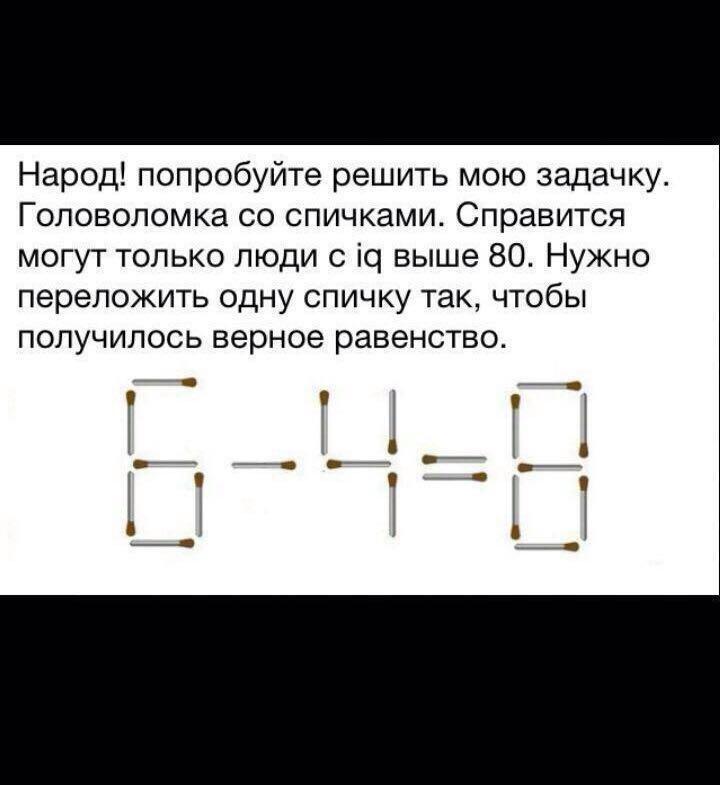
| ||
Задачи на логику по математике
На одной далёкой планете есть только один аэропорт, находящийся на Севеном полюсе.Бака самолёта хватает ровно до Южного полюса.
Самолёты имеют возможность дозаправляться (перекачивать горючее из одного в другой), находясь в полёте.
Как самолёт может облететь вокруг планеты так, чтобы все самолёты вернулись в аэропорт?
Решение:
Мысленно разделите весь путь от полюса до полюса на три части (от Северного полюса до Южного полюса 3 части. И от Южного полюса до Северного полюса 3 части). Стратегия состоит в следующем.
1. Два смолета летят до первой трети пути, один из них дозаправляет второй и поворачивает назад, а второй продолжает лететь до отметки 2/3 пути.
2. Два самолета вновь вылетают из аэропорта до первой третьей пути. Один из них дозаправляет второй и поворачивает назад, а второй продолжает путь до отметки 2/3 пути.
3. На отметке 2/3 пути теперь два самолета, бензобаки каждого заполнены на 2/3. Один из них дозаправляет второй и отправляется назад до отметки в 1/3 пути, где его встречает и дозаправляет 1/3 своего топлива третий самолет из аэропорта, оба летят обратно в аэропорт. В это время самолет, бывший на отметке 2/3 пути, с полным баком летит дальше, насколько это возможно (он пролетит над Южным полюсом, обогнет планету и долетит до отметки последней 1/3 пути до аэропорта).
4. Остальные действия очевидны. Из аэропорта вылетает еще один самолет (на этот раз в противоположном направлении, то есть навстречу обогнувшему планету самолету), чтобы поделиться 1/3 своего топлива с основным самолетом и вместе с ним вернуться в аэропорт.
———————
Волшебный пояс, исполняющий желания хозяина, уменьшается в два раза в длину и в 3 раза в ширину после каждого исполненного желания.
После исполнения трёх желаний площадь лицевой стороны стала 4 см2.
Какова была изначальная длина ремня, если его изначальная ширина была 9 см?
Ответ:
Изначальная длина пояса – 96см.
———————
У всех жителей города Болдвил разное количество волос на голове.
Нет ни одного жителя, у которого было бы точно 518 волос на голове.
Население города превышает число волос на голове любого из жителей Болдвил.
Каково максимально возможное население города Болдвил?
Решение:
Максимальное количество жителей города составляет 518 человек.
Причем один из жителей обязательно должен быть лысым, иначе в городе не будет ни одного человека.
———————
Кирпич весит 1 килограмм плюс половину собственного веса.
Сколько весит кирпич?
Решение:
Вам поможет обычное уравнение: 1 кирпич = 1кг + ½ кирпича, то есть x = 1 + x/2, откуда x — x/2 = 1,
откуда 2x — x = 2, откуда x = 2, то есть кирпич весит 2кг.
———————
Два поезда, находящиеся на расстоянии 200 км, движутся навстречу друг другу со скоростью 50 км/ч каждый. Муха берёт старт с одного из поездов и летит по направлению к другому со скоростью 75 км/ч. Долетев до другого поезда, муха разворачивается и летит назад к первому.
Муха берёт старт с одного из поездов и летит по направлению к другому со скоростью 75 км/ч. Долетев до другого поезда, муха разворачивается и летит назад к первому.
Так она летает туда и обратно, пока два поезда не сталкиваются, и насекомое погибает.
Какое расстояние успела пролететь муха?
Решение:
Расстояние, которое сможет пролететь муха за 2 часа (именно через два часа поезда столкнутся) с постоянной скоростью 75км/ч.
Она пролетит 150км.
———————
Из Бостона в Нью-Йорк выходит товарный поезд, двигаясь со скоростью 60 км/ч.
Через 30 минут навстречу ему из Нью-Йорка в Бостон выходит пассажирский поезд, двигающийся со скоростью 80 км/ч.
Который из поездов будет ближе к Нью-Йорку в момент встречи?
Решение:
Когда поезда встретятся, они оба будут приблизительно на одном и том же расстоянии от Нью-Йорка.
Поезд, выехавший из Нью-Йорка, будет ближе к Нью-Йорку примерно на расстояние, равное длине одного поезда, потому что поезда движутся во встречном направлении. Ну это если под словом «встретятся» Вы подразумеваете именно «встретятся», а не «пересекутся в тот самый момент, когда один из поездов поравняется всеми своими вагонами с вагонами второго поезда».
Ну это если под словом «встретятся» Вы подразумеваете именно «встретятся», а не «пересекутся в тот самый момент, когда один из поездов поравняется всеми своими вагонами с вагонами второго поезда».
———————
Половину пути до города, находящегося на расстоянии 60 км, я проехал со средней скоростью 30 км/ч.
С какой скоростью я должен ехать остаток пути,
чтобы общая средняя скорость всего путешествия была бы 60 км/ч?
Решение:
В данном случае невозможно найти желаемую среднюю скорость. Простая арифметика покажет, что даже при скорости 90км/ч, или любой другой скорости, результат не будет удовлетворять условиям задачи.
———————
Мало что известно о жизни одного греческого математика из Александрии, которого называют родоначальником алгебры. Предполагается, что он жил в 3-м веке нашей эры. По рассказам, на его надгробии была высечена следующая эпитафия:
«Детство Диофанта 1/6 жизни заняло; 1/12 жизни Диофант бороду растил; ещё 1/7 жизни Диофанта прошла до того, как он женился.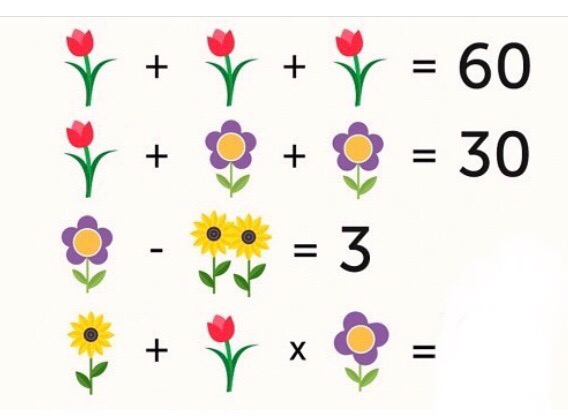 Через 5 лет после свадьбы у Диофанта родился сын, который прожил только половину лет, что прожил его отец. А через 4 года после смерти сына умер Диофант.»
Через 5 лет после свадьбы у Диофанта родился сын, который прожил только половину лет, что прожил его отец. А через 4 года после смерти сына умер Диофант.»
Сколько лет прожил Диофант?
Решение:
Следующее уравнение отображает все периоды жизни Диофанта:
1/6x + 1/12x + 1/7x + 5 + 1/2x + 4 = x ;
Диофант прожил 84 года (x = 84).
———————
Сто мер зерна надо поделить между пятью работниками так, чтобы второй получил настолько больше, чем первый, насколько третий больше, чем второй, и на столько же, насколько четвёртый больше, чем третий, и на столько же, насколько пятый больше, чем четвёртый. Сколько мер зерна должен получить каждый, если первый и второй работники вместе получат зерна в семь раз меньше, чем остальные три работника?
Решение:
Для решения задачи составим два равенства. 5w + 10d = 100; 7*(2w + d) = 3w + 9d, где w – количество зерна для первого работника, d – разница в количестве зерна между двумя (следующими по порядку) работниками. Ответ: первому работнику 10/6 мер зерна, второму работнику 65/6 мер зерна, третьему работнику 120/6 (20) мер зерна, четвертому работнику 175/6 мер зерна, пятому работнику 230/6 мер зерна.
Ответ: первому работнику 10/6 мер зерна, второму работнику 65/6 мер зерна, третьему работнику 120/6 (20) мер зерна, четвертому работнику 175/6 мер зерна, пятому работнику 230/6 мер зерна.
———————
Через два часа до полуночи останется в два раза меньше, чем оставалось бы через час.
Который сейчас час?
Ответ:
21:00
———————
В полдень часовая, минутная и секундная стрелки часов совпадают в одной точке циферблата.
Чуть больше, чем через час и пять минут, часовая и минутная стрелки совпадут снова.
Найдите с точностью до миллисекунды время, когда они совпадут.
Какой угол с ними будет в это время составлять секундная стрелка?
Решение:
Данная ситуация (когда часовая и минутная стрелки совпадают) повторяется 11 раз каждые 12 часов. Нетрудно догадаться, что отметка 1/11 окружности циферблата находится на моменте времени 1:05:27,273, то есть секундная стрелка будет стоять на отметке 27,273 сек.
Угол между часовой и секундной стрелкой в таком случае составит 131 градус.
———————
К бассейну подходят четыре трубы, по которым через краны можно контролировать скорость заполнения бассейна. Открыв первый кран, можно заполнить бассейн за 2 дня, второй – за 3 дня, третий – за 4 дня и четвёртый – за 6 часов.
Сколько понадобится времени, чтобы наполнить бассейн, открыв все четыре крана одновременно?
Решение:
Поскольку в сутках 24 часа, первый кран за час наполнит 1/48 бассейна, второй кран – 1/72, третий кран — 1/96, а четвертый наполнит бассейн на 1/6. Отсюда получаем: (6 + 4 + 3 + 48) / 288 = 61/288. Бассейн наполнится через 288/61 часов, то есть через 4 ч, 43 мин и примерно 17 сек.
———————
Военный автомобиль с важным посланием должен пересечь пустыню.
Однако полного бензобака хватает только на половину пути.
В распоряжении военной базы имеется несколько таких автомобилей, и бензин можно перекачивать из одного бака в другой.
Никакими канистрами и тросами они воспользоваться не могут.
Как доставить сообщение, не бросая ни одного автомобиля в пустыне?
Решение:
Всего понадобится 4 машины, включая ту, в которой находится ценное послание (та, что доедет до середины пустыни).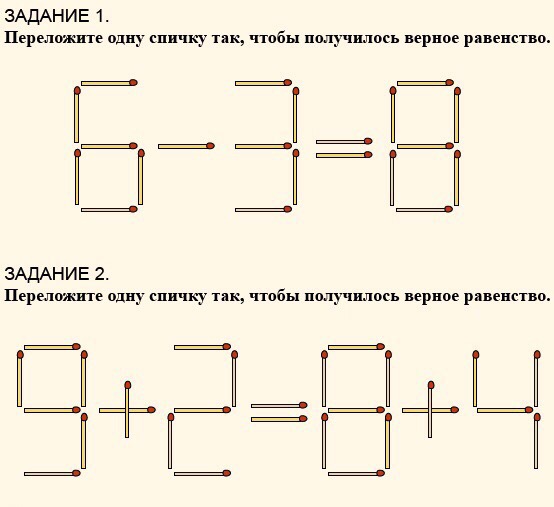 Чтобы она пересекла пустыню и достигла место назначения, надо будет на середине пути заново заполнить бензобак под горлышко. Путь от военной базы (где машины и бензин) до середины пустыни можно условно поделить на три части. Каждая из трех вспомогательных машин короткими «перебежками» между условными отметками и базой сможет при каждой поездке сливать треть бензобака в другую вспомогательную машину, находящуюся ближе к главной машине.
Чтобы она пересекла пустыню и достигла место назначения, надо будет на середине пути заново заполнить бензобак под горлышко. Путь от военной базы (где машины и бензин) до середины пустыни можно условно поделить на три части. Каждая из трех вспомогательных машин короткими «перебежками» между условными отметками и базой сможет при каждой поездке сливать треть бензобака в другую вспомогательную машину, находящуюся ближе к главной машине.
За несколько поездок туда-сюда методом эстафеты вспомогательные машины в конечном счёте смогут полностью заправить главную машину, чтобы та смогла продолжить свой путь через вторую половину пустыни.
———————
Антрополог, изучавший племя в отдалённом уголке джунглей Амазонки, обнаружил странный обычай. Когда муж узнавал, что его жена изменяет, он должен был публично её казнить в полночь того же дня. Про любую женщину, изменяющую мужу, всегда знали все жители племени, кроме её мужа. Но мужу никто никогда не рассказывал об изменах его жены, потому что это противоречило кодексу чести. Тот же кодекс чести не позволял жёнам известить ту жену, чей муж был ей неверен. В противном случае она в тот же вечер пристрелила бы своего мужа. В день своего отъезда антрополог созвал всех представителей племени и объявил: «Я знаю, что в этом племени есть неверные жёны.»
И на девятый день все неверные мужья были казнены.
Сколько было неверных мужей?
Решение:
Если принять количество неверных мужей за число «n», то количество неверных мужей, известных каждой жене неверного мужа, составляет «n — 1» (потому что всем обо всём точно известно – только о верности собственного мужа приходится догадываться). Теперь построим следующую логическую цепочку.
Предположим, что количество неверных мужей равно единице. Тогда всем, кроме одной, жёнам известно, что среди жителей есть один неверный муж, в то время как жена этого неверного мужа уверена, что все мужья верны своим жёнам. Как только она услышит, что среди жителей есть как минимум один неверный муж, она тут же поймёт, что может быть только её муж, поэтому в тот же вечер она его незадумываясь застрелит.
А теперь представьте, что среди жителей есть два неверных мужа. Каждая жена таких неверных мужей уверена, что среди жителей есть только один неверный муж, поэтому ждёт, пока какая-нибудь из жён пристрелит своего мужа. Но в этот вечер никто никого не застрелил, а это может означать только одно: её собственный муж ей тоже неверен и является вторым неверным мужем в племени. Первая жена первого неверного мужа приходит к точно таким же выводам (она также ждала, что кто-то из жён застрелит своего мужа). Таким образом, обе оскорбленные жены в первый же вечер понимают, что их мужья им изменяют,
и на следующий вечер (второго дня) пристреливают обоих мужей.
Следуя этой логике, нетрудно догадаться, что количество неверных мужей «n» будут пристрелены в «n» — нный вечер.
Логические загадки и задачи на английском языке
Предлагаем вам интересные логические загадки на задачки логику на английском языке. Английские задачи на логику не только полезны для развития логического мышления, но и помогут обогатить словарный запас.
Логические загадки на английском
Предлагаем вам несколько блоков логических загадок, рассчитанных на разный уровень владения английским языком.
БЛОК 1. НОВИЧКАМ.
Для того, чтобы решить следующие логические загадки на английском, вам понадобится лишь смекалка, особых знаний английского они не требуют, загадки построены на базовой лексике.
- What is the largest ant in the world?
- David’s father has 3 sons: Adam, Bob and …. who?
- What appears once in every minute, twice in every moment, but not once in thousand years?
- What part of London is in Brazil?
- What is the beginning of everything, also the end of life?
БЛОК 2. СРЕДНИЙ УРОВЕНЬ.
Логические загадки второго блока потребуют от вас более глубокого знания лексики.
- What starts with E, ends with E and only has one letter?
- What start with a «t» ,end with a «t» and is full of «t»?
- What runs but never walks?
БЛОК 3. СЛОЖНЫЙ УРОВЕНЬ.
Сложный или нет, решать вам, но для того, чтобы успешно справится с логическими загадками данного уровня вам потребуется неплохое знание устойчивых выражений в английском, так как загадки в той или иной степени построены на игре слов.
- Which is faster, hot or cold?
- What kind of dog never bites?
- Why did I throw the butter out of the window?
- What is that you ought to keep after you give it to somebody else?
- When you say this word, it disappears. What is it?
Логические задачи на английском
Задача 1. Who’s who?
In Red Street, there live five people with five different jobs. Their names are Nick, Simon, Gregory, Mike and Nelly.
Their jobs are a vet, entrepreneur, doctor, writer and lawyer.
Their annual incomes are 3 million, 4 million, 5 million, 10 million, 20 million.
Their ages are 25, 35, 40, 50, 60.
They all have between 0-3 kids.
Read the facts about the people and complete the chart below:
Name | Age | Kids | Job | Income |
Nick |
|
| lawyer |
|
Simon | 60 |
|
|
|
Gregory | 40 | 3 | vet |
|
Mike |
|
|
|
|
Nelly |
|
|
| 3 million |
- Nick earns half as much money as Simon.
- The entrepreneur earns the most.
- Mike has as many children as Nick.
- The oldest earns the second highest salary.
- Nick is twice as old as Nelly.
- The doctor has no kids.
- Mike is younger than Gregory.
- Nick has twice as many kids as Simon.
- The person who has one kid is a writer.
Логическая задача 2. Birthday Party!
Tim is 5 today. He has invited five friends to his birthday party. Can you tell who each child is?
- Kate is sitting next to Tim.
- Margareth is between two boys.
- Marik is opposite Lora.
- Dan is sitting beside Marik.
Логическая задачка 3. Friends.
Fill in the chart according to the info below.
- Alex, whose birthday is in August is in the middle and he’s 8 years old
- Kate is 6 years old and she is the first, her birthday is 2 months before Alex’s
- On the right is Sam and she is 10 years old. Her birthday is 2 months after Alex’s
- Sophie’s birthday is in July and she is 7 years old,
- Jack is between Sam and Alex he is 9 years old, and his birthday is 3 months after Kate’s
Name |
|
|
|
|
|
Birthday |
|
|
|
|
|
Age |
|
|
|
|
|
ОТВЕТЫ:
Блок 1.
- Elephant
- David
- Letter M
- Letter L
- Letter E
Блок 2
- envelope
- teapot
- Nose, river, etc.
Блок 3.
- Hot, you can easily catch cold
- A hot dog
- Because I wanted to see the butterfly.
- A promise
- Silence
Who’s who?
Name | Age | Kids | Job | Income |
Nick | 50 | 2 | lawyer | 5 |
Simon | 60 | 1 | write | 10 |
Gregory | 40 | 3 | vet | 4 |
Mike | 35 | 2 | entrepreneur | 20 |
Nelly | 25 | 0 | doctor | 3 |
Birthday Party!
- Lora 2. Kate 3. Tim 4. Margaret 5. Dan 6. Marik
Friends
Name | Kate | Sophie | Alex | Jack | Sam |
Birthday | June | July | August | September | October |
Age | 6 years old | 7 years old | 8 years old | 9 years old | 10 years old |
Понравилось? Сохраните на будущее и поделитесь с друзьями!
Загадки обманки для детей с ответами
Загадки обманки — умопомрачительно весёлые загадки с неожиданными ответами для детей и их родителей.
В чем суть загадок обманок?
Суть загадок обманок для детей в том, что ответ, который хочется дать в рифму стишка, не является правильным.
Как правильно разгадывать загадки обманки?
Загадки обманки с ответами заканчиваются словом в рифму, но ответ должен быть совершенно не таким. Прочитайте полностью стишок и, вы увидите, что «на автомате» как дети, так и взрослые дают неверный ответ. Нужно совсем немножечко подумать, чтобы догадаться, какое слово является разгадкой на самом деле.
ВНИМАНИЕ: Правильный ответ указан в скобках при нажатии на слово «ответ».
Белым снегом всё одето — |
лето (зима) ОТВЕТ |
Ночью каждое оконце |
солнце (луна) ОТВЕТ |
Друг зверей и друг детей |
Бармалей (Айболит) ОТВЕТ |
Кукарекает спросонок |
поросёнок (петух) ОТВЕТ |
Высокий, длинноногий, |
олень (аист) ОТВЕТ |
Лишь только свет дневной потух, |
петух (филин) ОТВЕТ |
Чик-чирик! Чик-чирик! — |
попугай (воробей) ОТВЕТ |
Под деревом четыре льва, |
два (три) ОТВЕТ |
Нашёл пять ягодок в траве |
две (четыре) ОТВЕТ |
Мышь считает дырки в сыре: |
четыре (пять) ОТВЕТ |
Кто взлетит с цветка вот-вот? |
бегемот (мотылёк) ОТВЕТ |
С пальмы вниз, на пальму снова |
корова (обезьяна) ОТВЕТ |
Простой вопрос для малышей: |
мышей (собак) ОТВЕТ |
Хвост веером, на голове корона. |
ворона (павлин) ОТВЕТ |
Мимо улья проходил |
крокодил (медведь) ОТВЕТ |
В чаще, голову задрав, |
жираф (волк) ОТВЕТ |
Дочерей и сыновей |
соловей (кабан) ОТВЕТ |
Кто грызёт на ветке шишку? |
мишка (белка) ОТВЕТ |
Ква-ква-ква — какая песня! |
соловей (лягушка) ОТВЕТ |
Скорей на берег выбегай! |
попугай (крокодил) ОТВЕТ |
Как? Неизвестно до сих пор: |
попугай (хамелеон) ОТВЕТ |
Cъела зайчонка и ловит второго |
корова (лиса) ОТВЕТ |
Он пиявок добывал, |
Буратино (Дуремар) ОТВЕТ |
Он гулял по лесу смело, |
Чебурашка (Колобок) ОТВЕТ |
Много дней он был в пути, |
Колобок (Иван-Царевич) ОТВЕТ |
И красива, и мила, |
Снегурочка (Дюймовочка) ОТВЕТ |
Я красивый, я летаю, |
воробей (снег) ОТВЕТ |
Он большой шалун и комик, |
Незнайка (Карлсон) ОТВЕТ |
Утром рано я встаю, |
овечка (корова) ОТВЕТ |
Жил в бутылке сотни лет, |
Дед Мороз (Старик Хоттабыч) ОТВЕТ |
Все меня боятся — |
тигр (комар) ОТВЕТ |
Я лаю и кусаю, |
коза (собака) ОТВЕТ |
С голубыми волосами |
Алиса (Мальвина) ОТВЕТ |
И капризна, и упряма, |
мама (дочка) ОТВЕТ |
На прививки и уколы |
школы (поликлиники) ОТВЕТ |
Загадки, викторины, головоломки: 10 загадочных диафильмов
Одна из прекрасных форм совместного досуга детей и взрослых, гарантирующая нескучный вечер в кругу семьи, – диафильмы. А диафильмы с загадками, викторинами и головоломками помогут провести время не только весело, но и с пользой!
Начнем с математики. Обратите внимание, что викторины рассчитаны на разный возраст.
Диафильм «Математическая викторина»
Данное пособие может быть использовано для занятий по развитию элементарных математических представлений в работе с детьми старшей группы детского сада или в семье.
Прямо наш случай – используйте в семье, не забывайте хвалить и поощрять детей за правильные ответы на вопросы викторины.
Диафильм «Занимательная математика. 1 класс»
Как следует из названия, этот диафильм – для ребят, которые уже ходят в первый класс школы. В диафильме даются задания на развитие внимания, наблюдательности, пространственных представлений, задачи по арифметике, логике, геометрии.
Диафильм «Занимательные задачи по математике. 3 класс»
А еще можно и историю метро вспомнить. На картинке схема московского метро 1977 года.
Диафильм можно использовать на октябрьских и пионерских сборах и при проведении конкурсов.
Вот и будем использовать для проведения семейных мини-конкурсов! Хотя при современном уровне развития конференц-связи можно и настоящий конкурс организовать.
Диафильм «Рассказы о математике. Алгебра»
Этот диафильм – для ребят постарше, учеников седьмого класса. Посвящен алгебре.
С тех пор Оля, как только хотела пожаловаться на математику, приходила к Соседу, который знал всё.
Мы к соседу не пойдем, пообщаемся с ним через экран, это не менее интересно.
Теперь переходим к географии. Будьте внимательны: часто ответы на географические вопросы надо давать с учетом исторических перемен – все диафильмы были сделаны в СССР, а сейчас многие правильные ответы уже вовсе не в «нашей стране». Но от этого еще интереснее!
Диафильм «Путешествие по родной стране»
Это диафильм-игра, и вам понадобятся бумага и карандаш, так как в первой половине диафильма идут вопросы, а во второй – ответы. Именно в этом диафильме важно помнить, что теперь родная страна не включает союзные республики.
Диафильм «Угадай-ка!»
Диафильм построен по принципу вопрос-ответ: один кадр – вопрос, следующий – ответ, так что листайте аккуратно.
Диафильмы «Географические загадки»
Это универсальный диафильм, построенный по принципу вопрос-ответ. Загадки будут интересены детям и взрослым.
Не обошли занимательным подходом и русский язык:
Диафильм «Буратино — деревянный человечек»
Этот диафильм сделали для уроков русского языка и развития речи в первом классе. Конкретно – для изучения темы «Слова, отвечающие на вопросы Какой? Какая? Какое?». Проверьте себя и детей, заодно вспомните сюжет сказки про Буратино.
Напоследок немного экзотики:
Диафильм «Астрономические загадки»
Хорошо ли вы знаете астрономию? Ведь в каждой квартире есть предметы, связанные с астрономией. Знаете, что это за предметы?
Диафильм «Викторина по гражданской обороне для учащихся общеобразовательных школ»
Этот диафильм-викторина – шанс блеснуть для пап, которые в школе изучали все, о чем идет речь в диафильме: поражающие факторы ядерного взрыва, типы противогазов и т.п. Неожиданный бонус – выкройка ватно-марлевой повязки.
Все диафильмы находятся в свободном доступе в Национальной электронной детской библиотеке.
Текст: канал НЭДБ на Яндекс.Дзен.
Загадки, викторины, головоломки – интеллектуальный спорт для всей семьи! Будьте здоровы!
Математические загадки на логику для детей читать онлайн
Какие три числа при сложении и умножении дают
один результат?
( 1 + 2 + 3 = 6, 1 * 2 * 3 = 6)
* * *
Больше часа, меньше минуты.
(секунда)
* * *
В парке 8 скамеек. Три покрасили.
Сколько скамеек стало в парке?
(восемь)
* * *
Какой знак нужно поставить между 6 и 7, чтобы результат оказался меньше 7 и больше 6?
(запятую)
* * *
В комнате 4 угла. В каждом углу сидела кошка, напротив каждой кошки — 3 кошки.
Сколько кошек находилось в комнате?
(4 кошки)
* * *
Как 2 литра молока поместить в литровую банку?
(получить
творог)
* * *
Шли муж с женой, брат с сестрой да муж с
шурином.
Сколько всего человек?
(три
человека)
* * *
На столе лежало 4 яблока. Одно из них разрезали пополам и положили на стол.
Сколько яблок осталось на столе?
(4 яблока)
* * *
На столе лежит 100 листов бумаги.
За каждые 10 секунд можно посчитать 10 листов.
Сколько секунд понадобится, чтобы посчитать 80 листов?
(20)
* * *
На столе лежат линейка, карандаш, циркуль,
резинка.
На листе бумаги нужно начертить окружность.
С чего начать?
(с листа
бумаги)
* * *
В каком числе цифр столько, сколько букв в его названии?
(100 — сто, 1000000 — миллион)
* * *
Горело 7 свечей. 2 свечи погасили.
Сколько свечей осталось?
(7 свечей)
* * *
Сколько различных цифр надо использовать, чтобы написать число 100?
(две — 0
и 1)
* * *
В каком случае число 1322 меньше 622?
(года до нашей эры)
* * *
В каком слове 3 буквы л и три буквы п?
(параллелепипед)
* * *
Пара лошадей пробежала 40 км.
По сколько километров пробежала каждая лошадь?
(40 км)
* * *
Сколько земли содержит яма диаметром 3 метра и глубиной 3 метра?
(нисколько, ямы пустые)
* * *
Какими нотами можно измерить расстояние?
(ми-ля-ми)
* * *
В комнате было 12 цыплят, 3 кролика, 5 щенят, 2 кошки, 1
петух и 2 курицы.
В комнату вошёл хозяин с собакой.
Сколько в комнате стало
ног?
(две, у животных нет ног)
* * *
Было два отца и два сына. И всего три яблока. Каждый съел по
яблоку.
Как такое возможно?
(сын, отец, дедушка)
* * *
У меня нет веса, но я бываю лёгкой, бываю тяжёлой.
Кто я?
(музыка)
* * *
В люстре горело пять лампочек. Две из них погасли.
Сколько лампочек осталось в люстре?
(осталось 5)
* * *
Суммарный возраст отца и сына — 66 лет.
Возраст отца — это
возраст сына, записанный справа налево.
Сколько лет каждому?
(51 и 15, 42 и 24, 60 и 06)
* * *
Электровоз идёт на запад со скоростью 90 км/ч.
Дует восточный
ветер, скорость ветра 10 км/ч.
В каком направлении идёт дым?
(у электровоза нет дыма)
* * *
Пять пломбиров пять ребят
Ровно в пять минут съедят.
А за сколько смогут съесть
Шесть ребят пломбиры, если
И пломбиров тоже шесть?
(сколько б ни было пломбиров,
если столько же ребят,
то ребята все пломбиры
в те же пять минут съедят)
* * *
Сколько раз можно вычесть 6 из 30?
(только один, потом 6 будет вычитаться из 24)
* * *
Две матери, две дочери и бабушка с внучкой.
Сколько всех?
(трое: бабушка, мать, внучка)
* * *
Как число 666 увеличить в полтора раза, не производя над ним никаких арифметических действий?
(написать 666 и повернуть её вверх ногами)
* * *
Когда мы смотрим на цифру 2, а говорим 10?
(когда смотрим на часы)
* * *
Сколько будет 2+2 х 2=?
(6)
* * *
Что тяжелее: килограмм железа или килограмм пуха?
(вес одинаков)
* * *
Одно яйцо варится 3 минуты.
Сколько минут будут вариться 2
яйца?
(3 минуты)
* * *
Сколько полосок у зебры?
(две: черная, белая)
* * *
Сколько яиц можно съесть натощак?
(одно, остальные не натощак)
* * *
Грузовик ехал в деревню.
По дороге он встретил 4 легковые машины.
Сколько машин ехало в деревню?
(одна)
* * *
Простая логическая загадка, демонстрирующая нелогичность людей / Хабр
Питер Васон
В 60-х годах психолог Питер Васон придумал эксперимент-загадку, «Задача выбора Васона». Говорят, что это наиболее часто исследуемая задача в психологии принятия решений.
Васон отличался чувством юмора и необычным мышлением. Он исповедовал отношение к психологии принятия решений как к загадке, которую надо изучать как критически, так и с долей развлечения. Он говорил своим коллегам, что будет изучать их работы только после того, как проведёт свои эксперименты, чтобы не искажать свою точку зрения. Также он сказал, что экспериментаторы никогда не должны точно знать, зачем они проводят эксперимент. «Целью его экспериментов было не проверить гипотезу, а изучить сущность мышления»,- так написали его ученики в его некрологе в 2003 году. «Он всегда хотел продемонстрировать некий феномен, чтобы показать, что мышление не такое, каким его представляют психологи, включая его самого».
Одна из версий задачи звучит так – испытуемому (который был всегда один, ибо Васон избегал групповых тестов) предлагались четыре карты – с одной стороны у каждой было число, с другой – один из двух цветов. Допустим, вы – испытуемый. У первой и второй карт вы видите лицевую сторону с числами 5 и 8, у третьей и четвёртой – обратную сторону, у одной – голубую, у другой — зелёную.
Экспериментатор сообщает вам следующее утверждение: если у карты на лицевой стороне изображено чётное число, то её обратная сторона – голубая. Вопрос: какие карты необходимо перевернуть для проверки этого утверждения?
Прим. перев. Мне показалось, что среди программистов и IT-специалистов распределение правильных ответов должно быть несколько другим, нежели 10% на 90%. Поэтому я потрудился сделать опрос. Если вам не трудно, перед просмотром правильного ответа выберите вариант, который вам нравится, в опросе внизу страницы.
Видео – интерактивное, там можно выбрать один вариант и нажать на него, чтобы проверить себя.
Если вы ошиблись – не отчаивайтесь. Задача проста лишь на первый взгляд. По статистике, справляются с ней лишь 10% людей.
Правильный ответ: — «5» переворачивать не нужно, т.к. в утверждении ничего не сказано про карты с нечётными числами. Утверждение «у карт с чётными числами обратная сторона – голубая», не означает автоматически, например, что у карт с нечётными числами должна быть зелёная обратная сторона— «8» перевернуть надо, чтобы проверить, действительно ли у неё обратная сторона – голубая
— голубую карту не надо переворачивать – какое бы число там не было изображено, это не нарушит утверждения
— зелёную карту нужно перевернуть – если там окажется чётное число, то утверждение будет опровергнуто
Итого, необходимо перевернуть карты «8» и зелёную.
Васон опубликовал в 1968 году работу, в которой назвал результаты экспериментов «тревожными», поскольку изначально предполагалось, что люди размышляют аналитически – но, как оказалось, на деле их рассуждения иррациональны. Васон задумался: была ли виной тому логическая структура правил игры, или людей сбивали с толку слова, формулирующие задачу?
В 1982 пара психологов, Ричард Григс и Джеймс Кокс попытались доказать, что сложность задачи проистекает из её формулировки. Они переформулировали задачу так: представьте, что вы полицейский, ищущий несовершеннолетних посетителей баров. Если человек пьёт пиво, его возраст должен быть больше 21 года. В этом случае правильно ответили на вопрос 75% испытуемых. Этот эффект назвали «эффект контекста» — влияние факторов окружающей среды на восприятие человеком стимула. То есть, сложность задачи зависит от её описания, хотя смысл её остаётся тем же. Но почему же слова оказывают такое влияние, если логическая структура не меняется?
В книжке от 2011 года «Мышление, быстрое и медленное», психолог Дэниел Кахнеман представил теорию «двойной обработки». Она утверждает, что разные слова заставляют вас использовать одну из двух систем распознавания. «Старая система», заложенная в человеке, интуитивная, или «система 1», работает быстрее, а «новая», «система 2» – медленнее. Столкнувшись с задачей, две системы начинают борьбу за выдачу правильного ответа. Если вы ошиблись с ответом – вините старую, интуитивную «систему 1», которая любит «срезать углы», работая со «склонностью к шаблонам». Люди склонны, отвечая на вопрос, выбирать те варианты, которые были упомянуты в самом вопросе. Поэтому чаще всего они выбирают карту «8» (правильный выбор) и голубую (неправильный), потому, что в вопросе есть слова «чётный» и «голубой». Но переворачивать голубую карту нет смысла, поскольку, что бы там ни было на другой стороне, это не будет противоречить утверждению.
Но отчего же люди склонны к нерациональным поступкам? Потому, что «это быстрее и кажется правильным», как написал один из психологов. Напротив, абстрактные рассуждения, которым занимается новая система – штука утомительная. Часто новая система, не осознавая этого, пропускает старую вперёд. Поэтому Кахнеман писал, что «одна из главных её характеристик – лень». Но в случае с пивом и совершеннолетием старая система справляется лучше, потому, что ей известны правила насчёт спиртных напитков и возраста, и она использует их, чтобы решить задачу.
Объяснение психологии методом «двойной обработки» получает подтверждение в других исследованиях. Например, если вы ответили правильно, скорее всего на вступительных экзаменах в институт вы наберёте больше баллов чем те, кто её не решил. Также была показана деградация «новой» системы по сравнению со «старой» с возрастом. Это объяснение делит наш разум на две части – новую систему принятия решений и старую, которая работает на автопилоте без особого контроля.
Если вас это не убедило – вы не одиноки. Эволюционные психологи сомневаются, что случайная эволюция так чётко разделила бы мышление на два разных процесса. С их точки зрения, людям легче решить задачку в форме, связанной с баром потому, что люди, как они говорят, эволюционировали в «социо-когнитивной нише». Им необходимо было адаптироваться, чтобы создавать и следовать правилам, чтобы функционировать, как «уникальный и конкурентный хищный организм».
Поэтому, с точки зрения эволюционного психолога, вариант с баром говорит о том, что человеку легко сказать, кто именно нарушает правила, принятые в социуме. В 1989 году Леда Космидес назвала эту возможность «модуль обнаружения жулика». С тех пор её коллеги использовали задачу выбора Васона для проверки социального фактора людей. В одном из исследований они установили, что родителям свойственно сильнее заботится о собственных детях. Родители хуже справлялись с заданиями, связанными с обработкой правил безопасности, если речь шла о чужих детях.
Сам Васон решил отстраниться от научных дебатов касательно его работы, и с удовольствием наблюдал рождение новых идей, связанных с ней. Он заинтересовался шахматами, написал книгу под названием (сюрприз) «Психология шахмат» и добился в ней звания гроссмейстера международного уровня. Как он позже писал про самого себя: «Возможно, меня всегда привлекала тема рассуждений и логики, потому, что большинство вещей в жизни – нелогичны».
30 лучших математических головоломок, которые должен попробовать каждый
Интервью Math Riddles Puzzles Комментариев нет Математические головоломки или математические головоломки основаны на логике и немного математике. Это очень важно для развития логического ума. Человек, имеющий привычку решать математические головоломки, развивает логическое мышление и считается человеком с очень высоким IQ. Эти головоломки не зависят от возрастной группы, поскольку для этого требуется лишь немного математики, но высокая логика.
Математические головоломки в наши дни становятся интересом работодателей во время собеседований, что позволяет работодателям проверять IQ кандидата. Здесь мы перечислили 30 самых известных математических головоломок, которые должен решить каждый в любой возрастной группе. Когда вы разберетесь со всеми 30 головоломками, вы будете хорошо подготовлены к любым головоломкам на собеседовании.
Решайте 2 головоломки из этого списка ежедневно, и все готово! 🙂
Список из 30 математических головоломок с ответами, основанных на математике и нестандартной логике (не пропустите ни одного, попробуйте все) —
- Неисправный шар из 8 шаров Пазл
- Проблема с горящей веревкой
- Пазл Famous Handshake
- Пазл с 10 монетами с завязанными глазами
- Знаменитая головоломка с математическим уравнением
- Пазл Верблюд и банан
- Пазл лавочник и поддельная записка
- Соотношение мальчиков и девочек в стране, где люди хотят только мальчиков
- Пазл для измерения 5 литров
- Вероятностная головоломка Marbles
- Жадные пираты и раздача золотых монет Головоломка
- Пазл о королевских бутылках и бутылках вина
- Пазл переходя мост
- Пазл Случайные места для самолетов
- 2 яйца и 100 этаж Google Classic вопрос
- Отмерьте 9 минут из пазла 2 песочных часа
- Пазл «Убийство и выживание на мечах» (проблема Иосифа)
- Пазл неисправная коробка для шоколада
- Красный и синий шарики Пазл
- Проблема с золотым слитком
- Пазл на 100 дверей
- Пазл Луковицы в круге
- Пазл на путаницу сумм и произведений
- Наибольшее число с использованием четырех троек Головоломка
- Пазл, образующий 6-значное число
- Математическая головоломка умножения пальцев
- Задача о муравье и треугольнике
- Загадка инвестора с Уолл-стрит
- Головоломка банковского кассира
- Пазл куб Каландара
Готово? Ух ты!! теперь вы чемпион по математике
математических головоломок
математических головоломок Присылайте нам свои комментарии и новые головоломки по электронной почте:
[email protected].
Наслаждаться! Эти головоломки не требуют никаких математических знаний, только логические рассуждения.Проверь, насколько ты умный. Если вы не можете их решить, расслабьтесь.
Почти все головоломки нам рассказали
компьютерно-математический гений Влад Митлин. Приходите к нам снова: мы намерены размещать здесь новые головоломки и решения.
1. Монеты
- Есть 12 монет. Один из них ложный; у него другой вес. Неизвестно, тяжелее или легче фальшивая монета, чем правильные монеты.Как найти фальшивую монету по трем весам на простых весах?
2. Мостовой переход
Эта проблема была недавно опубликована в MAA на сайте: Переход через шаткий мост ночью при свете фонарика.
- Группа из четырех человек должна перейти мост. Темно, и они должны осветить путь фонариком. Одновременно мост могут пересечь не более двух человек, а у группы есть только один фонарик. Люди в группе переходят мост разное время:
- A nnie пересекает мост за 1 минуту,
B ob пересекает мост за 2 минуты,
Володя Митлин пересекает мост за 5 минут,
D Ороти пересекает мост за 10 минут.
Решение:
кликните сюдаЧтобы увидеть анимированное решение, вам нужен браузер, поддерживающий JAVA.
3. Доставка яблок
Еще проблемы от Влада Митлина
Вечеринка!
На вечеринке группа людей. Покажите, что вы можете представить некоторые из их друг к другу так, чтобы после знакомства не более двух человек в группе будет одинаковое количество друзей (первоначальная конфигурация не работает, потому что у всех изначально 0 друзей).
Цифры
Покажите, что для любого натурального n хотя бы одно из двух чисел, n или n + 1, может быть представлены в следующем виде: к + S (к) для некоторого k, где S (k) — сумма всех цифр в k. Например, 21 = 15 + (5 + 1)
Проблема дзен
Буддийский монах получил задание от своего учителя: медитировать ровно 45 минут. У него нет часов; вместо этого ему дают две ароматические палочки, и он говорят, что каждая из этих палочек полностью сгорит за 1 час.В палочки не идентичны, и горят с разными, пока неизвестными скоростями (они сделаны вручную). Итак, у него есть эти два аромата и несколько совпадений: он устраивает медитацию ровно на 45 минут?
Счастливые билеты
В России садишься в автобус, берешь билет и иногда говоришь: Вау, а счастливое число! Автобусные билеты нумеруются шестизначными числами, а счастливый в билете сумма трех первых цифр равна сумме трех последних цифр. цифры. Когда мы учились в старших классах (ребята из математической школы No.N — 1
Расстояния
В прямоугольнике 6 точек со сторонами 3 и 4. Докажите, что расстояние между как минимум двумя из этих точек меньше квадрата корень 5.
король
Шахматный король помещается на шахматную доску 8×8. 2 + ab + ac + ad + bc + bd + cd не меньше 10.
Три планеты в галактике и обвал рынка
Галактика состоит из трех планет, каждая из которых движется по прямой линия с собственной постоянной скоростью. Если центры всех трех планет случайно лежат на прямой (какое-то затмение) жители каждая планета сходит с ума (они не могут видеть свои две соседние планеты сразу один раз), начните говорить о конце света, а фондовый рынок вылетает. Покажите, что таких обвалов рынка будет не более двух. каждая из этих планет.4 есть решения в простых числах? Найдите хотя бы один, если да, в противном случае приведите доказательство несуществования.
Последовательность
Последовательность натуральных чисел определяется по следующей формуле: A [n + 1] = a [n] + f (n) Где f (n) — произведение цифр в [n]. Есть ли [1] такая, что указанная выше последовательность не ограничена?
Интеллектуальная сила стаи драконов
Драконы должны встретиться для мозгового штурма в конференц-центре.В делегаты должны быть отобраны, чтобы обеспечить максимальную эффективность мозговой штурм. У дракона любое количество голов, и для любого N при необходимости доступно любое количество N-головных драконов. Проблема в что размер конференц-центра ограничен, поэтому не более 1000 головы могут поместиться в актовый зал. Интеллектуальная сила стая драконов — это произведение количества голов драконов в стае. Как должна выглядеть оптимальная стая (общее количество драконов, распределение голов)?
Истребитель вампиров
На поверхности планеты живет вампир, который может перемещаться скорость не больше u.Космический корабль истребителей вампиров приближается к планеты со скоростью v. Как только космический корабль видит вампира, он стреляет серебряной пулей — вампир мертв. Докажите, что если v / u> 10, убийца вампиров может выполнить свое миссии, даже вампир пытается спрятаться.
Проекторы
(2D) проектор освещает квадрант на плоскости. 4 проектора установить в 4 произвольных точках плоскости. Покажи, что их можно повернуть так что весь самолет будет освещен.(3D) Покажите, что все пространство может быть освещен 8 прожекторами, каждый из которых освещает октант, однако точки расположения есть.
Кампания бдительности в Солт-Лейк-Сити.
Солт-Лейк-Сити выглядит как прямоугольник, пересеченный улицами M , идущими от С севера на юг и с улицами N и , идущими с востока на запад. Город часто посещают туристы, которые предполагают бегать в автобусах. Губернатор штата Юта хочет следить за всеми перемещениями автобусов.Он планирует выставить на некоторых перекрестках полицейских, чтобы они наблюдали за движением автобусов. улицы, видимые с этих перекрестков. Какое минимальное количество полицейских необходимо для наблюдения за автобусом?
Блондинки (загадка из Oldaque P. de Freitas)
Две блондинки сидят в уличном кафе и разговаривают о детях. Один говорит, что у нее три дочери. Произведение их возраста равно 36 а сумма возрастов совпадает с номером дома через улицу.Вторая блондинка отвечает, что этой информации недостаточно, чтобы выяснить возраст каждого ребенка. Первый соглашается и добавляет, что у старшей дочери красивые голубые глаза. Затем второй решает загадку. Вы тоже можете это решить!
Это от Гжегожа Дзержановского.
Есть 12 зубочисток. Найдите многоугольники экстремального поля, используя все зубочистки. При построении этих полигонов соблюдайте правила: — зубочистки не сломаешь, — длина каждого ребра 1,2,3,… зубочистки, — края многоугольника не могут пересекать друг друга.
Помогите ребенку развить математические навыки с помощью логических головоломок. — IMACS
Пусть математика будет увлекательной, и ваши дети будут продолжать заниматься математикой. Привет, логические головоломки!Логические головоломки для детей — отличный способ пробудить интерес вашего ребенка к математике, поскольку логика и математика идут рука об руку. Каждый раз, когда дети увлекаются сложными головоломками, они развивают навыки, которые в конечном итоге будут использовать, чтобы сдать экзамен SAT, привести команду к победе на Первом соревновании по робототехнике и даже разделить счет в ресторане со своими будущими соседями по комнате.
Регулярное решение головоломок приносит больше пользы. Исследования показывают, что игра в интеллектуальные игры развивает навыки аналитического мышления, давая учащимся возможность неожиданно использовать стратегии решения проблем. Например, в English 101, когда вашему ученику нужно связать тезис с заключением, он будет вызывать свой набор навыков логического мышления. В робототехнике, если созданный ими робот для изготовления бутербродов кладет хлеб на сыр (вместо сыра на хлеб), аналитическое мышление позволит им отладить его и есть стильно.
Будь то задача ребуса, проблема нестандартного мышления или умопомрачительная головоломка судоку, каждая загадка делает вашего ребенка (и вас) лучшим писателем, мыслителем, стратегом и математиком.
Что такое логика и почему она необходима для критического мышления?Слово логика происходит от древнегреческого слова logos, первоначально означающего «слово» или «то, что говорится». Однако со временем этот термин стал означать «мысль» или «разум».«Логическая головоломка — это в буквальном смысле мысленная головоломка! Этимология объясняет, почему существует так много разновидностей логических головоломок для детей — от математических головоломок, построенных исключительно на отношениях между числами, таких как «24», до сложных загадок с игрой слов. Проверьте это:
Что становится влажнее и влажнее, чем больше сохнет?
Кто может бегать, но никогда не ходит, имеет рот, но никогда не разговаривает, имеет голову, но никогда не плачет, имеет кровать, но никогда не спит?
Я невесом, но вы меня видите. Положите меня в ведро, и я сделаю его легче.Что я?
В тупике? Вы найдете ответы внизу статьи.
Вау! Существует так много типов логических головоломок .Решение проблем включает в себя широкий спектр когнитивных инструментов, таких как индуктивная логика, дедуктивные рассуждения, аналогии, игра слов, упорядочивание и даже иногда просто очень, очень внимательное слушание.
Вот классический пример головоломки, которая полностью полагается на то, что ученые называют метакогнитивным слушанием, что является просто причудливым способом сказать: «Обращайте пристальное внимание на то, что задает вопрос.”
Фермер в Калифорнии владеет красивой грушей. Он поставляет фрукты в ближайший продуктовый магазин. Владелец магазина позвонил фермеру, чтобы узнать, сколько фруктов он может купить. Фермер знает, что у главного ствола 24 ветви. В каждой ветке ровно 12 ветвей, а в каждой — ровно шесть веток. Поскольку каждая веточка приносит по одному фрукту, сколько слив фермер сможет доставить?
Подождите? Какие! Вы сделали связку умножения? Вот подсказка: в этом нет необходимости.Почему? Что ж, приятно знать так много о прекрасном грушевом дереве фермера, но он разносит сливы!
Как у покупателя в магазине мороженого есть варианты, так и у поклонника логической головоломки. Как и в случае с мороженым, проблемы бывают разных вкусов, и у людей обычно есть свои любимые. Давайте изучим несколько и посмотрим, что вам больше всего нравится.
Классические математические задачи рассуждений.Учебная программа IMACS направлена на развитие у учащихся навыков математического мышления, поэтому неудивительно, что IMACS создал сотни уникальных логических задач.Попробуйте это из библиотеки IMACS:
Был морозный зимний вечер, когда сестры Аврора, Элизабет, Минни и Ророна сидели у камина и пили горячее какао. Когда они играли и пили из своих чашек, одна из сестер случайно пролила какао на ковер. Их мать вскоре проверила своих дочерей и спросила, взяв чашку: «Кто пролил какао?» Правду сказала только одна из сестер.
Элизабет сказала: «Чаша принадлежит Ророне.
Ророна сказал: «Чаша принадлежит сестре, в имени которой есть буквы, составляющие слово« рев »».
Аврора сказала: «Чаша принадлежит сестре с двумя буквами« о »в ее имени. . »
Минни просто смотрела на какао на полу.
Кто виновен в пролитии какао?
Этот тип логической задачи может оказаться чрезвычайно сложной задачей, прежде чем вы разовьете свои навыки рассуждения.Но во многих отношениях это небольшое препятствие для мышления, которое в малом масштабе имитирует сложности, с которыми изобретатели, инженеры и технологи сталкиваются в реальной жизни: оно требует понимания взаимосвязанных отношений и способности применять дедуктивное мышление. Любая сложная головоломка улучшит умственную гибкость человека, но логическое рассуждение является наиболее важным для развития, поскольку оно лежит в основе многих других важных стратегий решения проблем.
К счастью, логическое рассуждение является усвоенным, а не врожденным.Программа IMACS специально разработана для развития навыков мышления, необходимых для решения более сложных задач. Фактически, IMACS даже предлагает каждое лето веселые и увлекательные уроки, посвященные логическим головоломкам для детей с первого по восьмой класс.
Ищете ответ на проблему пролитого какао? Вы можете найти его (и другие) в конце статьи. Пожалуйста, не расстраивайтесь, если эти проблемы сложны! Имейте в виду, что математические рассуждения имеют много общего с изучением языка:
- лучше и легче всего овладеть им в молодом возрасте;
- Вы должны потратить время, чтобы научиться бегло говорить;
- Как только вы начнете свободно говорить, навык станет настолько автоматическим, что кажется, будто вы всегда знали, как это делать!
Хотите попробовать другой? Большой! Попробуйте:
Лори, Мэтт и Нэнси заказали бутерброд, гарнир и напиток в ресторане быстрого питания.Когда их заказы были доставлены: Лори получила бутерброд с рыбой, картофель фри и воду. Мэтт получил бутерброд с курицей, луковые кольца и корневое пиво. Нэнси получила овощной бутерброд, картофельные чипсы и лимонад.
К сожалению, заказы не были доставлены должным образом.
Лори сказала: «Правильно только одно — и это определенно не вода».
Мэтт сказал: «И только один из моих пунктов верен!»
Нэнси сказала: «Только один из моих предметов неправильный.
Один из сотрудников сказал: «Я знаю, что бутерброд с курицей подходит к воде».
Другой сотрудник сказал: «Я знаю, что картофельные чипсы подходят к корневому пиву, но не к сэндвичу с рыбой».
Помогите менеджеру разобраться! Каждое утверждение верно. Кто что заказывал?
Проблема путаницы в фаст-фуде очень сложна! Бумага и карандаш могут оказаться большим подспорьем. Не сдавайся. Решение находится в конце статьи.
Головоломки.Еще одна категория логических задач — классическая «головоломка». Логические дразнилки часто бывают сложными, потому что они полагаются на навык, называемый «нестандартным мышлением». Проблемы нестандартного мышления заставляют вас пересмотреть свои предположения по поводу вопроса. Вот классическая головоломка с нестандартным мышлением:
Что уникального в этом числе?
8,549,176,320
Спойлер! Мы собираемся дать ответ.Взгляните на минутку и посмотрите, сможете ли вы сначала во всем разобраться. Если вы застряли, взгляните на подсказки, прежде чем искать решение!
Подсказка № 1: Вы, наверное, заметили, что представлены все цифры (от 0 до 9). Хороший! И вы знаете, что это проблема латерального мышления (потому что это то, о чем этот раздел!) В задачах латерального мышления решение заключается в мышлении, выходящем за рамки предположений, которые вы привносите в проблему.
Поскольку эта логическая задача представляет вам числа, вы, вероятно, думаете, что должны использовать свои математические навыки, чтобы найти решение.Другими словами, как только ваш мозг видит числа, он быстро предполагает: «Ага! Ищите числовые отношения между числами! »
Суть проблем нестандартного мышления заключается в том, что решение останется неуловимым, пока вы остаетесь привязанными к предпосылкам, которые приносите с собой. Итак, есть ли другой способ думать о математической головоломке, которую вы видите?
Подсказка № 2: Что, если бы вам пришлось записать это число словами?
Подсказка № 3: Какова связь между первой буквой каждого слова, которое вы написали в предыдущей подсказке?
Поняли? Потрясающие! Это все цифры, записанные в виде слов в алфавитном порядке.
Сможете ли вы отгадать загадку тридцати центов?
Некоторые люди расстраиваются, когда находят решение проблемы нестандартного мышления. Это расстраивает, когда наши умственные ярлыки, которые обычно полезны, становятся источником наших неудач. Тем не менее, когда люди особенно искусны в мышлении, выходящем за рамки ограничений этих рамок, они часто становятся изобретательными предпринимателями и предприимчивыми изобретателями. Они развивают способность мыслить нестандартно и создавать революционные инновации.
Теперь, когда вы знаете, что этот раздел посвящен нестандартному мышлению и проверке ваших предположений, посмотрите, сможете ли вы решить следующую задачу самостоятельно. Вы можете начать с вопроса: «Какие предположения я делаю, которые могут быть перевернуты словами этого вопроса?» Давайте попробуем!
В руке у меня ровно две американские монеты. Вместе они составляют тридцать центов. Один из них — не пятак. Кто они такие?
Кажется невозможным, правда? Преимущество проблемы нестандартного мышления заключается в осознании того, что многие предположения о «невозможном» являются всего лишь функцией наших собственных ограничивающих убеждений.Если вы можете переосмыслить проблему по-новому, то, что когда-то считалось «невозможным», внезапно становится тривиальным!
Сдаться? Хотите ответ? Мы действительно сказали, что было две монеты, и действительно, одна из них — это не монета. Тот — это не никель — четверть. А другой ? Да, это никель. 😊
Тайна двух братьев. Невозможно?
На этом, посмотрим, сможете ли вы сломать свои предположения, чтобы найти ответ.
У женщины было два сына.Они родились в один и тот же час, в один и тот же день одного месяца одного года. Однако близнецами они не были. Как это возможно?
Хотя некоторые люди отвергают головоломки с латеральным мышлением как «настоящие логические головоломки», они имеют огромное значение в обучении детей (и взрослых) разнице между мышлением и тем, что ученые называют «метакогнитивным мышлением».
В типичной логической головоломке наша работа — думать. Но с боковыми рассуждениями наша работа — думать о мышлении.Когда в вопросе говорится, что сыновья не близнецы, мы всецело думаем о близнецах.
Это то «замкнутое мышление», которое мешает нам увидеть, что двух мальчиков, рожденных от одной матери в одно и то же время, условно называют близнецами, когда их всего двое. Но что, если трех братьев родились одновременно? В задаче все верно, но мы бы не стали называть этих мальчиков близнецами; мы бы назвали их тройняшками!
Отличительный признак боковых проблем: они всегда кажутся «невозможными» на основании информации.Однако невозможно сохранить логическую связь между нашими предположениями и простыми фактами вопроса.
Если вам нравится ощущение, что ваш разум скручивается в узлы, задачи с самореферентной информацией могут быть вашим любимым видом логической головоломки.Головоломки со ссылками на себя, иногда называемые рекурсивными задачами, — это задачи, которые заставят вас почувствовать, как ваш мозг крутится в узлах. В этих задачах вопросы относятся к вопросам, которые относятся к вопросам… Вы понимаете.Это сложно. Давайте посмотрим на один классный, созданный инженером-программистом и создателем головоломок по совместительству Лаури Тервонен:
1. Каков ответ на второй вопрос?
A. A
B. B
C. C
D. D
2. Сколько правильных ответов в этом тесте — B?
A. 0
B. 1
C.2
D. 3
3. Есть ли вопрос с правильным ответом A?
A. Нет
B. Да, 1
C. Да, 2
D. Да, все 3
Забавьте учителей ссылочная головоломка.
Если вам понравилась эта задача, вот одна из самых коротких версий задачи со ссылками на себя. Этот замечательный, потому что его достаточно легко запомнить.Вы можете попытаться поставить в тупик своих учителей и родственников!
Угадайте следующие три буквы в серии GTNTL.
Возможно, вы сразу поняли ответ на этот вопрос, но если вы еще этого не сделали, не сдавайтесь слишком быстро! Еще одна причина работать над головоломками — стать более усидчивыми.
Все еще застрял? Подсказка: этот раздел посвящен самодостаточным головоломкам!
Вы уловили последний намек? Следующие три буквы в последовательности: «I, T, S.», Которые являются начальными буквами слов« в серии ». Начальные буквы слов в задаче: G для предположения, T для, N для следующего, и так далее, создавая последовательность: GTNTLITS…
Если вам нравятся эти примеры и вам интересна рекурсия, ознакомьтесь с этим отличная статья о рекурсии, языке и логике.
Есть другие типы? Да! Головоломки с логической сеткой, головоломки Какуро, головоломки Судоку, Ребус, Хитори, Ханджи, Нурикабе, Скользящая ссылка, Футосики, кроссворды, Магический квадрат, Механика, Криптос.И это только начало.Вау. Это много разных видов, и это даже не касается всего! Компании и юридические школы даже используют логические головоломки при приеме на работу и приеме на работу, потому что они могут выявить когнитивные способности.
Если вам нравятся головоломки с логической сеткой, и вы научитесь их хорошо решать, попасть в лучшую юридическую школу будет намного проще. На LSAT, вступительном экзамене юридической школы, головоломки с логической сеткой составляют 23% вашего балла! Вот увлекательная статья о головоломках, которые ведущие технологические компании задают в своих интервью.
Как помочь ребенку разобраться в логических головоломках?Лучший способ научиться решать головоломки — это разгадывать их! А как это сделать проще всего? Если вы хотите, чтобы у ваших детей был постоянный поток логического времени, свяжите его с другими привычками, которые у вас уже есть.
Вы всегда обедаете вместе после спортивной тренировки во вторник вечером?
Попробуйте найти этот фантастический источник задач «Московские головоломки: 359 математических увлечений» и каждую неделю задавайте один из вопросов за ужином.Тот, кто это выясняет первым, не должен мыть посуду!
Вот еще один пример использования связывания привычек для последовательной работы над логическими проблемами. Вы и ваш ребенок читаете книги вместе каждую ночь? На ночь или две в неделю добавляйте простую загадку с логическими рассуждениями, прежде чем читать!
Время в машине — еще одно отличное время для решения сложной головоломки. То, где вы их делаете, имеет меньшее значение, чем последовательность. Лучший способ быть последовательным — сделать интеллектуальные игры частью деятельности, которая уже происходит регулярно.Эту технику, называемую накоплением привычек, можно использовать для выработки любой здоровой привычки. Всего через несколько месяцев вы увидите, как у вашего ребенка возрастет способность решать проблемы. В течение сезона вы увидите, как улучшение аналитических навыков вашего ребенка положительно повлияет на его математические способности и любовь к предмету.
Настольные игры и головоломки для развития аналитического мышления.Логические головоломки могут принимать разные формы. Даже знаменитый кубик Рубика — это логическая головоломка.Он относится к категории «механические головоломки». Такие занятия, как кубик Рубика и настольные игры, — отличный способ поощрить и развить аналитическое мышление, одновременно прекрасно проводя время! Настольная игра, такая как Splendor, которая основана на совершении сделок и оценке стоимости относительных предметов, отлично подходит для оттачивания навыков аналитического мышления.
Если вам нужна настоящая головоломка, а не соревновательная настольная игра, обратите внимание на линейку головоломок ThinkFun или головоломки Puzzle Baron’s Logic Grid.Учебная программа IMACS также отлично подходит для развития этих навыков. Фактически, один из разработчиков головоломок ThinkFun является выпускником IMACS. Вы можете прочитать историю Марка Энгельберга, чтобы узнать больше о том, как он придумал большую головоломку «Шоколадное исправление». Если вы хотите увидеть, как программа IMACS может сделать из вашего ребенка будущего конструктора головоломок, изобретателя, предпринимателя или отличного всестороннего мыслителя, приведите своего ребенка (виртуально!) На наш бесплатный класс оценивания. Мы поиграем с ними в математические игры в течение примерно тридцати минут и дадим вам бесплатный анализ размещения, чтобы вы знали, как лучше всего помочь вашему ребенку повысить уровень его математических способностей.
Собираем все вместе. Пять причин начать вместе с детьми решать логические головоломки.- Логические задачи учат детей различным подходам к решению проблем. Такие методы, как устранение, обратная работа, «нестандартное мышление» и навыки критического мышления — все это подходы, которые получают тренировку и улучшаются.
- Активные мозги растут. Если мозг похож на мышцу, математические головоломки — это штанги. Часто тренируйте свой мозг, чтобы поддерживать форму и становиться сильнее.
- Интересная математика, которую делают инженеры-математики, изобретатели и математики, намного увлекательнее, чем механический счет и применение некоторых уравнений к набору чисел. Во многих отношениях логические головоломки так же важны, как и «школьная математика», в плане набора навыков, которые понадобятся вашим детям в будущем.
- Иногда одаренные дети учатся бояться математики. Иногда дети, которые испытывают трудности с изучением предмета, отключаются, потому что думают, что это скучно. Однако часто это происходит потому, что их единственное воздействие — запоминание формулы или заполнение рабочего листа.Головоломки — отличный способ помочь детям, которые бросают учебу в школе, увидеть, насколько прекрасна и увлекательна математика.
- Логические головоломки — это замаскированные словесные задачи. «Нет! Это не страшная проблема со словами », — стонут многие дети, когда видят стену текста в учебнике по математике. Но для успеха в математике необходимы навыки понимания прочитанного. Головоломки чаще всего представляют собой задачи со словами, поэтому дети учатся получать удовольствие от формата, а не бояться его.
Иногда сложно увлечь детей тем, чего нет на экране. Мы получим это; мы тоже родители. Но за тридцать лет обучения детей навыкам логического мышления мы придумали один верный трюк, который заставит детей увлечься усердной работой над сложными проблемами: сказать им ответ.
Эй! Пока не нажимайте кнопку возврата! Вот как ответ помогает им взволноваться. Получите несколько логических головоломок; отличный источник — шоу NPR «Car Talk», которое заканчивает каждую серию блестящей головной болью.Пусть ваш ребенок покажет вам задачу. Переверни сценарий! Позвольте им наблюдать, как вы боретесь с этим, работаете над этим и, самое главное, получайте от этого удовольствие. Эти головоломки — это забавные головоломки, но все равно решите их. Когда вы попробуете еще один (может быть, через несколько дней или неделю), настаивайте на том, чтобы вы сначала попробовали его. Неделя третья, скажите, что вы хотите попробовать первым, но вы готовы, отпустить их первыми.
Моделируя, насколько весело решать головоломки, вы даете им повод попробовать.Этот принцип работает и в наших классах. Наши учителя так весело преподают математику ученикам IMACS, что дети с нетерпением ждут этого. Если вы еще не посещали наши занятия, вы можете узнать больше о детях, которые их посещали; если вы хотите сами увидеть наши занятия, подпишитесь на бесплатную пробную версию.
Спасибо за чтение! Вот вам еще одна забавная задача.У отца Петра пятеро сыновей. Имена четырех сыновей — Фефе, Фифи, Фафа и Фуфу соответственно.Как зовут пятого сына?
Если они вам понравились, вам понравится IMACS. Попробуйте бесплатное занятие по размещению и посмотрите, насколько увлекательны математические рассуждения.
Ответы:Загадки для игры слов:
Что намокнет? Полотенце.
Что можно запустить? Река
Я невесомая? Отверстие
Случай с пролитым какао:
Решение: Аврора
Пояснение:
Утверждения 1 (Элизабет) и 3 (Аврора) по сути говорят об одном и том же.Оба эти утверждения не могут быть правдой, поэтому Элизабет и Аврора должны лгать. Следовательно, Ророна должен говорить правду. Поскольку мы знаем, что какао пролила не Ророна, это, должно быть, Аврора, поскольку она единственная сестра, помимо Ророны, в имени которой есть буквы, которые могут «рычать».
Фиаско с фастфудом:
Решение:
Лори заказала бутерброд с рыбой, луковые кольца и лимонад.
Мэтт заказал бутерброд с курицей, картофель фри и воду.
Нэнси заказала овощной бутерброд, картофельные чипсы и корневое пиво.
Пояснение:
Поскольку картофельные чипсы идут с пивом, либо сторона Нэнси неправильная, либо ее напиток неправильный. Итак, ее вегетарианский бутерброд правильный. Лори не получила сэндвич с курицей (потому что он идет с водой, которую она не получила). Отсюда следует, что:
Лори заказала бутерброд с рыбой, ________ и ________.
Мэтт заказал сэндвич с курицей, ________ и воду.
Нэнси заказала вегетарианский бутерброд, ________ и ________.
Поскольку только один из пунктов Мэтта был правильным, он не получил луковые кольца. Поскольку чипсы идут с пивом, Мэтт чипсов не получил. Итак, он получил картошку фри.
Решение головоломки со ссылками на себя:- (A)
- (A)
- (C)
Логические головоломки с ответами по математике — Математические головоломки с ответами
Логические головоломки являются неотъемлемой частью банковских PO, SSC, государственных экзаменов и многих вступительных испытаний.Вопросы, основанные на головоломках, предназначены для проверки ваших аналитических, дедуктивных способностей и способностей к решению проблем. Здесь мы собрали ряд вопросов и ответов на различные логические головоломки в порядке сложности. Вы научитесь решать аналитические головоломки и вопросы логического мышления. Эта статья содержит 10 вопросов и ответов на головоломки среднего уровня.
Решите заданные вопросы и проверьте свои умственные способности:
Q.1. Внимательно прочтите следующую информацию и ответьте на вопросы, заданные ниже.- P, Q, R, S и T — пять друзей.
- Q старше Т, но не такой высокий, как R.
- R младше P и выше S и T.
- P выше S и не самый высокий, но моложе T.
- S старше P, но самый короткий в группе.
Кто из следующих самый высокий?
Решение и объяснение
 Сколько времени играл каждый мальчик?
Сколько времени играл каждый мальчик?
 02.2011, 22:54
02.2011, 22:54

 02.2011, 22:53
02.2011, 22:53 Мастера попросили изготовить номера для всех домов от 1 до 100. Чтобы выполнить заказ, он должен запастись цифрами. Не пользуясь карандашом и бумагой, подсчитайте в уме, сколько девяток потребуется мастеру?
Мастера попросили изготовить номера для всех домов от 1 до 100. Чтобы выполнить заказ, он должен запастись цифрами. Не пользуясь карандашом и бумагой, подсчитайте в уме, сколько девяток потребуется мастеру? 02.2011, 22:53
02.2011, 22:53