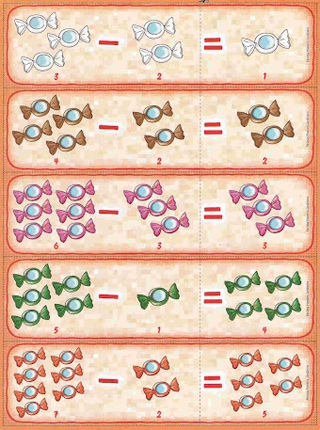
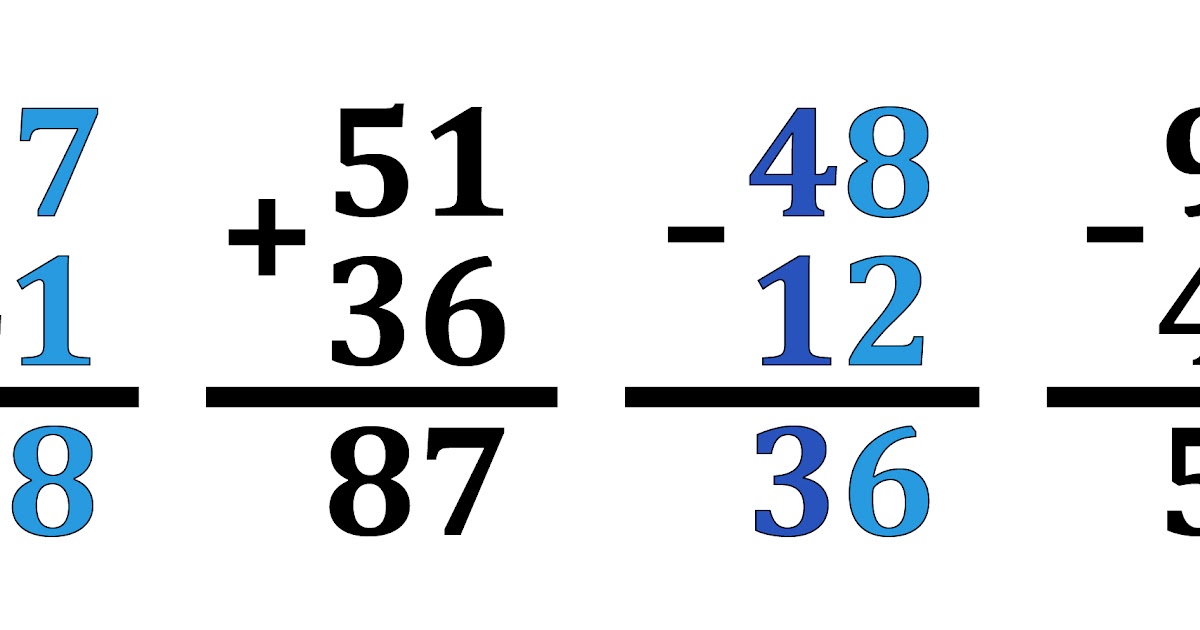Складываем и вычитаем | Развитие детей | Раннее развитие детей
Что вас ждет под обложкой:
«Сложение и вычитание» — обучающее пособие новой серии «Я люблю учиться. Подготовка к школе», наряду с развитием навыка счета, прививает грамотность, знакомит ребенка с окружающим миром. Помимо адаптированного для детей изложения заданий в пособии вы найдете интересного героя, который на протяжении всех заданий сопровождает ребенка, и в игровой форме помогает считать и писать цифры. Как вычесть 5 из 6, сколько насекомых нарисовано на страничке, как лягушонку сложить 7 и 8, сосчитай мороженое – вот несколько примеров заданий. Обучающее пособие «Сложение и вычитание» создано при участии опытных методистов и полностью соответствует образовательным программам детских садов в России. Неизменным преимуществом тетради является множество полезных советов для родителей, которые находятся внизу странички на каждом развороте тетради.
Гид для родителей:
Тетрадь «Сложение и вычитание» ориентирована на занятия с детьми от 5 до 7 лет и содержит советы родителям, как стимулировать раннее развитие ребёнка.
Изюминки книжки:
• Обучающая тетрадь «Сложение и вычитание» содержит золотые наклейки для поощрения успехов ребенка.
• Все упражнения соответствуют школьной программе и составлены в соответствии с требованиями ФГОС НОО.
• Удобный формат тетради, который позволяет взять ее с собой в любое путешествие.
• Обучение счету, сложению и вычитанию в игровой форме. • Высочайшее качество полиграфии, точная цветопередача.
• Соберите все рабочие тетради серии и подготовьте ребенка к школе!
«Складываем и вычитаем» Елена Бортникова
Купить рабочую тетрадь для детей 5-6 лет в Иваново «Складываем и вычитаем» Елена Бортникова
Хотите купить рабочую тетрадь для детей в Иваново? Ищите магазин, в котором можно приобрести недорогие рабочие тетради-тренажеры для детей для эффективного обучения? Приходите в магазин игрушек,канцтоваров и книг «Знай-ка» и покупайте рабочую тетрадь для детей 5-6 лет в Иваново «Складываем и вычитаем» Елена Бортникова.
Характеристика рабочей тетради для детей 5-6 лет «Складываем и вычитаем» Елена Бортникова
- Автор: Бортникова Елена Федоровна
- Художник: Чудинова Т.
- Редактор: Кайсина Т.
- Издательство: Литур, 2016 г.
- Серия: Рабочие тетради
Особенности рабочей тетради для детей 5-6 лет «Складываем и вычитаем» Елена Бортникова
Предлагаем Вашему вниманию задания для развития математических способностей у детей 5-6 лет, которые помогут Вашему ребенку успешно подготовиться к школе.
- Дети познакомятся с действиями «сложение» и «вычитание», научатся решать равенства на сложение и вычитание чисел первого десятка с опорой как на наглядный геометрический материал, так и на знание состава чисел.
- Также дети познакомятся с понятиями «уменьшение — увеличение числа», опираясь на числовой отрезок.

- Тетрадь рассчитана на совместную работу взрослых и детей. Она может быть использована в детских дошкольных учреждениях.
Если Вы хотите купить рабочую тетрадь для детей 5-6 лет в Иваново «Складываем и вычитаем» Елена Бортникова, приходите в магазин игрушек,канцтоваров и книг «Знай-ка» в Иваново по адресу: г. Иваново, ул.Громобоя, 13.
Телефон: +7(960)500-35-35 +7(960)50-99-00 +7(961)118-14-14
Пожалуйста, скажите, что узнали номер на СКИДКОМ
Показать телефонСкладываем и вычитаем числа. Решение задач на сложение и вычитание
Цели:

Тип урока: урок открытия нового знания.
Оборудование:
- учебник математики 1 класс, автор Рудницкая В.Н.;
- рабочая тетрадь №1 Математика, автор Рудницкая В.Н.;
- мультимедийный аппарат;
- презентация к уроку;
- индивидуальные нетбуки;
- карточки 1-4 варианты.
Ход урока
Организационный момент. (Слайд 1)
— Доброе утро! Посмотрите, ребята, друг на друга, улыбнитесь своему соседу или соседке и пожелайте удачи! Долгожданный дан звонок! Начинается урок!
— Девиз нашего урока: “Кто думает, тот всегда додумается!”. (Слайд 2)
Звукотерапия.
— Садитесь удобнее. Прежде чем приступить к работе, мы с вами вначале настроимся на рабочий лад при помощи звуков. Руки положите на свои коленочки, закройте глазки. Произнесите звуки так долго, пока я не назову вам следующую.
Н – активизация мыслительной деятельности.
О, А – настрой на работу.
Актуализация знаний.
Работа с нетбуками. (Академия младшего школьника. Состав числа 10).
А мы начнем, наверное, с самого приятного – это
работа с нетбуками. Сегодня мы усложняем нашу
работу. На прошлом уроке мы остановились на
составе числа 10 в третьем подъезде числового
дома. Но не все смогли пройти до самого верхнего
этажа подъезда и включить в нем свет. Значит, кто
не получил грамоту на прошлом уроке, они
возвращаются в состав числа 10 в 3-й подъезд (№62) и
постараются включить свет и получить грамоту. А
другие усложняют свою работу и переходят сразу
на два: на 2-й и 3-й (№63) подъезды.
№1. Группировка предметов. (Слайд 3)
— Молодцы! Вы замечательно справились с работой! И мы продолжим работу над числами. Посмотрите на примеры и скажите, на какие группы можно разложить примеры? (На сложение и вычитание).
— Прочитайте примеры разными способами.
— Теперь усложняем нашу работу. Посмотрите на данные примеры и скажите, чем похожи эти примеры?
— А чем отличаются? (Один пример на сложение, а другой на вычитание).
— А чем отличается сложение от вычитания? (Одно число увеличивается, а другое – уменьшается).
— Какой вывод можно сделать? (При сложении число увеличивается, а при вычитании – уменьшается).
— Что нужно исправить в задачах?
— А при решении задач может происходить то же самое?
— Из каких частей состоит задача? (Из условия и
вопроса).
— Внимательно прослушайте мои задачи и скажите, что нужно исправить в задаче?
- У девочки 7 шариков. Один шарик лопнул, девочка заплакала.
- В детском саду 8 резиновых мячей. Один мяч упал и разбился. Сколько мячей осталось?
- Бабушка испекла 8 пирожков. Несколько пирожков съели. Сколько пирожков осталось?
Физминутка.
Спортивно-арифметический диктант.
— Мы будем сейчас с вами решать примеры. Только числа не будем записывать, а выполнять их упражнениями. Ответ, который вы получите, решив пример, вам подскажет, сколько раз надо выполнить упражнение.
1. Наклоны вперед 9-2.
2. Выпады вперед 7-2.
3. Рывки руками вверх-вниз 10-5.
4. Наклоны в сторону 6+2.
5. Подтягивание 5+1.
6. Приседания 4+2.
Создание проблемной ситуации.
— Ребята, а в жизни вам приходится складывать и вычитать? А в каких ситуациях?
— Да, конечно, мы в жизни всегда встречаемся с
задачами. Например, в магазине. (Слайд 5).
Давайте вместе с Ирой отправимся в магазин и
попробуем составить задачи. Ира купила мороженое
и шоколадку. Какой вопрос нужно задать, чтобы она
решилась сложением?
Например, в магазине. (Слайд 5).
Давайте вместе с Ирой отправимся в магазин и
попробуем составить задачи. Ира купила мороженое
и шоколадку. Какой вопрос нужно задать, чтобы она
решилась сложением?
— А какой вопрос нужно задать, чтобы задача решалась вычитанием?
— Посмотрите еще раз на слайд и скажите, одинаковое ли условие у задач, которые мы составили? А вопросы задач были одинаковые?
— От чего же зависел выбор действия в решении этих задач? (От вопроса).
— Предположите, какая тема урока?
— Да, ребята, мы научимся отличать задачи, которые решаются сложением от задач, которые решаются вычитанием.
(Слайд 6)
— Прочитайте две задачи и скажите, какую из них нужно решить сложением, а какую – вычитанием.
— Как отличить задачу на сложение от задачи на вычитание?
— А когда же надо складывать, а когда отнимать?
(Дети выдвигают свои гипотезы)
— Я не знаю, какое из ваших мнений правильное. Как же мы будем проверять?
Как же мы будем проверять?
(Сравнивать задачи!)
Сравнительный анализ задачи.
— Еще раз прочитайте первую задачу. Решите. Какое слово помогло вам выбрать действие? (Всего).
— Прочитайте вторую задачу. Решите. Какое слово помогло сейчас вам выбрать действие? (Осталось).
(Слайд 7)
— А где эти слова находятся? В условии задачи или в вопросе?
— Давайте попробуем сделать вывод: Скажите еще раз, какие слова встречаются в задачах на сложение, а какие на вычитание.
— А где эти слова находятся? (В вопросах).
| + | — |
| Всего | Осталось |
| На… больше | Завяло |
| Было | На… меньше |
| Старше | Взяли |
| Стало, выше, дальше, длиннее | Ниже, короче, уже |
Практическая работа (парная работа).
— А теперь мы поработаем в паре со своим соседом. У вас на каждой парте лежит карточка. У кого-то карточка №1, у другого №2, 3. В этой карточке по две задачи. Мы договариваемся с вами работать следующим образом. Внимательно прочитайте первую задачу, обсудите со своим соседом, каким действием её нужно решать, найдите слова, которые помогли вам сделать правильный выбор и отметьте в кружочке знак действия + или — . На эту работу вам дается 3 минуты.
Проверка.
— У кого карточка №1? Отвечать нужно красивым математическим языком. (Мы решили задачу сложением, поставили знак +. Нам помогло слово “на 2 больше”).
Одновременно дополняется памятка на слайде.
— А какие слова еще можно добавить в эту памятку?
— А для чего мы вывели эту памятку? Нужна ли она нам?
Закрепление.
№4 в рабочей тетради.
— А теперь попробуем, используя эту памятку,
самостоятельно вставить нужные знаки действия.
— Откройте рабочую тетрадь на стр. 57. Прочитайте задание. Что нужно сделать? На выполнение этой работы дается 2 минуты.
— Оцените свою работу самостоятельно при помощи пасты зеленого цвета. Если вы поставили себе все 3 плюса, значит, у вас 3 балла; 2 плюса – 2 балла, 1-1 балл.
— Какие слова вам помогли выбрать нужное действие?
— Где они находились: в условии или в вопросе задачи?
Итог.
— Чему мы научились на уроке?
— Справились ли мы с этим заданием?
— Как же отличить задачи? (По словам).
— Какие действия нам помогают выбрать верный знак действия?
Рефлексия
— Давайте оценим свою работу на уроке. У вас на парте смайлики. Выберите тот смайлик: 1. Я все понял, смогу справится самостоятельно.
2. Я все понял, но у меня еще остались вопросы по теме.
3. Я мало что понял. Мне нужно объяснить еще раз.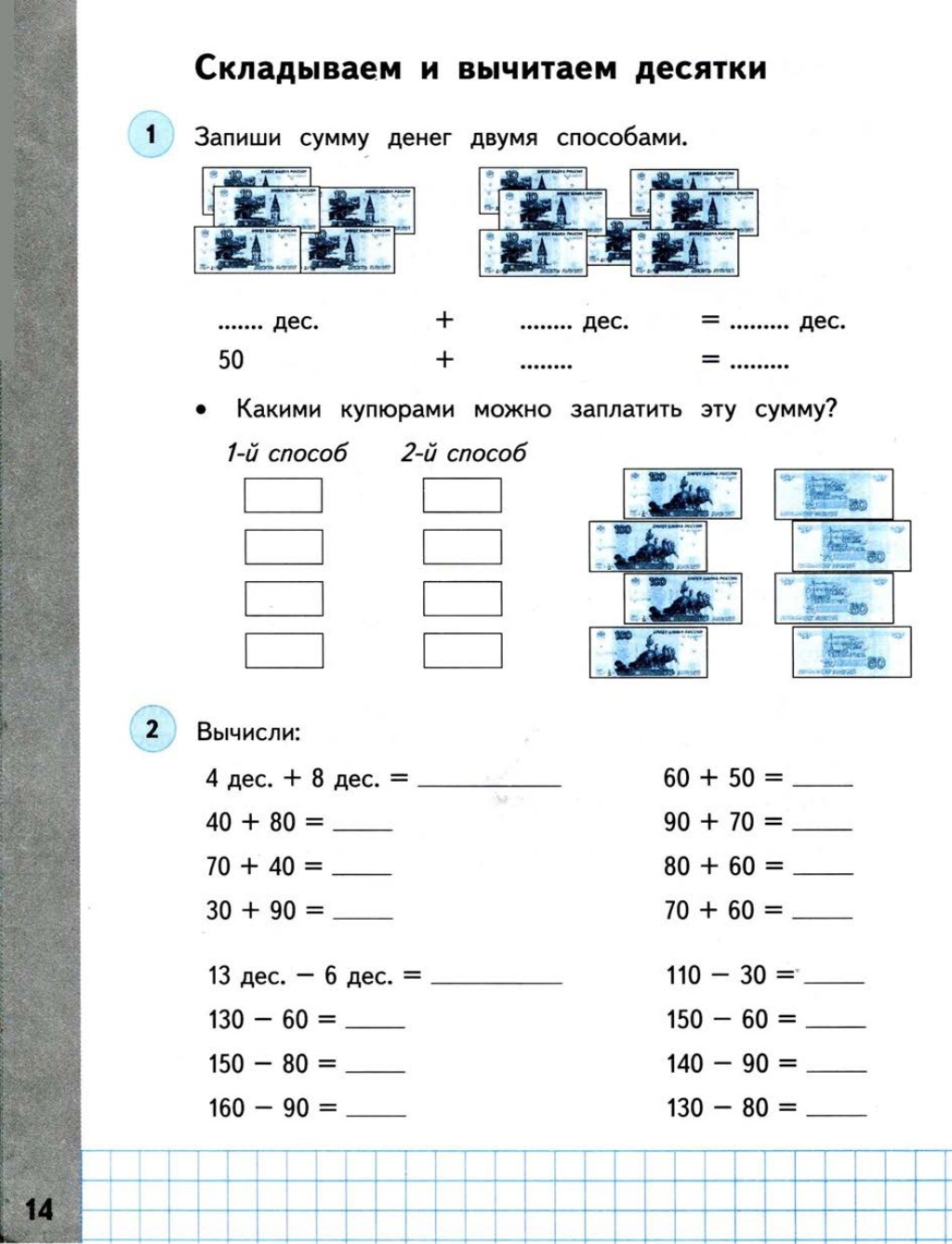
Спасибо за урок! Вы молодцы.
P.S.
Дополните задачу.
- Почтальон Печкин принес 4 письма Шарику и 5 писем Матроскину.
- Шарик снял с одной грядки 3 огурца, а другой – на 2 больше.
Складываем и вычитаем числа
Конспект урока по ФГОС второго поколения. Технологическая карта урока
Складываем и вычитаем числа
Гаврилова Марина Александровна,
учитель начальных классов ГБОУ школы № 337
Невского района Санкт-Петербурга
Предмет: математика Класс: 1 “Б “ Учебник (УМК): В.Н. Рудницкая, Е.Э. Кочурова О.А. Рыдзе «Математика»
Тема урока: Складываем и вычитаем числа. Тип урока: комбинированный.
Тип урока: комбинированный.
Оборудование: учебник, рабочая тетрадь, компьютер ,интерактивная доска,”смайлы”,карточки для индивидуальной работы.
Характеристика учебных возможностей и предшествующих достижений учащихся класса, для которого проектируется урок:
предметные результаты – умение
Цели урока как планируемые результаты обучения, планируемый уровень достижения целей: повторить арифметические действия сложение и вычитание; закреплять умение читать математические записи.
Задачи урока.
Отработка навыка счета, сложения и вычитания в пределах 10
Расширять кругозор, осуществлять связь с жизнью, развивать речь учащихся
Развивать умения наблюдать, сравнивать, делать выводы
Активизировать воображение, память
Прививать интерес к математике
Учить культуре общения
Воспитывать положительные качества личности учащихся, активность, аккуратность, умение преодолевать трудности.
Формировать культуру умственного труда
Содействовать развитию навыка самоконтроля. Развитие навыков сотрудничества.
|
Вид планируемых учебных действий |
Учебные действия |
Планируемый уровень достижения результатов обучения |
|
Предметные |
Овладение алгоритмами решения организационных задач и операций. Применение новых знаний в жизненных ситуациях. |
2 уровень — понимание, обоснованное применение операций. |
|
Регулятивные |
Умение выявлять проблему Умение определять и сохранять цель
Умение контролировать свою работу и полученный результат. |
2 уровень — самостоятельное выполнение действий по алгоритму. |
|
Познавательные |
Выбор наиболее оптимальных средств и способов решения задачи Умение использовать научные методы познания Умение сравнивать делать выводы. |
2 уровень — совместные действия учащихся в условиях взаимопомощи и взаимоконтроля |
|
Коммуникативные |
Умение вести учебное сотрудничество на уроке с учителем, одноклассниками в группе и коллективе. Умение воспринимать различные точки зрения ;воспринимать мнение других людей
Умение использовать простые речевые средства для передачи своего мнения, выражать свою точку зрения. |
1 уровень — выполнение действий по алгоритму под управлением учителя. |
|
Личностные |
Умение провести самооценку, организовать взаимооценку и взаимопомощь в группе. |
2 уровень — самостоятельное выполнение действий с опорой на известный алгоритм. |
|
Этап урока, время этапа |
Задачи этапа |
Методы, приемы обучения |
Формы учебноговзаимодей-ствия |
Деятельность учителя |
Деятельность учащихся |
Формируемые УУД и предметные действия |
|
|
Мотивационно-целевой этап |
Орг.
Самоопределение к учебной деятельности(2 минут) |
Организовать самоопределение детей к деятельности на уроке.
|
|
фронтальная |
Приветствует учеников. Проверяет готовность к уроку. Учащиеся Мы гостей сегодня ждали И с волнением встречали Хорошо ли мы умеем И решать, и отвечать? Не судите очень строго Ведь учились мы немного.(слайд1)
Учитель: Создадим дружелюбное хорошее настроение Улыбнитесь друг другу
(слайд2) Ну-ка, посмотри, дружок Ты готов начать урок? Все ль на месте? Все ль в порядке? Ручка, книжка и тетрадка? Цифры в ряд у вас лежат? Все ли правильно сидят? Все ль внимательно глядят? Все ль готовы слушать?
Тогда начинаем наш урок.
|
Воспринимают на слух, визуально контролируют свою готовность к уроку. |
Личностные: самоорганизация. Регулятивные: способность регулиро-вать свои действия, прогнозировать деятельность на уроке. |
|
Актулизация знаний ( 5 мин) |
Целеполага-ние и постановка задач.
Систематизировать имеющиеся у учащихся знания: сложения и вычетания |
Беседа по уточнению и конкрети-зации знаний . |
Фронтальная и групповая |
Слайд – сова (Разминка) Холодный белый пушистый? (снег) Как звали девочку вступившую в борьбу со Снежной королевой?(Герда) Какой сегодня день недели? (четверг)а какой он по счету? (4)а как получить число 4? А какой был вчера? (среда) Сколько урок по расписанию в среду ?(5) как получить число 5? Какое время наступило? Какой зимний месяц ? (декабрь) Какой он по счету в году? (12) Как получить число 12? Двенадцать увеличить на два. (14) Слайд 3 (2014) Кто может прочитать это число? Какое событие в жизни нашей страны будет в 2014 году в феврале?
(Олимпийские игры). (стук в дверь) В класс приходит письмо. |
|
Личностные: осознание своих возможностей.
Регулятивные: умение регулировать свои действия, взаимодействовать в группе.
Познавательные: Умение анализировать, выделять и формулировать задачу; умение осознанно строить речевое высказывание. |
|
|
Поисково-исследователь-ский этап (10 мин) |
|
|
|
Слайд 4 (олимпийские символы) ТЕКСТ ПИСЬМА
Оказалось, что рысь ,заяц и медведь столкнулись с разными ситуациями.
1 этап. Рабочая тетрадь
Задание № 1 (выполняют по командам) Организует работу пар и групп, следит за правильным выполнением операций, контролирует и корректирует действия учеников.
Проверка. Слайд 5 (примеры по столбикам) ФИЗКУЛЬТМИНУТКА (слайд 6) Задание № 2 Какие операции мы производим в задании.(складываем). В задании №1, какие действия мы проводили? (вычитали) Как вы считаете, чем мы будем заниматься на уроке. Слайд 7 (тема нашего урока) Складываем и вычитаем числа
3 этап Работа в учебнике. Задание № 1 стр.57 Когда мы прибавляем к числу, что происходит с числом? (увеличивается) Когда мы вычитаем из числа, что происходит с числом? (уменьшается)
Задание № 5. Работа с задачами.
|
Выбирают сравнивают анализируют и объясняют свой выбор.
|
Личностные: проявление интереса и активности в выборе решения; установление личностного смысла знания. Регулятивные: умение составлять план и последовательность действий, осуществлять контроль по результату.
Познавательные: умение рационально использовать информацию;, ориентироваться в материале.
|
|
|
Практический этап (17 мин) |
Умение ана-лизировать полученную информацию и применять на практике. умение сотрудничать на уроке с учителем, одноклассниками, в группе и коллективе. |
Практическая работа |
В парах группе и индивидуально. |
ФИЗКУЛЬТМИНУТКА для глаз
Этап 4 Работа в тетради. Задание №4. Устная проверка.
Этап 5 Работа с компьютером.
|
Определяют и выполняют технологические операции, осуществляют самоконтроль выполнения операции. |
Лчностные: умение овладеть нормами и правилами научной организации труда; Развитие трудолюбия и ответственности за качество своей и коллективной деятельности. Регулятивные: умение составлять план и последовательность действий, осуществлять контроль по результату. Познавательные: умение выделять необходимую инфор-мацию; умение ориентироваться в средствах и технологиях обработки материалов; умение планировать свою трудовую деятельность; умение обосновывать показатели качества промежуточных операций. |
|
|
Рефлексивно-оценочный этап (8 мин)
|
Умение построить алгоритм действия (технологическая цепочка)
умение сотрудничать на уроке с учителем, одноклассниками, в группе и коллективе. |
|
Фронталь-ная |
Предлагаю вам соединить точки по порядку. Что у нас получилось? |
Сравнивают работы, оценивают свою работу и работы членов группы, отвечают на вопросы учителя. Делают вывод о значимости сложности и трудоёмкости работы. Проговаривают последовательность своих действий. . |
Личностные: умение провести самооценку и организовать взаимооценку (прогнозирование и контроль). Регулятивные: построение логической цепочки рассуждений и доказательство.
Познавательные: умение сформулировать алгоритм действия; выявлять допущенные ошибки и обосновывать способы их исправления обосновывать показатели качества конечных результатов. |
|
Р/т младшего школьника. Складываем и вычитаем
Серия:
Р/т дошкольника.Автор:
СавранскаяКоличество страниц:
32Год издания:
2020Возрастные ограничения:
0+Оплата банковским переводом (напр., через Сбербанк РФ или иной удобный для Вас банк)
Данный способ оплаты предполагает, что вы предварительно оплачиваете 100% стоимости заказа (вместе с доставкой) переводом на наш расчетный счет. После оформления заказа перед Вами отображается уже заполненная счет-квитанция для оплаты через Сбербанк РФ или иной удобный для Вас банк, Вы можете ее распечатать или переписать реквизиты, а затем отнести квитанцию в ближайшей отделение банк и произвести оплату по реквизитам через кассу отделения выбранного Вами банка.
Оплата банковской картой Visa, MasterСard, Maestro, Visa Electron, МИР
Данным способом Вы можете оплатить заказ непосредственно после оформления заказа (предполагается 100 % оплата Товара).
*Данный способ оплаты можно использовать только при оформлении заказа на физическое лицо. Для юридических лиц и индивидуальных предпринимателей данный способ оплаты недоступен.
**к сожалению, не все банковские карты пригодны для оплаты через интернет. Однако некоторые банки начали выпуск специальных карт «электрон» этого типа, имеющих коды CVC2 и CVV2, которые могут быть использованы для оплаты заказов через интернет. Код CVV2/CVC2 — это контрольный номер, состоящий из трех цифр, который напечатан на обратной стороне банковской карты. Этот номер, обычно, напечатан в верхнем правом углу специальной полосы для подписи. Ввод номера необходим, чтобы убедиться, что карта используется настоящим владельцем.
При оформлении заказа просим Вас указывать реальный адрес электронный почты, на него после совершения платежа будет автоматически направлен кассовый чек, подтверждающий оплату Товара.
Внимание! До поступления денежных средств за заказанный Товар интернет – магазин Стрекоза не резервирует Товары на складе и не приступает к формированию заказа.
Формирование заказа осуществляется только после подтверждения оплаты или поступления денежных средств на расчетный счет интернет – магазина Стрекоза (срок зачисления денежных средств на расчетный счет интернет – магазина обычно составляет от 1 до 3 рабочих дней). Вы можете ускорить формирование и отправку заказа, прислав нам копию банковской квитанции на адрес электронной почты [email protected] или воспользовавшись на сайте вкладкой для обратной связи. Обратите внимание, что в разных банках могут взиматься комиссионные сборы при совершении платежей.
Какие платежи НЕ принимаются:
- Для заказов, оформленных физическими лицами НЕ допускается оплата заказа юридическими лицами или индивидуальными предпринимателями.

Возврат денежных средств покупателю по безналичному расчету
Возврат денежных средств осуществляется на банковскую карту, с которой происходила оплата заказа. Срок перечисления средств занимает до 10- ти рабочих дней. Сроки окончательного зачисления средств на банковскую карту зависят от платежных систем MC и VISA, а также от Вашего банка и могут составлять до 30 рабочих дней.
При оформлении возврата денежных средств Вам необходимо предоставить требование, о возврате направив его на адрес электронной почты [email protected] или воспользовавшись на сайте интернет – магазина вкладкой обратная связь, приложить к нему копию паспорта или иной документ удостоверяющий личность покупателя, кассовый чек.
ЗАЯВЛЕНИЕ НА ВОЗВРАТ ДЕНЕЖНЫХ СРЕДСТВ
| Считаем от 1 до 10 | розпочати роботу | ||
| Определяем количество объектов | розпочати роботу | ||
| Определяем порядковый номер объекта | розпочати роботу | ||
| Разбиваем объекты на группы по общему признаку | розпочати роботу | ||
| Изучаем число и цифру 2 | розпочати роботу | ||
| Изучаем число и цифру 6 | розпочати роботу | ||
| Сравниваем числа (с. 24) | розпочати роботу | ||
| Исследуем состав числа 6 | розпочати роботу | ||
| Повторяем числа 1–6 | розпочати роботу | ||
| Складываем и вычитаем по числовому лучу | розпочати роботу | ||
| Складываем и вычитаем в пределах 6 | розпочати роботу | ||
| Изучаем число и цифру 7 | розпочати роботу | ||
| Сравниваем числа (с. 30) | розпочати роботу | ||
| Повторяем числа 1–7 | розпочати роботу | ||
| Изучаем число и цифру 8 | розпочати роботу | ||
| Сравниваем числа (с. 34) | розпочати роботу | ||
| Исследуем состав числа 8 | розпочати роботу | ||
| Повторяем числа 1–8 | розпочати роботу | ||
| Изучаем число и цифру 9 | розпочати роботу | ||
| Сравниваем числа (с. 38) | розпочати роботу | ||
| Исследуем состав числа 9 | розпочати роботу | ||
| Повторяем числа 1–9 | розпочати роботу | ||
| Изучаем число 10 | розпочати роботу | ||
| Сравниваем числа (с. 42) | розпочати роботу | ||
| Исследуем состав числа 10 | розпочати роботу | ||
| Проверяем свои достижения (с. 44) | розпочати роботу | ||
| Повторяем числа 1–10 | розпочати роботу | ||
| Исследуем состав чисел первого десятка | розпочати роботу | ||
| Называем компоненты и результат действия сложения | розпочати роботу | ||
| Открываем способ сложения и вычитания числа 2 | розпочати роботу | ||
| Получаем число нуль. Вычитаем равные числа | розпочати роботу | ||
| Открываем способ рассуждения при сложении и вычитании числа 0 | розпочати роботу | ||
| Учимся складывать и вычитать числа | розпочати роботу | ||
| Прибавляем и вычитаем числа 0, 1, 2 | розпочати роботу | ||
| Исследуем таблицы сложения и вычитания числа 1 | розпочати роботу | ||
| Открываем переместительный закон сложения | розпочати роботу | ||
| Измеряем длины отрезков | розпочати роботу | ||
| Исследуем взаимосвязь сложения и вычитания | розпочати роботу | ||
| Прибавляем и вычитаем число 2 | розпочати роботу | ||
| Прибавляем и вычитаем числа 0, 1, 2 | розпочати роботу | ||
| Исследуем таблицы сложения и вычитания числа 2 | розпочати роботу | ||
| Исследуем разностное сравнение | розпочати роботу | ||
| Увеличиваем или уменьшаем на несколько единиц (с. 63) | розпочати роботу | ||
| Увеличиваем или уменьшаем на несколько единиц (с. 64) | розпочати роботу | ||
| Узнаём о математическом выражении «Разность» | розпочати роботу | ||
| Открываем способ сложения и вычитание числа 3 | розпочати роботу | ||
| Прибавляем и вычитаем число 3 | розпочати роботу | ||
| Открываем правило нахождения неизвестного слагаемого | розпочати роботу | ||
| Называем компоненты и результат действия вычитания | розпочати роботу | ||
| Складываем и вычитаем числа (с. 70) | розпочати роботу | ||
| Изучаем выражения на два действия | розпочати роботу | ||
| Исследуем таблицы сложения и вычитания числа 3 | розпочати роботу | ||
| Прибавляем и вычитаем числа 0, 1, 2, 3 (с. 77) | розпочати роботу | ||
| Готовимся к изучению задач | розпочати роботу | ||
| Проверяем свои достижения (с. 79) | розпочати роботу | ||
| Прибавляем и вычитаем число 4 (с. 80) | розпочати роботу | ||
| Прибавляем и вычитаем число 4 (С. 81) | розпочати роботу | ||
| Знакомимся с задачей | розпочати роботу | ||
| Исследуем структуру задачи | розпочати роботу | ||
| Исследуем задачи (с. 84) | розпочати роботу | ||
| Исследуем таблицы сложения и вычитания числа 4 | розпочати роботу | ||
| Прибавляем и вычитаем числа 0, 1, 2, 3, 4 | розпочати роботу | ||
| Открываем способ сложения и вычитания числа 5 | розпочати роботу | ||
| Прибавляем и вычитаем число 5 | розпочати роботу | ||
| Исследуем таблицы сложения и вычитания числа 5 | розпочати роботу | ||
| Выполняем арифметические действия с величинами | розпочати роботу | ||
| Складываем и вычитаем числа по частям. Сравниваем величины | розпочати роботу | ||
| Исследуем таблицы сложения чисел второй пятёрки | розпочати роботу | ||
| Готовимся к изучению вычитания чисел 6, 7, 8, 9 (с. 93) | розпочати роботу | ||
| Готовимся к изучению вычитания чисел 6, 7, 8, 9 (с. 94) | розпочати роботу | ||
| Составляем краткую запись задачи (с. 95) | розпочати роботу | ||
| Вычитаем числа 6, 7, 8, 9 | розпочати роботу | ||
| Составляем краткую запись задачи (с. 98) | розпочати роботу | ||
| Находим неизвестные уменьшаемое и вычитаемое | розпочати роботу | ||
| Вычитаем числа второй пятёрки | розпочати роботу | ||
| Сравниваем число и математическое выражение (с. 101) | розпочати роботу | ||
| Сравниваем число и математическое выражение (с. 103) | розпочати роботу | ||
| Сравниваем математические выражения | розпочати роботу | ||
| Измеряем массы предметов | розпочати роботу | ||
| Измеряем ёмкости сосудов | розпочати роботу | ||
| Проверяем свои достижения (с. 107) | розпочати роботу | ||
| Двузначные числа. Записываем задачу кратко | розпочати роботу | ||
| Сравниваем, складываем и вычитаем десятки | розпочати роботу | ||
| Получаем круглые числа. Складываем и вычитаем круглые числа | розпочати роботу | ||
| Исследуем единицу измерения длины «Дециметр» | розпочати роботу | ||
| Образуем числа второго десятка | розпочати роботу | ||
| Записываем числа второго десятка (с. 115) | розпочати роботу | ||
| Записываем числа второго десятка (с. 116) | розпочати роботу | ||
| Записываем числа первой сотни | розпочати роботу | ||
| Сравниваем числа в пределах 100 | розпочати роботу | ||
| Складываем и вычитаем на основе состава чисел второго десятка | розпочати роботу | ||
| Складываем и вычитаем на основе состава чисел первой сотни (с. 120) | розпочати роботу | ||
| Складываем и вычитаем на основе состава чисел первой сотни (с. 121) | розпочати роботу | ||
| Прибавляем и вычитаем число 1 | розпочати роботу | ||
| Складываем и вычитаем числа на основе нумерации (с. 123) | розпочати роботу | ||
| Обобщаем нумерацию чисел первой сотни | розпочати роботу | ||
| Прибавляем и вычитаем однозначное число | розпочати роботу | ||
| Складываем и вычитаем числа (с. 126) | розпочати роботу | ||
| Складываем и вычитаем числа (с. 127) | розпочати роботу | ||
| Исследуем задачи (с. 129) | розпочати роботу | ||
| Находим неизвестное вычитаемое и уменьшаемое | розпочати роботу | ||
| Знакомимся с задачами на нахождение неизвестного уменьшаемого или вычитаемого | розпочати роботу | ||
| Решаем задачи | розпочати роботу | ||
| Исследуем составляющие задач | розпочати роботу | ||
| Знакомимся со сложением и вычитанием двузначных чисел | розпочати роботу | ||
| Знакомимся с единицей измерения времени «Сутки» | розпочати роботу | ||
| Определяем время по часам | розпочати роботу | ||
| Узнаём о продолжительности суток | розпочати роботу | ||
| Складываем и вычитаем числа (с. 138) | розпочати роботу | ||
| Определяем стоимость товара | розпочати роботу | ||
| Знакомимся с единицей измерения длины «Метр» | розпочати роботу | ||
| Складываем и вычитаем числа. Повторяем изученное | розпочати роботу | ||
| Складываем и вычитаем числа. Повторяем изученное | розпочати роботу | ||
| Проверяем свои достижения (с. 143) | розпочати роботу | ||
Складываем и вычитаем круглые числа. | Уроки по Математике
Складываем и вычитаем круглые числа.
30.10.2016 2693 465 Бакулина Светлана СергеевнаДата: Класс: 1 46 урок
Тема: Складываем и вычитаем круглые числа
Цель урока:
познакомить с записью и названием круглых чисел;
научить графически представлять круглые числа, сравнивать их, складывать и вычитать; закрепить умение понимать смысл сложения и вычитания, сравнивать числа с помощью соответствующих знаков, повторить счёт в пределах 10, решение задач;
развивать речь, аналитическое и логическое мышление, память, внимание
Ожидаемый результат:
умение понимать смысл сложения и вычитания, сравнивать числа с помощью соответствующих знаков, повторить счёт в пределах 10, решение задач..
Деятельность учителя Деятельность обучающихся наглядности
3 мин. I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. Для создания психологической атмосферы проводит игру «Рисунок на спине» Ученики осмысливают поставленную цель. Проводят игру «Рисунок на спине».
Бумага А4
5 мин. II. Проверка домашней работы. С помощью метода «Ассоциативная карта» осуществляет проверку домашней работы.
Математический диктант.
1. Состав числа 9. «Весёлые задачи».
1.Дружно муравьи живут
И без дела не снуют.
Три несут травинку,
Три несут былинку,
Три несут иголки.
Сколько их под ёлкой?
2. В кружку сорвала Марина
Девять ягодок малины.
Пять дала подружке.
Сколько ягод стало в кружке?
3.Два гуся летят над нами,
Два других за облаками,
Пять спустились за ручей.
Сколько было всех гусей?
4. Ёж спросил Ежа-соседа:
«Ты откуда, непоседа?»
«Запасаюсь я к зиме.
Видишь — яблоки на мне?
Собираю их в лесу.
Шесть принёс да три несу».
Призадумался сосед:
«Это много или нет?»
Поскорее дай ответ
5.Взял девять вишенок Сергей
И угостил своих друзей:
Четыре вишни дал он Вите,
А остальные все Никите.
Сколько вишен у Никиты?
Сосчитайте и скажите.
1. Сравнение выражений.
— Поставьте знаки «больше, меньше или равно»
10-8…10-5 4+2…6-1
3+6…6+3 5-3…8-4
2.Действия с десятками.
— Найдите значения выражений:
9д-4д= 6д-1д= 7д-2д=
8д-3д= 5д+0д=
— Что объединяет все эти выражения?
( Одинаковое значение выражений – 5д).
— Назовите лишнее выражение.
(5д+0д – сумма, остальные – разности).
— Придумайте ещё одно выражение, чтобы ответ был 5д.
Проверим сигнальными карточками.
— Первый орешек раскусили! Ученики демонстрируют свои знания. На бумагах пишут все, что узнали о юморе и сатире. Бумага А4
20 мин. III. Актуализация знаний. .Проводит усвоение тему. Составляют Класстер
Повторение задачи для групп
Сосчитайте от 11 до 20, от 12 до 7.
Дан ряд чисел 6 7 8 9 10.
• В каком порядке расположены числа?
• Назовите самое большое и самое маленькое число в данном ряду.
• Какое число “лишнее”? Почему?
• Расскажите все, что знаете о числе 10.
На сколько 1 0? Каким действием искали? Почему?
-Посмотрите на ряд чисел и скажите, какое число лишнее и почему?
2 5 10 8
— -Заполните таблицу, опираясь на образец (с показом на доске).
-Какие числа написали? Прочитайте хором.
-Эти числа называют «круглые числа». Как вы думаете – почему?
— Справились и со вторым орешком!
Игра с мячом.
1. Запись круглых чисел )
-Объясните, какое задание надо выполнить?
(Дети самостоятельно выполняют задание в учебнике).
1. Сравнение круглых, а так же круглых чисел с нулём и единицами.
— Какой вывод можно сделать?
(Чтобы сложить или вычесть круглые числа, надо сложить/вычесть десятки и приписать справа нуль).
Выполнение второй части номера с показом на доске.
— Третий орешек готов!
Надо немного размяться.
Как называются числа с 0 на конце?
Почему их так назвали
Вывод. Такие ч Эти числа содержат 0. При записи 0 приписываем справа исла называются круглыми.
Задание для групп:
А) состав числа 7
Б) назови число
В по какому признаку можно разбить числа на группы
7, 18, 16, 4, 28, 93, 5, 17, 3 (однознач. и двузначные)
71, 64, 79, 67, 78, 60, 75, 62 (число десятков 6 и7)
30, 27, 40, 37, 57, 60, 77, 80, 97 (дес.,ед. и круглые десятки)
С какой из групп чисел последнего ряда мы работали на предыдущем уроке?
Какие действия мы можем производить с этими числами? (сложение и вычитание)
Кто же сформулирует тему урока? (сложение и вычитание круглых десятков)
.Осознание целей, задач и возможностей своего развития и саморазвития.
Какую работу учимся выполнять на уроке математики? (записывать и читать двузначные числа, складывать и вычитать круглые десятки)
Кто считает, что он уже легко справляется с этой работой?
Кому еще трудно? Где затрудняетесь? Какую учебную задачу каждый поставит для себя?
В конце урока каждый из вас сам подведет итоги выполнения этой задачи для себя.
.Участие учащихся в деятельности, дающей опыт успеха и тренинг достижений.
а) Уменьшить число 80 на 2 десятка, увеличь число 40 на 2 десятка. Запишите равенства. ( ученик записывает на доске, проверка)
Кому было сложно? Что помогло понять приемы вычитания круглых десятков? (число десятков складываем и вычитаем как единицы) Нужно ли еще потренироваться?
б) Выполните сложение и вычитание
Физминутка
в) Чем похожи и чем отличаются выражения? (работа в паре)
8 – 6 6 + 3 9 — 2
80 — 60 60 + 30 90 – 20
Найдите значения выражений.
Взаимопроверка в парах.
Кто справился с заданием?
г) Работа по учебнику
Какое задание можно предложить к данным числам?
3, 5, 9, 4, 8 30, 50, 90, 40, 80
Составить верные числовые равенства, используя данные числа.
Кому сложно, выполните задание только с числами первой группы. Кому все понятно, с числами обеих групп.
Проверка с доски самостоятельно.
Ребята, кто быстрее стал решать примеры с круглыми десятками?
д) Выполнить действие
90 – 20 — 50 + 40 – 10 — 40 =
(проверка )
10 мин. IV. Закрепление урока. По методу «Толстые и тонкие вопросы» проводит закрепление урока.
1. Сравнение выражений.
— Рассмотрите запись на доске. Попробуйте объяснить, что нужно сделать.
а — 8 * а – 5 с – 3 * с +2
б +4 * 4 +б 10 – д * 8 – д
— Обоснуйте своё решение.
3. Действия с десятками:
— Найдите значения выражений:
9д – 4д = 6д – 1д =
8д – 3д = 5д + 0д =
— Что объединяет все эти выражения? (Одинаковое значение выражений – 5д)
— Назовите лишнее выражение. ( 5д + 0д – сумма, а остальные — разности)
— Чтобы сохранить закономерность, какое выражение вы предложили бы записать Проводят обсуждение по творчеству поэта. Отвечают на вопросы учителя. Карточки
5 мин. V.Итог урока. Этап рефлексии: Стратегия «Телеграмма»
Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить.
— Что тебе понравилось?
— Что было трудным для тебя?
— Что ты смог сделать без труда? Оценивают работу своих одноклассников.
На стикерах записывают свое мнение по поводу урока.
стикеры
оценочный лист
2 мин. VI. Домашнее задание. Объясняет особенности выполнения домашней работы. Выучить задание по учебникам Записывают домашнюю работу в дневниках.
дополнительная информация
дифференциация. Как вы планируете поддерживать учащихся? Как вы планируете стимулировать способных учащихся оценивание. Как вы планируете увидеть приобретенные знания учащихся? межпредметные связи, соблюдение СанПиН ИКТ компетентность. Связи с ценностями
рефлексия.
были ли цели обучения реалистичными?
Что учащиеся сегодня узнали? На что было направлено обучение?
Хорошо ли сработала запланированная дифференциация? Выдерживалось ли время обучения?
Какие изменения из данного плана я реализовал и почему? Проводит рефлексию.
-Какую цель мы поставили сегодня на уроке?
-Достигли мы целей, которые ставили в начале урока?
Итоговая оценка
Какие два аспекта в обучении прошли очень хорошо( с учетом преподавания и учения)?
Какие два обстоятельства могли бы улучшить урок( с учетом преподавания и учения)?
Что узнал об учениках в целом или отдельных лицах?
1.
2.
1.
2.
Полный текст материала смотрите в скачиваемом файле.
На странице приведен только фрагмент материала.
Сложение и вычитание положительных и отрицательных чисел
Числа могут быть положительными или отрицательными
Это числовая строка:
| Отрицательные числа (-) | Положительные числа (+) |
| «-» — отрицательный знак. | «+» — положительный знак |
Отсутствие знака означает положительный результат
Если число имеет без знака , это обычно означает, что это положительное число .
Воздушные шары и гиря
Давайте подумаем о числах как о воздушных шарах (положительных) и весах (отрицательных):
К этой корзине привязаны воздушные шары и гирьки: |
Добавление положительного числа
Сложение положительных чисел — это просто сложение.
Мы можем добавить шары (мы добавляем положительное значение ) корзина тянется вверх (положительно) |
Пример: 2 + 3 = 5
действительно говорит
«Положительное 2 плюс Положительное 3 равно Положительное 5»
Мы могли бы записать это как (+2) + (+3) = (+5)
Вычитание положительного числа
Вычитание положительных чисел — это просто вычитание.
Воздушные шары можно забрать ( вычитаем положительное значение ) корзина тянется вниз (минус) |
Пример: 6 — 3 = 3
действительно говорит
«Положительных 6 минус Положительных 3 равно Положительных 3»
Мы могли бы записать это как (+6) — (+3) = (+3)
Добавление отрицательного числа
Теперь посмотрим, как выглядит сложение и вычитание отрицательных чисел :
Мы можем добавлять веса (мы добавляем отрицательные значения ) корзина тянется вниз (минус) |
Пример: 6 + (−3) = 3
действительно говорит
«Положительные 6 плюс отрицательные 3 равны положительным 3»
Мы могли бы записать это как (+6) + (−3) = (+3)
Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного числа) или прибавление веса (добавление отрицательного числа) заставляют корзину опускаться.
Значит, результат тот же :
- (+6) — (+3) = (+3)
- (+6) + (−3) = (+3)
Другими словами вычитание положительного то же самое, что добавление отрицательного .
Вычитание отрицательного числа
Наконец, мы можем убрать веса (мы вычитаем отрицательных значений ) корзина тянется вверх (положительно) |
Пример: Что такое 6 — (−3)?
6 — (- 3) = 6 + 3 = 9
Да, действительно! Вычесть отрицание — это то же самое, что и сложить!
Два отрицания дают положительный результат
Что мы нашли?
Добавление положительного числа — это простое сложение…
Добавление положительного значения Добавление
Положительное и отрицательное вместе …
Вычитание положительного
или
Добавление отрицательного
равно
Вычитание
Пример: Что такое 6 — (+3)?
6 — (+ 3) = 6 — 3 = 3
Пример: Что такое 5 + (−7)?
5 + (- 7) = 5 — 7 = −2
Вычитание негатива…
Вычитание отрицательного числа аналогично Добавление
Пример: Что такое 14 — (−4)?
14 — (- 4) = 14 + 4 = 18
Правила:
Все это можно поместить в два правила :
| Правило | Пример | ||||
|---|---|---|---|---|---|
| + (+) | Два одинаковых знака превращаются в знак плюс | 3 + (+ 2) = 3 + 2 = 5 | |||
| — (-) | 6 — (- 3) = 6 + 3 = 9 | ||||
| + (-) | Два непохожих знака превращаются в знак минуса | 7 + (- 2) = 7 — 2 = 5 | |||
| — (+) | 8 — (+ 2) = 8 — 2 = 6 | ||||
Они «как знаки», когда они похожи друг на друга (другими словами: одинаковые).
Итак, все, что вам нужно запомнить, это:
Два знака типа становятся положительным знаком
Два знака , отличных от , становятся отрицательным знаком
Пример: Что такое 5 + (- 2)?
+ (-) — это в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .
5 + (- 2) = 5 — 2 = 3
Пример: Что такое 25 — (- 4)?
— (-) — это , как знак , поэтому они становятся положительным знаком .
25 — (- 4) = 25 + 4 = 29
Пример: Что такое −6 + (+ 3)?
+ (+) — это , как и знак , поэтому они становятся положительным знаком .
−6 + (+ 3) = −6 + 3 = −3
Начните с −6 на числовой прямой, двигайтесь вперед на 3, и вы получите −3
А теперь поиграйте!
| Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха! |
Объяснение здравого смысла
И есть объяснение «здравого смысла»:
Если я скажу «Ешь!» Я призываю вас поесть (положительный результат)
Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).
Теперь, если я говорю: « НЕ, не ешь!», Я говорю, что не хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).
Итак, два отрицания дают положительный результат, и если это вас устраивает, тогда вы сделали!
Другое объяснение здравого смысла
Друг +, враг —
| + + ⇒ + | .друг друга мой друг | |
| + — ⇒ — | друг врага — мой враг | |
| — + ⇒ — | враг друга — мой враг | |
| — — ⇒ + | враг врага мой друг |
Пример банка
Пример. В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.
Итак, банк должен забрать отрицательные 10 долларов.
Допустим, ваш текущий баланс составляет 80 долларов США, поэтому у вас будет:
80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90 долларов
Итак, вы получаете на свой счет долларов, еще 10 .
Длинный пример, который вам может понравиться
Очки союзника
Элли может быть непослушным или милым. Так родители Элли сказали
«Если вы будете любезны, мы добавим 3 балла (+3).
Если непослушный, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку ».
| Союзник начинает день с 9 очками: | 9 | |
| Мама Элли обнаруживает пролитое молоко: | 9 — 3 = 6 | |
Тогда папа признается, что пролил молоко и пишет «отменить». Как «отменить» минус 3? | ||
| Итак, мама считает: | 6 — (−3) = 6 + 3 = 9 |
Итак, когда мы вычитаем отрицательное, мы получаем
баллов (т.е.е. так же, как добавление очков).
Таким образом, вычитание отрицательного числа аналогично добавлению
| Несколько дней спустя. У Элли 12 очков. | ||
| | | |
| Мама добавляет 3 очка, потому что комната Элли чистая. | 12 + 3 = 15 | |
| | | |
| Папа говорит: «Я убрал эту комнату» и пишет «отменить» на диаграмме.Мама считает: | 15 — (+3) = 12 | |
| | | |
| Папа видит, как Элли чистит собаку. Пишет на графике «+3». Мама считает: | 12 + (+3) = 15 | |
| | | |
| Элли бросает камень в окно. Папа пишет на диаграмме «−3».Мама считает: | 15 + (−3) = 12 |
См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.
Итак:
Неважно, вычтете ли вы положительные
баллов или добавите отрицательные,
вы все равно потеряете баллы.
Таким образом, вычитание положительного
или
Добавление отрицательного
равно
Вычитание
Попробуйте эти упражнения…
Теперь попробуйте этот лист и посмотрите, как у вас дела.
А еще попробуйте эти вопросы:
дополнительных игр | Игры на вычитание
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
Веселые игры для детей
Потрясающие игры на сложение и вычитание
Обзор игры: Щенки каноэ
Реклама | Без рекламыСупер стартеры
Объявление
Дополнительные факты 20
Alien Addition
Дополнение для гидроциклов
Вычитание монстров
Ducky Race
Количество облигаций 20
Koala Karts
Число пар 10
Match Kitten Match
Вычитание острова
Факты вычитания 20
Прыгающие цыпочки
Строители мозга
Вечеринка по размеру стоимости
Treasure Quest Numbers
Monster Addition
Вычитание супергероев
Дополнение Treasure Quest
Математические планки
Galaxy Pals 20
Минус Миссия
Пары бинго-номеров
Найдите автобусную остановку
Дополнение к строительству мостов
Корм для дельфинов
Candy Cashier — Деньги
Bingo Tens
Math Surpass Сравнить
Кодовые суммы
Galaxy Pals 100
Дополнительные блоки
Необычные числовые имена
Прогулка с монстрами
Добавление номера следа
Math Racer Дополнение
Galaxy Pals 200
Number Trails Pro
Бинго Сотни
Щенки для скейтборда
Дополнение к команде буксиров
Сложение двух цифр
Суммы под прикрытием
Бинго 3 числа
Тандемные черепахи Rounding
Space Jaunt Rounding
Округление бинго
Take the Cake Дополнение
Dolphin Dash
Дополнение к 100
Сложенная змея
Поп-пингвин
Дополнение к парку развлечений
Головоломка Венна
Загадочное число
Добавить / отменить добавление
Вычитание до 100
Зоги и монстры +
Пазл фото: деньги
Зоги и монстры $
Черепные испытания
Math Surpass Prime
Головоломки с целыми числами
Объединение целых чисел
Сумботы
2048
Дополнение ко всем на борту
Monster Mischief
Добавление секретного кода
Суммы перекрытия
Числовая последовательность
Цепные суммы
Суммарные блоки
Сложение Math Man
Добавление недостающих цифр
Сложение целых чисел
Сложение целых чисел
Магический треугольник
Вычитание отсутствующих цифр
Сумма фигур
Пазлы с целыми числами
Сумма связей 2
Проблемы со словами, видео и манипуляторы
Значение места
Добавление перегруппировки
Перегруппировка трех цифр
Перегруппировка с вычитанием
Вычитание с нулем
Задачи с математическим словом
Дополнение к блокам мышления
Решение проблем со словами
МАТЕМАТИЧЕСКАЯ ИГРОВАЯ ПЛОЩАДКАИгры для 1-го класса
Игры для 2-го класса
Игры для 3-го класса
Игры для 4-го класса
Игры для 5-го класса
Игры для 6-го класса
Блоки мышления
Видео по математике МАТЕМАТИЧЕСКИЕ ИГРЫ
Сложительные игры
Игры на вычитание
Игры на умножение
Игры на деление
Игры на дроби
Игры на соотношение
Игры на предварительную алгебру
Игры на геометрию ОБУЧАЮЩИЕ ИГРЫ
Логические игры
Классические игры
Правописание
Грамматические игры
Наборы текста
Географические игры
Математические головоломки
Пространственное мышление
ДЕТСКИЕ ИГРЫ
Веселые игры
Приключенческие игры
Автомобильные игры
Спортивные игры
Endless Runner
Perfect Timing
Многопользовательские игры
Все игры Реклама | Без рекламы
О нас Политика конфиденциальности Условия использования Условия оплаты Получить помощь
Авторские права © ООО «Математическая площадка, 2021» • Все права защищены.
Сложение и вычитание в пределах 20
Я все о том, чтобы научить студентов использовать стратегии при сложении и вычитании .Наши стандарты для второго класса требуют, чтобы учащиеся плавно складывали и вычитали в пределах 20 , но, чтобы научиться бегло говорить, учащиеся должны взять на себя ответственность за математические факты и создать свои собственные пути к поиску решения.
Мне нравится знакомить учащихся с различными стратегиями, а затем видеть, что находит отклик у каждого учащегося и помогает им лучше разбираться в математике. В предыдущем посте я затронул важность разработки 10 как эталонного числа. Я также привел пример некоторых математических станций, которые мы используем при добавлении математических фактов +8 и +9.
У меня есть еще больше информации об использовании стратегий сложения для разработки +9 фактов и довольно крутого «трюка», которому я научил своего сына.
Сложение и вычитание в 20 рабочих листах
В этом сообщении в блоге я подробно расскажу о том, как Â строить с помощью 10 для сложения и вычитания , разработав примерно , сделав 10 и добавив 10 стратегий . Â
Рабочие листы, которые вы видите ниже, взяты из моих сложений и вычитаний в пределах 20: сделать 10, сложить 10, использовать 10 для сложения, использовать 10 для вычитания ресурса. Этот ресурс содержит 200 страниц рабочих листов, которые подходят к этим концепциям различными способами, от числовых связей, десяти рамок, числовых линий и забавных партнерских игр.
Также доступны бесплатные игры и задания, в которых используйте 10, чтобы добавить +9 и +8 фактов. Рабочие листы предоставляют отличные инструкции и практические занятия, в то время как игры веселые и помогают ученикам углубляться и развивать гибкость в своем мышлении.
Сделать 10, сложить 10, использовать 10 для сложения и вычитания
Я различаю между Make 10, Add 10 и Use 10 в этом наборе ресурсов
- Make 10 просто находит два числа, которые в сумме дают 10 , вроде 7 + 3.
- Добавить 10 добавляет 10, например 10 +7. Â
- Использование 10 — это поиск факта make 10, который можно использовать для поиска ответа. Â Обычно это относится к фактам +8 и +9. Хотя его можно использовать с другими числами, этот набор рабочих листов сконцентрирован только на +/- 9 и 8.
Большинство рабочих листов, которые вы видите ниже, дублируются для каждой из математических стратегий с разными числами. Â Если вам нужна дополнительная информация о различиях между стратегиями и моделями, я подробно расскажу об этой теме в этом сообщении в блоге.
Сделай 10
Сделай 10 — это базовый навык для большинства стратегий сложения, которым я учу во втором классе. Конечно, дети изучают свои двойные факты и свои плюс один и плюс два факта, но когда мы узнаем о том, чтобы быть эффективными математиками, все дело в стратегиях более высокого уровня, использующих make 10 в качестве основы.
У меня есть целая запись в блоге о стратегиях, которые студенты могут использовать для разработки 10 в качестве контрольного числа.
Вот несколько примеров действий в разделе Make 10.Существует множество листов, в которых используются десять рамок, числовые связи и уравнения. Это разнообразие не только позволяет вам различать разных учеников, но и развивать у них гибкость в математическом мышлении.
Нижний рабочий лист помогает учащимся увидеть комбинацию из десяти рамок и цифр. Â Это отличный инструмент для перехода от использования моделей к числам. Ниже приведен тот же рабочий лист целиком.
Что мне нравится в моих рабочих листах для вырезания и вставки, так это то, что у студентов есть все ответы прямо на рабочем листе.У каждой проблемы на приведенном ниже листе есть четыре возможных «ответа». Учащиеся используют наглядные десять рамок и числа, чтобы помочь написать уравнения.
Мы также работаем над сопоставлением десяти полос и сопоставления десяти рамок. Â Этот рабочий лист является более простой версией концепции, поскольку он просто требует сопоставления. Учащиеся сопоставляют десять полосок и пишут соответствующие уравнения.
Этот лист также помогает понять, что порядок добавлений не имеет значения при добавлении.
Я включил и десять рамок, и десять полос, потому что ученики будут резонировать с разными моделями.Â Я хочу, чтобы студенты могли гибко мыслить независимо от модели.
После работы с двумя десятью фреймами на приведенном выше рабочем листе студентам предлагается создать один из десяти фреймов и написать семейство фактов. Â Этот лист помогает студентам обнаружить закономерность и практиковать как сложение, так и вычитание при написании семейства фактов.
Сделайте 10 с помощью числовых связей
Числовые связи — еще один отличный инструмент для использования в классе. Â Обычно ученики учатся использовать числовую связь в детском саду и в первом классе, так что это не новый инструмент.Однако я хочу, чтобы мои второклассники научились свободно пользоваться ими независимо от ориентации числовой связи. Â
Я создал этот лист числовых связей во всех различных направлениях, чтобы студенты могли практиковаться в ориентировании. Иногда ученики приходят в класс с установкой на данность в математике и нуждаются в помощи в разработке более гибких стратегий мышления.
Сделайте 10 игр-прядильщиков
В каждый раздел также включены игры-прядильщики, в которые учащиеся могут играть с партнером.Вот пример игры Make 10 spinner.
Задачи из 10 слов
Еще одним ресурсом на каждом уровне являются задачи со словами, где учащиеся могут практиковать математические навыки в контексте. Студентам предлагается нарисовать картинку, чтобы проиллюстрировать свое мышление.
Эти проблемы со словами совпадают с моими ресурсами Word по типам проблем. Задачи со словами по типу задачи — это бесчисленные задачи со словами, которые побуждают учащихся читать в контексте. Бесчисленные задачи со словами также позволяют учителям различать вычисления.Учителя могут легко создавать задачи с помощью сложения 10, сложения 10 или сложения или вычитания +9 или +8 фактов.
Добавить 10 к однозначному числу
Добавить 10 — это довольно простой навык для развития учащихся, поэтому мы не тратим на это слишком много времени. Однако это не то, что нужно пропускать. Â
Почему? Â
Когда ученики начинают использовать числовые линии и делать скачки на десять при сложении и вычитании двузначных чисел, наличие этого навыка в качестве основы действительно поможет им увидеть структуру однозначного числа с большими числами.
Вверху указан номер листа облигации. Â Вы заметите, что я продолжаю разную ориентацию. Â Существует несколько версий листа с номерами с разными числами.
Выше представлен лист вырезания и вставки, на котором учащимся предлагается добавить 10 в различных форматах. Это способствует гибкости мышления. Мне нравится, что листы вырезания и вставки дают все ответы.
Веселые партнерские игры
Вот еще одна веселая партнерская игра.  Учащиеся вращают вертушку и добавляют 10 к вращаемой цифре. Это помогает учащимся развивать умственные математические навыки, весело проводя время с одноклассником. Â
Учащиеся могут сыграть в простую версию игры, в которой они просто раскрашивают квадраты, или сыграют в более сложную версию, где им нужно соединить четыре квадрата вместе.
На картинке ниже представлены различные рабочие листы из этого раздела ресурса. Учащиеся используют числовые связи, уравнения, обращенные в разные стороны, и десять рамок. Все эти модели помогают учащимся развить гибкость в математическом мышлении.
Нижний лист выше помогает учащимся увидеть комбинацию из десяти рамок и цифр. Â Учащиеся разовьют беглость, когда увидят, что цифра в разряде единиц такая же, как и в десятичной рамке справа. Â Это отличный инструмент, который поможет студентам перейти от использования моделей к числам.
Используйте 10 для сложения и вычитания
Наконец, мы достигли нашей конечной цели: ученики использовали 10 для сложения и вычитания чисел с суммами от 10 до 20 . Â Это место, где мы хотим, чтобы учащиеся разработали различные стратегии и способы разбиения чисел на части.Â
В этом разделе представлены различные рабочие листы для разделения одного из дополнений. В ресурсе есть сложение +8, сложение +9, вычитание -8 и вычитание -9, а также сочетание всех четырех стратегий. Ниже приведены некоторые виды деятельности.
На листе выше ученики вырезают и сопоставляют десять рамок, имеющих то же значение, что и слева.  Если ученикам нужно, они могут сосчитать точки, но я надеюсь, что на этом этапе ученики смогут переместить точки, чтобы найти эквивалентный набор из десяти кадров. После сопоставления ученики напишут уравнения, соответствующие десяти рамкам.
Второй лист — это еще один рабочий лист для вырезания и вставки, в котором ученикам предлагается выполнить математику без десяти рамок. Â Обычно я даю студентам десять рамок и счетчиков для использования, но с таким объемом практики, который мы проделали, большинство моих студентов могут делать это и без десяти рамок. Â
На этой странице много уравнений, и все они являются фактами +8 и +9. Â Я считаю, что большинство студентов прибавляют десять при добавлении фактов +8 и +9, но не с +7 и +6 фактов. Для них это совсем немного.
Ниже приведен рабочий лист, на котором студенты практикуют сложение. Учащиеся начинают с 8 или 9, складывают до 10, а затем добавляют к уменьшенному.
Вот еще несколько примеров рабочих листов в Используйте 10, чтобы добавить раздел . Существует игра с прядильщиками, в которой студенты тренируются разбивать вычитаемое и складывать от 1 до 9. Это рабочий лист +9.
Также доступны действия с числовой строкой и десятью кадрами, оба смешанные +9 и +8.Вы можете легко дифференцировать занятия и предоставить студентам именно то, что им нужно.
Игры с прядильщиками для отработки стратегий вычитания -9 и -8
Как и в других разделах, учащиеся могут практиковать эти новые математические навыки, используя игры с прядильщиками. Есть несколько версий игр, которые обеспечивают гибкость мышления и разные способы разбить числа.
Ниже представлены две игры со спиннером. Один для -9 и один, который представляет собой смесь -9 и -8.
Использовать числовую строку +8 и +9 Факты
Числовые строки — один из моих любимых инструментов для сложения двух- и трехзначных чисел. Мы начинаем работу с числовой линией со сложения однозначных чисел, разбивая одно из слагаемых при добавлении фактов +9 и  +8.
Этот рабочий лист также изображен выше. Вот вид всего листа.
Идея состоит в том, чтобы перейти к десятке, а затем сделать оставшиеся прыжки к сумме. Â Включено несколько вариантов рабочих листов с числовыми линиями, чтобы студенты могли попрактиковаться.
Сделайте 10, сложите 10, используйте 10 плакатов
В этот ресурс «Сложение и вычитание в пределах 20» также включены плакаты, которые учителя могут показывать в своем классе.На плакатах есть все факты, которые учащиеся используют для каждой стратегии, а также вопросы, которые побуждают глубже задуматься о стратегии.
Number Bond Matching
Еще один ресурс — карточки для сопоставления чисел. Карты доступны и включают номера на плакатах выше. Карточки доступны в каждом разделе ресурса, чтобы учителя могли выделить стратегии, которые ученики могут практиковать.
Вы можете приобрести эти Сложение и Вычитание в пределах 20: Сделать 10, Добавить 10, Использовать 10 для добавления, Использовать 10 для вычитания ресурсов на моем веб-сайте или на сайте Teachers Pay Teachers.
В дополнение к сложению и вычитанию в пределах 20 печатных форм, у меня также есть набор математических станций и центров, специально предназначенных для использования 10 для сложения +9 и +8.
Я разработал эти математические станции после того, как заметил, что моим ученикам нужно немного больше попрактиковаться с использованием 10 в качестве контрольного числа. Â
Дополнительные идеи для преподавания математики
Хотите еще идеи и ресурсы для обучения математике в начальной школе? Взгляните на эти сообщения в блоге.
Что такое сложение и вычитание десятичных знаков?
Сложение и вычитание десятичных знаков
Десятичное число
Десятичное число — это дробь, знаменатель которой является степенью 10. Например, дробь 4 ⁄ 10 может быть записана в десятичной форме как 0,4, где:
Точка называется десятичной точкой.
Число справа от десятичной точки обозначает числитель дроби, то есть дробную часть.
Число слева от десятичной точки обозначает целую часть дроби.
Например, 4 3 ⁄ 10 выражается как 4,3, где 4 — это целая часть числа, а 0,3 — дробная часть.
Десятичная точка отделяет целую часть числа от дробной части.
Десятичные числа в реальной жизни
Мы занимаемся сложением и вычитанием десятичных дробей в повседневной жизни, имея дело с:
десятичных знаков можно складывать или вычитать так же, как мы складываем или вычитаем целые числа.
шагов для сложения или вычитания десятичных знаков:
Преобразует десятичные дроби в десятичные. (Десятичные дроби с одинаковым количеством цифр после запятой похожи на десятичные дроби).
Запишите десятичные дроби друг под другом в соответствии с местами цифр.
Добавляйте или вычитайте, начиная с крайней правой цифры и двигаясь к крайней левой цифре.
Поставьте десятичную точку под десятичной точкой в ответе.
Пример : прибавить 23,45; 13,101 и 345,5
1. Преобразовать в аналогичные десятичные числа : Наивысший десятичный разряд равен 3, поэтому мы добавляем нули в другие числа и получаем в них 3 десятичных разряда.
13.101
23,45 = 23,450
345,5 = 345,500
2. Выровняйте десятичные знаки :
3. Добавить :
4. Место десятичной дроби в ответе :
Пример : У Кайли было 25 м ленты. Для украшения юбки она использует 8 м и 13 см. Сколько ленты осталось у Кайли?
Решение :
Длина ленты у Кайли = 25 м = 25,00
Длина ленты Кайли = 8 м 13 см = 8,13
Оставшаяся длина ленты = 25,00 — 8,13
= 16.87
Интересные факты
|
Как складывать и вычитать дроби: 3 простых шага
На первый взгляд сложение и вычитание дробей может показаться устрашающим. Вы не только работаете с дробями, которые, как известно, сбивают с толку, но и внезапно сталкиваетесь с преобразованием числителей и знаменателей.
Но сложение и вычитание дробей — полезный навык. Как только вы выучите словарный запас и основы, вы с легкостью сможете складывать и вычитать дроби. Это руководство проведет вас через все, что вам нужно знать для сложения и вычитания дробей , включая некоторые примеры задач для проверки ваших навыков.
Ключевые слова для сложения и вычитания дробей
Прежде чем мы перейдем к математике сложения и вычитания дробей, вам необходимо знать терминологию. Мы будем использовать эти термины на протяжении всего периода , поэтому освежите их, чтобы быть уверенным, что вы всегда знаете, какую часть дроби мы имеем в виду.
Дробь : число, не являющееся целым числом; часть целого. Для наших целей дробь будет относиться к числу, записанному с числителем и знаменателем , например, 1/5 $ или 147/4 $.
Числитель : верхнее число в дроби, отражающее количество частей целого, например 1 в 1/5 $.
Знаменатель : нижнее число в дроби, представляющее общее количество частей, например 5 в 1/5 $.
Общий знаменатель : Когда две дроби имеют один и тот же знаменатель, например, $ 1/3 $ и $ 2/3 $.
Наименьший общий знаменатель : Наименьший знаменатель, который могут иметь две дроби. Например, наименьший общий знаменатель для $ 1/2 $ и $ 1/5 $ равен 10, потому что наименьшее число, в которое входят 2 и 5, равно 10.
Из пирогов получаются большие фракции.
Как складывать и вычитать дроби?
Теперь, когда у вас есть словарный запас, пора применить его на практике. Вы не можете просто складывать или вычитать дроби, как, например, целое число $ 1 / 4–1 / 2 $ не равно $ 0/2 $.
Вместо вам нужно будет найти общий знаменатель, прежде чем прибавлять или вычитать . Есть много способов найти общий знаменатель, некоторые из которых проще или эффективнее других.
Один из самых простых способов найти общий знаменатель, хотя и не обязательно лучший, — это просто перемножить два знаменателя вместе.
Например, возможный наименьший общий знаменатель для 1/2 $ и 1/12 $ будет равен 24, что вы найдете, умножив знаменатель 2 на знаменатель 12. Вы можете решить проблему, используя общий знаменатель 24, используя следующие шаги, но если вы это сделаете, вы столкнетесь с проблемой — вашу дробь нужно будет уменьшить.
Чтобы избавиться от необходимости уменьшать после сложения или вычитания, попробуйте найти наименьший общий знаменатель. Иногда это будет то же самое, что умножить два знаменателя вместе, но часто это не так.
Однако найти наименьший общий знаменатель нетрудно — , вам просто нужно будет ознакомиться с таблицей умножения . Например, давайте попробуем найти наименьший общий знаменатель, а не просто общий знаменатель для тех же дробей, которые мы использовали выше:
$$ 1/2 \: \ и \: 1/12 $$.
Для этого перечислите несколько значений, кратных каждому знаменателю
Кратное 2 : 2, 4, 6, 8, 10, 12 , 14, 16, 18, 20, 22, 24
Кратное 12 : 12 , 24, 36, 48, 60
Затем просмотрите оба списка кратных и найдите наименьшее число, которое у них обоих.В этом случае и 2, и 12 делят кратное 12. Если мы продолжим, мы получим другие кратные, которые они разделяют, например 24, но 12 является наименьшим, что означает, что это наименьшее общее кратное .
Вы можете сделать это с любой парой чисел, хотя большие числа могут представлять большую проблему. Для сложения или вычитания вы всегда можете вернуться к простому умножению одного знаменателя на другой, если у вас возникнут проблемы с нахождением наименьшего общего знаменателя , но имейте в виду, что вам, вероятно, придется уменьшить.
Дроби — самая вкусная часть математики.
Как сложить дроби — метод 1
Теперь, когда вы знаете, как найти общий знаменатель, вы готовы приступить к сложению и вычитанию.
Вернемся к примеру с 1/2 $ и 1/12 $ — в данном случае давайте рассмотрим эту задачу:
$$ 1/2 + 1/12 $$
Помните, что нельзя складывать прямо поперек; $ 1/2 + 1/12 $ не равно $ 2/14 $.
# 1: Найдите общий знаменатель
Сначала мы найдем наименьший общий знаменатель, так как это, как правило, лучший способ решить эту проблему.
Мы уже выполнили описанную выше работу, но напомним, что вы захотите записать серию кратных каждому числу, пока не найдете совпадение . В этом случае и 2, и 12 кратны 12.
# 2: Умножьте, чтобы получить каждый числитель по одному знаменателю
Всегда помните, что все, что вы делаете со знаменателем, должно происходить и с числителем. Итак, давайте посмотрим на эти две дроби, которые нам нужно преодолеть знаменатель 12.
$ 1/12 $ — это просто — оно уже превышает знаменатель 12, поэтому нам не нужно ничего с этим делать.
$ 1/2 $ потребует доработки. Какое число, умноженное на 2, будет равно 12?
Перефразируя этот вопрос как проблему, которую мы можем решить, $ 2 *? = 12 $. Или, что еще проще, , мы можем инвертировать операцию , чтобы получить $ 12/2 =? $, Что мы можем легко решить.
Итак, теперь мы знаем, что для перехода от знаменателя 2 к знаменателю 12 нам нужно умножить на 6. Опять же, помните, что все, что вы делаете со знаменателем, нужно делать и с числителем, поэтому умножьте верхнюю и снизу на 6, чтобы получить $ 6/12 $.
# 3: Добавьте числители, но оставьте знаменатели в покое
Теперь, когда у вас те же знаменатели, вы можете складывать числители прямо поперек.
В данном случае это будет означать, что $ 6/12 + 1/12 = 7/12 $. Спросите себя, можно ли уменьшить дробь, разделив числитель и знаменатель на одно и то же число. В этом случае вы не можете, поэтому ваш ответ — 7 долларов / 12 долларов.
Как сложить дроби — метод 2
В качестве альтернативы мы могли бы просто перемножить два знаменателя, чтобы найти другой общий знаменатель. Это другой способ решения проблемы, но ответ будет таким же.
# 1: Умножаем знаменатели вместе
Никаких хитростей — просто умножьте 2 на 12, чтобы получить 24. Это будет ваш общий знаменатель.
# 2: Умножьте, чтобы получить каждый числитель по одному знаменателю
Так же, как мы это сделали, когда нашли наименьший общий знаменатель, нам нужно будет умножить верхнее и нижнее число каждой дроби. В этом случае используйте обратные операции, чтобы узнать, какое число вам нужно умножить.
Если $ 1/2 $ должно быть $? / 24 $, вы можете сделать $ 24 ÷ 2 $, чтобы вычислить, какое число вам нужно умножить на -12. Умножьте верхнюю и нижнюю на 12, чтобы получить 12/24 доллара.
Повторите процесс с $ 1/12 $. Если $ 1/12 $ должно быть $? / 24 $, решите $ 24 ÷ 12 $, чтобы получить 2. Теперь умножьте числитель и знаменатель $ 1/12 $ на 2, чтобы получить $ 2/24 $.
# 3: сложите числители вместе
Теперь вы можете просто добавлять прямо поперек.$$ 12/24 + 2/24 = 14/24 $$.
# 4: Уменьшить
Вот здесь-то и появляется дополнительный шаг. 14/24 доллара — это не дробь в самом низком виде, поэтому нам нужно ее уменьшить. Чтобы уменьшить, нам нужно разделить числитель и знаменатель на одно и то же число.
Для этого нам нужно найти наибольший общий множитель. Во многом аналогично поиску наименьшего общего кратного, это означает перечисление чисел до тех пор, пока мы не найдем два общих множителя, которые являются общими для числителя и знаменателя, за исключением 1, например:
14 : 2 , 7
24 : 2 , 3, 4, 6, 8, 12
Какое у них общее число? 2.Это означает, что 2 — наш наибольший общий делитель, и, следовательно, число, на которое мы будем делить числитель и знаменатель.
$ 14 ÷ 2 = 7 $ и 24 ÷ 2 = 12 $, что дает нам ответ 7/12 $.
Ответ такой же, как и в случае, когда мы решили использовать наименьшее общее кратное, и не может быть сокращен дальше, так что это наш окончательный ответ!
Если вы когда-нибудь обнаружите, что записываете множество факторов без особой удачи, есть несколько быстрых способов выяснить потенциальные факторы.
- Если число четное, его можно разделить на 2.
- Если вы можете сложить цифры числа, число, которое делится на 3, число делится на 3, например 96 (9 + 6 = 15 $ и 1 + 5 = 6 $, что делится на 3).
- Если число заканчивается на 5 или 0, оно делится на 5.
- Если вы не уверены, когда прекращать поиск факторов, вычтите меньшее число из большего. Это число будет наибольшим возможным общим делителем , но не самим наибольшим общим множителем.
Например, возьмем 50 и 32.Конечно, мы могли бы просто разделить оба значения на 2 и продолжать уменьшать оттуда, но если вы сделаете 50-32 доллара, вы получите 18, что говорит нам прекратить искать наибольший общий фактор, когда мы достигнем 18.
На практике это выглядит так. это:
50 : 2 , 5, 10
32 : 2 , 4, 8, 16
Вместо продолжения мы знаем, что нужно остановиться, когда следующий множитель будет 18 или выше, не позволяя нам тратить больше времени на выяснение факторов, которые нам не нужны. Мы можем намного быстрее увидеть, что наибольший общий множитель равен 2, и приступить к решению проблемы!
$ 1/1 — 1 /? = ням $
Как вычесть дроби
Как только вы научитесь складывать дроби, вычитание дробей станет проще простого! Процесс точно такой же, хотя вы, естественно, будете вычитать, а не складывать.
# 1: Найдите общий знаменатель
Давайте посмотрим на следующий пример:
$$ 2 / 3-3 / 10 $$
Нам нужно найти наименьшее общее кратное для знаменателей, которое будет выглядеть так:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
10 : 10, 20, 30
Первое общее число — 30, поэтому мы поставим оба числителя над знаменателем 30.
# 2: Умножьте, чтобы получить оба числителя над одним знаменателем
Во-первых, нам нужно выяснить, на сколько нам нужно умножить числитель и знаменатель каждой дроби, чтобы получить знаменатель 30. Для 2/3 доллара какое число, умноженное на 3, равно 30? В форме уравнения:
$$ 30 ÷ 3 =? $$
Наш ответ — 10, поэтому мы умножим числитель и знаменатель на 10, чтобы получить 20/30 долларов.
Затем мы повторим процесс для второй дроби.Какое число нам нужно умножить на 10, чтобы получить 30? Итак, $ 30 ÷ 10 = 3 $, поэтому мы умножим верхнюю и нижнюю часть на 3, чтобы получить $ 9/30 $.
Это делает нашу задачу $ 20 / 30-9 / 30 $, а это значит, что мы готовы продолжить!
# 3: Вычесть числители
Так же, как мы это делали со сложением, мы вычтем один числитель из другого, но знаменатели оставим в покое.
$$ 20 / 30-9 / 30 = 11/30 $$.
Поскольку мы нашли наименьшее общее кратное, мы уже знаем, что проблему нельзя решить дальше.
Однако, допустим, мы просто умножили 3 на 10, чтобы получить знаменатель 30, поэтому нам нужно проверить, можем ли мы уменьшить. Давайте воспользуемся этим маленьким приемом, который мы изучили, чтобы найти наибольший возможный общий множитель . Независимо от того, какие делят множители 11 и 30, они не могут быть больше, чем $ 30-11, или 19.
11 : 11
30 : 2, 3, 5, 6, 10, 15
Поскольку у них нет общих факторов, ответ не может быть сокращен дальше.
$ 1/10 $ пицца все равно 10 $ / 10 $ вкусная.
Примеры сложения и вычитания дробей
Давайте рассмотрим еще несколько примеров задач!
$$ 8 / 15-4 / 9 $$
# 1: Найдите общий знаменатель
15 : 15, 30, 45 , 60
9 : 9, 18, 27, 26, 45
# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем
$$ 45/15 = \ bo3 $$
$$ 8 ÷ 3 = 24 $$
$$ 15 * 3 = 45 $$
$$ 24/45 $$
$$ 45 ÷ 9 = \ bo5 $$
$$ 4 * 5 = 20 $$
$$ 9 * 5 = 45 $$
$$ 20/45 $$
# 3: вычесть числители
$$ 24 / 45-20 / 45 = \ bo4 / \ bo45 $$
$$ 6/11 + 3/4 $$
# 1: Найдите общий знаменатель
11 : 11, 22, 33, 44
4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44
# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем
$$ 44 ÷ 11 = \ bo4 $$
$$ 6 * 4 = 24 $$
$$ 11 * 4 = 44 $$
$$ 24/44 $$
$$ 44 ÷ 4 = \ bo11 $$
$$ 3 * 11 = 33 $$
$$ 4 * 11 = 44 $$
$$ 33/44 $$
# 3: сложить числители
$$ 24/44 + 33/44 = \ bo57 / \ bo44 $$ или $$ \ bo1 \ bo13 / \ bo44 $$
$$ 4 / 7-11 / 21 $$
# 1: Найдите общий знаменатель
7 : 7, 14, 21
21 : 21 , 42, 63
# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем
$$ 21 ÷ 7 = \ bo3 $$
$$ 3 * 4 = 12 $$
$$ 3 * 7 = 21 $$
$$ 12/21 $$
$ 11/2 $ уже старше 21, поэтому нам не нужно ничего делать.
# 3: вычесть числители
$$ 12 / 21-11 / 21 = \ bo1 / 21 $$
$$ 8/9 + 7/13 $$
# 1: Найдите общий знаменатель
9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117
13 : 13, 26, 39, 52, 65, 78, 91, 104, 117
# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем
$$ 117 ÷ 9 = \ bo13 $$
$$ 8 * 13 = 104 $$
$$ 9 * 13 = 117 $$
$$ 104/117 $$
$$ 117 ÷ 13 = \ bo9 $$
$$ 7 * 9 = 63 $$
$$ 13 * 9 = 117 $$
$$ 63/117 $$
# 3: сложить числители
$$ 104/117 + 63/117 = \ bo167 / \ bo117 $$
Что дальше?
Сложение и вычитание дробей станет еще проще, если вы начнете преобразовывать десятичные дроби в дроби!
Если вы не уверены, какие уроки математики в старшей школе вам следует посещать, это руководство поможет вам составить расписание, чтобы быть уверенным, что вы готовы к поступлению в колледж!
Теперь, когда вы являетесь экспертом в сложении и вычитании дробей, испытайте себя, научившись переводить градусы Цельсия в градусы Фаренгейта!
чисел — сложение и вычитание целых чисел
ср может использовать числовую линию в качестве модели, чтобы помочь нам визуализировать сложение и вычитание целых чисел со знаком.Просто думайте о сложении и вычитании как о указаниях на числовая строка. Есть также несколько правил и свойств, которые определяют, как для выполнения этих основных операций.
Чтобы добавить целые числа с тем же знаком, сохраните тот же знак и добавьте абсолютное значение каждого номер.
Чтобы добавить целые числа с разными знаками держите знак числа с наибольшим абсолютным значение и вычтите наименьшее абсолютное значение из наибольшего.
Вычесть целое число, добавив его противоположность.
Осторожно! В отрицательное отрицательное число — противоположное положительное число. То есть по-настоящему числа,
— (- а) = +
Вот как сложить два положительных целых числа:
4 + 7 =?
Если начать при положительном числе четыре на числовой прямой и перемещении на семь единиц вправо, вы в конечном итоге положительный одиннадцать.Кроме того, эти целые числа имеют одинаковый знак, поэтому вы можно просто оставить знак и сложить их абсолютные значения, чтобы получить тот же ответ, положительный одиннадцать.
Вот как сложите два отрицательных целых числа:
-4 + (-8) =?
Если начать при отрицательном значении четырех на числовой прямой и перемещении восьми единиц влево, вы в конечном итоге на двенадцать. Кроме того, эти целые числа имеют одинаковый знак, поэтому вы можно просто оставить отрицательный знак и сложить их абсолютные значения, чтобы получить тот же ответ, двенадцать отрицательных.
Вот как добавить положительное целое число к отрицательному:
-3 + 6 =?
Если начать при отрицательных трех на прямой числовой строке и переместите шесть единиц вправо, в итоге вы получите три положительных числа. Кроме того, эти числа имеют разные знаки,
так что держите знак из целого числа, имеющего наибольшее абсолютное значение, и вычесть наименьшее абсолютное значение из наибольшего.
Вычесть три от шести и сохраните положительный знак, снова дав положительную тройку.
Вот как добавить отрицательное целое число к положительному целому:
5 + (-8) =?
Если начать при положительном пятерке на прямой числовой строке и переместите восемь единиц влево, в итоге вы получите минус три. Кроме того, эти целые числа имеют разные знаки, поэтому сохраните знак целого числа, имеющего наибольшее абсолютное значение, и вычтите наименьшее абсолютное значение из наибольшего или вычтите пять из восьми и снова оставьте отрицательный знак давая отрицательные три.
Вычесть число, добавьте его противоположность:
5-8 =?
Потому что они дают тот же результат, вы можете видеть, что вычитание восьми из пяти эквивалентно к добавлению отрицательных восьми к положительным пяти. Ответ — 3.
Вычесть число, добавьте его противоположность:
-3 — (-6) =?
Потому что они дают тот же результат, вы можете увидеть, что вычитая отрицательные шесть из отрицательных три эквивалентно добавлению положительных шести к отрицательным трем.Ответ 3.
назад наверх
Чем сложение похоже на вычитание?
Большое спасибо классу Деб Фрейзер (@ Frazier1st) в Огайо за номинирование на сегодняшнее чудо!
Когда вы впервые изучаете основную математику, это может показаться таким же простым, как 1 + 1 = 2. Легко, правда? Конечно, становится сложнее, но вскоре вы запомните все эти базовые факты с помощью флеш-карточек.
Затем однажды ваш учитель меняет дело против вас.Внезапно вы сталкиваетесь с вычитанием. Вы больше не считаете две группы вещей, чтобы получить простую сумму. Вместо этого вы забираете вещи и пытаетесь вычислить, сколько осталось.
Детям часто кажется, что вычитание труднее. В конце концов, это совсем не то же самое, что сложение, верно? Не так быстро! На самом деле сложение и вычитание имеют особые отношения.
Как любят говорить математики, между сложением и вычитанием существует обратная зависимость.Итак, что означает обратное? Не вдаваясь в технические подробности, вы можете думать об обратном как о «противоположном».
Например, горячее — холодное, обратное. Точно так же обратное сложение — вычитание. И угадай что? Обратное вычитание — сложение! Почему? Сложение и вычитание — противоположности. По сути, они уничтожают друг друга.
Давайте посмотрим, как это работает. Если мы сложим 1 + 1, мы получим 2. Это сложение. Если затем мы уберем 1 из наших 2, мы отменим только что выполненное сложение и в итоге получим 1.Это вычитание.
Чтобы понять взаимосвязь между сложением и вычитанием на еще более глубоком уровне, нам нужно узнать еще о двух вещах: числовые факты и семейства фактов. Числовой факт — это простое уравнение, состоящее из трех разных чисел. Например, 1 + 2 = 3 — это числовой факт.
Для каждого набора из трех разных чисел вы можете создать два связанных факта числа сложения и два вычитания. Мы называем эти четыре числовых факта семьей фактов, поскольку они связаны между собой как члены семьи.
Если мы будем придерживаться 1, 2 и 3 в качестве наших трех чисел, мы можем создать следующее семейство фактов:
1 + 2 = 3
2 + 1 = 3
3–2 = 1
3 — 1 = 2
Если 1 + 2 = 3, то, очевидно, следует, что 2 + 1 = 3, поскольку вы просто меняете порядок двух складываемых чисел. Связанные факты числа вычитания также следуют, поскольку они противоположны двум фактам числа сложения.
Если вам нужно визуализировать это, просто представьте факт сложения числа в обратном порядке, поменяв местами знак равенства и знак плюс, а затем переключив знак плюс на знак минус.1 + 2 = 3 становится 3-2 = 1!
Думая об этом так, вы сможете лучше понять вычитание. Всегда сложно освоить новый навык, но когда вы можете связать его с чем-то, что уже знаете, становится проще!
Стандарты: CCSS.



 момент 2 мин.
момент 2 мин.