Решение логических задач
Основные приемы и методы решения логических задач
Рассмотрим разные способы решения логических задач.
Каждый из приемов имеет свою область применения.
Логические (или нечисловые задачи) относятся к нестандартным задачам. К ним относят текстовые задачи, в которых необходимо распознать объекты или расположить их в определенном порядке. При этом часть утверждений в условии задачи может быть истинной или ложной. К логическим задачам относят также задачи на переливания и взвешивания (фальшивые монеты и т.п.).
Можно выделить несколько различных способов решения логических задач, которые можно назвать следующим образом:
метод рассуждений;
метод таблиц;
метод графов;
метод блок-схем;
метод бильярда;
метод кругов Эйлера.
Метод рассуждений
Метод рассуждений является самым примитивным способом и его обычно применяют для решения самых простых логических задач. Идея метода заключается в проведении рассуждений при последовательном использовании всех условий задачи, вследствие чего приходят к выводу, который является ответом задачи.
Пример 1
Владимир, Семен и Олег изучают разные иностранные языки: английский, французский и немецкий. На вопрос, какой язык изучает каждый из них, один ответил: «Владимир изучает английский, Семен не изучает английский, а Олег не изучает немецкий». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из студентов?
Решение:
Имеем три утверждения. Если принять за истину первое утверждение, то правдиво и второе, т.к. студенты изучают разные языки, что противоречит условию задачи. Таким образом первое утверждение ложно.
Если правдивым является второе утверждение, то первое и третье должны быть ложными. В таком случае получаем, что никто не изучает английский. Это противоречит условию, таким образом, второе утверждение также является ложным.
Остается третье утверждение, которое можем считать верным, а первое и второе — ложными. Таким образом, Владимир не изучает английский, его изучает Семен.
Ответ: Семен изучает английский язык, Олег — французский, Владимир — немецкий.
Метод таблиц
Основным приемом для решения текстовых логических задач является метод таблиц. С помощью таблиц можно наглядно представить условие задачи или ее ответ, кроме того их использование значительно помогают в принятии правильных логических решений.
Пример 2
У трех кукол Маши, Даши и Алены были платья трех разных цветов: красного, зеленого и синего. Туфли у них были таких же цветов. У Маши цвет платья и туфель совпадали. У Алены ни туфли, ни платье не были красными. Даша была в зеленых туфлях и в платье другого цвета. Как были одеты куклы?
Решение:
Составим таблицу, в которой отметим возможные цвета платьев и туфель кукол. По условию задачи заполним таблицу:
туфли Даши зеленые, а платье не зеленое. Следовательно, у Маши и Алены туфли уже не могут быть зелеными, так же как не могут быть туфли Даши синими или красными. Отмечаем все в таблице:
туфли и платье Алены не являются красными. Из таблицы видим, что красные туфли могут быть только у Маши, а, следовательно, туфли Алены — синие. Правая часть таблицы заполнена.
Рисунок 1.
- Цвет платья Маши совпадает с цветом ее туфель, значит оно красное. Теперь легко увидеть, что у Алены — зеленое платье, а у Даши — синее.
Рисунок 2.
Таблица полностью заполнена и в ней однозначно установлены цвета туфель и платьев кукол.
Ответ: Маша одета в красное платье и красные туфли, Даша в синем платье и зеленых туфлях, Алена в зеленом платье и синих туфлях.
Метод блок-схем
Этим методом решаются задачи, в которых с помощью сосудов требуется отмерить необходимое количество жидкости или связанные со взвешиванием на чашечных весах. Простейшим приемом решения таких задач является перебор всех возможных вариантов, который не является удобным и не дает возможности выделения общего подхода к решению подобных задач.
Суть метода блок-схем состоит в следующем:
выделяют операции для точного отмеривания жидкости, которые называются командами;
устанавливают последовательность выполнения команд, которая оформляется в виде блок-схемы (как в программировании). Составленная блок-схема является программой, выполнение которой должно привести к решению задачи, в ходе которой достаточно отмечать получаемые количества жидкости.
При выполнении программы удобно заполнять отдельную таблицу, в которую заносится количество жидкости в каждом из имеющихся сосудов.
Метод математического бильярда
Игра в бильярд стала предметом серьезных научных исследований в области механики и математики. Если представить горизонтальный бильярдный стол произвольной формы без луз, по которому без трения будет двигаться точечный шар, абсолютно упруго отражаясь от бортов стола, то возникал вопрос: какой может быть траектория этого шарика. В поисках ответа на этот вопрос появилась теория математического бильярда (теория траекторий).
С помощью данного метода можно очень легко решать задачи на переливание жидкостей.
Пример 3
Дано два сосуда — объемом $3$ л и $5$ л. С помощью этих сосудов необходимо получить $1$, $2$, $3$, $4$, $5$, $6$, $7$ и $8$ литров воды. Имеется водопроводный кран и раковина, в которую можно выливать воду.
Решение:
Построим для данной задачи параллелограмм со сторонами $3$ и $5$ единиц. По горизонтали будет откладываться количество воды в литрах в пятилитровом сосуде, а по вертикали — в трехлитровом. На всем параллелограмме нанесем сетку из одинаковых равносторонних треугольников:
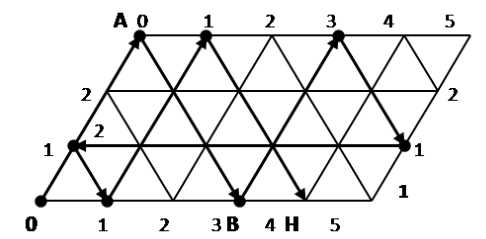
Рисунок 3.
Бильярдный шар может перемещаться только вдоль прямых, которые образуют сетку на параллелограмме. При ударе о сторону параллелограмма шар отражается и движется вдоль борта. При этом каждая точка соударения о сторону параллелограмма полностью характеризует, сколько воды находится в каждом из сосудов.
spravochnick.ru
Методы решения логических задач
Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.
Формальный способ решения логических задач
Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций.
Составить единое логическое выражение для всех требований задачи.
Используя законы алгебры логики, попытаться либо упростить полученное выражение и вычислить все его значения, либо построить таблицу истинности для рассматриваемого выражения, либо доказать истинность (ложность) некоторых утверждений методом рассуждений.
Выбрать решение — набор значений простых высказываний, при котором построенное логическое выражение является истинным.
Проверить, удовлетворяет ли полученное решение условию задачи.
Рассмотрим, как можно использовать эти способы для решения задач.
Решение логических задач средствами алгебры логики
Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Решение. Введём обозначения:
Р1 – первый учащийся изучал логику;
Р2 – второй учащийся изучал логику;
Р3 – третий учащийся изучал логику.
Из условия задачи следует истинность высказывания . Воспользуемся соотношением (20) и упростим исходное высказывание:
.
Высказывание 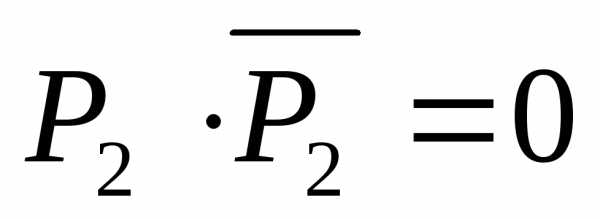 (согласно
(11)), а, следовательно, ложно и высказывание
(согласно
(11)), а, следовательно, ложно и высказывание 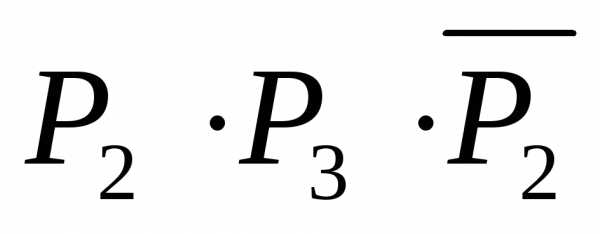 .
Поэтому должно быть истинным высказывание
.
Поэтому должно быть истинным высказывание 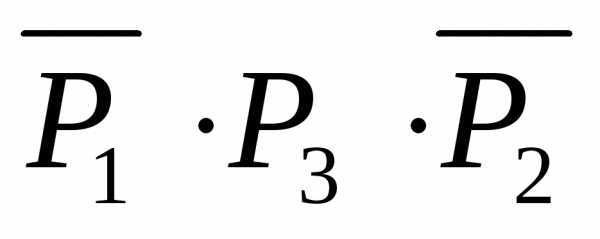 .
.
Ответ. Логику изучал третий учащийся, а первый и второй не изучали.
Задача «Прогноз». Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение. Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Джон: 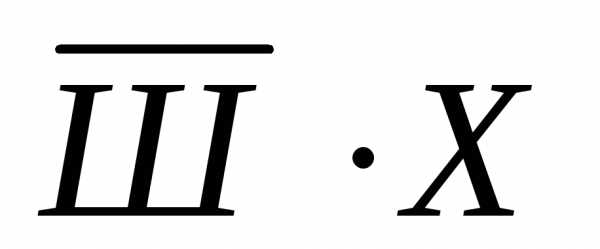 ,Ник:
,Ник: 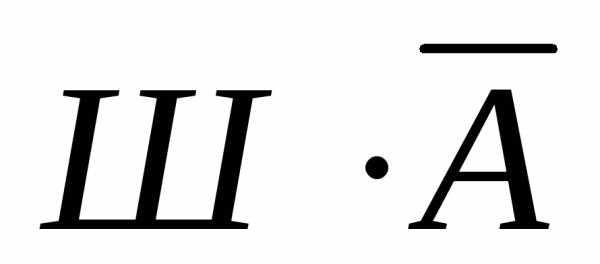 ,
Питер:
,
Питер: 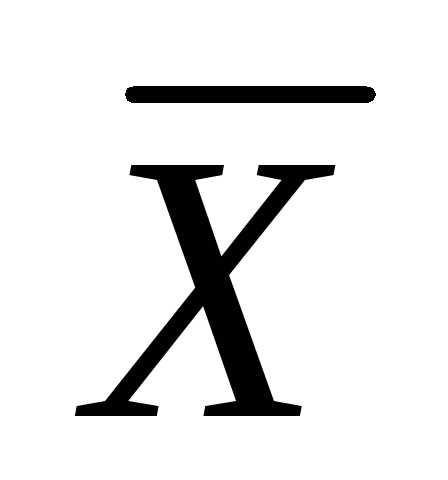 .
.
Учитывая то, что предположения лишь двух друзей подтвердились, а предположения третьего неверны, запишем все возможные комбинации истинности двух из трёх высказываний. Тогда истинное высказывание будет иметь вид:
=1.
Упростим это выражение. Используя (11), установим, что первые два слагаемые тождественно-ложные. Тогда, с учётом формул де Моргана для третьего слагаемого:
Произведение будет истинным только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
studfiles.net
Решение логических задач с помощью таблиц
Разделы: Математика
Класс:
#}В книге “Занимательная логика” Э.Кольмана и О.Зиха имеется много интересных логических задач. Вот одна из них.
1. В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. “Замечательно, что один из нас имеет белые, один черные и один рыжие волосы, но ни у одного из нас нет волос того цвета, на который указывает его фамилия”, - заметил черноволосый. “Ты прав”, — сказал Белов. Какой цвет волос у художника?
Решение. Для решения подобных логических задач полезно составить таблицу.
| Белов | Чернов | Рыжов | |
| блондин | |||
| брюнет | |||
| рыжий |
Ответ.
| Белов | Чернов | Рыжов | |
| блондин | — | + | — |
| брюнет | — | — | + |
| рыжий | + | — | — |
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан стоит около банки и сосуда с молоком.
Куда налита каждая жидкость?
Ответ.
| бутылка | стакан | кувшин | банка | |
| Молоко | — | — | + | — |
| Лимонад | + | — | — | — |
| Квас | — | — | — | + |
| вода | — | + | — | — |
3. В течение последних четырех лет Алексеев, Фомин, Дементьев и Иванов получали очередной отпуск в мае, июне, июле или в августе. Причем, если один из них отдыхал в мае, то другой — в июне, третий – в июле, а четвертый – в августе. Каждый их них получал отпуск в эти четыре года в разные месяцы. Так в первый год Дементьев отдыхал в июле, во второй год – в августе. Алексеев во второй год отдыхал в мае, Иванов в третий год – в июне, а Фомин в четвертый год – в июле.
Кто в каком месяце отдыхал в каждом из этих четырех лет?
Ответ.
| 1 –й год | 2 –й год | 3 –й год | 4 –й год | |
| Алексеев | июнь | май | июль | август |
| Фомин | май | июнь | август | июль |
| Дементьев | июль | август | май | июнь |
| Иванов | август | июль | июнь | май |
Три подруги вышли в белом, зеленом и синем платьях. Их туфли тоже были белого, зеленого и синего цветов. Известно, что только у Ани цвет платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми, Наташа была в зеленых туфлях.
Определить цвет платья и туфель каждой из подруг.
Решение: можно решать, составляя две таблицы, а можно таблицы объединить в одно целое.
| Аня | Валя | Наташа | Аня | Валя | Наташа | |||
| Белые туфли | + | — | — | Белое платье | + | — | — | |
| Зеленые туфли | — | — | + | Зеленое платье | — | + | — | |
| Синие туфли | — | + | — | Синее платье | — | — | + |
| белое платье | зеленое платье | синее платье | белые туфли | зеленые туфли | синее платье | |
| Аня | ||||||
| Валя | ||||||
| Наташа | ||||||
| белые туфли | ||||||
| зеленые туфли | ||||||
| синие туфли | ||||||
5. Три друга – спортсмена — Алеша, Вася и Сережа – учились в одном классе. Каждый из них увлекался двумя видами спорта из следующих шести: футбол, волейбол, баскетбол, теннис, плавание и велоспорт. Известно, что:
- все трое – Сережа, теннисист и пловец ходят из школы домой вместе,
- пловец и футболист – соседи по дому,
- Алеша самый старший из троих, а теннисист старше велосипедиста,
- Наиболее интересные спортивные передачи по телевизору все трое – Алеша, велосипедист и волейболист – смотрят вместе.
Надо узнать, кто каким спортом увлекается.
Ответ.
- Алеша – баскетбол и плавание,
- Вася – волейбол и теннис,
- Сережа – футбол и велоспорт.
6. На школьном вечере четыре юноши: Валентин, Николай, Владимир и Алексей все из разных классов, и их одноклассницы танцевали танец, но каждый юноша танцевал не своей одноклассницей.
Лена танцевала с Валентином, Аня – с одноклассником Наташи, Николай — с одноклассницей Владимира, а Владимир танцевал с Олей.
Ответ.
Танцевали Лена с Валентином, Оля с Владимиром, Аня с Николаем, Наташа с Алексеем.
Учатся в одних классах Аня и Владимир, Оля и Валентин, Лена и Алексей, Наташа и Николай.
Кто с кем танцевал?
А вот эту задачу придумали дети после очередного занятия математического кружка в 6 классе.
7. В одном поселке живут три товарища: Саша, Коля и Петя, которые осваивают новую профессию. Один из них готовится стать дизайнером, другой - садоводом, третий — парикмахером. Кроме того, все они имеют и другую профессию: один строитель, другой – руководитель драмкружка, а третий ведет дискотеки. В разное время они сказали разные фразы:
- Петя, ты меня не жди, я должен доделать прическу,
- Эх, Коля, вести дискотеку – сложно, но мне очень нравится,
- Завтра, Коля, ко мне не приходи, я буду на конкурсе парикмахеров,
- На днях я получу новый диск “ Комнатные растения”.Для меня, как для будущего садовода, он будет интересным и полезным.
- Наблюдал я вчера за тобой во время репетиции и подумал, что тебе поставить пьесу не легче, чем мне вывести новый сорт роз.
- С применением новых технологий в строительстве я совершенно не знаком, хотя как дизайнеру надо сними познакомиться.
Попробуйте по этим фразам установить, кто из друзей осваивает какую профессию и какую профессию они уже имеют?
Ответ.
- Саша – парикмахер и строитель,
- Коля – дизайнер и руководитель драмкружка,
- Петя — садовод и ведущий дискотек.
8. Сокровиша.
Три пирата: Нытик, Стрелец и Барс зарыли свои сокровища на одном острове. Один из них зарыл возле дерева лимона, другой – банана, а третий – абрикоса. Ёмкость для хранения тоже у каждого была своя: один использовал сундучок, второй – большую морскую ракушку, а третий – кожаный мешочек.
Определите имя пирата, а также где и чем хранил свои сокровища каждый из них, если известно, что:
- Ракушку использовал не Нытик.
- Тот, кто закопал сокровища под абрикосом, использовал мешочек.
- Барс закопал сундучок, но не под лимоном.
| банан | абрикос | лимон | сундучок | ракушка | мешочек | |
| Нытик | ||||||
| Стрелец | ||||||
| Барс | ||||||
| сундучок | ||||||
| ракушка | ||||||
| мешочек | ||||||
Ответ.
| имя | дерево | тара |
| Нытик | абрикос | мешочек |
| Стрелец | лимон | ракушка |
| Барс | банан | сундучок |
9. После традиционного вечера встречи с бывшими выпускниками школы в стенгазете появилась заметка о трех бывших учениках школы. В этой заметке было написано, что Иван, Борис и Андрей стали учителями. Теперь они преподают разные дисциплины: один – математику, второй – физику, третий – химию. Живут они тоже в разных городах: Минске, Витебске и Харькове. В заметке было еще написано, что первоначальные их планы осуществились не полностью: Иван работает не в Минске, Андрей – не в Витебске; житель Минска преподает не математику, Андрей преподает не физику. Повезло только жителю Витебска: он преподает любимую им химию. Кто есть кто?
Ответ.
- Иван – химик — Витебск
- Борис — физик — Минск
- Андрей — математик – Харьков
10. Арташ, Отар, Гурам и Сурен занимаются в разных спортивных секциях. Один из них играет в баскетбол, другой – в волейбол, третий – в футбол, четвертый – в теннис. У них различные увлечения: один из них любит кино, другой – театр, третий – эстраду, а четвертый – цирк. Арташ не играет ни в волейбол, ни в баскетбол. Отар играет в футбол и любит театр. Сурен не играет в волейбол. Тот из ребят, кто играет в волейбол, любит ходить в кино, а тот, кто играет в баскетбол, не любит цирк. Какое у каждого из них увлечение, и каким видом спорта занимается каждый?
Ответ.
- Арташ – теннис – цирк, Отар – футбол – театр,
- Гурам – волейбол – кино, Сурен – баскетбол – эстрада.
11. Первоклашки.
Год назад с нашего двора первый раз в первый класс пошли 5 мальчиков. Их имена: Петя, Коля, Ваня, Гена и Миша. Получилось так, что все пятеро попали в разные классы: один в класс “А”, другой – в “Б”, третий – в “В”, четвертый — в “Г”, пятый – в “Д”. Каждому из ребят досталась в качестве классного руководителя добрая учительница: Лидия Михайловна, Елена Анатольевна. Екатерина Кирилловна. Татьяна Григорьевна и Виктория Николаевна. Дети учились прекрасно, напротив их фамилий ( Анисин, Белов, Кукушкин, Степанов и Харитонов) всегда были практически одни пятерки.
Определите имя, фамилию, класс и добрую учительницу для каждого из первоклашек, если известно, что
- Ваня учится у Татьяны Григорьевны и его фамилия не Степанов.
- В классе “Д” преподает не Екатерина Кирилловна.
- Коля учится в классе “Б”. Он старше на 1месяц, чем Белов, и младше на 12 дней, чем тот, кто учится у Татьяны Григорьевны.
- Елена Анатольевна преподает в классе “Г” и у нее нет ученика по фамилии Белов.
- Харитонов Гена дружит с Петей и с тем, кто ходит в класс “А”.
- Кукушкин учится в классе “А”. Его учительница не Лидия Михайловна и не Екатерина Кирилловна.
- Анисин учится в классе “В” и его имя не Петя и не Миша.
| Имя | Учительница |
Класс | ||||||||||||||
| Петя | Коля | Ваня | Гена | Миша | Лидия Михайловна | Елена Анатольевна | Екатерина Кирилловна | Татьяна Григорьевна | Виктория Николаевна | А | Б | В | Г | Д | ||
| Фамилия | Анисин | |||||||||||||||
| Белов | ||||||||||||||||
| Кукушкин | ||||||||||||||||
| Степанов | ||||||||||||||||
| Харитонов | ||||||||||||||||
| Класс | А | |||||||||||||||
| Б | ||||||||||||||||
| В | ||||||||||||||||
| Г | ||||||||||||||||
| Д | ||||||||||||||||
| Учительница | Лидия Михайловна | |||||||||||||||
| Елена Анатольевна | ||||||||||||||||
| Екатерина Кирилловна | ||||||||||||||||
| Татьяна Григорьевна | ||||||||||||||||
| Виктория Николаевна | ||||||||||||||||
Ответ.
| фамилия | имя | учительница | класс |
| Анисин | Ваня | Татьяна Григорьевна | В |
| Белов | Петя | Лидия Михайловна | Д |
| Кукушкин | Миша | Виктория Николаевна | А |
| Степанов | Коля | Елена Анатольевна | Б |
| Харитонов | Гена | Елена Анатольевна | Г |
На математическую олимпиаду в город Киров поехало четыре девятиклассника: Лева, Коля, Миша и Петя. В первый день они решили позавтракать в разных местах: один пошел в кафе, другой – в столовую, третий – в закусочную, четвертый – в буфет. После завтрака они снова собрались вместе. Разговор, естественно, зашел о том, кто как позавтракал. Выяснилось, что все они пили разные напитки, так как в каждом из этих мест, где они завтракали, оказалось в наличии только по одному напитку: в одном месте – только кофе, в другом – только молоко, в третьем – только ряженка, в четвертом – только чай. В буфет
urok.1sept.ru
Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
|
wiki.iteach.ru
Решение логической задачи разными способами и сравнение их эффективности
Статья посвящена обзору различных способов решения логических задач и сравнению их эффективности. Логические задачи можно решать различными способами. У каждого из них есть свои достоинства и недостатки. Поэтому для решения подобного типа задач нужно найти такой способ, который имеет наименьшее количество недостатков, а следовательно, дает уверенность в правильности решения.
Ключевые слова: логика, логическая задача, алгебра логики, метод таблиц, метод рассуждений.
Abstract. This article is dedicated to various methods of solving logic exercises and comparing their effectiveness. Logic exercises can be solved by different methods. Each method has its own pros and cons. That’s why for solving logic exercises it’s necessary to find such method, that’s has she least number of cons.
Keywords: logic, logical exercise, the algebra of logic, method tables, method of reasoning.
На протяжении всех лет обучения в школе, начиная с начальных классов, мы решаем множество задач, в том числе и логических. Для успешного решения такого типа задач нужно: научиться выделять их общие признаки, выдвигать различные гипотезы, подмечать закономерности, строить цепочки рассуждений, проверять их на истинность, делать выводы. Существуют разные способы решения логических задач. К ним относят: применение законов алгебры логики, табличный способ, использование рассуждений [4, с. 223].
У каждого способа есть свои достоинства и недостатки. Поэтому для нахождения наиболее эффективного из них, в зависимости от задачных ситуаций, рассмотрим решение задач разными способами и проанализируем эти решения. Под эффективностью понимается большее количество преимуществ решения.
Традиционно к логическим задачам относят задачи на соответствия между множествами [5, с. 67].
Задача 1.Три девочки были в белом, красном и голубом платьях. Их туфли были тех же трёх цветов.
1. Только у Тамары цвет платья и туфель совпали.
2. Валя была в белых туфлях.
3. Ни платье, ни туфли Лиды не были красными.
Определите цвет платья и туфель каждой из девочек [3, с. 197].
Решение.
I способ. С помощью совмещенной таблицы.
Данная задача трехмерная, следовательно, нужно найти соответствия между множествами (имена и туфли, имена и платья, платья и туфли). Для этого используют 3 таблицы, которые затем совмещаются. Таблица заполняется из условий. Знак «+» ставится тогда, когда выясняется точное соответствие между элементами множеств, знак «-» ставится тогда, когда выясняется несоответствие. Если в какой-то строке малой таблицы получается два знака «-», то в третьей нужно поставить знак «+». Из условия 2 в таблице ставится знак «+» на пересечении графа «Валя» и «Белые туфли». Также из условия 2 получается, что Валя была в белых туфлях, а туфли Лиды не были красными, следовательно, Лида была в голубых туфлях, а Тамара в красных. У Тамары цвет туфель и платья совпали по условию 1, а у двух других девочек нет, следовательно, у Вали было голубое платье, а у Лиды белое.
Таблица 1
Таблица соответствия имен и одежды
|
|
Белые туфли |
Красные туфли |
Голубые туфли |
Белое платье |
Красное платье |
Голубое платье |
|
|
|
Тамара |
— (2) |
+ |
— |
— |
+ (1) |
— |
|
|
|
Валя |
+(2) |
— (2) |
— (2) |
— |
— |
+ |
|
|
|
Лида |
— (2) |
— (3) |
+ (3) |
+ |
— (3) |
— |
|
|
|
|
+ |
— |
— |
Голубые туфли |
|
|||
|
|
— |
+ |
— |
Красные туфли |
|
|||
|
|
— |
— |
+ |
Белые туфли |
|
|||
Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.
IIспособ. С помощью рассуждений.
По условиям задачи туфли Лиды не были красными, а у Вали были белые туфли, значит, красные туфли были у Тамары, а Лиды голубые. Так как у Тамары цвет платья и туфель совпали, то платье у Тамары было красное. У Вали и Лиды цвета не совпадали, значит у Вали было голубое платье, а у Лиды белое.
Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.
Оба выше приведенных способа дают результат при решении данной задачи. Решение с помощью таблицы дает наглядность и логичность, что способствует уверенности в правильности ответа, но занимает большое количество времени. Решение с помощью рассуждений занимает меньше времени, но в рассуждениях легко допустить ошибку.
Задача 2. Выяснить, кто из трёх людей участвовал в преступлении, исходя из двух посылок:
1) «Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не участвовал».
Решение.
А – Иванов участвовал в преступлении;
В – Петров участвовал в преступлении;
С – Сидоров участвовал в преступлении.
Iспособ. С использованием таблицы истинности.
Конструируем формулы, соответствующие 1) и 2) посылке задачи: (В)→С и →. Так как обе посылки истинны, то составим таблицу истинности для конъюнкции полученных формул:
Таблица 2
Таблица истинности
|
А |
В |
С |
||||
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Из таблицы видно, что преступление совершил А, то есть Иванов.
I аспособ. С помощью законов алгебры логики.
Снова запишем конъюнкцию формул, выражающих условия задачи. Преобразуем получившуюся формулу, пользуясь законами алгебры логики.
Так как обе посылки верны, то это выражение должно быть истинно. Это возможно только при А = 1, значит преступник – Иванов. Также , следовательно, исключается вариант B = 1, а C = 0, все остальные варианты возможны.
Ответ: исходя из предложенных посылок, можно определить, что Иванов участвовал в преступлении.
IIспособ. Cпомощью рассуждений.
Предположим, что Иванов не участвовал в преступлении, тогда выполняется условия 1 и 2. По условию 2 получается, что Сидоров не участвовал. Получается противоречие. Следовательно, Иванов участвовал, а про остальных нельзя сказать ничего определенного.
Решение данной задачи с помощью таблицы после ее построения сразу дает наглядный ответ. Решая задачу с помощью алгебры логики, наглядный ответ сразу получить сложно, для этого нужно делать определенные выводы. Минусы данного способа в том, что можно легко допустить ошибку, преобразуя формулы. Второй способ занимает меньше времени, но при рассуждениях легко запутаться в высказываниях.
Задача 3. Три одноклассника – Влад, Тимур и Юра встретились спустя 10 лет окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, а страсть третьего – регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра – единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
У двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время, и у кого какая профессия? [5, с. 385]
Решение.
Iспособ. Традиционная таблица. Кроме предложенного выше метода совмещения таблиц можно рассмотреть модификацию различных методов. Задача является трехмерной (множество имен, профессий и хобби), поэтому для ее решения используют кубическую таблицу [1, стр. 99].
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
Так как у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен, то следует что буква «а», присутствующая в слове «врач», указывает на то, что врач не Влад, следовательно, врач – Тимур. Второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени является Юра.
В имени Тимур встречаются буквы «т» и «р», которые присутствуют в слове «туризм». Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р».
Из получившихся предположений можно составить следующую кубическую таблицу:
Таблица 3
Таблица соответствия имен, профессии и хобби
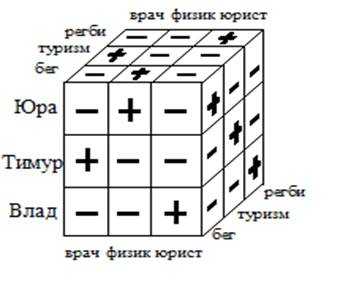
IIспособ. Нестандартная таблица.
Из высказывания Юры следует, что он не врач и не турист.
А из дальнейшего текста врач является туристом. Это отражает таблица.
Таблица 4
Таблица соответствия условий задачи
|
Имя |
Юра |
|
|
|
Профессия |
|
врач |
|
|
Увлечение |
|
туризм |
|
Далее из условия с буквами следует, что врач не Влад, следовательно, врач – Тимур; Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р». Можно составить следующую таблицу.
Таблица 5
Таблица соответствий условий задачи
|
Имя |
Юра |
Тимур |
Влад |
|
Профессия |
физик |
врач |
юрист |
|
Увлечение |
бег |
туризм |
регби |
Ответ:Влад – юрист и регбист, Тимур – врач и турист, Юра – физик и бегун.
Решая задачи с помощью традиционной и нестандартной таблиц, сразу после построения можно получить наглядный ответ. Нестандартная таблица удобная в применении, в ней наименьшая вероятность допустить ошибки. Минусы традиционной кубической таблицы в том, что для решения необходимо наличие опыта в заполнении такого рода таблиц.
Из приведенного выше анализа решения логических задач можно дать следующие рекомендации по применению того или иного способа:
1. Табличный метод и его модификации (кубическая и совмещенные таблицы, таблица соответствий) дают наглядность, логичность, прозрачность всех шагов рассуждений, следовательно, могут быть рекомендованы для решения задач любого уровня сложности.
2. Метод рассуждений можно рекомендовать только для решения простых задач с малым количеством объектов и множеств, так как при усложненном условии легко допустить ошибки, следовательно, он не дает уверенности в правильности решения.
3. Применение законов алгебры логики требуется осуществление перевода на язык математической логики, то есть выделяют элементарные высказывания и составляют более сложные в соответствие с условиями задачи. Следовательно, для применения этого способа необходимы знания законов Булевой алгебры и наличие опыта преобразований выражений и составлении таблицы. В то же время данный способ дает строгость и обоснованность полученных результатов.
Литература:
1. Бизам Д, Герцег Я. Многоцветная логика. – М.: Мир,1978. – 436 с.
2. Беррандо М. Занимательные задачи. – М.: Мир, 1983. – 457 с
3. Горбачев Н. Сборник олимпиадных задач по математике. – М: МЦНМО, 2004. – 560 с.
4. Игошин В.И. Математическая логика и теория алгоритмов. – 2-е изд. – М.: Изд. центр «Академия», 2008. – 448 с.
5. Сангалова М.Е. Курс лекций по математической логике. – Арзамас: Арзамас. гос. пед. ин-т, 2006. – 98 с.
moluch.ru
Логические задачи и методы их решения
Новосибирский государственный педагогический университет.
Математический факультет.
Кафедра геометрии и МПМ.
Логические задачи и методы их решения
Курсовая работа по математике.
Выполнила: студентка 35гр. Голобокова О.В.
Новосибирск 2009 г.
СОДЕРЖАНИЕ
Введение
1. Типы и способы решения логических задач
1.1 Задачи типа «Кто есть кто?»
1.2 Тактические задачи
1.3 Задачи на нахождение пересечения множеств или их объединения
1.4 Буквенные ребусы и примеры со звездочками
1.5 Истинностные задачи
1.6 Задачи типа «Шляпы»
1.7 Задачи типа «Два города»
Заключение
Список литературы
ВВЕДЕНИЕ
Тема моей курсовой работы: «Логические задачи и методы их решения».
Для расширения основного курса желательно выбирать темы, срособствующие развитию общеучебных умений школьников, обладающие значительным развивающим потенциалом. Привлекательными занятия по выбору сделает система методов организации внеурочной учебной деятельности школьника, использование групповых и индивидуальных занятий.
Содержательная и интересно поставленная внеурочная работа по математике позволяет выявить математически одаренных школьников, развить культуру мышления учащихся, разумно организовать их время.
Развитию творческой активности, инициативы, любознательности, смекалки способствует решение нестандартных задач.
У любого нормального ребенка есть стремление к познанию, желание проверить себя. Чаще всего способности школьников так иостаются не раскрыты для них самих, они не уверены в своих силах, равнодушны к математике.
Задачи повышенной трудности, в решении которых следует опираться на твердое знание изученных на уроках математических фактов, не следует сразу предлагать этим учащимся. Задачи должны быть доступны, будить сообразительность, овладевать их вниманием, удивлять, пробуждать их к активной фантазии и самостоятельному решению.
Несмотря на то, что школьный курс математики содержит большое количество интересных задач, многие полезные задачи не рассматриваются.
К эти задачам можно отнести логические задачи. Эти задачи могут быть рассмотрены на кружковых и факультативных занятиях, начиная с 5 класса.
1. Типы и способы решения логических задач
1.1 Задачи типа «Кто есть кто?»
Задачи типа «Кто есть кто?» очень разнообразны по сложности, содержанию и способности решения. Они, несомненно, представляют интерес для математического кружка.
а) Метод графов
Один из способов решения – решение с помощью графов. Граф – это несколько точек, часть которых соеденены друг с другом отрезками или стрелками (в таком случае граф называется ориентированным). Пусть нам требуется установить соответствие между двумя типами объектов (множествами). Точками обозначаются элементы множеств, а соответствие между ними – отрезками. Штриховой отрезок будет объеденять два элемента, не соответствующих друг другу.
Задача 1. Леня, Женя и Миша имеют фамилию Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов – члены математического кружка, а Миша и Ястребов занимаются музыкой?
Решение. Решить задачу просто, если учесть, что:
1. Каждому элементу одного множества обязательно соответствует элемент другого множества,но только один (у каждого мальчика есть фамилия и фамилии у мальчиков разные).
2. Если элемент каждого множества соединен со всеми элементами (кроме одного) другого множества штриховыми отрезками, то с последним он соединен сплошным отрезком.
Вместо сплошных штриховых отрезков можно использовать цветные, в таком случае решение получается более красочным, больше нравится младшим школьникам (рис. 1.).
Женя Миша Леня
Ястребов Соколов Орлов
Рис. 1.
Таким же способом можно находить соответствие между тремя множествами.
Задача 2. Три товарища, Иван, Дмитрий и Степан преподают различные предметы в школах Москвы, Санкт-Петербу
mirznanii.com
Логические задачи / math5school.ru
Немного теории
Часто знакомство с олимпиадной математикой начинается с логических задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания.
В логических задачах нет «серьёзной» математики – нет ни сложных числовых выражений, ни функций, ни соотношений в треугольнике, ни векторов, но есть лжецы и мудрецы, фальшивые монеты и необычные шахматные фигуры, разноцветные фишки и сказочные герои. В то же время дух математики в таких задачах чувствуется весьма ярко. Половина решения логической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.
Существуют несколько различных способов решения логических задач. Вот некоторые из них:
Способ рассуждений – самый простой способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.
Способ таблиц – распространённый прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.
Способ «с конца» – довольно часто применим в задачах с предугадываемым ответом, и состоит в анализе ответа или конечной стадии некоторого процесса, описанного в задаче.
Способ блок-схем – подходит, например, к решению задач «на переливание». Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов.
Задачи с решениями
1. На ступеньках дома сидят рядышком мальчик и девочка.
– Я мальчик, – говорит ребёнок с чёрными волосами.
– А я девочка, – говорит ребёнок с рыжими волосами.
Если по крайней мере один из детей говорит неправду, то кто из них мальчик, а кто девочка?
РешениеДля двух произвольных высказываний существуют четыре возможные комбинации типа «истина – ложь», а именно:
И – И, И – Л, Л – И, Л – Л.
Первая из них исключается, поскольку в условии оговаривается, что по крайней мере одно из высказываний является ложным. Вторая и третья комбинации также исключается, потому что если один ребёнок врал, то и другой не мог говорить правду, иначе мы бы имели дело с двумя мальчиками или с двумя девочками, что противоречит условию. Следовательно, оба говорили неправду.
Итак, у мальчика рыжие волосы, а у девочки чёрные.
2. В одной урне лежат два белых шара, в другой – два чёрных, в третьей – один белый шар и один чёрный. На каждой урне висела табличка, указывающая её состав: ББ, ЧЧ, БЧ. Но какой-то шутник перевесил все таблички так, что теперь каждая из них указывает состав урны неправильно. Разрешается вынуть шар из любой урны, не заглядывая в неё. Какое наименьшее число извлечений потребуется, чтобы определить состав всех урн? (Вы осведомлены о проделке шутника. После каждого извлечения шар опускается обратно.)
РешениеДостаточно извлечь один шар из урны с табличкой БЧ. Если он окажется белым, то в этой урне белые шары, а чёрные шары должны быть в урне с табличкой ББ, ведь не могут же они быть в урне с табличкой ЧЧ. В урне ЧЧ находятся шары разного цвета.
Если же вынут чёрный шар, то в урне с табличкой БЧ чёрные шары, в урне ЧЧ – белые, а в ББ – разного цвета.
3. Абрахам, хилый старик, подрядился выкопать канаву за 2 доллара. Он нанял Бенджамина, здоровенного парня, чтобы тот ему помог. Деньги они должны были поделить в соответствии с «копательными» способностями каждого. Абрахам копает так же быстро, как Бенджамин выбрасывает грунт, а Бенджамин копает в четыре раза быстрее, чем Абрахам выбрасывает грунт.
Каким образом они должны поделить деньги? Разумеется, соотношение сил старика и молодого человека как при копке, так и при выбрасывании грунта мы принимаем одинаковым.
РешениеПусть, например, Бенджамин (Б) может выкопать канаву за время t, и выбросить грунт за время 2t. Тогда Абрахам (А) выкапывает канаву за время 2t часа и выбрасывает весь грунт за 4t. Следовательно, при рытье канавы их силы относятся как t к 2t, а при выбрасывании грунта – как 2t к 4t (отношение сил остаётся неизменным). При этом А может выкопать канаву за то же время, за которое Б может выбросить весь грунт (время 2t), а Б может выкопать канаву за четвёртую часть того времени, которое А тратит на выбрасывание грунта.
Следовательно, Абрахаму причитается треть всей суммы, а Бенджамину – две трети.
4. Андерсон покинул отель в Сан-Ремо в 9 часов и находился в пути целый час, когда Бакстер вышел вслед за ним по тому же пути. Собака Бакстера выскочила одновременно со своим хозяином и бегала всё время между ним и Андерсоном до тех пор, пока Бакстер не догнал Андерсона. Скорость Андерсона составляет 2 км/ч, Бакстера – 4км/ч и собаки – 10 км/ч. Сколько километров пробежала собака к моменту, когда Бакстер догнал Андерсона?
РешениеВполне очевидно, что Бакстер догонит Андерсона через один час, поскольку к этому времени они пройдут по 4 километра в одном направлении. Так как скорость собаки составляет 10 км/ч, то за этот час она пробежит 10 километров.
Ответ: 10 км.
5. Можно ли расставить по окружности 20 красных и несколько синих фишек так, чтобы в каждой точке, диаметрально противоположной красной фишке, стояла синяя и никакие две синие фишки не стояли рядом?
РешениеИз условия следует, что красные и синие фишки должны чередоваться (на окружности), значит, всего их 40. Фишки по окружности размещаются равномерно в том смысле, что две диаметрально противоположные фишки делят множество оставшихся 38 фишек на две части по 19 фишек, расположенные в одной и другой полуокружностях относительно двух данных фишек. Это так, потому что согласно условию, каждая фишка имеет диаметрально противоположную. Диаметрально противоположные фишки имеют разный цвет, поэтому 19 фишек, расположенные в одной из полуокружностей должны чередоваться по цвету и начинаться и заканчиваться фишками разного цвета, что невозможно при нечётном 19. Следовательно, указанная в задаче расстановка фишек не возможна.
Ответ: нельзя.
6. Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления.
Браун: «Я не делал этого. Джонс не делал этого.»
Джонс: «Браун не делал этого. Смит сделал это.»
Смит: «Я не делал этого. Браун сделал это.»
Было установлено далее, что один из них дважды солгал, другой дважды сказал правду, третий – раз солгал, раз сказал правду. Кто совершил преступление?
РешениеЕсли вор – Смит, то и Браун, и Джонс оба сказали правду. Если вор – Джонс, то и Браун, и Смит одновременно сказали и правду, и ложь. Итак, Браун – преступник. Джонс оба раза солгал, Смит оба раза сказал правду, Браун один раз солгал, второй раз сказал правду.
7. «Суперкоролева» – это шахматный ферзь, который может ходить еще и как конь. Надо разместить четырех суперкоролев на доске 5 на 5 таким образом, чтобы ни одна из них не могла атаковать другую. Если вам это удастся, то попробуйте 10 суперкоролев разместить на доске 10 на 10 так, чтобы ни одна не имела возможности напасть на другую. Обе задачи имеют единственное решение, если не учитывать повороты доски и ее зеркальные отражения.
РешениеОба решения показаны на следующем рисунке.
8. У автомобиля новые шины. Шина на заднем колесе выдерживает пробег 16000 км, а на переднем – 24000 км. Какой максимальный пробег можно осуществить на этих калёсах?
РешениеБудем считать, что скорость роста износа колеса является постоянной и не зависит от того насколько оно давно служит.
Очевидно, что задние колёса изнашиваются в 1,5 раза быстрее передних. Значит, когда задние колёса износятся на 60%, то передние – только на 40%. Это произойдёт после пробега
0,6 · 16000 = 0,4 · 24000 = 9600 (км).
В этот момент и следует сменить колёса. Оставшийся 40%-й ресурс задних колёс, поставленных спереди, и 60%-й ресурс передних колёс, поставленных сзади, очевидно, исчерпается одновременно, и произойдёт это ещё через 9600 км. Таким образом максимальный пробег составляет 2·9600 = 19200 км.
Замечание. Это лишь одно из множества возможных решений этой задачи. Попробуйте найти своё.
Ответ: 19200 км.
9. Переаттестация Совета Мудрецов происходит так: король выстраивает их в колонну по одному и надевает каждому колпак белого или чёрного цвета. Все мудрецы видят, какого цвета колпак каждого впереди стоящего мудреца, а цвет своего и всех стоящих сзади не видят. Раз в минуту один из мудрецов должен выкрикнуть один из двух цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувшего цвет, отличный от цвета его колпака. Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казнённых. Скольким из них гарантированно удастся избежать казни?
РешениеЯсно, что мудрец, стоящий в колонне последним, может спастись только случайно, ведь его колпака не видит никто из мудрецов. Но он может спасти всех остальных, сообщив им чётность числа белых колпаков, надетых на них (по договоренности он скажет «белый», если это число нечетно, и «чёрный» в противном случае). Теперь мудрецы должны вычислять и называть цвета своих колпаков по порядку от предпоследнего к первому: сначала предпоследний, видя колпаки впереди стоящих и зная чётность числа белых колпаков (среди колпаков впереди стоящих и своего), легко определит цвет своего колпака и назовет его; затем мудрец, стоящий перед ним, зная цвета всех тех же колпаков, кроме своего (передние он видит, а про задний только что услышал), по чётности может определить цвет своего колпака и назвать его. Остается продолжать описанную процедуру до тех пор, пока первый мудрец не определит цвет своего колпака.
Ответ: всем, кроме, быть может, одного.
10. В тюрьму поместили 100 узников. Надзиратель сказал им: «Я дам вам вечер поговорить друг с другом, а потом рассажу по отдельным камерам, и общаться вы больше не сможете. Иногда я буду одного из вас отводить в комнату, в которой есть лампа (вначале она выключена). Уходя из комнаты, вы можете оставить лампу как включенной, так и выключенной. Если в какой-то момент кто-то из вас скажет мне, что вы все уже побывали в комнате, и будет прав, то я всех вас выпущу на свободу. А если неправ — скормлю всех крокодилам. И не волнуйтесь, что кого-нибудь забудут — если будете молчать, то все побываете в комнате, и ни для кого никакое посещение комнаты не станет последним.»
Придумайте стратегию, гарантирующую узникам освобождение.
РешениеУзники выбирают одного определённого человека (будем называть его «счётчиком»), который будет считать узников по такой системе: если, приходя в комнату, он обнаруживает, что свет включён, то он прибавляет к уже посчитанному числу узников единицу и выключает свет, если же свет не горит, то он, ничего не меняя, возвращается обратно в свою камеру. Каждый из оставшихся узников действует по такому правилу: если, приходя в комнату, он обнаруживает, что свет не горит, и он до этого ни разу не включал свет, то он его включает. В остальных случаях он ничего не меняет. Когда число посчитанных узников становится равным 99, «счётчик» говорит, что все узники уже побывали в комнате.
Действительно, каждый узник, кроме «счётчика», включит свет в комнате не более одного раза. Когда «счётчик» насчитает 99, он может быть уверен, что все остальные узники уже побывали в комнате хотя бы раз, кроме того он сам уже побывал в комнате. Получается, что к этому моменту все узники заведомо побывали в комнате хоть раз.
Остаётся доказать, что каждый из 99 узников включит свет. Предположим, что это не так – свет будет включён менее 99 раз. Тогда, начиная с некоторого дня n, свет включаться не будет. Так как никакой заход в комнату не будет для счётчика последним, он побывает в комнате после этого дня (например, на m-й день, m > n). Если свет при этом горел, он его выключит. Значит, начиная с (m+1)-го дня свет будет всё время выключен. Рассмотрим узника, который свет ещё ни разу не зажигал. Так как и для него никакой заход в комнату не последний, он побывает в комнате после m-го дня. Но тогда он должен включить свет – противоречие.
Задачи без решений
1. Каково наибольшее число утверждений из приводимых ниже, которые одновременно могут быть истинными:
а) Джо ловкач,
б) Джо не везет,
в) Джо везет, но он не ловкач,
г) если Джо ловкач, то ему не везет,
д) Джо является ловкачом тогда и только тогда, если ему везет,
е) либо Джо ловкач, либо ему везет, но не то и другое одновременно.
2. Мать разделила между своими сыновьями груши. Первому она дала половину всех груш и ещё половину груши, второму – половину остатка и ещё половину груши и, наконец, третьему – половину нового остатка и ещё половину груши. Ни одной груши при этом не нужно было разрезать. Сколько груш получил каждый сын, если мать раздала все груши?
3. В гостиницу приехал путешественник. Денег он не имел, а обладал лишь серебряной цепочкой, состоящей из семи звеньев. За каждый день пребывания в гостинице он расплачивался одним звеном цепочки, при этом хозяин предупредил, что согласен взять не более одного распиленного звена.
Подскажите, как путешественнику распилить цепочку, чтобы прожить в гостинице семь дней и ежедневно расплачиваться с хозяином.
4. Имеется 10 мешков монет. В девяти мешках монеты настоящие, весят по 10 г, а в одном мешке все монеты фальшивые, весят по 11 г. Одним взвешиванием определить, в каком мешке фальшивые монеты. (Взвешивание осуществляется на весах способных показать точный вес.)
5. Переаттестация Совета Мудрецов происходит так: король выстраивает их в колонну по одному и надевает каждому колпак белого, синего или красного цветов. Все мудрецы видят цвета всех колпаков впереди стоящих мудрецов, а цвет своего и всех стоящих сзади не видят. Раз в минуту один из мудрецов должен выкрикнуть один из трех цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувшего цвет, отличный от цвета его колпака. Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казненных. Скольким из них гарантированно удастся избежать казни?
math4school.ru
