Теория и методика математического развития. Конспект занятия «Звёздная математика» | План-конспект занятия по математике (средняя группа):
Муниципальное автономное дошкольное общеобразовательное учреждение
Детский сад № 1 «Ромашка»
Теория и методика математического развития
Конспект занятия «Звёздная математика»
Подготовил: воспитатель
Бикметова В.Х.
Учалы – 2019
Теория и методика математического развития.
Конспект занятия «Звёздная математика»
- Цель: Формирование элементарных математических представлений. Повышение у детей среднего дошкольного возраста интереса к математике посредством создания условий для исследовательской деятельности по изучению геометрических фигур, цифр и линий во взаимосвязи с окружающей жизнью, с предметами ближайшего окружения.
II. Задачи:
— формировать умение распознавать фигуры независимо от их пространственного положения, изображать, располагать на плоскости, упорядочивать по размерам, классифицировать, группировать по цвету, форме, размерам;
— развивать геометрическую зоркость: умение анализировать и сравнивать предметы по форме, находить в ближайшем окружении предметы одинаковой и разной формы, конструировать фигуры по словесному описанию и перечислению их характерных свойств;
— учить составлять тематические композиции из фигур по собственному замыслу;
— развивать математическое мышление, логические мыслительные операции.
III. Тип занятия: познавательный с элементами исследования.
IV. Форма занятия: игровая.
V. Продолжительность: 30 минут.
VI. Участники проекта: группа детей в количестве 10-15 человек, воспитатель.
VII. Возраст обучающихся: 6 лет
VIII. Оборудование и материалы: мяч, набор геометрических фигур, музыкальная аудиозапись для физкультминутки, карточки в виде планет солнечной системы, листы бумаги в клеточку, простые карандаши, ноутбук, проектор, интерактивная доска.
IX. Предварительная подготовка: Разучивание движений физкультминутки «Инопланетяне», исследование объёмных геометрических фигур, ощупывание, придумывание задач и их решения. Просмотр обучающих мультфильмов о геометрических фигурах. Чтение сказки Сытовой Н. Б. «Как геометрические фигуры город строили», коллективная аппликация «Город геометрических фигур».
X. Методы и приемы работы с детьми: поисковые (моделирование, эксперименты), игровые (развивающие игры, соревнования, конкурсы, развлечения), практические упражнения, использования занимательного материала (ребусы, лабиринты), наглядный, использование ИКТ.
XI. Структура занятия:
1. Организационный момент (3 минут)
2. Основная часть (17 минут)
3. Физкультминутка (2 минуты)
4. Заключение (8минут)
Ход занятия.
Организационный момент.
— Дети, вы любите путешествовать? (Да).
— А куда бы вы хотели отправиться в путешествие? (Ответы детей. В Африку к слонам, вокруг света, путешествие по сказкам, в космос…)
— Отгадайте загадку: «Рассыпался горох на тысячу дорог»? (Звездное небо).
— Сколько интересного в небе, в звездах! Как хочется отправиться в путешествие к далеким звездам и, может быть, встретить звездных обитателей.
— Слушайте, ребята, следующую загадку: «Ночь приходит – она восходит.
В небе сияет, тьму разгоняет.» (Луна).
— Мне бы очень хотелось слетать вместе с вами на Луну. Кто хочет со мной на Луну? ( Я, мы).
— Какую геометрическую форму имеет луна? (шар, круг, мяч).
— На какого сказочного героя похожа Луна? (колобок).
— Мы полетим на луну на космическом корабле, ракете.
— На доске рисунок ракеты из геометрических фигур. Давайте нарисуем ракету! Из каких геометрических фигур составлена наша ракета? (треугольник, прямоугольник, круг, квадрат).
— Чем они похожи, а чем отличаются? (цвет, форма, углы)
— Дети, поднимите свой треугольник, затем прямоугольник, потом круг.
— Путешествовать по Луне будем на луноходе. Экскурсию проведет Лунтик. (на экране воспитатель показывает Лунтика)
— Дети, нам нужно выбрать командира корабля с помощью считалки. Дети считают и выбирают командира.
— Я буду руководителем полета. Занять места в корабле, надеть комбинезон, шлем, пристегнуть ремни.
Командир из детей: Внимание, внимание. Объявляется трехминутная готовность! Ключ на старт! Начинаем вместе обратный отсчет времени.
Все вместе: 10,9,8,7,6,5,4,3,2,1 (дети показывают цифры)
Командир: пуск!
Основная часть. (17 минут)
Лунтик: Будьте внимательны, мы ведем наблюдение за космическими объектами. Посмотрите в иллюминатор, мы видим Солнце. На какую геометрическую форму похоже солнце? (Шар, круг).
На какую геометрическую форму похоже солнце? (Шар, круг).
Лунтик: На какую фигуру похоже солнце? (яблоко, мандарин, апельсин).
Лунтик: Давайте нарисуем круг и раздели пополам. (Дети рисуют)
Лунтик: Этот полукруг и похож на месяц.
Лунтик: Наш полет продолжается и чтобы вам не было скучно предлагаю поиграть в игру «Найди себе пару». У каждого из вас геометрическая фигура (половинки круга или квадрата разного размера). Посмотрите внимательно и сделайте так, чтобы у вас получилась правильная фигура: круг или квадрат. (дети ищут свои пары и показывают получившиеся фигуры.) Пусть каждая пара назовет получившуюся фигуру.
Лунтик: Молодцы! Вот яблоко. Оно целое. Какой фигуркой его можно обозначить? (дети показывают круги и квадратики.) А теперь я разрежу яблоко пополам. Как половинки можно обозначить? (дети показывают половинки кругов и квадратиков.) Как это на Земле называется? (Части).
Лунтик: Мы почти прилетели, но чтобы нам удачно прилуниться, нужно решить несколько задач. Давайте вспомним, из каких частей состоит задача? (Условие, вопрос, ответ. Если дети сомневаются, воспитатель подсказывает).
Давайте вспомним, из каких частей состоит задача? (Условие, вопрос, ответ. Если дети сомневаются, воспитатель подсказывает).
— Сколько чисел, как минимум должно быть в условии задачи? (Два числа).
— Если в вопросе есть слово «стало», то какой арифметический знак нужно поставить? (Плюс).
— А если слово «осталось»? (Минус).
Лунтик: Внимание, внимание! Наш космический корабль идет на посадку! Толчок, и мы прилунились (на экран выводится рисунок луны)
Лунтик : Дети, что на луне вы видите? (Горы).
Лунтик: На какие геометрические фигуры они похожи. (На треугольник). Показывают треугольник.
— На луне кроме гор есть еще кратеры. Вы узнали героя книги, который побывал на Луне? (Это Незнайка).
— Лунтик приготовил вам подарки. Это «лунный камень», и вы можете взять его с собой на память о Луне. Камни будете искать в песке, как найдёте, определите на ощупь и, не вытаскивая его из песка, скажите какой он формы. (Лунный камень в форме шара, вформе конуса, в форме цилиндра, в форме куба).
Лунтик: Вам пора возвращаться на землю.
Все прощаются с Лунтиком. Дети садятся в корабль и отправляются домой.
Физкультминутка (2 минуты)
— Подними ладошки выше.
И сложи их уголком.
Что же вышло?
Крыша вышла,
А под крышей мы с тобой. (Опустить руки).
Нарисуй квадрат ладошкой. (Ладошками рисовать большой и маленький квадраты).
Что же вышло?
Стенка вышла
И окошко нам с тобой.
Вот так дом, хороший дом.
Два хлопка слева, два справа.
Будем счастливы мы в нем.
Заключение (8 минут)
— Ребята, выберите фигуры, которые вам понравились и покажите. А я попытаюсь объяснить значение каждой.
Круг – самая добрая из всех фигур. Именно он скрепляет коллектив, семью, близких. Это семейная фигура.
Треугольник – сильная личность. Он решителен, энергичен, ставит ясные цели и, как правило, достигает их. Треугольник — очень уверенный человек.
Квадрат. Если вы выбрали в качестве своей основной формы квадрат, то вы — неутомимый труженик! Человек, который любит трудиться.
Прямоугольник. Прямоугольник нередко находится в состоянии замешательства, неопределенности в отношении себя. Он отличается низкой самооценкой, стремится стать в чем-то лучше, ищет новые методы работы, пытается изменить стиль жизни.
— Вот и подошло к концу наше путешествие «Звездная математика». С чем мы сегодня работали на занятии? (С геометрическими фигурами).
— Чему вы научились на занятии? Понравилось ли вам оно? А теперь оцените свою работу на занятии. Если у вас хорошее настроение, вам было интересно на занятии, у вас все получалось, то поднимите руки вверх, а если вы чувствовали себя неуютно, у вас что-то не получалось, тогда опустите руки вниз.
С математикой дружите, знания свои копите. Пусть помогут вам старание, память, логика, внимание.
Список используемой литературы:
1. Буренина А. И. Коммуникативные танцы-игры для детей: учебное пособие. – СПб: Музыкальная палитра, 2011.
2. Касицына М. А. Дошкольная математика. 1и 2-й год обучения: учебно-практическое пособие для педагогов и родителей. / М. А. Касицина, В. Д. Смирнова. – М. : Гном, 2004.
/ М. А. Касицина, В. Д. Смирнова. – М. : Гном, 2004.
3. Лыкова И. А. Изобразительная деятельность в детском саду: планирование, конспекты занятий, методические рекомендации. – М. : Карапуз-дидактика, 2009.
4. Метлина Л. С. Математика в детском саду / Л. С. Метлина. – М. : Просвещение, 1984
5. Стародубова Н. А. Теория и методика развития речи дошкольников. – М. : Академия, 2006.
«ТЕОРИЯ И МЕТОДИКА МАТЕМАТИЧЕСКОГО РАЗВИТИЯ» | План-конспект занятия по математике (младшая группа):
МЕТОДИЧЕСКАЯ РАЗРАБОТКА КОНСПЕКТА ЗАНЯТИЯ
На тему:
«ТЕОРИЯ И МЕТОДИКА МАТЕМАТИЧЕСКОГО РАЗВИТИЯ».
Составитель занятия: Мурадова Оксана Павловна
Методическая разработка конспекта занятия по математическому развитию в младшей группе «Математические игры».
Цель: Развитие интеллектуально-творческих способностей детей через освоение
ими логико-математических представлений и способов познания.
Задачи:
1. Образовательные задачи:
Продолжать учить различать и называть геометрические фигуры; основные
признаки предметов; цвет, форму, величину.
Учить устанавливать соответствие между множествами. Закрепить навыки счета
до 4-х.
2. Развивающие задачи:
Продолжать осваивать умение различать правую и левую руки, составлять из
частей целое.
Развивать память, воображение, логическое мышление, сообразительность.
3. Воспитывающие задачи:
Воспитывать интерес к занятию, трудолюбие, аккуратность, развивать
доброжелательные отношения.
Тип занятия:
Занятие на повторение пройденного материала
Форма занятия:
Интегрированное занятие
Продолжительность:
15 минут
Участники:
2 Младшая группа
Возраст обучающихся:
3-4 года
Оборудование и материалы:
сундучок, кукла, бабочки, зайка, ключи; образцы бус,
набор геометрических фигур, полянка с цветами, ручеек, разрезанные картинки;
музыкальное сопровождение.
Предварительная подготовка: Чтение стихов и сказок с математической тематикой; отгадывание загадок, дидактические игры «кто лишний?» разучивание физкультминутки, пальчиковой гимнастики.
Методы и приёмы работы с детьми:
Словесные — беседа, вопросы, объяснение.
Наглядные — демонстрация игр, пособий.
Игровые — проведение игр «Найди, какой же?», «Собери бусы», «Собери
картинку».
Практические — действия с дидактическим материалом.
Поощрение, анализ занятия.
Структура занятия:
Этап занятия | Содержание | Время |
Вводная часть | Разминка; сюрп. момент | 1.5 мин |
Основная часть | Беседа; вып. задания; д/и «Найди, какой же?»; д/и «Собери бусы»; д/и «Разрезные картинки». | 12.5 мин |
Заключительная часть | Подведение итогов. | 1 мин |
Ход занятия:
1 часть (вводная )
Дети заходят в группу, здороваются с гостями. Начинает звучать музыка.
Воспитатель: Посмотрите, дети, какой прекрасный сундучок стоит. Хотите
знать, что в нем находится?
Дети: Да.
Воспитатель: Давайте его откроем. Посмотрите, какой большой замок, но у нас есть три ключа. Какой они формы?
Дети: Треугольник, квадрат, круг.
2 часть (основная)
Проводится игра «Найди, какой же?»
Замок сундучка и ключи имеют определенную геометрическую форму. Дети подбирают каждый ключик. Выбор определяется путем приложения фигуры на изображение. Правильно выполненное задание позволяет открыть замок.
В сундучке будет кукла.
Воспитатель: Посмотрите, кто оказался в этом сундучке.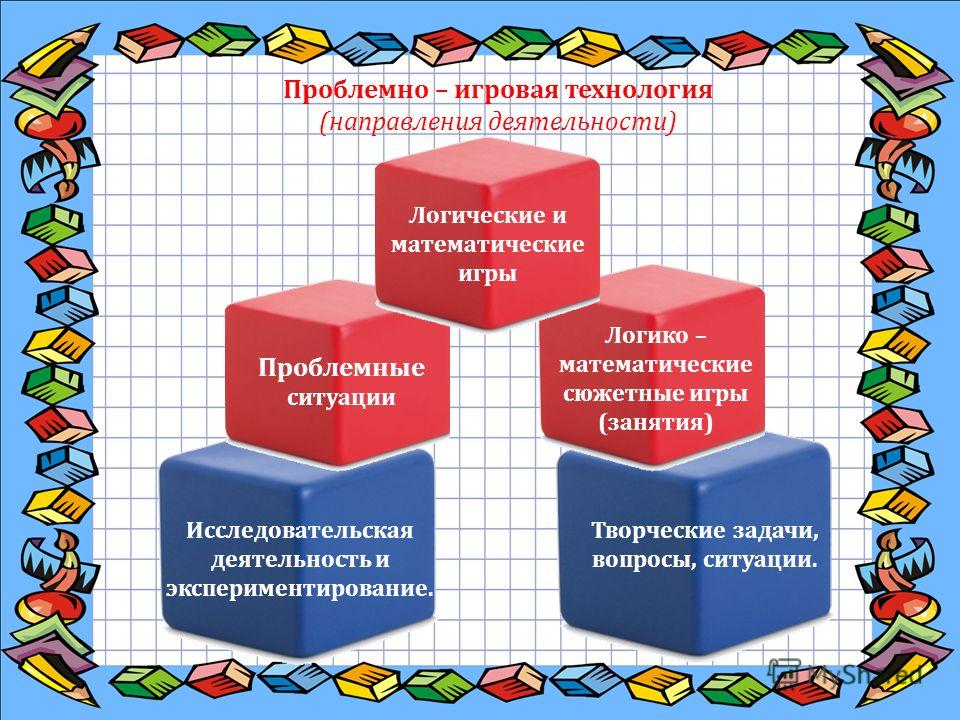 Это кукла Таня. Она большая или маленькая?
Это кукла Таня. Она большая или маленькая?
Дети: Маленькая.
Воспитатель: Посмотрите она веселая или грустная?
Дети: Грустная.
Воспитатель: Давайте узнаем, что с ней случилось. Она собиралась к нам в
гости. Надела красивое платье и разноцветные бусы. Но по дороге веревочка разорвалась и бусинки рассыпались. Давайте поможем их собрать.
Проводится игра «Собери бусы».
Воспитатель показывает детям часть нитки бус и говорит, что они рассыпались.
Их нужно собрать, используя для них круги двух цветов. У каждого ребенка
набор геометрических фигур и образец (начало нитки бус, круги чередуются по цвету). Ребенок собирает так как показано в начале нитки, отбирая фигуры по цвету.
Воспитатель: Посмотрите, дети, какая сейчас стала кукла? Почему?
Дети: Веселая. Потому что собрали бусы.
Пальчиковая гимнастика.
Мы капусту рубим, рубим.
Мы капусту трем, трем.
Мы капусту солим, солим.
Мы капусту жмем, жмем.
Воспитатель: Давайте посмотрим, что еще есть в нашем волшебном сундучке
(достает бабочки). Посмотрите, дети, какие красивые бабочки. Какие они по
цвету?
Дети: Красные, синие.
Воспитатель: Хотите поиграть с ними?
Дети: Хотим.
Воспитатель: Какое у нас сейчас время года?
Дети: Зима.
Воспитатель: А что делают бабочки зимой?
Дети: Спят.
Воспитатель: А наши бабочки из волшебного сундучка. В наших руках они сейчас оживут и полетят на полянки, искать красивые цветочки, такого же цвета, как они сами. Возьмите бабочек в правую руку, (рассматривает с детьми полянку с красными цветами). Сколько цветов на полянке? Давайте посчитаем.
Дети: Один, два, три, четыре.
Воспитатель: Давайте посчитаем сколько бабочек? (Спросить одного ребенка).
Дети: Один, два, три, четыре.
Воспитатель: Что из этого следует? Что бабочек столько, сколько и цветов.
Одинаковое количество, поровну.(Рассматривает другую полянку). Сколько цветов?
Сколько цветов?
Дети: четыре.
Воспитатель: Сколько бабочек?
Дети: три.
Воспитатель: Чего у нас больше? Цветов или бабочек?
Дети: Цветов.
Воспитатель: На сколько?
Дети: На один.
Воспитатель: Почему?
Дети: Потому что без бабочки остается один цветок.
Физкультминутка.
Спал цветок и вдруг проснулся,
Больше спать не захотел.
Шевельнулся, потянулся,
Взвился вверх и полетел.
Солнце утром лишь проснется,
Бабочка кружит и вьется.
Воспитатель: Вы слышите, ребята, кто-то плачет? Давайте посмотрим.
Дети и воспитатель собираются пойти посмотреть, кто плачет, но на пути им
встречается речка.
Воспитатель: Ребята, что это?
Дети: Речка.
Воспитатель: Она какая? Широкая или узкая?
Дети: Широкая.
Воспитатель: Как нам перейти через речку?
Дети: По мостику.
Идут дальше. На пути встречается ручеек.
Воспитатель: Дети, посмотрите, это что?
Дети: Ручеек.
Воспитатель: Какой он? Широкий или узкий?
Дети: Узкий.
Воспитатель: Мы можем его перейти?
Дети: Да.
Воспитатель и дети находят зайку.
Воспитатель: Дети, кто это?
Дети: Зайка.
Воспитатель: Давайте с ним познакомимся и спросим, почему он плачет.
Дети: Зайчик, как тебя зовут?
Зайчик: Степашка.
Дети: Почему ты плачешь?
Зайчик: Потому что я заблудился и очень хочу есть.
Воспитатель: Ребята, поможем зайчику?
Дети: Да.
Проводится игра «Разрезные картинки». Дети составляют картинки из четырех частей.
Воспитатель: Посмотри, Степашка, какую мы тебе морковку собрали.
Воспитатель угощает зайчика морковкой (муляж).
Зайчик: Спасибо вам ребята.
Заключительная часть.
Воспитатель: Давайте, ребятки, попрощаемся с зайчиком. Мы помогли зайчику, составили картинки из частей.
Дети: До свидания, Степашка.
Воспитатель: Давайте попрощаемся с Таней. Мы помогли ей собрать бусы.
Бусинки были разные по цвету.
Дети: До свидания, Таня.
Воспитатель: Давайте попрощаемся с бабочками. Мы с вами сегодня узнали, что на полянке было больше синих цветов, чем синих бабочек на один, а красных цветов и бабочек поровну.
Дети: До свидания, бабочки.
Воспитатель: Ребята, вам понравилось помогать нашим друзьям? Что вам
больше всего понравилось? В какие игры вы играли?
Воспитатель благодарит детей и раздает угощенье.
МОДЕЛИ И ОТНОШЕНИЯ МАТЕМАТИКА, НАУКИ, И ТЕХНОЛОГИЯ МАТЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ Глава 2: ПРИРОДА МАТЕМАТИКИ Математика опирается как на логику, так и на творчество, и ею занимаются
как для различных практических целей, так и для его внутреннего интереса. В этой главе основное внимание уделяется математике как части научной
усилия, а затем математику как процесс или способ мышления.
Рекомендации, относящиеся к математическим идеям, представлены в главе
9, «Математический мир», и те, которые касаются математических навыков, включены
в главе 12 «Привычки ума».
МОДЕЛИ И ОТНОШЕНИЯ Математика — это наука о закономерностях и отношениях. В качестве теоретического
дисциплина, математика исследует возможные отношения между
абстракции, не заботясь о том, есть ли у этих абстракций аналоги
в реальном мире. Абстракциями могут быть любые строки
числа к геометрическим фигурам к системам уравнений. Обращаясь,
скажем: «Формирует ли интервал между простыми числами закономерность?»
как теоретический вопрос, математиков интересует только нахождение
закономерность или доказательство того, что ее нет, но не в чем польза такая
знания могли иметь. При выводе, например, выражения для
изменение площади поверхности любого правильного твердого тела в зависимости от его объема
приближается к нулю, математиков не интересует никакая переписка
между геометрическими телами и физическими объектами в реальном мире. Центральным направлением исследований в теоретической математике является выявление
в каждой области исследования небольшой набор основных идей и правил, из которых
все другие интересные идеи и правила в этой области могут быть логически
выведено. Математики, как и другие ученые, особенно довольны
когда обнаруживается, что ранее не связанные части математики могут быть выведены
друг от друга или от какой-либо более общей теории. Часть смысла
красоты, которую многие люди восприняли в математике, заключается не в
в нахождении наибольшей сложности или сложности, а, наоборот,
в нахождении наибольшей экономии и простоты представления и
доказательство. По мере развития математики все больше и больше соотношений
были обнаружены между его частями, которые разрабатывались отдельно — для
например, между символическими представлениями алгебры и пространственным
представления геометрии. Математика также является прикладной наукой. Многие математики обращают внимание
их внимание на решении проблем, которые возникают в мире
опыт. Они тоже ищут закономерности и отношения, и в
процесса они используют методы, аналогичные тем, которые используются в
заниматься чисто теоретической математикой. Разница во многом одна
намерения. В отличие от математиков-теоретиков, прикладные математики,
в примерах, приведенных выше, мог бы изучить шаблон интервала простого
чисел для разработки новой системы кодирования числовой информации,
а не как абстрактная проблема. Или они могут заняться площадью/объемом
проблема как шаг в создании модели для изучения поведения кристалла. МАТЕМАТИКА, НАУКИ, И ТЕХНОЛОГИЯ Благодаря своей абстрактности математика в некотором смысле универсальна.
МАТЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ Использование математики для выражения идей или решения проблем требует
как минимум три этапа: (1) абстрактное представление некоторых аспектов вещей,
(2) манипулирование абстракциями по правилам логики для поиска новых отношений
между ними, и (3) посмотреть, говорят ли новые отношения что-то
полезно об оригинальных вещах. Математическое мышление часто начинается с процесса абстракции, который
то есть замечание сходства между двумя или более объектами или событиями. Аспекты
что у них есть общего, будь то конкретное или гипотетическое, может быть
представлены такими символами, как цифры, буквы, другие знаки, диаграммы,
геометрические конструкции или даже слова. Целые числа — это абстракции.
которые представляют размер наборов вещей и событий или порядок
вещей в наборе. Круг как понятие является абстракцией
полученные из человеческих лиц, цветов, колес или распространяющейся ряби; в
буква А может быть абстракцией площади поверхности объектов
любой формы, для ускорения всех движущихся объектов или для всех
объекты, имеющие определенное свойство; символ + представляет собой
процесс добавления, будь то добавление яблок или апельсинов, часов,
или миль в час. Такая абстракция позволяет математикам сосредоточиться на некоторых функциях вещей и избавляет их от необходимости постоянно поддерживать другие функции в уме. Что касается математики, то не имеет значения, треугольник представляет собой площадь поверхности паруса или схождение двух линий визирования на звезду; математики могут работать с понятие таким же образом. Полученная в результате экономия усилий очень полезна при условии, что что при абстракции стараются не игнорировать особенности которые играют существенную роль в определении исхода событий изучается. Манипуляции с математическими выражениями После того, как были сделаны абстракции и символические представления
они были выбраны, эти символы можно комбинировать и повторно комбинировать
различными способами по четко определенным правилам. Обычно строки символов объединяются в операторы, выражающие
идеи или предложения. Например, символ A для области
любого квадрата может использоваться с символом s для длины
стороны квадрата, чтобы составить предложение A = s 2 .
Это уравнение определяет, как площадь связана со стороной и
также означает, что он не зависит ни от чего другого. Правила обычного
Затем с помощью алгебры можно обнаружить, что если длина сторон
площади квадрата удвоится, площадь квадрата увеличится в четыре раза. Математическое понимание абстрактных отношений выросло
тысячи лет, и они до сих пор продлеваются, а иногда и
исправлено. Хотя они начинались с конкретного опыта подсчета
и измерения, они прошли через многие слои абстракции и
теперь гораздо больше зависят от внутренней логики, чем от механической демонстрации.
Таким образом, в некотором смысле манипулирование абстракциями очень похоже на
игра: начните с некоторых основных правил, а затем делайте любые ходы, соответствующие этим
правилав том числе изобретать дополнительные правила и находить новые
связи между старыми правилами. Тест на обоснованность новых идей
являются ли они непротиворечивыми и связаны ли они логически с
остальные правила. Математические процессы могут привести к своего рода модели вещи, от
какое понимание можно получить о самой вещи. Любой математический
отношения, полученные путем манипулирования абстрактными утверждениями, могут или
может не передать что-то правдивое о моделируемой вещи. За
например, если 2 стакана воды добавить к 3 стаканам воды и абстрактный
математическая операция 2+3 = 5 используется для вычисления суммы, т.е.
правильный ответ 5 стаканов воды. Однако, если 2 стакана сахара
добавить к 3 чашкам горячего чая и использовать ту же операцию, 5 — это
неверный ответ, так как такое добавление на самом деле приводит лишь к незначительному
более 4 чашек очень сладкого чая. Простое добавление томов
подходит для первой ситуации, но не для второй что-то
можно было бы предсказать, только зная кое-что о физическом
различия в двух ситуациях. Иногда достаточно здравого смысла, чтобы решить, стоит ли
результаты математики соответствуют. Например, для оценки
рост через 20 лет девушки ростом 5 футов 5 дюймов и
растет со скоростью один дюйм в год, здравый смысл подсказывает
простой ответ «скорость умножить на время» 7 футов 1 дюйм
маловероятно, и вместо этого обращаются к какой-либо другой математической модели, например
как кривые, приближающиеся к предельным значениям. Однако иногда может
трудно понять, насколько уместны математические результаты для
Например, при попытке предсказать цены на фондовом рынке или землетрясения. Часто один раунд математических рассуждений не дает удовлетворительных результатов. выводы и изменения в том, как делается представление или в самих операциях. Действительно, прыжки обычно делаются назад и далее между шагами, и нет никаких правил, определяющих, как продолжать. Процесс обычно протекает рывками, с много неправильных поворотов и тупиков. Этот процесс продолжается до тех пор, пока результаты достаточно хороши. Но какой степени точности достаточно? Ответ зависит от
как будет использоваться результат, о последствиях ошибки и о
вероятная стоимость моделирования и вычисления более точного ответа.
Например, ошибка в 1 процент при расчете количества сахара
в рецепте торта может быть неважным, тогда как подобная степень
ошибка в вычислении траектории космического зонда может иметь катастрофические последствия. | |
Copyright © 1989, 1990 Американской ассоциации по развитию науки |
математика | Определение, история и значение
Вавилонская математическая табличка
Посмотреть все медиа
- Ключевые люди:
- Глэдис Уэст Исаак Ньютон Галилео Бертран Рассел Альфред Норт Уайтхед
- Похожие темы:
- анализ теория вероятности Информатика комбинаторика процент
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
математика , наука о структуре, порядке и отношениях, возникшая из элементарных практик подсчета, измерения и описания форм объектов. Он имеет дело с логическими рассуждениями и количественными расчетами, и его развитие связано с возрастающей степенью идеализации и абстракции его предмета. С 17 века математика была незаменимым дополнением к физическим наукам и технике, а в более поздние времена она взяла на себя аналогичную роль в количественных аспектах наук о жизни.
Он имеет дело с логическими рассуждениями и количественными расчетами, и его развитие связано с возрастающей степенью идеализации и абстракции его предмета. С 17 века математика была незаменимым дополнением к физическим наукам и технике, а в более поздние времена она взяла на себя аналогичную роль в количественных аспектах наук о жизни.
Во многих культурах — под влиянием потребностей практических занятий, таких как торговля и сельское хозяйство — математика развилась далеко за пределы простого счета. Этот рост был самым большим в обществах, достаточно сложных, чтобы поддерживать эту деятельность и предоставлять досуг для размышлений и возможность развивать достижения более ранних математиков.
Все математические системы (например, евклидова геометрия) представляют собой комбинации наборов аксиом и теорем, которые могут быть логически выведены из аксиом. Исследования логических и философских основ математики сводятся к вопросам о том, обеспечивают ли аксиомы данной системы ее полноту и непротиворечивость. Для полного рассмотрения этого аспекта см. математика, основы.
Для полного рассмотрения этого аспекта см. математика, основы.
Эта статья предлагает историю математики с древнейших времен до наших дней. Вследствие экспоненциального роста науки большая часть математики развивалась с 15 века н. . По этим причинам основная часть этой статьи посвящена европейским событиям, начиная с 1500 г.
Викторина «Британника»
Математика: правда или вымысел?
Сойдутся ли когда-нибудь параллельные линии? У прямоугольника три прямых угла? Отделите факты от вымысла — и посмотрите, все ли у вас есть правильные ответы — в этой викторине по математике.
Это не означает, однако, что события в других местах были незначительными. Действительно, чтобы понять историю математики в Европе, необходимо знать ее историю хотя бы в древней Месопотамии и Египте, в древней Греции и в исламской цивилизации с 9 в.го до 15 века. То, как эти цивилизации влияли друг на друга, и важный непосредственный вклад Греции и ислама в более поздние события обсуждаются в первых частях этой статьи.


 Для некоторых людей, и не только профессиональных математиков, суть
математики заключается в ее красоте и ее интеллектуальной сложности.
Для других, включая многих ученых и инженеров, главной ценностью
математики, как это применимо к их собственной работе. Потому что математика
играет такую центральную роль в современной культуре, некоторое базовое понимание
природы математики необходимо для научной грамотности.
Для этого учащиеся должны воспринимать математику как часть
научное стремление, понять природу математического мышления,
и ознакомьтесь с ключевыми математическими идеями и навыками.
Для некоторых людей, и не только профессиональных математиков, суть
математики заключается в ее красоте и ее интеллектуальной сложности.
Для других, включая многих ученых и инженеров, главной ценностью
математики, как это применимо к их собственной работе. Потому что математика
играет такую центральную роль в современной культуре, некоторое базовое понимание
природы математики необходимо для научной грамотности.
Для этого учащиеся должны воспринимать математику как часть
научное стремление, понять природу математического мышления,
и ознакомьтесь с ключевыми математическими идеями и навыками.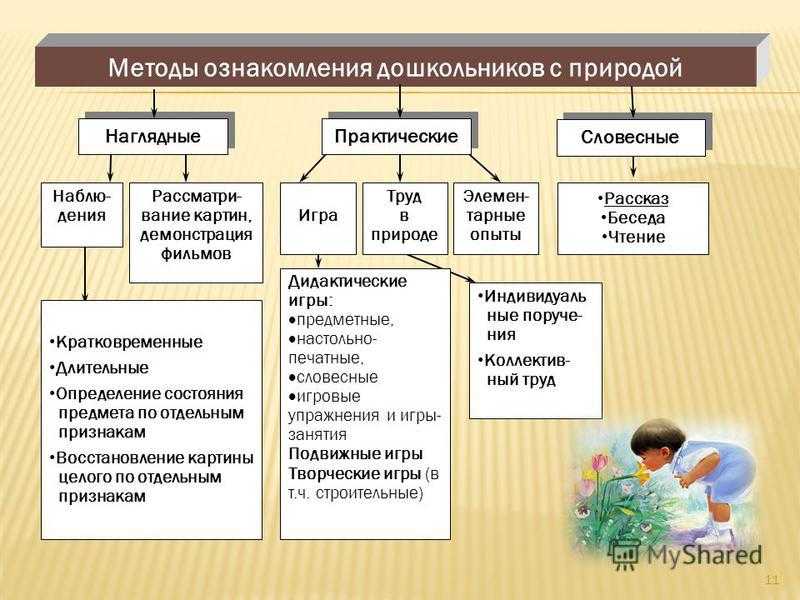

 что другие области человеческой мысли не являются. Находит полезные применения
в бизнесе, промышленности, музыке, исторической науке, политике, спорте,
медицина, сельское хозяйство, инженерия, социальные и естественные науки.
Отношения между математикой и другими областями фундаментальной
и прикладная наука особенно сильна. Это так по нескольким причинам,
в том числе:
что другие области человеческой мысли не являются. Находит полезные применения
в бизнесе, промышленности, музыке, исторической науке, политике, спорте,
медицина, сельское хозяйство, инженерия, социальные и естественные науки.
Отношения между математикой и другими областями фундаментальной
и прикладная наука особенно сильна. Это так по нескольким причинам,
в том числе:

 А абстракции делаются не только из конкретного
объекты или процессы; они также могут быть сделаны из других абстракций,
например, виды чисел (например, четные числа).
А абстракции делаются не только из конкретного
объекты или процессы; они также могут быть сделаны из других абстракций,
например, виды чисел (например, четные числа). Иногда это
делается с определенной целью; в других случаях это делается в
контекст эксперимента или игры, чтобы увидеть, что происходит. Иногда подходящее
манипуляция может быть легко идентифицирована по интуитивному смыслу
составляющие слова и символы; в другое время полезная серия
манипуляций приходится отрабатывать методом проб и ошибок.
Иногда это
делается с определенной целью; в других случаях это делается в
контекст эксперимента или игры, чтобы увидеть, что происходит. Иногда подходящее
манипуляция может быть легко идентифицирована по интуитивному смыслу
составляющие слова и символы; в другое время полезная серия
манипуляций приходится отрабатывать методом проб и ошибок. В более общем плане это знание позволяет выяснить, что
происходит с площадью квадрата независимо от длины его сторон
изменяется, и наоборот, как любое изменение площади влияет на
стороны.
В более общем плане это знание позволяет выяснить, что
происходит с площадью квадрата независимо от длины его сторон
изменяется, и наоборот, как любое изменение площади влияет на
стороны.
 Чтобы иметь возможность использовать и интерпретировать
математика хорошо, поэтому нужно заниматься
больше, чем математическая обоснованность абстрактных операций и
также учитывать, насколько хорошо они соответствуют свойствам
из представленных вещей.
Чтобы иметь возможность использовать и интерпретировать
математика хорошо, поэтому нужно заниматься
больше, чем математическая обоснованность абстрактных операций и
также учитывать, насколько хорошо они соответствуют свойствам
из представленных вещей.
 Однако важность «достаточно хорошего» вопроса привела к тому, что
к разработке математических процессов для оценки того, насколько далеко
от результатов могут быть и сколько вычислений потребуется, чтобы
получить желаемую степень точности.
Однако важность «достаточно хорошего» вопроса привела к тому, что
к разработке математических процессов для оценки того, насколько далеко
от результатов могут быть и сколько вычислений потребуется, чтобы
получить желаемую степень точности.