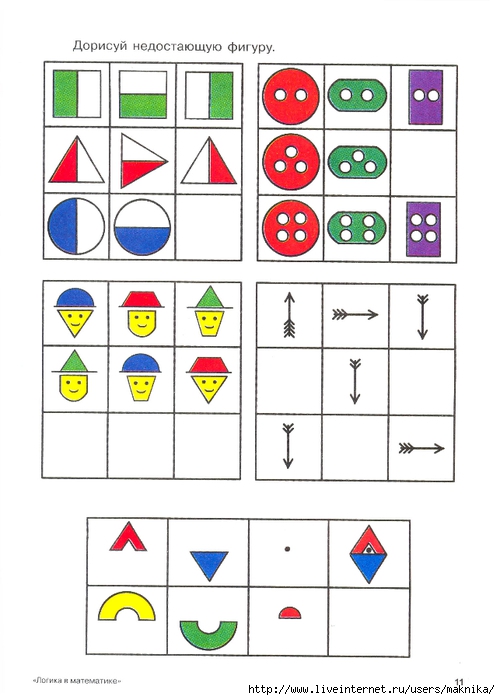
Лучшие игры и упражнения на логику для детей 7 лет
Современным школьникам нужно уделять много времени развитию своих собственных способностей, одной из которых является логическое мышление. Без него трудно решать какие-либо сложные математические задачи и отгадывать загадки, поэтому родители стараются помочь своим малышам и дополнительно занимаются с ними. Но какие упражнения лучше всего подходят для тренировки логики у школьников семи лет?
Развитие логического мышления в 1 классе
Когда ребенок приходит учиться в первый класс, он постепенно привыкает к школьным будням. В первые дни нагрузка может и не показаться такой уж большой, но со временем ученик замечает, что он все больше времени тратит на подготовку домашних заданий. Чтобы повысить свою успеваемость по таким предметам как родной язык, литературное чтение и окружающий мир, достаточно побольше читать и внимательно готовиться к уроку. А вот с математикой дела обстоят иначе.
Задания по этому школьному предмету достаточно разнообразны: сейчас ребенок решает простой пример, а через несколько минут столкнется с задачей или головоломкой.
Поэтому, чтобы хорошо понимать математику, недостаточно просто выучить правила и научиться применять их. Без развитого логического мышления ребенку сложно будет постигать точные науки не только в школе, но и в профильных учебных заведениях. Именно поэтому развивать эту сторону человеческого интеллекта так важно.
Но, так как основной формой деятельности у детей 7 лет все еще является игра, лучше развивать логику с помощью интересных упражнений, которые позволяют одновременно играть и тренировать полезные навыки.
Детские игры на логику в 7 лет
Программа в первом классе направлена на то, чтобы научить ребенка новому в формате игры. Но и дополнительные занятия в кружках или дома должны быть выстроены похожим образом. Важнейшая задача на данном этапе – привить детям желание учиться, показать им, что образовательный процесс может протекать весело.
Никакие упражнения не смогут заменить для малыша игру. Поэтому, тренируя логическое мышление, нужно обязательно делать перерывы на развлечения.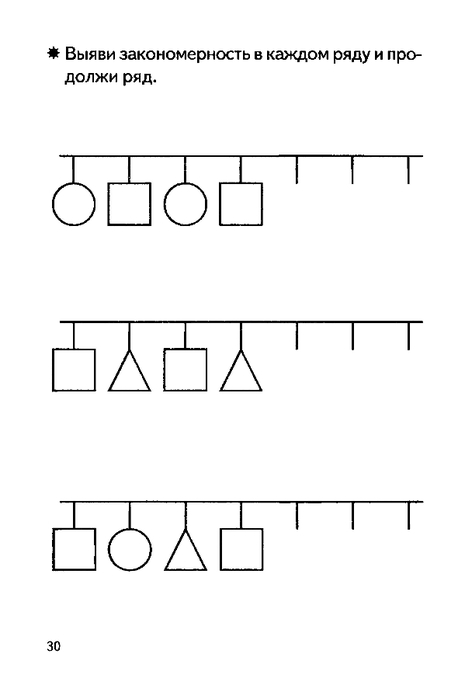
Но и это время можно потратить весело и с пользой. Существует множество интересных занятий, способствующих развитию логики: шарады, игры в слова, паззлы и некоторые настольные игры.
Такое времяпрепровождение позволяет малышу переключиться, отдохнуть и провести время с семьей, а после небольшого перерыва можно снова продолжать тренировки.
Логические упражнения для первоклассников
В интернете есть немало примеров упражнений на логику для детей 7 лет. Рассмотрим самые популярные из них:
- логические задачи. Многим взрослым с детства знакомы различные задачки с подвохом. Чтобы легко решать их, нужно научиться смотреть на описанную в задаче ситуацию под непривычным углом. Нестандартное мышление, которое развивается благодаря подобным играм и упражнениям, очень полезно и для школьников, и для взрослых.
- поиск лишнего предмета. Это задание предлагает ребенку рассмотреть несколько картинок, на которых изображены различные объекты. Нужно найти тот из них, который является здесь лишним.
Для того, чтобы справится с этой игрой, малыш должен детально изучить свойства каждого предмета и их назначение. Например, самолет – это транспорт, он белого цвета, летает, начинается на букву «с». По этим признакам малыш ищет отличия со всеми другими изображениями и выбирает из них то, которое больше всего отличается от других. - ребусы. Это упражнение знакомо большинству взрослых. Когда ребенок часто решает ребусы, он развивает свое ассоциативное мышление. Но выполнение подобных упражнений может быстро ему наскучить, поэтому лучше превращать их в игру и заниматься вместе с родителями. Можно играть на время – это сделает тренировку веселее и добавит соревновательного духа привычным занятиям.
Для того, чтобы справится с этой игрой, малыш должен детально изучить свойства каждого предмета и их назначение. Например, самолет – это транспорт, он белого цвета, летает, начинается на букву «с». По этим признакам малыш ищет отличия со всеми другими изображениями и выбирает из них то, которое больше всего отличается от других.Подобные игры и упражнения – это хорошая возможность развивать навыки ребенка. Но существуют и другие, более эффективные способы тренировать логическое мышление.
Тренажер для детской логики
Как бы не хотелось взять все лучшее и от серьезных занятий, и от игр, совместить все это в одном упражнении не всегда удается.
Но существует головоломка, которая несколько десятков лет назад захватила умы человечества и не теряет своей актуальности до сих пор – это Кубик Рубика.
Эта прекрасная игрушка способствует развитию сразу нескольких навыков и способностей – тренирует моторику рук, участвует в формировании логического, образного и пространственного мышления, укрепляет память. Все это делает Кубик Рубика не только интересным увлечением, но и отличным учителем.
Но все те, кто пытался собрать эту головоломку без предварительной подготовки, чаще всего терпели неудачу. Сегодня есть немало возможностей освоить эту игрушку самостоятельно, но далеко не всем хватит на это терпения. Поэтому многие родители отдают малышей на занятия по обучению скоростной сборке Кубика Рубика, ведь она является отличным тренажером на логику для детей от 7 лет.
Занятия по спидкубингу – это отличная возможность тренировать навыки малышей в интересной и понятной для них форме. Подобный подход разносторонне развивает интеллект школьников и приучает их к полезному и удивительному хобби.
Задания для детей 6-7 лет на логику и мышление: загадки и развивающие игры на развитие логического мышления для девочек и мальчиков
Зачем детям логические задачи?
Можно задаться вопросом: почему малыши очень любят решать различные головоломки, загадки и логические задачки?
Все очень просто. В первую очередь это очень любопытно и интересно. Второй причиной является то, что, когда ребенок решает какие-либо задачки, он старается решить все правильно. И если добивается верного ответа, тогда у малыша поднимается настрой, а также это помогает развитию умственных способностей. Еще одной причиной для решения задачек на логику является то, что увлекательные загадки расширяют кругозор, увеличивают внимательность и сообразительность ребенка.
Логические задачи также помогают детям систематизировать материал и искать скрытый смысл, более того учат размышлять и подводить итоги.
Как легко развивать мышление школьнику при помощи загадок?
Какой самый быстрый путь развить мышление ребенка? Верно! Мышление ребенку 7-8 лет помогут активировать загадки на логику для детей.
А ответы покажут возможный, может быть, неожиданный путь для размышления.
Что тоже очень важно. Зачем ребенку мышление в школе, когда достаточно вроде бы развитого внимания и памяти?
Ан нет. Без мышления он не решит новую задачу. Без мышления он видит каждую как в первый раз, хотя предыдущая была точно такая же, но с другими цифрами и объектами.
Почему ребенок не может применить правила по русскому языку, хотя знает его на зубок? Где была его голова, когда он писал, почему не включилась?
За все это отвечает мышление — умение сравнивать, сопоставлять, делать выводы, критически оценивать. А когда ребенок пойдет в среднюю школу, там начнется геометрия и алгебра, тогда станет совсем грустно.
Поэтому нужно как можно раньше начать отгадывать загадки на логику!
Как же все таки связаны логика и мышление?
Логика, если следовать определениям словарей, это наука о том, как правильно размышлять. А мышление — это то, что изучает логика. Поэтому правильней было бы назвать загадки по логике)
Но это все крючкотворство.
Зачем нужны загадки на логику или на мышление? Чтобы разбудить интерес к мыслительной деятельности. Активизировать его.
Пробудить любопытство к жизни. Чтобы было интересно жить, думать, а не опираться на выученные шаблоны и чужое мнение.
Все это дают загадки и в особенности загадки с неожиданными ответами, с подвохом. Потому что если мы удивляемся неожиданному ответу, радуемся мы испытываем положительные эмоции.
И такой путь мышления закрепляется в памяти без особых усилий. Как закрепляется в памяти информация, полученная на эмоциональном подъеме.
Это одно из важных условий запоминания информации на долгое время. Об этом можно почитать по этой ссылке (откроется в новой вкладке).
Ниже вы увидите загадки-задачки и просто загадки. Решая загадки-задачки, ребенок будет учиться делать выводы из суждений, которые изложены в условии, учиться рассуждать. Это чистая логика.
В логическом мышлении нет ничего сложного. А вот в нижеследующих загадках нужно подключать воображение, творчество, поиск ответа.
Именно поэтому они сложны и ответы порой бывают самыми неожиданными.
Поэтому приступим.
Какие задания нравятся детям?
Чтобы завоевать и удержать внимание ребенка, задания на логику должны быть интересными, яркими, красочными и разнообразными.
Загадки и задачи
Задания, которые побуждают детей мыслить логически, довольно разнообразны. С помощью упражнений, подходящих для детей 6-7 лет, можно:
- научить детей анализировать и сравнивать предметы, систематизировать их, находить закономерности;
- приучить к работе с рисунками и схемами;
- развивать речь;
- освоить порядковый и количественный счет;
- дать понимание взаимосвязей природных явлений.
Для развития логики полезно много беседовать и обсуждать, создавать что-то своими руками. Значительное место отводится и работе с наглядными пособиями – рисунками, книжками, распечатками, раскрасками, фото, разнообразными игрушками.
В 6 и 7 лет уже можно активно использовать математические задачи.
Рассмотрим несколько интересных загадок.
- У Антона большое кислое яблоко, у Ани – большое сладкое. Чем они похожи, а что разное?
- Света и Оля рассматривали картинки в журнале и в книге. Где рассматривала картинки Света, если это не книга?
- У Даши есть 3 пары носков. Сколько всего у нее носков?
- На площадке играли 5 детей. Двое ушли домой, а потом вернулись. Сколько теперь детей на площадке?
- Маша взяла 3 конфеты, а Саша – на 1 больше. Сколько конфет съест Саша?
- По двору ходят утки. Ваня насчитал у них 8 ног. Сколько всего уток?
- В коробке лежит 7 машинок. Сколько мне нужно забрать, чтобы там осталось 3 машинки?
- На дереве висит 6 груш. Дети сорвали по одной, и на дереве осталось 2 груши. Сколько было детей?
- В плитке шоколада есть 6 долек. Сколько раз ее надо разломать, чтобы поделить всю плитку на отдельные дольки?
- Денис принес 3 кубика, а Максим – 4. Сколько кубиков будет в башне, которую вместе построят ребята?
- В кошельке есть деньги, на которые можно купить 2 пачки печенья или 1 коробку конфет. Что стоит дороже?
- На двух полках стоит одинаковое количество книг. С одной забрали 2 книги и поставили на вторую. Сколько книг стало на каждой полке?
- В тарелке лежат 3 апельсина, а в коробке – вдвое больше. Сколько апельсинов находится в коробке?
- Торт разрезали на половины, а потом каждую из них – на 3 части. Сколько кусков получилось?
- Диме 10 лет, Маша на 5 лет младше. Сколько лет Маше?
- Мама испекла к завтраку 12 кексов. Все съели, кроме двух. Сколько осталось?
- На столе лежало 3 яблока. Одно разрезали на половинки. Сколько яблок на столе теперь?
Сколько мне нужно забрать, чтобы там осталось 3 машинки?
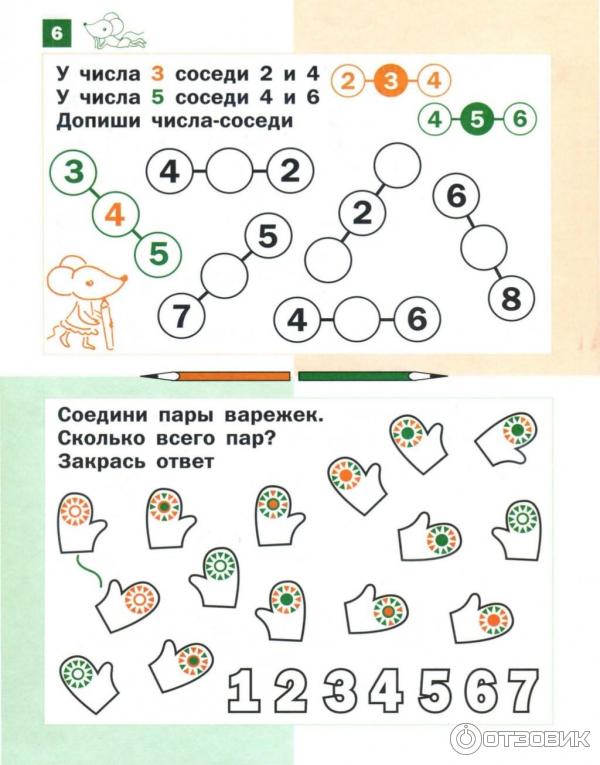Одно разрезали на половинки. Сколько яблок на столе теперь?Задача 1. Про лягушек
Условие: Лягушка ЖУ любит сидеть на розовой кувшинке.
Лягушка ИЯ никогда не выбирает ни розовую, ни голубую.
Вопрос: На какой кувшинке должна сидеть каждая из лягушек?
Ответ:
ЖУ — на розовой, ИЯ — на жёлтой, ЖА — на голубой.
Решение:
Сначала выбираем лягушку, о которой точно известно, на какой кувшинке она хотела бы сидеть. ЖУ – на розовой кувшинке.
Так как ИЯ не выбирает ни розовую, ни голубую, поместим её на жёлтую.
ЖА сидит на оставшейся голубой кувшинке.
Задача 2. Про рыбок и аквариум
Догадайся, сколько рыбок нужно запустить в пустой аквариум.
В каждом последующем аквариуме на одну рыбку больше, чем в предыдущем.
Задача 3. Продолжи ряд изображений
Условие: Картинки расставили в определённом порядке (в виде закономерности).
Задание: Подумай, какой элемент ряда будет следующим.
Закономерность состоит в чередовании неживых и живых предметов.
Задача 4. Карандаши
Выбери подходящий карандаш с соблюдением следующих условий: не синий и не жёлтый, не самый длинный и не самый короткий.
Ответ: Зелёный карандаш.
Задача 5. На постранственное мышление
Условие: На столе лежат квадратные салфетки одинакового размера одна на одной так, как на рисунке. Юра играл с канцелярскими кнопками и приколол салфетки к столу.
Вопрос: Салфетка какого цвета не будет приколота кнопкой?
Ответ: Синяя.
Задача 6. Найди правильное отражение
Условие: Девочка стала перед зеркалом.
Задание: Найди зеркало с её отражением.
Ответ: Зеркало №1.
Комментарий: Девочка смотрит вправо, значит, в отражении она смотрит влево.
Зеркало «разворачивает» изображение.
Развивающие игры для детей 6 лет на логику в домашних условиях
Практически любые виды активности дошкольника, будь то лепка, рисование, чтение, общение и т.
п., активизируют мыслительные процессы. Именно поэтому развивать логическое мышление можно и нужно в домашних условиях на примере самых простых и привычных ситуаций. К примеру, если дошкольник разбросал игрушки по комнате, попросите его собрать их не просто так, а сложив похожие по группам. Затем предложите малышу объяснить, почему он сделал именно так.
Навык сравнения можно тренировать и по дороге домой из детского сада. Предложите ребенку найти, чем отличаются между собой разные деревья, строения, транспорт и т. д.
Приведем и более сложные развивающие игры на логику для детей 5 лет. Прочитайте малышу сказку, а затем вместе перескажите и подробно разберите ее содержание. Затем попросите ребенка выделить, к примеру, наиболее хитрых героев. При этом обратите внимание дошкольника на то, что не все находчивые персонажи являются добрыми. С помощью подобных задач-вопросов на развитие логики дети 5—6 лет учатся классифицировать предметы и явления по переменным признакам.
Приведем еще один пример.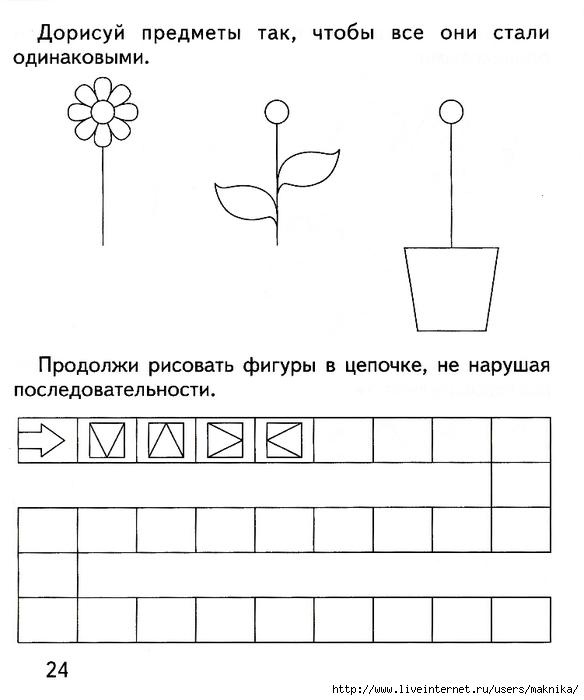
Возьмите три игрушки: тигра, корову и зайца. Разделите их на две группы таким образом, чтобы тигр и заяц оказались вместе, а корова — отдельно. Затем предложите малышу объяснить, по какому принципу созданы группы. Выполняя такие задания, ребенок учится анализировать, классифицировать, обобщать понятия.
Графические
Этот тип развивающих заданий на логику стимулирует мелкую моторику и готовит руку ребенка к письму, поэтому графическим играм в 6-7-летнем возрасте стоит уделить достаточно внимания. К ним относятся все занятия, во время которых ребенок рисует или пишет. К примеру, можно предложить дошкольнику раскрасить картинку, ориентируясь на цифровые обозначения, соответствующие определенному оттенку.
Многим детям нравится писать графические диктанты. Для них используют листы в крупную клетку, взрослый диктует, на сколько клеточек провести линию и в какую сторону, в результате чего возникает какое-то изображение, например, кошки, домика или кораблика.
С помощью подобных диктантов ребенок учится не только проводить ровные линии, но и ориентироваться в пространстве.
Не менее популярны и задания «продолжить узор», «соединить точки», разные прописи и раскраски. Все такие игры активно развивают и логическое мышление, и внимание. Они учат ребенка концентрироваться на задаче, воспитывают усидчивость.
Речевые
Такие игры одновременно с развитием логики стимулируют речевой аппарат. Их использование делает речь ребенка более четкой и чистой, увеличивает словарный запас. Они особенно важны, если ребенку нужны занятия с логопедом из-за каких-либо дефектов речи.
В ходе речевых игр ребенок должен проанализировать информацию, которую услышал, а затем выполнить задание. К примеру, взрослый начнет называть несколько разных слов, а задачей дошкольника будет отыскать между ними различия или что-то общее.
Хорошей речевой игрой является составление рассказа по картинке, ведь он должен быть логичным и последовательным. Эффективны также описания заданных предметов, придумывания ассоциаций, поиск слов, у которых противоположное значение.
Настольные
Эти игры интересны большинству детей. Психологи относят их к самым эффективным для развития мышления и логики, ведь в ходе игры ребенок планирует и размышляет, обдумывает общую стратегию и ходы. Если же привлечь к занятию несколько участников, это будет дополнительно улучшать коммуникативные навыки и учить, как работать в команде.
Ассортимент настольных игр в наши дни довольно большой, поэтому одновременно с освоением таких традиционных вариантов, как нарды, лото или шашки, можно подобрать для ребенка с учетом его интересов и множество других игр. Кроме того, можно использовать и разнообразные подручные материалы, например, спички или счетные палочки.
Логические вопросы и текстовые головоломки
Данные вопросы и головоломки можно загадывать детям по дороге в школу, в поездке, а также можно устроить соревнование на детском торжестве. Если ребенок затрудняется ответить на заданную задачку, можно постепенно делать подсказки, так ребенку будет интереснее.
Задание 1. На ветке сидит птичка. Как отпилить эту веточку так, чтобы не беспокоить птичку?
Ответ: Подождать, пока птичка сама улетит.
Задание 2. Можно ли из капли сделать цаплю?
Ответ: Поменять буквы «к» и «ц».
Задание 3. Поезд мчит на восток со скоростью 80 км/час. В какую сторону летит дым?
Ответ: Когда поезд едет, он не дымит (только если он не загорелся).
Задание 4. Правой или левой рукой правильно мешать сахар в кружке с чаем?
Ответ: Сахар в кружке с чаем правильно мешать ложкой.
Компьютерные
Эта группа игр, пожалуй, наиболее востребована у современных детей. Хотя многие родители и педагоги относятся к таким занятиям настороженно или негативно, но компьютерные игры имеют определенные плюсы, если контролировать их длительность (до 30 минут в день) и контекст (это не должны быть «стрелялки» или «бродилки»). Выполняя квесты, дети учатся мыслить логически, решать интересные задачи, выбирать правильные ответы.
Полезные советы
Стараясь развить у ребенка логическое мышление, занимайтесь регулярно.
При планомерном подходе, отсутствии длительных перерывов и подборе соответствующих возрасту заданий успехи будут наиболее выраженными.
При этом тренировки логики не должны быть слишком длинными, иначе они быстро наскучат ребенку. Дошкольник потеряет интерес и перестанет воспринимать новую информацию, что лишь затруднит дальнейшее развитие. Для детей 6-7 лет продолжительность занятий составляет 20-30 минут.
Подбирая подходящую игру, руководствуйтесь интересами и наклонностями дошкольника. Занятие, которое больше будет привлекать его внимание, непременно станет стимулом к размышлениям и отложится в памяти. К примеру, увлеченному автомобилями мальчику можно предложить задания с использованием разных видов транспорта, а интересующимся пони девочкам отлично подойдут раскраски и головоломки с Пинки Пай, Искоркой и другими любимыми персонажами.
Если задание незнакомое и новое, убедитесь, что перед выполнением ребенок правильно понял его суть.
Если его размышления зашли в тупик, задайте несколько наводящих вопросов.
Будьте терпеливы и не ругайте, если упражнение оказалось сложным, или ребенок отказывается его выполнять. В такой ситуации лучше отложить занятие ненадолго, вернувшись к нему позже, когда дошкольник будет в хорошем расположении духа.
Помните также о том, что хорошую работу мозга обеспечивают правильно спланированный режим дня и полноценное питание. Не перегружайте ребенка дополнительными занятиями, следите за длительностью ночного сна, ограничивайте время у телевизора или компьютера. Ежедневные прогулки, сбалансированный рацион, достаточный отдых – это крайне важные факторы, способствующие лучшему развитию мышления и других психических процессов.
Вместо заключения
Для того чтобы без трудностей решать логические задания, нужно научиться выделять их единые особенности, отмечать закономерности, извлекать предположения, делать проверку, выстраивать ряды доводов, делать выводы.
Таким образом, развитое логическое мышление не только помогает успешно учиться ребенку в школе, но и способствует правильной ориентировке по жизни, принимать нужные решения и идти в верном направлении. Когда человек пытается найти решение логической задаче, то применяет различные виды закономерных построений, повышая тем самым существующие у него знания.
Семь лучших логических игр для обучения детей STEM
Делиться — значит заботиться!
Вовлечение детей в науку, технологии, инженерию и математику (STEM) — это не только программирование или решение математических задач. По сути, STEM действительно направлен на оттачивание способности логически мыслить, чтобы решить насущную проблему.
Один из лучших способов потренировать логическое мышление в юности — играть в веселые логические игры. Во многие игры интересно играть всей семьей или в одиночку.
Как правило, эти игры требуют от ребенка проб и ошибок и пространственного мышления, чтобы решить головоломку.
Попутно они начинают понимать, что если я переверну этот кусочек головоломки, он может подойти! Ребенок подсознательно научился думать о решениях проблем с разных точек зрения. Это основная суть STEM.
Вот некоторые из наших любимых логических игр и головоломок, в которые наши дети играют уже более 5 лет.
В Camelor Jr вам предлагается 48 испытаний с 4 различными уровнями навыков: Starter, Junior, Expert и Master. Цель состоит в том, чтобы использовать блоки, чтобы построить путь, чтобы помочь рыцарю спасти принцессу.
Наличие тем Принцессы и Рыцаря абстрагирует логическое мышление во что-то более конкретное для маленького ребенка. Вместо того, чтобы относиться к этому как к задаче построить путь, ребенок, естественно, хочет найти способ привести Рыцаря к Принцессе.
Блоки со ступенями и башнями разной высоты дополнительно создают игровую среду, знакомую им в реальном мире. Например, как и в реальном мире, вам нужно подниматься по ступенькам, если вы хотите подняться выше.
Игра Camelot Jr со всеми этими красочными кубиками рекомендуется для детей от 4 лет.
Обзоры Camelot Jr
В Trucky 3 цель состоит в том, чтобы заполнить грузовики блоками разного размера. Есть три грузовика разного размера и десять блоков разной геометрической формы.
Изображение с сайта smartgames.eu.Буклет с игрой содержит 48 заданий, в которых вам нужно поместить заданные части блоков в определенные грузовики. Есть 12 испытаний для каждого из четырех уровней сложности (стартер, юниор, эксперт, мастер).
Как и в Camelot Jr, в Trucky 3 элемент игры очень силен. Естественный инстинкт ребенка — наполнить грузовик и иметь возможность толкать его. При этом они постепенно вводят понятие пространственного ограничения и то, что можно сделать, чтобы обойти это ограничение.
Вначале может показаться, что это просто метод проб и ошибок, но подсознательно ребенок учится решать задачу, поворачивая один блок на 90 градусов или пробуя разные наборы блоков, чтобы поместить его в грузовик.
Игра Trucky 3 со всеми этими красочными грузовиками и блоками рекомендуется для детей от 3 лет и старше.
Trucky 3 Reviews
Гравитационный лабиринт — еще одна классика нашей семьи. Это немного похоже на Marble Run, но сложнее, потому что каждый уровень башни имеет разные точки входа и выхода.
По общему признанию, это намного сложнее, чем Camelot Jr и Trucky 3. Много раз я сам попадал в тупик.
Гравитационный лабиринт содержит 60 заданий от новичка до эксперта. Каждое испытание показывает вам начальную и конечную точку испытания, а также конкретные башни, которые должны быть размещены в заранее определенном месте. Цель состоит в том, чтобы разместить оставшиеся башни на сетке так, чтобы шарик мог падать от начала до конца через фиксированные башни.
В этой игре нужно думать о нескольких измерениях. Вы должны думать о том, как вторая башня соединяется с первой башней, и какая вторая башня имеет правильный вход и выход, чтобы правильно соединиться с третьей башней, и так далее, и тому подобное.
Гравитационный лабиринт рекомендуется для детей от 8 лет.
Гравитационный лабиринт Обзоры
На самом деле мы получили настольную игру Gobblet в подарок, и я не особо придал ей значение, когда она ее получила. Но это оказалось настоящей жемчужиной. Это игра в хорошо известную игру крестики-нолики. Цель состоит в том, чтобы сформировать линию из четырех кубков.
Изюминка в том, что кубки (шахматные, как деревянные фигуры) похожи на русских матрешек, которые бывают четырех разных размеров. Таким образом, вы можете поглощать шахматные фигуры своих противников большим кубком, чтобы сделать эту фигуру своей.
В отличие от крестиков-ноликов, в эту игру можно играть без ограничений. Это как смесь крестиков-ноликов, шашек и шахмат, которая требует, чтобы вы думали на пару шагов впереди своих противников.
Настольная игра Gobblet рекомендуется для детей от 7 лет и старше. Хотя я думаю, что ребенок младше 5-7 лет тоже сможет насладиться игрой.
Обзоры настольных игр Gobblet
Ссылка SmartGames IQ Link содержит 120 заданий пяти различных уровней: Starter, Junior, Expert, Master и Wizard.
Каждая задача начинается с размещения некоторых ссылок в заранее определенных областях. Цель состоит в том, чтобы разместить все оставшиеся ссылки на доске, не перемещая начальные ссылки.
SmartGames IQ Link поставляется в автономном компактном футляре, что делает его чрезвычайно удобным для путешествий. Мы использовали их в длительных перелетах. Мы также использовали их, ожидая подачи еды в ресторанах.
SmartGame IQ Link рекомендуется для детей от 8 лет и старше.
SmartGame IQ Link Обзоры
SmartGames IQ Blox похож на IQ Link. Цель состоит в том, чтобы разместить все фигуры на доске. В IQ Blox также есть 120 заданий для уровней Starter, Junior, Expert, Master и Wizard.
Основное отличие состоит в том, что IQ Blox размещает белые стержни на заранее определенных местах на доске, и ребенок должен установить цветные кубики вокруг белых стержней, чтобы выполнить задания.
IQ Blox также немного удобен для детей младшего возраста. Рекомендуется для детей от 6 лет и старше.
У нас есть как IQ Blox, так и IQ Link, так что детям не придется ломать голову над головоломками.
Обзоры SmartGame IQ Blox
Ни один список не будет полным без классической любимой игры Mastermind Game. Это классическая игра, на которой я вырос!
Это игра для двух игроков, в которой один игрок (Codemaker) выбирает последовательность цветных фишек, которую другой игрок должен попытаться сопоставить.
Эта игра — отличное начало для маленьких детей, чтобы они могли весело провести время, изучая основные понятия цветов и узоров. Это также начало дедуктивных рассуждений, поскольку они собирают подсказки от Создателя кодов, чтобы решить, как им следует настроить свою следующую последовательность.
Обзоры SmartGame IQ Blox
Что вам больше всего нравится?
Эти игры были у нас в течение пяти или более лет, и мои дети все еще часто выбирали их, чтобы играть самостоятельно. Также, безусловно, является преимуществом то, что эти игры хорошо сделаны и хорошо спроектированы, так что все можно легко хранить вместе в коробке.
Легко собрать вещи для детей, значит меньше стресса и для мамы.
Эти игры определенно стоят вложений, потому что в них не только играют снова и снова, с течением времени, мы видим, как улучшаются пространственные и аналитические способности наших детей по мере того, как они переходят к более сложным уровням задач в играх. .
Эти навыки в дальнейшем применяются в реальной жизни и в их академической работе. Они учатся пробовать снова и думать о разных способах решения проблемы.
Тебе тоже нравятся логические игры? Какие ваши любимые?
Критическое мышление для детей: занятия, игры и книги
Критическое мышление для детей помогает детям думать за пределами очевидного. Это важный жизненный навык, который требуется во всех сферах жизни.
Критическое мышление — это инструмент, который помогает нам принимать обоснованные и рациональные решения. Это позволяет нам «как» думать и понимать данные и информацию, представленные нам.
Проще говоря, это способность анализировать имеющуюся информацию для принятия логического решения.
Ребенок с критическим складом ума может задавать вопросы, связывать информацию и идеи, делать рациональный выбор и, что наиболее важно, оправдывать свои собственные решения.
Это имеет решающее значение для развития человеческого мозга, поскольку он смещает акцент с пассивного слушателя на активного ученика.
Перейти к интересующему вас разделу!
- Почему важно критическое мышление?
- Критическое мышление для детей
- Игры на критическое мышление для детей
- Книги по критическому мышлению для детей
По мере нашего продвижения в будущее этот навык будет цениться больше, чем когда-либо. Поскольку искусственный интеллект и автоматизация выполняют большую часть работы, основанной на обработке и знаниях, именно этот навык будет поддерживать потребность людей в работе.
Для маленьких детей эта способность превращается в мышление, способствующее росту и обучению на протяжении всей жизни.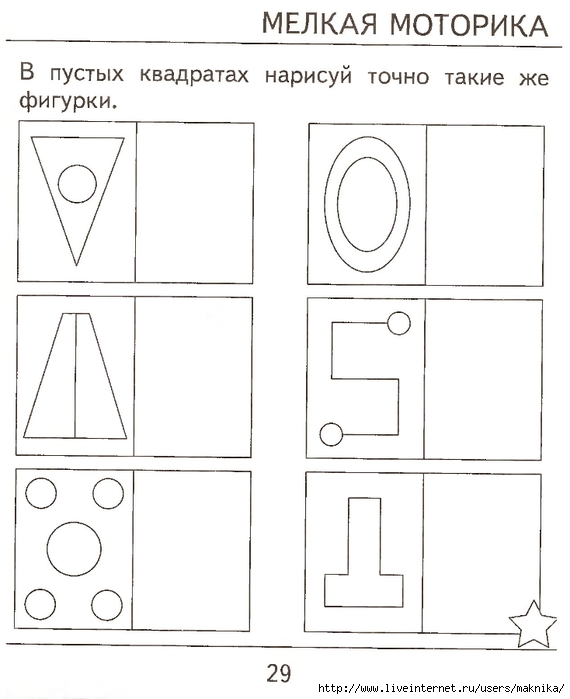
Критическое мышление позволяет детям развивать мышление роста , которое готово поглощать новую информацию, устанавливать значимые связи между существующими знаниями и вновь полученной информацией и, что наиболее важно, использовать свой банк знаний для решения проблем.
Это делает критическое мышление грозным оружием в умственных способностях. Значение критического мышления настолько велико, что оно стало одним из самых жизненно важных навыков 21 века.
При этом маленькие дети, по словам швейцарского психолога Жана Пиаже, до 12 лет умеют мыслить конкретно. Они учатся в основном путем проб и ошибок и не могут мыслить «критически», если их явно не поощрять.
Несмотря на то, что у юных учеников может не быть врожденной схемы для критического мышления, наставник или ободряющий родитель, безусловно, могут изменить ситуацию, заставив их мыслить логически.
Вот где мы, родители и опекуны, должны работать. Нам нужно научить наших детей мыслить критически, чтобы они могли пережить трудности будущего.
Вот наши предложения.
Критическое мышление для детей
1. Развивайте творческие способностиПредложите ребенку нарисовать сцену, чтобы объяснить свои мысли. Нам нужны навыки критического мышления, чтобы изображать наши мысли в картинках.
Вот почему ценится искусство. Это непростая задача. Для детей старшего возраста поиграйте в такие игры, как Pictionary, и попросите их объяснить, что они нарисовали.
2. Играйте в игры на сортировкуНавыки классификации и сортировки отлично подходят для логических рассуждений.
Попросите ребенка отсортировать один и тот же список животных/предметов, используя различные признаки, такие как размер, цвет, геометрия, форма и т. д. Сгруппируйте животных по категориям в зависимости от их среды обитания, пищевых привычек, строения тела, механизма размножения и т. д.
Эти занятия по сортировке помогают детям увидеть различия и сходства между различными группами, тем самым улучшая их понимание.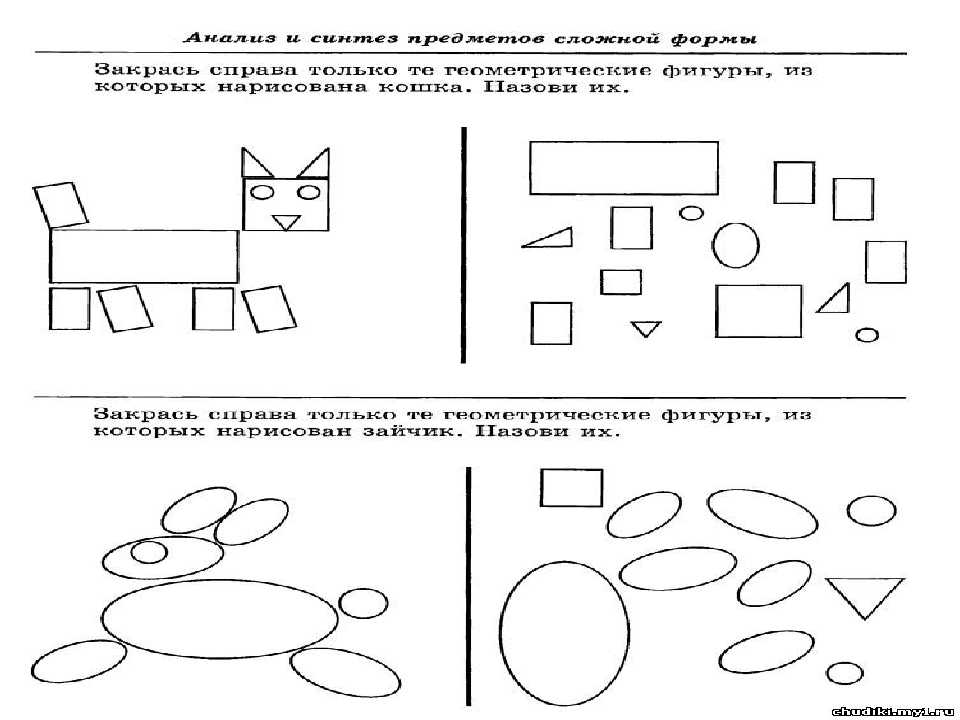
Они отлично подходят для решения проблем у детей. Будь то головоломка, крестики-нолики, лабиринты или что-то еще, что любит ваш ребенок.
Совместное решение головоломок и головоломок поможет вашим детям учиться у вас и формулировать собственную стратегию.
В то время как выполнение этих действий в одиночку может расстраивать детей, игривый ободряющий родитель может иметь большое значение.
Добавьте несколько математических анекдотов между занятиями, чтобы поднять настроение и добавить юмора во время тренировки мозга.
4. Притворная игра с реальной проблемойПридумайте реальную проблему, например нехватку воды, чтобы притвориться, что играете, и попросите их придумать решения. Такие игры помогают детям узнать об окружающей их среде и окружении.
Это также помогает им понять проблемы, с которыми они сталкиваются в реальном мире.
Мотивируйте их не только думать о решениях, но и реализовывать их на своем уровне.
Как будто мы думали, что использование стальной соломинки может уменьшить количество отходов, производимых соломинками, и спасти так много морских жизней. Что касается пластиковых пакетов, мы провели мозговой штурм и сделали тканевые пакеты многоразового использования из старой футболки.
Связанный: Узнайте, как дизайн-мышление для детей помогает вырастить новое поколение людей, решающих проблемы.
5. Творите с кубикамиКубики отлично подходят для развития логических навыков. Они помогают детям дать смысл их воображению. Также они отлично подходят для игры незакрепленными частями.
Каждый раз, когда вы поощряете своего детсадовца использовать старые кубики для новых игр, в его мозгу активизируются нейроны.
6. Вдохновляйте мысли Попросите их подумать над ответами на свои вопросы. Помогите процессу получения ответа, а не предоставления ответа.
Когда они придут к возможному объяснению, попросите их аргументировать свои собственные ответы.
Этот процесс размышления о мышлении – Метапознание поможет им найти недостатки (или поддержку) в своих собственных аргументах и уточнить свое мнение. Таким образом, делая их более критическими мыслителями.
7. Объясните причины и следствияПусть они исследуют и тестируют самостоятельно в безопасной среде. Много открытий было сделано простыми исследованиями. Такие экспедиции часто преподают хороший урок причин и следствий.
Прекрасная игра для обучения причин и следствий — старая классическая игра Marbles. То же самое касается пула и снукера.
Связанный: Научные эксперименты — идеальный способ изучения причин и следствий. Попробуйте несколько из нашего обширного списка дошкольных научных экспериментов.
8. Позвольте им H выдвинуть гипотезыЧитая рассказ, остановитесь на полпути и спросите, что, по их мнению, должно произойти, чем закончится рассказ?
Подобные открытые вопросы активизируют серые клетки и заставляют думать о логических и творческих результатах.
Дайте им время подумать и придумать развернутый ответ.
Вы даже можете использовать ситуации из реальной жизни, чтобы задавать открытые вопросы, например, если вы попали в пробку, попросите их придумать решение, которое могло бы разгрузить пробки.
9. Играйте в игры на угадываниеИгры на угадывание отлично развивают навыки рассуждения. Наш фаворит — «Угадай животных». Дайте подсказки, описывающие животное, а затем пусть ваш ребенок угадает его.
10. Загадывай ихЗагадки — отличный способ активировать нейроны и научить ребенка мыслить логически и критически. И самое приятное — загадки — это СУПЕР весело!
Ваши дети даже не узнают, что вы тайно работаете над их навыками критического мышления. Вот исчерпывающий список загадок, которые помогут вам начать.
11. Dumb Charades Это еще одна простая семейная игра, в которой ребенка просят угадать название фильма (STEM или научно-фантастические фильмы усложняют задачу) — или что-то еще — путем декодирования языка жестов его товарищ по команде.
12. Пусть поиграют в детектива
Оттачивайте навыки критического мышления и мышления вашего ребенка, позволяя ему надеть шляпу детектива.
Простая охота за сокровищами, чтобы найти спрятанный предмет радости, может превратиться в большое удовольствие и критическое мышление для детей.
Для детей постарше познакомьте с основами подходящего для детей исследования места преступления, чтобы они ощутили настоящий азарт и безопасную игровую площадку для тренировки своего критического мышления.
13. Ребусы
Эти креативные визуальные пазлы идеально подходят для развития навыков критического мышления у детей. Они отлично подходят для визуальных учеников, а также тайно работают над навыками грамотности.
Игры на критическое мышление для детей1. Угадай, кто
Это отличная семейная настольная игра, которая развивает критическое мышление. Задача состоит в том, чтобы угадать карту противника, задавая ей/ему правильные вопросы.
Подходит для детей от 6 лет и старше.
2. Connect Four
Connect 4 – это классическая стратегическая игра, которая побудит вашего ребенка критически мыслить и планировать свои действия, чтобы выиграть игру. Connect 4 очень прост в освоении и игре, он отлично помогает развивать мыслительные способности, развлекаясь.
Связанный: Также проверьте эти Увлекательные игрушки для детей , которые тайно учатся играть!
3. Othello
Еще одна игра на критическое мышление для детей от 6 лет, Othello доставляет массу удовольствия! Помимо того, что эта классическая игра вызывает сильное привыкание, она отлично развивает пространственное мышление и навыки логического мышления.
Ищете настольные игры? Ознакомьтесь с нашим Огромным списком настольных игр для детей, чтобы весело провести время всей семьей.
4. Бункеры
Эта игра для одного игрока отлично прогоняет скуку и является идеальной игрой для развития мозга для детей от 5 лет и старше.
Это связано с растущим уровнем проблем, которые постепенно наращивают навыки логического мышления. Аккуратно упакованный, он также отлично подходит для игры в путешествие!
5. Пазл с парковкой
Пазл с парковкой развивает навыки рассуждения и критического мышления у детей от 6 лет и старше. Задача состоит в том, чтобы назначить парковочные места автомобилям в соответствии с карточками-заданиями.
Карточки с заданиями начинаются с простого уровня и расширяются до экспертного уровня, чтобы дети (и взрослые!) искренне чесали затылки.
6. Brainvita
Эта игра с удалением шариков — настоящее удовольствие и идеальная игра для всей семьи. Эта игра-головоломка достаточно проста для понимания, но таит в себе большие трудности.
Есть сообразительный ребенок? Ознакомьтесь с викторинами для детей, чтобы проверить свои знания.
7. Mastermind
Возьмите на себя роль дешифровщика в этой игре Mastermind. Захватывающая и увлекательная игра развивает дедуктивные и логические навыки.
Адаптированная для детей младшего возраста, эта версия поставляется с колышками в виде животных из джунглей и 3 уровнями игры, что делает ее более подходящей для детей от 6 лет и старше.
8. Домино-лабиринт
Домино-лабиринт отлично подходит для геймификации навыков логического и критического мышления. Эта одиночная игра основана на вызове, в котором игрок должен добавить указанные жетоны на доску, чтобы вызвать эффект домино. Подходит для детей от 8 лет и старше.
9. Swish
Это замечательная карточная игра с критическим мышлением для детей от 8 лет и старше. Swish — одна из немногих игр, которая одинаково нравится детям и взрослым. Она отмечена наградами!
10. Игровая площадка Noggin Порыв Дракона
Порыв Дракона — это совместная игра, которая не только учит сплочению команды, но и развивает навыки критического мышления. Эта игра с критическим мышлением, предназначенная для детей от 5 лет и старше, проста в понимании и доставляет массу удовольствия!
Книги по критическому мышлению для детей1.
More-igamiЭто чудесная книга, которая поможет детям научиться критическому мышлению самым простым способом!
Ваши дети даже не подозревают, какие навыки они приобретают, читая эту трогательную историю о мальчике, который открыл для себя радость оригами и готов погрузиться в искусство складывания бумаги.
2. Плоская Земля? Круглая Земля?
Это еще одна жемчужина книги, когда речь идет о том, чтобы научить детей важности критического мышления. Плоская Земля? Круглая Земля? побуждает детей задавать вопросы и не принимать вещи за чистую монету. Настоятельно рекомендуется!
Также см. «Вдохновляющие книги STEM для детей», чтобы добавить STEM к чтению вашего ребенка.
3. Большие идеи для любознательных: введение в философию
Что может быть лучше для поощрения любознательности и критического мышления, чем познакомить детей с давними вопросами жизни.
Дети часто задаются вопросом об этих жизненных истинах, и их чаще затыкают, чем поощряют.
Это ваш шанс вдохновить на размышления о великих вещах жизни!
4. Что делать с коробкой?
Превратите своих детей в новаторов с помощью этой очаровательной книги, в которой рассказывается, что можно сделать из картонной коробки.
Эта книга побудит ваших детей задавать вопросы, удивляться и воплощать в жизнь свои идеи… идеальный способ развить у детей навыки критического мышления.
5. Thingamabob
Thingamabob — это милая юмористическая книга, которая обязательно вызовет критическое мышление у детей в возрасте от 3 лет. Присоединяйтесь к главному герою, который задается вопросом, что же такое на самом деле штуковинабоб, и подвергает сомнению свои собственные предположения.
6. Учимся летать
Это история о невероятной дружбе между человеком и пингвином, который верит, что умеет летать!
Вместе они задают вопросы, проектируют и строят, чтобы открыть секреты летания. Очень рекомендую, эта книга — настоящее сокровище!
7.
Покусывая мозг Эйнштейна: хорошее, плохое и фальшивое в наукеЕсли и может быть краткий курс критического мышления для детей, то эта книга возглавляет список. Это идеальное руководство по критическому мышлению.
Он предлагает отличный способ отличить фальшивые факты от реальной науки. Веселая и интерактивная, эта книга просто восхитительна!
8. Дом для птички
Это красивая история о дружбе и о том, как можно использовать критическое мышление не только для решения научных задач, но и для помощи другу. Отличная книга по разным оценкам — грамотность, иллюстрации и важные уроки, которые она преподносит. Идеально подходит для детей от 5 лет и старше.
9. Совершенно логично
Если вы ищете книгу, чтобы проверить навыки критического мышления вашего ребенка, не ищите дальше. Perfectly logic содержит 100 головоломок и головоломок, которые будут постепенно бросать вызов вашему ребенку.
10. Thinking Like a Lawyer
Выйдя из учителя, адвоката, педагога, а затем новатора, вы можете многого ожидать от этой книги, и это правильно! Одна из лучших книг для ознакомления детей с инструментами критического мышления.