Индивидуальные достижения в вузах России 2020
Выберите город, в который хотите поступать АбаканАльметьевскАнапаАрхангельскАстраханьБакуБалашихаБарнаулБелгородБелорецкБиробиджанБлаговещенскБрянскБуденновскВеликий НовгородВладивостокВладикавказВладимирВолгоградВологдаВоронежВыборгВышний ВолочекГеленджикГрозныйДмитровДушанбеЕкатеринбургЕлабугаЕлецЕреванЕссентукиЖелезногорскЗлатоустИвановоИжевскИркутскКазаньКалининградКалугаКаменск-УральскКемеровоКировКирово-ЧепецкКисловодскКонаковоКраснодарКрасноярскКурганКурскЛипецкМагаданМагнитогорскМайкопМахачкалаМинскМичуринскМоскваМурманскНабережные ЧелныНижневартовскНижнекамскНижний НовгородНижний ТагилНовомосковскНовороссийскНовосибирскНорильскНур-Султан (Астана)ОбнинскОмскОрелОренбургОрскПензаПермьПетрозаводскПетропавловск-КамчатскийПодольскПсковПятигорскРжевРостов-на-ДонуРязаньСалехардСамараСанкт-ПетербургСаранскСаратовСаяногорскСевастопольСерпуховСимферопольСмоленскСосновый БорСочиСтавропольСтарый ОсколСтерлитамакСургутСыктывкарТаганрогТамбовТашкентТверьТольяттиТомскТулаТюменьУлан-УдэУльяновскУфаУхтаХабаровскХанты-МансийскХимкиЧебоксарыЧелябинскЧереповецЧеркесскЧитаЭлектростальЮжно-СахалинскЯкутскЯрославль
Пожалуйста, выберите, кем вы являетесь Я абитуриент Я сотрудник ВУЗа Я родитель абитуриента Студент колледжа Школьник до 11-го класса Специалист Бакалавр Магистр Я учитель в школе
Регистрируясь через данную форму, я соглашаюсь с политикой конфеденциальности и согласен на обработку персональных данных.
Хочу, что вы отправляли мне индивидуальные подборки и лучшие предложения от вузов по нужным мне критериям.

Сводная таблица нормативов комплекса ГТО создана на основании Приказа Министерства спорта Российской Федерации от 19.06.2017 г. № 542 «Об утверждении государственных требований Всероссийского физкультурно-спортивного комплекса «Готов к труду и обороне» (ГТО) на 2018-2021 годы»
6 Ступень (возрастная группа от 18 до 29 лет)
Б — бронзовый знак
С — серебряный знак
З — золотой знак
Мужчины
| Обязательные испытания | |||||||
| 1. | Бег на 30 м. (секунд) | 4,8 | 4,6 | 4,3 | 5,4 | 5 | |
| …или бег на 60 м. (секунд) | 9 | 8,6 | 7,9 | 9,5 | 9,1 | 8,2 | |
| …или бег на 100 м. (секунд) | 14,4 | 14,1 | 13,1 | 15,1 | 14,8 | 13,8 | |
| 2. | Бег на 3 км (минут, секунд) | 14.30 | 13.40 | 12.00 | 15.00 | 14.40 | 12.50 |
| 3. | Подтягивание на высокой перекладине (раз) | 10 | 12 | 15 | 7 | 9 | 13 |
| …или сгибание и разгибание рук в упоре лежа на полу (раз) | 28 | 32 | 44 | 25 | 39 | ||
| …или рывок гири 16 кг (раз) | 21 | 25 | 43 | 19 | 23 | 40 | |
| 4. | Наклон вперед из положения стоя (от уровня скамьи – см) | 6 | 8 | 13 | 5 | 7 | 12 |
| Испытания по выбору | |||||||
| 5. | Челночный бег 3х10 м. (секунд) | 8 | 7,7 | 7,1 | 8,2 | 7,9 | 7,4 |
| 6. | Прыжок в длину с разбега (см) | 370 | 380 | 430 | — | — | |
| …или прыжок в длину с места толчком двумя ногами (см) | 210 | 225 | 240 | 205 | 220 | 235 | |
| 7. | Метание спортивного снаряда весом 700 г (метров) | 33 | 35 | 37 | 33 | 35 | 37 |
| 8. | Поднимание туловища из положения лёжа на спине (раз за 1 мин) | 33 | 37 | 48 | 30 | 35 | 45 |
| 9. | Бег на лыжах на 5 км.(минут, секунд) | 27.00 | 25.30 | 22.00 | 27.30 | 26.30 | 22.30 |
| …или кросс на 5 км (минут, секунд) | 26.00 | 25.00 | 22.00 | 26.30 | 26.00 | 22.30 | |
| 10. | Плавание на 50 м. (минут, секунд) | 1.10 | 1.00 | 0.50 | 1.15 | 01.05 | 0.55 |
| 11. | Стрельба из пневматической винтовки из положения сидя или стоя с опорой локтей о стол или стойку, дистанция – 10 м. (очки) | 15 | 20 | 25 | 15 | 20 | 25 |
| …или стрельба из пневматической винтовки с диоптрическим прицелом или из «электронного оружия» | 18 | 25 | 30 | 18 | 25 | 30 | |
| 12. | Самозащита без оружия (очки) | 15-20 | 21-25 | 26-30 | 15-20 | 21-25 | 26-30 |
| 13. | Туристский поход с проверкой туристских навыков (протяженность не менее, км) | 15 | |||||
| Количество испытаний, которые необходимо выполнить для получения знака отличия | 7 | 8 | 9 | 7 | 8 | 9 | |
Женщины
| Обязательные испытания | |||||||
| 1. | Бег на 30 м. (секунд) | 5,9 | 5,7 | 5,1 | 6,4 | 6,1 | 5,4 |
| …или бег на 60 м. (секунд) | 10 , 9 | 10,5 | 9,6 | 11,2 | 10,7 | 9,9 | |
| …или бег на 100 м. (секунд) | 17,8 | 17,4 | 16,4 | 18,8 | 18,2 | 17 | |
| 2. | Бег на 2 км (минут, секунд) | 13.10 | 12.30 | 10.50 | 14.00 | 13.10 | 11.35 |
| 3. | Подтягивание на низкой перекладине 90 см (раз) | 10 | 12 | 18 | 9 | 11 | 17 |
| …или сгибание и разгибание рук в упоре лежа на полу (раз) | 10 | 12 | 17 | 9 | 11 | 16 | |
| 4. | Наклон вперед из положения стоя (от уровня скамьи – см) | 8 | 11 | 16 | 7 | 9 | 14 |
| Испытания по выбору | |||||||
| 5. | Челночный бег 3х10 м. (секунд) | 9 | 8,8 | 8,2 | 9,3 | 9 | 8,7 |
| 6. | Прыжок в длину с разбега (см) | 270 | 290 | 320 | — | — | — |
| …или прыжок в длину с места толчком двумя ногами (см) | 170 | 180 | 195 | 165 | 175 | 190 | |
| 7. | Поднимание туловища из положения лежа на спине (раз за 1 мин) | 32 | 35 | 43 | 24 | 29 | 37 |
| 8. | Метание спортивного снаряда весом 500 г. (метров) | 14 | 17 | 21 | 13 | 15 | 18 |
| 9. | Бег на лыжах на 3 км. (минут, секунд)… | 21.00 | 19.40 | 18.10 | 22.30 | 20.45 | 18.30 |
| …или кросс на 3 км. (минут, секунд) | 19.15 | 18.30 | 17.30 | 22.00 | 20.15 | 18.00 | |
| 10. | Плавание на 50 м. (минут, секунд) | 1.25 | 1.15 | 1.00 | 1.25 | 1.15 | 1.00 |
| 11. | Стрельба из пневматической винтовки из положения сидя или стоя с опорой локтей о стол или стойку, дистанция – 10 м. (очки) | 15 | 20 | 25 | 15 | 20 | 25 |
| …или стрельба из пневматической винтовки с диоптрическим прицелом или из «электронного оружия» | 18 | 25 | 30 | 18 | 25 | 30 | |
| 12. | Самозащита без оружия (очки) | 15-20 | 21-25 | 26-30 | 15-20 | 21-25 | 26-30 |
| 13. | Туристский поход с проверкой туритских навыков (протяженность не менее, км) | 15 | |||||
| Количество испытаний, которые необходимо выполнить для получения знака отличия | 7 | 8 | 9 | 7 | 8 | 9 | |
Испытания по бегу на лыжах проводятся при наличие климатических и погодных условий. В противном случае эта дисциплина заменяется на кросс — бег по пересеченной местности.
сколько баллов добавляет к ЕГЭ
Стопроцентные шансы попасть в престижный вуз дают максимально высокие результаты по нужным дисциплинам единого госэкзамена и победа или призовые места в предметных олимпиадах школьников. Но и спортивные достижения абитуриентов при поступлении в университеты и институты тоже идут в зачет: от одного до пяти баллов к итоговой сумме, заработанной на ЕГЭ, добавляет ГТО. Это станет хорошим подспорьем абитуриентам, подающим заявления в вузы с большим конкурсом, на итог которого могут повлиять даже полбалла.Как получить
Сдать нормативы ГТО может любой желающий, начиная с 6 летнего возраста. Но при поступлении в вуз вес будут иметь результаты только последнего года – значок за 9 класс учитываться не будет. Кроме того, в зачет идут лишь высшие (золотые) достижения ГТО.
Для возрастной категории от 16 до 17 лет тест предполагает обязательные и дополнительные испытания. В первую группу входят:
- бег на 30,60, 100, 2000 или 3000 метров;
- подтягивание, отжимания или рывок гири в 16 кг;
- наклоны веред на гимнастической скамье.
По выбору можно сдать:
- челночный бег;
- прыжки в длину;
- пресс на время;
- плавание;
- лыжи или кросс по пересеченной местности;
- стрельба;
- самозащита;
- туристический поход.
Чтобы получить золотой значок ГТО, нужно пройти тест по высшей планке нормативов. Они дифференцированы для юношей и девушек. Причем различны не только итоговые значения, но и техника выполнения некоторых заданий (подтягиваний). Необходимый для зачета диапазон результатов обязательных испытаний представлен на рисунке.
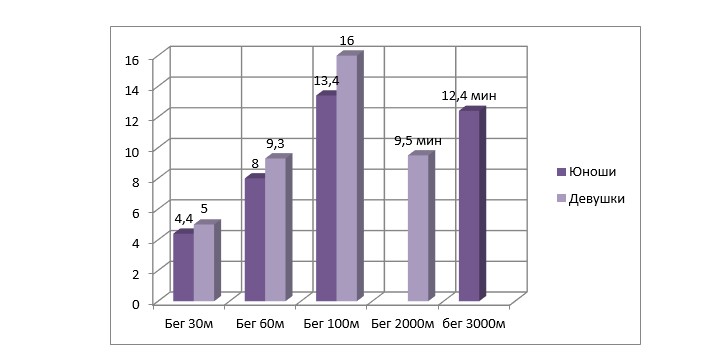
Все нормативы сдаются по собственному желанию, никакой оплаты за участие в сдаче не предусмотрено. От физкультурника требуется только документ, удостоверяющий личность и справка от врача об отсутствии медицинских противопоказаний к физическим нагрузкам.
Сколько баллов дает ГТО
Единого норматива по начислению баллов за ГТО для поступающих в вузы не существует. Каждое высшее учебное заведение самостоятельно определяет для себя приемлемые пороги.
Зачет баллов за золотой значок ГТО вузы начали практиковать с 2015 года. Естественно, все максимально возможные за личные достижения 10 дополнительных бонусных пунктов только за один здоровый дух рейтинговые учебные заведения не зачтут. Некоторые университеты к спортивным достижениям могут отнестись более лояльно и предоставить сразу 4 балла или принять к рассмотрению серебряный значок. А в других максимум, на что можно рассчитывать, – 1 балл.
Актуальный на 2019 год разброс значений допустимых бонусов за спортивные достижения представлен ниже.
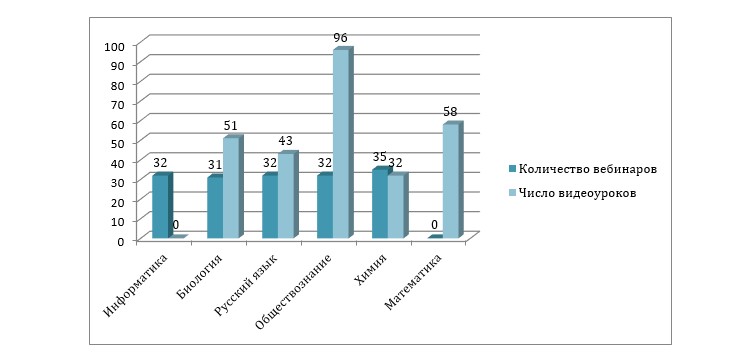
В общем, при поступлении в вузы баллы за ГТО помогут увеличить сумму, набранную на ЕГЭ, но больше всего спортивные достижения абитуриентов по понятным причинам ценят институты физкультуры – они и дают максимум бонусов (до 5) за здоровый дух и приверженность активному образу жизни.
Нормы ГТО 2020: таблица нормативов для школьников
В 2020 году продолжает свою работу физкультурно-оздоровительный комплекс ГТО, целью которого является популяризация среди граждан РФ спорта и здорового образа жизни. Таблицы нормативов отличаются в зависимости от возрастных групп, которые разделены на 11 ступеней и имеют три уровня сложности. За выполнение нормы, которая оценивается в соответствии с видом испытания, участник получает знак отличия, благодаря которому можно будет получить дополнительные привилегии при поступлении в ВУЗ.
Организационные моменты
Физкультурно-спортивный комплекс «Готов к труду и обороне» был разработан по инициативе президента РФ. Эта идея не является ноу-хау и уже использовалась в Советском Союзе, однако, после его распада прекратила свое существование. В 2014 году Владимир Путин внес предложение о возобновлении старой доброй традиции, которая играет важную роль в поддержке здоровья граждан.
Главными задачами комплекса являются:
- привлечение к спорту населения всех возрастов;
- пропаганда здорового образа жизни, начиная со школьной скамьи;
- улучшение общего состояния здоровья каждого гражданина;
- патриотическое воспитание.
При успешном прохождении всех утвержденных испытаний участник может получить один из трех видов знаков отличия, которые имеют различное достоинство:
- бронза;
- серебро;
- золото.
Награда представляет собой значок с обязательным подтверждающим документом, выполненный из железа с покрытием, имитирующим соответствующий драгоценный металл.

В ГТО могут участвовать граждане РФ в возрасте от 6 до 70 лет и старше, если они здоровы и могут заниматься физкультурой в основной группе. Для этого необходимо иметь подтверждающее медицинское заключение.
Для участия в ВФСК «Готов к труду и обороне» необходимо выполнить следующие несложные шаги:
- Зарегистрироваться на официальном портале www.gto.ru.
- Заполнить заявку участника.
- Пройти медицинский осмотр и получить документ, который отвечает требованиям медико-санитарных норм для присвоения группы здоровья и получения разрешения для участия в спортивных соревнованиях.
- Непосредственное прохождение самих испытаний.
Прохождение комплекса ГТО предусмотрено в специализированных Центрах тестирования, которые организованы в пределах субъектов РФ. Организационный комитет составляет график прохождения тестов с указанием соответствующей спортивной площадки. Узнать, где расположен ближайший Центр, можно на официальном сайте ГТО в Личном кабинете, который будет доступен после регистрации.

Нельзя пройти все установленные испытания за один день. Это противоречит Положению о прохождении ГТО и не может причислять к оздоровительному мероприятию. Необходимо правильно рассчитывать свои силы для достижения лучших показателей.
Участие в ГТО может быть реализовано в годовой отчетный период, который будет отличаться в зависимости от ступени тестирования. В 2020 календарном году пройти испытания согласно установленным нормам смогут мужчины и женщины, которым уже исполнилось 18 и более лет, и они не являются школьниками (VI-XI ступени). Для взрослого населения отчетный период совпадает с календарным годом и имеет поквартальную градацию (с I по IV квартал). В 2020 году график тестирований для взрослых будет выглядеть следующим образом:
- I квартал: с 01.01.2020 по 31.03.2020;
- II квартал: с 01.04.2020 по 30.06.2020;
- III квартал: с 01.07.2020 по 30.09.2020;
- IV квартал: с 01.10.2020 по 31.12.2020.
Для школьников предусмотрены другие временные рамки. Дети школьного возраста могут участвовать в комплексе спортивных мероприятий в течение учебного года. Таким образом, для них отчетный период в новом учебном году считается с 01.07.2019 по 30.06.2020.
Участие в комплексе ГТО не может быть навязано детям (или гражданам из других возрастных групп) и не является обязательной составляющей школьных уроков физкультуры. Прохождение испытаний в ВФСК осуществляется исключительно на добровольной основе. Также, нежелание их выполнять или отсутствие достижений в ГТО не могут влиять на итоговую оценку учащегося.

Нормы ГТО для школьников
В 2019-2020 учебном году дети школьного возраста должны будут сдать определенное количество упражнений в зависимости от принадлежности к возрастной группе. Нормы ГТО описаны в таблицах нормативов и утверждаются уполномоченными органами правительства РФ.
Результаты успешно выполненных упражнений записываются в протокол, после чего вносятся в базу данных ВФСК «ГТО» и отображаются в Личном кабинете участника на официальном портале. Получение нагрудного знака будет основано на следующих нормативах для детей школьного возраста:
Нормативы для возрасты 6-8 лет
Нормативы для возраста 9-10 лет
Нормативы для возраста 11-12 лет
Нормативы для возраста 13-15 лет
Нормативы для возраста 16-17 лет
Если участник не смог достигнуть установленного минимума, у него еще будет шанс пересдать тест. В общей сумме можно три раза перевыполнять одно упражнение в течение одного учебного года. Для пересдачи составляется отдельный индивидуальный график с обязательным условием – перерыв в две недели между прохождением тестов.

Почетный значок будет соответствовать нижней планке полученных результатов. Например, если участник получил хотя бы одну «бронзу» за выполненные упражнения, то в итоге ему будет присвоена бронзовая награда.
Бонусы и привилегии для школьников
Наличие награды за прохождение ГТО, которая соответствуют нормам, будет учитываться при поступлении учащегося в ВУЗ. Абитуриенту могут быть начислены дополнительные баллы на основании правил и требований данного высшего учебного заведения. Информацию о количестве дополнительных баллов при предоставлении нагрудного значка и удостоверения к нему следует уточнять непосредственно в ВУЗе.
В таблице ниже приведены несколько примеров поощрения индивидуальных достижений в ГТО в крупных ВУЗах:
| ВУЗ | Баллы на золотой знак |
|---|---|
| МГУ им. М.В. Ломоносова | 2 |
| РАМ им. Гнесиных | 1 |
| МГТУ им. Н.Э. Баумана | 4 |
| РГУФКСМиТ | 5 |
| МГПУ | 5 |
| РУДН | 3 |
| МГИМО | 1 |
При наличии золотого знака отличия студенту может быть увеличена государственная стипендия, что регулируется нормативными документами Министерства образования и науки.
Читайте также:
 Загрузка…
Загрузка…Заметили опечатку на сайте? Мы будем благодарны вам, если вы выделите ее и нажмете Ctrl + Enter
Получать дополнительные баллы к сумме ЕГЭ — это всегда приятно, согласитесь? И здесь есть возможность выбора с учетом собственных талантов и навыков. Посмотрим, как именно значок ГТО и другие спортивные достижения могут помочь в поступлении в вуз.
В этой статье:
Что такое дополнительны баллы?
Дополнительные баллы — это про ваши индивидуальные достижения. Вузы все чаще ценят абитуриентов, которые заняты в различных других активностях помимо учебы. Такие критерии университеты могут вводить сами, поэтому одни вузы будут давать баллы за волонтерскую деятельность, а другие не будут. Здесь, как говорится, хозяин — барин.
Получается такая незатейливая схема:
Баллы ЕГЭ/Вступительные испытания + Дополнительные баллы (максимум — 10) = Ваш итоговый вступительный балл

ГТО и спортивные заслуги как способ получить дополнительные баллы
Важно: при совпадении количества баллов у абитуриентов каждый случай приемная комиссия будет рассматривать в индивидуальном порядке. Иными словами, в некоторых случаях отдать предпочтение могут абитуриенту с более высокими баллами ЕГЭ по профильному предмету.
ГТО
ГТО («готов к труду и обороне») — еще одна аббревиатура, которая помогает будущим студентам попасть в вузы. На самом деле истоки программы ГТО идут к одной простой цели — мотивировать людей больше заниматься спортом и вести здоровый образ жизни.
Чтобы получить заветный значок нужно сдать установленные Министерством спорта РФ нормативы для пододящей возрастной группы. Имейте в виду, что нормативы для мужчин сложнее нормативов для женщин. По результатам можно получить золотой, серебряный или бронзовый значок.
Важно: в основном вузы дают дополнительные баллы только за золотой знак!
Чтобы пройти такое испытание необходима регистрация на сайте ГТО, однако во многих школах сами учителя координируют этот процесс.

Прецедура регистрации выглядит на удивление просто
После регистрации подаете заявку, подтверждаете свою личность и ждете своего уведомления, куда и когда явиться для сдачи. Обычно в каждом населенном пункте есть специальные центры тестирования.
Сдать нормативы можно с сентября по июнь. Также в течение года можно пересдать 3 раза, но интервал должен быть не менее двух недель.
Бонус: при получении золотого значка можно претендовать на повышенную стипендию в университете.
Другие спортивные заслуги
Это не про «Я во дворе лучше всех бегаю». Это про серьёзные спортивные достижения, которые (в отличие от ГТО) нельзя так быстро и просто получить.
Таким образом, получить дополнительные баллы за спортивные заслуги можно, если вы:
- чемпион или призер Олимпийских, Паралимпийских и Сурдлимпийских игр;
- чемпион мира или Европы.
Также эти достижения могут помочь поступить на профильные специальности в спортивные вузы.
Важно: любое ваше спортивное достижение должно быть подтверждено документом.
Сколько баллов дают вузы за ГТО и спортивные заслуги?
Посмотрим по вузам, на какое количество баллов можно претендовать:

Челночный бег, его достоинства. Бег и ходьба – естественные упражнения, которые человек использует по замыслу природы, как средство передвижения и обеспечения жизненных потребностей. Эти упражнения физически развивают человека, стимулируют мышечный тонус, гармонически улучшают форму тела.
Челночный бег разработан человеком для развития дополнительных качеств (выносливости, быстроты реакции, ловкости, умения координировать движения), при подготовке футболистов, баскетболистов, боксеров, легкоатлетов, других спортсменов к соревнованиям.
Дополнительные качества вырабатываются благодаря специфике челночного бега: повторяющиеся движения в противоположном направлении с резким изменением направления движения в конце промежуточной дистанции.
Нормативы по челночному бегу
Нормативы челночного бега для школьников по классам
Упражнение челночный бег в школах | Мальчики | Девочки | ||||
| 5 | 4 | 3 | 5 | 4 | 3 | |
| 3х10 м (сек.) | 9.9 | 10.8 | 11,2 | 10.2 | 11,3 | 11,7 |
| 4×9 м, сек | 12,0 | 12,8 | 13,2 | 12,4 | 12,8 | 13,2 |
| 3×10 м, сек | 9,1 | 10,0 | 10,4 | 9,7 | 10,7 | 11,2 |
| 3×10 м, сек | 8,8 | 9,9 | 10,2 | 9,3 | 10,3 | 10,8 |
| 3×10 м, сек | 8,6 | 9,5 | 9,9 | 9,1 | 10,0 | 10,4 |
| 4×9 м, сек | 10,2 | 10,7 | 11,3 | 10,5 | 11,0 | 11,7 |
| 4×9 м, сек | 10,0 | 10,5 | 11,5 | 10,3 | 10,7 | 11,5 |
| 4×9 м, сек | 9,8 | 10,3 | 10,8 | 10,1 | 10,5 | 11,3 |
| 4×9 м, сек | 9,6 | 10,1 | 10,6 | 10,0 | 10,4 | 11,2 |
| 4×9 м, сек | 9,4 | 9,9 | 10,4 | 9,8 | 10,2 | 11,0 |
| 4×9 м, сек | 9,3 | 9,7 | 10,2 | 9,7 | 10,1 | 10,8 |
| 4×9 м, сек | 9,2 | 9,6 | 10,1 | 9,8 | 10,2 | 11,0 |
Используются для оценки уровня физической подготовки человека. Нормативы челночного бега 3*10 м для школьников разработаны в зависимости от возраста (7-17 лет), пола и уровня подготовки (высокий, средний, низкий). Например, для мальчиков 7 лет с низким уровнем подготовки норматив составляет 11, 2 сек., а для девочки 11,7 сек. Для юноши 17 лет с высоким уровнем подготовки норматив 7,2 сек., а для девушки 8,7 сек.
В нормах ГТО челночный бег 3*10 м предусмотрен в качестве обязательного упражнения для 1-ой возрастной группы (6-8 лет). Для сдачи норматива золотого, серебряного и бронзового знака мальчик должен преодолеть эту дистанцию соответственно за 9,2; 10,1 и 10,4 сек., а девочка за 9,7; 10,7 и 10,9 сек.
ГТО нормативы по челночному бегу 3х10м
| Челночный бег 3*10 м (с) | Мальчики | Девочки | ||||
 |  |  |  |  |  | |
| 1 ступень (6-8 лет) | 10,3 | 10,0 | 9,2 | 10,6 | 10,4 | 9,5 |
| 2 ступень (9-10 лет) | 9,6 | 9,3 | 8,5 | 9,9 | 9,5 | 8,7 |
| 3 ступень (11-12 лет) | 9,0 | 8,7 | 7,9 | 9,4 | 9,1 | 8,2 |
| 4 ступень (13-15 лет) | 8,1 | 7,8 | 7,2 | 9,0 | 8,8 | 8,0 |
| 5 ступень (16-17 лет) | 7,9 | 7,6 | 6,9 | 8,9 | 8,7 | 7,9 |
Мужчины | Женщины | |||||
| 6 ступень (18-24 лет) | 8,0 | 7,7 | 7,1 | 9,0 | 8,8 | 8,2 |
| 6 ступень (25-29 лет) | 8,2 | 7,9 | 7,4 | 9,3 | 9,0 | 8,7 |
| 7 ступень и далее | не проводится | |||||
Нормативы 3х10 для студентов ВУЗов
Для вузов | Юноши | Девушки | ||||
5 | 4 | 3 | 5 | 4 | 3 | |
| 3х10 м (сек.) | 7,3 | 8,0 | 8,2 | 8,4 | 8,7 | 9,3 |
Для студентов также предусмотрены уроки физкультуры, и нормативы могут отличаться по ВУЗам.
Челночный бег нормативы мвд
Для вступления на службу по контракту
| Упражнение | Минимальные требования | |||
Мужчины | Женщины | |||
до 30 лет | >30 лет | до 25 лет | >25 лет | |
| Челночный бег 10×10 м | 28,5 | 29,5 | 38,0 | 39,0 |
Нормативы 10х10м для МВД и МЧС на оценку по возрастам / (сек) | |||
| Возраст | Оценка | ||
5 | 4 | 3 | |
| Для мужчин | |||
| до 30 лет | 25 | 26 | 27 |
| 30-35 лет | 26 | 27 | 28 |
| 35-40 лет | 29 | 30 | 31 |
| 40-45 лет | 32 | 33 | 34 |
| 45-50 лет | 34 | 35 | 36 |
| 50 и старше | 37 | 38 | 39 |
| Для женщин | |||
| до 25 лет | 32 | 34 | 36 |
| 25-30 лет | 34 | 36 | 38 |
| 30-35 лет | 40 | 42 | 44 |
| 35-40 лет | 48 | 50 | 52 |
В спецназе ориентируются на результат меньше 25 секунд 10*10 метров
Нормативы челночного бега для военнослужащих / таблица начисления балов 10х10м | ||||
Балы | Мужчины (сек) | Женщины < 30 лет | Женщины > 30 лет | |
| 100 | 24,0 | 29,0 | 31,0 | |
| 99 | 24,1 | 29,1 | 31,1 | |
| 98 | 24,2 | 29,2 | 31,2 | |
| 97 | 24,3 | 29,3 | 31,3 | |
| 96 | 24,4 | 29,4 | 31,4 | |
| 95 | 24,5 | 29,5 | 31,5 | |
| 94 | 24,6 | 29,6 | 31,6 | |
| 93 | 24,7 | |||
| 92 | 24,8 | 29,7 | 31,7 | |
| 91 | 24,9 | 29,8 | 31,8 | |
| 90 | 25,0 | 29,9 | 31,9 | |
| 89 | 25,1 | |||
| 88 | 25,2 | 30,0 | 32,0 | |
| 87 | 25,3 | 30,1 | 32,1 | |
| 86 | 25,4 | 30,2 | 32,2 | |
| 85 | 25,5 | |||
| 84 | 25,6 | 30,3 | 32,3 | |
| 83 | 25,7 | 30,4 | 32,4 | |
| 82 | 25,8 | 30,5 | 32,5 | |
| 81 | 25,9 | |||
| 80 | 26,0 | 30,6 | 32,6 | |
| 79 | 30,7 | 32,7 | ||
| 78 | 30,8 | 32,8 | ||
| 77 | 26,1 | |||
| 76 | 30,9 | 32,9 | ||
| 75 | 31,0 | 33,0 | ||
| 74 | 26,2 | 31,1 | 33,1 | |
| 72 | 31,2 | 33,2 | ||
| 71 | 26,3 | 31,3 | 33,3 | |
| 70 | 31,4 | 33,4 | ||
| 68 | 26,4 | 31,5 | 33,5 | |
| 66 | 31,6 | 33,6 | ||
| 65 | 26,5 | 31,7 | 33,7 | |
| 63 | 31,8 | 33,8 | ||
| 62 | 26,6 | |||
| 61 | 31,9 | 33,9 | ||
| 60 | 32,0 | 34,0 | ||
| 59 | 26,7 | 32,2 | 34,2 | |
| 58 | 32,4 | 34,4 | ||
| 57 | 32,6 | 34,6 | ||
| 56 | 26,8 | 32,9 | 34,9 | |
| 55 | 33,1 | 35,1 | ||
| 54 | 33,3 | 35,3 | ||
| 53 | 26,9 | 33,5 | 35,5 | |
| 52 | 33,7 | 35,7 | ||
| 51 | 34,0 | 36,0 | ||
| 50 | 27,0 | 34,1 | 36,1 | |
| 49 | 34,2 | 36,2 | ||
| 48 | 34,3 | 36,3 | ||
| 47 | 27,1 | 34,4 | 36,4 | |
| 46 | 34,5 | 36,5 | ||
| 45 | 34,6 | 36,6 | ||
| 44 | 27,2 | 34,7 | 36,7 | |
| 43 | 34,8 | 36,8 | ||
| 42 | 34,9 | 36,9 | ||
| 41 | 27,3 | 35,0 | 37,0 | |
| 40 | 35,1 | 37,1 | ||
| 39 | 35,2 | 37,2 | ||
| 38 | 27,4 | 35,3 | 37,3 | |
| 37 | 35,4 | 37,4 | ||
| 36 | 35,5 | 37,5 | ||
| 35 | 27,5 | 35,6 | 37,6 | |
| 34 | 35,7 | 37,7 | ||
| 33 | 35,8 | 37,8 | ||
| 32 | 27,6 | 35,9 | 37,9 | |
| 31 | 36,0 | 38,0 | ||
| 30 | 36,1 | 38,1 | ||
| 29 | 27,7 | 36,2 | 38,2 | |
| 28 | 36,3 | 38,3 | ||
| 27 | 36,4 | 38,4 | ||
| 26 | 27,8 | 36,5 | 38,5 | |
| 25 | 36,6 | 38,6 | ||
| 24 | 36,7 | 38,7 | ||
| 23 | 27,9 | 36,8 | 38,8 | |
| 22 | 28,0 | 36,9 | 38,9 | |
| 21 | 28,4 | 37,0 | 39,0 | |
| 20 | 28,8 | 37,1 | 39,1 | |
| 19 | 29,9 | 37,2 | 39,2 | |
| 18 | 29,6 | 37,3 | 39,3 | |
| 17 | 30,0 | |||
| 16 | 30,4 | |||
| 15 | 30,8 | |||
| 14 | 31,2 | |||
| 13 | 31,6 | |||
| 12 | 32,0 | |||
| 11 | 32,4 | |||
| 10 | 32,8 | |||
| 9 | 33,2 | |||
| 8 | 33,6 | |||
| 7 | 34,0 | |||
| 6 | 34,4 | |||
Нормативы челночного бега 10*10 и 4*9 м разработаны для военнослужащих и мальчиков 9-11 классов. Для школьников 8-х классов применяют оценивание челночного бега 5*10 м, а для девушек 3*10 и 3*9 м при низком уровне развития. Например, для получения оценки «5» ученику 11 класса необходимо пробежать дистанцию 4*9 м за 9,2 сек., а ученице за 9,8 сек.
Дистанции челночного бега.
Челночный бег применяется на дистанциях до 100 м с преодолением промежуточных дистанций (чаще всего 9-10 м) в прямом и обратном направлениях до 10 раз. Челночный бег требует большего времени и энергозатрат при пробеге одинаковой дистанции, т.к. спортсмену приходится несколько раз обегать препятствие и снижать скорость для недопущения травм при поворотах на 1800 в конце промежуточной дистанции.
Челночный бег позволяет проводить тренировки в спортзале при неблагоприятной погоде, т.к. для этого упражнения нужна небольшая площадка с разметкой начала и конца промежуточных дистанций. При благоприятной погоде можно проводить тренировки по челночному бегу на стадионе или любой спортивной площадке.
Наиболее популярные дистанции челночного бега 10*10, 4*9 и 3*10 м, реже в методике подготовки школьников используются дистанции 5*10 и 3*9 м. При подготовке спортсменов тренер индивидуально подбирает дистанцию челночного бега в зависимости от подготовленности спортсмена и специфики задач, решаемых в процессе тренировки.
Техника челночного бега. На каждом этапе челночного бега (старте, прохождении промежуточной дистанции, повороте, финише) применяется определенная техника.
Видео, как тренер тренирует будущих футболистов
И техника выполнения на видео как правильно бегать челночный бег от тренера
Первоначальный старт чаще всего применяется высокий с опорой на одну руку, но допускаются и другие варианты старта. После прохождения каждой промежуточной дистанции в обратном направлении на старте используется техника торможения и последующего ускорения. Линии старта и поворота размечаются, ширина линий входит в длину промежуточной дистанции. Прохождение промежуточной дистанции включает правильную постановку первого шага и способность увеличивать на дистанции частоту укороченных шагов, которая первоначально вырабатывается быстрыми прыжками со скакалкой. В конце промежуточной дистанции нужно отметить это событие, например, касанием земли (пола) рукой и повернуться на 180°.

Повороты требуют освоения стопорящего шага, такой шаг, кроме челночного бега, наиболее часто используется в баскетболе. Нельзя использовать на повороте любые неровности или предметы в качестве опоры. Туловище спортсмен наклоняет в сторону измененного направления бега.
Финиш требует оснащения места из условий безопасности: защита стен спортзала в месте финиша матами, в районе финиша не должно быть предметов, столкновение с которыми угрожает получением травмы. Все элементы техники челночного бега вырабатываются повторениями в замедленном темпе.
SAT Score to GPA Таблица перевода
Хотите конвертировать ваш средний балл в баллы SAT или наоборот? Возможно, вам интересно, какой балл по аттестату вы можете получить на основе ваших оценок в старшей школе. В этой статье мы изучили статистику, чтобы вы могли сделать именно это! Прежде чем мы перейдем к данным, у нас есть несколько предостережений, о которых нужно знать.
Возможно ли преобразование между баллами GPA и SAT?
Во-первых, вы должны знать, что SAT измеряет совершенно разные вещи, чем GPA. SAT — это одиночный тест, который проводится всего за несколько часов, в то время как GPA требует много лет работы для построения и основан на классной работе и общей производительности класса.
Следовательно, вы не можете сравнить их в прогнозном смысле. Вы не можете сказать это только потому, что у вас есть отличный средний балл, который вы получите отличный балл SAT, или наоборот. Предположим, что самое быстрое 100-метровое время было 9,7 секунды, а самое быстрое марафонское время — два часа и 10 минут. Начало 9.7 секунд в тире не означают, что вы наверняка получите 2:10 в марафоне!
Несмотря на это, вы можете приблизительно конвертировать между баллами GPA и SAT, посмотрев, насколько «хорош» каждый из них. Другими словами, вы можете сказать, что самый быстрый спринтер пробегает 100 метров за 9,7 секунды, что превращается в самого быстрого марафонца в 2:10. Эта шкала сопоставляет SAT и GPA в зависимости от того, насколько хорош каждый из них, точнее — процентилей людей, зарабатывающих каждый.
Преобразованиемежду результатами SAT и GPA
Ниже мы создали таблицу, которая содержит преобразования между составными баллами SAT и GPA (для невзвешенных 4.0 шкала).
,- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса 9
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal Class 9
- Решения RS Aggarwal Class 8
- Решения RS Aggarwal Class 7
- Решения RS Aggarwal Class 6
- Решения RD Sharma
- Решения RD Sharma класса 9
- Решения RD Sharma Class 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- 80003 Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Предыдущий год Вопросник
- CBSE Предыдущий год Вопросники Класс 10
- CBSE Предыдущий год Вопросник класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классу
- Учебная программа по экономическому классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
Z-оценка может быть определена как число стандартных отклонений от среднего. Точка данных является мерой того, сколько стандартных отклонений ниже или выше среднего значения. Необработанная оценка в виде Z-оценки также может называться стандартной оценкой и может быть размещена на кривой нормального распределения. Z-баллы варьируются от -3 стандартных отклонений до +3 стандартов.
Z-оценка может помочь нам определить разницу или расстояние между значением и средним значением.Когда вы «стандартизируете» переменную, ее среднее значение становится равным нулю, а ее стандартное отклонение становится равным единице.
Как рассчитать Z-показатель?
Для выборки базовая формула z-показателя составляет
z = (x — μ) / σ
Где,
μ — это среднее значение
x — это тестовое значение
σ — это стандартное отклонение
Или можно использовать другую формулу,
Z \ [_ {i} \] = \ [\ frac {x_ {i} — \ bar {x}} {S} \]
Где,
x̄ — это выборочное среднее
с — стандартное отклонение выборки.
Пример
Давайте рассмотрим пример и лучше поймем это. Ниже приведен пример проблемы.
У вас тестовая оценка 190. Тест имеет среднее значение (μ) 140 и стандартное отклонение (σ) 30. Предполагая, что это нормальное распределение, ваша оценка z будет такой.
Решение
Из вышеприведенного вопроса мы можем сделать вывод, что
Значение x равно 190 (оценка теста)
Значение среднего (μ) равно 140
И значение стандартного отклонения (σ) равно 30
. Положив значения в уравнении, указанном выше,
z = (x — μ) / σ
= (190 — 140) / 30 = 1.6
Формула оценки Z: стандартная ошибка среднего
Если у вас есть несколько выборок и вы хотите описать стандартное отклонение этих средних значений (стандартная ошибка), используйте эту формулу оценки z:
z = (x — μ ) / (σ / √n)
Этот z-показатель скажет вам, сколько стандартных ошибок существует между средним значением выборки и средним значением совокупности.
Таблицы Z-показателей:
Площадь под нормальной кривой:
Чтобы найти определенную область под нормальной кривой, сначала найдите z-показатель значения данных, а затем используйте таблицу Z-показателей для поиска площадь.Таблица Z-показателей — это таблица, которая показывает процент значений (или процент площади) слева от заданного z-показателя в стандартном нормальном распределении.
Существует две таблицы Z-показателей:
1) Таблица положительных Z-показателей
Положительные значения Z-значений означают, что наблюдаемое значение выше среднего значения общих значений.
2) Таблица отрицательных Z-баллов
Отрицательное значение Z-баллов указывает на то, что наблюдаемое значение ниже среднего общего значения.
Эти таблицы специально разработаны для стандартного нормального распределения, которое имеет среднее значение 0 и стандартное отклонение 1.
Приведенная выше таблица специально разработана для стандартного нормального распределения. Среднее значение этих таблиц равно 0, а 1 — их стандартное отклонение.
• В первом столбце таблицы мы можем узнать количество стандартных отклонений выше или ниже среднего значения с точностью до одного десятичного знака. (Целая часть и первое десятичное число Z-показателя присутствуют в метке строки)
• В самой верхней строке таблицы часть, которая обозначает z-показатель, обозначает сотую.
• Затем точка пересечения столбцов и строк дает нам площадь под нормальной кривой или вероятность.
Давайте рассмотрим следующий пример
Представьте группу из 300 кандидатов, которые сдали тест по математике. Сара набрала 700 баллов (X) из 1000. Средний балл составил 500 (µ), а стандартное отклонение — 120 (σ). Узнайте, насколько хорошо Сара сыграла по сравнению со своими сверстниками.
Решение
1) Определить Z-счет
Из приведенных выше данных можно вывести, что
Значение x равно 700
Значение μ равно 600
И значение σ составляет 150
Z балл = (x — μ) / σ
= (700-600) / 150
= 0.68
2) Используя таблицу Z-показателей, мы можем узнать, насколько хорошо она выступила по сравнению со своими сверстниками. Теперь нам нужно определить процент сверстников, чей счет становится выше и ниже, чем у Сары.
В этом примере рассчитанная Z-оценка является положительной, поэтому мы ссылаемся на все положительные значения в таблице Z-оценки.
При использовании таблицы Z-баллов необходимо выполнить определенные шаги.
Шаги, которые необходимо выполнить при обращении к таблице Z-шкалы,
1) Сначала найдите первые две цифры на оси у (в нашем примере первые две цифры равны 0).6).
2) Затем перейдите к оси x, чтобы найти второе десятичное число (в нашем примере это 0,7), это число 0,7486.
3) Затем умножьте это число на 100, чтобы получить процент
Итак,
0,7486 x 100 = 74,86%.
4) Это означает, что почти 75% студентов набрали баллы ниже, чем у Сары, и только 25% баллов выше, чем у нее. 75% из 200 учеников — 150. Это означает, что Сара справилась лучше, чем 150 учеников.
Итак, вот как решить вопрос на основе таблиц Z-показателей.
Форматы Z-показателей
Таблицы Z-показателей представлены в различных форматах. Ниже приведены два самых популярных формата z-счета:
1. Уступная область или вероятность
2. Первый формат помогает нам определить площадь или вероятность. Начните со среднего значения и затем двигайтесь к правому значению среднего до требуемого z-показателя. Эти таблицы обычно называются «кумулятивными от среднего». Таблица работает с использованием половины площади под нормальной кривой, и пользователь позаботился о том, чтобы они приняли это во внимание и внесли соответствующие коррективы при использовании таблицы.В этой таблице присутствуют только положительные z-оценки. Кумулятивный слева
Этот формат таблицы помогает определить площадь или вероятность, начиная с отрицательной бесконечности (последней слева) и затем направляясь прямо выше требуемого z-показателя. Эти таблицы, таким образом, называются «кумулятивными слева». Таблица работает со всей областью под нормальной кривой и не требует большой корректировки по сравнению с первым вариантом. В этом формате могут использоваться как положительные z-значения, так и отрицательные значения z-значения.
Z-оценки и стандартные отклонения
Z-оценка — это, в основном, число стандартных отклонений от среднего значения эталонной совокупности (совокупности, чьи известные значения были записаны, как в этих диаграммах, которые CDC составляет о весах людей ). Например:
z-оценка 1 равна 1, и стандартное отклонение присутствует выше среднего.
Оценка -2 равна -2, а стандартное отклонение присутствует ниже среднего.
Оценка 1.8 равно 1,8, и стандартное отклонение присутствует выше среднего.
z-оценка указывает, где именно находится оценка на кривой нормального распределения. Нулевой z-показатель говорит о том, что значения точно являются средними, а показатель +3 говорит о том, что значение намного выше среднего.
Применение Z-показателей
При нормальном распределении переменной центр распределения является средним значением, а стандартное отклонение является показателем существующей изменчивости.
Можно использовать z-таблицу, чтобы найти области для вычисленной z-оценки, если она заинтересована в определении вероятности конкретного значения, чтобы определить область при любом нормальном распределении. Это может помочь узнать шансы возникновения значения. Также следует отметить, что не все таблицы z-показателей одинаковы.
Недостатки Z-показателя
Одним из основных недостатков стандартных показателей является то, что они всегда предполагают, что все распределения являются нормальными.В тех случаях, когда это предположение не так, то оценки не могут быть интерпретированы как стандартная пропорция данного распределения, из которого они были рассчитаны. Рассматривая пример распределения с перекосом, область со стандартным отклонением 3 слева от среднего значения не равна области в пределах того же расстояния справа от среднего значения.
,ТаблицаZ (стандартное нормальное распределение)
Найдите значение, представляющее область слева от положительного значения Z в этой стандартной таблице нормального распределения.
Найдите значение, представляющее область слева от отрицательного Z-балла в этой стандартной таблице нормального распределения.
Z Score Lookup Объяснение Видео
Это короткое видео быстро объясняет , как найти область слева от Z Score . Он также показывает разницу в между использованием таблицы Z левого хвоста и правого хвоста.
Z балл Формула
- Z — балл az
- X — необработанный балл
- μ — средний показатель численности населения
- σ — стандартное отклонение популяции
Что такое Z-оценка?
Z-оценка, которая также известна как стандартная оценка, является числом стандартных отклонений от среднего значения, которым является точка данных. Если вы ищете более техническое определение, то мы можем сказать, что z-оценка — это мера того, сколько стандартных отклонений выше или ниже среднего значения по совокупности.
Одна из вещей, которую вам необходимо знать о z-значении, состоит в том, что при вычислении его среднего значения результат всегда будет равен 0. Кроме того, стандартное отклонение или дисперсия всегда будут с шагом 1.
A z Оценка может быть размещена на кривой нормального распределения. Он просто показывает положение необработанного показателя в терминах расстояния этого показателя от среднего значения при измерении в единицах стандартного отклонения. В случае, если вы получаете положительный z балл, вы знаете, что значение выше среднего.С другой стороны, когда вы получите отрицательное значение, оно будет ниже среднего.
Чтобы использовать z-оценку, вам нужно знать не только среднее значение — μ, но и стандартное отклонение совокупности — σ.
Правда состоит в том, что оценка z также позволяет сравнивать оценки различных переменных путем стандартизации распределения. На изображении ниже показано стандартное нормальное распределение, когда среднее значение равно 0, а стандартное отклонение равно 1.
Как рассчитать оценку Z?
Важно, чтобы вы знали, что, хотя z-балл обычно не рассчитывается вручную (поскольку данных так много), вы также можете это сделать.Чтобы сделать это, вам нужно будет использовать следующую формулу:
Как вы можете видеть, вам сначала нужно будет определить разницу между необработанной оценкой и средним значением выборки, а затем разделить результат на стандартное отклонение выборки.
Вот простой пример, чтобы вы могли легко определить z-оценку.
Предположим, что у вас тестовый результат 190. Этот тест имеет стандартное отклонение (σ) 25 и среднее значение (μ) 150. Также при условии, что вы имеете дело с нормальным распределением, вам потребуется:
z = (x — μ) / σ
z = (190 — 150) / 25
z = 1.6
Как вы уже знаете, z-оценка позволяет узнать, сколько стандартных отклонений от среднего значения имеет ваша оценка. Таким образом, в этом конкретном примере, учитывая, что у нас положительный z-показатель, мы можем сказать, что полученный вами показатель на 1,6 стандартного отклонения выше среднего.
Вычисление Z-баллов в Excel
Как мы уже упоминали, в реальной жизни большинство расчетов Z-баллов необходимо выполнять в Excel. Это не только позволяет исследователям и статистикам быстрее определять баллы, так как будет меньше ошибок и ошибок.Итак, вот шаги, которые вам нужно предпринять:
Шаг № 1:
Основная цель — найти z-оценку определенного значения. Давайте назовем это х.
По формуле, которую мы вам уже показали, вам нужно будет рассчитать среднее значение. Это где вы должны начать.
Чтобы определить среднее значение выборки, вам нужно использовать формулу AVERAGE. Если вы выполняете такие вычисления впервые, давайте предположим, что у вас есть выборка, которая начинается в ячейке A1 и заканчивается в ячейке A20.Используя формулу = AVERAGE (A1: A20), вы получите среднее значение этих чисел.
Шаг № 2:
Теперь пришло время рассчитать стандартное отклонение выборки. Для этого вам необходимо использовать формулу STDEV.S.
Давайте снова предположим, что ваши результаты начинаются в ячейке A1 и заканчиваются в ячейке A20. Итак, используя формулу = STDEV.S (A1: A20), вы получите стандартное отклонение этих чисел.
Шаг № 3:
Теперь, наконец, пришло время определить z-оценку.Если вы помните, формула z балла (х — среднее) / стандартное отклонение. Чтобы рассчитать его, вам нужно будет использовать пустую ячейку и ввести следующую формулу: = (x — среднее) / [стандартное отклонение].
Хотя это легко сделать, когда у вас небольшой объем данных, это может быть немного сложнее, если вы используете большую выборку. Таким образом, всегда предпочтительно использовать немного другую формулу, чтобы избежать записи всех средних значений и значений стандартного отклонения в формуле вручную. Если это то, что вы предпочитаете, тогда вы можете использовать следующую формулу: = (A12 — B1) / [C1].
Шаг № 4:
Но ваша работа еще не выполнена. Правда в том, что вам нужно будет рассчитать вероятность для меньшего z балла. Это означает, что вы будете определять вероятность наблюдения значения меньше x, которое соответствует области под кривой и слева от x. В этом случае вам нужно использовать пустую ячейку и ввести формулу = NORMSDIST (и ввести рассчитанную вами z-оценку).
Шаг № 5:
Чтобы определить вероятность большего значения z-балла, которое определяет вероятность наблюдения значения, превышающего x и соответствующего области под кривой и справа от x, вам необходимо использовать формула: = 1 — NORMSDIST (и введите рассчитанную вами z-оценку).Заметил, что этот также должен быть напечатан в пустой ячейке.
Интерпретация A Z Score
Когда вы закончите вычислять z z, пришло время интерпретировать результаты. Как краткий итог, значение z-балла позволяет точно узнать, на сколько стандартных отклонений вы находитесь от среднего значения. Итак,
- Если оценка z равна нулю, это означает, что оценка z равна среднему значению.
- Если вы получили положительный z-результат, это показывает, что необработанный результат выше среднего значения.Так, если, например, вы получаете z балл, равный +1,3, то вы можете сказать, что это на 1,3 стандартных отклонения выше среднего.
- Если вы получаете отрицательный z-балл, это показывает, что необработанный балл ниже среднего значения. Так, если, например, вы получите z-оценку, равную -2,3, то вы можете сказать, что она на 2,3 стандартных отклонения ниже среднего значения.
Некоторые люди предпочитают интерпретировать результаты, посмотрев на стандартную нормальную диаграмму распределения и отобразив там свои значения. Обратите внимание, что стандартное нормальное распределение также называется распределением вероятности или z-оценки.
Несколько быстрых замечаний о стандартном нормальном распределении:
- Среднее значение стандартного нормального распределения всегда равно 0.
- Стандартное отклонение стандартного нормального распределения всегда равно 1. Это означает, что одно стандартное отклонение необработанного показателя, независимо от исходное значение всегда конвертируется в 1 балл.
- Стандартное нормальное распределение всегда имеет одинаковую форму исходного распределения баллов. Таким образом, когда у вас есть необработанные оценки, которые обычно распределяются, распределение оценок z также будет нормально распределено.
Существует еще одно полезное применение для исследователей, когда они решают использовать стандартное нормальное распределение. В конце концов, они могут легко определить вероятность получения оценки из распределения или выборки.
Как вы можете легко увидеть на изображении выше:
- Вероятность случайного выбора значения от -1 до +1 стандартного отклонения от среднего значения составляет 68,27%.
- Существует 95,45 %% вероятность случайного выбора оценки между -1.96 и +1,96 стандартных отклонений от среднего.
- Если вероятность случайного выбора необработанного результата составляет менее 5%, мы можем сказать, что это статистически значимый результат.
# 5: Пример использования таблицы оценок AZ (т. Е. Стандартной нормальной таблицы)
Таблица оценок z или стандартная нормальная таблица, как на нее также ссылаются, является, как мы уже упоминали выше, одним очень эффективным способом, который исследователи и статистики используют для определения вероятности или области, которая соответствует конкретному z-баллу.Но как вы можете определить это и применить на практике? Давайте проверим практический пример, чтобы вы могли легко понять все необходимые шаги.
Давайте предположим, что мы случайным образом отобрали 50 добровольцев для прохождения теста IQ. Сьюзен, один из добровольцев, получил 74 (х) из возможных 120 баллов. Мы также знаем, что средний балл (µ) был 62, а стандартное отклонение (σ) было 11. Итак, какой вывод мы можем вывести отсюда? Насколько хорошо Сьюзен прошла тест по сравнению с другими добровольцами?
Шаг № 1: преобразование в A Z балл
Первое, что вам нужно сделать, — это конвертировать тестовые баллы IQ Сьюзен в стандартизированный балл или в конкретный z балл, который вы собираетесь использовать.
Итак, в соответствии с приведенным примером и с использованием формулы z-оценки, которую вы можете найти выше:
z = (74 — 62) / 11
z = 1.09090909
Хотя мы можем использовать все это число z, это часто округлять его. Итак, мы будем говорить, что z = 1,09. И это стандартная оценка z, которую мы собираемся использовать.
Шаг № 2: Найти область, которая соответствует Z-баллу
Как только вы вычислите стандартизированный балл, настало время взглянуть на область или вероятность.Это делается путем проверки таблицы Z. Сначала вам нужно будет найти две цифры в левой части таблицы Z, которая в данном случае равна 1.0. Затем, что касается оставшегося числа, вам нужно будет посмотреть через таблицу (вверху) и найти 0.09.
Как вы легко увидите, соответствующая область составляет 0,8621, что означает 86,21%. Обратите внимание, что в некоторых таблицах z-баллов вы увидите, что область, соответствующая z-баллу 1,09, равна 0,3621. Поскольку результаты разные, у вас может возникнуть соблазн думать, что вы не все делаете правильно или что вы смотрите не на тот стол.Это тоже не так. Реальность такова, что есть несколько таблиц z-баллов, которые просто показывают площадь справа и слева от среднего значения. Таким образом, когда вы проверяете одну из этих таблиц z-баллов и у вас есть положительный z-балл, вам нужно будет сложить 0,5 (или 50%), чтобы вычислить область слева от z-балла.
Таким образом, в этом случае это будет 0,5 + 0,3621 = 0,8621. Как видите, оба значения идентичны, независимо от того, используете ли вы одну таблицу z или другую.
Шаг № 3: Нарисуйте действительное заключение
На изображении выше вы можете увидеть представление результатов, полученных Сьюзен по сравнению с остальными добровольцами, когда она сдала IQ-тест.
Обратите внимание, что также возможно определить количество людей, которые Сьюзен превзошли на тесте. Чтобы сделать это, вам просто нужно умножить число людей, сдавших тест (50), на 0,8621:
50 X 0,8621 = 43,1
Таким образом, вам нужно округлить число до 43, так как нет частичных человеческих существа. Мы пришли к выводу, что Сьюзен смогла справиться лучше, чем 43 других добровольца.
Объяснение нормального распределения
Нормальное распределение также известно как распределение Гаусса или даже как стандартная или нормальная кривая колокола.
Как вы можете легко видеть на изображении выше, нормальное распределение сужается в обоих хвостах и является более плотным в середине. Это означает, что все значения всегда центрированы вокруг среднего значения, которое является центральной и самой высокой точкой кривой, и обычно известно как μ. Остальные баллы попадают куда-то вокруг.
Если вы думаете о представлении баллов студентов в пределах нормального распределения, то мы можем сказать, что большинство из них будет располагаться в средней и более толстой области кривой.В конце концов, большинство студентов, как правило, получают баллы B, C и D. Что касается более тонких хвостов, они только утверждают, что здесь меньше учащихся. Эта область относится к студентам, которые получают оценки.
Одна из самых важных вещей, которые вы должны иметь в виду, это то, что нормальное распределение очень важно, особенно в логической статистике. Это связано с тем, что существует много случайных величин, которые имеют тенденцию следовать этой же схеме.
Вот практический пример.
Согласно статистике Колумбийского университета, средний рост женщины в США составляет 63,1 дюйма (или около 5 футов 3 дюйма) со стандартным отклонением 2,7 дюйма.
Одна из вещей, которые вам нужно знать о высоте, это то, что она попадает под нормально распределенные переменные. Если вы думаете об этом, большинство людей имеют средний рост. Например, редко можно увидеть кого-то с 7 футами.
Кроме того, важно также отметить, что высота непрерывна.Реальность такова, что у вас может быть женщина ростом 63,1 дюйма, другая с 63,2 дюйма и еще одна с 63,05 дюйма. В принципе, нет никаких ограничений. Вот почему мы можем сказать, что переменная непрерывна.
Обратите внимание, что с нормальным распределением и непрерывными переменными, как в случае роста, вы не можете ответить на вопрос «Какова вероятность того, что случайная женщина в Нью-Йорке имеет рост 63,1 дюйма?». Однако вы можете ответить на другой вопрос: «Какова вероятность того, что случайная женщина в Нью-Йорке будет между 60.4 и 63,8 дюйма?
68-95-99.7 Правило
Это очень простое правило, которое показывает, что для любой нормально распределенной случайной величины:
- 68% населения будет лежать в пределах 1 стандартного отклонения, 1σ от среднего значения.
- 95% населения будет находиться в пределах 2 стандартных отклонений, 2σ от среднего значения.
- 99,7% населения будут находиться в пределах 3 стандартных отклонений, 3σ от среднего значения.
Используя это правило в нашем примере роста, средний рост женщин в Соединенных Штатах равен 63.1 дюйм Кроме того, мы также знаем, что стандартное отклонение составляет 2,7 дюйма.
Согласно правилу 68-95-99.7, мы можем сказать, что 68% всех женщин имеют рост в пределах 1 стандартного отклонения или 2,7 дюйма от среднего значения:
63,1 ± 2,7 = {60.4,65.8}
Как вы Можно видеть, мы можем сказать, что 68% женщин в Соединенных Штатах имеют рост от 60,4 до 65,8 дюймов.
Z Score PDF
Чтобы вы могли легко определить значение z-оценки, мы предоставляем вам таблицу Z-показателей в PDF.Таким образом, вы можете легко открыть его или даже загрузить.
Z Таблица двусторонняя нормальная кривая: как найти область
Хотя вы, вероятно, уже слышали о двухсторонней нормальной кривой, вы можете не знать, что это такое или для чего она используется. Правда заключается в том, что нормальная кривая с двумя хвостами — это кривая, как следует из названия, но в каждом из двух хвостов есть область. Итак, чтобы определить эту область, вам нужно знать, как читать таблицу z-результатов.
Как мы уже упоминали, таблицы z-оценок представляют собой списки процентов.Вы должны знать, что общая площадь под кривой составляет 100%, а площадь ботинок сказки z — это доля этого процента.
Вот шаги, которые вам нужно предпринять:
Шаг # 1: Посмотрите в таблице Z Для одного из значений z, найдя пересечение
Предположим, вы хотите найти область в левом хвосте z = -0,46. В этом случае вам нужно будет найти 0,4 с левой стороны, а затем посмотреть на верхнюю строку и найти 0,06. Пересечение столбца с линией дает вам 0.1772.
Шаг № 2: Вычтите значение Z из 0.50
Следующее, что вам нужно будет сделать, это вычесть значение z, которое вы только что нашли (0.1772), из 0.50:
0.50 — 0.1772 = 0.3228.
Шаг № 3: Повторите процесс
Пока вы смотрели только на левый хвост до сих пор, вам нужно будет повторить шаги 1 и 2 и для правого хвоста.
Одна из вещей, которые вам нужно знать, это то, что в большинстве случаев оба хвоста симметричны.Давайте предположим, что это так, и в результате вы также получите 0.3228.
Шаг # 4: Добавьте оба значения Z вместе:
В двухстороннюю нормальную кривую вам нужно будет добавить значение, полученное для левого хвоста, с тем, которое вы получили для правого хвоста:
0,3228 + 0,3228 = 0,6456
Кривая Белла
Кривая Белла — не что иное, как нормальное распределение, которое мы уже упоминали выше. Это относится к распределению, которое происходит естественным образом во многих ситуациях.
Хотя вы, возможно, никогда не слышали о кривой Белла, вы, вероятно, уже видели ее в действии. В конце концов, кривую Белла часто можно увидеть в таких тестах, как GRE или SAT. Принимая во внимание, что большинство студентов получают среднюю оценку (C), меньше получают баллы B или D. Процент будет еще меньше, если принять во внимание такие оценки, как A или F. И это создает распределение, похожее на колокол и отсюда и название.
Одна из вещей, которую вам нужно знать о кривой Белла, это то, что она симметрична, и что половина данных попадет в правую сторону от среднего значения, а другая половина в левую часть от среднего значения.
Есть много групп, которые следуют этому шаблону, и именно поэтому кривая Белла очень используется. Некоторые из примеров, где вы можете видеть это, могут быть связаны с бизнесом, государственными органами, такими как FDA, статистикой, показателями IQ, кровяным давлением, ростом людей, зарплатой, ошибками измерения, баллами на тесте, и многими другими.
