15 интересных логических задачек для детей и взрослых
15 интересных логических задачек для детей и взрослых

Логические игры и головоломки — это отличное развлечение как для детей, так и для взрослых. Они вырабатывают привычку думать, рассуждать, делать выводы и всегда стараться найти решение проблемы.
Задачка про волка, козу и капусту
Помните старинную задачу про волка, козу и капусту? Кто не решал ее в детстве! Предложите задачу своему ребенку! Мужику нужно перевезти через реку волка, козу и капусту. Но в лодке может поместиться только он сам, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как мужику перевезти свой груз?
Решение:
Нужно начать с козы. Перевезя ее, мужик возвращается на другой берег и берет волка. Переправив волка, он оставляет его на другом берегу, но зато берет козу и везет ее обратно на первый берег. Здесь он оставляет ее и перевозит к волку капусту. Затем, вернувшись, берет козу — переправа благополучно заканчивается.
Детективная задачка
На лугу лежат пять кусочков угля, одна морковь и шарф. Никто не клал их туда. Почему они там лежат?
Решение:
Дети использовали эти предметы, когда лепили снеговика зимой. С приходом весны снеговик растаял, и пять кусочков угля, морковка и шарф остались лежать уже на лугу.
Летная задачка
Мужчина выпрыгивает без парашюта из самолета. Высадка небезопасная, но мужчина остается целым и невредимым. Почему?
Решение:
Самолет находится ещё на взлётно-посадочной полосе.
Задачка про ноги
Ваня идет к лесному озеру. Ему навстречу движется класс из 25 учеников и двух преподавателей. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку. Сколько ног идут по дороге к лесному озеру?
Решение:
По дороге к лесному озеру идут только две ноги — Ванины. Все, кого он встретил, возвращаются с озера.

Сколько ворон?
Вишня у Маши плодоносит в большом количестве. К сожалению, на дерево садятся вороны и безжалостно клюют плоды. Вечером Маша считает ворон. Их 38! Это настолько выводит ее из себя, что она ловит одну ворону сачком. Сколько ворон осталось на дереве?
Решение:
Осталась только одна ворона, пойманная Машей. Остальные вороны испугались и улетели.
Задачка на внимательность
Молодая девушка заказывает в кафе яблочный сок, рулет и шоколадное мороженое. Официант, который принимает заказ, приносит ей вскоре все желаемое. После того как девушка оплатила заказ, официант спросил: «Трудно работать в полиции?» Как он догадался, что девушка — полицейский?
Решение:
Девушка была в полицейской форме.
День рождения князя
Когда князь празднует день рождения, его подданные должны принести ему достойный подарок: самую сочную ветчину, самый пряный сыр, самую упитанную курицу, искусно выделанные шкурки, плетеные корзинки, глиняные кувшины и резные изделия. Крестьянин сделал князю необычный подарок: бутылку с яблочным соком. Отличие этого подарка — яблоко находится в бутылке. Князь поражен: каким образом тот смог засунуть яблоко в бутылку? «Как ты сделал это? При помощи колдовства?» — спрашивает князь. Крестьянин отвечает: «Догадайтесь сами, но я вовсе не чародей!» Как яблоко попадает в бутылку?
Решение:
Крестьянин надевает бутылку на яблоневую ветку вскоре после цветения. Таким образом, плод развивается в бутылке.

Еще один вид логических игр придется всем по вкусу — это игры с палочками. Для игры понадобится набор счетных палочек или любые палочки одинаковой длины и толщины (например, спички, с которых предварительно счистили серу), подойдут и полоски картона. Если вы играете вместе с детьми, то можно давать устные задания. Если ребенок играет один, подготовьте карточки с рисунком и условием игровой задачи.
Задание № 1
Переложи одну палочку так, чтобы дом смотрел в другую сторону.
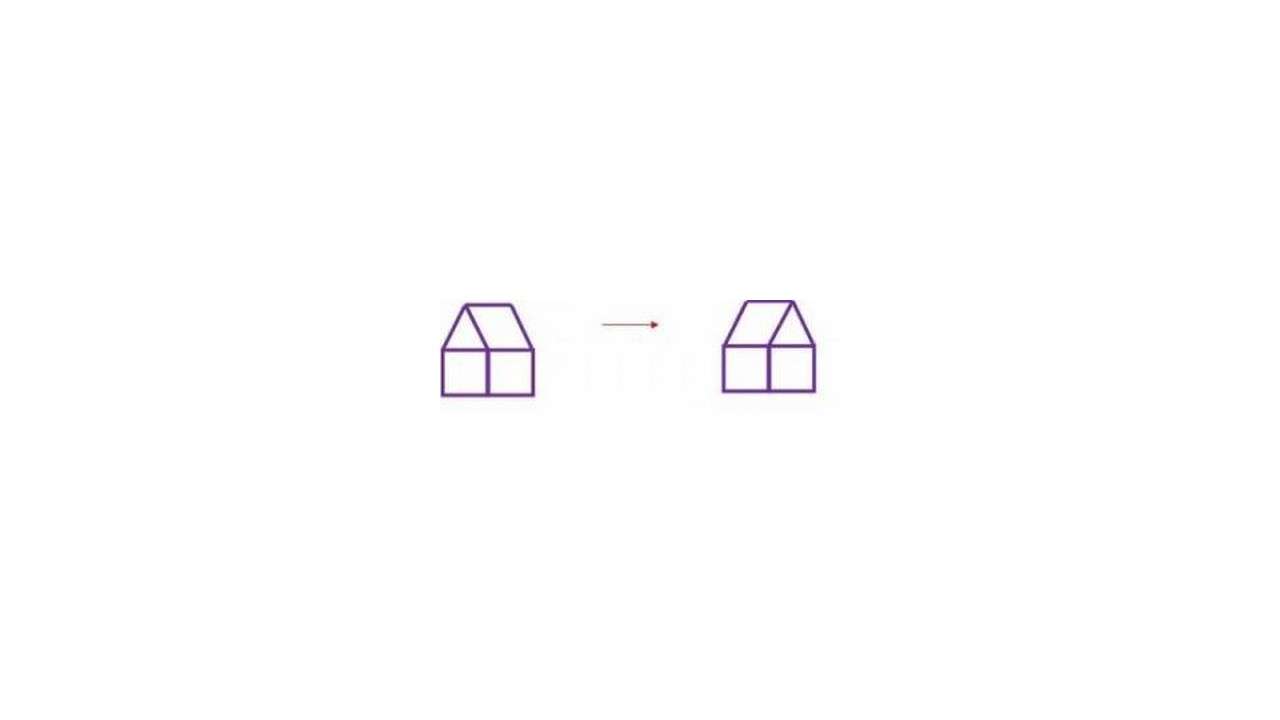
Задание № 2
Переложи 3 палочки так, чтобы корова оглянулась и подняла хвост.
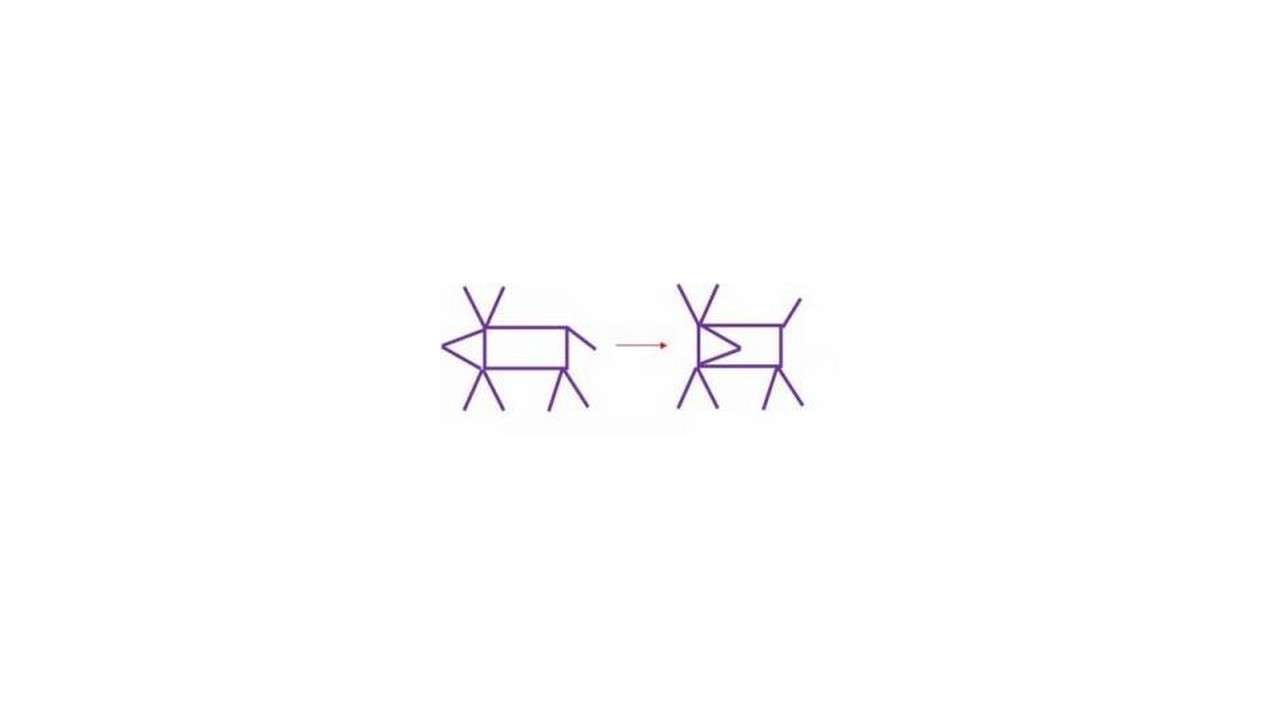
Еще несколько заданий с палочками из пособия С. И. Волковой «Математика и конструирование» (1−4 классы):
А в завершении мы хотим предложить вам самостоятельно изготовить знаменитую китайскую головоломку «Танграм». И в этом нам опять поможет пособие С. И. Волковой «Математика и конструирование».
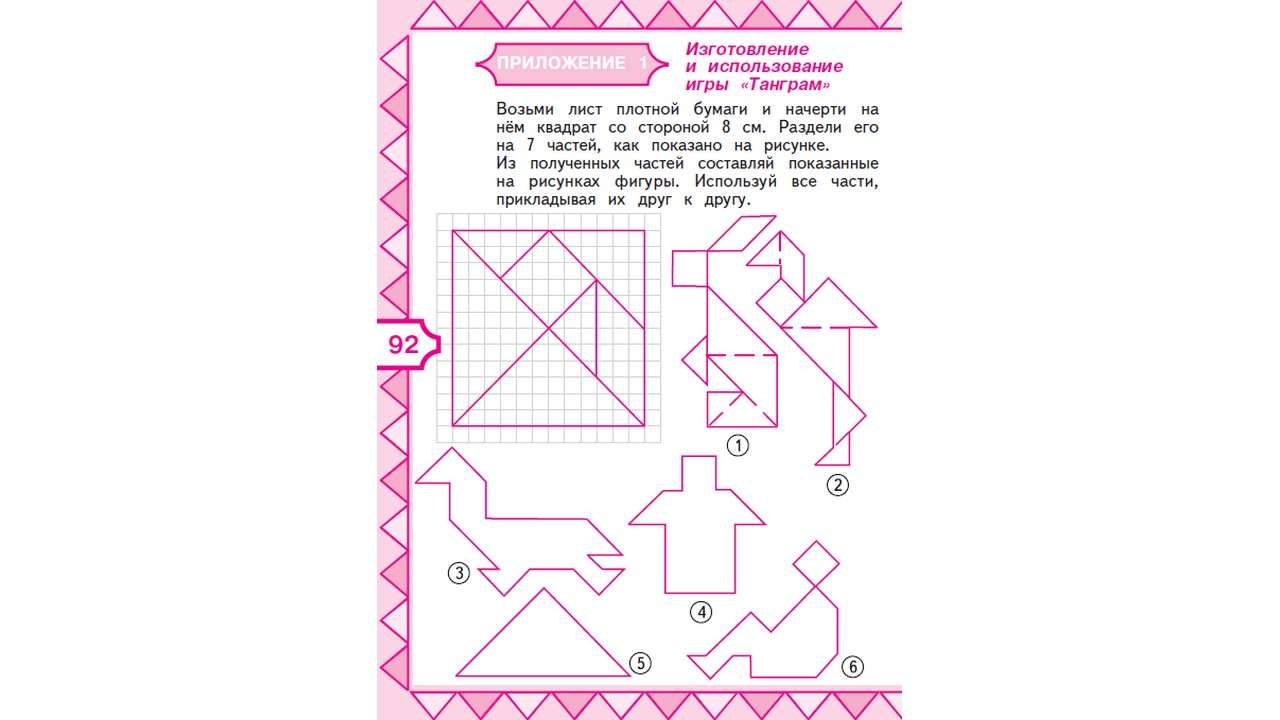
Из деталей этой головоломки можно складывать разные фигуры. Сложите для начала 1 и 2 фигуры. Рисунок вам поможет. Теперь попробуйте сложить фигуры 3, 4, 5, 6. И с этим справились? Поздравляем!
Надеемся, что выполняя предложенные задания, вы и ваш ребенок не раз испытали радость от приложенных интеллектуальных усилий, а главное — от самостоятельно найденного решения.
Фото: NadyaEugene/masterone/Shutterstock.com, архив пресс-службы,
Логические задачи для детей 10-12 лет с ответами, с подвохом
Логические задачи для детей 10-12 лет
Логические задачи для детей 10-12 лет с ответами станут настоящей находкой для родителей, которые хотят, чтобы их мальчишки и девчонки учились последовательно мыслить и формулировать свои мысли. Логические задачи – это не просто математика в чистом виде. Это еще и великолепная разминка для ума, в процессе которой детям приходится сталкиваться с необычными заданиями, оригинальными решениями и неожиданными ответами.



Интересно! Кроссворды для детей 11 лет
Предлагаем вашему вниманию подборку интересных логических задачек для детей в возрасте 10-12 лет.
Простые логические задачи для детей 10-12 лет
Для начала, рассмотрим несколько легких задачек.
Пример №1
Условие. У женщины имеется 5 кексов, которые ей нужно разделить поровну между 6 детьми. Как ей это сделать? При этом в условии говорится, что каждый кекс разрезать на 6 частей – нельзя.
Решение и ответ. Для начала женщине необходимо взять 3 кекса и разделить их напополам. Так она получит 6 равных частей. Затем ей нужно взять оставшиеся 2 кекса и разрезать каждый из них на 3 части. Она снова получит 6 одинаковых кусочков. Получается, что теперь она может дать каждому из детей одинаковое количество лакомства.

Пример №2
Условие. У мальчика есть три коробки палочек. В первой 11 штук, во второй 7 штук, а в третьей – 6. За три действия мальчику нужно сделать так, чтобы в каждой из коробок оказалось по 8 палочек. При этом в условии указано, что в каждую из коробок можно добавить такое число палочек, которое в ней имеется на текущий момент.

Решение и ответ. Первым делом необходимо из первой коробки переложить во вторую 7 палочек. Получится: 4, 14 и 6. Затем перекладываем 6 палочек из второй коробки в третью. Получается: 4, 8 и 12. Теперь дело за малым – перекладываем 4 палочки из третьей коробки в первую. По итогу получается, что в каждой из коробок стало по 8 палочек.
Логические задачи для детей 10-12 лет средней сложности
Теперь переходим к более сложным логическим задачам для детей 10-12 лет по математике. Для их решения придется применить еще и находчивость.
Пример №1
Условие. У хозяина магазина имеется большой бочонок лимонада. Также у него есть две пустые бутылки объемом в 3 и 5 литров. Клиент хочет купить у него 1 литр напитка. Как хозяину отмерить ровно 1 литр при помощи двух пустых бутылок, которые есть у него в наличии?
Решение и ответ. Первым делом мужчине нужно наполнить до краев бутылку объемом 3 литра. После этого перелить эти 3 литра в пятилитровую бутылку. Затем хозяину магазина необходимо снова наполнить трехлитровую тару до краев и начать переливать в пятилитровую бутыль. Как только она наполнится до краев, в трехлитровой таре останется 1 литр лимонада.

Пример №2
Условие. Два друга играли в настольный теннис. Они были настолько увлечены процессом, что один из парней не рассчитал силу удара, и шарик улетел в сторону и попал прямо во вкопанную в землю трубу. Получается, что шарик оказался на дне полутораметровой трубы. Другого шарика у них не было, поэтому им пришлось придумывать, как достать этот инвентарь. Выкапывать трубу им было нечем – при себе была только большая бутылка с водой. Каким способом ребята сумели достать теннисный шарик?

Решение и ответ. Для решения этой задачки необходимо применить смекалку, или же базовые знания из области физики. Если заполнить трубу водой, шарик тут же всплывет и его можно будет достать.
Задачи с «изюминкой» на логику для детей 10-12 лет
Некоторые задачи для учеников средних классов решаются путем несложных математических вычислений. Однако существуют и такие логические задания для детей 10-12 лет, о которых принято говорить «задачи с подвохом». Далее приведем несколько таких примеров.
Пример №1
Условие. Давайте представим, что в ящике вашего комода имеются носки разного цвета: 5 серых, 3 коричневых, 8 черных и 4 белых. Определите, какое минимальное количество носков необходимо не глядя достать из шкафа, чтобы быть на 100% уверенными, что у вас соберется пара одинаковых носков?

Решение и ответ. В этой задаче имеются отвлекающие факторы. Например, то, что количество носков разное, и некоторых видов – нечетное количество. Нам же следует обращать внимание лишь на то, что у нас имеется 4 вида носков. Это означает, что пятый носок, вытащенный вами, совершенно точно образует пару с одним из четырех носков, которые вы достали из ящика перед этим.
Пример №2
Условие. У мужчины имеется 4 монеты, и он знает, что одна из них точно фальшивая. Также ему известно, что отличить подделку можно по весу – фальшивая монета будет весить или больше или меньше настоящей. Как определить, какая из монет поддельная, проведя процедуру взвешивания всего два раза?
Решение и ответ. Для начала, поместим на чаши весов первую и вторую монету. Здесь возможны два сценария.

Интересно! Оригами: делаем самолеты из бумаги
Первый. Если весы не уравновесились, тогда убираем вторую монету и кладем на ее место третий экземпляр. Если весы окажутся в равновесии, значит, вторая монета была поддельной. Если же весы не уравновесятся, это означает, что фальшивой была первая монета.
Второй. Если весы уравновесились, тогда убираем вторую монету и кладем на ее место третью. Если весы окажутся в уравновешенном положении, значит, четвертая монета – фальшивка. Если же весы не уравновесятся, это означает, что поддельной является третья монета.
Пример №3
Условие. Известно, что если сложить возраст мамы и ее дочери, то получится число 66. Также мы знаем, что если цифры из возраста матери поменять местами, то тогда получится точный возраст ее дочери. Сколько лет маме и дочке, если, согласно условию задачи, дочь не может быть младше 7 лет, а ее мама не может быть старше 59 лет?

Решение и ответ. Путем логических размышлений и математических подсчетов мы можем выделить несколько возможных вариантов: 66 и 0, 60 и 6, 42 и 24, а также 51 и 15. Последний вариант является правильным. Так как первые три не соответствуют условиям задачи. В некоторых вариантах мать получается старше 59 лет, а дочь – младше 7.
Задачи на логику для детей 10-12 лет с математическими расчетами
Предлагаем вашему вниманию примеры задач, для решения которых ребенку придется применить определенные математические знания и навыки.
Пример №1
Условие. Туристы прогуливались по экзотическому лесу и наткнулись на три больших красивых камня. Возле них стояла табличка с интересной надписью, поэтому путешественникам стало интересно определить вес каждого из них. Итак, табличка гласила: «Первый камень весит вдвое меньше, чем второй. А третий – в три раза больше, чем первый. Общий вес камней составляет 360 кг». Помогите туристам определить, какова масса каждого из камней.

Решение и ответ. Итак, первый камень следует обозначить как х (икс). Тогда вес второго камня будет равняться 2х, а третьего – 3х. Таким образом, мы можем составить уравнение: (х+2х+3х)=360. Упрощаем его до такого вида: 6х=360 и решаем. х=360:6=60. Мы нашли массу первого камня – 60 кг. Следовательно, масса второго камня будет равняться 120 кг, а третьего – 180 кг.
Пример №2
Условие. Известно, что из 40 тонн руды рабочие выплавляют 20 тонн металла, который содержит в себе 6% различных примесей. Определите, какой процент примесей имеется в руде.

Решение и ответ. Для начала, определим вес примесей в металле 20х0,06=1,2 т. Теперь найдем массу «чистого» металла 20-1,2=18,8 т. Так, мы можем найти массу примеси в 40 тоннах руды 40-18,8=21,2 т. Теперь находим процент примесей в руде 21,2÷40=0,53. Ответ: 53%.
Логические задачи по математике для детей 10-12 лет с картинками
Предлагаем вашему вниманию задачи на логику с картинками.
Пример №1
Условие. Рассмотрите картинку. Сколько цифр вы в ней видите?


Интересно! Поделки из кофейных зерен
Ответ. На данной картинке можно найти десять цифр.
Пример №2
Условие. Рассмотрите картинку. Как, по-вашему, она будет выглядеть сверху?

Ответ. Правильный вариант под номером три.
Надеемся, что логические задачи для детей 10-12 лет с ответами, приведенные в нашей статье, будут интересны юным математикам и просто всем любознательным мальчикам и девочкам.
Задачи для первого класса по математике

- Рубрики:
- Школьное образование
Оправляя ребенка в первый класс, родители всегда мечтают о том, что их чадо будет отлично учиться и по всем предметам получать только высшие оценки. И если чтению научить малыша совсем не сложно, то понимать и решать математические задачи детям не всегда легко. Чтобы первоклассник успевал по математике в школе, родители либо нанимают репетитора, что не всегда финансово оправдано, либо пытаются заниматься с детьми самостоятельно. В этом материале мы расскажем, как подтянуть первоклассника по математике в домашних условиях, расскажем о различных типах задач и о методах их решений.
Как учить ребенка математическому счету
Родители первоклассников должны помнить о том, что в возрасте 5-7 лет у детей еще плохо развито абстрактное мышление. Вспомните сказку о Буратино, когда он считал яблоки, которые якобы забрал «Некто». Так и ребенок 5-7 лет еще не в состоянии представить условие задачи.
Лучше всего пользоваться наглядными пособиями, которые ребенок сможет увидеть, потрогать. Это могут быть счетные палочки, кубики или картинки, вырезанные из картона (например, набор картонных ежиков, цветочков, листиков и прочего). Выкладывайте перед ребенком все условие задачи из наглядных материалов: было столько-то, добавили или отняли столько-то. Так ему будет проще понимать условие задачи и легче находить ее решение.
Еще один важный момент при обучении детей состоит в том, что ребенок должен научиться отличать задачи друг от друга по типам. Для этого можно ориентир&
примеры с ответами :: SYL.ru
Идея софизмов зародилась еще во времена Древней Греции, постепенно распространившись и в Рим. Мудрецов специально обучали тому, чтобы доказывать какое-либо мнение с помощью заведомо ложных аргументов. Но эти доказательства выглядели очень правдоподобными.

Отличие софизма от паралогизма
Прежде чем рассмотреть конкретные примеры софизмов, необходимо отметить: любой из них представляет собой ошибку. Помимо этих философских уловок, также в логике существует и такое понятие, как паралогизм. Отличие его от софизма заключается в том, что паралогизм допускается случайно, в то время как софизм – это намеренная ошибка. Речь многих людей практически изобилует паралогизмами. Если даже умозаключение построено согласно всем законам логики, то в самом конце оно может быть искажено и уже не соответствовать реальной действительности. Хотя паралогизмы и допускаются без злого умысла, они могут все равно использоваться в личных целях – иногда такой подход называется подгонкой под результат.

Интересные примеры софизмов
В отличие от паралогизма, софизм представляет собой намеренное нарушение законов логики. При этом софизмы тщательнейшим образом маскируются под истинные умозаключения. Есть немало подобных примеров, которые сохранились с древности до наших дней. И заключение большей части из этих уловок носит достаточно курьезный оттенок. Например, таким образом выглядит софизм о воре: «Вор не испытывает желания воровать что-то дурное; приобретение чего-либо хорошего – благое дело; стало быть, вор занимается благим делом». Забавно звучит и такое утверждение: «Лекарство, которое нужно принимать больному, – это добро; чем больше добра, тем лучше; стало быть, лекарства нужно пить как можно больше».
Еще один интересный пример софизма – это знаменитое умозаключение о Сократе: «Сократ является человеком; понятие «человек» – это не то же самое, что понятие «Сократ»; стало быть, Сократ представляет собой нечто иное, нежели Сократ». Подобные софизмы нередко применялись в Древнем Риме для того, чтобы ввести в заблуждение своего оппонента. Не будучи вооруженными логикой, собеседники софистов совершенно ничего не могли противопоставить этим уловкам, хотя вся нелепость их была очевидна. Нередко споры в Древнем Риме заканчивались кровавыми драками.

Польза философских уловок
Несмотря на свое отрицательное значение, многочисленные примеры софизмов в философии имели и свою положительную сторону. Эти уловки способствовали развитию логики, поскольку они в неявной форме содержали в себе проблему доказательства. Именно с ними философы начали осмыслять проблему доказательства утверждения и его опровержения. Поэтому можно смело утверждать, что софизмы могут нести пользу, так как содействуют правильному, логически выверенному мышлению.
Уловки из математики
Немало известно и примеров математических софизмов. Для их получения уже неизвестные нам авторы подтасовывали значения чисел так, чтобы получить нужный результат. К примеру, можно доказать, что 2 х 2 = 5. Делается это таким образом: 4 делится на 4, а 5 – на 5. Стало быть, результат выходит таким: 1 / 1 = 1 / 1. А значит, 4 = 5, а 2 х 2 = 5. Разрешить этот пример софизма в математике очень просто – необходимо вычесть два разных числа, затем выявить неравенство этих двух чисел.
С софистами всегда нужно было держать ухо востро. Среди них было немало мудрых философов. Они мастерски владели искусством спора и придумали такие мыслительные уловки, которые и по сей день используют не только любители философии, но и политики.

Забавные софизмы
Эти философские уловки всегда использовались для того, чтобы ввести собеседника в заблуждение, а иногда над ним и потешиться. Следующие примеры логических софизмов показывают, что авторы древности не были лишены чувства юмора. Например:
Чтобы видеть, глаза человеку не нужны. Ведь он видит без правого глаза. И без левого он тоже способен видеть. Стало быть, глаза не являются необходимым условием, чтобы называться зрячим.
Следующий софизм построен в форме диалога, в котором мудрец задает вопросы крестьянину:
— А что, крестьянин, есть ли у тебя собака?
— Да, есть.
— Есть ли у нее кутята?
— Да, недавно появились на свет.
— Иными словами, получается, что эта собака – мать?
— Именно так, моя собака – мать.
— И эта собака твоя, крестьянин, не так ли?
— Моя, я же тебе сказал.
— Вот, ты сам признал, что твоя мать – собака. Значит, ты – пес.
И еще несколько примеров древних софизмов:
- Что человек не терял, то у него есть. Рога он не терял. Значит, у него есть рога.
- Чем больше самоубийц, тем меньше самоубийц.
- Девушка – это человек. Девушка является молодой, а значит, она – молодой человек. Последний, в свою очередь, является парнем. Стало быть, девушка не является человеком, так как здесь наблюдается противоречие. (Данный софизм является доказательством от противного).
Эти 5 примеров софизмов показывают, что с мудрецами лучше не спорить, по крайней мере, до той поры, пока не обретены навыки логического мышления.

Другие примеры
Известен и пример уловки о крокодиле, укравшем ребенка. Крокодил пообещал отцу ребенка, что вернет его, если тот угадает, станет ли возвращать крокодил малыша или же нет. Вопрос в этой дилемме звучит так: что нужно сделать крокодилу, если отец скажет, что крокодил не собирается возвращать ему ребенка?
Известен также и софизм о куче песка. Одна песчинка не является кучей песка. Если n песчинок не образуют собой кучу песка, стало быть, и n + 1 песчинок тоже не представляют собой кучу. Следовательно, никакое количество песчинок не смогут образовать собой кучу песка.
Еще один софизм называется «Всемогущий волшебник». Если волшебник всемогущ, может ли он создать камень, который ему не удастся поднять? Если такое колдовство он совершить сможет, то, стало быть, этот волшебник не всемогущ, ведь он не сможет поднять этот камень. А если у него это не получится, значит, он все равно не всемогущ. Ведь у него не получается создать такой камень.

Пример софизма о нарушителе
Данная философская уловка понравится тем, кто ищет примеры софизмов с ответами. В парк некоего богатого князя вход был воспрещен. Если кто-то попадался, то он должен был быть казнен. Однако нарушителю предоставлялось право выбрать казни: через повешение или обезглавливание. Перед наказанием преступник мог сделать какое-либо заявление. И если оно будет верным, то его обезглавят, если же ложно, то повесят. Какое это утверждение? Ответ таков – «вы меня повесите».
Софизм «Эпименид»
Выше были приведены примеры софизмов с ответами. Однако есть и такие уловки, над которыми можно тщетно биться годами, но так и не найти правильного ответа. Мыслитель будет ходить по замкнутому кругу, однако не сможет отыскать ключ к этой загадке. Пример софизма, который невозможно решить, повествует о критянине Эпимениде. Однажды он произнес фразу: «Все критяне – лжецы». Но ведь сам философ тоже являлся жителем Крита. Значит, он тоже лгал.

Парадокс критянина и судьбы несчастных философов
Но если Эпименид лжет, то, значит, его утверждение истинно? Но тогда он не является жителем Крита. Однако, согласно условию софизма, Эпименид – критянин, а значит… Все это значит только одно – мыслителю предстоит снова и снова ходить по замкнутому кругу. И не только ему. Известно, что стоик Хрисипп написал три книги, посвященные анализу этого примера софизма. Его известный коллега по имени Филет Косский не смог одолеть логической задачи и наложил на себя руки.

А знаменитый логик Диодор Кронос, уже будучи в преклонных годах, дал обет – не есть до тех пор, пока ему не удастся решить эту задачку. Об этом случае пишет Диоген Лаэртский. По свидетельству историка, когда мудрец Диодор находился при дворе Птолемея, ему было предложено решить этот софизм. Так как справиться с ним философ не смог, то Птолемей прозвал его Кронос (в переводе это слово не только обозначает имя древнего бога времени, но и просто «глупец, болван»). Ходили слухи, что Диодор погиб то ли от голода, то ли оттого, что не смог выдержать подобного позора. Таким образом, кому-то слишком серьезное восприятие софизмов стоило жизни. Однако не стоит уподобляться древним философам и воспринимать софизмы слишком серьезно. Они являются хорошими упражнениями для развития логики, но ради них не стоит рисковать карьерой, а уж тем более жизнью.
Философия для детей (Стэнфордская энциклопедия философии)
Известная теория когнитивного развития Жана Пиаже (1933) предполагает, что до 11 или 12 лет большинство детей не способны к философское мышление. Это потому, что, по его мнению, до этого времени дети не способны «думать о мышлении», своего рода метауровневое мышление, которое характеризует философское мышление. Этот «формальный операционный» уровень когнитивной развитие включает аналогичные рассуждения об отношениях, например как: «Велосипед относится к рулю, как корабль к рулю, с «Рулевой механизм» является аналогичным отношением » (Госвами, стр.XXI). Тем не менее, есть прочный корпус психологической исследование, которое указывает на то, что отчет Пиаже серьезно недооценивает познавательные способности детей (Astington, 1993; Gopnik, et al., 1999; Гопник, 2009).
Философ Гарет Мэтьюз идет дальше и подробно утверждает, что Пиаже не смог увидеть проявление философского мышления в самом детей он учился. Мэтьюз (1980) приводит ряд восхитительных примеры философского недоумения очень маленьких детей. Для пример:
- ТИМ (около шести лет), занимаясь облизыванием горшка, спросил: «Папа, как мы можем быть уверены, что все не так? мечта?» (п.1)
- ИОРДАН (пять лет), ложась спать в восемь вечера, спросил: «Если я ложусь спать в восемь и встаю в семь утра, как я действительно знаю, что маленькая стрелка часов ходила только один раз? Должен ли я не спать всю ночь, чтобы его посмотреть? Если я отвернусь даже на короткое время, может быть, маленькая стрелка обойдет два раза «. (п. 3)
- Однажды ДЖОН ЭДГАР (четыре года), видевший взлет самолетов, подняться и постепенно исчезнуть вдаль, взял свой первый самолет поездка.Когда самолет прекратил набирать высоту и погас знак ремней безопасности, Джон Эдгар повернулся к отцу и сказал с облегчением, но все же озадаченный тон голоса: «Вещи на самом деле не становятся меньше Вот.» (стр. 4)
Мэтьюз узнал многие из своих анекдотов от друзей, которые знали о его интерес к философскому мышлению детей. Это не редкость чтобы внимательные взрослые могли столкнуться с такими примерами.
Однако можно возразить, что таких анекдотов нужно больше. показать, что дети способны на серьезные философские мышление.Требуются доказательства того, что дети способны поддержал философских дискуссий. Мэтьюз (1984) дает иллюстрации этого тоже. Встречаясь с группой 8–11 лет, он использовал следующий пример для создания истории для обсуждения:
Ян (шестилетний) к своему огорчению обнаружил, что трое дети друзей его родителей монополизировали телевидение; они сохранили ему от просмотра его любимой передачи. «Мать», — спросил он. в отчаянии: «Почему троим детям лучше быть эгоистичный, чем один? » (Мэтьюз 1984, 92–3)
Это вызвало оживленную дискуссию, в которой дети прокомментировали невнимательность троих посещающих детей, желательность разработать решение, которое удовлетворило бы всех четверых детей, важность уважения прав людей, и что можно почувствовать, если он или она была на месте Яна.Затем Мэтьюз представил возможного утилитарного подход: «А как насчет этого аргумента, если мы позволим трем посетители добиваются своего, осчастливят трех человек вместо только один?» Один ответ был, что это было бы несправедливо для трех люди получают то, что хотят, за счет четвертых. это вызвали дискуссию о справедливости, направленную на более конкретные опасения по поводу относительного возраста детей, являются ли они друзей, братьев и сестер или незнакомцев и какие типы телевидения программы задействованы.
Без сомнения, это часть объяснения способностей детей и готовность продолжить подробное обсуждение обстоятельств Яна в том, что они столкнулись с аналогичными проблемами. Тем не менее, дети продемонстрировал довольно сложное концептуальное понимание проблем руки, чего можно ожидать от детей, когда они предлагается поразмышлять о собственном опыте.
Рассказы о людях примерно их возраста могут предоставить возможности
для детей, чтобы обсудить идеи, которые наиболее важны
их.Рассмотрим пример из романа Мэтью Липмана
«Я не мог позволить им избежать наказания за это», Тимми заметили, когда увидели, что их не преследуют и они могут замедлить до прогулки.«Ему не нужно было выставлять ногу наружу». Затем он добавил: «Конечно, мне тоже не нужно было делать то, что я делал. Но, как я сказал ранее, поворот — это честная игра ».
«Почему-то, — подумал Гарри, — это не совсем то же самое. вещь.» Но он не мог понять почему. «Я не знаю, — наконец сказал он Тимми. «Цель вашего Марочный клуб предназначен для обмена марок. Итак, когда вы дарите кому-то марки, ты должен что-то отдать. Также как если кто-то одолжит мне деньги, я должен их вернуть.Но если кто-то тянет грязный обмануть тебя, ты должен сделать то же самое с ним? Я не такой конечно.»
«Но я должен был отомстить», — возразил Тимми. «Я не мог позволить ему уйти с рук, сбив меня с ног причина «.
Чуть позже они познакомились с Лизой и Лаурой. Гарри рассказал девушкам, что случилось и почему он был озадачен. «Это напоминает мне», — заметил Лиза: «В прошлом году, когда мы узнали о том, как некоторые предложения могут быть изменены и останутся верными, в то время как другие, когда вы их перевернете, станет ложным.” «Да, — согласился Гарри, — но мы нашли правило. Какое здесь правило? » Лиза отбросила свои длинные волосы так, что они свисали через ее правое плечо. «Похоже, бывают случаи, когда правильно отдавать то, что у нас есть, и в других случаях, когда это неправильно. Но как определить, что есть что? » ( Лиза , стр. 23–4)
Этот отрывок — приглашение исследовать моральные нюансы
взаимность, или «возвращение натурой». Что может группа
Что об этом говорят дети 10–11 лет? Вот отрывок из
30-минутное обсуждение отрывка
- Что может произойти, когда мы ответим? Это просто начнется длинная цепочка попыток «уравнять», что никто (кроме разве что инициатора) хочет?
- Может ли ответный удар действительно «свести на нет»? Можем ли мы даже иметь смысл «уравнять вещи»?
- Действительно ли правильно отвечать на ошибку, возвращаясь натурой? Является это попытка исправить две ошибки?
- Какие альтернативы попыткам «уравнять» могут там быть? Что произойдет, если вы просто проигнорируете того, кто пытается получить от тебя подъем?
- Когда самооборона лучшая стратегия?
- Есть ли разница между попытками «получить вещи»? даже »и пытаясь« преподать кому-нибудь урок »?
- Чем отличается от: (а) обмена товаров; (б) платит вернуть долг; (c) возвращение услуги; (d) предложение услуги; (д) не делать кому-то одолжение, если они не сделают его для вас?
- Может ли здесь нам помочь Золотое правило? Что означает золотое правило значит ? Правило — хорошее правило
Подобные вдумчивые и проницательные дискуссии не редкость для дети, которым дана возможность их иметь.Это обсуждение подсказал детский роман. Однако регулярные учебные материалы, произведения искусства, мысленные эксперименты или даже ежедневные новости могут быть использованы, чтобы вызвать философские обсуждения моральные заботы.
Даже если допустить, что дети вполне способны заниматься расширенное обсуждение моральных концепций, связанных с их собственными опыты, а как насчет философских идей, менее непосредственно связанных с их практические дела? Вот иллюстрация, которая начинается с логики и заканчивается метафизикой.
Истинное предложение «Все дубы — деревья» становится ложным, когда наоборот. То же самое и со словами «Вся морковь — овощи». Мы можем говорят, что каждое истинное предложение, начинающееся со слова «все» становится ложным при обратном?
По крайней мере, уже в 3 классе дети легко находят исключения. Что насчет «Все тигры — тигры», многие скажут просить. Другие могут ответить, что это «скучное» предложение, предлагая что-то вроде «Все кролики — зайцы» или Альтернатива «У всех матерей есть дети».С участием относительно небольшая поддержка, они могут придумать хорошие определения геометрических фигур и отличать их от предложенных определения, которые нельзя отменить. Например, «Все квадраты являются прямоугольниками »истинно, но становится ложным при перевороте. «Все квадраты — это прямоугольники с равными сторонами», однако можно поменять местами.
Хотя изучение логики традиционно рассматривается как часть философии, скептики могут не найти отражения детей на Правила логики ужасно интересны с философской точки зрения.(Конечно, некоторые можно сказать это об элементарной логике в классе колледжа, поскольку ну.) Это не сильно отличается от базовой математики и грамматики, они может возразить. Является ли это справедливой оценкой, для многих дети, от логики до метафизики совсем немного. Вот пример из класса 4 th , который только что спросили всегда ли истинные предложения, начинающиеся со «все», становятся ложно при обратном (Pritchard 1996). После обычного «Все тигры — тигры »и« Все кролики — зайцы ». предложил, студент спросил: «Как насчет» Все ответы вопросы »и« На все вопросы есть ответы »?» К счастью, учитель остановился, чтобы обсудить это с классом.«У всех ответов есть вопросы?» он спросил. Конечно, — ответили студенты, иначе мы не сказали бы, что у нас есть ответ .
Учитель продолжил: «Как насчет другого предложения? Вы думаете, что на все вопросы есть ответы? » За этим последовал поток отзывов:
- Студент №1: «Есть ли жизнь в центре солнце?»
- Студент №2: «Хотя мы не можем пойти туда, чтобы узнать, на вопрос еще есть ответ ».
- Студент №3: «Сколько песчинок на земной шар?»
- Студент №4: «Есть определенное число, хотя мы не знаю, что это такое.”
- Студент № 3: «Ветер развеет их всех, и мы посчитай несколько раз ».
- Студент № 5: «Их слишком много, чтобы сосчитать».
- Студент №6: «Сколько песчинок на всех планеты?»
- Студент № 7: «Сколько деревьев на земле?»
- Студент №4: «Это легче, чем песчинки. Мы могли бы посчитай их.»
- Студент № 7: «Когда вы закончите их считать, некоторые упали, и другие начали бы расти.”
- Студент № 8: «Разве Бог создал время?»
- Студент № 9: «Вы имеете в виду, , если есть Бог, неужели он заставить время начать? »
- Студент № 7: «Есть ли ограничения?»
- Студент №5: «Ага, что будет, если вы дойдете до конца пространство и пытались протянуть руку? Если бы вы не могли, что бы сдерживает его снаружи? »
- Студент № 6: «Может быть, то, что сдерживает вашу руку, находится на внутри. Снаружи никого не будет «.
В ходе обсуждения этих вопросов студентам показалось, что изо всех сил стараться отойти от сложных вопросов, если не невозможно, ответить из-за наших практических ограничений (Е.g., не будучи уверенным в том, что конкретная песчинка не уже подсчитано) на вопросы, что в принципе неопровержимый. Наконец, с озорной ухмылкой на лице один из студенты спросили: «Время кончится?» Проблема, он объяснил, что, если время действительно закончится, никто не сможет позже подтверждаю, что это было так.
Вот еще одна иллюстрация того, как быстро обсуждение логики может перейти к обсуждению глубоких философских вопросов. (Притчард, 1985) Это группа из 5 -го классников с учетом приговора, «Все люди животные.Один из студентов предложил это как еще один пример истинного предложения, которое становится ложным, когда наоборот. Джефф возразил, что «Все люди — животные» — это не правда. Чип приступил к разработке таксономии, которая низводила людей, наряду со слонами и тиграми, в разделе млекопитающие, млекопитающие под животными, а животные под живыми существами. Джефф продолжал объект.
Чип: «Джефф, какие люди? Просто скажи мне, что такое люди? Ты же не можешь на это ответить?
Джефф: «Да, могу.”
Чип: «Ты что?»
Джефф: «Человек».
Чип: «Что такое человек?»
Джефф: «Кто-то живой».
Чип: «Живой кто-то может быть китом».
Джефф: «Я сказал, , кто-то , а не животное … «.
Чип: «Вы можете проверить каждую книгу в библиотека — ну, все, что о нас … »
Ларри: «Я хочу знать, почему все так раздражаются из-за маленькая тема.”
Рич: «Мы думаем ! Вот что мы здесь для.»
Эми: «Есть ли здесь у кого-нибудь энциклопедия, чтобы мы могли посмотреть животные, млекопитающие или люди? »
Джефф: «Мы все люди. Итак, если бы этот парень с Марса увидел нас, он бы сказать: «Эй, посмотри, здесь есть люди». Он не стал бы скажи: «Эй, посмотри, внизу есть животные. там »
Майк: «Марсиане, если они есть, сказали бы:« Эй, смотрите на этих странно выглядящих существ »или что-то в этом роде.Oни не знал бы, , что мы такое . Они ничего о нас не знают. [Возвращаясь к изначальному отличию Джеффа, Майк продолжает.] Если это человек, скажете вы, «какой-то , тело ». Если это животное, вы говорите: « штука ». Кто-то человек тело «.
Чип: «Есть живая жизнь, хорошо? Затем вы отходите от там. У вас есть животные, растения и все остальное это… ну знаете, молекулы и тому подобное. Теперь вы идете в животные, и вы ответвляетесь — млекопитающие, амфибии, рептилии и что бы там ни было.Затем вы разветвляетесь, и у вас есть все эти особенные люди. Это так, Джефф?
Джефф: «Просто продолжай».
Чип: «Ну, я просто хочу знать, согласны ли вы с этим».
Джефф: «Просто продолжай. Продолжай. Я не собираюсь менять свое мнение. Вот и все…. Я не животное. Я человек, и я собираюсь оставайся такой.
Чип: «Ты животное типа ».
Джефф: «Я не собираюсь подходить к доктору Джекилу и говорить: «Эй, преврати меня в животное»….”
Эми: «Люди — это такие животные, как птицы. Это отличается от слона. Птица отличается от слон. И мы разные, чем птица. Майк говорит, что мы не называем наши собака человека или кого-то. Но кто-то может быть очень близок со своим питомцем и считайте это частью семьи ».
Обсуждение продолжалось еще несколько минут. Как группа разойдясь, один студент заметил другому: «Если мы хотим, мы мог спорить часами! » «В течение нескольких дней», — ответил второй.Еженедельные встречи после уроков в местной публичной библиотеке. группа детей вернулась на следующей неделе с энциклопедией решить вопрос. После нескольких минут обсуждения учитель спросил студентов, считают ли они, что все в энциклопедии правда.
Эмили: «В некоторых вещах мы не уверены; и энциклопедия мог записать каждое слово о том, как образовалась солнечная система, и он, вероятно, сказал бы, что была большая пыль, которая кружилась, как верхняя. Но мы не уверены в этом.Итак, это могло быть неправильно.»
Учитель спросил, говорит ли в таких случаях энциклопедия: «Мы не уверены».
Майк: «Здесь написано« гипотеза »- это угадать.»
Курт: «Скорее всего, мы еще не уверены».
Таким образом, дискуссия сохранила философскую жизненность. это конкретная группа продолжала встречаться в течение всего учебного года, обсуждение широкого круга философских тем, в том числе: отношения между разумом и мозгом, различия (и сходство) между мечтами и реальностью, знание других умов, самопознание и отношения между свидетельствами и знаниями.
Учитывая и без того загруженный учебный план и растущее давление с целью обеспечить поддающиеся количественной оценке свидетельства овладения студентами стандартных предметов истории, литературы, математики и естествознания учителя могут задавать вопросы целесообразность добавления философии в учебную программу. Где пора быть найденным для компромисса философских дискуссий? Добавление Они могут возразить, что философия смешения только имеет значение хуже. Это не только еще одна тема, но и незнакомы большинству учителей, и они могут опасаться, что философия с ее постоянными вопросами действительно будет мешать с овладением студентами предметов уже в учебный план.Учитывая тревожный характер многих философских исследований, они могут чувствовать себя уязвимыми как учителя, потому что не уверены в свои ответы на поставленные вопросы.
Эта проблема усугубляется растущим давлением на учителей. продемонстрировать, что их ученики успевают на удовлетворительном уровне по общепринятым предметам. Стандартные тесты обычно используются в качестве мера успеваемости учащихся. Отмечено окончательным, недвусмысленным вопросы и ответы, эти тесты не делают упор на философская рефлексия.Поскольку успеваемость студентов обычно связано с финансированием школы, учителя не могут легкомысленно, как бы скептически они ни относились к образовательной ценности подготовки своих учеников к успешной сдаче стандартных тестов.
В ответ те, кто выступает за то, чтобы философии в школах подчеркивают способы, которыми философия может повысить весь образовательный опыт студентов. Цель больше чем просто введение еще одного предмета в школах.По предлагая студентам поразмышлять об отношениях между различными областями исследование и осмысление их образовательного опыта в целом, философия может повысить значимость образования учащихся как все. Кроме того, философия может внести важный вклад в еще одна область, вызывающая беспокойство, которая выходит за рамки учебной программы, критическая мышление.
В середине 1960-х философ Мэтью Липман встревожился низкое качество аргументации предположительно хорошо образованных граждане обсуждают войну во Вьетнаме и беды общества в целом.Убежденный, что преподавание логики следует начинать задолго до колледжа, он пытался придумать способ сделать это, чтобы стимулировать интерес 10–11 лет. Оставив Колумбийский университет на Государственный колледж Монтклера, он начал свои усилия со своей первой детский роман, Открытие Гарри Стоттлмайера (1974). Беспокойство Липмана по поводу уровень критического мышления в обществе в целом и школах в частности, были не только его. К 1970-м годам оттенок и крик о преподавание критического мышления в школах было если не ясно, то по крайней мере громкий; и это продолжается в значительной степени неизменным до настоящего времени.
Что подразумевается под «критическим мышлением»? характеризации диапазон сложности от удивительно краткого Роберта Энниса, «Разумное рефлексивное мышление, направленное на решение того, что верить или делать »(Эннис, 1987) на сложное заявление группы 46 участников дискуссии, созванной Американской философской ассоциацией Комитет по довузовской философии использовать метод Дельфи стремление к консенсусу:
Мы понимаем критическое мышление как целенаправленное, суждение саморегулирования, которое приводит к интерпретации, анализу, оценка и вывод, а также объяснение доказательств, концептуальный, методологический, критериологический или контекстный соображения, на которых основано это суждение….Идеал критическое мышление обычно любознательно, хорошо осведомлено, доверчиво разум, открытый, гибкий, объективный в оценке, честный в сталкивается с личными предубеждениями, осторожен в суждениях, готов пересматривать, ясно решать вопросы, организовывать сложные вопросы, усердно поиск соответствующей информации, разумной при выборе критериев, сосредоточен на исследованиях и настойчив в поисках результатов, столь же точных, как предмет и обстоятельства дознания позволяют. (Facione, 1989)
Липман был членом этой группы, и ясно, что его романы и Все руководства для учителей направлены на достижение этих целей.Его короче описание критического мышления состоит в том, что оно включает суждения, основанные на критерии или причины. По его словам, критерии можно оценивать с точки зрения «Мегакритерии», такие как надежность, актуальность, сила, согласованность и последовательность (Липман, 1991, с. 119). Критическое мышление, он добавляет, характеризуется как «мышление, которое (1) способствует суждение, потому что оно (2) опирается на критерии, (3) самокорректируется, и (4) зависит от контекста ». (Липман, 1991, с. 116)
Уловив идею о том, что критическое мышление зависит от контекста, некоторые критики оспаривают представление о том, что критическое мышление может быть полезно преподается независимо от конкретных дисциплинарных областей (Макпек, 1985).Признавая, что есть некоторые общие черты критическое мышление, пересекающее дисциплины, они утверждают, что даже эти особенности приобретают свое значение только в определенных контекстах, которые варьируются в зависимости от дисциплины (например, история, социология, биология, химия). Однако, если разные дисциплины не задают вопросы об их собственных основных предположениях и их отношениях с одним другое, критическое мышление в рамках этих дисциплин не учитывает важные вопросы, требующие внимания. Философия действительно спрашивает вопросы о других дисциплинах, а также о себе.
Липман надеялся, что философия займет центральное место в Учебная программа K-12, что позволяет учащимся развивать свои критические навыки мышления через философские вопросы. В то же время, он утверждал, что философия может помочь студентам лучше понять образовательный опыт. Стремясь разработать комплексные перспективы, философия пытается понять связи. учебная программа, которая делит обучение студентов на отдельные, автономные дисциплины, не вызывающие философских вопросов о природе этих дисциплин и их отношении к одному другой предлагает фрагментарный взгляд на образование.Предложенный Липманом Альтернатива описана в следующем разделе, где описывается K-12 программа, разработанная Институтом Развития Философии для детей (IAPC) он основал.
Если не считать амбициозной программы Липмана и его коллег из IAPC, для школ есть более скромные, но стоящие способы философское исследование уже существующих дисциплинарных структура в школах. Учителя могут приглашать своих учеников в размышлять о философских аспектах изучаемых ими предметов.На В то же время, когда они изучают историю, студенты могут уделить время, чтобы спросить вопросы о том, в какой степени исторические отчеты могут быть объективность — и вопросы о том, что такое «объективность» может означать, и почему это важно или не важно искать. Аналогичный можно задать вопросы о естественных и социальных науках, включая вопросы о том, в какой степени наука является или должна быть «свободным от ценностей». На самом деле, если есть место для таких вопросов, не поощряется, можно спросить, до какой степени критическое мышление себя поощряет.
Образовательное движение, известное как Философия для детей, получило началась в начале 1970-х с публикацией книги Мэтью Липмана философский роман для детей, Harry Stottlemeier’s Открытие . В 1970 году Harry вошел в Государственные школы Монклера в Нью-Джерси. К середине 70-х годов институт за развитие философии для детей (IAPC) формально место в Государственном колледже Монклера (ныне Государственный университет Монклера). СМИ быстро обратили внимание на сообщения о значительном улучшении навыки чтения и критического мышления у детей средней школы, которые были вовлечены в программы IAPC.Впоследствии IAPC произвел материалы, состоящие из детских романов Липмана и под руководство коллеги IAPC Энн Маргарет Шарп, сопровождающего учителя рабочие тетради для всей учебной программы K-12. Тысячи детей в Новом Джерси в Соединенных Штатах и даже во всем мире ознакомлен с образовательными программами МАПК.
Непритязательный 96-страничный роман для учеников средней школы, Гарри В Discovery Стоттлемайера изображен Гарри и его 5 th класс одноклассников.Взрослые изредка входят, но основной философская работа — детская. Гарри и его друзья открывают несколько основных понятий и правил аристотелевской логики; И они ломать голову над вопросами о природе мысли, разума, причинности, реальность, знание и вера, правильное и неправильное, справедливость и нечестность. Рассказ не вводит никакой специальной лексики философии (даже само слово «философия» не делает внешний вид). Философское исследование инициируется детьми в рассказ, а не взрослые.
«Что — это открытие Гарри Стоттлмейера ?» Гарри могут спросить читатели. Этот вопрос не прямо ответил. Однако один кандидат выделяется среди множества вещей, которые Гарри обнаруживает, исследуя вопросы о логике, знания, реальность и разум. Гарри и его одноклассников спрашивают написать статью на тему «Самое интересное в мир.» Под названием Thinking , эссе Гарри начинается:
Для меня самое интересное в мире — это мышление.Я знаю, что многие другие вещи тоже очень важны и чудесно, как электричество, магнетизм и гравитация. Но хотя мы их понимаем, они не могут понять нас. Так что мышление должно быть чем-то особенным.
Написав еще несколько абзацев, Гарри откладывает газету. Позже он думает: «В школе мы думаем о математике, и мы думаем, о правописании, и мы думаем о грамматике. Но кто все слышал о думаешь о мышлении? » Итак, он добавляет еще одно предложение к своему бумага: «Если мы подумаем об электричестве, мы сможем понять его лучше, но когда мы думаем о мышлении, мы, кажется, понимаем нам лучше.”
Без использования слова «философия» ни здесь, ни где-нибудь еще в Гарри Липман показывает, что Гарри занимается серьезным философская мысль, «размышление о мышлении». Это мы можно сказать, показывает открытие Гарри радостей философского мышление. Но это еще не все. Гарри также замечает, что, как интересно и, как ни важно думать о мышлении, кажется, особое место в школе. Наконец, хотя его статья начинается в от первого лица, оно быстро переходит на «мы» и фокусируется на том, что может быть выполнено с другими в классе.
Одна из наиболее привлекательных черт подхода IAPC к философии для детей для многих учителей было то, что он продвигает идею класс как «исследовательское сообщество», в котором учащиеся открыто и уважительно обмениваться идеями. Каждый студент рассматривается как иметь возможность внести ценный вклад в темы на рассмотрении. Студентам рекомендуется развивать умение слушать навыки, отзывчивость на то, что говорят другие, готовность попытаться поддерживать собственные идеи с уважением, и открытость возможность того, что следует изменить свои убеждения в свете новых соображения.Короче говоря, класс призван усилить потенциал ученика разумность . Это включает в себя больше чем умение рассуждать. Как отмечает Лоранс Дж. Сплиттер и Энн Маргарет Шарп написали (Splitter and Sharp, стр. 6):
Разумность — это прежде всего социальная предрасположенность: разумный человек уважает других и готов учитывать их взгляды и чувства, вплоть до изменения ее собственного мнения о важных вопросах и сознательно позволяя себе перспектива быть изменена другими.Другими словами, она желает быть аргументированным.
Учителя, которые положительно относятся к идее, что класс должен быть Тем не менее «исследовательское сообщество» может сопротивляться идее что философия должна быть в центре обсуждения. Они могли бы утверждать, что другие предметы хорошо поддаются формированию такая среда совместного обучения, которая может быть называется «исследовательское сообщество». Философия для детей адвокатам, однако, нужно только настаивать на том, что Поддерживая философию.К сожалению, Энн Маргарет Шарп прошла прочь в 2011 году. Особенность расследования, которое она и Липман, отстаиваемый Липманом, подробно рассматривается в недавнем сборнике сочинения о ней и о ней, посвященные ее памяти (Григорий и Лаверти, 2017).
Можно подумать, что философия — в лучшем случае подходящий предмет для относительно небольшое количество студентов на довузовском уровне. Поскольку философия традиционно преподается только на уровне колледжей в США. Государства, можно подумать, что он может подойти только для небольшого сегмент студентов дошкольного уровня — два процента студенты, отнесенные к категории «одаренных и талантливых».» Однако программы «Философия для детей» показали себя замечательно удалось привлечь практически всех студентов в класс вместе в расследовании. Учителя часто удивляются, и приятно видеть многих из их самых скрытных, «Отстающие» студенты активно участвуют в дискуссии философских идей.
Тем не менее, поскольку им не хватает опыта в формальном изучении философии, многие учителя не хотят поощрять философские думают о своих учениках.Однако их опасения преувеличены. Знакомство с некоторой стандартной философской литературой может быть желанным, но не обязательно приносить философию для Дети в класс. Что требуется, так это способность способствовать философской дискуссии. Для этого гораздо больше важно, чтобы учителя сами проявляли философское любопытство чем знакомство с академической философской литературой. Как их студенты, преподаватели, незнакомые с дисциплиной философия, могут тем не менее, иметь склонность к философскому мышлению — или хотя бы умение распознавать, когда другие занимаются философскими мысль.
Содействие обсуждению философии для детей не означает доминировать над ним; для учителей важно позволять своим ученикам разрабатывать собственные идеи. Учителя не должны предоставлять или даже есть, ответы на все вопросы. Они могут разделить недоумение с своих учеников, будьте открыты для неожиданных, но наводящих на размышления ответов на вопросы, которые задают они и их ученики, и с удовольствием наблюдают обмен студентами друг с другом. Это означает избавление от традиционная роль учителя как лектора и ответчика.Особенно для учителей, которые не уверены, что это влечет за собой, такие семинары, как те, что предлагаются IAPC, дают хорошее введение в педагогику Философия для детей.
Философия для детей побуждает детей думать на самих себя в то же время, что это побуждает их думать с другими. Однако философия часто рассматривается как вопрос одиночного размышления, возможно, вовлекающий обмены между несколько других мыслителей-одиночек — то, что «Массы» не вовлечены и не привлекаются.Возможно многие утверждал бы, что это философия в лучшем виде; как физика или математика, «философия для всех» размыта. Философии для детей нет необходимости оспаривать это аналогия. Фактически, это может повернуть его в свою пользу. Однако эзотерический физика и математика в лучшем виде, но школы тем не менее признают важность того, чтобы эти предметы были доступны всем ученики. Точно так же сторонники философии для детей могут противодействовать что должно быть место для всего класса, включая «Одаренные и талантливые», «неуспевающие» и «Обычные» студенты — занимающиеся философскими вопросы вместе.
Чтобы это сработало, дети в классе должны иметь возможность участвуйте в длительных философских дискуссиях с другими. Как уже отмечалось, что труды Гарета Мэтью предоставляют достаточно доказательств того, что многие дети способны на интересные, если не на глубокие, философские мысли. Однако менее очевидны способности детей поддерживать и развивать это вместе с другими. Анекдоты маленьких детей спонтанный обмен философской мыслью с наблюдательным взрослым не достаточно.Мэттьюз Диалоги с детьми является убедительным доказательством того, что дети могут пойти дальше этого. Примеры содержательных философских бесед детей, найденных в Lone (2012), МакКолл (2009), Притчард (1996), Шапиро (2012) и Wartenberg (2009), среди многих других, не оставляет сомнений в том, что у детей есть эта способность.
В свете быстро растущего международного интереса к философии для детей, Международный совет по философским расследованиям с Дети (ICPIC) была основана в 1985 году.ICPIC продолжает спонсировать международная конференция раз в два года, с ведущими, в том числе Австралия, Австрия, Бразилия, Англия, Мексика, Испания (дважды) и Тайвань. Самая последняя конференция (июнь 2017 г.) проходила в Мадриде, Испания. Кто организовал Felix Garcia-Moriyon (Universidad Autonoma de Мадрид), конференцию посетили более 400 участников. со всего света.
Даже после ухода пионеров IAPC Мэтью Липмана (2010 г.) и Энн Маргарет Шарп (2011), под руководством Мона Грегори IAPC сохраняет сильное присутствие в ICPIC.Однако многие члены ICPIC сейчас создали свои собственные институциональные структуры и разработали центры, ассоциации и программы. В Северной Америке есть Североамериканская ассоциация расследователей (NAACI), которая собирается раз в два года (годы, когда ICPIC не собирается). Недавно с начальным поддержка со стороны пред-колледжа Американской философской ассоциации Комитет по философии, PLATO (Изучение и преподавание философии Организация). Теперь это некоммерческая организация, поддерживаемая Фонд семьи сквайров, он спонсирует ежегодные собрания и работает в тесном сотрудничестве с Центром философии для детей Вашингтонского университета.PLATO также спонсирует два периодических издания: Questions и онлайн Precollege Philosophy and Public Practice . Австралия и Новая Зеландия организованы под Федерация австралазийской философии в школьных ассоциациях (FAPSA), которая собирается ежегодно и издает журнал по философии. в школах в качестве официального журнала. (Бург и Торнтон, 2016). В 1992 Общество по продвижению философских исследований и Reflection in Education (SAPERE) была основана в Оксфорде, Англия.В 2007 году Английский философский фонд был установлено. (Уорли, 2011). С 2005 г. журнал Philosophy. и Детство спонсировалось ICPIC и выпускником программа обучения в Государственном университете Рио-де-Жанейро (UERJ), с Уолтером Коханом и Дэвидом Кеннеди в качестве редакторов. Эти организаций, наряду со многими другими центрами и опытными практикующих по всему миру, продолжают поддерживать программы обучения для учителей, которые позволяют им познакомить тысячи детей с философия, как в обычных классах, так и за их пределами.
Хотя материалы IAPC продолжают использоваться, в последние годы был отмечен распространением альтернативных учебных ресурсов и способы вовлечения детей в философские дискуссии. Годами Гарет Мэтьюз написал обзоры детских рассказов. на Thinking , затем в официальный журнал IAPC (хотя собственные учебные материалы не использовали чужие детские литература). Это вдохновило Тома Вартенберга (2009, 2013) на разработку своего очень успешная программа довузовской философии в Mt.Хольок College (MA), отмеченная наградами программа, основанная на классическом детские сказки. Карен Мюррис была одним из первых противников Липмана устойчивость к использованию иллюстрированных материалов. (Моррис, 1992) Она и Джохана Хейнс предлагает подробный отчет о философском значении книжек с картинками. (Мюррис и Хейнс, 2012 г. и Мюррис, 2016 г.). Питер Уорли из Англии написал несколько вдохновляющих книг для учителя и студенты, не использующие материалы IAPC. Австралии Фил Кэм собрал множество рассказов, подходящих для философских использовать с детьми.Короче говоря, существует быстро растущий список ресурсы, которые показывают большие перспективы для вовлечения детей в философские дискуссии. (См., Например, DeHaan et al. 1995; Fisher 1998; Keen 1997; Льюис и Чендли 2012; Одинокий 2012; McCall 2009; Мюррис 1992, 2016; Sprod 2001 и White 2000). Вопросы: Философия для молодежи , периодическое издание, спонсируемое Комитет доуниверситетской философии Американской философской ассоциации, публикует сочинения молодежи по специальным философским темам. Первый выпуск (весна 2001 г.) был посвящен правам детей.
К счастью, Интернет позволяет неплохо успевать с последними разработками по всему миру и быстро общайтесь с другими преподавателями, интересующимися философией для Дети. К сожалению, многие из этих сайтов кажутся недолговечный. Тем не менее, см. Раздел Интернет-ресурсов ниже, чтобы список надежных веб-сайтов, на которых есть ссылки на другие полезные сайты.
,заданий по английскому для детей
! Английские задания для детей, фразовые глаголы — , , Английские задания для детей — ,
Превращение изображений в ощущения для помощи слепым
Я Алекс Вильярреал со Специальным английским отчетом о здоровье VOA, от …
Лекция или интерактивное обучение? Новое исследование старого номера
Это отчет о специальном английском образовании VOA от voaspecialenglis…
Может ли сканирование мозга маленьких детей предсказать проблемы с чтением?
Это отчет о специальном английском образовании VOA, подготовленный voaspecialengli …
Дроны: не только для использования в военных целях
Это специальный отчет по технологиям на английском языке VOA, изданный voaspecialengl …
, Английский язык для детей —
,
,!
