Учимся решать примеры до 10.
Ваш ребенок уже знает цифры, может отыскать названную вслух цифру, а также отвечает, как называется цифра, которую вы показываете? Не откладывайте обучение счету, решайте примеры вместе со своим малышом. Ниже несколько примеров в пределах 10.
Чтобы проверить, правильно ли ребенок соотносит цифру и количество предметов, которые она обозначает, попросим малыша выполнить задание.
Положите на стол 2 небольших предмета — например, пуговки. Спросите, сколько пуговок на столе? Попросите малыша показать столько пальчиков на руке, сколько предметов на столе, между делом потренируем и мелкую моторику. Добавьте 1 пуговку, спросите, сколько стало? Далее будем добавлять пуговки по одной в достаточно быстром темпе, проговаривая результат – фактически называя цифры по-порядку. Дойдя до десяти, начинаем убирать пуговки по одной. Здесь уже поможем малышу – будем называть результат вместе, одновременно изучая обратный счет. Поясните, что добавляя пуговки, мы совершаем действие – сложение, обозначаем это действие знаком плюс, а убирая – вычитание, и его обозначаем минусом.
Наглядно прямой и обратный счет можно показать с помощью лесенки, она – наш помощник в счете.
Чтобы решить пример: 3 + 1, малышу надо пальчиком встать на третью ступеньку, а затем сделать 1 шаг вверх. Ответом на пример будет ступенька, на которой он окажется. Для решения примера 5 – 2 мы встаем на пятую ступеньку и делаем 2 шага вниз. Спросите у ребенка – если в примере знак плюс, надо подниматься или опускаться по нашей лесенке? Какой знак написан в примере, если я шагаю вниз? Если прибавляем или отнимаем ноль, надо ли делать шаги, или почему «шагнув на ноль ступенек вверх или вниз» мы остаемся на месте? Почаще играйте так с малышом, с опорой на зрительную память он хорошо запомнит лесенку. Совсем скоро он легко будет решать примеры, даже не имея подсказки-лесенки перед глазами.
Начните с простых шагов и обязательно занимайтесь регулярно, чтобы ребенок хорошенько усвоил принцип решения.
Не забудьте выполнять упражения на сложение и вычитание на IQsha! Затем можно будет усложнять задания, предлагая решать простые примеры в уме.
Примеры по математике для 1, 2, 3 класса
1-й класс 2-й класс 3-й класс1 класс
В первом классе начинается обучение счёту. Сначала ученикам дают примеры в пределах первой десятки — сложение и вычитание. Когда примеры с однозначными числами решаются уверенно — добавляются примеры с переходом через десяток.
Для тренировки навыков устного счёта удобно воспользоваться генератором примеров:
Примеры на сложение и вычитание в пределах 10
Вычитание однозначных чисел
Примеры на сложение и вычитание в пределах 20
Сложение и вычитание однозначных и двузнычных чисел
Примеры на сложение и вычитание в пределах 100
Сложение и вычитание двузначных чисел
2 класс
Во втором классе изучают таблицу умножения, постепенно проходя каждую цифру доводят навыки умножение для автоматизма.
Для лучшего запоминания рекомендутся давать много разнообразных примеров вперемешку. В это поможет генератор примеров на умножение:
Примеры на умножение однозначных чисел
Сумма не превышает 10
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Помимо умножения во втором классе появляются примеры с пропусками значений — прообраз уравнений с одним неизвестным. В примерах с пропусками значений сначала необходимо правильно подобрать математическое действие, и только потом можно решить пример. Довести навыки счёта до автоматизмав поможет генератор примеров с пропусками значений.
Примеры на сложение и вычитание с пропусками двузначных и однозначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками двузначных чисел
Сумма не превышает 10
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Более слодные примеры — неравенства, где для решения нужно вычислить значения в левой и правой части.
Неравенства с примерами с однозначными числами
Сумма не превышает 10
Неравенства с примерами с двузначными числами
Сумма не превышает 10
3 класс
В третьем классе продолжается отработка навыков счёта. Примеры становятся более сложными, и для их решения применяется решение в столбик. Для развития навыков быстрого счёта рекомендутся давать ученику большое количество разнообразных примеров. Их можно взять здесь:
Примеры на сложение и вычитание в пределах 1000
Сложение двузначных чисел с суммой не превышащей 100
Примеры на сложение и вычитание в пределах 10000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 1000
Сложение двузначных чисел с суммой не превышащей 1000
Примеры на сложение и вычитание с пропусками в пределах 10000
Сложение двузначных чисел с суммой не превышащей 10000
Примеры на умножение в третьем классе включают уже двузначные числа.
Также полезно отработать счёт с «опорными» числами, которые часто встречаются в различных расчётах.
Примеры на умножение однозначных и двузначных чисел
Сумма не превышает 10
Примеры на умножение опорных чисел «12», «15», «25», «75», «125»
Сумма не превышает 10
Конспект открытого урока математики «Число 10. Решение примеров в пределах 10» 1 класс
Конспект открытого урока математики
«Число 10. Решение примеров в пределах 10» 1 класс
Цель:
закрепление умения детей числа 10, учить решать примеры на сложение и вычитание в пределах 10.
Задачи урока:
• Закрепить знания письменного сложения и вычитания в пределах 10;
• Воспитание аккуратности, доброжелательности, взаимопомощи, вежливости.
Оборудование:
1. тетрадь,
2. линейка,
3. карандаш,
4. ручка,
5. карточки с изображением сказочных персонажей с заданиями.
6. мультимедийная система.
Ход урока.
1. Организационный момент.
Здравствуйте, ребята, гости!
Ребята, посмотрите, что у меня в руках? Круг, квадрат, прямоугольник, треугольник.
У вас на столах лежат предметные картинки по форме похожие на геометрические фигуры.
Сейчас сядет тот, чья предметная картинка, напоминает форму круга, треугольника, квадрата.С каким числом мы познакомились на прошлых уроках? Мы познакомились с числом 10.
Тема нашего урока: «Число 10. Решение примеров на сложение и вычитание в пределах 10».
Ребята к нам в гости пришла гостья, а кто это отгадайте из загадки:
Прыгает зверюшка
Не рот, а ловушка.
Попадут в ловушку
И комар, и мушка. Лягушка
Верно.
А поможет нам на уроке сказка «Царевна-лягушка».
Давайте посмотрим на экран, кого мы видим? Давайте посчитаем, сколько цыплят изображено на экране?
А сейчас посмотрим на экран, правильно ли мы посчитали?
А теперь вспомним, как пишется число 10.
А теперь открываем тетради. От сегодняшнего числа отступаем вниз 2 клеточки, пропишем одну строчку числа 10.
2. Устный счет.
А теперь сказка. У царя было три сына. И велел царь сыновьям, пока совсем не состарился, жениться.
Вывел он их в чисто поле и велел пустить стрелы, куда упадет стрела, значит там их и судьба. Но стрелы, ребята, не простые, а с заданиями. Чтобы стрелы долетели до места, поможем сыновьям царя выполнить задания? Задания: Посмотрите у меня в руках картинка, что на ней изображено? Какая это птица? Посчитайте и покажите мне цифрой. Как вы думаете, грачи уже прилетели?
А это, что за птицы? Посчитайте и покажите цифрой, сколько изображено скворцов. Скоро на уроках мы будем знакомиться с этими птицами.
Молодцы, ребята. Стрелы долетели до места: одна – до барского дома. Другая – до купеческого. А третья – на болото к лягушке.
А мы попадем с вами на весеннюю полянку. Смотрите глазками на движущие предметы. (Электроннаяфизминутка для глаз).
3. Арифметический диктант.
Царь женил сыновей, дал задание невесткам – испечь хлеб.
Ребята, поможем испечь хлеб Царевне-лягушке. Для этого нужно выполнить игровые задания. Я буду называть числовой ряд и пропускать числа, а вы должны показать, что я пропустила:
4 … 6, 7, 8
6 … 8, 9, 10
10, 9, 8, 7 … 5
назовите предыдущее 10, последующее 9,
назовите соседей числа 9.
Молодцы! Вы помогли испечь хлеб Царевне.
Царю понравилось.
4.Физминутка
Под пение весенних птиц, изображаем полет птиц (релаксация)
5. Изучение нового материала.
Следующим заданием царя было – соткать ковер. Чтобы он получился красивым, мы должны его украсить. Для этого нужно решить пример, найти ответ с рисунком. И пример на ковре заменить узором.
Сильный уровень:
6+4
10-5
8+2
Средний уровень
7+2
6 -6
8 -3
Молодцы, ребята, справились с заданием, помогли Царевне. Царю очень понравился ковер.
Царь пригласил всех на бал. Мы тоже с вами давайте отдохнем.
6. Физминутка.
Как живешь?
Как бежишь?
Вдаль глядишь?
Ждешь обед?
Машешь вслед?
Ночью спишь?
А шалишь?
7. Закрепление изученного материала.
Понравилась Василиса Ивану-Царевичу, взял он и сжег её шкурку.
Улетела голубкой Василиса и велела искать её (у кого?). У Кощея Бессмертного.
Пошел Иван искать Василису.
Шел, шел и увидел избушку на курьих ножках, а в ней Баба-Яга сидит и говорит:
-Если решишь мою задачу, дам тебе за это клубок, который покажет тебе дорогу. Поможем Ивану решить задачу?
У пенечков 7 грибочков
И под елкой 3
Ребята, подумайте и выложите на партах в кассах решение этой задачи.
Сколько будет всех грибочков,
Ну-ка, посмотри?
Сколько грибочков всего? Как вы узнали?
Молодцы, справились с заданием. Отдала Баба-Яга клубок Ивану- Царевичу и он пошел спасать Василису.
А мы с вами пойдем по другой дорожке. Посмотрите, что начерчено на доске. Как называется эта линия? Прямая линия.
Отступите вниз две клетки, начертите прямую линию.
Молодцы! С заданием справились.
И прямая дорожка привела нас к дубу, где находится смерть Кощея.
Ребята, давайте снимем сундук. А для этого нужно выполнить неравенство:
Слабый уровень
8…10
Поймали зайца.
Теперь поймаем утку:
9…2
А из утки выкатилось яйцо. Давайте его разобьем:
5…5
Разбилось яйцо, достали мы иголку. Давайте сломаем её:
10…0
Молодцы, ребята. Вы помогли Ивану спасти Василису. Она вам очень благодарна, что вы ее спасли. Были активными, смелыми, дружными.
8. Итог урока.
Чем мы сегодня занимались на уроке?
Что вам понравилось?
Какие задания вызывали у вас трудности?
Закрепление счёта до 10, дней недели, решение примеров на сложение и вычитание. | План-конспект занятия по математике (подготовительная группа) по теме:
ОД по математике в подготовительной группе с использованием ИКТ «Выручим Царицу Математику»
Цель: обобщение и закрепление полученных ранее знаний по ФЭМП.
Задачи:
Образовательная: способствовать закреплению знаний о числах первого десятка, счет прямой и обратный в пределах 10.
Закреплять умение пользоваться математическими знаками +, -, >,. Упражнять в решении примеров на сложение и вычитание.
Воспитательная: воспитывать у детей желание откликаться на просьбы о помощи, желание трудиться во благо других.
Развивающая: развивать умение ориентироваться на листе бумаги, развивать моторику кистей рук.
Материал: индивидуальные задания на каждого ребенка, проектор, слайды, звукозапись физкультурной минутки, простой карандаш, цветные карандаши
Предварительная работа: решение задач, ориентировка на листе бумаги, решение примеров.
Ход занятия
Воспитатель: К нам на занятие пришли гости, давайте поздороваемся:
Дети вместе с воспитателем становятся в круг.
В круг широкий, вижу я,
Встали все мои друзья.
Мы сейчас пойдем направо,
А теперь пойдем налево,
В центре круга соберемся,
И на место все вернемся.
Улыбнемся, подмигнем,
Заниматься мы начнем.
1 слайд
Интригующая проблемная ситуация: слайд “с замком”,
Мы не можем попасть на занятие, чтобы попасть нужно, разгадать секрет замка.
Упражнение прямой и обратный счет до 10
Наш замок открылся, можем начинать занятие.
2 слайд
В одном красивом месте, где журчал ручей, цвели необыкновенной красоты цветы и воздух был чист и свеж, стоял великолепный замок.
3 слайд
В этом замке жила одна замечательная девушка – Царица Математика. Много времени она проводила за книгами и поэтому была очень образованна и умна. За ум и сообразительность
4 слайд
Ее невзлюбил злой волшебник, он опутал замок злыми чарами.
5 слайд
Солнце перестало появляться над зАмком. ЗАмок погрузился в темноту. Без солнечного света и тепла перестали расти цветы и деревья, птицы не пели своих чудесных песен. Весь животный и растительный мир стал гибнуть.
6 слайд
Царица Математика очень грустила, целую неделю сидела со слезами на глазах и не знала, как ей быть, как справиться с чарами злого волшебника.
7 слайд
Но вот однажды, над ее мрачным замком пролетала волшебница Фея. Она увидела, какая беда приключилась с Царицей Математикой и решила ей помочь.
Фея сказала: «Я знаю, как сбросить злые чары и победить злого волшебника. Надо выполнить все его математические задания без ошибок именно сегодня, и чары спадут».
«Но я сама не успею, как мне быть. ведь заданий очень много» – сказала Царица Математика. 8 слайд
«Я знаю, кто тебе поможет. В одном детском садике в подготовительной группе дети очень любят математику, они с удовольствием тебе помогут выполнить часть заданий. Обратись к ним за помощью».
Царица Математика написала письмо и вместе с заданиями отправила нам с голубиной почтой.
9 слайд (фото группы детей)
Воспитатель: ребята, вы хотите прочитать это письмо.
10 слайд письмо
Тогда давайте быстрее прочтем.
«Здравствуйте, дорогие ребята! Пишет вам царица Математика. Мне очень нужна ваша помощь. Дело в том, что мой математический зАмок заколдовал злой волшебник. И одолеть его я смогу только с вашей помощью. Вам необходимо очень постараться, чтобы выполнить все задания правильно и тогда над моим замком снова засияет ласковое солнце, зацветут цветы, защебечут птицы.
Вы сообразительные, умные, внимательные дети. Помогите мне.
Ваш друг Царица Математика».
Воспитатель: ребята, вы хотите помочь?
Дети: да.
Воспитатель: тогда нам надо поторопиться.
Задание №1.
Вспомните, сколько времени была печальна Царица Математика.
Дети: неделю.
В.: неделя – это сколько дней. Какой первый день недели?. Какой сегодня день недели?. Какой был вчера, будет завтра, позавчера, послезавтра. Сколько дней рабочих, сколько выходных.
Дети: называют дни недели.
11 слайд
В.: посмотрите, ребята. Перед вами закрытый, заколдованный слайд, вам надо правильно отвечать на все вопросы, решать правильно задания, и тогда мы выручим царицу Математику.
12 слайд
Задание №2. Решение неравенств
В.: Знаки спорят, где чье место, где здесь больше, где равно нужно им помочь, ребята, знаю вам на все равно. Сосчитай предметы так, чтоб поставить нужный знак.
Дети выполняют задания.
13слайд зАмок
14 слайд
Задание №3.
Решение примеров.
В.: перед вами новое задание. Примеры. Вы должны определить, какой знак поставить + или — чтобы ответ был верным. Дети работают самостоятельно. После окончания сверяются с примерами на доске.
— какой знак вы поставили в первом примере? (во втором, в третьем и т. д.)
За правильно выполненное задание появляется зАмок.
15 слайд зАмок расколдовывается
16 слайд Задание № 4 « Домики»
Посмотрите на домики. Окна в домиках закрыты не везде, вам нужно вставить пропущенные цифры. Будьте внимательны. Ошибок допускать нельзя, ведь мы помогаем Царице Математике
17 слайд зАмок расколдовывается
.
18 слайд Музыкальная разминка. «Снежки»
Воспитатель: вы хорошо работаете, но впереди еще много работы, поэтому предлагаю провести музыкальную разминку. Выходите из – за столов.
19 слайд Задание № 5 «Собери фигуру из треугольников»
20 слайд зАмок расколдовывается
21 слайд Замок и царица.
Тренажеры по математике онлайн для любого класса, игры по математике онлайн | Клуб любителей математики
Мы рады видеть Вас на сайте Клуба любителей математики! Здесь Вы сможете быстро и легко выучить Таблицу Умножения, «прокачать» свои навыки устного счета, либо просто с интересом и пользой провести время.
Умеете с ходу разбираться в любых вещах? Тогда начните свое знакомство с сайтом сразу в приложениях:
Простой онлайн тренажер поможет легко и эффективно выучить таблицу умножения за счет плавного увеличения сложности и подсказок в трудных местах.
Удобный интерфейс приложения поможет быстро и легко развить навыки счета. А наличие игровой формы превратит скучные занятия в увлекательную игру.
32 режима счета с разными дробями — простыми, неправильными, смешанными и десятичными. Ведение протокола примеров, подсказка с решением примера.
Пройдя все этапы игры, Вы откроете графический цифровой код и сможете разгадать его тайну.
Считаете себя профессионалом, готовым показать мастер класс, быстро и правильно решая любые примеры?
Значит докажи это!
Онлайн-тренажер для быстрого запоминания и проверки значений тригонометрических функций с наглядным отображением на тригонометрическом круге.
Подробнее о сайте
Matematika.Club – это активно развивающийся интернет-ресурс, включающий в себя разнообразие онлайн тренажеров по математике, обладающих удобным интерфейсом, подходящим под большинство современных устройств.
Наши онлайн тренажеры по математике позволяют в виде игры эффективно учить Таблицу Умножения и совершенствовать навыки устного счета при помощи специальных алгоритмов генерации математических примеров различных уровней сложности.
Сайт обладает средствами сбора персональной статистики, формирования подробных протоколов решения, анализа ошибок, наглядного отображения процесса и результатов собственного обучения.
как успеть за 3 месяца до школы
У многих детей трудности с математикой, очень часто они возникают еще в первых классах. При этом типична такая ситуация: ребенок не понял какую-то тему на уроке, родители уже забыли школьную программу и не могут объяснить ему материал. Итог: одна непонятая тема постепенно обрастает новыми пробелами в знаниях и в результате к концу четверти приходится нанимать репетитора.
Как же избежать таких проблем? Как помочь ребенку? Как сделать так, чтобы он полюбил математику с первого класса, с удовольствием решал задачки, а примеры щелкал, как орешки?
Для этого стоит начать знакомство с математикой еще до поступления в школу. Это поможет ребенку лучше адаптироваться в школе и чувствовать себя увереннее на уроках.
Сегодня мы расскажем, как познакомить малыша с математикой всего за 3 месяца.
Наши советы помогут ребенку освоить простейшие математические навыки: познакомят с цифрами и числами, научат складывать и вычитать, а также решать текстовые задачки.
3 месяца до школы. Первый шаг в обучении математике
Самое время познакомить ребенка с цифрами и числами, порядковым и количественным счетом, научить его считать и писать числа от 1 до 30. Лучше всего сделать это в игре. Занимайтесь с малышом не более получаса в день и следите за тем, чтобы он не переутомлялся.
Для начала познакомьте ребенка с порядковым счетом от 1 до 10, затем предложите ему упражнения для закрепления знаний.
Для знакомства с числами лучше всего подойдут игровые задания. Вот лишь несколько типов:
1. Соедини числа на картинке и напиши число в трафарете. Во время выполнения подобных упражнений следите за тем, чтобы ребенок соединял числа по порядку и называл каждое вслух.
2. Посчитай предметы.
Впиши пропущенные числа
2 месяца до школы. Второй шаг в обучении математике
Когда ваш ребенок запомнил все числа, можно знакомить его с простыми арифметическими действиями: сложением и вычитанием. Предлагайте ребенку задания, которые усложняются постепенно. Сначала научите его сложению и только, когда будете уверены в том, что он его полностью освоил, переходите к вычитанию.
Прежде чем предлагать ребенку примеры, вспомните с ним цифры и счет. Например, с помощью таких упражнений.
Затем можно предложить ему первые примеры. Сначала научите ребенка прибавлять 1, затем 2, 3, 4 и так далее. То же самое с вычитанием. Не спешите и переходите на следующий этап занятий только тогда, когда ребенок освоит предыдущий.
Вот несколько типов заданий, которые помогут в обучении:
1. Прибавь или вычти одно и то же число.
2.
Прочитай и обведи пример.
3. Сложи разные числа
Месяц до школы. Третий шаг в освоении математики
Когда ребенок освоил сложение и вычитание, очень важно закрепить эти навыки. Сделать это можно с помощью упражнений на скорость.
Сначала предложите ребенку определенное количество примеров и засеките время, за которое он с ними справиться. Затем предложите ребенку решать примеры на скорость. Для этого немного уменьшите исходное время, которое он потратил на решение самых первых примеров. Повторяйте тренировки ежедневно. Со временем ребенок будет выполнять задания без ошибок и за довольно короткое время.
Еще один вид математических упражнений, которые хорошо бы освоить до школы — простые текстовые задачи. Они особенно понравятся детям, потому что основаны на игровых элементах.
Решайте ежедневно по несколько подобных задачек.
Вконтакте
как научиться считать самому / TeachMePlease
Ментальная арифметика — это мгновенное совершение арифметических операций в уме.
Сначала они выполняются с помощью японских счётов — соробана, на которых ученик впоследствии считает в воображении. Существует множество организаций, предлагающих обучить данной технике. Мы же разберёмся, можно ли изучить её самостоятельно.
Инструменты счёта
Начинается обучение ментальной арифметике со счёта на соробане — японском варианте счёт. Они представляют собой доску с вертикальными спицами и пятью нанизанными на них костяшками. Отличительная черта соробана — горизонтальная перегородка, которая отделяет четыре костяшки в столбцах от пятой.
Четыре нижние косточки японцы называют «земными», они означают единицы. Пятая, верхняя костяшка, «небесная», считается сразу за пять единиц.
Для обучения ментальной арифметике необходимо обзавестись именно соробаном, а не просто счётами. Учиться считать можно также на бумаге с помощью изображения соробана или использовать специализированные сайты и приложения, но такое выполнение вычислений будет менее наглядным.
Основы работы с числами
В начале занятий соробан нужно привести в нулевую позицию, косточки соробана не должны касаться разделителя: верхние необходимо поднять к рамке, а нижние — наоборот опустить.
Для совершения действий с соробаном традиционно используют большой и указательный пальцы: первый перемещает бусины из нижнего ряда к разделителю, второй — выполняет остальные манипуляции.
Первая спица справа — это единицы (от 1 до 9). Чтобы отложить цифры от 1 до 4 необходимо перемещать косточки под разделителем в правом крайнем столбце вверх, для обозначения цифры 5 опускаем 1 костяшку из верхнего правого ряда. Числа от 6 до 9 обозначаем как 5, то есть 1 опущенная костяшка из верхнего ряда, плюс от 1 до 4 костяшек, поднятых к разделителю из нижнего ряда: 6 — это 5+1, 7 — это 5+2.
Переходим к десяткам (числа от 1 до 99): они находятся на следующей спице.
Двигаясь на столбец влево, мы меняем разряд — от единиц переходим к десяткам, далее к сотням, тысячам, десяткам тысяч и так далее.
Например, чтобы набрать число 129 необходимо поднять 1 косточку снизу в столбце сотен, 2 костяшки на столбце десятков, и 5 — опустить одну косточку к разделителю сверху и поднять 4 снизу в столбце единиц.
Изучив способы обозначения чисел, переходим к практике. Один человек вслух называет числа, а другой набирает их на доске. После того как навык доведён до автоматизма, можно переходить к арифметическим действиям.
Занятия с ребёнком можно сделать интереснее, называя числа со значением: например, посчитать количество дней в неделе, году, набрать номер дома, квартиры, годы рождения родственников, количество материков, стран, человек, населяющих город и страну.
Простые сложение и вычитание
Главное правило счёта на соробане: «считать нужно слева направо», что не соответствует привычному нам способу вычисления.
Внимание: техники счёта могут отличаться, мы используем те, что встречаются в рекомендации японской организации The Abacus Committee.
Начинать вычисления стоит с чисел, сумма и разность которых даёт не более 9 при сложении и не менее 1 при вычитании.
Примеры вроде 1+6, 2+7, 12+24 или 123+432 подойдут на первых порах.
- Начнём со сложения единиц: для примера 1+2 поднимите на крайней правой спице 1 костяшку вверх, а затем добавьте к ней ещё 2.
- Для примера:12+32. Откладываем в колонке десятков — 1 косточку, в единицах — 2. Затем к 1 костяшке придвигаем 3, к 2 костяшкам единиц ещё 2.
Изучать вычитание также стоит с простых примеров:
- Рассмотрим вычитание на единицах. Простой пример: 4 — 2 = 2. Из четырёх поднятых костяшек убираем 2 и получаем результат.
- Простой пример с десятками: 24 — 13 = 11. Из столбца десятков убираем 1 костяшку остаётся 1. Переходим к единицам: от 4 костяшек отнимаем 3, у нас остаётся 1 костяшка. Результат готов.
- По тому же принципу работаем с сотнями: 432 — 322 = 110. Из столбца сотен от 4 отнимем 3, из 3 вычтем 2 останется 1, из 2 вычтем 2 — все костяшки из столбца единиц возвращаются в нулевую позицию.
Для более сложных вычислений необходимо познакомиться с принципом дополнительных чисел.
Дополнительные числа
Высокая скорость работы на соробане зависит от того, насколько механизированы действия считающего.
Смысл заключается в том, чтобы снять лишнюю нагрузку с ума и выполнять арифметические действия механически, без размышлений или колебаний, отсюда и сравнение людей, обладающих этим навыком, с калькулятором. И если со сложением и вычитанием простых чисел всё ясно, то с более сложными примерами нужно освоить концепцию дополнительных чисел. Нужно просто запомнить, что:
- цифру 5 можно разложить на дополнительные числа: 4 и 1, 5 и 2.
- цифру 10 можно разложить на дополнительные числа: 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5.
При сложении дополнительное число вычитается. При вычитании — дополнительное число прибавляется. Как это работает на практике рассмотрим далее.
Сложное сложение
Пример: 4 + 8 = 12
Как решать?
- Установите 4 костяшки в столбце единиц.
- Для 8 костяшек места уже не найдётся.
- Вспоминаем принцип дополнительных чисел: число 10 даёт наша 8 и цифра 2.
- Вычтите дополнительную цифру 2 из 4.
- Добавьте единицу в столбик десятков.
- Результат — 12.
Принцип вычисления на соробане в привычной записи можно представить так:
4 + 8 = 12 превращаем в 4 — 2 +10 = 12
Важно запомнить: в сложных заданиях на сложение всегда вычитайте дополнительное число.
Сложное вычитание
Пример: 12 — 7 = 5.
Как решать?
- Установите 1 костяшку на столбец с десятками, добавьте 2 к единицам.
- Вспомните, что 7 — это 10 и 3.
- Уберите 1 костяшку из столбца десятков.
- Прибавьте в столбце единиц к 2 костяшкам дополнительные 3. Получается 5 — верните в нулевую позицию нижние костяшки и опустите «небесную».
Принцип вычисления на соробане в привычной записи можно представить так:
12 — 7 = 5 мы превращаем в 12 — 10 + 3 = 5
Важно запомнить: в подобных вычислениях на вычитание всегда прибавляйте дополнительное число.
Порядок столбцов при счёте
В приведённых выше примерах мы использовали по 2 столбца — для десятков и единиц.
Особое внимание стоит уделить тому, в каком порядке стоит добавлять и убирать костяшки из столбцов.
Для сложения:
- Вычтите дополнительное число и соответственное количество костяшек из правого столбца.
- Затем добавьте костяшку в левый стержень.
Для вычитания:
- Сначала вычтите числа в левом столбце.
- Добавьте дополнительное число на правый стержень.
Умножение
Есть несколько возможных способов умножения на соробане, мы рассмотрим один из самых распространённых.
Обратите внимание: чтобы умножать на соробане, нужно хорошо знать таблицу умножения.
Также необходимо запомнить следующие термины, которые мы рассмотрим на примере a x b = c, где:
a — это множимое;
b — это множитель;
с — произведение.
Пример: 43 x 8 = 344.
Шаг 1
В первом столбце слева устанавливаем множитель — 8, отступаем один столбец и откладываем множимое — 43. Отступаем 2 столбца — с этого столбца начнём записывать результат.
Шаг 2
Умножаем 3 на 8. Результат 24 записываем в 7 и 8 столбцах. Завершая операцию, убираем цифру 3 с доски, сдвинув костяшки вверх.
Шаг 3
Умножьте 4 на 8. Результат 32 запишите следующим образом: 3 в 6 столбец — перед прошлым результатом, а 2 сложите с результатом в 7 столбце, то есть с 2. Три цифры в результате дают ответ — 344.
Сложнее выполнить умножение с двумя двузначными числами, рассмотрим это на следующем примере:
Пример: 35 x 18
Шаг 1
Откладываем множитель, то есть 18 с начала доски. Делаем отступ и откладываем 35.
Шаг 2
Умножаем 1 на 5, записываем результат через 2 пробела.
Шаг 3
Умножаем 8 на 5, получаем 40. 4 записываем под прошлым результатом, т.е. складываем с 5. В столбцах результата остаётся цифра 90.
Шаг 4
Умножаем 3 на 1 и записываем результат — 3 — перед предыдущими столбцами. Получается 390.
Шаг 5
Умножаем 3 на 8, результат 24 записываем под первыми двумя цифрами прошлого результата.
Получаем 630.
Деление
Для деления мы также используем стандартные математические термины a ÷ b = c, где:
a — делимое;
b — делитель;
c — частное.
Делимое набирается на спицах в правом конце соробана, делитель — в левом конце. Результат записывается посередине.
Между делимым и делителем рекомендуют оставить минимум 4 пустых столбца для записи результата.
Также существуют правила размещения первой цифры частного:
- Если количество цифр в делителе меньше (или равно) количеству цифр в делимом, расположите первую цифру частного, отступив 2 столбца слева от делимого.
- Если количество цифр в делителе больше, нежели в делимом, начните располагать частное, отступив 1 столбец слева от делимого.
Пример: 72 ÷ 2
- Помещаем делитель 2 в левую часть счёт, делимое — 72 — в правую.
- Делим первое число 7 на 2. Цифра 2 помещается в 7 полностью три раза — поднимаем 3 костяшки в соответствии с правилом №1, отступив 2 столбца влево от делимого.
- Умножим полученное число 3 на делитель — 2. Результат — 6 — вычтем из первой цифры делимого — 7. Убираем лишние костяшки, остаётся единица.
- Остаток от делимого — 12 делим на делитель — 2. Полученный результат — 6 помещаем в следующий свободный столбец для записи результата. Получаем в итоге — 36.
Полезные ресурсы
- Подвигать косточки на соробане: ссылка
- Посмотреть пошаговое решение примеров: ссылка
- Приложение «Игры соробан»: ссылка
Мы разобрали самые простые способы вычисления на соробане. Чтобы выполнять манипуляции с трёхзначными и дробными числами необходимо на высоком уровне научиться работать с однозначными и двузначными числами.
Следующей ступенью после тщательного освоения каждой техники счёта становится его представление соробана в уме и мысленное выполнение вычислений. Последовательно, правильно и адаптировано для каждого возраста учат считать подготовленные тренеры в специализированных центрах.
Подобрать такой в своём городе вы можете на TeachMePlease.
Решение проблем Стратегии
для этой публикации услуг по оценке и оценкеАвторизация право на воспроизведение данного документа предоставляется лицам, действующим в официальном качестве в государственной системе народного образования как определено в Разделе 228.041 (1), Закон о Флориде. Авторское право уведомление внизу этой страницы должно быть включено во все копии. Администратор Авторские права © 2000 | |||||||||||||||
+ 6 = 12 или 3 ( 3 +1) = 3 (4).
Подсказка: если n — количество сторон, то 
Персона
за счетчиком срезов 0.53 фунта. Сколько это должно стоить?
Миссис Уильямс прочитала
20 книг . Их сын Джед прочитал 12 книг. Их дочь Джози
прочитала 14 книг, а их дочь Джули прочитала 7 книг. Как много
книги сделали дети мистера и миссисУильямс вообще читал?
Вы не знаете
если Джози, Джули и Джед — единственные дети.Использование стратегии решения проблем для решения числовых задач
Результаты обучения
- Применяйте общую стратегию решения проблем к числовым задачам
- Определите, сколько чисел вы решаете для данной числовой задачи
- Решить последовательные целочисленные задачи
Теперь переведем и решим числовые задачи.
В числовых задачах вам даются некоторые подсказки об одном или нескольких числах, и вы используете эти подсказки для построения уравнения. Проблемы с числами обычно возникают не каждый день, но они дают хорошее введение в практику стратегии решения проблем. Не забудьте найти ключевые слова, такие как , разница , из и и .
Пример
Разница между числом и шестью [латекс] 13 [/ латекс]. Найдите номер.
Решение:
| Шаг 1. Прочтите задачу. Вы все слова понимаете? | |
| Шаг 2. Определите то, что вы ищете. | номер |
| Шаг 3. Имя. Выберите переменную для представления числа. | Пусть [латекс] n = \ text {число} [/ latex] |
| Шаг 4. Translate. Перефразируйте одним предложением. Переведите в уравнение. | [латекс] n-6 \ Enspace \ Rightarrow [/ latex] Разница числа и 6 [latex] = \ enspace \ Rightarrow [/ latex] равно [латекс] 13 \ Enspace \ Rightarrow [/ латекс] тринадцать |
Шаг 5. Решите уравнение.Добавьте 6 с обеих сторон. Упростить. | [латекс] n-6 = 13 [/ латекс] [латекс] n-6 \ color {red} {+ 6} = 13 \ color {red} {+ 6} [/ latex] [латекс] n = 19 [/ латекс] |
| Шаг 6. Проверка: Разница между [латексом] 19 [/ латексом] и [латексом] 6 [/ латексом] составляет [латекс] 13 [/ латекс]. Это проверяет. | |
| Шаг 7. Ответьте на вопрос. | Номер [латекс] 19 [/ латекс]. |
пример
Сумма двойного числа и семи составляет [латекс] 15 [/ латекс]. Найдите номер.
Показать решениеРешение:
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите то, что вы ищете. | номер |
Шаг 3. Имя. Выберите переменную для представления числа. | Пусть [латекс] n = \ text {число} [/ latex] |
| Шаг 4. Translate. Переформулируйте проблему одним предложением. Переведите в уравнение. | [латекс] 2n \ enpace \ Rightarrow [/ latex] Сумма удвоенного числа [латекс] + \ Enspace \ Rightarrow [/ latex] и [латекс] 7 \ Enspace \ Rightarrow [/ латекс] семь [latex] = \ enspace \ Rightarrow [/ latex] равно [латекс] 15 \ Enspace \ Rightarrow [/ латекс] пятнадцать |
| Шаг 5. Решите уравнение. | [латекс] 2n + 7 = 15 [/ латекс] |
| Вычтите 7 с каждой стороны и упростите. | [латекс] 2n = 8 [/ латекс] |
| Разделите каждую сторону на 2 и упростите. | [латекс] n = 4 [/ латекс] |
| Шаг 6. Проверка: — это сумма удвоенных [латекс] 4 [/ латекс] и [латекс] 7 [/ латекс], равная [латексу] 15 [/ латексу]? [латекс] 2 \ cdot {4} + 7 = 15 [/ латекс] [латекс] 8 + 7 = 15 [/ латекс] [латекс] 15 = 15 \ квадратик \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. | Номер [латекс] 4 [/ латекс]. |
Посмотрите следующее видео, чтобы увидеть еще один пример решения числовой задачи.
Решение двух или более чисел
В некоторых задачах с числовыми словами вам предлагается найти два или более чисел. Может возникнуть соблазн назвать их все разными переменными, но до сих пор мы решали уравнения только с одной переменной. Мы определим числа в терминах одной и той же переменной.Обязательно внимательно прочтите задачу, чтобы узнать, как все числа соотносятся друг с другом.
пример
Одно число на пять больше другого. Сумма чисел — двадцать один. Найдите числа.
Показать решениеРешение:
| Шаг 1. Прочтите проблему. | ||
Шаг 2. Определите то, что вы ищете. | Вы ищете два числа. | |
| Шаг 3.{\ text {nd}} \ text {number} [/ latex] | ||
| Шаг 4. Translate. Переформулируйте проблему одним предложением со всей важной информацией. Переведите в уравнение. Подставьте переменные выражения. | Сумма чисел [латекс] 21 [/ латекс]. Сумма 1-го числа и 2-го числа составляет [латекс] 21 [/ латекс]. [латекс] n \ Enspace \ Rightarrow [/ latex] Первое число [латекс] + \ Enspace \ Rightarrow [/ latex] + [латекс] n + 5 \ Enspace \ Rightarrow [/ latex] Второй номер [латекс] = \ enpace \ Rightarrow [/ latex] = [латекс] 21 \ Enspace \ Rightarrow [/ латекс] 21 | |
| Шаг 5. Решите уравнение. | [латекс] n + n + 5 = 21 [/ латекс] | |
| Объедините похожие термины. | [латекс] 2n + 5 = 21 [/ латекс] | |
Вычтите пять с обеих сторон и упростите. | [латекс] 2n = 16 [/ латекс] | |
| Разделите на два и упростите. | [латекс] n = 8 [/ латекс] 1-й номер | |
| Найдите и второе число. | [латекс] n + 5 [/ латекс] 2-й номер | |
| Заменитель [латекс] n = 8 [/ латекс] | [латекс] \ color {красный} {8} +5 [/ латекс] | |
| [латекс] 13 [/ латекс] | ||
| Шаг 6. Чек: | ||
| Эти номера определяют проблему? Одно число 5 больше, чем другое? Тринадцать, 5 больше, чем 8? Да. Сумма двух чисел равна 21? | [латекс] 13 \ stackrel {\ text {?}} {=} 8 + 5 [/ латекс] [латекс] 13 = 13 \ четырехугольник \ галочка [/ латекс] [латекс] 8 + 13 \ stackrel {\ text {?}} {=} 21 [/ латекс] [латекс] 21 = 21 \ квадратик \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. | Номера: [латекс] 8 [/ латекс] и [латекс] 13 [/ латекс]. |
Посмотрите следующее видео, чтобы увидеть еще один пример того, как найти два числа с учетом отношения между ними.
пример
Сумма двух чисел равна четырнадцати отрицательным. Одно число на четыре меньше другого. Найдите числа.
Показать решениеРешение:
| Шаг 1.{\ text {nd}} \ text {number} [/ latex] | ||
| Шаг 4. Translate. Напишите как одно предложение. Переведите в уравнение. Подставьте переменные выражения. | Сумма двух чисел равна четырнадцати отрицательным. [латекс] n \ Enspace \ Rightarrow [/ latex] Первое число [латекс] + \ Enspace \ Rightarrow [/ latex] + [латекс] n-4 \ Enspace \ Rightarrow [/ latex] Второй номер [латекс] = \ enpace \ Rightarrow [/ latex] = [латекс] -14 \ Enspace \ Rightarrow [/ латекс] -14 | |
Шаг 5. Решите уравнение. | [латекс] n + n-4 = -14 [/ латекс] | |
| Объедините похожие термины. | [латекс] 2n-4 = -14 [/ латекс] | |
| Добавьте по 4 с каждой стороны и упростите. | [латекс] 2n = -10 [/ латекс] | |
| Разделить на 2. | [латекс] n = -5 [/ латекс] 1-й номер | |
| Замените [латекс] n = -5 [/ латекс], чтобы найти 2 и номер . | [латекс] н-4 [/ латекс] 2-й номер | |
| [латекс] \ color {red} {- 5} -4 [/ латекс] | ||
| [латекс] -9 [/ латекс] | ||
| Шаг 6. Чек: | ||
| Неужели −9 четыре меньше −5? Их сумма равна −14? | [латекс] -5-4 \ stackrel {\ text {?}} {=} — 9 [/ латекс] [латекс] -9 = -9 \ четырехугольник \ галочка [/ латекс] [латекс] -5 + (- 9) \ stackrel {\ text {?}} {=} — 14 [/ латекс] [латекс] -14 = -14 \ четырехугольник \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. | Номера: [латекс] −5 [/ латекс] и [латекс] −9 [/ латекс]. |
пример
Одно число на десять больше, чем другое. Их сумма равна единице. Найдите числа.
Показать решениеРешение:
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите то, что вы ищете. | два числа | |
| Шаг 3. Имя. Выберите переменную. Одно число на десять больше, чем другое.{\ text {nd}} \ text {number} [/ latex] | ||
| Шаг 4. Translate. Перефразируйте одним предложением. | Их сумма равна единице. | |
| Перевести в уравнение | [латекс] x + (2x + 10) \ enspace \ Rightarrow [/ latex] Сумма двух чисел [latex] = \ enspace \ Rightarrow [/ latex] равно [латекс] 1 \ enpace \ Rightarrow [/ латекс] 1 | |
Шаг 5. Решите уравнение. | [латекс] x + 2x + 10 = 1 [/ латекс] | |
| Объедините похожие термины. | [латекс] 3x + 10 = 1 [/ латекс] | |
| Вычтите 10 с каждой стороны. | [латекс] 3x = -9 [/ латекс] | |
| Разделите каждую сторону на 3, чтобы получить первое число. | [латекс] x = -3 [/ латекс] | |
| Замените, чтобы получить второй номер. | [латекс] 2x + 10 [/ латекс] | |
| [латекс] 2 (\ color {red} {- 3}) + 10 [/ латекс] | ||
| [латекс] 4 [/ латекс] | ||
| Шаг 6. Проверить. | ||
| Неужели 4 десять больше, чем в два раза −3? Их сумма равна 1? | [латекс] 2 (-3) +10 \ stackrel {\ text {?}} {=} 4 [/ латекс] [латекс] -6 + 10 = 4 [/ латекс] [латекс] 4 = 4 \ четырехугольник \ галочка [/ латекс] [латекс] -3 + 4 \ stackrel {\ text {?}} {=} 1 [/ латекс] [латекс] 1 = 1 \ четырехугольник \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. | Цифры: [латекс] −3 [/ латекс] и [латекс] 4 [/ латекс]. |
Решение для последовательных целых чисел
Целые числа, идущие подряд, — это целые числа, следующие друг за другом. Вот несколько примеров последовательных целых чисел:
[латекс] \ begin {массив} {c} \ phantom {\ rule {0.2} {0ex}} \\ \ phantom {\ rule {0.2} {0ex}} \\ \ phantom {\ rule {0.2} {0ex }} \\ \ phantom {\ rule {0.2} {0ex}} \\ \ hfill \ text {…} 1,2,3,4 \ text {,…} \ hfill \ end {array} [/ latex]
[латекс] \ text {…} -10, -9, -8, -7 \ text {,…} [/ latex]
[latex] \ text {…} 150,151,152,153 \ text {,…} [/ latex]
Обратите внимание, что каждое число на единицу больше, чем предшествующее ему.Итак, если мы определим первое целое число как [latex] n [/ latex], следующее последовательное целое число будет [latex] n + 1 [/ latex]. Следующий за ним на единицу больше, чем [latex] n + 1 [/ latex], так что это [latex] n + 1 + 1 [/ latex] или [latex] n + 2 [/ latex].
[латекс] \ begin {array} {cccc} n \ hfill & & & \ text {1-е целое число} \ hfill \\ n + 1 \ hfill & & & \ text {2-е целое число подряд} \ hfill \\ n + 2 \ hfill & & & \ text {3-е целое число подряд} \ hfill \ end {array} [/ latex]
пример
Сумма двух последовательных целых чисел равна [латекс] 47 [/ латекс].Найдите числа.
Решение:
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите то, что вы ищете. | два последовательных целых числа | |
| Шаг 3. Имя. | Пусть [латекс] n = \ text {1-е целое число} [/ latex] [латекс] n + 1 = \ text {следующее последовательное целое число} [/ латекс] | |
| Шаг 4. Translate. Перефразируйте одним предложением. Переведите в уравнение. | [латекс] n + n + 1 \ Enspace \ Rightarrow [/ latex] Сумма целых чисел [latex] = \ enspace \ Rightarrow [/ latex] равно [латекс] 47 \ Enspace \ Rightarrow [/ латекс] 47 | |
Шаг 5. Решите уравнение. | [латекс] n + n + 1 = 47 [/ латекс] | |
| Объедините похожие термины. | [латекс] 2n + 1 = 47 [/ латекс] | |
| Вычтите по 1 с каждой стороны. | [латекс] 2n = 46 [/ латекс] | |
| Разделите каждую сторону на 2. | [латекс] n = 23 [/ латекс] 1-е целое число | |
| Замените, чтобы получить второй номер. | [латекс] n + 1 [/ латекс] 2-е целое число | |
| [латекс] \ color {красный} {23} +1 [/ латекс] | ||
| [латекс] 24 [/ латекс] | ||
| Шаг 6. Проверка: | [латекс] 23 + 24 \ stackrel {\ text {?}} {=} 47 [/ латекс] [латекс] 47 = 47 \ квадратик \ галочка [/ латекс] | |
| Шаг 7. Ответьте на вопрос. | Два последовательных целых числа: [латекс] 23 [/ латекс] и [латекс] 24 [/ латекс]. |
пример
Найдите три последовательных целых числа, сумма которых равна [латекс] 42 [/ латекс].
Показать решениеРешение:
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите то, что вы ищете. | три последовательных целых числа | |
| Шаг 3. Имя. | Пусть [латекс] n = \ text {1-е целое число} [/ latex] [латекс] n + 1 = \ text {2-е целое число подряд} [/ латекс] [латекс] n + 2 = \ text {3-е целое число подряд} [/ латекс] | |
| Шаг 4. Translate. Перефразируйте одним предложением. Переведите в уравнение. | [латекс] n \ enpace + \ enspace n + 1 \ enspace + \ enspace n + 2 \ enspace \ Rightarrow [/ latex] Сумма трех целых чисел [latex] = \ enspace \ Rightarrow [/ latex] равно [латекс] 42 \ Enspace \ Rightarrow [/ латекс] 42 | |
Шаг 5. Решите уравнение. | [латекс] n + n + 1 + n + 2 = 42 [/ латекс] | |
| Объедините похожие термины. | [латекс] 3n + 3 = 42 [/ латекс] | |
| Вычтите по 3 с каждой стороны. | [латекс] 3n = 39 [/ латекс] | |
| Разделим каждую сторону на 3. | [латекс] n = 13 [/ латекс] 1-е целое число | |
| Замените, чтобы получить второй номер. | [латекс] n + 1 [/ латекс] 2-е целое число | |
| [латекс] \ color {красный} {13} +1 [/ латекс] | ||
| [латекс] 24 [/ латекс] | ||
| Замените, чтобы получить третий номер. | [латекс] n + 2 [/ латекс] 3-е целое число | |
| [латекс] \ color {красный} {13} +2 [/ латекс] | ||
| [латекс] 15 [/ латекс] | ||
| Шаг 6. Проверка: | [латекс] 13 + 14 + 15 \ stackrel {\ text {?}} {=} 42 [/ латекс] [латекс] 42 = 42 \ квадратик \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. | Три последовательных целых числа: [латекс] 13 [/ латекс], [латекс] 14 [/ латекс] и [латекс] 15 [/ латекс]. |
Посмотрите это видео, чтобы увидеть еще один пример того, как найти три последовательных целых числа по их сумме.
Задачи со словами — Полный курс алгебры
10
Примеры
Проблемы
ПРОБЛЕМЫ СО СЛОВАМИ требуют практики в переводе словесного языка на алгебраический язык. См. Урок 1, Задача 8.Тем не менее, проблемы со словами делятся на разные типы. Ниже приведены некоторые примеры.
Пример 1. ax ± b = c . Все проблемы, подобные следующей, в конечном итоге приводят к уравнению в такой простой форме.
Джейн потратила 42 доллара на обувь.
Это было на 14 долларов меньше, чем вдвое, чем она потратила на блузку. Сколько была кофточка?
Решение. У каждой проблемы со словом неизвестный номер. В этой проблеме цена на кофточку.Всегда позволяйте x представлять неизвестное число. То есть пусть на вопрос ответит x .
Пусть тогда x будет, сколько она потратила на блузку. В задаче говорится, что «Это» — то есть 42 доллара — было на 14 долларов меньше, чем два раза x .
Вот уравнение:
| 2 x — 14 | = | 42. |
| 2 x | = | 42 + 14 (Урок 9) |
| = | 56. | |
| x | = | 56 2 |
| = | 28. | |
Блузка стоила 28 долларов.
Пример 2. В классе б мальчиков. Это в три раза больше, чем в четыре раза девушек.Сколько девочек в классе?
Решение. Опять же, пусть x представляет неизвестное число, которое вас просят найти: Пусть x будет количеством девушек.
(Хотя b неизвестно — это произвольная константа — это не то, что вас просят найти.)
В задаче указано, что «Это» — b — на три больше, чем в четыре раза x :
| 4 x + 3 | = | б . | ||
| Следовательно, | ||||
| 4 х | = | б — 3 | ||
| x | = | б — 3 4 | . | |
Решение здесь не число, потому что оно будет зависеть от значения b .Это тип «буквального» уравнения, очень распространенного в алгебре.
Пример 3. Целое равно сумме частей.
Сумма двух чисел равна 84, одно из них на 12 больше другого. Какие два числа?
Решение. В этой задаче нам предлагается найти два числа. Следовательно, мы должны позволить x быть одним из них. Тогда пусть x будет первым числом.
Нам говорят, что другое число — еще 12, x + 12.
В задаче указано, что их сумма равна 84:
= 84
Линия размером x + 12 является символом группировки, называемым vinculum . Это избавляет нас от написания скобок.
У нас:
| 2 x | = | 84–12 |
| = | 72. | |
| x | = | 72 2 |
| = | 36. | |
Это первый номер. Следовательно, другой номер —
.x + 12 = 36 + 12 = 48.
Сумма 36 + 48 равна 84.
Пример 4.Сумма двух последовательных чисел составляет 37. Какие они?
Решение . Два последовательных числа равны 8 и 9 или 51 и 52.
Пусть тогда x будет первым числом. Тогда число после него будет x + 1.
В задаче указано, что их сумма равна 37:
= 37
| 2 x | = | 37 — 1 |
| = | 36. | |
| x | = | 36 2 |
| = | 18. | |
Два числа — 18 и 19.
Пример 5. Одно число на 10 больше другого.
Сумма, состоящая из удвоенного меньшего и трехкратного большего, равна 55.Какие два числа?
Решение. Пусть x будет меньшим числом.
Тогда большее число на 10 больше: x + 10.
Состояние проблемы:
| 2 x + 3 ( x + 10) | = | 55. |
| Это означает | ||
| 2 x + 3 x + 30 | = | 55.Урок 14. | .
| 5 x | = | 55–30 = 25. |
| x | = | 5. |
Это меньшее число. Чем больше число, тем больше на 10: 15.
Пример 6. Разделите 80 долларов между тремя людьми так, чтобы у второго было вдвое больше, чем у первого, а у третьего было на 5 долларов меньше, чем у второго.
Решение .
Опять же, нас просят найти более одного числа. Мы должны начать с того, что допустим x как то, сколько получает первый человек.
Затем второй получает вдвое больше, 2 x .
А третий получает на 5 долларов меньше, 2 x — 5.
Их сумма 80 $:
| 5 x | = | 80 + 5 |
| x | = | 85 5 |
| = | 17. | |
Вот сколько получает первый человек. Следовательно, второй получает
| 2 x | = | 34. |
| А третий получает | ||
| 2 x — 5 | = | 29. |
Сумма 17, 34 и 29 фактически равна 80.
Пример 7.Нечетные числа. Сумма двух подряд идущих нечетных чисел равна 52. Какие два нечетных числа?
Решение . Во-первых, четное число кратно 2: 2, 4, 6, 8 и так далее. В алгебре принято представлять четное число как 2 n , где при вызове переменной « n » понимается, что n будет принимать целые числа: n = 0, 1, 2 , 3, 4 и так далее.
Нечетное число на 1 больше (или на 1 меньше) четного.И поэтому представим нечетное число как 2 n + 1.
Пусть 2 n + 1 будет первым нечетным числом. Далее будет еще 2 — это будет 2 n + 3. В задаче указано, что их сумма 52:
.| 2 n + 1 + 2 n + 3 | = | 52. |
Теперь мы решим это уравнение для n , а затем заменим решение в 2 n + 1, чтобы найти первое нечетное число.У нас:
| 4 n + 4 | = | 52 |
| 4 n | = | 48 |
| n | = | 12. |
Следовательно, первое нечетное число 2 · 12 + 1 = 25.Итак, следующее 27. Их сумма 52.
Проблемы
Задача 1. У Джули есть 50 долларов, что на восемь долларов больше, чем у Джона. Сколько у Джона? (Сравните Пример 1.)
Во-первых, что вы позволите представить в формате x ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
Неизвестный номер — сколько у Джона.
Что такое уравнение?
2 x + 8 = 50.
Вот решение:
x = 21
долларов СШАПроблема 2. Карлотта потратила на рынке 35 долларов. Это было на семь долларов меньше, чем в три раза, чем она потратила в книжном магазине; сколько она там потратила?
Вот уравнение.
3 x — 7 = 35
Вот решение:
x = 14
долларов США Проблема 3.
Есть b черных мраморов. Это на четыре больше, чем в два раза больше красных шариков. Сколько там красных шариков? (Сравните Пример 2.)
Вот уравнение.
2 x + 4 = b
Вот решение:
Проблема 4. Джанет потратила 100 долларов на книги. Это было на тыс. долларов меньше, чем в пять раз больше, чем она потратила на обед.Сколько она потратила на обед?
Вот уравнение.
5 x — к = 100
Вот решение:
Задача 5. Целое равно сумме частей.
Сумма двух чисел равна 99, и одно из них на 17 больше другого. Какие два числа? (Сравните Пример 3.)
Вот уравнение.
Вот решение:
Задача 6. Класс из 50 учеников делится на две группы; в одной группе на восемь меньше, чем в другой; сколько их в каждой группе?
Вот уравнение.
Вот решение:
Проблема 7.Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа?
Вот уравнение.
x + 5 x = 72.
Вот решение:
x = 12. 5 x = 60.
Задача 8. Сумма трех последовательных чисел 87; кто они такие? (Сравните Пример 4.)
Вот уравнение.
Вот решение:
28, 29, 30.
Задача 9. Группа из 266 человек состоит из мужчин, женщин и детей. Мужчин в четыре раза больше, чем детей, и в два раза больше женщин, чем детей. Сколько их там?
(Чему вы положите равным x — количеству мужчин, женщин или детей?)
| Пусть x | = | Количество детей.Тогда |
| 4 x | = | Количество мужчин. И |
| 2 x | = | Количество женщин. |
| Вот уравнение: | ||
x + 4 x + 2 x = 266
Вот решение:
х = 38.4 x = 152. 2 x = 76,
Задача 10. Разделите 79 долларов между тремя людьми так, чтобы у второго было в три раза больше, чем у первого, а у третьего было на два доллара больше, чем у второго. (Сравните Пример 6.)
Вот уравнение.
Вот решение:
11, 33, 35 долларов.
Задача 11. Разделите 15,20 доллара между тремя людьми так, чтобы у второго было на доллар больше, чем у первого, а у третьего — на 2,70 доллара больше, чем у второго.
Вот уравнение.
Вот решение:
3,50 доллара, 4,50 доллара, 7,20 доллара.
Задача 12. Два последовательных нечетных числа таковы, что три раза первое будет 5 больше, чем в два раза больше второго.Что это за два нечетных числа?
(см. Пример 7, где мы представляем нечетное число как 2 n + 1.)
Решение . Пусть первое нечетное число будет 2 n + 1.
Тогда следующий 2 n + 3 — потому что будет еще 2.
Задача состоит в следующем:
| 3 (2 n + 1) | = | 2 (2 n + 3) + 5. | |
| Это означает: | |||
| 6 n + 3 | = | 4 n + 6 + 5. | |
| 2 n | = | 8. | |
| n | = | 4. | |
Следовательно, первое нечетное число — 2 · 4 + 1 = 9. Следующее — 11.
И это верное решение, потому что в соответствии с проблемой:
3 · 9 = 2 · 11 + 5.
Следующий урок: Неравенство
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Решение вопросов Word
МНОГО примеров!
В алгебре мы часто задаем вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Превращение английского в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте набросок , если возможно
- Назначьте букв для значений
- Найдите или разработайте формул
Вам также следует записать , что на самом деле требуется для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!
Также ищите ключевые слова:
| Когда вы видите | Думаю | |
|---|---|---|
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более | + | |
минус, меньше, разница, меньше, уменьшилась, уменьшилась | – | |
умноженное на умножение на произведение, множитель | × | |
разделенное, частное, на, из, соотношение, соотношение, процент, ставка | ÷ | |
| увеличить или уменьшить | геометрия формулы | |
| Скорость, скорость | расстояние формулы | |
| Сколько дней, часов, минут, секунд | время |
Ясное мышление
Некоторые формулировки могут быть хитрыми, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.
Как нам записать это в виде уравнения?- Пусть S = долларов у Сэма
- Пусть A = долларов У Алекса
Теперь … вот что: S — 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ: S = A — 2
( S — 2 = — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как нам записать это в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь … это то, что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как вопрос написан «дважды … собаки … кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы увидеть, как это делается:
Пример: прямоугольный сад размером 12 на 5 м, какова его площадь?
Превратите английский в алгебру:
Эскиз:
.
Письма:
- Используйте w для ширины прямоугольника: w = 12 м
- Используйте h для высоты прямоугольника: h = 5m
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь 60 кв.м .
Теперь давайте попробуем пример сверху страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?
Превратите английский в алгебру:
Письма:
- Используйте S , чтобы узнать, сколько игр Сэм сыграл
- Используйте A , чтобы узнать, сколько игр сыграл Алекс
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начать с: S + A = 12
S = A + 4 , поэтому мы можем
заменить S на «A + 4»: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычтем 4 с обеих сторон: 2A = 12 — 4
Упростить: 2A = 8
Разделите обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!
Пример посложнее:
Пример: Алекс и Сэм также создают таблицы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая один, может заработать 10 за 30 дней.
Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?
Превратите английский в алгебру:
Письма:
- Используйте a для скорости работы Алекса
- Используйте с для скорости работы Сэма
12 дней Alex и Sam — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день) составляет: a = 10/30 = 1/3
Начать с: 12a + 12s = 10
Положите «1/3» для a: 12 (1/3) + 12s = 10
Упростить: 4 + 12 = 10
Вычтем 4 с обеих сторон: 12s = 6
Разделите обе стороны на 12: s = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).
Итак, 10 столов займет у Сэма всего 20 дней.
Интересно, стоит ли Сэму платить больше?
И еще пример «подстановки»:
Пример: Дженна усиленно тренируется, чтобы пройти отбор на Национальные игры.
У нее обычный еженедельный распорядок, в одни дни она тренируется по пять часов в день, а в другие — по 3 часа в день.
В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?
Письма:
- Количество «5 часовых» дней: d
- Количество «3 часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из которых d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решить:
d + e = 7
Итак: e = 7 — d
Положим в 5d + 3e = 27 5d + 3 (7 − d) = 27
Упростить: 5d + 21 — 3d = 27
Вычтем 21 с обеих сторон: 5d — 3d = 6
Упростить: 2d = 6
Разделим обе части на 2: d = 3
Количество «5 часовых» дней — 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Некоторые примеры из Geometry:
Пример: круг имеет площадь 12 мм
2 , каков его радиус?Письма:
- Используйте A для Area: A = 12 мм 2
- Используйте r для радиуса
И формула для площади: A = π r 2
У нас спрашивают радиус.
Решить:
Нам нужно переставить формулу, чтобы найти площадь
Начать с: A = π r 2
Поменять местами стороны: π r 2 = A
Разделим обе части на π : r 2 = A / π
Извлечь квадратный корень из обеих частей: r = √ (A / π)
Теперь мы можем использовать формулу: r = √ (12/ π)
И получаем: r = 1.954 (до 3-х мест)
Пример: куб имеет объем 125 мм
3 , какова его площадь поверхности?Сделайте быстрый набросок:
Письма:
- Используйте В для объема
- Используйте A для Area
- Используйте s для длины стороны куба
Формулы:
- Объем куба: В = с 3
- Площадь куба: A = 6s 2
У нас спрашивают площадь.
Решить:
Первая тренировка с по формуле объема:
Начать с: В = с 3
Поменять местами стороны: с 3 = V
Извлечь кубический корень с обеих сторон: s = ∛ (V )
И получаем: с = ∛ (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начать с: A = 6s 2
И получаем: А = 6 (5) 2
A = 6 × 25 = 150 мм 2
Пример о деньгах:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.
Одну неделю Джоэл проработал 40 часов по обычной ставке, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?
Письма:
- Обычная ставка оплаты труда Джоэла: N $ в час
Формулы:
- Джоэл работает 40 часов по цене N $ в час = 40N
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар. 25N в час
- Джоэл работает 12 часов по цене 1,25 доллара США в час = (12 × 1 доллар США) = 15 долларов США
- А вместе он заработал 660 долларов, итак:
25N в час40N + $ (12 × 1¼N) = 660 $
Нас спрашивают, какова нормальная ставка зарплаты Джоэла — N долларов.
Решить:
Начните с 40N $ + (12 × 1¼N) = 660 $
Упростить: 40N + 15N = 660 $
Еще больше упростите: 55 $ N = 660 $
Разделим обе стороны на 55: $ N = 12 $
Итак, нормальная ставка оплаты труда Джоэла составляет 12 долларов в час.
Чек
Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная ставка составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная зарплата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в сумме 660
долларов.Подробнее о деньгах с этими двумя примерами, включающими сложный процент
Пример: Алекс вкладывает 2000 долларов в банк под 11% годовых.
Сколько это будет стоить через 3 года?Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Текущая стоимость PV = 2000 долларов США
- Процентная ставка (в десятичном формате): r = 0.11
- Количество периодов: n = 3
- Будущая стоимость (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3
Вычислить: FV = $ 2000 × 1,367631
Вычислим: FV = 2735 долларов.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
с:
- Текущая стоимость PV = 1000 долларов США
- Процентная ставка (желаемое значение): р.
- Количество периодов: n = 9
- Будущая стоимость: FV = 1551 доллар.33
Нас спрашивают о процентной ставке:
р.Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) 9
Поменять стороны: 1000 $ × (1 + r) 9 = 1551,33 $
Разделите обе стороны на 1000: (1 + r) 9 = 1551,33 доллара США / 1000 долларов США
Упростить: (1 + r) 9 = 1.55133
корень 9-й степени: 1 + r = 1,55133 (1/9)
Вычислить: 1 + r = 1.05
Вычислить: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долларов × (1,05) 9 = 1000 долларов × 1,55133 = 1551,33 доллара
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2: 1
Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки.
Соотношение мальчиков и девочек сейчас составляет 4: 3
Сколько всего студентов сейчас?
Письма:
- Количество мальчиков сейчас: б
- Количество девочек сейчас: г
Коэффициент текущей ликвидности 4: 3
b г = 4 3
Что можно переставить на 3b = 4g
На начало года было (b + 4) мальчиков и (g — 2) девочек, и соотношение было 2: 1
b + 4 г — 2 = 2 1
Что может быть преобразовано в b + 4 = 2 (g — 2)
Нас спрашивают, сколько всего студентов сейчас: b + g
Решить:
Начать с: b + 4 = 2 (г — 2)
Упростить: b + 4 = 2g — 4
Вычтем 4 с обеих сторон: b = 2g — 8
Умножаем обе стороны на 3 (получаем 3b): 3b = 6g — 24
Запомнить 3b = 4g : 4g = 6g — 24
Вычтем 6g с обеих сторон : −2g = -24
Разделим обе части на −2: g = 12
Есть 12 девушек !
И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , так что есть 16 мальчиков
Таким образом, сейчас в классе 12 девочек и 16 мальчиков, всего учеников 28 .
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3.
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1
А теперь для некоторых квадратных уравнений:
Пример. Произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?
Последовательные означают один за другим. И их , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2
И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:
п (п + 2) = 168
У нас спрашивают целые числа
Решить:
Начать с: n (n + 2) = 168
Развернуть: n 2 + 2n = 168
Вычтем 168 с обеих сторон: n 2 + 2n — 168 = 0
Это квадратное уравнение, и есть много способов его решить.
Используя метод решения квадратного уравнения, получаем −14 и 12.
Чек −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА
Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА
Итак, есть два решения: -14 и -12 — одно, 12 и 14 — другое.
Примечание: мы также могли попробовать «угадать и проверить»:
- Мы могли бы попробовать, скажем, n = 10: 10 (12) = 120 NO (слишком мало)
- Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА
Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).
А:
Пример: вы архитектор. Вашему клиенту нужна комната вдвое длиннее, чем ширина. Им также нужна веранда шириной 3 метра по длинной стороне.
У вашего клиента 56 квадратных метров красивой мраморной плитки, чтобы покрыть всю площадь.
Какой должна быть длина комнаты?
Давайте сначала сделаем набросок, чтобы все было правильно !:
Письма:
- Длина помещения: л
- Ширина помещения: Вт
- Общая площадь с верандой: А
Мы знаем:
- ширина комнаты равна половине ее длины: W = ½L
- общая площадь равна (ширина помещения + 3), умноженная на длину: A = (W + 3) × L = 56
Нас спрашивают о длине комнаты: L
Решить:
Начать с: (Ш + 3) × Д = 56
Заменитель W = ½L : (½L + 3) × L = 56
Упростить: ½L 2 + 3L = 56
Умножьте все члены на 2: L 2 + 6L = 112
Вычесть 112 с обеих сторон : L 2 + 6L — 112 = 0
Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторизацией:
Начать с: L 2 + 6L — 112 = 0
Два числа, которые умножаются и дают ac = −112,
и
сложить, чтобы получить b = 6, получится 14 и −8: L 2 + 14L — 8L — 112 = 0
Группа: L (L +14) — 8 (L + 14) = 0
Группа: (L — 8) (L + 14) = 0
Итак, L = 8 или -14
Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!
Итак, длина помещения 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56
Вот и мы.
..
… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?
Решение нестандартных математических задач
Что такое нестандартное решение проблем?Нестандартное решение проблем, также называемое творческим решением проблем, требует определенной степени творчества или оригинальности. Для нестандартных проблем обычно нет очевидной стратегии их решения. Часто эти проблемы можно решить разными способами и с помощью различных стратегий.Как и в случае с вычислительными упражнениями (например, делением в столбик), ученикам необходимо явно учить нестандартных задач.
Почему решение нестандартных проблем всегда будет частью моей инструкции:
- Он готовит студентов к решению реальных жизненных проблем. Реальные проблемы не содержат предписанных шагов по их решению. Чтобы их решить, люди должны мыслить творчески и логически.
- Это дает студентам возможность выбора. Я использую слово «дар», однако для многих учеников этот аспект очень ошеломляет.Они привыкли, что им говорят, что и как делать. Это буквально калечит студентов, когда приходит время решать задачу, которая не следует выученному алгоритму. В случае нестандартных задач учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определять подходящие стратегии использования и уверенно решать эти проблемы.
- Как упоминалось выше, это вселяет в студентов уверенность. Студенты вскоре понимают, что они могут самостоятельно выбрать подходящую стратегию (или стратегии) и успешно ее применять.
- Это дает студентам здоровую дозу «борьбы». Я полностью за то, чтобы преподавать на уровне обучения студентов. Однако я твердо убежден, что студенты также должны иногда чувствовать себя немного некомфортно, даже расстраиваться. Решение нестандартных задач расстроит некоторых ваших учеников, особенно поначалу. Не сдавайся! Поговорите со своими учениками о том, что они чувствуют. Обеспечьте соответствующие строительные леса, чтобы помочь им справиться с этой проблемой. Со временем ваши ученики поразят вас тем, на что они способны.
- Это весело !!! Я говорю это не просто потому, что я математик. Это действительно весело, и вашим ученикам понравится это разнообразие. Даже мои ученики, которые не получают правильный ответ, получают удовольствие от процесса.
- Он способствует развитию коммуникативных навыков учащихся. Студенты должны задокументировать и объяснить стратегии, которые они используют.
- Это для ВСЕХ. Я никогда не прибегал к этим занятиям для своих «более успешных» учеников. Фактически, многие студенты, которые боролись с вычислительными концепциями, ЖИВАЛИ, решая нестандартные задачи.
Я использую слово «дар», однако для многих учеников этот аспект очень ошеломляет.Они привыкли, что им говорят, что и как делать. Это буквально калечит студентов, когда приходит время решать задачу, которая не следует выученному алгоритму. В случае нестандартных задач учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определять подходящие стратегии использования и уверенно решать эти проблемы.
Обеспечьте соответствующие строительные леса, чтобы помочь им справиться с этой проблемой. Со временем ваши ученики поразят вас тем, на что они способны.Шаги для решения нестандартных проблем:
Есть четыре широко используемых шага, которые должны быть смоделированы для ваших учеников, чтобы дать им основу при работе с этими проблемами.
- Понять
- План
- Выполнить
- Обзор
Приложения с инструкциями:
У вас есть несколько вариантов того, как вы можете представить эти
проблемы для ваших студентов.
- Целая группа: Вы можете спроецировать задачу на весь класс для просмотра с помощью ЖК-дисплея или диапроектора. Студенты могут работать на досках или просто использовать бумагу и карандаш для решать проблему. Работа может быть сделана самостоятельно, или вы можете попросить учащихся работать вместе в парах или небольших группы. В последнем варианте я бы потребовать от всех студентов записать работу на своей доске или бумага. Этот вариант всей группы может следовать с несколькими студентами, представляющими свой план решения проблемы; это отличная возможность для класса увидеть несколько стратегий, которые можно использовать для решить ту же проблему.
- Самостоятельная работа: Студенты могут подготовить свою задачу в любое время, когда им нужно работать независимо (например, финишеры, центры, утренняя работа и т. д.)
- Совместное обучение:
Объедините учащихся в пары для совместной работы над проблемой. Это ценный вариант, потому что он добавляет
обучающие преимущества общения и сотрудничества для процесса.
Представительство:
И последнее, что следует учесть: в дополнение к вышеуказанным приложениям, подумайте, как бы вы хотели, чтобы ваши ученики поделились или представили свои работай.Это важный компонент для ряд причин:- Вмещает студенты несут ответственность за свою работу.
- Обеспечивает студенты с важной возможностью объяснить решение своих проблем процессы.
- Позволяет другим ученикам, чтобы увидеть различные способы решения проблемы.
- Обеспечивает у студентов «время проявить себя», когда они представляют свою работу другим.
- Они могут представить свою работу всему классу, в основном проводя собственное «размышление» вслух »аналогично тому, что сделал учитель, когда непосредственно моделировал процесс в класс.
- Они могут представить свою работу другому студенту или небольшой группе студентов.
- Они могут представить
свою работу родителю или старшему брату или сестре.
- Они могут представить свою работу на онлайн-форуме (например, Edmodo и т. д.), организованном учитель.
Приведенные выше задачи взяты из моей книги по математике Brain Power .Если ваши дети «жаждут» большего, проверьте их!
Как научить детей (в возрасте от 3 до 14 лет) решать проблемы — Big Life Journal
ЭТА СТАТЬЯ ВКЛЮЧАЕТ БЕСПЛАТНУЮ ПЕЧАТЬ
Будь то конфликт, связанный с игрушкой, сложное математическое уравнение или отрицательное давление со стороны сверстников, дети ВСЕХ возрастов ежедневно сталкиваются с проблемами и проблемами.
Как родители или учителя, мы не всегда можем решить из каждых проблем наших детей. На самом деле это не наша работа. Наша работа — УЧИТЬ наших детей, как решать проблемы сами .
Таким образом они могут стать уверенными, независимыми и успешными людьми.
Вместо того, чтобы сдаваться или расстраиваться, когда они сталкиваются с проблемой, дети, обладающие навыками решения проблем, управляют своими эмоциями, творчески думают и настойчивы, пока не найдут решение. Естественно, эти способности идут рука об руку с установкой на рост.
Прежде чем двигаться дальше, не забудьте подписаться на наши БЕСПЛАТНЫЕ еженедельные распечатки , тщательно разработанные, чтобы научить ваших детей мышлению роста, устойчивости и многому другому.Зарегистрируйтесь ниже, чтобы убедиться, что вы в списке!
После регистрации вы сразу же получите наше популярное руководство для родителей по методу роста .
Итак, КАК вы учите детей навыкам решения проблем?
Ну это зависит от возраста . По мере того как познавательные способности и размер проблем ребенка со временем растут / развиваются, ваш подход к обучению навыкам решения проблем должен измениться.
Прочтите, чтобы узнать об основных стратегиях обучения детей решению проблем, а также о некоторых идеях и упражнениях для разных возрастов.
3 общие стратегии обучения решению проблем в любом возрасте
1. Модель эффективного решения проблем
Когда ВЫ сталкиваетесь с проблемой, сделайте «подумай вслух» на благо своего ребенка. МОДЕЛИРУЙТЕ, как применить те же навыки решения проблем, над которыми вы работали вместе, приводя примеры из реального мира, которые она может применить в своей жизни.
В то же время покажите своему ребенку готовность совершать ошибки.Все сталкиваются с проблемами, и это нормально. Иногда первое решение, которое вы попробуете, не сработает, и это тоже нормально!
При моделировании решения проблем объясните, что есть некоторые вещи, которые находятся вне нашего контроля. Решая проблему, мы должны сосредоточиться на том, что мы МОЖЕМ реально контролировать.
Вы можете показать распечатку Circle of Control , входящую в комплект для печати Growth Mindset Printables Kit.
2. Спросите совета
Спросите совета у детей, когда у вас возникнет проблема.Это учит их тому, что ошибаться и сталкиваться с проблемами — обычное дело. Это также дает им возможность практиковать навыки решения проблем.
Плюс, когда вы укажете, что их идеи оценены в и оценены в , они обретут уверенность и попытаются решить проблемы самостоятельно.
3. Не давай «ответ»
Как бы трудно это ни было, позвольте вашему ребенку бороться, иногда терпеть неудачу и, в конечном итоге, УЧИТЬСЯ на своих последствиях.
Теперь давайте взглянем на возрастных стратегий и мероприятий .Указанные ниже возрасты являются общими рекомендациями. Не стесняйтесь выбирать любые стратегии или занятия, которые, по вашему мнению, будут работать для ВАШЕГО ребенка.
3-5 летИспользуйте коучинг эмоций
Чтобы сформировать образ мыслей о решении проблем, маленькие дети должны сначала научиться управлять своими эмоциями .
В конце концов, маленькому ребенку трудно логически обдумывать решения проблемы, если он в разгаре.
Один из способов добиться этого — использовать процесс тренировки эмоций, описанный Джоном Готтманом.
Во-первых, научите своих детей, что ВСЕ эмоции допустимы. НЕТ «плохих» эмоций. Даже такие, казалось бы, отрицательные эмоции, как гнев, печаль и разочарование, могут преподать нам ценные уроки. Важно то, как реагирует на эти эмоции .
Во-вторых, выполните этот процесс:
- Шаг первый: наименование и подтверждение эмоций. Когда ваш ребенок расстроен, помогите ему справиться с тем, как он себя чувствует. Скажите, например, : «Я понимаю, что вы расстроены, потому что Джессика играет с игрушкой, которую вы хотели.”
- Шаг второй: Обработка эмоций. Поместите ребенка в его успокаивающее пространство. Если у нее его нет, неплохо создать его. Позвольте ей успокоить свое тело и обработать свои эмоции, чтобы она могла решать проблемы, учиться и расти.
Позвольте ей успокоить свое тело и обработать свои эмоции, чтобы она могла решать проблемы, учиться и расти.- Шаг третий: решение проблемы. Обсудите с ребенком решения, делая больше СЛУШАТЬ , чем говорить во время разговора.Это позволяет вашему ребенку практиковать свои навыки решения проблем, и он с большей вероятностью действительно реализует решения, которые придумал сам.
Скажите: «Покажи мне трудную часть»
Когда ваш ребенок борется или чувствует разочарование, попробуйте методику, предложенную мамой и блоггером по воспитанию детей Лорен Тамм. Просто скажите «Покажи мне самое сложное».
Это поможет вашему ребенку определить ROOT проблемы, что сделает ее менее пугающей и более простой для решения.
Повторите то, что говорит ваш ребенок, «Итак, вы говорите…»
Как только вы оба поймете реальную проблему, предложите ребенку предложить решений .
«Должен быть способ исправить это…» или «Должно быть что-то, что ты можешь сделать…»
Теперь, когда ваш ребенок определил «сложную часть», он, вероятно, сможет придумать решение. Если нет, помогите ей придумать несколько идей. Вы можете попробовать задать вопрос: «Если бы вы ЗНАЛИ , что бы вы подумали?» и посмотрим, что она придумает.
Ваш ребенок может попрактиковаться в поиске решений для препятствий, с которыми он сталкивается, с My Mighty Treasure Coins для печати из набора Self-Esteem & Confidence Kit.
Решение проблем с помощью Creative Play
Позвольте ребенку выбирать занятия и игры в соответствии с его интересами . Бесплатная игра предоставляет множество возможностей для поиска и решения проблем.
Дети часто лучше всего учатся через ИГРУ.Игра с такими предметами, как блоки, простые головоломки и наряды, может научить вашего ребенка решать проблемы.
Даже во время игры ваш ребенок думает критически: Куда подходит этот пазл? Что это значит? Я хочу нарядиться королевой. Что мне надеть? Куда я положил диадему? Это под диваном?
Поощряйте творческие игры, творческое мышление и решение проблем с помощью нашего потрясающего набора для занятий с мышлением роста для детей!
Решение проблем с помощью сборников рассказов
Прочтите соответствующие возрасту рассказы с участием персонажей, которые испытывают проблемы, например:
- Ladybug Girl и Bumblebee Boy Джеки Дэвиса: история двух друзей, которые хотят играть вместе, но не могут найти игру, о которой можно было бы договориться.По очереди внося предложения, они приходят к игре, в которую оба хотят играть: Ladybug Girl и Bumblebee Boy.
- Серия «Любопытный Джордж» Маргарет и Х. Рей: Любопытная обезьянка попадает в дилеммы и выходит из них, обучая детей находить собственные решения проблем.
- Ира спит более чем Бернарда Вабера: Ира очень рад ночевать в доме своего друга Реджи. Но есть одна проблема: брать с собой плюшевого мишку или нет? Это может показаться незначительным, но это тот тип ранней социальной проблемы, с которой может иметь отношение ваш ребенок.
Свяжите эти переживания с аналогичными событиями в жизни вашего ребенка и СПРОСИТЕ своего ребенка, КАК герои этих историй могут решить свои проблемы. Поощряйте различные решения и обсуждайте возможные результаты каждого из них.
Это форма диалога , читающего , или активного ВОВЛЕЧЕНИЯ вашего ребенка в процесс чтения. Взаимодействие с текстом вместо пассивного слушания может «ускорить» развитие у детей дошкольного возраста таких навыков грамотности, как понимание.
Задавая вопросы о проблемах персонажей, вы также можете повысить способность вашего ребенка решать проблемы.
Вы можете даже попросить вашего ребенка разыграть проблему и возможные решения, чтобы закрепить урок.
Рекомендации по книгам можно найти в печатной версии Топ-85 книг о мышлении роста для детей и взрослых в нашем наборе для печати «Образ мышления роста».
5-7 лет
Обучайте этапам решения проблем
Придумайте для вашего ребенка простой процесс решения проблем, который вы можете последовательно реализовать .Например, вы можете попробовать выполнить следующие пять шагов:
- Шаг 1: Что я чувствую? Помогите своему ребенку понять, что он чувствует в данный момент (разочарование, гнев, любопытство, разочарование, волнение и т. Д.). Обращение к эмоциям и наименование эмоций ослабят их заряд и дадут вашему ребенку шанс сделать шаг назад.
- Шаг 2: В чем проблема? Помогите вашему ребенку определить проблему , характерную для .В большинстве случаев помогите ей взять на себя ответственность за случившееся, а не указывать пальцем. Например, вместо слов «Джои доставил мне неприятности на перемене» ваш ребенок может сказать: «У меня проблемы на перемене из-за того, что я спорил с Джоуи».
Например, вместо слов «Джои доставил мне неприятности на перемене» ваш ребенок может сказать: «У меня проблемы на перемене из-за того, что я спорил с Джоуи».- Шаг 3: Какие есть решения? Поощряйте своего ребенка придумать как можно больше решений. На данный момент они даже не должны быть «хорошими» решениями. Здесь они просто проводят мозговой штурм, но еще не оценивают идеи, которые они сгенерировали.
- Шаг 4: Что произойдет, если…? Что произойдет, если ваш ребенок попробует каждое из этих решений? Является ли решение безопасным и справедливым? Как это заставит других чувствовать себя? На этом этапе вы также можете попробовать ролевую игру. Вашему ребенку важно учитывать как положительные, так и отрицательные последствия своих действий.
- Шаг 5: Какой мне попробовать? Попросите ребенка выбрать одно или несколько решений, чтобы попробовать. Если решение не сработало, обсудите ПОЧЕМУ и переходите к другому. Поощряйте ребенка продолжать попытки, пока проблема не будет решена.
Если решение не сработало, обсудите ПОЧЕМУ и переходите к другому. Поощряйте ребенка продолжать попытки, пока проблема не будет решена.Последовательно выполняйте эти шаги, чтобы они стали вашей второй натурой, и таким же образом моделируйте решение собственных проблем. Хорошая идея — отразить : Что сработало? Что не сделали? Что вы можете сделать по-другому в следующий раз?
Помогите своему ребенку визуализировать и практиковать этот процесс с помощью красочной печатной формы «Мое решение проблем » из комплекта для самооценки и уверенности .
Решение проблем с помощью ремесленных материалов
Ремесло — это еще одна форма игры, которая может научить детей творчески решать проблемы.
Дайте вашему ребенку маркеры, пластилин, картонные коробки, скотч, бумагу и т. Д. Из этих простых материалов они придумают всевозможные интересные творения и изобретательные игры.
В этих «открытых игрушках» нет «правильного способа игры», позволяющего ребенку проявлять творческий подход и генерировать идеи самостоятельно .
Задавайте открытые вопросы
Задание открытых вопросов улучшает способность ребенка мыслить критически и творчески, что в конечном итоге делает его лучше решать проблемы. Примеры открытых вопросов:
- Как мы могли бы работать вместе, чтобы решить эту проблему?
- Как у вас это получилось? или как вы это узнали?
- Расскажите мне о том, что вы построили, сделали или создали.
- Как вы думаете, что будет дальше?
- Как вы думаете, что произойдет, если…?
- Что вы узнали?
- Что было легко? Что было сложно?
- Что бы вы сделали по-другому в следующий раз?
Открытые вопросы не имеют правильного ответа, и на них нельзя ответить простым «да» или «нет».”
Вы можете задавать открытые вопросы, даже если ваш ребенок в настоящее время не решает проблему, чтобы помочь ему практиковать свои мыслительные навыки, что пригодится, когда у него есть проблема, которую нужно решить.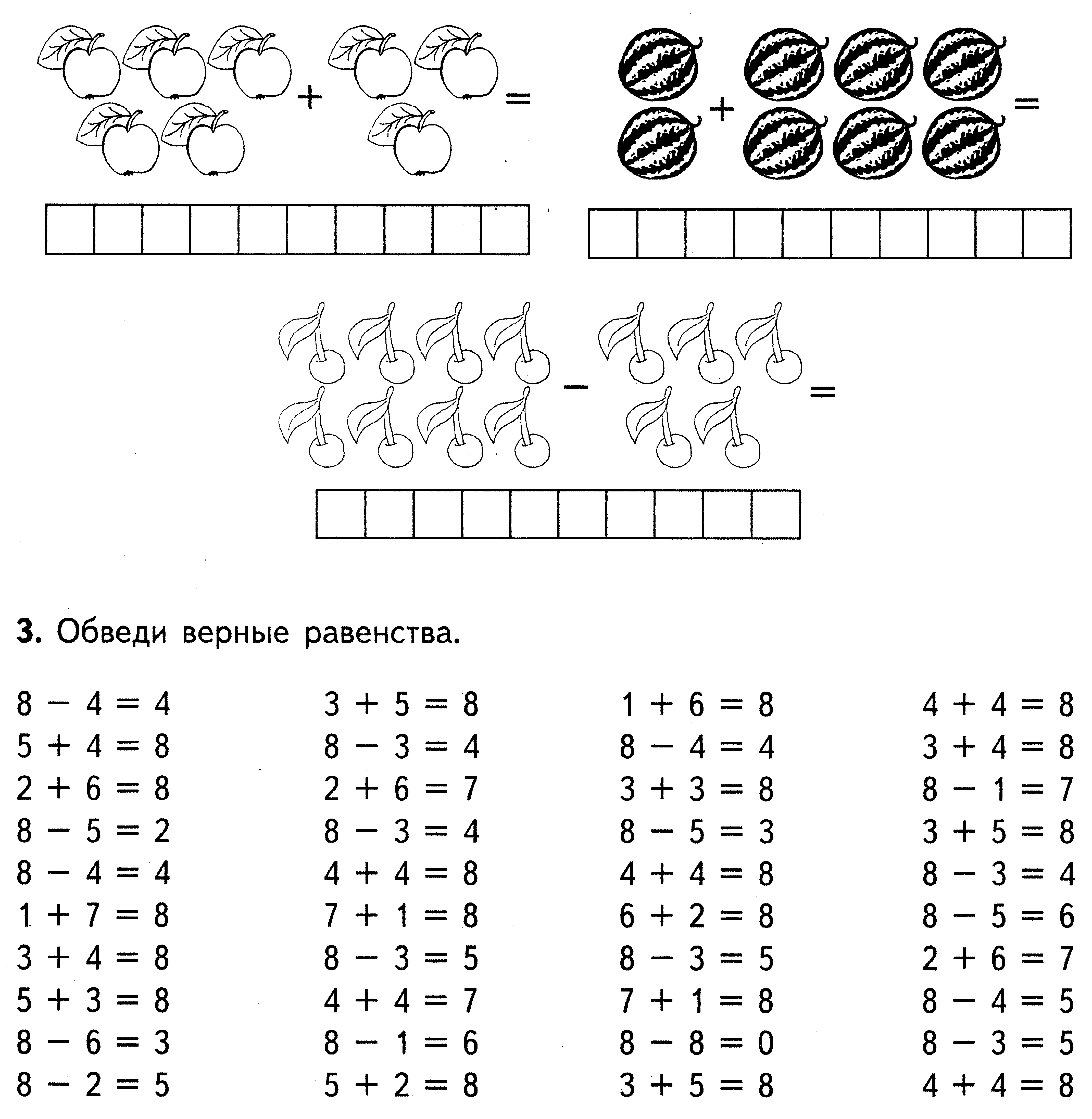
Для получения дополнительных идей используйте «10 вопросов о мышлении роста, которые нужно задать своим детям за обеденным столом» в нашем наборе для печати мышления о росте .
7-9 летРазбивка задач на части
Эта стратегия является более продвинутой версией «Покажи мне сложную часть.”
Чем больше становится ваш ребенок, тем больше становятся его проблемы. Когда ваш ребенок сталкивается с проблемой, которая кажется непреодолимой или непреодолимой, предложите ему разбить ее на более управляемых частей.
Например, у вашего ребенка плохая оценка на уроке истории. Почему оценка такая низкая? Каковы причины этой проблемы?
Как обычно, СЛУШАЙТЕ, как ваш ребенок проводит мозговой штурм, задавая открытых вопросов , чтобы помочь, если он застрял.
Если низкая оценка является результатом невыполнения заданий, возможно, ваш ребенок сможет составить список этих заданий и выполнять одно за другим.
Или, если проблема заключается в тестах, что заставляет вашего ребенка с трудом сдавать экзамены?
Возможно, ее отвлекают друзья в классе, ей трудно просить о помощи и она не проводит достаточно времени за учебой дома. Как только вы определили эти «кусочки», помогите ребенку решать их по одному, пока проблема не будет решена.
Обязательно используйте наши распечатанные карточки «Шаги по решению проблем для детей» (доступны в наборе действий для установки мышления роста). Это забавный и интерактивный способ, которым ваш ребенок может узнать, как решать проблемы и быть уверенным в процессе.
Показать «Видео о сломанном эскалаторе»
Обсудите важность решения проблем и самостоятельного решения проблем с помощью «видео о сломанном эскалаторе».
На видео неожиданно ломается эскалатор. Люди на эскалаторе «застревают» и кричат о помощи. В этом возрасте, вероятно, ваш ребенок найдет видео забавным и сразу предложит решение: «Просто гуляй! Сойдите с эскалатора! »
Скажите ребенку, что это простой пример того, как люди иногда действуют в трудных ситуациях.
Спросите: «Как вы думаете, почему они не сошли с эскалатора?» (не умели, помощи ждали и т. д.)
Иногда ваш ребенок может чувствовать «застрявшим» , когда сталкивается с проблемами. Они могут остановиться и попросить о помощи еще до того, как попытаются найти решение. Поощряйте ребенка принимать вызовы и вместо этого работать над их решением.
9-11 летРешение проблем с помощью подсказок
Обеспечьте вашего ребенка или группу детей такими материалами, как соломка, ватные шарики, пряжа, прищепки, скотч, скрепки, липкие заметки, палочки для мороженого и т. Д.
С помощью этих материалов предложите детям решить необычные задачи, например:
- Сделать ловушку для лепрекона
- Создать трамплин для машин
- Создайте свою игру с правилами
- Сделайте устройство для общения двух людей друг с другом
Это интересный способ попрактиковаться в критическом мышлении и творческом решении проблем.
Скорее всего, потребуется несколько попыток, чтобы найти работающее решение, применимое практически к любому аспекту жизни.
Заставьте их работать на это
Когда ваш ребенок просит новую игрушку, технологию или одежду, попросите его составить план, как получить желаемый предмет самостоятельно. Вашему ребенку придется не только провести мозговой штурм и оценить решения, но и обрести уверенность.
Спросите своего ребенка, КАК он может заработать деньги на предмет, который он хочет, и подбодрите его, когда он будет добиваться своей цели.
Положи это на бумагу
Например, используйте этот графический органайзер, разработанный The New York Times Learning Network.Ваш ребенок может определить свою проблему и найти решения.
Но теперь она продвигает этот процесс еще дальше: после попытки каждого решения, которое было успешным? Какие были неудачными? Почему ?
Это помогает вашему ребенку задуматься о различных результатах, узнавая, что работает, а что нет.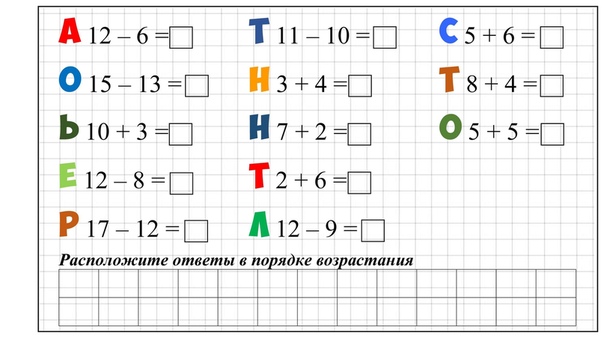
Уроки, которые она усвоит здесь, будут полезны, когда она столкнется с подобными проблемами в будущем.
Играем в шахматы вместе
Обучение игре в шахматы — отличный способ для детей научиться решать проблемы И строит своих мозгов одновременно.Он требует от игроков критического мышления, творчества, анализа доски, распознавания закономерностей и многого другого. Есть онлайн-версии игры, книги о том, как играть, видео и другие ресурсы. Не умеете играть? Научитесь вместе со своим подростком, как соединить , и проблемы решать вместе!
Пусть они научатся кодировать
Наши подростки и подростки уже технически подкованы и могут использовать свои навыки для решения проблем путем обучения программированию. Кодирование способствует творчеству, логике, планированию и настойчивости .Существует множество отличных инструментов, онлайн-программ или программ для личного общения, которые могут улучшить навыки программирования вашего ребенка.
Поощрение к началу значимого проекта
Этот проект должен быть значимым для вашего подростка, например, запуск канала YouTube. Ваш подросток будет практиковать навыки решения проблем, поскольку он будет выяснять, как расширить свою аудиторию, как сделать так, чтобы их видео были обнаружены, и многое другое.
В журнале Big Life Journal — Teen Edition есть раздел, который поможет им спланировать свой канал на YouTube и начать процесс решения проблем.
Примените метод SODAS
Ищете план игры, который ваш подросток может использовать, столкнувшись с проблемой? Метод SODAS можно использовать для больших или малых проблем. Просто запомните этот простой акроним и следуйте этим идеям:
- S ituation
- O частей
- D достоинства
- A Преимущества
- S olution
Поощряйте вступление в группы по решению проблем
Любит ли ваш подросток решать задачи в команде? Предложите им присоединиться к группе или клубу , который помогает им отточить свои навыки в различных условиях — от науки и робототехники до дискуссий и международных отношений.
Некоторые примеры групп включают:
- Одиссея разума
- Модель U.N.
- Дебатная группа
- Научная олимпиада
5 шагов к решению проблем со словами
Задачи со словами часто сбивают с толку учащихся просто потому, что вопрос не представлен в виде готового к решению математического уравнения. Вы можете ответить даже на самые сложные задачи со словами, если понимаете рассматриваемые математические концепции. Хотя степень сложности может измениться, способ решения текстовых проблем включает в себя спланированный подход, который требует определения проблемы, сбора соответствующей информации, создания уравнения, решения и проверки вашей работы.
Определите проблему
Начните с определения сценария, который проблема требует от вас решения. Это может быть вопрос или заявление. В любом случае слово «проблема» предоставляет вам всю информацию, необходимую для ее решения.
Определив проблему, вы сможете определить единицу измерения для окончательного ответа. В следующем примере вопрос просит вас определить общее количество носков между двумя сестрами. Единицей измерения этой задачи являются пары носков.
«У Сюзи восемь пар красных носков и шесть пар синих носков. У брата Сюзи, Марка, есть восемь носков. Если ее младшая сестра владеет девятью парами фиолетовых носков и теряет две пары из них Сюзи, сколько пар носков есть у сестер? оставили?»
Сбор информации
Создайте таблицу, список, график или диаграмму, в которых будет представлена информация, которую вы знаете, и оставьте поля для любой информации, которую вы еще не знаете. Каждая проблема со словом может потребовать разного формата, но визуальное представление необходимой информации облегчает работу.
В этом примере вопрос спрашивает, сколько носков принадлежит сестрам вместе, так что вы можете не обращать внимания на информацию о Марке.
Также не имеет значения цвет носков. Это удаляет большую часть информации и оставляет вам только общее количество носков, с которых сестры начали, и сколько маленькая сестра потеряла.
Создайте уравнение
Переведите любые математические выражения в математические символы. Например, слова и фразы «сумма», «больше, чем», «увеличился» и «в дополнение к» означают сложение, поэтому напишите символ «+» над этими словами.Используйте букву для неизвестной переменной и создайте алгебраическое уравнение, которое представляет проблему.
В этом примере возьмем общее количество пар носков, которыми владеет Сюзи — восемь плюс шесть. Возьмите общее количество пар, которыми владеет ее сестра — девять. Общее количество пар носков, принадлежащих обеим сестрам, составляет 8 + 6 + 9. Вычтите две недостающие пары и получите окончательное уравнение (8 + 6 + 9) — 2 = n, где n — количество пар носков, которые есть у сестер. оставили.
Решение проблемы
Используя уравнение, решите проблему, подставляя значения и решая для неизвестной переменной.
Попутно перепроверяйте свои расчеты, чтобы не допустить ошибок. Умножайте, делите и вычитайте в правильном порядке, используя порядок операций. Сначала идут экспоненты и корни, затем умножение и деление и, наконец, сложение и вычитание.
В этом примере после сложения чисел и вычитания вы получите ответ n = 21 пара носков.
Проверьте ответ
Проверьте, соответствует ли ваш ответ тому, что вы знаете. Используя здравый смысл, оцените ответ и посмотрите, приблизитесь ли вы к тому, чего ожидали.Если ответ кажется абсурдно большим или слишком маленьким, поищите проблему, чтобы найти, где вы ошиблись.
В этом примере вы знаете, сложив все числа сестер, что у вас есть максимум 23 носка. Поскольку в задаче упоминается, что младшая сестра потеряла две пары, окончательный ответ должен быть меньше 23. Если вы получили большее число, вы сделали что-то не так. Примените эту логику к любой проблеме со словами, независимо от сложности.
.