Как решать линейные уравнения — формулы и примеры решения простейших уравнений
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:
если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;
если а = 0 — уравнение корней не имеет;
если а и b равны нулю, то корнем уравнения является любое число.
Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
- кубические,
- уравнения четвертой степени,
- иррациональные и рациональные,
- системы линейных алгебраических уравнений и другие.
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5.
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Как решаем:
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
6x — 5x = 10
Приведем подобные и завершим решение.
x = 10
Ответ: x = 10.
Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12
Как решаем:
- Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.
-4x = 12 | : (-4)
x = −3
Ответ: x = −3.
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
Решаем так:
ЮПеренести 1 из левой части в правую со знаком минус.
6х = 19 − 1
Выполнить вычитание.
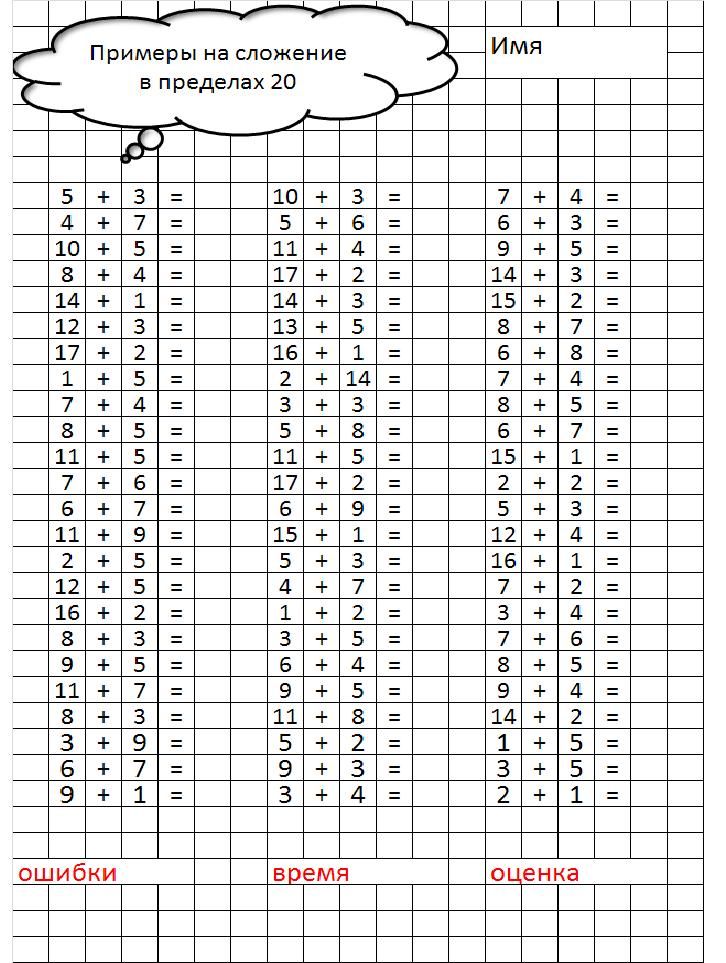
6х = 18
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
х = 3
Ответ: 3.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
Решаем так:
Раскрыть скобки
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
0х = 0
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
Решаем так:
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
х = 1/8 : 4
х = 1/32
Пример 4. Решить: 4(х + 2) = 6 − 7х.
Решаем так:
4х + 8 = 6 − 7х
4х + 7х = 6 − 8
11х = −2
х = −2 : 11
х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
Решаем так:
3(3х — 4) = 4 · 7х + 24
9х — 12 = 28х + 24
9х — 28х = 24 + 12
-19х = 36
х = 36 : (-19)
х = — 36/19
Ответ: 1 17/19.
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
Решаем так:
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
х – х = 4 — 7
Приведем подобные члены.
0 * х = — 3
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Решаем так:
2х + 6 = 5 − 7х
2х + 7х = 5 − 6
9х = −1
х = −1/9
Ответ: −1/9.
youtube.com/embed/h0T61H6jSk0?start=791″ ssmarticle=»»> Нахождение неизвестного слагаемого, множителя, и т.п.: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9. Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x.
Согласно первоначальному условию, это число вместе с 4 образуют 9, значит, можно записать уравнение 4+x=9. Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x? Для этого надо использовать правило:
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a+b=c, то c−a=b и c−b=a, и наоборот, из выражений c−a=b и c−b=a можно вывести, что a+b=c.
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Пример 1Возьмем то уравнение, что у нас получилось выше: 4+x=9. Согласно правилу, нам нужно вычесть из известной суммы, равной 9, известное слагаемое, равное 4.
Вычтем одно натуральное число из другого: 9-4=5. Мы получили нужное нам слагаемое, равное 5.
Обычно решения подобных уравнений записывают следующим образом:
- Первым пишется исходное уравнение.
- Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
- После этого пишем уравнение, которое получилось после всех действий с числами.
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
4+x=9,x=9−4,x=5.
Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4+x=9 и получим: 4+5=9. Равенство 9=9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки.
Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Определение 2Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Пример 2Например, у нас есть уравнение x-6=10. Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6, получим 16. То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:
x−6=10,x=10+6,x=16.
Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16-6=10. Равенство 16-16 будет верным, значит, мы все подсчитали правильно.
Переходим к следующему правилу.
Определение 3Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Пример 3Воспользуемся правилом для решения уравнения 10-x=8. Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10-8=2. Значит, искомое вычитаемое равно двум. Вот вся запись решения:
10-x=8,x=10-8,x=2.
Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10-2=8 и убедимся, что найденное нами значение будет правильным.
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных 0, c: a=b, c: b=c и наоборот.
Пример 4Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·0=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0, а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0. Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Определение 5Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Пример 5Решим с его помощью уравнение x:3=5. Перемножаем между собой известное частное и известный делитель и получаем 15, которое и будет нужным нам делимым.
Вот краткая запись всего решения:
x:3=5,x=3·5,x=15.
Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5. Верное числовое равенство – свидетельство правильного решения.
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Определение 6Для нахождения неизвестного делителя нужно разделить делимое на частное.
Пример 6Возьмем простой пример – уравнение 21:x=3. Для его решения разделим известное делимое 21 на частное 3 и получим 7. Это и будет искомый делитель. Теперь оформляем решение правильно:
21:x=3,x=21:3,x=7.
Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21:7=3, так что корень уравнения был вычислен верно.
Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0. Если же частным будет нуль, возможны два варианта.
Если делимое также равно нулю и уравнение выглядит как 0:x=0, то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0, с делимым, отличным от 0, решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5:x=0, которое не имеет ни одного корня.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
Пример 7У нас есть уравнение вида 3·x+1=7. Вычисляем неизвестное слагаемое 3·x, отняв от 7 единицу. Получим в итоге 3·x=7−1, потом 3·x=6. Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.
Вот краткая запись решения еще одного уравнения (2·x−7):3−5=2:
(2·x−7):3−5=2,(2·x−7):3=2+5,(2·x−7):3=7,2·x−7=7·3,2·x−7=21,2·x=21+7,2·x=28,x=28:2,x=14.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
словесных задач с одним неизвестным
Все ресурсы по алгебре
11 диагностических тестов 177 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Pre-Algebra Help » Алгебраические уравнения » Текстовые задачи » Словесные задачи с одним неизвестным
Джон зарабатывает $12,50/час садоводством. На этой неделе он заработал 275 долларов. Напишите уравнение для определения его заработной платы, а затем решите его, чтобы узнать, сколько часов он отработал.
Возможные ответы:
Правильный ответ:
Объяснение:
Шаг 1: Чтобы узнать, сколько часов работает Джон, сначала нужна формула для расчета его заработной платы:
(почасовая оплата)(часы) = общая заработная плата
Шаг 2: подставьте известные значения ( почасовая оплата, общая заработная плата)
Шаг 3: изолируйте неизвестную переменную (часы), разделив обе части на его почасовую заработную плату, затем решите
Сообщить об ошибке
3 человека могут проложить дорогу за 4 часа.
За какое время 8 человек покроют дорогу?
Возможные ответы:
Правильный ответ:
Пояснение:
С обратной пропорциональностью, когда одна величина увеличивается, другая уменьшается, и наоборот. Ключ к решению этой проблемы заключается в том, чтобы помнить, что каждый человек работает с одинаковой скоростью, независимо от того, сколько людей разделяет рабочую нагрузку.
Пусть:
= константа пропорциональности (коэффициент работы на человека)
= время
= количество людей
Используя эти переменные, мы можем составить уравнение, которое даст нам общее время:
Решите для использования исходной информации для 3 человек.
Используя эту константу, мы можем вернуться к первому уравнению и решить для времени, когда работают 8 человек:
Сообщить об ошибке
Читая книгу, Сара замечает, что прочитала 3 страницы за 10 минут.
Если она продолжит читать с такой скоростью, сколько страниц она прочитает за 1 час?
Возможные ответы:
Правильный ответ:
Объяснение:
Количество прочитанных страниц прямо пропорционально времени, затраченному на чтение. Чтобы решить эту задачу, нам нужно найти константу пропорциональности, которая представлена в следующем соотношении:
Здесь — количество прочитанных страниц, а — время. Переставьте, чтобы найти константу:
Используя полученную информацию:
Один час равен 60 минутам, поэтому повторное использование уравнения прямой пропорциональности дает:
Сообщить об ошибке
4 часов для 4 человек, чтобы построить сарай, сколько человек потребуется, чтобы построить такой же тип сарая за одну треть времени?
Возможные ответы:
Правильный ответ:
Пояснение:
Константа пропорциональности равна произведению времени () и количества людей ().
Пусть представляет собой время и количество людей, работающих на первом навесе, и представляет время и количество людей, работающих на втором навесе. Поскольку одинаково для обеих ситуаций (это константа), мы можем установить первый и второй сценарии равными друг другу.
Теперь в этой задаче нужно указать количество людей, необходимое для постройки второго сарая. Это означает, что нам нужно найти способ решения для . Мы можем разделить обе части нашего уравнения на :
Используйте данные значения для решения. Обратите внимание, что будет равно 3 (одна треть от исходных 9).
Сообщить об ошибке
Дорога до ближайшего боулинга занимает 45 минут по городским улицам со скоростью 30 миль в час (миль в час). Сколько времени потребуется, чтобы добраться туда по автостраде со скоростью 65 миль в час, если расстояние такое же?
(Округлить до ближайшей минуты).
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем составить уравнение скорости, в котором расстояние равно скорости (скорости), умноженной на время:
Наша скорость и время могут меняться в зависимости от разных маршрутов, но расстояние остается неизменным.
Городской маршрут:
Автострада:
Мы можем приравнять эти уравнения друг к другу, поскольку оба равны .
Решите для времени автострады, переставляя и заменяя заданные значения.
Округляя до ближайшей минуты, мы получаем 21 для нашего окончательного ответа.
Сообщить об ошибке
Отец покупает чизбургеры для своих детей. Каждый чизбургер стоит 3,50 доллара. Он тратит 17,50 долларов на чизбургеры. Сколько чизбургеров он купил?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение, где равно количеству чизбургеров:
Решите для c:
Сообщить об ошибке
Грейс на 4 года старше Елены. Если Грейс 9 лет, то сколько лет Елене?
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть число Елены будет равно:
Сообщить об ошибке
Сьюзи нужно ехать на велосипеде в продуктовый магазин, который находится в 15 милях от нее.
Сьюзи едет на велосипеде до продуктового магазина за 45 минут. Какая средняя скорость у Сьюзи? Экспресс-ответ в милях в час.
Возможные ответы:
Правильный ответ:
Объяснение:
Расстояние равно произведению скорости и времени:
Подставьте информацию, данную в задаче, помня, что в вопросах сказано изложить ответ в милях в час, а мы даем ей время в минутах. Изменить минуты на часы:
Сьюзи понадобилось 0,75 часа, чтобы доехать до продуктового магазина.
Ставка Сьюзи .
Сообщить об ошибке
Стоимость рожка мороженого плюс налог с продаж. За сколько рожков мороженого можно купить?
Возможные ответы:
Правильный ответ:
Объяснение:
Рассчитайте стоимость рожка мороженого с налогом:
Определите, сколько рожков можно купить за , составив следующее уравнение:
Разделите обе части на 3,18:
Следовательно, рожки для мороженого можно приобрести за .
Сообщить об ошибке
Тридцать шесть друзей арендуют автобус для вечеринок на школьный выпускной. Аренда автобуса для вечеринок будет стоить 300 долларов США вперед плюс 18 долларов США в час. У друзей есть автобус с 17:00 до 3:00.
Каждый друг согласился внести по 12 долларов. Один из учителей средней школы, мистер Джонс, предложил скинуться на остальное. Если да, то сколько он заплатит?
Возможные ответы:
Правильный ответ:
Объяснение:
У друзей есть автобус с 17:00 до 3:00 — это
часов.
Стоимость аренды автобуса составит
.
Тридцать шесть студентов внесут по 12 долларов каждый, всего
.
Оставшаяся сумма, которую мистер Джонс заплатит, составляет
.
Сообщить об ошибке
← Назад 1 2 3 4 5 Далее →
Уведомление об авторских правах
Все ресурсы Pre-Algebra
11 Диагностические тесты 177 практических тестов Вопрос дня Карточки Learn by Concept
Решение линейных уравнений с одним неизвестным
Все ресурсы по математике GMAT
22 диагностических теста 693 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
GMAT Math Help » Проблемные вопросы » Алгебра » Линейные уравнения, одно неизвестное » Решение линейных уравнений с одним неизвестным
При каком значении следующее уравнение не имеет решения?
Возможные ответы:
Уравнение всегда должно иметь хотя бы одно решение независимо от значения .
Правильный ответ:
Объяснение:
упростите обе стороны уравнения как можно больше и решайте для уравнения с точки зрения:
— то есть, . Мы убеждаемся, что это значение не дает решения, заменяя:
Уравнение не имеет решения и является правильным ответом.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Решить для:
Возможные ответы:
Правильный ответ:
Объяснение:
Отчет о ошибке
Решение для:
Возможные ответы:
Правильный ответ:
959959959959959995959995999595999959 9005 .
Объяснение:
Сообщить об ошибке
Что такое координата средней точки и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Что такое координата средней точки и?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Что такое координата средней точки?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Решите следующее уравнение:
.
Возможные ответы:
Правильный ответ:
Объяснение:
Мы начинаем с выделения выражения абсолютного значения:
Это дает нам два случая, когда мы удаляем абсолютное значение:
и
Затем мы решаем для каждого случая:
Сообщить об ошибке
Найти:
Возможные ответы:
Уравнение не имеет решения.
Правильный ответ:
Объяснение:
Отчет о ошибке
Решение для:
.
Правильный ответ:
Объяснение:
Отчет о ошибке
← Предыдущий 1 2 3 4 следующие →
.