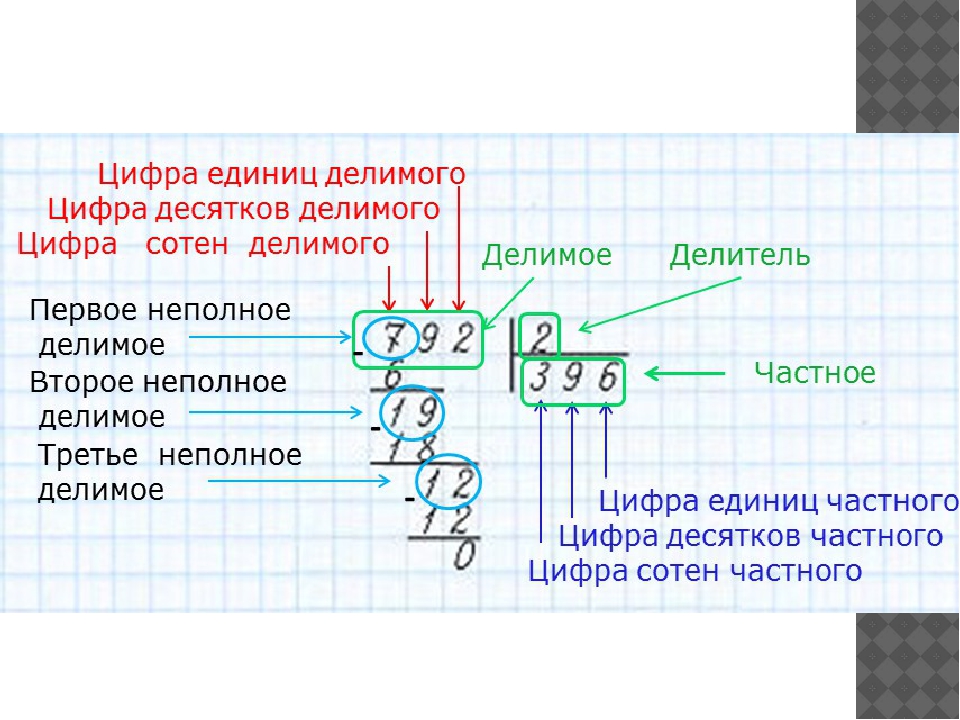
Деление в столбик | ПОЛЕЗНЫЕ ПРОГРАММЫ ДЛЯ УЧЕБЫ И РАБОТЫ
Описание
Примеры на деление в столбик решать просто. Но они требуют концентрации и внимания, особенно для очень торопливых детей. Практика счета таких примеров поможет развить внимательность и закрепить навыки счета больших чисел, а также добиться автоматизированного счета.
Программа представляет собой тренажер для счета. Она имеет внутренние настройки, изменяя которые можно создать примеры для детей разного возраста и уровня подготовки: на однозначное , двузначное или трехзначное число. Поэтому программа будет полезна как для учеников начальной школы 3-4 классов, так и для более старших классов.
Программа счета написана в Excel с помощью макросов.
Формируются примеры на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. При записи примеров разряды чисел формируются друг под другом, что позволяет легко ориентироваться в примерах.
В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.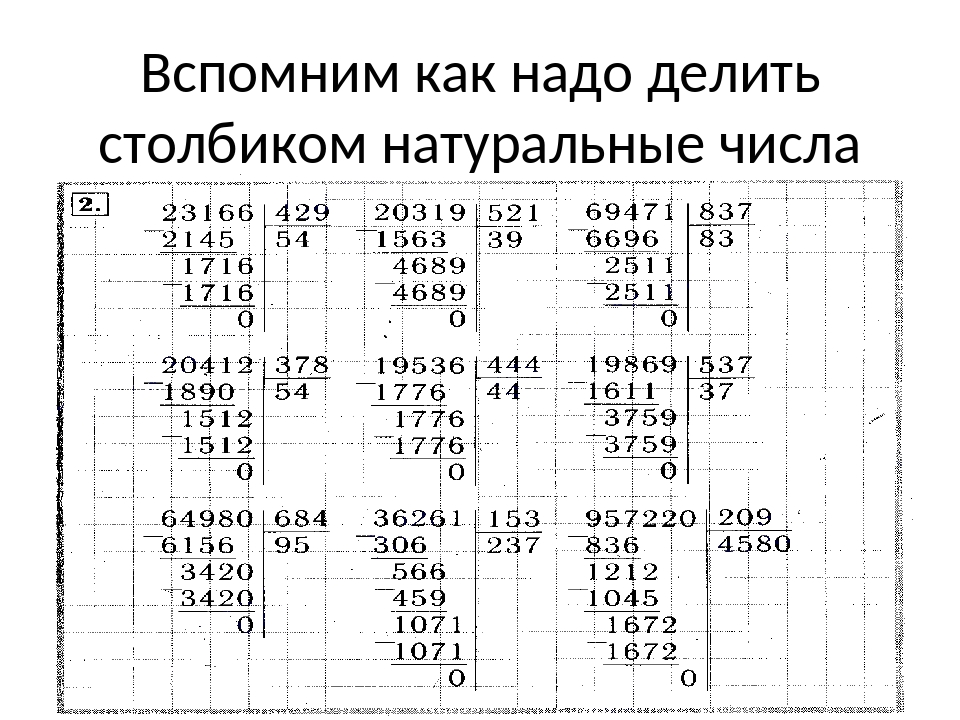
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.
На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
5.5.5. Деление десятичной дроби на натуральное число.
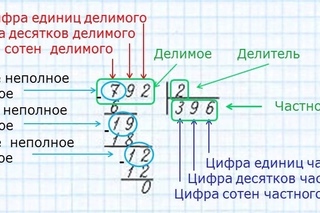
I. Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа и поставить в частном запятую тогда, когда закончится деление целой части.
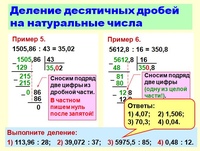
Примеры.
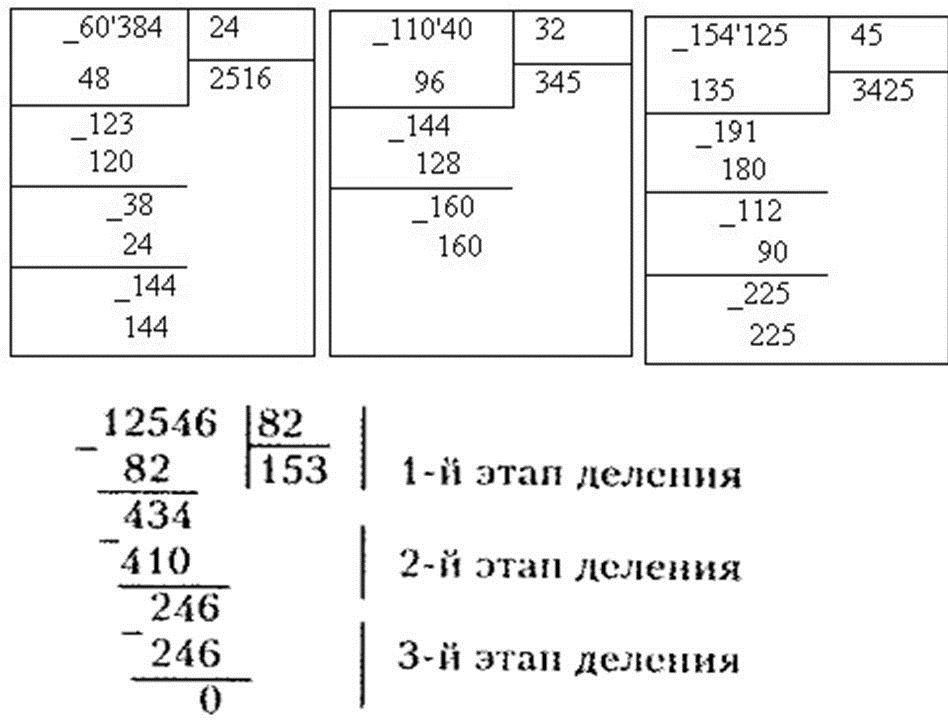
Выполнить деление: 1) 96,25:5; 2) 4,78:4; 3) 183,06:45.
Решение.
Пример 1) 96,25:5.
Делим «уголком» так, как делят натуральные числа. После того, как сносим цифру 2 (число десятых — первая цифра после запятой в записи делимого 96,25), в частном ставим запятую и продолжаем деление.
Ответ: 19,25.
Пример
Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 7 — первую цифру после запятой в делимом 4,78. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.
Ответ: 1,195.
Пример 3) 183,06:45.
Делим как 18306 на 45. В частном поставим запятую как только снесем цифру
Ответ: 4,068.
Вывод: при делении десятичной дроби на натуральное число в частном ставим запятую сразу после того, как сносим цифру в разряде десятых делимого. Обратите внимание: все выделенные красным цветом цифры в этих трех примерах относятся к разряду десятых долей делимого.
Смотрите видео: «Как разделить десятичную дробь на натуральное число».
Примеры.
Выполнить деление: 1) 41,56:10; 2) 123,45:100; 3) 0,47:100; 4) 8,5:1000; 5) 631,2:10000.
Решение.
Перенос запятой влево зависит от того, сколько в делителе нулей после единицы. Так, при делении десятичной дроби на
В примерах 3) и 4) пришлось приписать нули перед десятичной дробью, чтобы удобнее было переносить запятую. Однако, приписывать нули можно мысленно, и вы будете это делать, когда хорошо научитесь применять правило II для деления десятичной дроби на 10, 100, 1000 и т. д.
Смотрите видео: «Как разделить десятичную дробь на 10, 100, 1000 и т.д.»
Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.Я. за 1, 2, 3 и 4 четверти
Дата публикации: .
Самостоятельные на темы: «Натуральные числа и их обозначения», «Сложение и вычитание натуральных чисел», «Сравнение натуральных чисел», «Отрезок, прямая, луч», «Умножение натуральных чисел», «Деление натуральных чисел», «Выражения и уравнения», «Квадрат и куб числа», «Окружность и круг», «Обыкновенные дроби», «Сравнение дробей» и др.
Некоторые понятия к учебному материалу.
1. Натуральные числа – используются для счета предметов в повседневной жизни.2. Отрезок. Длина отрезка – расстояние между его крайними точками, концами. Обозначается заглавными латинскими буквами, например AB.
4. Единичный отрезок – отрезок с длиной равной единице.
5. Меньше и больше. Меньше, число, которое при счете называется раньше. Больше, число, которое при счете называется позже.
6. Слагаемые числа – числа, которые складываются.
7. Вычитание. Число из которого вычитают – это уменьшаемое. Число, которое вычитается – это вычитаемое.
В итоге получаем разность.Самостоятельная работа №1 (входная работа на повторение)
Вариант I.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 699.в) Определите натуральное число, которое на единицу больше числа 239 999.
г) Определите натуральное число, которое на единицу меньше числа 394 000.
2. Решите задачу.
В городском сквере посажено 340 деревьев. А в парке посажено 270 деревьев. На сколько деревьев больше в городском сквере, чем в парке?3. Решите примеры.
| а) 492 + 1 220 = | б) 3 495 — 593 = |
| в) 5112 : 6 = | г) 56 * 23 = |
Вариант II.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 879.б) Определите натуральное число, которое на единицу меньше числа 2 000.
г) Определите натуральное число, которое на единицу меньше числа 24 000.
2. Решите задачу.
Рыбаки за первую неделю поймали 395 кг рыбы, а за вторую неделю – 239 кг. На сколько кг было поймано меньше за вторую неделю, чем за первую?3. Решите примеры.
| а) 638 + 1 445 = | б) 6 112 — 2 598 = |
| в) 2688 : 3 = | г) 24 * 45 = |
Вариант III.
1. Определение числа.
б) Определите натуральное число, которое на единицу меньше числа 3 000.
в) Определите натуральное число, которое на единицу больше числа 28 999.
г) Определите натуральное число, которое на единицу меньше числа 12 000.
2. Решите задачу.
В огороде посадили 2 грядки помидор. С первой грядки было собрано 427 помидор, а со второй грядки – 311. На сколько меньше помидор было собрано со второй грядки, чем с первой?3. Решите примеры.
| а) 455 + 3 412= | б) 5 332 — 593 = |
| в) 3648 : 8 = | г) 29 * 41 = |
Самостоятельная работа №2 на тему: «Натуральные числа и их обозначения»
Вариант I.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 20;б) число 49.
2. Представьте следующие словосочетания в числовом виде.
а) Шесть миллиардов пятьсот три тысяча семь.б) На единицу больше чем пятьсот девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 2, 3 и 7.b) 4, 0 и 9.
Вариант II.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 60;б) число 38.
2. Представьте следующие словосочетания в числовом виде.
б) На единицу больше чем сто девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 1, 3 и 9.b) 2, 4 и 0.
Вариант III.
1.
Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
б) число 58.
2. Представьте следующие словосочетания в числовом виде.
а) Два миллиарда шестьсот два миллиона триста.3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 5, 2 и 8.b) 1, 3 и 0.
Самостоятельная работа №3
Вариант I.
1. Переведите из одной единицы измерения в другую.
| а) 8 дм 43 см = … см | б) 5 км 549 м = … м |
| в) 7 см 18 мм = … мм | г) 249 см =… дм … см |
2. Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D. AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 18 столбах, расстояние между столбами составляет пять метров.
4. Начертите четырехугольник ABCD. Отметьте точкой T середину стороны BC. Соедините точки B и D, А и T. Выпишите все многоугольники, которые образовались.
Вариант II.
1. Переведите из одной единицы измерения в другую.
| а) 4 дм 23 см = … см | б) 25 км 50 м = … м |
| в) 16 см 65 мм = … мм | г) 456 см =… дм … см |
2. Начертите отрезок AB, равный 15 см 4 мм, отметьте на нем точки C и D. AC равен 8 см 2 мм, CD равен 3 см 7 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 19 столбах, расстояние между столбами составляет 4 метра. Каково расстояние между третьим и восьмым столбами?4. Начертите четырехугольник ABCD. Отметьте середину AB и поставьте точку N. Проведите отрезки DN и АС. Выпишите все многоугольники, которые образовались.
Вариант III.
1. Переведите из одной единицы измерения в другую.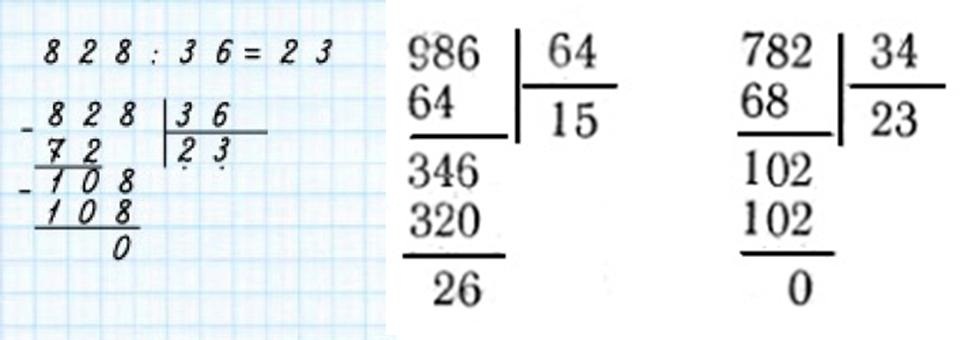
| а) 19 дм 5 см = … см | б) 21 км 678 м = … м |
| в) 43 см 8 мм = … мм | г) 503 см =… дм … см |
2. Начертите отрезок AB, равный 13 см 2 мм, отметьте на нем точки C и D. AC равен 7 см 3 мм. CD равен 3 см 6 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 16 столбах, расстояние между столбами составляет 3 метра. Каково расстояние между пятым и одиннадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС. Выпишите все многоугольники, которые образовались.
Самостоятельная работа №4 на тему: «Сравнение натуральных чисел»
Вариант I.
1. Сравните числа.
| а) 3 485 660 … 3 458 660 | б) 303 559 … 330 559 |
| в) 2 596 440 … 2 569 440 | г) 45 696 … 44 696 |
2. Представьте в виде двойного неравенства: 18 т 347 кг .
.. 18 т 4 ц 59 кг … 18 568 кг.
Вариант II.
1. Сравните числа.
| а) 34 686 887 … 34 868 887 | б) 3 855 … 3 585 |
| в) 40 955 999 … 40 595 999 | г) 455 776 … 445 776 |
2. Представьте в виде двойного неравенства: 13 км 845 м … 14675 м … 13 км 845 м 3 дм.
Вариант III.
1. Сравните числа.
| а) 678 881 … 687 881 | б) 782 223 … 728 223 |
| в) 2 490 606 … 2 490 660 | г) 13 799 … 13 977 |
2. Представьте в виде двойного неравенства: 15 т 475 кг … 15657 кг … 157 ц 35 кг.
Самостоятельная работа №5 на тему: «Сложение и вычитание натуральных чисел»
Вариант I.
1. Выполните сложение.
| а) 348 588 667 + 239 586 394 = | б) 93 955 483 + 495 868 991 = |
| в) 23 394 596 + 5 697 345 = | г) 3 949 532 + 405 669 = |
2. Выполните вычитание.
| а) 348 588 667 — 283 745 733 = | б) 93 955 483 — 22 394 583 = |
| в) 23 394 596 — 192 485 = | г) 3 949 532 — 4 348 483 = |
3. Решите задачу.
Мастерская закупила 560 гаек. На ремонт первой машины потребовалось 203 гайки, а на ремонт второй машины – еще 293 гайки. Сколько гаек осталось в мастерской?4. Решите задачу.
В концертном зале стояло 454 стула. Для проведения концерта принесли 123 новых стула, а после антракта – еще 13 стульев. Сколько всего стульев стало в концертном зале?Вариант II.
1. Выполните сложение.
| а) 3 484 558 + 9 499 834 = | б) 93 955 483 + 394 585 665 = |
| в) 3 495 863 + 35 384 588 = | г) 5 697 291 + 34 405 669 = |
2. Выполните вычитание.
| а) 4 856 342 — 3 495 384 = | б) 283 495 864 — 232 485 965 = |
| в) 5 965 493 — 3 449 594 = | г) 23 455 303 — 19 485 588 = |
3.
Решите задачу.
4. Решите задачу.
В магазине находилось 4 т 150 кг сахара. В первый день привезли 340 кг сахара, а во второй день – еще 4 ц сахара. Сколько кг сахара стало в магазине?Вариант III.
1. Выполните сложение.
| а) 2 399 388 + 239 586 394 = | б) 435 483 + 495 868 991 = |
| в) 34 567 784 + 13 412 345 = | г) 6 563 544 + 23 876 554 = |
2. Выполните вычитание.
| а) 455 586 661 — 283 745 733 = | б) 40 954 586 — 22 394 583 = |
| в) 495 568 222 — 448 568 338 = | г) 3 949 532 — 2 349 588 = |
3. Решите задачу.
В моток смотано 459 м провода. В первый день истратили 119 м, а на второй день – 239 м провода. Сколько метров провода осталось в мотке?4. Решите задачу.
На складе находилось 3 т и 450 кг муки.
В первый день привезли 560 кг, через неделю привезли еще 5 ц муки. Сколько кг муки стало на складе?Самостоятельная работа №6
Вариант I.
1. Найдите значение выражения: ( а + 46 ) : ( b — 48 ), если а = 35 и b = 57.
2. Упростите выражения.
а) с + 239 — 93;б) 485 — 483 + d.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. К нему прибавили число 194, а потом прибавили ещё число 110 и получили число 322. Какое число было задумано?4. Решите уравнения.
a) (305 — ( ( 45 + х ) — 32 ) + 96 = 223;б) 38 + ( 69 — y ) + 74 = 172.
Вариант II.
1. Найдите значение выражения: ( а — 34 ) * ( b + 9 ), если а = 60 и b = 11.
2. Упростите выражения.
а) 594 — 69 — а;б) 149 + b — 54.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 424, а затем прибавили число 392. В итоге, получилось число 632. Какое число было задумано?4.
Решите уравнения.
б) 18 + ( 159 — y ) + 34 = 172.
Вариант III.
1. Найдите значение выражения: ( а — 68 ) : b + 2 339, если а = 92 и b = 8.
2. Упростите выражения.
а) с + 239 — 193;б) 485 — d + 384.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 209, а затем прибавили число 47. В итоге, получилось число 217. Какое число было задумано?4. Решите уравнения.
a) ( 111 — ( 45 + х ) ) + 96 = 123;б) 29 + ( 59 — y ) + 15 = 72.
После завершения второй четверти, учащиеся должны:
1. уметь умножать натуральные числа и использовать эти знания;
2. уметь производить деление натуральных чисел, в том числе и деление с остатком, и использовать эти навыки при решении задач;
3. знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
4. знать, что такое возведение числа в степень.
Понимать, что такое корень и куб числа;
5. понимать, что такое формула, и как производить вычисления по формуле.
Самостоятельная работа №7 на тему: «Действия с натуральными числами. Умножение»
Вариант I.
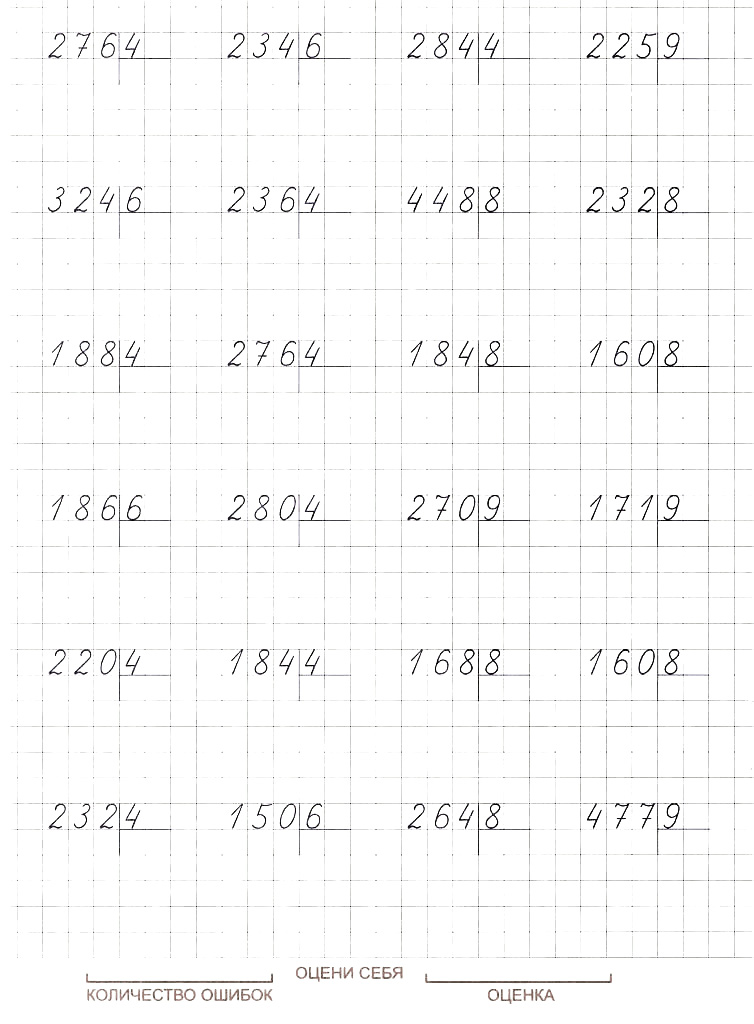
1. Выполните умножение.
| а) 283 * 46 = | б) 29 * 473 = | в) 841 * 93 = | г) 19 * 632 = |
| д) 570 * 340 = | е) 930 * 730 = | ж) 5100 * 360 = | з) 560 * 230 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 491 * 4 * 200 =б) 4 * 324 * 25 * 300 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 35 * 34 = | 34 * 33 = | 34 * 36 = | 32 * 32 = |
4. Решите задачу.
В двухэтажной школе всего 32 кабинета и в каждом кабинете по 12 парт. В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?Вариант II.
1. Выполните умножение.
| а) 342 * 57 = | б) 64 * 268 = | в) 342 * 89 = | г) 32 * 864 = |
| д) 920 * 560 = | е) 470 * 990 = | ж) 2300 * 630 = | з) 430 * 540 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 500 =б) 4 * 265 * 25 * 200 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 85 * 84 = | 84 * 83 = | 84 * 86 = | 82 * 82 = |
4. Решите задачу.
В поселке построено 18 домов. Из них 4 трехэтажных, 6 двухэтажных, остальные одноэтажные дома. В трехэтажных домах – 18 окон, в двухэтажных – 14 окон, в одноэтажных – 8 окон. Сколько окон необходимо для 4 таких же посёлков?Вариант III.
1. Выполните умножение.
| а) 563 * 24 = | б) 32 * 441 = | в) 324 * 87 = | г) 23 * 728 = |
| д) 220 * 680 = | е) 240 * 580 = | ж) 7500 * 290 = | з) 920 * 630 = |
2.
Умножьте числа, используя наиболее удобный порядок действий.
б) 4 * 641 * 25 * 100 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 65 * 64 = | 64 * 63 = | 64 * 66 = | 62 * 62 = |
4. Решите задачу.
В один мешок помещается 26 кг картофеля, или 34 кг муки, или 38 кг сахара. Сколько всего весит груз, если в машину погрузили 32 мешка картофеля, 38 мешков муки и 52 мешка сахара?Самостоятельная работа №8 на тему: «Деление натуральных чисел»
Вариант I.
1. Выполните деление.
| а) 475 860 : 5 = | б) 8 412 : 4 = | в) 492 000 000 : 1 000 = |
| г) 270 930 : 3 = | д) 386 240 : 5 = | е) 19 688 : 23 = |
2. Решите уравнения.
| а) X : 85 = 2 210 | б) 36 690 : Y = 10 | в) 792 : X = 4 |
| г) 15 * ( 39 : X ) = 45 | д) Y : 42 = 168 | е) 65 065 : Y = 1 001 |
3.
Решите задачу.
4. Остаток равен 18, неполное частное – 35 и делитель – 23. Найдите делимое.
Вариант II.
1. Выполните деление.
| а) 489 560 : 5 = | б) 36 690 : 3 = | в) 657 000 : 1 000 = |
| г) 960 552 : 6 = | д) 522 240 : 2 = | е) 67 065 : 85 = |
2. Решите уравнения.
| а) X : 26 = 456 | б) 4 760 : Y = 85 | в) 792 : X = 8 |
| г) 35 * ( 54 : X ) = 315 | д) Y : 3 = 3015 | е) 524 : Y = 131 |
3. Решите задачу.
Станок производит 1200 заготовок за 1 час. Сколько минут нужно машине, чтобы приготовить 48 000 заготовок?4. Остаток равен 33, неполное частное – 41 и делитель – 25. Найдите делимое.
Вариант III.
1. Выполните деление.
| а) 236 560 : 4 = | б) 36 690 : 6 = | в) 612 345 000 : 1 000 = |
| г) 960 440 : 8 = | д) 678 350 : 2 = | е) 31 464 : 69 = |
2.
Решите уравнения.
| а) X : 25 = 14 | б) 1 820 : Y = 28 | в) 1 836 : X = 6 |
| г) 52 * Y = 468 | д) Y : 3 = 7 659 | е) 1048 : Y = 131 |
3. Решите задачу.
Комбайн убирает 30 га пшеницы за 1 час. Сколько дней ему нужно, чтобы убрать площадь равную 1200 га, если в день он будет работать по 10 часов?4. Остаток равен 24, неполное частное – 25 и делитель – 28. Найдите делимое.
Самостоятельная работа №9 на темы: «Выражения, уравнения и решение уравнений», «Квадрат и куб числа»
Вариант I.
1. Решите примеры.
а) 34 + ( 239 — 606 : 6 ) * 4 — 393 : 3 =б) 152 =
в) 73 =
г) ( 14 + 7 )2 — ( 5 + 13 )2 + 287 =
2. Упростите выражение и найдите его значение при с=34: 47с + 34 — 58 + 12с — 58.
3. Решите уравнения.
а) 15 * х = 945б) 3 * y — 45 = 44
4. Решите задачу.
Бабушка и внучка слепили 124 пельмени. Сколько пельменей слепили бабушка и сколько внучка, если бабушка лепила в 3 раза быстрее, чем внучка?Вариант II.
1. Решите примеры.
а) 472 — ( 29 + 124 : 4 ) — 72 : 8 =б) 182 =
в) 63 =
г) ( 5 + 27 )2 — ( 4 + 12 )2 — 64 =
2. Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
3. Решите уравнения:
а) 15 * х = 180б) 12 * y + 36 = 96
4. Решите задачу.
Инженер и студент отремонтировали 248 приборов. Инженер ремонтировал приборы в 3 раза быстрее, чем студент. Сколько приборов починил каждый?Вариант III.
1. Решите примеры.
а) 365 + ( 299 — 342 : 2 ) * 5 — 687 : 3 =б) 172 =
в) 83 =
г) ( 4 + 7 )2 — ( 5 + 23 )2 + 787 =
2. Упростите выражение и найдите его значение при с=12: 47 + 56с — 6с + 34 — 12с.
3. Решите уравнения.
а) 32 * х = 1280б) 8 * y + 36 = 356
4. Решите задачу.
Портной и его ученик сшили 213 фартуков. Портной работал в 2 раза быстрее, чем его ученик. Сколько фартуков сшил портной, а сколько ученик?Самостоятельная работа №10 на темы: «Окружность и круг».
«Обыкновенные дроби» Вариант I.
1. Нарисуйте окружность с центром в точке X и радиусом 4 см 6 мм. Нарисуйте отрезок CD так, чтобы он проходил через центр окружности и пересекал ее в точках C и D. Как называются отрезки СX и СD? Определите их длину.
2. Решите задачу.
Оля нашла 26 грибов, из них 18 маслят. Какую часть грибов составляют маслята?3. Решите задачу.
Рыбаки поймали 112 кг рыбы. Из них 10⁄28 – караси. Сколько карасей поймали рыбаки?4. Решите задачу.
Коля прочитал 85 страниц журнала, что составило 5⁄12 от общего числа страниц. Сколько страниц в журнале?Вариант II.
1. Нарисуйте окружность с центром в точке Y и радиусом 3 см 8 мм. Нарисуйте отрезок EF так, чтобы он проходил через центр окружности и пересекал ее в точках E и F. Как называются отрезки YE и EF? Определите их длину.
2. Решите задачу.
Коля собрал в корзину 31 фрукт, из них 22 фрукта – это груши. Какую часть собранных фруктов составляют груши?3.
Решите задачу.
4. Решите задачу.
Мастер отремонтировал 35 приборов, что составило 5⁄12 от общего количества приборов. Сколько всего приборов надо отремонтировать мастеру?Вариант III.
1. Нарисуйте окружность с центром в точке Z и радиусом 2 см 6 мм. Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
2. Решите задачу.
У Саши есть 29 карандашей. Из них 19 карандашей – это простые карандаши. Какую часть карандашей составляют цветные карандаши?3. Решите задачу.
Мастер сделал 312 деталей. Из них 3⁄24 часть деталей – деревянные. Сколько деревянных деталей сделал мастер?4. Решите задачу.
Ребята из 5 класса собрали 32 кг ягод. Это составляет 3⁄24 от всего количества собранных ягод.
Сколько всего ягод было собрано?Самостоятельная работа №11 на тему: «Сравнение дробей»
Вариант I.
1. Задан луч длиной в 12 единиц. Отметьте на числовом луче:
| а) 2⁄12 части | б) 6⁄12 части | 2⁄3 части | 5⁄4 части |
2. Сравните дроби.
а) 23⁄38 и 16⁄18б) 21⁄45 и 15⁄26
3. Найдите три решения неравенства.
а) 21⁄22< x < 22⁄22б) 7⁄11 < z < 8⁄11
4. При каких значениях х:
а) дробь х⁄22 будет правильной?б) дробь 15⁄х будет неправильной?
Вариант II.
1. Задан луч длиной в 15 единиц. Отметьте на числовом луче:
| 4⁄15 части | 3⁄15 части | 3⁄5 части | 2⁄3 части |
2.
Сравните дроби.
б) 22⁄49 и 18⁄21
3. Найдите три решения неравенства.
а) 19⁄20 < x < 20⁄20б) 7⁄9 < z < 8⁄9
4. При каких значениях y:
а) дробь y⁄19 будет правильной?б) дробь 23⁄y будет неправильной?
Вариант III.
1. Задан луч длиной в 18 единиц. Отметьте на числовом луче:
| 2⁄18 части | 6⁄18 части | 2⁄3 части | 5⁄6 части |
2. Сравните дроби.
а) 26⁄31 и 18⁄19б) 23⁄41 и 17⁄18
3. Найдите три решения неравенства.
а) 9⁄10< y < 10⁄10б) 5⁄7 < z < 6⁄7
4.
При каких значениях z:
б) дробь 13⁄z будет неправильной?
Самостоятельная работа №12 на тему: «Сложение и вычитание обыкновенных дробей»
Вариант I.
1. Решите примеры.
а) 26⁄31 + 18⁄31 — 6⁄31;б) 17⁄125 — 5⁄125 + 106⁄125;
в) 19⁄39 + ( 18⁄39 — 6⁄39 ) — 13⁄39;
2. Решите уравнения.
а) x + 6⁄18 = 16⁄18б) 13⁄25 — ( y + 6⁄25 ) = 4⁄25
3. Решите задачу.
Первый спортсмен пробежал 5⁄7 км, а второй спортсмен за тоже время пробежал 6⁄7 км. На сколько метров больше пробежал первый спортсмен?4.
Решите задачу.
Вариант II.
1. Решите примеры.
а) 15⁄38 + 12⁄38 — 11⁄38;б) 23⁄192 — 8⁄192 + 48⁄192;
в) 19⁄56 + ( 21⁄56 — 12⁄56 ) — 16⁄56;
2. Решите уравнения.
а) x — 5⁄12 = 3⁄12б) 18⁄23 — ( 7⁄23 + y ) = 5⁄23
3. Решите задачу.
Расстояние от дачи до пруда равно 3⁄5 км, а от дачи до леса равно 4⁄5 км. На сколько метров расстояние от дачи до пруда больше, чем расстояние от дачи до леса?4. Решите задачу.
Из погреба вытащили 3⁄12 части картофеля, а потом – ещё 2⁄12 части.
После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?Вариант III.
1. Решите примеры.
а) 19⁄28 + 12⁄28 — 16⁄28;б) 13⁄176 — 11⁄176 + 49⁄176;
в) 27⁄42 + ( 12⁄42 — 6⁄42 ) — 12⁄42;
2. Решите уравнения.
а) x + 12⁄23 = 20⁄23б) 28⁄35 — ( y + 16⁄35 ) = 4⁄35
3. Решите задачу.
Расстояние от школы до больницы равно 8⁄9 км, а от школы до бассейна равно 4⁄9 км. На сколько метров расстояние от школы до больницы больше, чем расстояние от школы до бассейна?4. Решите задачу.
Из рулона отрезали 3⁄8 части ткани, а потом – ещё 2⁄8 части.
После этого в рулоне осталось 32 метра ткани. Сколько метров ткани было в рулоне?Самостоятельная работа №13 на тему: «Сложение и вычитание смешанных чисел»
Вариант I.
1. Решите примеры.
а) 4 19⁄28 + 6 12⁄28;б) 5 13⁄176 — 2 11⁄176;
в) 12 27⁄43 + 3 12⁄43.
2. Решите уравнения.
а) 23 18⁄38 + х =36 12⁄28;б) 7 14⁄16 — y = 3 11⁄16;
в) y + 18 27⁄53 = 24 13⁄53;
3. Решите задачу.
В первый день в мастерской использовали 23 3⁄18 метра проволоки, а во второй день – ещё 18 2⁄18 части. После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?Вариант II.
1. Решите примеры.
а) 3 13⁄22 + 3 12⁄22;б) 8 15⁄126 — 4 15⁄126;
в) 13 22⁄49 + 3 14⁄49.
2. Решите уравнения.
а) 2 18⁄43 + х = 3 4⁄43;б) 17 15⁄19 — y = 12 12⁄19;
в) y — 18 38⁄56 = 24 27⁄56.
3. Решите задачу.
В первый день в школе покрасили 17 5⁄23 метра коридора, а во второй день – ещё 23 4⁄23 метра. Сколько метров было покрашено за 2 дня?Вариант III.
1. Решите примеры.
а) 5 19⁄23 + 6 12⁄23;б) 7 13⁄48 — 3 11⁄48;
в) 82 25⁄78 + 34 12⁄78
2. Решите уравнения.
а) 6 17⁄29 + х = 23 4⁄29;б) 8 15⁄128 — y = 6 12⁄128;
в) y — 18 38⁄47 = 5 27⁄47.
3. Решите задачу.
Фермер убрал 13 6⁄13 метра грядки в первый день, а на следующий день – ещё 18 3⁄13 метра.
После двух дней работы осталось убрать 6 метров. Какова длина грядки?Самостоятельная работа №14 на темы: «Десятичная запись дробных чисел». «Сравнение десятичных дробей»
Вариант I.
1. Заданные дроби представьте, как десятичные дроби.
а) 5 59⁄10б) 6 1⁄100
в) 17 137⁄1000
2. Сравните числа.
а) 5,596 и 5,629б) 7,34 и 7,339
в) 0,684 и 0,6840
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 92 ц; 887 кг; 14 т 12 кг;б) представьте в квадратных дециметрах: 8 м 2; 57 см 2; 8 м2 77 дм2.
4. Отметьте точки: 0,2; 0,8; 1,1; 2,3; 2,1; 3,7 на числовом отрезке, равном 5 единицам.
Вариант II.
1. Заданные дроби представьте, как десятичные дроби.
а) 18 59⁄1000б) 7⁄10
в) 7 137⁄100
2. Сравните числа.
а) 35,97 и 35,971б) 8,449 и 8,540
в) 0,92 и 0,920
3.
Переведите из одной единицы измерения в другую.
б) представьте в квадратных дециметрах: 13 м 2; 2 см 2; 87 м2 32 дм2.
4. Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Вариант III.
1. Заданные дроби представьте, как десятичные дроби.
а) 15 43⁄100б) 9 23⁄1000
в) 5⁄10
2. Сравните числа.
а) 29,345 и 29,354б) 171,89 и 171,889
в) 0,93 и 0,930
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 18 ц; 56 кг; 3 т 9 кг;б) представьте в квадратных дециметрах: 4 м 2; 23 см 2; 2 м2 56 дм2.
4. Отметьте точки: 0,4; 0,5; 1,4; 1,9; 2,4; 3,0 на числовом отрезке, равном 4 единицам.
Самостоятельная работа №15 на темы: «Сложение и вычитание десятичных дробей».
«Округление чисел» Вариант I.
1. Решите примеры на сложение десятичных дробей.
а) 29,3 + 4,35 =б) 68,9 + 19,1 =
в) 0,68 + 6,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 35,1 — 13,2 =б) 37 — 27,3 =
в) 13,28 — 5,327 =
3. Решите задачу:
В первый день плот проплыл 14,8 км, во второй день – на 1 км 700 м больше, чем в первый день. В третий день плот проплыл на 600 м меньше, чем во второй день. Сколько всего км проплыл плот?4. Округлите:
а) целую часть числа 2539,48190 до сотен, до десятков, до единиц;б) дробную часть числа 2539,48190 до тысячных, до сотен, до десятков.
Вариант II.
1. Решите примеры на сложение десятичных дробей.
а) 79,3 + 8,15 =б) 18 + 8,8 =
в) 0,93 + 23,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 48,2 — 4,98 =б) 96 — 48,6 =
в) 37,67 — 13,168 =
3. Решите задачу.
В первом пакете было 15,7 кг песка, во втором – на 350 г больше, чем в первом.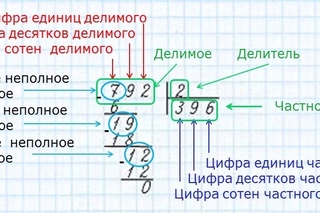
В третьем – на 1200 г меньше, чем в первом. Сколько кг песка в трех пакетах?4. Округлите:
а) целую часть числа 3462,9470 до сотен, до десятков, до единиц;б) дробную часть числа 3462,9470 до тысячных, до сотен, до десятков.
Вариант III.
1. Решите примеры на сложение десятичных дробей.
а) 34,3 + 13,11 =б) 8 + 47,7 =
в) 0,123 + 23,942 =
2. Решите примеры на вычитание десятичных дробей.
а) 69,2 — 7,88 =б) 91,76 — 18,6 =
в) 8,94 — 5,452 =
3. Решите задачу.
3 дня бабушка пекла блины. В первый день она использовала 1,2 кг муки, во второй день – на 500 г меньше, чем в первый день, а на третий день – на 300 г больше, чем во второй день. Сколько муки она использовала за три дня?4. Округлите:
а) целую часть числа 4392,73910 до сотен, до десятков, до единиц;б) дробную часть числа 4392,73910 до тысячных, до сотен, до десятков.
Самостоятельная работа №16 на тему: «Умножение десятичных дробей на натуральные числа»
Вариант I.
1. Выполните умножение.
| а) 8,3 * 8 = | б) 7,12 * 34 = | в) 0,235 * 93 = | г) 1,93 * 100 = |
2. Найдите значение выражения: х + ( 3,74х — 1,474х ) при х=3; 100; 374; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух деревень, расстояние между которыми составляет 45,8 км, вышли пешеходы. Скорость первого пешехода составляет 4,2 км/ч, а скорость второго – 4,5 км/ч. Какое расстояние будет между ними через 4 часа?4. Решите задачу.
Машина проехала 360 км за 6 часов. Какое расстояние она преодолеет, передвигаясь с той же скоростью, за 1⁄4 часа, за 2 1⁄3 часа?Вариант II.
1. Выполните умножение.
| а) 7,48 * 12 = | б) 3,57 * 7 = | в) 0,873 * 87 = | г) 1,698 * 1000 = |
2. Найдите значение выражения: 5х + ( 6,59х + 2,483х ) при х=5; 100; 324; 1000.
3. Решите задачу.
Одновременно в противоположных направлениях из города выехали 2 машины.
Скорость первой машины составляет 54,7 км/ч, а скорость второй – 76,2 км/ч. Какое расстояние будет между ними через 3 часа?4. Решите задачу.
Велосипедист преодолел 72 км за 3 часа. Какое расстояние он преодолеет, перемещаясь с той же скоростью, за 5⁄6 часа, за 2 1⁄3 часа?Вариант III.
1. Выполните умножение.
| а) 9,4 * 6 = | б) 8,34 * 56 = | в) 0,517 * 62 = | г) 6,787 * 1000 = |
2. Найдите значение выражения: ( 8,45х — 3,594х ) — х при х=8; 100; 843; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух городов выехали мотоциклы. Расстояние между городами составляет 234,8 км. Скорость первого мотоциклиста составляет 34,5 км/ч, а скорость второго – 56,2 км/ч. Какое расстояние будет между ними через 2 часа?4. Решите задачу.
Моторная лодка прошла 24 км за 2 часа. Какое расстояние она пройдет, перемещаясь с той же скоростью, за 1⁄4 часа, за 3 1⁄3 часа?Самостоятельная работа №17 на тему: «Деление десятичных дробей на натуральные числа»
Вариант I.
1. Выполните деление.
| а) 2,729 : 6 = | б) 283,85 : 4 = | в) 4 : 13 = | г) 0,095 : 10 = |
2. Решите уравнения.
| а) 5X — 0,4 = 23,6 | б) 48,2 : Y = 10,4 |
3. Решите задачу.
За два дня рабочие отремонтировали 3,6 км дороги. В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?4. Решите задачу.
4 класс и 5 класс собирали макулатуру. Пятиклассники собрали в 2 раза больше макулатуры, чем ребята из 4 класса. Вместе они собрали 239,7 кг. Сколько кг собрали ребята из 5 класса и сколько ребята из 4 класса?Вариант II.
1. Выполните деление.
| а) 5,837 : 7 = | б) 291,49 : 5 = | в) 5 : 18 = | г) 0,023 : 10 = |
2. Решите уравнения.
| а) 8X + 2,8 = 18,6 | б) 28,1 : Y = 12,4 |
3. Решите задачу.
За два дня бригада собрала 147,6 кг ягод.
В первый день они собрали 4/9 части урожая ягод. Сколько кг ягод они собрали во второй день?4. Решите задачу.
Две бригады собирали картофель. Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?Вариант III.
1. Выполните деление.
| а) 4,752 : 9 = | б) 472,49 : 6 = | в) 7 : 19 = | г) 0,044 : 10 = |
2. Решите уравнения.
| а) 5X + 2,5 = 24 | б) 14,2 : Y = 3,4 |
3. Решите задачу.
За 2 дня мотоциклист преодолел 394,1 км. В первый день он проехал 4⁄7 части пути. Сколько км он проехал во второй день?4. Решите задачу.
Мама собрала в 5 раз больше ягод, чем дочка. Вместе они собрали 34,5 кг ягод. Сколько ягод собрала мама и сколько дочка?Самостоятельная работа №18 на тему: «Среднее арифметическое»
Вариант I.
1. Найдите среднее арифметическое четырех чисел: 4,5; 5,6; 4,9; 5,1.
2. Решите задачу.
В течение часа машина двигалась со скоростью 67,5 км/ч, в течение второго часа – со скоростью 51,6 км/ч. В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 14,5. Первое число – 14,1, а второе число на 0,8 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями равно 340 км. Автомобиль преодолел половину пути со скоростью 58 км/ч, а вторую половину – со скоростью 49 км/ч. Какова средняя скорость автомобиля на протяжении всего пути?Вариант II.
1. Найдите среднее арифметическое четырех чисел: 12,3; 12,9; 11,6; 13,1.
2. Решите задачу.
В течение первого часа спортсмен шел со скоростью 11,2 км/ч, в течение второго часа – со скоростью 10,7 км/ч, а в течение третьего часа его скорость составила 9,8 км/ч.
Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 28,5. Первое число – 28,2, а второе на 0,9 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя городами составляет 52 км. Первую половину пути велосипедист передвигался со скоростью 18 км/ч, а вторую половину – со скоростью 22 км/час. Какова средняя скорость велосипедиста на всем протяжении пути?Вариант III.
1. Найдите среднее арифметическое четырех чисел: 9,1; 9,9; 11,1; 10,7.
2. Решите задачу.
В течение первого часа лодка двигалась со скоростью 15,5 км/ч, во второй час движения её скорость составила 17,4 км/ч, а в течение третьего часа – 12,7 км/ч. Какая средняя скорость лодки? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 13,2. Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.4. Решите задачу.
Самостоятельная работа №19 на тему: «Проценты, задачи на проценты»
Вариант I.
1. Решите задачу.
В спортивной секции занимается 60 учеников, из них 70% составляют девочки. Сколько мальчиков занимается в спортивной секции?2. Решите задачу.
Ребята четвертых и пятых классов собирали макулатуру. Ребята пятого класса собрали 150 кг макулатуры, что составило 60% общего веса собранной макулатуры. Сколько кг макулатуры собрали ребята?3. Решите задачу.
Из 15 кг яблок получается 12 кг яблочного пюре. Каков процент выхода пюре из яблок?Вариант II.
1. Решите задачу.
В 5 классе числится 30 учеников, 60% из них – мальчики. Сколько девочек учится в 5 классе?2. Решите задачу.
2 бригады собирали помидоры. Первая бригада собрала 320 кг помидор, что составило 40% от общего урожая.
Сколько всего помидор собрали обе бригады?3. Решите задачу.
Из 60 семян взошли 55 растений. Найдите процент всхожести семян.Вариант III.
1. Решите задачу.
В школе работает 40 человека. Из них 80% – женщины. Сколько мужчин работает в школе?2. Решите задачу.
Бабушка и внучка собирали яблоки. Бабушка собрала 30 кг яблок, что составило 80% от общего сбора. Сколько кг яблок собрали бабушка и внучка вместе?3. Решите задачу.
При перемалывании 40 кг зерна получили 25 кг муки. Найдите процент выхода муки.Конспект урока математики на тему «Деление многозначных чисел в столбик».
Разработка урока математики в 4 классе
Тема урока: Деление многозначных чисел в столбик.
Тип урока: урок обобщения и систематизации знаний.
Цель: Систематизировать навык деления многозначного числа на двузначное число.
Задачи:
— обучающие:
закрепить алгоритм деления на многозначное число и применять его на практике;
совершенствовать навыки по решению задач;
познакомить учащихся с уравнениями нового вида, имеющими более одного корня;
продолжать учить анализировать задачи.
— развивающие:
развивать умение осознавать и принимать учебную цель
развивать умение рассуждать и обобщать;
способствовать развитию внимания, памяти, логического мышления,а также математической речи.
— воспитывающие:
воспитывать усидчивость, аккуратность при работе в тетрадях;
воспитывать взаимопомощь к товарищам;
воспитывать осознанное отношение к своему здоровью.
Оборудование:
Учебник И. И. Аргинская, Е. И. Ивановская « Математика» 4 класс, тетради, карточки-сигналы, карточки с индивидуальными заданиями, компьютер и мультимедийная установка.
Структура урока
1. Организационный этап – 1 мин.
2. Постановка учебной проблемы — 4 мин.
3. Актуализация знаний — 12 мин.
4. Физкультминутка – 3 мин.
5.Систематизация знаний – 20 мин.
6. Рефлексивно-оценочный этап – 4 мин.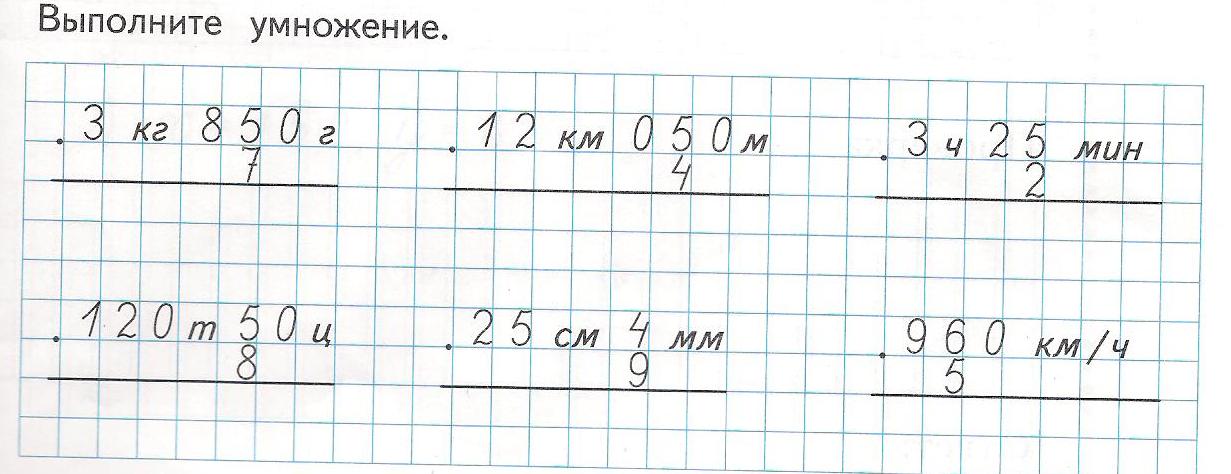
Ход урока.
1.Организационный этап.Эмоциональный настрой.
2. Постановка учебной проблемы.
— Доброе утро, ребята!
— А теперь проверь, дружок, ты готов начать урок?
Всё ль на месте, всё в порядке, книжка, ручка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получить
Только лишь оценку «5».
— Чтобы нам сегодня всё удалось, какими мы должны быть?
— Пусть нашим девизом и станут эти слова: Будь внимателен и трудолюбив!
— Ребята, сегодня на урок к нам пришли 3 смайлика: весёлый, задумчивый и грустный. (приложение 1). Они будут следить за вашими ответами в процессе всего урока. В конце урока, вы попробуете оценить себя и свои знания в математике, выберите себе тот смайлик, который посчитаете нужным.
— Посмотрите на запись, которая имеется на доске: (1слайд).
312:3= 2584:76=
1296:12=
-Решите, пожалуйста, выражения.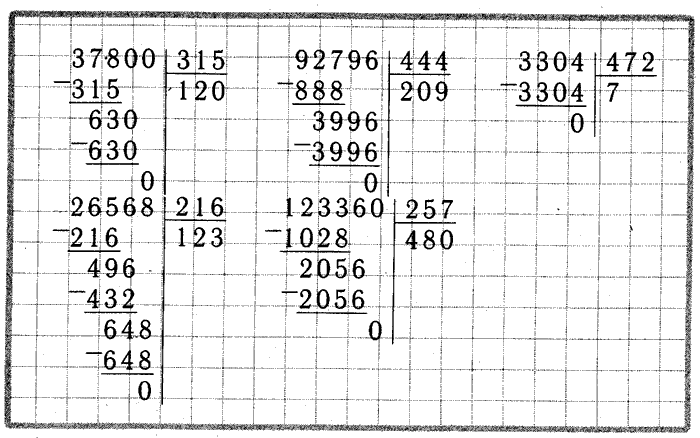
— Что нового в этих выражениях вы заметили?
— Какие из них вы можете решить, а какие нет и почему?
— Ребята, кто догадался и может уже назвать тему нашего сегодняшнего урока?
Деление многозначного числа на двузначное.
— Сегодня мы продолжим работу над этой темой.
— А как вы думаете, чему мы должны сегодня научиться?
Мы познакомимся с новым способом деления в столбик.
— Цель нашего урока — вспомнить алгоритм деления и научиться делить многозначные числа на двузначные в столбик.
Мотивационный компонент урока.
Эмоционально-положительный настрой на урок, создание ситуации успеха.
Постановка проблемной задачи.
Наблюдение над примерами.
Решение примеров в тетради.
Формулировка темы урока.
Рассуждения детей.
3.Актуализация знаний.
— Посмотрите на те выражения, которые вы не смогли решить.
(слайд 2).
2584:76=
— Скажите, что нужно знать, для того, чтобы решить эти выражения?
Алгоритм деления.
— Давайте его составим.
1. Находим первое неполное делимое.
2. Определяем число цифр в частном.
3. Округляем делитель с наименьшей погрешностью.
4. Делим первое неполное делимое. Получаем первую цифру в результате частного. Узнаём, сколько единиц разделили. Остаток сравниваем с делителем.
5. Сносим следующую цифру. Продолжаем деление в том же порядке. (слайд 3).
(Памятку с алгоритмом деления на многозначное число раздаю ученикам). (приложение 2).
— А теперь ребята, давайте потренируемся в решении примеров на деление в столбик.
— Не забывайте, пожалуйста, что если новым неполным делимым является 0, то его переписываем в частное.
— Ребята, сейчас мы с вами вместе решим один пример на деление в столбик, а два других вы решите самостоятельно.
1376 43
-А теперь давайте проверим ваши результаты.
(слайд 4).
-Решите два других выражения по вариантам:
I-вариант II-вариант
828 36 2584 76
-А теперь поменяйтесь тетрадочками и проверьте полученные результаты. (слайд 5).
Ответ при решении первого примера:23, второго -34.
— Ребята, эти выражения можно было выполнить и по-другому, сделав подробную запись.
-Кто из вас догадался как?
Разложив делитель в виде произведения двух чисел.
-Решите последний пример.
2.584:76=(2.280+304)=2.280:76+304:76=30+4=34
— Сверьте вашу запись с той, которая дана в учебнике на с.96 в №232(3). (приложение 3).
Рассуждение детей.
Повторение случаев табличного умножения и деления. Развитие логического мышления. Закрепление умения правильно вычислять.
Запись в тетрадь.
Работа в парах, запись в тетрадь
Работа в парах.
Запись в тетрадь.
Проверка знаний, умений и навыков.
4. Физкультминутка.
Используется физкультминутка «Бабочка».
Утром бабочка проснулась,
Потянулась, улыбнулась.
Раз – росой она умылась, Два – изящно покружилась.
Три – нагнулась и присела.
На четыре – улетела.
(по ходу физкультминутки ученики имитируют все движения бабочки).
Эмоциональное восприятие материала.
Переключение внимания.
Снятие напряжения.
Охрана здоровья.
5.Систематиза-ция знаний.
1. Реши задачу №233(1) с.97 (приложение 3), составив краткую запись.
1). 7+5=12(д)- яблонь и груш в одной части.
2). 4248:12=354(ч)- по 12 деревьев.
-Ребята, скажите, что нужно сделать для того, чтобы найти сколько яблонь посадили в саду?
—Нужно количество яблонь умножить на часть.
3). 7х354=2.478(д)- яблонь.
4). 5х354=1770(д)- груш.
Ответ: 2.478 яблонь, 1770 груш.
Развитие мыслительной деятельности.
Оценка деятельности учащихся.
Создание проблемной ситуации.
2. Выполняем №234(первые уравнения 1-го и 2-го столбика с.97).
-Кто сможет решить первое уравнение?
-Решите его.
х+38=113
х=113-38
х=75
75+38=113
113=113
— Давайте проверим ваш ответ. (слайд 6).
-А кто может решить второе уравнение?
-Давайте решим его вместе.
-Скажите, как найти произведение множителей, если оно равно нулю?
а в=0, когда а=0 или в=0
(у-3)х(4-у)=о
у-3=0 или 4-у=0
у=3 у=4
Если у=3, тогда
(3-3)х(4-3)=0
0х1=0
0=0
Если у=4, тогда
(4-3)х (4-4)=0
1х0=0
0=0
— Молодцы ребята, хорошо вы сегодня потрудились. А теперь давайте подведём итог урока.
Закрепление пройденного материала. Решение уравнений.
Постановка проблемной задачи.
7.
Рефлексивно-оценочный этап.
Итог урока.
Оценивание учащихся.
Домашнее задание.
— Ребята скажите, а какое открытие вы сегодня сделали на уроке?
-А над чем мы продолжим работу?
— Чем необходимо руководствоваться, для того, чтобы выполнить деление многозначных чисел в столбик?
— Итак, каждый из вас записал себе в тетрадь памятку с алгоритмом деления, давайте проведём проверку:
— Научились ли вы находить первое неполное делимое?
— Научились определять количество цифр в частном?
— Сумели ли вы определить цифру в частном?
— По результатам ответов выберите
тот смайлик, который считаете, что вам подходит и над чем предстоит вам ещё поработать.
— Если всё удалось на уроке, тогда весёлый смайлик. Если остались неразрешённые вопросы –задумчивый, если вам ещё понадобиться помощь, тогда – грустный.
Выставляются оценки ученикам, которые активно работали на уроке.
— Чтобы закрепить полученные на уроке знания и подготовиться к работе на следующем уроке, дома выполните:
№232 (7) 3,4,5 пример, №234 (2,7 уравнение) с.
97; №61 с.29 рабочая тетрадь (ребус по желанию). (приложение 4).
Регулирующий момент.
Совершенствовать умения анализировать, обобщать, делать выводы.
Оценивание своих способностей.
Вызвать у учащихся чувство удовлетворённости от урока.
Дифференциация по содержанию.
10 трюков, упрощающих математические операции
Недавно, прочитав книгу «Магия чисел», я почерпнул огромное количество информации. В книге рассказывается о десятках трюков, которые упрощают привычные математические операции. Оказалось, что умножение и деление в столбик — это прошлый век, и непонятно, почему этому до сих пор учат в школах.
Я выбрал 10 самых интересных и полезных трюков и хочу поделиться ими с вами.
Умножение «3 на 1» в уме
Умножение трёхзначных чисел на однозначные — это очень простая операция. Всё, что нужно сделать, — это разбить большую задачу на несколько маленьких.
2
- Умножаем 7 на 8 и получаем 56.
- Добавляем к числу 25 и получаем 5 625.
Деление на однозначное число
Деление в уме — это достаточно полезный навык. Задумайтесь о том, как часто мы делим числа каждый день. К примеру, счёт в ресторане.
Пример: 675 : 8
- Найдём приближенные ответы, умножив 8 на удобные числа, которые дают крайние результаты (8 × 80 = 640, 8 × 90 = 720). Наш ответ — 80 с хвостиком.
- Вычтем 640 из 675. Получив число 35, нужно разделить его на 8 и получить 4 с остатком 3.
- Наш финальный ответ — 84,3.
Мы получаем не максимально точный ответ (правильный ответ — 84,375), но согласитесь, что даже такого ответа будет более чем достаточно.
Простое получение 15%
Чтобы быстро узнать 15% от любого числа, нужно сначала посчитать 10% от него (перенеся запятую на один знак влево), затем поделить получившееся число на 2 и прибавить его к 10%.
Пример: 15% от 650
- Находим 10% — 65.
- Находим половину от 65 — это 32,5.
- Прибавляем 32,5 к 65 и получаем 97,5.
Банальный трюк
Пожалуй, все мы натыкались на такой трюк:
Задумайте любое число. Умножьте его на 2. Прибавьте 12. Разделите сумму на 2. Вычтите из неё исходное число.
Вы получили 6, верно? Что бы вы ни загадали, вы всё равно получите 6. И вот почему:
- 2x (удвоить число).
- 2x + 12 (прибавить 12).
- (2x + 12) : 2 = x + 6 (разделить на 2).
- x + 6 − x (вычесть исходное число).
Этот трюк построен на элементарных правилах алгебры. Поэтому, если вы когда-нибудь услышите, что кто-то его загадывает, натяните свою самую надменную усмешку, сделайте презрительный взгляд и расскажите всем разгадку. 🙂
Магия числа 1 089
Этот трюк существует не одно столетие.
Запишите любое трёхзначное число, цифры которого идут в порядке уменьшения (к примеру, 765 или 974). Теперь запишите его в обратном порядке и вычтите его из исходного числа.
К полученному ответу добавьте его же, только в обратном порядке.Какое бы число вы ни выбрали, в результате получите 1 089.
Быстрые кубические корни
Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1 000 |
»
Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.
Пример: кубический корень из 19 683
- Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27). 3. Следовательно, последняя цифра ответа — 7.
- Ответ — 27.
3. Следовательно, последняя цифра ответа — 7.Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.
Правило 70
Чтобы найти число лет, необходимых для удвоения ваших денег, нужно разделить число 70 на годовую процентную ставку.
Пример: число лет, необходимое для удвоения денег с годовой процентной ставкой 20%.
70 : 20 = 3,5 года
Правило 110
Чтобы найти число лет, необходимых для утроения денег, нужно разделить число 110 на годовую процентную ставку.
Пример: число лет, необходимое для утроения денег с годовой процентной ставкой 12%.
110 : 12 = 9 лет
Математика — волшебная наука. Я даже немного смущён тем, что такие простые трюки смогли меня удивить, и даже не представляю, сколько ещё математических фокусов можно узнать.
По материалам книги «Магия чисел»
Электронная книга Купить на amazon
Электронная книга на английском языке
Математика.
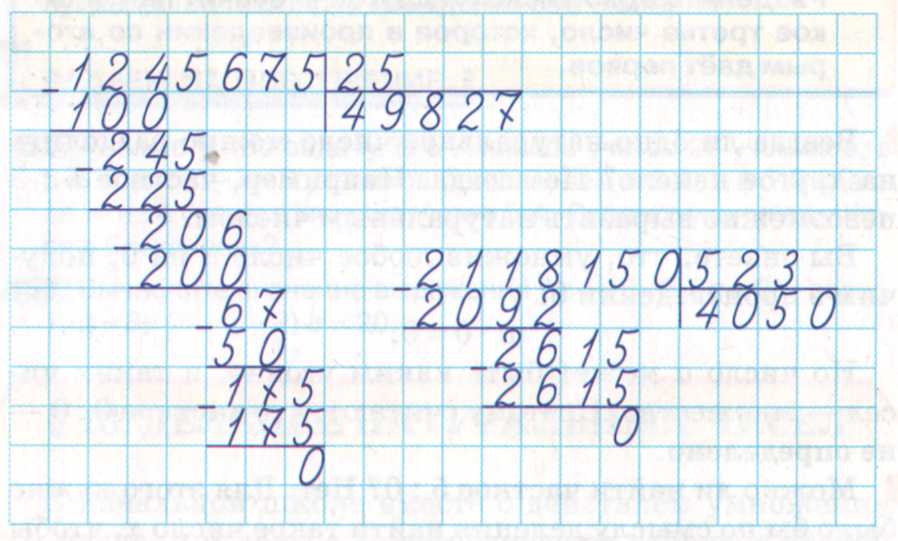Деление уголком | Сайт Леонида НекинаГлавная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
648 / 2.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
648 =
6 ∙ 100 + 4 ∙ 10 + 8 =
3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 =
( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 =
324 ∙ 2 .
После этого становится очевидно, что частное от деления равно
648 / 2 = 324.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель.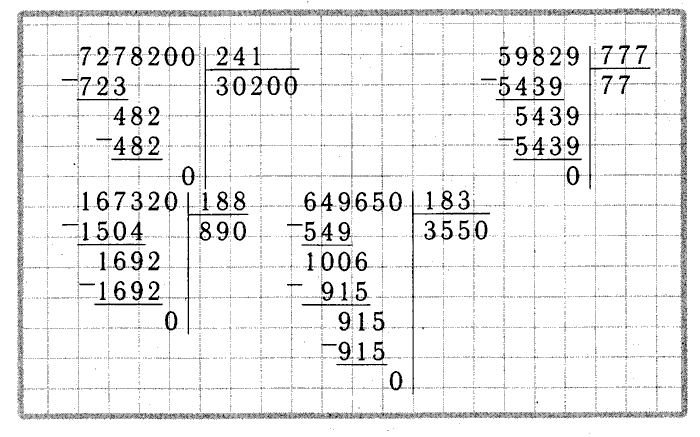
А вот пример несколько посложнее:
156 / 2 = ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
156 =
15 ∙ 10 + 6 .
Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
15 = 7 ∙ 2 + 1 = 14 + 1 .
Теперь мы можем продолжать расписывать наше делимое дальше:
156 =
15 ∙ 10 + 6 =
( 14 + 1 ) ∙ 10 + 6 =
14 ∙ 10 + 1 ∙ 10 + 6 =
14 ∙ 10 + 16 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 =
( 7 ∙ 10 + 8 ) ∙ 2 =
78 ∙ 2 .
Отсюда моментально получаем ответ:
156 / 2 = 78.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто.
Делимое и делитель запишем так:
1 | 5 | 6 | 2 |
|
|
|
|
|
|
При делении первых двух разрядов ( 15 ) на двойку получается 7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
1 | 5 | 6 | 2 |
|
|
|
| 7 |
|
Умножаем на эту семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
Теперь настало время вычислить остаток от деления 15-ти на 2 .
Он равен, очевидно,
15 − 2 ∙ 7 = 15 − 14 .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 |
|
|
|
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 | 6 |
|
|
В результате такого приписывания у нас получается число 16 .
Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
Вычитаем последнюю строку из предпоследней и получаем 0:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
|
| 0 |
|
|
Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
156 : 2 = 78 (ост.
0).
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
157 : 2 = 78 (ост. 1).
Таблица для этого примера выглядит так:
1 | 5 | 7 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 7 |
|
|
| 1 | 6 |
|
|
|
| 1 |
|
|
Здесь, опять-таки, остаток стоит в последней строке.
Для полноты картины распишем наше делимое в таком виде:
157 =
14 ∙ 10 + 17 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 + 1 =
( 7 ∙ 10 + 8 ) ∙ 2 + 1 =
7 8 ∙ 2 + 1
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
135674 : 259 = ?
Приступаем к заполнению таблицы:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
|
|
|
|
|
|
|
|
|
|
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ).
Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
1356 : 259 = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 = 5 .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
1356 : 259 = 5 (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик».
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
|
|
| 6 | 1 |
|
|
|
|
|
Внимательно приглядимся к полученной разности ( 61 ).
Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
1356 : 259 = 5 (ост. 61 ).
Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 | 2 | 3 |
|
|
| 6 | 1 | 7 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
259 ∙ 2 = |
|
| 5 | 1 | 8 |
|
|
|
|
|
|
|
| 9 | 9 | 4 |
|
|
|
|
|
|
| 1 | 2 |
|
|
|
|
259 ∙ 3 = |
|
|
| 7 | 7 | 7 |
|
|
|
|
|
|
| 2 | 1 | 7 |
|
|
|
Можно выписывать окончательный ответ:
135674 : 259 = 523 (ост.
217).
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
2 | 6 | 2 | 7 | 4 | 0 | 8 | 7 |
|
|
2 | 2 |
|
|
|
|
|
|
|
|
2 | 6 | 1 |
|
|
| 3 | 0 | 2 | 0 |
|
| 1 | 7 | 4 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
|
|
| 1 | 7 | 4 |
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).
Теперь остается только тренироваться, тренироваться и тренироваться.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
10 трюков, упрощающих математические операции — «Хакер»
В книге «Магия чисел» рассказывается о десятках трюков, которые упрощают привычные математические операции. Оказалось, что умножение и деление в столбик — это прошлый век, а есть гораздо более эффективные способы деления в уме.
Вот 10 самых интересных и полезных трюков.
Умножение «3 на 1» в уме
Умножение трёхзначных чисел на однозначные — это очень простая операция.
2
Деление на однозначное число
Деление в уме — это достаточно полезный навык. Задумайтесь о том, как часто мы делим числа каждый день. К примеру, счёт в ресторане.
Пример: 675 : 8
- Найдём приближенные ответы, умножив 8 на удобные числа, которые дают крайние результаты (8 × 80 = 640, 8 × 90 = 720). Наш ответ — 80 с хвостиком.
- Вычтем 640 из 675. Получив число 35, нужно разделить его на 8 и получить 4 с остатком 3.
- Наш финальный ответ — 84,3.
Мы получаем не максимально точный ответ (правильный ответ — 84,375), но согласитесь, что даже такого ответа будет более чем достаточно.
Простое получение 15%
Чтобы быстро узнать 15% от любого числа, нужно сначала посчитать 10% от него (перенеся запятую на один знак влево), затем поделить получившееся число на 2 и прибавить его к 10%.
Пример: 15% от 650
- Находим 10% — 65.
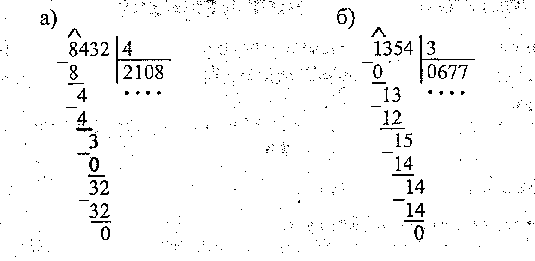
- Находим половину от 65 — это 32,5.
- Прибавляем 32,5 к 65 и получаем 97,5.
Банальный трюк
Пожалуй, все мы натыкались на такой трюк:
Задумайте любое число. Умножьте его на 2. Прибавьте 12. Разделите сумму на 2. Вычтите из неё исходное число.
Вы получили 6, верно? Что бы вы ни загадали, вы всё равно получите 6. И вот почему:
- 2x (удвоить число).
- 2x + 12 (прибавить 12).
- (2x + 12) : 2 = x + 6 (разделить на 2).
- x + 6 − x (вычесть исходное число).
Этот трюк построен на элементарных правилах алгебры. Поэтому, если вы когда-нибудь услышите, что кто-то его загадывает, натяните свою самую надменную усмешку, сделайте презрительный взгляд и расскажите всем разгадку. 🙂
Магия числа 1 089
Этот трюк существует не одно столетие.
Запишите любое трёхзначное число, цифры которого идут в порядке уменьшения (к примеру, 765 или 974). Теперь запишите его в обратном порядке и вычтите его из исходного числа.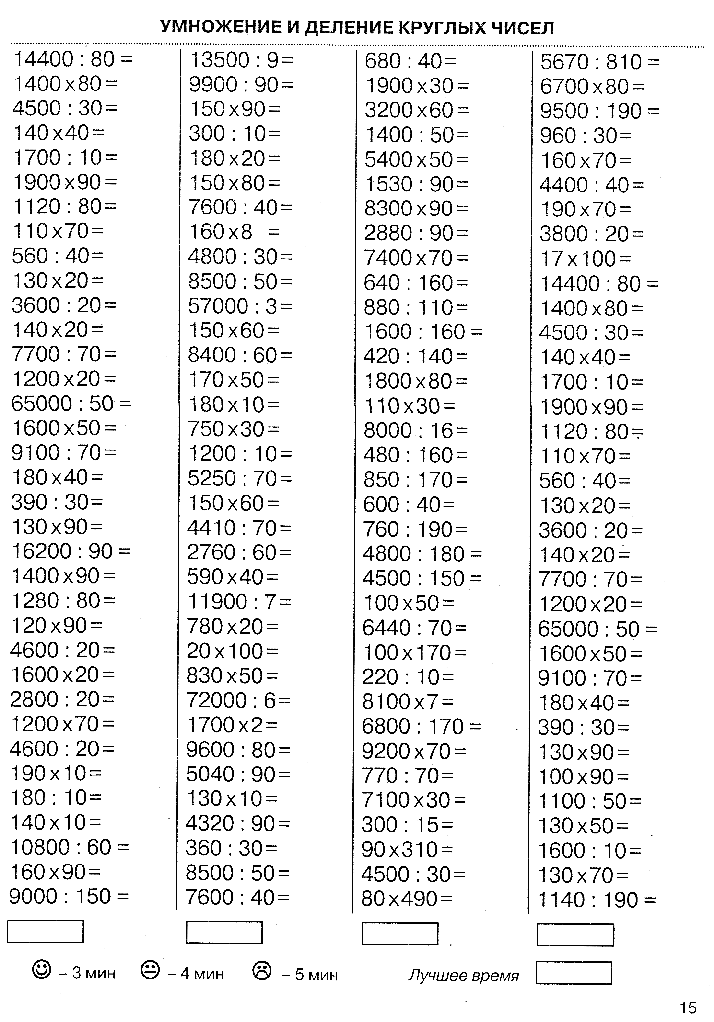
К полученному ответу добавьте его же, только в обратном порядке.
Какое бы число вы ни выбрали, в результате получите 1 089.
Быстрые кубические корни
Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1 000 |
Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.
Пример: кубический корень из 19 683
- Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27). 3. Следовательно, последняя цифра ответа — 7.
- Ответ — 27.
3. Следовательно, последняя цифра ответа — 7.Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.
Правило 70
Чтобы найти число лет, необходимых для удвоения ваших денег, нужно разделить число 70 на годовую процентную ставку.
Пример: число лет, необходимое для удвоения денег с годовой процентной ставкой 20%.
70 : 20 = 3,5 года
Правило 110
Чтобы найти число лет, необходимых для утроения денег, нужно разделить число 110 на годовую процентную ставку.
Пример: число лет, необходимое для утроения денег с годовой процентной ставкой 12%.
110 : 12 = 9 лет
Математика — волшебная наука. Если даже такие простые трюки удивляют, то какие ещё фокусы можно придумать?
Игры с длинными разделениями для 5-х классов
Чтобы научиться делить длинные руки, нужны терпение и практика. Вместо того, чтобы использовать рабочие листы для всей практики, позвольте учащимся время от времени играть в увлекательные игры.
Соревнуясь за победу в игре, учащиеся будут заинтересованы в правильном обучении и правильном выполнении процесса разделения.
Карточная игра
••• Jupiterimages / Photos.com / Getty Images
Мотивируйте студентов изучать процесс деления в столбик, научив их играть в простую карточную игру.Помогите детям найти партнеров и раздайте каждому партнеру колоду игральных карт с удаленными лицевыми картами. Каждый игрок берет четыре карты. Первые три числа — это делимое, а последняя карта — делитель. Оба игрока должны решить проблему с разделением. Каждый игрок будет использовать калькулятор, чтобы проверить ответ партнера. Игрок с большим частным сохраняет все карты. Игра продолжается до тех пор, пока один игрок не получит все карты.
Дивизия Дартс
••• Фото.com / Photos.com / Getty Images
Многие дети любят играть в дартс. Примените эту игру к делению в столбик, чтобы мотивировать учащихся овладеть процессом деления.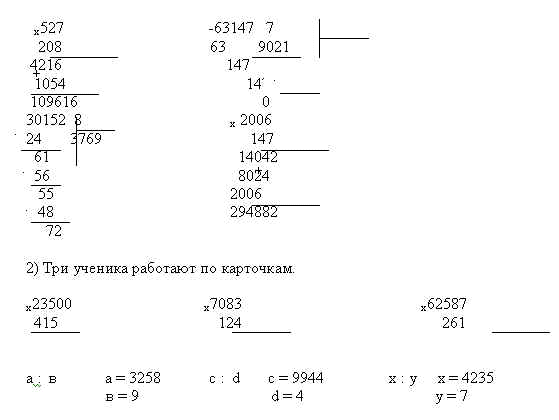
Нарисуйте на бумаге по три концентрических круга для каждой пары учеников. Выпишите 16 задач на разделение на отдельном листе, не давая ответов. Проработайте задачи на другой бумаге и напишите частные на доске для дротика в различных местах, включая одно в центральном кольце. Чтобы играть, ученики должны разрезать карточки с задачами на деление.Когда они переворачивают карточку и решают задачу деления, они должны найти частное на доске и вычеркнуть ответ. Центральный круг приносит 15 очков, следующее кольцо дает 10 очков, а внешний круг приносит 5 очков. Игрок, набравший наибольшее количество очков после того, как все карты были вытянуты, становится победителем.
Spill the Beans
••• Stockbyte / Stockbyte / Getty Images
Оставьте это на волю случая и немного бобов, чтобы увидеть, кто выиграет игру на разделение называется Spill the Beans.Помогите детям найти партнеров. Каждой команде потребуется два листа сетки. Одна сетка должна быть заполнена однозначными цифрами.
Другая сетка должна быть заполнена двузначными или трехзначными числами. В свой ход игрок бросает по одному бобу на каждую бумагу. Меньшее число нужно разделить на большее число. Частное должно быть записано в оценочной карточке. У каждого игрока есть 10 шансов бросить бобы. После последнего хода оба игрока складывают все 10 частных. Игрок с наибольшей суммой выигрывает.
Division Bingo
••• Creatas / Creatas / Getty Images
Учащиеся могут проверить свою удачу в увлекательной игре Division Bingo. Каждому ученику понадобится квадрат размером 5х5. Помогите ученикам правильно заполнить свои карточки: в первом столбце используются числа от 1 до 200, во втором столбце — числа от 201 до 400, в третьем столбце — числа от 401 до 600, в четвертом столбце — числа от 601 до 800 и последнем. столбец с числами от 801 до 1000.Назовите делитель и дивиденд. Каждый ученик должен решить задачу на макулатуре. Если учащиеся могут найти на своем листе число, которое находится в пределах 20 от частного, они могут поставить «Х» над этим числом.
Первый игрок, получивший пять крестиков подряд, становится победителем.
Интерактивные игры с длинным разделом — пошаговые задания и примеры
Наши бесплатные развивающие игры используют более 20 000 учителей и родителей, обучающихся на дому!
Отличная пошаговая игра с делением в столбик:
Возникнет проблема с длинным разделением.На каждом этапе Snork будет сообщать вам, какой расчет произвести. Введите ответ в пустой слот и переходите к следующему шагу.
Продолжайте отвечать так, и с помощью подсказок Snork вы легко решите проблему разделения.
www.thegreatmartinicompany.com
1. Заполните закрашенные блоки.Вы можете перемещаться между блоками с помощью клавиш со стрелками или щелкая мышью.
2. На каждом этапе вы можете получать немедленных отзывов для ваших ответов — просто наведите указатель мыши на символ V в левом нижнем углу, и вы увидите СИНИМ цветом ваши правильные ответы, а КРАСНЫМ — неправильные ответы.
3. Вы можете увидеть полное решение проблемы, наведя указатель мыши на символ =.
4.При нажатии на звездочку * откроется калькулятор.
5. Вы также можете установить количество цифр в задаче, щелкнув X в символе длинного деления в правом нижнем углу.
6. Щелкните символ утилизации, чтобы сбросить проблему и получить новую.
Длинное деление с трехзначным дивидендом
DivideRama
cemc2.
math.uwaterloo.ca
Нажмите кнопку «Пуск», и появится новая проблема с длинным разделением.
Решайте проблему по одной цифре. Мигающий курсор покажет вам, где ввести следующую цифру.
Если вам нужна помощь, установите флажок, где написано «Установите этот флажок для получения справки».
Вы можете исправить себя и вернуться, щелкнув мышью по цифре, которую хотите исправить.
Когда вы закончите, нажмите кнопку «Проверить ответ».
Можно установить количество цифр в делимом и делителе
Математические операции с перетаскиванием
www.mrnussbaum.com
Начните с выбора количества задач, количества цифр в делимом и количества цифр в делителе.
Введите свое имя и нажмите «Играть».
На экране появится проблема с длинным разделением. Перетащите цифры с левой стороны и аккуратно разместите их в нужных местах на листе, чтобы решить проблему. Если вы допустили ошибку, вы можете перетащить цифру за пределы рабочего листа, чтобы избавиться от нее.
Вы можете использовать небольшой калькулятор для помощи.
Когда у вас есть ответ, введите его в поле результатов вверху и нажмите кнопку «Проверить».
Эти игры ориентированы на деление в столбик и могут стать прекрасным подспорьем для учителей, которым нужны интерактивные интерактивные занятия для своих учеников.
Независимо от того, является ли студент абсолютным новичком в делении на столбики или изучает его в течение некоторого времени, он найдет здесь что-то ценное для своей учебы.
В каждом упражнении есть множество математических задач, которые представлены в простом, удобном для чтения формате, который детям понравится и увлекателен, и который очень способствует усвоению материала.
Инструкции для каждого модуля представлены пошагово, чтобы избежать путаницы, и содержат несколько примеров, чтобы учащиеся быстро усвоили концепции и начали работать над решением проблем.
Многие задания предлагают обратную связь, сообщая учащимся о неправильных ответах, чтобы они могли попробовать еще раз.Игры на этой странице в основном предназначены для учеников 4-х классов.
Стратегии разделения для 5-го класса
Вы боитесь преподавать разделение каждый год? Раньше я был в этом лагере. Мои ученики много боролись с делением, потому что им не хватало чувства числа и концептуального понимания.
Однако, к счастью, я понял, что так быть не должно. Я могу использовать стратегии разделения, которые не только подходят для развития, но и имеют смысл для моих учеников.
Фактически, как только я отказался от стандартного алгоритма в качестве моей стратегии деления, мои ученики начали осваивать деление влево и вправо. Некоторые все еще боролись? Да. К сожалению, ни одна из стратегий или советов, которыми я делюсь, не станет волшебной пилюлей, но они сделают разделение доступным и концептуальным для ваших учеников.
Частные частные с помощью Easy Breezy Math
Частные частные изменили правила игры для моих учеников. Частные частные — это стратегия деления, которая использует фрагменты для более эффективного многократного вычитания групп делителя.
Но мне пришлось добавить эшафот для моих учеников. Мы называем этот эшафот нашей «Легкой и легкой математикой». По сути, мы берем известное нам умножение и списываем их в сторону. Мы устраняем эти проблемы, чтобы помочь нам решить проблему.
Мы делаем это, потому что моим ученикам действительно не хватает чувства деления в начале года. Это также помогает им увидеть связь между умножением и делением.
По мере того, как год идет, они выйдут за рамки простой простой математики, поскольку они разовьют чувство числа и начнут видеть закономерности.
Совет: напомните им сложить множители вертикально в их Easy Breezy Math. Иногда я даю своим ученикам доски специально для этого, чтобы сделать их более интересными.
Чтобы получить более подробную информацию об этом методе разделения и получить помощь бесплатно, щелкните здесь.
Если эта стратегия для вас нова и вам нужно увидеть ее в действии, то посмотрите это видео и песню.
Коробочная модель или блочный метод с частичными частными
Box Model Division 1 была для меня новинкой год назад и работает лучше всего, когда студенты знакомы с использованием этого типа органайзера при умножении на частичные произведения.
Этот тип стратегии деления похож на частичное частное, но организован иначе.
Если это для вас в новинку, то посмотрите видео, на котором учитель и ее класс проходят этапы. Этот метод лучше всего «увидеть в действии», а не читать о нем.
Это видео длиннее, но оно отлично помогает учителям понять стратегию деления и послушать некоторый язык, чтобы помочь ученикам понять его.Примечание. Часть работы What I Know совпадает с тем, что я называю « Easy Breezy Math. ”
Я настоятельно рекомендую представить эту стратегию (и действительно любую стратегию, но определенно эту) в контексте проблемы со словом, чтобы помочь студентам осмыслить стратегию и действительно понять, что происходит. Полезно называть делимое и делитель в зависимости от контекста.
Советы для преподавателей дивизиона (с любой стратегией деления)
1.
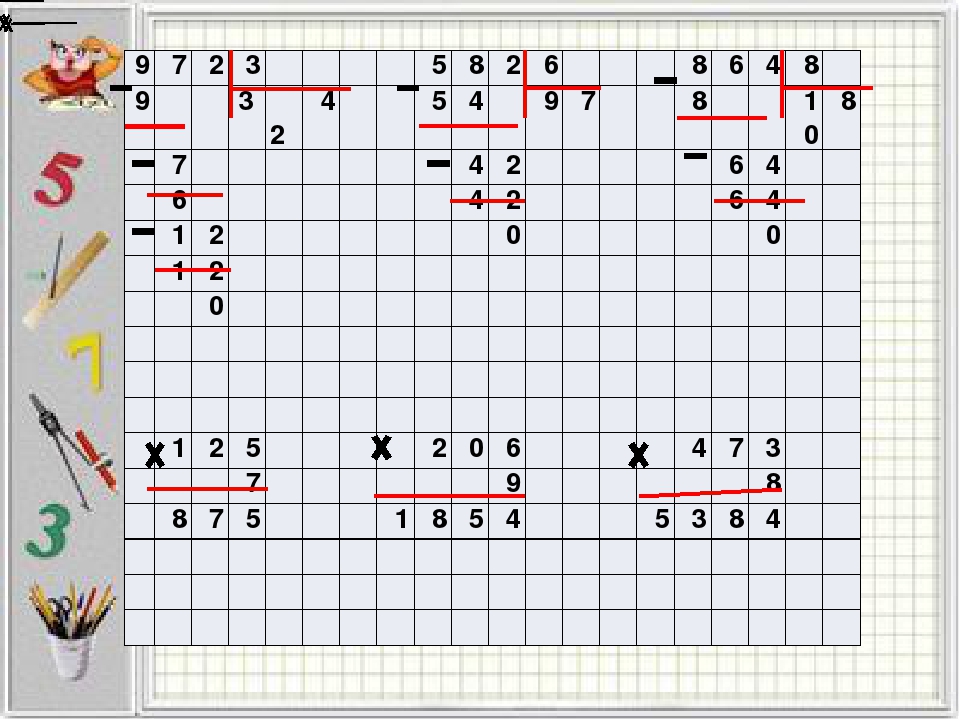) Представьте новые стратегии с увлекательным контекстом или проблемой со словом. По мере того, как вы проходите этапы стратегии, проходите через то, что может происходить в проблеме.
2.) Если эти стратегии совершенно новые, то потратьте день (или больше) с однозначными делителями, прежде чем переходить к двузначным делителям. Это будет того стоить!
3.) Убедитесь, что учащиеся понимают цель Easy Breezy Math, если вы решите использовать эту платформу. Кроме того, убедитесь, что они понимают, что это значит и как работает (в нем представлены частичные коэффициенты, которые уже готовы для учащихся на выбор).
4.) Научите студентов проверять свои ответы умножением. Это поможет им в самооценке и позволит им обнаруживать небольшие ошибки, которые они допускают при вычитании или другие ошибки вычислений.
А как насчет традиционного алгоритма деления?
Поскольку в моем штате используется общее ядро, я не преподаю традиционный алгоритм деления в рамках учебной программы пятого класса.
Однако после государственного тестирования мы делаем предварительный просмотр математики в шестом классе. В то время я всегда усиленно учил традиционный алгоритм.К этому моменту у моих учеников есть четкое понимание деления и лучшее чувство чисел. Это помогает им освоить алгоритм. Кроме того, я обнаружил, что многие учителя шестого класса ожидают, что они знают традиционный алгоритм, поэтому я определенно не хочу, чтобы мои ученики отставали, когда они пойдут в среднюю школу.
Требуется БОЛЬШЕ ресурсов для подразделения?
БЕСПЛАТНЫЕ печатные формы для тренировок «Дивизион»: Щелкните здесь, чтобы получить бесплатный пакет печатных материалов для «Дивизиона дня». Я использую их для утренней работы, проверки математики или домашних заданий после того, как ученики выучили деление и им нужно развить беглость речи и продолжить практику.
Дополнительные ресурсы отдела: У меня также есть пакет отдела, который содержит печатные формы, простые центры, карточки задач и оценки.
Ресурсы не требуют какой-либо конкретной стратегии, поэтому вы можете выбрать стратегии, которые вы хотите, чтобы ваши ученики применяли, или позволить им выбирать. Щелкните здесь, чтобы просмотреть дополнительные ресурсы Division в моем магазине Teachers Pay Teachers.
Используете ли вы какую-либо из этих стратегий разделения? Вы используете другую стратегию разделения? Дайте мне знать в комментариях.Я всегда ищу новые стратегии разделения для 5-го класса!
Как сделать длинное деление с двумя цифрами + пример
В сегодняшнем посте мы собираемся объяснить
, как решить двузначное деление.Прежде чем приступить к изучению решения двузначного деления, важно, чтобы вы познакомились с этими терминами, потому что мы будем использовать их позже.
Дивиденд: делимое число.
Делитель: число, на которое делится дивиденд.
Частное: результат деления.
Остаток: сумма, оставшаяся после разделения.
Как только вы это увидите, вы знаете, где разместить каждое число в делении. Теперь нам нужно выполнить следующие шаги:
- Возьмите первые цифры делимого, то же количество цифр, что и у делителя. Если число, взятое из делимого, меньше делителя, вам нужно взять следующую цифру делимого.
- Разделите первое число делимого (или два первых числа, если на предыдущем шаге была принята другая цифра) на первую цифру делителя. Запишите результат этого деления через частное.
- Умножьте цифру частного на делитель, запишите результат под делимым и вычтите его. Если вы не можете, потому что дивиденд меньше, вам придется выбрать меньшее число в частном, пока оно не будет вычитаться.
- После вычитания отбрасывает следующую цифру делимого и повторяет действия, начиная с шага 2, до тех пор, пока в делимом не останется больше чисел.
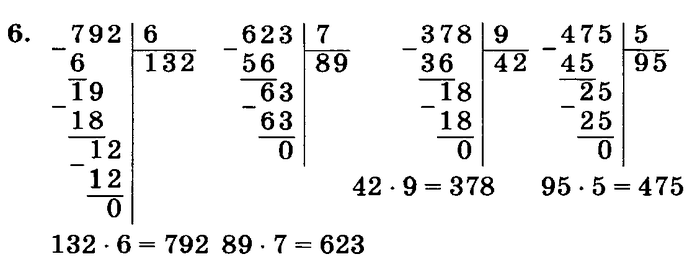
В этом суть концепции, но мы рассмотрим ее на примере.
Мы собираемся решить следующее двузначное деление:
- Возьмите первые цифры делимого: в данном случае 57. Но поскольку 57 меньше 73, вам нужно взять еще одну цифру: 573.
- Чтобы разделить 573 на 73, мы берем первые две цифры делимого: 57 и делим их на первую цифру делителя:
57 ÷ 7 = 8
- Запишите 8 в частном и умножьте его на делитель:
8 x 73 = 584
Но 584 больше 573; следовательно, 8 «не подходит».Вам нужно выбрать предыдущее число и снова умножить:
7 х 73 = 511
511 меньше дивиденда; поэтому 7 «подходит». Мы пишем 511 под цифрами делимого, а затем делим и вычитаем:
- Отбросьте следующую цифру делимого, которая равна 8. Теперь вам нужно разделить 628 на 73. Повторите предыдущие шаги:
Разделите первые две цифры делимого на первую цифру делителя и запишите его вместо частного:
62 ÷ 7 = 8
Умножьте эту цифру на делитель:
8 х 73 = 584
584 меньше 628; следовательно, мы можем вычесть:
628–584 = 44
Результат этого деления — 78, а остатка — 44.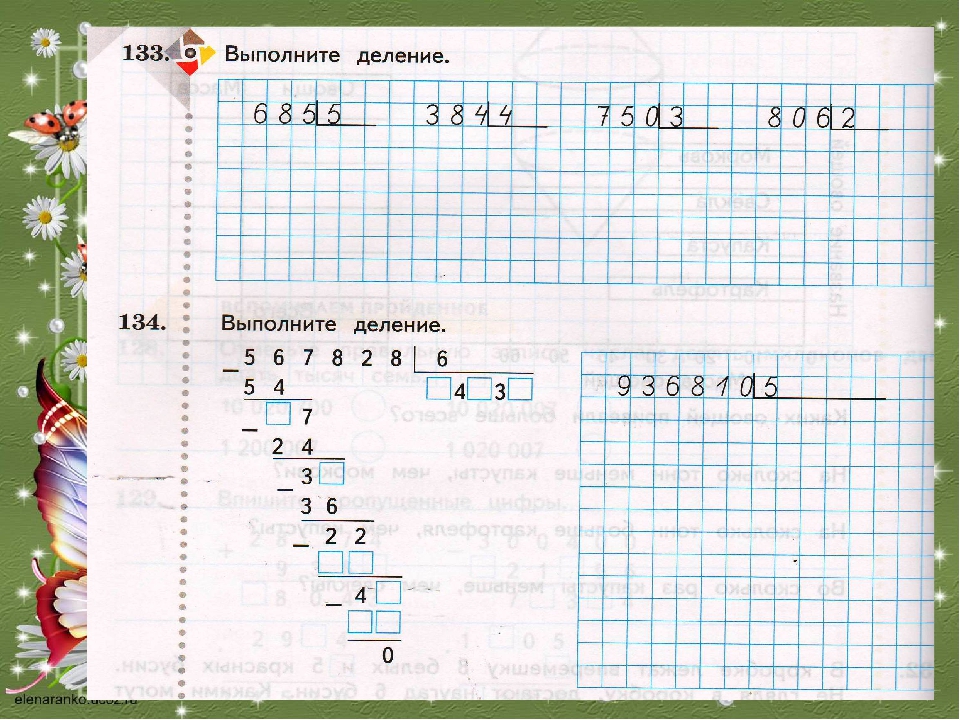
Я надеюсь, что в этом посте вы узнали, как делать двузначное деление.
Не стесняйтесь оставлять свои комментарии!
А если вы хотите узнать больше о математике, войдите в Smartick
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Как разделить по распределительной собственности.Пошаговые примеры и практические задачи
Как показывает приведенный выше пример деления в столбик, мы можем «разделить» дивиденд (693) на сумму и распределить наше деление по одному по каждой части.
Задача 1
Посмотрим, сможешь ли ты разобраться в следующем примере?
Показать ответ В этом случае мы разделяем дивиденд 964 на 900 + 60 + 4, и каждую часть делим на 3, а затем в конце суммируем их все.
Задача 2
Давайте посложнее … и добавим нули!
Показать ответВ этом случае мы разделяем дивиденд 401 на 400 + 0 + 1, и каждую часть делим на 4, а затем в конце суммируем их все.
Задача 3
А как насчет 4-значного числа?
Показать ответ В этом случае мы делим дивиденд 6 937 на 6000 + 900 + 30 + 7, и каждую часть делим на 3, а затем в конце суммируем их.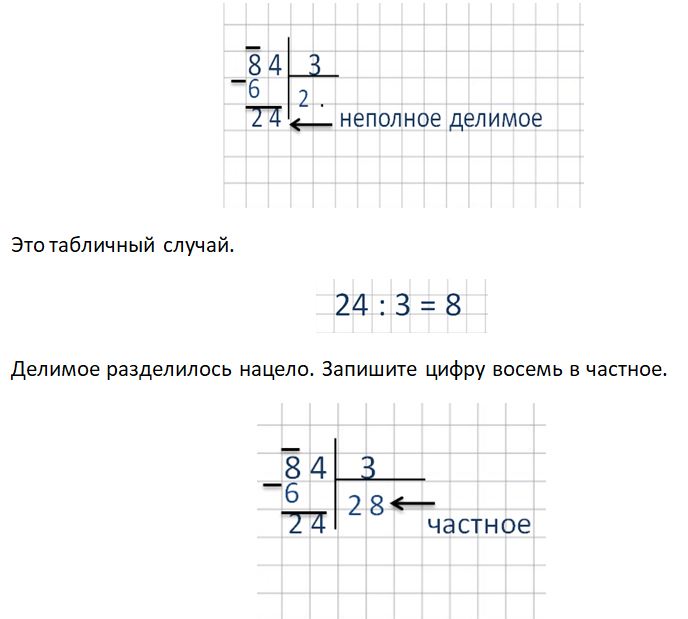
А как насчет переноски?
Все задачи, которые мы сделали до сих пор, не связаны с переносом остатков от одной части к другой.
Например, в предыдущей задаче $$ 6837 \ div 3 $$ наш делитель 3 равномерно разделен на следующие части.
- $$ 6,000 \ div 3 $$ дает нам хорошее четное частное 2,000.
- $$ 900 \ div 3 $$ дает 300.
- $$ 30 \ div 3 $$ дает 10.
Остаток вступает в игру только в самой последней части 7 . То же самое происходит с первой проблемой, которую мы сделали.
Или посмотрите на первую задачу, которую мы сделали, наш делитель 3 равномерно разделен на каждую часть.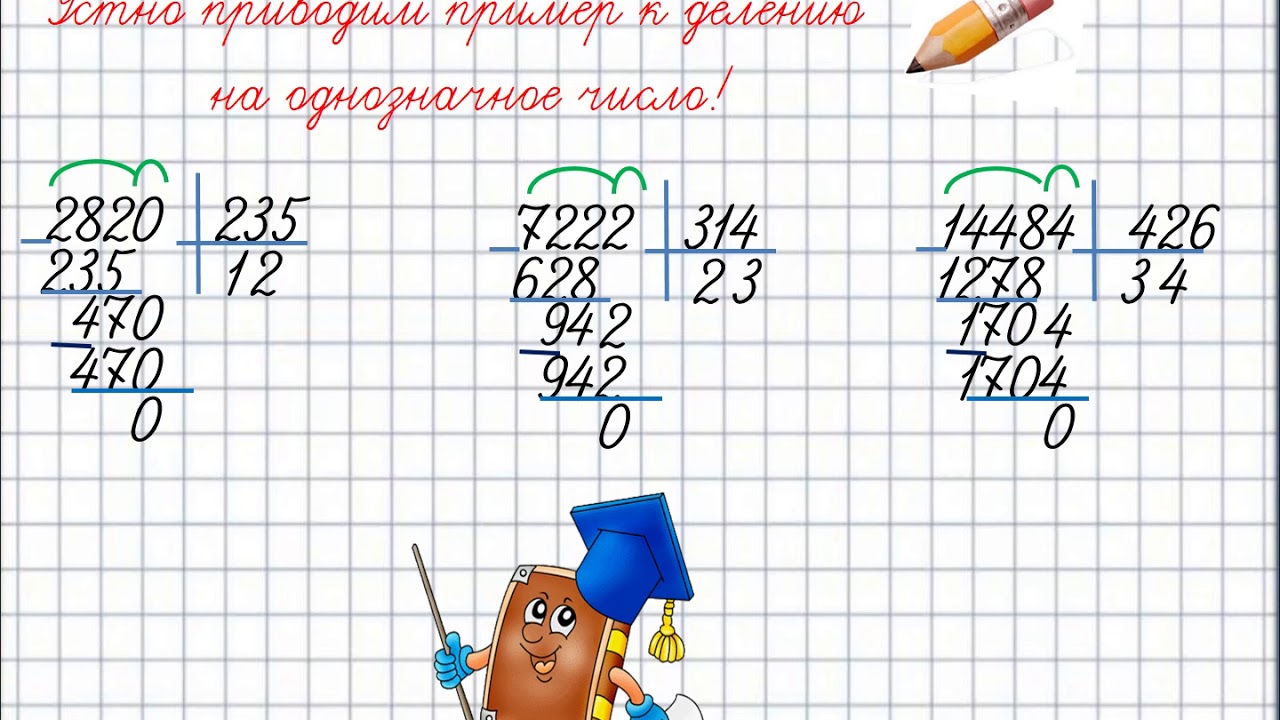
$$ 900 \ div 3 $$ дает нам хорошее четное частное 300, а $$ 600 \ div 3 $$ дает ровно 200 и т. Д.
Что если мы изменим
на одну цифру ?Мы собираемся заменить первую цифру из нашей первой задачи на одну.
Задача 4 (с переноской)
Давайте возьмем наш старый вопрос 1 и изменим первую цифру. Как нам теперь к этому подойти?
Задача 5
Что такое $$ 754 \ div 3 $$ при использовании метода распределения в столбик?
Показать ответОтвет:
Задача 6
Что такое $$ 806 \ div 3 $$ при использовании метода распределения в столбик?
Показать ответОтвет:
Задача 7
Что такое $$ 234 \ div 7 $$ при использовании метода распределения в столбик?
Показать ответОтвет:
Эта страница предназначена для родителей или других взрослых (например, владельца этого веб-сайта), которые пытаются помочь детям младшего возраста научиться работать с некоторыми из новых способов, которыми школы учат детей выполнять традиционное деление в столбик и работать с числами.
с остатками
Использование калькулятора
Разделите два числа, делимое и делитель, и найдите ответ как частное с остатком. Узнайте, как решать задачи деления в столбик с остатками, или попрактикуйтесь в решении собственных задач деления в столбик и используйте этот калькулятор, чтобы проверить свои ответы.
Деление в столбик с остатками — это один из двух методов ручного деления в столбик.Это несколько проще, чем решить задачу деления, найдя частный ответ с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш Калькулятор длинного деления с десятичными знаками.
Какие части подкласса
Для предложения деления 487 ÷ 32 = 15 R 7
- 487 — дивиденд
- 32 — делитель
- 15 — это частная часть ответа
- 7 — это оставшаяся часть ответа
Как сделать длинное деление с остатками
Из приведенного выше примера разделим 487 на 32, показывая работу.
Поместите 487, делимое, на внутреннюю часть скобки. Дивиденд — это число, которое вы делите.
Поместите делитель 32 на внешнюю сторону кронштейна. Делитель — это число, на которое вы делите.
4, разделенное на 32, равно 0, а остаток равен 4. Остаток пока можно проигнорировать.
Поместите 0 на верхнюю часть скобки деления.Это начало частного ответа.
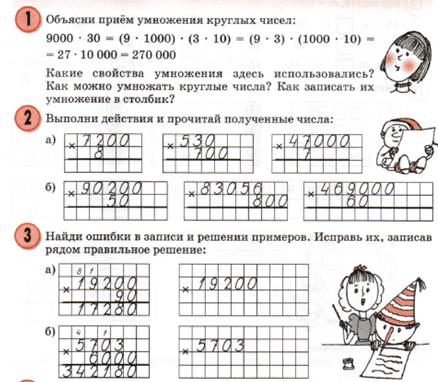
Затем умножьте 0 на делитель 32 и вставьте результат 0 под первым числом делимого внутри скобок.
0 * 32 = 0
Проведите линию под 0 и вычтите 0 из 4.4 — 0 = 4
Опустите следующее число делимого и вставьте его после 4, чтобы получилось 48.
Разделите 48 на делитель 32. Ответ: 1. Остаток пока можно проигнорировать.48 ÷ 32 = 1
Обратите внимание, что вы можете пропустить все предыдущие шаги с нулями и сразу перейти к этому шагу.
Вам просто нужно понять, сколько цифр в дивиденде вам нужно пропустить, чтобы получить первое ненулевое значение в ответе на частное.В этом случае вы можете сразу разделить 32 на 48.
1 * 32 = 32
Проведите линию и вычтите 32 из 48.48 — 32 = 16
Выполните следующее число из делимого и вставьте его после 16, чтобы получилось 167.
Разделите 167 на 32.
Видите, как возникает закономерность?167 ÷ 32 равно 5 с остатком 7
Поместите цифру 5 вверху полосы деления справа от единицы.Умножьте 5 на 32 и запишите ответ под 167.5 * 32 = 160
Проведите линию и вычтите 160 из 167.167 — 160 = 7
Поскольку 7 меньше 32, деление в столбик сделано.У вас есть свой ответ: частное равно 15, а остаток равен 7.Итак, 487 ÷ 32 = 15 с остатком 7
Для более длинных дивидендов вы должны продолжать повторять шаги деления и умножения, пока вы не уменьшите каждую цифру из divdend и не решите проблему.
Дополнительная литература
в Спросите доктораМатематика вы можете найти Инструкции по длинному делению для простых и более сложных задач.
Math is Fun также предоставляет пошаговый процесс деления в столбик с Длинное деление с остатками.
Калькулятор длинного деленияс пошаговой работой
Запишите частное и остаток для 9452, разделенное на 11, используя метод длинного деления.
Приведенный ниже решенный пример длинного деления 4 на 2 цифры с остатком может быть полезен для понимания того, как делать длинное деление вручную для задач, связанных с заданиями, классными и домашними заданиями.
- Расположите 4-значное делимое и 2-значное делительное число для метода длинного деления и сравните, больше ли первые две цифры делимого 9452, чем делитель 11.
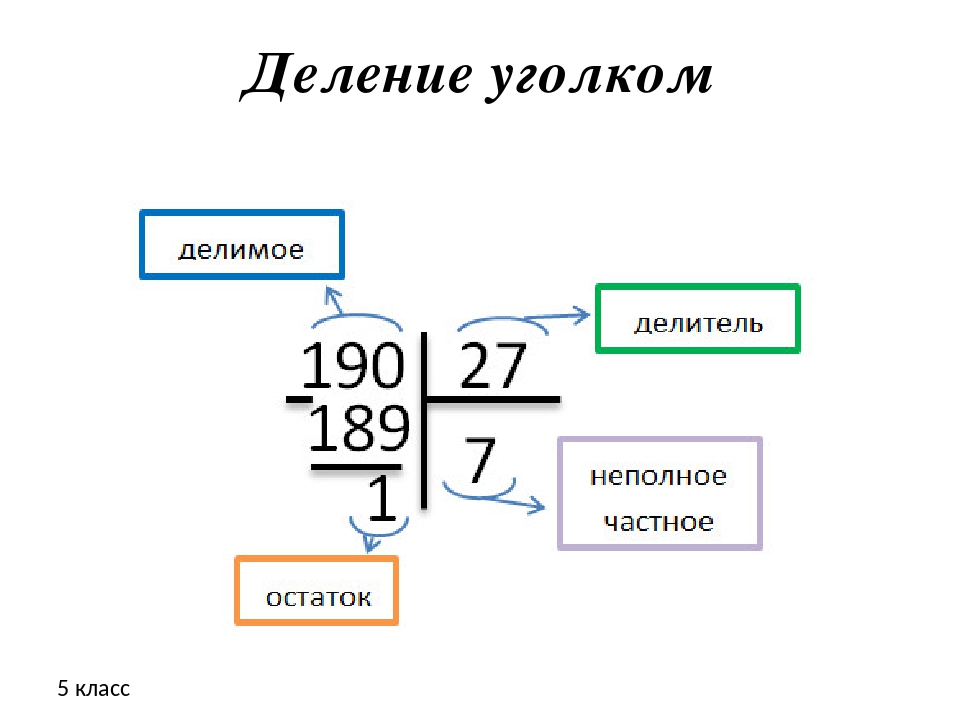
- Проверьте, сколько раз делитель может быть помещен в число 94, и запишите значение как часть частного.Делитель 11 может быть 8 раз помещен в 94. Запишите 8 как наиболее значимую цифру частного.
- Найдите разницу между 94 и произведением 8 и 11, если есть. 6 — разница между 94 и 88.
- Опустите третью цифру начального делимого и добавьте (не прибавляя) ее к правой части остатка 6, чтобы сформировать новый дивиденд. Следовательно, новый дивиденд равен 65 .
- Сравните, больше ли новый дивиденд 65, чем делитель 11, и проверьте, сколько раз делитель может быть помещен в новый дивиденд, образованный понижением 3-й цифры.Делитель 11 можно разместить 5 раз в 65. Добавьте значение 5 (количество раз) прямо к предыдущему частному 8. Следовательно, остаток теперь равен 85.
- Найдите разницу между 65 и произведением 5 и 11, если таковая имеется. 10 — разница между 65 и 55.
- Опустите и добавьте 4-ю цифру 2 к правой части более ранней разницы 10. Следовательно, новое делимое станет 102.
- Проверьте, сколько раз делитель 11 может быть включен в новый дивиденд, образованный понижением 4-й цифры.Делитель 11 может быть размещен 9 раз в 102. Добавьте значение 9 (количество раз) прямо к предыдущему частному 85. Следовательно, остаток теперь равен 859.
- Проверьте разницу между 102 и произведением 11 и 9. Из-за того, что больше нет цифр для уменьшения, окончательная разница 3 представляет собой десятичный остаток от дивиденда 9452, деленный на 11.
Следовательно, новое делимое станет 102.