Пример столбиком – Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.

Умножение столбиком. Примеры умножения в столбик, нахождения решения онлайн.

Нахождение произведения чисел

Метод умножения столбиком, позволяет упростить умножения чисел. Умножение столбиком предполагает последовательное умножения первого числа, на все цифры второго числа последующего сложения полученных произведений с учетом отступа, зависящего от положения цифры второго числа.

Рассмотрим как нужно умножать столбиком на примере нахождения произведения двух чисел 625 × 25.

• 1 Запишем числа одно под другим и проведем черту .
• 2 Число 25, состоит из 2 цифр, 2 и 5, будем умножать первое число 625, на цифры второго числа в обратном порядке. Начнем вычисление с нахождения произведения 625 × 5, запишем результат ниже черты, начинаем запись с правой стороны, получим: .
• 3 Теперь умножаем 625 на 2, и запишем результат на следующей строке, сместив запись на одну клетку левее, предыдущего произведения, получим .

  При большем количестве цифр во втором числе, мы получим что наши произведения выстраиваются справа в виде «лесенки».
• 4 В результате умножения получаем 2 произведения, 3125 и 1250, будем последовательно справа на лево складывать их цифры между собой, в том порядке как они идут, и записывать результат их сложения ниже. Если сумма цифр при сложение превысит 9, то делим сумму на 10, остаток от деления записываем под текущими цифрами, а целую часть от деления перенесем влево.
  В результате получаем .

Пример Умножить столбиком числа 687 и 253.

calcs.su

Сложение столбиком

Метод сложения столбиком, позволяет упростить сложения чисел. Сложение столбиком предполагает

последовательное сложения цифр первого и второго числа, складывают числа справа налево, начиная с единиц, потом десятки, сотни и т.д.

Рассмотрим как нужно складывать столбиком на примере нахождения суммы двух чисел 437 и 276.

• 1 Запишем числа одно под другим и проведем черту .
• 2 Складываем единицы, получаем:

  .

  Если в результате сложения цифр чисел получили двухзначное число 13, следовательно десяток переносим в следующий разряд, а 3 записываем в результат.

• 3 Складываем десятки чисел плюс перенесенную единицу, получим:

  .

  складывать
• 4 Складываем сотни чисел плюс перенесенную единицу, получим:

  .

Пример Сложить столбиком числа 304 и 58.

calcs.su

Умножение и деление в столбик: примеры

Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Советы тем, кто хочет хорошо знать математику

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

• Записать эти дроби нужно так, чтобы число 33 было под 25.
• Теперь правую тройку нужно умножить на 25. Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
• Потом умножать 25 на первую 3. Опять будет 75, но написано оно будет так, чтобы 5 оказалось под 7 предыдущего числа.
• После сложения этих двух чисел получается 825. В десятичных дробях запятыми отделены 4 цифры. Поэтому в ответе нужно отделить запятой тоже 4 цифры. Но их всего три. Для этого перед 8 придется написать 0, поставить запятую, перед ней еще один 0.
• Ответом в примере окажется число 0,0825.

С чего начать обучение делению?

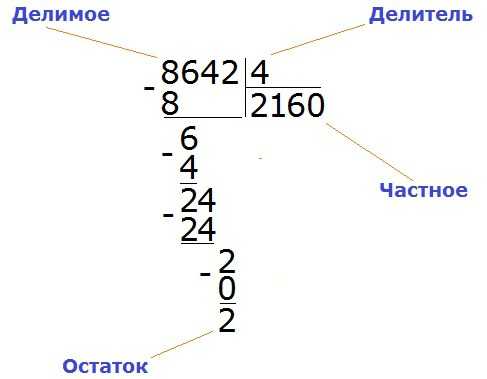
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него — делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082 : 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

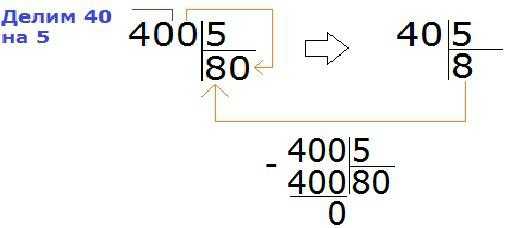
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

fb.ru

Сложение столбиком. Запись сложения столбиком. Онлайн калькулятор

При сложении однозначных чисел удобно использовать таблицу сложения, но желательно, конечно, знать результаты сложения однозначных чисел наизусть.

Многозначные числа складываются по разрядам, используя переместительный и сочетательный законы сложения. Например:

25 + 61 = (20 + 5) + (60 + 1) = 20 + 5 + 60 + 1 =

= (20 + 60) + (5 + 1) = 80 + 6 = 86

Такая запись слишком длинная и неудобная, поэтому сложение многозначных чисел обычно выполняется столбиком.

Сложение столбиком – это способ записи сложения, используемый при сложении чисел, состоящих из двух и более цифр. Сложение столбиком также называют сложением чисел в столбик.

Запись сложения столбиком

Рассмотрим запись сложения столбиком и вычисление суммы чисел на примере:

25 + 61

Чтобы сложить два числа столбиком, надо одно число записать под другим так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). То есть, при сложении столбиком, самая правая цифра одного числа должна располагаться под самой правой цифрой другого числа:

Обратите внимание, что мы записали меньшее число под большим это делается только для удобства вычисления суммы.

Затем, слева между числами ставится знак плюс, а под нижним слагаемым проводят горизонтальную черту:

Вычисление начинают с разряда единиц: складываем 1 + 5 = 6, результат записываем под чертой под единицами:

Теперь складываем разряд десятков: 6 + 2 = 8, результат записываем под чертой под десятками:

У нас получилось число 86, которое можно записать в исходный пример:

25 + 61 = 86

Рассмотрим ещё один пример: сложить два трёхзначных числа 735 и 426 столбиком.

Сначала запишем числа друг под другом, поставим слева знак плюс и проведём под нижним слагаемым черту:

Начинаем складывать с единиц: 5 + 6 = 11. Так как число 11 состоит из 1 десятка и 1 единицы, то под разрядом единиц мы запишем число 1, а один десяток можно либо держать в уме, либо подписать над разрядом десятков:

Складываем десятки: 3 + 2 = 5. К этим 5 десяткам надо прибавить ещё один, который мы получили при сложении единиц: 5 + 1 = 6, результат записываем под разрядом десятков:

Осталось сложить сотни: 7 + 4 = 11, 11 сотен это 1100 единиц, то есть у нас получилась одна сотня и одна тысяча. Под разрядом сотен записываем 1 и ещё одну единицу записываем в разряд тысяч:

На этом нахождение суммы окончено и можно записать сложение в обычном виде:

735 + 426 = 1161

Калькулятор сложения столбиком

Данный калькулятор поможет вам выполнить сложение столбиком. Просто введите слагаемые и нажмите кнопку Вычислить.

naobumium.info