10 увлекательных задач от советского математика
12 сентября 2021Отдых
Попробуйте решить головоломки от популяризатора математики Бориса Кордемского, не пользуясь подсказками.
Поделиться
01. Переправа через реку
Небольшой воинский отряд подошёл к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Каким образом?
Показать ответ
Скрыть ответ
2. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить ещё одну заготовку. Сколько деталей можно сделать таким образом из тридцати шести свинцовых заготовок?
Показать ответ
Скрыть ответ
3.
Во время приливаНедалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы десять ступенек; расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды.
Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через какое время покроется водой третья ступенька верёвочной лесенки?
Показать ответ
Скрыть ответ
4. Девяносто девять
Сколько нужно поставить знаков «плюс» (+) между цифрами числа 987 654 321, чтобы в сумме получилось 99?
Показать ответ
Скрыть ответ
5. Для Цимлянского гидроузла
В выполнении срочного заказа по изготовлению измерительных приборов для Цимлянского гидроузла приняла участие бригада в составе опытного бригадира и девяти молодых рабочих.
В течение дня каждый из юных рабочих смонтировал по 15 приборов, а бригадир — на 9 приборов больше, чем в среднем каждый из десяти членов бригады. Сколько всего измерительных приборов было смонтировано бригадой за один рабочий день?
Показать ответ
Скрыть ответ
6.
Попробуйте отвеситьВ пакете находится 9 кг крупы. Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Показать ответ
Скрыть ответ
7. Смышлёный малыш
Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:
— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.
Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну.
Сколько же лет было малышу и каждому из остальных братьев?
Показать ответ
Скрыть ответ
8. Раздробить на части
Раздробите 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвёртую разделить на 2, то все результаты будут равными. Сумеете сделать?
Показать ответ
Скрыть ответ
9. Посадка деревьев
Пятиклассникам и шестиклассникам было поручено посадить деревья по обе стороны улицы по равному количеству на каждой стороне.
Чтобы не ударить лицом в грязь перед шестиклассниками, пятиклассники вышли на работу пораньше и успели посадить 5 деревьев, пока пришли старшие ребята, но оказалось, что они сажали деревья не на своей стороне.
Пришлось пятиклассникам идти на свою сторону и вновь начинать работу. Шестиклассники, конечно, справились с задачей раньше. Тогда учитель предложил:
— Пойдём, ребята, поможем пятиклассникам!
Все согласились. Перешли на другую сторону улицы, посадили 5 деревьев, отдали, значит, долг, да ещё успели посадить 5 деревьев, и вся работа была закончена.
— Хоть вы пришли раньше нас, а всё-таки мы вас обогнали, — посмеялся один шестиклассник, обращаясь к младшим ребятам.
— Подумаешь, обогнали! На 5 деревьев только, — возразил кто-то.
— Нет, не на 5, а на 10, — зашумели шестиклассники.
Спор разгорался. Одни настаивают на том, что на 5, другие пытаются как-то доказать, что на 10. Кто же прав?
Показать ответ
Скрыть ответ
10. Четыре теплохода
В порту пришвартовались 4 теплохода. В полдень 2 января они одновременно покинули порт. Известно, что первый теплоход возвращается в этот порт через каждые 4 недели, второй — через каждые 8 недель, третий — через 12 недель, а четвёртый — через 16 недель.
Когда в первый раз теплоходы снова сойдутся все вместе в этом порту?
Показать ответ
Скрыть ответ
Задачи для этой подборки взяты из сборника «Математическая смекалка» Бориса Кордемского, который выходил в издательстве «Альпина Паблишер».
Читайте также 🔥
- 15 занимательных задач для тренировки ума и сообразительности
- 11 хитрых советских головоломок для проверки логики и сообразительности
- 5 задач, которые предлагают решить на собеседованиях в Google и других компаниях
Нестандартные задачи по математике для 3 класса.
Задачи по математике 3 класс.
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
Задача 1
Сколько может быть трехзначных чисел все цифры, которых это 1, 2 или 3.
Решение:
- Первым может быть любое из этих 3-цифр на второе тоже, следовательно, два первых места могут быть заняты девятью способами: 11, 12, 13, 21, 22, 23, 31, 32, 33. В каждом из вышеописанных случаев третье место можно занять любой из этих трех цифр. Следовательно, все число можно записать двадцатью семью различными вариантами от 111 до 333.
- Короче данное решение можно выразить следующим образом: первой может быть любая из этих 3-х цифр, второй может быть любая из этих 3-х цифр, третей может быть любая из этих 3-х цифр. Поэтому этих чисел всего 3 * 3 * 3 = 27.
- Ответ: 27.
Задача 2.
Оксана нашла один гриб, Катя – два, Наташа – три. Мама дала им 18 конфет и предложила разделить их по заслугам. Сколько конфет должна получить каждая девочка?
Решение:
- Наташа собрала половину всех грибов, поэтому она должна получить половину конфет — 9. Катя должна получить вдвое больше конфет, чем Оксана, потому что она собрала вдвое больше чем Оксана грибов, следовательно, Оксана должна получить 3 конфеты, а Катя 6.
- Ответ: Наташа – 9, Катя – 6, Оксана – 3.
Задача 3.
На какое число нужно разделить разницу наибольшего трехзначного числа и наибольшего двухзначного числа, чтобы получить однозначное число?
Решение:
- (999 – 99) : 100 = 9
- Ответ: 100.
Задача 4.
За 4 дня велосипедисты проехали 88км.
Сколько километров они проехали в первый день, если каждый следующий день они проезжали на 2км. меньше чем в предыдущий?
Решение:
- За второй день велосипедисты проехали на 2км. меньше чем за первый, за третий на 4км., за четвертый на 6км меньше чем за первый. Если бы каждый день велосипедисты проезжали столько километров, сколько за первый день, то за четыре дня они бы проехали 88 + 2 + 4 + 6 =100км. Значит за первый день они проехали 100 : 4 = 25км.
Задача 5.
Улитка решила поползти по дереву вверх. За день она проползала шесть метров. А за ночь спускалась на четыре метра. За сколько она доползет до верхушки дерева, если высота этого дерева четырнадцать метров?
Решение:
- Утром второго дня он будет на высоте 6 – 4 = 2м. вечером на высоте 2 + 6 = 8м. Утром на третий день он будет на высоте 8 – 4 = 4м. вечером на высоте 4 + 6 = 10м. На четвертый день утром на высоте 10 – 4 = 6м.
вечером на 6 + 6 = 12м. На пятый день на высоте 12 – 4 = 8м вечером 8 + 6 = 14м – высота нашего дерева.
Ответ: к концу пятого дня.
вечером на 6 + 6 = 12м. На пятый день на высоте 12 – 4 = 8м вечером 8 + 6 = 14м – высота нашего дерева.Задача 6.
Первого февраля 1999 года был понедельник. Каким днем недели было 1 марта 1999 года?
Решение:
- Сколько дней разделяет первое февраля 1999года и первое марта 1999года, учитывая, что 1999год не високосный, то это 28 дней? Далее смотрим какой день недели, если у нас был понедельник прибавляем 28 дней(ровно 4 недели), следовательно день также будет понедельник.
- Ответ: понедельник.
Задача 7.
Запишите трехзначное число, у которого каждая последующая цифра больше предыдущей втрое.
Решение:
- Ответ: 139 единственное число, удовлетворяющее условиям задачи.
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
5 простых математических задач, которые никто не может решить
Введите ключевые слова для поискаГлавные новости дня
1
Запустит ли Россия свою торпеду «Апокалипсис»?
2
Мы могли бы жить в компьютере пришельца-подростка
3
Сможете ли вы разгадать загадку о колоде карт?
4
Тайны единственного животного, которое может жить в космосе
5
Как помыть автомобиль без воды
Редакторы, одержимые Gear, выбирают каждый продукт, который мы рассматриваем.
Мы можем заработать комиссию, если вы покупаете по ссылке.
Как мы тестируем снаряжение.
Легко понять, в высшей степени трудно доказать.
По Эйвери Томпсон
Justin LewisGetty Images
Математика может быть довольно сложной. К счастью, не все математические задачи должны быть неразрешимыми. Вот пять актуальных задач в области математики, которые может понять каждый, но решить пока не удалось никому.
Гипотеза Коллатца
Джон МакЛун
Выберите любой номер. Если это число четное, разделите его на 2. Если оно нечетное, умножьте его на 3 и прибавьте 1. Теперь повторите процесс с новым числом. Если вы продолжите, вы в конечном итоге окажетесь на 1. Каждый раз.
Математики перепробовали миллионы чисел и так и не нашли ни одного, которое в конце концов не равнялось бы 1. Дело в том, что они никогда не могли доказать , что не существует особого числа, которое никогда не ведет к 1.
Проблема с движущимся диваном
Клаудио Роккини
Итак, вы переезжаете в свою новую квартиру и пытаетесь привезти свой диван. Проблема в том, что коридор поворачивает, и вам нужно поставить диван за угол. Если это маленький диван, это может не быть проблемой, но действительно большой диван обязательно застрянет. Если вы математик, вы спросите себя: какой самый большой диван вы могли бы поставить за углом? Это не обязательно должен быть прямоугольный диван, он может быть любой формы.
Суть задачи о движущемся диване. Вот конкретика: вся задача в двух измерениях, угол — это угол 90 градусов, а ширина коридора равна 1. Какая наибольшая двумерная область может уместиться вокруг угла?
Самая большая площадь, которая может поместиться за углом, называется — я не шучу — диваном-константой.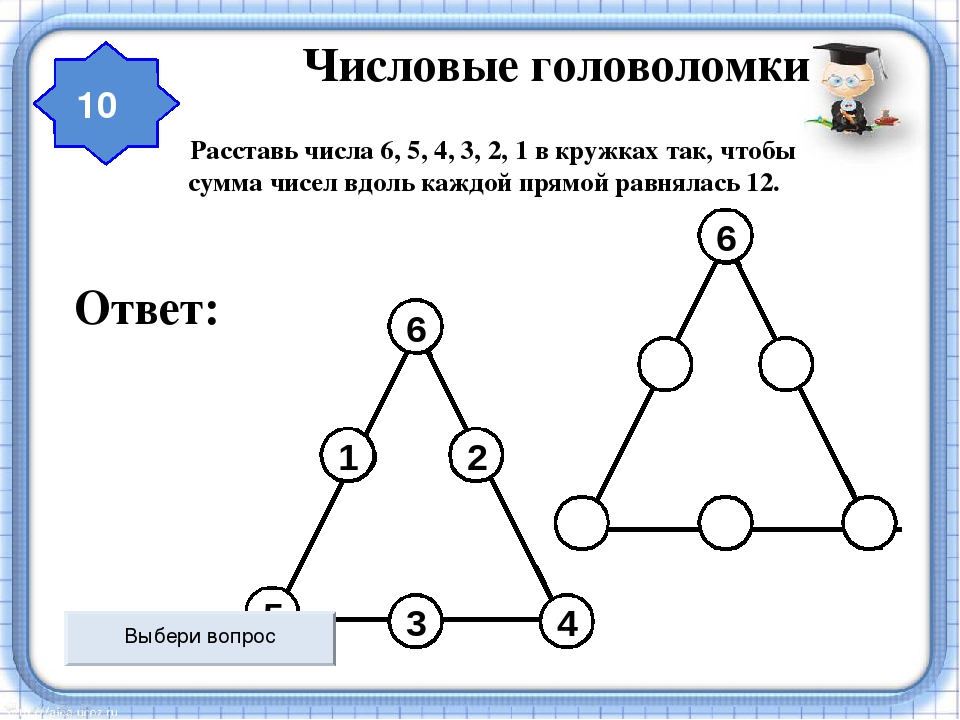
Никто точно не знает, насколько он велик, но у нас есть довольно большие диваны, которые работают, поэтому мы знаем, что он должен быть как минимум таким же большим, как они. У нас также есть несколько диванов, которые не работают, поэтому они должны быть меньше, чем те. Все вместе мы знаем, что константа дивана должна быть в пределах 2,219.5 и 2,8284.
Идеальная прямоугольная задача
Gfis
Помните теорему Пифагора, A 2 + B 2 = C 2 ? Три буквы соответствуют трем сторонам прямоугольного треугольника. В треугольнике Пифагора все три стороны — целые числа. Давайте расширим эту идею до трех измерений. В трех измерениях есть четыре числа. На изображении выше это A, B, C и G. Первые три — это размеры коробки, а G — диагональ, идущая от одного из верхних углов к противоположному нижнему углу.
Точно так же, как есть некоторые треугольники, у которых все три стороны являются целыми числами, существуют также прямоугольники, у которых три стороны и пространственная диагональ (A, B, C и G) являются целыми числами.
Но есть еще три диагонали на трех поверхностях (D, E и F), и это поднимает интересный вопрос: может ли существовать ящик, в котором все семь из этих длин являются целыми числами?
Цель состоит в том, чтобы найти ящик, в котором A 2 + B 2 + C 2 = G 2 и где все семь чисел являются целыми числами. Это называется совершенным кубоидом. Математики испробовали множество различных возможностей, но пока не нашли ни одной, которая работает. Но они также не смогли доказать, что такого ящика не существует, поэтому идет охота за идеальным прямоугольным параллелепипедом.
Задача о вписанном квадрате
Клаудио Роккини
Нарисуйте замкнутый контур. Петля не обязательно должна быть кругом, она может быть любой формы, которую вы хотите, но начало и конец должны встречаться, и петля не может пересекаться.
Должна быть возможность нарисовать квадрат внутри петли так, чтобы все четыре угла квадрата касались петли. Согласно гипотезе вписанного квадрата, каждая замкнутая петля (в частности, каждая плоская простая замкнутая кривая) должна иметь вписанный квадрат, квадрат, все четыре угла которого лежат где-то на петле.
Это уже решено для ряда других форм, таких как треугольники и прямоугольники. Но квадраты сложны, и до сих пор формальное доказательство ускользало от математиков.
Проблема со счастливым концом
Дэвид Эппштейн
Задача о счастливом конце названа так потому, что она привела к женитьбе двух математиков, которые работали над ней, Джорджа Секереса и Эстер Кляйн. По сути, проблема работает следующим образом:
Поставьте пять точек в случайных местах на листе бумаги. Предполагая, что точки не расположены преднамеренно, скажем, в линию, вы всегда должны быть в состоянии соединить четыре из них, чтобы создать выпуклый четырехугольник, который представляет собой форму с четырьмя сторонами, где все углы меньше 180 градусов.
Суть этой теоремы в том, что вы всегда сможете создать выпуклый четырехугольник с пятью случайными точками, независимо от того, где эти точки расположены.
Вот как это работает для четырех сторон. Но для пятиугольника, пятиугольника, оказывается, нужно девять точек. Для шестиугольника это 17 точек. Но кроме этого мы не знаем. Остается загадкой, сколько точек требуется для создания семиугольника или любой другой формы большего размера. Что еще более важно, должна быть формула, чтобы сказать нам, сколько точек требуется для любой формы. Математики подозревают, что уравнение имеет вид M=1+2 N-2 , где M — количество точек, а N — количество сторон фигуры. Но пока им удалось доказать только то, что ответ по крайней мере такой же большой, как ответ, который вы получаете таким образом.
Эйвери Томпсон twitter.com/physicallyavery
Удивительная математика внутри кубика Рубика
Сможете ли вы разгадать загадку о колоде карт?
Решение загадки о колоде карт
Мы могли бы жить в компьютере пришельца-подростка
Почему некоторые люди вызывают демонов сонного паралича
Радиоактивные отходы обнаружены в начальной школе
Синтетический «мозг» только что раздавил его в Pong
Земля — гигантский магнит: это причина нашего существования
Почему хилые человеческие мозги не могут понять Мультивселенную
Самая глубокая часть океана — чужой мир
Четыре странных и интересных неразрешимых математических задачи | Автор Самрат Дутта
Источник: Pexels.
У всех нас была математика в школе, но некоторые из нас выбрали академические или карьерные пути, которые больше не нуждаются в математике, а для других математика стала неотъемлемой частью их жизни. Однако все, от новичка до знатного человека, которые когда-либо касались математической задачи, согласятся, что наиболее отличительной чертой интригующей задачи является ее сложность.
По мере развития математика также становится все более и более сложной, но никогда не теряет своей первоначальной сущности. Однако даже величайшие математики сталкивались с проблемами, которые кажутся неразрешимыми и остаются таковыми до сих пор. Вот некоторые неразрешимые и почти мистические по своей сути проблемы.
Задача «Затерянный в лесу», впервые предложенная в 1955 году, была простой задачей, и это именно то, что следует из названия.
Представьте, что вы путешественник, заблудившийся в лесу, и у вас есть карта леса определенной формы, однако вы не знаете, где вы находитесь и в каком направлении смотрите – какой же тогда кратчайший путь из лес?
Что касается этой задачи, математики оказались не лучше, чем действительно заблудившийся турист.
При отсутствии конкретных факторов и переменных, на которых можно было бы основывать расчеты, теряется процесс изучения.
Математическая логика и теоремы, необходимые для решения этой задачи, если они будут изобретены, могут значительно помочь другим разделам математики. Один исследователь назвал эту задачу «задачей на миллион долларов», подразумевая, что это, возможно, одна из самых дискретных, но важных математических проблем, которые ждут своего решения.
Обычно для решения этой проблемы предлагается просто идти по прямой. Это также эффективно в реальном лесу. Однако решения во многом зависят от формы леса. Например, в случае равностороннего треугольника наилучшим возможным маршрутом будет определенная зигзагообразная линия, которая, как доказано, всегда не может уместиться внутри такого треугольника.
Эта задача также имеет определенное отношение к задаче о червях, поскольку они обратны друг другу. Если вы найдете самую маленькую форму червя, которая не помещается внутри определенной формы одеяла, то это то же самое, что найти форму кратчайшего пути, который выведет вас из леса.
По сути, то, что не работает с проблемой червя, работает с проблемой леса. Увлекательно, правда?
Представьте, что вы двигаете диван по узкому коридору. Даже если вы не выполняли задачу самостоятельно, вы можете хотя бы представить, насколько это может быть утомительно. Юмор некоторых ситкомов 90-х, безусловно, помогает этому воображению.
В любом случае, вопрос –
Какой самый большой диван (по площади), который можно сдвинуть за угол 90°, не поднимая его?
Эта проблема была впервые предложена Лео Мозером в 1966 году и до сих пор остается нерешенной. Вам может быть интересно, почему это так, ведь проблема кажется довольно простой. Ответ кроется в объективной природе математической логики.
В 1992 году математик Джозеф Гервер придумал диван в форме телефона (📞), который, казалось, был ответом. Однако, согласно вопросу, необходимо объективно доказать, что никакой другой диван любой формы и размера не может заменить этот диван.
Это должен быть абсолютно герметичный, полностью логичный аргумент, а не просто идея с большим количеством доказательств в свою пользу. Это требует противопоставления этого дивана всем возможным врагам дивана.
Для этого ученые в настоящее время проводят симуляции, но до сих пор проблема не решена. Мы только пришли к выводу, что предложение Гервера — один из самых больших диванов, а самый большой диван может быть всего на несколько процентов больше.
Мозер не остановился на диване и добавил к списку нелепых и неразрешимых задач еще одну. Этот называется «Червь Мозера». Вопрос:
Если мы предположим, что червяк-мать хочет накрыть червяка-детеныша одеялом, то какое наименьшее возможное одеяло может покрыть всего червяка независимо от его положения?
Простой ответ, который можно было бы придумать, состоит в том, чтобы сделать квадратное одеяло, каждая сторона которого в два раза длиннее червяка. Это кажется полной защитой, но того же эффекта можно добиться с помощью круглого одеяла с размером червя в качестве диаметра.
Это новое одеяло составляет всего 79% площади квадратного одеяла. Ну тогда в чем, кажется, дело? То же, что и первая проблема. Пока не будут опробованы все размеры и формы, невозможно доказать, какой размер одеяла является наименьшим из возможных.
Даже тогда ученые проводят симуляции и предсказывают, что наименьший размер одеяла должен составлять от 6% до 6,5% от изначально предложенного квадратного одеяла. Мы, конечно, надеемся, что достаточно скоро найдем применимый ответ, чтобы червь-мать мог эффективно работать, чтобы защитить своих детенышей.
Я думаю, что многие из нас слышали о магических квадратах и даже видели некоторые из них. Они представляют собой сетку чисел 4×4, где каждая строка, столбец и диагональ составляют одно и то же число. Магические квадраты были обнаружены в древних текстах и реликвиях со всей Индии, Китая и других частей Юго-Восточной Азии и даже в некоторых частях Европы. Следовательно, это то же самое, что сказать, что это не ново.
Задача о магических квадратах здесь относится к задаче «квадрат квадратов». Это один магический квадрат 3×3, где каждый квадрат магического квадрата будет содержать квадратное число.
Задача состоит в том, чтобы найти работающий магический квадрат квадратов, т. е. каждая строка, столбец и диагональ в сумме дают одно и то же число. 1996 г. в одной из своих статей в журнале Scientific American. Вы можете найти эту точную проблему самостоятельно, но никто не смог ее решить.
Было несколько промахов, но это не помогает. Возможно, у этой проблемы нет ответа, и этот магический квадрат квадратов не может быть решен… из-за кажущейся недоступности квадратов. Но даже тогда это нужно доказать, а доказательства — это то, чего нам не хватает.
Немногие занимаются этими математическими задачами, а те, кто этим занимаются, в основном любители. Они надеются, что эти проблемы можно решить или, по крайней мере, доказать их неразрешимость.
Все в математике основано на доказательствах, которые можно получить откуда угодно.
