Математика для 6 7 лет: Развивающие игры и задания по математике для детей 6-7 лет — Яркий Дворик

Содержание

Игры по математике для детей 6-7-8 лет

Начиная с раннего возраста, детки должны вникать в арифметические приемы и решать простенькие логические задачки – это закладывает основательный фундамент для их дальнейшего развития в социуме. Для первого знакомства малышей с азами математики обязательно нужно постараться создать увлекательную и красочную атмосферу, чтобы даже самый неусидчивый ребенок проявил интерес к новому для себя виду деятельности. Отличный выбор математических игр для детей 6-8 лет представлен в каталоге развлекательного портала Quicksave.

Полезные дидактические тесты на любой вкус

Здесь сорванцы узнают полезную информацию о цифрах и числах, научатся грамотно считать, ознакомятся с основами арифметики. Наглядные онлайн примеры несложных заданий дадут толчок развитию абстрактного мышления. Чтобы максимально быстро и эффективно понять и закрепить материал, интерактивные забавы на логику для детей 7 лет должны выгодно отличаться своей простотой и захватывающим геймплеем.

Мотивационный фактор играет здесь не последнюю роль – за каждый успешно пройденный уровень маленького игромана ожидает награда. Благодаря интерактивным развивающим пособиям, девочки и мальчики будут хорошо учиться в будущем и отличаться примерным поведением.

Что должны содержать и на что обязаны быть направлены такие тематические игры:

Наличие четких и ясных правил;
Ориентация на раскрытие детских талантов;
Красочный графический интерфейс и клевая озвучка.

Уникальная подборка анимированных упражнений дает заметный прогресс в улучшении интеллектуальных способностей у дошкольников. Разбираться с математическими премудростями значительно проще в компании сверстников – устройте импровизированное соревнование с друзьями, чтобы узнать, кто лучше всех складывает или умножает числа.

Шикарная коллекция математических флеш игр от Quicksave

Браузерные игры без регистрации– это действенный виртуальный инструмент для сохранения мотивации и желания учиться у юных пытливых умов. Чтобы достичь видимого успеха, целесообразно проводить регулярные 20-минутные математические тренировки, не забывая отвлекаться и отдыхать. Ребята имеют великолепную возможность бесплатно пройти познавательно-развлекательные квесты из категории: Игры с цифрами, игры учимся считать, обучающие игры, чтобы продолжать прогрессировать и поддерживать в тонусе мыслительные процессы.

Программа математического развития дошкольников «Игралочка»

Содержание

ПРЕДИСЛОВИЕ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Цели и задачи реализации Программы

Возрастные особенности и динамика формирования элементарных математических представлений у дошкольников

Планируемые результаты освоения содержания Программы

Особенности организации образовательного процесса

СОДЕРЖАНИЕ ПРОГРАММЫ

Первый год обучения (для детей 3-4 лет)

Второй год обучения (для детей 4-5 лет)

Третий год обучения (для детей 5-6 лет)

Четвертый год обучения (для детей 6-7 лет)

педагогическая диагностика ДОСТИЖЕНИЯ ДЕТЬМИ ПЛАНИРУЕМЫХ РЕЗУЛЬТАТОВ ОСВОЕНИЯ ПРОГРАММЫ

МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОГРАММЫ

Основной компонент

Вариативный (предшкольный) компонент

ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ СОДЕРЖАНИЯ РАБОТЫ ПО МАТЕМАТИЧЕСКОМУ РАЗВИТИЮ ДОШКОЛЬНИКОВ

Основной компонент программы

Примерное тематическое планирование к курсу «Игралочка» для детей 3-4 лет, часть 1 (26 занятий)

Примерное тематическое планирование к курсу «Игралочка» для детей 4-5 лет, часть 2 (29 занятий)

Примерное тематическое планирование к курсу «Игралочка – ступенька к школе» для детей 5-6 лет, часть 3 (32 занятия)

Примерное тематическое планирование к курсу «Игралочка – ступенька к школе» для детей 6-7 лет, часть 4 (64 занятия)

Вариативный компонент программы

Примерное тематическое планирование к курсу «Раз – ступенька, два – ступенька…» для детей 5-6 лет и 6-7 лет (64 занятия)

Взаимодействие педагогов с родителями дошкольников по вопросам математического развития детей

СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

ПРИЛОЖЕНИЕ 1 Схема анализа соответствия образовательного процесса дидактическим принципам деятельностного метода

ПРИЛОЖЕНИЕ 2 Схема анализа занятия «открытия» нового знания

ПРИЛОЖЕНИЕ 3 Краткая презентация Программы

Читать всю программу. ..

Введение

Социально-экономические процессы, происходящие в современном обществе, непосредственным образом затрагивают сферу образования на всех ее уровнях, в том числе и на дошкольном.

В настоящее время в системе отечественного дошкольного образования происходят изменения, которые без преувеличения можно назвать революционными. Впервые за всю историю существования в России системы образования дошкольное детство признано особым самоценным уровнем. Закон «Об образовании в Российской Федерации» (от 29 декабря 2012 года № 273-ФЗ) закрепил за дошкольной ступенью статус первого уровня системы общего образования. Таким образом, благодаря достижениям в педагогике, психологии и методологии в последние годы идея об определяющем, решающем значении дошкольного возраста для всего последующего развития личности получила правовое обоснование.

Перенос в современных нормативных документах акцента с подготовки ребенка к школе на полноценное проживание детства как самоценного и социально значимого периода способствует изменению представлений о результатах дошкольного образования

Этими результатами становятся, в первую очередь, социализация детей, свой для каждого ребенка уровень развития любознательности, активности, самостоятельности, познавательной инициативы, готовности к преодолению ошибок и неудач, поиску решений в новой, нестандартной ситуации, в условиях дефицита информации. Все это должно стать прочной основой не только для успешного обучения ребенка в школе, но и полноценной реализации его личностного потенциала на всех этапах жизни.

Преемственность между разными уровнями образования обеспечивается единой концепцией к построению образовательного процесса, а именно – системно-деятельностным подходом, пронизывающим все образовательные стандарты, в том числе и федеральные государственные образовательные стандарты дошкольного образования (ФГОС ДО).

В связи с этим особую актуальность приобретает проблема создания современного педагогического инструментария, основанного на системно-деятельностном подходе и обеспечивающего решение современных задач дошкольного образования, с одной стороны, с позиций уникальности дошкольного детства, а с другой, с позиций непрерывности образования на протяжении всей жизни человека.

Один из вариантов решения данных задач предложен в непрерывной образовательной системе деятельностного метода обучения Л.Г. Петерсон, реализующей системно-деятельностный подход на основе общей теории деятельности (Г.П. Щедровицкий, О.С. Анисимов).

На дошкольном уровне образовательная система Л.Г. Петерсон представлена в образовательной программе дошкольного образования «Мир открытий» (под научным руководством Л.Г. Петерсон, общей редакцией Л.Г. Петерсон, И.А. Лыковой) и парциальной образовательной программе математического развития детей дошкольного возраста «Игралочка» (под научным руководством Л.Г. Петерсон.).

Образовательная система Л.Г. Петерсон прошла

широкую апробацию, начиная с 1992-го года, более чем в 1000 образовательных организациях (в детских садах и школах) на всей территории РФ. В настоящее время по данной образовательной системе работают около 10 000 образовательных организаций России и стран СНГ.

Одним из показателей значимости достигнутых результатов является премия Президента РФ в области образования за 2002 год, которой была удостоена команда Центра системно-деятельностной педагогики «Школа 2000…» под руководством доктора педагогических наук Петерсон Людмилы Георгиевны, за разработку дидактической системы деятельностного метода обучения и ее реализацию в широкой образовательной практике.

Известно, что определяющее значение для решения современных задач образования имеет качество работы педагога. Поэтому принципиально важно создать условия для того, чтобы помочь педагогам проникнуться идеями и задачами нового этапа развития образования, освоить новые образовательные технологии, обеспечивающие решение современных задач образования с позиций его непрерывности.

Сегодня педагогам, как никогда раньше, важно не только владеть инструментами организации образовательного процесса деятельностного типа, но и уметь модифицировать эти инструменты в соответствии с возрастными и индивидуальными особенностями детей, своими профессиональными интересами.

С этой целью на базе Инситута системно-деятельностной педагогики организована многоуровневая курсовая подготовка педагогов различных уровней образования и система их методической поддержки на местах.

Читать всю программу…

Конспект занятия по математике для детей 6-7 лет: Целое и части

Конспекты занятий

Конспект занятия по математике

Организация непосредственно образовательной деятельности в рамках освоения образовательной области «Познание» по развитию элементарных математических представлений детей 6-7 лет в группе кратковременного пребывания «Логика для дошкольника»

(структура построения занятия по образовательной системе «Детский сад 2100»)

Корнаухова Т. А., воспитатель МБДОУ ЦРР-ДС №53 «Елочка» г.Тамбов

Тема: «Целое и части»

Цель:

Ввести понятие целое и части.

Сформировать представление о сложении, как объединении частей в целое.
Развивать логическое мышление средствами математических операций.
Воспитывать интерес к предмету «Математика».

Ход занятия:

I. Введение в игровую ситуацию.

Педагог: — Ребята, сегодня мы отправимся в увлекательное путешествие на поезде. Устраивайтесь поудобнее и поехали. Чух-чух-чух. Ту-ту-ту.

«Паровозик наш волшебный

Отправляется вперёд,

И посмотрим мы, ребята,

Он куда нас привезёт?»

2. Мотивационная игра.

Педагог:

— Наш поезд остановился.

— Куда же мы попали?

(в лес, на волшебную опушку)

— Посмотрите, ребята, что это? (грибы).

— Какие это грибы? Как называется? (белые и подосиновики).

— Какие правила сбора грибов вы знаете? (нельзя рвать грибы, с корнем, можно повредить грибницу, нужно осторожно выкрутить гриб, или срезать ножом, оставив корень гриба).

— Какое время года наступило? (осень)

— Что делают звери осенью? (готовятся к зиме).

— Смотрите, кто это? (это ёжи).

— Они отравились в лес заготавливать себе питание.

— Давайте поможем ежам собрать грибы, положим их в корзину.

— Рита положит белые грибы, а Игорь — подосиновики. А мы вместе посчитаем, сколько всего грибов положат в корзинку Игорь и Рита.

— Сколько белых грибов в корзинку положила Рита? (2)

— Сколько подосиновиков положил Игорь? (3)

— Сколько всего грибов положили в корзину Игорь и Рита? (5)

— Как получили «5» (2 и 3)

— Куда сложили грибы? (в корзинку)

— Каким словом можно заменить слово «сложили» (положили, объединили).

Вывод: Действие, которое мы выполнили, в математике называется — сложением.

— Молодцы. Садитесь на пенёчки (стулья), поработаем с геометрическим материалом.

3. Затруднения в игровой ситуации

Работа с геометрическим материалом

Педагог:

— Положите в первый мешочек 2 треугольника, а во второй мешочек-3 круга

— Проверьте, что лежит в первом мешочке? (2 треугольник)

— Что лежит во втором мешочке? (3 кружка)

— Сложите эти фигуры в один общий мешок.

— Сколько всего фигур в мешочке (2 треугольника и 3 кружка) «5»

— Что мы сделали с фигурами? (собрали, сложили, объединили в один большой мешок).

— Давайте ещё раз повторим:

— Что было в первом мешке? (2 треугольника) — Это первая часть

— Что было во втором мешке? (3 круга) — Это вторая часть.

— Что мы сделали? (все фигуры объединили в целое). Какое математическое действие с фигурами мы выполнили? (сложение).

— Как получить целое из частей?

Вывод: Чтобы получить целое из частей, части нужно объединить или сложить.

Педагог: — Мы вывели с вами важное правило сложения. Чтобы сложить, не обязательно ссыпать все фигуры в один мешок, между частями можно поставить математический знак, который показывает сложение частей.

— Кто знает, как называется этот знак (плюс +).

— Найдите и покажите знак сложения.

— Положите его между двумя частями.

— Мы получили две суммы.

— Равны ли они?

— Что находится слева? Справа?

— Слева 2 треугольника и 3 кружка и справа 2 треугольника и 3 кружка

— Значит, суммы равны?

— Какой знак поставим? (знак =)

— Найдите у себя этот знак и положите.

Физкультминутка

Ёжик шёл — шёл — шёл

Белый гриб он нашёл

Раз — грибок, два грибок,

Положил их в кузовок

4. Закрепление, применение нового материала.

Педагог:

— Ребята, а что ещё запасают ежи на зиму, кроме грибов? (лесные яблоки).

— Наши ежи пошли в лес за яблоками.

— Сосчитайте, сколько всего яблок собрали ежи.

— Назовите первую часть, вторую часть, целое значение.

5. Повторение и развивающие задания.

Педагог: — На нашей полянке живут не только ежи, но и другие обитатели. Придумайте название этой картинке. Мне кажется, здесь кто-то лишний. Как вы думаете, кто это? (ответы детей).

6. Физкультминутка

Утром по лесной дорожке.

Топтоп-топ топочут ножки

Ходит, бродит, вдоль дорожек

Весь в иголках старый ёжик

Ищет яблочки, грибочки

Для сыночка и для дочки.

7. Штриховка.

Педагог: — В лесу темнеет, чтобы наши ежи нашли дорогу домой, давайте зажжём им в лесу волшебные фонарики.

8. Работа с пазлами. Работа в микрогруппах .

Педагог:

— Где мы сегодня побывали? (в лесу)

— Кого повстречали? (ежей)

— Ёжи вернулись домой, а вам оставили задание. (2 конверта)

— Задание для первой группы, для второй группы.

9. Рефлексия.

Педагог:

— Какое математическое действие мы выполняли с грибами, яблоками, геометрическими фигурами? (ответы детей)

— Какой математический знак показывает, что мы части объединили в целое (ответы детей)

— Где в жизни могут пригодиться наши знания (ответы детей)

На этом наше путешествие закончилось, усаживайтесь поудобнее в наш поезд мы возвращаемся в детский сад.

занимательные задания и игры для дошкольников

Автор Alef На чтение 7 мин. Просмотров 612 Обновлено 30.12.2019

Дошкольники, в отличие от годовалых малышей, способны самостоятельно размышлять и анализировать. Математика для детей 5—6 лет научит сравнивать предметы по количеству, устанавливать связь между ними, решать примеры на логику. Процесс обучения дошкольников с помощью простых математических приемов — сложная задача. Для быстрого усвоения материала педагоги советуют проводить уроки с малышами в увлекательной форме.

Начальный этап

Математика для детей 5 лет должна начинаться с анализа свойств разных предметов, сравнения их между собой: яблоко легче арбуза, папа ростом больше мамы. На первых уроках лучше использовать числа до 10. Аналогичной методики преподавания рекомендуется придерживаться на первых уроках геометрии. Малышу нужно показать и рассказать, что значит круглый, короткий и длинный предмет.

Если дети уже знают основные понятия, занятия по математике проводят с целью усвоения определений «цифра» и «число». Каждый термин объясняется с примерами и сопровождается самостоятельным решением задач. Задания по математике в 5 лет должны быть похожи на веселую игру.

Если родители планируют заниматься с будущим первоклассником самостоятельно, можно воспользоваться специальными программами для подготовки к школе. Их разрабатывают педагоги и психологи совместно. В таких дидактических материалах есть раскраски, карточки, цифры и обучающие мультфильмы.

Математика в раскрасках заставляет «работать» память. С помощью таких книг малыш знакомится с треугольниками, квадратами, кругами. Некоторые раскраски учат порядковому счету: необходимо последовательно чертить ломаную линию от цифры к цифре.

В дидактических материалах с картинками есть легкие и тяжелые математические задания. Например, в большом круге изображена цифра. Необходимо нарисовать и раскрасить в нем маленькие кружки, количество которых должно соответствовать указанному числу.

Прописи и игры

Карточки с цифрами помогают малышам познакомиться с основными математическими понятиями. С таким материалом развиваются память и мышление. Чтобы привыкнуть к ручке, можно купить прописи либо самостоятельно написать в тетради фигуры и цифры. Подобные занятия проводят с 5 лет. Они развивают усидчивость. Прописи способствуют выработке навыков аккуратного письма.

Занимательная математика для детей 5 и 6 лет включает в себя задачи на логику и дидактические игры. Веселые логические задания можно придумать самостоятельно, к примеру, что тяжелее: 1 кг пуха либо 1 кг железа. Дидактические либо обучающие игры проводят в любой обстановке (на прогулке, сидя в очереди к педиатру и т. д. ).

Если малыш больше любит рисование, чем математику, родителям лучше проводить занятия в игровой форме:

Хлопки. Игра развивает математические способности и слуховое восприятие. Взрослый хлопает в ладоши с разной частотой и силой, а ребёнок считает количество ударов.
Фокус. Маленькие предметы зажимаются в кулаке, прячутся за спиной. Дошкольник, зная, сколько предметов в одной руке, должен подсчитать, сколько спрятано в другом кулаке. Если он ответил верно, угадывает взрослый. При неверном ответе предметы прячут в ином количестве.
Лишнее. Из журналов вырезают 20 картинок разной категории: растения, транспорт, продукты питания, мебель. Изображения одной тематики раскладывают на столе. К ним добавляют несколько картинок из другой категории. Дошкольник должен найти посторонние рисунки, подсчитав их количество. Также производится подсчет оставшихся изображений из одной категории.
Число. Эта групповая игра проводится с мячом. Дети становятся в круг, в центре которого должен находиться взрослый. Мяч поочередно бросается, при этом называется число. Каждый малыш должен вернуть мяч ведущему, произнося следующее по порядку число.
Рисование. Арифметика для детей 5 лет должна быть увлекательной. Для этого педагогами разработаны дидактические материалы с уроками рисования по точкам. Дети, соединения элементы, проводят по порядку линии от одной цифры к иной.
Ходилка. На игровом поле отмечается путь. По нему необходимо добраться из одного пункта к другому. Дети по очереди бросают игральные кости, считая количество выпавших точек, и совершают ходы. Счет ограничивается от 1 до 12. Если выпали 6 и 3, ребенок должен посчитать сумму этих чисел. Следующий ход выполняется после того, как игрок верно сложит цифры.
Магазин. Дети-продавцы предлагают взрослым-покупателям приобрести продукты по разным ценам. Можно произвести реальный расчет, если пойти в магазин с ребенком. Постепенно малыш сможет сам определять размер сдачи. Частые походы в магазин помогут ему быстрее научиться счету.

Знания ребенка

Математика считается сложной наукой. Чтобы исключить сложности в ее изучении, дошкольнику нужно иметь основные математические навыки. В летний период, перед началом учебного года, будущему первокласснику рекомендуется пройти подготовительные курсы. После такого обучения ребенок должен уметь считать до десяти, знать цифры, рисовать фигуры, разделять квадрат и круг на несколько одинаковых частей. Другие навыки:

умение измерить высоту, длину и ширину предметов;
понимать, что означает выше, ниже, шире, уже, больше и меньше;
решать простые задачи в одно действие.

Математика для детей до 6 лет легко усваивается, если ее объяснять правильно, придерживаясь советов психологов. Нельзя заставлять ребенка в возрасте 5—6 лет решать одну задачу дольше 40 минут. Во время занятий не следует сразу давать малышу подсказку. Урок должен проводиться с заданиями различного типа. Похвала — это то, чего ждет ребенок от родителей.

Некоторые малыши не хотят учиться даже в игровой форме. Это может быть связано с неправильным подходом родителей к методике проведения уроков. Нельзя заниматься математикой, следуя схеме «сиди и решай». Нелюбовь к счету объясняется и перегруженностью детей разными развивающими секциями. Возможно, ребенку не нравится реакция мамы или папы на неверный ответ. В таких случаях родителям требуется профессиональная помощь.

Советы психологов и педагогов

Нежелание изучать математику способно возникнуть по разным причинам. Ребенок может не понимать её из-за своего юного возраста. Иногда пятилетний малыш не обладает способностями к вычислению. Часто дошкольники с гуманитарным складом ума игнорируют цифры, но бегло читают и хорошо пишут.

Родителям нельзя остро реагировать на нежелание ребенка считать. Если у него есть способности к математике, но нет охоты заниматься, необходимо донести до него важность учебного процесса. Этот вопрос рекомендуется обсуждать часто, демонстрируя на практике необходимость математических вычислений.

Когда дошкольник не воспринимает цифры, нужно его ими окружить. Для этого используют рисунки и карточки с числами. Листы бумаги развешивают по дому, периодически акцентируя на них внимание. С помощью такого подхода ребенок быстро начнет складывать и вычитать числа.

Еще один практический совет педагогов — включение цифр в речь при общении с дошкольником. Можно играть в разные игры, в которых нужно отсчитывать время или рассказывать стихи с разрядом. Со временем ребенок сам проникнется интересом к точной науке. Если он не воспринимает игровые и классические методы обучения счету, используют сладости. Когда дошкольник дает верный ответ на поставленную задачу, он получает конфеты. Такая методика подстегнет в нём желание быстрее овладеть навыком счета.

Математика для детей 6 лет считается увлекательной и интересной наукой. Главное, сделать правильный выбор в форме обучения. Занятия не должны обременять малышей. Идеи для проведения занимательных уроков находятся вокруг нас, достаточно подключить свою фантазию. Если решать задачи по арифметике в игровой форме, тогда дошкольник получит дополнительную мотивацию для нахождения верного ответа. Он будет стремиться получить награду, став победителем. Ученые доказали, что именно в процессе игры отлично запоминается новая информация.

Плюсы обучения с помощью математических игр заключаются в наглядности изучаемого материала и развитии абстрактного мышления. Игры в числа с ярким оформлением, основанные на понятных примерах, помогут детям научиться самостоятельно анализировать, сопоставлять предметы и запоминать арифметические действия. При этом увлекательная математика для детей 5-6 лет поможет втянуться не только в мир цифр и логики, но и станет отправной точкой для моделирования — одной из составляющих развития творческих способностей дошкольника.

математических рассказов для детей 6-7 лет | Scholastic

Рассказы, объединяющие математику, улучшают мышление и обучение по многим направлениям: они расширяют навыки детей в решении проблем, привносят математику в реальные жизненные ситуации, расширяют мышление и расширяют словарный запас и навыки грамотности! Книги, которые просят детей мыслить математически или решать проблемы по-новому, не только укрепляют математические навыки и навыки грамотности, но и подчеркивают творческое решение проблем! Попробуйте некоторые из этих замечательных математических чтений:

One Grain of Rice от Деми — это отличный рассказ, который поможет вашему ребенку понять силу удвоения, а также урок творческого мышления. Чтобы провести урок еще дальше, предложите удвоить один пенни за неделю и попросите ребенка предсказать, сколько денег он получит в конце. Сделайте это бумажным упражнением на месяц, иначе у вас не будет больше денег, чем вы можете сэкономить (см. Математику здесь)! Вы можете связать это понятие с веб-сайтом Free Rice, где ваш ребенок может отвечать на математические вопросы и собирать миски с рисом для нуждающихся.
Zero Кэтрин Отоши (или любой другой из этой серии!): Зеро подружится с другими числами и в конечном итоге выясняет, чего она на самом деле стоит.Используйте его, чтобы поговорить с ребенком не только о ценности чисел и исчислении десятков, но и о синергетическом импульсе, который поддерживает друг друга и создает совместную работу в команде.
The Greedy Triangle Мэрилин Бернс — отличный способ поговорить о геометрии для первоклассников. У гуру математики Мэрилин Бернс есть множество замечательных идей, книг и занятий для учащихся всех возрастов.
Математика на все времена Грега Танга содержит больше загадок и способов решения проблем, которые расширяют кругозор детей и расширяют их возможности обучения! Эта забавная книга фокусируется на сложении, предлагая читателям использовать подсказки, которые он дает, чтобы определить, «сколько».’
Сэр Кумференс и все королевские десятки : Математическое приключение от Синди Швингер. Вся эта серия — отличный способ вывести математику в новое измерение. Книга позволит вашему ребенку применить группировку и добавить к «реальным жизненным» ситуациям (потому что, сколько вечеринок-сюрпризов Кинга собирается ваш ребенок?).
Место для нуля : Математическое приключение Ангелины Спарагны Лопрести и Филлис Хорнунг. Хорошая книга, чтобы поговорить о математической лексике и расстановке знаков.

математических навыков и этапов в зависимости от возраста | Разобрался

Дети начинают изучать математику в тот момент, когда они начинают познавать мир. Каждый навык — от определения форм до счета и поиска закономерностей — основан на том, что они уже знают.

Есть определенные математические вехи, которые большинство детей достигают примерно в одном возрасте. Но учтите, что математические навыки у детей развиваются с разной скоростью. Если дети еще не обладают всеми навыками, указанными для их возрастной группы, ничего страшного.

Вот как математические навыки обычно развиваются по мере взросления детей.

Младенцы (в возрасте 0–12 месяцев)

Начните предсказывать последовательность событий (например, проточная вода означает время купания)
Начните понимать основную причину и следствие (встряхивание погремушки вызывает шум)
Начните классифицировать вещи простыми способами (некоторые игрушки шумят, а некоторые нет)
Начните понимать относительный размер (ребенок маленький, родители большие)
Начните понимать слова, описывающие количество (еще , больше , достаточно )

Малыши (возраст 1–2 года)

Поймите, что числа означают «сколько» (используя пальцы, чтобы показать, сколько им лет)
Начните называть числа, но можете пропустить некоторые из них
Поймите слова, которые сравнивают или измеряют вещи ( меньше , позади , быстрее )

Сопоставьте базовые формы (треугольник с треугольником, круг с кругом)

Изучите измерения путем заполнения и опорожнения контейнеров
Начните видеть закономерности в повседневных делах и в таких вещах, как напольная плитка

Дошкольники (в возрасте от 3 лет) –4 года)

Распознавать формы в реальном мире
Начать сортировку по цвету, форме, размеру или назначению
Сравните и сопоставьте, используя такие классификации, как рост, размер или пол
Подсчитайте не менее 20 и точно укажите и подсчитайте элементы в группе
Помните, что цифры обозначают названия чисел (5 означает пять )
Используйте пространственное восприятие, чтобы складывать головоломки
Начните предсказывать причинно-следственные связи (например, что произойдет, если они уронят игрушку в ванну с водой)

900 02

Детсадовцы (возраст 5 лет)

Сложите, сосчитав пальцы на одной руке — 1, 2, 3, 4, 5 — и начиная с 6 на второй руке
Определите большее из двух чисел и распознавать цифры до 20
Копировать или рисовать симметричные формы
Начните использовать простые карты, чтобы найти «спрятанное сокровище»
Начните понимать основные понятия времени, такие как утро или дни недели
Следуйте многоступенчатым инструкциям, в которых используются такие слова, как первый и следующий
Поймите значение таких слов, как маловероятно или возможно

Предскажите, что будет дальше в шаблоне и создавать собственные шаблоны
Знать разницу между двухмерными и трехмерными формами и называть основные (кубики, конусы, цилиндры)
Считайте до 100 по единицам, двоек, пятеркам и десяткам
Запишите и узнайте цифры от 0 до 100 и слова для чисел от одного до двадцати
Выполните базовое сложение и вычитание до 20
Прочтите и создайте простую гистограмму
Распознайте и узнайте ценность монет

Переходите от практических методов к использованию бумаги и карандаша для решения математических задач
Работа с деньгами
Выполняйте сложение и вычитание с перегруппировкой (также известное как заимствование)
Понимайте значение разряда достаточно хорошо, чтобы решать задачи с десятичными точками
Знать, как выполнять умножение и деление с помощью семейств фактов (наборов связанные математические факты, например 3 × 4 = 12 и 4 × 3 = 12)
Составьте числовое предложение или уравнение из задачи со словами

Начните применять математические концепции к реальному миру (например, разрезать рецепт пополам)
Попрактикуйтесь в использовании более чем одного способа решения задач
Запишите и сравните дроби и десятичные дроби и расположите их в порядке числа строка
Сравните числа с помощью> (больше) и <(меньше)
Начните двух- и трехзначное умножение (например, 312 × 23)
Полное деление в столбик, с остатками или без них
Оценить и округлить

Начните базовую алгебру с одного неизвестного числа (например, 2 + x = 10)
Используйте координаты для определения точек на сетке, также известной как построение упорядоченных пар
Работа с дробями, процентами и пропорциями
Работа с линиями, углами, типами треугольников и другими основными геометрическими фигурами
Используйте формулы для решения сложных задач и для определения площади, периметра и объема фигур

Поймите, что числа могут быть представлены разными способами (дроби, десятичные числа, основания и переменные)
Использование числа в реальных ситуациях (например, расчет продажной цены или сравнение студенческих ссуд)
Начните видеть, как математические идеи дополняют друг друга
Начните понимать, что некоторые математические задачи не имеют реальных решений
Используйте математический язык для передачи мыслей и решений
Используйте графики, карты или другие представления для изучения и передачи информации

Помните, что дети развиваются разными темпами. Они могут получить некоторые математические навыки позже, чем другие дети, или могут иметь некоторые из них, которые уже старше их возраста.

Если вы наблюдаете за своим ребенком и беспокоитесь о его успехах в математике, узнайте, почему у некоторых детей возникают проблемы с математикой, и что нужно делать.

этапов математики 7-8 — Kidspot

В этой возрастной группе навыки счета приобретают все более формальный характер, поскольку дети работают над развитием чувства числа и уверенности, используя умственные и письменные стратегии для решения задач.

Дети в этой возрастной группе могут прогрессировать семимильными шагами или развивать навыки в стабильном темпе. Пожалуйста, рассмотрите то, что вы читаете ниже, в контексте уникального развития вашего ребенка.

Навыки счета в возрасте 7–8 лет могут включать:

Обычно дети могут заказывать, читать и записывать числа до 999 к восьми годам. Они начали использовать счетчики для записи итогов, но некоторые дети все еще могут использовать простые рисунки в качестве подкрепления своего объяснения решения проблем.
Дети понимают концепцию чисел, стоящих на числовой прямой, и могут использовать их в качестве инструментов для развития умственных стратегий счета. Большинство 8-летних могут обрабатывать большие числа на числовой прямой и могут определить, что такое число, как 3000, на числовой прямой ближе к 5000, чем 2000.
Дети в возрасте 7-8 лет могут создавать и продолжать числовые модели и связывать их со сложением и вычитанием до 20. Шаблоны могут быть связаны со стратегиями, такими как подсчет пропусков. Большинство детей в этом возрасте могут пропустить счет до 100 и определить закономерность, пропустив счет на 2, 4 и 5 секунд.
Некоторые дети в этом возрасте могут все еще учиться называть определенное число в сотнях, например, «Какое число идет после 192?».
Дети этого возраста в основном понимают, что десять единиц — это то же самое, что и десять.
Психологические стратегии улучшаются, и дети могут понять, что 3 + 4 = 4+ 3. Дети в возрасте 8 лет обычно способны понять, что 3 + 4 + 5 — это то же самое, что 3 + 9.
Теперь дети складывают, вычитают, умножают и делят. Они все еще говорят об умножении и делении, используя язык групп, справедливых долей, и еще не ожидают, что они будут знать свою таблицу умножения.Умножение называется повторным сложением. Дети в этом возрасте изучают множество способов счета и сложения чисел для сложения и вычитания. Эти стратегии связаны с распознаванием отношений между числами, таких как удвоение.
Дети могут понять концепцию «основания 10» и понять, что числа имеют разные значения в зависимости от позиции в числе. Ребенок узнает, что 4 в числе 14, 45 и 432 представляют разные значения.Дети в этом возрасте используют длинные, плоские и однотонные брюки, чтобы показать понимание в классе.
В этом возрасте дети также работают с дробями, используя термины половинки и четверти. Это связано с ситуациями из реальной жизни, такими как разрезание торта или пирога на половинки или четвертинки и определение количества частей. Дети понимают, что четверть — это половина, опять же вдвое.

Важно

Именно на этом этапе разработки вводятся формальные письменные алгоритмы.Это должно происходить только в том случае, если дети прочно усвоят основные понятия о числовом значении и смогут мысленно удерживать в уме двузначные числа. Если это не так, то настойчивое развитие чувства числа с помощью игр и действий будет более полезным, чем подталкивание ребенка к написанию алгоритмов.

Эта статья написана Мишель Баррингтон для Kidspot, ведущего австралийского образовательного ресурса для родителей из таких источников, как Совет по образованию, викторианские документы об образовании и учебная программа SA.Мишель — учительница и мать малыша, которая ведет блог на сайте Gee, You’re Brave.

7 секретов математики, которые увлекут вашего ребенка Математика

Будьте примером
Согласно национальным опросам, многие взрослые говорят, что ненавидят математику в школе. Если вы один из них, будьте осторожны, не передавайте такое отношение своему ребенку. Это может вызвать математическое беспокойство, которое, к сожалению, заразительно. Помогите своему ребенку улучшить его отношение к математике, продемонстрировав ему, что вы уверены в выполнении рутинных задач, таких как подсчет денег со школьного сбора средств, оценка стоимости покупки или заполнение налоговой декларации.Вы также можете указать на важность математики в различных профессиях, включая архитектуру, медицину, дизайн одежды, ресторанный менеджмент и компьютерное программирование. Эти маленькие переключатели в том, как вы говорите о математике, могут иметь значение и даже заинтересовать вашего ребенка математикой.
Помогайте своему ребенку использовать математику каждый день
Поощряйте ребенка решать задачи, связанные с математикой, вне школы. В продуктовом магазине попросите его выяснить цену на четыре банки тунца.В машине спросите ее, сколько времени займет поездка до пункта назначения в зависимости от вашей скорости. В магазине игрушек попросите ее подсчитать цену на игрушку со скидкой и сколько времени потребуется, чтобы накопить деньги на ее покупку.
Ознакомьтесь со стандартами обучения
Важно знать, какие математические навыки ваш ребенок должен освоить в своем текущем классе. (Вот что ваш ребенок должен изучать по математике в детском саду, 1-м классе, 2-м классе, 3-м классе, 4-м классе, 5-м классе, 6-м классе, 7-м классе и 8-м классе.Вы также можете увидеть математические навыки на уровне своего класса в действии, посмотрев наши видеоролики о вехах.) Если вы знаете, чему должен учиться ваш ребенок, будет проще дополнить эти навыки домашними занятиями.
Контролируйте домашнее задание по математике
Задания вашего ребенка по математике требуют только механической работы или учитель включает творческую «задачу недели», которая проверяет понимание учащимися математических понятий? Спросите учителя вашего ребенка, какие методы он использует, чтобы помочь ученикам освоить математику.
Обратите внимание на детали
Вы можете помочь своему ребенку с домашним заданием по математике, убедившись, что он показывает всю свою работу при решении уравнений и проверяет правильность вычислений и ответов. Лучше не отвлекаться и выделять одно и то же время каждый день на домашнюю работу.
Играйте в математические игры дома
Ваш ребенок может играть во многие игры, связанные с математикой. Начиная с младших классов, учащиеся могут научиться получать удовольствие от математики, играя в такие игры, как шахматы, домино, криббидж, шашки, сет, монополия, яхтзее и нарды.
Читайте книги, содержащие математику
Все больше и больше школ начинают включать различные предметные области в учебную программу, чтобы учащиеся могли установить более четкие связи. Но как включить математику в уроки истории или английского? Один из способов — читать книги, в которых главные герои решают задачу с помощью математики или логики. Примеры включают Сто злых муравьев Эллинор Дж. Пинчес, Королевские комиссары Эйлин Фридман и Сократ и три поросенка Туеси Мори.

Итоги

Мы, естественно, поощряем наших детей читать, писать и говорить вне школы. Тем не менее, мы часто оставляем изучение математических навыков 45 минутами в день в классе. Как и все остальное, навыки, уверенность и азарт вашего ребенка в математике будут улучшаться благодаря ежедневной практике, поддержке и поощрению.

Поделиться в Pinterest

Обновлено: 4 декабря 2019 г.

Глава 111. Подраздел B

Глава 111.Техас: основные знания и навыки математики,
Подраздел B. Средняя школа

Законодательные органы: положения данного Подглавы B выпущен в соответствии с Кодексом образования Техаса, 7.102 (c) (4), 28.002, 28.0021 (a) (1), и 28.008, если не указано иное.

111,25. Реализация Техасских основных знаний и навыков для математики, средняя школа, принята 2012.

(а) Положения пунктов 111.26-111.28 настоящего подраздела реализуются школьными округами.

(б) Не позднее 31 августа 2013 г., уполномоченный образование должно определить, было ли финансирование учебных материалов предоставлены в государственные школы Техаса для материалов, которые охватывают основные знания и навыки по математике, принятые в пунктах 111. 26-111.28 настоящего подраздел.

(c) Если комиссар принимает решение, что инструктивный финансирование материалов было предоставлено в соответствии с подразделом (b) этого раздела, 111.26-111.28 настоящего подраздела вводить в действие, начиная с 2014-2015 учебный год и распространяется на 2014-2015 и последующие учебные годы.

(d) Если комиссар не принимает решение финансирование учебных материалов доступно в подразделе (b) данного раздела комиссар не позднее августа определяет 31 каждого последующего учебного года ли финансирование учебных материалов был доступен.Если комиссар определит, что инструкция выделено финансирование материалов, уполномоченный должен уведомить Государственное управление образования и школьных округов, 111.26-111.28 г. подраздел вводится в действие на следующий учебный год.

Источник: Положения настоящего стандарта 111.25 приняты для вступления в силу. 10 сентября 2012 г. , 37 TexReg 7109; внесены изменения, вступающие в силу 31 декабря 2014 г., 39 TexReg 10470.

111.26. 6 класс, принято 2012.

(а) Введение.

(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.

(2) Стандарты процессов описывают способы, которыми Ожидается, что студенты будут вовлечены в содержание. Размещение процесса стандарты в начале знаний и навыков, указанные для каждого класса и конечно намеренно. Стандарты процессов объединяют другие знания и навыки вместе, чтобы учащиеся могли успешно решать проблемы и эффективно и эффективно использовать математику в повседневной жизни. Стандарты процесса интегрированы в каждый класс и курс.По возможности студенты будут применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте. Студенты будут использовать модель решения проблем, которая включает анализ заданных информация, формулирование плана или стратегии, определение решения, обоснование решение, а также оценка процесса решения проблем и разумности решения. Студенты выберут соответствующие инструменты, такие как реальные объекты, манипуляторы, алгоритмы, бумага и карандаш, а также технологии и техники такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция решать задачи.Студенты будут эффективно передавать математические идеи, рассуждения и их последствия с использованием нескольких представлений, таких как символы, диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические отношения для выработки решений, установления связей и прогнозов. Студенты будут анализировать математические отношения, чтобы общаться и общаться математические идеи. Студенты будут отображать, объяснять или обосновывать математические идеи и аргументы с использованием точного математического языка в письменной или устной форме общение.

(3) Основное внимание в 6 классе уделяется количеству и операции; соразмерность; выражения, уравнения и отношения; и измерения и данные. Студенты используют концепции, алгоритмы и свойства рациональных чисел, чтобы исследовать математические отношения и описывать все более сложные ситуации. Студенты используют понятия соразмерности исследовать, развивать и сообщать математические отношения. Ученики использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях приводит к изменению другого.Студенты соединяют словесные, числовые, графические, и символические представления отношений, включая уравнения и неравенства. Студенты используют геометрические свойства и отношения, а также пространственные рассуждения, моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения. делать выводы, оценивать аргументы и давать рекомендации. В то время важно использование всех видов техники, упор на готовность к алгебре навыки требуют внедрения графической технологии.

(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.

(b) Знания и навыки.

(1) Стандарты математических процессов. Студент использует математические процессы для получения и демонстрации математического понимания. Ожидается:

(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;

(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;

(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;

(D) передает математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;

(E) создавать и использовать представления для организации, записывать и передавать математические идеи;

(F) анализировать математические отношения к соединять и передавать математические идеи; и

(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные математический язык в письменном или устном общении.

(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается:

(A) классифицирует целые числа, целые числа и рациональные числа с использованием визуального представления, такого как диаграмма Венна, для описания отношения между наборами чисел;

(B) идентифицирует число, его противоположность и его абсолютная величина;

(D) порядок набора рациональных чисел, возникающих из математического и реального контекстов; и

(E) распространяет представления о делении на включить дробное обозначение, например a / b представляет то же число как a b , где b ≠ 0.

(3) Число и операции. Студент подает заявку стандарты математического процесса для представления сложения, вычитания, умножения, и разделение при решении проблем и обосновании решений. Студент ожидается:

(A) признать, что деление на рациональное число и умножение на обратный результат в эквивалентных значениях;

(B) определяет, с расчетом и без него, увеличивается или уменьшается количество при умножении на дробь, в том числе значения больше или меньше единицы;

(C) представляют собой целочисленные операции с конкретными моделирует и связывает действия с моделями со стандартизованными алгоритмами;

(D) складывать, вычитать, умножать и делить целые числа свободно; и

(E) умножить и разделить положительное рациональное числа бегло.

(4) Пропорциональность. Студент применяет математические стандарты процесса для развития понимания пропорциональных отношений в проблемных ситуациях. Ожидается:

(A) сравнить два правила словесно, численно, графически и символически в форма y = ax или y = x + a , чтобы различать между аддитивными и мультипликативными отношениями;

(B) применять качественные и количественные рассуждения для решения задач прогнозирования и сравнения реальных проблем с использованием соотношений и ставки;

(D) приведены примеры ставок для сравнения путем деления двух величин с разными атрибутами, включая ставки как частные;

(E) представляют собой отношения и проценты с бетоном модели, дроби и десятичные дроби;

(F) представляют собой контрольные доли и проценты, такие как 1%, 10%, 25%, 33 1/3%, и кратные этих значений с использованием сеток 10 на 10, ленточных диаграмм, числовых линий и чисел;

(G) генерировать эквивалент формы дробей, десятичных знаков и процентов с использованием реальных задач, в том числе проблемы, связанные с деньгами; и

(H) преобразовать единицы измерения система, включая использование пропорций и удельных ставок.

(5) Пропорциональность. Студент применяет математические стандарты процесса для решения проблем, связанных с пропорциональными отношениями. Ожидается:

(A) представляет математический и реальный мир проблемы, связанные с соотношениями и коэффициентами с использованием масштабных коэффициентов, таблиц, графиков и пропорции;

(B) решать реальные проблемы для найти целое с учетом части и процентов, чтобы найти часть с учетом целого и проценты, и найти проценты для части и целого, включая использование конкретных и графических моделей; и

(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений описывать алгебраические отношения. Ожидается:

(A) идентифицирует независимые и зависимые количества из таблиц и графики;

(B) напишите уравнение, которое представляет взаимосвязь между независимыми и зависимыми величинами из Таблица; и

(C) представляют данный ситуации с использованием словесных описаний, таблиц, графиков и уравнения в виде y = kx или y = x + b .

(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки концепций выражения и уравнения. Ожидается:

(A) генерировать эквивалентные числовые выражения, использующие порядок операций, включая целочисленные показатели и разложение на простые множители;

(B) различать выражения и уравнения устно, численно и алгебраически;

(C) определить, если два выражения эквивалентны с использованием конкретных моделей, графических моделей и алгебраических представлений; и

(D) генерировать эквивалентные выражения используя свойства операций: обратная, тождественная, коммутативная, ассоциативные и распределительные свойства.

(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для представления отношения и решать проблемы. Ожидается:

(A) расширить предыдущие знания о треугольниках и их свойства включают сумму углов треугольника, отношение между длинами сторон и величиной углов в треугольнике, и определение когда три длины образуют треугольник;

(B) модель формулы площади для параллелограммов, трапеций, и треугольники, разложив и переставив части этих фигур;

(C) написать уравнения которые представляют собой проблемы, связанные с областью прямоугольники, параллелограммы, трапеции, треугольники и объем справа прямоугольные призмы с положительными рациональными размерами числа; и

(D) определить решения проблем, связанных с областью прямоугольники, параллелограммы, трапеции, треугольники и объем справа прямоугольные призмы с положительными рациональными размерами числа.

(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. представлять ситуации. Ожидается:

(A) написать уравнения с одной переменной и одним шагом и неравенства для обозначения ограничений или условий в рамках проблем;

(B) представляют решения для одной переменной, одношаговые уравнения и неравенства на числовых прямых; и

(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. решать задачи. Ожидается:

(A) и решите одну переменную, одношаговое уравнения и неравенства, представляющие проблемы, включая геометрические понятия; и

(B) определить, соответствует ли данное значение (я) Однопеременные, одношаговые уравнения или неравенства верны.

(11) Измерения и данные. Студент подает заявку стандарты математического процесса для использования координатной геометрии для определения местоположений на плоскости. Ожидается, что ученик наберет точки во всех четырех квадрантах. с помощью упорядоченные пары рациональных чисел.

(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений анализировать проблемы. Ожидается:

(A) представляют числовые данные графически, включая точечные диаграммы, диаграммы стеблей и листьев, гистограммы и ящичковые диаграммы;

(B) использовать графическое представление числовых данные для описания центра, распространения и формы распределения данных;

(C) суммирует числовые данные с числовые сводки, включая среднее и медианное значение (меры центра), а также размах и межквартильный размах (IQR) (меры распространения), и используйте эти сводки для описания центра, распространения, и форма распределения данных; и

(D) суммирует категориальные данные с числовыми и графические сводки, включая режим, процент значений в каждом категории (таблица относительной частоты) и гистограммы процентов, и используйте их резюме для описания распределения данных.

(13) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений решать задачи. Ожидается:

(A) интерпретация числовых данных, представленных в виде точечных диаграмм, стебель-лист графики, гистограммы и коробчатые диаграммы; и

(B) различать ситуации дающие данные с вариабельностью и без нее.

(14) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора.Ожидается:

(A) сравните характеристики и стоимость проверки счет и дебетовая карта, предлагаемые различными местными финансовыми учреждениями;

(B) различают дебетовые и кредитные карты открытки;

(D) объясните, почему важно установить положительная кредитная история;

(E) описать информацию в кредитном отчете и как долго он сохраняется;

(F) описывает ценность кредитных отчетов для заемщикам и кредиторам;

(G) объясняет различные методы оплаты обучения в колледже, в том числе через сбережения, гранты, стипендии, студенческие ссуды и работу-учебу; и

(H) сравнить годовую зарплату нескольких профессий требующие различных уровней послесреднего образования или профессионального обучения и рассчитать влияние различных годовых зарплат на пожизненный доход.

Источник: Положения настоящего стандарта 111.26 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.

111,27. 7 класс, принято 2012.

(а) Введение.

(3) Основное внимание в 7 классе уделяется количеству и операции; соразмерность; выражения, уравнения и отношения; и измерения и данные. Студенты используют концепции, алгоритмы и свойства рациональных чисел, чтобы исследовать математические отношения и описывать все более сложные ситуации. Студенты используют понятия соразмерности для изучения, развития и передачи математических взаимосвязей, в том числе число, геометрия и измерение, статистика и вероятность.Ученики использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях приводит к изменению другого. Студенты соединяют словесные, числовые, графические, и символические представления отношений, включая уравнения и неравенства. Студенты используют геометрические свойства и отношения, а также пространственные рассуждения, моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения. делать выводы, оценивать аргументы и давать рекомендации. В то время важно использование всех видов техники, упор на готовность к алгебре навыки требуют внедрения графической технологии.

(b) Знания и навыки.

(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;

(E) создавать и использовать представления для организации, записывать и передавать математические идеи;

(F) анализировать математические отношения к соединять и передавать математические идеи; и

(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается, что студент расширит предыдущие знания наборы и подмножества с использованием визуального представления для описания отношений между наборы рациональных чисел.

(3) Число и операции. Студент подает заявку стандарты математического процесса для сложения, вычитания, умножения и деления решение проблем и обоснование решений.Ожидается:

(A) сложение, вычитание, умножение и деление рациональных чисел числа бегло; и

(B) применять и расширять предыдущие договоренности операций для решения задач с использованием сложения, вычитания, умножения, и деление рациональных чисел.

(4) Пропорциональность. Студент применяет математические стандарты процессов для представления и решения проблем, связанных с пропорциональными отношениями. Ожидается:

(A) представляют постоянную скорость изменения в математических и реальных задачах, заданных в графических, табличных, словесных, числовые, графические и алгебраические представления, в том числе d = rt ;

(B) рассчитать удельные расценки по ставкам в математической и проблемы реального мира;

(D) решать проблемы, связанные с соотношения, ставки и проценты, включая многоэтапные задачи с процентами рост и снижение процента, и проблемы с финансовой грамотностью; и

(E) преобразование между системами измерения, включая использование пропорций и использования единичных ставок.

(5) Пропорциональность. Студент применяет математические стандарты процессов для использования геометрии для описания или решения проблем, связанных с пропорциональные отношения. Ожидается:

(A) обобщить критические атрибуты сходство, включая соотношения внутри и между подобными формами;

(B) описывает π как отношение длины окружности к ее диаметру; и

(6) Пропорциональность. Студент применяет математические стандарты процессов для использования вероятности и статистики для описания или решения проблем вовлекающие пропорциональные отношения. Ожидается:

(A) представляют собой пробелы для простых и составные события с использованием списков и древовидных диаграмм;

(B) выберите и используйте различные модели для представляют простые и сложные события с технологиями и без них;

(D) делать прогнозы и определять решения использование теоретической вероятности для простых и сложных событий;

(E) найти вероятности простого событие и его дополнение и описывают отношения между ними;

(F) использовать данные из случайной выборки для делать выводы о населении;

(G) решить проблемы с использованием данных, представленных в виде гистограмм, точечных диаграмм и круговых диаграмм, включая сравнения и эквиваленты «от части к целому» и «от части к частям»;

(H) решать проблемы с помощью качественные и количественные прогнозы и сравнения из простых экспериментов; и

(I) определяют экспериментальные и теоретические вероятности, связанные с простыми и сложными событиями, с использованием данных и выборки пробелы.

(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для представления линейных отношений. с использованием нескольких представлений. Ожидается, что ученик будет представлять линейные отношения с помощью словесных описаний, таблиц, графиков, и уравнения, которые упрощаются до формы y = mx + b .

(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для построения геометрических соотношений. с объемом.Ожидается:

(A) моделирование отношений между объемом прямоугольной призмы и прямоугольной пирамиды, имеющей оба совпадающих основания и высоты и соединяются это отношение к формулам;

(B) объяснять словесно и символически соотношение между объемом треугольной призмы и треугольной пирамида, имеющая конгруэнтные основания и высоты и соединяющая это отношение к формулам; и

(C) использовать модели для определения приблизительных формул для окружности и площади круга и соедините модели с актуальными формулы.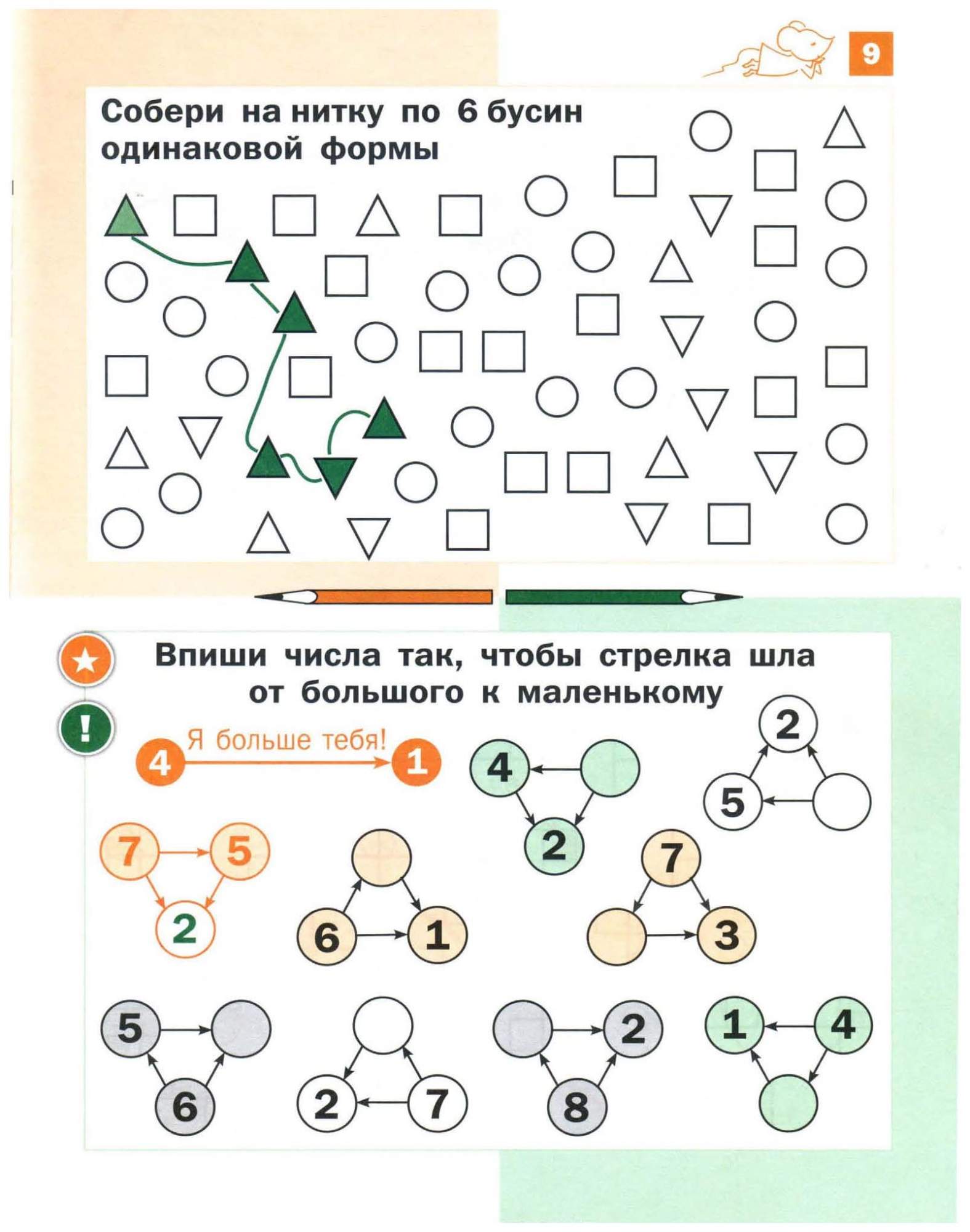

(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения геометрических задач. Ожидается:

(A) решить проблемы объемные прямоугольные призмы, треугольные призмы, прямоугольные пирамиды и треугольные пирамиды;

(B) определить окружность и площадь круги;

(C) определить площадь составных фигур содержащий комбинации прямоугольников, квадратов, параллелограммов, трапеций, треугольники, полукруги и четверти окружности; и

(D) решить проблемы, связанные с боковыми и общая площадь поверхности прямоугольной призмы, прямоугольной пирамиды, треугольная призма и треугольная пирамида путем определения площадь сетки фигуры.

(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной и неравенство для представления ситуаций. Ожидается:

(A) запись с одной переменной, двухступенчатая уравнения и неравенства для представления ограничения или условия в рамках проблем;

(B) представляют решения для одной переменной, двухшаговой уравнения и неравенства на числовых линиях; и

(11) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения уравнений с одной переменной. и неравенство. Ожидается:

(A) моделирование и решение двухэтапных уравнений и неравенств с одной переменной;

(B) определить, значение (я) составляют двухступенчатые уравнения с одной переменной и неравенство правда; и

(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических представлений для анализа данные. Ожидается:

(A) сравнить две группы числовых данных, используя сравнительные точечные или коробчатые диаграммы путем сравнения их форм, центров и спреды;

(B) использовать данные из случайная выборка, позволяющая делать выводы о совокупности; и

(C) сравнить две популяции на основе данных в случайных выборках из этих популяций, включая неформальные сравнительные выводы о различиях между двумя популяциями.

(13) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:

(A) рассчитать налог с продаж для данной покупки и рассчитать подоходный налог с заработной платы;

(B) идентифицируют компоненты личного бюджет, включая доходы; запланированные сбережения на колледж, пенсию и чрезвычайные ситуации; налоги; постоянные и переменные расходы, и посчитайте, какой процент каждый категория состоит из общего бюджета;

(D) используйте оценщик семейного бюджета для определения минимальный семейный бюджет и средняя почасовая оплата, необходимая семье для удовлетворить свои базовые потребности в студенческом городе или другом крупном городе поблизости;

(E) рассчитать и сравнить простые проценты и доход от сложных процентов; и

(F) анализировать и сравнивать денежные стимулы, включая продажи, скидки и купоны.

Источник: Положения настоящего стандарта 111.27 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.

111,28. 8 класс, принято 2012.

(а) Введение.

(3) Основные направления в 8-м классе — пропорциональность; выражения, уравнения, отношения и основы функций; и измерения и данные. Студенты используют концепции, алгоритмы и свойства действительных чисел исследовать математические отношения и описывать все более сложные ситуации. Студенты используют концепции соразмерности для изучения, развития, и сообщать математические отношения. Студенты используют алгебраическое мышление чтобы описать, как изменение одной величины в отношениях приводит к изменению в другом.Студенты соединяют словесные, числовые, графические и символические представления отношений, включая уравнения и неравенства. Студенты начинают развить понимание функциональных отношений. Студенты используют геометрические свойства и отношения, а также пространственные рассуждения для моделирования и анализа ситуации и решать проблемы. Студенты сообщают информацию о геометрических цифры или ситуации путем количественной оценки атрибутов, обобщить процедуры из измерения и использовать процедуры для решения проблем.Ученики использовать соответствующую статистику, представления данных и рассуждения для рисования выводы, оценивать аргументы и давать рекомендации. Хотя использование важны все виды техники, упор на навыки алгебры требует внедрения графической технологии.

(b) Знания и навыки.

(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;

(E) создавать и использовать представления для организации, записывать и передавать математические идеи;

(F) анализировать математические отношения к соединять и передавать математические идеи; и

(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования действительных чисел в различных форм. Ожидается:

(A) расширить предыдущие знания о множествах и подмножества с использованием визуального представления для описания отношений между наборами действительных чисел;

(B) приблизительное значение иррационального числа, включая π и квадрат корни чисел меньше 225 и расположите это приближение рационального числа на числовой прямой;

(D) заказать набор настоящих числа, возникающие из математических и контексты реального мира.

(3) Пропорциональность. Студент применяет математические стандарты процесса для использования пропорциональных соотношений для описания расширений. Ожидается:

(A) обобщают, что отношение соответствующих стороны одинаковых форм пропорциональны, включая форму и ее расширение;

(B) сравнить и сопоставить атрибуты формы и ее расширения (ов) на координатной плоскости; и

(C) использовать алгебраическое представление для объяснения влияния данного положительного рационального масштабного коэффициента, применяемого к двумерным фигурам, на координату плоскость с центром в центре расширения.

(4) Пропорциональность. Студент применяет математические стандарты процесса для объяснения пропорциональных и непропорциональных отношений с уклоном. Ожидается:

(A) используйте аналогичные прямоугольные треугольники для построения понимание этого уклона, м , заданного как скорость, сравнивающего изменение в и -значениях на изменение x -значений, (y ₂ — y ₁) / (x ₂ — x ₁), то же самое для любых двух точек (x ₁, y ₁) и (x ₂, y ₂) на той же строке;

(B) график пропорциональных отношений, интерпретация единичная ставка как наклон линии, моделирующей взаимосвязь; и

(C) использовать данные из таблицы или графика для определения скорость изменения или наклона и y — перехват в математическом и реальном мире проблемы.

(5) Пропорциональность. Студент применяет математические стандарты процесса использовать пропорциональные и непропорциональные отношения разработать основные концепции функций. Ожидается:

(A) представляют линейно-пропорциональный ситуации с таблицами, графиками и уравнениями в виде y = kx ;

(B) представляют линейные непропорциональные ситуации с таблицами, графики и уравнения в виде y = mx + b , где b ≠ 0;

(C) сопоставьте двумерные наборы данных, которые предполагают линейная связь с двумерными наборами данных, которые не предполагайте линейную зависимость от графического представления;

(D) используйте линию тренда, которая приближается к линейной взаимосвязь между двумерными наборами данных для прогнозирования;

(E) решать проблемы, связанные с прямая вариация;

(F) различают пропорциональные и непропорциональные ситуаций с использованием таблиц, графиков и уравнений в форма y = kx или y = mx + b , где b ≠ 0;

(G) идентифицирует функции с помощью наборов упорядоченных пары, таблицы, отображения и графики;

(H) определяет примеры пропорциональных и непропорциональных функций, которые возникают из математических и проблемы реального мира; и

(I) напишите уравнение в форме y = mx + b для моделирования линейной зависимости между двумя величинами с помощью словесного, числовые, табличные и графические представления.

(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки математических отношения и устанавливать связи с геометрическими формулами. Ожидается студент Кому:

(A) описывает формулу объема В = Bh цилиндра по площади основания и высоте;

(B) моделирование отношений между объемом цилиндра и конусом, имеющим равные основания и высоту, и соединяют это отношение к формулам; и

(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для решения проблемы. Ожидается:

(А) решить задачи, связанные с объемом цилиндров, конусов, и сферы;

(B) использовать предыдущие знания площади поверхности чтобы сделать связи с формулами для боковой и общей площади поверхности и определять решения проблем с прямоугольными призмами, треугольными призмы и цилиндры;

(D) определить расстояние между двумя точками на координатной плоскости с помощью теоремы Пифагора.

(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной или неравенство в проблемных ситуациях. Ожидается:

(A) написать уравнения или неравенства с одной переменной с переменными с обеих сторон, которые представляют проблемы, используя коэффициенты и константы рациональных чисел;

(B) напишите соответствующую реальную проблему когда задано уравнение с одной переменной или неравенство с переменными с обеих сторон знака равенства с использованием рационального числа коэффициенты и константы;

(C) и решите одну переменную уравнения с переменными по обе стороны от знака равенства, представляющие математические и реальные проблемы с использованием коэффициенты и константы рациональных чисел; и

(D) использовать неформальные аргументы для установления фактов о сумме углов и внешнем угле треугольников, углы, созданные при параллельные прямые пересекаются трансверсалью, а критерий угол-угол для подобие треугольников.

(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений разработать основные концепции одновременных линейных уравнений. Студент ожидается определение и проверка значений x и y , которые одновременно удовлетворяют двум линейным уравнениям вида y = mx + b из пересечения графических уравнений.

(10) Двумерные формы.Студент подает заявку стандарты математических процессов для разработки концепций трансформационной геометрии. Ожидается:

(A) обобщают свойства ориентации и согласованность вращений, отражений, переводов и растяжения двумерных фигур по координате самолет;

(B) различать преобразования сохраняющие конгруэнтность и несоответствующие;

(C) объяснить эффект переводов, отражений по оси x или y , а вращение ограничено до 90, 180, 270 и 360 в зависимости от ситуации к двумерным фигурам на координатной плоскости с помощью алгебраической представление; и

(D) моделирует влияние на линейные и площадные измерения расширенных двумерных форм.

(11) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических процедур для описания данных. Ожидается:

(A) построить диаграмму рассеяния и описать наблюдаемые данные для решения таких вопросов ассоциации, как линейные, нелинейные и нет связи между двумерными данными;

(B) определить среднее абсолютное отклонение и используйте эту величину как меру данные о среднем расстоянии взяты от среднего с использованием набора данных не более 10 данных точки; и

(C) моделировать генерацию случайных выборок того же размера из популяции с известными характеристиками для развития понятие случайной выборки, репрезентативной для населения, из которого он был выбран.

(12) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:

(A) решать реальные проблемы, сравнивая процентная ставка и срок кредита влияют на стоимость кредита;

(B) рассчитать общую стоимость погашения ссуды, включая кредитные карты и легкодоступные ссуды, по различным ставкам проценты и за разные периоды с помощью онлайн-калькулятора;

(C) объясните, как вложены небольшие суммы денег регулярно, включая деньги, откладываемые на учебу и пенсию, со временем растут;

(D) рассчитать и сравнить простые проценты и доход от сложных процентов;

(E) определить и объяснить преимущества и недостатки разных способов оплаты;

(F) анализирует ситуации, чтобы определить, представлять финансово ответственные решения и определять преимущества финансовых ответственность и издержки финансовой безответственности; и

(G) оценка стоимости двухлетнего и четырехлетнего высшее образование, включая семейный вклад, и периодические сбережения план накопления денег, необходимых для вклада в общую стоимость посещаемость не менее первого года обучения в колледже.

Источник: Положения настоящего стандарта 111.28 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.

Для дополнительная информация, электронная почта [email protected].

Математика Стандарты учебных ресурсов

Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него. Стандарты обучения (SOL) и тестирования
Новости и объявления
Инициатива по математике в Вирджинии
Инициатива подготовки к математике в Вирджинии (VMPI) — это совместная инициатива Департамента образования Вирджинии (VDOE), Государственного совета высшего образования штата Вирджиния (SCHEV) и системы общественных колледжей Вирджинии (VCCS).Инициатива поддерживает Профиль выпускника Вирджинии, переопределяя математические пути для студентов в Содружестве, чтобы обратиться к знаниям, навыкам, опыту и качествам, которые студенты должны достичь, чтобы добиться успеха в колледже и / или на рабочем месте и быть «готовыми к жизни». ”
Теперь доступны быстрые проверки по математике!
Just in Time Quick Checks по математике — это формирующие экзамены, соответствующие стандартам обучения по математике (SOL) 2016 года.Эти ресурсы, разработанные учителями и руководителями математики Вирджинии, предназначены для того, чтобы помочь учителям выявлять учащихся с незаконченным обучением и помочь в планировании обучения, чтобы заполнить потенциальные пробелы «вовремя».
Нарушения обучаемости в ресурсах по математике
Страница с ограниченными возможностями обучения математике включает информацию и ресурсы, а также два новых сопутствующих руководства VDOE:
Коронавирус (COVID-19) —
Обучение на месте Ресурсы по математике
23 марта 2020 года губернатор Ральф Нортам распространил свое распоряжение о закрытии всех государственных и частных школ K-12 в Вирджинии в связи с продолжающимся распространением COVID-19 до конца учебного года. Команда математики Министерства образования Вирджинии собрала несколько материалов по математике Learning in Place, , чтобы помочь учителям, родителям и ученикам в это беспрецедентное время.
2016
Математика Стандарты обучения Анализ результатов теста Результаты
общегосударственных тестов по математике на основе стандартов обучения (SOL), основанных на нормах обучения по математике 2016 года и проведенных весной 2019 года, были проанализированы для определения конкретного содержания, по которому общая успеваемость учащихся была слабой или непоследовательной.Эти презентации доступны и предназначены для того, чтобы дать преподавателям более глубокое понимание математических концепций, которые бросают вызов студентам всего штата.
Содержание страницы
Записки суперинтенданта относительно реализации
Ожидаемые результаты по математике в Вирджинии, готовые к поступлению в колледж и карьеру
Ожидаемые результаты по математике определяют уровень успеваемости, которого должны достичь учащиеся, чтобы быть академически подготовленными к успеху на начальных курсах кредитных курсов колледжа.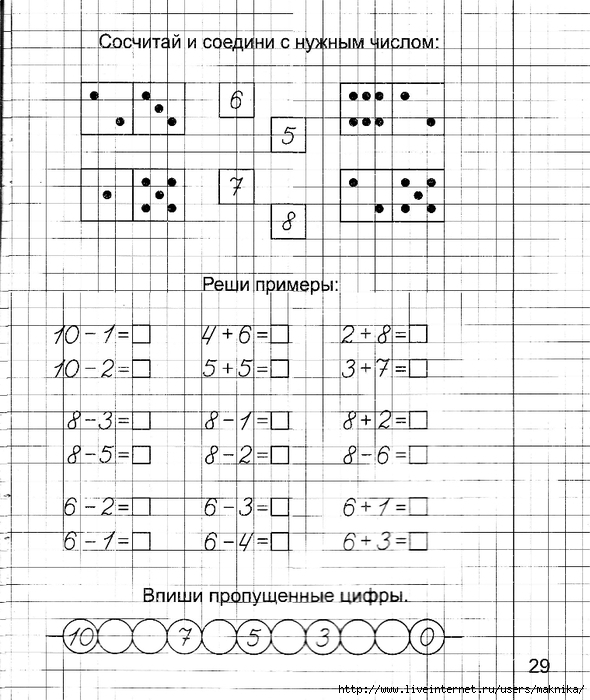 Ожидания были разработаны в рамках Инициативы готовности к колледжу и карьере — процесса, в котором участвовали преподаватели двух- и четырехлетних колледжей и университетов Вирджинии, представители бизнес-сообщества и преподаватели средних школ.
Ресурсы для инструкций
Своевременные быстрые проверки по математике — эти формирующие экзамены соответствуют Стандартам обучения по математике (SOL) 2016 года. Эти ресурсы, разработанные учителями Вирджинии и руководителями математики, предназначены для того, чтобы помочь учителям выявлять учащихся с незавершенным обучением и помогать в планировании обучения, чтобы «вовремя» заполнить потенциальные пробелы.«По мере того, как в течение учебного года вводится новый контент, учителя могут использовать эти быстрые проверки для выявления и диагностики незавершенного обучения на уровне класса и / или для оценки понимания необходимых знаний, которые могут потребоваться для доступа к контенту на уровне класса. Пробелы в понимании математики учащимися существуют по разным причинам, и эти ресурсы можно использовать, чтобы помочь вернуть учащимся математическое обучение в нужное русло.
Инструмент вертикального сочленения по математике (MVAT) — этот инструмент обеспечивает поддержку в определении концепций, соответствующих Стандартам обучения по математике (SOL) 2016 года, которые формулируются на разных уровнях математического обучения или курсов.
Учебные планы по математике — включают учебные планы, соответствующие Стандартам обучения по математике 2016 года , чтобы помочь учителям привести обучение в соответствие с основными знаниями и навыками.
Корреляция между VASOL и CCSS. Это таблица в формате Excel. (XLS) — Эта электронная таблица содержит черновик корреляций между детским садом и алгеброй II — 2016 Вирджинские стандарты обучения (VASOL) для математики с Общими основными государственными стандартами (CCSS) для математики. Эта корреляция была создана для поддержки преподавателей по всему Содружеству, поскольку они пытаются использовать материалы, которые могут обозначать только соответствие CCSS. Все VASOL и CCSS, а также цели процесса Вирджинии и математические практики CCSS связаны по всей таблице, чтобы упростить перекрестные ссылки.
Учебные планы по математике с совместным преподаванием — включают учебные планы, соответствующие Стандартам обучения по математике 2016 г. , разработанным учителями, участвующими в инициативе «Совершенство в области совместного обучения».Эти планы включают предложения по улучшению уроков и занятий в классе с совместным преподаванием.
Настенные карточки со словарным запасом математики (K-8, Алгебра I, Геометрия, AFDA и Алгебра II) — обеспечивают отображение слов математического содержания и связанных с ними визуальных подсказок, помогающих в развитии словарного запаса.
Нарушения обучаемости по математике — Эта страница содержит информацию и ресурсы, а также два новых сопутствующих руководства VDOE:
сложных математических заданий — (K-8, алгебра I, геометрия, алгебра II) Эти ресурсы предназначены для поддержки учителей во внедрении в их классах «Стандартов обучения по математике 2016» . Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.
Математические стандарты обучения (SOL) 2018 институты — Математические стандарты учебных заведений 2018 года обеспечили обучение, направленное на внедрение математических стандартов обучения 2016 года; усиление преподавания и изучения математики посредством содействия содержательному математическому дискурсу; и поддержка равных возможностей обучения математике для всех учащихся.Продукт Математических институтов 2018 года представляет собой набор онлайн-модулей профессионального развития, предназначенных для использования группой учителей определенного уровня или курса при содействии одного из членов команды.
Математические стандарты учебных заведений 2017 — предоставлены ресурсы для профессионального развития, направленные на углубление понимания участниками Стандартов обучения по математике 2016 и использование эффективных методов преподавания математики, как указано в Принципах действий NCTM : обеспечение успеха в математике для всех резюме.
Компьютерное адаптивное тестирование (CAT) — включает информационные видеоролики по CAT и ресурсы
Учебные видео для учителей — учебные видео, предназначенные для учителей в поддержку внедрения стандартов обучения по математике 2016
Практические задания
SOL в TestNav 8 — предоставьте примеры контента, согласованного со Стандартами обучения по математике 2016 , и возможности для практики с онлайн-инструментами и функциями, которые доступны в TestNav 8 во время онлайн-тестирования SOL.
Ресурсы для оценки
Начало страницы
Детские игры, фильмы и книги K-3
Starfall не имеет рекламы, не собирает личную информацию от детей, не продает никакой информации и использует файлы cookie только для внутреннего управления сайтом. Используя этот сайт, вы соглашаетесь на использование файлов cookie и обновленную Политику конфиденциальности OK
Звездопад.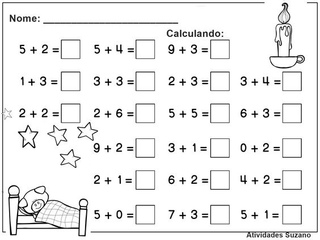 com® открылся в сентябре 2002 года как бесплатная общественная служба по обучению детей чтению. С тех пор он расширился, включив в него языковые искусства и математику для дошкольных учреждений, детских садов, первого, второго и третьего классов. Акцент Starfall на фонематической осведомленности, систематической последовательной фонетике и обычных словах в сочетании с аудиовизуальной интерактивностью оказался эффективным в обучении начинающих читателей. Мероприятия «Звездопад» основаны на исследованиях и соответствуют индивидуальным и общепринятым государственным стандартам по английской словесности и математике.
Программа делает упор на исследование, игру и позитивное подкрепление — побуждает детей стать уверенными и внутренне мотивированными. Starfall — образовательная альтернатива другим развлечениям для детей и особенно эффективна для специального образования, домашнего обучения и развития английского языка (ELD, ELL, ESL). Он широко используется в школах, которые обслуживают детей с особыми потребностями и трудностями в обучении.
No related posts.

Игры по математике для детей 6-7-8 лет

Полезные дидактические тесты на любой вкус

Шикарная коллекция математических флеш игр от Quicksave

Программа математического развития дошкольников «Игралочка»

Содержание

Введение

Конспект занятия по математике для детей 6-7 лет: Целое и части

Конспекты занятий

Конспект занятия по математике

занимательные задания и игры для дошкольников

Начальный этап

Прописи и игры

Знания ребенка

Советы психологов и педагогов

математических рассказов для детей 6-7 лет | Scholastic

математических навыков и этапов в зависимости от возраста | Разобрался

Младенцы (в возрасте 0–12 месяцев)

Малыши (возраст 1–2 года)

Дошкольники (в возрасте от 3 лет) –4 года)

Детсадовцы (возраст 5 лет)

этапов математики 7-8 — Kidspot

Навыки счета в возрасте 7–8 лет могут включать:

Важно

7 секретов математики, которые увлекут вашего ребенка Математика

Будьте примером

Помогайте своему ребенку использовать математику каждый день

Ознакомьтесь со стандартами обучения

Контролируйте домашнее задание по математике

Обратите внимание на детали

Играйте в математические игры дома

Читайте книги, содержащие математику

Итоги

Глава 111. Подраздел B

Математика Стандарты учебных ресурсов

Новости и объявления

Инициатива по математике в Вирджинии

Теперь доступны быстрые проверки по математике!

Нарушения обучаемости в ресурсах по математике

Коронавирус (COVID-19) —

2016

Содержание страницы

Записки суперинтенданта относительно реализации

Ожидаемые результаты по математике в Вирджинии, готовые к поступлению в колледж и карьеру

Ресурсы для инструкций

Ресурсы для оценки

Детские игры, фильмы и книги K-3

Добавить комментарий Отменить ответ