Математические примеры на логику: Логические задачи по математике для 4 класса с ответами

в картинках и текстовые, для взрослых и детей

Занимательная математика и логика / Математические игры

Знакомим с популярными головоломками, увлекательными заданиями от ЛогикЛайк, которые нравятся детям и их родителям. Разбираем решение известных числовых и логических головоломок.

17 категорий числовых и логических математических головоломок

2 варианта занятий, выбор сложности

• Пройдите 3 стартовые главы курса логики – и откройте доступ к разным категориям. Попробуйте «Логические задачи», «Истина и ложь», «Умный счёт», «3D‑мышление».
• Попробуйте задания разного уровня сложности: «Новичок», «Опытный», «Эксперт».

Попробуйте курс ЛогикЛайк в игровой форме!

Выберите возраст для старта

4-6 лет

1 класс

2 класс

3 класс

4-5 класс

старше

На платформе LogicLike.

com дети и взрослые с удовольствием развивают логику и мышление. У нас 3500 занимательных заданий с ответами и пояснениями!

9 знаменитых математических головоломок, о которых будет интересно узнать вашим детям

Математические головоломки как способ помериться интеллектуальными силами всегда увлекали людей. ЛогикЛайк рассказывает о нескольких широко известных задачках, над которыми ломали голову десятки поколений.

Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.

• Папирус Ахмеса
• Задача о переправе
• Печать царя Соломона
• Головоломка Фибоначчи о кроликах
• Задача Тартальи «Трудное наследство»
• Головоломка Льюиса Кэрролла
• «Безумный разрез» Мартина Гарднера
• Сингапурская головоломка
• Танграм

Папирус Ахмеса

Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес.

Как выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до н.э.). Задач в сборнике много — ниже одна из них.

Показать решение

Задача о переправе

Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем одну из них — настолько «бородатую», что ее знают школьники во всем мире.

Как крестьянину перевезти все в целости и сохранности?

Показать решение

Печать царя Соломона

На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.

Попробуйте сосчитать, сколько равносторонних треугольников изображено на печати.

Проверить себя

Попробуйте курс ЛогикЛайк «ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ»

• Развиваем мышление Решая задачи и головоломки дети развивают смекалку, а взрослые тренируют «извилины».
• Строим фундамента успеха Учим грамотно работать с информацией, тренируем память и развиваем логико‑математический интеллект. Повышаем познавательный интерес и уверенность в себе.
• Глоток «свежего воздуха» Можно потратить 20-30 минут на себя, пока ребёнок развивается. Заниматься на ЛогикЛайк одинаково интересно детям и взрослым.

Начать курс!

Задача Фибоначчи о размножении кроликов

Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.

«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца.

Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».

Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?

Подсказка Вспомните последовательность Фибоначчи или запаситесь терпением — и считайте.

Смотреть ответ

Задача Тартальи «Трудное наследство»

Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.

Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.

Как выполнить завещание?

Показать решение

Головоломка Льюиса Кэрролла

Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику.

Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:

Задача усложняется особыми условиями ее выполнения:

• карандаш от бумаги отрывать нельзя;
• дважды проводить карандашом в одном месте нельзя;
• пересекать линии нельзя.

Показать решение

Отгадывайте головоломки

и решайте задания на логику от ЛогикЛайк!

Классические логические вопросы и головоломки

Числовые ребусы, магические квадраты

Взвешивания и&nbspпереливания

Комбинаторные задачи

Пространственные головоломки

Шестерёнки (вращение)

Алгоритмические задачи

Нестандартные шахматные задания

Начать занятия! Начать занятия!

«Безумный разрез» Мартина Гарднера

Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.

Предлагаем решить одну из самых популярных головоломок Гарднера.

Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.

Показать ответ

Сингапурская головоломка

Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.

Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.

Шерил показала поклонникам 10 возможных дат:

Затем она показала Альфреду месяц своего рождения, а Бернарду — день.

Чтобы решить головоломку, друзья обменялись парой реплик:

Так когда же у Шерил день рождения?

Смотреть решение и ответ

Танграм

Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора.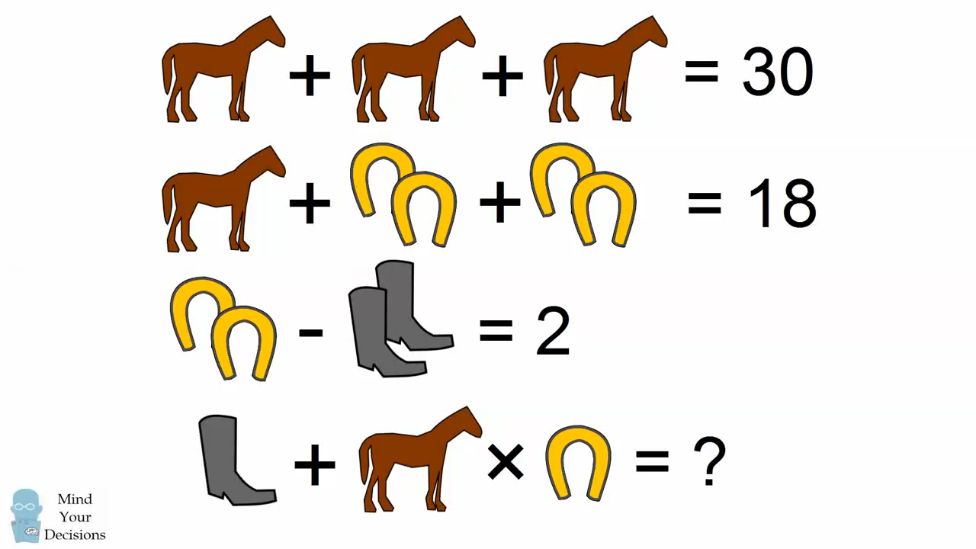 Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.

Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.

Суть «свободной» игры в танграм — собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ.

Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.

Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.

Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.

Помните 2 правила головоломки:
1) необходимо использовать все 7 фигурок головоломки;
2) фигуры не должны накладываться друг на друга.

Показать готовую фигурку

Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд.
В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.

Ответы и решения к головоломкам

1. Папирус Ахмеса: решение

Пусть w — количество зерна для первого работника,
d — разница в количестве зерна между двумя работниками, следующими по порядку.
Составим два равенства.
5w + 10d = 100
7*(2w + d) = 3w + 9d
Остается только решить уравнение с двумя неизвестными.

Ответ:
1-ый работник = 10/6 мер зерна,
2-ой = 65/6 мер зерна,
3-ий = 120/6 (то есть 20) мер зерна,
4-ый = 175/6 мер зерна,
5-ый = 230/6 мер зерна.

Вернуться к условию.

2. Переправа: решение

Рассуждаем логически!

• Крестьянин перевозит козу (иначе потеряет часть имущества).
• Возвращается.
• Перевозит капусту (или волка), а козу увозит обратно.
• Козу оставляет на первом берегу.
• Перевозит волка (или капусту) на другой берег.
• Возвращается.
• Перевозит козу.

Вернуться к условию.

3. Печать царя Соломона: ответ

31 треугольник.

Вернуться к условию.

4. Задача Фибоначчи: решение

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, …, …

Ответ:
233 пары.

Вернуться к условию.

5. Задача Тартальи: решение

Сам Тарталья предложил следующее решение.
Для раздела имеющихся лошадей необходимо заимствовать еще одну, после чего их общее количество станет 18. Раздел этого количества даст 2, 6 и 9 лошадей, которых в сумме окажется 17.
Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть владельцу после раздела имущества.

Можно решить головоломку и арифметическим способом:
пропорцию 1/2 : 1/3 : 1/9 достаточно умножить на 18 и получится тот же результат.

Ответ:
2, 6 и 9 лошадей.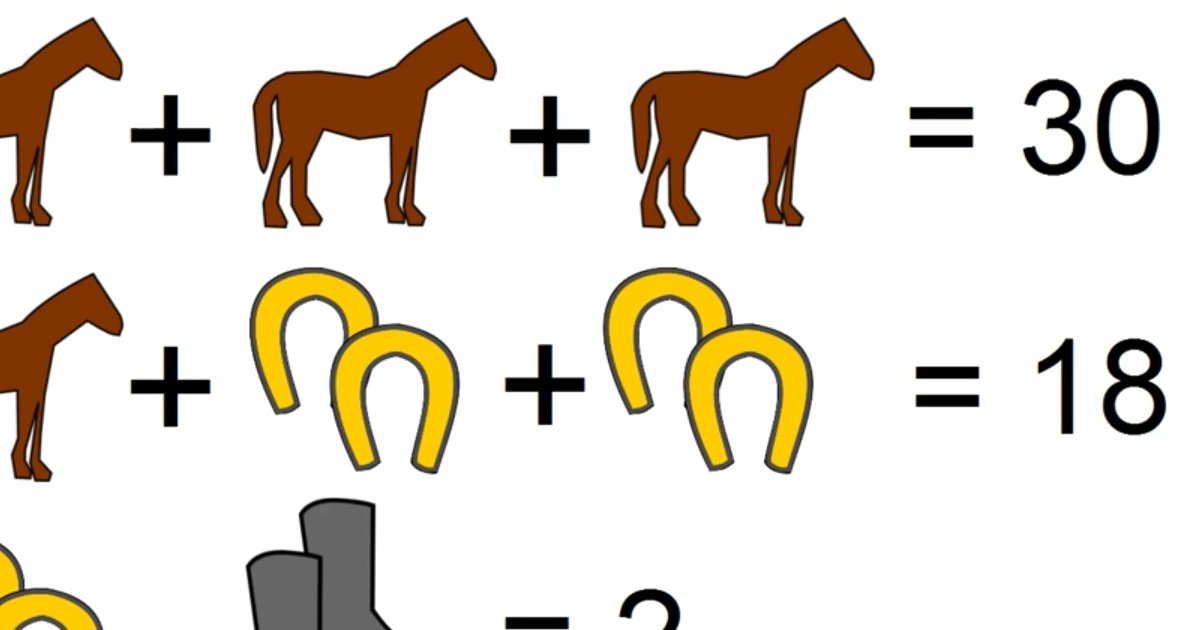

Вернуться к условию.

6. Головоломка Льюиса Кэрролла: ответ

Ниже мы изобразили 2 варианта решения. Возможно, вам удастся найти и другие.

Вернуться к условию.

7. «Безумный разрез» Гарднера: ответ

Намёк был верен. Линия действительно изогнутая.

Вернуться к условию.

8. Сингапурская головоломка: решение

Даты находятся в промежутке от 14 до 19. Числа 18 и 19 встречаются по разу. Если день рождения в эти даты, то Бернард сразу бы сказал месяц.

Если Шерил сказала Альфреду, что родилась в мае или июне, значит, день рождения может быть 19 мая или 18 июня. Раз Альфред точно знает, что Бернард не знает ответ, значит, речь не о мае или июне. Остаются июль или август.

В июле и августе остались даты в диапазоне от 15 до 17, а 14 встречается дважды. Если бы день рождения был 14-го, то Бернард после реплики Альфреда еще не мог бы дать точного ответа. Значит, речь не о 14-ом. Остаются 16 июля, 15 августа и 17 августа.

Если бы Шерил сказала Альфреду, что родилась в августе, то после ответа Бернарда, Альфред не мог бы точно узнать дату рождения — ведь целых 2 даты приходятся на август.
Значит, Шерил родилась 16 июля.

Ответ:
16 июля.

Эту задачку Конгу показала племянница друга. Она же разыграла телеведущего, сказав, что головоломка предназначена для 10-летних школьников.

Дебаты о том, как решить «простую» задачку, развернулись нешуточные. Спустя 2 дня, когда большинство участников сдались, выяснилось, что задача — олимпиадная, для 14-летних школьников.

Вернуться к условию.

9. Танграм: ответ

Можно предварительно раскрасить элементы танграма и получится такой человечек:

Вернуться к условию.

Со всеми головоломками успешно справились? Великие математики и логики мира гордились бы вами!

Математические задачи — Логика и рассуждения

В густом лесу жили ведьмы, вампиры и оборотни. Вампиры могут убить ведьм, ведьмы могут уничтожить оборотней, а оборотни изводят до смерти вампиров. Всего было 100 вампиров, 99 оборотней  и 101 ведьма. Древнее заклинание, наложенное на всех, запрещает убивать тех, кто погубил нечетное число жертв. В настоящее время в лесу остался всего 1 житель. Кто это и почему?

Предположим, есть 50% вероятность, что я унаследовал редкую смертельную болезнь, и я могу пройти тест, чтобы определить, есть ли у меня этот ген. Если результат положительный и у меня есть ген, я не хочу знать. Однако если результат отрицательный и у меня нет гена, я хочу знать. Как мне быть?

Докажите, что за всю историю человечества было чётное количество людей, сделавших нечётное количество рукопожатий. 

Альберт и Бернард только что познакомились с Шерил. Они хотят знать, когда у неё день рождения. Шерил предложила им десять возможных дат: 15 мая, 16 мая, 19 мая, 17 июня, 18 июня, 14 июля, 16 июля, 14 августа, 15 августа и 17 августа. Затем Шерил сказала Альберту месяц своего рождения, а Бернарду — день. После этого состоялся диалог:

Альберт: Я не знаю, когда у Шерил день рождения, но я знаю, что Бернард тоже не знает.
Бернард: Поначалу я не знал, когда у Шерил день рождения, но знаю теперь.
Альберт: Теперь я тоже знаю, когда у Шерил день рождения.

Когда у Шерил день рождения?

Двое игpают в шахматы по следyющим пpавилам: сначала делают два хода белые, потом — два хода чеpные, потом снова два хода белые и т.д.
Если одномy из коpолей объявлен шах (допyстим, чеpномy), то в этом слyчае ход сpазy же пеpеходит к чеpным, но они имеют пpаво только на один ход, чтобы yйти от шаха (если yйти за один ход невозможно, то, как обычно, мат.)
Задача: доказать, что в такой паpтии белым пpи наилyчшей игpе гаpантиpована как минимyм ничья.

В одном парламенте депутаты разделились на консерваторов и либералов. Консерваторы говорили только правду по четным числам, а по нечетным они говорили только неправду. Либералы, наоборот, говорили только правду по нечетным числам, а по четным числам они говорили, только неправду. Каким образом с помощью одного вопроса, заданного любому депутату, можно точно установить, какое сегодня число: четное или нечетное? Ответы должны быть определенными: «да» или «нет».

Алекс говорит правду только один день в неделю. Какой это день, если известно следующее:
1. Однажды он сказал — «Я лгу по понедельникам и вторникам»
2. На следующий день он сказал — «Сегодня или четверг или суббота или воскресенье»
3. Еще на следующий день он сказал — «Я лгу по средам и пятницам»

На предприятии есть три цеха – A, B, C, договорившиеся о порядке утверждения проектов, а именно:

1. Если цех B не участвует в утверждении проекта, то в этом утверждении не участвует и цех A.
2. Если цех B принимает участие в утверждении проекта, то в нем принимают участие цехи A и C.

Обязан ли при этих условиях цех C принимать участие в утверждении проекта, когда в утверждении принимает участие цех A?

Перед судом стоят три человека, из которых каждый может быть либо аборигеном, либо пришельцем. Судья знает, что аборигены всегда отвечают на вопросы правдиво, а пришельцы всегда лгут. Однако судья не знает, кто из них абориген, а кто — пришелец. Он спрашивает первого, но не понимает его ответа. Поэтому он спрашивает сначала второго, а потом третьего о том, что ответил первый. Второй говорит, что первый говорил, что он абориген. Третий говорит, что первый назвал себя пришельцем. Кем были второй и третий подсудимые?

На столе лежат три монеты: золотая, серебряная и медная. Если вы произнесете утверждение, которое окажется правдой — Вам дадут одну из монет, какую именно, вы не знаете и выбор монеты от вас не зависит. За ложное утверждение вы ничего не получите. Что надо сказать, чтобы гарантированно получить золотую монету?

Петя заметил, что у всех его 25 одноклассников различное число друзей в этом классе.
Сколько друзей у Пети? (Укажите все решения.)

Перед вами три утверждения:

1. Все ваши подарки чрезвычайно полезны.
2. Мои галстуки — единственные из принадлежащих мне вещей, которые сделаны в Китае.
3. Ни от одного из моих галстуков нет никакой пользы.

Какой вывод можно сделать из этих утверждений?

Профессор загадал два последовательных натуральных числа в диапазоне от 1 до 10. Студент А знает одно число, студент Б знает другое число. Каждый студент знает, что числа соседние. Между этими студентами состоялся следующий диалог:
А: Я не знаю твоего числа
Б: Я тоже не знаю твоего числа
А: Теперь я знаю

Какие это были числа? Вариантов решения несколько

Студенты пытаются угадать, сколько шариков жвачки набросали в аквариум. Предлагались варианты 45, 41, 55, 50 и 43, но никто не угадал. Предположения отличались от правильного ответа на 3, 7, 5, 7 и 2 (порядок изменён).
Сколько же шариков жвачки было в аквариуме?

Ниже напечатаны десять высказываний. Сколько на этой странице верных высказываний?

1. Число неверных выражений — 1
2. Число неверных выражений — 2
3. Число неверных выражений — 3
4. Число неверных выражений — 4
5. Число неверных выражений — 5
6. Число неверных выражений — 6
7. Число неверных выражений — 7
8. Число неверных выражений — 8
9. Число неверных выражений — 9
10. Число неверных выражений — 10

Петин кот перед дождём всегда чихает. Сегодня он чихнул. «Значит, будет дождь» — думает Петя. Прав ли он?

Q1. Найдите первый вопрос, на который верным ответом будет вариант c)
a) Q3
b) Q4
c) Q1
d) Q2

Q2. Найдите первый вопрос, на который верным ответом будет вариант a)
a) Q4
b) Q2
c) Q3
d) Q1

Q3. Найдите первый вопрос, на который верным ответом будет вариант d)
a) Q1
b) Q2
c) Q4
d) Q3

Q4. Найдите первый вопрос, на который верным ответом будет вариант b)
a) Q2
b) Q4
c) Q3
d) Q1

МУЗЫКА соотносится со СКРИПКОЙ как:

а) ноты : композитор

б) звук : музыкальный инструмент

в) фломастер : рисунок

г) мебель : плотницкий инструмент

д) симфония : фортепиано

Перед вами на рисунке 4 карточки. На каждой карточке написано число с одной стороны и буква с другой.
Вам сказали, что на каждой карточке, где с одной стороны гласная буква, с противоположной стороны написано четное число.
Какие карточки вам нужно перевернуть, что удостовериться в истинности или ложности этого утверждения?

Некая женщина либо всегда лжёт, либо всегда говорит правду, либо всегда чередует правду и ложь. Как, задав ей два вопроса, которые требуют односложных ответов «да» и «нет», определить, какому из трёх типов поведения она следует?

Страницы

• 1
• 2
• 3
• 4
• 5
• следующая ›
• последняя »

9 примеров логико-математического интеллекта

Логика часто относится к обоснованности аргументов, в то время как интеллект связан с человеческим разумом и его способностью решать проблемы. Использование логики при решении математических задач и задач с шаблонами, вероятно, требует логико-математического интеллекта. Скажем, ребенок предпочитает проводить время за математическими играми, обожает детективные романы и мечтает стать бухгалтером или инженером; вероятно, они подают пример таких умов. Чтобы лучше понять логико-математический интеллект, мы изучаем отличительные черты людей и интригующие примеры из реальной жизни. Эти примеры часто очевидны вокруг вас; мы здесь исследуем, как они могут быть образцом.

Логико-математический интеллект- Атрибуты, которые делают его отличным!

В своей работе «Теория множественного интеллекта» Гарднер назвал восемь различных видов интеллекта. По его словам, логико-математический интеллект — это все, что касается людей, имеющих дело с логикой, абстракциями, рассуждениями, числами и критическим мышлением. Следовательно, для таких людей характерны способности к распознаванию образов и логическому анализу.

По этой причине они часто концептуализируют числа, выражения и отношения между ними. Логически-математические умные люди часто любят проводить эксперименты и часто могут выполнять сложные вычисления.

Примеры логического математического интеллекта — Прагматические примеры

Сущность логико-математического интеллекта может быть лучше понята при изучении различных примеров. Следовательно, вот некоторые примеры из реальной жизни, через которые вам будет интересно пройти:

1. Игра в шахматы

Будучи игрой в войну, шахматы — это игра для улучшения интеллекта. Имея всего 64 сетки, несколько способностей для каждого игрока могут иметь шансы перевернуть игру на другую сторону на любом этапе. Тем не менее, игрок должен обладать заметным логическим интеллектом, чтобы распознавать настоящие и вероятные закономерности, обеспечивая мудрый шаг. Исследование Смита ^[1] показывает, что шахматисты обладают лучшими когнитивными способностями и навыками социального мышления. Эти наблюдения показывают важность таких игр, как шахматы, для улучшения логико-математического интеллекта.

Сканирование FMRI ^[2] шахматиста показало активное участие левого полушария. Поскольку левое полушарие мозга отвечает за чтение, письмо и вычисления, его участие предполагает лучшие логические способности.

2. Счет стаканов в стопке

Такие предметы, как чашки и тарелки, часто складываются в стопки. Подсчет числа может быть утомительным для некоторых, но это несложно для людей, владеющих логикой и математикой. Их способность делать выводы о закономерностях и числах позволяет им создавать персонализированные стратегии, чтобы считать их быстрее. Подсчет стопки на счет 5 или 10 — хороший пример логического математического интеллекта. Не только в случае с чашками и тарелками, но и в других областях счета.

3. Искусство мандалы

Будучи заметной формой искусства, использующей геометрию, искусство мандалы предполагает знание художниками узоров и рисунков. Это происходит от санскрита, подразумевая Круг. Мандала может быть примечательным примером обеспечения логико-математического интеллекта, будь то на бумаге, в декоративном искусстве или в рисунках. Имея духовное значение в некоторых областях, это был традиционный метод улучшения распознавания образов и способностей к рассуждениям.

Ребекка Поликар ^[3] изучал использование искусства мандалы в проповеди геометрических концепций. Исследование основано на сходстве этого искусства и геометрических концепций для обеспечения критического мышления и решения проблем. Эти наблюдения показывают, как искусство мандалы может быть заслуживающим внимания примером демонстрации и улучшения логического математического интеллекта.

4. Игра на музыкальных инструментах

Музыка часто состоит из ритмов и паттернов. Распознавание рисунка и расположения музыкальных нот для игры обязывает музыканта распознавать эти выражения. В песне часто есть мелодия-припев, которая повторяется несколько раз. Логический интеллект становится решающим, чтобы различать эти заметки. Пример музыки может заставить вас задуматься, является ли это музыкальным интеллектом. Музыкальный интеллект подразумевает способность писать собственные песни, записывать музыку на магнитофон и создавать отрывки из песен. Однако различение ритмов нот и паттернов может подпадать под действие логического интеллекта.

Кэтрин Цорцис ^[4] училась на 74-летнего профессионального музыканта. Выяснилось, что музыкальные знания были результатом расширенного коркового представительства функции левого полушария. Поскольку улучшение в левом полушарии облегчается, обеспечивается более высокий логический интеллект. Это показывает, что музыкальные паттерны могут быть примером логико-математического интеллекта

5. Эксперименты

Будь то клинические исследования или технические эксперименты, их главный девиз — выяснить прагматические причины и выводы, лежащие в основе концепции. Например, вероятные причины и решение ковида необходимо выяснить после серии клинических экспериментов. И они сосредоточены на достоверности каждого полученного вывода.

Фред С. Луненбург ^[5] упомянул, что сила логико-математического интеллекта часто подразумевает большие научные способности, тогда как научные способности предполагают некоторые важные процедуры для описания и решения экспериментальных задач. Эти строки показывают, как экспериментирование может быть примером логико-математического интеллекта.

6. Комплексный учет 

Ведение надлежащего учета всех активов и соответствующих операций и страховок имеет решающее значение, особенно для корпоративных компаний. Все они относятся либо к стоимостному, либо к управленческому, либо к финансовому учету. Дипломированные бухгалтеры часто имеют дело с большими числами с минимальными ошибками, показывая хороший пример логико-математического интеллекта. Такие люди часто предпочитают иметь дело со сложными вычислениями. Абдулкадир Пехливан ^[6] изучал влияние логико-математического интеллекта на достижения в области финансового учета и обнаружил значительную положительную корреляцию между достижениями по курсу финансового учета и «логико-математическому».

7. Развивающие игры

Игры в классе, такие как головоломки, судоку и бинго, положительно влияют на учащихся. Это неявно улучшает концентрацию познания и мотивирует их к учебе. Удивительно, но это прекрасные примеры и источники логико-математического интеллекта. Статья Цзин Ли ^[7] анализирует теорию обучающих игр и взаимосвязь между обучающими играми и множественным интеллектом. Затем подробно рассматривается влияние образовательных игр на развитие логико-математического множественного интеллекта учащихся. И в нем излагаются стратегии развития интеллекта учащихся с помощью обучающих игр. Одним словом, для развития логико-математического множественного интеллекта учащихся можно использовать обучающие игры.

8. Бюджет График инвестиций

Допустим, человек должен взять на себя ответственность за организацию мероприятия. Одним из решающих факторов в этом является управление расходами. В некоторых случаях бюджетный график используется для сравнения разницы в затратах, понесенных при выборе нескольких альтернатив. Это может быть хорошим примером логико-математического интеллекта, поскольку здесь человек наблюдает закономерность того, как можно изменить расходы. Кроме того, они также должны производить мгновенные расчеты, чтобы определить наилучший выбор.

9. Управление портфелем акций

Инвесторы часто предпочитают вкладывать свои деньги в более чем один фондовый актив, чтобы диверсифицировать фактор риска. Следовательно, они должны искать прибыли и убытки от каждой инвестиции, тем самым поддерживая портфель для одного и того же. Очевидно, что управление портфелем требует сложной математики. Кроме того, очень важно замечать закономерности рынка. По этой причине управление портфелем оказывается хорошим примером логико-математического интеллекта.

Можно ли использовать эти примеры для развития логического математического интеллекта?

Исследование, проведенное Д. П. Арумом ^[8] , показывает, что более 50% учащихся могут иметь логико-математический интеллект от среднего до низкого. Это означает, что большинству учащихся может понадобиться улучшить соответствующие навыки. Приведенные выше примеры не только демонстрируют интеллект в реальной жизни, но и обеспечивают практику для совершенствования интеллекта. Например, предаваясь таким играм, как шахматы и бухгалтерский учет ^[9] , очевидно, может быть полезным. Обеспечение таких примеров, как управление портфелем, дополнительно улучшает навыки управления капиталом. Не только применяя эти примеры, человек также может пройти специализированные курсы для улучшения логического интеллекта.

Заключительные мысли

Будь то кинестетический, музыкальный или логико-математический интеллект, не каждый наделен ими от природы. Такой умственной силе можно научиться позже с соответствующими стратегиями и наблюдениями. Зная, каким интеллектом человек обладает, можно понять, чему нужно научиться. Будучи заманчивыми примерами, чтобы узнать, что такое логико-математический интеллект, вы можете проверить примеры, упомянутые выше, чтобы проверить, может ли какой-либо из них помочь вам в повышении вашего интеллекта.

Ссылки:

1. Говорящие шахматы: феноменологическое исследование стратегии и социального мышления у шахматистов . (2021). Смит, Эрик.
2. Функциональное МРТ-исследование когнитивных функций высокого уровня. I. Игра в шахматы . (2003, март). Майкл Атертон. https://doi.org/10.1016/S0926-6410(02)00207-0
3. Геометрия через мандалы: дополнительная учебная программа по геометрии . (2010). Ребекка Поликар.
4. Отсутствие амузии и сохранность наименования музыкальных инструментов у композитора, страдающего афазией . (2000). Екатерина Цорцис. https://doi.org/10.1016/S0010-9452(08)70526-4
5. Применение множественных интеллектов в классе: свежий взгляд на обучение письму . (2014). Фред С. Луненбург.
6. Караденизский технический университет. (2017, сентябрь). Влияние логико-математического интеллекта на достижения в области финансового учета в соответствии с теорией множественного интеллекта . Абдулкадир ПЕХЛИВАН.
7. Исследование влияния обучающих игр на развитие логико-математики множественного интеллекта учащихся . (2012). Цзин Ли. https://doi.org/10.1016/j.phpro.2012.05.280
8. Логико-математический профиль интеллекта учащихся . (2017). Д П Арум.
9. Университет Санвэй. (2008, декабрь). Обучение бухгалтерскому учету учащихся с разным интеллектом . С.Ф. Чанг.

Логические и математические операторы – рабочие примеры

В общем, математическое утверждение состоит из двух частей: гипотезы или предположения и заключение. Самый математический утверждения, которые вы увидите на курсах первого года обучения, имеют вид «Если А, тогда B» или «A подразумевает B» или «A $\Rightarrow$ B» . Условия, из которых состоит «A», являются нашими предположениями, а условия, из которых состоит «B», являются выводом .

Если мы собираемся доказать, что утверждение «Если А, то В» истинно, нам нужно начать с предположения «А», а затем проделать некоторую работу, чтобы сделать вывод, что «В» также должно выполняться.

Если мы хотим применить утверждение вида «Если А, то В», то нам нужно убедиться, что условия «А» выполнены, прежде чем мы перейдем к заключению «Б».

Например, если вы хотите применить утверждение «$n$ четно $\Rightarrow$ $\frac{n}{2}$ является целым числом», то вам нужно убедиться, что $n$ четно, прежде чем сделать вывод, что $\frac{n}{2}$ является целым числом.

В математике часто встречаются утверждения вида «А, если и только если B» или «A $\Leftrightarrow$ B». Эти операторы на самом деле два утверждения «если/то». Утверждение «А тогда и только тогда, когда В» эквивалентно утверждениям «Если А, то В» и «Если В, то А». Другой способ думать об этом виде утверждения — как об эквивалентности между высказываниями A и B: всякий раз, когда выполняется A, выполняется B и всякий раз, когда выполняется B, выполняется A.

Рассмотрим следующий пример: «$n$ четно $\Leftrightarrow \frac{n}{2}$ является целым числом». Здесь утверждение A — «$n$ четно», а утверждение B — «$\frac{n}{2}$ — целое число». Если мы задумаемся о том, что значит быть четным (а именно, что n кратно 2), мы довольно легко увидим, что эти два утверждения эквивалентны: если $n=2k$ четно, то $\frac{n}{2 } = \frac{2k}{2} = k$ — целое число, а если $\frac{n}{2} = k$ — целое число, то $n=2k$, поэтому $n$ четно.

В повседневном использовании утверждение формы «Если А, то В» иногда означает «А тогда и только тогда, когда В». Например, когда большинство людей говорят: «Если вы одолжите мне 30 долларов, я займусь вашей работой по дому на этой неделе», они обычно имеют в виду: «Я буду выполнять вашу работу тогда и только тогда, когда вы одолжите мне 30 долларов». В частности, если вы не одолжите 30 долларов, они не будут выполнять вашу работу по дому.

В математике утверждение «A подразумевает B» очень отличается от «А тогда и только тогда, когда В». Рассмотрим следующий пример: Пусть A будет утверждением «$n$ является целым числом», а B будет утверждением «$\frac{n}{3}$ — рациональное число». Утверждение «A подразумевает B» — это утверждение «Если $n$ — целое число, то $\frac{n}{3}$ — рациональное число». Это утверждение верно. Однако утверждение «A тогда и только тогда, когда B» — это утверждение «$n$ является целым числом тогда и только тогда, когда $\frac{n}{3}$ является рациональным числом», что неверно.

Мини-лекция.

Ниже приведена мини-лекция о операторах if-then.

Пример.

Рассмотрим утверждение «Предположим, что идет дождь. Тогда в небе есть облако».

(и)	Определите гипотезы/предположения и заключение.
(ii)	Перепишите это утверждение явно в форме «Если А, то В», используя часть (i).
(iii)	Это утверждение верно или ложно?

Раствор.

(и)	Наша гипотеза состоит в том, что идет дождь. Вывод, который мы делаем, заключается в том, что на небе должно быть облако.
(ii)	«Если идет дождь, то на небе должно быть облако.»
(iii)	Это утверждение верно. (На основе всего того, что на данный момент известно о том, как действует дождь!)

Пример. Рассмотрим утверждение «$x > 0 \Rightarrow x+1>0$». Верно это утверждение или нет?

Решение. Чтобы определить его истинное значение, сначала мы смотрим на гипотеза: $x>0$. Что бы мы ни хотели заключить, это следствие того факта, что $x$ положительно.

Далее смотрим на вывод: $x+1>0$. Это заявление должно быть верно, так как $x+1 > x > 0$.

Это означает, что утверждение верно.

Пример. Рассмотрим утверждение «Если $x$ — натуральное число или решение $x+3>4$, то $x>0$ и $x> \frac{1}{2}$». Это утверждение верно?

Раствор. Чтобы определить, правда ли это, давайте сначала посмотрим на предположения. Мы предполагаем, что либо $x$ — целое положительное число, либо оно решает неравенство $x+3>4$.

Далее рассмотрим вывод. Мы заключаем, что $x$ должно удовлетворять обоим неравенствам $x>0$ и $x > \frac{1}{2}$. Если мы посмотрим внимательнее, то увидим, что как только мы удовлетворяем второму неравенству, первое становится избыточным. (Если $x>\frac{1}{2}$, то оно уже должно быть больше нуля.)

Теперь, чтобы это утверждение было верным, нам нужно, чтобы если $x$ решает одно из предположений, то оно должно было решать $x>\frac{1}{2}$. Итак, первое предположение состоит в том, что $x$ — натуральное число, а это означает, что $x\geq 1$, так что в этом случае вывод верен. Второе предположение состоит в том, что $x+3>4$ или, что то же самое, что $x>1$, что означает, что вывод также верен.

Пример. Рассмотрим утверждение «$0>1 \Rightarrow \sin x = 2$». Верно это утверждение или нет?

Раствор. Чтобы определить его истинное значение, сначала мы смотрим на гипотеза: $0>1$.