Математическая задача на логику: Логические задачи для детей 5

Решение задач с помощью математической логики. Информатика, 10 класс: уроки, тесты, задания.

1.	Алгебра высказываний Сложность: лёгкое	1
2.	Высказывание Сложность: среднее	1
3.	Составное высказывание Сложность: среднее	2
4.	Задача «Формула 1″ Сложность: среднее	2
5.	Задача про погоду Сложность: среднее	2
6.	Задача про сосуд Сложность: среднее	2
7.	Преступление Сложность: среднее	2
8.	Дорожно-транспортное происшествие Сложность: сложное	3
9.	Задача о максимальной прибыли Сложность: сложное	3

Математическая логика и теория алгоритмов

Составитель: д.ф.-м.н., проф. И.Л. Братчиков

---

---

Цели и задачи курса.

Его место в учебном процессе.

Цели и задачи данного курса определяются той ролью, которую играет математическая логика в современных математике и информатике. В первую очередь очевидно большое значение, которое имеет математическая логика в основаниях математики. Строгое, математически точное построение логических исчислений, решение проблемы дедукции, аксиоматические системы и доказательство теорем в их рамках прививают учащимся навыки работы с математическими объектами, математическую строгость мышления, совершенно необходимую для исследовательской работы в области математики и других точных наук.

В то же время быстрое развитие вычислительной техники способствует расширению как круга задач, решаемых с помощью математической логики, так и методов, применяемых для их решения. Это в первую очередь относится к задачам искусственного интеллекта, решение которых немыслимо без привлечения методов математической логики. Сказанное в полной мере относится и к теории алгоритмов, тесно связанной с математической логикой. Таким образом, знание основ математической логики и теории алгоритмов совершенно необходимо преподавателям математики и информатики высших и средних учебных заведений.

Содержание данного курса несколько изменено по сравнению с традиционными курсами математической логики, читаемыми на математических факультетах. В связи с быстрым развитием методов и средств логического программирования и фундаментальным значением, которое приобретает математическая логика для дальнейшего развития информатики в целом, большее внимание, чем обычно, уделено тем аспектам, которые особенно актуальны для информатики. Этим объясняется включение в курс метода резолюций, который лежит в основе логического программирования — относительно нового направления в программировании, с помощью которого решается большинство задач искусственного интеллекта. В то же время из-за недостатка часов в программу не включены теоремы Геделя, сокращено рассмотрение аксиоматических систем.

Последний раздел курса посвящен теории алгоритмов. Здесь рассматривается лишь один класс алгоритмов — машины Тьюринга как общего вида, так и наиболее важные их подклассы. Составитель настоящего курса исходит из того, что многие свойства алгоритмов изучаются в ряде других курсов, читаемых студентам факультета.

Содержание и методика изложения предмета ориентированы на его преподавание в рамках бакалавриата в четвертом или шестом семестрах очной формы обучения.

Итак, главной целью настоящего курса следует считать изучение студентами основ математической логики и теории алгоритмов, а также приобретение необходимых навыков работы с информационными, логическими и алгоритмическими объектами, которые рассматриваются в курсе.

В число основных задач курса следует включить:

1. Знакомство с основными методами логических рассуждений — дедукцией, индукцией, аналогией. Рассмотрение методов решения задач логического характера.
2. Изучение классических логических исчислений — исчисления высказываний, исчисления предикатов.
3. Освоение метода резолюций как основного метода решения проблемы дедукции в исчислениях высказываний и предикатов.
4. Знакомство с основами логического программирования.
5. Изучение основных свойств аксиоматических систем и ознакомление с методами формальных доказательств в рамках этих систем.
6. Изучение машин Тьюринга и разработанных на ее основе важнейших классов алгоритмов.

[Наверх]

---

После окончания курса студенты должны знать и уметь.

Студенты должны знать:

1. Место математической логики среди других математических дисциплин; задачи, решаемые в рамках математической логики.
2. Определение исчисления высказываний (ИВ) и основных понятий этого исчисления.
3. Методы преобразования произвольных формул ИВ в дизъюнктивные и конъюнктивные нормальные формы.
4. Проблему дедукции и ее решение методами прямой и обратной дедукции.
5. Метод резолюций для ИВ и его роль в решении проблемы дедукции.
6. Определение исчисления предикатов (ИП) и основных понятий этого исчисления.
7. Методы преобразования произвольных формул ИП в клаузальные формы.
8. Эрбранов универсум и его роль в доказательстве свойств формул ИП.
9. Подстановки и унификацию литер в ИП.
10. Метод резолюций для ИП и его роль в решении проблемы дедукции.
11. Проблематику искусственного интеллекта и способы представления баз знаний средствами ИП.
12. Понятие о логическом программировании.
13. Определение, свойства аксиоматических систем и приемы работы с ними.
14. Определение и классы машин Тьюринга и их роль в теории алгоритмов.

Студенты должны уметь:

1. Формулировать задачи логического характера в рамках ИВ и ИП.
2. Выполнять преобразования логических формул с использованием схем тождественных преобразований.
3. Проводить исследование логических формул для доказательства их свойств.
4. Применять метод резолюций для решения проблемы дедукции в ИВ и ИП.
5. Описывать базы знаний средствами логических исчислений.
6. Проводить доказательства в рамках аксиоматических систем.
7. Формулировать и решать задачи, пользуясь соответствующими классами машин Тьюринга.

По остальным вопросам программы необходимо иметь общее представление и уметь пользоваться литературой.

Ключевые понятия, которые должны быть усвоены: дедукция, индукция, аналогия, силлогизм, высказывание, предикат, логическое исчисление, логическая формула, интерпретация логических формул, общезначимость, выполнимость и невыполнимость логических формул, тождественные преобразования, дизъюнктивные и конъюнктивные нормальные формы, клаузальные формы, Эрбранов универсум, дизъюнкт, дизъюнкт Хорна, резолюция, унификация, унификатор, база знаний, аксиоматическая система, машина Тьюринга, распознаватель, преобразователь, линейно-ограниченный автомат, конечный автомат.

[Наверх]

---

Содержание курса.

Раздел 1. Введение.

Понятие информационно-логических систем и их место в математике и информатике. Роль математической логики, как теоретической основы математики. Влияние математической логики на развитие информатики. Понятие искусственного интеллекта.

Примеры задач, решаемых рассуждениями. Необходимость формализации рассуждений. Дедукция, силлогизм, индукция, математическая индукция.

Основные математические понятия, необходимые для изложения основ математической логики.

Раздел 2. Исчисление высказываний.

2.1. Формулы исчисления высказываний и их интерпретация.

Понятие высказывания. Синтаксис исчисления высказываний (ИВ). Интерпретация формул в ИВ. Общезначимые, выполнимые и невыполнимые формулы. Тривиальный алгоритм проверки выполнимости формул. Алгоритм Куайна.

2.2. Алгебраический подход к ИВ.

Алгебра логики и эквивалентные преобразования. Некоторые приложения алгебры логики.

2.3. Нормальные формы.

Дизъюнктивные и конъюнктивные нормальные формы в ИВ (ДНФ и КНФ). Методы построения ДНФ и КНФ, эквивалентных произвольным формулам ИВ: с помощью таблиц истинности, с помощью эквивалентных преобразований. Алгоритм Девиса-Патнема для проверки выполнимости нормальных форм.

2.4. Метод резолюций в ИВ.

Проблема дедукции и ее значение в математической логике и информатике. Прямая и обратная дедукции. Теорема Робинсона и правило резолюций. Метод резолюций для решения проблемы дедукции. Дизъюнкты Хорна. Метод резолюций для дизъюнктов Хорна. Оценка трудоемкости метода.

Раздел 3. Исчисление предикатов (первого порядка).

3.1. Понятие предиката.

Ограниченность ИВ. Примеры рассуждений, не формализуемых в рамках ИВ. Понятие предиката и примеры его использования в рассуждениях.

3.2. Синтаксис и семантика формул исчисления предикатов.

Синтаксис исчисления предикатов (ИП). Семантика формул в ИП. Кванторы и типы вхождения переменных в формулы. Интерпретация формул в ИП. Примеры интерпретаций. Общезначимые, выполнимые и невыполнимые формулы. Схемы общезначимых формул, используемых для эквивалентных преобразований.

3.3. Клаузальные формы.

Подстановка и конкретизация в ИП. Универсальное и экзистенциональное замыкания. Предваренные и нормальные формы. Сколемовские и клаузальные формы. Алгоритм преобразования произвольной формулы ИП в клаузальную форму.

3.4. Эрбранова интерпретация.

Эрбранов универсум множества дизъюнктов. Основные выражения и эрбранов базис. Н-интерпретация. Теорема о невыполнимости множества дизъюнктов. Следствия теоремы.

3.5. Метод резолюций в ИП.

Проблема дедукции в ИП. Фундаментальная резолюция. Унификация с помощью подстановки. Алгоритм унификации. Метод резолюций для ИП. Дизъюнкты Хорна и решение проблемы дедукции методом резолюций в ИП. Примеры применения метода резолюций для решения проблемы дедукции. Связь ИП с системами представления знаний в задачах искусственного интеллекта.

Раздел 4. Аксиоматические системы.

4.1. Определение аксиоматических систем.

Определение и свойства аксиоматических систем (АС). Области применения АС.

4.2. АС с правилом вывода Modus Ponens.

Ас исчисления высказываний (с правилом вывода М.Р.). Полнота и минимальность АС. Примеры доказательства теорем. Теорема Эрбрана-Тарского и ее использование для упрощения доказательств.

4.3. АС натурального вывода.

Определение и особенности АС натурального вывода. Правила вывода. Примеры доказательства теорем.

4.4. Теории первого порядка.

Понятие о теориях первого порядка. Примеры теорий и их использования.

Раздел 5. Основы теории алгоритмов.

5.1. Понятие алгоритма.

Неформальное определение алгоритма. Примеры алгоритмов. Основные свойства алгоритмов. Роль алгоритмов в информатике. Парадигма процедурного программирования.

5.2. Алгоритмические проблемы.

Проблема разрешимости. Примеры неразрешимых проблем. Понятие вычислимости и вычислительные процедуры.

5.3. Машины Тьюринга.

Определение машины Тьюринга. Примеры машин Тьюринга. Тезис Черча-Тьюринга. Проблема остановки для машины Тьюринга.

5.4. Машины Тьюринга с разрешимой проблемой остановки.

Линейно-ограниченные автоматы. Проблема остановки для линейно-ограниченных автоматов. Машина Тьюринга как распознаватель формальных языков. Двухленточные машины Тьюринга. Автоматы с магазинной памятью. Конечные автоматы. Синтаксический анализ языков с помощью автоматов с магазинной памятью и конечных автоматов.

Раздел 6. Заключение.

Обзор приложений математической логики в информатике. Парадигма логического программирования. Язык Пролог как реализация метода резолюций для решения задач искусственного интеллекта.

[Наверх]

---

Рекомендуемый перечень практических занятий.

Практические занятия проводятся в аудиториях; желательно некоторое количество лабораторных занятий в компьютерных классах для решения простейших задач в рамках языка Пролог.

На практических занятиях студенты под руководством преподавателя и самостоятельно решают задачи, соответствующие разделам лекционного курса. В случае организации лабораторных занятий студенты разрабатывают простейшие программы на языке Пролог и выполняют их в рамках программных систем, основанных на этом языке программирования.

[Наверх]

---

Темы практических занятий.

1. Решение задач логического характера методом логических рассуждений.
2. Работа с формулами ИВ и их интерпретацией. Задачи на алгебраическую интерпретацию формул ИВ и ее применение для исследования контактных схем.
3. Преобразование формул ИВ к ДНФ и КНФ.
4. Применение метода резолюций для решения проблемы дедукции в ИВ.
5. Работа с формулами ИП и их интерпретацией.
6. Преобразование формул ИП к клаузальным формам.
7. Задачи на эрбранов универсум множеств дизъюнктов и доказательство свойств множеств дизъюнктов.
8. Задачи на подстановки и унификаторы. Применение алгоритма вычисления наиболее общих унификаторов.
9. Применение метода резолюций для решения проблемы дедукции в ИП.
10. Решение задач содержательного характера с помощью метода резолюций.
11. Доказательства теорем в аксиоматической системе с правилом вывода М.Р.
12. Доказательства теорем в аксиоматической системе натурального вывода.
13. Задачи на разработку алгоритмов решения задач, основанные на неформальном определении понятия алгоритм.
14. Примеры использования машин Тьюринга общего вида.
15. Примеры использования машин Тьюринга с разрешимой проблемой остановки. Решение задач с помощью конечных автоматов.

Примечания.

1. При организации лабораторных занятий в компьютерных классах студенты решают задачи логического характера с использованием языка Пролог.
2. Темы практических и лабораторных занятий и их количество могут варьироваться в рабочих программах курса.

[Наверх]

---

Перечень вопросов, выделенных для самостоятельного изучения студентами.

• Дополнительное углубленное изучение основных понятий формальной логики и методов решения логических задач.
• Минимальные и кратчайшие ДНФ и КНФ.
• Применение методов математической логики в теории формальных языков. Формальные грамматики как логические исчисления.
• Углубленное изучение языка Пролог и систем логического программирования.
• Использование машин Тьюринга с разрешимой проблемой остановки для исследования формальных языков.

Примечание.Некоторые из этих тем могут быть освещены в лекциях и на практических занятиях при наличии соответствующего учебного времени.

[Наверх]

---

Рекомендуемое распределение часов по темам и видам работ для очной формы обучения.

№	наименование разделов и тем	Учебные часы
		всего	лекц.	пр.зан.
1.	Раздел 1. Введение	4	2	2
2. 2.1. 2.2. 2.3. 2.4.	Раздел 2. Исчисление высказываний (ИВ). Формулы ИВ и их интерпретация. Алгебраический подход к ИВ. Нормальные формы. Метод резолюций в ИВ.	28 4 4 10 10	12 2 2 4 4	16 2 2 6 6
3. 3.1. 3.2. 3.3. 3.4. 3.5.	Раздел 3. Исчисление предикатов (ИП). Понятие предиката. Синтаксис и семантика формул ИП. Клаузальные формы. Эрбранова интерпретация. Метод резолюций в ИП.	50 4 10 10 10 16	24 2 4 4 6 8	26 2 6 6 4 8
4. 4.1. 4.2. 4.3. 4.4.	Раздел 4. Аксиоматические системы (АС). Определение и свойства АС. АС с правилом вывода М.Р. АС натурального вывода. Теории первого порядка.	26 2 12 10 2	14 2 6 4 2	12 — 6 6 —
5. 5.1. 5.2. 5.3. 5.4.	Раздел 5. Основы теории алгоритмов. Понятие алгоритма. Алгоритмические проблемы. Машины Тьюринга. Машины Тьюринга с разрешимой проблемой остановки.	24 4 4 8 8	14 2 4 4 4	10 2 — 4 4
6.	Раздел 6. Заключение.	8	4	4
	ИТОГО	140	70	70

Примечания.

1. Трудоемкость настоящего курса составляет 280 часов, из них 140 часов — самостоятельная работа студентов.
2. В часы самостоятельной работы студентов включено время на написание реферата.
3. При организации лабораторных занятий используются часы, отведенные под практические занятия по разделу 6.

[Наверх]

---

ЛИТЕРАТУРА

1. Клини С.К. Математическая логика. М,. Мир, 1973.
2. Мендельсон Э. Введение в математическую логику. М., Наука, 1984.
3. Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. М., Наука, 1983.
4. Тей А., Грибомон П. и др. Логический подход к искусственному интеллекту, том 1. М., Мир, 1990.
5. Тей А., Грибомон П. и др. Логический подход к искусственному интеллекту, том 2. М., Мир, 1998.
6. Ковальски Р. Логика в решении проблем. М., Наука, 1990.
7. Барвайс Дж. (ред.) Справочная книга по математической логике. М., Наука, 1982.
8. Ин Ц., Соломон Д. Использование Турбо-Пролога. М., Мир, 1993.
9. Братчиков И.Л. Синтаксис языков программирования. М., Наука, 1975.

10 логических задач с собеседований, которые заставят застрелиться

Некоторые логические задачи с собеседований вгоняют в недоумение: зачем такое спрашивать? Чтобы создать сложную ситуацию и посмотреть, как быстро вы примете решение.

Разобраться и ответить правильно поможет наша подборка логических задач с собеседований.

Автомат с напитками

Начнём с простой логической задачи.

На склад привезли три машины для напитков. Одна из них выдаёт чай, вторая выдаёт кофе, а третья — чай или кофе (определяется случайно). Любой автомат продаст стакан напитка за одну монету. На каждом автомате приклеена этикетка с выдаваемым напитком. Но на заводе произошла ошибка, из-за чего на всех автоматах наклеены не те этикетки, которые должны быть.

Вопрос: сколько потребуется денег, чтобы определить, где какие автоматы?

Потребуется одна монета, которую нужно бросить в автомат с наклейкой «случайный». Мы знаем, что это неправильная наклейка, поэтому это автомат с чаем либо кофе. После этого определяются остальные два автомата методом исключения. Например, если автомат выдал чай, то автомат с наклейкой «чай» на самом деле выдаёт кофе, а автомат с наклейкой «кофе» выдаёт случайный напиток.

Инопланетяне и десяток храбрецов

В нашу планету вторглась инопланетная раса, чтобы уничтожить всё человечество. Но перед этим они решили дать нам возможность проявить свои интеллектуальные способности. Они отобрали десять умнейших людей планеты, построив их в ряд в полностью тёмной комнате. Каждому они надели чёрную или белую шляпу. После этого свет включился.

Инопланетянин просит стоящего в конце ряда человека назвать цвет своей шляпы. Если ответ правильный — этот человек остаётся жить, если нет — погибает. Подсмотреть цвет своей шляпы нельзя, однако можно обсудить с остальными определённый принцип ответа, которого будут придерживаться все. Распределение цветов шляп случайное, но вам виден цвет шляп всех остальных людей.

Вопрос: каким должен быть ответ, чтобы в живых осталось как можно больше людей?

Люди должны договориться о следующем принципе ответов: отвечающий считает количество чёрных шляп у остальных людей. Если шляп нечётное количество, он называет «чёрный», если чётное — «белый». Следующий человек в ряду, видя шляпы остальных и зная чётность чёрных, может вычислить цвет своей шляпы. Например, если чёрных всё ещё нечетное количество, то на нём белая шляпа. С такой тактикой выживут 9 из 10 человек. Один же из них героически погибнет, спасая остальных.

Поездки на мотоциклах

У вас есть 50 мотоциклов с полным баком, которого хватает на 100 км езды.

Вопрос: используя все мотоциклы, какое максимальное расстояние вы сможете проехать? Все мотоциклы в начале пути находятся условно в одной точке.

Самое простое решение, которое может прийти в голову — просто завести все мотоциклы и одновременно проехать на них 100 км. Но можно проехать и больше. Для этого сначала проедьте 50 км. Все мотоциклы будут с наполовину заполненными баками. Перелейте топливо с одной половины мотоциклов в другую половину. Теперь у вас 25 мотоциклов с полным баком. Проедьте ещё 50 км и повторите операцию. Таким образом можно проехать 350 км

3 лампы и 3 выключателя

Эта логическая задача особенно полюбилась на собеседованиях. Есть 2 комнаты. Первая комната закрыта дверью, в ней низкие потолки и висят 3 лампы накаливания. Во второй комнате есть 3 выключателя, подсоединённых к каждой из ламп. Можно как угодно переключать выключатели, но перейти из второй комнаты в первую можно лишь один раз.

Вопрос: как узнать, за какую лампу отвечает каждый из выключателей?

Ситуацию спасут низкие потолки, которые позволят дотронуться до лампы. Ещё очень важная деталь — лампы накаливания, которые очень сильно нагреваются. Вам нужно, находясь во второй комнате, включить любую лампу на несколько минут, потом выключить её и включить любую из двух других. После этого переходите в комнату с лампами. Первый выключатель, который вы трогали, будет присоединён к лампе, которая ещё тёплая. Второй выключатель — к светящей лампе. А выключатель, который вы не трогали, будет подсоединён к выключенной холодной лампе.

Два стражника

А такая логическая задача часто встречается на интервью от Apple. Игрок дошёл до финального задания в квесте. Перед ним оказались две двери. Первая приведёт к богатству и победе, другая — к поражению. Под дверьми стоит по одному стражнику. Они знают, куда ведут их двери. Но один из них скажет неправду. Не известно, кто именно солжёт. Игрок может спросить одного стражника всего один раз.

Вопрос: что нужно спросить у стража, чтобы выйти к богатству и выиграть квест?

У любого стражника нужно спросить: «какая дверь, по мнению другого стражника, ведёт к победе?». Если игрок спрашивает у правдивого стражника, то тот укажет на дверь с поражением, ведь второй стражник всегда врёт. Если же спросить у второго стражника, то он соврёт о мнении правдивого стражника и тоже укажет на дверь с поражением. Зная неправильную дверь, вам просто нужно выбрать другую.

Пьяные кролики

Как-то раз один наследник захотел убить своего короля, чтобы власть скорей перешла в его руки. У короля была 1000 бутылок вина его любимого сорта. Наследник послал убийцу, чтобы тот отравил любимое вино короля. Но убийцу поймали после того, как он успел отправить лишь одну бутылку. Правитель был умным, поэтому решил использовать десяток кроликов, чтобы определить, куда именно был подсыпан яд. От отравы погибали спустя 1 день.

Вопрос: сколько минимум потребуется времени, чтобы найти отравленную бутылку? Как именно это сделать?

Кролика можно представить в бинарном состоянии: он либо жив, либо мёртв (1 или 0).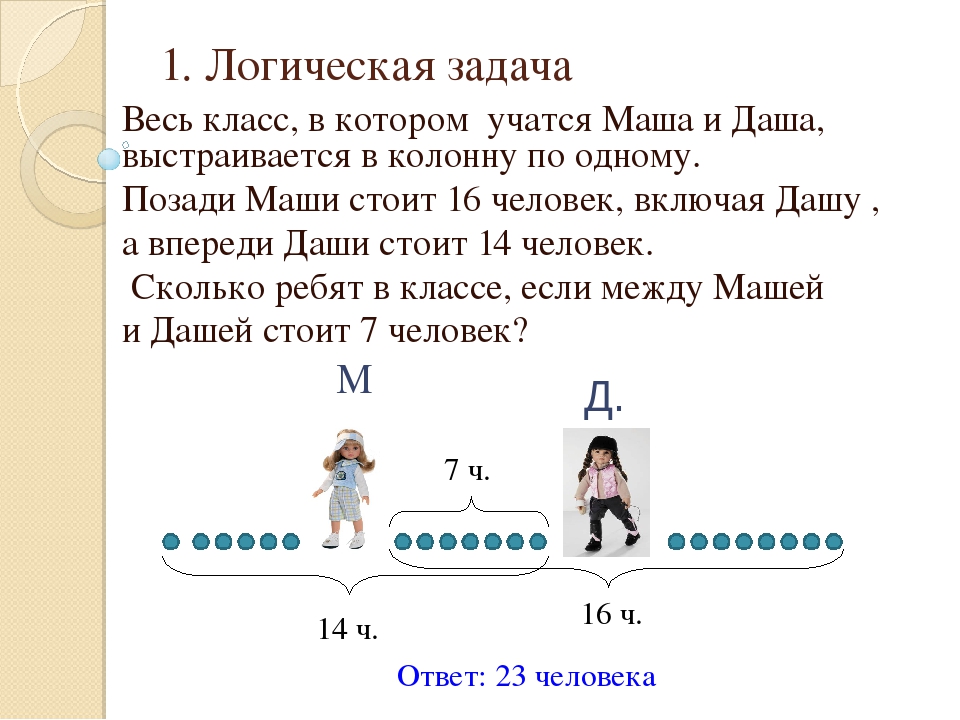 10) уникальных комбинаций состояний кроликов. Пронумеруем все бутылки в двоичной системе, для этого хватит 10 разрядов (в задаче нумерация регистров начинается с 1):

• 1-я бутылка = 0000000001
• 2-я бутылка = 0000000010
• 3-я бутылка = 0000000011
• …
• 999-я бутылка = 1111100111
• 1000-я бутылка = 1111101000

Кроликов нужно пронумеровать от 1 до 10. Каждый из них  будет соответствовать одному из 10 разрядов числа. Кроликов нужно поить из тех бутылок, где в соответствующем кролику разряде есть единица. Например, из первой бутылки пьёт только первый кролик; из третьей — первый и второй. Напоив кроликов из всех бутылок, нужно подождать один день. Номера кроликов, которые погибли, подскажут разряды числа, в которых должны быть единицы. Таким образом, если погибли только 3-й и 1-й кролики, то отравлена 5-я бутылка (0000000101 = 5).

Голодные белки

Данная логическая задача нередко задаётся на собеседованиях и выделяется среди прочих своей неординарностью. В её решении важны не особые математические способности, а умение абстрагироваться от странного условия. Полюбившаяся интервьюерам задача звучит так: 1,5 белки за 1,5 минуты поедают 1,5 жёлудя.

Вопрос: сколько желудей за 9 минут съедят 9 белок?

Если вы не зависли на моменте «1.5 белки», то у вас есть все шансы осилить эту логическую задачку — завсегдатая собеседований. Нужно лишь иначе представить заданные условия. Если 1,5 белки съедают 1,5 жёлудя за 1,5 минуты, то 1 белка за 1,5 минуты съедает 1 жёлудь. Тогда 9 белок за 1,5 минуты съедают 9 желудей. Но по условию нужно узнать количество желудей, съедаемых за 9 минут:

1. 9 / 1,5 = 6 — во столько больше раз нам даётся времени;
2. 9 * 6 = 54 — столько желудей съедят 9 белок за 9 минут.

Треугольник муравьёв

Есть треугольник с равными углами. На углах стоят по одному муравью. В какой-то момент муравьи начинают идти в другой угол вдоль стороны треугольника. В какой именно — определяется случайно.

Вопрос: каков шанс того, что ни один муравей не столкнётся с другим муравьём?

Может показаться, что вероятность 33%, но это не так. Есть два варианта необходимого движения муравьёв: по часовой стрелке и против. Давайте сконцентрируемся на одном муравье. После того, как он случайным образом выбрал направление, ему нужно, чтоб и остальные муравьи двигались в эту же сторону. Шанс того, что второй муравей пойдёт в его направлении — 50%. Аналогичная вероятность и у третьего муравья. Это значит, что общая вероятность того, что муравьи не столкнутся — 25%.

Котлета, котлета и ещё одна котлета

У вас есть 2 сковородки и 3 котлеты. На приготовление 1 котлеты с одной стороны уходит 1 минута. На одной сковороде вмещается лишь 1 котлета.

Вопрос: за какое минимальное время вы сможете полностью обжарить все 3 котлеты?

Первым в голову приходит ответ — 4 минуты. Но можно уложиться и в 3 минуты. Для этого придерживайтесь следующей последовательности:

1. положите жариться по 1 котлете на две сковороды;
2. через минуту переверните первую котлету, а вторую уберите. На место второй котлеты положите третью;
3. ещё через минуту первая котлета будет полностью готова. На её место положите дожариваться вторую котлету, которую вы убрали, а третью котлету переверните;
4. спустя минуту все 3 котлеты будут полностью обжарены.

Необычная оплата

В поместье пришёл путник. В кармане — ни гроша, лишь одна золотая цепь из 6 звеньев. Хозяин поместья предложил брать плату в виде одного кольца с цепочки за один день проживания, при условии, что будет распилено только одно звено. Хозяин должен получать плату каждый день. Он не хочет принимать предоплату или давать в долг.

Вопрос: как путник должен распилить цепочку, чтобы вносить оплату за жильё каждый день в течение 5 дней?

В условиях задачи не запрещался обмен звеньями цепи.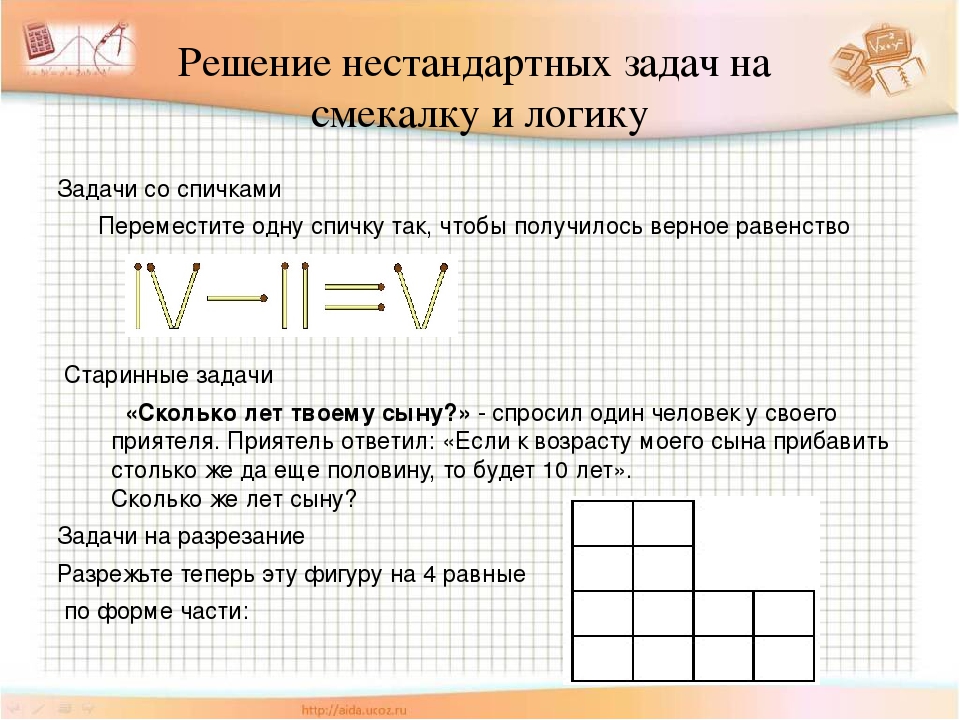 Было лишь требование, чтобы с каждым днём у хозяина жилья прибавлялось одно звенье. Нужно распилить третье звено цепи, чтобы получить 3 части по 1, 2 и 3 звена. За 1-е сутки странник платит одним звеном. На 2-е сутки он платит куском из 2 звеньев и получает сдачу — одно звено (которым он расплатился за 1-е сутки). На 3-и сутки платит куском из 3 звеньев и забирает кусок из 2 звеньев. По такому принципу странник и должен оплатить все оставшиеся дни.

Заключение

Возможно, вы уже сталкивались с подобными логическими задачами на собеседованиях. Если так, поделитесь своим опытом: что это были за задачки и удалось ли их решить?

А для любителей поломать голову мы подготовили тест на проверку логики и математики.

в чём польза и как развить

Преимущества математического мышления

Математическим называется теоретическое мышление, объекты которого лишены вещественности и объединены отношениями. Оно не только помогает нам решать уравнения, но и даёт преимущества в учёбе в целом.   

Человек с развитым математическим мышлением удерживает в голове большое количество информации, понимает, что у любой проблемы есть решение, умеет разбивать сложные задачи на более мелкие и выявлять взаимосвязи.

Математическое мышление помогает и в повседневной жизни. Когда проблема раскладывается на части и учитываются все варианты развития событий, обычно принимается наилучшее решение. А благодаря уверенности в решаемости любых задач дела реже откладываются на потом.

‍

Виды математического мышления

По мнению психолога Ильи Каплуновича, в человеке обычно в разных пропорциях развиты пять типов математического мышления:

1. Топологическое. Отвечает за связанность и целостность логических операций. Сначала нужно изучить суть, а потом последовательно решить задачу. Людям-топологам присуща аккуратность, размеренность и консерватизм.
2. Порядковое. Отвечает выработку конкретных алгоритмов и чёткое следование плану. Главное качество людей с порядковым мышлением — педантичность.
3. Метрическое. Оперирует цифрами и конкретными параметрами. Людям с таким мышлением свойственна предусмотрительность и осторожность.
4. Алгебраическое. Предполагает структурированное восприятие и выстраивание комбинаций. Люди с таким мышлением могут начинать работу с любого места и легко переключаются между задачами. Но им свойственна некоторая рассеянность.
5. Проективное. Заключается в умение смотреть на вещи с разных сторон. Люди с таким мышлением способны быстро оценить ситуацию.
   

Интересный факт: люди, у которых преобладает один и тот же тип мышления, неосознанно тянутся друг к другу.  

Как развить математическое мышление

Математическое мышление тесно связано с пространственным, поэтому его прокачку следует начать с упражнений для пространственного мышления:

• Представьте две сближающиеся линии и определите место их пересечения. Затем представьте треугольник, наложенный на две линии. Что вы видите?
• Закройте глаза и попросите друга дать вам в руки какой-нибудь предмет. Изучите объект на ощупь в течение минуты и скажите, что это.
• Посмотрите на какой-нибудь небольшой предмет и попробуйте перенести его в реальном размере на бумагу. Затем снова скопируйте тот же объект, только увеличив или уменьшив в два раза.
• Начертите план своей комнаты со всеми предметами и деталями.
• Попробуйте сложить оригами, в интернете вы найдёте для этого множество самоучителей. Сначала представьте желаемую фигуру и постарайтесь проговорить необходимый порядок действий.
  

Также для развития математического мышления полезно как можно больше работать с цифрами. При необходимости любых вычислений в повседневной жизни старайтесь производить их в уме, без калькулятора.

Выполняйте специальные задачи и упражнения на логику, играйте в математические игры, решайте головоломки и ребусы, играйте в шахматы.

Законы логики и логические задачи для ребенка

Понятия логики и логического мышления используются повсеместно. С точки зрения логики мы оцениваем поведение, поступки, ситуации. Школьникам знание законов логики необходимо как в обычной жизни, так и в учебе. Именно логикой приходится руководствоваться, решая математические задачи или проводя анализ. Сегодня мы поговорим о логике как науке, рассмотрим основные ее понятия и законы, узнаем, как развить ее у ребенка.

Немного теории

Логика – это наука о формах и законах правильного мышления. Это один из разделов философии. В школе логика редко изучается как самостоятельный предмет. Как правило, основные ее законы включаются в разделы математики, и зачастую им не уделяется должного внимания. Однако прививать ребенку логическое мышление необходимо, ведь именно на него приходится опираться в решении задач, оценке ситуации, анализе данных и пр. Вот основные понятия логики:

• Суждение. Это такая форма мышления, в которой утверждается/отрицается что-либо. Суждения могут касаться какого-то предмета (его качеств, свойств) или отношений между несколькими предметами/явлениями. Примеры: у кошки четыре лапы; собака друг человека; если завтра будет хорошая погода, то мы пойдем купаться.
• Рассуждение. Это ряд суждений, относящихся к одному предмету/явлению, следующих друг за другом таким образом, что одно вытекает из другого. Благодаря рассуждению можно найти ответ на поставленный вопрос. Пример: Если бы шел дождь, то земля была бы мокрой. Но земля сухая. Значит, дождя нет.
• Умозаключение. Это такая форма мышления, в которой истинность некоторого суждения выводится из истинности других суждений (двух и более). Суждения, из которых вытекает умозаключение или вывод, также называются предпосылками. Пример: Все дети любят играть (первая предпосылка). Миша – ребенок (вторая предпосылка). Значит, Миша любит играть (вывод, умозаключение).
• Индукция или индуктивное умозаключение. Это умозаключение, идущее от частного к общему. Пример: А1 имеет признак В. А2 имеет признак В. Все элемента от А3 до Аn имеют признак В. Значит, все элементы множества имеют признак В.
• Дедукция или дедуктивное умозаключение. Это умозаключение, идущее от общего к частному. Пример: Все люди смертны. Аристотель – человек. Значит, Аристотель смертен.

Понятия и операции логики позволяют человеку получать новые знания, не опирающиеся на личный опыт.

Основные законы логики

Источник фото

Существует четыре основных логических закона:

1. Закон тождества. Он гласит, что каждое истинное понятие о предмете, логическая мысль о нем должны оставаться неизменными и однозначными на протяжении всего рассуждения и вывода. Другими словами, если в начале рассуждения мы использовали предпосылку «Все люди смертны», то в конце рассуждения она не может измениться на «Некоторые люди смертны».
2. Закон противоречия (непротиворечия). Два противоположных по смыслу суждения не могут быть истинными одновременно. Хотя бы одно из них обязательно ложно. Т.е. мы не можем начинать рассуждения с предпосылок «Все люди смертны» и «Не все люди смертны».
3. Закон исключенного третьего. Два противоречащих друг другу суждения о предмете/явлении, взятом в одно и то же время и при одних и тех же условиях, не могут быть одновременно истинными. Правильным будет только одно из них, и при этом третьего не существует. Например, или «Все люди смертны», или «Все люди не смертны». При таких условиях мы может выбрать и принять за истинное только одно суждение.
4. Закон достаточного основания. Любая мысль, суждение может быть признана истинной только в том случае, если имеет достаточное основание, т.е. обоснована. Т.е. делая умозаключение, мы должны опираться на суждения, которые уже проверены и признаны истинными, являются аксиомами. Например, долька лимона меньше целого лимона, потому что целое всегда больше части.

Задания на развитие логического мышления

Источник фото

Задания на логику могут быть самыми разнообразными: шуточные загадки, задачки с подвохом, головоломки, упражнения на отработку основных логических понятий. Мы рассмотрим разные типы заданий, которые можно предложить ребенку.

Суждение

Предложите школьнику вынести несколько различных суждений, которые являются аксиомами (т.е. истинны и не требуют доказательств). Они могут опираться:

• На личный опыт. На столе лежит книга. Яблоко зеленого цвета. Шоколад сладкий. И т.д.
• На знания, полученные в школе. Земля вертится вокруг солнца. В году 365 дней. Часть всегда меньше целого. И др.

Рассуждение

Упражнение на отработку рассуждений может предлагаться школьнику в двух видах:

• Свободное рассуждение. Предложите ученику порассуждать об окружающих предметах и явлениях. Например, во время прогулки можно затронуть тему осени: почему опадают листья, а птицы улетают на юг?
• Заданное рассуждение. Ребенку задается вопрос, ответ на который ему нужно найти в вашем рассуждении. Например: Мы не сможем сегодня пойти гулять. (Почему?) На улице мокро и сыро. А у нас даже нет зонта. Мы можем промокнуть и заболеть. (Ответ: потому что на улице идет дождь).

Умозаключение

Предложите школьнику ряд различных предпосылок, из которых ему необходимо сделать вывод. После того как школьник освоил это действие и перестал делать ошибки, необходимо попросить его самостоятельно придумать предпосылки и сделать умозаключения на их основе.

Аналогичные задания даются на отработку индуктивных и дедуктивных умозаключений с учетом их специфики. Также можно дать ребенку предпосылки, а потом спросить, по какому из этих двух типов делался вывод.

Примеры предпосылок:

• Все птицы – животные. Все воробьи – птицы. Значит?
• Некоторые уроки трудны. Всё, что трудно, требует внимания. Значит?
• Тем, кто лыс, расчёска не нужна. Ни одна ящерица не имеет волос. Значит?

Занимательные задачки на логику

1. Человеку не нужны глаза, чтобы видеть. Ведь если мы закроем правый глаз, то все равно видим, если закроем левый глаз, то тоже видим. У человека только два глаза, поэтому получается, что ни левый, ни правый глаз необязательны, чтобы видеть. Верно ли это суждение? Если нет, то в чем ошибка?
2. После девяти стирок длина, ширина, высота кусочка мыла сократились вдвое от изначального размера. На сколько стирок хватит оставшегося мыла?
3. Единственный сын отца плотника – сапожник. Кем приходится плотник сапожнику?
4. Один рабочий способен построить дом за пять дней. А пять рабочих – за один день. Один корабль пересекает Индийский океан за пять дней. Значит, пять кораблей могут пересечь океан всего за один день. Где ошибка в данном рассуждении? Почему она возникла?
5. Шуточная загадка: у фермера 8 свиней. 5 из них розовые, 2 – черные, а одна – бурая. Сколько свиней могут сказать, что у фермера существуют еще свиньи той же масти, что и они сами?
6. Если к трехзначному числу приписать такое же число, то во сколько раз оно увеличится?
7. Миша говорил неправду с четверга по субботу. А его друг врал с понедельника по среду. Однажды они одновременно произнесли: «вчера был один из дней, когда я говорил неправду». Что это был за день?
8. У маленького мальчика спросили: «Сколько лет твоему отцу». «Столько же, сколько мне», — четко ответил малыш. Человек удивился, как такое возможно. Поэтому мальчик объяснил: «Мой отец стал моим отцом лишь тогда, когда я родился. До этого он им не был. Поэтому ему лет столько же, сколько и мне. Т.е. 5». Можно ли назвать данное утверждение верным? Почему?
9. Закончи предложения:
   1. Тарелка – это посуда, потому что…
   2. Диван – это мебель, потому что…
   3. Воробей – это птица, потому что…
   4. Сорока умеет летать, потому что у нее…
   5. Математика – это наука, потому что…
10. Из 12 счетных палочек собрали 4 квадрата. Убери 2 палочки так, чтобы осталось 2 квадрата.

Источник фото

11. Г-жа Роуз – богатая вдова. Она могла удовлетворить любую свою прихоть, но никогда не могла обмануть знаменитого сыщика Шерлока Холмса. Однажды она рассказала такую историю: «Было около трех часов утра, когда меня разбудил шум. Человек в маске стоял в моей комнате, направил на меня оружие и приказал, чтобы я не кричала. С ним были еще двое. Меня связали, заткнули рот и грубо бросили спиной на кровать, а эти ужасные люди пошли к моей шкатулке. Беспомощная, я наблюдала, как злодеи заполнили мешок драгоценными камнями. Я боялась и не смела предпринять что-либо, пока они были в моем доме. Но как только последний из них вылез, я закричала с призывом о помощи. К счастью, патрульный Кейси находился через квартал и услышал меня. Убегая от него, воры в спешке бросили драгоценности. Но страх будет со мной еще долго». Шерлок Холмс иронично улыбнулся и сказал, что эта история не может быть правдивой. Почему?
12. Когда-нибудь человек обязательно прилетит на Марс. Саша Петров – человек. А это значит, что когда-нибудь он обязательно прилетит на Марс. Что не так в этом рассуждении? Почему его нельзя назвать верным?
13. Чтобы получить оранжевую краску необходимо смешать желтую и красную краску в соотношении 6:2. У нас есть 3 г красной краски и 3 г – желтой. Сколько граммов оранжевой краски мы получим в этом случае?

Источник заглавной картинки

Понравилась статья? Поделитесь с друзьями:        

Мудрая сова 31 июля 2015

логических головоломок

логических головоломок

Попробуйте эти логические головоломки:

У 5 пиратов разного возраста есть клад в 100 золотых монет. На своем корабле они решают … Попробовать Puzzle >> У 5 пиратов разного возраста есть клад в 100 золотых монет. На своем корабле они решают … Попробовать Puzzle >> У вас есть корзина с десятью яблоками. У вас десять друзей, каждый из которых хочет по яблоку. Вы … Попробуйте головоломку >> У вас есть три сумки, в каждой по два шарика.В сумке A два белых шарика, в сумке B … Попробуйте головоломку >> Каннибалы устраивают засаду на сафари в джунглях и захватывают троих мужчин. Людоеды дают мужчинам … Головоломка >> Сколько шагов нужно сделать, чтобы разбить плитку шоколада размером m × n на 1 × 1 … Попробуйте Puzzle >> Мужчина оказался на острове, покрытом лесом. Однажды, когда дует ветер … Попробовать пазл >> Вы находитесь на немаркированном перекрестке … один путь — это Город лжи, а другой -… Попробовать пазл >> Вы работаете на фруктовой фабрике. Перед вами 3 ящика. В одном ящике только … Попробовать «Пазл» >> Цельный четырехдюймовый деревянный куб покрыт синей краской со всех шести сторон. Тогда кубик … Попробуйте пазл >> Вот обычный крест. Вы можете сделать два прямых разреза. Как ты … Попробуйте пазл >> Мужчина пойман на владении короля. Его приводят к королю для наказания …. Попробуйте Puzzle >> Мужчина работает на 10-м этаже и в конце всегда спускается на лифте на уровень земли… Попробовать пазл >> Мужчина несет своего сына в больницу, потому что у его сына гвоздь в ноге. Хирург … Решить головоломку >> Фермер хочет перейти реку и взять с собой волка, козу и капусту. Вот … Попробуйте пазл >> Четверо авантюристов (Алекс, Брук, Крис и Дасти) должны пересечь реку на небольшом каноэ. … Попробуйте головоломку >> Четыре человека едут в разные места на разных видах транспорта. Их имена … Попробуйте Puzzle >> У меня есть три специальных четырехгранных кубика.У них по одной букве с каждой стороны. Когда я качусь … Попробуйте головоломку >> Пять шестеренок соединены в ряд, первая соединена со второй, … Попробовать Головоломку >> Пять шестеренок соединены в ряд, первая соединена со второй, . .. Попробовать Головоломку >> Говорят мальчик и девочка. • «Я мальчик», — сказал ребенок с черными волосами. • … Попробовать пазл >> У старого фермера Палмера стадо коров, но он, кажется, всегда забывает, сколько там животных… Попробовать пазл >> Есть три человека (Алекс, Брук и Коди), один из которых рыцарь, один лжец и один … Попробуйте Puzzle >> Есть три человека (Алекс, Брук и Коди), один из которых рыцарь, один лжец и один … Попробуйте Puzzle >> Алекс, Брук, Коди, Дасти и Эрин недавно узнали, что все их дни рождения приходились на … Попробуйте Puzzle >> Несколько лет назад, чтобы озадачить своих друзей, ученый дал один из четырех контейнеров, содержащих синий и / или … Попробуйте Puzzle >> Вы собираетесь уехать в отпуск, но забыли носки! Вы бежите обратно в свою комнату, но ….. Попробовать пазл >> Ученый собрал четырех студентов-математиков. Затем их выстроили в ряд так, чтобы каждый мог видеть … Попробовать «Пазл» >> Два отца увезли сыновей на рыбалку. Каждый мужчина и сын поймали по одной рыбе, но когда они вернулись … Попробуйте Пазл >> Это знаменитая головоломка по мотивам шоу «Давайте заключим сделку». Ведущий, … Попробуйте головоломку >> У миссис Гудсуорти 6 великолепных шляп. 3 — зеленые, 2 — синие и 1 — канареечно-желтые. Четыре … Попробуйте головоломку >> Игра «НИМ» включает ряды спичек, уложенных в виде треугольника.Когда это … Попробуйте головоломку >> Идея состоит в том, чтобы проложить свой путь по всем улицам на этой карте, не идя по улицам … Попробуйте Puzzle >> Недавно на выставке домашних животных я заметил, что все, кроме двух, были кошками, все, кроме … Попробуйте Puzzle >> Посмотрите на треугольник из шести пенсов ниже: Я хочу перевернуть этот треугольник вверх ногами: … Попробуйте головоломку >> Есть монастырь безмолвных монахов без зеркал и одно важное правило: никаких красных глаз! Если … Попробовать пазл >> Мужчина на скамейке в парке смотрит на небольшой портрет.Вы спрашиваете его: «Кто это в . .. Попробуйте головоломку >> Вы хотите отправить секретное сообщение своему другу Алексу по почте. Но Сэм, ты не … Попробуй головоломку >> В ресторане в центре города мистер Ред, мистер Блю и мистер Уайт встречаются за обедом. Под их … Попробуйте Puzzle >> Вы должны принимать по две разные таблетки (А и В) каждый день. Если вы забудете один или возьмете еще … Попробуйте Puzzle >> Мост рухнет через 17 минут. 4 человека хотят пересечь его, пока он не рухнул ….Попробуйте головоломку >> В интернате пятнадцать школьниц, которые постоянно гуляют группами … Попробовать Пазл >> В первой коробке два белых шара. Во втором ящике два синих шара. В третьем ящике белый … Попробовать пазл >> Как в ресторане выбрать один из трех десертов с равной вероятностью … Попробовать Puzzle >> Есть три спортсмена (Алекс, Брук и Крис) и их индивидуальные тренеры (Мерфи, Ньюлин … Попробуйте головоломку >> Три человека входят в комнату и надевают на голову зеленую или синюю шляпу.Они не видят … Попробуйте головоломку >> Профессор Фрэнтик поставила эти три задачи своему классу маньяков в Clueless University …. Попробуйте Puzzle >> Разложите эти шесть шариков так, чтобы каждый из них касался всех четырех шариков разного цвета. Попробуйте головоломку >> Три сестры — однояйцевые тройни. Самая старая по минутам — Сара, и Сара всегда говорит … Попробуйте Puzzle >> В городе всего два парикмахера, у одного из них красивая, аккуратно подстриженная шевелюра …. Попробуйте Puzzle >> Ваш учитель сказал, что в полдень на этой неделе будет тест, но этот день будет сюрпризом.Вы … Попробуйте головоломку >> На приведенной ниже диаграмме показан узор, состоящий из квадратов: Сколько квадратов можно найти … Попробуйте пазл >>

Авторские права © 2020 MathsIsFun.com

головоломок с числами

головоломок с числами

Попробуйте решить эти головоломки с числами:

Найдите 10-значное число, где первая цифра — это количество нулей в номере, вторая цифра . .. Попробуйте Puzzle >> Используйте цифры 1, 9, 9 и 6 точно в указанном порядке, чтобы получить следующие числа: 28, 32 ,… Попробовать пазл >> Как я могу получить ответ 24, используя только числа 8, 8, 3 и 3. Вы можете использовать сложение, вычитание, … Попробуйте головоломку >> Какое 5-значное число имеет следующие особенности: Если поставить в начале лишнюю цифру 1, … Попробовать Головоломку >> Какое 9-значное число имеет следующие особенности: В нем все 9 цифр от 1 до 9 Можно … Попробовать Головоломку >> У меня десять коробок общим весом 75 кг: 15 кг, 13 кг, 11 кг, 10 кг, 9 кг, 8 кг, 4 … Попробуйте Puzzle >> В прошлом месяце я послал за одним из тех наборов, которые вы можете использовать, чтобы сделать свои собственные рождественские крекеры…. Попробовать пазл >> Найдите число с его буквами в алфавитном порядке. Пример: у «пятерки» есть «пятерка» … Попробовать пазл >> На вопрос о его дне рождения мужчина сказал: «Позавчера мне было всего 25 … Попробуйте Puzzle >> Найдите код! • Он состоит из 6 разных цифр • Чередуются четные и нечетные цифры (примечание: … Попробуйте головоломку >> Тим увидел, что цифровые часы его духовки показывают 1:23, и заметил, что каждое число равно единице … Попробуйте головоломку >> Используйте 8 ровно восемь раз, чтобы получить 1000 a) Используя только + — × / b) Также допускается… Попробовать пазл >> Я думаю об одной из этих пяти карт: Вы должны попытаться выяснить, какая я … Попробуйте головоломку >> Популярное математическое времяпрепровождение: используйте ровно четыре четверки, чтобы образовать каждое целое число от 0 … Попробуйте головоломку >> Существует одно четырехзначное целое число n, так что последние четыре цифры n ² равны … Попробуйте Головоломка >> Можете ли вы расположить цифры от 1 до 9 (1, 2, 3, 4, 5, 6, 7, 8 и 9) в одну дробь, которая … Попробуйте головоломку >> Том спросил свою бабушку, сколько ей лет.Вместо того чтобы дать ему прямой ответ, она ответила: . .. Попробуйте Puzzle >> Гораций купил сегодня пирожных, как объясняется в этой песне. Теперь, когда он взял свой … Попробуйте Puzzle >> Это Волшебный квадрат. Это означает, что числа в сумме дают одинаковую сумму во всех направлениях. Каждый … Попробуйте пазл >> Используя цифры 1,7,7,7 и 7 («1» и четыре «7»), создайте число … Попробуйте Puzzle >> Голодный Гораций зашел в музыкальный магазин, чтобы купить музыкальные сладости, которые они продавали.Вот … Попробуйте пазл >> Однажды днем ​​Голодный Гораций испек большое количество пирогов с фаршем для своей рождественской вечеринки … Попробуйте головоломку >> У вас есть калькулятор с клавиатурой, состоящей из 10 цифр и двух символов, [#] и … Попробуйте головоломку >> Мужчина, который жил по самому большому адресу на своей улице, переехал в другой дом на … Пазл >> Парень идет в магазин и покупает 4 вещи. Кассир сказал ему, что его счет составляет 7,11 доллара. «Подождите … Попробуйте головоломку >> Вот газета из 8 больших листов бумаги, сложенных пополам.В газете 32 … Попробуйте пазл >> Существует бесконечно много формул, подходящих для любой конечной серии. Попробуйте угадать следующий … Попробуйте Puzzle >> Если полторы курицы откладывают полтора яйца за полтора дня, сколько яиц делает одно … Пазл >> Людвиг Бамп управляет банком в Матсвилле. Но вы должны помочь ему, потому что он забыл … Попробуйте Puzzle >> Однозначные числа — это среднее само по себе. Пример: среднее 7 равно 7. Сможете найти… Попробовать пазл >> На школьном празднике людей просили угадать, сколько горошин в банке. Никто … Попробуйте пазл >> 25 человек участвуют в гонке-пикнике. Но трасса узкая, и одновременно могут участвовать только 5 человек …. Попробуйте Puzzle >> Две из четырех плиток головоломки имеют одинаковую сумму корней. Найдите эти плитки. Попробуйте головоломку >> Голодный Гораций на днях переписывал домашнее задание по математике, но, поскольку он был в … Попробуйте головоломку >> Сколько клеток на шахматной доске…? (Подумайте внимательно) Попробуйте головоломку >> Пятизначное число имеет сумму всех пяти цифр, равную 5. Первая цифра равна … Попробовать Головоломку >> Я думаю о шестизначном числе. Сумма цифр — 43. А всего две, … Попробовать пазл >> Жемчужное ожерелье состоит из 33 жемчужин, самый большой и самый ценный из которых находится в середине. Запускаем … Попробуйте головоломку >> Добро пожаловать в странный разум Эврики Блип. Он не всегда думает так же, как мы… Попробовать пазл >> В коробке было 100 конфет. Коробку передали ряду людей. … Попробуйте головоломку >> Возрастные проблемы были в моде в древности. Вот пример: я в два раза старше … Попробуйте Puzzle >> Учитель придумывает два последовательных (одно за другим) чисел в диапазоне от 1 до 10 и … Попробуйте головоломку >> Учитель говорит: «Первый ученик знает свой продукт, а другой — свой … Попробуйте головоломку >> Двое друзей вместе вкусно пообедают, а счет составляет 25 долларов. Друзья платят по 15 долларов каждый, что составляет… Попробовать пазл >> Трое друзей вместе вкусно пообедают, а счет составляет 25 долларов. Трое друзей платят по 10 долларов каждый, … Попробовать Puzzle >>

Авторские права © 2020 MathsIsFun.com

Математическая логика и математические задачи

Логика — это применение принципов рассуждения. Математика — это изучение характеристик и операций с числами. Раньше эксперты открывали несоответствия в математике и вынуждены были разгадывать эти загадки.Таким образом, их исследования превратились в математическую логику: применение принципов рассуждения и теории к числам и их отношениям, чтобы определить, является ли конкретное математическое утверждение истинным или ложным.

Здесь вы найдете всевозможные головоломки и игры. Чтобы решать головоломки или выигрывать в играх, вы будете использовать математическую логику. Эти игры веселые, и некоторые из них заставят вас по-настоящему напрячь мозги. Посмотрите их, и
увидите, , как вы думаете, !

Повседневные математические и логические задачи для всех

• Brain Games — Веселые игры с головоломками, играми в слова,
  и логикой.
• Brain Food — Множество логических задач, головоломок и игр со словами
  ; здесь есть что-то для всех.
• Brain Games — ссылки на веселые игры для мозга для студентов и семей.
• Пазлы с числами и словами — Бесплатные онлайн пазлы с числами и словами.
• Learning Math — Найдите здесь несколько ссылок на несколько подходящих для возраста игр.
• Семейные математические задания и игры — На сайте этой школы вы найдете игры, подходящие для различных возрастных групп.
• New Fruit Game — Это старая игра с новой привлекательностью. Проверить это.
• Дополнительные темы по математике — изучите множество математических ресурсов, перечисленных на этом сайте, от судоку до дискретной математики.
• Знай свою алгебру — наведите указатель мыши на ссылку, чтобы задать вопрос; знать ответ?
• Endless Math — На этом сайте вы найдете буквально СОТНИ математических головоломок!
• Kids ‘Play — Веселитесь с детьми, решая эти головоломки и играя в эти игры.

Задачи по математике и логике для детей

Задачи по математике и логике для подростков

Математические и логические задачи для математиков и логиков

• Papyrus Puzzle Game — Сможете ли вы снова собрать папирус?
• Нерешенные проблемы — действительно ли они неразрешимы? Может, ты найдешь решение.
• Логический калькулятор — научитесь использовать логический калькулятор, чтобы находить истину в логических утверждениях.
• Задача занятого бобра. Узнайте, что такое машина Тьюринга. Тогда вы сможете решить эту проблему.
• Puzzling — Это не для слабонервных.
Коллекция
• — На этой веб-странице вы найдете всевозможные головоломки с математикой и логикой. Испытывающий!
• Проверьте себя — Найдите здесь несколько задач со словами, для решения которых требуются логика и математика.
• Наноохота — это нужно делать в уме…бумага и письменные принадлежности запрещены!

Решение пропозициональной логической задачи со словом

В этом разделе мы будем использовать знакомые обозначения, используемые в логике высказываний. Возможно, вы сначала захотите познакомиться с логикой высказываний.

Как и при решении любых других вопросов, мы всегда должны спрашивать себя, что мы можем, а что не можем делать, записывая свои рассуждения. Первый шаг к тому, чтобы научиться решать проблемы логики высказываний, состоит в том, чтобы перечислить то, что нельзя сделать или что невозможно, чтобы мы могли сузить круг возможных сценариев.Помните, что очень легко сделать ошибочный вывод, основанный на ошибочных рассуждениях. Возьмите в качестве примера приведенные ниже утверждения. Если первое утверждение истинно, верно ли второе утверждение?

«Если идет дождь, то я не могу играть в футбол». «Если я не могу играть в футбол, значит идет дождь». \ Begin {array} {c} & \ text {«Если идет дождь, то я могу» t играть в футбол «.} & \ text {» Если я не умею играть в футбол, значит идет дождь. «} \ end {array}» Если идет дождь, то я не могу играть в футбол «.» Если я могу Не играю в футбол, значит идет дождь.«

Совершенно очевидно, что проблема здесь: могут быть другие причины, по которым я не могу играть в футбол, которые не обязательно зависят от погоды. Если мы допускаем такие простые ошибки в рассуждениях, когда контекст очень ясен, просто представьте, что произойдет, когда вы будете менее уверены в более расплывчатых утверждениях. В следующем абзаце мы познакомимся с этими ошибками.

Обратные и обратные ошибки

Как новичок, наиболее распространенная ошибка, которую вы можете сделать, — это предположить, что верно и обратное и / или обратное к исходному утверждению.Взгляните на два раздела ниже:

Введение в Converse Ошибка с ошибочными рассуждениями:

Предпосылка : Если идет дождь, я не могу играть в футбол.

Заключение : Если я не умею играть в футбол, значит идет дождь.

Объяснение : Из первого оператора мы получаем условие и результат: «дождь» как условие и «я не могу играть в футбол» как результат. Вся посылка сформулирована таким образом, что если условие выполнено, то результат наступит.Однако вывод показывает, что если результат будет выполнен, то условие будет выполнено. Это не имеет смысла, потому что условие не обязательно должно иметь место, если результат наступает первым. Это известно как обратная ошибка.

В общем виде аргумент обратной ошибки выглядит следующим образом:

• Если встречается P, значит Q.
• Q возникает.
• Следовательно, также встречается P.

Введение в обратную ошибку с ошибочными рассуждениями:

Предпосылка : Если идет дождь, я не могу играть в футбол.

Вывод : Если не идет дождь, то могу поиграть в футбол.

Объяснение : Из первого оператора мы получаем условие и результат: «дождь» как условие и «я не могу играть в футбол» как результат. Вся посылка сформулирована таким образом, что если условие выполнено, то результат наступит. Однако вывод показывает, что если условие не наступает, то не наступает и результат. Это не имеет смысла, потому что могут быть другие причины / факторы, которые могут привести к появлению результата.Это известно как обратная ошибка.

В общем виде аргумент обратной ошибки выглядит следующим образом:

• Если встречается P, значит Q.
• P не встречается.
• Следовательно, Q также не встречается.

Теперь может быть совершенно ясно, что легко определить, что мы сделали ошибочные рассуждения. Однако что, если приведенные утверждения кажутся более расплывчатыми? Это причина, по которой мы вводим две ошибки выше (обратная ошибка и обратная ошибка), чтобы показать, что не все неправильные утверждения легко идентифицировать.Проще говоря, взаимосвязь между двумя событиями не обязательно означает, что одно вызывает другое. Короче говоря, мы указываем на общий факт, что «корреляция не подразумевает причинно-следственной связи».

Теперь, когда мы увидели эти ошибки на собственном опыте, давайте рассмотрим другой пример, чтобы напомнить себе, что это ошибки, и мы надеемся избежать их в будущем. Имейте в виду, что некоторые обратные / обратные утверждения могут показаться нелепыми, а некоторые — нет.

Нам дается следующее утверждение: Если сегодня воскресенье, значит, погода солнечная.

(i) \ qquad \ text {(i)} (i) Запишите обратную и обратную форму этого утверждения.
(ii) \ qquad \ text {(ii)} (ii) Определите, какое из этих утверждений, которое вы сделали, не логично, и объясните, почему.

---

(i) \ text {(i)} (i) Обратные и обратные

• Обратное: Если сегодня не воскресенье, то погода не солнечная.
• Converse: Если погода солнечная, то сегодня воскресенье.

(ii) \ text {(ii)} (ii) Логический или нелогичный

Хотя они являются инверсией и противоположностью исходному утверждению, мы должны помнить, что они не обязательно могут быть ошибкой.Однако нет ничего плохого в том, чтобы проверить, верны они или нет.

• Обратное утверждение подразумевает, что день имеет прямое отношение к солнечной погоде или нет, что смехотворно , потому что также могут быть несолнечные дни, которые не выпадают на воскресенье.

• Обратное утверждение подразумевает, что только если погода солнечная, тогда день будет воскресным, что также смехотворно , потому что у них также может быть солнечная погода в дни, не приходящиеся на воскресенье.□ _ \ квадрат □

Определите точную ошибку

Теперь, когда мы можем определить, как возникают ошибки, давайте сделаем еще один шаг и применим эти методы, чтобы мы могли точно определить, где возникает ошибка. \ text {+} \ text {средний или лучший} \\ & \ text {(iii)} & \ text {Взять бухгалтерию} \\ \ end {array} (i) (ii) (iii) Специалист в области математики или информатики Получите средний балл B + или вышеБерите бухгалтерский учет

Поскольку вы стали изучать математику, критерий (i) \ text {(i)} (i) удовлетворяется.\ text {+} B + среднее, критерий (ii) \ text {(ii)} (ii) не выполняется.
Поскольку вы начали бухгалтерский учет, критерии (iii) \ text {(iii)} (iii) удовлетворены.

Поскольку вы не соответствовали всем критериям и получили отказ, персонал вам не лгал. □ _ \ квадрат □

Теперь, когда вы знакомы с записью этих операторов и выявлением возможных ошибок, давайте попробуем другой пример, в котором используется такое свойство!

Недостаточная информация Sharky Сатвик Кришна

В магазин совершили налет мародер (а), который уехал на машине.Трое известных преступников Сатвик, Кришна и Шарки доставлены в полицейский участок для допроса. Инспектор полиции Адитья извлекает следующие факты:

(1) (1) (1) Никто, кроме Сатвика, Кришны и Шарки, не участвовал в грабеже.
(2) (2) (2) Шарки никогда не выполняет работу без использования Сатвика (и, возможно, других) в качестве сообщников.
(3) (3) (3) Кришна не умеет водить машину.

Найдите человека, который в любом случае виноват.

Эта задача входит в мой набор «Это то, что вы называете логикой?»

Формальная терминология

В предыдущих разделах мы узнали о двух наиболее распространенных ошибках, которые допускают учащиеся при решении задачи логического рассуждения.Однако мы формально не касались терминологии для этих терминов: обратная ошибка и обратная ошибка. Давай начнем!

Контрапозитив : Утверждение логически эквивалентно своему контрапозитиву. Контрапозитив отрицает оба термина в импликации и меняет их позиции. Например, противоположность «P подразумевает Q» — отрицание Q подразумевает отрицание P.

• Converse : Обратное меняет положение терминов.Обратное к «P влечет Q» означает «Q влечет P».

• «Если и только если», иногда записываемое как iff и известное как эквивалентность, является импликацией, которая работает в обоих направлениях. «P тогда и только тогда, когда Q» означает, что и «P подразумевает Q», и «Q подразумевает P».

Давайте попробуем несколько примеров, охватывающих эту область!

(i) \ text {(i)} (i) Запишите контрпозитивное заявление для

«Если вы человек, значит, у вас есть ДНК.»\ text {» Если вы человек, то у вас есть ДНК. «}» Если вы человек, то у вас есть ДНК «.

(ii) \ text {(ii)} (ii) Запишите два оператора if-then для

«Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны.» \ Text {«Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны.»} «Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны «.

---

(i) \ text {(i)} (i) Contrapositive
\ qquad Если у вас нет ДНК, значит, вы не человек.

(ii) \ text {(ii)} (ii) утверждения «если-то»
\ qquad Если многоугольник является четырехугольником, то у него 4 стороны.
\ qquad Если у многоугольника 4 стороны, то это четырехугольник. □ _ \ квадрат □

Просто, не правда ли? Давайте попробуем решить некоторые задачи, в которых применяются методы, которые мы узнали выше.

Если Джефф хорошо справится со своим следующим тестом по математике, то он закончил домашнее задание по математике.Если Джефф потратит 5 часов на видеоигры, то следующий тест по математике он провалит. Если Джефф не провалит следующий тест по математике, значит, он не провел 5 часов, играя в видеоигры. Если Джефф не выполнит домашнее задание по математике, он потратит 5 часов на видеоигры. Если Джефф не играет в видеоигры, он успешно сдаст следующий тест по математике.Если Джефф не выполнит домашнее задание по математике, значит, он не справится со следующим тестом по математике. Если Джефф потратит 2 часа на видеоигры, он сможет закончить домашнее задание по математике. Если Джефф завершит домашнее задание по математике, значит, он не потратил 5 часов на видеоигры.

Если Джефф потратит 5 часов на видеоигры, он не сможет закончить домашнее задание по математике.

Если Джефф завершит домашнее задание по математике, то его следующий тест по математике будет успешным.

На основании этой информации, что из следующего является логически правильным?

Синий Не могу сказать Зеленый Желтый

Селена, Дженнифер и Майли носят синее платье, желтое платье и зеленое платье в неизвестном порядке.Известно, что:

1) Если Селена носит синее, то Дженнифер носит зеленое.
2) Если Селена носит желтое, то Майли носит зеленое.
3) Если Дженнифер не носит желтого цвета, то Майли носит синее.

Какого цвета платье на Селене?

Теперь, когда мы освоили эти методы, давайте перейдем к следующему разделу, чтобы узнать о других классных методах доказательства!

Сможете ли вы решить «самую сложную логическую головоломку»?

Несмотря на общую неприязнь к математике, о которой заявляет большинство, многим людям нравятся логические головоломки.Это странно, ведь многие логические головоломки — это всего лишь вариации математических задач. Радостно игнорируя этот факт, многие математофобы будут пытаться разгадывать загадки и головоломки огромной сложности, используя инструменты рассуждения, которые они боятся использовать, когда предметом является уравнение.

Сегодня мы рассмотрим головоломку, эрудита, который ее придумал, и почему вам стоит подумать о том, чтобы взять книгу логических головоломок в следующий раз, когда вы будете в библиотеке.

Эта головоломка была написана блестящим логиком Раймондом Смулляном.Смуллян родился в Нью-Йорке 101 год назад. Он получил степень бакалавра в Чикагском университете и докторскую степень по математике в Принстоне, где он также преподавал в течение нескольких лет.

Чрезвычайно плодовитый писатель, он опубликовал несколько книг по логическим головоломкам для массового потребления и бесконечный поток учебников и эссе по логике для академической аудитории. Его сборники головоломок хорошо известны за то, что знакомят людей со сложными философскими идеями, такими как теоремы Гёделя о неполноте, в увлекательной и нетехнической форме.

Смуллян, владеющий крупными планами, когда-то работал профессиональным фокусником. Он также был опытным пианистом и астрономом-любителем, построившим свой собственный телескоп. Помимо интереса к логике, он также восхищался даосской философией и опубликовал книгу по ней для широкой аудитории.

Он также нашел время появиться у Джонни Карсона, где, как и во многих его книгах, он утверждал, что люди, которым нравятся его головоломки, утверждают, что не любят математику только потому, что они не осознают, что они — одно и то же.

Проблема трех богов

Одна из наиболее популярных формулировок проблемы, которая, по словам профессора логики Массачусетского технологического института Джорджа Булоса, была самой сложной из всех, это:

«Три бога A, B и C называются в произвольном порядке, Верно, Ложно. , и Случайный. Истинный всегда говорит правду, Ложь всегда говорит ложно, но говорит ли Рэндом правдиво или ложно — это совершенно случайный вопрос. Ваша задача — определить личности A, B и C, задав три вопроса типа «да-нет»; каждый вопрос должен быть задан ровно одному богу.Боги понимают английский, но ответят на все вопросы на своем языке, в котором слова да и нет будут да и ja в некотором порядке. Вы не знаете, какое слово означает какое «.

Булос добавляет, что вам разрешено задавать конкретному богу более одного вопроса и что Random переключается между ответами, как если бы они говорили правду или лжецами, а не только между ответами» da «и» ja. «

Дайте себе минутку подумать, мы рассмотрим несколько ответов ниже.Готовый? Хорошо.

Решение Джорджа Булоса направлено на поиск истинного или ложного с помощью сложных вопросов.

В логике часто используется функция, которая часто записывается как «если и только если», что означает «если и только тогда». Его использовали, чтобы сказать что-то вроде «Небо голубое, если и только если Де-Мойн находится в Айове». Это мощный инструмент, поскольку он дает истинное утверждение только тогда, когда оба его компонента истинны или оба ложны. Если одно истинно, а другое ложно, у вас ложное утверждение.

Итак, если вы сделаете такое утверждение, как «Луна сделана из Горгонзолы, если и только если Рим находится в России», то вы сделали верное утверждение, поскольку обе его части ложны. Утверждение «На Луне нет воздуха, если и только если Рим находится в Италии» также верно, поскольку верны обе его части. Однако утверждение «Луна сделана из Горгонзолы в том и только в том случае, если Олбани является столицей Нью-Йорка» неверно, потому что одна из частей этого утверждения верна, а другая — нет (Тот факт, что эти предметы не полагайтесь друг на друга пока несущественно).

В этой головоломке iff может использоваться здесь для контроля неизвестных значений «da» и «ja». Поскольку ответы, которые мы получаем, можно сравнить с тем, что мы знаем, они были бы, если бы части нашего вопроса были все истинными, все ложными или если они различались.

Boolos хотел бы, чтобы мы начали с вопроса бога A: «Означает ли« да »да, если и только если вы истинны, тогда и только тогда, когда B — случайное?» Независимо от того, что говорит А, ответ, который вы получите, будет чрезвычайно полезным. Как он объясняет:

«Если A истинно или ложно, и вы получаете ответ da, то, как мы видели, B является случайным, и, следовательно, C либо истинно, либо ложно; но если A истинно или ложно, и вы получаете ответ ja, тогда B не является случайным, поэтому B либо истинно, либо ложно … если A является случайным, и вы получаете ответ da, C не является случайным (и B не является случайным, но это не имеет значения), и поэтому C либо истинно, либо Ложь; и если A случайное…и вы получите ответ ja, B не является случайным (как и C, несущественно), и поэтому B либо True, либо False ».

Независимо от того, какой бог A, ответ« da »гарантирует, что C не является ‘t Случайный, и ответ «ja» означает то же самое для B.

Отсюда можно просто задать любой из известных вам вопросов, которые не являются случайными, чтобы определить, говорят ли они правду, а затем один о том, кто последний бог. Булос предлагает начать с «Означает ли да, если и только если Рим находится в Италии?» Поскольку одна часть этого утверждения верна, мы знаем, что Истина скажет «да», а Ложь скажет «ja», если столкнулся с этим вопросом.

После этого вы можете спросить того же бога что-то вроде: «Да означает ли да, если и только если, A — случайное?» и точно знаете, кто есть кто, по их ответам и процессу исключения.

Если вы не понимаете, как это работает, попробуйте медленно повторить это снова. Помните, что важная часть — это знание того, каким будет ответ, если два положительных или два отрицательных результата всегда будут положительными, и что можно положиться на двух богов, которые будут действовать последовательно.

Смуллян написал несколько книг с другими логическими головоломками.Если вам понравился этот, и вы хотите узнать больше о философских проблемах, которые они исследуют, или, возможно, если вы хотите попробовать несколько, которые немного легче решить, вам следует подумать о их прочтении. Некоторые из его головоломок можно найти с объяснениями в этом интерактиве.

Разработчики учебных материалов: у нас более одного интеллекта (Часть четвертая: логико-математический интеллект)

Логико-математический интеллект и учебный дизайн

Профессор Ховард Гарднер, профессор познания и образования Хоббса в Гарварде, в семидесятые годы придумал радикальную идею:

«К 1981 году я утверждал, что все люди обладают не одним единственным разумом, скорее, мы, люди, лучше описываем как обладающие набором автономных разумов.”

Это из основополагающей книги Гарднера «Фреймы разума».

Логико-математический интеллект

Большинство из нас сразу же подумает о научном мышлении, когда мы прочитаем эту фразу, и будем правы. Однако эта логико-математическая способность также связана с нашей способностью распознавать образцы или абстрактные представления, такие как числа и геометрические фигуры, и работать с ними. Логика — математический интеллект позволяет нам видеть отношения между вещами, не являющимися буквами алфавита, такими как формы и символы, для решения проблем, которые считаются научными.В этом навыке больше всего нуждаются такие люди, как программисты, архитекторы, математики и статистики; но все мы в той или иной степени обладаем им и используем его, чтобы учиться. Это также важная часть решения проблем и критического мышления.

Гарднер определил следующие множественные интеллекты: вербально-лингвистический, логико-математический, визуально-пространственный, телесно-кинестетический, музыкально-ритмический, межличностный и внутриличностный. В этой статье я собираюсь сосредоточиться на логико-математическом интеллекте из этого арсенала интеллекта.

Навык решения проблем

Если кто-то использует свои логико-математические навыки в попытке решить математическую или логическую задачу, осознайте, что на самом деле они имеют дело с паттернами , симметрией , асимметрией и отношениями . Они также имеют дело с символическим языком, который в значительной степени не является английским, а представляет собой смесь английских и математических символов.

В следующей арифметической задаче есть как английские слова, так и другие символические представления: Если a = 9 и если b = 10, то чему равно a, умноженное на b? Здесь нас просят использовать логику, знание символов, отношений и чисел, а также английский язык, чтобы распознать закономерность — или, вернее, последовательность — для ответа на вопрос и решения проблемы.

Пробуждение логико-математического интеллекта

Логико-математический интеллект пробуждается, когда мозг / разум видит проблему, которую необходимо решить. Первое столкновение с проблемой, которая может быть решена только с помощью логико-математического интеллекта, вероятно, происходит в детской, когда ребенок видит закономерности в предметах вокруг комнаты и решает переставить предметы, чтобы они соответствовали другому образцу, который он имеет в виду. Так оно и во взрослой жизни, и после нее. Мы машины для установления взаимосвязи и распознавания образов.

Психологи делают из этого вывод, что как только ум ребенка начинает привыкать к конкретным образцам, представленным объектами на полу в детской, и манипулировать ими, ребенок осознает, что они могут иметь дело и с абстрактными образцами, и осознает, что они могут манипулировать образцами чисел — также хорошо. как и другие идеи — в их уме. Это пробуждение, и это начало математических способностей.

К сожалению, наша система образования США не использует эту врожденную способность и вместо этого обучает тестам.В результате в 2013 году Америка заняла 21-е место из 23 самых продвинутых стран в области математики или математики, как ее иногда называют. И в этой самой продвинутой нации на земле мы оказываемся только в середине стаи, когда исследуются взрослые.

Плохие математические навыки приводят к более высоким расходам как для частных лиц, так и для корпораций, в которых они работают. Это проявляется в исследовании за исследованием. В одном примере почти три четверти участников исследования купили лосьон для рук, когда он был помечен как «на 50 процентов больше», чем когда он был помечен как «скидка 35 процентов», хотя сделка немного лучше с лосьоном, цена которого снижена на 35 процентов.(Если вы обычно платите 3 доллара за восемь унций лосьона, предложение «на 50 процентов больше» будет составлять 3 доллара за 12 унций или 25 центов за унцию, а предложение «скидка 35 процентов» будет составлять 1,95 доллара за восемь унций, или около 24 центов за унцию. центов за унцию.

Фактические затраты только на экономику Великобритании, не умеющую читать, оцениваются в 3,2 миллиарда долларов. В США это было бы больше похоже на 6,8 миллиарда долларов потери производительности. Увеличение доли американцев до уровня владения математикой в ​​Канаде или Южной Корее приведет к увеличению роста в США почти на 1 процентный пункт.

Даже небольшое улучшение навыков счета у ваших сотрудников может иметь большое значение.

Что такое счет? Счисление — это знания и навыки, необходимые для эффективного управления математическими требованиями в различных ситуациях и реагирования на них. Он включает в себя развитие уверенности и компетентности с помощью логики и рассуждений и требует понимания того, как данные собираются и представляются в диаграммах, графиках, таблицах и диаграммах. Это жизненно важно для полноценного участия сотрудников в вашей компании.

Что такое безграмотность? Это математический аналог неграмотности, и, поскольку это в основном социальная деятельность — поскольку она требует способности интегрировать математические и коммуникативные навыки — она ​​неразрывно связана с языком, поскольку слова являются инструментами для перевода числового кода и придания ему смысла. .

Вероятность дорогостоящих ошибок из-за неграмотности даже больше, чем из-за неграмотности.

Логика = Шаблоны и отношения

Человеческий разум всегда ищет закономерности и взаимосвязи; математика — лишь один из формализованных способов, которыми мы это делаем.Даже очень маленькие дети могут расширить шаблон, сделав прыжок логики. Если бы вы спросили четырехлетнюю девочку, которая знала свой алфавит: «Какие две буквы алфавита идут после букв a, b, c и d?» ребенок почти наверняка определит правильный ответ, используя свой логико-математический интеллект.

Задавая это, вы фактически создаете проблему в уме ребенка; и человеческий разум, кажется, всегда, по крайней мере, пытается справиться с подобными проблемами распознавания образов.Точно так же, когда вы спрашиваете ребенка: «Какие два числа идут после 1, 2, 3, 4 и 5? Или с 1, 3, 5 и 7?

По сути, нет никакой разницы между молодым студентом, видящим закономерности в приведенных выше вопросах, и математиком (Евклид 2300 лет назад), который впервые увидел схему для простых чисел. Он увидел, что некоторые числа можно разделить только на себя и 1, и начал последовательность 2, 3, 5, 7, в которой следующее число — не 9, а 11; следующие числа в последовательности — 13 и 17, потому что они подчиняются другому закону развития, но по-прежнему основаны на шаблонах и отношениях.

Сотрудники должны владеть основами счета, чтобы иметь возможность полноценно участвовать в трудовой деятельности и расширять возможности своего образования и обучения. Повышение уровня этих навыков приведет к более гибкой, квалифицированной и адаптируемой рабочей силе, повышению производительности и конкурентному преимуществу для предприятий. На проекты рабочих мест положительно повлияет улучшение коммуникации и способности сотрудников заполнять рабочую документацию, а также сокращение количества ошибок и прогулов на рабочем месте, а также улучшение удержания и качества персонала.

Излагая свои идеи о необходимости оттачивать логические и математические навыки, возможно, вводя две предыдущие задачи, имеет смысл вступить в дискуссию о разнице между алфавитной и числовой системами счисления. Обсудите или, вернее, заставьте их поговорить об идее символизма на раннем этапе. Другие дисциплины, такие как производство или бухгалтерский учет, будут иметь больше смысла, и их важность возрастет.

Лучшие работодатели хотят лучших мыслителей в области распознавания образов

Почему? Потому что те, кто думают, чтобы заработать себе на жизнь, не только зарабатывают больше, но и вносят непропорционально большой вклад в предприятие.

«Сколько слов ты сказал за всю свою жизнь?» Очевидно, это больше связано с мыслительными процессами, чем с ответом. Если люди попытаются ответить на вопрос, они неизбежно начнут с шаблона и попытаются распознать его и продолжить его. Как бы это выяснить? Мои шаблоны использования и отношения.

Microsoft печально известна — или достойна восхищения, в зависимости от вашей точки зрения — тем, что просит респондентов попытаться за несколько минут выяснить, сколько квадратных футов газона есть во всех 32 парках Высшей лиги бейсбола.Они не ищут точного ответа; они ищут, насколько хорошо кандидат может распознавать закономерности, создавать закономерности, а затем разумно их интерпретировать.

Сколько кирпичей в доме соседа? Сколько карандашей, уложенных встык, нужно, чтобы растянуть отсюда до туда… ..вы выбираете начальную и конечную точки? Сколько секунд в день, год или в среднем за время жизни? Сколько банок газировки нужно, чтобы наполнить раковину?

Предположение имеет значение. Нанесение удара / втыкание кола в землю / угадывание имеет свою роль. Часто это лучший способ начать, потому что он запускает шаблон, который можно усовершенствовать. Постулирование чего-либо, уточнение и проверка его предположений и повторение всего этого иногда — это логический способ приближения только .

Я уверен, что вы видели людей в магазинах украшения дома, которые ужасно недооценивали свою потребность в обоях, или, возможно, вы слышали рассказы своего налогового инспектора о людях, которые откладывают подачу заявки в IRS, потому что им так неудобно иметь дело с числами.Хорошо это или плохо, но числа являются такой же частью ландшафта нашей цивилизации, как слова, и вашим сотрудникам необходимо овладеть ими. Хорошая новость заключается в том, что все мы до некоторой степени умеем считать; речь идет о том, чтобы разработчики учебных материалов пробуждали этот навык в своих учениках. Ваша задача как конструктора учебных материалов — пробудить научное, логическое и математическое любопытство и интеллект тех, кого вы обучаете.

Числовые игры обостряют математические чувства. Поощряйте своих людей играть в игры, которые обостряют их чувство чисел и закономерностей, такие как Clue, Dominoes и Go.У доктора Томаса Армстронга есть буквально десятки техник, перечисленных в его книге «7 видов умного». Предлагаю ли вашим людям проводить время на работе, играя в игры, улучшающие их логику? Абсолютно! Это отличное вложение. А школы этого не делали, так что вы должны.

Логические правила: это механизм самообороны вашей компании

Логическая ошибка приводит к ошибке в суждении или решении. Так что правильно делать это окупается: а делать это правильно — значит добраться до Истины.

Логика — это основа критического мышления. Логика чрезвычайно полезна для обнаружения ошибок и установления истины. Есть 3 первых принципа логики.

1. Закон идентичности.
   A — это A. Яблоко — это Яблоко. Что-то есть то, что есть. Все, что существует, имеет характеристики. Другими словами, если что-то существует, оно имеет уникальную природу, сущность. Это Sui generis — единственный в своем роде. У дерева есть ветви, листья, ствол и корни. Мы узнаем, что такое что-то, наблюдая за его характеристиками.Вы знаете, что дерево — это дерево, потому что вы видите его ветви, листья, ствол и корни. Более того, если у чего-то есть идентичность, у этого есть единственная идентичность. У него не более одной личности. Если что-то существует, у него есть набор атрибутов, согласующихся с его собственным существованием. У него нет набора несовместимых с ним атрибутов. Следовательно, мы можем легко сделать вывод, что дерево — это не дом.
2. Закон непротиворечия.
   A не может быть одновременно A и не A в одном и том же смысле. Что-то или какое-то утверждение не может быть истинным и ложным одновременно и одинаково. В дискуссиях и дебатах мы, естественно, способны распознать, когда кто-то противоречит сам себе. Противоречие возникает, когда одно истинное утверждение исключает возможность другого истинного утверждения, но при этом оба утверждаются как истинные. Поскольку мы знаем, что и то и другое не может быть правдой, мы видим противоречие. Исходя из этого принципа, мы можем заключить, что истина не противоречит самому себе .
3. Закон исключенного третьего гласит, что утверждение либо истинно, либо ложно.
   Я беременна. Утверждение либо верно, либо неверно. Поскольку я мужчина, я не могу забеременеть. Следовательно, утверждение неверно. Если бы я была женщиной, я могла бы забеременеть. Женщина не беременна. Она либо беременна, либо не беременна — средней позиции нет. Закон исключенного третьего важен, потому что он помогает нам иметь дело с абсолютными истинами. Компьютеры сейчас имеют дело только с абсолютом — вкл / выкл. Ситуация изменится с появлением квантовых вычислений, которые бросят вызов этому закону и улучшат нашу жизнь ради него, поскольку нет ничего изначально неправильного в том, чтобы держать в уме, приостановить в уме возможность того, что что-то есть или нет, истинно или ложно или что утверждение либо правда, либо ложь.Как только логика доказала, что что-то истинно или ложно, истина достигнута.

Это особенно важно в обществе, где пропагандируется релятивизм, а утверждения истины часто отрицаются.

Чтобы увидеть, как использовать команду для максимальной отдачи, посмотрите демонстрацию бесплатно здесь.

И, пожалуйста, поделитесь!

О логических рассуждениях — мост для входа в высшую математику

Почему логические рассуждения?

Как помочь учащимся использовать дедуктивное мышление для понимания математики? Ответить на этот вопрос — цель занятий по логическому мышлению.

Наши классы логики помогают учащимся развить навыки дедуктивного мышления, анализа случаев, методической работы и доказательства от противоречия. Кроме того, учащиеся учатся внимательно читать математические письма, чтобы понимать новые виды математических задач — все ключевые навыки для их будущего успеха в математике.

Разные классы

Студенты будут выбирать между тремя или четырьмя курсами логического мышления, каждый из которых основан на логической головоломке разного типа в качестве «крючка» для студентов.В каждом курсе студенты начинают с развития своих навыков решения выбранной логической головоломки, а затем переходят к выполнению математических вопросов, в которых используются те же навыки. Мы надеемся, что, проводя явные связи между двумя типами работы, учащиеся разовьют новые способы мышления о ситуациях, с которыми они сталкиваются.

BEAM Discovery — это гибкая программа, поэтому на уроках логики есть много возможностей для импровизации и творчества. Мы надеемся, что вы поможете нам разработать эти курсы и со временем расширять их.

Подробный обзор

Курс «Логическое рассуждение» начинается с решения классических логических задач, которые развивают основные навыки класса: дедуктивное рассуждение, анализ случаев, методическая работа и внимательное чтение. Мы также хотим заложить основу для доказательства противоречия: идея, что вы можете попробовать дело и идти до тех пор, пока не увидите противоречие; тогда вы можете вернуться и исключить этот случай.

No related posts.