Логические задачи для 8 класса с ответами
Логические задачи для 8 класса с ответами
#1
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ?Этим свойством обладает только шар
#2
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ?Получится не 12 десятков, а 120 десятков. То есть: 30 * 40 = 1200
#3
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
#4
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ?Книга стоит 2 доллара. Решение: полкниги стоит доллар, значит вся книга стоит 2 доллара
#5
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок.
Но в Японии на такие кроссовки накладываются очень большие пошлины.
Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? Никакой коррупционной и преступной составляющей здесь нет.
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями.
То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака.
В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе.
В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
#6
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г.
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке.
Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2, 25кг.
В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок.
И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
#7
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ?15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов
Два колхозника решили узнать, у кого больше овец.
Первый из них сказал: «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит: «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было)
У первого колхозника 7 овец, у второго только 5.
Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше.
#9
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ?Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
#10
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами)
Ответ?Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата.
У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка
#11
Попробуйте сообразить, какой из выводов, указанных ниже, верный:
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные
#12
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Получится равенство: 888 + 88 + 8 + 8 + 8 = 1000
#13
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Ответ?Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек.
Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения
#14
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые.
Варианты взвешиваний :
1) кладем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью.
Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных.
2) кладем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета
#15
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ?Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1
Как так могло оказаться, что половина числа 12 стало равно 7
Ответ?Нужно написать число 12 римскими цифрами: IIX, далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7
#17
Трехлитровый сосуд полностью заполнен тремя литрами воды.
Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды.
При этом больше нельзя пользоваться ничем, кроме этих трех сосудов.
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев.
Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ?Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
#19
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ?Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
aababy.ru
ВИКТОРИНА для 6-8 классов «Логические задачи»

Предлагаю учащимся 6-8 классов моей школы попробовать свои силы в дистанционной викторине. Вопросы в основном логические. А как у нас с логикой?… Правильно, тяжело! Попробуем изменить ситуацию и потренируем свое логическое мышление.
Все вопросы имеют порядковый номер. Решите как можно больше логических задачек и разместите в комментариях к этой статье ваши ответы. Обязательно указывайте номер вопроса, за ним – ваш ответ с пояснениями, если таковые требуются. Самые активные участники и наиболее интересные комментарии будут непременно отмечены учителем математики. Итак, вперед!
ВОПРОС 1. У вас в руках одна палочка. Как с её помощью образовать на столе треугольник? ВОПРОС 2.
ЗАДАЧА 23. В городе N живут три типа людей: такие, которые всегда говорят правду, всегда говорят неправду (лжецы), и шутники (они могут говорить и правду, и неправду). В этом городе кто-то угнал машину у шерифа. Полиция задержала троих человек: Джона, Джека и Билла. Полиции было известно, что один из них — лжец, один — всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь. Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду. Трое задержанных сказали следующее:
Джон: Я не виновен. Джек: Он говорит истинную правду. Билл: Я угнал машину. Кто угнал машину и кто лжец? ЗАДАЧА 24. Как без использования калькулятора найти три последние цифры произведения 1 x 2 x 3 x 4 x 5…x 17 x 18? ЗАДАЧА 25. У Петра 100 мышей. Некоторые белые, некоторые – серые. Известно, что хотя бы одна мышь серая, а из двух мышей хотя бы одна – белая. Сколько у Петра серых мышей?.
Ответы к задачам с комментариями будут непременно размещены после подведения итогов викторины. Желаю успехов в тренировке!
solodenkovagalina.blogspot.com
Логические задачи
1. Отправился человек в море и попал в шторм. Его отнесло на остров, где не было мужчин, а жили только девушки. Утром проснулся мужик на каком-то ритуале, весь обвязанный веревками, и узнал, что его хотят убить. Тогда попросил бедолага дать ему последнее слово. После того, как мужчина произнес его, девушки смастерили ему лодку, дали еду и отправили домой. Что же он сказал?
2. Эту загадку ученик первого класса решает за 5 минут, старшеклассник справляется за 15 минут, студент — за час, профессор же не решит никогда. А вот и вся головоломка: расшифруй ОДТЧПШСВДД.
3. Один поезд едет из Москвы в Санкт-Петербург с опозданием в 10 минут, а другой — в обратном направлении с опозданием в 20 минут. Какой из этих поездов будет ближе к Москве, когда они встретятся?
4. Известно, что среди девяти монет есть одна фальшивая, вес которой меньше, чем у остальных. Как с помощью чашечных весов всего за два взвешивания определить фальшивку?
5. Стоит стена из бетона высотой 3 метра, длиной 20 метров и весом 3 тонны. Как ее повалить, не имея никаких вспомогательных средств и инструментов?
6. Кошка – 3, лошадь – 5, петух – 8, ослик – 2, кукушка – 4, лягушка – 3, собака — ?
7. К реке подходят два человека. У берега стоит лодка, которая может выдержать только одного. Оба человека переправились на противоположный берег. Как?
8. Где встречается такое, что конь через коня перепрыгивает?
9. Шерлок Холмс шел по улице. И вдруг он увидел мертвую женщину, лежащую на земле. Сыщик подошел, открыл ее сумку и достал телефон. В телефонной книге нашел номер ее мужа и позвонил. Шерлок сказал: «Срочно приезжайте сюда. Ваша жена умерла». Через некоторое время приезжает муж, смотрит на жену и говорит: «Милая моя, что с тобой случилось?» Вскоре подоспела полиция. Шерлок указал пальцем на мужа женщины и промолвил: «Арестуйте этого человека, он убил свою жену». Вопрос: почему Шерлок так подумал?
10. Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться всем на другой берег?
Ответы.
1. Пусть меня убьет самая некрасивая.
2. 1, 2, 3, 4…
3. В момент встречи они будут на одинаковом расстоянии от Москвы.
4. Первое взвешивание: на каждой чаше весов по 3 монеты. Фальшивка находится в той кучке, которая меньше весит. Если равны, то фальшивая монета в третьей партии. Второе взвешивание: из тройки с наименьшим весом берем две монеты и взвешиваем. Какая чаша опуститься меньше, там и подделка. Если чаши весов равны, то фальшивка — оставшаяся монета из этой партии.
5. Толщина такой стены будет не более двух сантиметров, что позволяет толкнуть ее рукой.
6. Кошка говорит мяу (3 буквы), лошадь — и-го-го (5 букв), петух — ку-ка-ре-ку (8)… Собака, как известно, — гав, поэтому правильный ответ 3.
7. Они просто были на разных берегах.
8. В шахматах.
9. Ведь Холмс не назвал адрес, куда ехать.
10. Сперва переправляются оба сына. Один из них возвращается обратно к отцу. Папа перебирается на противоположный берег к сыну и остается на берегу, а второй сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
1.Ответ:
Всего 5 остановок (включая конечную).
2.Ответ
На эскалаторе 280 ступеней.
Если общее количество ступеней на открытой части эскалатора обозначить через N, то при движении вниз оно будет складываться из количества ступеней, на которые опустился сам эскалатор, и количества ступеней, пройденных по нему. В первом случае время движения составило 140 : 2 = 70 секунд, во втором — 56 секунд. Для постоянной скорости эскалатора V указанные соображения приводят к уравнениям:
140 + 70*V = N
168 + 56*V = N,
решение которых N = 280 ступеней и V = 2 ступени в секунду.
3.Ответ
У кого-то может денег не быть!
1 — 1,54
2 — 1,35
3 — 0
4.Ответ:
Пусть велосипедист вёз мальчика х километров. Скорость мальчика v км/ч, скорость велосипедиста 2v км/ч. Между 12-00 и 14-00 прошло времени x/2v+a/v=(x+2a)/(2v)=2 часа. На обратную дорогу уйдёт (x+2a)/v=4 часа
5.Ответ:
12345 23456 34567 45678 56789
и обратные:
98765 87654 76543 65432 54321
и одно 55555
1.Прочитайте условие, но только один раз, и попробуйте сразу же ответить на вопрос. На конечной остановке в автобус сели четырнадцать мужчин и две женщины. На первой остановке сошли двое мужчин и вошли две женщины. На следующей остановке вышли почти все мужчины (осталось только трое), а на следующей вошли пять женщин. Проехав с полкилометра, автобус остановился, и в него вошел еще один мужчина. Сколько всего было остановок на пути следования автобуса?
2.Человек опаздывал на работу и, чтобы наверстать потерянное в пробке время, побежал вниз по эскалатору метро. Спускаясь со скоростью две ступени в секунду, он насчитал сто сорок ступеней. Через день ситуация повторилась, но теперь ему грозило большее опоздание. Естественно, по тому же эскалатору он бежал быстрее — со скоростью три ступени в секунду, а насчитал на двадцать восемь ступенек больше.
Странно получилось: чем быстрее бежишь, тем длиннее эскалатор.
Сколько же всего ступенек на нем?
3. Трое друзей хотят купить книжку. Оказалось, что двоим на покупку книги не хватает 1 копейки, третьему 2 рубля 90 копеек. Когда они сложили свои деньги, то денег на покупку книги им все равно не хватило. Зная, что денег у первого из друзей на 19 копеек больше чем у второго, найдите, сколько денег было у каждого.
4. Мальчик пошел из лагеря в город. В 12 часов, в нескольких километрах от лагеря, его догнал велосипедист и подвез его немного. Затем велосипедист высадил мальчика недалеко от города, и в 14 часов мальчик добрался до города.
Сколько времени потратит мальчик на обратную дорогу пешком, если известно, что скорость велосипедиста в два раза больше скорости мальчика?
5. На доске выписаны все пятизначные числа, у которых каждая цифра либо равна обеим соседним, либо отличается от соседних ровно на единицу — от одного в меньшую, а от другого в большую сторону.
Сколько написанных на доске чисел содержат в своей записи цифру 5?
Задачи на взвешивание и переливания.
1.Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном — все фальшивые. Одна настоящая монета весит 5 грамм, а фальшивая — 4 грамма. Есть весы, показывающие вес в граммах.
Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты
Мешки можно раскрывать и вытаскивать монеты
2. Как, имея пятилитровое и девятилитровое ведро, набрать из крана ровно три литра воды?
3.Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?
4.Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л.
5.Три человека купили сосуд, полностью заполненный 24 унциями меда. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить мед на равные части используя эти четыре сосуда? Постарайтсь решить задачу за наименьшее количество переливаний.
Восемнадцать спичек образовывают 6 одинаковых прилегающих друг к другу квадратов. Заберите 2 спички так, чтобы осталось 4 таких же квадрата.

11.Что больше: сумма всех цифр или их произведение?
12.Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
13.В тот день в классе было 24 человека. Когда ученики писали контрольную работу, то они по мере завершения клали тетради в стопку одна на другую. Петя сдал тетрадь пятым по счёту. Каким по счёту его тетрадь проверят, если считать, что учитель проверяет тетрадь сверху стопки и строго по порядку?
1.Ответ:
Пронумеруем мешки от 1 до 10. Вытащим из первого 1 монету, из второго 2, из третьего 3 и так далее. Затем возьмем всю эту кучу монет и положим на весы. Если бы они все были настоящие, то общий вес составил бы 275 грамм (т.к. мы вытащили в общей сложности 55 монет). Но в одном из мешков были фальшивые. Если это был первый мешок, то вес будет на 1 грамм меньше (т.к. мы взяли оттуда 1 монету). Если фальшивые были во втором, то на 2 грамма меньше. И так далее.
2.Ответ:
Заполняем 9-литровое ведро и заливаем из него в 5-литровое ведро. (Далее 5-литровка и 9-литровка). в 9-литровке 4 литра. Выливаем воду из 5-литровки и заливаем туда 4 литра из 9-литровки. Заполняем 9-литровку и выливаем оттуда 1 литр в пятилитровку. Выливаем воду из 5-литровки, и заполняем пятилитровку из девятилитровки. Всё! В девятилитровке теперь 3 литра.
3.Ответ:
Сначала он наполнил 30-литровый кувшин и вылил его содержимое в 50-литровый. Потом опять наполнил 30-литровый и долил до полного заполнения в 50-литровый. В результате у него в кувшине останется 10 литров.
4.Ответ:
Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л.- 4 литра, в 8л — 3литра, а в 5л.- 5 литров. Переливаете из 5л. в 12л. всю воду, а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.
5.Ответ:
Сосуды могут содержать 24, 13, 11, и 5 унций соответственно:
Их начальное состояние 24, 0, 0, 0;
1 — 8, 0, 11, 5;
2 — 8, 11, 0, 5;
3 — 8, 13, 3, 0;
4 — 8, 8, 3, 5;
5 — 8, 8, 8, 0.
6. Ответ:

11.Ответ:
Больше сумма, так как произведение равно 0 (один из множителей — это цифра 0).
12.Ответ:
Один человек берет яблоко вместе с корзиной.
13.Ответ:
Подвох в том, что учитель тоже человек. Т.е. в классе было 23 ученика, и после Пети работу сдали 18 человек (23-5). Таким образом, Петину тетрадь проверят 19-ой.
videouroki.net
Проектная работа по математике на тему » Решение логических задач» ( 8 класс)
Муниципальное бюджетное образовательное учреждение
средняя общеобразовательная школа №1 с. Александров-Гай
Проектная работа на тему :
«Решение логических задач»
Выполнила:
Жусубалиева Мадина,
обучающаяся 8 «а» класса
МБОУ СОШ №1
с. Александров-Гай
Саратовской области
Руководитель: учитель математики
МБОУ СОШ №1 с. Александров-Гай
Пыхова Галина Владимировна
Александров-Гай
2016 г.
Оглавление
1.Введение___________________________________________________3
2.Основоположники науки «логика»______________________________4
3.Как решаются логические задачи?______________________________5
4. Типы и способы решения логических задач______________________5
метод графов ______________________________________________5
метод таблиц ______________________________________________6
метод рассуждений _________________________________________6
метод алгебры логики _______________________________________7
метод кругов Эйлера ________________________________________8
5. Копилка занимательных задач ______________________________9
6. Заключение______________________________________________12
7. Литература______________________________________________13
Предмет математики настолько
серьезен, что нельзя упускать случая
сделать его немного занимательным.
Блез Паскаль
Введение
Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики — нет ни чисел, ни функций, ни треугольников, а есть только лжецы и мудрецы, истина и ложь. В то же время дух математики в них чувствуется ярче всего — половина решения любой математической задачи состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.
Готовя данную работу, я ставила цель : изучение методов решения задач на логику. Только решение трудной, нестандартной задачи приносит радость победы.
Предмет исследования: логические задачи.
Актуальность. В наше время очень часто успех человека зависит от его способности четко мыслить, логически рассуждать и ясно излагать свои мысли.
Задачи: 1) ознакомление с понятиями «логика» и «математическая логика»;
2) изучение основных методов решения логических задач;
Ло́гика — раздел философии, нормативная наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка.
Логика получила основательное развитие изначально только в трёх традициях: в китайской, индийской и греческой. Современная логика происходит в конечном счёте из греческой традиции.
В конце XIX — начале XX веков были заложены основы математической, или символической, логики. Её суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.
Основоположники науки «логика»
Слово «логика» греческого происхождения. Логика как наука основана Аристотелем (384-320 гг до н.э.), который был необыкновенной фигурой в целой плеяде блестящих греческих ученых. Он был последователем Платона и посещал его Академию в Афинах. После смерти Платона (347 г.до н.э.) Аристотель покинул Афины. Он вернулся туда 12 лет спустя и основал свою школу — Лицей. Одним из учеников Аристотеля был Александр Великий. Аристотель не был математиком в полном смысле этого слова, его логика является скорее частью философии, но эта часть — основа всех наук. В своем выдающемся произведении «Аналитики» Аристотель создал и проверил около 20 схем рассуждений, которые назвал силлогизмами. Процитируем самый известный силлогизм: «Сократ — человек; все люди смертны; значит Сократ смертен». После Аристотеля силлогизмы и их трансформации стали основой дедуктивных рассуждений. Галилей говорил, что если бы ему пришлось начать снова свое будущее, то он последовал бы совету Платона и «принялся бы сперва за математику как науку, требующую точности и принимающую за верное то, что вытекает как следствие из доказанного».
Готфрид Лейбниц в начале 18 века сделал попытку создать формальную логическую систему, введя законы сочетания высказываний. Он высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам: «Можно придумать некий алфавит человеческих мыслей, и с помощью комбинации букв этого алфавита и анализа слов, из них составленных, все может быть открыто и разрешимо». Но эти работы не были опубликованы, и лишь в 19 веке Джордж Буль и Август де Морган основали математическую логику, независимую от философии.
Назовем известнейшие работы Буля (1815-1864): «Формальная логика», «Исследование законов мысли». Буль вводит в логику алгебраическую структуру, называемую сегодня кольцо Буля, две операции, свойства которых в чем-то подобны свойствам операции с числами (например, 1+0=1), и в чем-то расходятся с ними (например, 1+1=1). Это позволило описать логику высказываний как формальную алгебраическую структуру.
Как решаются логические задачи?
Логические задачи – это своеобразная «гимнастика ума», средство для утоления естественной для каждого мыслящего человека потребности испытывать и упражнять силу собственного разума. В разделе представлен ряд занимательных задач из области математики, физики, естествознания, полюбившиеся многим задачи на взвешивание, переливание, задачи на нестандартное логическое мышление. Итак, мы узнаем, как разными способами можно решать логические задачи. Оказывается таких приемов несколько, они разнообразны и каждый из них имеет свою область применения. Вы узнаете кое-что об этих приемах. Познакомившись подробно, поймете в каких случаях удобнее использовать тот или другой метод. Вам придется познакомиться с основными понятиями направления «математики без формул» — математической логики, узнать о создателях этой науки и об истории ее становления. Известно несколько различных способов решения логических задач: метод графов; метод рассуждений; метод таблиц; метод блок-схем; метод бильярда; метод алгебры логики; метод кругов Эйлера. Остановимся отдельно на каждом из выделенных методов, иллюстрируя их примерами решения конкретных задач.
Типы и способы решения логических задач
1.Метод графа.
Один из способов – решение с помощью графов. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в таком случае граф называется ориентированным). Пусть нам требуется установить соответствие между двумя типами объектов (множествами). Буквами обозначаются элементы множеств, а соответствие между ними – красными отрезками. Синий отрезок будет объединять два элемента, не соответствующих друг другу.
Решить задачу просто, если учесть, что:
Каждому элементу одного множества обязательно соответствует элемент другого множества, но только один
Если элемент каждого множества соединен со всеми элементами (кроме одного) другого множества штриховыми отрезками, то с последним он соединен сплошным отрезком.
Задача. Пятеро одноклассников: Маша, Андрей, Даша, Сергей и Паша стали победителями олимпиад школьников по физике, математике, информатике, литературе и географии. Известно, что:
-победитель олимпиады по информатике учит Машу и Андрея работе на компьютере;
-Даша и Сергей тоже заинтересовались информатикой;
-Андрей всегда побаивался физики;
-Даша, Андрей и победитель олимпиады по литературе занимаются плаванием;
-Андрей и Даша поздравили победителя олимпиады по математике;
-Маша сожалеет о том, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
2.Метод таблиц.
Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Способ решения логических задач – с помощью таблиц – также прост и нагляден, но его можно использовать только в том случае, когда требуется установить соответствие между двумя множествами. Он более удобен, когда множества имеют по пять-шесть элементов.
Задача. Пятеро одноклассников: Маша, Андрей, Даша, Сергей и Паша стали победителями олимпиад школьников по физике, математике, информатике, литературе и географии. Известно, что:
-победитель олимпиады по информатике учит Машу и Андрея работе на компьютере;
-Даша и Сергей тоже заинтересовались информатикой;
-Андрей всегда побаивался физики;
-Даша, Андрей и победитель олимпиады по литературе занимаются плаванием;
-Андрей и Даша поздравили победителя олимпиады по математике;
-Маша сожалеет о том, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
Решение.
Маша.
Андрей.
Даша.
Сергей.
Саша.
Физика.
+
Матем.
+
Информ.
+
Литер.
+
Геогр.
+
3. Метод рассуждений.
Способ рассуждений — самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Задачи на перемещение или правильное размещение фигур можно решать двумя способами: практическим (действия в перемещении фигур, подборе) и мысленном (обдумывание хода, предугадывание результата, предположение решения- метод рассуждений).
В методе рассуждений при решении помогают: схемы, чертежи, краткие записи, умение выбирать информацию, умение пользоваться правилом перебора. Этим способом обычно решают несложные логические задачи.
Задача. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение. Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
4.Метод алгебры логики.
Задача. Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым. Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение. Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
5.Метод кругов Эйлера.
Этот способ решать задачи придумал в 18 веке великий Леонард Эйлер.
Задачи , которые можно решить с помощью кругов Эйлера нельзя решить иначе, по сравнению с табличным методом или при помощи графов. Метод диаграмм Эйлера позволяет графически решать математические задачи на основе применения теории множеств. Этот метод прост, если в нем разобраться. Задачи на нахождение пересечения или объединение множеств (круги Эйлера). Ещё один тип задач – задачи, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Задача.
В классе 36 человек, 2 человека побывали и в кино и в театре и в цирке. В кино побывало 10 человек; в театре — 14 человек; в цирке — 18 человек;
и в театре, и в цирке — 8 человек; и в кино, и в цирке — 5 человек;
и в театре, и в кино — 3 человека.
Сколько учеников класса не посетили ни театр, ни кино, ни цирк?
Решение.
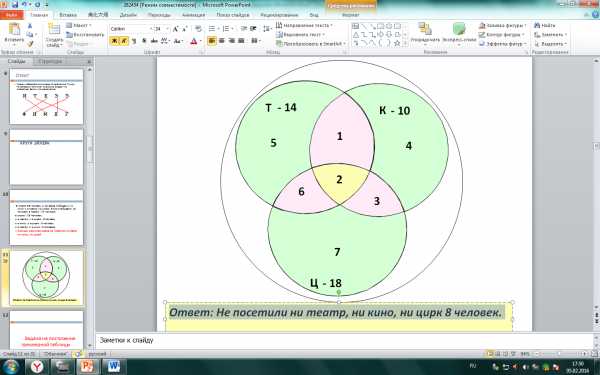
Ответ: Не посетили ни театр, ни кино, ни цирк 8 человек.
Копилка интересных задач
Задачи о переправах.
Задача. Отец, мать и двое детей – сын и дочь, должны переправиться через реку. Поблизости случился рыбак, который мог бы одолжить им свою лодку. Однако, в лодке могут поместиться только один взрослый или двое детей. Как семье переправиться через реку и вернуть рыбаку его лодку?
Решение. Первыми переправляются дети. Сын возвращается к маме-папе. Папа едет на берег к дочери, потом дочь едет за братом и возвращается с ним к папе. Сын едет к маме, отдает ей лодку, чтобы она переплыла к папе и дочери. После того, как мама переправилась, дочь садится в лодку и едет к брату, подбирает его, и вместе они едут к родителям. Дочь остается с родителями, а сын едет к рыбаку, отдает ему лодку. Рыбак едет к родителям и высаживается. Дочь садится и едет за братом, привозит его с собой обратно (наконец-то вся семья снова вместе), они отдают лодку рыбаку. Лодка пересекла реку 13 раз.
Задачи на переливание.
Задача. Отмерить 3 л, имея сосуд 5 л. Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Решение. Наливаем кастрюлю. Переливаем воду из кастрюли в банку. Наливаем кастрюлю. Доливаем полную банку, и в кастрюле остается 3 литра.
Задача. Как при помощи 5-ти литрового и 9-ти литрового ведра набрать из реки 3 литра воды?
(Решение : Заполняем водой из реки 9-ти литровое и переливаем из него воду в 5-ти литровое (в 9-ти литровом остается 4 литра). Освобождаем 5-ти литровое ведро и переливаем в него 4 литра из 9-ти литрового. Еще раз заполняем водой из реки 9-ти литровое и из него доливаем в 5-ти литровое 1 литр воды (в 9-ти литровом остается 8 литров). Освобождаем 5-ти литровое и переливаем в него из 9-ти литрового 5 литра воды. В 9-ти литровом ведре останется 3 литра воды.)
Задача . Лена, Оля, Таня участвовали в беге на 100 м. Лена прибежала на 2 с раньше Оли, Оля прибежала на 1 с позже Тани. Кто пришел раньше: Таня или Лена и на сколько секунд? ( ответ : раньше на 1с пришла Лена)
Задача . В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что у одного из нас белые, у другого черные, а у третьего рыжие волосы, но ни у кого цвет волос не соответствует фамилии», — заметил черноволосый. «Ты прав», — сказал Белов. Какой цвет волос у художника? ( ответ –черноволосый)
Задача . Однажды на семейном празднике собрались семь супружеских пар. Фамилии мужчин: Владимиров, Федоров, Назаров, Викторов, Степанов, Матвеев и Тарасов. Женщин зовут: Тоня, Люся, Лена, Света, Маша, Оля и Галя. На вечере Владимиров танцевал с Леной и Светой, Назаров — с Машей
и Светой, Тарасов — с Леной и Олей, Викторов — с Леной, Степанов — со Светой, Матвеев — с Олей. Затем стали играть в карты. Сперва Викторов и Владимиров играли с Олей и Галей, потом мужчин сменили Степанов и Назаров, а женщины продолжали игру. И, наконец, Степанов и Назаров сыграли одну партию с Тоней и Леной.
Задача . Четыре ученика — Витя, Петя, Юра и Сергей — заняли на математической олимпиаде четыре первых места. На вопрос, какие места они заняли, были даны ответы:
а) Петя — второе, Витя — третье;
б) Сергей — второе, Петя — первое;
в) Юра — второе, Витя — четвертое.
Указать, кто какое место занял, если в каждом ответе правильна лишь одна часть.
( ответ : первое место – Петя, второе место — Юра, третье место — Витя, четвертое место Сергей)
Задача . Три друга Коля, Олег и Петя играли во дворе, и один из них случайно разбил мячом оконное стекло. Коля сказал: «Это не я разбил стекло». Олег сказал: «Это Петя разбил стекло». Позднее выяснилось, что одно из этих утверждений верное, а другое — нет. Кто из мальчиков разбил стекло? ( ответ: стекло разбил Олег.)
Задача . Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 — и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекается коллекционированием? ( ответ 10)
Задача . Три курицы за три дня несут три яйца. Сколько яиц снесут 12 таких же курей за 12 дней? ( ответ 48)
Задача . В шкафу вперемешку лежат 15 носков черного цвета и 20 носков белого цвета. Какое минимальное количество носков необходимо достать (в полной темноте или просто не глядя), чтобы из них можно было получить пару одного цвета?
( ответ : необходимо достать всего 3 носка. При этом возможны следующие варианты комбинаций. 1. Все три носка черного цвета. 2. Все носка белого цвета. 3. Один носок черного, два носка белого цвета. 4. Один носок белого, два носка черного цвета. То есть при любом варианте можно получить пару одного цвета.)
Задача . Позавчера Пете было 17 лет. В следующем году ему будет 20 лет. Как такое может быть?
( ответ : если нынешний день 1 января, а День Рождения у Пети 31 декабря. Позавчера (30 декабря) ему было еще 17 лет, вчера (31 декабря) исполнилось 18 лет, в нынешнем году исполнится 19 лет, а в следующем году — 20 лет.)
Задача . Набор чисел 1, 3, 8, 120 обладает следующим свойством: если перемножить любые два числа и прибавить единицу, то получится точный квадрат. Какое пятое число можно к ним добавить, чтобы свойства набора не изменились?
(Ответ: Это число 0! Что касается шестого такого числа, то она не известно, но и не доказано, что его нет).
Заключение
В данной работе мы познакомились с логическими задачами. С тем, что такое логика. Вашему вниманию были предложены различные логические задачи, которые помогают развивать логическое и образное мышление.
У любого нормального ребенка есть стремление к познанию, желание проверить себя. Чаще всего способности школьников так и остаются не раскрыты для них самих, они не уверены в своих силах, равнодушны к математике.
Для таких школьников я и предлагаю применять логические задачи. Эти задачи могут быть рассмотрены на кружковых и факультативных занятиях.
Они должны быть доступны, будить сообразительность, овладевать их вниманием, удивлять, пробуждать их к активной фантазии и самостоятельному решению.
Также я считаю, что логика помогает нам в нашей жизни справиться с любыми трудностями, и все что мы делаем, должно быть логически осмысленно и построено.
С логикой и логическими задачами мы сталкиваемся не только в школе на уроках математики, но и на других предметах.
Освоение основных элементов математической логики пригодится в будущей профессиональной деятельности как в сфере экономики, так и в других сферах жизни общества.
Литература:
1.Дорофеев Г.В. Математика .-Просвещение,: 2013.
2.Матвеева Г. Логические задачи // Математика. — 1999. № 25. — С. 4-8.
3.Орлова Е. Методы решения логических задач и задач на числа // Математика. — 1999. № 26. — С. 27-29.
4.Шарыгин И.Ф.,Шевкин Е.А. Задачи на смекалку.-Москва,:Просвещение,1996.-65с.
5. Математическая логика // Википедия / http://ru.wikipedia.org
infourok.ru
Логические задачи для 7, 8 класса
Решение задачи 1.Прежде всего заметим, что обойтись менее чем шестью распилами не удастся. Действительно, рассмотрим один из восьми внутренних кубиков. У него шесть граней, и все они должны быть освобождены распилами. Но за один распил освобождается не более одной грани каждого кубика, поэтому менее чем шестью распилами обойтись не удастся. Проверим, что шести распилов достаточно, указав способ осуществления этих распилов. Действительно, за два распила, параллельные одной из граней, легко распилить куб на 4 «слоя» размером 4x4x1, сделав при этом одно перекладывание между распилами. Затем повторяя эти операции параллельно другим ребрам, можно добиться распила на единичные кубики.
Решение задачи 2.
Во-первых, опишем тактику, следуя которой, Глазок может гарантировать себе не менее 54 монет, тогда Хапок не может гарантировать себе более 46. Пусть Глазок забирает себе все те пригоршни, в которых не менее 6 монет, а все остальные отдает Хапку. Тогда в конце дележа Глазок либо возьмет 9 пригоршней, в которых не менее 54 монет, либо не возьмет 9 пригоршней. В этом случае Хапок возьмет не более 9 пригоршней, в которых не более 45 монет, и Глазку достанется не менее 55.
Во-вторых, покажем, как Хапок может гарантировать себе не менее 46 монет. Пусть Хапок берет одинаковые пригоршни по 6 монет. Таких пригоршней получится 16 и еще 4 монеты. Тогда в конце дележа либо Глазок возьмет 9 пригоршней, в которых 54 монеты, либо Хапок возьмет не менее 8 пригоршней, в которых 48 монет. В обоих случаях Хапок получит не менее 46 монет.
Решение задачи 3.
Расположение 16 коней показано на рисунке (а). Докажем, что большее число коней расположить нельзя.
Пусть шахматная доска 5×5 окрашена так, что угловые клетки (а, значит, и центральная тоже) черные. Получится 13 черных и 12 белых клеток. Пусть на доске расставлены кони в соответствии с условием. Каждый конь, стоящий на белой клетке, бьет двух коней, стоящих на черных, при этом каждого коня стоящего на черной клетке бьют два коня, стоящих на белых, следовательно, на белых клетках стоит столько же коней сколько на черных. Если на центральной клетке стоит конь, то из 8 белых клеток, которые он бьет, 6 клеток свободные, значит, занято не более 6 белых клеток, но тогда на доске не более 12 коней. Если на одной из угловых клеток стоит конь, то еще два коня должны стоять на белых клетках, которые он бьет (на рисунке (б) это клетки, отмеченные крестом). Тогда из отмеченных на рисунке (б) десяти черных клеток заняты не более трех, т.е. всего на черных полях стоит не более 6 коней, но тогда на доске не более 12 коней. Если же центральная и все угловые клетки свободны, то занято не более 8 черных клеток и на доске не более 16 коней.
Решение задачи 4.
Чтобы узнать через сколько дней они встретятся нужно найти НОК (3;4;5). Так как числа имеют только один общий делитель равный 1, то наименьшее общее кратное равно их произведению, есть НОК (3;4;5) = 60(дней). Так как они встретятся только в один день. А именно , в понедельник, то найдем остаток от деления периода их встречи на количество дней в неделю, то есть 60 : 7 = 8 (ост.4).
| Понедельник | Вторник | Среда | Четверг | Пятница | Суббота | Воскресенье |
| 0 | 1 | 2 | 3 | 4 | — | — |
Ответ: ребята встретятся через 60 дней, в пятницу.
Решение задачи 5.
Всего шариков в коробках первоначально 1 + 2 + 3 + 4 + 5 + 6 = 21, а после k ходов их станет 21 + 2k. С другой стороны, общее количество шариков в коробках в тот момент, когда во всех коробках станет шариков поровну, равно 6n, где n – число шариков в одной коробке.
Отсюда 21 + 2k = 6n.
Но равенство невозможно при натуральных k и n, так как его правая часть четна, а левая – нечетна.
Ответ: нельзя.
Решение задачи 6.
Рассмотрим остатки, которые может давать квадрат натурального числа при делении на 11. Результат вычислений можно оформить в виде таблицы:
| Остаток от деления a на 11 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Остаток от деления b на 11 | 0 | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 |
Заполняется она таким образом. Если натуральное число а при делении на 11 дает в остатке r:
а = 11k + r (k и r – целые неотрицательные, r то
а2 = (11k + r)2 = (121k2 + 22kr) + r2.
Следовательно, достаточно выяснить, какой остаток даст r2 при делении на 11 (в случае, если r2 > 11, нужно r2 разделить на 11 с остатком и записать в таблицу полученный остаток).
А теперь присмотримся к таблице: когда сумма остатков от деления на 11 квадратов двух натуральных чисел а и b равна 0 или 11? Только в одном случае – когда оба эти остатка равны нулю, т.е. когда и число а, и число b делятся на 11.
Ответ: верно.
Решение задачи 7.
Первое решение. Если бы все задачи, решенные Мишей, были трудными, то он получил бы за них 10 – 3 = 30 баллов. Однако он получил только 14 баллов и, значит, 16 баллов потерял. Если вместо трудной задачи он решил легкую, то вместо 3 баллов он получил 2, т. е. потерял 1 балл. За каждую нерешенную легкую задачу он по условию также терял 1 балл. Итак, за каждую легкую задачу (независимо от того, решил он ее или нет) Миша терял ровно 1 балл. Так как всего он потерял 16 баллов, то и число легких задач также равно 16.
Второе решение. Пусть х легких задач Миша решил, а у легких задач не решил. Тогда он решил 10 – х трудных задач. Поэтому по условию имеет место равенство 3 – (10 – х) + 2 • х – 1 • у = 14, откуда после упрощения х + y = 16. Следовательно, общее количество легких задач равно 16.
eruditu.ru
Логические задачи, задачи на логику. С ответами.
Размер | Толщина | Фон | ||
| Скрыть ответы | +шрифт —шрифт | +жирн —жирн | White Cyan LGreen GYellw DpSkBl Coral DPink1 DPink2 SkBlue Orange OlivD1 OlivD2 LBlue PGreen Yellow Gold Blue Green Wheat Chocol Salmon Red HPink DPink Pink VioRed Magent Violet Plum Purple OrRed Bisque Bisqu2 LemC1 LemC2 Corns2 Honey2 Turqu1 Turqu2 SGrn1 SGrn2 Orchi1 Orang1 Gray golrod | |
Как вы думаете, если полста разделить на половину, то сколько в итоге получится?
Ответ
Получится не 25, как многие могут подумать, а 100. Так как если 50 разделить на 1/2, то это равносильно умножению на 2.
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ
Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).
Ответ
Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата. Поэтому их если и делают, то только прикрепив к люку шарнирами. У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка.
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ
Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1.
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ
Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.
Ответ
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ
Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ
Этим свойством обладает только шар.
Попробуйте сообразить, какой из выводов, указанных ниже, верный :
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Ответ
Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные.
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ
Книга стоит 2 доллара. Решение : полкниги стоит доллар, значит вся книга стоит 2 доллара.
Поделитесь с друзьями: |
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
Ответ
Сейчас восемь часов.
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок. Но в Японии на такие кроссовки накладываются очень большие пошлины. Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? (Никакой коррупционной и преступной составляющей здесь нет).
Ответ
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями. То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака. В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе. В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ
15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г. Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Ответ
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке. Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2,25кг. В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок. И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
Два колхозника решили узнать, у кого больше овец. Первый из них сказал : «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит : «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было).
Ответ
У первого колхозника 7 овец, у второго только 5. Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше. Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5.
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Ответ
Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек. Если из первой половины добавить школьника в другую, то получится разница в 2 человека. Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения.
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Ответ
Получится равенство : 888 + 88 + 8 + 8 + 8 = 1000.
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые. Как определить эту монету за 2 взвешивания на чашечных весах?
Ответ
Варианты взвешиваний : 1) ложем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью. Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных. 2) ложем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета.
Как так могло оказаться, что половина числа 12 стало равно 7 ?
Ответ
Нужно написать число 12 римскими цифрами : IIX , далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7.
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ
Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
Поделитесь с друзьями: |
www.treningmozga.com
Сборник логических задач для школьников 8-9 классов
46. Вставить пропущенное число:
50. Вставить пропущенные числа.40
12
20
?
?
51. Вставить пропущенное число.
12
15
4
5
8
17
90
?
52. Вставить пропущенное слово.
53.Вставить пропущенное число.
3600
?
54. Вставить пропущенное число.
55. Вставить пропущенное число.
56. Вставить пропущенное число.Раздел ІІ
Решение задач
1.Пусть было х гусей, тогда по условию задачи получим уравнение x+х+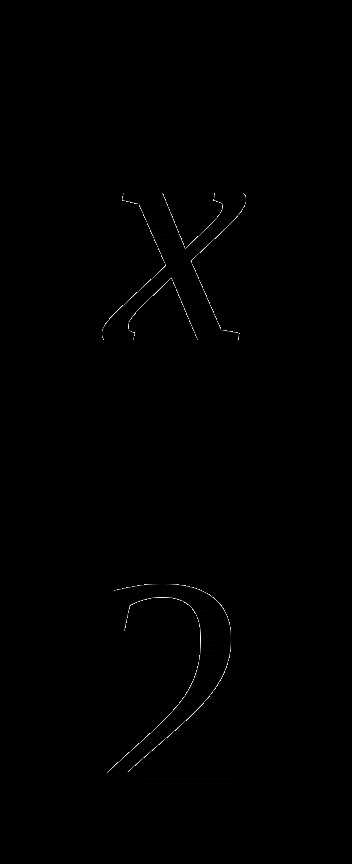 +
+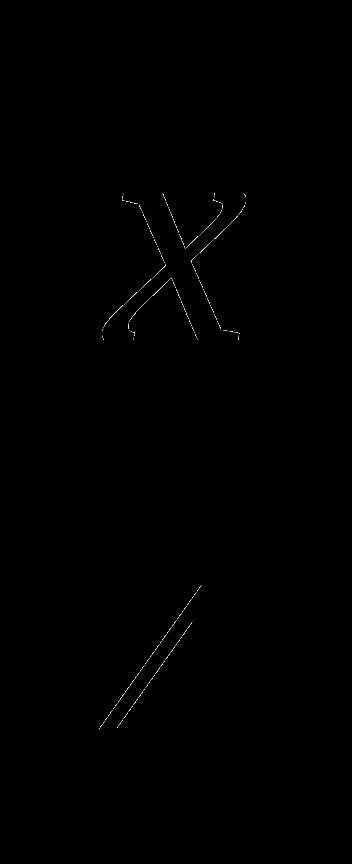 +1=100. После решения уравнения получим х=36.
+1=100. После решения уравнения получим х=36.
Итак, было 36 гусей.
Ответ: было 36 гусей.
2. Ответ: наседьмой день.
3.Ответ: число 666 нужно перевернуть и получим 999.
4.Справа – стандартный вид числа, которое записано слева, поэтому данный многочлен второй строки нужно записать в стандартном виде. Значит, получим: а3 + а2 — 3а -3.
Ответ: а3 + а2 — 3а -3.
5. Ответ:9ав – ас – вс.
6.Проанализируем данные первого ряда: 3 1058 : 5
1058 : 5 1023 = 6
1023 = 6 1034, тогда пропущенное выражение будет 63в9с : 7вс2 = 9в8с-1.
1034, тогда пропущенное выражение будет 63в9с : 7вс2 = 9в8с-1.
Ответ 9в8с-1.
7. Листопад – это опадание листьев осенью, поэтому нужно преобразовать данное выражение:
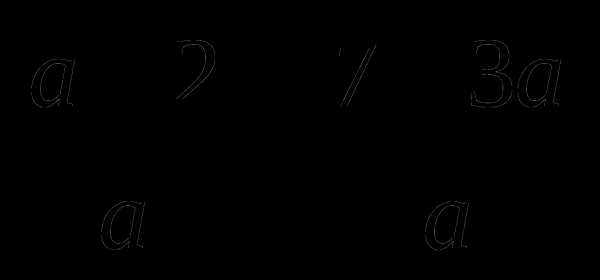 =
= 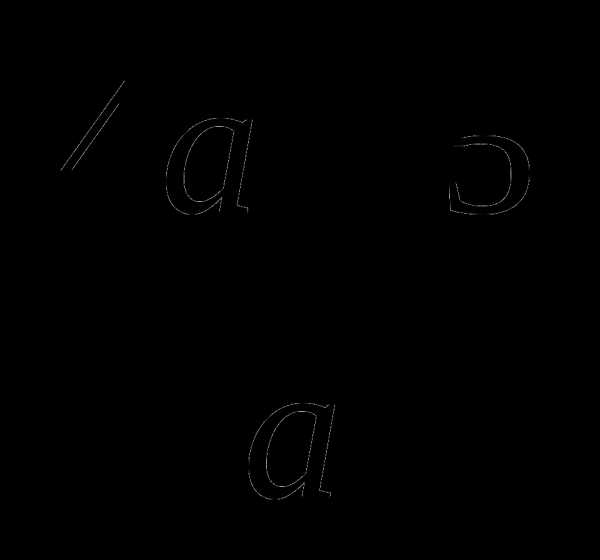 .
.
Ответ: 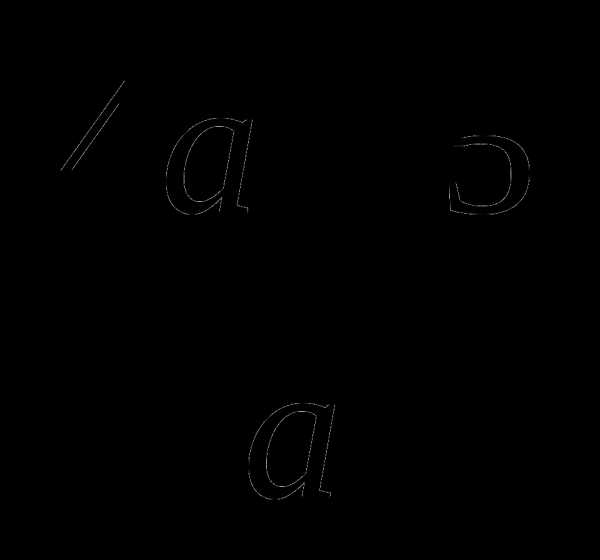 .
.
8. 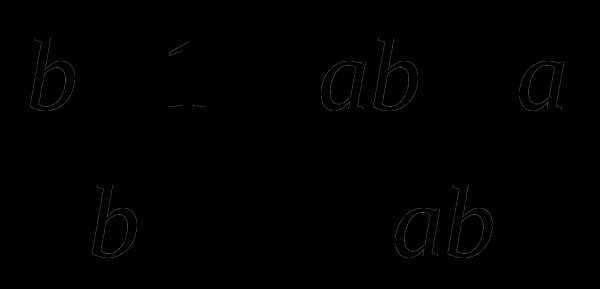 =
=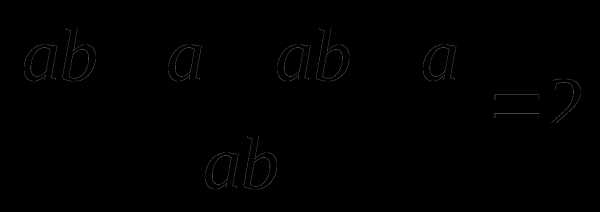 .
.
Ответ: 2.
9. Проаналируем данные первой строки: а15 : а3 = а12, тогда 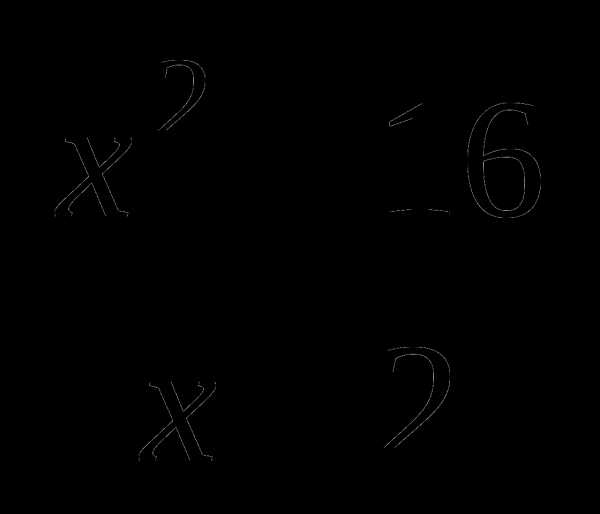 :
:  = х + 4.
= х + 4.
Ответ: х + 4.
10.х10  х8=х18, тогда найдем произведение дробей второй строки:
х8=х18, тогда найдем произведение дробей второй строки: 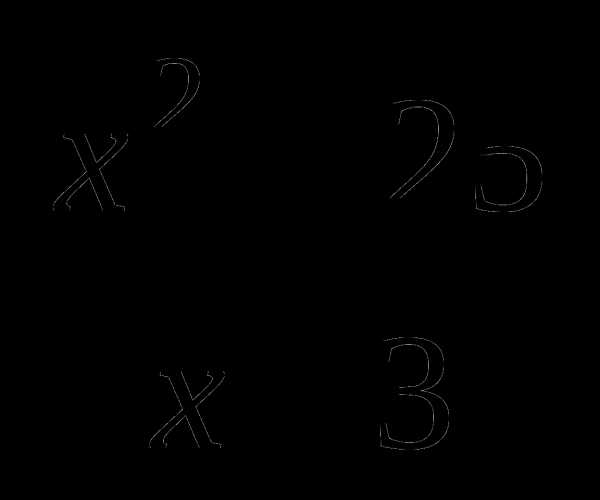

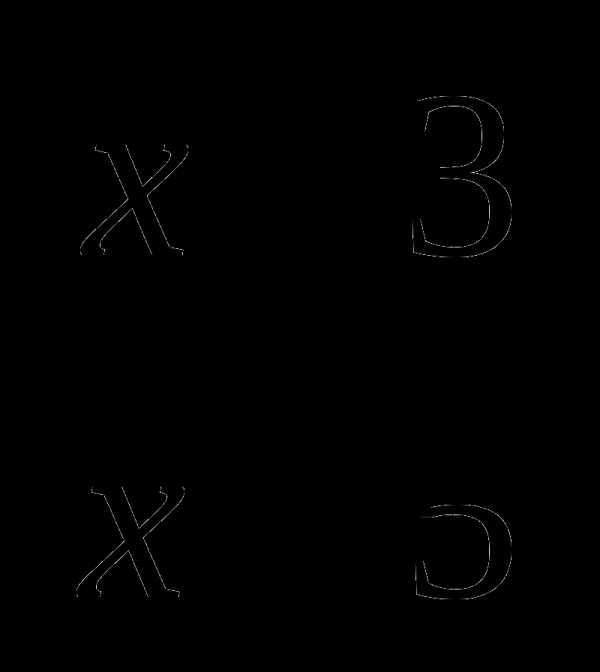 = х – 5.
= х – 5.
Ответ: х – 5.
11.В первой строке дробь 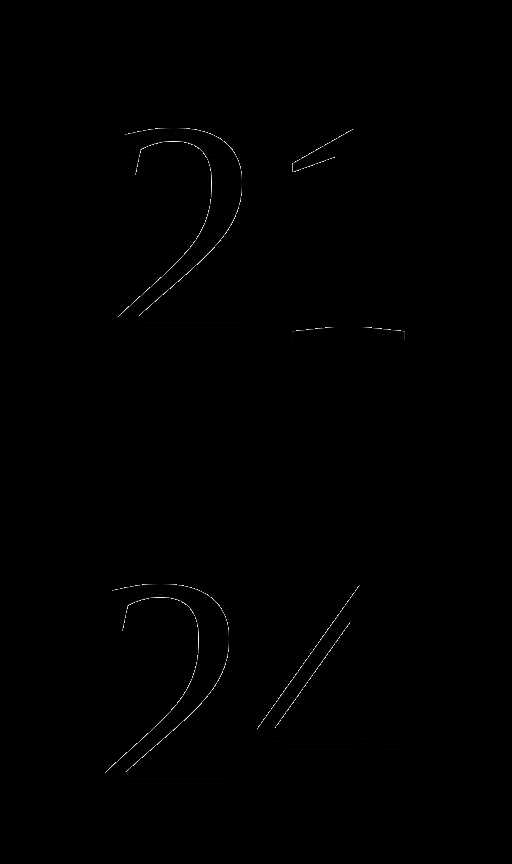 сократимая и получим
сократимая и получим  , поэтому неизвестный результат второй строки: а -3.
, поэтому неизвестный результат второй строки: а -3.
Ответ : а -3.
12.Если сократить дробь  , то получим
, то получим  , поэтому нужно сократить выражение:
, поэтому нужно сократить выражение:
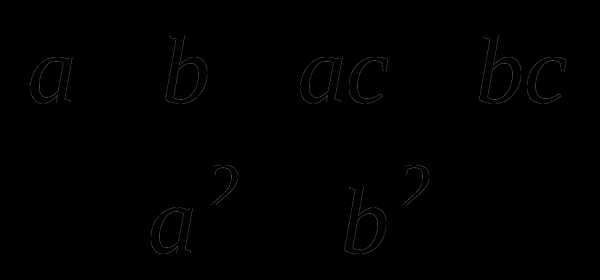 =.
=.
Ответ:  .
.
13.у(3)=4 – 32=-5, поэтому два пропущеных числа будут значениями данной функции при х=1 и х=2, значит это будут числа 0 та 3.
Ответ: 0 та 3.
14.Если воспользоваться неравенством треугольника для треугольника АВС, то получим 3<АС<13, поэтому ответом к заданию будет неравентсов 2<В1С1 <26.
Ответ: 2<В1С1 <26.
15.Воспользовавшись неравенством треугольника, имеем 2<m<12, поэтому лишним числом будет 1.
Ответ: 1.
16.Согласно свойству размещения двух окружностей на плоскости, якщо О1О2= R1 + R2, то данные окружности имеют только одну общую точку, т.е. касаются. А при другом условии имеем: О1О2>R1 + R2, тому окружности не имеют общих точек.
Ответ:
17.Корнями первого квадратного уравнения являются числа 2 и 3, а сумма их квадратов 13, аналогично сумма квадратов корней второго уравнения равна (-2)2+(-4)2=4+16=20, поэтому искомое число будет суммой корней уравнения х2+2х-3=0, т.е. (-3)2+12=10.
Ответ: 10.
18.
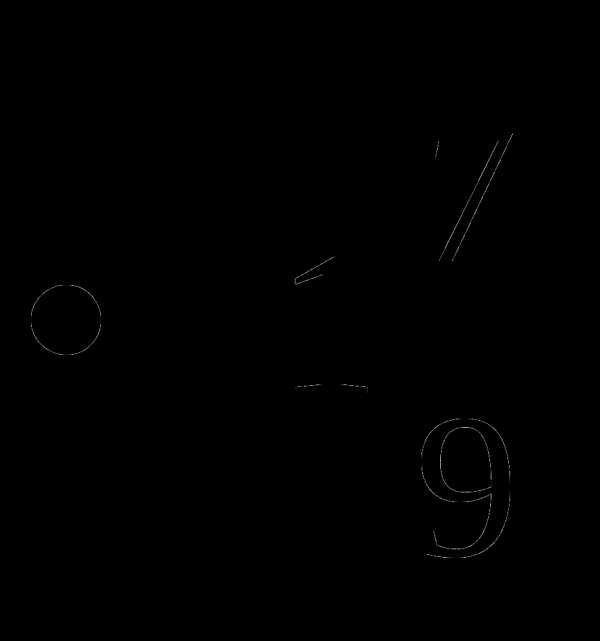 =2, поэтому нужно найти произведение двух выражений:
=2, поэтому нужно найти произведение двух выражений: 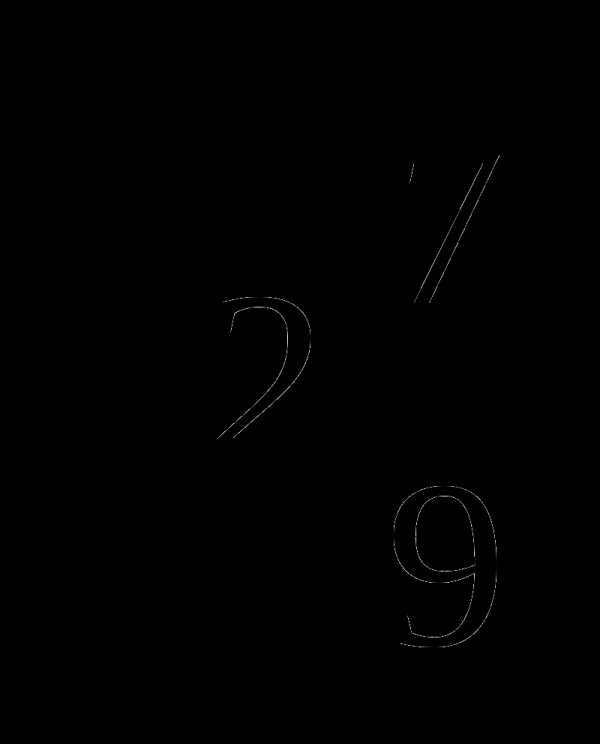
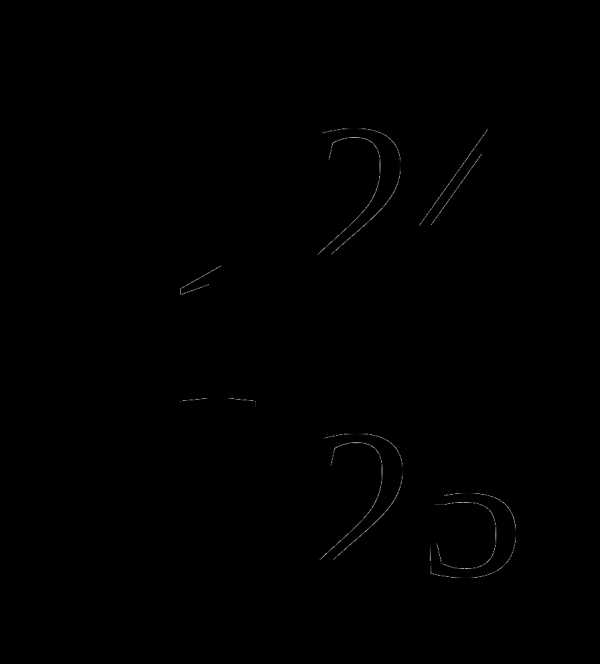 =
=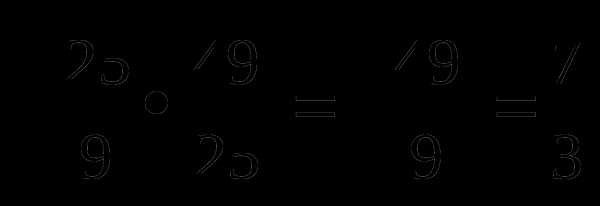 .
.
Ответ:  .
.
19.По условию первой строки: если х=4, то у=1, поэтому нужно найти целые значения х и у, удовлетворяющие данной функции. Такими значениями будут числа х=3 и у=1.
Ответ:
20. Точка А имеет координаты (3,4), поэтому расстояние до начала отсчета О(0, 0) равно . Значит, нужно вычислить ОМ=.Ответ: искомое число 13.
21. Точка А имеет координаты (4,1). Уравнение, записанное справа по теореме Виета имеет также корни х1=4 и х2=1. Поэтому нужно составить квадратное уравнение, корнями которого будут координаты точки В(-3,2).
Ответ: х2 + х -6=0.
22. 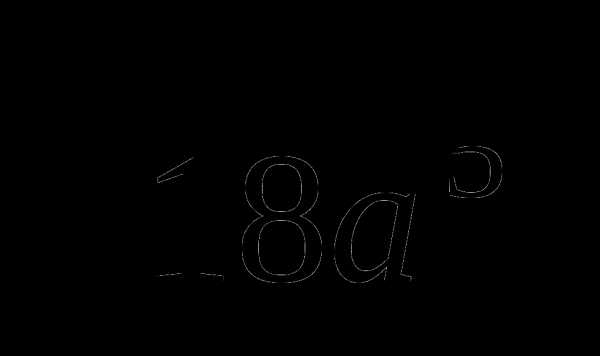 + а2
+ а2 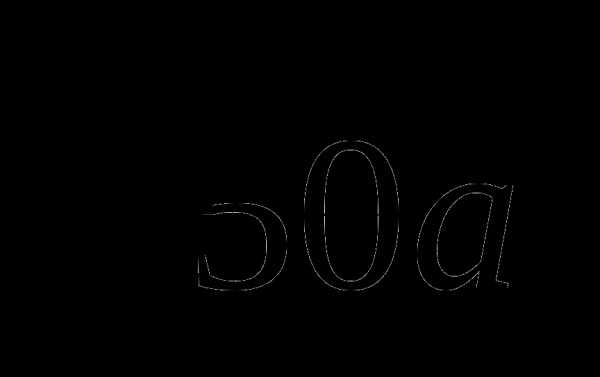 = 3а2
= 3а2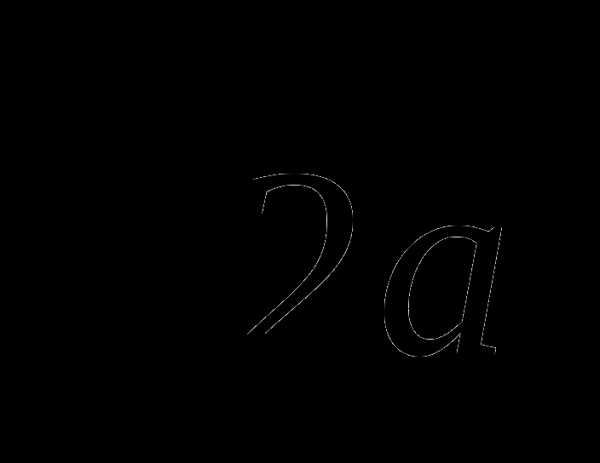 +5а2
+5а2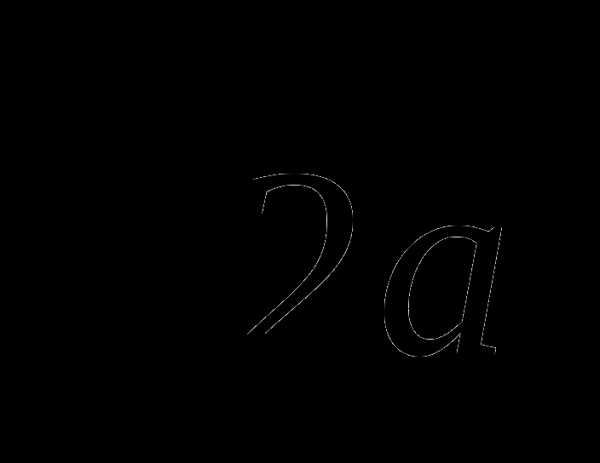 =8а2
=8а2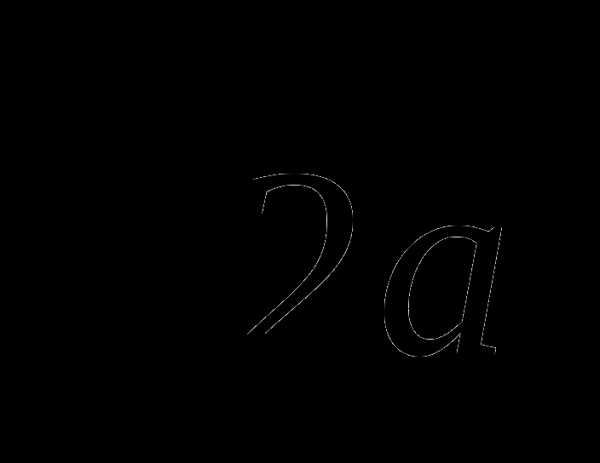 , поэтому искомое число будет равно сумме двух многочленов (
, поэтому искомое число будет равно сумме двух многочленов (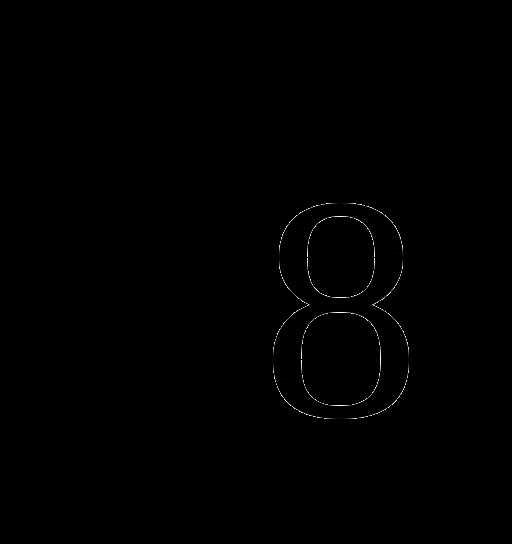 —
—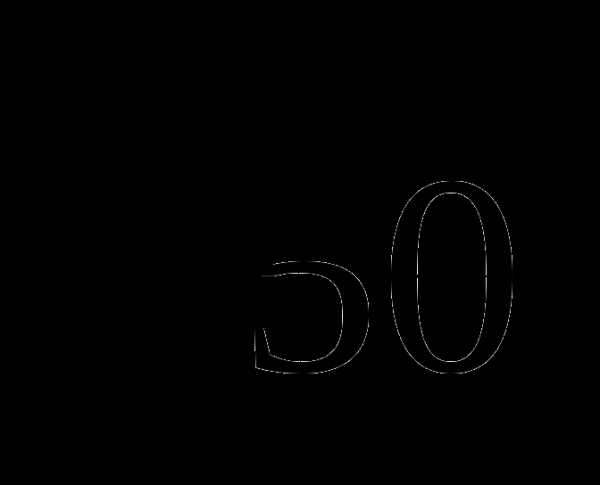 )+ (
)+ ( +
+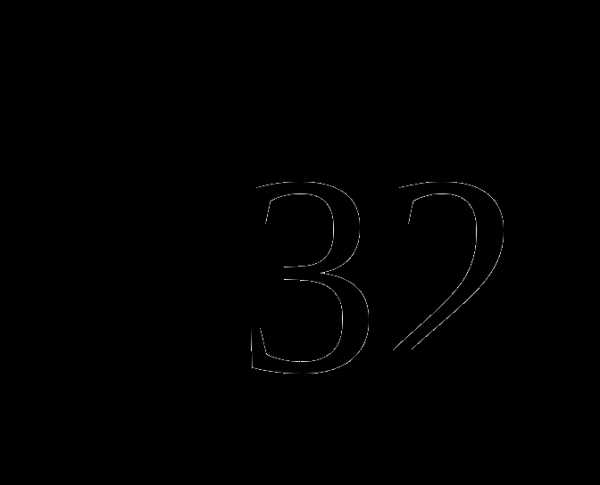 )=2
)=2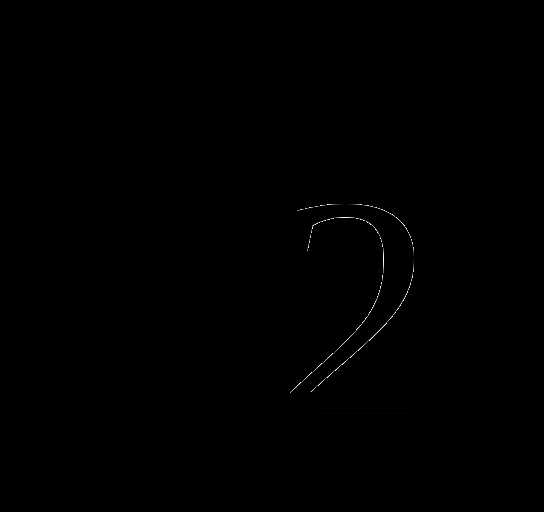 -5
-5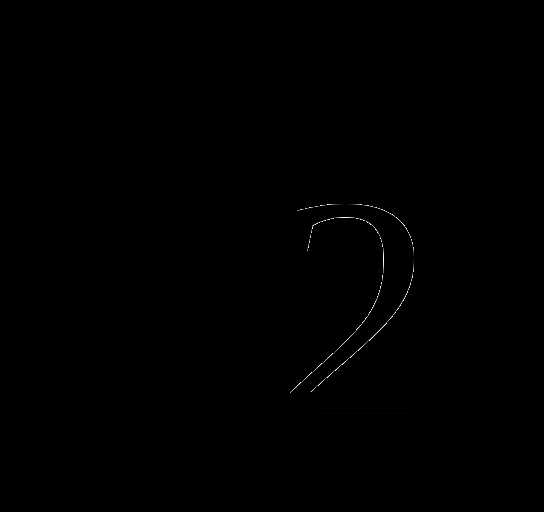 +3
+3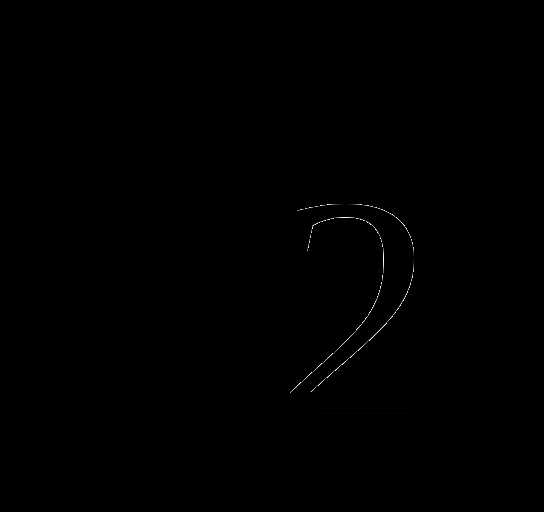 +4
+4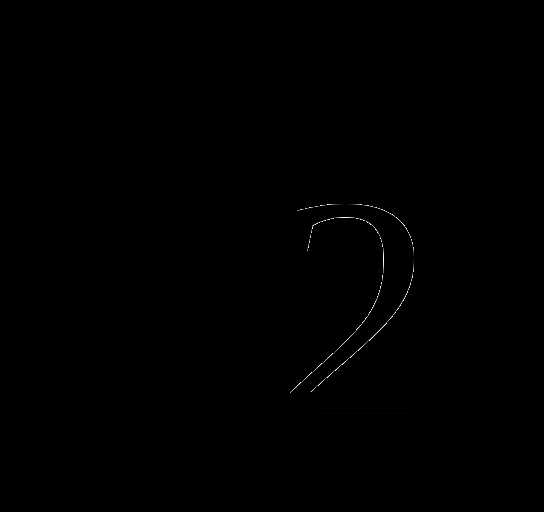 =4
=4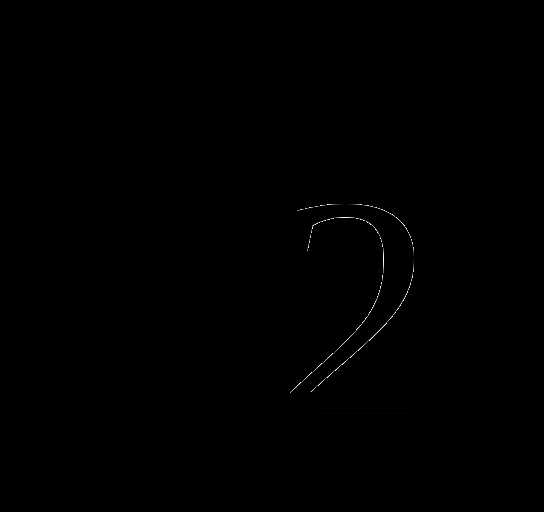 .
.
Ответ: 4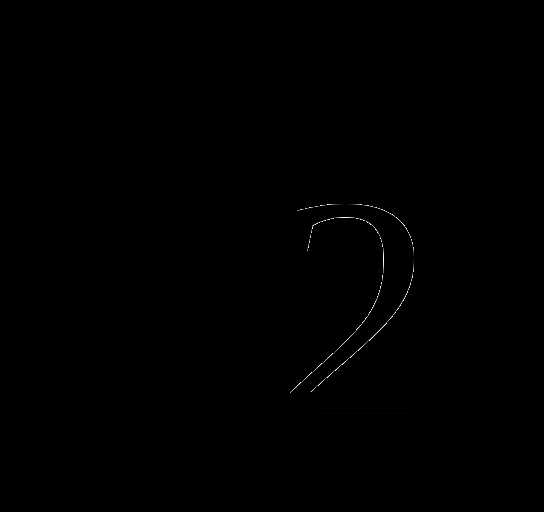 .
.
23.Произведение выражений, щвписанных в противоположных секторах, равно а21, поэтому, по часовой стрелке, получим а-3 и а18.
Ответ: а-3 и а18.
24. Произведение выражений первой и второй строк равно 1, поэтому пропущенным числом будет число, обратное к 2 , т.е.
, т.е.  .
.
Ответ:  .
.
25. Избавившись от иррациональности в знаменателе дроби  , получим
, получим 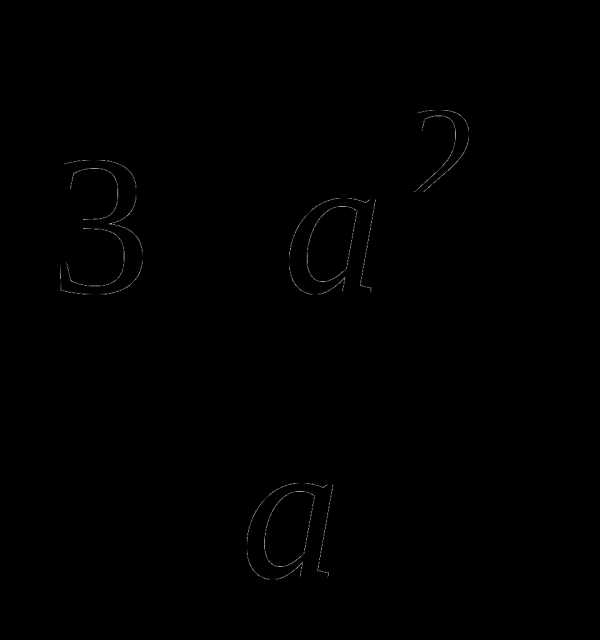 , поэтому во второй строке нужно дописать
, поэтому во второй строке нужно дописать 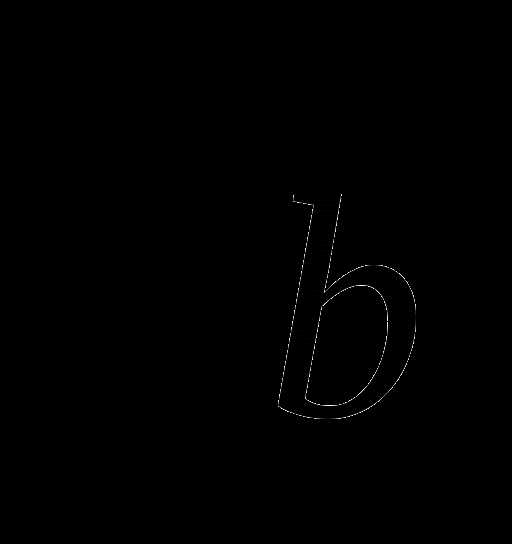 , а в третьей —
, а в третьей —  =
=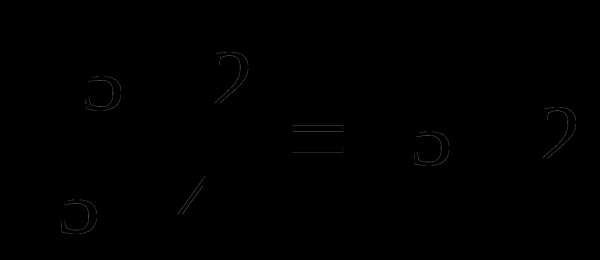 .
.
Ответ: 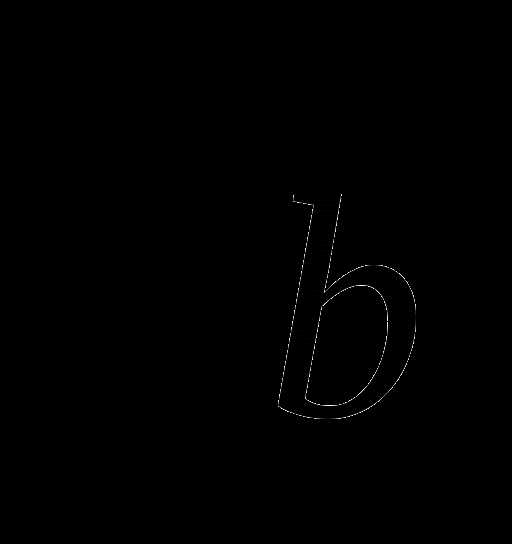 та
та  .
.
26. , поэтому искомое число будет результатом произведения .
Ответ: 24.
27.(а-7 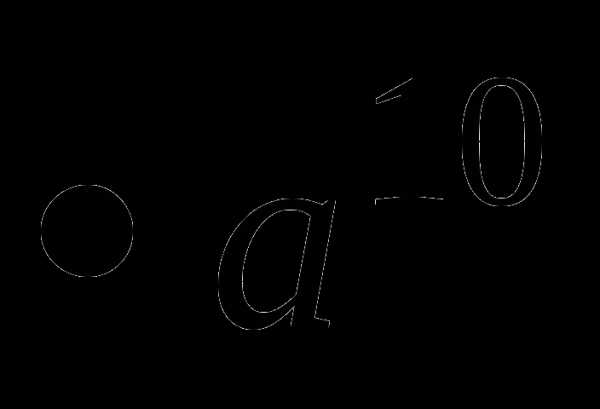 ): (а3
): (а3 а-2)=а2, поэтому искомое выражение будет равно (а-5
а-2)=а2, поэтому искомое выражение будет равно (а-5  а7): (а3
а7): (а3  а-4)=а3.
а-4)=а3.
Ответ: а3.
28. а2 – в2 =(а+в)(а-в), а3 + в3 = (а+в)(а2 – ав + в2), т.е. а+в является общим множителем в разложении многочленов. Таким образом, нужно данные многочлены разложить на множители.
Имеем: -2х2+7х-3= -2(х- )(х-3)=(1-2х)(х-3) та 10х2— х-2= 10(х-
)(х-3)=(1-2х)(х-3) та 10х2— х-2= 10(х- )(х+0,4)=(2х-1)(5х+2).
)(х+0,4)=(2х-1)(5х+2).
Ответ: 2х-1.
29.Воспользовавшись формулой расстояния между точками, ОА=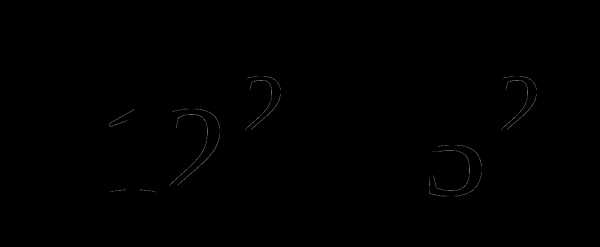 =13, поэтому нужно решить уравнение ОМ=10, т.е. х2+82=100. Таким образом, х1=6 и х2=-6.
=13, поэтому нужно решить уравнение ОМ=10, т.е. х2+82=100. Таким образом, х1=6 и х2=-6.
Відповідь: 6 и -6.
30. 6 10-7
10-7  8
8 1015=4,8
1015=4,8 109, поэтому найдем произведение выражений
109, поэтому найдем произведение выражений
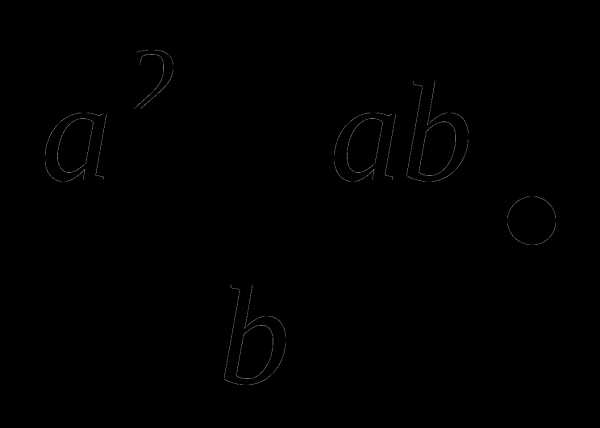
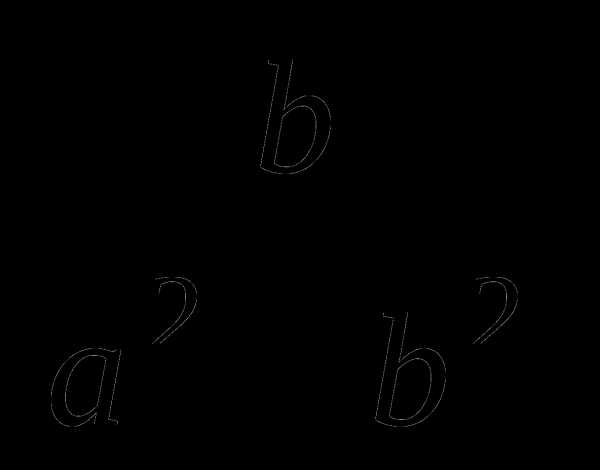 =
= .
.
Ответ:  .
.
31. Уравнение 2х-1=5 имеет корень х=3, поэтому числа 2 та -1 не являются корнями указанного уравнения, поэтому для решения задания нужно указать лишние числа, указанные на рисунке. Биквадратное уравнение х4-3х2=4 имеет два корня х1=2 и х2=-2, поэтому лишними будут числа 1 и -1.
Ответ: 1 и -1.
32. Произведение а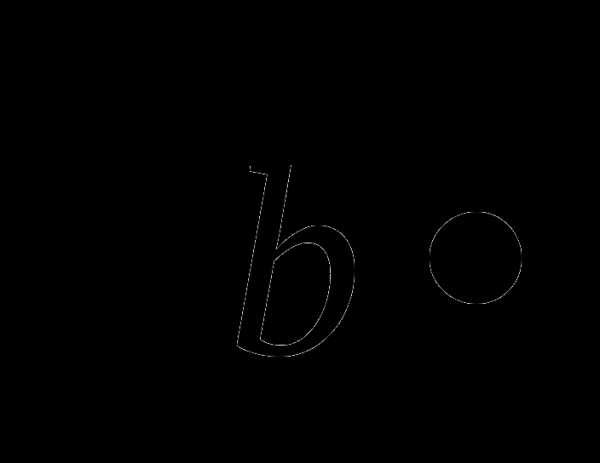
 =
= , поэтому (а-3
, поэтому (а-3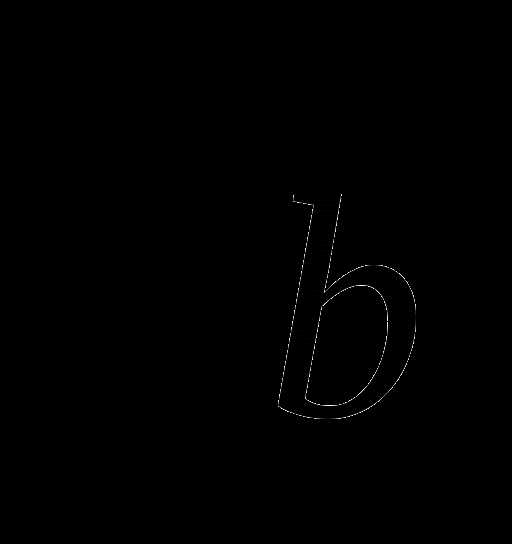 )(а+3
)(а+3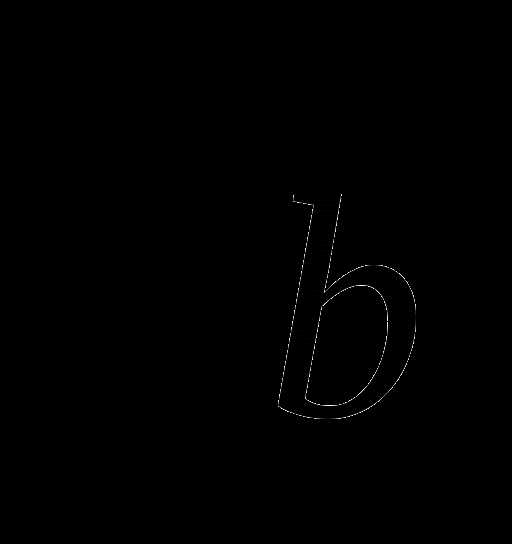 )=а2-9b.
)=а2-9b.
Ответ: а2-9b.
33. Если сократить дробь, которая стоит слева в первой строке, то получим дробь справа. Значит, 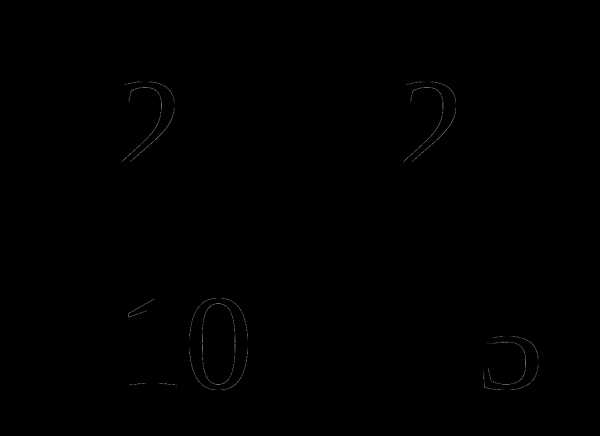 =
=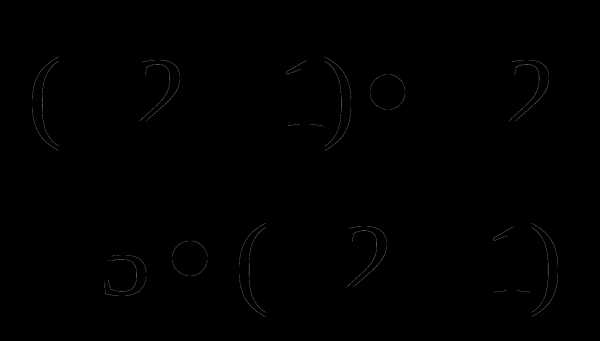 =
=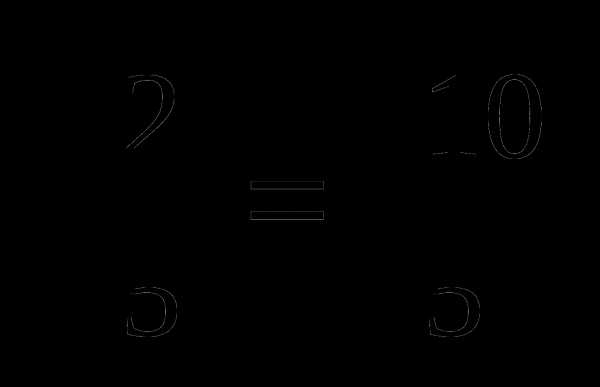 .
.
Ответ: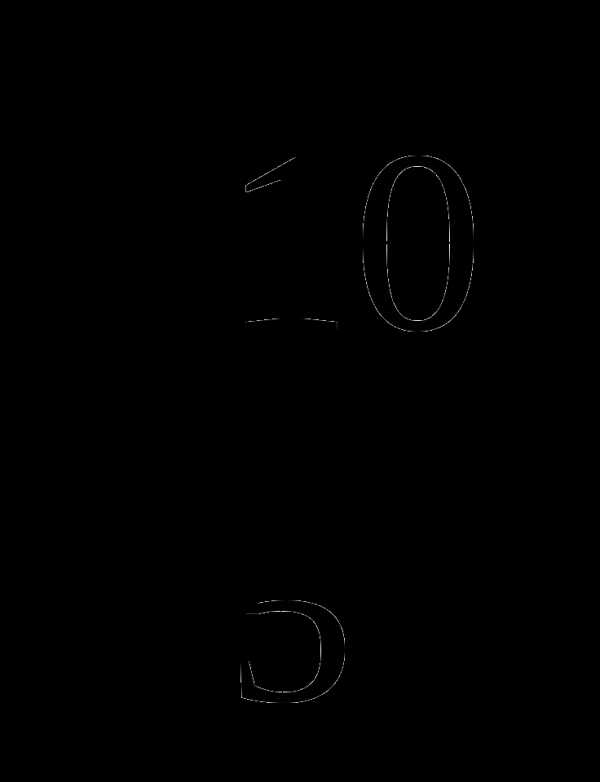 .
.
34. Рассмотрим первый рисунок: числа -1 и 2 являются корнями некоторого квадратного уравнения, а именно: х2 –х=2. Аналогично, числа — и 1 – корни уравнения 2х2 — х=1. Поэтому, искомые числа будут корнями уравнения х2 – 7х=-6, а это числа 1 и 6.
и 1 – корни уравнения 2х2 — х=1. Поэтому, искомые числа будут корнями уравнения х2 – 7х=-6, а это числа 1 и 6.
Ответ: 1 и 6.
35. Три из четирех указанных пар чисел не принадлежат графику функции у= , поэтому искомой будет точка (9,4).
, поэтому искомой будет точка (9,4).
Ответ: (9,4).
36.Это число  , потому что все другие пары чисел принадлежат области определения функции
, потому что все другие пары чисел принадлежат области определения функции 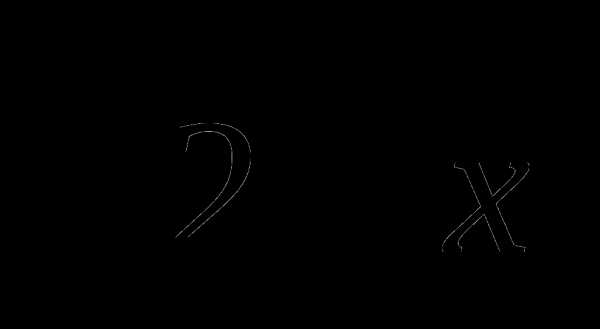 .
.
Ответ:  .
.
37. Только число — не принадлежит области определения функции
не принадлежит области определения функции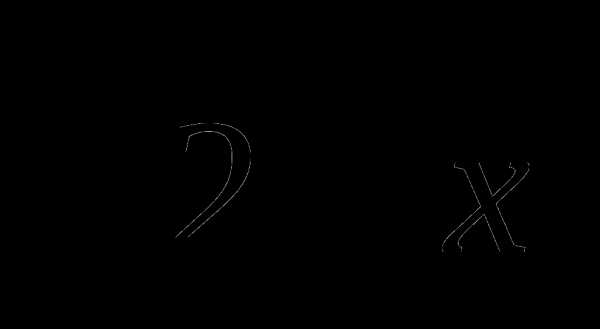 +
+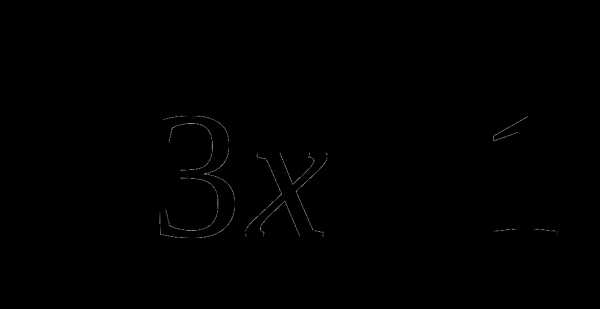 ,
,
Ответ : —  .
.
38. На первой строке справа стоит виражение, которое является квадратом выражения,стоящего слева, поэтому неизвестным выражением будет 49а10в14с2.
Ответ: 49а10в14с2.
39. Якщо у прямокутнику всі сторони рівні, то отримаємо квадрат, тому паралелограм, в якому всі сторони рівні – ромб.
Ответ: ромб.
40. Число -3 является нулем знаменателя дроби 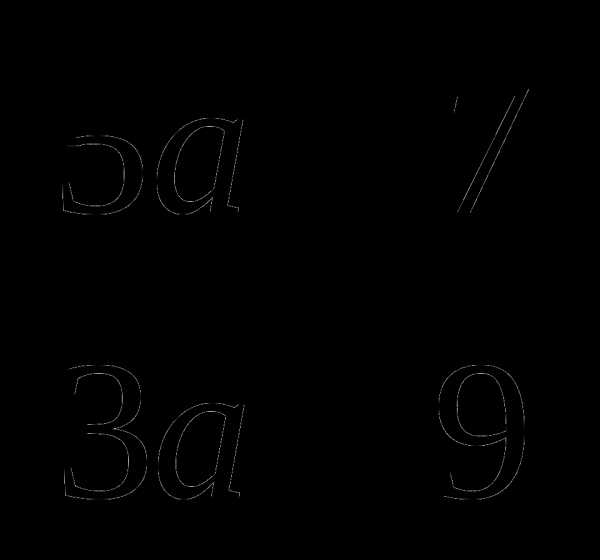 , поэтому нужно найти нуль знаменателя второй дроби, т.е. найдем коеінь уравнения 5а-3=0, а=0,6.
, поэтому нужно найти нуль знаменателя второй дроби, т.е. найдем коеінь уравнения 5а-3=0, а=0,6.
Ответ: а=0,6.
41. Число -2 является корнем уравнения а-2=0, поэтому найдем корень уравнения а2-25=0, т.е. а1=5 и а2=-5.
Ответ: а1=5 и а2=-5.
42. 5n – это формула n-го члена ряда 5,10,15,20,25, поэтому искомым будет выражение
2n-1.
Ответ: 2n-1.
43. Если найти произведение двух чисел, записанных в первых двух столбиках первой строки, то получим выражение третьего столбика первой строки, поэтому найдем произведение двух многочленов: (а+3) (а-5)=а2 +3а -5а-15= а2 -2а-15.
(а-5)=а2 +3а -5а-15= а2 -2а-15.
Ответ: а2 -2а-15.
44. Результат деления 8 107 на 2
107 на 2 103 равно 4
103 равно 4 104, поэтому неизвестным будет результат деления
104, поэтому неизвестным будет результат деления  :19а9b3=
:19а9b3=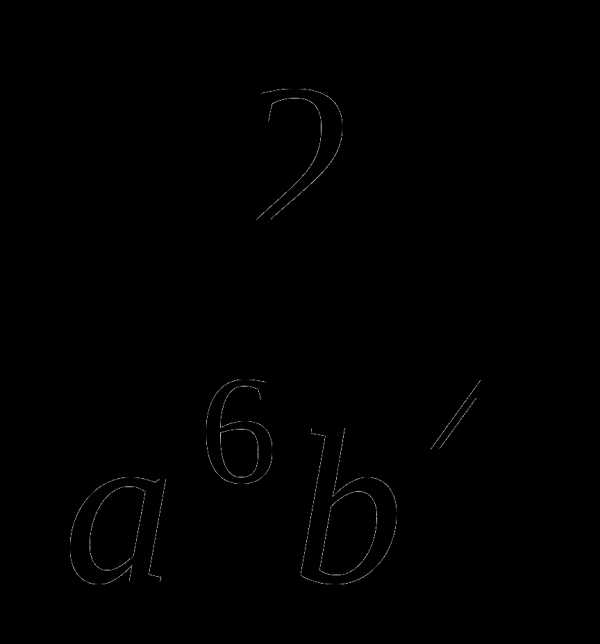 .
.
Ответ: 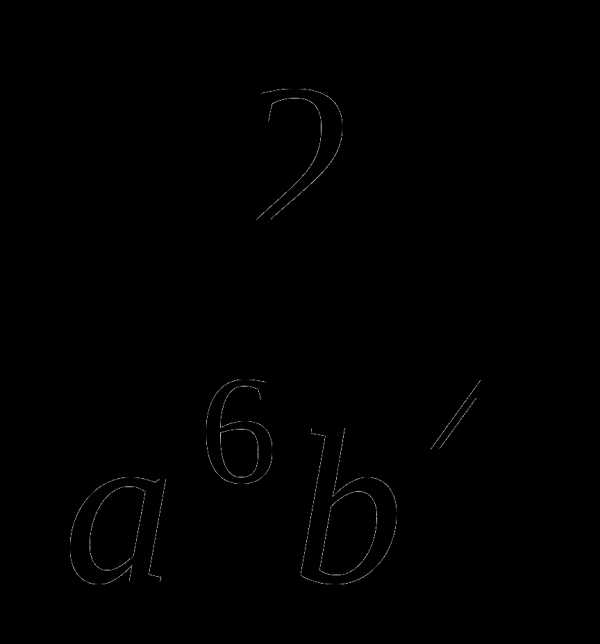 .
.
45. (х2 +х -6) : (х2-2х -15)= 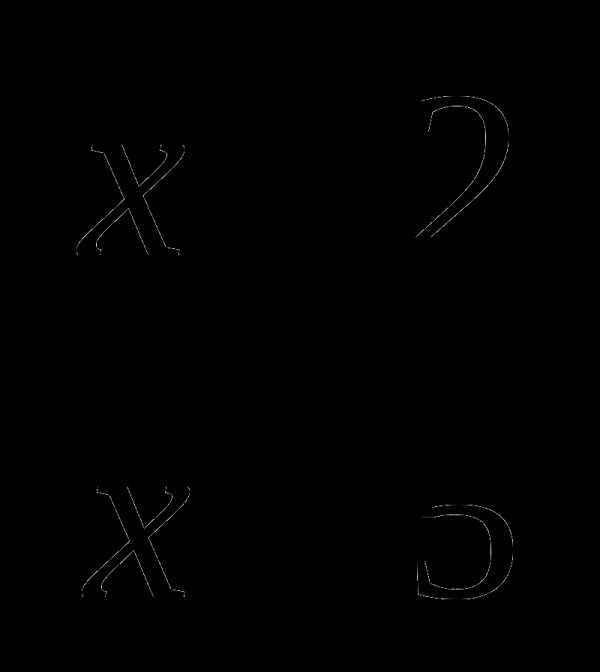 , поэтому: а3b: bс3=
, поэтому: а3b: bс3=
 .
.
Ответ:  .
.
46. Число 1 является корнем уравнения (2х+7) +(3х-11)=2-х. Поэтому искомое число будет корнем уравнения 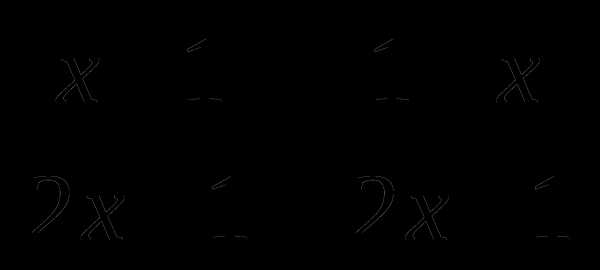 =
=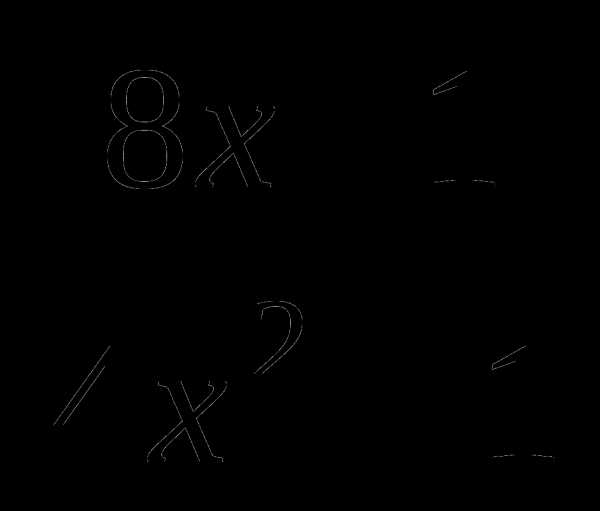 . Если решить уравнение, то получим х=
. Если решить уравнение, то получим х= .
.
Ответ: х= .
.
___
47. , тогда по правилу сложения векторов имеем результат АМ.
___
Ответ: АМ.
48. у=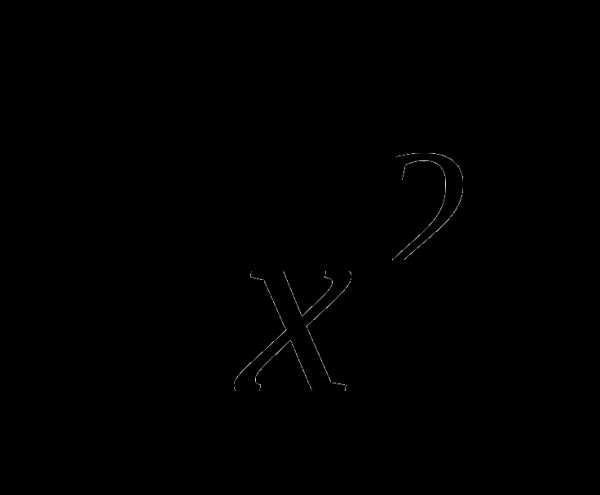 =|х|, поэтому графиком будет
=|х|, поэтому графиком будет

49.Из букв можно составит слова основание,, степень, показатель, число. Поэтому лишним будет слово «число», а три других относятся к теме «Степень с рациональным показателем».
Ответ: число.
50. Проанализируем рисунок: периметр треугольника со сторонами 7см, 10 см и 13 см равен 30см, а периметр прямоугольника со сторонами 8 см и 12 см – 40 см. Значит, 20 см – периметр квадрата, поэтому сторона данного квадрата будет 5см.
Ответ: 5см.
51.Площадь прямоугольного треугольника с катетами 12см и 15 см равна 90см2, а прмоцгольника — 20 см2. Значит, нужно вычислить площадь равнобедренного треугольника с основанием 17см и высотой 8см. S∆= 
 8
8 17= 68cм2.
17= 68cм2.
Ответ: 68cм2.
52.Ответ: периметр прямоугольника.
53. Сумма углов параллелограма равна 3600, поэтому нужно вычислить сумму углов шестиугольника. Сумма углов шестикугольника7200.
Ответ : 7200.
54. Проанализируем данных первых двух строк двторого столбика: сумма указанных углов равна 1800, поэтому их можно считать прилежащими к одной стороне паралелограмма. Итак, искомое значение будет 620.
Ответ: 620.
55. 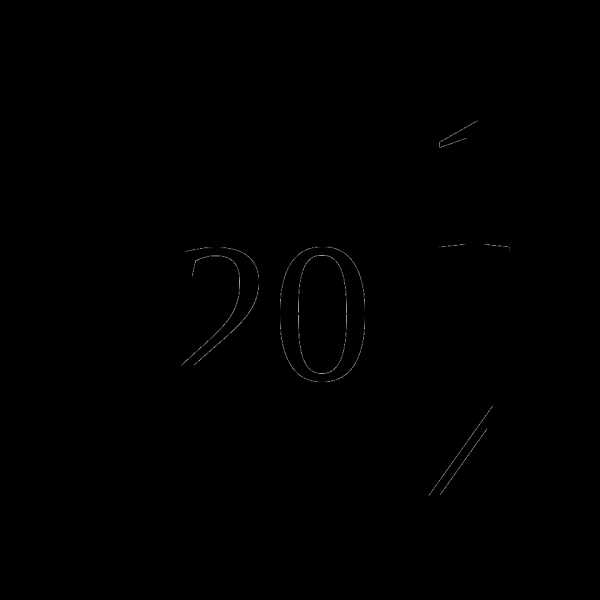 =
= , которое является обратной дробью для
, которое является обратной дробью для  , а
, а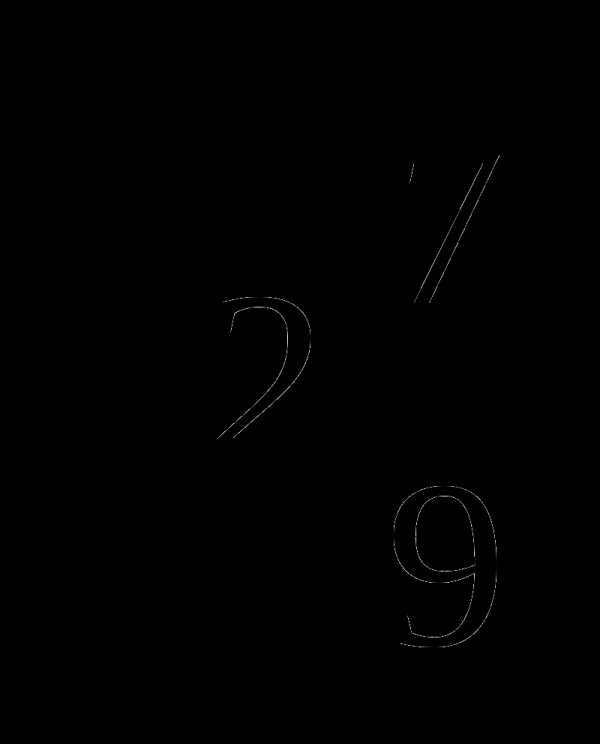 =
= . Значит, искомым числом будет
. Значит, искомым числом будет  .
.
Ответ:  .
.
56.  =
=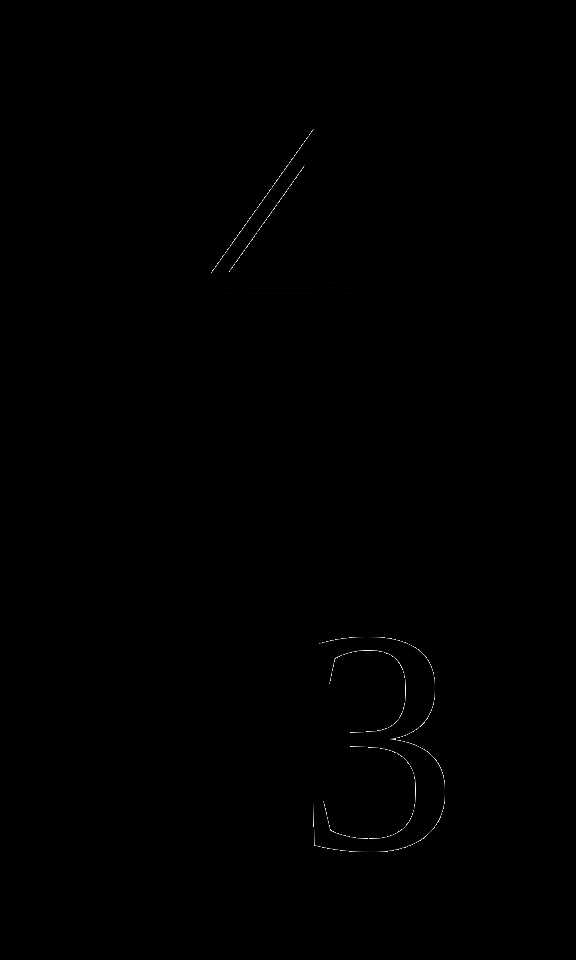 , которое является обратной дробью
, которое является обратной дробью 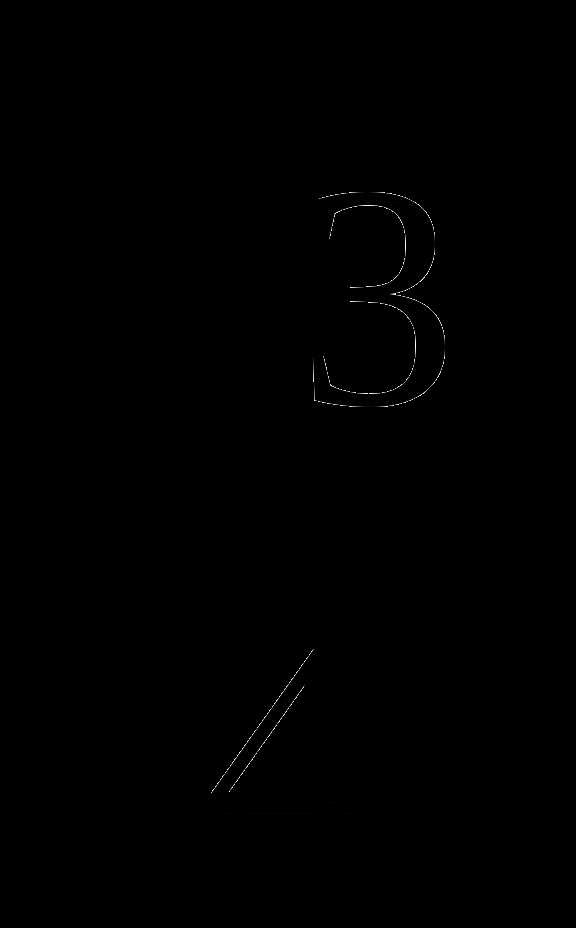 .
.  =
= , поэтому искомым числом будет
, поэтому искомым числом будет 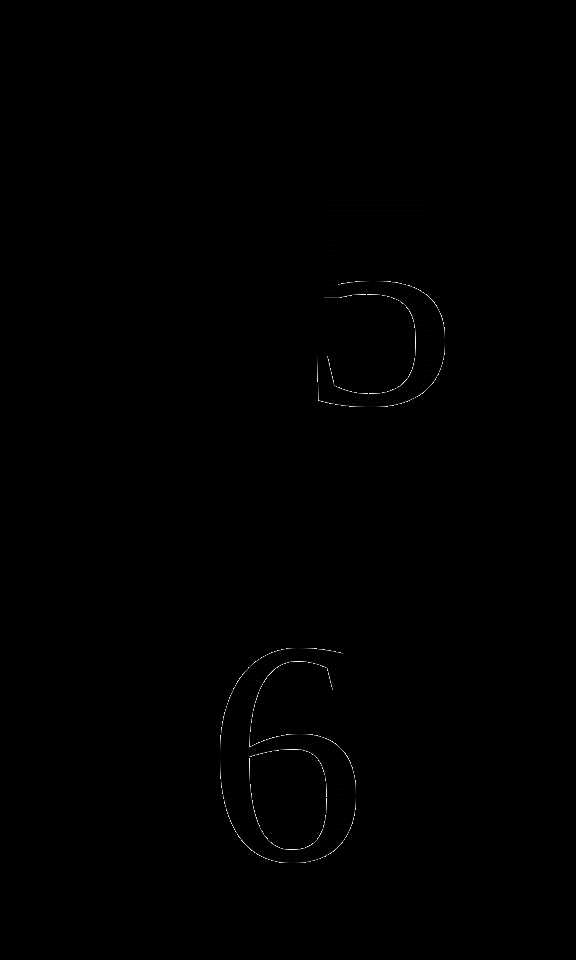 .
.
Ответ: 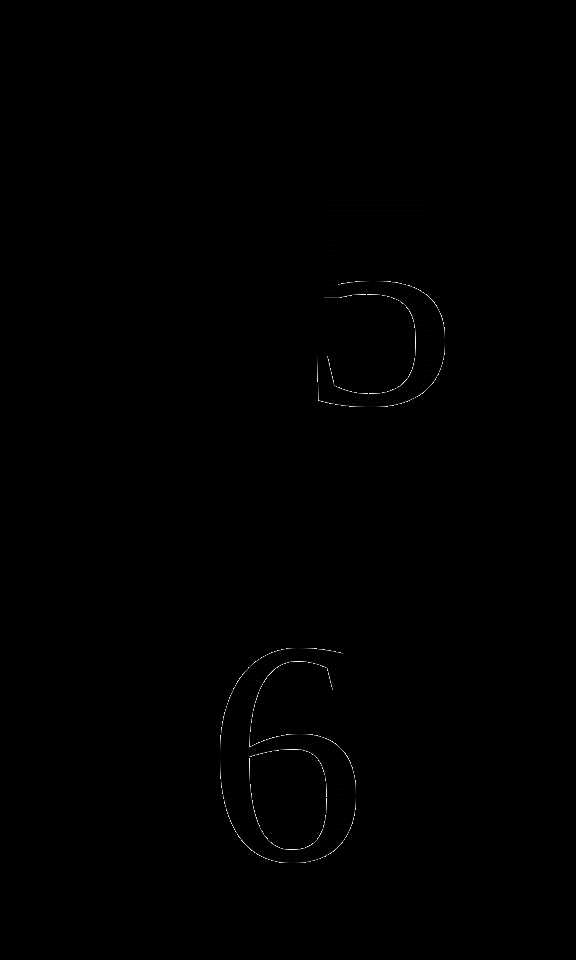 .
.
Список используемой литературы
365 логическиз задач и игр, Москва, «АСТ-ПРЕСС КНИГА», 2005;
И.Н. Сергеев, С.Н. Олехник, С.Б. Гашаков «Примени математику», Москва главная редакция физикоматематической литературы, 1990;
О.Б. Епишева, В.И. Крупич «Учить школьников учиться математике», Москва, «Просвещение». 1990;
Д.Пойа «Как решать задачу», Львов, журнал «Квантор», 1991.
infourok.ru
