Методика обучения решения логических задач в курсе математика начальной школы
Статья посвящена вопросам обучения в начальной школе решению логических задач. Дается краткое описание учебных пособий по математической логике для школьников; более подробно анализируются методы решения логических задач; приводятся примеры решения логических задач.
Развитие логического мышления, формирование самостоятельности, инициативы, творческого потенциала является одной из основных задач современного педагогического процесса. Успешность этого процесса зависит от сформированности познавательных интересов. Многие исследователи отмечают, что целенаправленная работа по развитию логического мышления младших школьников должна носить системный характер (Е.В. Веселовская, Е.Е. Останина, А.А. Столяр, Л.М. Фридман и др.). При этом исследования психологов (П.Я. Гальперин, В.В. Давыдов, Л.В. Занков, А.А. Люблинская, Д.Б. Эльконин и др.) позволяют сделать вывод о том, что результативность процесса развития логического мышления младших школьников зависит от способа организации специальной развивающей работы.
Особую роль при развитии логики играет школьный предмет математика. Именно математика считается теоретической наукой, где содержится высокий уровень абстракции. Уроки математики обладают развивающим эффектом, и создает предпосылки для развития логического мышления.
Решению задач в начальном курсе математике посвящено достаточно большое количество времени. Классифицировать решаемые задачи можно по разным основаниям [3]. Как показывает практика, самым эффективным способом для развития логики у обучающихся на ступени начального общего образования является решение логических задач [1].
На сегодняшний день в школьной программе применяются различные УМК по математики, которые содержат логические задачи на различном этапе обучения. Наиболее востребованной программой является «Школа России». В учебниках по математики данной программы логические задачи включены в дополнительную часть, так называемые «задания повышенной трудности». В первом классе логические задачи решаются приемом рассуждения. Во втором, третьем и четвертом классах задачи уже намного разнообразнее, чем в первом, и подразделяются на виды: задачи на переливание, установление временных рамок, разбиение предметов на группы.
Во втором, третьем и четвертом классах задачи уже намного разнообразнее, чем в первом, и подразделяются на виды: задачи на переливание, установление временных рамок, разбиение предметов на группы.
Начальное обучение математике закладывает основы для формирования приемов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, они усваивают определенные обобщенные знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. Универсальные учебные действия обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учиться.
На сегодняшний день существует несколько методов, которые помогут решить логическую задачу, а именно[2]:
- рассуждений;
- подбора цифровых значений;
- предположения;
- схемы и таблицы;
- метод обратного хода;
- метод «четно-не четно»
- метод граф;
- комбинированный метод.
Часто в условии логической задачи имеется такое обилие фактов, что удержать их все в памяти нелегко. Тогда прибегают к составлению схем, таблиц, выполнению рисунков и чертежей.
Более подробно мы рассмотрим способ решения с помощью таблиц словесных задач.
Детям предлагается задача «Коля, Боря, Вова, Юра заняли первые четыре места в соревнованиях. На вопрос, какие места они заняли, трое ответили: Коля — ни 1-е, ни 4-е; Боря — 2-е; Вова — не 4-е. Какие места заняли мальчики?».
Первый этап работы над логической задачей предполагает ознакомление с содержанием задачи. Данный этап так же называется подготовительный. Если дети не умеют читать бегло задачу, выделять главное, это делает учитель. Если в задачи встречаются неизвестные понятия, то они разъясняются на данном этапе.
Если в задачи встречаются неизвестные понятия, то они разъясняются на данном этапе.
Второй этап подразумевает составления краткой записи либо таблицы, которая позволит наглядно представить условие задачи. После прочтения текста задачи учитель в ходе беседы с учащимися обсуждает её условие. Для этого учитель задает ряд вопрос, на которые учащиеся должны ответить. Затем составляется таблица исходных данных:
Место | Коля | Боря | Вова | Юра |
1 | – | |||
2 | + | |||
3 | ||||
4 | – | – |
Третий этап это решение задачи. В нашем случае после того как внесены в таблицу известные данные начинают рассуждать логически. Так, если Коля ни занял ни 1-е и ни 4-е , и не 2-е место ( т. к. его занял Боря), значит он занял 3-е место. Далее, если 2-е и 3-е место уже известно, а Вова согласно условию задачи занял ни 4-е место, значит, он занял 1-е место. Следовательно, Юра занимает 4-е оставшееся место.
к. его занял Боря), значит он занял 3-е место. Далее, если 2-е и 3-е место уже известно, а Вова согласно условию задачи занял ни 4-е место, значит, он занял 1-е место. Следовательно, Юра занимает 4-е оставшееся место.
Место | Коля | Боря | Вова | Юра |
1 | – | – | + | – |
2 | – | + | – | – |
3 | + | – | – | – |
4 | – | – | – | + |
Ответ: 1- е место Вова, 2-е место Боря, 3-е место Коля, 4-е место Юра.
Между множеством имен мальчиков и множеством завоеванных мест должно быть взаимно однозначное соответствие.
Соответственно, согласно представленной таблице наглядно видно решение логической задачи. Табличный метод и его модификации (кубическая и совмещенные таблицы, таблица соответствий) дают наглядность, логичность, прозрачность всех шагов рассуждений, следовательно, могут быть рекомендованы для решения задач любого уровня сложности.
Табличный метод и его модификации (кубическая и совмещенные таблицы, таблица соответствий) дают наглядность, логичность, прозрачность всех шагов рассуждений, следовательно, могут быть рекомендованы для решения задач любого уровня сложности.
Рассмотрим ещё один из методов решения логических задач — метод рассуждений. Например: Оля, Ира, Катя изучают различные иностранные языки: английский, китайский и французский. На вопрос, какой язык изучаете, каждая из девочек ответила так: Оля изучает английский, Ира не изучает английский, а Катя не французский. Из всех утверждение одно только верное.
Решение задачи начнем с рассуждения. Имеется три утверждения, одно из которых считается верным. Если верно первое утверждение, значит верно, и второе, что противоречит условиям задачи. Если верно второе, значит, первое и третье будет ложным, а значит, английский ни кто не изучает. Это так же противоречит условию задачи. Значит, третье утверждение считается верным, в первое и второе ложным. Значит, Ира изучает английский, Катя китайский, а Оля французский.
Таким образом, систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на развитие логического мышления, организованных согласно приведенной выше схеме, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Логические задачи для начальной школы | Презентация к уроку по математике по теме:
Слайд 1
Задачи логического характера не требующие вычисленийСлайд 2
«Главная задача обучения математике, причём с самого начала, с первого класса, — учить рассуждать, учить мыслить» ведущий отечественный методист А.А. Столяр
Слайд 3
«Логика — это наука о законах правильного мышления, о требованиях, предъявляе- мых к последовательному и доказательному рассуждению» немецкий философ И. Кант
Слайд 4
ЗАДАЧИ ТИПА «КТО ЕСТЬ КТО?» Смысл задач под кодовым названием «Кто есть кто?» довольно прост. Вам даны отношения между предметами и следуя по цепочке этих отношений, вы приходите к правильному результату. Существует несколько методов решения задач типа «Кто есть кто?». Один из методов решения таких задач – метод графов . Второй способ, которым решаются такие задачи – табличный способ .
Вам даны отношения между предметами и следуя по цепочке этих отношений, вы приходите к правильному результату. Существует несколько методов решения задач типа «Кто есть кто?». Один из методов решения таких задач – метод графов . Второй способ, которым решаются такие задачи – табличный способ .
Слайд 5
Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по 1 шт. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш? Решение методом графов
Слайд 6
Решение логических задач методом таблиц Задача. В каких квартирах живут котята? Белый котёнок живёт не в квартире № 1. В квартирах № 1 и 2 живут не чёрные котята. В квартирах № 1, 2, 3 живут три котёнка – белый, чёрный, рыжий. В какой квартире какой котёнок живёт?
Слайд 7
Кто где живёт? Так как чёрный котёнок не живёт в квартирах №№ 1 и 2 ( по условию ), значит, чёрный живёт в квартире № 3. 2. Так как чёрный живёт в квартире № 3 ( по доказательству ), значит белый и рыжий не живут в квартире № 3. 3. Так как белый котёнок не живёт в квартире № 1 ( по условию ) и не в квартире № 3 ( по доказательству ), значит, белый живёт — в № 2. 4. Так как белый живёт — в № 2 ( по доказательству ), значит, рыжий не живёт — в № 2. 5. Так как рыжий не живёт — в № 2 и 3 (по доказательству ), значит, рыжий живёт – в № 1. белый черный рыжий № 1 № 2 № 3 Ответ: белый живёт в квартире № 2, чёрный — в № 3, рыжий — в № 1 .
2. Так как чёрный живёт в квартире № 3 ( по доказательству ), значит белый и рыжий не живут в квартире № 3. 3. Так как белый котёнок не живёт в квартире № 1 ( по условию ) и не в квартире № 3 ( по доказательству ), значит, белый живёт — в № 2. 4. Так как белый живёт — в № 2 ( по доказательству ), значит, рыжий не живёт — в № 2. 5. Так как рыжий не живёт — в № 2 и 3 (по доказательству ), значит, рыжий живёт – в № 1. белый черный рыжий № 1 № 2 № 3 Ответ: белый живёт в квартире № 2, чёрный — в № 3, рыжий — в № 1 .
Слайд 8
Решение логических задач методом рассуждений Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Слайд 9
1. Вадим изучает китайский; 2. Сергей не изучает китайский; 3. Михаил не изучает арабский. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Имеется три утверждения: Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Сергей не изучает китайский; 3. Михаил не изучает арабский. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Имеется три утверждения: Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Слайд 10
Решение логических задач методом блок-схем Сначала выделяются операции. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами и широко используются в программировании. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи.
Слайд 11
Задача! Имеются два сосуда — трехлитровый и пятилитровый. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды .
Слайд 12
Дальше эта последовательность будет полностью повторяться. Из таблицы видим, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда.
Слайд 13
КРУГИ ЭЙЛЕРА ЗАДАЧИ НА ПЕРЕСЕЧЕНИЕ ИЛИ ОБЪЕДИНЕНИЕ МНОЖЕСТВ Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Леонард Эйлер
Слайд 14
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»? Задача: «Обитаемый остров» и «Стиляги»
Сколько человек смотрели только фильм «Стиляги»? Задача: «Обитаемый остров» и «Стиляги»
Слайд 15
ТАКТИЧЕСКИЕ ЗАДАЧИ Решение тактических и теоретико-множественных задач заключается в составлении учащимися плана действий, который приводит к правильному ответу. Сложность состоит в том, что выбор нужно сделать из очень большого числа вариантов, т.е. эти возможности не известны учащимся, их нужно придумать.
Слайд 16
— Задаю тебе последнюю задачу, — сказала принцесса Иванушке, — найди единственно верный путь из этой комнаты в наш зимний сад и сорви для меня самую красивую розу. Из этой комнаты ты пройдешь через левую, или правую, или среднюю дверь во вторую комнату; такие же три вида дверей будут перед тобой при переходе из второй комнаты в третью и из третей — в сад. Учти мои советы, — продолжала принцесса, — первый: из этого зала пройди через правую дверь; второй: из второй комнаты — не через правую дверь, и третий совет: из третей — не через левую дверь. Иванушка знал, что обычно из трех советов принцессы ровно в двух указывают ложное направление, кроме того, служанка принцессы успела шепнуть ему, что надо пройти через дверь каждого вида по одному разу. Как и полагается сказке, принес Иванушка розу и был вознагражден. Какой же маршрут оказался верным?
Как и полагается сказке, принес Иванушка розу и был вознагражден. Какой же маршрут оказался верным?
Слайд 17
+ — + П С Л + + — + — + С Л П Л П С — + — + + + Л С Л П С П Для решения этой задачи нужно рассмотреть всевозможные маршруты, т. к. на избранном пути не должно быть одинаково расположенных дверей, то возможно лишь 6 различных маршрутов (3!). Воспользуемся графами (рис. 27). «Плюс» на соединительном отрезке означает правильный, а «минус» — ложный ответ принцессы. Так как верен один совет, то правильный маршрут тот, который отмечен одним знаком «+» и двумя «-», а именно Л — П — С. Решение
Слайд 18
Буквенные ребусы Буквенные ребусы и задачи со звездочками Методом подбора и рассмотрения различных вариантов решаются буквенные ребусы и примеры со звездочками. Такие задачи различны по сложности и схеме решения. Рассмотрим один такой пример:
Слайд 19
Перед началом бегов на ипподроме четыре знатока из числа зрителей обсуждали шансы фаворитов А, В или С. Ребусы Первый: Заезд выиграет А или С. Второй: Если А придет третьим, то С не выиграет. Третий: Если А будет вторым, то выиграет В. Четвертый: Вторым придет А или В. После заезда выяснилось, что три фаворита А, В, С действительно заняли первые три места и что все четыре утверждения знатоков оказались истинными. Как фавориты поделили между собой три первых места?
Ребусы Первый: Заезд выиграет А или С. Второй: Если А придет третьим, то С не выиграет. Третий: Если А будет вторым, то выиграет В. Четвертый: Вторым придет А или В. После заезда выяснилось, что три фаворита А, В, С действительно заняли первые три места и что все четыре утверждения знатоков оказались истинными. Как фавориты поделили между собой три первых места?
Слайд 20
Возможны 6 вариантов исхода заезда (з!): А В С А С В (4) В С А (1), (4) В А О (1) С А В (3) С В А (2)
Слайд 21
ИСТИННОСТНЫЕ ЗАДАЧИ Истинностные задачи – это задачи, в которых требуется установить истинность или ложность высказываний. Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису? Задание!
Слайд 22
Задачи, решаемые с конца Ответ.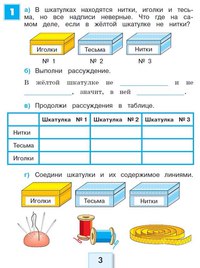 7 – искомое число. Задуманное число Я задумала число, умножила его на два, прибавила три и получила 17. Какое число я задумала? Решение: 17 – 3 = 14 – число до прибавления 3. 14 : 2 = 7 – искомое число.
7 – искомое число. Задуманное число Я задумала число, умножила его на два, прибавила три и получила 17. Какое число я задумала? Решение: 17 – 3 = 14 – число до прибавления 3. 14 : 2 = 7 – искомое число.
Слайд 23
ЗАДАЧИ НА ПЕРЕЛИВАНИЕ Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Слайд 24
Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л. Решение лучше и удобнее оформить в виде таблицы: ходы 1 2 3 4 5 6 5 л 5 2 2 — 5 4 3 л — 3 — 2 2 3 Решение
Слайд 25
Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена. Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр. Но тогда решение будет выглядеть следующим образом: Ходы ходы 1 2 3 4 5 6 7 8 5 л — 3 3 5 — 1 1 4 3 л 3 — 3 1 1 — 3 —
Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена. Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр. Но тогда решение будет выглядеть следующим образом: Ходы ходы 1 2 3 4 5 6 7 8 5 л — 3 3 5 — 1 1 4 3 л 3 — 3 1 1 — 3 —
Слайд 26
Задачи на взвешивание Задачи на взвешивание — достаточно достаточно распространённый вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.
Слайд 27
Задание У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?
Слайд 28
Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она — в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете — фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена. Решение
Логические задачи на уроках математики в начальной школе
Рассмотрим методику использования на уроках
математики в начальной школе специального типа
логических задач, связанных с внедрением в
сознание ребенка основных понятий
математической логики. Эта методика была
разработана ведущим отечественным методистом
А.А. Столяром.
Эта методика была
разработана ведущим отечественным методистом
А.А. Столяром.
«Главная задача обучения математике, причем с самого начала, с первого класса, — учить рассуждать, учить мыслить», — писал А.А.Столяр. Для достижения наилучших результатов в освоении учащимися основ логического мышления и в изучении геометрических фигур А.А. Столяр использовал в своей практике игру с кругами.
Игра с кругами, созданная на основе известных кругов Эйлера, позволяет обучать классифицирующей деятельности, закладывает понимание логических операций: отрицания — не, конъюнкции и, дизъюнкции — или. Перечисленные логические операции имеют важнейшее значение, так как различные их комбинации образуют всевозможные и сколь угодно сложные логические структуры. Из функциональных элементов, реализующих логические операции не, и, или, конструируются схемы современных ЭВМ.
К концу дошкольного возраста у ребенка
проявляются признаки логического мышления. В
своих рассуждениях он начинает использовать
логические операции и на их основе строить
умозаключения. Очень важно в этот период научить
ребенка логически мыслить и обосновывать свои
суждения.
В
своих рассуждениях он начинает использовать
логические операции и на их основе строить
умозаключения. Очень важно в этот период научить
ребенка логически мыслить и обосновывать свои
суждения.
Для игры с кругами нужны нарисованные на бумаге один, два или три пересекающихся круга разного цвета, разноцветные обручи и наборы геометрических фигур разных цветов и размеров, карточки с числами и буквами русского алфавита. В принципе необязательно использовать круги, можно работать с любыми замкнутыми плоскими фигурами. В этом случае замкнутые области выделяются на монтажной панели, к примеру, цветными веревочками. Возможна также работа на компьютере со специальной компьютерной программой. Комплексное обучение, сочетающее игры с обручами со всем классом, игру за столом в группе и индивидуальную работу за компьютером, является наиболее эффективным.
Вот некоторые фрагменты уроков, где
рассматривались подобные задачи.
Фрагмент урока “Задачи с одним кругом” для 4 класса
Цель работы над задачами с одним кругом:
1. Учить классифицировать предметы по одному признаку, понимать и применять логическую операцию отрицания не;
2. Развивать логическое мышление.
Игра проводится со всем классом. У учеников в руках наборы квадратов, кругов и треугольников разных цветов и размеров, цветные карандаши. В центре полотна на доске нарисован круг.
Приложение 1
Цель работы над задачами с двумя кругами:
1. Развить умение классифицировать предметы по двум свойствам, понимать и применять логическую операцию конъюнкции, выражаемую союзом и;
2. Развивать логическое мышление.
На первых этапах знакомства задачами такого
типа ученики работают с раздаточным материалом.
(У учащихся в руках тот же раздаточный материал,
но теперь они уже будут работать с двумя кругами
или обручами разных цветов с пересекающимися
областями). Далее при выполнении заданий с
числами, ученики работают в тетрадях, где будут
необходимы цветные карандаши.
Далее при выполнении заданий с
числами, ученики работают в тетрадях, где будут
необходимы цветные карандаши.
Приложение 2
Обратные задачи также развивают способность классифицировать предметы по двум свойствам, правильно использовать логическую операцию конъюнкции, выражаемую союзом и. Эти задачи требуют большей внимательности.
Выше были приведены фрагменты урока, где рассматривались только некоторые задачи, затрагивающие интуитивное понимание основных логических конструкций математики.
Материал для подобных задач может быть взят и из других учебных предметов, например, природоведения.
Умение классифицировать по трем признакам и применять более сложные логические операции отрабатывается на играх с тремя кругами.
Организация различных форм работы с логическими задачами
Выше неоднократно утверждалось, что развитие у
детей логического мышления — это одна из важных
задач начального обучения. Умение мыслить
логически, выполнять умозаключения без
наглядной опоры, сопоставлять суждения по
определенным правилам — необходимое условие
успешного усвоения учебного материала.
Умение мыслить
логически, выполнять умозаключения без
наглядной опоры, сопоставлять суждения по
определенным правилам — необходимое условие
успешного усвоения учебного материала.
Основная работа для развития логического мышления должна вестись с задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления. Нестандартные логические задачи — отличный инструмент для такого развития.
Однако что зачастую наблюдается на практике? Учащимся предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают ее. Но извлекается ли из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учащихся может вновь испытывать затруднения при решении.
Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей.
1. Работа над решенной задачей. Многие учащиеся
только после повторного анализа осознают план
решения задачи.
2. Решение задач различными способами. Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь это умение свидетельствует о достаточно высоком математическом развитии. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем. Но я считаю, что это доступно не всем учащимся, а лишь тем, кто любит математику, имеет особые математические способности.
Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать “”””что это доступно не всем учащимся, а лишь тем, кто любит математику, имеет особые математические способности.
3. Правильно организованный способ анализа
задачи — с вопроса или от данных к вопросу.
4. Представление ситуации, описанной в задаче (нарисовать «картинку»). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
5. Самостоятельное составление задач учащимися.
Составить задачу:
1) используя слова: больше на, столько, сколько, меньше в, на столько больше, на столько меньше;
2) решаемую в 1, 2, 3 действия;
3) по данному ее плану решения, действиям и ответу; 4) по выражению и т.д.
6. Решение задач с недостающими или лишними данными.
7. Изменение вопроса задачи.
8. Составление различных выражений по данным задачам и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
9. Объяснение готового решения задачи.
10. Использование приема сравнения задач и их решений.
11. Запись двух решений на доске — одного верного и другого неверного.
12. Изменение условия задачи так, чтобы задача решалась другим действием.
13. Закончить решение задачи.
14. Какой вопрос и какое действие лишнее в решении задачи (или, наоборот, восстановить пропущенный вопрос и действие в задаче).
15. Составление аналогичной задачи с измененными данными.
16. Решение обратных задач.
Систематическое использование на уроках
математики и внеурочных занятиях специальных
задач и заданий, направленных на развитие
логического мышления, организованных согласно
приведенной выше схеме, расширяет
математический кругозор младших школьников и
позволяет более уверенно ориентироваться в
простейших закономерностях окружающей их
действительности и активнее использовать
математические знания в повседневной жизни.
Приложение 1
Приложение 2
Решение логических текстовых задач в начальной школе как один из способов развития творческих способностей младших школьников Текст научной статьи по специальности «Науки об образовании»
© Гебекова А.Н.*
Дагестанский институт повышения квалификации педагогических кадров,
г. Махачкала
Чеченский государственный педагогический институт, г. Грозный
В статье автор аргументирует актуальность выбранной темы, рассматривает роль логических задач на развитие творческих способностей младших школьников в связи с реализацией федеральных государственных образовательных стандартов начального общего образования. Использование логических задач будет способствовать развитию у учащихся умение сравнивать наблюдаемые предметы, находить в них общие свойства и различия.
Использование логических задач будет способствовать развитию у учащихся умение сравнивать наблюдаемые предметы, находить в них общие свойства и различия.
Ключевые слова логические задачи, логика, логическое мышление, творческие способности.
В основе разработки федеральных государственных образовательных стандартов начального общего образования лежит представление об образовании как институте социализации личности. Целью начального образования на данном этапе является формирование личности младшего школьника с максимальным учетом его индивидуальных способностей, развитие его творческих способностей, которые обеспечивают такую ключевую компетенцию, как умение учиться. Важнейшей задачей современной системы образования является формирование универсальных учебных действий, которые обеспечивают школьникам умение учиться, т.е. способность к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта.
При проектировании современных стандартов начального общего образования второго поколения одним из главных ориентиров является «определение в качестве ведущей цели образования в информационную эпоху мотивации к обучению, познанию и творчеству в течении всей жизни и формирование способности к обновлению компетенций». Это связано обновлением содержания обучения, где одним из ведущих процессов является формирование творческой активности младших школьников, способной самостоятельно делать выбор, ставить, а затем и реализовывать цели, выходящие за рамки, предписанные стандартным требованиям, анализировать возникающие проблемы и осознанно оценивать свою учебную деятельность.
Доцент кафедры Дошкольного и начального образования, к.п.н., доцент
88
ОБУЧЕНИЕ И ВОСПИТАНИЕ: МЕТОДИКИ И ПРАКТИКА
Развитие творческих способностей младших школьников необходимо на всех этапах школьного обучения, но особое значение имеет формирование творческих способностей в младшем школьном возрасте.
«Главная задача обучения математике, с первого класса, — учить рассуждать, учить мыслить», — писал ведущий отечественный методист А.А. Столяр. Использование логических-нестандартных задач на уроке математики в начальной школе очень актуально сегодня в связи с реализацией федеральных государственных образовательных стандартов начального общего образования. Актуальность данной темы заключается в том, что учитель из-за отсутствия системы работы над этими задачами не всегда знает, как сформировать у учащихся способность мыслить последовательно, по законам логики.
Мы предполагаем, что никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к новым учебным программам. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что развитие логического мышления в значительной мере идёт стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевают начальными приёмами логического мышления.
В настоящее время в свете Федерального государственного образовательного стандарта начального общего образования содержание математического образования направлено главным образом на интеллектуальное развитие младших школьников, на формирование культуры и самостоятельной творческой активности. Поэтому учителя начальных классов должны особое внимание уделять решению логических задач.
Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному. Как показывает опыт, в младшем школьном возрасте одним из эффективных способов развития логического мышления является решение школьниками нестандартных логических задач [2].
Кроме того, решение нестандартных логических задач способно привить интерес ребёнка к изучению «классической» математики. В этом отношении весьма характерен следующий пример. Крупнейший математик современности, создатель московской математической школы, академик Николай Николаевич Лузин, будучи гимназистом, получал по математике сплошные двойки. Учитель прямо сказал родителям Н.Н. Лузина, что их сын в математике безнадёжен, что он туп и что вряд ли он сможет учиться в гимназии. Родители наняли репетитора, с помощью которого мальчик еле-еле перешёл в следующий класс.
Однако репетитор этот оказался человеком умным и проницательным. Он заметил невероятную вещь: мальчик не умел решать простые, прими-
Теория и методика обучения и воспитания
89
тивные задачи, но у него иногда вдруг получались задачи нестандартные, гораздо более сложные и трудные. Он воспользовался этим и сумел заинтересовать математикой этого, казалось бы, бездарного мальчика. Благодаря такому творческому подходу педагога из мальчика впоследствии вышел учёный с мировым именем, не только много сделавший для математики, но и создавший крупнейшую советскую математическую школу.
Он воспользовался этим и сумел заинтересовать математикой этого, казалось бы, бездарного мальчика. Благодаря такому творческому подходу педагога из мальчика впоследствии вышел учёный с мировым именем, не только много сделавший для математики, но и создавший крупнейшую советскую математическую школу.
Логика — это наука о законах правильного мышления, о требованиях, предъявляемых к последовательному и доказательному рассуждению (немецкий философ И. Кант). Отсюда следует, что мы должны научить учащихся анализировать, сравнивать, выделять главное, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, ставить и разрешать проблемы. Овладение этими методами и означает умение мыслить. Нельзя сформировать логическое мышление не изучая логику, нельзя надеяться, что логическое мышление развивается в полной мере спонтанно на уроках математики, литературы и др. Во многих ситуациях учащиеся поступают интуитивно, полагаясь на сообразительность и смекалку, а иногда жизненный опыт или подсказку старших. Но логическая интуиция нуждается в прояснении.
Но логическая интуиция нуждается в прояснении.
Но каков бы ни был подход к решению этого вопроса, т.е. развития логического мышления, большинство исследователей сходятся в том, что развивать логическое мышление в процессе обучения — это значит:
— развивать у учащихся умение сравнивать наблюдаемые предметы, находить в них общие свойства и различия;
— вырабатывать умение выделять существенные свойства предметов и отвлекать (абстрагировать) их от второстепенных, несущественных;
— учить детей расчленять (анализировать) предмет на составные части в целях познания каждой составной части и соединять (синтезировать) расчлененные мысленно предметы в одно целое;
— учить детей делать правильные выводы из наблюдений или фактов, уметь проверять эти выводы;
— следить за тем, чтобы мысли учащихся излагались определенно, последовательно, обоснованно.
Основная работа для развития логического мышления, как мы считаем, должна вестись с текстовой задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления и творческих способностей младших школьников. Нестандартные логические задачи — отличный инструмент для такого развития [1]. Однако, что зачастую наблюдается на практике? Учащимся предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают её. Но извлекается ли из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учащихся может вновь испытывать затруднения при ее решении. Для получения наибольшего эффекта мы предлагаем применить различные формы работы над задачей [1]:
90
ОБУЧЕНИЕ И ВОСПИТАНИЕ: МЕТОДИКИ И ПРАКТИКА
1. Работа над решённой задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твёрдых знаний по математике. Конечно, повторение анализа требует времени, но оно окупается [1].
Работа над решённой задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твёрдых знаний по математике. Конечно, повторение анализа требует времени, но оно окупается [1].
2. Решение задач различными способами. Учителя начальных классов мало внимания уделяют решению задач разными способами в основном из-за нехватки времени. А ведь это умение свидетельствует о достаточно высоком математическом развитии. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем, хотя это доступно не всем учащимся, а лишь тем, кто любит математику, имеет особые математические способности[1].
3. Правильно организованный способ анализа задачи — с вопроса или от данных к вопросу.
4. Представление ситуации, описанной в задаче (нарисовать «картинку»). Учителю необходимо обратить внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
5. Самостоятельное составление задач учащимися.
Составить задачу: 1) используя слова: больше на; столько, сколько; меньше в, на столько больше, на столько меньше; 2) решаемую в 1, 2, 3 действия; 3) по данному её плану решения, действиям и ответу; 4) по выражению и т.д.
6. Решение задач с недостающими или лишними данными.
7. Изменение вопроса задачи.
8. Составление различных выражений по данным задачам и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
9. Использование приёма сравнения задач и их решений.
10. Запись и сравнение двух решений на доске — одного верного и другого неверного.
11. Изменение условия задачи так, чтобы задача решалась другим действием.
12. Закончить решение задачи.
13. Какой вопрос и какое действие лишние в решении задачи (или, наоборот, восстановить пропущенный вопрос и действие в задаче).
14. Составление аналогичной задачи с измененными данными.
15. Решение обратных задач.
Для развития творческих способностей младших школьников можно использовать решение текстовых задач разными способами. Выработка привычки к поиску другого варианта решения играет большую роль в будущей работе. Применение различных способов решения текстовых задач развивает не только умственные способности, но и приучает их к исследователь-
Применение различных способов решения текстовых задач развивает не только умственные способности, но и приучает их к исследователь-
Теория и методика обучения и воспитания
91
ской работе. На уроках математики при решении тестовых задач, мы считаем, что необходимо соблюсти не только все этапы работы над текстом, но и применять различные формы работы над задачей.
Задачи с недостающими или лишними данными
Как показывает практика, интерес и активность учащихся начальной школы при решении задач повышается, если их текст сформулирован на основе разнообразных задачных ситуаций взятых из жизни.
Сформулированные на их основе задачи могут содержать избыточную информацию, то есть такую, которая не нужна для выполнения требования задачи.
На основе возникающих жизненных ситуаций могут быть сформулированы и задачи, в которых недостаточно информации для выполнения требований.
Незаконченные задачи (задача без вопроса)
Алгоритм работы выстроен на даче вопросов детям:
— Поставьте вопрос так, чтобы задача решалась в одно действие.
— Поставьте вопрос так, чтобы задача решалась в два действия.
— Поставьте вопрос к задаче.
Составление задач по имеющимся данным
Вначале даётся понятие «задача», затем «данные». После того как учащимися усвоены эти понятия, мы предлагаем перейти к системной поэтапной работе. Каждый этап имеет различный период времени и определяется усвоением учащимися технологии работы по данному алгоритму.
Каждый этап имеет различный период времени и определяется усвоением учащимися технологии работы по данному алгоритму.
— Данные предлагаются конкретные и отвлечённые.
— Предлагать детям цифровые и словесные данные (полные) «разрезанная задача».
— Предлагать числовые данные и главные словесные (по типу краткой записи)
— Предлагать только словесные данные (могут быть картинки, реальные жизненные ситуации)
— Предлагать только числовые данные.
Составление задач по краткой записи
Для данной работы предлагаем использовать схемы.
На первом этапе отрабатывается алгоритм записи задачи краткои алгоритм принятого сокращения, а также правила распределения схематических стрелок и знаков вопроса.
Учитель должен учить детей дифференцировать разные вопросы: Сколько…? Который…? Какова.? И начинать свой ответ, опираясь на вопрос.
92
ОБУЧЕНИЕ И ВОСПИТАНИЕ: МЕТОДИКИ И ПРАКТИКА
Для уяснения лексического значения слова необходимо использовать задания на подбор нужного слова в вопросе.
Решение задач разными способами
Например, «Турист отправился в путешествие, во время которого он ехал на автомашинах, плыл на пароходе и, конечно, шел пешком. На протяжении всего путешествия он наблюдал за очарованием природы и восхищался старинной архитектурой».
На основе приведенного текста составьте задачу так, чтобы ее решением было числовое выражение
264 — (146 + (146 — 50)) 146 + (146 — 40) + (146 — 40) : 2
Учащимся можно предложить задачи с возрастающей степенью трудности, которые решаются последовательно — от первого к последнему. По количеству и качеству решенных задач можно было судить о навыке ребенка. Если ребенок не смог справиться с каким-либо заданием, то он должен был объяснить, что вызвало у него затруднение. Это позволит учителю скорректировать свою обучающую деятельность относительно каждого ребенка.
По количеству и качеству решенных задач можно было судить о навыке ребенка. Если ребенок не смог справиться с каким-либо заданием, то он должен был объяснить, что вызвало у него затруднение. Это позволит учителю скорректировать свою обучающую деятельность относительно каждого ребенка.
Демонстрация разных способов решения задач стимулирует познавательный интерес слабых учащихся, способствует развитию творческого мышления.
Поиск новых способов решения
Одним из эффективных приёмов мышления учащихся, включений их в творческую деятельность, является поиск различных способов решения задачи.
На пошив 8 одинаковых платьев израсходовали 24 м ткани. Сколько метров ткани потребуется на 2 таких же платья?
1- й способ:
1) 24 : 8 = 3 (м) — ткани требуется для одного платья;
2) 3 • 2 = 6 (м) — ткани потребуется на 2 платья.
Ответ: 6 метров.
2- й способ
1) 8 : 2 = 4 (раза) — меньше изготовят платьев;
2) 24 : 4 = 6 (м) — ткани потребуется на 2 платья.
Ответ: 6 метров.
Если частично изменить условие и вопрос задачи, то можно решить новую задачу.
Использование приема сравнения задач и их решений
Здесь интересным для учащихся является то, что что им необходимо поискать алгоритм решения подобных задач, что тоже ведёт к развитию творчества учащихся в процессе обучения.
Теория и методика обучения и воспитания
93
1. Друзья утром съели 5 яблок, а днём — ещё 3. Сколько всего они съели яблок?
Друзья утром съели 5 яблок, а днём — ещё 3. Сколько всего они съели яблок?
2. Друзья утром съели 5 яблок, а днём — ещё 3. На сколько больше они съели яблок утром, чем днём?
Прочитай тексты и докажи, что это задачи.
Чем задачи похожи? Чем различаются? Как ты думаешь, решения этих задач будут одинаковыми? Объясни ответ.
Реши задачи и объясни выбор действий.
Придумай свою задачу, которую нужно решать тем же действием, что и первую задачу из данных.
Измени вопрос своей задачи так, чтобы её решение стало таким же, как у второй задачи.
Решение обратных задач
Эта форма работы над задачей привлекает внимание всех учащихся, так как всегда всё необычное является наиболее интересным.
1. В вазе было 15 конфет, 11 из них съели. Сколько конфет осталось в вазе?
2. Когда съели 11 конфет, в вазе осталось ещё 17. Сколько конфет было в вазе сначала?
Реши задачи.
Сравни решения задач. Какая между ними связь? От чего она зависит?
Как бы ты назвал эти задачи? Почему?
Какую ещё задачу, обратную данным, можно составить? Запиши такую задачу и её решение.
Вышеуказанные виды задач обеспечивают одновременное осмысленное усвоение противоположных понятий и помогают детям различать близкие и сходные между собой понятия.
На уроках математики необходимо использовать различные формы работы над задачей и считаем продуктивным в системе метод чередования задач, решаемых разными способами, сопоставление задач, различные преобразования, приводящие к упрощению и усложнению. Для развития творческих способностей младших школьников мы считаем, что необходимо создать проблемные ситуации, ориентирующие учащихся на поиск. В результате ученик выступает в роли исследователя, открывая для себя новые знания.
Для развития творческих способностей младших школьников мы считаем, что необходимо создать проблемные ситуации, ориентирующие учащихся на поиск. В результате ученик выступает в роли исследователя, открывая для себя новые знания.
В результате многократных изменяющихся и усложняющихся упражнений ум ребенка становится острее, а сам он — находчивее и сообразительнее. У детей меняется подход к решению задач, он становится более гибким, особенно развивается навык по решению задач, имеющих несколько вариантов решения.
Рассуждения учащихся становятся последовательными, доказательными, логичными, а речь — четкой, убедительной, аргументированной. Повы-
94
ОБУЧЕНИЕ И ВОСПИТАНИЕ: МЕТОДИКИ И ПРАКТИКА
шается интерес к предмету, формируется неординарность мышления, умение анализировать, сравнивать, обобщать и применять знания в нестандартных ситуациях.
Ведь в творческом поиске легких побед не бывает, поэтому развивается упорство в достижении поставленных целей и, что очень ценно, развиваются навыки самоконтроля и самооценки.
Формирование творчества на уроках математики через решение логических задач обогащает педагогический процесс, делает его более содержательным, влияет на развитие ребенка, как на творческую личность.
Список литературы:
1. Алексеева О.В.Логические задачи на уроках математики в начальной школе. — М., 2014.
2. Асмолов А.Г., Буркменская Г.В., Володарская И.А. и др. Формирование УУД в основной школе: от действия к мысли. — М.: 2011.
3. Богоявленская Д.Б. Психология творческих способностей: Учеб. пособие для студ. высш. учеб. заведений. — М.: Издательский центр «Академия», 2002. — 320 с.
пособие для студ. высш. учеб. заведений. — М.: Издательский центр «Академия», 2002. — 320 с.
4. Демидова Т.Е. Теория и практика решения текстовых задач / Т.Е. Демидова. — М.: издательский центр «Академия», 2002.
5. Залевская Т.И. Использование логических задач на уроках математики в начальной школе. — М.: 2012.
6. Иванова Е.В. Развитие логического мышления на уроках математики // Начальная школа плюс до и после. — 2006. — № 6. — С. 59-60.
7. Липина И. Развитие логического мышления на уроках математики // Начальная школа. — 1999. — № 8. — С. 37-39.
8. Еланская З.А. Активизация познавательной деятельности // Начальная школа. — 2001. — № 6. — С. 52-54.
ВЫПУСКИ ПОЗНАВАТЕЛЬНО-ИНФОРМАЦИОННОИ ГАЗЕТЫ «ВАРЕНЬЕ» КАК НОВЫЙ ВИД ИНФОРМАЦИОННО-ОТЧЕТНОЙ ДЕЯТЕЛЬНОСТИ В ДОШКОЛЬНОМ УЧРЕЖДЕНИИ
© Джафарова Ф. Х.*
Х.*
Детский сад № 546, г. Екатеринбург
В статье представлены результаты работы по проекту познавательно-информационная газета «Варенье», который был успешно реализо-
Воспитатель высшей категории.
Логические задачки для 2 класса
Логические задачи для активизации мыслительной деятельности учащихся начальной школы на уроках математики.
Можно использовать и для проведения дополнительных занятий, а также для внеклассных мероприятий по математике.
1.10 насосов за 10 минут выкачивают 1 тонну воды. За сколько минут 20 таких насосов выкачивают 2 тонны воды?
Решение: 10нас/10мин=1мин/10:10=1 (одна минута)1*20=20 (20 минут) Ответ: 20 минут
2.На участке дороги длиной 90 м. Школьниками поручено посадить деревья так, чтобы между ними были расстояния в 9 метров. Сколько деревьев должны посадить школьники?
Сколько деревьев должны посадить школьники?
Решение: 90:9=10(д.) Ответ: школьники должны посадить 10 деревьев.
3.На столе лежали три линейки. Жёлтая была длиннее зелёной на 2 см. Синяя короче зелёной на 3 см. Найти длину жёлтой линейки, если длина синей – 15 см.
Ответ:Синяя линейка- 15см Зеленая линейка -18 см Жёлтая линейка-20 см
4.К числу 67 прибавить 2 однозначных числа и получить 75. Какие числа прибавили?
Решение: 5-67=8 8/2=4 два по четыре Ответ: 4 и 4
5.В море плавало 9 пароходов. 2 парохода пристали к пристани. Сколько пароходов в море? (9).
6.Неожиданно пошел сильный дождь. Но Таня, Саша, Лена не промокли. Почему?(Они наблюдали из окна; у них были плащи, зонты).
7.В реке купались дети. Они постоянно ныряли в воду и невозможно их было пересчитать. На берегу были разбросаны кеды, всего 12 штук. Сколько детей купалось в реке? (6).
8. Какой знак нужно поставить между 4-мя и 5-ю, чтобы результат оказался больше 4-х и меньше 5-ти? (Запятую)
9. Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)
Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)
10. По улице шли два отца и два сына, да дедушка с внуком. Сколько всего человек шло по улице? (3 человека)
11. Если один петух закукарекает, то человек проснётся. Сколько петухов должны закукарекать, чтобы проснулись три человека? (Один петух)
12. На сколько больше наименьшее двузначное число, чем наибольшее однозначное? (На 1)
13. В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. Наследующей — вышли 9 человек, зашли 5. Далее — вышли 7, зашли 8. Сколько было остановок? (3 остановки)
14. На уроке физкультуры дети выстроились в одну шеренгу с интервалом 1 м. Шеренга растянулась на 20 м. Сколько детей было на уроке? (21 ученик).
15. Карина гуляла и видела у реки 4 уток, 2 гусей, жука, 4 бабочки и соседскую собаку. Сколько птиц видела Карина? (6 птиц)
Развитие логического мышления на уроках математики как основа повышения качества образовательного процесса
В данный момент одной из основных проблем учащихся начальных классов является то, что на уроках они не умеют находить рациональный выход из различных ситуаций, тем самым усложняют задачу обучения, не рационально используют время на уроке.
В число основных интеллектуальных умений входят логические умения, формируемые, прежде всего, при обучении математике. Объекты логических умозаключений и принятые в математике правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, формулировать четкие определения, развивают логическую интуицию, кратко и наглядно вскрывают механизм логических построений и учат их применению.
Психолого-педагогическими исследованиями отечественных и зарубежных ученых доказано, что основные логические умения на элементарном уровне можно сформировать у детей, начиная с 5-6-летнего возраста.
Цель исследования: выявление и описание наиболее продуктивных путей развития логического мышления у детей младшего школьного возраста.
Предметом исследования: выступает развитие логического мышления.
Для достижения поставленной цели планирую решить следующие задачи:
— описать теоретические основы формирования логического мышления у детей младшего школьного возраста;
— дать характеристику существующим обще методическим подходам к решению логических задач на уроках математики в начальной школе;
— раскрыть роль использования логических задач на уроках математики в начальной школе;
— подобрать подходящие логические задачи и классифицировать их в соответствии с возможными способами решения на уроках математики в начальной школе.
Практическая значимость исследования – умело и рационально организованная работа учителя по решению задач способствует развитию у детей логического мышления.
При написании работы были использованы следующие теоретические методы исследования:
— теоретические – анализ психолого-педагогической и методической литературы, периодических изданий, интернет-источников по теме исследования;
— эмпирические – анализ продуктов деятельности учащихся, проектирование, описание результатов апробирования.
— сформировать логическое мышление учащихся начальных классов;
— повысить качество знаний по математике через развитие логического мышления.
Актуальность опыта
Одной из основных задач современной школы является подготовка человека, способного самостоятельно принимать решения и эффективно, разумно действовать в жизненных ситуациях. За годы работы в школе я поняла, что успешная реализация этой задачи во многом зависит от сформированности у учащихся логического мышления.
Мышление – это особого рода умственная и практическая деятельность, предполагающая систему включённых в неё действий и операций преобразовательного характера. Мыслительная деятельность людей совершается при помощи мыслительных операций: сравнения, анализа, синтеза, абстракции, обобщения и конкретизации [5].
Различают три вида мышления: наглядно-действительное, наглядно-образное, словесно-логическое. Самой ранней ступенью в развитии мышления ребенка является наглядно-действительное мышление. Оно характеризуется тем, что задача, подлежащая мышлению, даётся наглядно и решается руками, т.е. с практическим действием. Эта форма «мышления руками» не исчезает с развитием более высоких форм логического мышления. С развитием речи и накоплением опыта ребенок приходит к наглядно-образному мышлению. Он мыслит образами, а слово, которым он владеет, помогает ему делать обобщения. Ребенок, придя в школу, в основном мыслит, опираясь на конкретные образы. Но полное и глубокое изучение программного материала способствует развитию словесно-логического мышления. Логическое мышление является высшей ступенью умственного развития ребенка, проходит длительный путь [3].
Логическое мышление является высшей ступенью умственного развития ребенка, проходит длительный путь [3].
С поступлением ребенка в школу происходят существенные изменения в его жизни, формируется учебная деятельность. На основе учебной деятельности развиваются основные психологические новообразования младшего школьника. Мышление становится доминирующей функцией. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определённым правилам – необходимое условие успешного усвоения учебного материала на уроках математики. О ребёнке, у которого хорошо развито логическое мышление, говорят, что он основательно мыслит, дисциплинированно рассуждает. Такой ученик, как правило, не допускает ошибок в своих рассуждениях и выводах. Процесс развития логического мышления довольно длителен. Поэтому и начинаться он должен с первых лет обучения ребенка в школе [1].
Мыслительная деятельность людей совершается при помощи мыслительных операций: сравнения, анализа, синтеза, абстракции, обобщения и конкретизации.
Сравнение – это сопоставление предметов и явлений с целью найти сходство и различие между ними.
Анализ – это мысленное расчленение предмета или явления на образующие его части, выделение в нем отдельных частей, признаков и свойств.
Синтез – это мысленное соединение отдельных элементов, частей и признаков в единое целое.
Анализ и синтез неразрывно связаны, находятся в единстве друг с другом в процессе познания. Анализ и синтез – важнейшие мыслительные операции.
Абстракция – это мысленное выделение существенных свойств и признаков предметов или явлений при одновременном отвлечении от несущественных. Абстракция лежит в основе обобщения.
Обобщение – мысленное объединение предметов и явлений в группы по тем общим и существенным признакам, которые выделяются в процессе абстрагирования. Процессам абстрагирования и обобщения противоположен процесс конкретизации.
Конкретизация – мыслительный переход от общего к единичному, которое соответствует этому общему. В учебной деятельности конкретизировать – значит привести пример.
В начальной школе учащиеся должны овладеть такими элементами логических действий, как: сравнение, классификация, выделение признаков предметов, определение знакомого понятия через род и видовое отличие, делать простейшие умозаключения, опираясь на данные посылки. Поэтому целесообразно начинать обучение логическим действиям с формирования соответствующих элементарных умений, постепенно усложняя задания.
Усвоение знаний – большой и нелегкий труд. Он требует от учащихся максимальных, длительных и напряженных усилий, постоянной мобилизации воли и внимания. Дорог каждый день жизни детей, начиная с самого рождения, а тем более нельзя упустить время в первые школьные годы, которые являются важнейшим периодом в развитии и формировании человека. В это время развитие логического мышления выступает как важнейший фактор, обеспечивающий эффективность его дальнейшего обучения в школе, успешность в профессиональной подготовке и жизни [4].
Хорошо развитое логическое мышление предостерегает от ошибок в практической деятельности. Это качество развивается главным образом в процессе изучения математики и является, по моему мнению, главной задачей уроков математики. В математике ученик с наибольшей полнотой может увидеть демонстрацию почти всех основных законов элементарной логики. От развития мышления зависит качество знаний учащихся.
Открытие, исследование, эксперимент – основа учебного процесса. Идея состоит в том, чтобы ещё до получения учениками конкретных знаний предоставить им возможность испытать на себе то, что испытывает любой исследователь, который должен ответить на поставленные вопросы.
Рассматривая процесс развития своих учеников, я обратила внимание на то, что обучение выдвигает мышление в центр сознания ребенка.
Развитие логического мышления младших школьников – одно из важнейших направлений обучения учащихся. На важность этого процесса указывают учебные программы и методическая литература. Актуальность проблемы развития мышления объясняется тем, что успешность любой деятельности как раз во многом и зависит от особенностей развития мышления. Именно в младшем школьном возрасте, как показывают специальные исследования, должно достаточно интенсивно развиваться логическое мышление. Мышление играет огромную роль в познании. Оно расширяет границы познания, дает возможность выйти за пределы непосредственного опыта ощущений и восприятия. Мышление дает возможность знать и судить о том, что человек непосредственно не наблюдает, не воспринимает.
Актуальность проблемы развития мышления объясняется тем, что успешность любой деятельности как раз во многом и зависит от особенностей развития мышления. Именно в младшем школьном возрасте, как показывают специальные исследования, должно достаточно интенсивно развиваться логическое мышление. Мышление играет огромную роль в познании. Оно расширяет границы познания, дает возможность выйти за пределы непосредственного опыта ощущений и восприятия. Мышление дает возможность знать и судить о том, что человек непосредственно не наблюдает, не воспринимает.
К сожалению, в средних классах учителя математики сталкиваются с проблемой несформированности у учащихся способности анализировать, конкретизировать, обобщать, планировать, делать выводы. Возникает вопрос, а как же улучшить мыслительную деятельность учащихся начальных классов на уроках математики, сделать их ум более гибким, научить мыслить, какие средства использовать.
Исходя из этой проблемы, я считаю, что развитие логического мышления на уроках математики в начальных классах актуально и определяется социальным заказом общества на творческую личность, способную осваивать, преобразовывать и создавать новые способы организации своей деятельности.
В начальной школе учащиеся должны овладеть такими элементами логических действий, как: сравнение, классификация, выделение признаков предметов, определение знакомого понятия через род и видовое отличие, делать простейшие умозаключения, опираясь на данные посылки.
У первоклассника мышление наглядно-образное, навыки анализа у него элементарны, в содержание обобщений и понятий входят лишь внешние и часто несущественные признаки, поэтому целесообразно начинать обучение логическим действиям с формирования соответствующих элементарных умений, постепенно усложняя задания. При помощи упражнений не только закрепляются, но и уточняются знания детей, формируются навыки самостоятельной работы, укрепляются навыки мыслительной деятельности. Детям непрерывно приходится заниматься анализом, сравнением, составлять словосочетания и предложения, абстрагировать и обобщать. При этом обеспечивается одновременное развитие ряда важнейших интеллектуальных качеств ребенка: внимания, памяти, различных видов мышления, речи, наблюдательности.
Таким образом, в процессе формирования логического мышления детей 7-10 лет, пожалуй, самое важное — научить ребят делать пусть маленькие, но собственные открытия. Ученик должен уже в младших классах решать задачи, которые требовали от него не простого действия по аналогии (копирование действий учителя), а таили бы в себе возможность для “умственного прорыва”. Полезен не столько готовый результат, сколько сам процесс решения с его гипотезами, ошибками, сравнениями различных идей, оценками и открытиями, что, в конечном счете, может привести к личным победам в развитии ума.
На своих уроках я всегда нахожу момент, когда можно предложить ученикам задачи-шутки, задачи на смекалку, задачи в стихах. Это помогает процесс обучения сделать более интересным, и способствует развитию логики.
Для развития математических способностей и развития мышления очень полезны и интересны логические задачи. Логические задачи – задачи, требующие умения проводить доказательные рассуждения, анализировать. Она позволяют организовать на уроках интересные ситуации, которые способствуют лучшему усвоению программного материала и развитию логического мышления [2].
Опыт показывает, что у основной массы учащихся здравый смысл опережает математическую подготовку. Это обуславливает высокий интерес школьников к решению таких задач. От обычных они отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – особая информация, которую не только нужно отработать в соответствии с заданным условием, но и хочется это сделать.
Для реализации плана я разработала систему использования разнообразных методов, приёмов, заданий, направленных на развитие логического мышления учащихся, тестирование учащихся по сформированности у них логического мышления. После того, как я убедилась в том, что ученики умеют логически мыслить, выполняя математические задания, стала осуществлять контрольно-коррекционную деятельность по выполнению математических заданий.
Экспериментируя свою научную работу на практике, я заметила, что практически у всех учащихся в итоге была повышена активность на уроках, так же в высокой степени было развито логическое мышление. Мы научились решать логические задачи за короткий срок.
Заключение. Так как математика даёт реальные предпосылки для развития мышления, я решила полнее использовать эти возможности на уроках при обучении детей. Как показывает мой опыт, уроки математики обладают уникальным развивающим эффектом и дают реальные предпосылки для развития логического мышления. Считаю, что систематичность в работе, выбранные мной формы и методы развития логического мышления, способствуют развитию самостоятельности логики мышления, которая позволит детям строить умозаключения, проводить доказательства, высказывания, делать выводы, обосновывать свои суждения, приобретать знания, а также активнее использовать эти знания на уроках математики и в повседневной жизни. Практической значимостью работы является то, что материалы используются в практике учителями начальных классов. Логическое мышление – основа школьного образования, залог успешного понимания технических и гуманитарных дисциплин. Развитие логического мышления как педагогический процесс необходимо осуществлять в соответствии с законами развития детского организма, в единстве и согласии с интеллектуальным развитием ребенка. Развитие логического мышления учащихся на всех уроках – одно из наиболее существенных требований, обеспечивающих качество обучения.
Список использованных источников:
1. Федеральный государственный образовательный стандарт начального общего образования, М.: Просвещение, 2010.
2. Афанасьева, О. В. Логика. – М.: Мастерство, 2002.
3. Выготский Л. С. Мышление и речь. – М.: Просвещение, 2010.
4. Ефанова, З. А. Развитие мышления. – Волгоград: Корифей, 2010.
5. Белошистая, А.В., Задания для развития логического мышления в начальных классах / А.В. Белошистая, В.В.Левитес. – Москва: Дрофа, 2008. – 65 с.
6. Берков, В.Ф. Логика: задачи, упражнения, практикум / В.Ф. Берков. – Минск: ТетраСистемс, 1998. – с. 5-6.
7. Зайцев, В.В. Математика для младших школьников / В.В. Зайцев. — Москва: Владос, 2001. – 20 с.
8. Немов, Р.С. Психология / Р.С. Немов. – Москва: Владос, 2003. с. 198-201.
9. Мельникова, Т.В. Математика. Развитие логического мышления / Т.В. Мельникова. – Волгоград: Учитель, 2009. – 131 с.
Источники:
http://nsc.1september.ru/
http://suhin.narod.ru/zag1.htm
http://www.ed.gov.ru
http://nssh.kostjukovichi.edu.by/be/main.aspx?guid=13231http://открытыйурок.рф/статьи/313900/
Как развивать логическое мышление у младших школьников
Развитие логического мышления младших школьников — одно из важнейших направлений обучения учащихся. На важность этого процесса указывают учебные программы и методическая литература. Совершенствовать логическое мышление лучше всего и в школе, и дома, однако далеко не все знают, какие методы для этого будут наиболее эффективными. Вследствие этого логическое обучение принимает форму стихийного, что негативно сказывается на общем уровне развития учеников. Бывает так, что даже старшеклассники не умеют логически мыслить, пользуясь приёмами анализа, синтеза, сравнения и пр. Как правильно развивать логическое мышление младших школьников — вы узнаете из нашей статьи.
Особенности мышления учеников начальной школы
Мышление учеников младших классов имеет особенностиК тому времени, когда ребёнок начинает ходить в школу, его психическое развитие характеризуется весьма высоким уровнем.
«Каждый возрастной период ребёнка характеризуется ведущим значением какого-либо психического процесса. В раннем детстве ведущую роль играет формирование восприятия, в дошкольном периоде — памяти, а у младших школьников основным становится развитие мышления».
Мышление учеников младших классов имеет особенности. Именно в этот период наглядно-образное мышление, имевшее ранее основное значение, трансформируется в словесно-логическое, понятийное. Вот потому в начальной школе чрезвычайно важно уделять внимание становлению логического мышления.
Младшие школьники развивают своё логическое мышление тем, что регулярно выполняют задания, учатся думать тогда, когда надо.
Учитель учит:
- находить взаимосвязи в окружающей жизни
- вырабатывать правильные понятия
- применять на практике изучаемые теоретические положения
- анализировать с помощью мыслительных операций (обобщения, сравнения, классификации, синтеза, и пр.).
Всё это позитивно влияет на развитие логического мышления младших школьников.
Педагогические условия
Правильно созданные педагогические условия стимулируют развитие логического мышления школьниковДля того чтобы развивать и совершенствовать логическое мышление младших школьников, необходимо создать способствующие этому педагогические условия.
Образование начальной школы должно быть направлено на то, чтобы учитель помог каждому ученику раскрыть свои способности. Это реально в том случае, когда учитель учитывает индивидуальность каждого. Кроме этого, раскрытию потенциала младшего школьника способствует разнообразная образовательная среда.
Рассмотрим педагогические условия, способствующие формированию логического мышление ученика:
- Задания на уроках, которые побуждают детей размышлять. Лучше, когда такие задания не только на уроках математики, а и на всех остальных. А некоторые учителя делают логические пятиминутки между уроками.
- Общение с учителем и сверстниками — в урочное и неурочное время. Размышляя над ответом, путями решения задачи, ученики предлагают разные варианты решения, а педагог просит их обосновывать и доказывать правильность своего ответа. Таким образом, младшие школьники учатся рассуждать, сопоставлять разнообразные суждения, делать умозаключения.
- Хорошо, когда учебный процесс наполнен элементами, где ученик:
- может сравнивать понятия (предметы, явления),
- понимать различия между общими признаками и отличительными (частными)
- выделять существенные и несущественные признаки
- не брать во внимание несущественные детали
- анализировать, сравнивать и обобщать.
«Успех полноценного формирования логического мышления младшего школьника зависит от того, насколько комплексно и системно происходит обучение этому».
Начальная школа — наилучший период для целенаправленной работы по активному развитию логического мышления. Помочь сделать этот период продуктивным и результативным могут всевозможные дидактические игры, упражнения, задачи и задания, направленные на:
- формирование умения самостоятельно мыслить
- обучение умению делать выводы
- эффективному использованию полученных знаний в мыслительных операциях
- поиск характерных признаков в предметах и явлениях, сравнение, группирование, классификацию по определённым признакам, обобщение
- использование имеющихся знаний в различных ситуациях.
Нестандартные задания, упражнения, игры для развития мыслительных операций полезно применять как на уроках, так и при домашних занятиях с детьми. Сегодня они не являются дефицитом, так как разработано большое количество полиграфической, видео- и мультимедийной продукции, разнообразных игр. Все эти средства можно использовать, подбирая с учётом целей, а также ориентируясь на индивидуальные особенности и предпочтения ребёнка.
Видео с примером игры для планшета, направленную на развитие логического мышления младших школьников
Упражнения и игры на логическое мышление
- «Четвёртый лишний». Упражнение заключается в том, чтобы исключить один предмет, у которого отсутствует некоторый признак, общий для остальных трёх (здесь удобно использовать карточки с изображениями).
- «Чего не хватает?». Нужно придумать недостающие части рассказа, (начало, середину или конец).
- «Не зевай! Продолжай!». Смысл в том, чтобы ученики быстро называли ответы на вопросы.
На уроках чтения:
- Кто последний тянул репку?
- Как звали мальчика из «Цветика-семицветика»?
- Как звали мальчика с длинным носом?
- Кого победил жених мухи-цокотухи?
- Кто пугал трёх поросят?
На уроках русского языка:
- Какое слово содержит три буквы «о»? (трио)
- Название какого города свидетельствует о том, что он сердитый? (Грозный).
- Какую страну можно носить на голове? (Панама).
- Какой гриб растёт под осиной? (Подосиновик)
- Как можно написать слово «мышеловка» с помощью пяти букв? ( «Кошка»)
На уроках природоведения:
- Паук — это насекомое?
- Вьют ли наши перелётные птицы гнёзда на юге? (Нет).
- Как называется личинка бабочки?
- Что ест ёжик зимой? (Ничего, он спит).
На уроках математики:
- Тройка лошадей пробежала 4 километра. Сколько километров пробежала каждая из лошадей? (по 4 километра).
- На столе лежало 5 яблок, одно из которых разрезали пополам. Сколько яблок лежит на столе? (5.)
- Назовите число, в котором три десятка. (30.)
- Если Люба стоит позади Тамары, то Тамара …(стоит впереди Любы).
«Совет. Для обогащения учебного процесса, а также для домашних занятий используйте логические задачи и загадки, головоломки, ребусы и шарады, многочисленные образцы которых вы легко найдёте в разных методических пособиях, а также в интернете».
Задания, активизирующие мозг
Существует множество заданий, активизирующих мозгЗадания на развитие умения анализировать и синтезировать
- Соединение элементов воедино:
«Вырежи нужные фигуры из разных предложенных для того, чтобы получился дом, корабль и рыбка».
- На поиск разных признаков предмета:
«Назови, сколько сторон, углов и вершин у треугольника?».
«Никита и Егор прыгали в длину. С первой попытки Никита прыгнул на 25 см дальше, чем Егор. Со второй Егор улучшил свой результат на 30 см, а Никита прыгнул так же, как и с первой. Кто прыгнул дальше со второй попытки: Никита или Егор? На сколько? Догадайся!».
- На узнавание или составление объекта по определённым признакам:
«Какое число идёт перед числом 7? Какое число стоит после числа 7? За числом 8?».
Задания на умение классифицировать:
«Что общего?»:
1) Борщ, макароны, котлета, компот.
2) Свинья, корова, лошадь, коза.
3) Италия, Франция, Россия, Беларусь.
4) Стул, парта, шкаф, табурет.
«Что лишнее?» — игра, позволяющая находить общие и неодинаковые свойства предметов, сравнивать их, а также объединять их в группы по основному признаку, то есть классифицировать.
«Что объединяет?» — игра, формирующая такие операции логики, как сравнение, обобщение, классификация по переменному признаку.
Например: взять три картинки с изображениями животных: коровы, овцы и волка. Вопрос: «Что объединяет корову и овцу и отличает их от волка?».
Задание на развитие умения сравнивать:
«У Наташи было несколько наклеек. Она подарила 2 наклейки подруге, и у неё осталось 5 наклеек. Сколько наклеек было у Наташи?».
Задания на поиск существенных признаков:
«Назови признак предмета». Например, книга — какая она? Из какого материала она изготовлена? Какого она размера? Какой она толщины? Каково её название? К каким предметам относится?
Полезные игры: «Кто живёт в лесу?», «Кто летает в небе?», «Съедобное — несъедобное».
Задания на сравнение:
Сравнение по цвету. Нужно назвать побольше предметов:
а) синего цвета
б) жёлтого цвета
в) белого цвета
г) розового цвета.
Сравнение по форме. Нужно назвать побольше предметов:
а) квадратной формы
б) круглой формы
в) треугольной формы
г) овальной.
Сравним 2 предмета:
а) грушу и банан
б) малину и клубнику
в) санки и телегу
г) автомобиль и поезд.
Сравним времена года:
Беседа с учащимися об особенностях времён года. Чтение стихов, сказок, загадок, пословиц, поговорок о временах года. Рисование на тему времён года.
Нестандартные логические задачи
Одним из самых эффективных способов развить логическое мышление в начальной школе является решение нестандартных задач.
«А знаете ли вы, что математике присущ уникальный развивающий эффект? Она стимулирует развитие логическое мышление, самым лучшим способом формируя приёмы мыслительной работы, расширяя интеллектуальные способности ребёнка. Дети учатся рассуждать, замечать закономерности, применять знания в различных сферах, быть более внимательными, наблюдательными».
Кроме математически задач, мозг младших школьников развивают головоломки, разные виды заданий с палочками и спичками (выкладывание фигуры из определённого числа спичек, перенос одной из них с целью получения другой картинки, соединение несколько точек одной линией без отрыва руки).
Задачи со спичками
- Нужно составить 2 одинаковых треугольника из 5 спичек.
- Нужно сложить 2 одинаковых квадрата из 7 спичек.
- Нужно составить 3 одинаковых треугольника из 7 спичек.
Всестороннее развитие мышления обеспечивают также игры-головоломки: «Кубик Рубика», «Змейка Рубика», «Пятнашки» и многие другие.
Хорошо развитое логическое мышление поможет ребёнку в учёбе, делая усвоение знаний легче, приятнее и интереснееПредложенные в данной статье игры, упражнения и задания направлены на развитие логического мышления младших школьников. Если эти задания постепенно усложнять, то результат будет лучше с каждым днём. А гибкое, пластичное мышление и быстрая реакция помогут ребёнку в учёбе, делая усвоение знаний легче, приятнее и интереснее.
Логических игр для учеников начальной школы, Мышление для детей детского возраста онлайн играть бесплатно
Blomster Match — уникальная игра, в которую может играть каждый!
Меняйте местами блоки, чтобы составить ряды из трех или более одинаковых цветов, прежде чем истечет таймер. Звучит просто, правда? Что ж, в этой игре есть одна загвоздка … Вы должны убедиться, что все блоки на доске совпадают! Фон станет синим, и вы сможете перейти на следующий уровень! Помните, что вы можете подбирать совпадения, только если три или более блоков с одним и тем же цветком, так что имейте это в виду! Вы всегда можете попросить подсказку и использовать приобретенные предметы, чтобы помочь вам на этом пути.В этой веселой игре-головоломке двадцать четыре уровня. Сможете ли вы выполнить их все?
Сыграть в эту игру
Nom Nom Yum — это игра-головоломка на тему суши от студии «Cut the Rope», в которой вам нужно перерезать веревки и лопать пузыри, чтобы доставить кусок суши ко рту Нома! На каждом уровне суши будут подвешены на одной или нескольких веревках. Если их разрезать, суши упадут или раскачиваются. Вам решать, как гравитация повлияет на движение, и сделать так, чтобы вы собирали звезды, прежде чем точно падать, чтобы накормить Ном Нома!
Сыграть в эту игру
Fantasy Jigsaw Deluxe: это классическая игра-головоломка, в которой вы можете выбрать сложность, легкую или сложную, в зависимости от вашего опыта! Чем быстрее вы соберете головоломку, тем выше будет результат! Так что не торопись.Покажи, из чего ты сделан!
Соберите лобзик как можно быстрее. Это проверит вашу наблюдательность. Сможете ли вы определить правильное место для головоломки и, кроме того, сможете ли вы справиться с давлением тикающих часов. Совет будет смотреть на форму части головоломки, если у них плоская сторона, которая должна означать, что они могут идти только снаружи!
Сыграть в эту игру
Vortex — это красивая веселая 2D-аркада, в которой легко заблудиться из-за простой в освоении игровой механики.Удовольствие для людей всех возрастов, которое можно подобрать и насладиться почти мгновенно, поскольку оно основано на одной базовой, но невероятно волнующей концепции — «Сохраняйте стрелу в безопасности».
Помимо того, что вихрь визуально привлекателен, в нем используется простой игровой процесс, требующий всего двух щелчков мышью. Геймплей увлекателен и увлекателен, но по мере того, как ваш уровень поднимается выше и возникает напряженность, временами он может стать разочаровывающим и сложным. Точность и быстрое время реакции — ключ к достижению высоких результатов и побитию личного рекорда.
Сыграть в эту игру
Проверьте свою память и наблюдательность в карточной игре-головоломке Genius Memory. Задача проста: сопоставьте все карты с одним лицом до того, как истечет время. Genius Memory — это не только отличная игра для улучшения вашей памяти и сохранения остроты ума, но и идеальная игра для семейных игровых вечеров. В Genius Memory есть до 120 уровней, каждый из которых сложнее предыдущего. Посмотрите, у кого в вашей семье самая лучшая или худшая память!
Сыграть в эту игру
Используйте навыки решения проблем и хорошую стратегию, чтобы помочь Джеку сбежать в этой сложной онлайн-игре-головоломке! Игра Prison Escape, в которую можно играть на мобильном телефоне, планшете, ноутбуке, ноутбуке и настольном ПК, не оставит вас равнодушным.Джек — невиновный человек, ставший жертвой правосудия. В тюрьме с ограниченным доступом трудно найти какие-либо инструменты, чтобы сбежать! Но умному Джеку удается спланировать идеальный побег из тюрьмы всего за 14 дней. Нарисуйте дорожную карту, по которой Джек сможет сбежать. Держитесь подальше от охранников !!!
Проверьте и проявите свою решительность в решении проблем, логическое и аналитическое мышление, чтобы выяснить, где находится непосредственный шанс на побег! Также в игру вступают терпение, выносливость и готовность к пробам и ошибкам.Продолжайте пытаться зайти как можно дальше с каждой новой попыткой!
Как играть: Используйте мышь или палец, чтобы нарисовать дорожную карту, и нажмите, чтобы ИДТИ! тщательно рассчитайте время бега для всех трех сокамерников. Начните рисовать с начального круга и закончите линию у X. Доставьте всех 3 заключенных до финиша, чтобы пройти уровень.Сыграть в эту игру
Halloween Crazy Match — карточная игра на память, в которой вы собираете все большее количество карт на тему вуду, чтобы выиграть деньги.Каждая карта, которую вы открываете, стоит 10 долларов, но если вы найдете пару, вы выиграете 100 долларов! Посмотрите, сколько денег вы можете накопить, используя свои навыки памяти и гоняясь со временем.
Сыграть в эту игру
Взаимодействуйте с игровой средой, чтобы направить кусок хлеба в тостер, собирая сыр с помощью множества предметов на кухне в этой веселой игре-головоломке, основанной на физике! Bread Pit — это многоуровневая головоломка, в которой вы должны устранять препятствия и изменять игровую площадку для прохождения каждого уровня! Можно играть на мобильном телефоне, планшете, ноутбуке, ноутбуке и настольном ПК.
Требуемых навыков: Эта стимулирующая головоломка на основе гравитации требует острых навыков аналитического мышления, зрительно-моторной координации, быстрой реакции, наблюдательности и упорной решимости. Умное принятие решений и решение проблем являются ключевыми, когда вы пытаетесь выяснить правильную последовательность устранения препятствий на каждом уровне. Метод проб и ошибок также важен — вы должны извлекать уроки из неудачных попыток и соответствующим образом корректировать свою стратегию!
Сыграть в эту игру
Сыграйте в онлайн-головоломку судоку с тремя уровнями сложности на своем телефоне, планшете, ноутбуке или настольном ПК! Master Sudoku — это увлекательная онлайн-версия классической игры для тренировки мозга, основанной на числах.Играть можно на устройствах Android и в веб-браузерах, есть три уровня сложности: легкий, нормальный или сложный. И новички, и опытные игроки в судоку могут наслаждаться головокружительной игрой, играя на время, чтобы решить каждую головоломку!
Судоку, в которую играют фанатики головоломок со всего мира, представляет собой логическую игру с расстановкой чисел. Если вы не знакомы с этой концепцией, ваша цель — заполнить квадратную сетку 9×9 цифрами так, чтобы каждый вертикальный столбец, горизонтальная строка и подсетка 3×3 содержали числа от 1 до 9 в любом порядке.
Эта онлайн-игра, основанная на HTML5, должна работать на устройствах Android, а также в большинстве веб-браузеров для ПК / Mac. Требуемые навыки включают быструю реакцию (из-за нехватки времени), острые навыки логического и аналитического мышления, способность сосредоточиться на более широкой картине и использовать процесс исключения, чтобы увидеть, какие числа лучше всего подходят для каждой позиции в сетке. Удачной игры в судоку!
Сыграть в эту игру
Проверьте и тренируйте свои навыки аналитического мышления в увлекательной обстановке, а также используйте эффекты гравитации и хорошее время, чтобы безопасно опустить своих мышей! 3 Mice — это увлекательная интерактивная игра-головоломка, основанная на физике, для детей младшего школьного возраста и старшеклассников, где вы должны стратегически и тактично направлять мышей вниз по опасным уступам!
Цель игры — безопасно опустить трех мышей как можно глубже; не проваливаясь через щели и не срываясь с края! Здесь требуется эффективное сочетание физических и психических качеств.Что касается физических навыков, вы должны проявлять хорошие навыки зрительно-моторной координации, рассудительность и расчет времени с помощью тактичного постукивания пальцами. Что касается умственных способностей, важны умное стратегическое планирование, острое аналитическое мышление и логические навыки, творческое решение проблем, хорошие навыки предвидения, высокий уровень концентрации и настойчивость.
Сыграть в эту игру
Tap My Water — это динамичная и увлекательная игра-головоломка, в которой вам предстоит мчаться на время, чтобы заставить работать водопроводные трубы.Но убедитесь, что вы делаете это правильно, иначе вы останетесь насквозь мокрым.
В игре есть несколько головоломок, каждая из которых имеет разную степень сложности. А различные препятствия и бонусы на протяжении всей игры делают ее всегда разной и всегда веселой.
Сыграть в эту игру
Catch the Apple — это простая, но увлекательная игра-головоломка, в которой вам нужно управлять возбудимым ежом и проводить его через несколько сложных уровней. Собирайте яблоки, чтобы выиграть, и не забывайте не торопиться! Это не гонка! Пошли!
Цель этой игры — пройти уровень.Вы делаете это, собирая яблоки и звезды … постарайтесь получить 3/3 звезды на каждом уровне, чтобы показать всем, что вы профессионал! Эта игра проверит ваши навыки суждения, поскольку вам нужно решить, когда лучше всего использовать вспомогательные средства … слишком рано, и вы не сможете в полной мере воспользоваться этим предметом! Кроме того, вам понадобится решимость, потому что иногда единственный способ учиться и совершенствоваться — это ошибиться, а затем учиться на своих ошибках … очень ценный навык в жизни! Наслаждаться!
Сыграть в эту игру
Проверьте свою память в этой веселой игре с парными плитками в милой и приятной пасхальной теме! Easter Card Memory deluxe — это веселая и простая игра-головоломка для детей младшего возраста, в которой вы должны находить и устранять совпадающие пары пасхальных плиток на время.Вы можете играть на мобильном телефоне, планшете, ноутбуке, ноутбуке и настольном ПК. Вам предстоит проходить все более сложные уровни с увеличивающимся количеством плиток в каждом испытании!
Требуемых навыков: Это динамичное занятие, основанное на сопоставлении, требует острого внимания и навыков концентрации, большой решимости и выносливости. Точные щелчки мышью / пальцами очень важны — в зависимости от того, играете ли вы на мобильном телефоне, Android или на компьютере. Ваши навыки памяти также проверяются, когда вы пытаетесь вспомнить, где каждая плитка расположена на сетке.Только не занимайте слишком много времени, потому что часы идут!
Сыграть в эту игру
Создавайте красочные рождественские печенья на заказ в этой обманчиво сложной головоломке, в которую можно играть на iOS, Android, ноутбуках, ноутбуках и настольных ПК! Christmas Cookies Jigsaw — это сложная многоуровневая логическая головоломка. Чтобы решить эту головоломку, вам нужно разместить 64 части в правильном порядке.
Эта онлайн-игра-головоломка на основе HTML5 должна работать на устройствах iOS и Android, а также в большинстве веб-браузеров для ПК / Mac.Требуемые навыки включают хорошее решение проблем, логическое / аналитическое мышление и стратегические навыки. Очень важно определить идеальное место для каждого кусочка печенья.
Сыграть в эту игру
Santa Present Delivery — яркая веселая игра-головоломка, в которой вы собираете Святого Ника и его заснеженную зимнюю страну чудес. Но
Как и все головоломки, эта игра одновременно напряженная и успокаивающая. Дополнительная возможность выбирать уровень сложности делает игру еще более увлекательной и добавляет много веселья, которое можно повторять.
Сыграть в эту игру
Heart Gems Connect — это красочная игра-головоломка, в которой вы объединяете соседние красочные сердца одного цвета в линии по три или более, чтобы удалить их из сетки и набрать очки. Создание совпадения на квадрате также изменяет цвет фона плитки, чтобы вы знали, что на нем есть совпадение. Сердечки можно совмещать по горизонтали, вертикали или диагонали, чтобы создать максимально длинную цепочку. Сопоставление каждого квадрата сетки в заданные временные рамки позволит вам перейти на следующий уровень.Различные уровни становятся все более сложными, с более сложными сетками и более точными временными рамками!
Сыграть в эту игру
Physics Drop — сложная игра-головоломка, в которой вам нужно использовать физику для прохождения уровней. Помогите мячу попасть в корзину в конце и заработайте заслуженную победу.
Сыграть в эту игру
Connecting Pipes 3D — это все о поливе растений. Что в этом может быть сложного? Ну, кажется, совсем немного, потому что эта игра намного сложнее, чем вы думаете.
На каждом уровне есть две вещи: пожарный гидрант, полный жидкости, и растение в горшке, которое нужно поливать. Ваша задача — доставить воду из гидранта на завод по ряду труб, которые вы должны вращать и поворачивать, чтобы выровняться прямо у гидранта. Это должно быть легко, а иногда и бывает, но иногда на самом деле довольно сложно.
Сыграть в эту игру
Coloruid 2 — сложная и уникальная игра, в которой вы очищаете каждый уровень, изменяя весь этап на один цвет.У вас есть ограниченное количество действий на каждом уровне, поэтому не тратьте их зря. Испытайте себя и очистите каждый доступный уровень.
Сыграть в эту игру
Стратегически и тактично убирайте блоки, чтобы доставить голодному желтому блоку вкусную конфету! Catch The Candy — это многоуровневая интерактивная игра-головоломка, основанная на физике, играющая на мобильных устройствах Android, ноутбуках, ноутбуках и настольных ПК, в которой вы должны тщательно изменить игровую среду, чтобы направить вихрь конфет в рот. статичного героя желтого блока.И леденец, и блок не могут двигаться сами по себе, поэтому вам нужно удалить бетонные блоки, чтобы создать импульс и заставить леденец двигаться, используя комбинацию эффекта гравитации и контуров уровня.
Эта игра-головоломка, основанная на физике и гравитации HTML5, должна работать на мобильных устройствах Android, а также в большинстве веб-браузеров для ПК / Mac. Требуемые навыки включают острое аналитическое мышление и навыки решения проблем, тактичное щелканье мышью / постукивание пальцами, хорошие навыки ожидания и быструю реакцию, чтобы быстро вычислить и создать лучший маршрут, по которому леденец достигнет голодного блока.Метод проб и ошибок также вступает в игру, особенно на более поздних уровнях, когда препятствия более сложные, и действия должны выполняться в определенной последовательности.
Сыграть в эту игру
Вы хотите проверить или освежить свои знания в области географии Европы, или, возможно, вы ищете такой инструмент, который поможет вашему ребенку в обучении? Если это так, Scatty Maps Europe — идеальная игра для таких нужд, делающая изучение и географию увлекательными благодаря своей головоломной формуле и забавным фактам. Каждый раз, когда вас просят указать местоположение страны, Scatty Maps Europe предоставит вам некоторую информацию о населении страны и ее столице.Иди учись и получай удовольствие!
Сыграть в эту игру
Dream Book Jigsaw — это красочная и веселая интерактивная игра-головоломка, в которой вы можете сложить яркие и красивые картинки. Есть ли что-нибудь более увлекательное, чем отличная головоломка?
Эта игра похожа на типичную игру-головоломку, но включенные цвета и изображения делают ее еще более увлекательной и идеальной для игроков всех возрастов. Кроме того, вы можете выбрать свой уровень сложности, что является дополнительным бонусом.
Сыграть в эту игру
Устройтесь поудобнее, расслабьтесь и наслаждайтесь разнообразными словесными играми, которые может предложить Microsoft Ultimate Word Game.Играйте в классические игры, такие как Wordament, Word Twister и Crosswords, в увлекательной игре, в которой вы можете расслабиться, сохраняя при этом остроту ума. В Microsoft Ultimate Word Game есть что предложить каждому, в том числе возможность изменить фоновую тему одним из четырех вариантов. Но хватит, приходите поиграть в игру и посмотрите, может быть, однажды вы сможете победить бабушку в кроссвордах.
Сыграть в эту игру
Сыграйте в увлекательную головоломку по удалению блоков на своем мобильном телефоне, планшете, ноутбуке, ноутбуке или настольном ПК, которая сочетает в себе навыки аналитического мышления. Lightbulb Physics — сложная игра, основанная на физике и гравитации, для решения проблем для детей, подростков и взрослых. где вы должны тщательно и методично изменять игровую среду (убирать предметы), пока ваша лампочка не коснется источника электричества.По мере того, как вы достигаете более высоких уровней, это становится все сложнее! Есть 60 прогрессивно сложных уровней. Сможете ли вы победить их всех?
Эта онлайн-игра-головоломка на основе HTML5 должна работать на устройствах iOS и Android, а также в большинстве веб-браузеров для ПК / Mac. Требуемые навыки включают общее понимание законов физики и гравитации, настороженное аналитическое мышление и навыки предвидения.
Сыграть в эту игру
Ловко направьте золотую монету в ожидающую копилку в этой милой, но сложной игре в стиле «перерезай веревку», основанной на времени, и головоломке для мобильных устройств, ноутбуков и настольных ПК! Piggy Bank Adventure — это веселая и увлекательная интерактивная игра, основанная на физике, и сложная головоломка для решения проблем для детей младшего возраста и старшеклассников, где вы должны перерезать веревки, которые привязывают золотую монету к верхней части игровой площадки, и использовать гравитацию и препятствия. , и контуры каждого уровня, чтобы монета попала вниз и в терпеливую розовую копилку внизу игрового экрана.
Piggy Bank Adventure — это игра на основе HTML5, которая должна работать на устройствах iOS и Android, а также в большинстве веб-браузеров для ПК / Mac. Поскольку это действие, основанное на времени, навыки тактичного управления мышью / касания пальцами действительно важны, особенно при работе с движущимися объектами и платформами на более поздних уровнях (всего 24 уровня становятся все более сложными). Другие необходимые ключевые навыки включают терпение, хорошее стратегическое планирование, острую реакцию и навыки аналитического мышления, а также готовность к пробам и ошибкам.
Секретный совет: Вам не нужно плавно вставлять монету в прорезь на спине свиньи, чтобы пройти каждый уровень. Как только монета падает и ударяется в любое место на вершине поросенка, она совершает один отскок и идеально приземляется в щель. Гоша, если бы только мои мячи для гольфа могли это делать!
Сыграть в эту игру
Джеймс Дэвис: Логика в классе, четыре занятия | ПЛАТО
Во многих программах дошкольного образования неформальная и формальная логика не существует как отдельный курс, хотя логическое мышление имеет решающее значение для большей части академической работы.По мере того, как учащиеся получают образование в начальной и средней школе, ожидается, что они будут все больше и больше поддерживать свое мнение хорошо обоснованными аргументами. В то время как школам может быть трудно включить курс логики в свою учебную программу, им может быть проще посвятить небольшие части своих существующих курсов изучению определенных логических инструментов. На протяжении многих лет я часто уделял время своим урокам истории, а также работал с моими коллегами-математиками, чтобы научить логическому мышлению.Однако я часто делал это, используя интерактивные демонстрации, чтобы помочь студентам понять инструменты, которым я обучаю. В этом блоге я поделюсь четырьмя упражнениями, которые учителя могут легко применить, если они захотят добавить логический компонент в свои курсы.
Диаграммы Венна человека
Ученики могут столкнуться с диаграммами Венна на уроках математики. Поскольку довольно много студентов борются с диаграммами Венна, иногда помогает показать им, как визуализировать происходящее, когда они строят диаграммы силлогизмов, особенно когда дело доходит до разработки диаграмм для двух предпосылок.Интерактивный способ сделать это — попросить их поиграть в «человеческие диаграммы Венна».
Начните с рисования диаграммы Венна для силлогизма на полу в классе или на игровой площадке. Для изображения кругов можно использовать различные методы: от скрепления или скрепления цветных ниток мелом и до большого плаката. Чтобы представить затененные области на диаграмме, используйте черную плотную бумагу, которую учащиеся могут поместить в соответствующие области. Затем создайте три категории, применимые к вашим ученикам.Например, «студенты в очках», «студенты в часах» и «студенты с мобильными телефонами». Затем, работая в группах, ученики должны построить несколько силлогизмов, используя категории. Например, одна группа могла бы сформулировать следующий аргумент:
(1) Все студенты, носящие часы, — это студенты, у которых есть мобильные телефоны.
(2) Некоторые студенты, у которых есть мобильные телефоны, — это студенты, которые не носят очков.
(3) Следовательно, ни один ученик, который носит очки, не является учеником, который носит часы.
Назначьте каждому студенту помещение. Затем учащиеся должны встать в правильное место на схеме и при необходимости заштриховать участки с помощью цветной бумаги. Любой студент, стоящий в регионе, означает, что существуют члены этой конкретной категории. Студенты должны разыгрывать одну предпосылку за раз, корректируя свои позиции на диаграмме, когда появляется новая информация из-за второй предпосылки. Наконец, ученик должен стоять в той области, которая представляет вывод на диаграмме.Студенты должны завершить упражнение, объяснив, как их человеческая диаграмма Венна установила достоверность или недействительность силлогизма.
Я успешно использовал этот метод с учениками средней школы, а также со школьниками первого и второго года обучения. Учащиеся считают, что это упражнение, хотя и увлекательное, помогает им лучше представить себе, что происходит на диаграммах. Я рекомендую учителям также получить доступ к пониманию своих учеников, попросив их объяснить, что происходит на их диаграмме, когда они это разыгрывают.Один из способов сделать это — попросить каждого участника рассказать, почему она стоит там, где находится, почему ее заставили переехать в новый регион или почему она использовала черный картон.
Заблуждение дня
Многие из моих студентов с нетерпением ждут, когда узнают о неформальных заблуждениях, если крики « ad hominem! »или« соломенный человек! »в холлах и классах моей школы есть хоть какое-то указание. Действительно, изучение заблуждений имеет неоценимое значение для развития у наших студентов способности оценивать и критиковать аргументы и позиции.
Я часто знакомил своих учеников с неформальными заблуждениями, посвящая около десяти минут классного времени раз в неделю объяснению и обсуждению конкретной ошибки. В течение обычного учебного года, состоящего из тридцати трех недель, учащиеся узнают изрядное количество типичных ошибок в рассуждении. Я обнаружил, что потраченное время часто того стоит, поскольку учащиеся чувствуют себя уполномоченными, распознавая эти заблуждения, и часто будут активно искать их в своих чтениях. Некоторые, естественно, перейдут на «темную сторону», намеренно софистично используя свои новые знания, но, что, возможно, неудивительно, им труднее уйти от манипулирования другими учениками, потому что их сверстники также усвоили заблуждения.Излишне говорить, что это довольно ясно демонстрирует моим ученикам ценность знания заблуждений.
Это помогает усилить ошибочность дня, имея пример этого в чтении, назначенном для того же класса. Например, рассмотрим призыв Папы Урбана II к Первому крестовому походу:
Пусть дела ваших предков вдохновят вас и побудят ваши умы к человеческим достижениям: величию короля Карла Великого и его сына Людовика, а также других ваших монархов, которые разрушили королевства турок и расширили власть Церковь над землями, ранее принадлежавшими язычникам.Пусть святая гробница нашего Господа и Спасителя, которой обладают нечистые народы, особенно возбудит вас и святые места, которые ныне подвергаются бесчестию и непочтительно осквернены нечистыми нечистыми. 1
Если бы ошибкой дня было argumentsum ad популярным, то можно было бы использовать этот текст не только для иллюстрации заблуждения, но и для обсуждения того, почему он был так эффективен.
« Что черепаха сказала Ахиллу»
Учителя, желающие добавить логику в свои классы, могут найти полезными « Алиса Приключения в стране чудес и « Зазеркалье » Льюиса Кэрролла.Моим ученикам интересно читать рассказы, и им также нравится обсуждать, как они в игровой форме используют логику. Один из подходов к использованию Кэрролла — разбить студентов на небольшие актерские труппы, задача которых — разыграть сцену из текста, иллюстрирующую логическую головоломку. После того, как они представят сцену, труппа может либо объяснить ее логическое значение, либо провести остальную часть класса в ее обсуждении.
Кэрролла также можно использовать для обучения студентов логическим парадоксам. Студенты часто испытывают личную потребность разрешить парадоксы Зенона или Рассела, и наличие раздела по ним может помочь студентам понять разницу между противоречием и парадоксом.Я часто пытаюсь показать своим ученикам, что логическое противоречие можно разрешить, просто отказавшись от одного из предложений, вызывающих проблему. Однако с парадоксом я хочу, чтобы мои студенты увидели, что отказ от любого противоречащего утверждения в конечном итоге неудовлетворителен. Парадоксы «Дихотомии» и «Ахиллес и черепаха» особенно беспокоят студентов, поскольку они «знают», что движение возможно, но рассуждения Зенона кажутся правильными.
Студенты также могут сформулировать парадокс для домашнего задания.Их можно либо попросить воспроизвести аргументы Зенона, либо — что еще лучше — попытаться развить свои собственные парадоксы. Студенты найдут последнее трудным, но их усилия могут быть использованы для поучительного обсуждения того, чем противоречие и парадокс отличаются друг от друга.
“ Утка; Утка; Опровергнуть! »
Одно упражнение, которое помогает студентам практиковать публичные выступления и мышление на ногах, является вариантом старой игры «Утка, утка, гусь». Студенты встают в круг, и первый говорит студент с теннисным мячом.Основываясь на чтении, прочитанном накануне вечером, у инструктора должно быть несколько спорных моментов по поводу начального задания. Первый ученик приводит доводы по этому поводу, обычно приводя аргументы за или против. Закончив, она бросает или передает теннисный мяч другому ученику, который должен попытаться опровергнуть позицию первого ученика. Третий ученик пытается защитить первого ученика, опровергая второго, и так далее.
Возьмем, к примеру, знаменитую проблему с тележкой, когда человек должен решить, позволить ли убить пять человек, стоящих на пути сбежавшей тележки, или нажать выключатель, который переключает тележку на другую колею, где убьет только одного. человек.Для этого упражнения первый ученик начал бы с аргументации, например, «человек должен отклонить трамвай, потому что пять жизней стоят больше, чем одна». Затем ученик бросал теннисный мяч другому ученику, который должен был бы возразить против первоначального аргумента: например, «Но убийство одного, чтобы спасти пятерых, нарушает права одного». Затем этот ученик бросал третьему ученику и так далее.
Я считаю, что это упражнение хорошо подходит для мозгового штурма по материалу, но я также использовал его для обучения студентов публичным выступлениям и аргументации на конференциях «Модель Организации Объединенных Наций».В зависимости от размера класса остальные студенты могут выступать в качестве жюри, которое может обсудить и решить, какая сторона аргумента имеет лучшую позицию.
В заключение, для школ, в которых отсутствуют неформальные и формальные курсы логики, эти и другие подобные упражнения могут помочь учащимся развить логическое мышление в увлекательной и минимально навязчивой форме в рамках установленной учебной программы. Студентам будет полезно мыслить более ясно и строго во многих своих курсах, особенно в тех, где формулировка и защита аргументированной позиции имеют центральное значение.
1 Urban II: Речь в Клермоне 1095 (версия Роберта Монаха) доступно по адресу http://www.fordham.edu/halsall/source/urban2a.html
Джеймс Дэвис имеет докторскую степень. Доктор философии в Бостонском университете и преподает философию и историю в Академии Бостонского университета. Он обучал своей логике и работал академическим деканом в Центре программы талантливой молодежи Университета Джона Хопкинса. Он также входит в совет директоров Организации изучения и преподавания философии (PLATO) и в редакционный совет журнала «Вопросы: философия для молодежи».
Comm, Джо — ЦЕЛЬ / Логические головоломки
Сделанные учителем логические головоломки PPT
1. 30-секундные тайны — Учитывая обстоятельства дела, загадочный вопрос и 4 подсказки, можете ли вы разгадывать каждую загадку за 30 секунд или меньше? (Щелкните Загадки 30 секунд, чтобы открыть Power Point. Загрузка занимает несколько секунд.) 2. Головоломки для бокового мышления — Сможете ли вы решить эти загадки, получив загадку и несколько полезных вопросов для размышления? (Щелкните Головоломки для бокового мышления, чтобы открыть Power Point.Загрузка занимает несколько секунд.) 3. Загадки о географии — Попробуйте решить эти рифмующиеся загадки на тему географии. Играйте всей группой или прочитайте загадку и молча запишите свой ответ. (Щелкните Загадки Geoscape, чтобы открыть Power Point. Загрузка занимает несколько секунд.) 4. Другие головоломки с боковым мышлением — Эти головоломки с боковым мышлением немного сложнее, чем приведенные выше. Сможете ли вы принять вызов? Урок Power Point также знакомит с человеком, придумавшим термин «нестандартное мышление», и знакомит с его «Шесть мыслящих шляп».»(Щелкните» Другие головоломки для бокового мышления, чтобы открыть Power Point. Загрузка занимает несколько секунд.) « 5. Логические головоломки — Тип головоломки, в которой ответ может быть выведен или разгадан из заданного набора предпосылок или Факты. В этом уроке Power Point представлены десятки различных примеров головоломок. (Нажмите «Логические головоломки», чтобы открыть Power Point. Загрузка занимает несколько секунд.) 3. Три одинаковых — в этой игре на мышление изучите три элемента перечисляются на экране и выясняют, что у них общего.(Нажмите «Три вида», чтобы открыть.)Логические головоломки онлайн
1. Mindbenders — Mind Benders похожи на загадки, которые вы должны разгадывать. Решите эти 15 загадок ума вместе с партнером или индивидуально. Сделайте столько, сколько сможете, а затем мы соберемся вместе и проверим ответы. Возможно, вам придется разыграть это, нарисовать картинку или использовать другие методы решения проблем, но вам определенно придется мыслить нестандартно. (Щелкните здесь, чтобы открыть: http: // www.cimt.plymouth.ac.uk/resources/puzzles/mindbend.htm. Предупреждение: нажатие «Ответить» открывает все 15 ответов.)
Цифровые математические задания для учеников начальной школы
В этом сообщении блога рассказывается о любимых упражнениях по цифровой математике NO PREP для учащихся начальных классов, которые можно использовать в Google Classroom для дистанционного обучения.
2020 год был удачным для всех, но особенно для учителей! Мы никогда не могли себе представить, что покидаем наши школы и классы, чтобы учить дома и общаться с нашими учениками только через Интернет.Но именно там мы находимся сегодня и ищем способы заставить это работать!
Несмотря на то, что дистанционное обучение сопряжено со множеством проблем, одна из них кажется большой — это выяснить, как предоставить учащимся качественные, увлекательные и сложные задания, которые они могут выполнять дома без вас.
Чтобы облегчить вам задачу, я создал БЕСПЛАТНЫХ цифровых обновлений некоторых из моих самых популярных занятий по чтению, письму и математике.Они мотивируют и бросают вызов студентам, обеспечивают надлежащую поддержку за счет естественной дифференциации и ZERO PREP для вас!
Сегодня я рад поделиться с вами подробностями о ЦИФРОВЫХ ВЕРСИЯХ моих Cognition Coins и Cognition Cube Logic Puzzles!
Эти логические головоломки с монетами представляют собой сложную математическую задачу для учащихся, которые узнали значение и могут считать смешанный набор монет (пенни, никель, десять центов, четверть).Учащиеся используют логические подсказки, чтобы расположить монеты на карточках с заданиями для самопроверки. Набор головоломок с монетами познания становится все сложнее, что делает задачи сложными, но доступными для учащихся .
Замечательная новость заключается в том, что теперь они включают ЦИФРОВЫЕ логические головоломки, отформатированные для учащихся, которые могут использовать их с Google Drive на iPad и настольных компьютерах! Если вы ранее приобрели версию для печати логических головоломок, , цифровое обновление для вас БЕСПЛАТНО ! Перейдите к своим покупкам, чтобы повторно загрузить цифровые файлы!
Если у вас еще нет этого ресурса, вы можете получить как распечатанные, так и цифровые пазлы ниже.
Эти головоломки — отличное математическое задание, которое будет держать учеников интересными и оттачивать навыки критического мышления. Головоломки идеально подходят, чтобы помочь ученикам научиться настойчиво решать сложные задачи.
Cognition Cubes Bundle 1 и 2 включает 56 головоломок и ориентирован на учеников 1 и 2 классов. Набор кубиков познания 3 и 4 включает 40 головоломок и ориентирован на учеников 3-го и 4-го классов. Все головоломки теперь доступны в ЦИФРОВОЙ форме для учащихся, которые могут использовать Google Диск на своих компьютерах и планшетах! Ух-у!
Если вы ранее приобрели версию для печати логических головоломок куба, цифровое обновление для вас БЕСПЛАТНО ! Перейдите к своим покупкам, чтобы повторно загрузить цифровые файлы!
Если у вас еще нет этого ресурса, получите приведенные ниже пазлы для печати и в цифровом формате.
Эти два цифровых математических ресурса станут прекрасным дополнением к вашему дистанционному обучению!
Во-первых, они оба требуют НУЛЕВОЙ подготовительной работы ! Все, что вам нужно сделать, это четко смоделировать, как выполнять действия. Структура каждой головоломки остается неизменной, поэтому, когда они решат одну, они могут независимо работать со слайдами в любом темпе, который вы им назначите!
Набор Cognition Coin Counting включает 40 различных логических головоломок , а набор Cognition Cube включает 96 головоломок !! Это ресурсы, с которыми студенты могут работать долгое время!
Во-вторых, эти головоломки сложные, ! Многие из нас упорно трудились, чтобы помочь нашим ученикам развить установку на рост.При этом мы создали классы, в которых студенты с готовностью принимают вызовы. Теперь, когда мы учим издалека, мы должны найти задачи и действия, которые заставят их упорно продолжать. Эти головоломки бывают разных уровней, поэтому вы можете убедиться, что все учащиеся мотивированы усердно трудиться и получают соответствующие вызовы.
Несмотря на то, что за последние месяцы многое изменилось, эти упражнения по цифровой математике могут предоставить вашим ученикам задачу, к которой они привыкли в вашем классе.Я надеюсь, что вы сочтете их полезными и что вы сможете с удовольствием их назначать!
1
— ПИН для ПОЗЖЕ —
Обучающих игр и головоломок для развлечения
Включение обучающих игр и головоломок в сегодняшнюю школьную программу — отличный способ заложить основы языковых и математических навыков. Этот сборник материалов для учителей для детей веселый, бесплатный и учит детей основам обучения для учащихся начальной и средней школы.Обучающие игры и головоломки могут развить навыки в языковых искусствах, математике, социальных науках, науках и многом другом. Используйте следующие ресурсы, чтобы найти образовательные инструменты для ваших планов уроков и сделать обучение интересным.
Головоломки
Пазлы
- Поисковые запросы, печатные формы и рабочие листы: Найдите различные варианты поиска слов, посвященные животным, книжной тематике, праздникам, математике, навыкам и т. Д.
- Brain Bashers: найдите широкий спектр логических головоломок японского типа, которые обновляются ежедневно.
- Пазлы для печати: Коллекция тематических пазлов для печати на праздники, времена года и многое другое.
- Неврология для детей: рабочие листы для печати по нейробиологии, включая головоломки с поиском слов, кроссворды и связанные с ними уроки.
- Математические и логические головоломки. На этой веб-странице представлены разнообразные математические и логические головоломки, такие как головоломки с измерением и симметрией.
- Математические загадки: Большой выбор математических загадок от простых до очень сложных по различным математическим подтемам, таким как геометрия и вероятность.
- Короткие загадки Покойо: список забавных загадок для учеников начальной и средней школы, которые помогут им задуматься.
- Загадки для пищевых групп: эти загадки можно включить в планы уроков, касающихся фруктов, овощей и питания.
Иллюзии
Другие образовательные развлечения
- Игры и головоломки: На этой образовательной странице есть научные игры, игры с элементами, математические игры и другие забавные игры и головоломки для учащихся.
- Обучающие видео, уроки и игры. Учителя средней школы могут использовать эти видео, задания и игры по естествознанию, математике, общественным наукам и английскому языку в своей повседневной учебной программе.
- Популярные печатные игры и головоломки: здесь вы найдете традиционные игры для средней школы, такие как кроссворды с положениями и поиск слов на теле человека.
План урока логики | Study.com
Продолжительность
2 — 2,5 часа
Стандарты учебных программ
- CCSS.ELA-LITERACY.RST.11-12.3
Точно соблюдайте сложную многоступенчатую процедуру при проведении экспериментов, измерений или выполнении технических задач; проанализировать конкретные результаты на основе пояснений в тексте.
Материалы
- Компьютер с проектором
- Экземпляры викторины урока
- листов судоку — достаточно, чтобы у каждой пары учеников было 2
- Бумага для принтера
- Линейки
- Прозрачность логической головоломки
Инструкция
- В начале урока расскажите ученикам, что существуют всевозможные головоломки. В молодости они могли решать простые головоломки с картинками.Есть головоломки посложнее, требующие использования логики.
- Объясните своим ученикам, что они узнают больше о решении логических головоломок, просмотрев видео-урок «Использование логики и стратегии для решения головоломок».
- Включите урок для учащихся и периодически приостанавливайте его для обсуждения.
- Начните видео с начала и приостановите его на 0:55, затем спросите и обсудите следующее:
- Что такое головоломка судоку?
- Какие числа должны появиться в подсетке головоломки Судоку?
- Что такое логические головоломки?
- Что вам дают для решения логических задач?
- Продолжите воспроизведение видео и снова поставьте его на паузу в 2:40, затем спросите и обсудите:
- Что такое логика?
- Сколько раз можно использовать число в строке или столбце в головоломке Судоку?
- Как сетка помогает решать логические головоломки?
- Продолжайте воспроизведение видео и снова поставьте его на паузу в 3:58, затем спросите и обсудите следующее:
- Что такое стратегия?
- Какова стратегия решения головоломок судоку?
- Что такое стратегия решения логических задач?
- Продолжайте воспроизведение оставшейся части видео, а затем ответьте на любые вопросы, которые могут возникнуть у учащихся на этом этапе.
- Проецируйте на доске прозрачную логическую головоломку.
- Решите логическую головоломку вместе как класс. Убедитесь, что вы ответили на любые вопросы или затруднения при решении головоломки .
Головоломки Судоку
- Соедините своих учеников
- Раздайте каждой паре по 2 головоломки судоку
- Объясните своим ученикам, что они должны решать головоломки вместе. Им следует записать свою стратегию решения головоломки по мере ее решения.Стратегия должна быть пошаговой.
- Каждая пара должна предоставить вам на проверку свои головоломки, а также свои пошаговые стратегии.
Создайте свое собственное судоку
- Раздайте каждой паре учеников несколько листов бумаги для принтера и линейку
- Объясните своим ученикам, что они собираются вместе создавать свои собственные головоломки Судоку.
- После того, как пары составили свои головоломки, попросите их передать их паре слева от них, чтобы они решали ее.
- Как только они будут решены, пары должны передать головоломки обратно паре, которая их создала, чтобы они проверили их точность.
Оценка
- Попросите каждого учащегося пройти тест на уроке
- Просмотрите ответы на викторины после того, как все учащиеся завершат свои тесты
Обучение дедуктивному мышлению — Логические головоломки для детей
Логические головоломки строят дедуктивные рассуждения — и это весело! Во-первых, научите своих детей исключать возможности.Таким образом, они могут найти решения. Затем научите их создавать свои собственные ситуации и подсказки.
Мисс Снид учит логическим головоломкам
Наша любимая учительница четвертого класса, г-жа Снид, стояла в передней части своего класса. «Сегодня, — сказала она, — мы продолжим нашу таинственную деятельность».
Все приветствовали. В начале своего загадочного подразделения они играли в игры-наблюдения. Затем взломали секретные коды. Совсем недавно класс поигрался с невидимыми чернилами и отпечатками пальцев.Одно можно сказать наверняка: им это понравилось!
«Кто решил логическую головоломку?» — спросил учитель. Несколько рук взлетели в воздух. Однако многие студенты выглядели неуверенно.
«Это включает дедуктивное рассуждение, — продолжила г-жа Снид. «Сначала вам будет представлена ситуация. Например, в нашей первой головоломке четыре человека владеют четырьмя домашними животными. С помощью всего лишь нескольких подсказок вы узнаете, кому какое животное принадлежит ». Говоря, она ходила по комнате, раздавая страницы.
Вы чувствуете себя «воодушевленным»? Не стесняйтесь прикреплять изображения из этого сообщения.
«Кто-нибудь может подсказать? Как вы будете использовать эту сетку? » Поднялось несколько рук.
«Вы используете чеки и бывшие», — крикнула девушка с косичками. «Если это неправда, поставьте бывшего. Но если это правда, поставьте галочку. Кроме того, если в строке или столбце остался только один пробел, это должно быть верно ».
Мисс Снид кивнула. «Отличный совет! А теперь приступим. Она ходила по комнате, помогая детям, которые были новичками в этой концепции.
Дети играют онлайн
В течение следующей недели ученики решили еще пять логических головоломок.Сначала некоторые с подозрением относились к процессу. Однако вскоре они потребовали большего.
«Некоторые из вас готовы к более серьезным испытаниям», — сказала г-жа Снид своему классу. «Поэтому я отправил вам ссылку на Puzzle Baron’s Logic Puzzles. Вы можете выбрать свой уровень сложности. Но предупреждаю, это вызывает привыкание! »
Класс делает свои собственные логические головоломки
На следующий день мисс Снид приготовила сюрприз для своего класса. «Сегодня мы составим наши собственные логические головоломки».
Ее ученики удивленно переглянулись.Некоторые выглядели в приподнятом настроении; другие немного напуганы.
«Позвольте мне рассказать вам об одном», — сказал их учитель. Она показала пустой стол.
«Я поделился с вами этим мероприятием TpT Digital. Как видите, это часть наших таинственных мероприятий «. Она указала на тему «Думай как детектив» вверху страницы.
Начало работы
«Сначала вы определите ситуацию и подумаете, какие подсказки вы будете использовать. Например, я выбрал ситуацию с ужином на День Благодарения.Она печатала во время разговора. «За круглым столом сидят пять членов семьи. У каждого есть любимый гарнир. Чтобы выяснить, кому что нравится, я буду использовать их позиции за столом, пол и категории еды.
«Во-вторых, вы пометите первый столбец и строку». В первом столбце она напечатала имена. «Как видите, я использую имена, которые помогают людям соответствовать полу. Другими словами, я бы не стал использовать такое имя, как Крис. Почему? Очевидно, это имя нейтрально с гендерной точки зрения ». Затем она написала пять продуктов в первой строке.«Кроме того, я выбираю продукты, которые можно разделить на категории. Например, картофель, начинка, макароны с сыром содержат крахмал. Кроме того, овощами являются картофель и стручковая фасоль. Вы уловили идею.
Мисс Снид отметила по одному продукту для каждого человека. «Наконец, я отмечаю, кому что нравится».
Добавление подсказок
Учитель глубоко вздохнул. «Хорошо, теперь мы добавим подсказки. Это сложная часть. Мы не хотим, чтобы подсказки были слишком простыми или слишком сложными. Вместо этого используйте принцип Златовласки: в самый раз.”
Она сделала еще один вдох. «Допустим, Рут не любит крахмалистую пищу. Это заставляет их задуматься. Но не так уж сложно отказаться от картофеля, начинки, макарон с сыром ».
Мисс Снид поставила бывших за эти блюда рядом с именем Рут.
«Вы также можете использовать простые подсказки. Например, мы просто скажем им, что Том любит картошку ». Она обвела чек в этой коробке и выделила Тома всю остальную еду. Кроме того, она выгнала картошку для всех остальных.
г-жаСнид на мгновение остановился. «Хм. Затем давайте попробуем что-нибудь с полом. Если мы скажем, что мама Квентина любит стручковую фасоль, это исключает и Квентина, и Тома. Мы также скажем, что Сиара их не любит ».
Мисс Снид напечатала еще одну простую подсказку. «Если мы скажем, что Мария любит овощи, у нас останется только две коробки».
«Напоследок скажем, что у Марии аллергия на сыр. Та-да! » Мисс Снид сияла от своей логической головоломки и поклонилась. Подыгрывая, ее ученики громко аплодировали и аплодировали.
Наслаждайтесь преподаванием
На протяжении своей карьеры г-жа Снид осознала, что есть 6 шагов, чтобы получить удовольствие от преподавания. Чтобы выжить, ей нужно было организовывать, планировать и упрощать. Затем, чтобы преуспеть, мисс Снид нужно было учиться, участвовать и, наконец, погрузиться в жизнь! Следите за сказочными обучающими приключениями г-жи Снид и узнайте, как вы тоже можете получать удовольствие от преподавания.
.