ГДЗ Математика 5 класс. Ответы и решения по Математике для 5 го класса на VipGDZ.ru
Еще со времен появления школ, в учебном процессе образовался такой раздел, как домашняя работа. Эта часть обучения всегда приносила немало трудностей школьникам. Больше всего их возникало с такой сложной дисциплиной как математика, по которой ученики 5 класса получают около десяти упражнений на домашнее выполнение. Но это было раньше. С момента появления специально разработанных учебных пособий – ГДЗ, облегчающих процесс усвоения знаний, математика стала для учеников легким и интересным предметом.
О том, как же влияют решебники на обучение пятиклассников, спорили довольно долго. Результат дискуссий показал, что ГДЗ за пятый класс приносят только положительное воздействие и на учебу, и на самих детей. Школьники, работая с такими справочниками, не только улучшают оценки, а как результат, и общую успеваемость, но и укрепляют свои личностные характеристики. Среди них, главным образом, выделяются: самостоятельность, уверенность в себе и желание добывать новые знания.
Из чего же сделаны ответы по математике?
Все плюсы работы с решебниками стали возможными благодаря их правильной и эффективной структуре. ГДЗ по математике выпущенные для 5 класса обладают очень похожей структурой. Как принято, эти книги начинаются из содержания. Данная часть хоть и небольшая, но очень хорошо помогает с поиском нужных заданий. Потом в ГДЗ по математике за 5 класс представлены полные решения упражнений, во всех возможных вариантах. Они демонстрируются в развернутой форме, чтобы ученик без труда смог проследить за алгоритмом применения правила.
Дальше идут правильные ответы на задачи. Главная их роль заключается в предоставлении возможности ученикам 5 класса самостоятельно проверять свои работы и, находя ошибки, исправлять их. В самом конце пособия находится список литературы, с помощью которого достаточно просто искать какие-то дополнительные материалы по теме, вызвавшей интерес ученика.
Основной проблемой родителей и школьников становится поиск качественных решебников.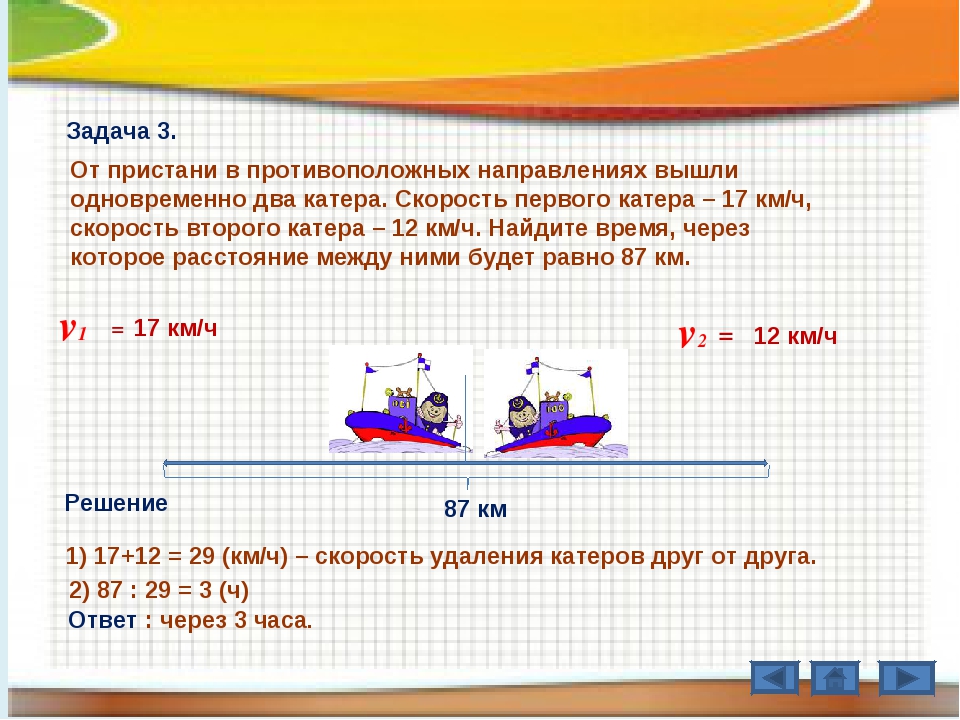
Но, наш сайт VIPGDZ.ru навсегда избавит от этих трудностей, ведь на его страницах находятся только тщательно подобранные книги такого формата.
Самое надежное место, где поселились правильные решения
Наш сайт VIPGDZ.ru завоевал доверие и взрослых, и детей, в первую очередь, благодаря большому количеству плюсов, которые приносит сотрудничество с ним. Главным достоинством нашего портала VIPGDZ.ru можно считать огромный ассортимент различных учебных материалов на его страницах. Сайт богат не только на решебники по математике за 5 класс, но и на учебники. Стоит отметить, что все книги на ресурсе полностью соответствуют требованиям Министерства образования. Отличным бонусом VIPGDZ.ru являются различные дополнительные материалы, которые предоставляет наш сайт. Среди них находятся увлекательные и интересные статьи, которые будут полезными не только школьникам 5 класса, но и их родителям, а также учителям.
Важным аспектом работы с материалами на нашем ресурсе VIPGDZ.ru считается то, что доступ ко всем книгам на нем можно получить абсолютно бесплатно.
Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах
Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.
Рассылка «Мела»
Мы отправляем нашу интересную и очень полезную рассылку два раза в неделю: во вторник и пятницу
Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.
Для развития мышления и речи детей начинать лучше с арифметического способа решения.
Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.
Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?
Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:
6: 2 = 3 кг.
Сахара надо взять 3 такие же части, то есть:
3 ∙ 3 = 9 кг.
Ответ: 9 кг.
В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.
Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?
Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.
1) Сколько частей составляют 120 книг?
1 + 3 = 4 (части).
2) Сколько книг приходится на 1 часть?
120: 4 = 30 (книг).
3) Сколько книг приходится на первую полку?
30 ∙ 3 = 90 (книг).
Ответ: 90 и 30 книг.
Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.
Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына. Сколько лет сыну сейчас?
Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.
Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.
В заключение задача посложнее.
Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов.
Решение:
1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,
2) 1800: 9 = 200 (г) — приходится на 1 часть,
3) 200 ∙ 4 = 800 (г) — было яблок,
4) 200 ∙ 3 = 600 (г) — было груш,
5) 200 ∙ 2 = 400 (г) — было слив.
Ответ: 800, 600 и 400 г.
Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.
Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?
Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.
1) 1 + 2 = 3 (части) — приходится на 36 книг,
2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),
3) 36 — 12 = 24 (книг) — стало на 2-й полке.
Вернём три книги на первую полку.
4) 12 + 3 = 15 (книг) — было на первой полке первоначально,
5) 24 — 3 = 21 (книга) — была на второй полке первоначально.
Ответ: 15 и 21 книга.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.Я. за 1, 2, 3 и 4 четверти
Дата публикации: .
Самостоятельные на темы: «Натуральные числа и их обозначения», «Сложение и вычитание натуральных чисел», «Сравнение натуральных чисел», «Отрезок, прямая, луч», «Умножение натуральных чисел», «Деление натуральных чисел», «Выражения и уравнения», «Квадрат и куб числа», «Окружность и круг», «Обыкновенные дроби», «Сравнение дробей» и др.
Некоторые понятия к учебному материалу.
1. Натуральные числа – используются для счета предметов в повседневной жизни.2.
Отрезок. Длина отрезка – расстояние между его крайними точками, концами. Обозначается заглавными латинскими буквами, например AB.4. Единичный отрезок – отрезок с длиной равной единице.
5. Меньше и больше. Меньше, число, которое при счете называется раньше. Больше, число, которое при счете называется позже.
6. Слагаемые числа – числа, которые складываются.
7. Вычитание. Число из которого вычитают – это уменьшаемое. Число, которое вычитается – это вычитаемое. В итоге получаем разность.
Самостоятельная работа №1 (входная работа на повторение)
Вариант I.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 699.б) Определите натуральное число, которое на две единицы меньше числа 1001.
г) Определите натуральное число, которое на единицу меньше числа 394 000.
2. Решите задачу.
3. Решите примеры.
| а) 492 + 1 220 = | б) 3 495 — 593 = |
| в) 5112 : 6 = | г) 56 * 23 = |
Вариант II.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 879.б) Определите натуральное число, которое на единицу меньше числа 2 000.
в) Определите натуральное число, которое на единицу больше числа 722 999.
г) Определите натуральное число, которое на единицу меньше числа 24 000.
2. Решите задачу.
Рыбаки за первую неделю поймали 395 кг рыбы, а за вторую неделю – 239 кг. На сколько кг было поймано меньше за вторую неделю, чем за первую?3. Решите примеры.
| а) 638 + 1 445 = | б) 6 112 — 2 598 = |
| в) 2688 : 3 = | г) 24 * 45 = |
Вариант III.
1. Определение числа.
б) Определите натуральное число, которое на единицу меньше числа 3 000.
в) Определите натуральное число, которое на единицу больше числа 28 999.
г) Определите натуральное число, которое на единицу меньше числа 12 000.
2. Решите задачу.
В огороде посадили 2 грядки помидор. С первой грядки было собрано 427 помидор, а со второй грядки – 311. На сколько меньше помидор было собрано со второй грядки, чем с первой?3. Решите примеры.
| а) 455 + 3 412= | б) 5 332 — 593 = |
| в) 3648 : 8 = | г) 29 * 41 = |
Самостоятельная работа №2 на тему: «Натуральные числа и их обозначения»
Вариант I.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 20;б) число 49.
2. Представьте следующие словосочетания в числовом виде.
а) Шесть миллиардов пятьсот три тысяча семь.
б) На единицу больше чем пятьсот девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 2, 3 и 7.b) 4, 0 и 9.
Вариант II.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 60;б) число 38.
2. Представьте следующие словосочетания в числовом виде.
а) Восемь миллиардов триста одна тысяча три.б) На единицу больше чем сто девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 1, 3 и 9.b) 2, 4 и 0.
Вариант III.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 30;б) число 58.
2. Представьте следующие словосочетания в числовом виде.
а) Два миллиарда шестьсот два миллиона триста.
б) На единицу больше чем семьсот пять тысяч девятьсот девяносто восемь.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 5, 2 и 8.b) 1, 3 и 0.
Самостоятельная работа №3
Вариант I.
1. Переведите из одной единицы измерения в другую.
| а) 8 дм 43 см = … см | б) 5 км 549 м = … м |
| в) 7 см 18 мм = … мм | г) 249 см =… дм … см |
2. Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D. AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 18 столбах, расстояние между столбами составляет пять метров. Каково расстояние между шестым и четырнадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте точкой T середину стороны BC. Соедините точки B и D, А и T. Выпишите все многоугольники, которые образовались.
Вариант II.
1. Переведите из одной единицы измерения в другую.
| а) 4 дм 23 см = … см | б) 25 км 50 м = … м |
| в) 16 см 65 мм = … мм | г) 456 см =… дм … см |
2. Начертите отрезок AB, равный 15 см 4 мм, отметьте на нем точки C и D. AC равен 8 см 2 мм, CD равен 3 см 7 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 19 столбах, расстояние между столбами составляет 4 метра. Каково расстояние между третьим и восьмым столбами?4. Начертите четырехугольник ABCD. Отметьте середину AB и поставьте точку N. Проведите отрезки DN и АС. Выпишите все многоугольники, которые образовались.
Вариант III.
1. Переведите из одной единицы измерения в другую.
| а) 19 дм 5 см = … см | б) 21 км 678 м = … м |
| в) 43 см 8 мм = … мм | г) 503 см =… дм … см |
2. Начертите отрезок AB, равный 13 см 2 мм, отметьте на нем точки C и D.
AC равен 7 см 3 мм. CD равен 3 см 6 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 16 столбах, расстояние между столбами составляет 3 метра. Каково расстояние между пятым и одиннадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС. Выпишите все многоугольники, которые образовались.
Самостоятельная работа №4 на тему: «Сравнение натуральных чисел»
Вариант I.
1. Сравните числа.
| а) 3 485 660 … 3 458 660 | б) 303 559 … 330 559 |
| в) 2 596 440 … 2 569 440 | г) 45 696 … 44 696 |
2. Представьте в виде двойного неравенства: 18 т 347 кг … 18 т 4 ц 59 кг … 18 568 кг.
Вариант II.
1. Сравните числа.
| а) 34 686 887 … 34 868 887 | б) 3 855 … 3 585 |
| в) 40 955 999 … 40 595 999 | г) 455 776 … 445 776 |
2.
Представьте в виде двойного неравенства: 13 км 845 м … 14675 м … 13 км 845 м 3 дм.
Вариант III.
1. Сравните числа.
| а) 678 881 … 687 881 | б) 782 223 … 728 223 |
| в) 2 490 606 … 2 490 660 | г) 13 799 … 13 977 |
2. Представьте в виде двойного неравенства: 15 т 475 кг … 15657 кг … 157 ц 35 кг.
Самостоятельная работа №5 на тему: «Сложение и вычитание натуральных чисел»
Вариант I.
1. Выполните сложение.
| а) 348 588 667 + 239 586 394 = | б) 93 955 483 + 495 868 991 = |
| в) 23 394 596 + 5 697 345 = | г) 3 949 532 + 405 669 = |
2. Выполните вычитание.
| а) 348 588 667 — 283 745 733 = | б) 93 955 483 — 22 394 583 = |
| в) 23 394 596 — 192 485 = | г) 3 949 532 — 4 348 483 = |
3. Решите задачу.
Мастерская закупила 560 гаек. На ремонт первой машины потребовалось 203 гайки, а на ремонт второй машины – еще 293 гайки.
Сколько гаек осталось в мастерской?4. Решите задачу.
В концертном зале стояло 454 стула. Для проведения концерта принесли 123 новых стула, а после антракта – еще 13 стульев. Сколько всего стульев стало в концертном зале?Вариант II.
1. Выполните сложение.
| а) 3 484 558 + 9 499 834 = | б) 93 955 483 + 394 585 665 = |
| в) 3 495 863 + 35 384 588 = | г) 5 697 291 + 34 405 669 = |
2. Выполните вычитание.
| а) 4 856 342 — 3 495 384 = | б) 283 495 864 — 232 485 965 = |
| в) 5 965 493 — 3 449 594 = | г) 23 455 303 — 19 485 588 = |
3. Решите задачу.
В рулоне было смотано 327 м ленты. В первый день использовали 103 м, а во второй день – ещё 205 м. Сколько метров осталось в рулоне?4. Решите задачу.
В магазине находилось 4 т 150 кг сахара. В первый день привезли 340 кг сахара, а во второй день – еще 4 ц сахара. Сколько кг сахара стало в магазине?Вариант III.
1. Выполните сложение.
| а) 2 399 388 + 239 586 394 = | б) 435 483 + 495 868 991 = |
| в) 34 567 784 + 13 412 345 = | г) 6 563 544 + 23 876 554 = |
2. Выполните вычитание.
| а) 455 586 661 — 283 745 733 = | б) 40 954 586 — 22 394 583 = |
| в) 495 568 222 — 448 568 338 = | г) 3 949 532 — 2 349 588 = |
3. Решите задачу.
В моток смотано 459 м провода. В первый день истратили 119 м, а на второй день – 239 м провода. Сколько метров провода осталось в мотке?4. Решите задачу.
На складе находилось 3 т и 450 кг муки. В первый день привезли 560 кг, через неделю привезли еще 5 ц муки. Сколько кг муки стало на складе?Самостоятельная работа №6
Вариант I.
1. Найдите значение выражения: ( а + 46 ) : ( b — 48 ), если а = 35 и b = 57.
2. Упростите выражения.
а) с + 239 — 93;б) 485 — 483 + d.
3. Составьте уравнение для решения задачи и решите его.
4. Решите уравнения.
a) (305 — ( ( 45 + х ) — 32 ) + 96 = 223;б) 38 + ( 69 — y ) + 74 = 172.
Вариант II.
1. Найдите значение выражения: ( а — 34 ) * ( b + 9 ), если а = 60 и b = 11.
2. Упростите выражения.
а) 594 — 69 — а;б) 149 + b — 54.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 424, а затем прибавили число 392. В итоге, получилось число 632. Какое число было задумано?4. Решите уравнения.
a) 209 — ( ( 145 + х ) — 12 ) + 96 = 123;б) 18 + ( 159 — y ) + 34 = 172.
Вариант III.
1. Найдите значение выражения: ( а — 68 ) : b + 2 339, если а = 92 и b = 8.
2. Упростите выражения.
а) с + 239 — 193;б) 485 — d + 384.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число.
Из этого числа вычли число 209, а затем прибавили число 47. В итоге, получилось число 217. Какое число было задумано?4. Решите уравнения.
a) ( 111 — ( 45 + х ) ) + 96 = 123;б) 29 + ( 59 — y ) + 15 = 72.
После завершения второй четверти, учащиеся должны:
1. уметь умножать натуральные числа и использовать эти знания;
2. уметь производить деление натуральных чисел, в том числе и деление с остатком, и использовать эти навыки при решении задач;
3. знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
4. знать, что такое возведение числа в степень. Понимать, что такое корень и куб числа;
5. понимать, что такое формула, и как производить вычисления по формуле.
Самостоятельная работа №7 на тему: «Действия с натуральными числами. Умножение»
Вариант I.
1. Выполните умножение.
| а) 283 * 46 = | б) 29 * 473 = | в) 841 * 93 = | г) 19 * 632 = |
| д) 570 * 340 = | е) 930 * 730 = | ж) 5100 * 360 = | з) 560 * 230 = |
2.
Умножьте числа, используя наиболее удобный порядок действий.
б) 4 * 324 * 25 * 300 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 35 * 34 = | 34 * 33 = | 34 * 36 = | 32 * 32 = |
4. Решите задачу.
В двухэтажной школе всего 32 кабинета и в каждом кабинете по 12 парт. В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?Вариант II.
1. Выполните умножение.
| а) 342 * 57 = | б) 64 * 268 = | в) 342 * 89 = | г) 32 * 864 = |
| д) 920 * 560 = | е) 470 * 990 = | ж) 2300 * 630 = | з) 430 * 540 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 500 =б) 4 * 265 * 25 * 200 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 85 * 84 = | 84 * 83 = | 84 * 86 = | 82 * 82 = |
4. Решите задачу.
В поселке построено 18 домов. Из них 4 трехэтажных, 6 двухэтажных, остальные одноэтажные дома. В трехэтажных домах – 18 окон, в двухэтажных – 14 окон, в одноэтажных – 8 окон. Сколько окон необходимо для 4 таких же посёлков?Вариант III.
1. Выполните умножение.
| а) 563 * 24 = | б) 32 * 441 = | в) 324 * 87 = | г) 23 * 728 = |
| д) 220 * 680 = | е) 240 * 580 = | ж) 7500 * 290 = | з) 920 * 630 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 300 =б) 4 * 641 * 25 * 100 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 65 * 64 = | 64 * 63 = | 64 * 66 = | 62 * 62 = |
4. Решите задачу.
В один мешок помещается 26 кг картофеля, или 34 кг муки, или 38 кг сахара.
Сколько всего весит груз, если в машину погрузили 32 мешка картофеля, 38 мешков муки и 52 мешка сахара?Самостоятельная работа №8 на тему: «Деление натуральных чисел»
Вариант I.
1. Выполните деление.
| а) 475 860 : 5 = | б) 8 412 : 4 = | в) 492 000 000 : 1 000 = |
| г) 270 930 : 3 = | д) 386 240 : 5 = | е) 19 688 : 23 = |
2. Решите уравнения.
| а) X : 85 = 2 210 | б) 36 690 : Y = 10 | в) 792 : X = 4 |
| г) 15 * ( 39 : X ) = 45 | д) Y : 42 = 168 | е) 65 065 : Y = 1 001 |
3. Решите задачу.
Фермеру необходимо вспахать поле размером 318500 м. За сколько дней он вспашет поле, если известно, что за день он может вспахать 45 500 м?4. Остаток равен 18, неполное частное – 35 и делитель – 23. Найдите делимое.
Вариант II.
1. Выполните деление.
| а) 489 560 : 5 = | б) 36 690 : 3 = | в) 657 000 : 1 000 = |
| г) 960 552 : 6 = | д) 522 240 : 2 = | е) 67 065 : 85 = |
2.
Решите уравнения.
| а) X : 26 = 456 | б) 4 760 : Y = 85 | в) 792 : X = 8 |
| г) 35 * ( 54 : X ) = 315 | д) Y : 3 = 3015 | е) 524 : Y = 131 |
3. Решите задачу.
Станок производит 1200 заготовок за 1 час. Сколько минут нужно машине, чтобы приготовить 48 000 заготовок?4. Остаток равен 33, неполное частное – 41 и делитель – 25. Найдите делимое.
Вариант III.
1. Выполните деление.
| а) 236 560 : 4 = | б) 36 690 : 6 = | в) 612 345 000 : 1 000 = |
| г) 960 440 : 8 = | д) 678 350 : 2 = | е) 31 464 : 69 = |
2. Решите уравнения.
| а) X : 25 = 14 | б) 1 820 : Y = 28 | в) 1 836 : X = 6 |
| г) 52 * Y = 468 | д) Y : 3 = 7 659 | е) 1048 : Y = 131 |
3. Решите задачу.
Комбайн убирает 30 га пшеницы за 1 час. Сколько дней ему нужно, чтобы убрать площадь равную 1200 га, если в день он будет работать по 10 часов?4.
Остаток равен 24, неполное частное – 25 и делитель – 28. Найдите делимое.
Самостоятельная работа №9 на темы: «Выражения, уравнения и решение уравнений», «Квадрат и куб числа»
Вариант I.
1. Решите примеры.
а) 34 + ( 239 — 606 : 6 ) * 4 — 393 : 3 =б) 152 =
в) 73 =
г) ( 14 + 7 )2 — ( 5 + 13 )2 + 287 =
2. Упростите выражение и найдите его значение при с=34: 47с + 34 — 58 + 12с — 58.
3. Решите уравнения.
а) 15 * х = 945б) 3 * y — 45 = 44
4. Решите задачу.
Бабушка и внучка слепили 124 пельмени. Сколько пельменей слепили бабушка и сколько внучка, если бабушка лепила в 3 раза быстрее, чем внучка?Вариант II.
1. Решите примеры.
а) 472 — ( 29 + 124 : 4 ) — 72 : 8 =б) 182 =
в) 63 =
г) ( 5 + 27 )2 — ( 4 + 12 )2 — 64 =
2. Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
3. Решите уравнения:
а) 15 * х = 180б) 12 * y + 36 = 96
4. Решите задачу.
Инженер и студент отремонтировали 248 приборов. Инженер ремонтировал приборы в 3 раза быстрее, чем студент. Сколько приборов починил каждый?Вариант III.
1. Решите примеры.
а) 365 + ( 299 — 342 : 2 ) * 5 — 687 : 3 =б) 172 =
в) 83 =
г) ( 4 + 7 )2 — ( 5 + 23 )2 + 787 =
2. Упростите выражение и найдите его значение при с=12: 47 + 56с — 6с + 34 — 12с.
3. Решите уравнения.
а) 32 * х = 1280б) 8 * y + 36 = 356
4. Решите задачу.
Портной и его ученик сшили 213 фартуков. Портной работал в 2 раза быстрее, чем его ученик. Сколько фартуков сшил портной, а сколько ученик?Самостоятельная работа №10 на темы: «Окружность и круг». «Обыкновенные дроби»
Вариант I.
1. Нарисуйте окружность с центром в точке X и радиусом 4 см 6 мм.
Нарисуйте отрезок CD так, чтобы он проходил через центр окружности и пересекал ее в точках C и D.
Как называются отрезки СX и СD? Определите их длину.
2. Решите задачу.
Оля нашла 26 грибов, из них 18 маслят. Какую часть грибов составляют маслята?3. Решите задачу.
Рыбаки поймали 112 кг рыбы. Из них 10⁄28 – караси. Сколько карасей поймали рыбаки?4. Решите задачу.
Коля прочитал 85 страниц журнала, что составило 5⁄12 от общего числа страниц. Сколько страниц в журнале?Вариант II.
1. Нарисуйте окружность с центром в точке Y и радиусом 3 см 8 мм. Нарисуйте отрезок EF так, чтобы он проходил через центр окружности и пересекал ее в точках E и F. Как называются отрезки YE и EF? Определите их длину.
2. Решите задачу.
Коля собрал в корзину 31 фрукт, из них 22 фрукта – это груши. Какую часть собранных фруктов составляют груши?3. Решите задачу.
Школьники собрали 104 кг овощей. 13⁄26 от общего числа овощей составляют помидоры. Сколько кг помидор собрали школьники?4.
Решите задачу.
Вариант III.
1. Нарисуйте окружность с центром в точке Z и радиусом 2 см 6 мм. Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
2. Решите задачу.
У Саши есть 29 карандашей. Из них 19 карандашей – это простые карандаши. Какую часть карандашей составляют цветные карандаши?3. Решите задачу.
Мастер сделал 312 деталей. Из них 3⁄24 часть деталей – деревянные. Сколько деревянных деталей сделал мастер?4. Решите задачу.
Ребята из 5 класса собрали 32 кг ягод. Это составляет 3⁄24 от всего количества собранных ягод. Сколько всего ягод было собрано?Самостоятельная работа №11 на тему: «Сравнение дробей»
Вариант I.
1.
Задан луч длиной в 12 единиц. Отметьте на числовом луче:
| а) 2⁄12 части | б) 6⁄12 части | 2⁄3 части | 5⁄4 части |
2. Сравните дроби.
а) 23⁄38 и 16⁄18б) 21⁄45 и 15⁄26
3. Найдите три решения неравенства.
а) 21⁄22< x < 22⁄22б) 7⁄11 < z < 8⁄11
4. При каких значениях х:
а) дробь х⁄22 будет правильной?б) дробь 15⁄х будет неправильной?
Вариант II.
1. Задан луч длиной в 15 единиц. Отметьте на числовом луче:
| 4⁄15 части | 3⁄15 части | 3⁄5 части | 2⁄3 части |
2.
Сравните дроби.
б) 22⁄49 и 18⁄21
3. Найдите три решения неравенства.
а) 19⁄20 < x < 20⁄20б) 7⁄9 < z < 8⁄9
4. При каких значениях y:
а) дробь y⁄19 будет правильной?б) дробь 23⁄y будет неправильной?
Вариант III.
1. Задан луч длиной в 18 единиц. Отметьте на числовом луче:
| 2⁄18 части | 6⁄18 части | 2⁄3 части | 5⁄6 части |
2. Сравните дроби.
а) 26⁄31 и 18⁄19б) 23⁄41 и 17⁄18
3. Найдите три решения неравенства.
а) 9⁄10< y < 10⁄10б) 5⁄7 < z < 6⁄7
4.
При каких значениях z:
б) дробь 13⁄z будет неправильной?
Самостоятельная работа №12 на тему: «Сложение и вычитание обыкновенных дробей»
Вариант I.
1. Решите примеры.
а) 26⁄31 + 18⁄31 — 6⁄31;б) 17⁄125 — 5⁄125 + 106⁄125;
в) 19⁄39 + ( 18⁄39 — 6⁄39 ) — 13⁄39;
2. Решите уравнения.
а) x + 6⁄18 = 16⁄18б) 13⁄25 — ( y + 6⁄25 ) = 4⁄25
3. Решите задачу.
Первый спортсмен пробежал 5⁄7 км, а второй спортсмен за тоже время пробежал 6⁄7 км. На сколько метров больше пробежал первый спортсмен?4.
Решите задачу.
Вариант II.
1. Решите примеры.
а) 15⁄38 + 12⁄38 — 11⁄38;б) 23⁄192 — 8⁄192 + 48⁄192;
в) 19⁄56 + ( 21⁄56 — 12⁄56 ) — 16⁄56;
2. Решите уравнения.
а) x — 5⁄12 = 3⁄12б) 18⁄23 — ( 7⁄23 + y ) = 5⁄23
3. Решите задачу.
Расстояние от дачи до пруда равно 3⁄5 км, а от дачи до леса равно 4⁄5 км. На сколько метров расстояние от дачи до пруда больше, чем расстояние от дачи до леса?4. Решите задачу.
Из погреба вытащили 3⁄12 части картофеля, а потом – ещё 2⁄12 части.
После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?Вариант III.
1. Решите примеры.
а) 19⁄28 + 12⁄28 — 16⁄28;б) 13⁄176 — 11⁄176 + 49⁄176;
в) 27⁄42 + ( 12⁄42 — 6⁄42 ) — 12⁄42;
2. Решите уравнения.
а) x + 12⁄23 = 20⁄23б) 28⁄35 — ( y + 16⁄35 ) = 4⁄35
3. Решите задачу.
Расстояние от школы до больницы равно 8⁄9 км, а от школы до бассейна равно 4⁄9 км. На сколько метров расстояние от школы до больницы больше, чем расстояние от школы до бассейна?4. Решите задачу.
Из рулона отрезали 3⁄8 части ткани, а потом – ещё 2⁄8 части.
После этого в рулоне осталось 32 метра ткани. Сколько метров ткани было в рулоне?Самостоятельная работа №13 на тему: «Сложение и вычитание смешанных чисел»
Вариант I.
1. Решите примеры.
а) 4 19⁄28 + 6 12⁄28;б) 5 13⁄176 — 2 11⁄176;
в) 12 27⁄43 + 3 12⁄43.
2. Решите уравнения.
а) 23 18⁄38 + х =36 12⁄28;б) 7 14⁄16 — y = 3 11⁄16;
в) y + 18 27⁄53 = 24 13⁄53;
3. Решите задачу.
В первый день в мастерской использовали 23 3⁄18 метра проволоки, а во второй день – ещё 18 2⁄18 части. После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?Вариант II.
1. Решите примеры.
а) 3 13⁄22 + 3 12⁄22;б) 8 15⁄126 — 4 15⁄126;
в) 13 22⁄49 + 3 14⁄49.
2. Решите уравнения.
а) 2 18⁄43 + х = 3 4⁄43;б) 17 15⁄19 — y = 12 12⁄19;
в) y — 18 38⁄56 = 24 27⁄56.
3. Решите задачу.
В первый день в школе покрасили 17 5⁄23 метра коридора, а во второй день – ещё 23 4⁄23 метра. Сколько метров было покрашено за 2 дня?Вариант III.
1. Решите примеры.
а) 5 19⁄23 + 6 12⁄23;б) 7 13⁄48 — 3 11⁄48;
в) 82 25⁄78 + 34 12⁄78
2. Решите уравнения.
а) 6 17⁄29 + х = 23 4⁄29;б) 8 15⁄128 — y = 6 12⁄128;
в) y — 18 38⁄47 = 5 27⁄47.
3. Решите задачу.
Фермер убрал 13 6⁄13 метра грядки в первый день, а на следующий день – ещё 18 3⁄13 метра.
После двух дней работы осталось убрать 6 метров. Какова длина грядки?Самостоятельная работа №14 на темы: «Десятичная запись дробных чисел». «Сравнение десятичных дробей»
Вариант I.
1. Заданные дроби представьте, как десятичные дроби.
а) 5 59⁄10б) 6 1⁄100
в) 17 137⁄1000
2. Сравните числа.
а) 5,596 и 5,629б) 7,34 и 7,339
в) 0,684 и 0,6840
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 92 ц; 887 кг; 14 т 12 кг;б) представьте в квадратных дециметрах: 8 м 2; 57 см 2; 8 м2 77 дм2.
4. Отметьте точки: 0,2; 0,8; 1,1; 2,3; 2,1; 3,7 на числовом отрезке, равном 5 единицам.
Вариант II.
1. Заданные дроби представьте, как десятичные дроби.
а) 18 59⁄1000б) 7⁄10
в) 7 137⁄100
2. Сравните числа.
а) 35,97 и 35,971б) 8,449 и 8,540
в) 0,92 и 0,920
3.
Переведите из одной единицы измерения в другую.
б) представьте в квадратных дециметрах: 13 м 2; 2 см 2; 87 м2 32 дм2.
4. Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Вариант III.
1. Заданные дроби представьте, как десятичные дроби.
а) 15 43⁄100б) 9 23⁄1000
в) 5⁄10
2. Сравните числа.
а) 29,345 и 29,354б) 171,89 и 171,889
в) 0,93 и 0,930
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 18 ц; 56 кг; 3 т 9 кг;б) представьте в квадратных дециметрах: 4 м 2; 23 см 2; 2 м2 56 дм2.
4. Отметьте точки: 0,4; 0,5; 1,4; 1,9; 2,4; 3,0 на числовом отрезке, равном 4 единицам.
Самостоятельная работа №15 на темы: «Сложение и вычитание десятичных дробей».
«Округление чисел» Вариант I.
1. Решите примеры на сложение десятичных дробей.
а) 29,3 + 4,35 =б) 68,9 + 19,1 =
в) 0,68 + 6,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 35,1 — 13,2 =б) 37 — 27,3 =
в) 13,28 — 5,327 =
3. Решите задачу:
В первый день плот проплыл 14,8 км, во второй день – на 1 км 700 м больше, чем в первый день. В третий день плот проплыл на 600 м меньше, чем во второй день. Сколько всего км проплыл плот?4. Округлите:
а) целую часть числа 2539,48190 до сотен, до десятков, до единиц;б) дробную часть числа 2539,48190 до тысячных, до сотен, до десятков.
Вариант II.
1. Решите примеры на сложение десятичных дробей.
а) 79,3 + 8,15 =б) 18 + 8,8 =
в) 0,93 + 23,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 48,2 — 4,98 =б) 96 — 48,6 =
в) 37,67 — 13,168 =
3. Решите задачу.
В первом пакете было 15,7 кг песка, во втором – на 350 г больше, чем в первом.
В третьем – на 1200 г меньше, чем в первом. Сколько кг песка в трех пакетах?4. Округлите:
а) целую часть числа 3462,9470 до сотен, до десятков, до единиц;б) дробную часть числа 3462,9470 до тысячных, до сотен, до десятков.
Вариант III.
1. Решите примеры на сложение десятичных дробей.
а) 34,3 + 13,11 =б) 8 + 47,7 =
в) 0,123 + 23,942 =
2. Решите примеры на вычитание десятичных дробей.
а) 69,2 — 7,88 =б) 91,76 — 18,6 =
в) 8,94 — 5,452 =
3. Решите задачу.
3 дня бабушка пекла блины. В первый день она использовала 1,2 кг муки, во второй день – на 500 г меньше, чем в первый день, а на третий день – на 300 г больше, чем во второй день. Сколько муки она использовала за три дня?4. Округлите:
а) целую часть числа 4392,73910 до сотен, до десятков, до единиц;б) дробную часть числа 4392,73910 до тысячных, до сотен, до десятков.
Самостоятельная работа №16 на тему: «Умножение десятичных дробей на натуральные числа»
Вариант I.
1. Выполните умножение.
| а) 8,3 * 8 = | б) 7,12 * 34 = | в) 0,235 * 93 = | г) 1,93 * 100 = |
2. Найдите значение выражения: х + ( 3,74х — 1,474х ) при х=3; 100; 374; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух деревень, расстояние между которыми составляет 45,8 км, вышли пешеходы. Скорость первого пешехода составляет 4,2 км/ч, а скорость второго – 4,5 км/ч. Какое расстояние будет между ними через 4 часа?4. Решите задачу.
Машина проехала 360 км за 6 часов. Какое расстояние она преодолеет, передвигаясь с той же скоростью, за 1⁄4 часа, за 2 1⁄3 часа?Вариант II.
1. Выполните умножение.
| а) 7,48 * 12 = | б) 3,57 * 7 = | в) 0,873 * 87 = | г) 1,698 * 1000 = |
2. Найдите значение выражения: 5х + ( 6,59х + 2,483х ) при х=5; 100; 324; 1000.
3. Решите задачу.
Одновременно в противоположных направлениях из города выехали 2 машины.
Скорость первой машины составляет 54,7 км/ч, а скорость второй – 76,2 км/ч. Какое расстояние будет между ними через 3 часа?4. Решите задачу.
Велосипедист преодолел 72 км за 3 часа. Какое расстояние он преодолеет, перемещаясь с той же скоростью, за 5⁄6 часа, за 2 1⁄3 часа?Вариант III.
1. Выполните умножение.
| а) 9,4 * 6 = | б) 8,34 * 56 = | в) 0,517 * 62 = | г) 6,787 * 1000 = |
2. Найдите значение выражения: ( 8,45х — 3,594х ) — х при х=8; 100; 843; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух городов выехали мотоциклы. Расстояние между городами составляет 234,8 км. Скорость первого мотоциклиста составляет 34,5 км/ч, а скорость второго – 56,2 км/ч. Какое расстояние будет между ними через 2 часа?4. Решите задачу.
Моторная лодка прошла 24 км за 2 часа. Какое расстояние она пройдет, перемещаясь с той же скоростью, за 1⁄4 часа, за 3 1⁄3 часа?Самостоятельная работа №17 на тему: «Деление десятичных дробей на натуральные числа»
Вариант I.
1. Выполните деление.
| а) 2,729 : 6 = | б) 283,85 : 4 = | в) 4 : 13 = | г) 0,095 : 10 = |
2. Решите уравнения.
| а) 5X — 0,4 = 23,6 | б) 48,2 : Y = 10,4 |
3. Решите задачу.
За два дня рабочие отремонтировали 3,6 км дороги. В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?4. Решите задачу.
4 класс и 5 класс собирали макулатуру. Пятиклассники собрали в 2 раза больше макулатуры, чем ребята из 4 класса. Вместе они собрали 239,7 кг. Сколько кг собрали ребята из 5 класса и сколько ребята из 4 класса?Вариант II.
1. Выполните деление.
| а) 5,837 : 7 = | б) 291,49 : 5 = | в) 5 : 18 = | г) 0,023 : 10 = |
2. Решите уравнения.
| а) 8X + 2,8 = 18,6 | б) 28,1 : Y = 12,4 |
3. Решите задачу.
За два дня бригада собрала 147,6 кг ягод.
В первый день они собрали 4/9 части урожая ягод. Сколько кг ягод они собрали во второй день?4. Решите задачу.
Две бригады собирали картофель. Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?Вариант III.
1. Выполните деление.
| а) 4,752 : 9 = | б) 472,49 : 6 = | в) 7 : 19 = | г) 0,044 : 10 = |
2. Решите уравнения.
| а) 5X + 2,5 = 24 | б) 14,2 : Y = 3,4 |
3. Решите задачу.
За 2 дня мотоциклист преодолел 394,1 км. В первый день он проехал 4⁄7 части пути. Сколько км он проехал во второй день?4. Решите задачу.
Мама собрала в 5 раз больше ягод, чем дочка. Вместе они собрали 34,5 кг ягод. Сколько ягод собрала мама и сколько дочка?Самостоятельная работа №18 на тему: «Среднее арифметическое»
Вариант I.
1. Найдите среднее арифметическое четырех чисел: 4,5; 5,6; 4,9; 5,1.
2. Решите задачу.
В течение часа машина двигалась со скоростью 67,5 км/ч, в течение второго часа – со скоростью 51,6 км/ч. В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 14,5. Первое число – 14,1, а второе число на 0,8 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями равно 340 км. Автомобиль преодолел половину пути со скоростью 58 км/ч, а вторую половину – со скоростью 49 км/ч. Какова средняя скорость автомобиля на протяжении всего пути?Вариант II.
1. Найдите среднее арифметическое четырех чисел: 12,3; 12,9; 11,6; 13,1.
2. Решите задачу.
В течение первого часа спортсмен шел со скоростью 11,2 км/ч, в течение второго часа – со скоростью 10,7 км/ч, а в течение третьего часа его скорость составила 9,8 км/ч.
Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 28,5. Первое число – 28,2, а второе на 0,9 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя городами составляет 52 км. Первую половину пути велосипедист передвигался со скоростью 18 км/ч, а вторую половину – со скоростью 22 км/час. Какова средняя скорость велосипедиста на всем протяжении пути?Вариант III.
1. Найдите среднее арифметическое четырех чисел: 9,1; 9,9; 11,1; 10,7.
2. Решите задачу.
В течение первого часа лодка двигалась со скоростью 15,5 км/ч, во второй час движения её скорость составила 17,4 км/ч, а в течение третьего часа – 12,7 км/ч. Какая средняя скорость лодки? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 13,2. Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.4. Решите задачу.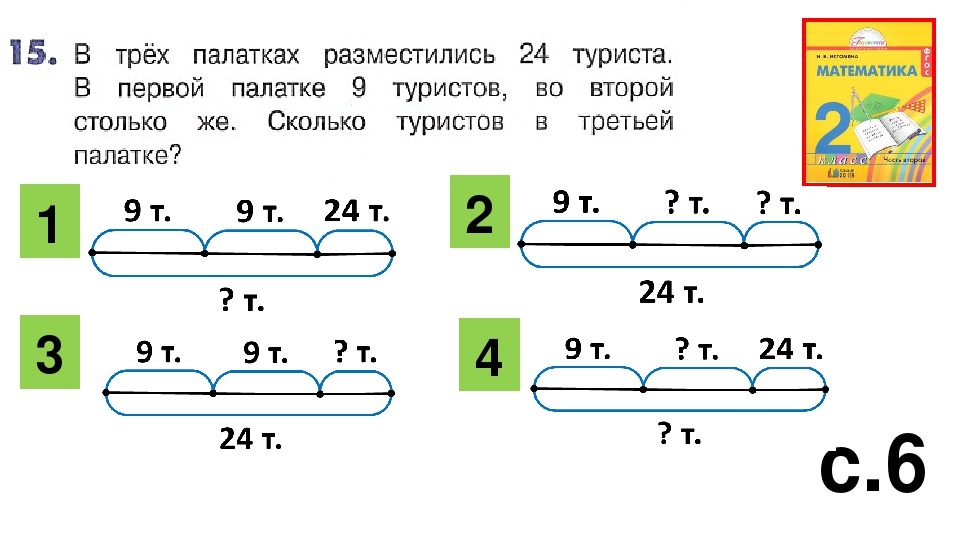
Самостоятельная работа №19 на тему: «Проценты, задачи на проценты»
Вариант I.
1. Решите задачу.
В спортивной секции занимается 60 учеников, из них 70% составляют девочки. Сколько мальчиков занимается в спортивной секции?2. Решите задачу.
Ребята четвертых и пятых классов собирали макулатуру. Ребята пятого класса собрали 150 кг макулатуры, что составило 60% общего веса собранной макулатуры. Сколько кг макулатуры собрали ребята?3. Решите задачу.
Из 15 кг яблок получается 12 кг яблочного пюре. Каков процент выхода пюре из яблок?Вариант II.
1. Решите задачу.
В 5 классе числится 30 учеников, 60% из них – мальчики. Сколько девочек учится в 5 классе?2. Решите задачу.
2 бригады собирали помидоры. Первая бригада собрала 320 кг помидор, что составило 40% от общего урожая.
Сколько всего помидор собрали обе бригады?3. Решите задачу.
Из 60 семян взошли 55 растений. Найдите процент всхожести семян.Вариант III.
1. Решите задачу.
В школе работает 40 человека. Из них 80% – женщины. Сколько мужчин работает в школе?2. Решите задачу.
Бабушка и внучка собирали яблоки. Бабушка собрала 30 кг яблок, что составило 80% от общего сбора. Сколько кг яблок собрали бабушка и внучка вместе?3. Решите задачу.
При перемалывании 40 кг зерна получили 25 кг муки. Найдите процент выхода муки.50, 51. Задачи на части
Купили 2700 г сухофруктов. Яблоки составляют 4 части, чернослив — 3 части и курага — 2 части массы сухофруктов. Сколько граммов яблок, чернослива и кураги в отдельности купили?Решение:
1) 4+3+2=9(ч.) — всего
2) 2700 : 9 = 300 (г) — на одну часть
3) 300 * 4 = 1200 (г) — яблок
4) 300 * 3 = 900 (г) — чернослива
5) 300 * 2 = 600 (г) — кураги
Ответ: 1200г, 900г, 600г.
2. Известно количество частей некоторых элементов и разность этих элементов.
Тетрадей в клетку купили на 60 больше, чем тетрадей в линейку. Тетрадей в клетку было в 3 раза больше, чем тетрадей в линейку. Сколько купили тетрадей?
Решение:
Пусть тетради в линейку составляют одну часть, тогда тетради в клетку составляют 3 части.
1) 3-1=2 (ч.) — это 60 тетрадей
2) 60 : 2 = 30 (т.) — на одну часть
2) 3 + 1 = 4 (ч.) — всего
3) 30 * 4 = 120 (т.) — купили
Ответ: 120 тетрадей.
Для компота взяли 6 частей яблок, 5 частей чернослива и 3 части кураги. Оказалось, что чернослива и кураги вместе взяли 2 кг 400 г. Определите массу взятых яблок; массу всех фруктов.
Решение:
1) 5 + 3 = 8 (ч.) — чернослива и кураги
2) 2400 : 8 = 300 (г) — на одну часть
3) 300 * 6=1800 (г) — яблок
4) 1800 + 2400 = 4200 (г) — фруктов
Ответ: 1 кг 800 г; 4 кг 200 г.
Домашнее задание К уроку 50 (на 17.11)
п. 3.14
№ 3.212, 3.213
Дополнительное задание
Для приготовления абрикосового джема берут 5 частей абрикосов, 3 части сахара и 1 часть воды. Сколько килограммов абрикосового варенья получится, если сахара потребовалось на 2 кг 400 г меньше, чем абрикосов.
К уроку 51 (на 18.11)
Подготовиться к контрольной работе
п. 3.14
№ 3.214(2), 3.215
Дополнительное задание
Для приготовления яблочного повидла на 5 частей массы яблочного пюре берут 3 части массы сахара. Сколько яблочного пюре и сколько сахара потребуется, чтобы подготовит 6 кг смеси?
| Класс | Название урока | Ссылка на учебные материалы |
| 5 | Ряд натуральных чисел. Десятичная система записи натуральных чисел |
https://resh.edu.ru/subject/lesson/7719/main/234018/ |
| 5 | Сравнение натуральных чисел | https://resh.edu.ru/subject/lesson/7718/main/235258/ |
| 5 | Сравнение именованных чисел | https://interneturok.ru/lesson/matematika/5-klass/bnaturalnye-chislab/izmerenie-velichin-edinitsy-izmereniya?block=player |
| 5 | Измерение отрезков | https://resh.edu.ru/subject/lesson/7740/main/234855/ |
| 5 | Длина отрезка | https://resh.edu.ru/subject/lesson/6914/main/235937/ |
| 5 | Прямая, луч, отрезок | https://resh.edu.ru/subject/lesson/7741/main/235227/ |
| 5 | Координатный луч | https://resh.edu.ru/subject/lesson/7756/main/234421/ |
| 5 | Представление натуральных чисел на координатном луче | https://resh. edu.ru/subject/lesson/7738/main/233801/ |
| 5 | Сложение натуральных чисел. Законы сложения | https://resh.edu.ru/subject/lesson/7723/main/ |
| 5 | Арифметические действия с натуральными числами | https://mosobr.tv/release/7856 |
| 5 | Вычитание | https://resh.edu.ru/subject/lesson/7717/main/235289/ |
| 5 | Правила вычитания суммы из числа и числа из суммы | https://znaika.ru/catalog/5-klass/matematika/Svoystva-vychitaniya-naturalnykh-chisel.html |
| 5 | Решение текстовых задач с помощью сложения и вычитания | https://resh.edu.ru/subject/lesson/7716/main/233832/ |
| 5 | Числовые выражения | https://resh.edu.ru/subject/lesson/7708/main/266123/ |
| 5 | Углы. Измерение углов | https://resh.edu. ru/subject/lesson/589/ |
| 5 | Углы. Измерение углов | https://resh.edu.ru/subject/lesson/7735/main/234886/ |
| 5 | Многоугольники | https://resh.edu.ru/subject/lesson/7727/main/267638/ |
| 5 | Треугольники | https://resh.edu.ru/subject/lesson/7734/main/234917/ |
| 5 | Четырёхугольники | https://resh.edu.ru/subject/lesson/7733/main/233522/ |
| 5 | Симметрия относительно точки, относительно прямой и относительно плоскости | https://resh.edu.ru/subject/lesson/983/ |
| 5 | Умножение. Законы умножения | https://resh.edu.ru/subject/lesson/7722/main/235069/ |
| 5 | Распределительный закон | https://resh.edu.ru/subject/lesson/7724/main/266247/ |
| 5 | Умножение. Законы умножения | https://resh. edu.ru/subject/lesson/7712/main/235041/ |
| 5 | Деление нацело | https://resh.edu.ru/subject/lesson/7712/main/235041/ |
| 5 | Деление с остатком | https://resh.edu.ru/subject/lesson/7709/main/235165/ |
| 5 | Степень с натуральным показателем | https://resh.edu.ru/subject/lesson/7713/main/234793/ |
| 5 | Решение текстовых задач с помощью умножения и деления | https://resh.edu.ru/subject/lesson/7711/main/234760/ |
| 5 | Площадь прямоугольника. Единицы площади | https://resh.edu.ru/subject/lesson/7732/main/233181/ |
| 5 | Прямоугольный параллелепипед | https://resh.edu.ru/subject/lesson/7731/main/234669/ |
| 5 | Объём прямоугольного параллелепипеда. Единицы объёма | https://resh.edu.ru/subject/lesson/7730/main/272356/ |
| 5 | Объём прямоугольного параллелепипеда | https://resh. edu.ru/subject/lesson/7753/main/234824/ |
| 5 | Понятие дроби | https://resh.edu.ru/subject/lesson/7782/main/233643/ |
| 5 | Сравнение обыкновенных дробей | https://resh.edu.ru/subject/lesson/16/ |
| 5 | Задачи на дроби (нахождение части целого) | https://resh.edu.ru/subject/lesson/7780/main/234203/ |
| 5 | Дроби и деление натуральных чисел | https://znaika.ru/catalog/5-klass/matematika/Delenie-i-drobi.html |
| 5 | Нахождение целого по его части | https://resh.edu.ru/subject/lesson/7779/main/233956/ |
| 5 | Задачи на дроби (нахождение части целого) | https://resh.edu.ru/subject/lesson/7780/main/234203/ |
| 5 | Сложение дробей с одинаковым знаменателем | https://resh.edu.ru/subject/lesson/7774/main/233212/ |
| 5 | Понятие смешанной дроби | https://resh. edu.ru/subject/lesson/7761/main/233026/ |
| 5 | Сложение смешанных дробей | https://resh.edu.ru/subject/lesson/7760/main/233336/ |
| 5 | Вычитание смешанных дробей | https://resh.edu.ru/subject/lesson/7759/main/233615/ |
| 5 | Понятие положительной десятичной дроби | https://resh.edu.ru/subject/lesson/6903/main/235413/ |
| 5 | Сравнение положительных десятичных дробей | https://resh.edu.ru/subject/lesson/6902/main/236096/ |
| 5 | Округление натуральных чисел. Теоретическая часть | https://resh.edu.ru/subject/lesson/23/ |
| 5 | Округление десятичных дробей | https://resh.edu.ru/subject/lesson/27/ |
| 5 | Чтение и запись десятичных дробей | https://video-ypoku.com/dlya-detej-i-roditelej/shkolnikam/1383-matematika-5-klass-desyatichnye-drobi |
| 5 | Сложение положительных десятичных дробей | https://resh. edu.ru/subject/lesson/6901/main/236064/ |
| 5 | Вычитание положительных десятичных дробей | https://resh.edu.ru/subject/lesson/6900/main/236033/ |
| 5 | Сложение и вычитание десятичных дробей | https://resh.edu.ru/subject/lesson/719/ |
| 5 | Умножение и деление десятичной дроби на 10, 100, 1000 | https://resh.edu.ru/subject/lesson/720/ |
| 5 | Умножение положительных десятичных дробей. Часть 1 | https://resh.edu.ru/subject/lesson/6898/main/235559/ |
| 5 | Умножение положительных десятичных дробей. Часть 2 | https://resh.edu.ru/subject/lesson/6897/main/236204/ |
| 5 | Деление натуральных чисел | https://mosobr.tv/release/7932 |
| 5 | Деление десятичной дроби на целое число | https://resh.edu. ru/subject/lesson/722/ |
| 5 | Умножение и деление десятичной дроби на 10, 100, 1000 | https://resh.edu.ru/subject/lesson/720/ |
| 5 | Деление положительных десятичных дробей. Часть 1 | https://resh.edu.ru/subject/lesson/6896/main/236240/ |
| 5 | Деление положительных десятичных дробей. Часть 2 | https://resh.edu.ru/subject/lesson/6895/main/237500/ |
| 5 | Среднее арифметическое | https://resh.edu.ru/subject/lesson/715/ |
| 5 | Среднее арифметическое нескольких чисел | https://resh.edu.ru/subject/lesson/22/ |
| 5 | Понятие о проценте | https://resh.edu.ru/subject/lesson/6846/main/237181/ |
| 5 | Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах | https://resh. edu.ru/subject/lesson/1060/ |
| 5 | Задачи на проценты. Часть 1 | https://resh.edu.ru/subject/lesson/6848/main/237738/ |
| 5 | Задачи на проценты. Часть 2 | https://resh.edu.ru/subject/lesson/6839/main/237149/ |
| 5 | Занимательные задачи по теме «Смешанные дроби» | https://resh.edu.ru/subject/lesson/7752/main/233553/ |
| 5 | Итоговое обобщение и систематизация знаний по темам «Делимость натуральных чисел» | https://resh.edu.ru/subject/lesson/7790/main/234080/ |
| 5 | Итоговое обобщение и систематизация знаний по темам «Обыкновенные дроби и смешанные дроби» | https://resh.edu.ru/subject/lesson/7789/main/266061/ |
| 5 | Единицы длины | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/687915 |
| 5 | Шкала. Примеры шкал |
https://infourok.ru/videouroki/2947 |
| 5 | Буквенное выражение и его значение | https://infourok.ru/videouroki/2952 |
| 5 | Формулы | https://infourok.ru/videouroki/2922 |
| 5 | Уравнение | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4369029 |
| 5 | Биссектриса угла | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/2680471 |
| 5 | Равные фигуры | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4909803 |
| 5 | Прямоугольник. Периметр прямоугольника | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/1299188 |
| 5 | Порядок действий | https://infourok.ru/videouroki/2920 |
| 5 | Понятие площади | https://uchebnik.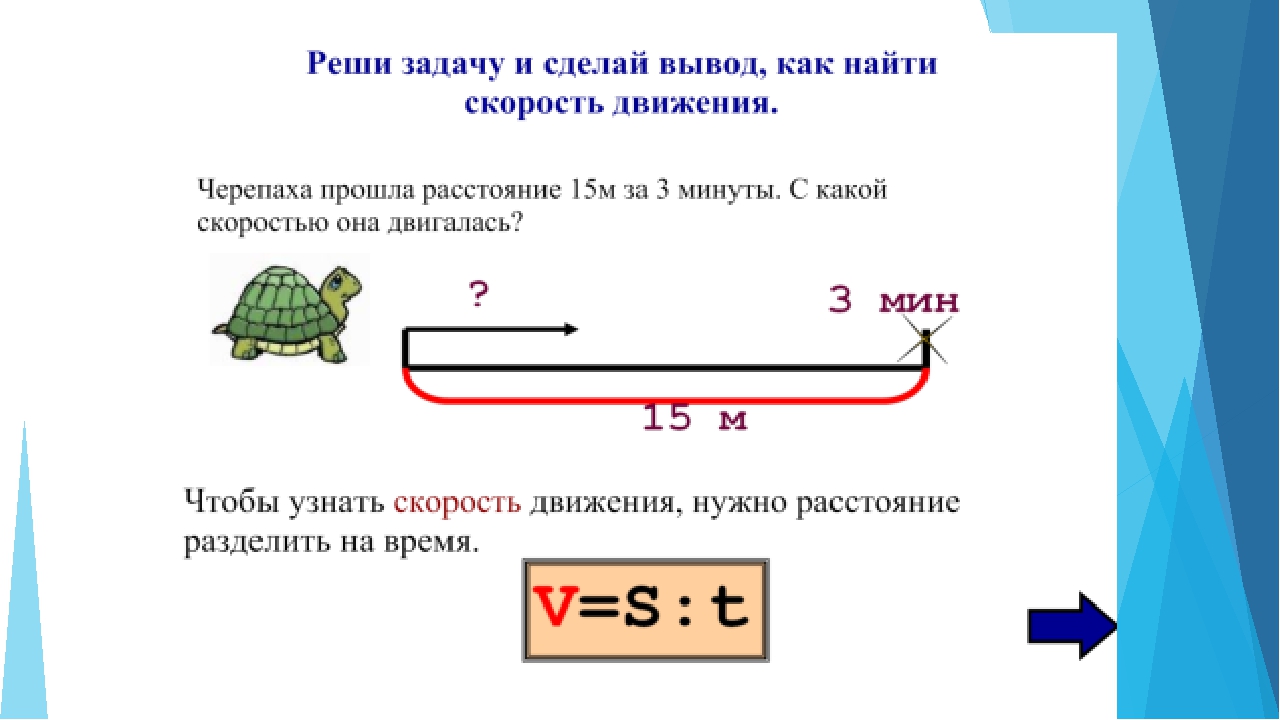 mos.ru/catalogue/material_view/atomic_objects/856976 |
| 5 | Пирамида | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3149941 |
| 5 | Ломаная. Длина ломаной | https://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/4454434 |
| 5 | Развёртки геометрических фигур | https://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/5795070 |
| 5 | Округление чисел. Прикидки | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/5206540 |
| 5 | Умножение десятичных дробей на 0,1, 0,01, 0,001 и т. д. | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/439985 |
| 5 | Деление десятичной дроби на 0,1, 0,01, 0,001 и т. д. | https://znaika.ru/catalog/5-klass/matematika/Delenie-na-desyatichnuyu-drob. html |
| 6 | Делители натурального числа | https://resh.edu.ru/subject/lesson/694/ |
| 6 | Признаки делимости | https://resh.edu.ru/subject/lesson/7750/main/234576/ |
| 6 | Простые и составные числа | https://resh.edu.ru/subject/lesson/7749/main/234979/ |
| 6 | Наибольший общий делитель (НОД) | https://resh.edu.ru/subject/lesson/7747/main/233739/ |
| 6 | Наименьшее общее кратное (НОК) | https://resh.edu.ru/subject/lesson/7746/main/234266/ |
| 6 | Равенство дробей | https://resh.edu.ru/subject/lesson/7781/main/269492/ |
| 6 | Понятие дроби | https://resh.edu.ru/subject/lesson/7782/main/233643/ |
| 6 | Приведение дробей к общему знаменателю. Сокращение дробей | https://resh. edu.ru/subject/lesson/7777/main/233115/ |
| 6 | Приведение дробей к общему знаменателю. Сокращение дробей | https://resh.edu.ru/subject/lesson/7778/main/233708/ |
| 6 | Сравнение дробей | https://resh.edu.ru/subject/lesson/7776/main/233243/ |
| 6 | Сравнение дробей. Сравнение с единицей. Сравнение остатков до единицы | https://resh.edu.ru/subject/lesson/7775/main/233398/ |
| 6 | Сложение дробей с одинаковым знаменателем | https://resh.edu.ru/subject/lesson/7774/main/233212/ |
| 6 | Сложение дробей с разными знаменателями | https://resh.edu.ru/subject/lesson/7773/main/233057/ |
| 6 | Вычитание дробей | https://resh.edu.ru/subject/lesson/7771/main/233150/ |
| 6 | Решение задач с использованием вычитания дробей | https://resh. edu.ru/subject/lesson/7770/main/233925/ |
| 6 | Умножение натурального числа на дробь | https://resh.edu.ru/subject/lesson/7769/main/234483/ |
| 6 | Законы умножения. Распределительный закон | https://resh.edu.ru/subject/lesson/7767/main/234545/ |
| 6 | Нахождение части целого и целого по его части | https://resh.edu.ru/subject/lesson/7764/main/233584/ |
| 6 | Решение задач на применение умножения дроби на натуральное число и умножение дробей | https://resh.edu.ru/subject/lesson/7768/main/234142/ |
| 6 | Умножение и деление обыкновенной дроби на обыкновенную дробь | https://resh.edu.ru/subject/lesson/710/ |
| 6 | Деление дробей | https://resh.edu.ru/subject/lesson/7766/main/234948/ |
| 6 | Свойства деления | https://znaika. ru/catalog/5-klass/matematika/Delenie-naturalnykh-chisel-i-ego-svoystva.html |
| 6 | Понятие положительной десятичной дроби | https://resh.edu.ru/subject/lesson/6903/main/235413/ |
| 6 | Бесконечные периодические десятичные дроби | https://resh.edu.ru/subject/lesson/6915/main/236435/ |
| 6 | Разложение положительной обыкновенной дроби в конечную десятичную дробь | https://resh.edu.ru/subject/lesson/6919/main/237273/ |
| 6 | Отношение чисел и величин | https://resh.edu.ru/subject/lesson/6844/main/235847/ |
| 6 | Пропорции | https://resh.edu.ru/subject/lesson/6841/main/237211/ |
| 6 | Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах | https://resh.edu.ru/subject/lesson/1060/ |
| 6 | Прямая и обратная пропорциональность | https://resh. edu.ru/subject/lesson/6849/main/237769/ |
| 6 | Деление числа в данном отношении | https://resh.edu.ru/subject/lesson/6842/main/235816/ |
| 6 | Окружность и круг. Сфера и шар | https://resh.edu.ru/subject/lesson/588/ |
| 6 | Длина окружности. Площадь круга | https://resh.edu.ru/subject/lesson/6913/main/236498/ |
| 6 | Куб, шар, пирамида, цилиндр, конус | https://resh.edu.ru/subject/lesson/557/ |
| 6 | Столбчатые и круговые диаграммы | https://resh.edu.ru/subject/lesson/1228/ |
| 6 | Отрицательные целые числа | https://resh.edu.ru/subject/lesson/6872/main/237087/ |
| 6 | Координатная ось. Часть 1 | https://resh.edu.ru/subject/lesson/6912/main/236158/ |
| 6 | Представление целых чисел на координатной оси | https://resh.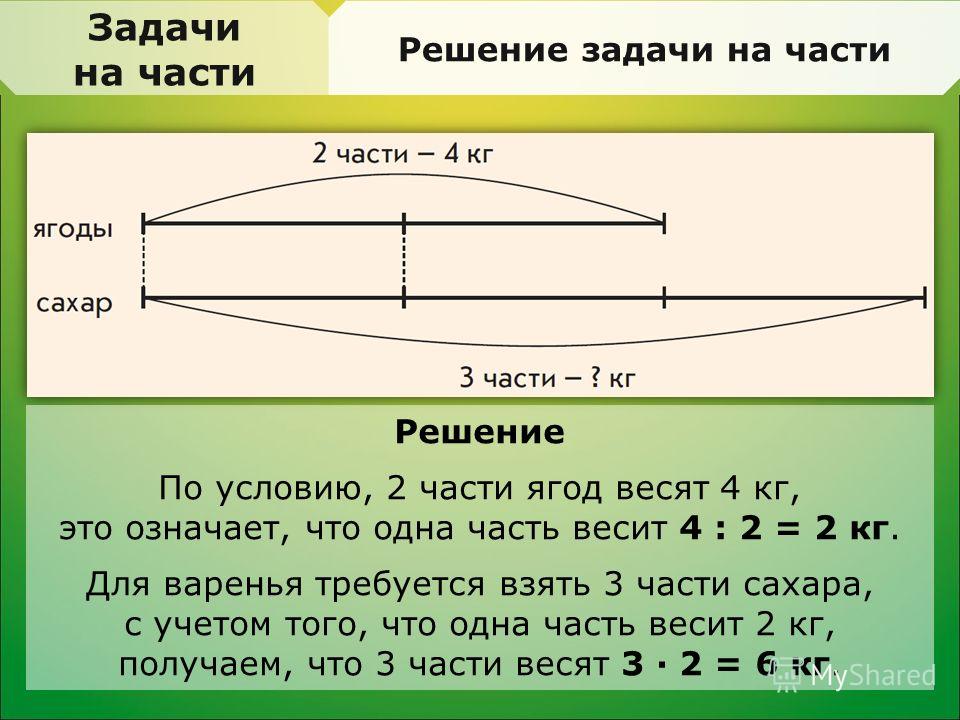 edu.ru/subject/lesson/6866/main/236343/ |
| 6 | Координатная ось. Часть 2 | https://resh.edu.ru/subject/lesson/6920/main/236020/ |
| 6 | Противоположные числа. Модуль числа | https://resh.edu.ru/subject/lesson/6862/main/237056/ |
| 6 | Сравнение целых чисел | https://resh.edu.ru/subject/lesson/6861/main/237025/ |
| 6 | Сложение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6863/main/236994/ |
| 6 | Сложение целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6864/main/236963/ |
| 6 | Сложение целых чисел. Часть 3 | https://resh.edu.ru/subject/lesson/6865/main/236933/ |
| 6 | Законы сложения целых чисел | https://resh.edu.ru/subject/lesson/6860/main/237335/ |
| 6 | Рациональное вычисление значений арифметических выражений с применением вычитания, как алгебраического сложения. Часть 1 (теория) |
https://resh.edu.ru/subject/lesson/1380/ |
| 6 | Разность целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6859/main/237552/ |
| 6 | Разность целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6858/main/236901/ |
| 6 | Произведение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6857/main/236870/ |
| 6 | Произведение целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6856/main/237301/ |
| 6 | Произведение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6857/main/236870/ |
| 6 | Распределительный закон | https://resh.edu.ru/subject/lesson/6871/main/236746/ |
| 6 | Раскрытие скобок и заключение в скобки | https://resh.edu. ru/subject/lesson/6855/main/235382/ |
| 6 | Частное целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6869/main/237521/ |
| 6 | Частное целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6870/main/236808/ |
| 6 | План и этапы решения задачи. Анализ решения, Проверка решения, проверка обратным действием | https://resh.edu.ru/subject/lesson/608/ |
| 6 | Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость | https://resh.edu.ru/subject/lesson/346/ |
| 6 | Использование таблиц, схем, чертежей, других средств представления данных при решении задачи | https://resh.edu.ru/subject/lesson/340/ |
| 6 | Построение фигур, симметричных относительно заданной точки или прямой. Часть 1 | https://resh. edu.ru/subject/lesson/1392/ |
| 6 | Построение фигур, симметричных относительно заданной точки или прямой. Часть 2. | https://resh.edu.ru/subject/lesson/1120/ |
| 6 | Декартова система координат на плоскости | https://resh.edu.ru/subject/lesson/6921/main/236560/ |
| 6 | Столбчатые диаграммы. Графики | https://resh.edu.ru/subject/lesson/6911/main/235706/ |
| 6 | Построение столбчатых диаграмм. Чтение графиков | https://resh.edu.ru/subject/lesson/6922/main/236622/ |
| 6 | Обобщение и систематизация знаний по теме «Декартова система координат на плоскости» | https://resh.edu.ru/subject/lesson/6917/main/236653/ |
| 6 | Занимательные задачи на проценты | https://resh.edu.ru/subject/lesson/6918/main/235909/ |
| 6 | Сложные задачи на проценты | https://resh. edu.ru/subject/lesson/6910/main/236839/ |
| 6 | Обобщение и систематизация знаний по темам «Десятичные дроби, проценты, решение задач на проценты» | https://resh.edu.ru/subject/lesson/6923/main/236777/ |
| 6 | Случайные события | https://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost.html |
| 6 | Вероятность случайного события | https://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost.html |
| 6 | Арифметические действия с рациональными числами | https://clck.ru/MWVCo |
| 6 | Свойства умножения рациональных чисел | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4033089 |
| 6 | Свойства вычитания рациональных чисел | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4368360 |
| 6 | Коэффициент | https://infourok. ru/videouroki/2988 |
| 6 | Перпендикулярные прямые | https://infourok.ru/videouroki/2991 |
| 6 | Параллельные прямые | https://infourok.ru/videouroki/2992 |
ГДЗ по Математике 5 класс Мерзляк. Решебник заданий
ГДЗ по математике за 5 класс Мерзляк – это решебник или сборник готовых домашних заданий, которые выполнены на основе упражнений одноименного учебника по арифметике для российских средних школ от авторитетных авторов – Мерзляка А.Г., Полонского В.Б., Якира М.С.
Чем решебник по математике Мерзляка А.Г. в пятом классе поможет ученикам и их родителям?
В чем заключается удобство использования готовых домашних заданий? Онлайн-сборники включают в себя не только готовые ответы, но и детальные решения примеров и задач по арифметике. Такой вариант удобен для родителей, которые желают помочь пятикласснику разобраться в примерах и задачках, а также детально проверить его успеваемость по предмету.
Сайт ВИП ГДЗ – это способ быстрого поиска ответов и решений по решебнику по математике за 5 класс Мерзляк. Достаточно указать в поисковой строке номер задачки или часть ее условия, как система предложит соответствующий запросу результат.
Решения и ответы на сайте соответствуют последнему изданию учебника Мерзляка А.Г. 2014 года. Более того, ресурс обладает массой значимых для пользователей достоинств:
- искать ответы и решения можно с любых электронных гаджетов;
- продвинутый поиск существенно экономит время пользователя;
- наличие нескольких вариантов выполнения одного и того же упражнения расширяет кругозор школьника относительно использования различных способов выполнения упражнений.
Учебник по математике за 5 класс Мерзляк А.Г. – содержание пособия
Онлайн-решебник нашего сайта составлен на основе учебника А.Г. Мерзляка за 2014 год – дату его последнего издания. В нем можно найти подробные решения задач, примеров, уравнений по таким темам школьной арифметики, как:
- натуральные числа, использование шкал и система координат;
- простые фигуры – отрезки, прямые, лучи, углы;
- действия с натуральными числами, равенство многоугольников, виды треугольников, оси симметрии;
- определение степени числа;
- расчет площади квадрата и прямоугольника;
- обыкновенные и десятичные дроби, смешанные числа;
- расчет среднего арифметического и процентов.
Поскольку большая часть материала в дальнейшем используется школьниками в ходе изучения алгебры, геометрии, а порой – химии и физики, то важно детально разобраться в правилах и теоремах на базе ГДЗ по математике за 5 класс Мерзляк.
Благодаря удобному функционалу сайта можно найти решение задачки всего за пару секунд, а подробные алгоритм решения позволяет родителям добиться высокой успеваемости школьника, его высоких оценок на контрольных и экзаменах даже без помощи репетитора.
Формулы для решения задач на дроби для 5 класса
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачуПример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $\frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.
3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всегоПример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$
Сократим ещё раз на 2:
$\frac{24}{60} = \frac{12}{30}$
И ещё раз:
$\frac{12}{30} = \frac{6}{15}$
Теперь можно сократить на 3:
$\frac{6}{15} = \frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников.
Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$
Ответ: школьники составляют $\frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$
Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».
Как решить математическую задачу с помощью PEMDAS
Обновлено 15 декабря 2020 г.
Крис Дезил
Взгляните на следующее равенство:
x = 7 + 2 × (11-5) ÷ 3
Решите для x , выполняя математические операции в порядке слева направо, и вы получите 18, что является неправильным ответом.
Чтобы получить правильный ответ — 11, вы должны соблюдать правильный порядок действий. Если вы не можете вспомнить правильный порядок, PEMDAS может вам помочь.Это аббревиатура, обозначающая круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
В общем, PEMDAS не так уж сложно запомнить, но если вы не можете это сделать, вам может помочь пара крылатых фраз. Один из них — «Прошу прощения, моя дорогая тетя Салли». Первая буква в каждом слове этой фразы является одной из букв в PEMDAS. Если вы предпочитаете называть круглые скобки скобками, вспомните аббревиатуру BEDMAS и крылатую фразу «Большие слоны уничтожают мышей и улиток».В этой фразе D и M меняются местами, но это нормально. Когда вы доходите до умножения и деления, вы обычно делаете то, что идет первым в выражении.
Некоторые люди, которым сложно запомнить PEMDAS, ищут порядок операций с помощью поиска PADMAS math. Это не поможет. Он игнорирует E для экспонент, а экспоненты — важная операция, которую необходимо выполнить, прежде чем вы перейдете к любой из других арифметических операций.
Как применять порядок операций
Всякий раз, когда вам нужно выполнить длинную цепочку операций, правила математики ясны.Вы всегда начинаете с выполнения операций в круглых скобках (скобках), а затем решаете экспоненты, которые представляют собой числа в форме x a . Следующие две операции — это умножение и деление. Если деление идет первым в выражении, вы делаете это в первую очередь. Точно так же, если сначала идет умножение, сделайте это в первую очередь. То же верно и для двух последних операций — сложения и вычитания. Выполняйте вычитание перед сложением, если они идут первыми в выражении, и наоборот.
Пример расчета
Еще раз взгляните на выражение в начале этой статьи. Применяя PEMDAS, вы решаете это следующим образом:
Начните с чисел в скобках
Выполните Умножение и деление
Завершить с сложением и вычитанием
11-5 = 6
Таким образом, выражение теперь принимает вид
x = 7 + 2 × 6 ÷ 3
Умножение идет первым, так что начнем с него.
Теперь выражение выглядит следующим образом:
x = 7 + 12 ÷ 3
Теперь выполните деление, чтобы в итоге получилось:
x = 7 + 4
Осталось выполнить только одно сложение. , что дает окончательный ответ:
x = 11
Иногда вы увидите несколько скобок или скобок.Правило состоит в том, чтобы упростить все внутри скобок, начиная с внутренних, прежде чем переходить к остальным арифметическим операциям. Не забывайте следовать PEMDAS или BEDMAS даже при работе с числами в скобках. Это означает, что нужно решить экспоненты, прежде чем переходить к другим операциям.
Дополнительные примеры использования PEMDAS или BEDMAS
15 — [5 + (7-4)]
- Начните с внутренних скобок: 15 —
[5 + 3}
2. Теперь выполните внешние кронштейны: 15
—
8
3.
2 × 4
- E — Решите все экспоненты:
4 + 4 × 4
- M, D — Произведите умножение и деление:
4 + 16
- A, S — Выполните сложение и вычитание:
Порядок операций — Бесплатная справка по математике
Введение
Порядок операций — очень простая концепция, жизненно важная для правильного понимания математики.В отличие от чтения, где мы всегда работаем слева направо, иногда с математикой нам нужно проработать одну часть задачи перед другой, иначе окончательный ответ может быть неверным! Мы используем термин «порядок операций», чтобы описать, с какой частью проблемы нужно работать в первую очередь. Возьмите это уравнение в качестве примера:
$$ 4 + 6 \ div 2 * 11 =? $$ Если бы вы просто решали слева направо, ответ был бы неверным. Давайте сделаем это сейчас: 4 + 6 = 10. Разделите это на 2, чтобы получить 5.
Умножьте 5 на 11, чтобы получить 55.К сожалению, хотя это казалось нормальным, это неверный ответ.
Правильный порядок действий
Порядок действий позволит вам решить эту проблему правильно. Порядок следующий: Скобка , Показатели , Умножение и деление и, наконец, Сложение и вычитание . Всегда сначала выполняйте операции внутри скобок, а затем выполняйте операции с показателями. После этого выполняйте все умножение и деление слева направо и, наконец, все операции сложения и вычитания слева направо.
Популярным способом запоминания порядка является аббревиатура PEMDAS. Круглые скобки, экспоненты, умножение и деление, сложение и вычитание. Вы также можете создать небольшую фразу, например « P lease E xcuse M y D ear A unt S ally». Что бы вы ни выбрали, убедитесь, что вы хорошо знаете все шесть этапов порядка действий.
Давайте попробуем решить это уравнение еще раз, на этот раз с помощью PEMDAS.
Шаг 1) Круглые скобки.Нет ни одного. Двигаться дальше.
Шаг 2) Показатели. Никто. Продолжай …
Шаг 3) Умножение и деление. Идите слева направо, выполняя все операции умножения и деления по мере того, как вы сталкиваетесь с этим, поэтому разделите 6 на 2, чтобы получить 3, и умножьте это на 11, чтобы получить 33.
Шаг 4) Сложение и вычитание. Слева направо: 4 + 33 = 37.
$$ 4 + 6 \ div 2 * 11 $$ $$ 4 + 3 * 11 $$ $$ 4 + 33 $$ $$ 37 $$Вся идея состоит в том, чтобы просто следовать правилу: PEMDAS. Теперь мы можем попытаться решить проблему со скобками и показателями степени.2 \ div 5 $$ $$ 5 + 144 \ div 5 $$ $$ 5 + 28,8 $$ $ 33,8 $
К настоящему моменту вы должны иметь базовое представление о порядке операций. Чтобы продолжить изучение этой темы, вы можете продолжать просматривать наш сайт или попробовать поискать в Интернете на Yahoo или Google. MathGoodies.com также предлагает отличный урок о порядке операций.
Как решить вирусную математическую задачу 2019
Вот оно появилось в Твиттере, как жестокая насмешка:
Этот контент импортирован из Twitter.Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.
Каждые несколько месяцев Интернет пожирает себя какой-нибудь вирусной загадкой или иллюзией, каждая из которых выводит из себя больше, чем предыдущая. И так, как по маслу, эта сводящая с ума математическая задача стала вирусной, следуя великой традиции таких травмирующих событий, как «Платье» и «Янни / Лорел».
Такого рода загадки преднамеренно созданы для того, чтобы разделять и подчинять, и, как и ожидалось, кажущаяся простая проблема, изложенная в оскорбительном твите — 8 ÷ 2 (2 + 2) — на практике вызвала гражданскую войну в офисе Popular Mechanics . которыми мы также делимся с нашими (бывшими) друзьями в журналах Runner’s World и Bicycling .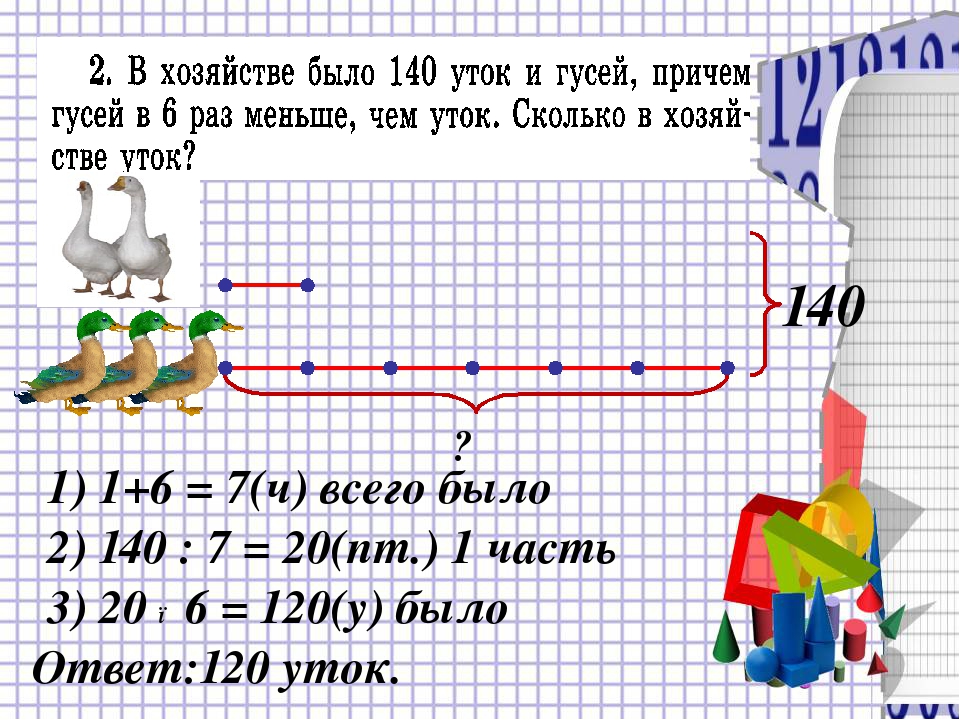
➗ Вы любите сложные математические задачи. И мы тоже. Решим их вместе.
Естественно, мы обратились к Slack, чтобы устранить наши различия. Вот горячая беседа между редакторами, которые перестали делать хоть какое-то подобие реальной работы в течение дня, чтобы решить уравнение, созданное, чтобы сбить с толку четвероклассников — и нажить много врагов в процессе, — за которым следует понимание реальных математиков и физиков, которые неохотно откликнулись на наш запрос за комментарий, чтобы раз и навсегда разрешить яростные математические дебаты.
The Slack War, часть I
Дерек Колл, видеопродюсер: 8 разделить на 8 равно 1.
Джефф Денгейт, Runner’s World Главный бегун: PEMDAS. 16.
Бобби Ли, редактор тестов (и трехкратный олимпийский велосипедист): i ride bikes
Пэт Хайне, продюсер видео: .
.. она пишет PEMDAS, а затем PEDMAS
Matt: Вы явно не слушали
Pat: Я не слушал…я была занята исправлением своей математики.
Дерек: Когда они изобретают математику заново?
Мэтт: хорошо, Дерек, видео для вас
Пат: если вы получили 16, это потому, что вы не знаете разницы между скобками и скобками.
Википедия
Морган Петруни, редактор тестирования: Я согласен с Дереком и не согласен с YouTube. Что, если вы хотите проделать долгий путь и использовать свойство распределения, а сначала распространить 2? Вы бы сделали: 8 / (4 + 4) = 1.
Или свойство распределения вдруг перестало действовать?
Я бы сказал, что это доказывает, что 1 правильный.
Дерек: Я доверяю Морган, потому что в это десятилетие у нее был урок математики.
Pat: Википедия говорит, что вы ненавидите Америку, если получаете 16.
Википедия
Дэн Роу, редактор теста: Верно, но это умножение / деление, а не умножение, а затем деление
Морган: НО умножение с круглыми скобками превосходит деление.Так что у вас все еще остается 8/2 (4). Так что сначала вам нужно сделать 2х4. По крайней мере, так меня учили.
Дэн: умные люди из Беркли говорят, что это слишком двусмысленно, чтобы говорить; PEMDAS — это не столько математическое соглашение, сколько метод обучения
Pat: умножение / деление :: правильно / неправильно
Тейлор Ройек, помощник редактора функций: Главный вывод не в том, что кто-то плохо разбирается в математике, но этот человек не умеет писать четкие уравнения
Билл Стрикленд, редакторский директор : СДЕЛАЙТЕ ЭТО СОДЕРЖАНИЕ!
инстаграм-история, в которой наши сотрудники обсуждают?
можно назвать известного математика?
Бобби: Это похоже на разговор, который относится к сегменту «Не моя работа» Подожди, подожди, не говори мне
Кэти Фогель, редактор социальных сетей: сейчас опрашивает нашу аудиторию IG по этому поводу.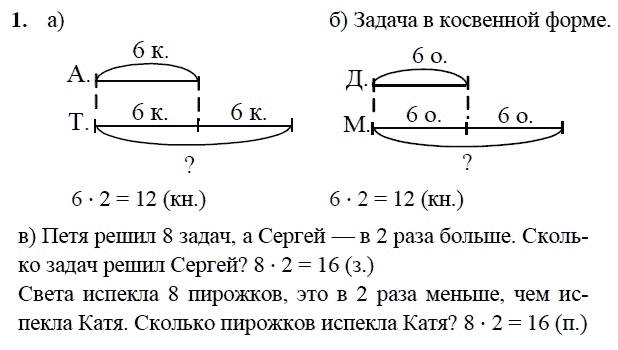
..
Pat: Уравнение написано не в соответствии со стандартами ISO, что оставляет неоднозначность интерпретации, и настоящий ответ заключается в том, что нам нужно научить лучше писать математику.
Неоднозначный PEMDAS
Неоднозначные проблемы, порядок операций, PEMDAS, BEMDAS, BEDMAS
он же … как сказал Тейлор, но из Гарварда
Морган: он же … научить распределительному свойству вместо случайных сокращений
Pat: Если написано в соответствии со стандартом ISO, ответ — 1.
Пэт Хайне
Эндрю Дэниэлс, редактор с практическими рекомендациями: честно, мы могли бы опубликовать эту слабую ветку слово в слово, а затем попросить ученого присоединиться к нам и обучить нас
Кэти Фогель: Из нашей аудитории IG …
Кэти Фогель / Instagram
Кит Фокс, редактор специальных проектов: Не возникает ли вопрос и двусмысленность, когда исчезают круглые скобки? Мол, остаются ли парены после того, как вы сделаете 2 + 2? Или они исчезнут, как только вы сначала решите мини-уравнение внутри скобок.
Я говорю, что они никуда не денутся. Я в команде 1
Я также не посещал математические классы более 10 лет
Тревор Рааб, фотограф: Мой вопрос в том, к какому сценарию реального мира это применимо к
Брэд Форд, редактор теста: Класс математики?
Тревор: ах, классический учись математике, чтобы научиться больше заниматься математикой
Бобби: школа — не настоящий мир
Морган: Создание горячих и поляризационных офисных дискуссий
Брэд: Бобби, скажи это шестикласснику.
Бобби: Я буду работать над подготовкой моего аргумента сейчас
Тейлор: У вас есть, что, 11 лет, чтобы улучшить его
Бобби: время на моей стороне
, что является кодом для: Я могу отложить это на очень долгое время
Пат: , который является кодом для «спроси свою мать»
Бобби: она любит утверждать, что она хороша в математике.
Она может пожалеть о том дне, когда хвасталась этим
Pat: «Это не поможет мне выиграть миллионы долларов, играя в Fortnite, хотя»
Краткое заявление Майка Брина, специалиста по общественной осведомленности Американского математического общества , Чья работа — «рассказывать людям, насколько велика математика»
В соответствии с порядком операций вы сначала решаете то, что указано в скобках.Это дает вам 4. Затем в PEMDAS умножение и деление имеют равный приоритет, поэтому вы должны делать первое, что происходит слева направо. Итак, сначала вы должны разделить 8 на 2, то есть 4. Таким образом, получится 16 в соответствии с классическим порядком операций.Но как написано, неоднозначно. В математике очень часто возникают двусмысленности. Математики стараются делать правила как можно точнее. По строгому порядку действий вы получите 16, но я бы не стал бить кого-нибудь линейкой по запястью, если он скажет 1.
The Slack War, часть II
Эндрю: уууу мальчик
я только что разговаривал по телефону с американским математическим обществом
какие американские горки это оказывается
мой человек микрофон с AMS, чья работа состоит в том, чтобы прямо отвечать на такие вопросы, как этот, говорит, что ответ такой .
..
Брэд: 42
Тайлер Дасвик, помощник редактора функций: тайно лучший ответ здесь
Эндрю: ШЕСТНАДЦАТЬ
Эндрю, минуты спустя: , почему никто не реагирует должным образом на эту новость
Брэд: Потому что он неправ.
Trevor: но разве это не противоречит PEMDAS?
Эндрю: он говорит (и мне придется вернуться к стенограмме), что при использовании * традиционного * порядка операций ответ будет 16
Мэтт Филлипс, старший редактор тестирования: Эндрю, у моего брата имеет степень доктора теоретической физики и пишет статьи с такими названиями, как… «Угловая зависимость для ν ‘, j’-разрешенных состояний в реактивном рассеянии F + h3 → HF (ν’, j ‘) + H с использованием нового источника пучка атомного фтора» I может посмотреть, хочет ли он взвесить…
Андрей: да! пожалуйста, сделайте [Примечание редактора: брат Мэтта не ответил.
]
Тейлор: есть ли способ, которым 1 также является правильным ответом для этого?
Тревор: PEMDAS
Эндрю: Я также отправлю запрос своему физику, который также только что ответил на вопрос POP о том, как прыгнуть с движущегося поезда
Тейлор: tbh, это было бы было бы здорово, если бы мы смогли найти экспертов, которые не согласны
Тревор: подождите, вернул мою интерпретацию PEMDAS обратно к 16
вот почему я пошел в художественную школу
Тейлор: Я спросил моего друга [УДАЛЕНО], кто такой собирается закончить университет с докторской степенью по статистике из [УДАЛЕНО], имеет три или четыре степени магистра математики
, и я так рад сообщить, что она на моей стороне
Тейлор Ройек
Дерек: [УДАЛЕНО] побеждает
Эндрю: но что [УДАЛЕНО] было ответом ??!
Тейлор: нет ответа, фальшивый вопрос, созданный, чтобы разжечь возмущение
Билл: , может быть, наш умный взгляд таков: математика не является субъективной, никто не пишет математику так, вот что не так
Тейлор: она только начинает
Тейлор Ройек
Комплект: Похоже, [УДАЛЕНО] нужно написать потную математику.
Take
Эндрю: daaaaang [УДАЛЕНО]
go off
Бобби: нет, мы на что-то наткнулись!
Прощальный выстрел от Ретта Аллена, доктора философии.D., доцент кафедры физики Университета Юго-Восточной Луизианы, вынесший окончательный вердикт и решительно закрыл нас всех
Это математическая версия вопроса «Какого цвета это платье? Синий и черный или золотой и белый? »Я отвечу, что вы сначала заключаете скобки, так что получается:
8/2 * 4
Затем вы идете слева направо.
8/2 равно 4, поэтому это
4 * 4
Теперь вы получаете 16.
Конечно, это не математика. Это условность.У нас есть соглашения о том, как писать эти вещи, точно так же, как у нас есть соглашения о том, как писать что-то по буквам. Но все же есть разные условности. Некоторые люди пишут это как «серый», а другие как «серый».
Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Вот так:8 / (2 * (2 + 2)), если это то, что вы пытаетесь сделать. Таким образом, никто не ошибется.
Футболки Popular Mechanics на Amazon
Футболка с обложки Popular Mechanics, апрель 1940 г.
Футболка на обложке Popular Mechanics, январь 1951
Футболка с обложкой журнала Popular Mechanics, июль 1982 года
Футболка с обложкой Popular Mechanics, октябрь 1943
Футболка на обложке Popular Mechanics, март 1936 года
Футболка с обложкой Popular Mechanics, июнь 1935
Футболка с обложкой Popular Mechanics, ноябрь 1923
Футболка с обложкой Popular Mechanics, ноябрь 1922
Футболка с обложкой Popular Mechanics, январь 1994
Футболка на обложке Popular Mechanics, апрель 1915 года
Футболка с обложкой Popular Mechanics, январь 1931
Футболка с обложкой журнала Popular Mechanics, июнь 1926 года
Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты.
Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
— эквивалентные уравнения, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если к обоим элементам прибавляется или вычитается одинаковое количество уравнения, полученное уравнение эквивалентно исходному уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получим
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим
.2x + 1-1 = x — 2-1
2x = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2.
В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1).
В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Разделив оба элемента на -4, получим
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
РешениеСначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить
Решение Во-первых, умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решить.
Решение Во-первых, упростите над дробной чертой, чтобы получить
Затем умножьте каждый член на 3, чтобы получить
Наконец, разделив каждого члена на 5, получим
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства.
Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить
В следующем примере мы упрощаем над дробной чертой перед применением свойств, которые мы изучали.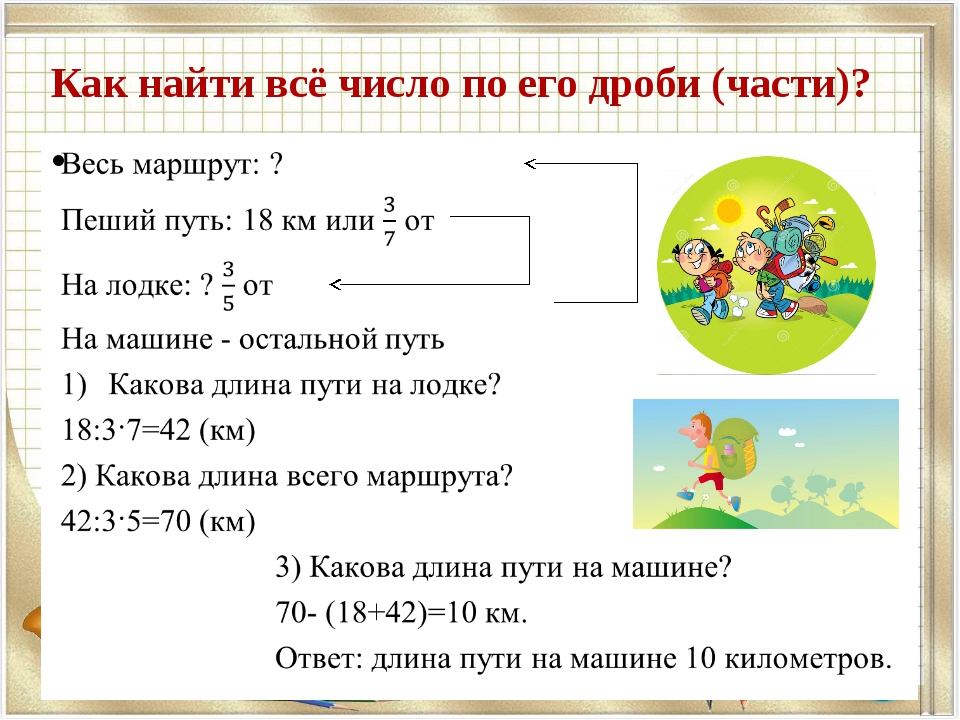
Пример 2 Решить
Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы разделим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.
Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
из которых по закону симметрии
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить
, затем разделив каждый член на a, мы получим
Эта математическая задача для пятого класса ставит в тупик всех
Здесь, в DYR, мы любим проверять ваши знания (и свои собственные) с помощью вопросов по математике, которые мы, вероятно, смогли бы решить в пятом классе. Это еще один, который докажет, действительно ли вы умнее пятиклассника! Эта математическая задача сейчас ставит в тупик всех в Интернете.
Может ты сможешь это решить
Математическое уравнение: «9 — 3 ÷ 1/3 + 1 =?». и лучший способ решить эту проблему — использовать мнемоническое устройство PEMDAS. Это также означает «скобки, показатели, умножение, деление, сложение, вычитание» или порядок операций! Однако в этом есть изюминка (слышимый стон). Многие люди выбрали 9 в качестве ответа, но это неверно.
Математическая задача / AWMИтак, каков ответ? Ответ — 1 . Как получить такой ответ? TipHero объясняет, как получить этот ответ.
«Здесь вы хотите начать сначала с решения 3 ÷ 1/3, и нет, вам здесь не положено умножаться. Разделять! Подсказка: 3 делить на 1/3 на самом деле 9. Возьмите это оттуда. Скорее всего, при использовании калькулятора соотношение между 3 и 1/3 будет восприниматься как забавный способ прийти к 1, прежде чем вычислять остальную часть уравнения. Если вы это сделали, мы понимаем, как вы пришли к своему окончательному ответу ».
Математические задачи на классной доске / Pixabay Reader’s Digest также добавляет: «Теперь, , правила PEMDAS призывают вас решать все задачи на сложение и вычитание в том порядке, в котором они появляются.
.Поэтому вместо того, чтобы складывать первым, вы будете решать уравнение слева направо ».
«Если вам все еще нужно наглядное объяснение того, как решить проблему, посмотрите видео [не включено], в котором компонент деления извлекается из середины, показывая, как решить 3 ÷ 1/3, что становится 3/1 ÷ 1/3, что равно 9. После того, как вы решите это, вы можете двигаться слева направо с помощью операций: 9-9 + 1. 9–9 — это 0, прибавьте это к 1, и вы получите 1. »
Выполнение математики на калькуляторе / pxhereТеперь, если вы похожи на меня и никогда не разбирались в математике в школе, это для вас просто куча лабиринта.Тем не менее, постарайтесь изо всех сил и посмотрите, сможете ли вы предложить 1 в качестве ответа! Один человек прокомментировал нечто удивительное, что могло либо запутать вас, либо помочь вам.
«Это просто… ДРОБИ. Деление инвертированное. Отменить и умножить… это делается перед вычитанием… так что возьмите середину… 3/1 разделите на 1/3.
это то же самое, что 3/1 X 3/1, которое равно 9. Теперь верните это в уравнение … 9-9 + 1 = 1. Просто … если вы помните свои дроби ».
Можете ли вы решить эту математическую задачу? Пожалуйста, ПОДЕЛИТЬСЯ с друзьями и семьей и узнайте, смогут ли они решить эту проблему!
Посмотрите видео ниже об одной из самых сложных математических задач SAT за всю историю:
Решатель математических уравнений
Использование калькулятора
Решайте математические задачи, используя порядок операций, такой как PEMDAS, BEDMAS и BODMAS.(Предупреждение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и экспоненциальные числа.
5 равно 2 в степени 5)
r Корни (2r3 — это 3-й корень из 2)
() [] {} Кронштейны
Вы можете попытаться скопировать уравнения из других печатных источников и вставить их сюда, и, если они используют ÷ для деления и × для умножения, этот калькулятор уравнений попытается преобразовать их в / и * соответственно, но в некоторых случаях вам может потребоваться повторно ввести скопированные и вставленные символы или даже полные уравнения.(2/3) 5 повышено до 2/3
Ввод дробей
Если вы хотите, чтобы такая запись, как 1/2, рассматривалась как дробь, введите ее как (1/2). Например, в уравнении 4, деленном на ½, вы должны ввести его как 4 / (1/2). Тогда сначала выполняется деление 1/2 = 0,5, а последним — 4 / 0,5 = 8.
Если вы неправильно введете его как 4/1/2, то сначала решается 4/1 = 4, а затем 4/2 = 2.2 — неправильный ответ. 8 был правильным ответом.
Математический порядок операций — PEMDAS, BEDMAS, BODMAS
PEMDAS — это аббревиатура, которая может помочь вам запомнить порядок операций при решении математических уравнений. PEMDAS обычно расширяется до фразы: «Прошу прощения, моя дорогая тетя Салли». Первая буква каждого слова во фразе образует аббревиатуру PEMDAS. Решайте математические задачи в стандартном математическом порядке операций слева направо:
- Круглые скобки — работая слева направо в уравнении, сначала найдите и решите выражения в скобках; если у вас есть вложенные круглые скобки, работайте от самого внутреннего к самому внешнему
- Экспоненты и корни — работая слева направо в уравнении, вычислите все экспоненциальные и корневые выражения секунды
- Умножение и деление — затем решите оба выражения умножения И деления одновременно, работая слева направо в уравнении.
- Сложение и вычитание — затем решите оба выражения сложения И вычитания одновременно, работая слева направо в уравнении
Предупреждение PEMDAS
Умножение НЕ всегда выполняется перед Делением. Умножение и деление происходят одновременно слева направо.
Сложение НЕ всегда выполняется перед вычитанием. Сложение и вычитание выполняются одновременно слева направо.
Порядок «MD» (DM в BEDMAS) иногда путают, когда он означает, что умножение происходит до деления (или наоборот). Однако умножение и деление имеют одинаковый приоритет. Другими словами, умножение и деление выполняются на одном и том же шаге слева направо. Например, 4/2 * 2 = 4 и 4/2 * 2 не равно 1.
Такая же путаница может произойти и с «AS», однако сложение и вычитание также имеют одинаковый приоритет и выполняются на одном и том же шаге слева направо.Например, 5-3 + 2 = 4 и 5-3 + 2 не равно 0.
Чтобы запомнить это, можно записать PEMDAS как PE (MD) (AS) или BEDMAS как BE (DM) (AS).
Порядок операций Сокращения
Сокращения, обозначающие порядок операций, означают, что вы должны решать уравнения в этом порядке, всегда работая слева направо в вашем уравнении.
PEMDAS означает « P арентес, E xponents, M ultiplication и D ivision, A ddition и S убирание «
Вы также можете увидеть BEDMAS и BODMAS в качестве сокращений порядка операций.В этих акронимах «квадратные скобки» совпадают с круглыми скобками, а «порядок» совпадает с показателями степени.
BEDMAS означает «ракетки B , компоненты E , D ivision и M ultiplication, A ddition и S убирание «
BEDMAS похож на BODMAS.
BODMAS означает « B ракетки, O rder, D ivision и M ultiplication, A ddition и S убирание «
Ассоциативность операторов
Умножение, деление, сложение и вычитание левоассоциативны.Это означает, что при решении выражений умножения и деления вы переходите от левой части уравнения к правой. Точно так же, когда вы решаете выражения сложения и вычитания, вы действуете слева направо.
Примеры левоассоциативности:
- а / б * с = (а / б) * с
- а + б — с = (а + б) — с
Показатели и корни или радикалы правоассоциативны и решаются справа налево.(4/5))
Для вложенных скобок или скобок: сначала решите самые внутренние скобки или выражения скобок и двигайтесь к самым внешним скобкам.
Для каждого выражения в круглых скобках следуйте остальной части порядка PEMDAS: сначала вычислите экспоненты и радикалы, затем умножение и деление и, наконец, сложение и вычитание.
Вы можете решить умножение и деление на одном и том же этапе математической задачи: после решения скобок, степеней и радикалов и перед сложением и вычитанием.Для умножения и деления действуйте слева направо. Решение сложения и вычитания следует после скобок, показателей степени, корней и умножения / деления. Снова действуйте слева направо для сложения и вычитания.
Сложение, вычитание, умножение и деление положительных и отрицательных чисел
Этот калькулятор следует стандартным правилам для решения уравнений.
Правила сложения (+)
Если знаки одинаковые, оставьте знак и складывайте числа.
-21 + -9 = — 30
(+7) + (+13) = (+20)
Если знаки разные, вычтите меньшее число из большего числа и сохраните знак большего числа.
(-13) + (+5) = (-8)
(-7) + (+9) = (+2)
Правила для операций вычитания (-)
Сохраните знак первого числа.Замените все следующие знаки вычитания на знаки сложения. Измените знак каждого следующего числа так, чтобы положительное стало отрицательным, а отрицательное стало положительным, затем следуйте правилам для задач сложения.
(-15) — (-7) =
(-5) — (+6) =
(+4) — (-3) =
(-15) + (+7) = (-8)
(-5) + (-6) = (-11)
(+4) + (+3) = (+7)
Правила операций умножения (* или ×)
Умножение отрицательного на отрицательное или положительного на положительное дает положительный результат.
Умножение положительного на отрицательное или отрицательного на положительное дает отрицательный результат.
-10 * -2 = 20
10 * 2 = 20
10 * -2 = -20
-10 * 2 = -20
-10 × -2 = 20
10 × 2 = 20
10 × -2 = -20
-10 × 2 = -20
Правила для операций дивизии (/ или ÷)
Подобно умножению, деление отрицательного на отрицательное или положительного на положительное дает положительный результат.Разделение положительного на отрицательный или отрицательного на положительное дает отрицательный результат.
-10 / -2 = 5
10/2 = 5
10 / -2 = -5
-10 / 2 = -5
-10 ÷ -2 = 5
10 ÷ 2 = 5
10 ÷ -2 = -5
-10 ÷ 2 = -5
Мармелад | 10 методов для более быстрого решения математических задач
29 апр. 10 Методы более быстрого решения математических задач
“ Разница между поэтом и математиком состоит в том, что поэт пытается забраться головой в небеса, а математик пытается вбить небеса в свою голову.”
— Г.
К. Честертон
В современном мире бесчисленное множество людей боятся математики. Сложность решения проблем с большим количеством пользователей — обычная проблема, с которой борются многие люди. В этой статье я хочу поделиться с вами некоторыми простыми математическими приемами. Техники заключаются в следующем.
Большие числа
Сложить большие числа без калькулятора может быть очень сложно, но вы можете сделать этот процесс очень простым и легким, преобразовав все числа в числа, кратные 10.Например, если вам нужно добавить 644 + 238:
- Прежде всего округлите числа до 650 и 240.
- Сложите оба округленных числа; ответ — 890.
- Найдите разницу между исходными и округленными числами, например 650 — 644 = 6 и 240 — 238 = 2,
- Добавьте разницу, например 6 + 2 = 8.
- Наконец, вычтем 8 из 890; ответ — 882.
Вычитание
Если вы хотите вычесть большое число из 1000, просто вычтите последнее число из 10 и вычтите все остальные числа из 9.Предположим, например, что вы хотите вычесть 1000 — 556.
- Прежде всего, отработайте 9 — 5 = 4.
- Во-вторых, сделать 9 — 5 + 4.
- Наконец, вычислим 10-6 = 4.
- 444 — ваш ответ.
Отдел
Хотите узнать, как можно разделить число поровну? См. Несколько примеров ниже:
- 10, если число заканчивается нулем.
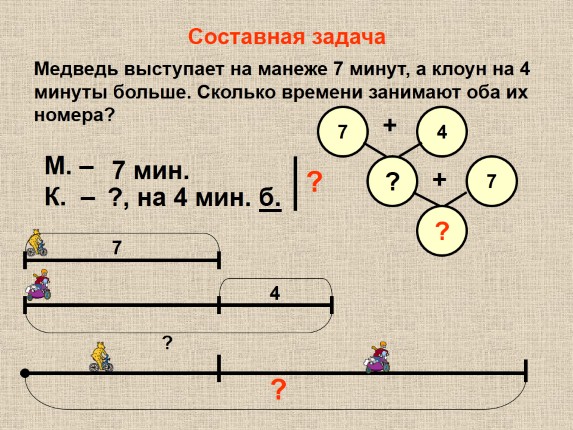
- 9, когда числа сложены и полученная сумма может быть разделена на 9.
- 8, если случай таков, что последние 3 числа можно разделить на 8.
Умножение на 9
С помощью этой техники вы можете умножить любую цифру до 9. Рассмотрим для примера 9 x 3:
- Вычтите 1 из цифры, которую нужно умножить на 9, например 3 — 1 = 2.
- Вычтите ответ из 9, например 9 — 2 = 7.
- Объедините 2 и 7, например 27.
- Смотрите, работает! 9 х 3 = 27.
5-кратное умножение (четное число)
Возможно, вы умножили 5 на множество четных чисел.
Что ж, это умножение можно сделать быстрее. Рассмотрим на примере 5 x 4.
- Разделите 4 на 2 — ответ 2.
- Добавьте ноль к приведенному выше ответу, чтобы получилось 20.
Уловка в 10 раз
Если вы хотите умножить любую цифру на 10 и получить быстрый ответ, просто добавьте 0 в конце цифры. Рассмотрим пример: 62 x 10 = 620.
%%%
С помощью этого метода можно быстро найти проценты. Например, если вы хотите найти 5% от 235, выполните шаги ниже
.- Перемещение десятичной запятой на одно место, e.грамм. 23.5.
- Разделил указанное выше значение на 2.
- Ответ: 11,75.
Быстрое выравнивание
Рассмотрим число 35.
- Разделите 3 из 35 на 3, ответ — 1
- Поместите 25 в конце.
- «[3 x (3 + 1)] x 25»
- Решите первую часть уравнения сначала «[3 x (3 + 1)] = 12»
- Умножьте ответ на 25, чтобы получить окончательный ответ: «12 x 25 = 1225»
Жесткое умножение
При умножении больших чисел, если одна из цифр четная, вы можете сделать следующее:
- Например, вы хотите умножить 20 x 120.
- Прежде всего, разделите 20 на 2, чтобы получилось 10, затем удвойте 120, чтобы получить 240.
- Умножьте 10 x 240, чтобы получить 2400 — это окончательный ответ.
Числа, заканчивающиеся на «0»
Для быстрого умножения чисел, оканчивающихся на «0», рассмотрите следующие
- Предположим, вы хотите умножить 200 на 400.
- Умножьте 4 на 2, чтобы получить 8.
- Поместите все нули после 8, чтобы получилось 80 000 (это окончательный ответ).
Заключение
Это некоторые из основных приемов, которые вы можете использовать, чтобы немного упростить решение математических задач.
