Главная → Видеоуроки → Математика. 5 класс. Натуральные числа. Описание видеоурока: Деление столбиком — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым, делится на другое, называемое делителем, производя результат, называемый частным. Этот способ позволяет выполнять деление произвольно больших чисел, разбивая процесс на серию последовательных простых шагов. 00:15:58 Валерий Волков 38 15.09.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
10 — 11 класс.
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице.
Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое.
Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.
. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого.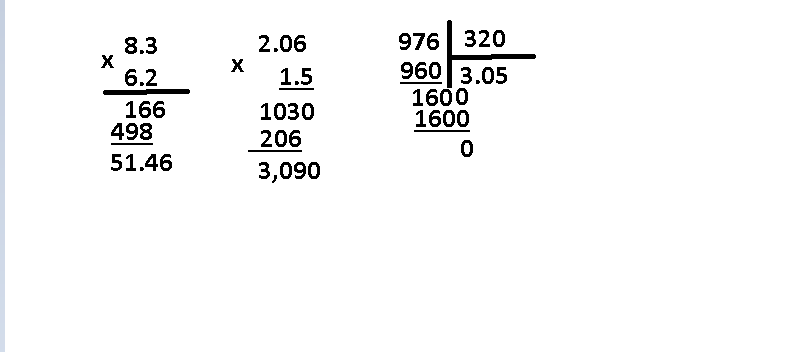
Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0. В итоге отмечаем новое рабочее число — 20.
Важно!Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8.
В самой нижней строчке записываем число 0. Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбикРазделим натуральное число 7136 на натуральное число 9.
Запишем:
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбикРазделим число 7042035 на 7.
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбикРазделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Разделим натуральное число 238079 на 34.
Ответ: 7002
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Объяснение короткого деления и длинного деления
Мы работали с экспертами по начальной математике, чтобы создать руководство для родителей и новых учителей по короткому делению (включая метод автобусной остановки) и страшному длинному делению.
В этой статье мы объяснили все, что вам нужно знать, чтобы помочь вашему ребенку разобраться с этими сложными темами!
Неважно, короткое это деление или длинное, для многих детей и их родителей одно только упоминание слова «Д» может вызвать мурашки по спине у многих юных математиков, но это не так. должно быть дело!
Здесь, в Third Space Learning, мы стремимся сделать математику доступной для всех, включая деление на короткое и длинное деление… представляют собой математическую задачу), поэтому неудивительно, что многие из нас до сих пор находят ее сложной.
В настоящее время, когда дети проводят много времени в школе, понимая , как работает деление , а не просто запоминая метод, страх перед делением KS2 тает, но подведение итогов и поиск будут иметь большое значение, особенно если родители могут поддержка из дома.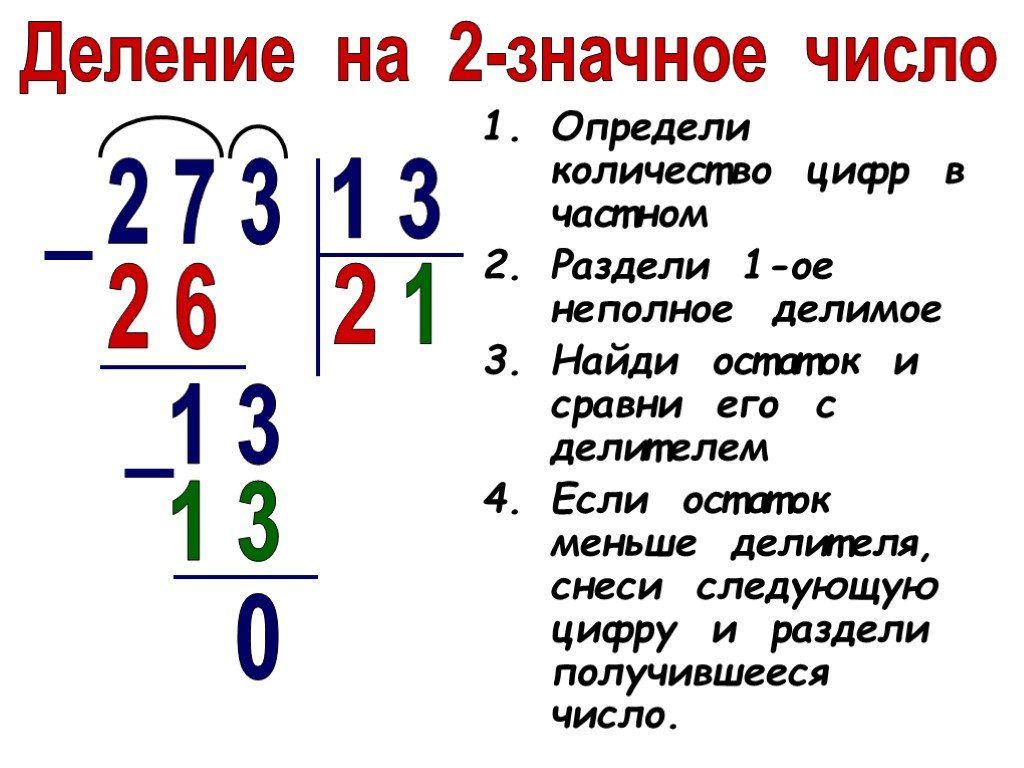
Но прежде чем вы узнаете все, что вам нужно знать о дивизионах для детей, мы подготовили для вас краткий обзор дивизий!
Этот блог является частью нашей серии блогов, предназначенных для учителей, школ и родителей, поддерживающих домашнее обучение.
Рабочие листы на деление в длинное число для 3-6 классов
Этот БЕСПЛАТНЫЙ ресурс содержит 3 готовых к использованию рабочих листа для вашего класса, которые помогут им со всеми аспектами деления в длинное число, от однозначных чисел до вычисления кратных!
Как учить делению:
Вкратце о методах деленияМы знаем, насколько чертовски сложным может быть деление, поэтому давайте начнем с некоторых определений и резюме того, что вы, возможно, забыли со школы.
Что такое деление в математике?Деление — это операция, обратная умножению и заключающаяся в разделении на равные части или группы.
В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности.
Их:
- Разделение на части
- Короткое деление (также известное как метод автобусной остановки)
- Длинное деление
Подробнее: Что такое деление?
Что такое фрагментация?Разбиение на части — это метод, используемый для деления больших чисел, которые невозможно разделить в уме.
При использовании метода фрагментации дети будут многократно вычитать делитель из делимого, пока не будет получен ответ. Например, 12 ÷ 3 можно решить, выполнив 12 – 3, чтобы получить 9., 9 – 3, чтобы получить 6, 6 – 3, чтобы получить 3, а затем 3 – 3, чтобы получить 0.
Когда все 3 вычитаются из 12, подсчитываются (4), становится ясно, что ответ 4.
Что такое короткое деление?Короткое деление — это быстрый и эффективный метод деления больших чисел.
После того, как ваш ребенок освоится с делением на фрагменты, он перейдет к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым, выполнив ряд простых шагов.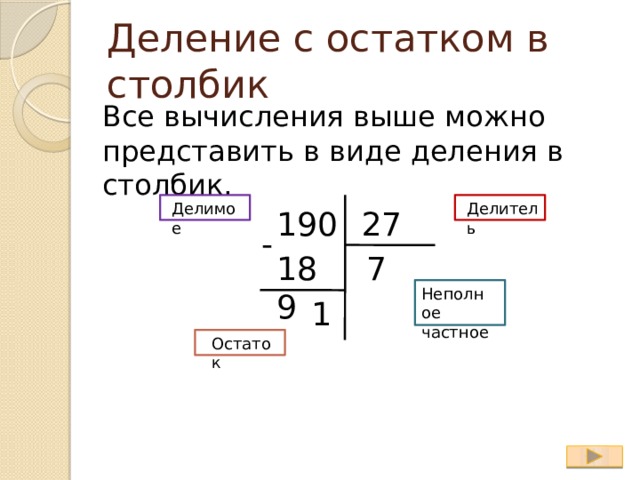
Например:
В этом примере у нас есть 9 десятков, которые нужно разделить на четыре. 9 десятков ÷ 4 = 2 десятка, и у нас остался один десяток.
Этот остаток затем передается следующему числу (шесть), чтобы получилось 16 единиц. 16 единиц ÷ 4 равно 4, поэтому при суммировании ответ становится 24.
Какой метод автобусной остановки?
Метод деления на автобусной остановке — это просто еще одно название сокращенного деления. Он получил свое название от идеи, что делимое (число, которое вы хотите разделить) находится внутри автобусной остановки, а делитель ждет снаружи.
Учителя расходятся во мнениях относительно того, действительно ли это изображение полезно при изучении деления, поэтому в большинстве случаев мы просто будем называть его коротким делением.
Что такое длинное деление? Длинное деление — это метод, который используется при делении большого числа (обычно трех или более цифр) на двузначное (или большее) число.
Он изложен аналогично методу автобусной остановки, который используется для короткого деления.
Взгляните на наш пример ниже, чтобы увидеть, как деление в длину объясняется наглядным примером.
Лучше всего это объяснить на примере – см. ниже.
У нас есть очень подробная статья, написанная для учителей на эту тему, которая может вам понравиться, если вы хотите более подробно изучить метод деления в KS2.
Терминология, которую необходимо знать при обучении разделу
В наших блогах мы стараемся избегать слишком большого количества профессионального жаргона, но следующие три термина действительно важны для всех, кто изучает раздел.
- Дивиденд — это число, которое вы делите (число внутри «автобусной остановки»).
- Делитель — это число, на которое вы делите.
- Частное — это сумма, которую получает каждый делитель, т.е. ответ в большинстве случаев.
Хороший способ запомнить это делимое ÷ делитель = частное .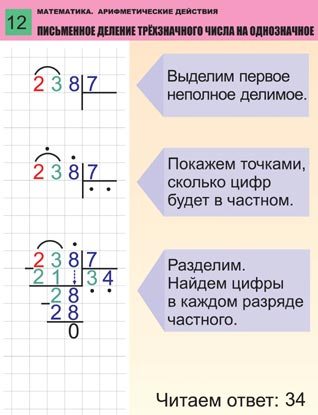
Изучив правильный словарный запас всех частей задачи на деление, ваш ребенок найдет многие элементы задачи на деление намного проще.
Что мой ребенок должен знать о коротком и длинном делении в KS1 и KS2?
В связи с тем, что дети меняются из года в год на протяжении всей начальной школы, в кратком и длинном делении в блоге есть что рассказать, но чтобы помочь вам, мы разбили его по годам.
Как обучать разделу
1-й годВ 1-м классе раздел обычно называется , разделяя , и это делается с использованием конкретных предметов, таких как прилавки, кубики или даже продукты питания, такие как макароны.
Это помогает детям понять разделение как разделение между группами.
Простой пример этого можно найти ниже.
Несколько простых задач на деление для 1-го класса Возьмите математические манипуляторы или кубики, чтобы помочь юным ученикам решить эти задачки на деление.
Убедитесь, что вы не забыли использовать такие слова, как разделить и разделить повсюду, чтобы ваш ребенок познакомился с понятиями, где делитель — это количество групп, между которыми должен быть разделен дивиденд.
Начните с 4 блоков. Разделите их на 2 равные группы.
Начните с 10 блоков. Разделите их на 2 равные группы.
Начните с 6 блоков. Разделите их на 3 равные группы.
Как преподавать деление Год 2Во втором классе дети начинают более глубоко изучать принцип деления, а это значит, что вашему ребенку предстоит научиться еще кое-чему.
Ключевая концепция, которую нужно понять и освоить в этом возрасте, — 9 лет.0003 коммутативность .
Если вы изо всех сил пытаетесь вспомнить, что именно означает коммутативность, определение простое.
В математике свойство коммутативности утверждает, что порядок не имеет значения.
Умножение коммутативное ; вы можете поменять местами числа, и это не имеет значения.
2 x 3 = 6
3 x 2 = 6
Деление не коммутативное . Если вы поменяете порядок чисел, это изменит ответ.
4 ÷ 2 = 2
2 ÷ 4 = 0,5
Деление и коммутативность во 2-м классе
В этом возрасте полезно практиковаться в изучении таблиц умножения на 2, 5 и 10 с соответствующими фактами деления. Например:
Факт умножения:
2 x 5 = 10
Соответствующие факты деления:
10 ÷ 5 = 2
10 ÷ 2 = 5
обратное умножению, и они являются отличным примером того, почему коммутативность важна.
Если вашего ребенка устраивает разница между 10 ÷ 5 и 10 ÷ 2, даже после того, как он увидит, что 5 x 2 равно 2 x 5, он будет лучше подготовлен для комфортного перехода к короткому дивизиону KS2 и длинному KS2. разделение.
Как научить делению Год 3 В 3-м классе ваш ребенок сосредоточится на записи вычислений деления и решении основных задач на деление, связанных с пропущенными числами.
Здесь очень пригодятся знания об умножении и делении, поэтому, как и в случае со 2-м классом, очень важно практиковать их со своим ребенком.
Эта проблема пропущенных чисел поможет вам понять, почему знание таблицы умножения значительно упрощает деление:
5 x 4 = 20
__ ÷ 5 = 4
20 ÷ __ = 5
Также есть два письменных метода деления, которые вводятся в этом возрасте, и они разбиты ниже.
Письменные методы деления для детей
Объяснение метода деления на фрагменты
Хотя этот метод немного медленнее, чем деление на автобусной остановке, он отлично подходит для развития умственных навыков, необходимых детям для более сложного деления в дальнейшем.
Как сделать разбиение на части метод деленияРазбиение на части — это когда вы определяете, сколько раз одно число входит в другое число.
Вы вычисляете это, многократно вычитая делитель (или кратные делителю), пока не доберетесь до нуля, чтобы увидеть, сколько раз делитель может войти в число, которое вы делите (делимое).
Разделение на фрагменты — это хороший способ познакомить вашего ребенка с некоторыми из основных понятий деления, и как только они с этим смирятся, они смогут перейти к методу краткого деления.
Объяснение метода короткого деления или метода деления на автобусной остановкеЧасто называется методом автобусной остановки из-за того, что при выводе на лист бумаги расчет имеет некоторое визуальное сходство с автобусной остановкой, этот метод короткого деления KS2 является одним из самых популярных методов, которым обучают в школах.
Этот метод быстрее, чем фрагментация, но важно, чтобы дети понимали, что они делают (а не просто следовали методу).
Это значительно облегчит деление на части в будущем, но рекомендуется убедиться, что ваш ребенок научился разделять на фрагменты, прежде чем переходить к делению на короткие.
Как выполнить краткое деление В этом возрасте краткое деление будет включать однозначные делители и 3- или 4-значные дивиденды.
Сядьте вместе с ребенком и посмотрите на схему ниже, чтобы узнать названия и места для каждой части задачи на деление.
Они могут выглядеть очень незнакомыми, когда вы привыкли выписывать свои суммы в строку, поэтому поработайте с ребенком, чтобы убедиться, что он знает свой делитель по делимому!
Как помочь ребенку разделить трех- или четырехзначное число на однозначное числоТак как эти типы вопросов на деление составляют большинство вопросов на деление в 3-м классе, вот рисунок, в котором подробно показано, как разделить трех- или четырехзначное число число однозначным числом.
Как учить деление Год 4В 4 классе ваш ребенок будет использовать краткое деление (метод деления на автобусной остановке, описанный выше), чтобы делить числа до четырех цифр на двузначные числа.
Метод точно такой же, как и с однозначными цифрами, за исключением того, что первый шаг всегда включает группировку.
На этом этапе процесс деления становится гораздо более трудным, если ваш ребенок не выучил наизусть свою таблицу умножения, поэтому лучшее, что вы можете сделать для него, — это помочь ему выучить ее.
Им также нужно будет выбрать, какой остаток использовать в зависимости от вопроса, а некоторые распространенные вопросы будут связаны с реальными ситуациями, например, с разделением групп между автомобилями или предметами между ящиками.
Вопросы на деление с остаткомДеление с остатком может быть сложной концепцией для понимания, когда дети впервые знакомятся как с коротким, так и с длинным делением, но важно, чтобы дети хорошо их понимали, поскольку они могут резко измениться в зависимости от вопроса, который спрашивают.
Практикуйтесь в использовании пар множителей в 4-м классе, чтобы облегчить письменное деление Пары множителей — это два множителя (числа), которые при умножении вместе дают определенный продукт (результат).
Упражнения с парами факторов могут помочь вашему ребенку ускорить процесс деления, так как знание того, что 4 x 5 = 20, поможет ему, когда дело доходит до вычисления 20 ÷ 4 = _ .
Попросите вашего ребенка найти как можно больше пар множителей для приведенного ниже числа, и почему бы не превратить это в игру?
Сядьте вместе со своим ребенком, возьмите ручку и лист бумаги и посмотрите, кто сможет вычислить наибольшее количество пар множителей для следующих чисел за минуту. Результаты могут быть ближе, чем вы думаете!
- 20
- 68
- 12
- 30
- 100
Подробнее: Что является самым высоким общим фактором
Как обучить год 5. должен уметь быстро мысленно уменьшать сумму вдвое или вчетверо. Если им трудно, внедрение математики в реальный мир может стать отличным способом помочь им справиться с половинками и четвертинками. Например, когда вы находитесь вне дома, спросите их, сколько будет стоить предмет, если он будет стоить половину, или сколько граммов будет в половине 1-килограммового мешка сахара.
Умение быстро делить на 2 (деление пополам) и 4 (четвертование) станет важной частью деления по мере того, как ваш ребенок будет учиться в школе, поэтому будет очень полезно, если он сможет научиться этому прямо сейчас.
Сокращенное деление с десятичными знакамиСокращенное деление будет использоваться для чисел, содержащих десятичные дроби, впервые в 5-м классе.
Это означает, что самое время пересмотреть разрядность, чтобы ваш ребенок понял, как работают десятичные дроби.
Десятичные числа являются частями целого (аналогично дробям), но при делении десятичных дробей важно помнить, что столбцы разрядных значений уменьшаются в значении каждый раз, когда вы перемещаетесь вправо.
Пример десятичного деления Как научить деление Год 6В 6-м классе ваш ребенок впервые познакомится со страшным делением на две части!
Однако хорошая новость заключается в том, что как только вы освоите деление на фрагменты и короткое деление, длинное деление совсем не так уж плохо!
Ключевым моментом, когда дело доходит до деления в длину для детей, является не торопиться и поощрять их аккуратно представлять свою работу, чтобы они могли легко замечать ошибки и работать над их исправлением.
Даже зная об этом, деление в длинное число все еще может быть пугающей перспективой для детей (и родителей!), поэтому взгляните на наш пример ниже, чтобы понять, как решить задачу деления в длинное число.
Вы учитель, который ищет поддержку в обучении делению в столбик? Ознакомьтесь с нашими идеями и советами по обучению делению в столбик, написанными опытными математиками-практиками.
Объяснение деления в длинное деление для детейВ приведенном ниже примере показан самый популярный метод деления в длинное деление для детей, а также тот, с которым вы, возможно, знакомы еще со времен начальной школы.
Все, что вам нужно для завершения вычисления 528 ÷ 24, это ручка, немного бумаги и ребенок, который хочет освоить этот метод!
После того, как вы попробуете ответить на несколько вопросов на деление на длинное деление (с вашей помощью для начала), ваш ребенок вскоре увидит, что этот метод может помочь ему понять, как решать задачи на деление на длинное деление, независимо от задействованных чисел, и окажется неоценимым.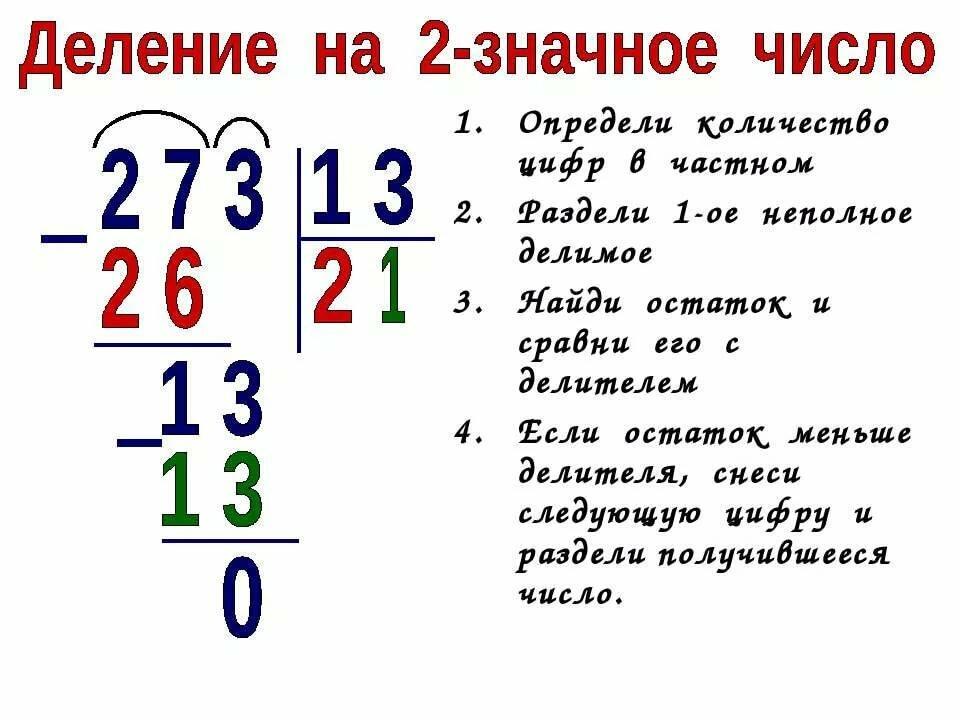
когда дело доходит до SAT.
Не беспокойтесь, если для полного внедрения процесса потребуется некоторое время. Это длинная цепочка вещей, которые нужно запомнить, поэтому потребуется регулярная практика, чтобы запомнить этот метод. Ознакомьтесь с нашими вопросами о длинном делении и примерами длинного деления для получения дополнительной поддержки.
Просто запомните процесс: делить, умножать, вычитать, сводить; и повторить.
Тяжелая работа окупится в долгосрочной перспективе, поэтому стоит уделить время своему ребенку сейчас, чтобы убедиться, что деление в столбик хорошо объяснено на раннем этапе, чтобы уменьшить количество раз, когда вы услышите неизбежное:
Откуда мы знаем, когда делить и какой метод использовать?« Муммммм…….Как вы делаете деление в длинное…?»
Различные вопросы на деление требуют разных методов деления для их решения, но вот краткое и простое руководство, которое покажет, какой метод и когда должен использовать ваш ребенок:
- Разбиение лучше всего подходит для небольших чисел и арифметики.
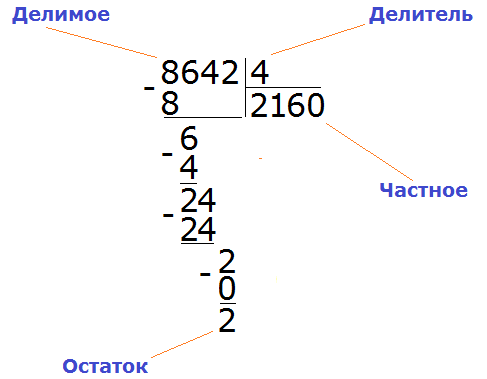
- Сокращенное деление отлично подходит для деления больших чисел на однозначные числа.
- Длинное деление удобно для деления больших чисел на числа, состоящие из 2 и более цифр.
Конечно, могут быть случаи, когда каждый из вышеперечисленных методов можно использовать в немного разных сценариях, но, как правило, этого должно быть достаточно, чтобы помочь вашему ребенку принять правильное решение.
Вопросы по разделу SAT для 6-го классаКогда придет время сдавать экзаменационные работы по математике, более чем вероятно, что вашему ребенку придется отвечать на некоторые вопросы по разделу.
Решение задач и рассуждения (бумаги 2 и 3) в 6-м классе могут быть сложными, когда речь идет о задачах на деление. Часто задачи требуют решения более чем одной операции, что может добавить элемент сложности в и без того напряженную обстановку, поэтому поощряйте ребенка обращать внимание на такие слова, как , делиться или , группировать , чтобы помочь им идентифицировать что нужно сделать для решения проблемы.
Задачи на деление в задании 1 (арифметика) будут представлены в виде числовых предложений, и ваш ребенок должен будет продемонстрировать свое решение, если вопрос оценивается более чем в 1 балл.
Эти вопросы легко определить, потому что они будут использовать символы деления:
÷
или
, или они могут включать дроби.
Как правило, поощряйте ребенка к мысленному разделению, когда это возможно.
Хотя письменные методы отлично подходят для больших чисел, возможность мысленного деления даст им преимущество. Это означает, что когда они выполнят письменный метод, они смогут увидеть, является ли их ответ примерно правильным, путем оценки.
Помимо бесплатных печатных рабочих листов и вопросов на деление, вы также можете загрузить набор бесплатных вопросов SAT по делению и умножению, чтобы расширить свою практику.
Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч учащихся начальной школы.
С 2013 года мы помогли более 130 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
Обучение математике для детей в возрасте от 5 до 12 лет в соответствии с национальной учебной программой и проводится онлайн
Отдел ÷ | Основы арифметики
На этой странице описаны основы деления (÷) .
См. другие наши арифметические страницы для обсуждения и примеров: сложение ( + ), вычитание (-) и умножение ( × ).
Раздел
Обычный письменный символ деления (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять вычисления деления.
Как только мы хорошо разберемся в методе и правилах, мы сможем использовать калькулятор для более сложных вычислений, не делая ошибок.
Разделение позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте подумаем, как найти ответ на 10 ÷ 2 (десять разделить на два). Это то же самое, что «делить» 10 конфет между двумя детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ 5.
Некоторые краткие правила деления:
При делении 0 на другое число ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 конфет делится поровну между 2 детьми — каждый ребенок получает 0 сладости.
Когда вы делите число на 0, вы вообще не делите (это серьезная проблема в математике). 2 ÷ 0 невозможно. У вас есть 2 конфеты, но нет детей, чтобы разделить их между собой. На 0 делить нельзя.
При делении на 1 ответ совпадает с числом, которое вы делили. 2 ÷ 1 = 2. Две конфеты разделить на одного ребенка.
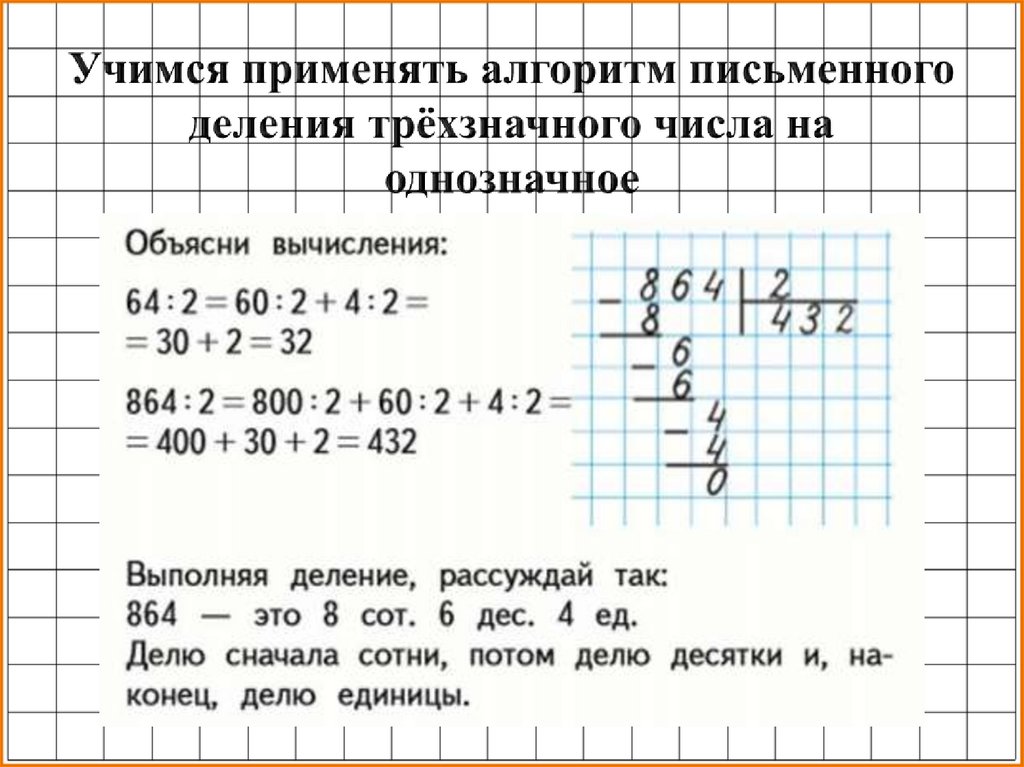
При делении на 2 число уменьшается пополам. 2 ÷ 2 = 1.
Любое число, деленное на одно и то же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет разделить на двадцать детей — каждый ребенок получает по одной конфете.
Числа должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять конфет, разделенных на двоих детей, сильно отличаются от 2 конфет, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ равно 1 ÷ 2. Одна конфета делится на двоих детей. См. нашу страницу Фракции для получения дополнительной информации.
Множественные вычитания
Точно так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.
Например:
Если у Джона в машине 10 галлонов топлива, и он использует 2 галлона в день, сколько дней до того, как у него закончится топливо?
Мы можем решить эту задачу, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.
- В день 1 Джон начинает с 10 галлона и заканчивает 8 галлона. 10 — 2 = 8
- В день 2 Джон начинает с 8 галлона и заканчивает 6 галлона. 8 — 2 = 6
- В день 3 Джон начинает с 6 галлона и заканчивает 4 галлона. 6 — 2 = 4
- В день 4 Джон начинает с 4 галлона и заканчивает 2 галлона. 4 — 2 = 2
- В день 5 Джон начинает с 2 галлона и заканчивает 0 галлонов. 2 — 2 = 0
У Джона закончилось топливо на 5-й день.
Более быстрый способ выполнить это вычисление — разделить 10 на 2. То есть, сколько раз 2 делится на 10 или сколько партий по два галлона содержится в десять галлонов? 10 ÷ 2 = 5,
Таблица умножения (см.
умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (красный заштрихованный заголовок). Двигайтесь вниз по столбцу, пока не найдете искомый номер 10 . Переместитесь по строке влево, чтобы увидеть ответ (красный заштрихованный заголовок) 5 .
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Мы можем выполнить другие простые вычисления деления, используя тот же метод.
56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки 8 .
Если возможно, постарайтесь выучить приведенную выше таблицу умножения, потому что она значительно ускоряет выполнение простых операций умножения и деления.
Деление больших чисел
Вы можете использовать калькулятор для выполнения вычислений с делением, особенно когда вы делите большие числа, которые труднее вычислить в уме. Однако важно понимать, как выполнять вычисления деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также необходимо, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может показаться пугающим, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и со всей математикой, проще всего это понять, если мы рассмотрим пример:
Машине Дейва нужны новые шины.
Ему нужно заменить все четыре шины на машине плюс запаску.
Дэйв получил предложение от местного гаража на 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 будет входить в 480?
Условно запишем так:
| 5 | 4 | 8 | 0 |
Работаем слева направо в логической системе.
Начнем с деления 4 на 5 и сразу наткнемся на проблему. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 входит в 4?».
Мы знаем, что 2 дважды входит в число 4 (4 ÷ 2 = 2), и мы знаем, что 1 входит в число 4 четыре раза (4 ÷ 1 = 4), но 5 не входит в число 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно входить в число, на которое мы делим (в данном случае 4), целое число раз.
Как вы увидите, это не обязательно должно быть точное целое число.
Так как 5 не входит в 4, мы ставим 0 в первую колонку (сотни). Для получения справки о столбцах сотен, десятков и единиц см. нашу страницу о числах .
| Сотни | Десятки | Единицы | |
| 0 | |||
| 5 | 4 | 8 | 0 |
Далее мы двигаемся вправо, чтобы включить столбец десятков. Теперь мы можем увидеть, сколько раз 5 входит в число 48.
5 входит в число 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно входит в число 48.
Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 число, которое мы ищем, находится между этими двумя значениями. Помните, нас интересует , сколько раз всего 5 входит в число 48.
Десять раз — это слишком много.
Мы видим, что 5 входит в число 48 целое число (9) раз, но не точно, с оставшимися 3.
9 × 5 = 45
48 – 45 = 3
Теперь мы можем сказать, что 5 входит в число 48 девять раз, но с остатком 3. нашли из числа, на которое мы делим: 48 — 45 = 3 .
Таким образом, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбце десятков в качестве ответа для второй части вычисления и поставить наш остаток перед нашим последним числом в единицах измерения. столбец. Наше последнее число становится 30.
| Сотни | Десятки | Единицы | |
| 0 | 9 | ||
| 5 | 4 | 8 | 30 |
Теперь мы разделим 30 на 5 (или узнаем, сколько раз 5 входит в 30). Используя нашу таблицу умножения, мы видим, что ответ равен ровно 6 без остатка.
5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
| Сотни | Десятки | Единицы | |
| 0 | 9 | 6 | |
| 5 | 4 | 8 | 30 |
Поскольку остатка нет, мы закончили расчет и получили ответ 96 .
Новые шины Дэйва будут стоить 96 фунтов стерлингов каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Раздел рецептов
Наш последний пример разделения основан на рецепте. Часто при приготовлении пищи рецепты сообщают вам, сколько еды они собираются приготовить, например, достаточно, чтобы накормить 6 человек.
Ингредиенты, указанные ниже, необходимы для приготовления 24 волшебных тортов, однако нам нужно сделать только 8 волшебных тортов. Мы немного изменили ингредиенты для этого примера (оригинальный рецепт: BBC Food).
Первое, что нам нужно установить, это сколько восьмерок в числе 24.
Воспользуйтесь таблицей умножения выше или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Поэтому нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 сказочных пирожных.
Ингредиенты
- 120 г сливочного масла, размягченного при комнатной температуре
- 120 г сахарной пудры
- 3 куриных яйца, слегка взбитых
- 1 чайная ложка ванильного экстракта
- 120 г самоподнимающейся муки
- 1-2 столовые ложки молока
Количество масла, сахара и муки одинаковое, 120г. Следовательно, необходимо вычислить 120 ÷ 3 только один раз, так как ответ будет одинаковым для этих трех ингредиентов.
| 3 | 1 | 2 | 0 |
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, так как 3 больше 1. Далее мы смотрим, сколько раз 3 входит в 12.
Используя таблицу умножения, если нужно, мы можем увидеть, что 3 входит в число 12 ровно 4 раза по без остатка.
| 0 | 4 | 0 | |
| 3 | 1 | 2 | 0 |
120 г ÷ 3 равно 40 г. Теперь мы знаем, что нам понадобится 40 г сливочного масла, сахара и муки.
В исходном рецепте указано 3 яйца, и мы снова делим на 3. Таким образом, 3 ÷ 3 = 1, значит, нужно одно яйцо.
Далее по рецепту требуется 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 — это то же самое, что ⅓ (одна треть). Вам понадобится ⅓ чайной ложки ванильного экстракта, хотя на самом деле может быть сложно точно отмерить ⅓ чайной ложки!
Оценка может быть полезна, и единицы измерения можно изменить!
Мы можем посмотреть на это по-другому, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.
(Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3), а 2 остаются. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!
Мы можем оценить ответ, чтобы убедиться, что мы правы. Три партии по 1,5 мл дают нам 4,5 мл. Таким образом, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшая оценка может быть забавой и хорошей практикой для нашей ментальной арифметики.
Далее по рецепту требуется 1–2 ст.л. молока. Это от 1 до 2 столовых ложек молока. У нас нет определенного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.