Как правильно делить числа в столбик? Как научить ребенка делить столбиком двузначные и трехзначные числа за 3 и 4 класс, как ему объяснить, как делить столбиком?
Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.
Содержание статьи
- Как правильно делить числа в столбик: алгоритм деления
- Как объяснить ребенку деление и научить делить столбиком?
- Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
- Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
- Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
- Как делить в столбик с остатком?
- Как делить столбиком десятичные дроби с запятой?
- Как делить столбиком меньшее число на большее?
- Как делить столбиком числа с нулями?
- Видео: как правильно делить числа в столбик?
Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам.
Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.
Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.
Как правильно делить числа в столбик: алгоритм деления
алгоритм деления чисел столбиком
Для деления чисел столбиком следуйте по таким шагам:
- правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
- разлинейте место между делимым и делителем.
Вам поможет схема ниже.
схема и назнвания составных элементв действия деления чисел столбиком
- планируйте пространство для деления в столбик.
Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение, - первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
- перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
- завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
- допишите следующую цифру делимого к остатку и продолжайте решение,
- последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,Как объяснить ребенку деление и научить делить столбиком?
дети-школьники тренируются делить числа столбиком
Во-первых, учтите ряд вводных факторов:
- ребёнок знает таблицу умножения
- хорошо разбирается и умеет применять на практике действия вычитания и сложения
- понимает разницу между целым и его составными элементами
Дальше акценты в ваших действиях выглядят так:
- поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
- объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
- превратите процесс в игру, придумайте историю про цифры и действие деления,
- подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
- первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.
Положите её перед ребёнком и на примерах покажите удобство использования при делении,Сам процесс освоения деления столбиком:
- запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
- предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
- подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
- помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
- следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
- снова помогите с записью действия,
- продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
- закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.
Её удобно изобразить точками, которые потом превратятся в цифры,Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
обучение ребёнка делению методом солнышка
Приступим к пошаговому разбору примеров на деление в столбик.
Осуществите действие над цифрами 25 и 2:
- запишите их рядом и разделите линиями границы,
- определите нужное количество цифр делимого для первого действия,
- запишите значение под делителем и результат умножения под делимым,
- выполните вычитание,
- допишите вторую цифру делимого и повторите действия на умножение и вычитание.
Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:
незаконченное решение примера на деление столбиком двузначного числа на однозначное
Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.
Второй пример. Разделите 87 на 26 в столбик.
Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя.
Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.
Ниже пример деления столбиком двузначного числа на двузначное с остатком.
пример деления столбиком двузначного числа на двузначное с остатком
Третий пример. Как разделить число в столбик с нулем в ответе.
Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.
Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
рисунок из презентации на тему деления трёхзначного числа столбиком
Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.
Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.
Схематически он выглядит так:
пример деления трехзначного числа на однозначное столбиком
В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.
Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.
Схема деления трехзначного на двузначное числа такая:
примеры деления столбиком трехзначных чисел на двузначные
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.
Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.
Схема деления трёхзначного на трёхзначное числа.
пример деления в столбик трёхзначного числа на трёхзначное с остатком
Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
на доске решены примеры на деление столбиком трёх- и более значных чисел
В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:
- определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
- появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
- проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,Ниже пример решения.
алгоритм деления столбиком четырёхзначного числа
пример деления столбиком четырёхзначного числа на двузначное
Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.
Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:
- количество знаков у частного, то есть результата
- цифры у делимого для первого действия
- правильность переноса остальных чисел
Примеры подробного решения ниже.
примеры деления столбиком многочленов
При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:
- у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
- для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
- совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.
В первом случае запишите его в числителе, а делитель в знаменателе,Ниже ряд подробных примеров с решениями.
примеры деления многочленов в столбик
Как делить в столбик с остатком?
слайд из презентации о делении чисел с остатком
Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.
Запишите его в ответе либо:
- как дробь, где в числителе остаток, а в знаменателе — делитель
- словами, например, 73 целых и 6 в остатке
Как делить столбиком десятичные дроби с запятой?
рисунок с алгоритмом действий при делении десятичной дроби столбиком
Существует несколько особенностей при подобном делении.
Если вы совершаете действие с:
- десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
- числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
- десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.
Как делить столбиком меньшее число на большее?
девочка-школьница устала от решения примеров на деление столбиком
При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.
Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:
- первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
- поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
- когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.Ниже пример.
примеры деления столбиком меньшего числа на большее
Как делить столбиком числа с нулями?
улыбчивая девочка у школьной доски
Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.
Из нюансов отметим:
- при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
- если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.
Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.
Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.
Практикуйте полученные знания и помогайте своему чаду осваивать математику.
Видео: как правильно делить числа в столбик?
Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
- Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8).
Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному.
Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.
Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Как сделать длинное деление | Математика 3 класса
Деление — это деление числа на равные части.
Ранее вы узнали, что уравнения деления можно записывать в длинной форме, например:
До сих пор вы научились делить в основном одно- или двузначные числа.
Теперь давайте выучим длинное деление, , чтобы мы могли делить еще большие числа.
Давайте научимся вместе решать пример:
682 ÷ 2 = ?
Шаги длинного деления
Чтобы выполнить длинное деление , вы делите каждую цифру делимого или большого числа по одному, начиная с наибольшего.
Вы переносите любые остатки на меньшие разрядные значения по мере продвижения.
Давайте попробуем вместе выполнить шаги на 682 ÷ 2.
Сначала мы разделим наибольшую цифру в делимом, 6, на 2.
Сколько двоек вписывается в 6? 🤔
Правильно, 3.
Итак, пишем 3 сверху .
Далее нам нужно посмотреть, есть ли у нас остаток. Это занимает два шага: умножение, а затем вычитание. Мы думаем об этом как о комбо-ходах в видеоиграх.
Вот два этапа комбо:
1⃣ Мы Умножьте 3 и 2 и написать продукт ниже 6.
2⃣ Далее, мы 0003 вычесть это произведение из цифры в делимое ( 6), и записать ответ ниже с новой строки.
Отлично! 0 под новой строкой — это наш остаток.
Итак, что мы выяснили на данный момент?
Мы вычислили первую цифру нашего ответа, или частное, 3__ ! Мы также обнаружили, что до сих пор нет остатка. ✅ Продолжаем.
Мы приносим вниз рядом цифра, 8.
Почему?
Это поможет нам включить остаток от первого шага. 👍 В данном случае остаток был равен 0.
Далее мы спрашиваем себя, сколько двоек может вместиться в 8?
8 ÷ 2 = 4.
Сверху пишем 4 .
Затем мы делаем нашу комбинацию из двух ходов, чтобы найти остаток в этом столбце.
1️⃣ Умножаем 4 и 2 и пишем произведение ниже 8.
2️⃣ Затем вычитаем этого произведения из 8.
Хорошо. Разницу пишем ниже новой строки.
Итак, чего мы достигли на данный момент?
Мы нашли первые две цифры нашего ответа, или частное, 34_ ! Мы также обнаружили, что у нас пока нет остатка. ✅
Теперь давайте сократим до последней цифры, 2 .
Внизу осталось разделить только 2.
Спросите себя: «Сколько двоек входит в двойку?» 🤔
Правильно! Просто 1.
Итак, пишем 1 сверху .
Мы закончили? Не да. Нам нужно посмотреть, есть ли остатки. Давайте снова проделаем это двухходовое комбо.
1️⃣ Умножаем 1 и 2 и записываем произведение под 2.
2️⃣ Затем вычитаем .
У нас больше нет цифр в делимом, которые нужно уменьшить, и у нас нет остатка.
Итак, мы нашли ответ, 341!
682 ÷ 2 = 341
Отличная работа.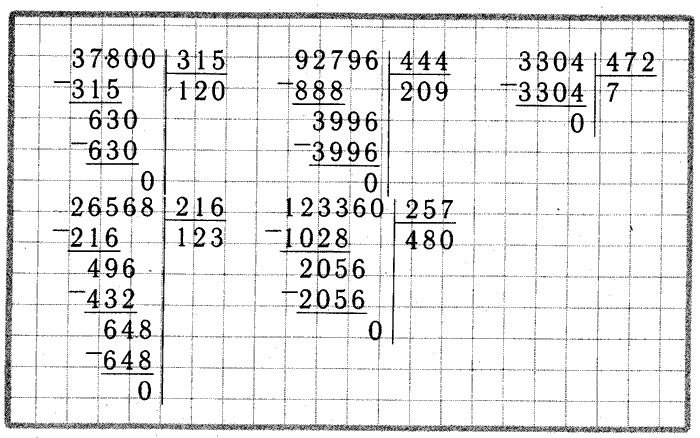
👏
Длинное деление — классный набор шагов, которые придумали люди для деления больших чисел.
Подсказка: Шаги для деления в большую сторону похожи на откусывание от делимого, по одному разряду за раз.
Полное деление очень важно, поэтому давайте попробуем другой пример.
Пример длинного деления 2
249 ÷ 3 = ?
Вы помните первый шаг?
Начните с написания задачи в виде длинное деление форма:
Теперь посмотрим на первую цифру , 2.
Сколько троек поместится в a2? 🤔
Нет или ‘0’.
Итак, давайте поместим 0 на сверху.
Подсказка : То, что мы пишем сверху, является нашим ответом или частным.
Теперь нам нужно найти остаток для переноса, прежде чем мы разделим следующую цифру.
Чтобы найти остаток, мы снова делаем комбо-ход умножение-вычитание.
0 × 3 = 0.
2 — 0 = 2. Таким образом, у нас есть остаток 2 из столбца сотни.
Затем мы переносим 4 вниз.
Совет : Поскольку в частном у нас был 0, мы могли бы пропустить несколько шагов и просто разделить первые две цифры, например:
Тем не менее, сколько 3 влезет в 24? 🤔
Очень хорошо! 8.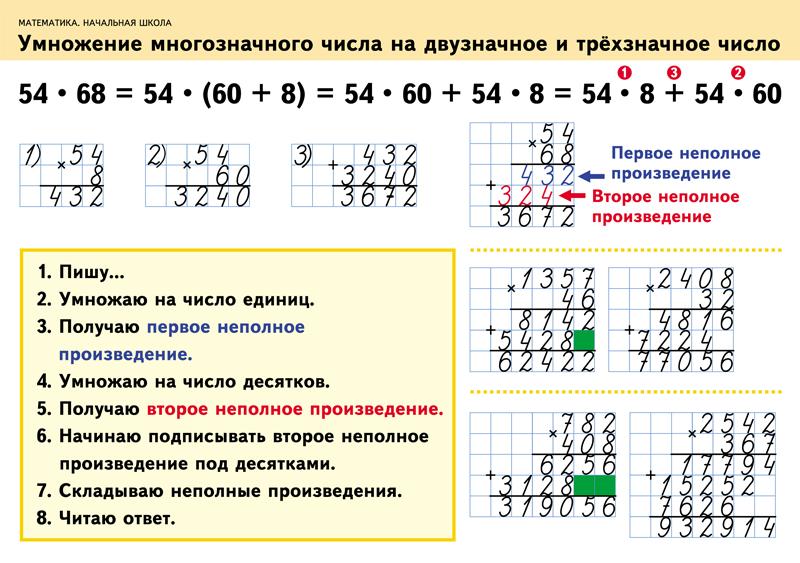
Итак, пишем 8 на Top, и напишите продукт из 8 и 3 ниже 24.
Тогда WE Suptract 24. Идеальный! Пока остатка нет, и мы нашли две цифры нашего частного. ✅
Помните следующий шаг? 😀
Мы приводим вниз следующая цифра, 9 .
Затем мы вычисляем, сколько троек умещается в 9.
Наконец, мы выполняем комбинированное движение умножение-вычитание, чтобы увидеть, остался ли остаток. На этот раз у нас нет остатка.
Итак, каков окончательный ответ?
Очень хорошо! Это 83.
249 ÷ 3 = 83
Отличная работа.
Теперь вы знаете, как делить в большую сторону. 👏
Бонус: Анимация шагов длинного деления
Вот как выглядит ускоренное длинное деление:
По сути, мы продолжаем увеличивать цифры в частном или ответе, чтобы получить как можно больше кусочков от делимого, по одному столбцу за раз.
Теперь приступайте к практике. Это лучший способ самостоятельно освоить длинное деление.
Деление трехзначных и четырехзначных чисел без остатка | Математика для 4 класса
На прошлом уроке вы научились выполнять простое деление в большую сторону.
В этом уроке вы будете использовать длинное деление для деления еще больших чисел.
Деление трехзначных чисел
Давайте попробуем решить это:
378 ÷ 6 = ?
Вы помните первый шаг деления в большую сторону? 🤔
Верно.
Начнем с того, что запишем задачу в форме деления .
Теперь посмотрим на первую цифру делимого.
Совет: делимое означает большое число, которое мы хотим разделить на части.
Первая цифра делимого, 3 78, это 3.
Сколько шестерок поместится в тройку?
Правильно. Нет или «0».
Итак, давайте положим 0 поверх 3 в частном.
Совет: частное — это ответ на задачу деления. Он идет выше длинной разделительной полосы.
Теперь давайте запишем 7.
Совет : Мы заносим только 1 цифру за раз.
У нас 37.
Сколько шестерок в числе 37?
Ты понял! 6.
Напишите 6 поверх 7 в области частного.
Затем умножьте 6 на 6.
Получится 36. Запишите ниже 37.
Затем вычтите.
Теперь сократим 8, третью цифру делимого.
Можете ли вы сказать, сколько 6 вписывается в 18? 🤔
Очень хорошо! 3.
Итак, мы пишем 3 поверх 8.
Есть остаток?
Нет.
Итак, каков наш ответ или частное?
Очень хорошо! 63.
Совет : Игнорируйте «0», если он стоит в начале числа.
378 ÷ 6 = 63 ✅
Отличная работа! 🎉
Деление четырехзначных чисел
Давайте попробуем это на примере:
8792 ÷ 7 = ?
Действия те же.
Что нужно сделать в первую очередь?
Да! Запишите задачу в форме длинного деления .
Что дальше?
Да! Подумайте, сколько семерок может поместиться в числе 8.
8 — первая цифра делимого.
Итак, сколько семерок может поместиться в 8?
Верно! 1. Мы можем уместить 7 в 8 только один раз.
Напиши 1 сверху 8.
Затем умножь это на 7, наш делитель.
Запишите произведение ниже 8 и вычтите.
Теперь сократите 7. Это вторая цифра делимого.
Это дает нам 17.
Сколько семерок может поместиться в 17?
Очень хорошо! 2.
Напишем 2 поверх 7.
Затем умножаем 7 на 2.
Что получится?
Да! Это 14.
Запишите это ниже 17.
Теперь вычитаем 14 из 17.
У нас осталось 3. Теперь давайте опустим 9.
У нас есть 39.
Сколько семерок может поместиться в 39?
Ты понял! 5.
Напишем это поверх 9.
Затем умножаем 7 на 5. Помните, 7 — наш делитель.
Произведение равно 35. Пишем ниже 39.
Потом вычитаем.
Что дальше?
Очень хорошо! Сбиваем 2.
Теперь у нас 42.
Сколько семерок может поместиться в 42?
Вот оно! 6.
👍
Умножим 6 на 7, наш делитель.
Что мы получаем?
Верно! 42
Пишем что под 42.
Потом вычитаем.
Остались цифры, которые нужно сбить?
Нет.
Это означает, что наше подразделение готово.
8792 ÷ 7 = 1,256
Отличная работа!
Давайте рассмотрим
Шаги для деления чисел одинаковы независимо от того, состоят ли они из 3 или 4 цифр.