| 1. |
Компоненты деления с остатком
Сложность: лёгкое |
2 |
| 2. |
Возможный остаток при делении на двузначное число
Сложность: лёгкое |
1 |
3.
|
Деление многозначного числа на двузначное число с остатком устно
|
1 |
| 4. |
Деление с проверкой
|
2 |
5.
|
Сложность: среднее |
2 |
| 6. | Сложность: среднее |
2 |
7. |
Деление шестизначного числа на двузначное с остатком (1)
Сложность: среднее |
2 |
| 8. |
Деление семизначного числа на двузначное с остатком
Сложность: среднее |
2 |
9. |
Неизвестный делитель
Сложность: среднее |
5 |
| 10. |
Текстовая задача (ткань)
Сложность: сложное |
2 |
11. |
Текстовая задача (картофель)
Сложность: сложное |
5 |
Письменное деление на двузначное число (без остатка и с остатком)
Как давно мы с вами не встречались! И вот, наконец, мы вместе.
Сегодня я хочу рассказать вам, как выполнять письменное деление на двузначное число.
Ещё в третьем классе вы
знакомились с темой «Деление двузначного числа на двузначное» и знаете,
что такое деление выполняется методом подбора. Вот, например, при
делении восьмидесяти семи на двадцать девять мы сначала подбирали в качестве
частного число один.
Но, проверив деление умножением и вычитанием, поняли, что остаток пятьдесят восемь больше делителя, что недопустимо. Попробовали в качестве частного число два. Остаток получился равным делителю. И только, когда попробовали число три, всё получилось.
А вот при делении числа девяносто восемь на четырнадцать было просто сплошное мучение! – семь чисел пришлось попробовать.
Вот одно из них:
Сегодня я расскажу вам о письменном приёме деления трёхзначных чисел на двузначные и поделюсь небольшим секретом, который поможет облегчить и ускорить процесс подбора нужного числа в частном. Итак, приступим.
Предположим, надо разделить триста сорок четыре на сорок три. А вот теперь – мой маленький секрет! Для того, чтобы делить было легче,
 Ведь вы помните, ребята, что сорок – это
произведение чисел десять и четыре. И мы можем делить последовательно на эти
множители. Делим триста сорок четыре на десять, а теперь тридцать четыре делим
на четыре. Получается восемь. Хочу предупредить вас, ребята, что это пока
только пробная цифра, поэтому в частное мы её не записываем, а умножаем
на неё делитель сорок три. Получается триста сорок четыре. Отлично, частное действительно
равно восьми.
Ведь вы помните, ребята, что сорок – это
произведение чисел десять и четыре. И мы можем делить последовательно на эти
множители. Делим триста сорок четыре на десять, а теперь тридцать четыре делим
на четыре. Получается восемь. Хочу предупредить вас, ребята, что это пока
только пробная цифра, поэтому в частное мы её не записываем, а умножаем
на неё делитель сорок три. Получается триста сорок четыре. Отлично, частное действительно
равно восьми.Давайте попробуем разобрать ещё
один пример. Пятьсот тридцать четыре разделим на восемьдесят девять. Помните, сначала
делитель заменяем круглым числом – восемьдесят. Делим пятьсот
тридцать четыре на восемьдесят, то есть на десять, а потом пятьдесят три на
восемь. Получается примерно шесть. Не забываем! Пока мы не выполним проверку
умножением, взятая нами цифра только пробная, и записывать её в
частное ещё не нужно. Перемножаем восемьдесят девять и шесть. Ура! Получилось
пятьсот тридцать четыре. Частное равно шести.
Ура! Получилось
пятьсот тридцать четыре. Частное равно шести.
Ну что же, я надеюсь, вы всё поняли и сможете самостоятельно решить парочку примеров. Вот этих: 228 : 76 и 256 : 32.
Ну как, справились? У вас такое решение?
А теперь давайте вместе найдём частное чисел триста девяносто восемь и пятьдесят шесть:
Заменяем делитель круглым числом пятьдесят. Триста девяносто восемь делим на десять, а потом тридцать девять делим на пять. Кажется, получается по семь. Перемножаем пятьдесят шесть и семь. Получается триста девяносто два. Так-так…
При умножении получилось не то
число, которое было в делимом. Может быть, я неправильно выполнила деление? Сейчас
проверю! Вычитаю из делимого полученное произведение — триста
девяносто два. Остаток – шесть, он меньше делителя. Значит, деление выполнено
верно, и в частное можно смело писать ответ семь.
Давайте попробуем найти частное чисел сто шестьдесят два и тридцать девять. Вместо тридцати девяти берём тридцать, сто шестьдесят два делим на десять и шестнадцать делим на три, получается пять. Перемножаем пять и тридцать девять, получается… упс…сто девяносто пять! Полученное число больше делимого! Такого быть не может! Не зря я говорила, что пока в частное цифру писать не стоит – она пробная. Так как полученное произведение больше делимого, пятёрку надо заменить на меньшее число. Попробую умножить не на пять, а на четыре. Тридцать девять умножаю на четыре, получается сто пятьдесят шесть. Уффф… это число меньше делимого. Теперь узнаем на сколько. Вычитаем его из ста шестидесяти двух. Остаток равен шести. Ну что же, частное чисел сто шестьдесят два и тридцать девять равно четырём, остаток – шесть.
А теперь вы попробуйте сами найти частные вот в таких примерах:
261 : 63; 376 : 68.
Итак, ребята, давайте проверим вашу работу.
Конечно, со вторым примером пришлось повозиться.
Но я надеюсь, что вы были внимательны и справились с ним.
А теперь пришло время прощаться. Удачи вам в освоении приёма письменного деления. Пока, ребята!
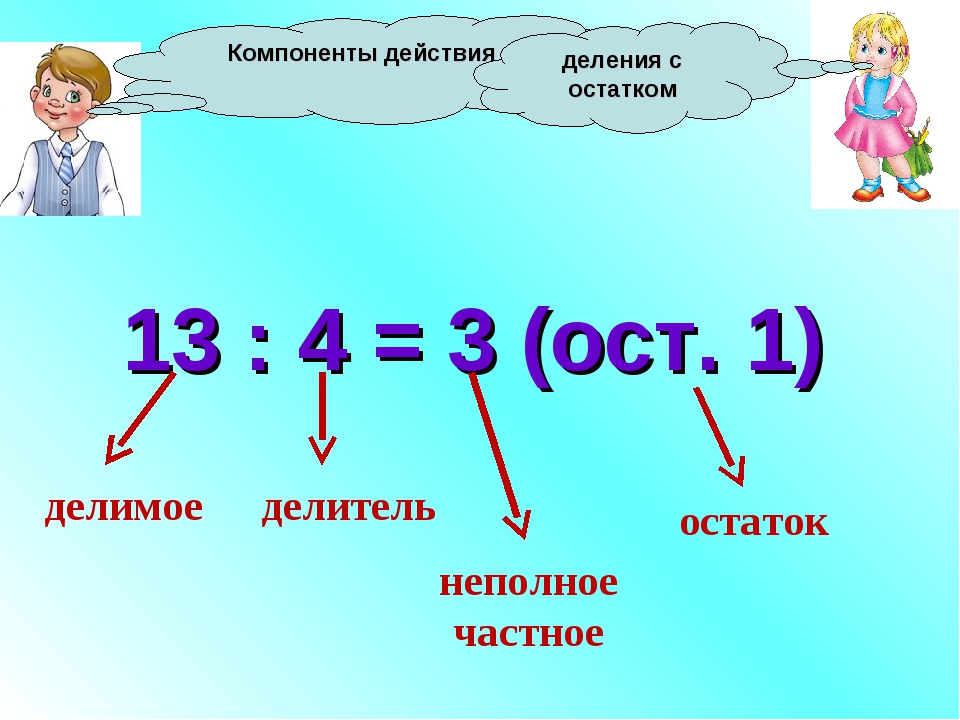
Деление с остатком | Математика
Если одно натуральное число не делится на другое нацело, можно выполнить деление с остатком.
Как и при делении нацело, числа, которые делим, называются делимое и делитель.
Результат деления называется неполным частным.
Число, которое остаётся от делимого в результате деления (это число меньше делителя), называется остаток.
Чтобы выполнить проверку, надо:
- Неполное частное умножить на делитель.
- К полученному произведению прибавить остаток.
- В результате должно получиться делимое.
Рассмотрим конкретные примеры деления с остатком.
Примеры.
Выполнить деление чисел с остатком и сделать проверку:
1) 29 : 8;
2) 613 : 6;
3) 279 : 10;
4) 784 : 23;
5) 4057 : 35;
6) 8591 : 62;
7) 52779 : 2524;
8) 15 : 79.
Решение: 1)
29 : 8 = 3 (остаток 5).
Проверка:
3 · 8 + 5 = 24 + 5 = 29.
2)
513 : 6 = 85 (остаток 3).
513 — делимое, 6 — делитель, 85 — неполное частное, 3 — остаток.
Проверка:
85 · 6 + 3 = 510 + 3 = 513.
3)
279 : 10 = 27 (остаток 9).
279 — делимое, 10 — делитель, 27 — неполное частное, 9 — остаток.
Проверка:
27 · 10 + 9 = 270 + 9 = 279.
4)
784 : 23 = 34 (остаток 2).
784 — делимое, 23 — делитель, 34 — неполное частное, 2 — остаток.
Проверка:
34 · 23 + 2 = 782 + 2 = 784.
5)
4057 : 35 = 115 (остаток 32).
4057 — делимое, 35 — делитель, 115 — неполное частное, 32 — остаток.
Проверка:
115 · 35 + 32 = 4025 + 32 = 4057.
6)
8591 : 62 = 138 (остаток 35).
8591 — делимое, 62 — делитель, 138 — неполное частное, 35 — остаток.
Проверка:
138 · 62 + 35 = 8556 + 35 = 8591.
7)
52779 : 2524 = 20 (остаток 2299).
52779 — делимое, 2524 — делитель, 20 — неполное частное, 35 — 2299.
Проверка:
20 · 2524 + 2299 = 50480 + 2299= 52779.
8) 15 : 79 = 0 (остаток 15).
15 — делимое, 79 — делитель, 0 — неполное частное, 15 — остаток.
( Если делимое меньше делителя, неполное частное всегда равно нулю, а остаток — делимому).
примеры в столбик для 3, 4 класса, алгоритм, двузначное на двузначное, проверка, формула, основные правила, видеоурок
Деление с остатком – это арифметическая операция, в ходе которой проводится деление одного числа на другое, а в результате получается 2 целых числа: неполное частное и остаток от деления. Причем сам остаток всегда должен быть меньше делителя. В то же случае, если во время данной операции в результате образовался ноль, говорят, что делимое делится нацело.
Находясь в строгих рамках только натуральных чисел, во время проведения арифметических операций приходится различать деление с остатком и нацело. Здесь важно помнить, что 0 – это не натуральное число. Также еще один важный момент, на который нужно обратить внимание – неполное частное при делении меньшего на большее должно приравниваться к 0. Это также несколько выходит за рамки натуральных чисел. Все эти искусственные ограничения усложняют формулировку и дальнейшие вычисления. Деление с остатком может были проведено не только с целыми числами, но и с другими математическими объектами. Например, с многочленами.
Делению дети начинают обучаться еще в младших классах. Это одна из основных операций, которые можно проводить с цифрами. Можно сказать, что это основа для того, чтобы в дальнейшем проводить более сложные подсчеты. Поэтому правила нужно запоминать обязательно.
На первый взгляд может показаться, что деление с остатком никогда в будущем не пригодится. Но это не так. Данную операцию часто применяют в компьютерной технике и телекоммуникационном оборудовании с целью получения случайных и создания контрольных чисел. Сама операция исчисления ост-ка в разных языках программирования указывается по-своему.
Данную операцию часто применяют в компьютерной технике и телекоммуникационном оборудовании с целью получения случайных и создания контрольных чисел. Сама операция исчисления ост-ка в разных языках программирования указывается по-своему.
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример для детального объяснения:Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета.
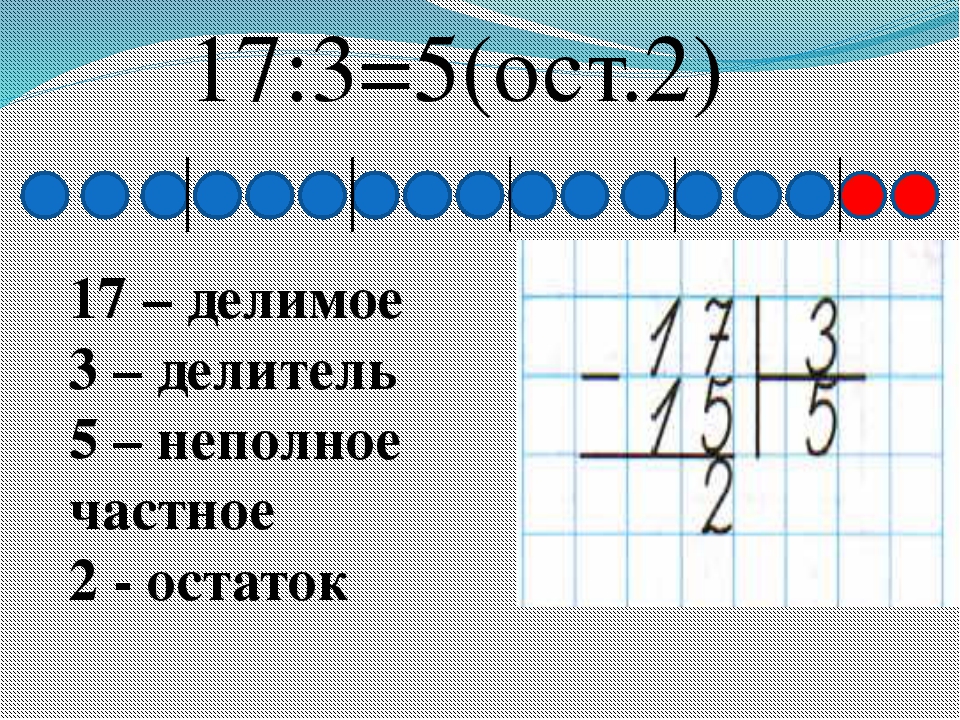
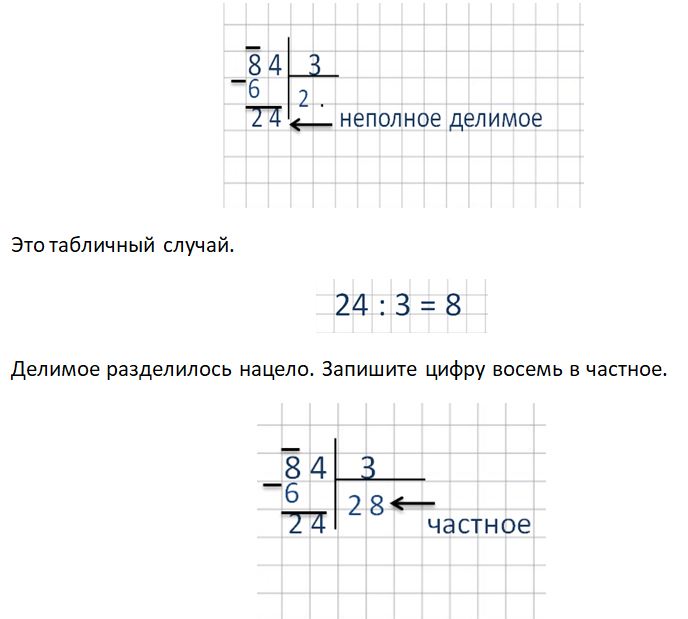
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель. Основная черта обозначена оранжевым цветом.
- Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
- Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма).
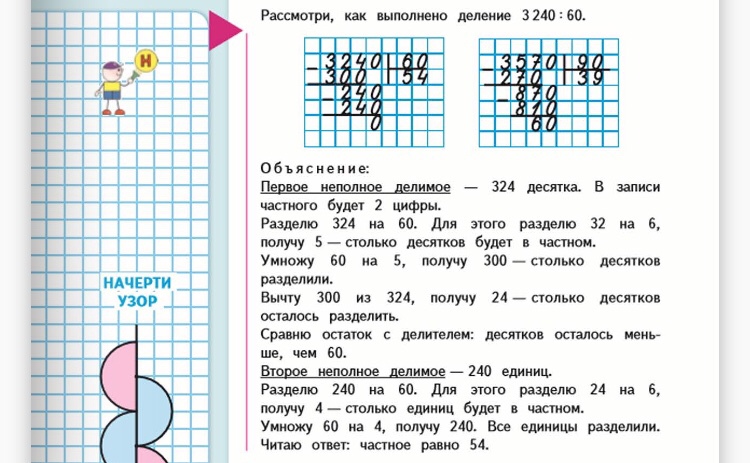 2 – это остаток.
2 – это остаток.
[warning]При делении таким образом, остаток всегда должен быть меньше делителя.[/warning]
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо приводить в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику подсчета ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
[warning]Существует правило для случаев, когда делитель больше делимого: НЧ равно 0, ост-к равен делимому.[/warning]
Как разделить число 5 на число 6? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6>5.По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. После всех подсчетов получаем: НЧ = 0, ост-к = 5.
Эту тему начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры: 14:3
Находим НЧ: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Ост-к: 3*4=12, 14-12=2.
Ответ: НЧ 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача:
- 3 пирожка надо разделить на двоих;
- 4 пирожка на двоих;
- 5 пирожков на двоих.
Читайте также: Натуральные числа
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами свыше 100.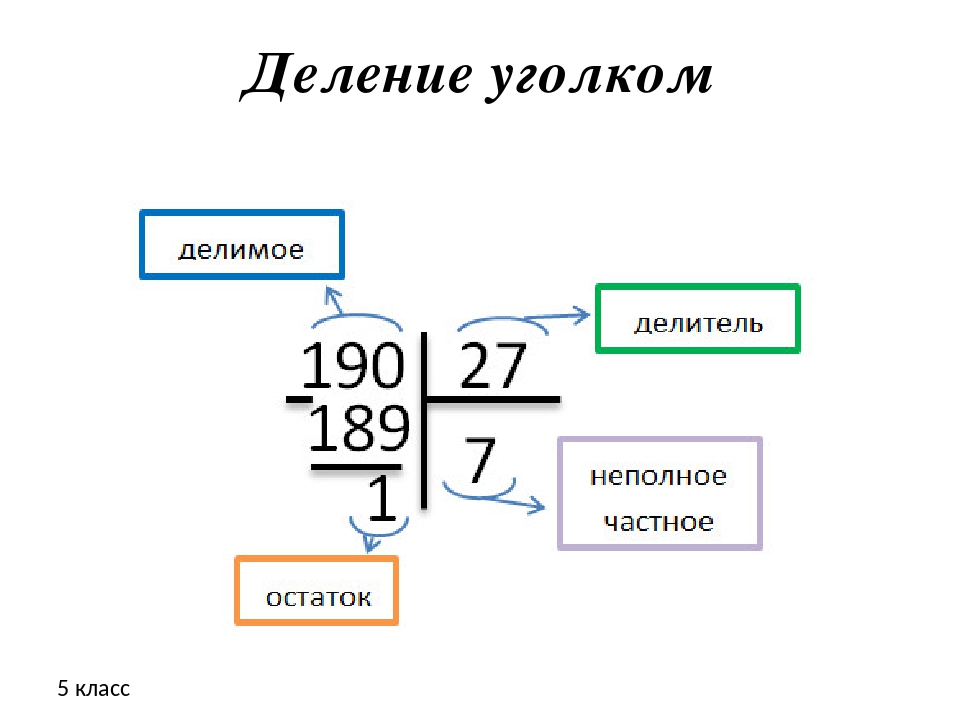
Данное действие удобнее всего выполнять в столбик, так как НЧ также будет двузначным (в большинстве случаев), а алгоритм столбика облегчает подсчет и делает его более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя подсчет проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить ост-к.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у последнего первые две левые цифры – это 38. Сравниваем их с делителем. 38>25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50>38, возвращаемся на один шаг назад.
Ответ – 1. Вписываем единицу в зону не полного частного.
Далее:
38-25=13. Вписываем 13 под чертой.
Второй уровень
13>25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136>25? Да – значит можно его вычесть. Определяем, сколько 25 поместиться в 136.
Получилось 136. 136>25? Да – значит можно его вычесть. Определяем, сколько 25 поместиться в 136.25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150>136 – возвращаемся назад на один шаг. Добавляем цифру 5 в зону неполного частного, справа от единицы.
Определяем остаток:
136-125=11. Приводим под чертой. 11>25? Нет – действие провести нельзя. У делимого не остались цифры. Значит, делить больше нечего. Подсчет закончен.
Ответ: НЧ равно 15, в ост-ке 11.
Если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого, то в таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в подсчете сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38>75? Нет – деление провести нельзя. Берем все 3 цифры. 386>75? Да – действие провести можно. Проводим расчет.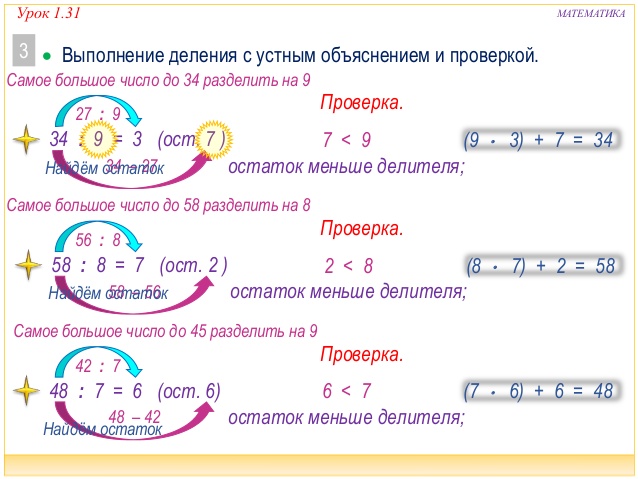
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450>386 – возвращаемся на шаг назад. Вписываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11>75? Нет. Также не остались цифры у делимого. Подсчет закончен.
Результат: НЧ = 5, в ост-ке — 11.
119:35
Выполняем проверку: 11>35? Нет – математическую операцию провести нельзя. Подставляем третье число – 119>35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140>119 – возвращаемся на один шаг назад. Вписываем 3 в зону неполного ост-ка.
Находим ост-к: 119-105=14. 14>35? Нет, и у делимого не остались цифры. Вычисления закончены.Результат: НЧ = 3, осталось — 14.
1195:99
Проверяем: 11>99? Нет – подставляем еще одну цифру. 119>99? Да – начинаем вычисления.
11<99, 119>99.
99*1=99, 99*2=198 – перебор. Вписываем 1 в неполное частное.
Находим ост-к: 119-99=20. 20<99. Опускаем 5. 205>99. Вычисляем.
Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим ост-к: 205-198=7.
Результат: НЧ = 12, остаток — 7.
Деление с остатком — примеры:
Учимся делить в столбик с остатком:
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно. Этой теме необходимо уделить больше внимания, чтобы разобраться со всеми тонкостями подсчета.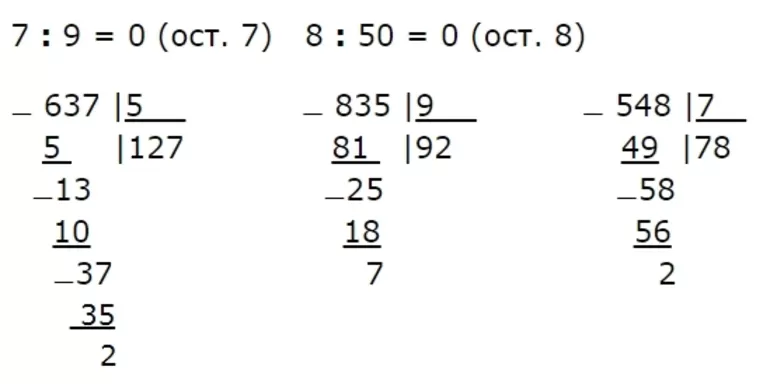 В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
Читайте также: Легкие правила округления чисел после запятой
Деление с остатком объяснение. Деление столбиком. Деление в столбик
Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы :
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается.
 Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное. - Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные : 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного .
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 5, в остатке — 11.
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 3, осталось — 14.
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
1199.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 2099. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ: неполное частное = 12, остаток — 7.
Деление с остатком — примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?
Разделим натуральное число 273844 на натуральное число 97 .
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823 , а остаток равен 13 .
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 — 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 — 3 = 1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7 ÷ 3 = 2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3 .
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.
Вычислим: 145 ÷ 46 .
Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:
Повторяем эту операцию еще раз:
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .
В нашем случае остатком является число 7 .
145 ÷ 46 = 3 (остаток 7) .
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a
Например:
12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.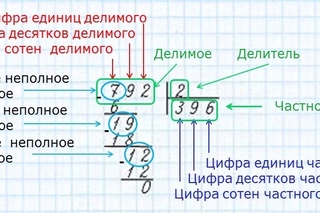 д.
д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a — b · c . Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т.д. Применяя формулу d = a — b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбора
Разделим 267 на 21 .
a = 267 ; b = 21 . Подберем неполное частное.
Используем формулу d = a — b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.
Если с = 0 , имеем: d = a — b · c = 267 — 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.
Число 267 больше, чем 21 , поэтому продолжаем подстановку.
При с = 1 имеем: d = a — b · c = 267 — 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.
При с = 2 имеем: d = a — b · c = 267 — 21 · 2 = 267 — 42 = 225 ; 225 > 21 .
При с = 3 имеем: d = a — b · c = 267 — 21 · 3 = 267 — 63 = 204 ; 204 > 21 .
При с = 12 имеем: d = a — b · c = 267 — 21 · 12 = 267 — 252 = 15 ; 15
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a b .
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b .
Найти нужно неполное частное c и остаток d .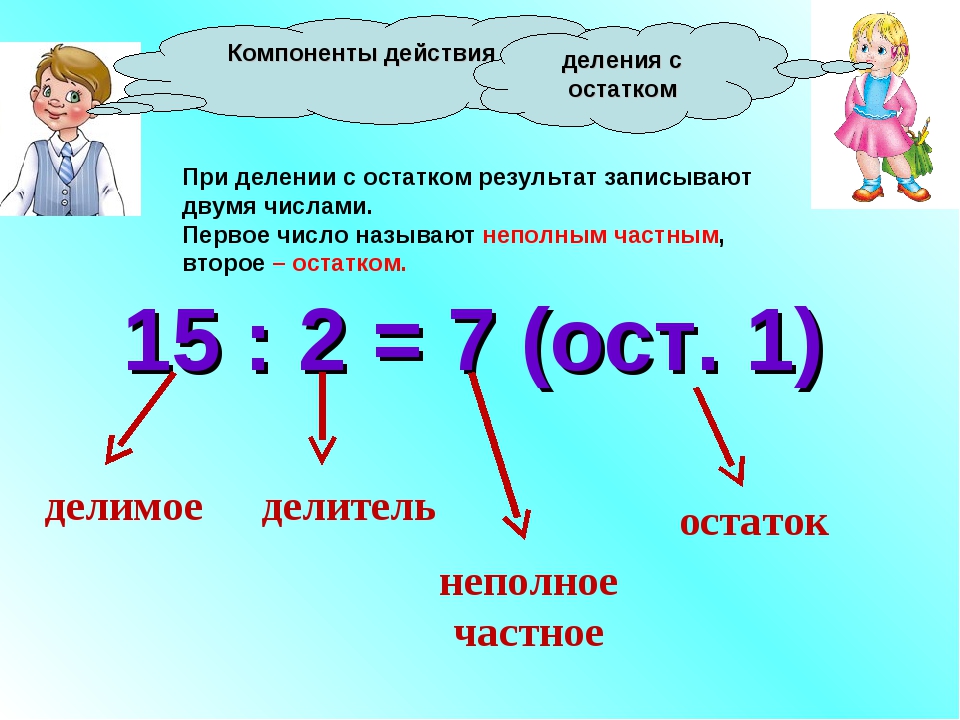
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.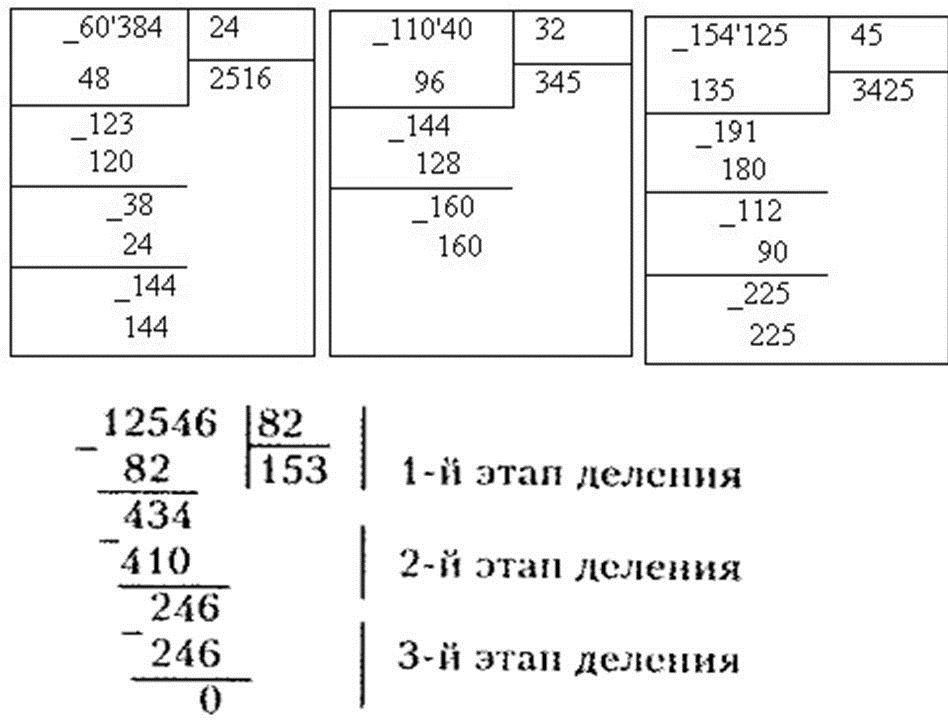
В нашем примере справа от 47 дописываем нуль. Так как 470
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .
470 899 .
Число, которое мы получили на предпоследнем шаге (470 = 47 · 10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1 — 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 — 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899 — 470 = 429 , 429 > 47 . Повторяем шаги 1 — 5 алгоритма с числом 429 , взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу — число 1 .
2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 — 1 = 0 . Запоминаем 0 .
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 429 . Таким образом, второе искомое слагаемое — 47 · 9 = 423 .
5. Разность между 429 и 423 равна числу 6 . Так как 6
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:
899 = 47 · 10 + 47 · 9 + 6
Применим распределительное свойство умножения.
899 = 47 · 10 + 47 · 9 + 6 = 47 · (10 + 9) + 6
899 = 47 · 19 + 6 .
Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .
Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Пример 5. Деление натуральных чисел с остатком
Разделим числа 42252 и 68 .
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800 = 68 · 600 .
Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 — 40800 и получаем второе слагаемое 1360 = 68 · 20
Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 — 1360 .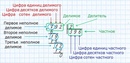 Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 — 68 .
Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 — 68 .
В результате получаем:
42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · (600 + 20 + 1) + 24 = 68 · 621 + 24
Неполное частное равно 621 , остаток равен 24 .
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Важно!
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Пример 6. Проверка результата деления натуральных чисел с остатком.
Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .
Сравниваем остаток и делитель: 30 > 28 .
Значит, деление выполнено неверно.
Пример 7. Проверка результата деления натуральных чисел с остатком.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .
Подставляем значения и сравниваем результаты
13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122
Значит, в вычисления школьника где-то закралась ошибка.
Пример 8. Проверка результата деления натуральных чисел с остатком.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 .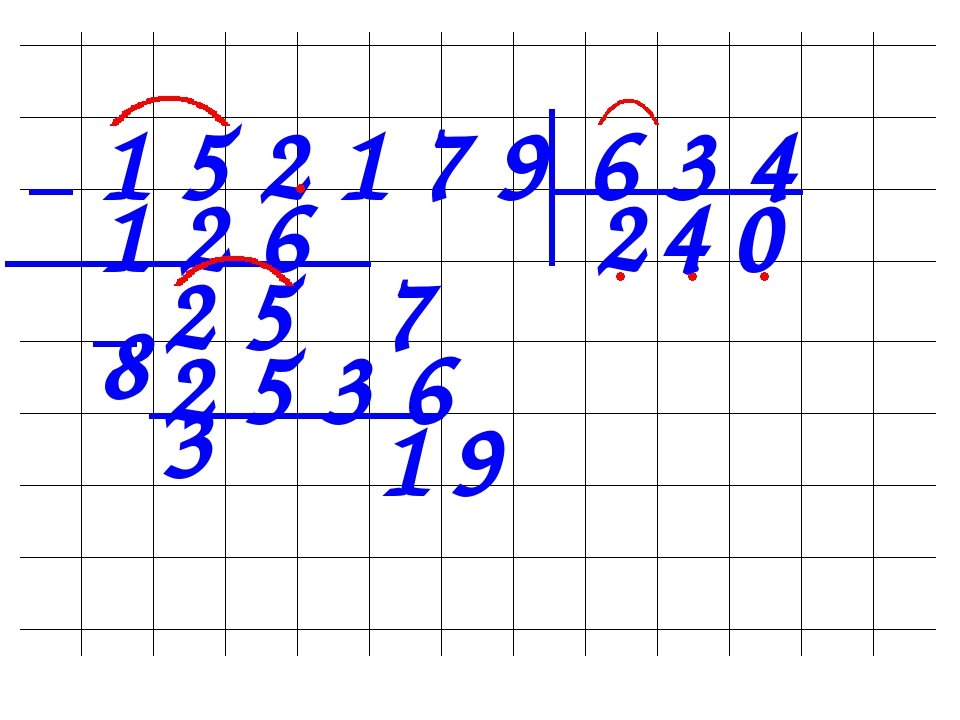 Все ли правильно посчитано?
Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.
Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .
После подстановки, имеем:
5998 = 111 · 54 + 4 = 5994 + 4 = 5998 .
Равенство корректно, а значит, и деление выполнено верно.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Деление с остатком проходят в третьем классе начальной школы. Тема довольно сложная для понимания ребенком и требует от него практически идеального знания таблицы умножения. Но все математические знания улучшаются с практикой, и поэтому, решая задания, ребенок с каждым примером будет выполнять его все быстрее и с меньшим количеством ошибок. Наш тренажер предполагает отработку навыка быстрого деления с остатком.
Как делить с остатком
1. Определяем, что деление с остатком (не делится нацело).
34:6 не решается без остатка
2. Подбираем ближайшее меньшее число к первому (делимому), которое делится на второе (делитель).
Подбираем ближайшее меньшее число к первому (делимому), которое делится на второе (делитель).
Ближайшее к 34 меньшее число, которое делится на 6 — это 30
3. Выполняем деление этого числа на делитель.
4. Пишем ответ (частное).
5. Чтобы найти остаток, от первого числа (делимого) вычитаем то число, которое подобрали. Записываем остаток. При делении с остатком остаток всегда должен получиться меньше делителя.
34-30=4 (ост. 4) 4
Проверяем деление так:
Умножаем ответ на делитель (второе число) и прибавляем к ответу остаток. Если получается делимое (первое число), то деление выполнил верно.
5*6+4=34 Деление выполнено верно.
Большие числа легко и просто делятся столбиком. При этом в уголке под делителем у нас запишется целое число, а в самом низу останется остаток, который меньше делителя.
Если при делении с остатком делимое меньше делителя, то их неполное частное равно нулю, а остаток равен делимому.
Например:
6: 10 = 0 (ост. 6)
14: 112 = 0 (ост. 14)
Скачать карточки-тренажеры на деление с остатком
Сохраните лист-карточку себе на компьютер и распечатайте на А4. Одного листа хватит на 5 дней отработки деления с остатком. В нем 5 столбиков с примерами. Вы можете даже разрезать лист на 5 частей. Над каждым столбиком — тучка, смайлик и солнышко, пусть ребенок оценит свою работу, когда закончит столбик.
Чем занимается на математике 3 класс? Деление с остатком, примеры и задачи — вот что изучается на уроках. О делении с остатком и алгоритме таких вычислений пойдет речь в статье.
Особенности
Рассмотрим темы, включенные в программу, которую изучает 3 класс. Деление с остатком выделено в специальный раздел математики. О чем идет речь? Если делимое не делится на делитель нацело, то остается остаток. Например, делим 21 на 6. Получается 3, но в остатке остается 3.
В случаях, когда во время деления натуральных чисел остаток равен нулю, говорят о том, что произведено деление нацело. Например, если 25 нужно поделить на 5, получается число 5. Остаток равен нулю.
Например, если 25 нужно поделить на 5, получается число 5. Остаток равен нулю.
Решение примеров
Для того чтобы произвести деление с остатком, используется определенная запись.
Приведем примеры по математике (3 класс). Деление с остатком в столбик можно не записывать. Достаточно записи в строчку: 13:4=3 (остаток 1) или 17:5=3 (остаток 2).
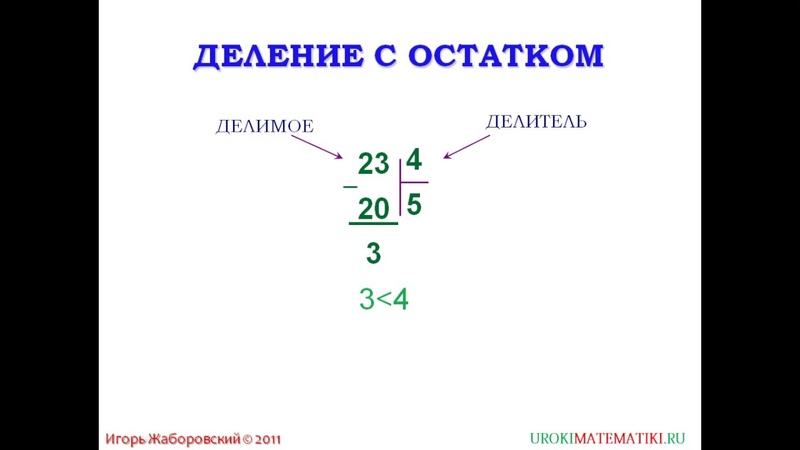
Разберем все подробнее. Например, при делении 17 на три получается целое число пять, кроме того, получается остаток два. Каков порядок решения такого примера на деление с остатком? Сначала необходимо отыскать максимальное число до 17, разделить которое можно без остатка на три. Самым большим будет 15.
Далее проводится деление 15 на число три, результатом действия будет цифра пять. Теперь вычитаем из делимого число, найденное нами, то есть из 17 отнимаем 15, получаем два. Обязательным действием является сверка делителя и остатка. После проверки обязательно записывается ответ совершенного действия. 17:3=15 (остаток 2).
Если остаток будет больше делителя, действие выполнено неправильно. Именно по такому алгоритму выполняет 3 класс деление с остатком. Примеры сначала разбирает учитель на доске, затем ребятам предлагается проверка знаний путем проведения самостоятельной работы.
Именно по такому алгоритму выполняет 3 класс деление с остатком. Примеры сначала разбирает учитель на доске, затем ребятам предлагается проверка знаний путем проведения самостоятельной работы.
Пример с умножением
Одна из самых трудных тем, с которой сталкивается 3 класс, — деление с остатком. Примеры могут быть сложными, особенно когда требуются дополнительные расчеты, записываемые в столбик.
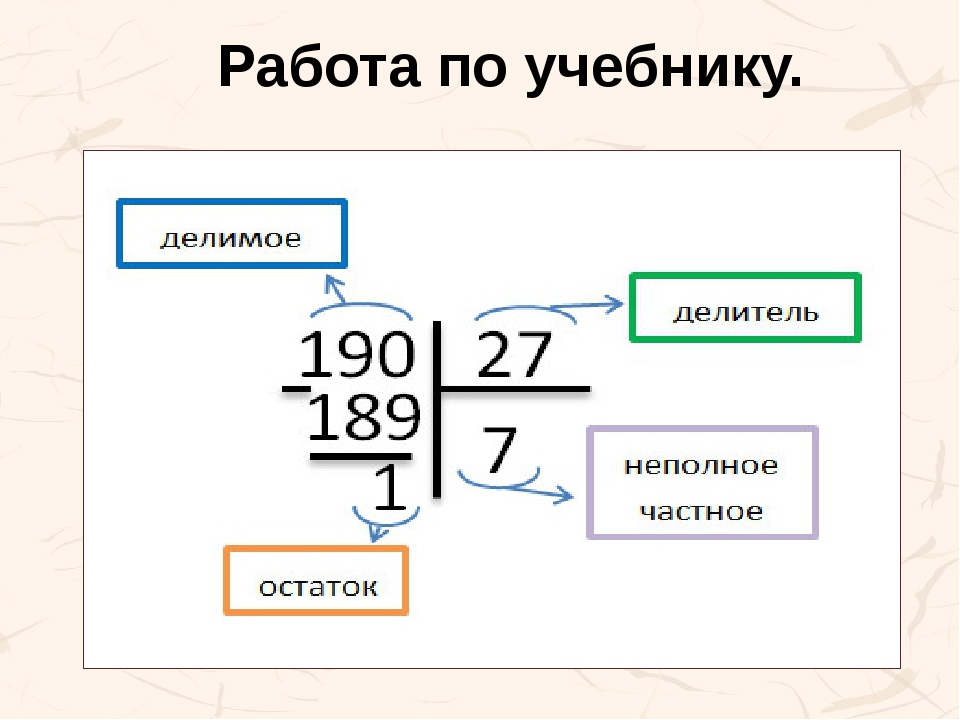
Допустим, необходимо разделить число 190 на 27 с получением минимального остатка. Попробуем решить задачу, пользуясь умножением.
Подберем число, которое при умножении будет давать цифру, максимально приближенную к числу 190. Если умножить 27 на 6, получим цифру 162. Вычтем из 190 число 162, остаток будет 28. Он получился больше, чем исходный делитель. Следовательно, число шесть не подходит для нашего примера в качестве множителя. Продолжим решение примера, взяв для умножения число 7.
Умножая 27 на 7, мы получим произведение 189. Далее проведем проверку правильности решения, для этого вычтем из 190 полученный результат, то есть отнимем число 189.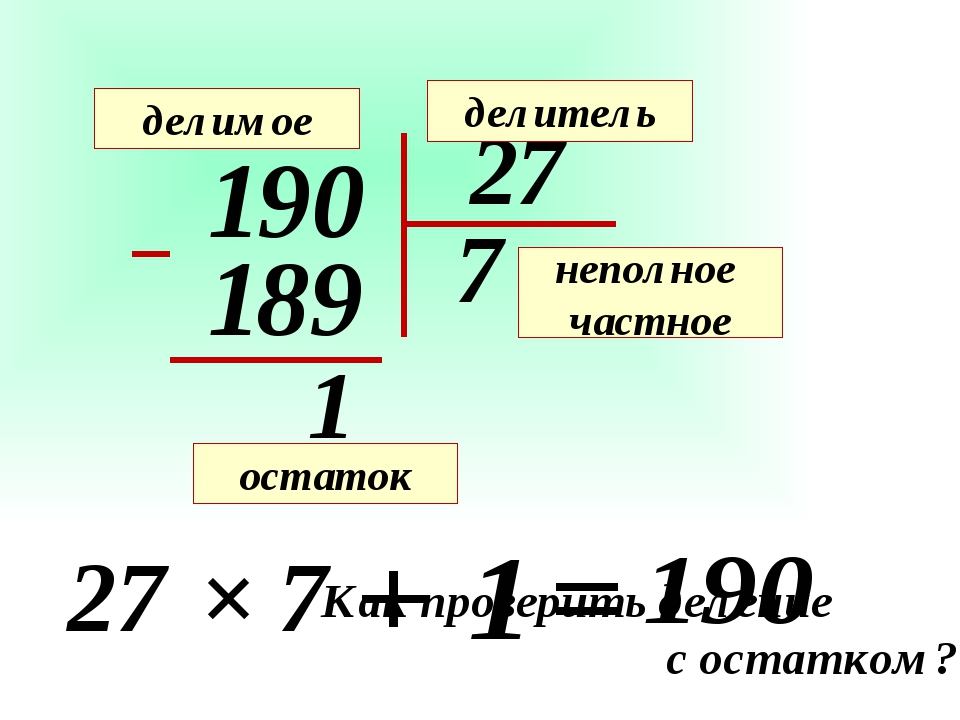 Остатком будет 1, что явно меньше 27. Именно так решаются сложные выражения в школе (3 класс, деление с остатком). Примеры всегда предусматривают запись ответа. Все математическое выражение можно оформить так: 190:27=7 (остаток 1). Подобные вычисления можно производить и в столбик.
Остатком будет 1, что явно меньше 27. Именно так решаются сложные выражения в школе (3 класс, деление с остатком). Примеры всегда предусматривают запись ответа. Все математическое выражение можно оформить так: 190:27=7 (остаток 1). Подобные вычисления можно производить и в столбик.
Именно так осуществляет 3 класс деление с остатком. Примеры, приведенные выше, помогут разобраться в алгоритме решения подобных задач.
Заключение
Для того чтобы у учеников начальных классов были сформированы правильные вычислительные навыки, педагог во время проведения занятий по математике обязан уделять внимание пояснению алгоритма действий ребенка при решении заданий на деление с остатком.
По новым федеральным государственным образовательным стандартам особое внимание уделяется индивидуальному подходу к обучению. Учитель должен подбирать задания для каждого ребенка с учетом его индивидуальных способностей. На каждой ступени обучения правилам деления с остатком педагог должен осуществлять промежуточный контроль. Он позволяет ему выявлять основные проблемы, возникающие с усвоением материала у каждого ученика, своевременно проводить коррекцию знаний и навыков, устранять появляющиеся проблемы, получать желаемый результат.
Он позволяет ему выявлять основные проблемы, возникающие с усвоением материала у каждого ученика, своевременно проводить коррекцию знаний и навыков, устранять появляющиеся проблемы, получать желаемый результат.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление столбиком на двузначное число. Обучение делению с помощью игр
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.

- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.

- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.

21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Давайте сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5. Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим . Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном.
И 26 разделим на 5, будет 5. Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим . Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном.
Значение частного чисел 265 и 53 — 5. Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 — это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим . А 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим . Мы видим, что цифра 8 подходит. Можем ее записать в частном.
Значение частного чисел 184 и 23 — 8.
Рассмотрим более сложные случаи деления. Найдем значение частного чисел 768 и 24.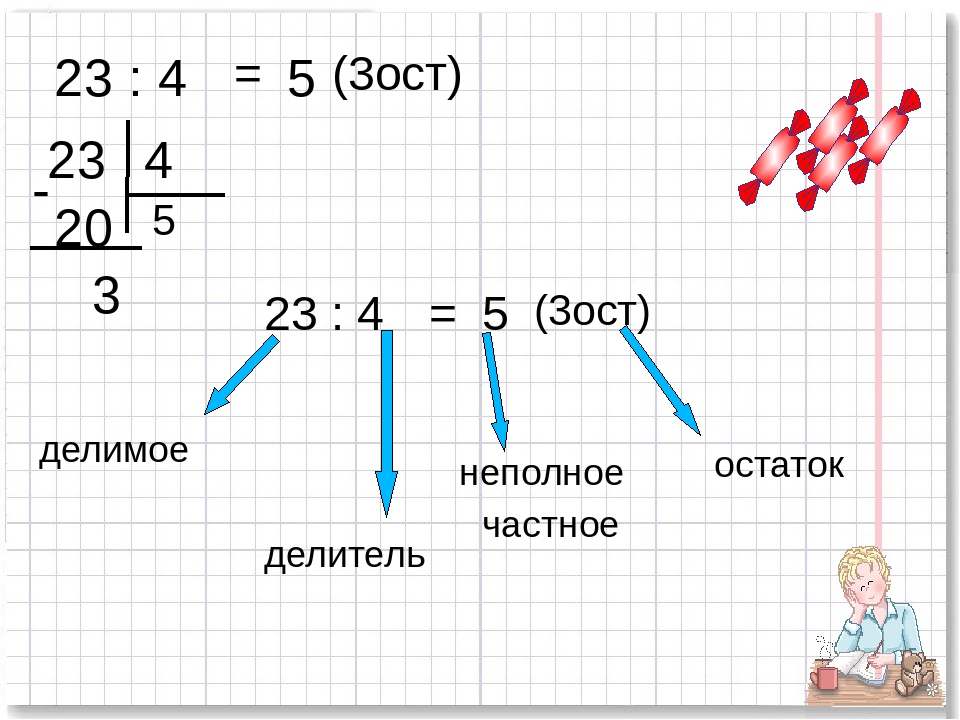
Первое неполное делимое — 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 — это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим . . Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного.
Продолжим деление. Следующее неполное делимое — 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим . Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного.
Значение частного чисел 768 и 24 — 32.
Найдем значение частного чисел 15 344 и 56.
Первое неполное делимое — 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 — это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим . А 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим . А . Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. Это 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. . . Помните: 8 — это пробная цифра. Проверим ее. . А 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. . Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Значит, цифра подошла и в частном на месте десятков можем записать 7.
Продолжим деление. Следующее неполное делимое — 224 единицы. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 — это пробная цифра, проверим ее, подойдет ли она. . И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном.
Значение частного чисел 15 344 и 56 — 274.
Мы сегодня учились делить письменно на двузначное число.
Список литературы
- Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова — М.: Просвещение, 2010.
- Узорова О.В., Нефедова Е.А. Большой задачник по математике. 4 класс. — М.: 2013. — 256 с.
- Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.Л. Дрозд, А.А. Столяр; пер. с бел. яз. Л.А. Бондаревой. — 3-е изд., перераб.
 — Минск: Нар. асвета, 2008. — 134 с.: ил.
— Минск: Нар. асвета, 2008. — 134 с.: ил. - Математика. 4 класс. Учебник. В 2 ч./Гейдман Б.П. и др. — 2010. — 120 с., 128 с.
- Ppt4web.ru ().
- Myshared.ru ().
- Viki.rdf.ru ().
Домашнее задание
Выполните деление
>> Урок 13. Деление на двузначное и трехзначное число
Разделим 876 на 24. Прикидка 800: 20 = 40 показывает, что в ответе должно получиться число, близкое к 40.
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
Число сотен 8 является однозначным, поэтому делим 87 десятков на 24. Получится 3 десятка и еще 15 десятков останется (87 — 3 24 = 15). 15 десятков и 6 единиц — это 156. А если 156 разделить на 24, то получится 6 и 12 в остатке (156 — 24 6 = 12). Всего получится 3 десятка и 6 единиц, то есть 36, а в остатке 12. Это записывают так:
10*. Найди сумму всех возможных двузначных чисел, все цифры которых нечетные.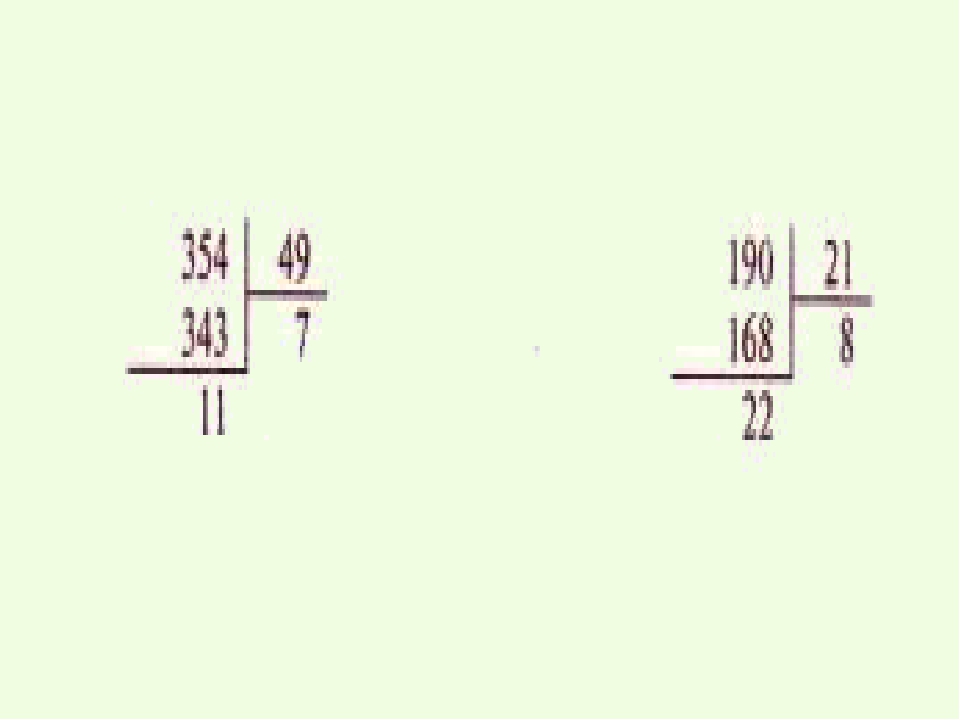
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 1. — М.: Издательство «Ювента», 2005, — 64 с.: ил.
Планы конспектов уроков по математике 4 класса скачать , учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиДеление на двузначное число — сложная операция, требующая тренированной памяти для запоминания начальной и промежуточной
информации.
Как и в других разделах, начинайте с отработки наиболее простых упражнений, параллельно осваивая более сложные.
Методика деления
При устном делении запоминайте цифры парами разрядов, например, 3542 как «тридцать пять — сорок два».
Если делимое четырехзначное, то первым делом определите число сотен в ответе, поделив первую пару цифр на делитель. Дальше работайте с остатком от этого деления и второй парой. Например, при делении 3542 на 11, число сотен в ответе — 3, а деление 242 на 11 дает 22, то есть ответ — 322.
Способы деления для различных комбинаций чисел даны в следующих примерах.
На первом этапе не обращайте внимания на остатки от деления — на практике обычно достаточно приближенного ответа.
Во всех примерах в круглых скобках показывается остаток от деления.
Деление на 11-19
A.1. Умножение до 19×9.
Деление — операция, обратная умножению. Выучите наизусть таблицу умножения до 19×9 — это позволит быстро делить на числа, меньшие 20. Для тренировки используйте пример:
Для тренировки используйте пример:
× =
A.2. Деление двузначного числа.
Вычислите целую часть и остаток:
: =
A.3. Деление на 11.
: =
Деление на 11 проще всего выполнить обычным способом, «в столбик».
- При делении четырехзначного числа сначала определите число сотен в ответе, поделив первые две цифры числа на 11. Дальше работайте с остатком и второй парой цифр.
- Полезно помнить, что 1001 = 7 × 11 × 13 = 91 × 11. Например, при делении 1023 на 11 сразу получаем 93.
Трехзначные числа можно научиться делить на 11 сразу, если помнить правило умножения двузначного числа на 11. Например:
- 577: 11 = 52 (5). Сразу видно, что 572 делится нацело на 11 (5 + 2 = 7) и дает 52.
- 642: 11 = 58 (4). Сразу видно, что 638 делится нацело на 11 и дает 58 (5 + 8 = 13).
A.4. Деление на 13.
: =
При делении на 13 полезно помнить:
- 1001 = 7 × 11 × 13 = 77 × 13.
- 104 = 8 × 13.
Алгоритм деления на 13 на примере числа 6357:
- Сначала воспользуемся тем, что 1001 = 7 × 11 × 13. Значит, 6006: 13 = 42 × 11 = 462 (используем правило умножения на 11).
- Далее, нужно поделить 357 − 6 = 351 на 13. Так как 104 = 8 × 13, то 312: 13 = 24.
- Остается поделить 351 − 312 = 39 на 13, что дает 3.
- Складываем, получаем ответ: 489.
Иногда проще делить обычным способом, «в столбик», например, 5265: 13 = 405, так как 52: 13 = 4, 65: 13 = 5.
A.5. Деление на 15.
: =
При делении на 15:
- Определите число сотен в ответе, поделив первые две цифры четырехзначного числа на 15.
- Оставшееся число умножьте на 2, затем поделите на 30.
A.6. Деление на 17.
: =
При делении на 17 полезно помнить:
- 102 = 6 × 17.
- 1020 = 60 × 17.
- 1003 = 59 × 17.
Алгоритм деления на 17 на примере числа 4493:
- Сначала определим число сотен в ответе: 44: 17 = 2 (10).

- При делении 1093 на 17 используем то, что 1020: 17 = 60, а 73: 17 = 4 (5).
- Складываем, получаем ответ: 264 (5).
Иногда проще делить обычным способом «в столбик», например, 3572: 17 = 210 (2), так как 34: 17 = 2, 172: 17 = 10 (2).
A.7. Деление на 19.
: =
При делении на 19 полезно помнить: 100: 19 = 5 (5).
Алгоритм деления на 19 на примере числа 4126:
- Сначала определим число сотен в ответе: 41: 19 = 2 (3).
- Чтобы поделить 326 на 19, воспользуемся тем, что 100: 19 = 5 (5), поэтому 300: 19 = 15 (15), а 41: 19 = 2 (3). Значит, 326: 19 = 17 (3).
- Складываем, получаем ответ: 217 (3).
Иногда проще делить обычным способом «в столбик», например, 1938: 19 = 102.
A.8. Деление на 12, 14, 16, 18.
: =
При делении на четное число сначала определите число сотен в ответе, поделив первые две цифры четырехзначного числа на делитель.
Для оставшегося числа либо сократите делимое и делитель на 2 и дальше делите на однозначное число, либо используйте свойства:
- 96 = 8 × 12.

- 96 = 6 × 16.
- 98 = 49 × 2 = 7 × 14.
- 90 = 18 × 5.
- 2149: 12 = 1 (сотня) + 9 × 8 + (9 × 4 + 49)/12 = 179 (1).
- 2149: 18 = 1 (сотня) + 3 × 5 + (3 × 10 + 49)/18 = 119 (7).
Деление на 21-99
Б.1. Деление на 91-99.
: =
- В первом приближении ответ — число сотен в делимом (45).
- Число 100 больше 94 на 6. Чтобы посчитать следующее приближение, умножьте число сотен делимого на 6 и добавьте две последние цифры: 45 × 6 + 35 = 305.
- Поделите его на 94 тем же способом: 305: 94 = 3 (3×6+5) = 3 (23).
- Сложите ответы. Итого: 4535: 94 = 48 и 23/94.
Иногда таким же способом удобно делить на 89 (так как легко умножать на 11 в промежуточных вычислениях).
Б.2. Деление на числа, заканчивающиеся на 9.
: =
В этом случае также удобно применять метод округления. Например, нужно поделить 3426 на 29.
- Округлите делитель в большую сторону (из 29 получаем 30).

- Поделите на 30 и вычислите остаток: 3426: 30 = 114 (6). Это уже дает приближенный ответ — примерно 114.
- Чтобы посчитать следующее приближение, сложите ответ и остаток: 114 + 6 = 120.
- Поделите на 30 и вычислите остаток: 120: 30 = 4 (0). Таким образом, целая часть ответа равна 114 + 4 = 118. А остаток равен сумме последнего ответа (4) с последним остатком (0), то есть 4. Итого: 3426: 29 = 118 и 4/29.
Б.3. Деление на числа, заканчивающиеся на 7 и 8.
: =
Метод округления можно применять и в этом случае.
Пример деления 6742 на 48 методом округления (до 50):
- Первое приближение: 67 × 2 = 134.
- Новое делимое: 134 × 2 + 42 = 310.
- Второе приближение: 134 + 6 = 140 (число 6 — это 300:5).
- Остаток: 6 × 2 + 10 = 22.
- Ответ: 6742: 48 = 140 (22).
По мере освоения метода им можно также пользоваться при делении на числа, заканчивающиеся на 5 и 6 (что сложнее, так как требует умножения на 5 и 4 в промежуточных вычислениях).
Б.4. Деление на числа, кратные 11.
: =
При делении на числа, кратные 11:
- Если делимое четырехзначное, то сначала определите число сотен в ответе. Для этого поделите первую пару цифр делимого на делитель. Дальше работайте с остатком от этого деления и второй парой.
- Сократите числитель и знаменатель на 11. Обычно это нетрудно, так как на 11 легко делить, и при этом делимое сокращается на один разряд. Если делимое не делится на 11, отбросьте от него несколько единиц, которые потом можно будет добавить в остаток.
- Далее делите на оставшийся множитель исходного делителя.
При делении на 33 иногда удобнее умножить делимое и делитель на 3. Тогда число сотен в новом делителе сразу дает приближенный ответ.
Пример 1. Деление 4359 на 33.
- Сначала определяем число сотен в ответе: 43: 33 = 1 (10). Далее работаем с числом 1059.
- Умножим делимое и делитель на 3: 1059: 33 = 3177: 99. Первое приближение равно числу сотен в новом делителе: 31.
 Остаток — 31 + 77 = 108. Таким образом, 3177: 99 = 32 и 9/99.
Остаток — 31 + 77 = 108. Таким образом, 3177: 99 = 32 и 9/99. - Ответ: 132 и 3/33 (остаток приведен к исходному делителю 33).
Иногда проще сократить не на 11, а на другой множитель делителя.
Пример 2. Деление 6230 на 55.
- Сократим делимое и делитель на 5 (для делимого — отбросим ноль и умножим на 2): 6230: 55 = 1246: 11.
- Делим 1246 на 11 «в столбик», получаем 113 и 3/11.
- Ответ: 113 и 15/55 (остаток приведен к исходному делителю 55).
Б.5. Деление на числа, заканчивающиеся на 1.
: =
Числа, заканчивающиеся на 1, как правило, проще всего делить «в столбик».
Б.6. Деление на числа, заканчивающиеся на 5.
: =
В этом случае можно применить метод округления из примера Б.3, деление «в столбик» или метод сокращения на 5, как описано здесь.
Пример. Деление 8117 на 65:
- Если делимое четырехзначное, то сначала определите число сотен в ответе.
 Для этого поделите первую пару цифр делимого на делитель.
Дальше работайте с остатком от этого деления и второй парой. В данном случае: число сотен — 1, новое делимое — 1617.
Для этого поделите первую пару цифр делимого на делитель.
Дальше работайте с остатком от этого деления и второй парой. В данном случае: число сотен — 1, новое делимое — 1617. - Округлите делимое вниз до десятков и сократите его на 5, то есть поделите на 10 и умножьте 2: 1610: 5 = 161 × 2 = 322.
- Поделите результат на делитель, также сокращенный на 5: 322: 13 = 24 и 10 в остатке.
- Определите остаток: 7 + 10 × 5 = 57. Таким образом, 8117: 65 = 124 и 57/65.
- Умножьте сотни делимого на 4: 32 × 4 = 128.
- Поделите две последние цифры делимого на 25 и посчитайте остаток: 68: 25 = 2 и 18 в остатке.
- Сложите два ответа: 3268: 25 = 130 и 18/25 (т.е. 130,72).
Если делитель — 75, то поделите сначала на 25, затем на 3.
Б.7. Деление трехзначных чисел.
: =
- Первым делом определите и запомните число десятков в ответе — это позволит избежать крупной ошибки. Для этого поделите первые две цифры делимого на делитель.
 Например, при делении 943 на 34, количество десятков в ответе — 2, а при делении 325 на 43 — 0 (32 меньше 43).
Например, при делении 943 на 34, количество десятков в ответе — 2, а при делении 325 на 43 — 0 (32 меньше 43).
Б.8. Деление четырехзначных чисел.
: =
- Первым делом определите и запомните число сотен в ответе — это позволит избежать крупной ошибки. Для этого поделите первые две цифры делимого на делитель.
- Попытайтесь применить методы из упражнений Б.1-Б.6, а если они не подходят, делите обычным способом, «в столбик».
- Если делитель — кратное небольшого числа, попробуйте сократить на него делимое и делитель. При этом, если делимое не делится на это число, отбросьте от него нужное количество единиц, чтобы делилось (затем учтите их при расчете остатка). Для двузначного числа нетрудно определить, разлагается ли оно на множители — для этого нужно проверить делимость на числа 2, 3, 5 и 7.
Деление с остатком: примеры в столбик для 4 класса, алгоритм, как научить ребенка разделять в 3 классе
Как научить ребенка делению? Самый простой метод – выучить деление столбиком.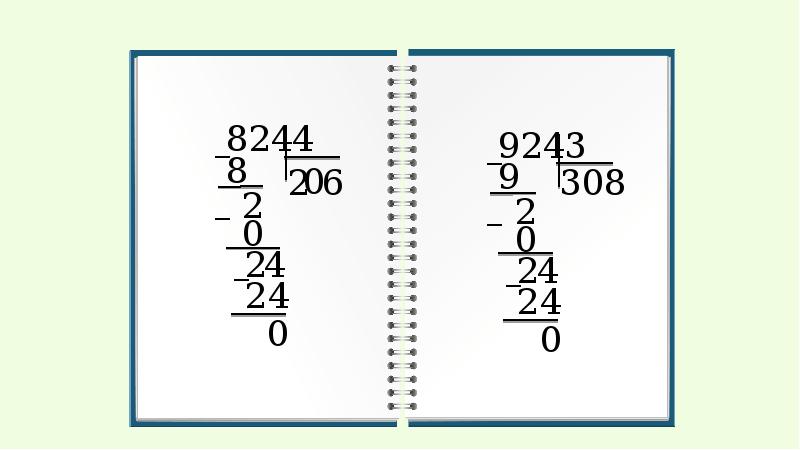 Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….
Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 помещается, 5*2=10 помещается, 5*3=15 помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2.
 Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
14:3
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного.
Далее:
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 5, в остатке 11.
119:35
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет.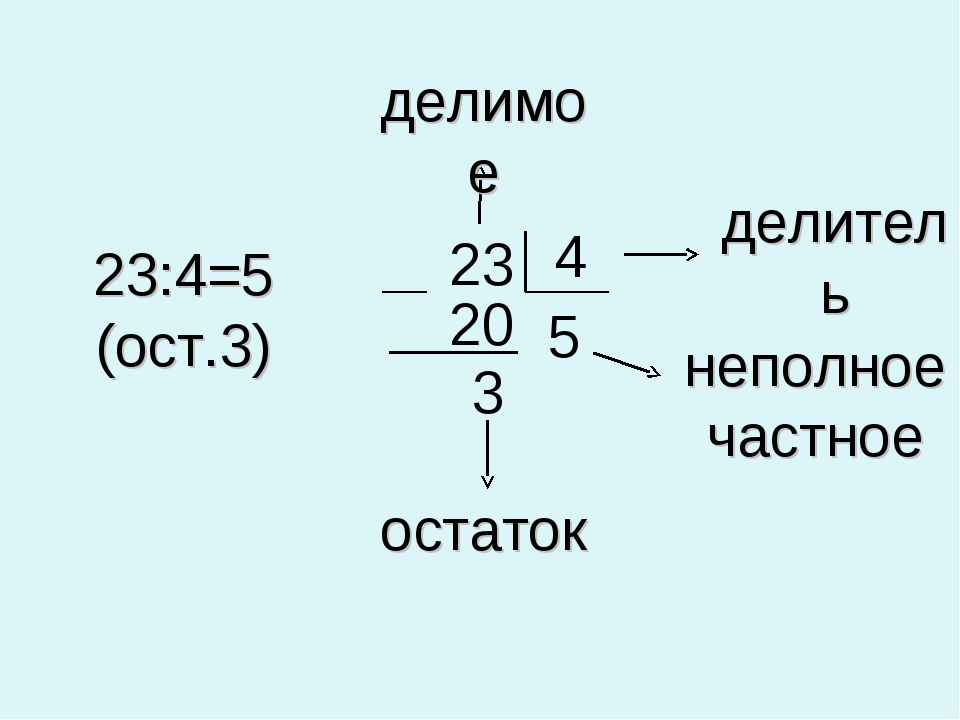 Остались цифры у делимого? Нет. Вычисления закончены.
Остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 3, осталось 14.
1195:99
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
11<,99, 119>,99.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 20<,99. Опускаем 5. 205>,99. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ: неполное частное = 12, остаток 7.
Деление с остатком примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Это интересно! Легкие правила округления чисел после запятой
Что такое делитель? — Определение, факты и пример
Что такое делитель?
Делитель — это число, которое делит другое число полностью или с остатком.Делитель представлен в уравнении деления как:
Дивиденд ÷ Делитель = Частное. |
Разделив 20 на 4, мы получим 5. Здесь 4 — это число, которое полностью делит 20 на 5 частей и известно как делитель.Его уравнение деления —
Аналогично, если мы разделим 20 на 5, получим 4. Таким образом, 4 и 5 являются делителями 20.
Делитель и множители Делитель — это любое число, которое делит другое число. Однако множитель — это делитель, который полностью делит число и не оставляет остатка.
Итак, все множители числа являются его делителями. Но не все делители будут факторами.
В приведенном выше примере 4 и 5 являются множителями 20.
В то время как, если мы разделим 20 на 3, это не будет полностью разделить 20. Таким образом, 3 не является множителем 20.
Рассмотрим другой пример,
деление 15 на 5 дает 3. Здесь 5 — делитель. Кроме того, разделив 15 и разделив на 3, мы получим 5. Здесь 3 — делитель.
Множители и делители 15: 1, 3, 5, 15
Множители числа
Чтобы найти множители числа, скажем 12, мы выполняем следующие шаги:
1.Начните с 1 и запишите факты умножения так, чтобы произведение было 12, например 1 × 12.
2. Продолжайте тем же способом найти другие факты умножения, пока не дойдете до пары ближайших множителей или делителей, как указано:
1 × 12, 2 × 6, 3 × 4
3. Запишите все числа в факте умножения, так как они являются делителями 12.
4. Итак, делители или множители числа 12 равны 1,2,3,4,6 и 12.
Различные способы представления делителя
Существуют разные стили выражения уравнения деления.На изображениях ниже показаны различные методы записи делителя:
Особые случаи
1. Число 1 — делитель всех чисел.
Причина : Когда делитель равен 1, то частное совпадает с делимым.
Посмотрите на приведенные примеры,
34 1 = 34
15 1 = 15
2. Само число всегда является одним из делителей числа.
Причина : Когда делитель совпадает с делимым, тогда ответ на такое деление всегда 1.
Посмотрите на приведенные примеры,
34 34 = 1
15 15 = 1
3. Если делитель меньше делимого, то ответ будет не целым, а десятичным числом.
Например,
510 = 0,5
Интересные факты
|

 {2} + 4x + 5 [/ latex] на [latex] x + 2 [/ latex], используя алгоритм длинного деления.
{2} + 4x + 5 [/ latex] на [latex] x + 2 [/ latex], используя алгоритм длинного деления. 2} -7x + 18 [/ latex], а остаток –31. Процесс будет более понятен в Примере 3.
2} -7x + 18 [/ latex], а остаток –31. Процесс будет более понятен в Примере 3. Д.{2} -3x — 36 [/ латекс] по [латекс] х — 3. [/ Латекс]
Д.{2} -3x — 36 [/ латекс] по [латекс] х — 3. [/ Латекс] Мы начинаем с разделения на цифры дивиденда, которые имеют наибольшее значение. Мы делим, умножаем, вычитаем, включаем цифру в позицию следующего разряда и повторяем. Например, разделим 178 на 3 в столбик.
Мы начинаем с разделения на цифры дивиденда, которые имеют наибольшее значение. Мы делим, умножаем, вычитаем, включаем цифру в позицию следующего разряда и повторяем. Например, разделим 178 на 3 в столбик. Умножить:}}} 18 (x + 2) \\
Умножить:}}} 18 (x + 2) \\  2 + 3x − 2 \) на \ (x + 1 \).2 + 5x}}} {\ color {Cerulean} {)}} & {\ color {green} {\ text {Шаг 2. Умножьте:}}} 5x (x + 1) \\
2 + 3x − 2 \) на \ (x + 1 \).2 + 5x}}} {\ color {Cerulean} {)}} & {\ color {green} {\ text {Шаг 2. Умножьте:}}} 5x (x + 1) \\ 

 2 + 2x − 10 \).2 + 21x − 150 + \ frac {1,090} {x + 7} \)
2 + 2x − 10 \).2 + 21x − 150 + \ frac {1,090} {x + 7} \) Когда вы делите 9 (здесь не 37) на 5, вы получаете остаток 4.
Когда вы делите 9 (здесь не 37) на 5, вы получаете остаток 4. Если вы разделите 4 на 5, остаток будет 4. Теперь, если на предыдущем шаге, когда вы делили n на 4, если частное было 4, а остаток был 1, то число n должно было быть 4 * 4 + 1 = 17 (n = частное * делитель + остаток). Итак, каков будет остаток, если вы разделите 17 на 20? Будет 17.
Если вы разделите 4 на 5, остаток будет 4. Теперь, если на предыдущем шаге, когда вы делили n на 4, если частное было 4, а остаток был 1, то число n должно было быть 4 * 4 + 1 = 17 (n = частное * делитель + остаток). Итак, каков будет остаток, если вы разделите 17 на 20? Будет 17. Давайте теперь рассмотрим вопрос, связанный с тремя отделами.
Давайте теперь рассмотрим вопрос, связанный с тремя отделами. Разделите 157 на 8, 7 и 5 в таком порядке:
Разделите 157 на 8, 7 и 5 в таком порядке:  Она преподает GMAT Prep для Veritas Prep и регулярно участвует в проектах по разработке контента, таких как этот блог!
Она преподает GMAT Prep для Veritas Prep и регулярно участвует в проектах по разработке контента, таких как этот блог! 
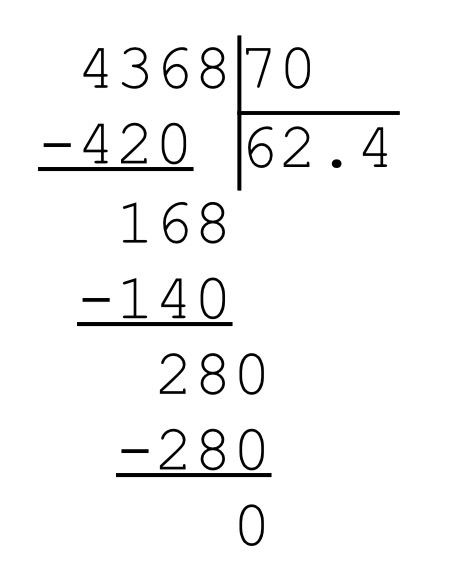 Похоже, что синтетическое деление может помочь нам в нескольких разных типах
проблем. Я думаю, вы готовы открыть для себя
чудесный мир синтетического деления.
Похоже, что синтетическое деление может помочь нам в нескольких разных типах
проблем. Я думаю, вы готовы открыть для себя
чудесный мир синтетического деления.
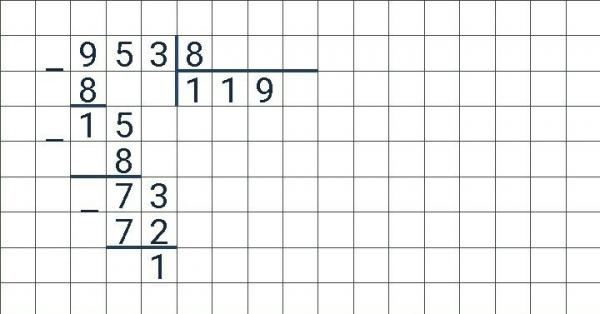 Включите любые 0, которые были вставлены вместо отсутствующих терминов.
Включите любые 0, которые были вставлены вместо отсутствующих терминов.
 д.
д. Окончательное значение справа — остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.
Окончательное значение справа — остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д. Окончательное значение справа — остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.
Окончательное значение справа — остаток.
Работая справа налево, следующее число — ваша константа, следующее — значение
коэффициент для x , следующий коэффициент
для x в квадрате и т. д.
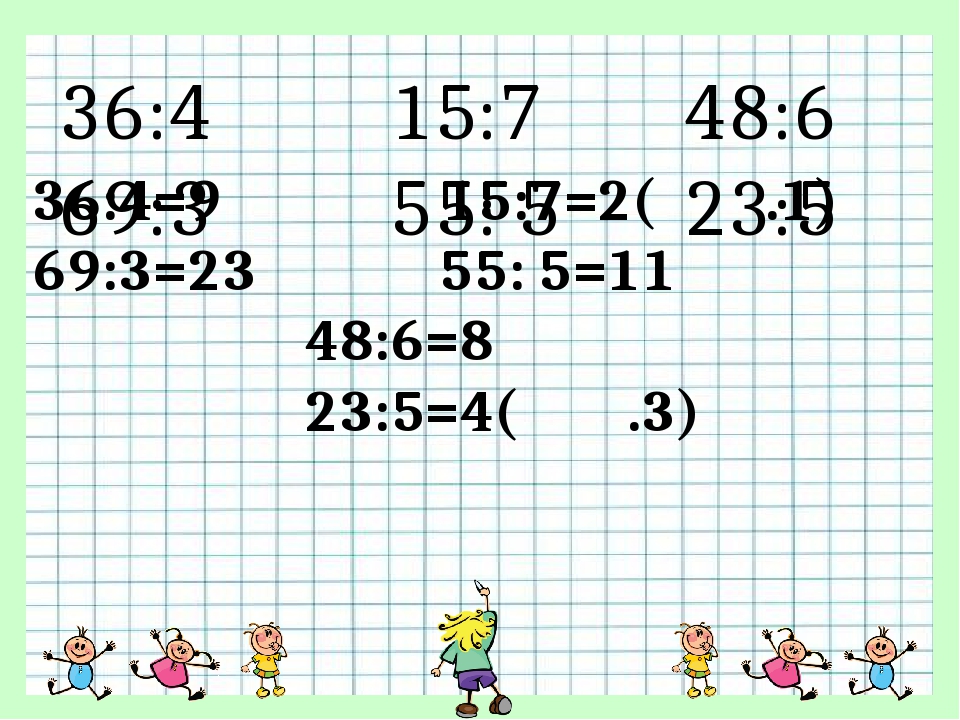 Если x — c — коэффициент,
вы можете переписать исходный многочлен как ( x — c ) (частное).
Если x — c — коэффициент,
вы можете переписать исходный многочлен как ( x — c ) (частное). Это означает, что ( x — 2) является множителем.
Это означает, что ( x — 2) является множителем.
