Урок 58. деление на трёхзначное число — Математика — 4 класс
Математика, 4 класс
Урок № 58. Деление на трёхзначное число.
Перечень вопросов, рассматриваемых в теме:
— Как делить многозначное число на двузначное?
— Как правильно выполнять запись деления?
— Как подобрать пробную цифру частного?
Глоссарий по теме:
Частное – результат деления одного числа на другое.
Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.
Основная и дополнительная литература по теме урока:
1. Петерсон Л.Г. Математика. 4 класс. 1 ч. – М.: 2013. – стр. 40-43.
2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2017.
3. Математика. Проверочные работы. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова — М.: Просвещение, 2017.
4. Математика. Тетрадь учебных достижений. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова — М.: Просвещение, 2017. – стр. 79-80.
Теоретический материал для самостоятельного изучения
Рассмотрим деление на трёхзначное число. Деление на трёхзначное число выполняется по тем же правилам, что и деление на двузначное число.
936:234.
Первое неполное делимое — это само число 936. Поэтому в частном будет только одна цифра.
Алгоритм деления: 1.Образую неполное делимое. 2.Определю количество цифр в частном. 3.Делю неполное делимое на делитель. 4.Умножаю делитель на пробную цифру. 5. Нахожу остаток от деления вычитанием. 6. Сравниваю остаток с делителем. |
Чтобы легче было найти цифру частного, будем делить 936 не на 234, а на 200. Для этого нужно 9 разделить на 2, получим 4. Это пробная цифра. Нужно проверить, подходит ли она. Проверку делаем устно.
Проверку делаем устно.
234 · 4 = 200 · 4 + 30 · 4 + 4 · 4 = 936
Полученное число равно делимому, значит, пробная цифра 4 подходит. Записываем ее в частном. Закончим запись деления столбиком. Умножаем 234 на 4, будет 936. Находим остаток от деления. Он равен нулю. Остаток меньше делителя. Деление закончено.
Найдём значение частного 219296 : 352
Выделим первое неполное делимое 2192 сотни.
Так как деление начинаем с сотен, в частном получим 3 цифры. Определяем первую цифру частного: 21:3=7, получили пробную цифру 7.
В запасе сотен нет, а требуется ещё 3 сотни, так как 5 дес. · 7 = 35 десятков. Значит, частное должно быть меньше 7.
Проверим 6.
3 сот. ·6 = 18 сот.
5 дес. ·6 = 30 дес. = 3 сот.
2 · 6 = 12
1800 + 300 + 12 = 2112
2112 < 2192, значит, цифра 6 подходит. Записываем ее в частном.
Умножаем 352 на 6, будет 2112. Вычитаем 2112 из 2192, будет 80. Остаток 80 меньше делителя 352.
Второе неполное делимое 809 десятков. Определяем цифру частного.
Определяем цифру частного.
8 : 3 = 2, получили пробную цифру 2.
Проверяем:
352 · 2 = 704
704 < 809, значит, цифра 2 подходит. Записываем ее в частном.
Умножаем 352 на 2, будет 704. Вычитаем 704 из 809, будет 105. Остаток 105 меньше делителя 352.
Третье неполное делимое 1056 единиц. Определяем цифру частного.
Делим 10 на 3, получаем пробную цифру 3. Проверяем, 352 умножаем на 3. Складываем 900, 150 и 6, получаем 1056. Это число равно третьему неполному делимому. Значит, цифра 3 подходит, записываем ее в частном. Умножаем 352 на 3, будет 1056. Вычитаем 1056 из 1056. Остаток равен нулю. Деление окончено.
Задания тренировочного модуля:
1. Определите значение выражения, используя запись деления столбиком.
92400:462+1386:462
Варианты ответа: 23; 203; 263
Правильный вариант: 203
2. Расшифруйте слово, с которого начинается четверостишие из поэмы М.Ю. Лермонтова.
(40 ∙ 40 ∙ 40 : 2 + 486850 : 650) ∙ 18
О | Е | М | А | Т |
З | Р | И | К | Н |
Ц | Ы |
_____ воет, дик и злобен,
Меж утёсами громад.
Буре плач его подобен,
Слёзы брызгами летят.
Правильный вариант: Терек
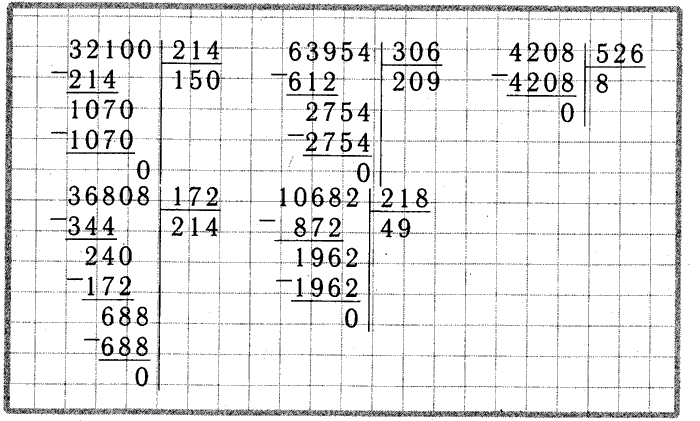
4. Выберите пропущенные числа в записи деления столбиком.
Варианты ответа: 0; 4; 7; 114; 141; 1141
Правильный вариант: 1141; 7; 0
| 1. |
Какое число в частном?
|
1 |
2.
|
Деление шестизначного числа на трёхзначное число устно
|
1 |
| 3. |
Частное по делимому и делителю
|
2 |
4. |
Деление четырёхзначного числа на трёхзначное число (1)
Сложность: среднее |
1 |
| 5. |
Деление четырёхзначного числа на трёхзначное число (2)
Сложность: среднее |
2 |
6. |
Деление пятизначного числа на трёхзначное число
Сложность: среднее |
2 |
| 7. |
Деление шестизначного числа на трёхзначное число. Краткая запись
Сложность: среднее |
2 |
8.
|
Деление круглого семизначного числа на трёхзначное число
Сложность: среднее |
2 |
| 9. |
Составление и решение уравнения
Сложность: среднее |
3 |
10.
|
Значение выражения
Сложность: среднее |
3 |
| 11. |
Текстовая задача (два участка)
Сложность: среднее |
3 |
12.
|
Неизвестное частное
Сложность: сложное |
3 |
| 13. |
Решение уравнения
Сложность: сложное |
4 |
14.
|
Во сколько раз меньше?
Сложность: сложное |
3 |
Как научить ребенка делить в столбик на однозначное, двузначное и трехзначное число | В помощь родителям младшего школьника
В конце 3 и 4 классов дети учатся делить в столбик. Если с умножением в столбик все достаточно понятно, то деление в столбик вызывает у детей замешательство. С первого раза с этой темой разобраться бывает сложно. В этой статье я расскажу, как научить ребёнка делить в столбик на однозначное, двузначное и трехзначное число.
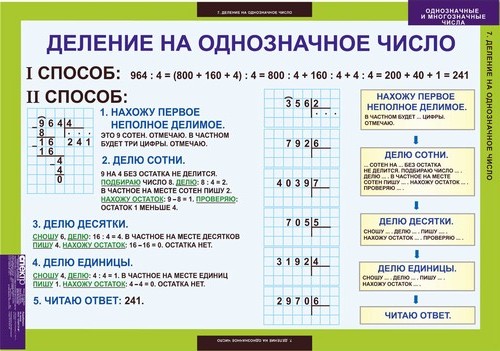
Как научить делить в столбик на однозначное число
Разделим 938 на 2.
При записи деления в столбик знак деления записывают углом. Над чертой пишут делитель. Под чертой записывают ответ (частное).
1. Ищем первое неполное делимое. Т. е. число, которое мы будем делить первым.
Для этого существует правило: сколько цифр в делителе, столько цифр в первом неполном делимом.
В нашем примере делитель 2. Для записи этого числа используют одну цифру. Значит и первое неполное делимое будет состоять из одной цифры. Это 9.
2. 9 разделить на 2 без остатка нельзя. Ищу близкое к девяти число, которое делится без остатка на 2. Это число 8. 8 : 2 = 4. 4 записываю под чертой. Проверяю себя. 4 × 2 = 8. Но я делила 9. Из 9 вычитаю 8. Получается 1.
3. 1 нельзя разделить на два. Сношу следующую цифру (3) и записываю рядом с 1. Получилось число 13. Это второе неполное делимое.
4. 13: 2 без остатка нельзя. Близкое число, которое делится без остатка на 2, — 12. 12 : 2 = 6. 6 записываю под чертой. 6 × 2 = 12. Из 13 вычитаю 12. Получается 1.
Близкое число, которое делится без остатка на 2, — 12. 12 : 2 = 6. 6 записываю под чертой. 6 × 2 = 12. Из 13 вычитаю 12. Получается 1.
5. 1 разделить на 2 нельзя. Сношу еще одну цифру. Это 8. Получилось число 18. 18- третье неполное делимое. 18 : 2 = 9. 9 × 2 = 18. 18 — 18= 0. Деление закончено.
938 : 2 = 469
Рассмотрим ещё один пример
4914 : 7
1. Сколько цифр в делителе, столько цифр в первом неполном делимом. Но 4 разделить на 7 нельзя. Поэтому первое неполное делимое — 49. 49 : 7 = 7. Проверяю себя. 7 ×7 = 49. 49 — 49 = 0. Но ноль в середине примера не пишем.
2. Сношу следующую цифру — 1. 1 на 7 не делится. В частном пишу 0.
Теперь внимательно! В в предыдущем примере мы не писали в частном 0 потому, что остался остаток при вычитании. В этом примере остатка при вычитании нет. Снесли цифру, число не разделилось. Пишем в частном 0.
Итак, 1 нельзя разделить на 7 без остатка. Пишу в частном 0.
3. Сношу следующую цифру — 4. Получилось число 14. 14 : 2 = 7. Проверяю себя. 7 × 2 = 14. 14 — 14 = 0. 4914 : 7 = 702.
Как делить в столбик на двузначное число
Потренируемся.
8508 : 12
1. В делителе две цифры. Поэтому первое неполное делимое — 85. Решаем методом подбора.
На сколько нужно умножить 12, чтобы получить число, близкое к 85? На 7. 12 × 7 = 84. 85 — 84 = 1.
2. 1 на 12 разделить нельзя. Сношу следующую цифру. Получилось число 10. 10 разделить на 12 нельзя. В частном пишу 0.
3. Сношу следующую цифру. Получилось число 108. 108 : 12 =9.
Как разделить в столбик на трехзначное число
Деление на трехзначное число происходит аналогично делению на двузначное число.
Разделим 29876 на 308.
1. Ищем первое неполное делимое. Сколько цифр в делителе, столько цифр в первом неполном делимом. Но 298 нельзя разделить на 308. Поэтому первое неполное делимое будет число 2987.
2. Подбираем, на сколько нужно умножить 308, чтобы получилось число, близкое к 2987. Это число 9. 308 × 9 = 2772. 9 пишу в ответ. Из 2987 вычитаю 2772. Получается 215.
3. 215 нельзя разделить на 308. Сношу 6. Получилось число 2156. Оно делится на 308 без остатка. Получается 7. 7 пишу в ответ. Из 2156 вычитаю 2156. Получается 0. Деление закончено.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Как делить четырехзначное число на трехзначное. Как научиться делить столбиком: примеры и решения
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.
Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.
Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.
Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.
Как правильно делить числа в столбик: алгоритм деления
Для деления чисел столбиком следуйте по таким шагам:
- правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку.
 Так вы сохраните визуальную последовательность решения,
Так вы сохраните визуальную последовательность решения, - разлинейте место между делимым и делителем.
Вам поможет схема ниже.
- планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
- первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
- перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
- завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
- допишите следующую цифру делимого к остатку и продолжайте решение,
- последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя.
 Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Как объяснить ребенку деление и научить делить столбиком?
Во-первых, учтите ряд вводных факторов:
- ребёнок знает таблицу умножения
- хорошо разбирается и умеет применять на практике действия вычитания и сложения
- понимает разницу между целым и его составными элементами
- поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
- объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
- превратите процесс в игру, придумайте историю про цифры и действие деления,
- подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
- первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:
- запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
- предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
- подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
- помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
- следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
- снова помогите с записью действия,
- продолжайте до момента, когда результат от разницы составит ноль.
 Это актуально только для деления чисел без остатка,
Это актуально только для деления чисел без остатка, - закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.
Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
Приступим к пошаговому разбору примеров на деление в столбик.
Осуществите действие над цифрами 25 и 2:
- запишите их рядом и разделите линиями границы,
- определите нужное количество цифр делимого для первого действия,
- запишите значение под делителем и результат умножения под делимым,
- выполните вычитание,
- допишите вторую цифру делимого и повторите действия на умножение и вычитание.
Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:
Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.
Второй пример. Разделите 87 на 26 в столбик.
Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.
Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.
Ниже пример деления столбиком двузначного числа на двузначное с остатком.
Третий пример. Как разделить число в столбик с нулем в ответе.
Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.
Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.
Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.
Схематически он выглядит так:
В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.
Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.
Схема деления трехзначного на двузначное числа такая:
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.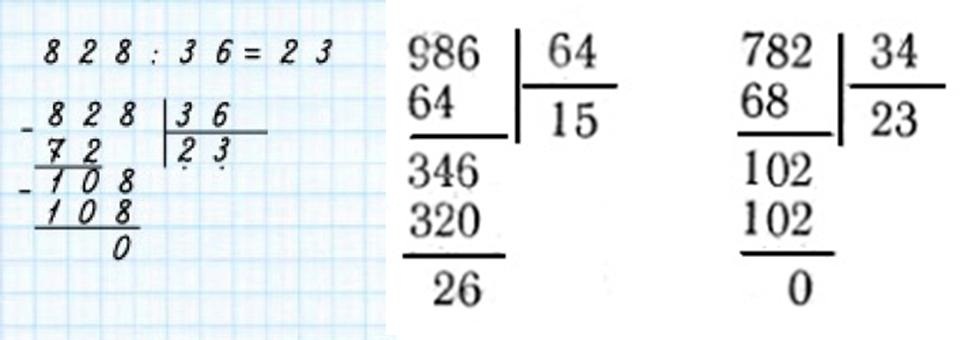
Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.
Схема деления трёхзначного на трёхзначное числа.
Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:
- определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
- появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
- проверку полученного результата посредством выполнения действия умножения.
 Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Ниже пример решения.
Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.
Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:
- количество знаков у частного, то есть результата
- цифры у делимого для первого действия
- правильность переноса остальных чисел
Примеры подробного решения ниже.
При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:
- у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
- для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
- совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов.
 Тогда их сократите и получится результат без остатка.
Тогда их сократите и получится результат без остатка.
Ниже ряд подробных примеров с решениями.
Как делить в столбик с остатком?
Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.
Запишите его в ответе либо:
- как дробь, где в числителе остаток, а в знаменателе — делитель
- словами, например, 73 целых и 6 в остатке
Как делить столбиком десятичные дроби с запятой?
Существует несколько особенностей при подобном делении. Если вы совершаете действие с:
- десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
- числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя.
 Например, 749,5:100=7,495,
Например, 749,5:100=7,495, - десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.
Как делить столбиком меньшее число на большее?
При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.
Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:
- первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
- поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
- когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка.
 В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
Ниже пример.
Как делить столбиком числа с нулями?
Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.
Из нюансов отметим:
- при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
- если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.
Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.
Пример, 1000:2=500 — вы перенесли два последних нуля.
Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.
Практикуйте полученные знания и помогайте своему чаду осваивать математику.
Видео: как правильно делить числа в столбик?
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.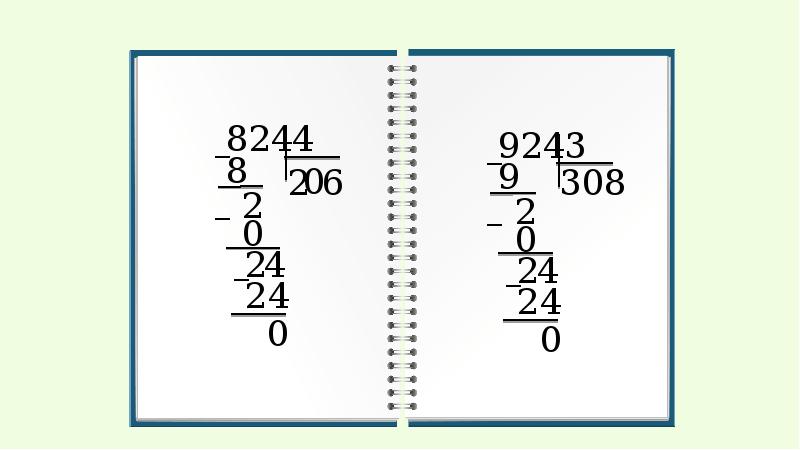
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7.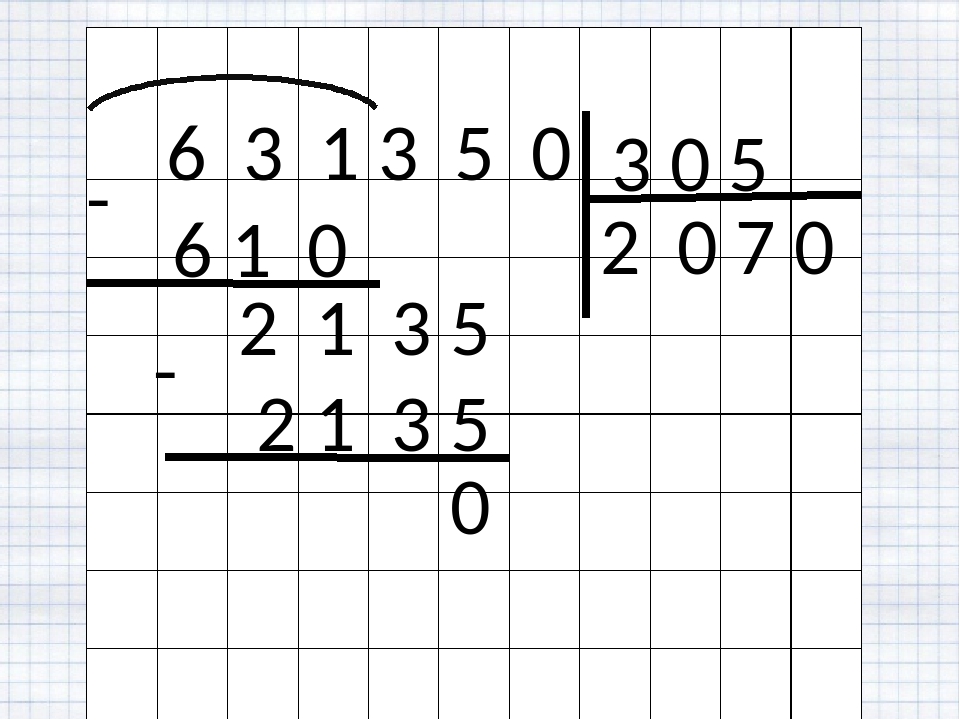 Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление.
 Уровень 4. Рабочая тетрадь» от Kumon
Уровень 4. Рабочая тетрадь» от Kumon - «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Как в столбик делить — один из основных навыков, необходимых для работы с двух- и трёхзначными числами. Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Этот полезный математический навык необходим не только для успешного освоения школьной программы по математике и ряду других предметов. Умение делить наверняка поможет каждому в повседневной жизни.
Умение делить наверняка поможет каждому в повседневной жизни.
Итак, делимое, то есть число, которое нужно разделить, надо записать слева. Число, на которое делят, называют делителем и записывают справа.
Под делителем проводится черта, под которой пишут частное (решение).
Под делимым необходимо оставить место, требующееся для вычислений.
Сама задача выглядит следующим образом: пакет, где лежат шесть грибов, весит 250 грамм. Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Сейчас предстоит вычислить, сколько целых раз делится первая цифра (отсчёт ведётся с левого конца) делимого на делитель.
Для решения нашей задачи нужно узнать, сколько раз цифра 2 делится на 6. Так как это невозможно, то в ответе — 0, который записывается под делителем. В этом случае нуль является первым числом частного, однако допускается отказ от такой записи.
Теперь предстоит узнать, сколько целых раз делятся две первые цифры делимого на делитель.
Если в предшествующем действии в ответе был получен 0, надо рассмотреть две первые цифры делимого. В рассматриваемой задаче надо вычислить, сколько раз 25 делится на 6.
Если делитель является двух- и более значным числом, надо разделить на него первые три (четыре, пять и т. д.) цифры делимого. Наша цель: получить целое число.
Далее начинается работа с целыми числами. Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Результат, полученный в третьем этапе, записывается прямо под соответствующей цифрой делителя — под чертой. Данный итог будет первой цифрой искомого частного, то есть ответа.
Результат обязательно нужно писать под соответствующей цифрой делителя. Если пренебречь этим требованием, будет допущена ошибка, которая скажется и на конечном результате: он будет неверным.
В рассматриваемом случае 4 записывается под 5, так как на 6 делится число 25, а не 2.
Часть вторая. УмножениеЭтот этап представляет собой переход к новой части работы «как считать в столбик». Деление в данном случае сменятся… умножением.
Делитель умножается на число, которое было под ним записано. Это означает, что речь идёт о первой цифре искомого частного.
Результат этого произведения размещается под делимым.
В рассматриваемом примере 6 х 4 = 24. Число, стоящее в ответе, то есть 24, записывается под 25. Важно: 2 должна стоять под 2, а 4 — под 5.
Результат произведения подчёркивается. В нашем случае речь идёт о подчёркивании числа 24.
Здесь происходит переход к вычитанию и опусканию цифр.
Результат записывается под чертой, которая в свою очередь проводится под числом, поставленным под делимым.
Нам предстоит произвести вычитание 24 из 25. Получаемый при этом результат: 1.
Получаемый при этом результат: 1.
Опускается третья цифра делимого, то есть она записывается рядом с результатом вычитания.
В нашем случае 1 не может делиться на 6. В силу этого спускают третью цифру делимого (третьей цифрой числа 250 является 0). Она размещается рядом с 1. Мы получаем число 10, которое может быть разделено на 6.
Теперь требуется повторить процесс с новым числом.
Для этого полученное число делится на наш делитель, а получаемый при этом результат размещается под делителем, в качестве которого будет выступать вторая цифра частного, то есть нашего ответа.
В решаемом примере 10 делим на 6, что даёт в итоге 1. Единичка записывается в частное — рядом с 4. После этого 6 умножается на 1 и из 10 вычитают результат. У нас должно получиться 4 (остаток).
Если делимое представляет собой двух-, трёх-, четырёх- и более значное число, изложенный процесс повторяется до тех пор, пока не будут опущены все цифры делимого. Пример для иллюстрации: если известно, что вес грибов равен 2 506 г, надо опустить цифру 6, то есть записать её рядом с 4.
Теперь переходим к записи частного с остатком или в виде десятичной дроби.
Наш остаток был равен 4, что связано с тем, что это число — 4 — не делится на 6 и у нас не осталось цифр, которые можно спустить.
Ответ при этом будет выглядеть следующим образом: 41 (ост. 4).
Вычисления на данном этапе могут быть завершены, если в задаче сформулировано требование найти что-то, выражаемое исключительно в целых числах. Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Если есть необходимость в ответе в виде десятичной дроби, можно перейти к следующим действиям алгоритма «как разделить в столбик».
Если нет желания записывать ответ с остатком, можно найти ответ в виде десятичной дроби. При получении остатка, не поддающегося делению на делитель, надо добавить десятичный знак (к частному).
В нашем случае число 250 может быть записано в виде десятичной дроби: 250. 000.
000.
Теперь, когда в наличии цифры (только нули), которые могут быть опущены, можно продолжить вычисления. Опускаем нуль и подсчитываем, сколько целых раз можно поделить полученное число на делитель.
В нашем примере после частного 41 (которое размещаем прямо под делителем) пишем десятичную запятую и приписываем 0 к остатку (4). Затем делим полученное число, то есть 40, на делитель (в роли которого выступает 6). Получаем опять 6, которую пишем в частное после десятичного знака. Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
В ряде ситуаций при поиске ответа в виде десятичной дроби приходится столкнуться с повторяющимися числами. Для этого надо прервать вычисления и округлить уже полученный ответ — вниз или вверх.
В частности, в рассматриваемом примере надо отказаться от бесконечного получения цифры 4. Нужно просто прервать вычисления и округлить частное. В силу того, что 6 больше 5, округление производится вверх, в результате чего получается ответ в виде дробного числа 41.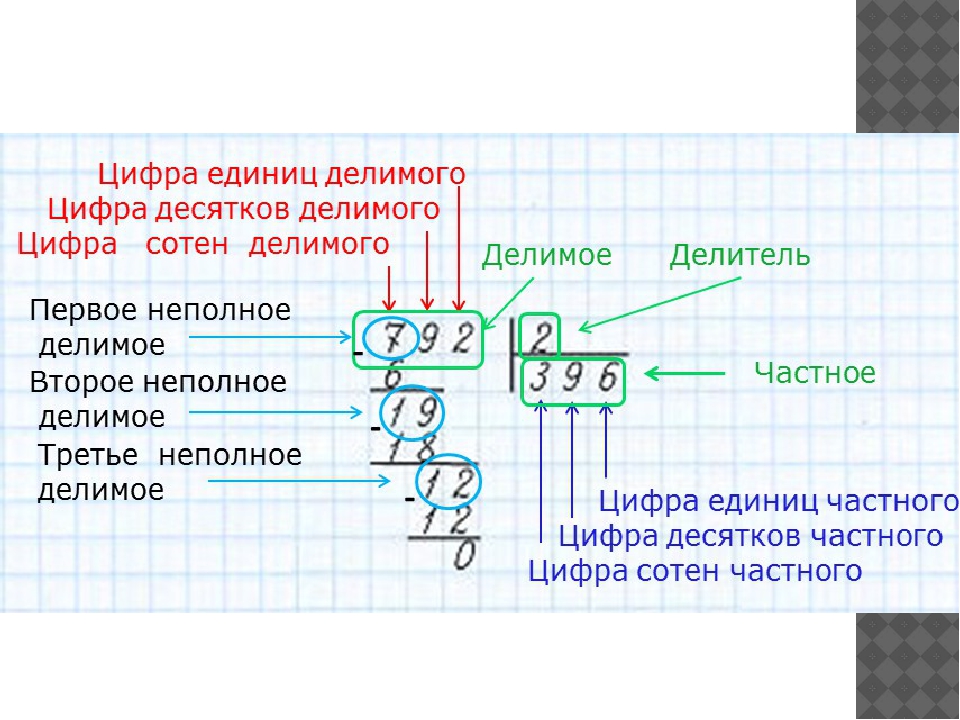 67.
67.
Деление столбиком (также можно встретить название деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными
числами изображается символ вида
.
Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.Как делить в столбик лучше всего объяснить на примере. Вычислить :
512:8=?
Для начала запишем делимое и делитель в столбик.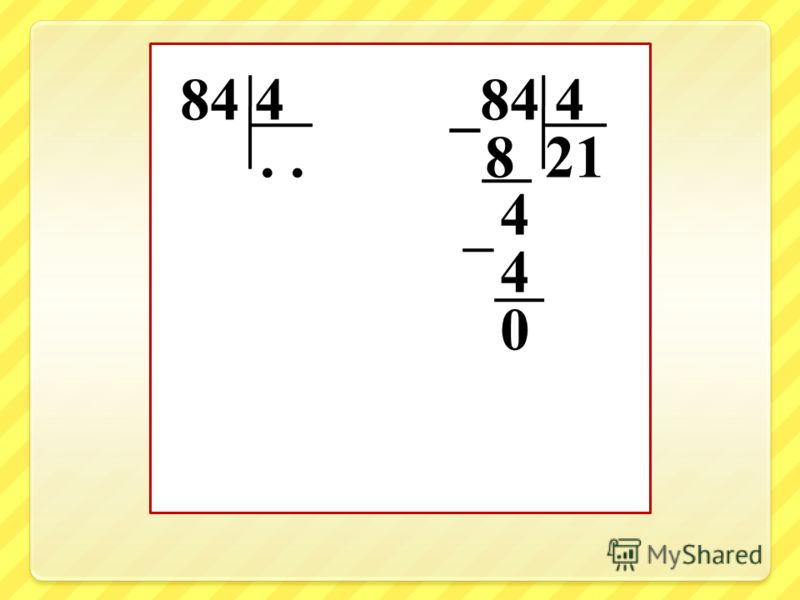 Выглядеть это будет так:
Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения .
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не
стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в
записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.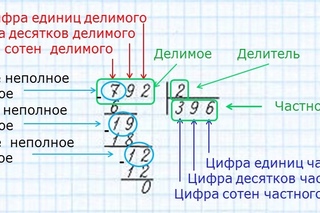
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.

- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число
получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего,
меньшего разряда и продолжать деление.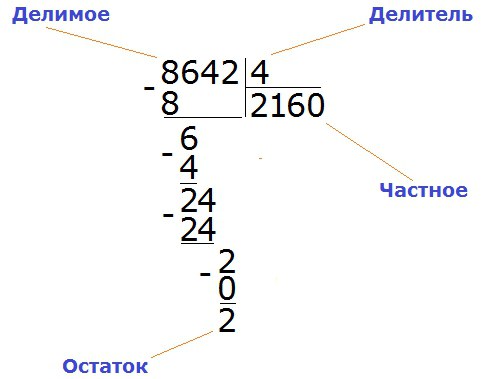
Алгоритм деления в столбик. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.

Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).

На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Одним из наиболее важных этапов обучения вашего ребенка математическим операциям является обучение действиям деления простых чисел. Для обучения делению ребенка, нужно, чтобы к моменту обучения он уже освоил и хорошо понимал такие математические действия, как вычитание, сложение.
Кроме того, важно иметь четкое представление о самой сущности таких действий, как деление и умножение. Таким образом, он должен понимать, что в действии с делением заключается метод разделения чего-либо на равные доли. В заключение необходимо также обучиться операциям по умножению и хорошо знать таблицу умножения.
Обучаемся операции по делению на части
На данном этапе лучше сформировать понимание того, что главное в процессе деления, это разделение чего-то на равные части. Самым простым способом научиться этому для ребенка, это будет предложить ему поделить несколько предметов между ним и членами семьи или друзьями.
К примеру, возьмите 6 одинаковых предметов и предложите ребенку поделить их на две равные части. Можно немного усложнить задание, предложив поделить не на две, а на три равные части.
Важным моментом здесь считается проводить операции по делению четных количеств предметов. Такое действие окажется полезным на дальнейшем этапе, когда ребенку будет необходимо понимание того, что разделение, это действие, обратное умножению.
Делим и умножаем, при помощи таблицы умножения
Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.
Например : 2 умножить на 4 будет восемь. Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения.
Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.
Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное». Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!
Разделяем столбиком – легко и быстро
Перед тем, как начинать обучение следует вспомнить с ребенком, какое название имеет каждое число в процессе операции разделения. Главное, научиться быстро и безошибочно научиться определять данные категории.
Наглядный пример:
Попробуем разделить 938 на 7. В этом приведенном примере число 938 будет являться делимым, а число 7 будет делителем. В результате действия, ответ будет называться частное.
В результате действия, ответ будет называться частное.
- Необходимо записать числа, разделив их «уголком».
- Предложите ученику из наименьшего числа делимого выбрать то, что больше делителя. Из цифр 9, 3, 8, наибольшим будет цифра 9. Предложите проанализировать, сколько семерок может содержать в цифре 9. Одним правильным ответом здесь будет только один. Первым результатом записываем 1.
- Оформляем деление в столбик.
Умножим делитель 7 на 1, ответ будет 7. Полученный результат вписываем под первое число нашего делимого, затем вычитаем в столбик. Таким образом, из 9 отнимаем 7 и в ответе получаем 2. Это тоже записываем.
- Видим число, получившееся меньше делителя, поэтому увеличиваем его. Чтобы это сделать, объединим его вместе с неиспользованным числом делимого, то есть с цифрой 3. Дописываем 3 к полученной 2.
- Затем анализируем сколько раз делитель 7 будет содержаться в числе 23. Ответ 3 раза и фиксируем его в частном. Результат произведения 7 на 3 (21) вписываем снизу в столбик под число 23.

- Остается только найти последнее число частного. Применяя тот же алгоритм, продолжает вычисления в столбике. Вычитает в столбике 23-21 получает разницу, равной числу 2. Из всего делимого, у нас остается только неиспользованное число 8. Его объединяем с полученным результатом 2, получаем в ответе 28.
- В заключение анализируем, какое количество, раз делитель 7 содержится в полученном нами числе. Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Самым наиболее главным при обучении ребенка методу деления, будет усвоение и четкое понимание алгоритма действий, ведь на самом деле он предельно прост.
Если ваш ребенок отлично умеет оперировать таблицей умножения, то с «обратным» делением у него не должны возникнуть трудности. Поэтому очень важно все время тренировать полученные навыки. Не стоит останавливаться на достигнутом.
Для легкого обучения юного ученика методу деления следует:
- в возрасте трех лет правильно усвоить термины «целое» и «часть».
 Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта.
Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта. - правильно понимать и разбираться в методах деления и умножения.
Чтобы занятия доставили ребенку удовольствие, следует возбуждать интерес к математике в ситуациях в быту, а не только в процессе учебы.
Поэтому тренируйте наблюдательность у ребенка, придумывайте аналогии математических действий во время игр, в процессе конструирования либо же в простых наблюдениях за природой.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.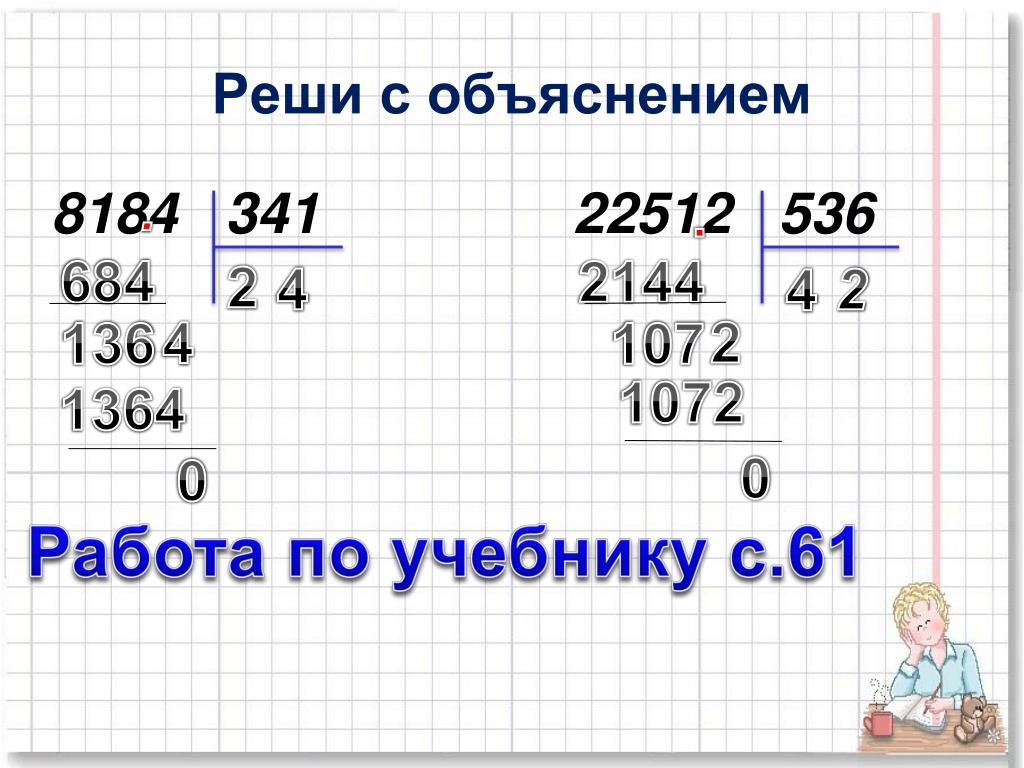 6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть».
 У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.

- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Как делить большие числа с остатком. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком.
 Когда делитель больше делимого
Когда делитель больше делимогоПрочитайте тему урока: «Деление с остатком». Что вы уже знаете по этой теме?
Можете ли вы разложить 8 слив поровну на две тарелки (рис. 1)?
Рис. 1. Иллюстрация к примеру
В каждую тарелку можно положить по 4 сливы (рис. 2).
Рис. 2. Иллюстрация к примеру
Действие, которое мы выполнили, можно записать так.
8: 2 = 4
Как вы думаете, можно ли 8 слив поровну разложить на 3 тарелки (рис. 3)?
Рис. 3. Иллюстрация к примеру
Будем действовать так. Сначала в каждую тарелку положим по одной сливе, потом по второй сливе. У нас останется 2 сливы, но 3 тарелки. Значит, дальше поровну мы разложить не можем. Мы положили в каждую тарелку по 2 сливы, и 2 сливы у нас осталось (рис. 4).
Рис. 4. Иллюстрация к примеру
Продолжим наблюдение.
Прочитайте числа. Среди данных чисел найдите те, которые делятся на 3.
11, 12, 13, 14, 15, 16, 17, 18, 19
Проверьте себя.
Остальные числа (11, 13, 14, 16, 17, 19) на 3 не делятся, или говорят «делятся с остатком».
Найдем значение частного.
Узнаем, сколько раз по 3 содержится в числе 17 (рис. 5).
Рис. 5. Иллюстрация к примеру
Мы видим, что поместилось по 3 овала 5 раз и 2 овала осталось.
Выполненное действие можно записать так.
17: 3 = 5 (ост. 2)
Можно записать и в столбик (рис. 6)
Рис. 6. Иллюстрация к примеру
Рассмотрите рисунки. Объясните подписи к этим рисункам (рис. 7).
Рис. 7. Иллюстрация к примеру
Рассмотрим первый рисунок (рис. 8).
Рис. 8. Иллюстрация к примеру
Мы видим, что 15 овалов разделили по 2. По 2 повторилось 7 раз, в остатке — 1 овал.
Рассмотрим второй рисунок (рис. 9).
Рис. 9. Иллюстрация к примеру
На этом рисунке 15 квадратов разделили по 4. По 4 повторилось 3 раза, в остатке — 3 квадрата.
Рассмотрим третий рисунок (рис. 10).
10).
Рис. 10. Иллюстрация к примеру
Можно сказать, что 15 овалов разделили по 3. По 3 повторилось 5 раз поровну. В таких случаях говорят, что остаток — 0.
Выполним деление.
Семь квадратов разделим по три. Получим две группы, и один квадрат останется. Запишем решение (рис. 11).
Рис. 11. Иллюстрация к примеру
Выполним деление.
Узнаем, сколько раз по четыре содержится в числе 10. Видим, что в числе 10 по четыре содержится 2 раза и 2 квадрата остаются. Запишем решение (рис. 12).
Рис. 12. Иллюстрация к примеру
Выполним деление.
Узнаем, сколько раз по два содержится в числе 11. Видим, что в числе 11 по два содержится 5 раз и 1 квадрат остается. Запишем решение (рис. 13).
Рис. 13. Иллюстрация к примеру
Сделаем вывод. Разделить с остатком — значит узнать, сколько раз делитель содержится в делимом и сколько единиц останется.
Деление с остатком можно выполнить и на числовом луче.
На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и одно деление осталось (рис. 14).
Рис. 14. Иллюстрация к примеру
Запишем решение.
10: 3 = 3 (ост.1)
Выполним деление.
На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и два деления осталось (рис. 15).
Рис. 15. Иллюстрация к примеру
Запишем решение.
11: 3 = 3 (ост.2)
Выполним деление.
На числовом луче отметим отрезки по 3 деления и увидим, что получили ровно 4 раза, остаток отсутствует (рис. 16).
Рис. 16. Иллюстрация к примеру
Запишем решение.
12: 3 = 4
Сегодня на уроке мы познакомились с делением с остатком, научились выполнять названное действие с помощью рисунка и числового луча, потренировались в решении примеров по теме урока.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник.
 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Выпиши числа, которые делятся на 2 без остатка.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
2. Выполни деление с остатком с помощью рисунка.
3. Выполни деление с остатком с помощью числового луча.
4. Составь задание для своих товарищей по теме урока.
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?
Разделим натуральное число 273844 на натуральное число 97 .
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823 , а остаток равен 13 .
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 — 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 — 3 = 1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7 ÷ 3 = 2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3 .
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.
Вычислим: 145 ÷ 46 .
Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:
Повторяем эту операцию еще раз:
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .
145 ÷ 46 = 3 (остаток 7) .
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a
Например:
12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a — b · c . Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т. д. Применяя формулу d = a — b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.
д. Применяя формулу d = a — b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбора
Разделим 267 на 21 .
a = 267 ; b = 21 . Подберем неполное частное.
Используем формулу d = a — b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.
Если с = 0 , имеем: d = a — b · c = 267 — 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.
При с = 1 имеем: d = a — b · c = 267 — 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.
При с = 2 имеем: d = a — b · c = 267 — 21 · 2 = 267 — 42 = 225 ; 225 > 21 .
При с = 3 имеем: d = a — b · c = 267 — 21 · 3 = 267 — 63 = 204 ; 204 > 21 .
При с = 12 имеем: d = a — b · c = 267 — 21 · 12 = 267 — 252 = 15 ; 15
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a b .
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b .
Найти нужно неполное частное c и остаток d .
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
В нашем конкретном примере в делимом три знака, а в делителе — два.
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .
470 899 .
Число, которое мы получили на предпоследнем шаге (470 = 47 · 10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1 — 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 — 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899 — 470 = 429 , 429 > 47 . Повторяем шаги 1 — 5 алгоритма с числом 429 , взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу — число 1 .
2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 — 1 = 0 .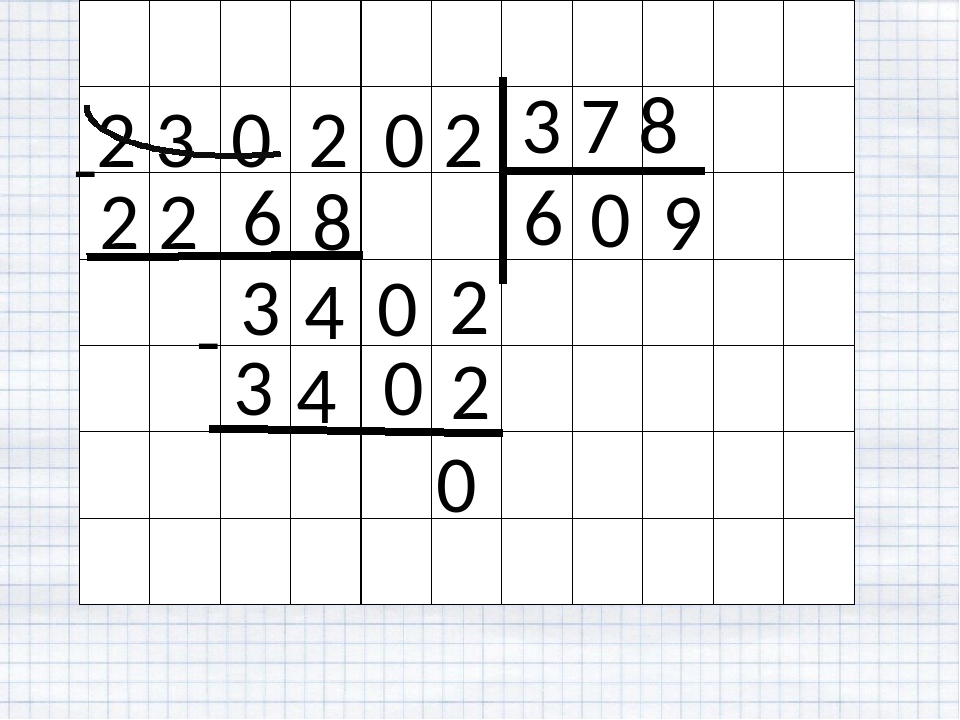 Запоминаем 0 .
Запоминаем 0 .
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 429 . Таким образом, второе искомое слагаемое — 47 · 9 = 423 .
5. Разность между 429 и 423 равна числу 6 . Так как 6
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:
899 = 47 · 10 + 47 · 9 + 6
Применим распределительное свойство умножения.
899 = 47 · 10 + 47 · 9 + 6 = 47 · (10 + 9) + 6
899 = 47 · 19 + 6 .
Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .
Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Пример 5. Деление натуральных чисел с остатком
Разделим числа 42252 и 68 .
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800 = 68 · 600 .
Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 — 40800 и получаем второе слагаемое 1360 = 68 · 20
Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 — 1360 . Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 — 68 .
В результате получаем:
42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · (600 + 20 + 1) + 24 = 68 · 621 + 24
Неполное частное равно 621 , остаток равен 24 .
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый.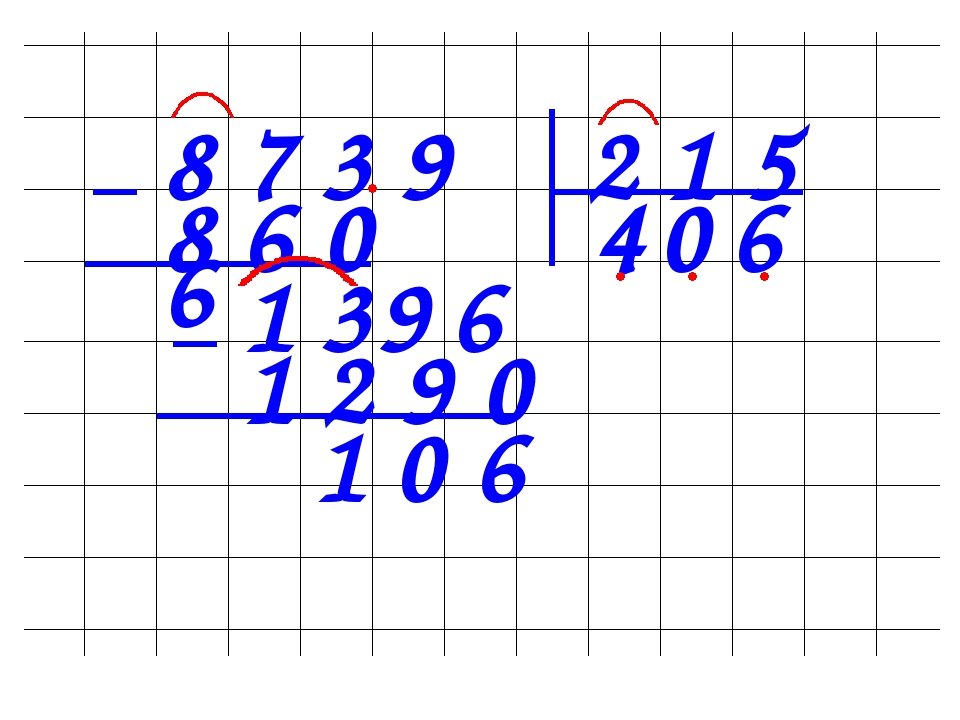 Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Важно!
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Пример 6. Проверка результата деления натуральных чисел с остатком.
Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .
Сравниваем остаток и делитель: 30 > 28 .
Значит, деление выполнено неверно.
Пример 7. Проверка результата деления натуральных чисел с остатком.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5
Первый пункт проверки пройден, переходим ко второму.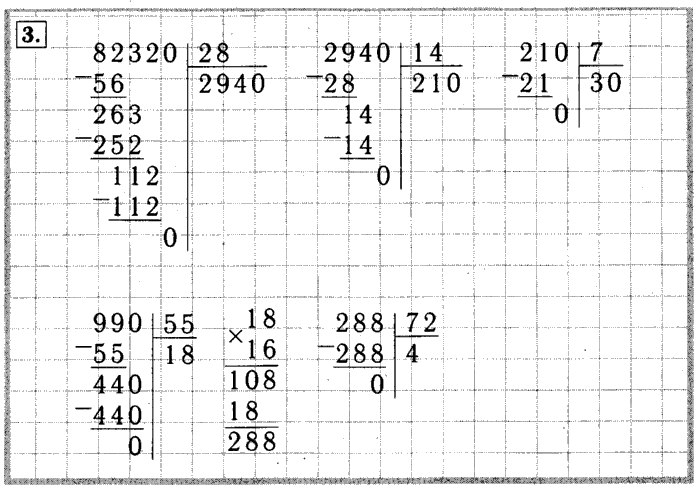
Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .
Подставляем значения и сравниваем результаты
13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122
Значит, в вычисления школьника где-то закралась ошибка.
Пример 8. Проверка результата деления натуральных чисел с остатком.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 . Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.
Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .
После подстановки, имеем:
5998 = 111 · 54 + 4 = 5994 + 4 = 5998 .
Равенство корректно, а значит, и деление выполнено верно.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление.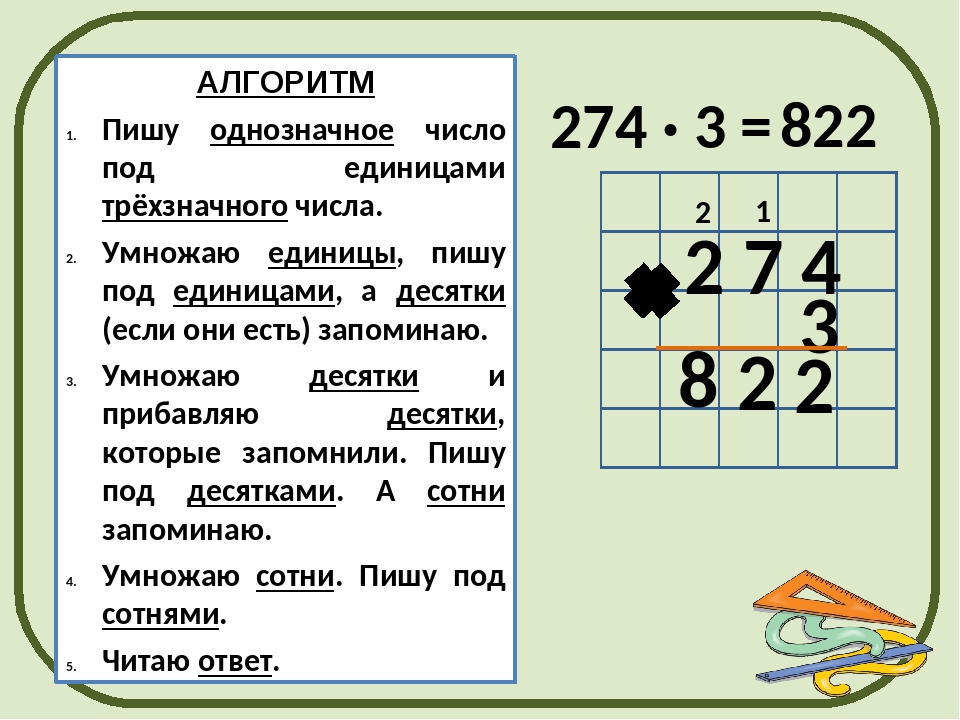 В качестве примера, разделим 17 на 5.
В качестве примера, разделим 17 на 5.
Основные этапы :
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2.
 Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные : 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного .
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 5, в остатке — 11.
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 3, осталось — 14.
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
1199.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 2099. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ: неполное частное = 12, остаток — 7.
Деление с остатком — примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Чем занимается на математике 3 класс? Деление с остатком, примеры и задачи — вот что изучается на уроках. О делении с остатком и алгоритме таких вычислений пойдет речь в статье.
Особенности
Рассмотрим темы, включенные в программу, которую изучает 3 класс. Деление с остатком выделено в специальный раздел математики. О чем идет речь? Если делимое не делится на делитель нацело, то остается остаток. Например, делим 21 на 6. Получается 3, но в остатке остается 3.
В случаях, когда во время деления натуральных чисел остаток равен нулю, говорят о том, что произведено деление нацело. Например, если 25 нужно поделить на 5, получается число 5. Остаток равен нулю.
Решение примеров
Для того чтобы произвести деление с остатком, используется определенная запись.
Приведем примеры по математике (3 класс). Деление с остатком в столбик можно не записывать. Достаточно записи в строчку: 13:4=3 (остаток 1) или 17:5=3 (остаток 2).
Разберем все подробнее. Например, при делении 17 на три получается целое число пять, кроме того, получается остаток два. Каков порядок решения такого примера на деление с остатком? Сначала необходимо отыскать максимальное число до 17, разделить которое можно без остатка на три. Самым большим будет 15.
Далее проводится деление 15 на число три, результатом действия будет цифра пять. Теперь вычитаем из делимого число, найденное нами, то есть из 17 отнимаем 15, получаем два. Обязательным действием является сверка делителя и остатка. После проверки обязательно записывается ответ совершенного действия. 17:3=15 (остаток 2).
После проверки обязательно записывается ответ совершенного действия. 17:3=15 (остаток 2).
Если остаток будет больше делителя, действие выполнено неправильно. Именно по такому алгоритму выполняет 3 класс деление с остатком. Примеры сначала разбирает учитель на доске, затем ребятам предлагается проверка знаний путем проведения самостоятельной работы.
Пример с умножением
Одна из самых трудных тем, с которой сталкивается 3 класс, — деление с остатком. Примеры могут быть сложными, особенно когда требуются дополнительные расчеты, записываемые в столбик.
Допустим, необходимо разделить число 190 на 27 с получением минимального остатка. Попробуем решить задачу, пользуясь умножением.
Подберем число, которое при умножении будет давать цифру, максимально приближенную к числу 190. Если умножить 27 на 6, получим цифру 162. Вычтем из 190 число 162, остаток будет 28. Он получился больше, чем исходный делитель. Следовательно, число шесть не подходит для нашего примера в качестве множителя.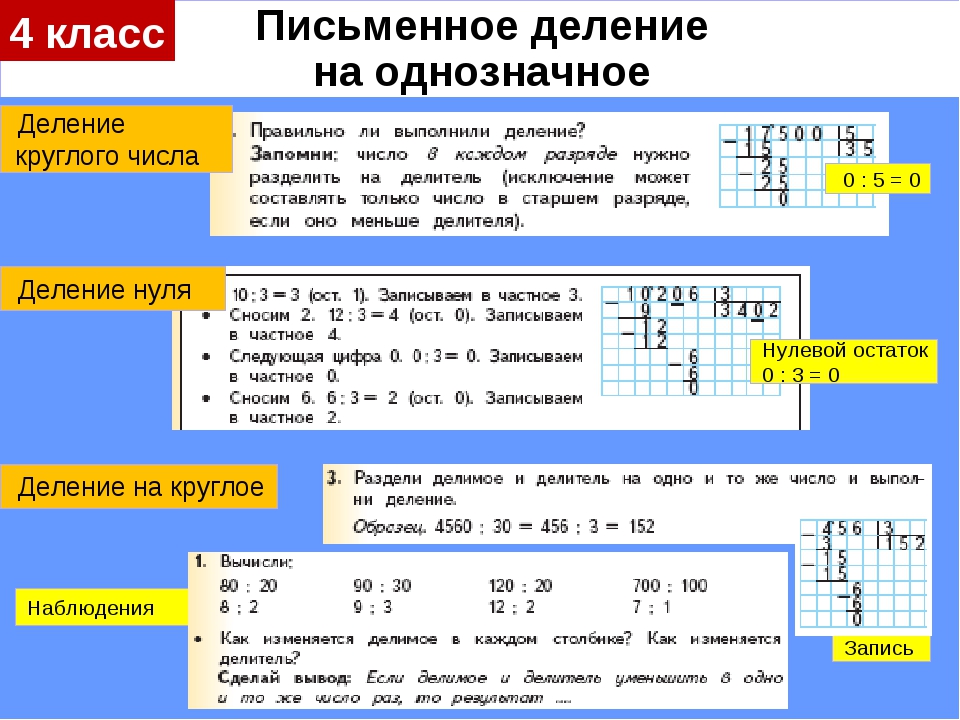 Продолжим решение примера, взяв для умножения число 7.
Продолжим решение примера, взяв для умножения число 7.
Умножая 27 на 7, мы получим произведение 189. Далее проведем проверку правильности решения, для этого вычтем из 190 полученный результат, то есть отнимем число 189. Остатком будет 1, что явно меньше 27. Именно так решаются сложные выражения в школе (3 класс, деление с остатком). Примеры всегда предусматривают запись ответа. Все математическое выражение можно оформить так: 190:27=7 (остаток 1). Подобные вычисления можно производить и в столбик.
Именно так осуществляет 3 класс деление с остатком. Примеры, приведенные выше, помогут разобраться в алгоритме решения подобных задач.
Заключение
Для того чтобы у учеников начальных классов были сформированы правильные вычислительные навыки, педагог во время проведения занятий по математике обязан уделять внимание пояснению алгоритма действий ребенка при решении заданий на деление с остатком.
По новым федеральным государственным образовательным стандартам особое внимание уделяется индивидуальному подходу к обучению. Учитель должен подбирать задания для каждого ребенка с учетом его индивидуальных способностей. На каждой ступени обучения правилам деления с остатком педагог должен осуществлять промежуточный контроль. Он позволяет ему выявлять основные проблемы, возникающие с усвоением материала у каждого ученика, своевременно проводить коррекцию знаний и навыков, устранять появляющиеся проблемы, получать желаемый результат.
Учитель должен подбирать задания для каждого ребенка с учетом его индивидуальных способностей. На каждой ступени обучения правилам деления с остатком педагог должен осуществлять промежуточный контроль. Он позволяет ему выявлять основные проблемы, возникающие с усвоением материала у каждого ученика, своевременно проводить коррекцию знаний и навыков, устранять появляющиеся проблемы, получать желаемый результат.
Деление столбиком (также можно встретить название деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида .
Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет
записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже
делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
512:8=?
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого.
Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать
с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую
слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми
цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения .
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в
этом пункте не является самым последним действием, полностью завершающим процесс деления
столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое
«промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
При этом, в первое
«промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.
- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить
поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Деление столбиком. Онлайн калькулятор | Математика
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30.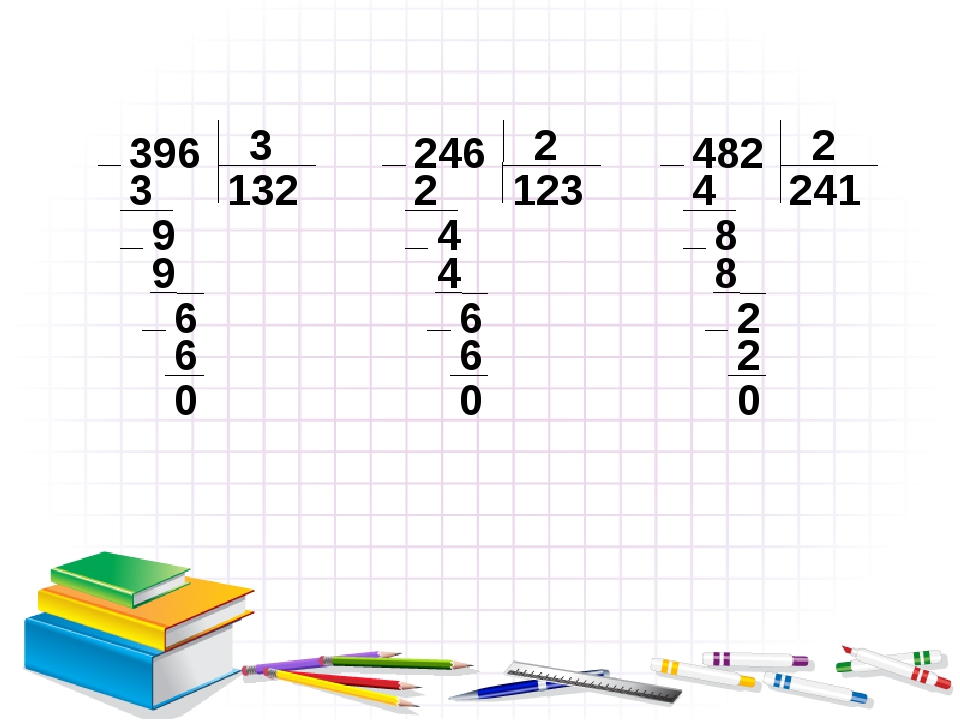 В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить
.
Как разделить трехзначное число
Деление — это математический процесс, в котором вы определяете, сколько раз одно значение уместится в другое значение. Деление противоположно умножению. Некоторых студентов расстраивает деление, особенно при делении значений на более крупные числа, такие как трехзначные числа. Вы сможете делить трехзначные числа, если поймете процессы оценки, умножения и заимствования. После небольшой практики у вас не должно возникнуть проблем с обработкой трехзначных чисел в задачах деления.
Напишите данное трехзначное число под скобкой деления. Это называется «дивидендом».
Напишите число, которое будет разделено на трехзначное число в левой части скобки. Это называется «делителем».
Оцените, сколько раз делитель уместится в делимом, на основе округленных чисел. Например, если у вас есть 309 в качестве делителя и 675 в качестве дивиденда, вы можете мысленно округлить 309 до 300 и 675 до 700. Число 300 уместится в 700 дважды, поэтому вы можете попробовать 2 в качестве первой оценки.
Умножьте свою оценку на фактический делитель в стороне от проблемы или на листе бумаги. В этом примере вы умножите 2 на 309, что даст результат 618. Если бы вы использовали 3 в качестве первой цифры вашего частного, ваш ответ был бы более 900, что слишком велико. Таким образом, вы знаете, что 2 будет первой цифрой вашего частного.
Запишите первую цифру вашего частного над столбцом единиц вашего дивиденда. Напишите это число в верхней части скобки деления.В этом случае вы должны написать 2.
Умножьте первую цифру вашего частного на ваш делитель, запишите ответ под своим дивидендом и проведите линию под произведением. В этом примере вы умножите 2 на 309, чтобы получить 618.
Вычтите ответ из шага 6 из вашего дивиденда. В этом примере вы должны вычесть 618 из 675. Поскольку 8 в столбце единиц больше, чем 5, вы должны «позаимствовать» 1 из разряда десятков, что делает 5 равным 15. Вычтите 8 из 15, чтобы получить 7 в одном месте.Переходя к столбцу десятков, вы должны вычесть 1 из 7, так как вы ранее занимали. Это делает цифру десятков равной 6. Таким образом, вы вычтете 1 из 6, чтобы получить 5. Наконец, в позиции сотен вы вычтете 6 из 6, в результате останется ноль. Следовательно, ваш ответ на этом шаге будет 57, который вы должны написать под линией, которую вы нарисовали на шаге 6.
Добавьте десятичную дробь к вашему разделенному, что в данном случае составляет 675,0. Сбросьте ноль до предыдущей разницы 57, получив 570.Затем разделите свой делитель на это число. В этом примере вы разделите 309 на 570, что подойдет только 1 раз. Поэтому вы должны написать десятичную дробь после первой цифры вашего частного (равного 2), а затем числа 1.
Умножьте вторую цифру вашего частного на ваш делитель и запишите произведение внизу задачи с линия под ним. В этом случае вы должны умножить 1 на 309, чтобы получить 309. Вы должны написать 309 под 570 и вычесть, чтобы получить 261.
Продолжайте процесс прибавления нуля к делимому, опускания нуля, деления делителя на новое число, умножения и вычитания, пока вы не решите задачу до желаемого разряда.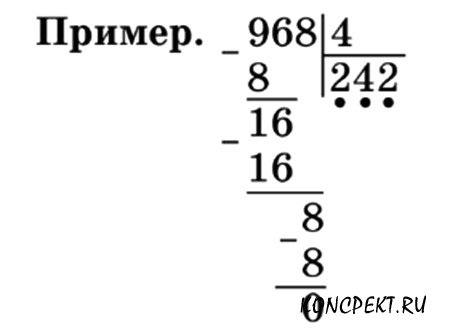
iDevBooks — Раздел столбцов
для iPad, iPhone, Mac и ПК с Windows 10
Это приложение можно использовать для обучения и изучения метода разделения столбцов. Приложение простое в использовании и имеет интуитивно понятный интерактивный интерфейс с настраиваемыми цветами и другими настройками.Пользователь может решать задачи произвольного и произвольного деления.
Метод разделения по столбцам
Метод деления на столбцы — это простой вариант традиционного метода деления столбиком. Линии проводятся для разделения цифр делителя. Каждый столбец с размеченными значениями решается слева направо.
В программе повседневной математики метод деления на столбцы является одним из алгоритмов деления.
Приложение Column Division
Числа выравниваются автоматически, так что пользователь может сосредоточиться на решении операций для каждого столбца.
После того, как вы решите операцию для каждого частичного продукта, правильный ответ попадет в нужное место. Если вы нажмете не ту кнопку, ответ появится над клавиатурой, но не будет двигаться.
Если вы нажмете не ту кнопку, ответ появится над клавиатурой, но не будет двигаться.
Сложность может быть установлена
- Дивиденд может содержать от 2 до 5 цифр
- Делитель может состоять из 1 или 2 цифр
- Текущая операция может быть скрыта
- Можно выделить операнды текущей операции
- Цвета интерфейса можно менять
- Скорость анимации можно установить
Column Division Видео
Разделение на столбцы с трехзначным делением
324 ÷ 6
Разделение на столбцы с пятизначным делением и двузначным делителем
÷ 33
Column Division в Apple VPP Store для образовательных учреждений
Программа оптовых закупок позволяет участвующим образовательным учреждениям приобретать математические приложения iDevBooks в больших количествах и распространять их среди студентов. Все математические приложения iDevBooks предлагают специальную скидку 50% на покупку 20 или более приложений для участвующих учебных заведений.
Все математические приложения iDevBooks предлагают специальную скидку 50% на покупку 20 или более приложений для участвующих учебных заведений.
Колонный отдел в магазине ВПП
Как научить деление в столбик: пошаговый метод
В этой статье я объясню, как обучить делению в столбик в несколько шагов. Вместо того, чтобы показывать студентам сразу весь алгоритм, мы искренне воспринимайте это «шаг за шагом».
До ребенок готов учить деление в столбик, он должен знать:
- таблицы умножения (по крайней мере неплохо)
- базовая концепция деления, основанная на таблицах умножения
(например, 28 ÷ 7 или 56 ÷ 8) - базовое деление с остатками (например 54 ÷ 7 или 23 ÷ 5)
Одна из причин, по которой деление в столбик затруднено
Деление в столбик — это алгоритм, который повторяет основные шаги
1)
Разделять; 2) Умножить; 3) Вычесть; 4) Отбросьте следующую цифру.
Из этих шагов №2 и №3 могут стать трудными и запутать учащихся, потому что они, по-видимому, не имеют отношения к разделению — они имеют отношение к нахождению остатка. На самом деле, чтобы указать на это, мне нравится объединять их в один «умножить и вычесть» шаг.
Чтобы избежать путаницы, я рекомендую обучать полному делению в таком мода на то, что дети сначала НЕ подвергаются всем этим шагам. Вместо этого вы можете научить этому в несколько «ступенек»:
- Шаг 1: Все цифры деления четные.Здесь студенты отрабатывают только разделительную часть.
- Шаг 2: Остаток в единицах. Сейчас же, студенты практикуют часть «умножить и вычесть» и связать это с поиском остаток.
- Шаг 3: остаток в десятках. Студенты теперь используйте весь алгоритм, в том числе «отбрасывание следующей цифры», с использованием 2-значного дивиденды.
- Шаг 4: Остаток в любом месте
значения. Студенты практикуют весь алгоритм, используя более длинные дивиденды.

Шаг 1: Все цифры деления четные
Мы делим числа, в которых каждая из цифр сотен, десятков и единиц без остатка делится на делитель. ЦЕЛЬ на этом первом легком шаге — это приучить студентов к двум вещам:
- Чтобы привыкнуть к большему делению «угол», чтобы частное писалось сверху.
- Чтобы привыкнуть спрашивать, сколько раз делитель переходит в разные цифры делимого.
Ниже приведены примеры проблем для этого шага. Студенты должны проверить каждый
деление на умножение.
На этом этапе ученики также учатся смотреть на первые две цифры делимого, если делитель не «входит» в первую цифру:
4 не входит в 2. | |||||||||||||||||||||
Пояснение: 2 из 248, конечно, 200 на самом деле. Если вы разделите 200 на 4, результат будет меньше 100, поэтому частное не будет иметь любые целые сотни. Но тогда вы комбинируете 2 сотни с 4 десятками.Это составляет 24 десятка, и вы МОЖЕТЕ разделить 24 десятка на 4. Результат 6 десятков входит в частное. Отметьте окончательный ответ: 4 × 62 = 248. |
Далее следуют другие примеры проблем. Разделять. Проверьте свой ответ умножение частного на делитель.
| а. | б. | ||
г. | г. | ||
Шаг 2: Остаток в единицах
Теперь есть остаток в единицах (единицах). Тысячи, сотни, и десятки цифр по-прежнему делятся на делитель. Во-первых, студенты могут остальное решить мысленно и просто напишите остаток сразу после частное:
4 балла
не входить в 1 (сотку). 4 переходит в 16 четыре раза. 4 идет в 5 раз, оставив остаток 1. |
8 шт. не входить в 3 тысячи.Так что объедините 3 тысячи с 2 сотни (3200). 8 идет
в 32 четыре раза (3200 ÷ 8 = 400) |
Далее студенты учатся
на номер найдите
остаток с использованием процесса «умножить и вычесть» . Это
очень важный шаг! Часть «умножить и вычесть» часто очень
запутывает студентов, поэтому здесь мы практикуем это в максимально простых
место: в самом конце деления, в колонке единиц (вместо
в столбце десятки или сотни).Конечно, это предполагает, что студенты
уже научились находить остаток в задачах простого деления
основанные на таблицах умножения (например, 45 ÷ 7 или 18 ÷ 5).
Это
очень важный шаг! Часть «умножить и вычесть» часто очень
запутывает студентов, поэтому здесь мы практикуем это в максимально простых
место: в самом конце деления, в колонке единиц (вместо
в столбце десятки или сотни).Конечно, это предполагает, что студенты
уже научились находить остаток в задачах простого деления
основанные на таблицах умножения (например, 45 ÷ 7 или 18 ÷ 5).
В проблемах раньше вы просто записывали оставшуюся часть. Обычно мы записываем вычитание, которое фактически находит остаток. Смотрите внимательно:
|
|
Вот несколько примеров проблем. Теперь студенты проверяют ответ, умножая делитель на частное, а затем добавляем остаток.
| а. | б. | ||
| | | |
| г. | г. | ||
| |
Шаг 3: остаток в десятках
На этом этапе студенты впервые практикуют все основные шаги. алгоритма длинного деления: делить, умножать и вычитать, раскрывать
следующая цифра.Для простоты мы используем двузначные числа. Умножить
& вычитание связано с нахождением остатка, а после нахождения
остаток мы объединяем со следующим блоком, к которому мы готовимся
разделить (опустив цифру).
алгоритма длинного деления: делить, умножать и вычитать, раскрывать
следующая цифра.Для простоты мы используем двузначные числа. Умножить
& вычитание связано с нахождением остатка, а после нахождения
остаток мы объединяем со следующим блоком, к которому мы готовимся
разделить (опустив цифру).Пример:
| 1. Разделять. | 2. Умножить и вычесть. | 3. Выпустите следующую цифру. | ||||||||||||||||||||||||||||||
Два переходит в 5 два раз, или 5 десятков ÷ 2 = 2 целых десятки — но есть остаток! |
Чтобы найти, умножьте 2
× 2 = 4, напишите это 4 под пятеркой и вычтите, чтобы найти
остаток от 1 десятки. |
Затем выпадайте 8 из один следующий к оставшейся 1 десять.Вы объединяете остаток десять с 8 единицами, получаем 18. |
1. Разделять. Разделять. | 2. Умножить и вычесть. | 3. Выпустите следующую цифру. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Разделите 2 на 18. |
Умножить 9 × 2 = 18,
напишите, что 18 меньше 18, и вычтите. |
Разделение окончено
так как в дивиденде больше нет цифр. |
Шаг 4: остаток в любом из значений разряда
Освоив предыдущий шаг, студенты долго практикуются. деление с трех- и четырехзначными числами, куда им придется идти выполните основные шаги несколько раз.| 1. Разделять. | 2. Умножить и вычесть. | 3.Выпустите следующую цифру. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Два переходят в 2 одного
раз, или 2 сотни ÷ 2 = 1 сотня. |
Умножить 1 × 2 = 2, напишите это 2 под двумя и вычтите, чтобы найти остаток от нуля. |
Затем выпадайте 7
из десятков рядом с нулем. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Разделить. | Умножить & вычесть. | Капля вниз на следующую цифру. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Разделите 2 на 7. |
Умножить
3 × 2 = 6, запишите это 6 под 7 и вычтите, чтобы найти остаток от 1 до десяти. |
Затем выпадайте 8
из тех, что рядом с 1 оставшимися десятью. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. Разделять. | 2. Умножить и вычесть. | 3. Выпустите следующую цифру. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Разделите 2 на 18. |
Умножить 9 × 2 = 18,
напишите, что 18 меньше 18, и вычтите, чтобы найти остаток от нуля. |
Больше нет
цифры, которые нужно раскрыть. |
Эти идеи также объясняются в видео на YouTube ниже:
Почему работает длинное деление
Я чувствую, что алгоритм длинного деления И почему он работает, представляет собой довольно сложную вещь для изучения студентами, поэтому в этом случае я не вижу проблемы с учениками, которые сначала изучают алгоритмические шаги («как»), а затем углубляются в «почему».Попытка сделать и то, и другое одновременно может оказаться для некоторых слишком сложной задачей.
Однако, как только ученик овладевает базовыми навыками , как выполнять долгое деление, пора также изучить, на чем он основан. Чтобы узнать больше об этом, посетите:
Деление в столбик как повторное вычитание
Почему работает длинное деление (на основе повторного вычитания)
Рабочие листы
Листы с длинным делением
Создайте неограниченное количество листов для деления в столбик (классы 4-6), в том числе с 2-значными и 3-значными делителями. Рабочие листы могут быть выполнены в формате html или PDF — оба легко распечатать. Вы также можете настроить их с помощью генератора.
Рабочие листы могут быть выполнены в формате html или PDF — оба легко распечатать. Вы также можете настроить их с помощью генератора.
Деление на 1000 — Математика с мамой
Чтобы разделить число на 1000, мы перемещаем каждой цифры в этом числе трех столбцов значений разряда вправо на .Разделение целого числа , которое заканчивается тремя нулями , на 1000 имеет тот же эффект, что и удаление трех нулей.
Этот прием работает только с целыми числами, оканчивающимися на три нуля (или числами, кратными 1000).Вот пример деления такого числа на 1000.
В приведенном выше примере каждая цифра в числе 9000 перемещена на три позиции вправо.
Цифра «9» в столбце тысяч перемещается в столбец единиц.
При делении на тысячу любая цифра в столбце тысяч всегда будет перемещаться в столбец единиц слева от десятичной точки.
«0» в столбце сотен перемещается на три позиции в столбец десятых, сразу после десятичной точки.
«0» в столбце десятков перемещается на три позиции в столбец сотых.
Наконец, «0» в столбце единиц переместится в столбец тысячных.
Итак, 9000 становится 9.000, что совпадает с 9.
Если число имеет только цифру «0» после десятичной точки, тогда это целое число, и мы не записываем нули или десятичную точку.
Легче написать 9, чем 9.000.
Вы также можете знать, что когда мы делим целое число, заканчивающееся тремя нулями, на 1000, мы можем просто «удалить нули» из конца этого числа.
Этот трюк не сработает, если у нас есть десятичное число.
Важно понимать, как работает деление на 1000, потому что не все числа, которые мы делим на 1000, заканчиваются тремя нулями.
Например:
Чтобы разделить 604 на 1000, мы перемещаем каждой цифры на 604 на три позиции вправо .
Начнем с перемещения «6» из столбца сотен на три позиции вправо в столбец десятых .
Затем «0» и «4» будут следовать за 6 в том же порядке. «0» перемещается из столбца десятков в столбец сотых , а «4» перемещается из столбца единиц в столбец тысячных долей .
«0» перемещается из столбца десятков в столбец сотых , а «4» перемещается из столбца единиц в столбец тысячных долей .
Поскольку в столбце единиц измерения больше нет цифр, мы пишем ноль.
Итак, 604 ÷ 1000 = 0,604.
Мы всегда записываем одну цифру «0» в столбце единиц перед десятичной точкой, если не осталось другой цифры для записи.Неправильно начинать число с десятичной точки, поэтому мы пишем «0,604», а не «.604». Это позволяет избежать путаницы в письменном тексте с использованием чисел. Это позволяет избежать путаницы между запятыми, точками и десятичными точками.
Десятичная точка маленькая и иногда ее не замечают. Включая ноль перед десятичной точкой, он помогает читателю понять, что после нуля, вероятно, будет десятичная точка. Это связано с тем, что целые числа не начинаются с нуля, и единственный способ сделать ноль первой цифрой числа — это десятичное число.
В следующем примере мы делим десятичное число на 1000.
Начнем с того, что переместим цифру «1» на три позиции вправо . Он перемещается из столбца десятков в столбец сотых . Затем последуют 2 и 8. Мы перемещаем 2 из столбца единиц в столбец тысячных и перемещаем 8 из столбца десятых долей в столбец десятитысячных.
Поскольку больше нет цифр ни в столбце единиц, ни в столбце десятых, мы пишем ноль в каждое из этих мест.
Следовательно, 12,8 ÷ 1000 = 0,0128
В следующем примере мы делим десятичное число меньше 1 на 1000.
Для этого переместим цифру «5» на три позиции вправо , из столбца десятых долей в столбец десятитысячных .
Поскольку в столбце десятых, сотых или тысячных нет цифр, мы записываем ноль в каждый из этих столбцов, чтобы показать, что их значения равны нулю.
Следовательно, 0,5 ÷ 1000 = 0,0005.
Правила отдела
Правила Дивизиона
Задача состоит в том, чтобы разделить трехзначное число на однозначное.

Начните с решения, на какое число вы собираетесь делить. Это ваш делитель.
Ваша задача будет заключаться в том, чтобы придумать некоторые правила для этого делителя.
Теперь сгенерируйте трехзначное число. Это ваши дивиденды.
Здесь вы можете использовать счетчики для генерации цифр, вы можете использовать кости или просто использовать свое воображение!
Теперь разделите ваш дивиденд на делитель.Запишите ответ.
Создайте другие дивиденды и разделите их на тот же делитель. Запишите ответы.
Внимательно посмотрите ответы. Когда ответ — целое число? Когда останется 1?
Можете ли вы заметить какие-нибудь закономерности?
Можете придумать какие-нибудь правила?
Почему это действие?
Это упражнение дает контекст для практики деления трехзначного числа на однозначное число. Он побуждает детей замечать закономерности и догадки, а также проверять правила.Это может привести к установлению способов распознавания трехзначных чисел в таблицах умножения.
Возможный подход
Урок может начаться с повторения любых шаблонов, которые дети распознали в таблицах умножения, вплоть до x10 или x12. Они могут знать, что числа в таблице 5 всегда заканчиваются на 5 или 0, например. В этом упражнении эти правила распространяются на трехзначные числа.Перед тем, как приступить к выполнению задания, возможно, стоит напомнить детям о методах, которые они могут использовать для деления.
В качестве класса вы можете изучить делитель 2 и записать результаты, как показано ниже:
| Расчет | Целый ответ | Остаток от 1 |
| 269 ÷ 2 = 134 r1 | 269 | |
| 547 ÷ 2 = 273 r1 | 547 | |
| 466 ÷ 2 = 233 | 466 | |
| 728 ÷ 2 = 364 | 728 | |
Призовите класс внимательно посмотреть на числа, приводящие к различным типам ответов, найти сходства и использовать эту информацию для создания правила для типов чисел, которые появляются в каждом столбце.
 Сделайте предположение, а затем проверьте его!
Сделайте предположение, а затем проверьте его!Помните, что ответы целыми числами означают, что дивиденд является кратным делителю.
Тогда все классы могут исследовать один и тот же делитель, или разные группы могут смотреть на разные делители (возможность дифференцировать деятельность).
Некоторые дети могут перейти к дополнительному заданию (см. Ниже).
Ключевые вопросы
Что общего у чисел с целым числом?Вы можете придумать правило?
Как вы думаете, вы могли бы найти кратные… без необходимости выполнять расчет деления?
Возможные расширения
Другой способ решения проблемы — сохранять постоянный дивиденд и изменять делители. Итак, вы можете исследовать, что происходит, когда вы делите 123 (например) на 2, затем на 3, затем на 4 и так далее. Сможете ли вы найти какие-нибудь трехзначные простые числа? Есть ли способ быстро определить эти числа?Возможная поддержка
Сетка умножения и калькулятор были бы полезны (последнее, только если упор не на отработку письменного метода).
математических приемов — ядро исследования поведенческих наук
Эта веб-страница посвящена невероятной идее
о том, что математика может быть увлекательной!
Попробуйте эти уловки:
Вот несколько интересных ссылок:
- Список для чтения книг по сложной математике, большинство из которых я использовал для этого сайта.
- Узнайте об исходном компьютере: Abacus (http://www.ee.ryerson.ca:8080/~elf/abacus/)
- Сыграйте в математическую погоню (http: // dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape, Не прокручивать страницу вниз, пока загружается .
- Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Проверьте свои знания таблиц умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.
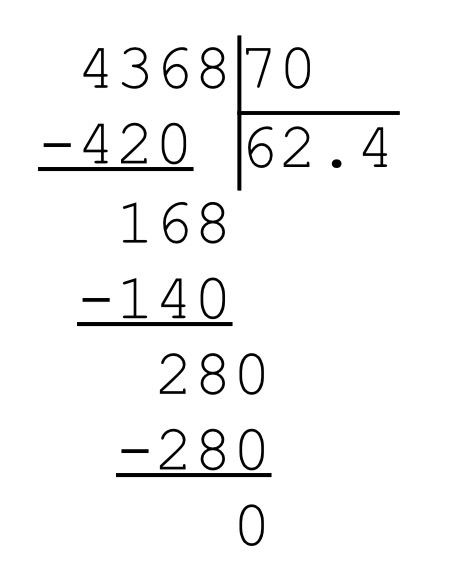 html)
html) - Попробуйте свои силы в оценке (http: //www.fi.uu.nl / wisweb / en / applets / bollen / Welcome.html).
- Исследуйте геометрию в увлекательной и интерактивной форме.
- Попробуйте загадку Ханойской башни (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
- Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
- Посмотрите, что такое сет Мандельброта (http://www.franceway.com/java/fractale/mandel_b.htm).
- Если вам нужно больше математических задач , попробуйте новый сайт PBS MATHLINE MATH CHALLENGESsite. Попробуйте, вам понравится.(Но помните, что мы были первыми.)
Трюк с добавлением магии # 1
Поразите батраков этим. Все просто. Это эффективно. Он их получает каждый раз.
- Спросите свою оценку, чтобы выбрать три (3) различных номеров от 1 до 9.
- Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, наибольшее первое и наименьшее последнее, чтобы получилось одно трехзначное число.
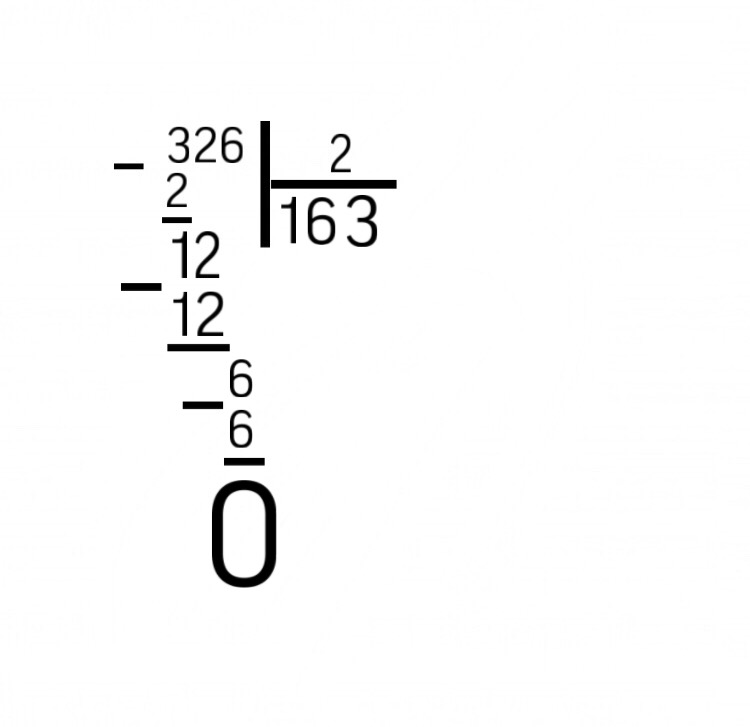 Скажите ему / ей, чтобы он не называл вам цифры.
Скажите ему / ей, чтобы он не называл вам цифры. - Затем попросите ее или ее сформировать новое трехзначное число, поменяв местами цифры, поместив наименьшее первым и наибольшее последнее. И напишите это число прямо под первым числом.
- Теперь попросите его или ее вычесть нижнее (и меньшее) трехзначное число из верхнего (и большего) трехзначного числа. Скажите им, чтобы они не рассказывали вам, каков результат.
- Теперь у вас есть выбор подытоживания:
- Попросите друга сложить три цифры числа, полученного в результате вычитания меньшего из большего трехзначного числа.Затем поразите его или ее, сказав им, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
- Скажите своему другу, что если он или она скажет вам первую ИЛИ последнюю цифру ответа, вы скажете ей или ему, каковы остальные две цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет равна 9! Итак, чтобы получить цифру, отличную от средней (то есть 9) и отличную от цифры, которую говорит вам ваш друг, просто вычтите цифру, которую ваш друг говорит вам, из 9, и это неизвестная цифра.

В начало
Магический квадрат №15
Сумма в каждой строке и столбце этого магического квадрата равна 15. Так что сделайте обе диагонали!
В начало
Магический квадрат №34
Сумма в каждой строке и столбце равна 34 в этом магическом квадрате. Так что сделайте обе диагонали!
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |
В начало
Рецепт для вашего собственного волшебного квадрата 3 x 3
Вот рецепт для создания собственного квадрата с магическим числом 3 х 3.Этот рецепт и оба вышеупомянутых магических квадрата взяты из одной чертовой книги Ланселота Хогбена под названием «Математика на миллион », изданной Norton and Company. Я очень рекомендую это. Вам совсем не нужно много математики, чтобы окунуться в приключение чисел, рассказанное в этой классической книге.
Я очень рекомендую это. Вам совсем не нужно много математики, чтобы окунуться в приключение чисел, рассказанное в этой классической книге.
Некоторые необходимые правила и определения:
- Пусть буквы a , b и c обозначают целые числа (то есть целые числа).
- Всегда выбирайте a так, чтобы оно было больше суммы b и c .То есть a > b + c . Это гарантирует, что никакие записи в магическом квадрате не являются отрицательными числами.
- Не позволяйте 2 X b = c . Это гарантирует, что вы не получите одинаковый номер в разных ячейках.
- Используя формулы в таблице ниже, вы можете составить магические квадраты, в которых сумма строк, столбцов и диагоналей равна 3 X независимо от того, какое значение — .
| a + c | a + b — c | а — б |
| a — b — c | a | a + b + c |
| a + b | a — b + c | a — c |
Чтобы создать первый Магический квадрат # 15, приведенный выше, вы позволяете a быть равным 5, пусть b равно 3, и пусть c будет равно 1.Вот еще несколько:
- a = 6, b = 3, c = 2
- a = 6, b = 3, c = 1
- a = 7, b = 3, c = 2
- a = 7, b = 4, c = 2
- a = 8, b = 6, c = 1
- a = 8, b = 5, c = 2
- a = 8, b = 4, c = 3
Попробуйте придумать что-нибудь свое.
В начало
Волшебный квадрат вверх ногами
Вот магический квадрат, который не только дает в сумме 264 во всех направлениях, но и делает это, даже когда он перевернут! Если вы мне не верите, посмотрите на него, пока стоите на голове! (Или просто скопируйте его и переверните вверх дном.)
| 96 | 11 | 89 | 68 |
| 88 | 69 | 91 | 16 |
| 61 | 86 | 18 | 99 |
| 19 | 98 | 66 | 81 |
В начало
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм.
Эта таблица дает 8 различных итогов.
В начало
Выиграйте ставки с этим Magic Square
Хорошо, вот отличный способ выигрывать ставки с помощью магического квадрата. Позвоните другу по телефону. Попросите его или ее взять карандаш и бумагу и принести их к телефону, чтобы он или она могли записать числа от 1 до 9. Скажите своему другу, что вы будете по очереди набирать номера от 1 до 9. Никто из вас не может. повторить номер, который вызывает другой.Затем вы оба запишите числа от 1 до 9. Затем, когда ваш друг говорит одно из чисел, он или она обводит это число кружком, и вы тоже. Когда вы произносите число, вы рисуете квадрат вокруг этого числа, и ваш друг тоже. Побеждает тот, кто первым наберет три числа, которые в сумме составляют 15.
Допустим, вы идете первым, а вы зовете 8. Ваш друг может позвонить 6. Затем вы зовете 2. Ваш друг зовет 5, а вы зовете 4. Ваш друг зовет 7, а вы звоните 3.Затем вы говорите своему другу, что вы только что выиграли, потому что вы назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет сыграть. Итак, на этот раз вы можете поспорить с ним, что выиграете, при условии, что в случае ничьей (когда вы используете числа от 1 до 9, но никто из вас не наберет 15) никто ничего не должен.
Если вы знаете фокус, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.
Уловки На самом деле трюк основан как на крестиках-ноликах, так и на магическом квадрате.Магический квадрат выглядит так:
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме составляют 15. Итак, если у вас есть этот квадрат перед собой с вашим другом по телефону, вы можете поставить крестик в квадратах. номер, который вы вызываете, и букву O в квадратах номеров, которые называет ваш друг. Затем, как и в крестиках-ноликах, вы пытаетесь получить три крестика подряд, потому что они всегда в сумме дают 15.
Итак, в приведенном выше примере, когда вы вызываете 8, вы ставите X в верхнем левом углу.Когда ваш друг говорит 6, вы ставите) в правом верхнем углу. И так далее.
В начало
Математический карточный фокус
Для этого вауера вам понадобится обычная колода карт. Никакой сложной перетасовки не требуется. Просто выполните следующие простые шаги:
- Перетасуйте карты, чтобы тщательно перемешать их.
- Разложите 36 карт в стопку.
- Попросите друга выбрать одну из 36 карточек, посмотреть на нее и запомнить, а затем положить обратно в стопку, не позволяя вам ее увидеть.
- Перемешайте 36 карт.
- Разложите 36 карт в 6 рядов по 6 карт в каждом. Обязательно наносите верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее с каждой последующей строкой, лежащей под предыдущей.
- Попросите друга взглянуть на карточки и сказать, в каком ряду находится выбранная карточка. Запомните, какой номер в строке.
- Осторожно возьмите карты в том же порядке, в котором вы их положили .Таким образом, первая карта слева от верхнего ряда находится наверху стопки, а последняя карта справа от нижнего ряда находится внизу стопки.
- Теперь выложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карту по столбцу за раз . Вместо того чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Положите первые шесть карт в столбец сверху вниз в крайнем левом углу. Затем выложите следующие шесть карт во втором столбце из шести карт справа от первого столбца из шести карт.Продолжайте делать это, пока у вас не будет 6 столбцов по 6 карт в каждом (что выглядит так же, как 6 рядов по 6 карт в каждом — потому что — это то же самое).
- Еще раз спросите друга, в какой строке находится выбранная карта.
- Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, какая именно карта выбрана. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта находится во втором столбце пятой строки.Это потому, что вы располагаете карточки, то, что было строками в первый раз, во второй раз становятся столбцами.
В начало
Калькулятор молний
Вот трюк, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите их изменить их на любое другое число от 1 до 9.Затем попросите их скопировать свои девять чисел в том же порядке рядом с исходными девятью числами. Это даст им номер из 18 цифр, первая половина которого такая же, как и вторая. Затем измените вторую цифру на 7, а одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Затем сделайте ставку на то, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они смогут вычислить это вручную.Ответ: 0 — 7 делится на это новое число ровно без остатка!
В начало
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Развлечений в теории чисел Альберта Х. Байлера, изданной Dover Publications. Эта книга фактически объясняет математические причины, по которым эти уловки работают.
3 х 37 = 111 и 1 + 1 + 1 = 3 6 х 37 = 222 и 2 + 2 + 2 = 6 9 х 37 = 333 и 3 + 3 + 3 = 9 12 х 37 = 444 и 4 + 4 + 4 = 12 15 х 37 = 555 и 5 + 5 + 5 = 15 18 х 37 = 666 и 6 + 6 + 6 = 18 21 х 37 = 777 и 7 + 7 + 7 = 21 24 х 37 = 888 и 8 + 8 + 8 = 24 27 x 37 = 999 и 9 + 9 + 9 = 27 1 х 1 = 1 11 х 11 = 121 111 х 111 = 12321 1111 х 1111 = 1234321 11111 х 11111 = 123454321 111111 х 111111 = 12345654321 1111111 х 1111111 = 1234567654321 11111111 х 11111111 = 123456787654321 111111111 х 111111111 = 12345678987654321 1 х 9 + 2 = 11 12 х 9 + 3 = 111 123 х 9 + 4 = 1111 1234 х 9 + 5 = 11111 12345 х 9 + 6 = 111111 123456 х 9 + 7 = 1111111 1234567 х 9 + 8 = 11111111 12345678 х 9 + 9 = 111111111 123456789 х 9 +10 = 1111111111 9 х 9 + 7 = 88 98 х 9 + 6 = 888 987 х 9 + 5 = 8888 9876 х 9 + 4 = 88888 98765 х 9 + 3 = 888888 987654 х 9 + 2 = 8888888 9876543 х 9 + 1 = 88888888 98765432 х 9 + 0 = 888888888 1 х 8 + 1 = 9 12 х 8 + 2 = 98 123 х 8 + 3 = 987 1234 х 8 + 4 = 9876 12345 х 8 + 5 = 98765 123456 х 8 + 6 = 987654 1234567 х 8 + 7 = 9876543 12345678 х 8 + 8 = 98765432 123456789 х 8 + 9 = 987654321 7 х 7 = 49 67 х 67 = 4489 667 х 667 = 444889 6667 х 6667 = 44448889 66667 x 66667 = 4444488889 666667 x 666667 = 444444888889 6666667 x 6666667 = 44444448888889 и Т. Д. 4 х 4 = 16 34 х 34 = 1156 334 х 334 = 111556 3334 х 3334 = 11115556 33334 х 33334 = 1111155556 и Т. Д.В начало
Знаете ли вы …?
Каждое двузначное число, оканчивающееся на 9, является суммой кратных двух цифр и суммы двух цифр. Таким образом, например, 29 = (2 X 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что когда оно написано как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.
Простое число — это целое число больше 1, которое не может делиться равномерно на любое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые простые числа подряд, различающиеся на 10.
69 — единственное число, в квадрате и кубе между ними по одному разу используются все цифры от 0 до 9:
69 2 = 4761 и 69 3 = 328,509.
Один фунт железа содержит приблизительно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля ежедневно проходит более полутора миллионов миль.
В Эйфелевой башне 2 500 000 заклепок.
Если все кровеносные сосуды в человеческом теле проложить встык, они растянутся на 100 000 миль.
В начало
Математический трюк на этот год
Предположительно, он будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, в которые вы хотели бы выходить (1-7).
2. Умножьте это число на 2.
3. Добавить 5.
4. Умножьте полученную сумму на 50.
5. В 1998 году, если у вас уже был день рождения в этом году, прибавьте 1748. Если нет, добавьте 1747. В 1999 году просто прибавьте 1 к этим двум числам (поэтому прибавьте 1749, если у вас уже был день рождения, и 1748, если у вас нет). В 2000 году число изменится на 1749 и 1748. И так далее.
6. Вычтите четырехзначный год вашего рождения (19XX).
Результатов:
У вас должно получиться трехзначное число.
Первой цифрой этого числа было количество дней, на которое вы хотите выходить каждую неделю (1-7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
В начало
Где строка?
В следующий раз, когда вы будете с группой людей и захотите поразить их своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до числа.Возьмите веревку и попросите привязать ее к кому-нибудь на пальце, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто сделают для вас простую математику и скажут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
2. Добавить 3.
3. Умножьте результат на 5.
4. Если строка справа, добавьте 8.
Если строка слева, добавьте 9.
5. Умножить на 10.
6. Сложите номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем вычтите мысленно 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что веревка находится на третьем пальце левой руки игрока №6:
1. Умножить на 2 = 12.
2. Складываем 3 = 15.
3.Умножить на 5 = 75.
4. Поскольку строка находится слева, прибавляем 9 = 84.
5. Умножить на 10 = 840.
6. Сложите число пальца (3) = 843.
7. Складываем 2 = 845.
Теперь мысленно вычтите 222 = 623. Правая цифра (3) говорит вам, что строка находится на третьем пальце. Средняя цифра говорит о том, что он находится слева (правая рука = 1). Левая цифра говорит о том, что строка у игрока №6.
Кстати, когда число людей больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ цифры слева будут номером Игрока.
В чем секрет?
(Это из замечательной книги Шейлы Энн Барри, Giant Book of Puzzles & Games, . Издана Sterling Publishing Co., Inc., Нью-Йорк, 1978, недавно переиздана в мягкой обложке.)
Следите за новостями, чтобы узнать больше о математических трюках. Они будут добавляться время от времени, поэтому обязательно зарегистрируйтесь снова.
CBA Генератор математических пробников совокупных навыков: несколько навыков
Тип задачи:
Вычитание
1.Два однозначных числа: от 0 до 9
2. Двухзначное число из двухзначного числа:
без перегруппировки
3. 3. цифровой номер из трехзначного числа:
без перегруппировки
4. Два 4-значных числа: без перегруппировки
5. 2-значное число из 2-значного числа:
перегруппировка
6. Трехзначное число из трехзначного числа:
перегруппировка только из 1-го столбца
7. Трехзначное число из трехзначного числа:
перегруппировка только из 10-го столбца
8.3-значное число из 3-значного числа:
перегруппировка из столбцов 1 и 10
9. 4-значное число из 4-значного числа:
перегруппировка только из 1-го столбца
10. 4-значное число из 4-значного числа:
перегруппировка только из 10-го столбца
11. 4-значное число из 4-значного
число: перегруппировка из столбцов единиц и десятков
12. 4-значное число из 4-значного числа:
перегруппировка из столбцов 1, 10 и 100
13.5-значное число из 5-значного числа:
перегруппировка только из 1-го столбца
14. 5-значное число из 5-значного числа:
перегруппировка только из 10-го столбца
15. 5-значное число из 5-значного числа:
перегруппировка из столбцов 1 и 10
16. 5-значное число из 5-значного
число: перегруппировка из столбцов 1, 10 и 100
17. 5-значное число из 5-значного числа:
перегруппировка в любой столбец
18.


 Вы можете поставить ноль в частном разряда сотен или опустить его.
Но 4 действительно входит в 24, шесть раз. Поставьте 6 в частном.
Вы можете поставить ноль в частном разряда сотен или опустить его.
Но 4 действительно входит в 24, шесть раз. Поставьте 6 в частном. Так что объедините 1 сотню с 6 десятками
(160).
Так что объедините 1 сотню с 6 десятками
(160). Умножим 1 × 4 = 4, запишем это четыре под 7,
и вычесть. Это дает нам остаток от 3.
Умножим 1 × 4 = 4, запишем это четыре под 7,
и вычесть. Это дает нам остаток от 3. Умножим 2 × 4 = 8, запишем это восемь под знаком
9 и вычесть. Это дает нам остаток от 1.
Умножим 2 × 4 = 8, запишем это восемь под знаком
9 и вычесть. Это дает нам остаток от 1.
 Поставьте 9 в частное.
Поставьте 9 в частное.
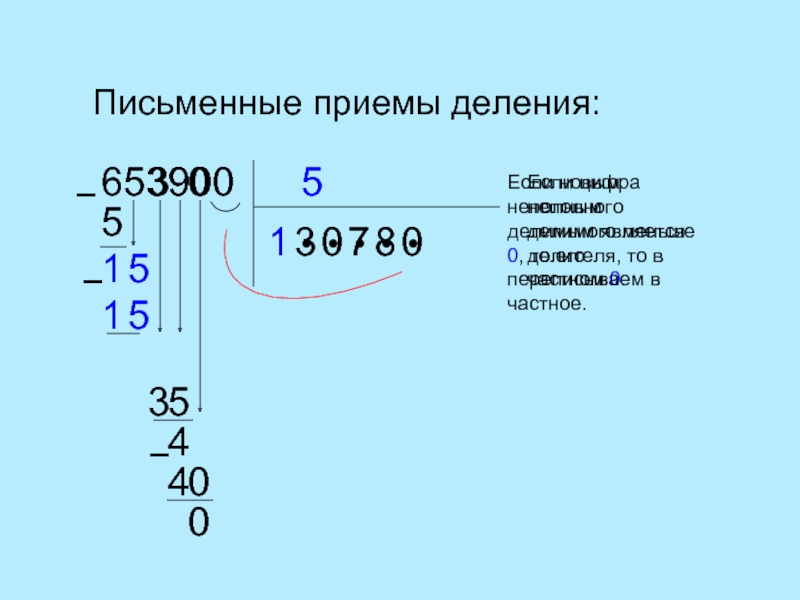 Частное 29.
Частное 29.

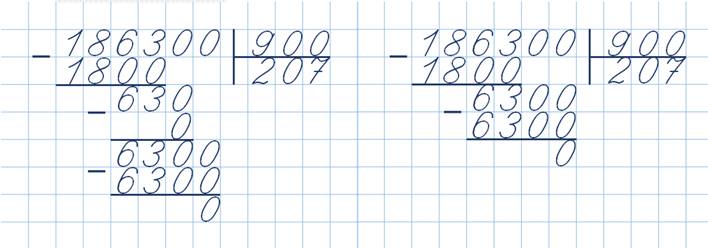 Поместите 3 в частное.
Поместите 3 в частное.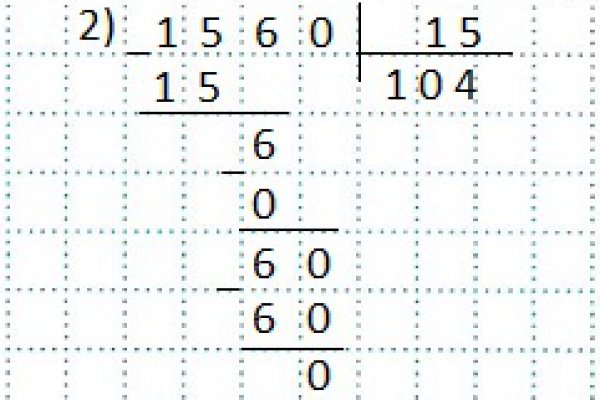

 Поставьте 9 в частное.
Поставьте 9 в частное.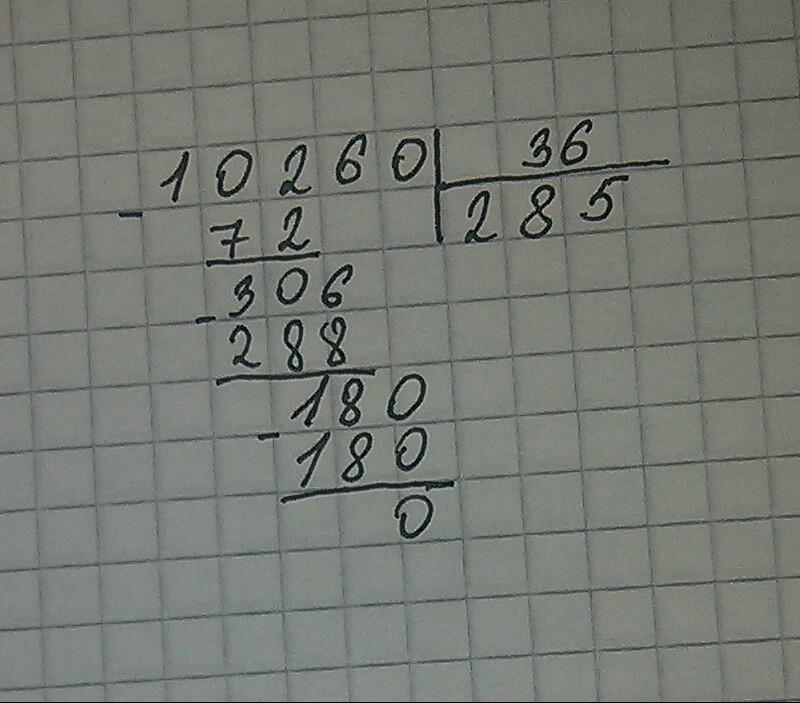
 Частное — 139.
Частное — 139.