Введите два числа: делимое и делитель.
Для простоты вычислений умножим делимое 1.1 и делитель 1.4 на 10. Результат (частное) от этого не изменится. В результате пример сводится к делению следующих чисел:
1.1÷1.4 = 11÷14
| — | 1 | 1 | 1 | 4 | ||||||||||||
| 9 | 8 | 0 | . | 7 | 8 | 5 | 7 | 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 | |
| — | 1 | 2 | 0 | |||||||||||||
| 1 | 1 | |||||||||||||||
| — | 8 | 0 | ||||||||||||||
| 7 | 0 | |||||||||||||||
| — | 1 | 0 | 0 | |||||||||||||
| 9 | 8 | |||||||||||||||
| — | 2 | 0 | ||||||||||||||
| 1 | 4 | |||||||||||||||
| — | 6 | 0 | ||||||||||||||
| 5 | 6 | |||||||||||||||
| — | 4 | 0 | ||||||||||||||
| 2 | 8 | |||||||||||||||
| — | 1 | 2 | 0 | |||||||||||||
| 1 | 1 | 2 | ||||||||||||||
| — | 8 | 0 | ||||||||||||||
| 7 | 0 | |||||||||||||||
| — | 1 | 0 | 0 | |||||||||||||
| 8 | ||||||||||||||||
| — | 2 | 0 | ||||||||||||||
| 1 | 4 | |||||||||||||||
| — | 6 | 0 | ||||||||||||||
| 5 | 6 | |||||||||||||||
| 4 |
Окончательный ответ: 1,1÷1,4 = 0.785714285714
Повторяем термины
Если вы уже немного знакомы с арифметическими действиями, то, наверное, знаете, как называются числа, с которыми придется иметь дело:- делимое — это то, что вам нужно разделить;
- делитель — на него всегда делят;
- частное — то, что получается в итоге.
Важно! Если вы хотите объяснить принцип деления ребенку, не забудьте проверить, помнит ли он правила умножения.Без умения перемножать числа в этом случае никак не обойтись, ведь результат всегда нужно проверить, а сделать это можно только обратным действием, то есть умножением. Конечно, навыки сложения и вычитания при освоении деления тоже не повредят.
Как записать?
I_
Такой способ записи называется “уголком”. Слева от вертикальной линии пишется число, которое мы будем делить, над горизонтальной черточкой — делитель, а под ней — частное. Обычный тетрадный лист подходит для такой записи больше, но при желании все возможно и в ворде Деление с остатком и без
Иметь дело мы будем с целыми числами, а вот в результате может получиться и десятичная дробь, в зависимости от того, допустимо ли в задании частное с остатком. Для начала попробуем разделить трехзначное число на однозначное.Пример 1
Возьмем 216 разделить 3. Попробуем записать пример:Посмотрим, какая из первых цифр делится нацело на 3. Двойка? Нет. Значит, берем две цифры — 21. Получится 7, а промежуточное действие будет выглядеть так: Теперь остается разделить на 3 последнюю цифру — 6, потому после первого шага остаток не образовался. Шестерку в столбике надо написать строго под той, что стоит в примере — в этом главный фокус, иначе можно очень легко сбиться. Что ж, давайте запишем аккуратно. Например, вот так:
Пример 2
Но может быть и другая ситуация. Например, когда первые две цифры на однозначное число нацело не делятся. Ничего страшного. Записываем: Первым делом придется делить 76, никуда не денешься. Ближайшее число, кратное 8 (то есть то, которое делится без остатка), — 72. Его и будем отнимать. Получим 9, которое сразу запишем в частное, и 4 в остатке — его нужно поместить под чертой: Следующий шаг — дописать к этой четверке последнюю цифру. Получится 48, его мы на 8 и разделим, от этого действия получится вторая цифра в результате — 6. Наш пример будет выглядеть теперь вот так:Двузначный делитель
Что будет, если попробовать выполнить другую операцию — разделить то же самое число 768 не на 8, а, скажем, на 16? Да то же самое. Возьмем первые две цифры, посмотрим, какое ближайшее число кратно 16 — это 64. Отнимаем его от 72, получаем 8. К восьмерке приписываем цифру делимого, которую мы еще не задействовали, то есть 8. Пример принимает следующий вид: Да, но 88 на 16 тоже не делится! Во всяком случае, без остатка. Что ж, тогда поступаем так: Можно, конечно, больше ничего не делать и записать ответ как 45 (остаток 8). Но есть и другие варианты решения. Если бы число было четырехзначным — все оказалось бы куда проще! А почему бы и не превратить его в четырехзначное? Представим, что делимое у нас записано иначе — 768,0. Тогда мы можем после пятерки тоже поставить запятую и превратить целое число в десятичную дробь. В данном случае она конечна, но бывают примеры и с бесконечными дробями. Вот что получается:Деление меньшего числа на большее
А можно ли в столбик разделить меньшее число на большее? Ничто не помешает это сделать. Вообще-то арифметика — это веселая и увлекательная игра со своими правилами. Главное — учимся соблюдать порядок. Итак, пробуем быстро разделить 36 на 540. Записываем выражение так: Поскольку первое число меньше второго, то и результат будет меньше единицы, то придется иметь дело с нулями. Объяснение простое: частное показывает, сколько раз делитель укладывается в делимое. Если нисколько — значит, результат начинается с нуля: А дальше действуем, как в предыдущих примерах: Числа в столбике начинают повторяться, то есть получается бесконечная десятичная дробь.Как проверить результат деления?
Результат, как и всегда, проверяется умножением. Если остатка не было, просто перемножаем частное и делитель любым удобным способом — кстати, умножать в столбик тоже удобно. Если делить нацело не получилось, опять же, перемножаем частное и делитель, а затем прибавляем остаток.Важно! Если результатом получилась бесконечная десятичная дробь, проверка может быть лишь приблизительной — в результате умножения у вас должно получиться число, очень близкое к делимому.Эти навыки очень помогут потом, когда придется считать не числа, обозначенные цифрами, а действовать в мире одночленов и многочленов. Ведь полиномы — это тоже числа, только выраженные иначе. Еще больше наглядных примеров деления в столбик смотрите в предложенном ниже видео.
Как делить в столбик | BeginPC.ru
В настоящее время современные технологии развиваются стремительными темпами, и все больше работы за нас выполняют компьютеры и различные другие электронные устройства. Тем не менее, умение выполнять арифметические операции без помощи калькулятора остаются все еще востребованными.
Ранее мы уже рассматривали, как складывать, вычитать и умножать в столбик на листе бумаги. Поэтому сегодня давайте освежим в памяти, а возможно кто-то узнает впервые алгоритм деления столбиком без калькулятора. В этом нет ничего сложного, главное внимательность и аккуратность.
Для начала запомним, что число которое делится называется делимое. Число на которое делят называют делителем, а результат деления частным. Чтобы было проще, давайте рассмотрим деление в столбик на конкретном примере и разделим 834 на 6. Первое что нам необходимо сделать, это записать их соответствующим образом.
Пишем делимое, затем правее него делитель и отделяем их друг от друга так называемым уголком. Все подготовительные операции выполнены и переходим непосредственно к делению в столбик.
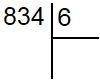
Для этого необходимо в делимом двигаясь слева на право найти наименьшее число большее или равное делителю. Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
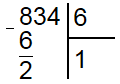
Теперь сносим вниз следующую цифру исходного делимого (3) и проверяем чтобы получившееся число (23) было больше делителя (6). В данном случае это так. Снова находим сколько раз делитель помещается в неполном делимом, получается 3 раза. Поэтому под делителем записываем 3, а под делимым находим разность 23 и 18 (6*3), которая равна 5.
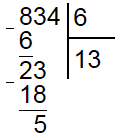
Дальше делаем все точно также, сносим вниз следующее число из делимого (4), получается число 54 и находим сколько раз в нем умещается делитель (6). Он умещается 9 раз, значит под делителем записываем 9, а под неполным делимым 54 (6*9). Поскольку 54 отнять 54 равно нулю и в делимом не осталось больше чисел, то деление закончено и частное равно 139. Можете проверить на калькуляторе или выполнив умножение в столбик 6 на 139.
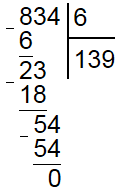
Чтобы закрепить навык деления столбиком давайте рассмотрим еще один пример и разделим 1587 на 23. Согласно уже известному нам алгоритму находим в делимом наименьшее число большее или равное делителю, таким числом является 158. Делитель 23 умещается в неполном делимом 6 раз. Соответственно под делителем пишем 6, а под делимым 138 (23*6) и находим разность 158 и 138.
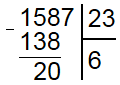
Поскольку 20 меньше делителя все сделано правильно, теперь сносим вниз следующее число (7) и находим сколько раз умещается делитель в получившемся числе 207. Он умещается 9 раз, а поскольку 207-207=0 и в делимом больше нет чисел, то деление в столбик законченно и ответ равен 69.
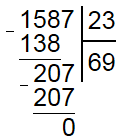
Как видите, ничего особо сложного нет, главное внимательность. Хотя внимательный читатель наверняка уже обратил внимание, что в обоих приведенных примерах делитель помещается в делимом целое число раз. Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Поскольку 4 меньше 8, то наименьшим неполным делимым является 46. В числе 46 делитель содержится 5 раз, следовательно под делителем пишем 5, а под делимым 40 (5*8).
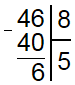
Разность 46 и 40 равна 6. Число 6 меньше делителя, значит мы все сделали верно, но в делимом больше не осталось чисел, а разность не равна 0. Это значит, что разделить эти два числа без остатка нельзя. Чтобы найти остаток поступаем следующим образом. В разности ставим запятую, а к остатку приписываем 0. В остатке имеем число 60. Делитель умещается в нем 7 раз, значит пишем в разность 7 и вычитаем из 60 число 56 (8*7).
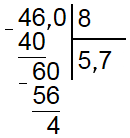
В остатке имеем 4, снова приписываем 0. Получается 40 и делитель умещается в нем 5 раз. В частное записываем 5 и вычитаем из остатка 40, получается 0.
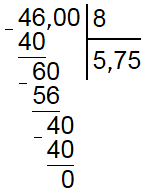
Таким образом, мы разделили 46 на 8 столбиком и получили ответ 5,75. Теперь вы знаете, как делить в столбик без калькулятора. Кстати в Windows есть встроенный калькулятор «Пуск» ⇒ «Стандартные» ⇒ «Калькулятор», в котором всегда можно быстро выполнить необходимые вычисления.
Деление столбиком — LoveGDZ
- 1 класс
- Математика
- Русский язык
- Английский Язык
- Информатика
- Окружающий мир
- Литература
- 2 класс
- Математика
- Русский язык
- Английский язык
- История
- Немецкий язык
- Информатика
- Окружающий мир
- Литература
- 3 класс
- Русский язык
- Математика
- Английский язык
- История
- Немецкий язык
- Информатика
- Окружающий мир
- Литература
- 4 класс
- Русский язык
- Математика
- Английский язык
- История
- Немецкий язык
- Информатика
- Окружающий мир
- Литература
- 5 класс
- Математика
- Английский язык
- Русский язык
- Биология
- География
- ОБЖ
- Обществознание
- Немецкий язык
- Информатика
- Литература
- Физика
- Окружающий мир
- История
- 6 класс
- Математика
- Русский язык
- Английский язык
- История
- Обществознание
- Информатика
- Литература
- Биология
- Химия
- Физика
- Немецкий язык
- География
- ОБЖ
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Химия
- Геометрия
- Физика
- Литература
- Биология
- Информатика
- География
- История
- Обществознание
- Немецкий язык
- ОБЖ
- 8 класс
- Английский язык
- Русский язык
- Алгебра
- Геометрия
- Физика
- Химия
- Немецкий язык
- Информатика
- Литература
- ОБЖ
- Биология
- География
- История
- Обществознание
- 9 класс
- Английский язык
- Русский язык
- Алгебра
- Геометрия
- Физика
- Химия
- Немецкий язык
- Информатика
- Литература
- География
- ОБЖ
- Биология
- История
- Обществознание
- 10 класс
- Английский язык
- Русский язык
- Алгебра
Long Division — Введение
Long Division легко, , как только вы получите идею .
Надеюсь, что некоторые из этих страниц будут «кликать» с вами, и вы станете мастером!
Почему Long Division
Простейший способ деления — повторное вычитание :
Пример: что такое 48/12?
- Начнем с 48, вычтем 12, получим 36
- Повтор: 36-12 = 24
- Повтор: 24-12 = 12
- Повтор: 12-12 = 0
Мы сделали 4 вычитания, поэтому 48/12 = 4
Но это может занять много времени для чего-то вроде 3768/12
Пример: что такое 3768/12?
- Начнем с 3768, вычтем 12, получим 3756
- Повтор: 3756-12 = 3744
- Повтор: 3744-12 = 3732
- Повтор: 3732-12 = 3720
- .. о нет! Это займет много времени!
Может быть, мы могли бы сделать 100 вычитаний за один раз
- Начнем с 3768, вычтем из 100 лотов из 12 , получим 3768-1200 = 2568
- Повтор: 2568-1200 = 1368
- Повтор: 1368-1200 = 168
Теперь давайте перейдем к 10 вычитаниям за один раз.
- 168, вычитаем из 10 лотов из 12 , получаем 168-120 = 48
Теперь давайте перейдем к синглу:
- 48, отнимем 12, получим 36
- Повтор: 36-12 = 24
- Повтор: 24-12 = 12
- Повтор: 12-12 = 0
Итак, мы сделали 3 лота из 100 , 1 лот из 10 и 4 отдельных вычитания из 12, что в сумме составляет 314 вычитаний из 12
, т. 3768/12 = 314
Это идея за длинным дивизионом
Длинное деление выглядит так:
0314
12) 3768
0
37
36
16
12
48
48
0
Поначалу это может показаться немного странным, но видите ли вы «3768» в верхней части?
А затем «12» слева и фактический ответ «314» вверху.
Это показывает, что мы разработали 3768/12 = 314
- Теперь посмотрите на «36»: вот где мы взялись за 100s (3 × 12 = 36)
- И чуть ниже это «12», где мы сделали 10s (1 × 12 = 12)
- А внизу находится «48» (4 × 12 = 48)
Итак, мы взяли 100, затем 10, затем единицы, как и выше.
А «0» внизу означает, что после всех вычитаний ничего не осталось.
Продолжайте и узнайте, как сделать это самостоятельно!
Понимание Long Division
Long Division
Практика
Продвинутый
,полиномов — длинное деление
Полином выглядит так:
| пример полинома у этого есть 3 условия |
Деление
Полиномы иногда можно разделить, используя простые методы, показанные в разделе Деление полиномов.
Но иногда лучше использовать «длинное деление» (метод, аналогичный длинному делению чисел)
Числитель и Знаменатель
Мы можем дать каждому многочлену имя:
- , вершина , полином , числитель , , .
- , полис , полином , знаменатель , ,
Если у вас проблемы с запоминанием, подумайте, что знаменатель — это знаменатель , а не .
метод
Запишите аккуратно:
- знаменатель идет первым,
- тогда «)»,
- то числитель с линией выше
Оба полинома должны иметь сначала термины «высшего порядка» (те, которые имеют наибольшие показатели, например «2» в x 2 ).
Тогда:
| |
| Повторите , используя новый полином |
Проще показать на примере!
Пример:
Запишите его аккуратно, как показано ниже, а затем решите его постепенно (нажмите кнопку воспроизведения):
Проверьте ответ:
Умножьте ответ на нижний полином, мы должны получить верхний полином:
Остатки
Предыдущий пример работал отлично, но это не всегда так! Попробуйте это:
После деления у нас осталось «2», это «остаток».
Остаток — это то, что осталось после деления.
Но у нас все еще есть ответ: поместите остаток , разделенный на нижний полином , как часть ответа, как это:
«Пропавшие» условия
Могут быть «пропущенные термины» (пример: может быть x 3 , но не x 2 ). В этом случае либо оставьте пробелы, либо включите пропущенные члены с нулевым коэффициентом.
Пример:
Запишите это с коэффициентами «0» для пропущенных терминов, затем решите это нормально (нажмите play):
Посмотрите, как нам нужно место для «3x 3 «?
Более одной переменной
До сих пор мы делили полиномы только с одной переменной ( x ), но мы можем обрабатывать полиномы с двумя или более переменными (например, x и y ), используя один и тот же метод.
Пример:
,Long Division — Википедия переиздано // WIKI 2
Стандартный алгоритм деления для многозначных чисел
В арифметике длинное деление — это стандартный алгоритм деления, подходящий для деления многозначных чисел, который достаточно прост для выполнения вручную. Это разбивает проблему деления на ряд более простых шагов.
Как и во всех задачах деления, одно число, называемое дивидендом, делится на другое, называемое делителем, в результате чего получается результат, называемый частным.Это позволяет выполнять вычисления с использованием сколь угодно больших чисел, выполняя ряд простых шагов. [1] Сокращенная форма длинного деления называется коротким делением, которое почти всегда используется вместо длинного деления, когда делитель имеет только одну цифру. Чанкинг (также известный как метод частичных отношений или метод Палача) — это менее механическая форма длинного деления, известная в Великобритании, которая способствует более целостному пониманию процесса деления. [2]
Хотя связанные алгоритмы существуют с 12-го века нашей эры, [3] конкретный алгоритм в современном использовании был введен Генри Бриггс c. 1600 н.э. [4]
Энциклопедия YouTube
1/3
Просмотров:834 706
22 405
1 222 892
✪ Длинный трюк с делением — быстрый расчет!
✪ Другой способ сделать длинное деление — математика легко
Ant Математические выходки — десятичная арифметика
Содержание
место в образовании
Недорогие калькуляторы и компьютеры стали наиболее распространенным способом решения проблем деления, устраняя традиционные математические упражнения и уменьшая образовательную возможность показать, как это сделать с помощью методов бумаги и карандаша.(Внутренне эти устройства используют один из множества алгоритмов деления, более быстрые из которых основаны на аппроксимациях и умножениях для решения задач). В Соединенных Штатах, долгое разделение было особенно предназначено для снижения акцента, или даже исключения из школьной программы, реформатской математикой, хотя традиционно вводится в 4-х или 5-х классах. [5]
Метод
В англоязычных странах длинное деление не использует косую черту⟩ ∕⟩ или знак деления ⟨÷⟩, а вместо этого создает таблицу . [6] Делитель отделен от делимого правой круглой скобкой ⟨)⟩ или вертикальной чертой ⟨|⟩; дивиденд отделяется от фактора винкулюмом (то есть надстрочным элементом). Комбинация этих двух символов иногда называется символом с длинным делением или скобкой с делением . [7] Он возник в 18 веке из более ранней однострочной записи, отделяющей дивиденд от частного с помощью левой круглой скобки. [8] [9]
Процесс начинается с деления самой левой цифры дивиденда на делитель.Частное (округленное до целого числа) становится первой цифрой результата, а остаток вычисляется (этот шаг записывается как вычитание). Этот остаток переносится вперед, когда процесс повторяется со следующей цифрой дивиденда (обозначается как «понижение» следующей цифры до остатка). Когда все цифры были обработаны, а остатка не осталось, процесс завершен.
Ниже показан пример, представляющий деление 500 на 4 (с результатом 125).
125 (Пояснения)
4) 500
4 (4 × 1 = 4)
10 (5 - 4 = 1)
8 (4 × 2 = 8)
20 (10 - 8 = 2)
20 (4 × 5 = 20)
0 (20 - 20 = 0)
Пример длинного деления без калькулятора.
Более подробная разбивка шагов выглядит следующим образом:
- Найдите самую короткую последовательность цифр, начиная с левого конца делимого, 500, в которую делитель 4 входит хотя бы один раз.В данном случае это просто первая цифра 5. Самое большое число, на которое можно умножить делитель 4, не превышая 5, равно 1, поэтому цифра 1 ставится выше 5, чтобы начать построение частного.
- Затем 1 умножается на делитель 4, чтобы получить наибольшее целое число, кратное делителю 4, не превышая 5 (в данном случае 4). Эта 4 затем помещается под 5 и вычитается из 5, чтобы получить остаток 1, который находится под 4 под 5.
- После этого первая еще неиспользованная цифра в дивиденде, в данном случае первая цифра 0 после 5, копируется непосредственно под собой и рядом с остальной частью 1, чтобы сформировать число 10.
- В этот момент процесс повторяется достаточно много раз, чтобы достичь точки остановки: наибольшее число, на которое делитель 4 можно умножить, не превышая 10, равно 2, поэтому 2 записывается выше как вторая крайняя слева цифра. Это 2 затем умножается на делитель 4, чтобы получить 8, которое является наибольшим кратным 4, которое не превышает 10; так что 8 записано ниже 10, и вычитание 10 минус 8 выполняется, чтобы получить остаток 2, который находится ниже 8.
- Следующая цифра дивиденда (последние 0 из 500) копируется непосредственно под собой и рядом с оставшейся частью 2, образуя 20.Затем наибольшее число, на которое можно умножить делитель 4, не превышая 20, то есть 5, помещается выше в качестве третьей самой левой частной цифры. Это 5 умножается на делитель 4, чтобы получить 20, которое записано ниже и вычтено из существующих 20, чтобы получить остаток 0, который затем записывается ниже второго 20.
- В этот момент, так как больше нет цифр для уменьшения из дивиденда и последний результат вычитания был равен 0, мы можем быть уверены, что процесс завершен.
Если бы последний остаток, когда у нас заканчивались цифры дивидендов, был чем-то отличным от 0, было бы два возможных варианта действий:
- Мы могли бы просто остановиться на этом и сказать, что дивиденд, деленный на делитель, представляет собой частное, записанное сверху, а остаток внизу, и написать ответ как частное, за которым следует дробь, являющаяся остатком, деленным на делитель. ,
- Мы могли бы увеличить дивиденд, написав его, скажем, 500.000 … и продолжить процесс (используя десятичную точку в частном прямо над десятичной точкой в дивиденде), чтобы получить десятичный ответ, как в следующем примере.
31,75
4) 127.00
12 (12 ÷ 4 = 3)
07 (0 остаток, опустить следующую цифру)
4 (7 ÷ 4 = 1 р 3)
3.0 (сбить 0 и десятичную точку)
2.8 (7 × 4 = 28, 30 ÷ 4 = 7 р 2)
20 (дополнительный ноль сбит)
20 (5 × 4 = 20)
0
В этом примере десятичная часть результата вычисляется путем продолжения процесса за цифрой единиц измерения, «сбрасывая» нули как десятичную часть дивиденда.
Этот пример также иллюстрирует, что в начале процесса этап, который производит ноль, может быть опущен. Поскольку первая цифра 1 меньше делителя 4, вместо этого выполняется первый шаг для первых двух цифр 12.Точно так же, если бы делителем было 13, можно было бы выполнить первый шаг на 127, а не на 12 или 1.
Основная процедура для длительного деления n ÷ м
- Найти расположение всех десятичных точек в делимом n и делителе m .
- При необходимости упростите задачу длинного деления, переместив десятичные дроби делителя и делимого на одинаковое количество десятичных разрядов вправо (или влево), чтобы десятичная дробь делителя находилась справа от последнего цифра.
- Делая длинное деление, держите числа выровненными прямо сверху вниз под таблицей.
- После каждого шага убедитесь, что остаток для этого шага меньше делителя. Если это не так, возможны три проблемы: неправильное умножение, неправильное вычитание или необходим больший коэффициент.
- В конце, остаток, r , добавляется к коэффициенту роста как фракция, r / m .
Пример с многозначным делителем

Анимированный пример многозначного длинного деления
Можно использовать делитель любого количества цифр.В этом примере 1260257 нужно разделить на 37. Сначала проблема устанавливается следующим образом:
37) 1260257
Цифры числа 1260257 берутся до тех пор, пока не появится число, большее или равное 37. Таким образом, 1 и 12 меньше 37, а 126 больше. Затем вычисляется наибольшее кратное из 37, меньшее или равное 126. Таким образом, 3 × 37 = 111 <126, но 4 × 37> 126. Множество 111 написано под 126, а 3 написано сверху, где появится решение:
3
37) 1260257
111
Внимательно обратите внимание, в какой столбец значений места записаны эти цифры.3 в частном случае идет в том же столбце (десяти тысячном месте), что и 6 в дивиденде 1260257, то есть в том же столбце, что и последняя цифра 111.
Затем 111 вычитается из строки выше, игнорируя все цифры справа:
3
37) 1260257
111
15
Теперь цифра от следующего меньшего значения места дивиденда копируется вниз и добавляется к результату 15:
3
37) 1260257
111
150
Процесс повторяется: вычитается наибольшее кратное из 37, меньшее или равное 150.Это 148 = 4 × 37, так что 4 добавляется к вершине как следующая частная цифра. Затем результат вычитания увеличивается еще на одну цифру, взятую из дивиденда:
34
37) 1260257
111
150
148
22
Наибольшее значение, кратное 37, меньшему или равному 22, равно 0 × 37 = 0. Вычитая 0 из 22, получаем 22, мы часто не записываем шаг вычитания. Вместо этого мы просто берем еще одну цифру из дивиденда:
340
37) 1260257
111
150
148
225
Процесс повторяется до тех пор, пока 37 точно не разделит последнюю строку:
34061
37) 1260257
111
150
148
225
222
37
Смешанный режим с длинным делением
Для недесятичных валют (таких как британская система sd до 1971 года) и мер (таких как Avirirdupois) необходимо использовать смешанный режим деления .Рассмотрим деление 50 миль на 600 ярдов на 37 частей:
миль - фут - фут - дюйм
1 - 634 1 9 р. 15 "
37) 50 - 600 - 0 - 0
37 22880 66 348
13 23480 66 348
1760 222 37 333
22880 128 29 15
===== 111 348 ==
170 ===
148
22
66
==
Каждый из четырех столбцов работает по очереди.Начиная с миль: 50/37 = 1 остаток. возможно, поэтому выполните длинное умножение на 1760, чтобы преобразовать мили в ярды, в результате получается 22 880 ярдов. Несите это к вершине колонки ярдов и добавьте это к 600 ярдам в дивиденде, дающем 23 480. Длинное деление 23 480/37 теперь происходит как обычно, давая 634 с остатком 22. Остаток умножается на 3, чтобы получить ноги, и переносится в столбец ног. Длинное деление ног дает 1 остаток 29, который затем умножается на двенадцать, чтобы получить 348 дюймов.Длинное деление продолжается с последним 15-дюймовым показателем в строке результата.
Интерпретация десятичных результатов
Когда частное не является целым числом и процесс деления выходит за пределы десятичной точки, может произойти одно из двух:
- Процесс может завершиться, что означает, что достигнут остаток от 0; или
- Остаток может быть достигнут, который идентичен предыдущему остатку, который возник после того, как были записаны десятичные знаки.В последнем случае продолжать процесс было бы бессмысленно, поскольку с этого момента одна и та же последовательность цифр будет появляться в частном числе снова и снова. Таким образом, над повторяющейся последовательностью отображается полоса, указывающая, что она повторяется вечно (то есть каждое рациональное число является либо десятичным, либо завершающим, либо повторяющимся).
Система обозначений в неанглоязычных странах
Китай, Япония, Корея используют те же обозначения, что и англоязычные страны, включая Индию. В других местах используются одни и те же общие принципы, но цифры часто располагаются по-разному.
Латинская Америка
В Латинской Америке (за исключением Аргентины, Боливии, Мексики, Колумбии, Парагвая, Венесуэлы, Уругвая и Бразилии) расчеты практически одинаковы, но записаны по-разному, как показано ниже, с теми же двумя примерами, использованными выше. Обычно частное записывается под полосой, нарисованной под делителем. Длинная вертикальная линия иногда проводится справа от расчетов.
500 ÷ 4 = 125 (пояснения)
4 (4 × 1 = 4)
10 (5 - 4 = 1)
8 (4 × 2 = 8)
20 (10 - 8 = 2)
20 (4 × 5 = 20)
0 (20 - 20 = 0)
и
127 ÷ 4 = 31.75
124
30 (снизьте 0; десятичное к частному)
28 (7 × 4 = 28)
20 (добавлен дополнительный ноль)
20 (5 × 4 = 20)
0
В Мексике используется англоязычная система обозначений мира, за исключением того, что аннотируется только результат вычитания, а расчет выполняется мысленно, как показано ниже:
125 (Пояснения)
4) 500
10 (5 - 4 = 1)
20 (10 - 8 = 2)
0 (20 - 20 = 0)
В Боливии, Бразилии, Парагвае, Венесуэле, Квебеке, Колумбии и Перу используется европейское обозначение (см. Ниже), за исключением того, что частное не разделено вертикальной линией, как показано ниже:
127 | 4
- 124 31,75
30
- 28
20
- 20
0
Та же процедура применяется в Мексике, Уругвае и Аргентине, аннотируется только результат вычитания, а расчет делается мысленно.
Евразия
В Испании, Италии, Франции, Португалии, Литве, Румынии, Турции, Греции, Бельгии, Беларуси, Украине и России делитель находится справа от дивиденда и разделен вертикальной чертой. Деление также происходит в столбце, но частное (результат) записывается под делителем и разделяется горизонтальной линией. Этот же метод используется в Иране и Монголии.
127 | 4
- 124 | 31,75
30
- 28
20
- 20
0
На Кипре, как и во Франции, длинная вертикальная черта отделяет дивиденды и последующие вычитания от коэффициента и делителя, как в примере ниже 6359, деленное на 17, то есть 374 с остатком 1.
| 6 | 3 | 5 | 9 | 17 |
| — 5 | 1 | 374 | ||
| 1 | 2 | 5 | ||
| — 1 | 1 | 9 | ||
| 6 | 9 | |||
| — | 6 | 8 | ||
| 1 |
Десятичные числа не делятся напрямую, деление и делитель умножаются на степень десяти, так что деление включает в себя два целых числа.Следовательно, если делить 12,7 на 0,4 (вместо десятичных запятых используются запятые), дивиденд и делитель сначала изменятся на 127 и 4, а затем деление будет выполнено, как указано выше.
В Австрии, Германии и Швейцарии используется нотационная форма нормального уравнения.
127: 4 = 31,75
- 12
07
- 4
30
- 28
20
- 20
0
Такие же обозначения приняты в Дании, Норвегии, Болгарии, Северной Македонии, Польше, Хорватии, Словении, Венгрии, Чехии, Словакии, Вьетнаме и в Сербии.
В Нидерландах используются следующие обозначения:
12/135 \ 11,25
12
15
12
30
24
60
60
0
Алгоритм произвольной базы
Каждое натуральное число N {\ displaystyle n} может быть уникально представлен в произвольной числовой базе б > 1 {\ displaystyle b> 1} как последовательность цифр N знак равно α 0 α 1 α 2 ,{К-я-1}}
лет N {\ displaystyle n} быть дивидендом и м {\ displaystyle m} быть делителем, где L {\ displaystyle l} это количество цифр в м {\ displaystyle m} , Если К <
L {\ displaystyle k за каждую итерацию я {\ displaystyle i} , позволять Q я {\ displaystyle q_ {i}} быть коэффициентом, извлеченным до сих пор, d я {\ displaystyle d_ {i}} быть промежуточным дивидендом, р я {\ displaystyle r_ {i}} быть промежуточным остатком, α я {\ displaystyle \ alpha _ {i}} быть следующей цифрой исходного дивиденда, и β я {\ displaystyle \ beta _ {i}} быть следующей цифрой частного.По определению цифр в базе б {\ displaystyle b} , 0
≤ β я <
б {\ displaystyle 0 \ leq \ beta _ {i} Википедия Википедия Эти примеры взяты из Кембриджского английского корпуса и из источников в Интернете.Любые мнения в примерах не соответствуют мнению редакторов Cambridge Dictionary или издательства Cambridge University Press или его лицензиаров. Больше примеров
Меньше примеров Википедия Это было похоже на переход от длиной к делению до бинома
