Математика 5 класс. Сложные задачи на дроби. Дидактика репетитора
Предлагаю репетиторам по математике специально подготовленный комплект базовых сложных задач на дроби, рассчитанный для учащихся 5 класса. Ориентировочное время на его проработку на уроке — 60 минут. Регулярно использую данный комплект в ситуациях, когда родителям нужна олимпиадная помощь репетитора по математике (подготовка в Курчатовскую школу, в лицей «Вторая школа» и др.) Большинство задач составлены мной по мотивам известных классических номеров повышенной сложности. Комплект можно также использовать в работе с сильным учеником 4 класса, параллельно осваивающим с репетитором по математике программу учебника Петерсона.
Для подготовки к олимпиадам по математике в 5 классе. Задачи на дроби.
1) Тетя Нюра пожарила блинчики. Ира съела половину приготовленных блинчиков и еще один блинчик. Максим съел половину остатка и еще один блинчик, а Никита съел половину последнего остатка и последний блинчик. Сколько блинчиков пожарила тетя Нюра?
3) Папа пошел в магазин. На первую покупку он истратил всех своих денег и еще одну монету. На вторую покупку он истратил остатка и еще одну монету. На последнюю покупку он снова истратил остатка и последнюю монету. Сколько монет было у папы?
4) Андрей прочитал книгу за 2 дня. Во второй день он прочел того, что он прочитал в первый день. Сколько страниц он прочитал во второй день, если во всей книге 80 страниц?
5) Турист проехал намеченный путь за 2 дня. В первый день он проехал того, что проехал во второй. Сколько километров он проехал во второй день, если весь путь составил 140км?
6) Столб врыт в землю. Часть столба, находящаяся в земле, составляет той части, которая находится над землей. Найдите глубину, на которую врыт столб, если его длина составляет 3м40см.
7) Полина прочитала книги, а Софья — такой же книги. Сколько страниц в этой книге, если Полина прочла больше Софьи на 63 страницы?
8) В первый день в магазине продали всей завезенной вишни, а во второй — всей завезенной вишни. Сколько килограммов вишни завезли, если во второй день продали на 90 кг больше, чем в первый?
9) Имеются две одинаковые бочки с водой. Из первой вылили бочки, а из второй — бочки. Сколько литров воды было в каждой бочке, если из второй бочки вылили на 220литров воды больше, чем из первой.
10) Количество отсутствующих учеников в классе составляет числа присутствующих. Когда из этого класса вышло 6 учеников, число отсутствующих составило числа присутствующих. Сколько всего учеников в этом классе?
11) Преподаватель по математике проверял тетради с итоговой контрольной работой за 6 класс. До обеда число проверенных работ составляло числа не проверенных. После обеда он проверил еще 4 работы, и число проверенных составило от числа не проверенных. Сколько всего имелось работ?
12) В коробке лежат красные и белые шары. Количество красных шаров составляет числа белых. После того как 12 белых шаров покрасили в красный цвет, количество красных составило числа белых. Сколько шаров в коробке?
13) После того как почтальон проехал 1 км и еще половину оставшегося пути до почты, ему осталось проехать всего пути и еще 1 км. Чему равен путь почтальона?
14) После того как черепаха проползла 10 см и еще оставшегося пути, ей осталось проползти всей дистанции и последние 10 см. Чему равна длина дистанции черепахи?
15) После того как туристы проехали 2 км на машине и еще остатка всего маршрута, им осталось до конца маршрута проехать всего пути и последние 3 км. Найдите длину туристического маршрута?
Пояснение репетитора по математике: данные задачи представляют собой полноценный комплект упражнений для одного урока с сильным учеником 4 — 5 класса по теме: «задачи на дроби». Он представлен пятью блоками полуолимпиадных номеров, рассчитанных на решение без применения уравнений. Рекомендую репетиторам по математике разбирать одну задачу самостоятельно, другую оставлять для самостоятельную работы ученика в присутствии репетитора, а еще одну задавать на дом. В каждом блоке для этого имеется соответствующее количество задач.
Колпаков А.Н Репетитор по математике в Москве. Строгино
Логические задачи для 5 класса с ответами
Логические задачи для 5 класса с ответами
#1
Пете и Коле купили по коробке конфет. В каждой коробке находится 12 конфет. Петя из своей коробки съел несколько конфет, а Коля из своей коробки съел столько конфет, сколько осталось в коробке у Пети.
Сколько конфет осталось на двоих у Пети и Коли?
#2
Пять землекопов за 5 часов выкапывают 5 м канавы.
Сколько потребуется землекопов, для того чтобы выкопать 100 м канавы за 100 часов?
Пять землекопов за 5 часов выкапывают 5 м канавы; следовательно, пять землекопов за 1 час вырыли бы 1 м канавы, а за 100 часов — 100 м.
Люди, приезжавшие в одну деревушку, часто удивлялись местному дурачку.
Когда ему предлагали выбор между блестящей 50-центовой монетой и мятой пятидолларовой купюрой, он всегда выбирал монету, хотя она стоит в десять раз меньше купюры.
Почему он никогда не выбирал купюру?
#4
Человек живет на 17-м этаже. На свой этаж он поднимается на лифте только в дождливую погоду или тогда, когда кто-нибудь из соседей с ним едет в лифте. Если погода хорошая и он один в лифте, то он едет до 9-го этажа, а дальше до 17-го этажа идет пешком по лестнице.
#5
Образно представьте себе нашу планету, плотно стянутую кольцом по всему ее экватору.
После увеличения длины окружности кольца на 10 метров, между кольцом и поверхностью земли образовался зазор определенной величины.
Как Вы считаете, сможет ли человек пройти, или хотя бы протиснуться в этот зазор? Известно, что экватор имеет длину приблизительно равную 40 000 километров.
по сравнению с его длиной в 40 000 км будет способствовать образованию практически незаметного зазора.
Однако, исходя из формулы определения длины окружности L = 2П * R видно, что радиус Земли (кольца) R = L/2П и при увеличении длины кольца на 10м, его радиус приблизительно увеличиться на 1,59м (10м / 6,28), образуя соответствующий зазор, в который человек сможет не только протиснуться, но и даже пройти, немного нагнувшись.
#6
Инспектор, проверявший некую школу, заметил, что, когда бы он ни задал классу вопрос, в ответ тянули руки все ученики.
#7
Возвращаясь с рыбалки домой, рыболов встретил своего приятеля, который поинтересовался его уловом.
Но, так как наш рыболов помимо рыбалки был также большим любителем всякого рода загадок, ответил приятелю следующим образом: «Если к количеству пойманной мною рыбы добавить половину улова и еще десяток рыбин, то мой улов составил бы ровно сотню рыб». Сколько рыбы поймал рыболов?
#8
У Вас есть два шнура (фитиля). Каждый шнур, подожженный с конца, полностью сгорает дотла ровно за один час, но при этом горит с неравномерной скоростью.
Как при помощи этих шнуров и зажигалки отмерить время в 45 минут?
Считается, что есть веская причина, по которой у птичьих яиц один конец тупее другого. Что это за причина?
Ответ? Сферические и овальные яйца катились бы по прямой. Асимметричные же яйца, у которых один конец тупее, а другой острее, при скатывании стремятся катиться по кругу. Если яйцо лежит на краю обрыва или в другом ненадежном месте, стремление катиться по кругу, а не по прямой — большое преимущество.#10
Воздушный шар уносится непрерывным ветром в южном направлении.
#11
Трехзначное число состоит из возрастающих (слева направо) цифр.
Если это число прочитать, то все слова будут начинаться на одну и туже букву. Что это за число?
#12
Имеется круглое глубокое озеро диаметром 200 метров и два дерева, одно из которых растет на берегу у самой воды, другое — по центру озера на небольшом островке.
Человеку, который не умеет плавать, нужно перебраться на островок при помощи веревки, длина которой чуть больше 200 метров.
Как ему это сделать?
#13
Предположим Вам надо повалить бетонную стену длиной в 20 метров, высотой в 3 метра и весом в 3 тонны.
Как вы выполните эту задачу, если в вашем распоряжении нет абсолютно никаких инструментов?
#14
Человек прыгает со стула. В руках он держит весы, на чашке которых лежит груз 10 кг.
На каком делении будет стоять стрелка весов во время падения?
#15
На обыкновенных чашечных весах лежат: на одной чашке — булыжник, весящий ровно 2 кг, на другой — железная гиря, весящая так же 2 кг.
Весы осторожно опустили под воду. Остались ли чашки в равновесии?
#16
Все мы неоднократно слышали журчание ручья. Как Вы считаете, отчего он журчит?
Ответ? Ручей журчит оттого, что струя воды при небольшом падении захватывает частицы воздуха и погружает их в воду, отчего образуются пузырьки. Лопаньем этих пузырьков и объясняется журчание ручья.#17
Для чего между рельсами оставляют зазоры?
Ответ? Между стыками рельсов всегда оставляют пустые промежутки — зазоры. Делается это специально. Если зазоров не оставить и укладывать рельсы вплотную один к другому, железная дорога скоро придет в негодность. Дело в том, что все предметы при их нагревании раздаются во все стороны. Удлиняется и стальной рельс летом, когда его нагревает солнце. Если же не дать рельсам простора для удлинения, то, упираясь концами друг в друга с большой силой, они изогнутся вбок, вырвут удерживающие их костыли и исковеркают путь. В зимнюю пору происходит противоположное — сжатие рельса.#18
Мужчина ночью долго ворочался в кровати и никак не мог заснуть…
Потом он взял телефон, набрал чей-то номер, прослушав несколько длинных гудков — положил трубку и спокойно заснул.
Вопрос: почему он до этого не мог заснуть?
#19
На гладкую доску положили 2 кирпича — один плашмя, а другой на ребро. Кирпичи весят одинаково.
Какой кирпич соскользнет первым, если наклонять доску?
#20
С борта парохода был спущен стальной трап. Нижние 4 ступеньки трапа погружены в воду.
Каждая ступенька имеет толщину в 5 см; расстояние между двумя соседними ступеньками составляет 30 см.
Начался прилив, при котором уровень воды стал поднимается со скоростью 40 см в час.
Как Вы считаете, сколько ступенек окажется под водой через 2 часа?
#21
В больницу Сент-Джеймс направляли всех пострадавших в результате несчастных случаев в городе.
Больше всего было водителей и пассажиров, пострадавших в ДТП.
Чтобы уменьшить их число, городские власти сделали обязательным пользование ремнями безопасности.
Водители и пассажиры стали пристегиваться этими ремнями, но число ДТП осталось неизменным, а число пострадавших в них людей,
которые поступали в больницу, даже увеличилось. Почему?
aababy.ru
Олимпиадные задачи по математкие 5-6 класс — Колпаков Александр Николаевич
В последнее время увеличился поток писем от посетителей сайта с просьбами о помощи в решении олимпиадных задач для самых маленьких (5 — 6 класс). Это приятно, ибо работать с талантливыми и целеустремленными детьми одно удовольствие. Кто обычно пишет репетитору по математике? Как правило, это родители учеников, решающих сложные задачи для собственного удовлетворения и развития. Чуть меньше писем от самих участников математических олимпиад и конкурсов «Кенгуру». Последние присылают задачи, оказавшиеся им не по зубам на школьном или на районном туре. Репетитор по математике он-лайн в таких случаях является хорошим источником проверки правильности решения, а иногда и единственной надеждой узнать его вообще. Не каждому родителю удается справиться с олимпиадной задачей (и тем более объяснить ее в 5 классе), а возможности придти после олимпиады домой и посмотреть решение задачи в учебнике нет. Именно для таких посетителей я решил открыть новую узкоспециализированную страницу: олимпиадные задачи по математике для 5 — 6 класса.
К сожалению, не всегда удается найти время на полное оформление задач в том объеме, в котором ни приходят ко мне по e-mail. Не забывайте, что я реальный репетитор по математике, а не виртуальный. Поэтому заранее прошу прощения, если в силу своей занятости не смогу ответить Вам оперативно. Оформление каждого решения (особенно если нужны рисунки и схемы) отнимает много времени и отвлекает репетитора от самого главного — от реальных занятий. Но мне интересно развитие сайта, интересно расширение базы занимательных задач (дефицит которых испытывает каждый репетитор по математике), поэтому в свободное время с удовольствием работаю с Вашими письмами. Пишите, присылайте интересные и сложные задачки (для 5 класса, для 6 класса !!!), присылайте все что Вам показалось занимательным и необычным, сложным, тонким или противоречивым.
Олимпиадные задачи для 5 — 6 класса. Ответы на Ваши вопросы.
Вопрос репетитору по математике от Валентины
Часы Юры отстают на 8 минут, но он считает, что часы спешат на 2 минуты. Часы Коли спешат на 2 минуты, однако он думает, что они отстают на 8 минут. Друзья договорились, что встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут?
Решение репетитора (Колпаков А.Н.)
Отметим, что мальчики приходят в точку встречи по своему «внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо узнать, каково реальное время в момент прихода каждого. Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17 ч 10 мин.
Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16 ч 50 мин. Поэтому Коля пришел раньше Юры на 20 минут.
Задача репетитору по математике от Катерины.
Доброе утро, ребёнку в школе задали решить задачу с олимпиады, ну ни как не получается! Задача: Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
Решение (А.Н.Колпаков) Прежде всего, нужно понять, что означает «в два раза быстрее». Это значит, что скорость больше в два раза. А поэтому в два раза больше будет пройденное расстояние (не важно, за какое время). Тогда, если Петя идет в два раза быстрее Васи и в 4 раза медленнее трамвая, то Вася проходит за минуту в раз меньшее расстояние, чем трамвай.
Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут. Ответ: 9 мин.
Вопрос репетитору по математике от Ибрагилава.
Как решить задачу? Свете втрое больше лет, чем было Максиму тогда, когда она была в его нынешнем возрасте. Когда Максим будет в возрасте Светы, то им вместе будет 28 лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?
Решение (Колпаков А.Н.)
Запутанные (олимпиадные) задачи на возраст удобно показывать на временной оси, на которой возраста представляются точками. Если у нас 2 человека и их возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас лет, а Свете сейчас лет.
Вопрос репетитору по математике от Миши
Здравствуйте! Помогите решить олимпиадную задачку за 5 — 6 класс. Вася написал в тетради 4 числа. Сложил их по два всеми возможными способами получил шесть таких сумм: 2, 4, 9, 9, 14, 16. Какие числа записал Вася?
Решение (Колпаков А.Н.)
Пусть a, b, с, d – искомые числа, расположенные в порядке возрастания. Составим последовательность их суммы также в порядке возрастания используя неравенство a < b < c < d. Получим такой ряд:
1) a+b=2
2) a+c=4
3,4) b+c и a+d
5) b+d=14
6) c+d=16
Первые две суммы явно наименьшие и поэтому равны 2 и 4. Две последние явно наибольшие и равны соответственно 14 и 16. Осталось выяснить судьбу двух оставшихся: b+с и a+d. Но так на них приходятся две девятки, то каждая из них равна 9. По первым двум суммам делаем вывод, что с на 2 больше чем b. Поэтому c=b+2. Подставляя выражение для числа с в равенство b+c=9 получим, что b+b+2=9. Поэтому b=3,5 и значит c=3,5+2=5,5. Из первого равенства вытекает, что a=2-3,5=-1,5, а из последнего, что d=16-5,5=10,5
В итоге ответ оказывается таким: -1,5; 3,5; 5,5 и 10,5
Задача репетитору от Эльдара. Помогите решить: Всего 5555 человек, на 10 солдат приходится 1 капрал, на 5 капралов 1 офицер, на 9 офицеров 1 генерал. Решение: сколько всего было солдат?
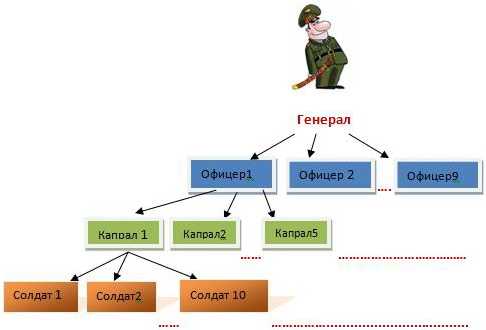
Репетитор по математике Ермакова Диана
Для начала определим, сколько человек в одном таком «наборе», состоящем из генерала, капралов, офицеров и солдат.
Один генерал и девять офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится капралов.
Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится солдат.
Всего человек в «наборе»
Так как всего в армии 5555 человек, то количество «наборов» равно
. В одном «наборе» солдат, поэтому в 11 «наборах» будет солдат.
Ответ: солдат.
Иногда мне помогают оформлять решения другие репетиторы по математике. Я рассылаю условия тем, кто дал свое согласие на участие в виртуальной работе. Для репетитора по математике такая активность — хороший шанс обратить на себя внимание будущих учеников. Поэтому, если Вы регистрируетесь у меня на сайте как репетитор по математике — укажите при заполнении анкеты (в поле дополнительной информации) готовы ли Вы к такому сотрудничеству. Тот репетитор по математике, кто будет присылать решения для публикации регулярно, скорее всего, может рассчитывать на размещение еще и в рекомендованном списке репетиторов.
Pages: 1 2
ankolpakov.ru
Математика 5 класс. Задания и упражнения. Натуральные числа.
Натуральные числа
Сравнение, сложение и вычитание натуральных чисел.
Базовый уровень
Задание 1
Какое из чисел 2/7, 837, 9/15, 1592 может означать количество кирпичей на строительном складе? Как называются эти числа?
- Решение
- 837, 1592.
- Эти числа называются натуральными.
Задание 2
Прочитайте каждое из чисел:
| 1) 385 | 2) 703 | 3) 1 907 | 4) 34 856 |
| 5) 591 | 6) 862 | 7) 8 057 | 8) 82 930 |
- Решение
- 1 — триста восемьдесят пять,
- 2 — семьсот три,
- 3 – тысяча девятьсот семь,
- 4 – тридцать четыре тысячи восемьсот пятьдесят шесть,
- 5 – пятьсот девяносто один,
- 6 – восемьсот девяносто два,
- 7 — восемь тысяч пятьдесят семь,
- 8 – восемьдесят две тысячи девятьсот тридцать.
Задание 3
Назовите сколько единиц, десятков, сотен и тысяч в каждом из чисел:
| 1) 793 | 2) 6 004 | 3) 201 |
| 4) 39 862 | 5) 856 398 | 6) 6 836 539 |
- Решение
- 1 – 793 единицы, 79 десятков, 7 сотен;
- 2 – 6 004 единицы, 600 десятков, 60 сотен, 6 тысяч;
- 3 — 201 единица, 20 десятков, 2 сотни;
- 4 – 39 862 единицы, 3 986 десятков, 398 сотен, 39 тысяч;
- 5 – 856 398 единиц, 85 639 десятков, 8 563 сотен, 856 тысяч;
- 6 — 6 836 539 единиц, 683 653 десятков, 68 365 сотен, 6 836 тысяч.
Задание 4
Запишите числа цифрами:
- 1) Семьсот девяносто четыре;
- 2) Три тысячи триста сорок восемь;
- 3) Восемьсот двадцать один;
- 4) Триста восемь тысяч семьдесят четыре;
- 5) Один миллион пятьсот тридцать одна тысяча шестьсот семьдесят три;
- 6) Тринадцать миллионов 98 тысяч сто тридцать один.
Решение
| 1) 794 | 2) 3 348 | 3) 821 |
| 4) 308 074 | 5) 1 531 673 | 6) 13 098 131 |
Задание 5
Запишите каждое из чисел словами:
30, 857, 208, 1029, 14845.
Решение
Тридцать, восемьсот пятьдесят сем, двести восемь, тысяча двадцать девять, четырнадцать тысяч восемьсот сорок пять.
Задание 6
Расставьте знаки больше или меньше:
| 308 … 380 | 7 591 … 7 951 | 47 805 … 91 000 | 359 000 … 68 000 |
| 192 … 180 | 3 829 … 6 350 | 71 003 … 17 300 | 296 038 … 269 380 |
Решение
| 308 < 380 | 7 591 < 7 951 | 47 805 < 91 000 | 359 000 < 68 000 |
| 192 > 180 | 3 829 < 6 350 | 71 003 > 17 300 | 296 038 > 269 380 |
Задание 7
Выполните сложение:
| 200 + 300 = | 700 + 59 = | 340 + 60 = | 37 + 163 = |
| 417 + 162 = | 417 + 82 = | 3002 + 6003 = | 450 + 540 = |
Решение
| 200 + 300 = 500 | 700 + 59 = 759 | 340 + 60 = 400 | 37 + 163 = 200 |
| 417 + 162 = 579 | 417 + 82 = 499 | 3002 + 6003 = 9005 | 450 + 540 = 990 |
Задание 8
Выполните вычитание:
| 133 — 33 = | 860 — 177 = | 500 — 387 = | 1384 — 1262 = |
| 457 — 391 = | 293 — 290 = | 5827 — 2268 = | 7545 — 5676 = |
Решение
| 133 — 33 = 100 | 860 — 177 = 683 | 500 — 387 = 113 | 1384 — 1262 = 122 |
| 457 — 391 = 66 | 293 — 290 = 3 | 5827 — 2268 = 3559 | 7545 — 5676 = 1869 |
Задание 9
Решите задачу:
До обеда в магазине было продано 48 кг помидор, а после обеда на 14 кг меньше. Сколько кг помидор было продано в магазине после обеда?
- Решение
- 1) 48 – 14 = 34 (кг).
- Ответ: после обеда в магазине было продано 34 кг помидор.
Задание 10
Найдите значение выражения:
| (34 + 15) — 24 = | 64 — (25 + 14) = | (36 + 34) — 24 = |
| (13 + 58) — 28 = | 36 — (16 + 29) = | (43 + 29) — 23 = |
Решение
| (34 + 15) — 24 = 25 | 64 — (25 + 14) = 25 | (36 + 34) — 24 = 46 |
| (13 + 58) — 28 = 43 | 36 — (16 + 19) = 1 | (43 + 29) — 23 = 49 |
Задание 11
В вазе было 37 конфет. Шестеро детей съели по 3 конфеты и двое по 4 конфеты. Сколько конфет осталось в вазе?
- Решение
- 1) 6 * 3 = 18 (конфет) съели шестеро детей;
- 2) 3 * 4 = 12 (конфет) съели четверо детей;
- 3) 18 + 12 = 30 (конфет) всего съели дети;
- 4) 37 – 30 = 7 (конфет).
- Ответ: в вазе осталось 7 конфет.
Средний уровень
Задание 1
Запишите числа цифрами:
- 1. Восемьсот семьдесят миллионов девять;
- 2. Два миллиарда четыреста пятьдесят девять миллионов триста шестьдесят восемь тысяч пятьсот семьдесят девять;
- 3. Тридцать миллиардов четыре миллиона двадцать три;
- 4. Восемьсот миллиардов шесть;
- 5. 248 миллиарда 6 миллионов 18 тысяч сто;
- 6. 503 миллиарда 241 тысяча 64.
Решение
| 1) 87 000 009 | 2) 2 459 368 579 | 3) 30 004 000 023 | 4) 800 000 000 006 | 5) 248 006 018 100 | 6) 503 000 241 064 |
Задание 2
Запишите числа, как сумму разрядных слагаемых:
| 1) 349 | 2) 809 | 3) 2475 | 4) 3008 |
Решение
| 1) 349 = 300 + 40 + 9 | 2) 809 = 800 + 9 | 3) 2475 = 2000 + 400 + 70 + 5 | 4) 3008 = 3000 + 8 |
Задание 3
Расставьте знаки больше или меньше:
| 852 618 … 852 681 | 2 545 033 … 2 545 300 | 300 300 003 … 300 003 300 |
Решение
| 852 618 < 852 681 | 2 545 033 < 2 545 300 | 300 300 003 > 300 003 300 |
Задание 4
Запишите числа в порядке возрастания:
98362, 6395, 1103672, 492031, 10238, 2958, 300271, 300713, 490952, 192, 74.
Решение
74, 192, 2 958, 6 395, 10 238, 98 362, 300 271, 300 713, 490 952, 492 031, 1 103 672.
Задание 5
Запишите натуральные числа, которые меньше 82 и больше 74.
Решение
75, 76, 77, 78, 79, 80, 81.
Задание 6
Какое количество натуральных чисел расположено между числами:
| 1) 57 и 64; | 2) 238 и 261; | 3) 167 и 192; | 4) 342 и 409; |
Решение
| 1) 6; | 2) 21; | 3) 24; | 4) 66. |
Задание 7
Выполните сложение:
| 27 592 + 593 089 = | 59 003 + 12 903 = | 129 301 + 739 912 = |
| 60 018 + 224 983 = | 30 283 + 45 037 = | 884 916 + 294 001 = |
Решение
| 27 592 + 593 089 = 620 681 | 59 003 + 12 903 = 71 906 | 129 301 + 739 912 = 869 213 |
| 60 018 + 224 983 = 285 001 | 30 283 + 45 037 = 75 320 | 884 916 + 294 001 = 1 178 917 |
Задание 8
Вычислите:
| 18м 48см + 26м 39см = ; | 45т 390 кг + 21т 31кг = . |
Решение
| 18м 48см + 26м 39см = 44м 87 см; | 45т 390 кг + 21т 31кг = 66т 421кг. |
Задание 9
Выполните вычитание:
| 49 081 — 19 090 = | 18 928 — 18 098 = | 397 802 — 65 834 = |
| 72 305 — 50 923 = | 25 730 — 21 829 | 450 038 — 375 340 = |
Решение
| 49 081 — 19 090 = 29 991 | 18 928 — 18 098 = 830 | 397 802 — 65 834 = 331 968 |
| 72 305 — 50 923 = 21 382 | 25 730 — 21 829 = 3 901 | 450 038 — 375 340 = 74 698 |
Задание 10
Найдите значения выражений:
| 469 + 1 843 — 1 992 = | 4 578 — 2640 + 3 654 = |
| 9 029 — 6 230 — 1 389 = | 19 463 + 7 356 + 35 230 = |
Решение
| 469 + 1 843 — 1 992 = 320 | 4 578 — 2640 + 3 654 = 5 592 |
| 9 029 — 6 230 — 1 389 = 1 410 | 19 463 + 7 356 + 35 230 = 62 049 |
Задание 11
Вычислите:
| 6 036 — (1 343 + 2 876) = | 9 803 — (6 357 + 1 996) = |
| 4 378 — (2 195 — 1 880) = | 6 306 — (4 381 — 2 270) = |
Решение
| 6 036 — (1 343 + 2 876) = 1 817 | 9 803 — (6 357 + 1 996) = 1 450 |
| 4 378 — (2 195 — 1 880) = 4 063 | 6 306 — (4 381 — 2 270) = 4 195 |
Задание 12
В швейную мастерскую привезли 150 м ткани. В первую неделю было израсходовано 46 метров, а во вторую 38 метров. Сколько метров ткани осталось в мастерской?
Решение
- 1) 46 + 38 = 84 (м) ткани израсходовали за 2 недели;
- 2) 150 – 84 = 66 (м) ткани.
- Ответ: в мастерской осталось 66 метров ткани.
Задание 13
Сравните не вычисляя:
| 1 487 + 372 … 183 + 1 394 | 48 391 + (3 409 + 2 809) … (2 893 + 1 908) + 48 391 |
| 8 934 + 490 … 822 + 8 943 | 17 429 + (6 830 + 3 402) … (7 620 + 3 420) + 17 429 |
Решение
| 1 487 + 372 > 183 + 1 394 | 48 391 + (3 409 + 2 809) > (2 893 + 1 908) + 48 391 |
| 8 934 + 490 < 822 + 8 943 | 17 429 + (6 830 + 3 402) < (7 620 + 3 420) + 17 429 |
Задание 14
Решите задачу:
В овощной магазин привезли картофель и лук. Картофеля привезли 185 кг, а лука на 48 кг меньше. Сколько всего картофеля и лука привезли в магазин?
Решение
- 1) 185 — 48 = 137 (кг) лука привезли в магазин;
- 2) 185 + 137 = 322 (кг).
- Ответ: всего привезли 322 кг лука и картофеля?
mat-zadachi.ru
Олимпиадные задания по алгебре (5 класс) на тему: Олимпиадные задачи. Математика 5 класс
Аннотация.
Задания школьной олимпиады по математике рассчитаны на обучающихся 5 классов. При подборе заданий олимпиады использовался принцип, при котором должны быть задачи посильные для большинства участников, задачи повышенной трудности (их может решить половина участников), сложные, требующие особой математической смекалки навыков решения нестандартных задач.
Для каждой задачи приводится решение и ответы. Даны рекомендации по оцениванию решений участников олимпиады.
Олимпиада по математике в 5 классе (школьный этап).
- Напишите наименьшее десятичное число, у которого все цифры различны.
(2 балла)
- В четырехэтажном доме Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. Кто на каком этаже живет? (3 балла)
- Переложите 4 спички таким образом, чтобы образовались три квадрата:
(4 балла)
- Катя и Юра купили лотерейные билеты с номерами 625517 и 322324 и обнаружили, что в каждом из номеров можно расставить знаки арифметических действий и скобки так, что в каждом случае результат будет равняться 100. Как это можно сделать? (4 балла)
- В корзине лежат яблоки, груши и персики – всего 37 плодов. Яблок в корзине в два раза больше, чем персиков, и на 3 штуки больше, чем груш. Сколько в корзине яблок, груш и персиков? (5 баллов)
Решение и ответы:
- Ответ: 1023456789.
- Ответ:
4 этаж | Сеня |
3 этаж | Ваня |
2 этаж | Петя |
1 этаж | Коля |
- Ответ:
- Ответ: например, 62+55-17 и (3+22)*(3-2)*4
- По условию задачи всего 37 плодов, составим уравнение х+2х+2х-3=37,
5х-3=37, 5х=40,
х=8 – персиков
2*8=16 – яблок
16-3=13 – груш
Ответ: 8 персиков, 16 яблок, 13 груш.
Решение считается неполным, если оно:
1. Содержит основные идеи, но не доведено до конечного результата;
2. Опирается на недоказанные утверждения, которые нельзя считать известными или очевидными.
nsportal.ru
Логические задачи для 5 класса
Тема: «Задачи на перевозки»
Цель: отработать навыки решения задач на перевозки с помощью интерактивного модуля.
1.Решение задач по теме.
Переправы без условий. Переправляющиеся находятся на одном берегу.
Переправы без условий. Переправляющиеся находятся на разных берегах.
Переправы с условиями. Условия на вместимость лодки.
Переправы с условиями. Затрудненные переправы. Возможно наличие острова.
Рассматривается разное количество героев, участвующих в переправе, и различная вместимость лодки.
1. Паромщик многие годы зарабатывал на жизнь тем, что перевозил через реку людей, их скарб и животных. Платы он большой не взимал, поэтому люди охотно пользовались его услугами, но за всю жизнь так и не удалось ему скопить денег на новый большой паром. На его маленьком паромчике хватало место только для самого паромщика и ещё чего-нибудь одного. Однажды ему надо было переправить через реку волка, козу и капусту. Но вот неудача волка с козой без присмотра оставлять нельзя, козу с капустой тоже. Объясните паромщику как в целости и сохранности переправить через реку капусту животных?
Ответ: Сначала переправить на другой берег козу, оставив волка с капустой. За тем перевезти капусту, а козу вернуть назад. Оставив козу и переправив волка на берег, где лежит капуста, паромщик может спокойно вернуться и переправить волка.
2. Волк и волчонок, медведь и медвежонок, лис и лисёнок решили переправиться с левого берега реки на правый берег. У них была лодка, в которую помещались любые двое из них. Как им переправиться на другой берег, если нельзя оставлять детёнышей с чужими папами без своего папы.
3. Отряд солдат подходит к реке, через которую необходимо переправиться. Но мост сломан, а река глубока. Как быть? Вдруг командир замечает двух мальчиков, которые — катаются на лодке недалеко от берега. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Как это было сделано?
4. Три рыцаря, каждый в сопровождении оруженосца, съехались на берегу реки, намереваясь переправиться на другую сторону. Им удалось найти маленькую двухместную лодку, и переправа произошла бы легко, но все оруженосцы, словно сговорившись, наотрез отказались оставаться в обществе незнакомых рыцарей без своих хозяев. И все же переправа состоялась, все шесть человек благополучно перебрались на другой берег с помощью одной двухместной лодки. При этом соблюдалось условие, на котором настаивали оруженосцы. Как это было сделано?
Составьте решение и апробируйте его с помощью мультимедийных средств.
5. Двое мальчиков катались на лодке. К берегу подошел отряд солдат. Лодка так мала, что на ней может переправиться только один солдат или двое мальчиков. Однако все солдаты переправились через реку именно на этой лодке. Как?
6. По длинному узкому каналу один за другим идут три парохода. Навстречу им – еще три парохода (см. рисунок). Канал такой узкий, что два парохода в нем разъехаться не могут, но в канале есть залив, где может поместиться один пароход. Могут ли пароходы разъехаться?
7. В кабине лифта 20-этажного дома есть две кнопки. При нажатии на одну из них лифт поднимается на 13 этажей, а при нажатии на другую опускается на 8 этажей. Как попасть с 13-го этажа на 8-й?
8. На рисунке изображен план яблоневого сада (точки — яблони). Садовник собирал яблоки со всех яблонь. Начал он с клетки, отмеченной звездочкой, и обошел одну за другой все клетки, как занятые яблонями, так и свободные, ни разу при этом, не возвращаясь на пройденную клетку. По диагонали он не ходил и на заштрихованных клетках не был, так как там помещались различные строения. Закончив обход, садовник оказался на той же клетке, с которой начинал путь. Нарисуйте путь садовника.
9. На станции железной дороги остановился грузовой поезд в составе паровоза и пяти вагонов. На этой станции есть небольшой тупичок, где в случае необходимости помещается паровоз с двумя вагонами (см. рисунок). Вскоре, вслед за грузовым поездом, к этой же станции (по тем же рельсам) подошел пассажирский поезд. Как его пропустить?
10. Однажды по лесу гуляли три рыцаря, каждый со своей дамой. Подойдя к реке, они захотели переправиться на другой берег. В их распоряжении оказалась одна лодка без гребца, поднимающая всего двух человек. Как им переправиться, если ни одна из дам не согласна ехать в лодке или быть на берегу в окружении чужих рыцарей без своего рыцаря? Дамы тоже умеют грести.
Дополнительные задачи
11. В лодке, вмещающей только двух человек, через реку должны переправиться три миссионера и три каннибала. Миссионеры боятся оставаться на каком-нибудь берегу в меньшинстве. Только один миссионер и один каннибал умеют грести. Как им переправиться?
12. Трём хирургам необходимо последовательно прооперировать в полевых условиях больного, страдающего заразным заболеванием. Сами хирурги тоже больны, причём все — разными болезнями. В распоряжении хирургов есть лишь две пары стерильных перчаток. Подскажите план операции, после которой ни хирурги, ни больной не заразятся друг от друга. Помогать друг другу во время операций хирурги не должны. Оперировать одной рукой нельзя.
13. Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама – за 2, малыш – за 5, а бабушка – за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? Если переходят двое, то они идут с меньшей скоростью. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя. Кидаться фонариком тоже нельзя.
infourok.ru
Логические задачи Математика 5 класс
Математический тренажер 5 класс
Математический тренажер 5 класс Сайт «Все Для Детей» http:// Математический тренажер. 5 класс Основная функция устных упражнений актуализация опорных для конкретной темы знаний и умений, подготовка учащихся
ПодробнееРебусы по русскому языку 6 класс
Библиотека сайта «Все Для Детей» Ребусы по русскому языку 6 класс http:// Ребусы по русскому языку. 6 класс Ребусы прекрасный игровой метод для активизации детей на уроке. Ребусы любят все и сами школьники,
ПодробнееКроссворды по русскому языку 5 класс
Библиотека сайта «Все Для Детей» Кроссворды по русскому языку 5 класс http:// Кроссворды по русскому языку. 5 класс Кроссворд на уроке самый насыщенный метод опроса и даже проверки знаний. По активности
Подробнее0:1 Винни-Пух обходит полянку квадратной формы за 12 минут. За сколько минут обойдет он полянку, периметр которой в три раза больше? 0:3 У Кати вдвое больше пятерок, чем у Вовы, а у него на 5 пятерок меньше,
Подробнее0:1 Винни-Пух обходит полянку квадратной формы за 12 минут. За сколько минут обойдет он полянку, периметр которой в три раза больше? 0:3 У Кати вдвое больше пятерок, чем у Вовы, а у него на 5 пятерок меньше,
ПодробнееМ А Т Е М А Т И К А В Ш К О Л Е
Тесты по математике по учебнику М. И. Моро для 1 класса. 1 и 2 четверти Тесты по математике для 1 класса, 1 четверть Тест 1 Вариант I 1. На рисунке изображены круги и квадраты. Закрась синим цветом фигуры,
Подробнее426 + ( ) ( ) ( ) ( ) ( ) 4589 ( ) 1 6 (I) Вычисли:
м (4 класс) Дорогой друг! Стартовая работа помогла тебе выявить трудности, а карточки, размещѐнные здесь, помогут тебе с этими трудностями справиться. Старайся, и у тебя всѐ получится! Карточку надо аккуратно
ПодробнееУВАЖАЕМЫЕ ПЕДАГОГИ И РОДИТЕЛИ!
УВАЖАЕМЫЕ ПЕДАГОГИ И РОДИТЕЛИ! Федеральный государственный образовательный стандарт второго поколения рекомендует по-новому оценивать не только знания, умения, но и компетентности обучающихся в начальной
ПодробнееПояснительная записка
Пояснительная записка Все задания предполагают творческое применение программных знаний, умений и навыков по данным предметам. Материалы данной работы могут быть использованы учителем при подготовке к
Подробнее«Думай, считай, отгадывай!»
«Думай, считай, отгадывай!» Цели игры: — создать условия для развития математического мышления, быстроты реакции; — содействовать формированию интереса к математике; — обобщать ранее изученный материал.
ПодробнееМ А Т Е М А Т И К А В Ш К О Л Е
Контрольные работы по математике по учебнику Петерсон. 1 класс Контрольная работа 1, уроки 1-18, на темы: «Сложение и вычитание», «Свойства предметов: больше, меньше», «Группа предметов: сложение, вычитание»,
ПодробнееМ А Т Е М А Т И К А В Ш К О Л Е
Задачи и примеры для самостоятельной работы по математике 1 класс, 1 четверть по учебнику Петерсон Задачи и примеры для самостоятельной работы 1 на темы: «Свойства и сравнения предметов» Вариант I 1. Продолжи
ПодробнееВнимание. Ответ: Ответ:
Задание 1. «Отыщи поросят» Внимание. Внимательно посмотрите на картинку. Отыщите всех поросят на полянке. Каждого поросёнка, которого найдёте, зачеркните карандашом. (вписать цифрой число зачёркнутых поросят)
ПодробнееМАТЕМАТИКА 4 КЛАСС ЯНВАРЬ
1 В 3 носка. Вытащив из ящика 2 носка, можно вытащить 1 синий носок и 1 чёрный носок. Третий носок будет или синий, или чёрный, и в руках Васи обязательно окажется пара носков одинакового цвета. 2 Г 15
ПодробнееТест готовности ребенка к школе :00
Первый класс! Для всех родителей это очень важное и запоминающееся событие, поскольку ваш кроха, который ещё вчера практически ничего не умел делать без вашей помощи, сегодня уже достаточно самостоятельная
ПодробнееЗанятие 1 Задачи на смекалку
Занятие 1 Задачи на смекалку В этом занятии не требуется никаких навыков, знаний или умений производить сложные вычисления. Понадобится лишь смекалка и воображение ребенка. В данном разделе собраны фольклорные
ПодробнееЗАНЯТИЕ 3 ОН МОЙ ОНА МОЯ ОНО МОЁ
ЗАНЯТИЕ 3 ОН МОЙ ОНА МОЯ ОНО МОЁ 1. Подпиши картинки. Вставь слова МОЙ, МОЯ ИЛИ МОЁ. СОБАКА ЯБЛОКО СТУЛ _Она моя КРЕСЛО ПЛАТЬЕ ТИГР ДОМ МЯЧ КНИГА КОШКА КОНФЕТА ВАРЕНЬЕ 8 2. Соедини слова с картинкой. Соедини
ПодробнееРусский язык, 1 класс, декабрь 2016
Русский язык, 1 класс, декабрь 2016 1 КЛСС ЕКРЬ 2016 Маленькая Майя хочет, чтобы ей почитали. Она просит старшую сестру: «Почитай мне книжку, где доктор лечит всех зверей! И ещё про крокодила, который
ПодробнееРешения для 4 5 класса
1 1. Первая часть Задача 1: Решения для 4 5 класса Сколькими способами можно поставить двух королей одного цвета на доске 3х3 так, чтобы они не били друг друга? А. 4 Б. 8 В. 12 Г. 16 В центре доски король
ПодробнееМатематическое домино. Задания
Математическое домино Правила математической игры «Математическое домино» 1. Представитель каждой команды выбирает доминошку. На обороте каждой доминошки написана задача. На каждую задачу отводится два
ПодробнееУмножение числа на 10.»
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа 2 Урок математики в 3 классе «Сочетательное свойство умножения. Умножение числа на 10.» Учитель: Гурьянова Е.С. г. Навашино
ПодробнееМ А Т Е М А Т И К А В Ш К О Л Е
Карточки по математике для 1 класса, 3 и 4 четверти Карточки по математике для 1 класса, 3 четверть Тема: «Сложение чисел от 0 до 10» 5 + 1 = 4 + 3 = 3 + 6 = 1 + 7 = 4 + 2 = 2 + 2 = 3 + 5 = 2 + 7 = 3 +
ПодробнееМежшкольная олимпиада. 4 класс
Межшкольная олимпиада 30.01.16 4 класс 1. Соедините пять звеньев цепи в одну цепь при помощи только шести операций (операции состоят из расковывания и заковывания колец) 2. Скорый поезд вышел из Москвы
Подробнееdocplayer.ru
