Умножение / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
В математике существует знак для умножения — это точка посередине строки между числами, которые нужно перемножить.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
6 — первый множитель
4 — второй множитель
24 — произведение
Числа при умножении
Первый множитель
Второй множитель
Результат умножения, или Произведение

Чтение числовых выражений
6 • 4 = 24
Этот пример можно прочитать по-разному.
- 6 умножить на 4 равняется 24.
- 6 увеличить в 4 раза – получится 24.
- Первый множитель – 6, второй множитель – 4, произведение – 24.
- Произведение 6 и 4 равно 24.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.

Умножение на 0

8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10

8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения

8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
2 + 2 + 2 + 2 = 4 (к.)
Заменяем сложение умножением и получаем:
2 • 4 = 8 (к.)
Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Свойства умножения
Правило встречается в следующих упражнениях:
2 класс
Страница 58. Вариант 1. № 1, Моро, Волкова, Проверочные работы
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 56, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 57, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 58, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 26, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 17, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 27, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 102, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Упражнение 36, Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
😃 Умножение — правила, секретные примеры, упражнения, игры
Основа математики – это четыре операции с числами и переменными: сложение, вычитание, деление и умножение. Как раз об операции умножения и пойдет речь в этой статье.
Умножение чисел
Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.
Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.
Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.
Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Формулы умножения
Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:
a1+a2+…+an=n*a.
Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.
Сокращенное умножение
Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:
Формулы сокращенного умножения
Пусть a, b принадлежат R, тогда:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a+b)^2 = a^2 + 2ab + b^2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a-b)^2 = a^2 — 2ab + b^2
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Формула: a^2 — b^2 = (a — b)(a + b)
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Формула: (a + b)^3 = a^3 + 3a(^2)b + 3ab^2 + b^3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Формула: (a-b)^3 = a^3 — 3a(^2)b + 3ab^2 — b^3
Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 + b^3 = (a + b)(a^2 — ab + b^2)
Разность кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 — b^3 = (a — b)(a^2 + ab + b^2)
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Умножение дробей
Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.
Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.
Умножение 2 класс
Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:
Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?
В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?
Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?
В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?
Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?
В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?
Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?
В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?
Умножение 3 класс
В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление.
Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.
Умножение столбиком:
Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.
1 шаг. Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.
2 шаг. Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.
Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.
3 шаг. Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.
4 шаг. Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.
Итак, умножив 427 на 6, получился ответ 2562
ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!
5 шаг. Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281
6 шаг. Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.
Умножение 4 класс
Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.
Например, найти произведение следующих пар чисел:
- 988 * 98 =
- 99 * 114 =
- 17 * 174 =
- 164 * 19 =
Презентация на умножение
Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!
Презентация
Таблица умножения
Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Примеры на умножение
Умножение на однозначное
- 9 * 5 =
- 9 * 8 =
- 8 * 4 =
- 3 * 9 =
- 7 * 4 =
- 9 * 5 =
- 8 * 8 =
- 6 * 9 =
- 6 * 7 =
- 9 * 2 =
- 8 * 5 =
- 3 * 6 =
Умножение на двузначное
- 4 * 16 =
- 11 * 6 =
- 24 * 3 =
- 9 * 19 =
- 16 * 8 =
- 27 * 5 =
- 4 * 31 =
- 17 * 5 =
- 28 * 2 =
- 12 * 9 =
Умножение двузначное на двузначное
- 24 * 16 =
- 14 * 17 =
- 19 * 31 =
- 18 * 18 =
- 10 * 15 =
- 15 * 40 =
- 31 * 27 =
- 23 * 25 =
- 17 * 13 =
Умножение трехзначных чисел
- 630 * 50 =
- 123 * 8 =
- 201 * 18 =
- 282 * 72 =
- 96 * 660 =
- 910 * 7 =
- 428 * 37 =
- 920 * 14 =
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Быстрый счет»
Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Играть сейчас
Игра «Математические матрицы»
«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».
Играть сейчас
Игра «Числовой охват»
Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.
Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.
Играть сейчас
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Математические сравнения»
Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
- Научится запоминать на более длительный срок
- Увеличится скорость воспоминания нужной информации
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Свойства умножения / Умножение / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
- Свойства умножения
1) Переместительное свойство: от перестановки множителей произведение не изменится.
3 • 4 = 12
4 • 3 = 12
Значит, 3 • 4 = 4 • 3
2) Сочетательное свойство: два соседних множителя можно заменить их произведением.
(6 • 2) • 5 = 6 • (2 • 5)
3) Распределительное свойство: при умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
(3 + 10) • 7 = 3 • 7 + 10 • 7 = 91.
4) Чтобы умножить сумму на число, можно сначала выполнить сложение и полученный результат умножить на число:
(3 + 10) • 7 = 13 • 7 = 91.
5) Чтобы умножить число на произведение, можно сначала выполнить умножение в скобках, а затем умножить число на полученный результат:
4 • (3 • 5) = 4 • 15 = 60.
6) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат:
2 • (3 + 5) = 2 • 8 = 16
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Умножение
Правило встречается в следующих упражнениях:
3 класс
Страница 46. Вариант 1. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 47. Вариант 2. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 101, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
4 класс
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 33, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 17, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 24, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 42, Моро, Волкова, Рабочая тетрадь, 2 часть
© budu5.com, 2020
Пользовательское соглашение
Copyright
Умножение | Математика
Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.
Определение умножения
Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.
Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.
Умножение есть сложение равных слагаемых.
Данные в умножении называются множимым и множителем, а искомое — произведением.
В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.
Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.
Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.
Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.
Множимое и множитель вместе называются производителями.
При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.
Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.
Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать
7 + 7 + 7
пишут при помощи знака умножения короче:
7 × 3 или 7 · 3
Умножение есть сокращенное сложение равных слагаемых.
Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).
Связь между данными и искомым числом выражается в умножении
письменно:
7 × 3 = 21 или 7 · 3 = 21
словесно:
семь, умноженное на три, составляет 21.
Чтобы составить произведение 21, нужно 7 повторить три раза
21 = 7 + 7 + 7
Чтобы составить множитель 3, нужно единицу повторить три раза
3 = 1 + 1 + 1
Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:
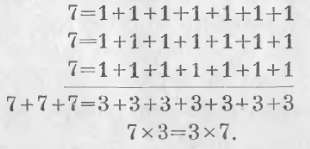
Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
Умножение однозначных чисел. Таблица Пифагора
Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.
Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).
Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.
Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде
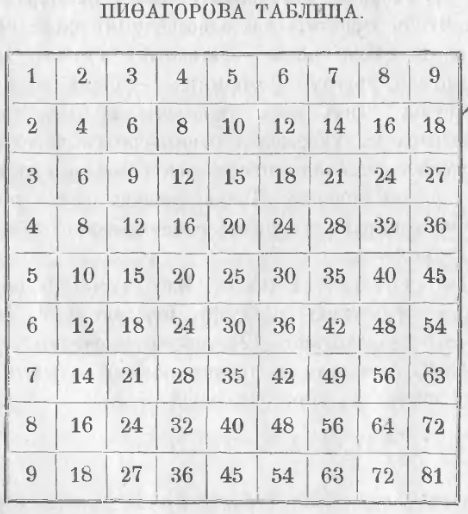
Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.
Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
Умножение продолжается до тех пор, пока не получат полного произведения.
Умножение чисел на 10, 100, 1000 …
Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.
Этого достигают, приписывая к числу два нуля.
Отсюда заключаем:
Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.
Умножение числа 6035 на 1000 выразится письменно:
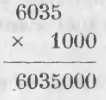
Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.
Умножение на число с нулями в конце
Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.
Ход вычисления выразится письменно:
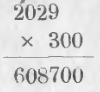
Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.
Умножение многозначного числа на многозначное
Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.
Три произведения

называются частными произведениями.
Полное произведение 3029 × 429 равно сумме трех частных:
3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.
Найдем величины этих трех частных произведений.
Умножая 3029 на 9, находим:
3029 × 9 27261 первое частное произведение
Умножая 3029 на 20, находим:
3029 × 20 60580 второе частное произведение
Умножая 3026 на 400, находим:
3029 × 400 1211600 третье частно произведение
Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.
Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.
Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.
Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.
Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,
нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.
Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.
Пример. Найти произведение 342 на 2700.
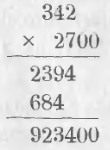
Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.
Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35
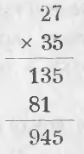
Приписывая к 945 пять нулей, получаем искомое произведение:
2700 × 35000 = 94500000.
Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).
Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.
В нашем произведении может содержаться или 7 или 6 цифр.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
2 × 2 = 4, 3 × 3 = 9.
Квадраты. Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы. Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями.
Произведения трех равных множителей или кубы называются третьими степенями, и т. д.
Умножение натуральных чисел / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Умножение натуральных чисел
Определение
Умножение — одна из операций математики, предназначена для упрощения сложения одинаковых чисел.
Например: 4 + 4 + 4 = 4 · 3 = 12.
Умножение обозначают точкой «·» или крестиком «х».
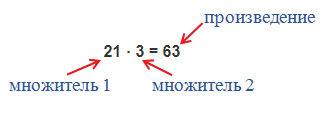
Числа, которые умножаются, называют «множителями», результат умножения, называют «произведением»
Пример:
Алгоритм умножения чисел
Разберем порядок умножения чисел на примере. Умножим число 25 на 16
1. Сначала записываем множители в столбик.
Второй множитель записывается под первым множителем так, что разряды второго множителя находились под соответствующими разрядами первого множителя, т.е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
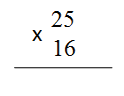
2. Производим последовательное умножение.
Сначала число, обозначающее разряд единиц класса единиц второго множителя последовательно умножаем на все разряды первого множителя.
Умножим цифру 6 на 5, получаем 30 — 3 десятка 0 единиц. 0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
3. Найдем второе неполное произведение. Последовательно умножим десятки второго множителя — 1 на все разряды первого слагаемого. Сначала 1 умножим на 5, получаем 5, запишем полученное произведение под десятками. После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
4. Последовательно сложим цифры полученных неполных произведений по правилам сложения.
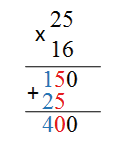
Свойства умножения натуральных чисел.
1. Переместительное свойство умножения.
a · b = b · a
От перемены мест множителей произведение не изменится.
12 · 4 = 4 · 12
12 · 4 = 48
4 · 12 = 48
2. Сочетательное свойство умножения.
a · (b · c) = (a · b) · c
Произведение не зависит от группировки сомножителей.
2 · (3 · 6) = (2 · 3) · 6
2 · (3 · 6) = 36
1) 3 · 6 = 18; 2) 18 · 2 = 36
(2 · 3) · 6 = 36
1) 2 · 3 = 6; 2) 6 · 6 = 36
3. Распределительное свойство умножения относительно сложения.
a · (b + c) = ab + ac
При умножении числа на сумму двух других чисел, можно данное число умножить на каждое из слагаемых, а полученные результаты сложить.
3 · (5 + 4) = 3 · 5 + 3 · 4
3 · (5 + 4) = 27
1) 5 + 4 = 9; 2) 9 · 3 = 27
3 · 5 + 3 · 4 = 27
1) 3 · 5 = 15; 2) 3 · 4 = 12; 3) 12 + 15 = 27
4. Распределительное свойство умножения относительно вычитания
a · (b — c) = ab — ac
При умножении числа на разность двух других чисел, можно данное число умножить на уменьшаемое и на вычитаемое, а полученные результаты вычесть.
6 · (7 — 5) = 6 · 7 — 6 · 5
6 · (7 — 5) = 12
1) 7 — 5 = 2; 2) 2 · 6 = 12
6 · 7 — 6 · 5 = 12
1) 6 · 7 = 42; 2) 6 · 5 = 30; 3) 42 — 30 = 12
5. Свойство умножения единицы на натуральное число
a · 1 = a
При умножении единицы на любое число, получим равное ему число.
1 · 76 = 76
6. Свойство умножения нуля на натуральное число
0 · a = 0
При умножении 0 на любое число, получим 0
0 · 123 = 0
Произведение всех натуральных чисел от 1 до 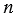 называют
называют 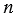 факториал, записывают:
факториал, записывают: 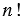 , читают: «эн факториал». Следовательно, справедливо равенство:
, читают: «эн факториал». Следовательно, справедливо равенство:
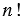 = 1
= 1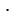 2
2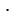 3
3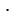 …
…
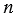
Пример:
3! = 1 2
2 3 = 6;
3 = 6;
5! = 1 2
2 3
3 4
4 5 =120.
5 =120.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 663, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 834, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 835, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 878, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1023, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1199, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1552, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 619, Мерзляк, Полонский, Якир, Учебник
Упражнение 1078, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 99, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 409, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 412, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 477, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 481, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 517, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 539, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 570, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 594, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 615, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Табличное умножение / Умножение / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
- Табличное умножение
Напомним смысл умножения и его связь с делением
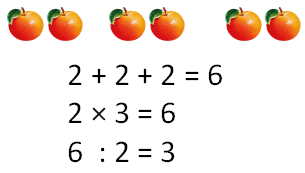
Первое: Было 3 пары яблок. Сколько всего яблок было?
2 + 2 + 2 = 6 (яб.)
Было всего 6 яблок.
Второе: Все слагаемые одинаковые, значит, сложение можно заменить умножением. По 2 яблока взяли 3 раза.
2 • 6 = 6 (яб.)
Было всего 6 яблок.
Проверка:
2 • 3 = 6 6 : 2 = 3
6 : 3 = 2 3 • 2 = 6
Выучи наизусть:
2 • 1 = 2 (2 повторить 1 раз – получим 2)
2 • 2 = 4 (2 повторить 2 раза – получим 4)
2 • 3 = 6 (2 повторить 3 раза – получим 6)
2 • 4 = 8 (2 повторить 4 раза – получим 8)
2 • 5 = 10 (2 повторить 5 раз – получим 10)
2 • 6 = 12 (2 повторить 6 раз – получим 12)
2 • 7 = 14 (2 повторить 7 раз – получим 14)
2 • 8 = 16 (2 повторить 8 раз – получим 16)
2 • 9 = 18 (2 повторить 9 раз – получим 18)
Таблица умножения на 2 и 3
Таблица умножения на 4 и 5
Таблица умножения на 6 и 7
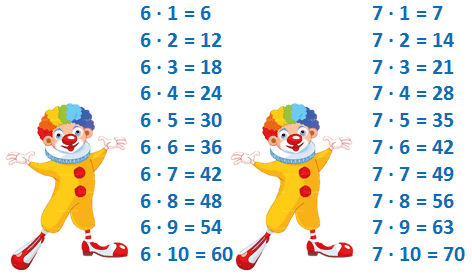
Таблица умножения на 8 и 9

Таблица умножения на 10
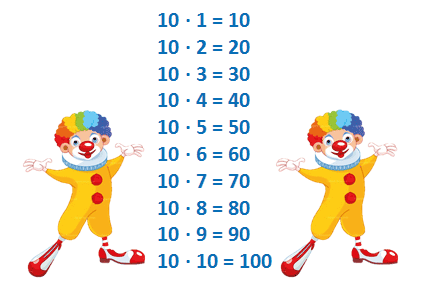
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Свойства умножения
Умножение
Правило встречается в следующих упражнениях:
2 класс
Страница 61. Вариант 2. № 2, Моро, Волкова, Проверочные работы
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 97, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 46, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 104, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 22. Вариант 1. Тест 2, Моро, Волкова, Проверочные работы
Страница 24. Вариант 1. № 5, Моро, Волкова, Проверочные работы
Страница 35. Вариант 2. № 3, Моро, Волкова, Проверочные работы
4 класс
Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 14, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 16, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 23, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 16, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 65, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Задание 53, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 56, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 4, Мерзляк, Полонский, Якир, Учебник
Упражнение 140, Мерзляк, Полонский, Якир, Учебник
Упражнение 253, Мерзляк, Полонский, Якир, Учебник
Упражнение 261, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 402, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правила умножения, сложения и общей вероятности
Правило сложения
Дополнительное правило определяет вероятность наступления хотя бы одного из событий.
Если A и B исключают друг друга, то P (A и B) = 0, поэтому правило можно упростить следующим образом:
Правило умножения
Правило умножения определяет совместную вероятность двух событий.
Совместная вероятность A и B равна вероятности A для данного B, умноженной на вероятность B.
Если A и B независимы, то P (A / B) = P (A) и правило умножения упрощается до:
Правило общей вероятности
Правило полной вероятности определяет безусловную вероятность события в терминах вероятностей, обусловленных сценариями.
Давайте рассмотрим пример, чтобы понять это.
Событие A: цена акций компании X вырастет.
Событие B: Инфляция упадет. Р (В) = 0,6. Следовательно, вероятность того, что инфляция не снизится, P (B C ) = 0.4
Вероятность роста курса акций при падении инфляции, P (A | B) = 0,8
Вероятность роста стоимости акций при отсутствии снижения инфляции, P (A | B C ) = 0,6
Мы можем использовать правило полной вероятности для вычисления вероятности роста цены акций следующим образом:
Это полная вероятность возникновения события A при всех сценариях.
.Раздел 5.4: Условная вероятность и общее правило умножения
Цели
К концу этого урока вы сможете …
- вычислить условные вероятности
- используйте общее правило умножения
- определить независимость событий
Чтобы получить краткий обзор этого раздела, посмотрите это короткое резюме видео:
Условная вероятность
Вспомните пример 3 в разделе 5.3, о бросании двух кубиков? В В этом примере мы сказали, что события E (первый кубик — 3) и F (второй кубик — 3) были независимыми , потому что появление E не повлияло на вероятность F. Ну, это не всегда так, что приводит нас к другому типу вероятности, называемому условной вероятностью .
Условная вероятность
Обозначение P (F | E) читается как «вероятность F для данного E» и представляет собой вероятность это событие F происходит, учитывая, что событие E уже произошло.
Давайте еще раз посмотрим на Пример 1 из того же раздела.
Пример 1
Рассмотрим эксперимент, в котором две карты вытягиваются без замены. ( Без замены означает один рисуется, а затем второй рисуется, не кладя первый обратно.) Определите события E и F так:
E = первая вытянутая карта — король
F = вторая вытянутая карта — король
Найдите P (F | E).
[открыть ответ]
P (F | E) — вероятность того, что вторая карта окажется королем, если первая взятая карта была король. В этом случае из 51 карты останется 3 короля, поэтому
P (F | E) = 3/51
Может оказаться полезным снова взглянуть на диаграмму Венна, чтобы проиллюстрировать эту идею. Посмотрим на это который мы использовали еще в разделе 5.2.
Пример 2
Найдите P (E | F).
[открыть ответ]
Хорошо, это немного сложнее. P (E | F) — вероятность того, что событие E произойдет при данном событии. F уже произошло. Немного изменим изображение. Поскольку F произошло, мы можем сосредоточиться только на те «результаты» в F.
И затем из этих , нам нужна вероятность того, что «результат» находится в E. 2 из них в E и 5 всего,
P (E | F) = 2/5.
Еще один пример.
Пример 3
Рассмотрим опрос, проведенный среди 52 студентов курса базовой алгебры в ECC, со следующими ответы на утверждение «Мне нравится математика».
| Сильно Согласен | Согласен | нейтральный | Не согласен | Сильно Не согласен | Всего | |
| Мужской | 6 | 10 | 3 | 0 | 0 | 19 |
| Женский | 8 | 14 | 7 | 4 | 0 | 33 |
| Всего | 14 | 24 | 10 | 4 | 0 | 52 |
Какова вероятность того, что ученик увлекается математикой ( согласен, или полностью согласен, ) учитывая, что студентка женщина?
[открыть ответ]
Всего учатся 33 студентки.Из них 22 ответили, что им нравится математика, так что …
P (увлекается математикой | женщина) = 22/33 = 2/3
Проблема Монти Холла
Интересным примером условной вероятности является классическая Задача Монти Холла . Это основано на старом игровом шоу, где ведущий показывает три двери. За одной была новая машина, а за другими — козы. Суть в том, что как только вы сделаете свой выбор, Монти откроет одну из других дверей, показывая козу.Тогда вопрос — стоит переключать? Ответ отличается от того, что вы думаете. Вот еще одно видео Клайва Рикса из Университета Лестера в Лестере, Англия:
Не верите? Попробуйте эту интерактивную функцию из New York Times или посмотрите это видео с шоу Numb3rs.
Ух ты, никогда не знаешь, где можно применить условную вероятность!
Общее правило умножения
Давайте еще раз посмотрим на эксперимент из Примера 1 в Разделе 5.3.
Пример 4
Рассмотрим эксперимент, в котором две карты вытягиваются без замены. ( Без замены означает один рисуется, а затем второй рисуется, не кладя первый обратно.) Определите события E и F так:
E = первая вытянутая карта — король
F = вторая вытянутая карта — король
Как найти P (E и F)?
Мы знаем из примера 1, что E и F не независимы, поэтому мы знаем, что мы не можем использовать умножение Правило независимых событий.Хотя, вероятно, не так уж сложно понять, как мы можем это сделать.
| P (E и F) | = P (первый король, второй король) |
| = P (первый — король) • P (второй — король, первый — король) | |
| = (4/52) (3/51) | |
| ≈ 0.0045 |
Или, другими словами, P (E и F) = P (E) • P (F | E)
Эта идея на самом деле является версией правила умножения для независимых событий и является назвал General Правило умножения .
Общее правило умножения
Вероятность того, что происходят два события E и F, равна
.P (E и F) = P (E) • P (F | E)
Пример 5
Давайте попробуем новый вероятностный эксперимент.На этот раз рассмотрим мешок шариков, содержащий 10 красных, 20 синих и 15 зеленых шариков. Предположим, что два шарика нарисованы без замены. (Первый мрамор не кладут обратно в мешок до нанесения второго.)
Какова вероятность того, что оба нарисованных шарика красные?
[открыть ответ]
Определим пару событий:
E = первый шарик красный
F = второй мрамор красный
Мы хотим P (E и F).Используя общее правило умножения, мы видим
P (E и F) = P (E) • P (F | E) = (10/45) • (9/44) ≈ 0,0455
Проверка на независимость
Если вы помните, в Разделе 5.3 мы определили, что означает независимость двух событий:
Два события E и F являются независимыми , если наступление события E не влияет на вероятность события F.
Рассматривая это с точки зрения условной вероятности, если появление E не влияет на вероятность F, то P (F | E) = P (F).Это хороший способ проверить независимость. Фактически, мы можем переопределить независимость используя эту концепцию.
Два события E и F независимы , если P (F | E) = P (F).
Давайте используем это новое определение в примере, чтобы определить, являются ли два события независимыми.
Пример 6
Давайте снова воспользуемся данными из Примера 3 и опроса 52 студентов по базовой алгебре. конечно в ECC, со следующими ответами на утверждение «Мне нравится математика.«
| Сильно Согласен | Согласен | нейтральный | Не согласен | Сильно Не согласен | Всего | |
| Мужской | 6 | 10 | 3 | 0 | 0 | 19 |
| Женский | 8 | 14 | 7 | 4 | 0 | 33 |
| Всего | 14 | 24 | 10 | 4 | 0 | 52 |
Предположим, что студент выбран случайным образом из числа опрошенных, и мы определяем события E и F следующим образом:
E = выбранный студент — женщина
F = студент увлекается математикой
Независимы ли события E и F?
[открыть ответ]
Чтобы ответить на этот вопрос, нам нужно посмотреть, равно ли P (F | E) = P (F).
P (F) = 38/52 ≈ 0,7308
P (F | E) = 22/33 ≈ 0,6667
Поскольку P (F) ≠ P (F | E), события E и F зависят.
.
