Способы умножения.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Солдатова В.А. 1
1МБОУ СОШ №3 г.Тосно
Неизвестный Е.В. 1
1МБОУ СОШ №3 г.Тосно
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения. В школе мы изучаем таблицу умножения, а затем учимся умножать числа в столбик. Это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел.
Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи:
Найти и разобрать различные способы умножения.
Научиться демонстрировать некоторые способы умножения.
Рассказать о новых способах умножения и научить одноклассников ими пользоваться.
Основная часть
История появления таблицы умножения.
При раскопках здания в городе Нара, древней столице Японии, археологами была найдена деревянная табличка с фрагментом таблицы умножения. Из всех табличек, обнаруженных в Японии, найденная – самая древняя.
Из всех табличек, обнаруженных в Японии, найденная – самая древняя.
Каким же образом жители Японии впервые узнали о математической «запоминалочки»? Судя по тому, что иероглифы, которыми записаны цифры напоминают китайское письмо, скорее всего, она была просто скопирована из китайского учебника арифметики того времени. А откуда она взялась в Китае? Не исключено, что именно там ее впервые и придумали.
Эту версию подтверждает находка, сделанная китайскими археологами на юге страны. Там была обнаружена дощечка, на которой был фрагмент таблицы умножения, возраст которой ученые оценили в 2700 -3000 лет.
На основании этой находки ученые Китая предложили гипотезу, согласно которой впервые таблица умножения была составлена в Древнем Китае, а потом вместе с караванами проникли в Индию, а оттуда в страны Передней Азии и Европу. Однако этой версии противоречат многие находки, сделанные ранее. Например, в Индии в свое время были обнаружены более древние варианты таблицы умножения, возраст которых оценивается в 3000-3200 лет.
Самые старые в мире таблицы умножения были найдены при раскопках городов Древней Месопотамии. Они были нанесены с помощью клинописи на глиняные таблички, возраст которых составляет 5000 лет. Скорее всего, таблица умножения появилась где-то в тех краях.
Хотя не исключено также и то, что данная система устного счета появилась независимо в разных местах. Узнать имя гениального математика, который первым додумался записать результаты умножения в виде таблицы, скорее всего, не удастся. Это пришло в голову сразу нескольким людям. В европейской культуре автором таблицы умножения считается знаменитый греческий математик Пифагор. [1, с.78]
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть ли не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
За тысячелетия развития математики было придумано множество способов умножения чисел, и все эти приемы соперничали друг с другом и усваивались с большим трудом. [2, с.16]
Давайте рассмотрим наиболее интересные и простые способы умножения.
Способы умножения
Русско-крестьянский способ умножения.
Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоений другого числа.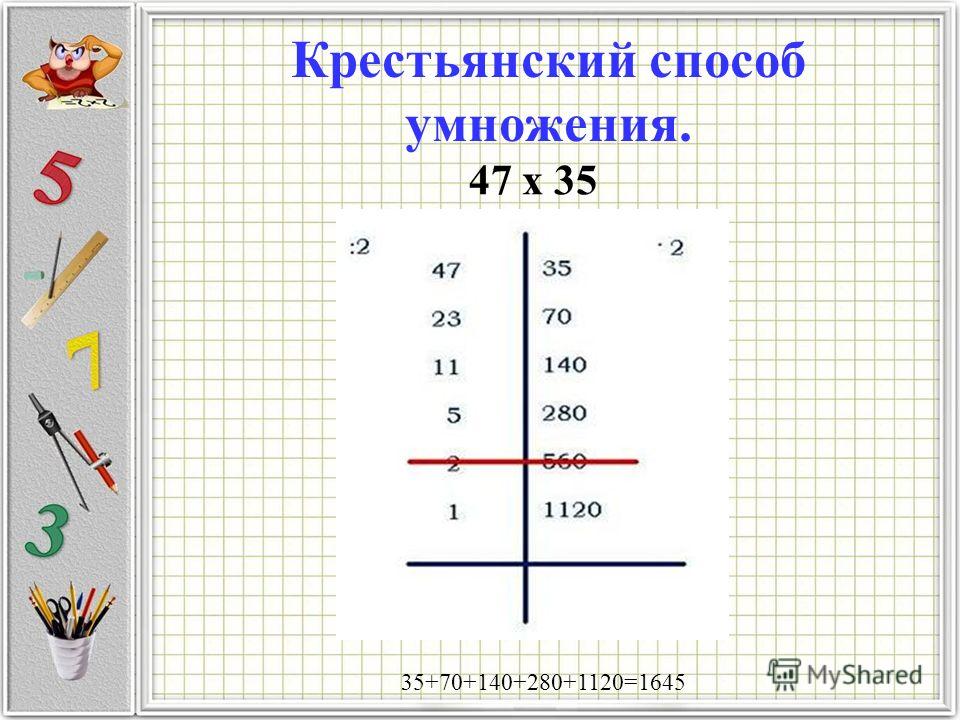 Пример: 32 х 13
Пример: 32 х 13
|
Множимое =32 |
Множитель = 13 |
|
32 |
13 |
|
16 |
26 |
|
8 |
52 |
|
4 |
104 |
|
2 |
208 |
|
1 |
416 |
Таблица 1.
Деление пополам (см. левую половину Табл.1) продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число (правая часть Табл.1). Последнее удвоенное число и дает искомый результат.
Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение:( 32 х 13 ) = ( 1 х 416 ) [3, с.54]
Особо внимательные заметят «А как быть с нечетными числами, которые не кратны 2-м?».
Итак, пусть нам необходимо умножить два числа: 987 и 1998. Одно запишем слева, а второе — справа на одной строчке. Левое число будем делить на 2, а правое — умножать на 2 и результаты записывать в столбик. Если при делении возникнет остаток, то он отбрасывается.
Операцию продолжаем, пока слева не останется 1. Затем вычеркнем те строчки, в которых слева стоят четные числа и сложим оставшиеся числа в правом столбце.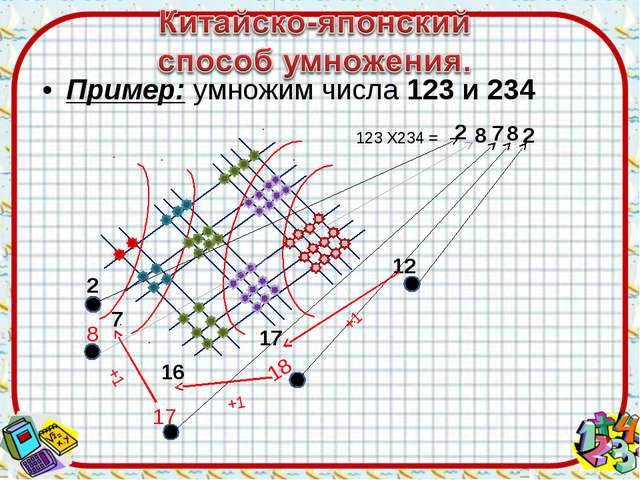 Это и есть искомое произведение. [3, с.67] Дана графическая иллюстрация по данному описанию. ( см. Таблицу 2.)
Это и есть искомое произведение. [3, с.67] Дана графическая иллюстрация по данному описанию. ( см. Таблицу 2.)
Таблица 2.
Квадрат Пифагора.
1 2 3
4 5 6
7 8 9
Это всем известный Квадрат Пифагора, отражающий мировую систему счисления, состоящую из девяти цифр: от 1 до 9. Выражаясь современным языком – это девяти разрядная числовая матрица, в которой цифры, являющиеся основой для дальнейших вычислений любой сложности расположены в порядке возрастания. Квадрат Пифагора называют и Эннеадой, а тройку цифр — триада. Можно рассматривать тройки цифр расположенные по горизонтали (123, 456, 789) и по вертикали(147, 258, 369). Причем, записанные таким образом, тройки цифр начинают обозначать уже особые числа, подчиняющиеся законам математической пропорции и гармонии.
Вспомним главное правило древнеегипетской математики, в котором сказано, что умножение производится при помощи удвоения и сложения полученных результатов; то есть каждое удвоение есть сложение числа с самим собой. Поэтому интересно посмотреть на результат подобного удвоения цифр и чисел, но полученному современным методом складывания « в столбик», известному даже в начальных классах школы. Это будет напоминать египетскую систему счисления, по сути, с разницей в том, что все цифры либо числа записываются в один столбик (без указания того или иного действия в соседнем столбике — как у египтян). [4, с.97]
Поэтому интересно посмотреть на результат подобного удвоения цифр и чисел, но полученному современным методом складывания « в столбик», известному даже в начальных классах школы. Это будет напоминать египетскую систему счисления, по сути, с разницей в том, что все цифры либо числа записываются в один столбик (без указания того или иного действия в соседнем столбике — как у египтян). [4, с.97]
Начнем с цифр, составляющих Квадрат Пифагора: от 1 – до 9.
1 2 3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
3 6 9 12 15 18 21 24 27
4 8 12 16 20 24 28 32 36
5 10 15 20 25 30 35 40 45
6 12 18 24 30 36 42 48 54
7 14 21 28 35 42 49 56 63
8 16 24 32 40 48 56 64 72
9 18 27 36 45 54 63 72 81
10 20 30 40 50 60 70 80 90
Цифра 1: обычный последовательный ряд цифр.
Цифра 9: левый столбик — четкий восходящий ряд («поток»).
правый столбик — четкий нисходящий ряд последовательных цифр. Условимся называть восходящим ряд, значения чисел в котором увеличиваются сверху вниз ; в нисходящем же – наоборот: уменьшаются значения чисел сверху вниз.
Условимся называть восходящим ряд, значения чисел в котором увеличиваются сверху вниз ; в нисходящем же – наоборот: уменьшаются значения чисел сверху вниз.
Цифра 2: в правом столбике повторяются четные цифры 2,4,6,8 («в периоде»).
Цифра 8: такой же повтор — только в обратном порядке- 8,6,4,2.
Цифры 4 и 6: четные цифры «в периоде» 4,8,2,6 и 6,2,8,4.
Цифра 5: подчиняется правилу сложения цифры 5- чередование 5 и 0.
Цифра 3: правый столбик — нисходящий ряд уже не цифр, а чисел, образующих тройки вертикальных рядов в квадрате Пифагора- 369, 258, 147. Причем, отсчет идет «из правого угла квадрата» или справа налево. Здесь также действует принятое выше правило восходящего — нисходящего ряда. Но восходящий ряд – это движение от тройки чисел 147 до тройки 369; нисходящий — от 369 до 147.
Цифра 7: восходящий ряд чисел 147,258,369 из «левого угла» или слева направо. Впрочем, все зависит от того, как изображена сама девятиразрядная числовая матрица — где поставить цифру 1.
Китайский способ умножения.
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 13 на 24. Начертим следующий рисунок:
Этот рисунок состоит из 10 линий (количество может быть любым)
Эти линии обозначают число 24 (2 линии, отступ, 4 линии)
А эти линии обозначают число 13 (1 линия, отступ, 3 линии)
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим способом: (пересечения на рисунке указаны точками)
Количество пересечений:
Верхний левый край: 2
Нижний левый край: 6
Верхний правый: 4
Нижний правый: 12
1) Пересечения в верхнем левом крае (2) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (6+4) – второе число ответа
3) Пересечения в нижнем правом крае (12) – третье число ответа.
Получается: 2; 10; 12.
Т.к. два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему.
3(2+1)1(0+1)2
Ответ: 312 [5, с.48]
Итальянский способ умножения.
В Италии, а также во многих странах Востока, этот способ приобрел большую известность. [5, с.74]
Использование приема:
Например, умножим 6827 на 345.
Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
Умножаем число каждого ряда последовательно на числа каждой колонки.
т.е.
6*3 = 18. Записываем 1 и 8
8*3 = 24. Записываем 2 и 4
Если при умножении получается однозначное число, записываем вверху 0, а внизу это число.
(Как у нас в примере при умножении 2 на 3 получилось 6. Вверху мы записали 0, а внизу 6)
Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Ответ: 2355315.
Таблица Оконешникова.
Рис.1. Таблица Оконешникова
Умножение не стоит на месте, о чем доказывает новый способ умножения, который разработал Василий Иванович Оконешников. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе и «теперь ребята смогут умножать и складывать в уме не только единицы, десятки, но также миллионы, триллионы и даже, не пугайтесь, секстиллионы с квадриллионами»При этом каждая кнопка делится еще на 9 квадратов, в которой записываются результаты перемножения числа данной кнопки на числа от одного до девяти, т.е. получаем своеобразную таблицу умножения. Данный метод имеет ограничение — умножение делается на однозначное число. Например, найдем произведение чисел 148 и 4. Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке. Получаем: 04 16 32. Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами. [8, с.32]
Для этого обратимся к квадрату соответствующему четверке, выбираем числа, соответствующие цифрам числа по порядку: единице, четверке, восьмерке. Получаем: 04 16 32. Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие складываем попарно: четверку с единицей, шестерку с тройкой.. Последняя цифра также без изменений. 0(4 + 1)(6+3)2 = 0592. Число 592 и есть результат умножения. Произведя расчет по методу Василия Ивановича Оконешникова при умножении многозначного числа на однозначное, этот метод достаточно прост и быстр, если имеется готовая таблица в уме или перед глазами. [8, с.32]
Индийский способ умножения.
В древней Индии применяли два способа умножения: сетки и галеры. На первый взгляд они кажутся очень сложными, но если следовать шаг за шагом в предлагаемых упражнениях, то можно убедиться, что это довольно просто.
Умножаем, например, числа 6827 и 345:
1. Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток.
В предложенном примере можно использовать одну из этих сеток.
Сетка 1 Сетка 2
2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке.
Сетка 1
3. Посмотри, как выглядит сетка со всеми заполненными клетками.
Сетка 1
4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.
Сетка1
Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315. [8, с.65]
Египетский способ умножения.
Древнеегипетское умножение является последовательным методом умножения двух чисел.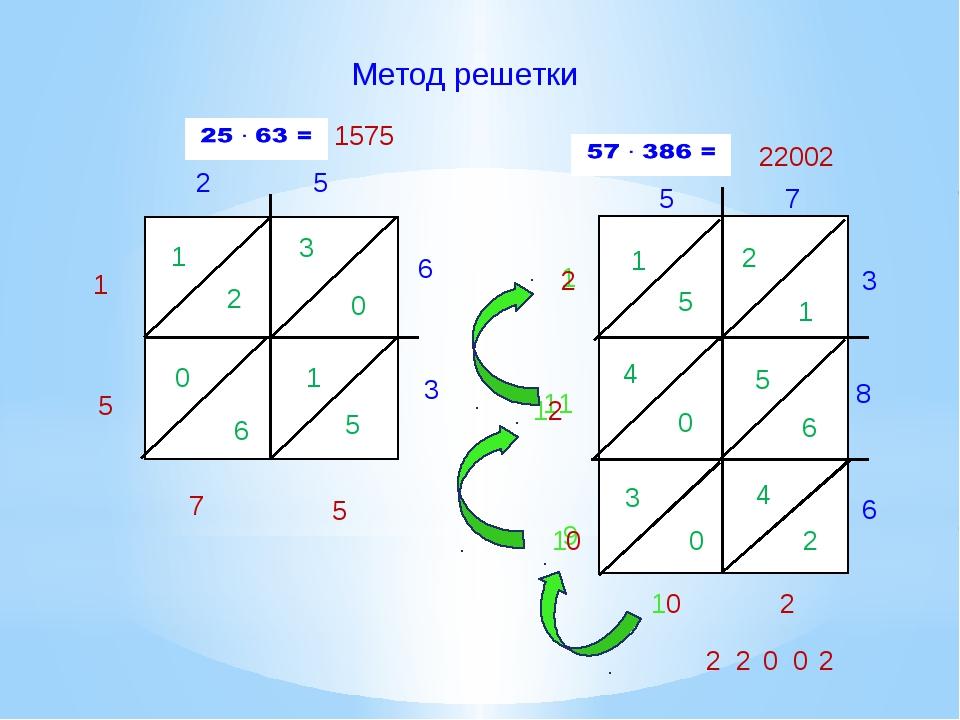 Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах.
Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать. Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное перемножение на второй множитель (см. пример). Этот метод можно и сегодня встретить в очень отдаленных регионах.
Разложение. Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число.
Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений:
1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32
Пример разложения числа 25: Кратный множитель для числа «25» — это 16; 25 — 16 = 9. Кратный множитель для числа «9» — это 8; 9 — 8 = 1. Кратный множитель для числа «1» — это 1; 1 — 1 = 0. Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1. [9, с.28]
[9, с.28]
Пример: умножим «13» на «238» . Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: ✔ 1 х 238 = 238 ✔ 4 х 238 = 952 ✔ 8 х 238 = 1904
13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 =1904 + 952 + 238 = 3094.
Заключение
Существует много различных, забавных и интересных способов умножения чисел, но не все они удобны в использовании. Из всех найденных мною необычных способов счета более интересным и простым показался мне «Итальянский способ».
Я показал некоторые способы умножения своим одноклассникам, и многие очень заинтересовались необычными вычислениями.
Работая над этим проектом, я пришла к выводу, что самый простой и привычный способ умножения, это тот, который мы изучаем в школе. А чтобы пользоваться этим способом, нужно всем знать наизусть таблицу умножения!
Список литературы и Интернет — ресурсы
1. 1. Арутюнян Е., Левитас Г. Занимательная математика. — М.: АСТ — ПРЕСС, 1999. — 368 с.1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. — ЛКИ ,2012.-208 с.1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.1.4. Ликум А. Все обо всем. Т. 2. — М.: Филологическое общество «Слово», 1993. — 512 с.1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.1.6. Перельман Я.И. Занимательная арифметика. — М.: Русанова, 1994 – 205с.1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. — М.: Детская литература, 1998 — 175 с.1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.2. Другие источники информацииИнтернет – ресурсы: 2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс]
1. Арутюнян Е., Левитас Г. Занимательная математика. — М.: АСТ — ПРЕСС, 1999. — 368 с.1.2. Беллюстина В. Как постепенно дошли люди до настоящей арифметики. — ЛКИ ,2012.-208 с.1.3. Депман И. Рассказы о математике. – Ленинград.: Просвещение, 1954. – 140 с.1.4. Ликум А. Все обо всем. Т. 2. — М.: Филологическое общество «Слово», 1993. — 512 с.1.5. Олехник С. Н., Нестеренко Ю. В., Потапов М. К.. Старинные занимательные задачи. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.1.6. Перельман Я.И. Занимательная арифметика. — М.: Русанова, 1994 – 205с.1.7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л.: Лениздат, 1941 — 12 с. 1.8. Савин А.П. Математические миниатюры. Занимательная математика для детей. — М.: Детская литература, 1998 — 175 с.1.9. Энциклопедия для детей. Математика. – М.: Аванта +, 2003. – 688 с.2. Другие источники информацииИнтернет – ресурсы: 2.1. Корнеев А.А. Феномен русского умножения. История. [Электронный ресурс]
Приложение 1
Анкетирование
Мною было проведено анкетирование учащихся 5а класса, в котором приняли участие 25 человек.
На основании анкетирования выявлено, что все опрошенные умеют умножать традиционным способом, а вот о нетрадиционных способах умножения большинство ребят не знают. И есть желающие познакомиться с ними.
Вопросы в анкете были следующие:
Когда была неделя математики в нашей школе, видели ли вы мою стенгазету о разных способах умножения?
Рис.2. Круговая диаграмма. Опрос учащихся к 1-му вопросу
Ответ: да – 20 человек, нет – 5 человек.
Знаете ли вы нетрадиционные способы умножения? Приведите пример.
Рис.3. Круговая диаграмма. Опрос учащихся к 2-му вопросу
Ответ: знают – 7 человек, не знают – 18 человек.
Хотели бы вы научиться нетрадиционным способам умножения?
Рис.3. Круговая диаграмма. Опрос учащихся к 3-му вопросу
Ответ: хотят – 19 человек, не хотят – 6 человек.
Приложение 2
Сравнение результатов по вычислению примеров (по эффективности затраченного времени)
|
Время, за которое мне и моим одноклассникам удалось решить один и тот же пример разными способами |
||||
|
Китайский способ |
Таблица Оконешникова |
Итальянский способ |
Столбик |
|
|
Я |
56 секунд |
30 секунд |
25 секунд |
8 секунд |
|
Ученик №1 |
58 секунд |
32 секунд |
28 секунд |
10 секунд |
|
Ученик №2 |
1 минута 6 секунд |
50 секунд |
42 секунды |
10 секунд |
|
Ученик №3 |
1 минута 10 секунд |
56 секунд |
48 секунды |
11 секунд |
|
Ученик №4 |
1 минута 25 секунд |
1 минута |
55 секунд |
12 секунд |
Вывод: самым эффективным способом умножения является умножение столбиком.
Приложение 3
Моя работа на неделе математики в школе
Приложение 4
Памятка для учащихся
Просмотров работы: 4035
Урок 6. Умножение в уме любых чисел до 100
Чтобы умножать любые числа до 100 в уме важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее удобные случаи для каждой методики умножения.
Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).
Универсальные методики
Применимость универсальных методик умножения чисел до 100 такова:
Использование одного опорного числа (Урок 5):
- все числа в диапазонах до 30, 40-60, 85-100 – если оба множителя рядом с опорным числом.
Например: 13*17, 18*23, 29*22, 53*61, 88*97 и т.д.
- если одно число очень близко к удобному опорному (+/- 3 от 10, 20, 50, 100), второе может быть любым.

Например: 21*67 (21 близко к 20), 48*33 (48 близко к 50), 98*32 (98 близко к 100)
Использование двух опорных чисел (Урок 5):
- Если одно опорное число является кратным другому и если одно из опорных чисел является удобным (10, 20, 50, 100)
Например: 98*24, 12*44, 43*103, 23*62
Иные числа удобно умножать традиционными методами из третьего урока, когда разряды десятков и единиц не очень большие (Урок 3). Кроме того, традиционный метод удобен, когда вы не знаете, какой другой метод вам применить.
- Например: 42*32 = 12 (2*4+3*2) 4 = 1344
Частные методики
Также полезно помнить о частных методиках, существенно упрощающих решение некоторых примеров:
Умножение на 10, 20, 25, 50 – должно осуществляться практически на автомате (Урок 2):
- Например: 88*25 = 2200 (деление на 4)
Умножение на 11 всегда по методике из урока 4
- Например: 57*11= 5 (5+7) 7 = 627
Числа, заканчивающиеся на 5 удобно возводить в квадрат по методу из четвёртого урока
- Например: 65*65 = (6*7)25 = 4 225
Любые числа удобно возводить в квадрат используя формулы сокращенного умножения четверного урока
- Например: 69*69 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Теперь, вы имеете серьезный алгоритмический аппарат для решения примеров на умножение чисел до 100. Кроме того, вы уже можете умножать и некоторые примеры с множителями больше 100. Главным фактором, влияющим на вашу способность умножать в уме, в дальнейшем должен стать опыт и тренировка. Пройти тренировку можно ниже.
Кроме того, вы уже можете умножать и некоторые примеры с множителями больше 100. Главным фактором, влияющим на вашу способность умножать в уме, в дальнейшем должен стать опыт и тренировка. Пройти тренировку можно ниже.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Cтатистика На весь экран
Евгений Буянов
← 5 Опорное число7 Возведение в квадрат →
1PRO
Ненавижу математику? Эти умственные трюки заставят вас умножать быстрее, чем когда-либо мог Эйнштейн! « Взлом разума :: WonderHowTo
- org/Person»> By Осас Обайза
2 + 2 = 4.
Это примерно столько, сколько я могу ежедневно обрабатывать без калькулятора. Я буквально ненавижу заниматься математикой больше всего на свете, в основном потому, что у меня плохо получается, и я ненавижу заниматься тем, в чем не силен.
Итак, когда я натыкаюсь в сети на классный математический трюк, который, как утверждается, облегчает жизнь таким людям, как я, я внимательно слушаю. В то время как исчисление (в основном) бесполезно для повседневной жизни среднего человека, умножение, сложение, вычитание и проценты — это все, что мы должны уметь делать — и без калькулятора.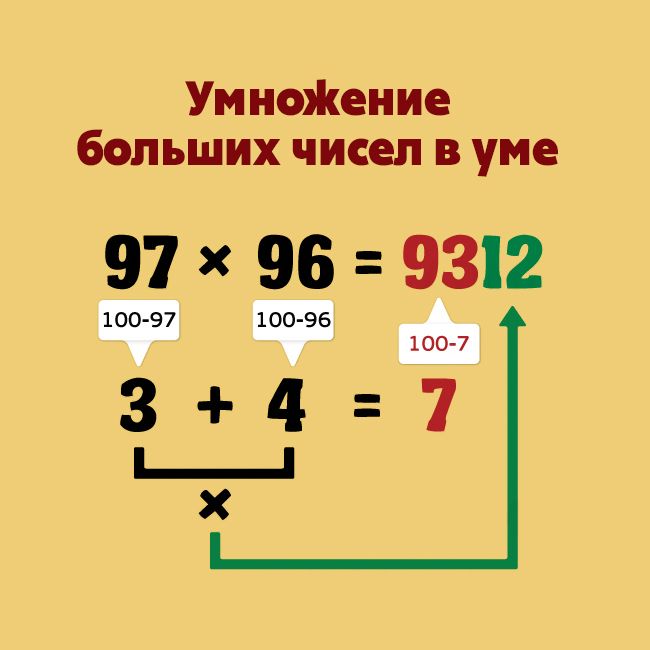
Как большой поклонник TED Talks, я наткнулся на следующее видео Gaurav Tekriwal, демонстрирующее преимущества так называемой ведической математики, которая представляет собой базовый набор стратегий, помогающих упростить сложные вычисления.
Хотя происхождение этих учений несколько загадочно, стратегии весьма эффективны, и я буду помнить их каждый день. Может быть, математика не так уж и сложна?
Вот некоторые советы и рекомендации.
Как умножать двузначные числа на 11
Моя таблица умножения остановилась на 10, так что кроме этого, я произвожу вычисления, основываясь на своей памяти или считаю в уме. Однако, используя ведическую математику, умножить на 11 проще простого.
Однако, используя ведическую математику, умножить на 11 проще простого.
Все, что вам нужно сделать, это сложить цифры числа, которое вы умножаете на 11, и поместить это в середину исходного числа. Если сумма цифр 10 или больше, просто перенесите ее. Лучше увидеть, чем мне написать.
Видите, как это было просто? По сути, если вы знаете, как складывать, вы знаете, как умножать на 11.
Теперь давайте рассмотрим другой пример.
- 11 x 11
Просто разделите число, умноженное на 11 (в данном случае также 11 ), чтобы между ними было место для вашего номера. Теперь просто сложите две цифры этого числа вместе ( 1 + 1 = 2 ) и бросьте сумму в то место, которое вы оставили открытым. Это дает вам 121 .
- 58 x 11
Просто добавьте 5 + 8 , что даст вам 13 . Вставьте его между 5 и 8 , и вы получите 5138 . Но это неправильно, так как вам нужно нести это. Идите вперед и перенесите его, и вы получите 638 .
Но это неправильно, так как вам нужно нести это. Идите вперед и перенесите его, и вы получите 638 .
Излишне говорить, что теперь, когда я знаю это, я чувствую себя полным задирой.
Как умножать числа, близкие к степени 10
В этом базовом методе используются степени 10 (десятки, сотни, тысячи и т. д.), а также перекрестное вычитание и умножение сумм. Опять же, гораздо лучше видеть то, что я говорю, чем пытаться это прочитать. Вот пример умножения двух двузначных чисел (по основанию сотен).
То, что делает Гаурав, на самом деле довольно простое.
- 99 x 97
Он берет разность каждого числа от 100 и помещает эти числа в правый столбец ( 99 — 100 = -01 и 97 — 100 = -03 ).
Затем он складывает один набор чисел (подходит любая пара), чтобы получить первое число ответа. Итак, 99 + -03 или 97 + -01 = 96 .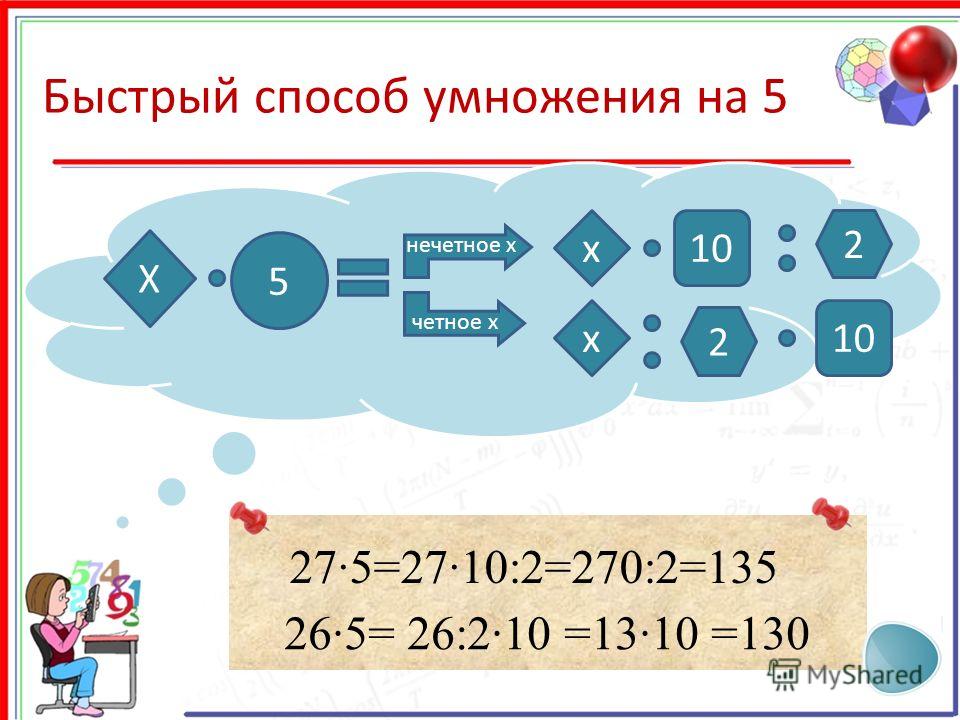 Итак, это будет первая часть ответа.
Итак, это будет первая часть ответа.
Теперь умножьте два меньших числа ( -01 x -03 ), чтобы получить вторую часть ответа. -01 х -03 = 03 . Таким образом, получается ответ 9603 .
Круто, правда?
Этот же метод работает для любого основания десяти. 999 x 987 или 9 878 x 9 999 будут работать с базой 1000 и 10 000 соответственно. Вы можете увидеть это на отметке 3:45 в видео.
Как умножить двузначное число на любое другое двузначное число
Самое интересное в математике — наблюдать за тем, как, казалось бы, невозможные комбинации в конце концов выходят идеально. Выполняя определенные операции, вы можете превратить чрезвычайно сложные уравнения в простые пошаговые решения.
Используя схему «Вертикально и крестообразно», мы можем легко умножать большие двузначные числа, подобные изображенному ниже.
Вместо постоянного метода умножения мы будем разделять и властвовать.
- 12 x 34
Сначала умножаем вертикально вверх правую сторону. 2 х 4 = 8 . Итак, 8 будет последней цифрой в нашем ответе.
Далее перекрестно умножаем. 3 х 2 = 6 и 4 х 1 = 4 . Теперь добавьте 6 + 4 , чтобы получить 10 . Перенесите 1 , как обычно, и у вас останется 0 , который будет стоять перед 8 , который у нас уже есть.
Итак, на данный момент в строке ответа должно быть 08 .
Наконец, мы вертикально умножаем левую сторону. 3 x 1 = 3 и добавить переносимое 1 . Поместите это перед нашей строкой ответа, и мы получим 408 9.0005 .
Как умножать, используя линии вместо чисел
Если вы предпочитаете визуальное обучение и действительно ненавидите числа, вы также можете полностью использовать их на японском языке и заменить эти цифры линиями, как это делает YouTuber kimelicious. Я не собираюсь объяснять это — просто посмотрите, и вы увидите.
Я не собираюсь объяснять это — просто посмотрите, и вы увидите.
Вы уже не любите математику?
Есть несколько действительно удивительных математических трюков, использующих математику в ведическом стиле, поэтому не забудьте посмотреть полное видео, чтобы получить более четкое представление об этом и начать использовать его в своей повседневной жизни.
А у тебя есть свои крутые математические трюки? Дайте нам знать в разделе комментариев.
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.
Купить сейчас (скидка 97%) >
Другие выгодные предложения:
- Скидка 97 % на The Ultimate White Hat Hacker Certification Bundle 2021
- Скидка 98 % на комплект Accounting Mastery Bootcamp 2021
- Пакет
- Скидка 59 % на XSplit VCam: пожизненная подписка (Windows)
- Скидка 98 % на сертификационный комплект Premium Learn To Code 2021
- Скидка 62 % Программное обеспечение MindMaster Mind Mapping: Бессрочная лицензия
- Скидка 41 % NetSpot Home Wi-Fi Analyzer : Пожизненные обновления
7 комментариев
- Горячий
- Последние
хитростей и советов по умственному умножению, чтобы быстрее считать в уме
Приемы и советы по умножению в уме, приведенные в этом посте, позволят вам выполнять вычисления в уме быстрее, чем калькулятор, полностью действующий у вас в голове. Существует много умственных стратегий умножения, но рассмотренные здесь стратегии умственного умножения можно применять для умножения любого набора чисел. Изучение советов по умственному умножению в этом посте будет похоже на обучение езде на велосипеде. Однажды выучив его, действительно очень трудно его забыть.
Существует много умственных стратегий умножения, но рассмотренные здесь стратегии умственного умножения можно применять для умножения любого набора чисел. Изучение советов по умственному умножению в этом посте будет похоже на обучение езде на велосипеде. Однажды выучив его, действительно очень трудно его забыть.
Прежде чем мы продолжим, вы должны освоить умножение однозначных чисел. Обязательным условием является знание таблицы умножения однозначных чисел от 1 x 1 до 9.x 9, прежде чем мысленно умножать большие числа. Если вы немного заржавели, добавьте этот пост в закладки и убедитесь, что вы сначала выучили свою таблицу умножения с одной цифрой. Если вы хорошо разбираетесь в умножении однозначных чисел, можете читать дальше.
Этот пост является второй частью серии математических трюков в уме. Настоятельно рекомендуется прочитать первый пост этой серии — Уловки ментальной арифметики для быстрой математики, прежде чем приступить к изучению того, как выполнять ментальную арифметику в умножении.
Секрет трюков с умножением в уме
В первой части «Уловок с ментальной арифметикой» мы узнали, что вычисление в уме становится труднее, если считать справа налево. Следовательно, секрет ментальной арифметики заключается в том, чтобы делать наоборот и вместо этого считать слева направо. Решая слева направо, вы начнете называть ответ, прежде чем закончите полный расчет. Вычисление слева направо поначалу может показаться немного странным, но после небольшой практики оно станет естественным. В этом посте мы увидим, как применить это к умственному умножению.
Что такое множимое и множитель?
Прежде чем мы приступим к умножению в уме, давайте быстро определим, что такое множимое и множитель. Возьмем, к примеру, задачу на умножение 43 x 23. Здесь число 43 является множимым — числом, которое нужно умножить. Число 23 — это множитель — число, на которое умножается первое число.
В этом посте есть несколько трюков с умножением для ментальной арифметики. Каждый метод мысленного умножения будет иметь два примера. Первый пример, видимый всем, познакомит вас с трюком умножения. Второй пример, видимый только вошедшим в систему пользователям, будет иметь варианты, не описанные в первом примере. Так что войдите или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.
Каждый метод мысленного умножения будет иметь два примера. Первый пример, видимый всем, познакомит вас с трюком умножения. Второй пример, видимый только вошедшим в систему пользователям, будет иметь варианты, не описанные в первом примере. Так что войдите или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.
Трюки с умножением для однозначного числа
Общее умное умножение для однозначного множителя
Общий метод умственного умножения заключается в умножении слева направо. Хотя общий метод можно применять для любого числа, лучше всего он работает, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельная техника для чисел, оканчивающихся на 7, 8 и 9. А пока давайте применим метод умственного умножения для умножения 5321 x 4.
Правило простое. Умножать слева направо. Одна цифра за раз.
Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньшее количество чисел, чтобы потом их вспомнить и использовать. Вы сразу начнете называть ответ с самого первого шага расчета.
Вы сразу начнете называть ответ с самого первого шага расчета.
Теперь попробуйте умножить 7142 x 6. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение в уме с округлением до 1-значного множителя
Использование приемов умножения в уме после округления полезно, когда числа заканчиваются на 7, 8 или 9. Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножьте 68 x 3.
1. Округлите число
2. Умножьте слева направо
3. Умножьте округленную сумму
4. Вычтите числа из двух предыдущих шагов
Если вы попытаетесь сделать так, как вы обычно делаете это на бумаге, вы поймете, что это занимает больше времени, чем то, что вам нужно сейчас, чтобы сделать это в своей голове. Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы для умственного умножения, которые вы можете скачать и попрактиковаться.
Теперь попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение в уме двузначных чисел
Общие приемы умножения
Давайте теперь посмотрим, как выполнять умножение в уме для теперь двухзначные числа. Трюки с умножением, которые мы видели ранее, нужно немного изменить. Давайте посмотрим, как это сделать на примере. Умножить 36 x 32.
1. Разбить множимое
2. Умножить слева направо
3. Сложите отдельные ответы вместе, чтобы получить окончательный ответ
Вы можете решить ту же проблему, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Попробуйте выбрать число с меньшей цифрой, потому что в большинстве случаев это обычно приводит к тому, что вы добавляете меньшие числа.
Теперь попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Округление для двузначного множителя
Как и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:
Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:
1. Округлить число
2. Умножить округленное значение и сумму, округленную слева направо
3. Вычесть два числа
Теперь попробуйте умножить 41 x 57. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Умножение в уме с использованием коэффициентов
Как и при округлении, один из приемов умножения заключается в том, чтобы перед умножением числа разложить его на множители. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22.
1. Разложить число на множители
2. Умножить число на первый множитель (слева направо)
4. Умножить произведение на второй множитель (слева направо)
В трюках с умножением, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы сложить/вычесть произведение второй цифры. Однако при умственном умножении с использованием множителей вы просто умножаете второй множитель на первый продукт, поэтому вам не нужно запоминать столько чисел, сколько вы вычисляете.
Теперь попробуйте умножить 21 x 63, используя метод множителей. Процедура такая же, как и раньше, и вы можете найти ее ниже:
Упражнения по умножению в уме
Ниже вы можете загрузить рабочие листы по умножению в уме в формате PDF, чтобы применить описанные приемы умножения.
Стать человеком-калькулятором
Вы изучили основные приемы умножения. Но Мы коснулись только поверхности, и еще многое предстоит осветить. Если вы действительно хотите стать человеком-калькулятором и вывести свои математические способности в уме на новый уровень, посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я добился того, что имею сегодня. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к мастерству ментальной математики. Чтобы посмотреть видео кликните здесь.
Заключение
Вопросы, уточнения и отзывы оставляйте в комментариях. Потребуется практика, прежде чем применение трюков с умножением станет легким и легким.
