Решение ребусов и логических задач: Математические ребусы для 4 класса с ответами и решениями — Яркий Дворик

Содержание

Решение логических задач — как решать задачи на логику

Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.

Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.

Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.

Самое главное в решении логических задач

Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.

Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.

Все задачи на развитие логики можно разделить на группы:

Математические ребусы;
Задачи на истинность утверждений;
Задачи на перемещение, взвешивание или переливание;
Задачи, которые решаются с конца;
Работа с множествами;
Задачи на сопоставление «Кто есть кто?»

Выбор способа решения зависит от того, к какой группе относится задание.

Известные техники решения логических задач

Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):

таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы.
Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.

Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.

Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:

Табличный метод

Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.

Задача:

У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?

Решение:

Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:

1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).

8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).

Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).

Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.

Круги Эйлера

Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.

Задача:

Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?

Решение:

Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.

1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».

Ответ: 5 человек.

Метод рассуждений

Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.

Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?

Решение:

1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.

Ответ: голубая ваза.

Метод рассуждений «с конца»

Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.

Задача:

Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?

Решение:

1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы

Ответ: 27, 48 и 50 лет.

Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.

Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».

Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере

Поробуйте решить задачу Умназии прямо сейчас!

Попробовать

Математика

Умназисты соревновались в поедании пирожков.

Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.

Посмотри на информацию о соревнующихся на рисунке. Можешь ли ты сказать, кто из умназистов занял почётное третье место?

Выбери ответ:

Третье место заняла Ума Коала.

Третье место занял Мышлен.

Третье место занял Грамотигр.

Третье место занял Ква-Квариус.

Третье место заняла Сообразебра.

ответить

Логика решения:

Мы знаем, что Мышлен ел по 1 пирожку в минуту, значит за 45 минут соревнования он съел 45 пирожков (1 х 45 = 45).

Если Мышлен съел на 10 пирожков больше, чем Сообразебра, то Сообразебра съела 35 пирожков (45 – 10 = 35).

Если Ума-Коала съела на 5 пирожков меньше, чем Сообразебра, то Ума-Коала съела 30 пирожков (35 – 5 = 30).

Чтобы выяснить, сколько съели Грамотигр и Ква-Квариус, сложим все пирожки, которые съели Мышлен, Ума-Коала и Сообразебра. Получается 45 + 35 + 30 = 110 пирожков.

От общего количества съеденных пирожков вычтем съеденное тремя умназистами: 179 – 110 = 69. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.

Из условия мы знаем, что Грамотигр съел пирожков в 2 раза больше, чем Ква-Квариус.

Допустим, Ква-Квариус съел 23 пирожка, тогда Грамотигр съел в два раза больше, то есть 23 х 2 = 46 пирожков.

Теперь снова сложим их пирожки, чтобы проверить себя: 23 + 46 = 69. Сходится.

Значит, Грамотигр (46 пирожков) занял первое место, Мышлен (45 пирожков) – второе, а Сообразебра (35 пирожков) – третье.

Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:

1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?

Ждем вас, будет весело и интересно!

Развитие логики у детей 7-10 лет

Развиваем критическое нестандартное мышление, учим работать с информацией и принимать верные решения

узнать подробнее

Читайте также:

Решение логических задач и ребусов.

Конспект урока: Решение логических задач и ребусов.

Цели: рассмотреть понятие логические задачи, основные способы решения таких задач, выяснить для чего они применяются.

Задачи:

1. Познакомиться с понятием логических задач

2. Рассмотреть способы решения логических задач

3. Привести примеры логических задач, загадок, ребусов и головоломок

4. Сделать вывод

Ход урока

1 Орг. Момент. Психологический настрой «Похвали себя»

Я предлагаю вам очень интересную разминку. Называется она необычно – «Похвали себя». Похвалить же себя нам поможет волшебное зеркало. При этом каждый, у кого будет находиться волшебный предмет, будет хвалить себя. Прошу вас не стесняться. Давайте игру начнем с меня. «Я, хочу похвалить себя и сказать, что я очень умная и добрая, всегда прихожу на помощь своим ученикам и их родителям, а также другим людям».

Решите примеры.

20+10 2Х5 100-50 12:3

45 +15 3Х3 47-7 130:10

32+60 8Х4 90-70 72:8

23+50 6Х10 12-7 56:7

84+6 5Х9 86-6 32:4

99+1 7Х8 55-15

Кто решал примеры на сложение и на умножение 1 группа, на

Деление и на вычитание 2 группа. Деление на группы : 1группа-« Круг», 2группа- «Квадрат»

2.Представление команд:
Учитель. Сегодня в нашем соревновании участвуют две команды.

Команды по очереди дружно говорят своё название и девиз
1.»Круг» Наш девиз: «В кругу друзей лучше считать, легче решать и побеждать!»

4.»Квадрат» Наш девиз: «У нашего квадрата все стороны равны. Наши ребята дружбой сильны».

Сегодня, ребята, мы побываем в мире математики. Вы увидите, как разнообразен и увлекателен этот мир. А для чего надо изучать математику?

Сегодня на занятии мы с вами будем решать логические задачи, отгадывать ребусы.

-Вам нужно было узнать , что такое ребус? Что значить логическая задача? (ответы детей)

Ребус — это загадка, в которой вместо слов или части слова поставлены знаки, нарисованы предметы, которые помогают прочитать весь ребус. Предлагается три ребуса:

На обратной стороне открываются слова: СЧИТАТЬ, РЕШАТЬ, ОТГАДЫВАТЬ

— Так какие слова были зашифрованы в ребусах?

— Правильно. Эти слова будут девизом нашего занятия.

1.Конкурс «Разминка».

Кто знает ответ на вопрос, поднимает руку.

1 Ребята измеряли шагами длину игровой площадки. У Лизы получилось 25 шагов, у Полины – 27, у Максима – 22, а у Юры – 24.
У кого из ребят самый короткий шаг? Ответ: У Полины.

2. Назови наибольшее двухзначное число? (99)

3.Запиши число 7 при помощи четырех троек и знаков действий.
Найди несколько решений.
Ответ: (7 = 3 : 3 + 3 + 3, 7 = 3 + 3 + 3 : 3, 7 = 3 + 3 : 3 + 3)

4 На столе лежало 4 яблока. Одно из них разрезали пополам. Сколько яблок осталось? (4)

5. Сколько кг в центнере?(100)

6.Начерти квадрат периметром 12 см. Затем дополни его до прямоугольника периметром 16 см. Вычисли стороны прямоугольника.

2. Конкурс Кто это или что это»

Рыбок дома держат в нем, что это за водоем? (Аквариум.)
Как зовем мы человека, что зимой ползет он в реку? (Морж.)
Ствол дерева покрывает и надежно защищает? (Кора.)
Если месяцев двенадцать, как им вместе называться? (Год.)
Служит он на корабле, его узнаешь на земле: на голове фуражка, а на груди – тельняшка. (Моряк.)
По реке плывет бревно, ох и злющее оно! Тем кто в речку угодил, нос откусит… (Крокодил.)
Он в телевизоре сидит и четко, ясно говорит, все новости он вам расскажет. (Диктор.)
Какое колесо не вращается при движении (запасное)

3Конкурс «Размышляй-ка».

1. Из 12 палочек сложили 5 квадратов. Уберите две палочки так, чтобы остались только два разных по величине квадрата.

2.Дана фигура необходимо сосчитать, сколько треугольников в ней .

4.Конкурс «Считать умею , не собьюсь»

5. Конкурс «Математические ребусы»

Каждой команде предлагается математический ребус в картинках. Решить ребус и назвать ответ.

Домашнее задание придумать ребус с цифрами и положить в «корзину идей».

6. Конкурс «Побеждай-ка».

Задачки-шутки.

— На березе росло 90 яблок. Подул сильный ветер, и 10 яблок упало. Сколько осталось?
Ответ: На березе яблоки не растут.

-Под каким деревом сидит заяц, когда идет дождь?
Ответ: Под мокрым.

— Из какой посуды нельзя ничего поесть?
Ответ: Из пустой.

— Куда идет цыпленок, переходя дорогу?
Ответ: На другую сторону дороги.

— Если пять кошек ловят пять мышей за пять минут, то, сколько времени нужно одной кошке, чтобы поймать одну мышку?
Ответ: Пять.
— Сколько месяцев в году имеют 28 дней?
Ответ: Все 12, т.к. если в месяце 30 дней, то и 28 дней среди них есть.

— Что бросают, когда нуждаются в этом, и поднимают, когда в этом нет нужды?
Ответ: Якорь (морской, а не ресурсный)

-Можно ли зажечь спичку под водой?
Ответ: Если ты в подводной лодке, то да.

-Как спрыгнуть с десятиметровой лестницы и не ушибиться?
Ответ: Спрыгнуть с нижней ступеньки. Или положить лестницу на землю.

7Подведение итогов.

Объявление лучшего игрока. Награждение медалью.

Логические задачи, ребусы, загадки и головоломки | Статья:

Логические задачи, ребусы, загадки и головоломки

Задача на логику – это такая задача, для решения которой, как правило, требуется логическое мышление, сообразительность, иногда применение нестандартного мышления, а не специальные знания высокого уровня. Поэтому ее решение поможет вам, как проверить, так и повысить вашу сообразительность, логическое мышление. Логические задачи нужны для того, чтобы развивать логику. Решение логических задач помогает развивать нашу способность к рассуждению, к построению цепочек от общего к частному и наоборот. Задачи на логическое мышление, как правило, требуют не столько большого объема знаний, сколько умения эти знания применить.

Логические задачи можно решать разными способами. Таких приемов несколько, они разнообразны и каждый из них имеет свою область применения. Все логические задачи делятся на определенные группы:

задачи, решаемые с конца
задачи на переливание
задачи на взвешивание

Способы решения логических задач

Магия чисел. Я задумала число, прибавила к нему 5, потом разделила сумму на 3, умножила на 4, отняла 6, разделила на 7 и получила число 2. Какое число я задумала? Решение. Решаем задачу с конца: 1) 2 ∙ 7 = 14 – число до деления на 7. 2) (14 + 6) : 4 = 5 – число до умножения на 4. 3) 5 ∙ 3 = 15 – число до деления на 3. 4) 15 – 5 = 10 – искомое число. Ответ: задумано число 10.

Задача: Отмерить 3 л, имея сосуд 5 л. Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды? Ответ: Наливаем кастрюлю. Переливаем воду из кастрюли в банку. Наливаем кастрюлю. Доливаем полную банку, и в кастрюле остается 3 литра.

Задача: Имеется 8 с виду одинаковых монет. Одна из них фальшивая и известно, что она легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В Вашем распоряжении только лабораторные весы, которые показывают только больше-меньше. Ответ: Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый, то взвешиваем оставшиеся 1 и 1 монеты и выявляем фальшивую (более легкую). Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1 и 1 и действуем по предыдущему алгоритму: если вес одинаков, значит, фальшива третья, а если нет, то та, которая легче.

Загадки – это изображение или выражение, нуждающееся в разгадке. Загадки позволяют разглядеть в самых обычных вещах поэтическую и неожиданную сторону. Также благодаря загадкам можно тренировать смекалку, учиться мыслить логически. Помимо обычных, традиционных загадок, которые основаны на игре слов, есть также шуточные загадки, и кроме этого – головоломки и шарады. Иногда загадка может быть сформулирована в виде прямого, но каверзного вопроса, например, «Что будет козе после семи лет?», ответ будет такой – ей всего лишь пойдёт восьмой год.

Ребусы – это игра, в которой зашифрованы слова, фразы или целые высказывания при помощи рисунков в сочетании с буквами и знаками.

Головоломка — это задача или загадка, для решения которой требуется проявить сообразительность и знания в области, о которой идет речь в головоломке (Перед вами симпатичный спичечный домик. Требуется, передвинув всего две спички, повернуть его к нам другой стороной).

Действительно, существует не один способ решения логических задач. И все эти задачи, ребусы и головоломки тренируют и развивают логическое мышление.

Источники

http://fizmatolimp.ru/zanimatelno2.html

http://festival.1september.ru/articles/609124/

http://ptil2006.narod.ru/weight/answer_weight_08.html

http://fomuvi.ru/zadachki/logical

http://www.treningmozga.com/tasks/logicheskie_zadachi_1_01.html

http://elhow.ru/ucheba/opredelenija/z/chto-takoe-zagadka

http://nazva.net/rubric/16

Ребусы. Логические задачи, головоломки, тесты на интеллект, логические игры

Ребусы — это игра, в которой зашифрованы слова, фразы или целые высказывания при помощи рисунков в сочетании с буквами и знаками. Название образовано от латинского rebus — (вещь, предмет).

Правило 1. Изображенные на рисунках предметы и живые существа чаще всего (за редким исключением) читаются как слова в именительном падеже и единственном числе. Иногда нужный объект на картинке указывается стрелкой.

Правило 2. Если картинка нарисована вверх ногами, читаем слово задом наперед. Например, нарисован вверх ногами кот — читаем ТОК.

Правило 3. Запятые после картинки указывают, сколько букв нужно убрать с конца слова, обозначающего то, что изображено на картинке. Например, нарисована коза с двумя запятыми после нее — читаем КО.

Правило 4. Перевернутые запятые перед картинкой указывают, сколько букв нужно убрать в начале слова, обозначающего то, что изображено на картинке. Например, нарисован слон с запятой перед картинкой — читаем ЛОН.

Правило 5. Над картинкой или под ней могут появиться цифры. Каждая цифра — это номер буквы в слове: 1 — первая буква слова, 2 — вторая буква, 3 — третья, и так далее. Определенный набор цифр под или над картинкой говорит о том, что нужно взять только эти буквы и прочитать их в указанном порядке. Перечеркнутая цифра означает, что данная буква должна быть опущена. Например, нарисован конь и цифры 2,1 под ним — читаем ОК. При объединении примеров в правилах 3, 4 и 5 получаем загаданное слово КОЛОНОК.

Правило 6. Знак равенства между буквами означает замену определенной буквы (или сочетания букв) слова на другую букву (или на сочетание букв). Знак равенства может быть заменен на стрелку. Действие замены обозначается и третьим способом — буквы, которые заменяются, перечеркиваются, а над ними пишутся заменяющие. Например, нарисован крот, а рядом перечеркнутые буквы РО и сверху буква И — читаем КИТ.

Правило 7. Буквы могут быть изображены внутри других букв, над другими буквами, под и за ними. В таких случаях необходимо понять, в каких пространственных отношениях состоят изображенные буквы. Например, внутри буквы О нарисованы буквы ЛК — читаем ВОЛК (хотя можно прочесть и как ЛКВО). Сверху написаны буквы АР, снизу ОК — читаем ПОДАРОК (можно было прочесть и ОКПОДАР, НАДОКАР, АРНАДОК — но здесь уж приходится выбирать то, что подходит по смыслу). Впереди написаны буквы ДА, сзади ЧА — читаем ЗАДАЧА.

Правило 8. Буквы могут быть изображены по поверхности других букв. Например, изображена большая буква Н, а по ней разбросаны маленькие И — читаем ПОНИ (хотя можно прочитать и как ИПОН, НИЗИ или ИЗИН). Правило 9. Перечисленные выше приемы могут объединяться друг с другом.

Праздник головоломок

Любители всевозможных шарад, ребусов, нестандартных задач, пазлов и прочих затей, объединенных названием «головоломка», должны знать, что 13 июля, в день рождения венгерского изобретателя, скульптора и профессора архитектуры Эрно Рубика в мире отмечается Международный день головоломки (International Puzzle Day).

Головоломка — непростая задача, для решения которой, как правило, требуется сообразительность, а не специальные знания высокого уровня. При решении головоломки происходит развитие логического и стратегического мышления, пространственного восприятия, памяти, способности к нестандартному взгляду на ситуацию. Головоломки для детей — это не только прекрасный развивающий инструмент, но и — увлекательный способ досуга, благодаря которому ребенок сможет получить настоящее удовольствие от процесса поиска ответа на сложные вопросы.

Задачи, над которыми можно было бы «поломать голову» известны человечеству с глубокой древности. Из различных исторических источников, изображений на стенах египетских пирамид, в древнегреческих манускриптах учёные в наше время находят оригинальные логические задачи.

Эпохой расцвета в средневековой истории головоломок можно считать конец IX века. Рост уровня образования и снижение религиозной нетерпимости к наукам привели к расширению круга любителей логических задач. В это время появилась и первая книга головоломок в Европе — сборник ирландского просветителя Алкуина «Задачи для развития молодого ума». Наиболее широкое распространение головоломки получили на рубеже XIX и XX веков. Благодаря деятельности американца Сэма Лойда и англичанина Генри Дьюдени головоломки проникли во многие периодические издания, стали популярны среди широких слоев населения. Следующим толчком в развитии головоломок стало изобретение в 1974 году венгром Эрно Рубиком знаменитого кубика. Кубик Рубика стал не только игрушкой, но и объектом исследований математиков и инженеров. С тех пор по всему миру регулярно проводятся соревнования по скоростной сборке кубика.

Решение головоломки не приносит, как правило, конкретных знаний, однако дает и малышам, и взрослым гораздо более широкие возможности по восприятию самых разных наук, в частности, математики, геометрии, логики. Гибкость мышления, умение рассматривать проблему под разными углами, развитое воображение — это те качества, которые пригодятся как в обучении, так и в повседневной жизни. Вот почему решение головоломок является одним из самых полезных развлечений для всей семьи.

Праздники 13 июля

Виды головоломок

Гэри Грубер «170 cамых сложных в мире головоломок. Задачи, ребусы и каверзные вопросы для ума» (0+)

В книге известного эксперта по стандартизированным тестам собрано более 170 увлекательных задач, ребусов, головоломок, которые заставят вас хорошенько задуматься и потренировать свой мозг. Головоломки доктора Г. Грубера помогут вам повысить остроту и скорость мышления, научиться работать в условиях многозадачности, принимать верные решения в стрессовых ситуациях. Вам будет значительно проще проходить разного рода тестирование, включая тесты на определение академических способностей, ЕГЭ, тесты для проверки профессиональных способностей и т.д. И, что немаловажно, головоломки могут стать вашим любимым развлечением.

«Новые головоломки Шерлока Холмса» (12+)

Хотите весело и с пользой провести время? Множество оригинальных головоломок: от простейших до самых сложных ждут вас в книге «Новые головоломки Шерлока Холмса»! Разгадывайте задачки, достойные великого физика! Тренируйте свой мозг с помощью увлекательных заданий.

«Головоломки для юных детективов» (6+)

На теплоход проник вор. Супердетективы Макс и Зоя ждут тебя на набережной. Они надеются, что ты поможешь им решить все головоломки и найти преступника. Чтобы успешно справиться с заданием, советуем тебе держать ухо востро, не упускать мельчайших деталей, а главное – действовать как можно осторожнее!

Помоги юным детективам разгадать все загадки и разоблачить преступников. Тебя попросят опознать подозреваемых, проанализировать улики, восстановить картину преступления, выйти на след, взломать коды и вернуть похищенное…

Стань настоящим сыщиком!

А. Н. Ядловский, М. В. Талер, Т. С. Шабан «Головоломки»(6+)

Разгадывать головоломки не только интересно, но и полезно. Эта книга предназначена для юных ценителей логических задач и примеров на сообразительность, умеющих не только учиться, но и веселиться. Приведенные здесь задания разного уровня сложности понравятся и любителям математики, и знатокам из гуманитарных классов. Подобранные в этом издании головоломки помогут в развитии пространственного, абстрактного и креативного мышления, сообразительности, а где-то и интуиции. И, конечно же, оставят ощущение удовольствия от интересно проведенного времени.

Для среднего школьного возраста.

Ирина Парфенова «Лучшие головоломки в дорогу» (6+)

Если ты хочешь весело и увлекательно провести время в дороге, а заодно напрячь свои извилины, то эта книга для тебя! И совершенно не важно, едешь ли ты полчаса в метро или летишь на другой край Земли. Мы собрали самые интересные, забавные и непростые загадки под одной обложкой. Их можно отгадывать в одиночестве, с семьей или друзьями. Отличной дороги!

Михаил Гершензон «Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач» (6+)

Что может быть интереснее и увлекательнее загадок, лабиринтов и головоломок? Ведь иногда простая задачка может завести в тупик и лишить спокойствия на целый день.

Головоломки М. А. Гершензона разнообразны и необычны – это рисунки-лабиринты, оптические иллюзии, загадки по принципу оригами, фокусы, шутки, задания на логику и внимательность. Каждый сможет найти интересную для себя задачу и придумать свое оригинальное решение! Примерьте на себя роль веселого художника или всезнайки, придумавшего собственные загадки, найдите несоответствия и ошибки в обычных художественных текстах, поразмышляйте над головоломками и задачами.

Анна Спектор «Эйнштейновы головоломки для детей»(12+)

Эта книга представляет собой сборник лучших головоломок и задач, решение которых сделало бы честь, пожалуй, и самому Эйнштейну. Здесь есть и веселая компания для их решения. Это обаятельные и неунывающие IQ-детки: озорник Прохор и его рассудительная сестричка Варя. Они уже готовы вступить в шуточное соревнование с читателем на страницах этой книги. Книга будет интересна и детям, и взрослым, которые осознают жизненную необходимость регулярной тренировки интеллекта.

Для среднего школьного возраста.

А. Н. Ядловский, Ирина Никитенко, Т. С. Шабан

«Самые известные головоломки мира» (12+)

Эта книга приглашает всех смекалистых, веселых и находчивых в путешествие по миру головоломок. Разнообразие этого мира безгранично, а национальный колорит придает некоторым из его обитателей особую таинственность. Ведь одно дело разбираться в детективных приключениях в центре европейской столицы, и совсем другое, когда приходится решать запутанную задачу о разделе наследства многодетного султана или торговца верблюдами. Для решения подобных головоломок потребуются логическое мышление, умение концентрироваться, наблюдательность и, конечно же, чувство юмора. Веселые игры, загадочные рисунки, оптические иллюзии – все это вы найдете на страницах данного издания. Уверены, оно поможет каждому освежить умение строить логические цепочки, находить скрытые закономерности, делать выводы и раздвигать границы воображения.

Игоря Сухина «Какуро для детей. Математическая игра-головоломка для будущих отличников» (6+)

Одна из центральных задач любого начального курса математики заключается в том, чтобы довести вычислительные навыки ученика до автоматизма. Новые удивительные возможности предоставляет в этом плане какуро – оригинальная игра-головоломка, пришедшая на смену судоку.

В какуро играет уже весь мир. Но если для пап и мам какуро – нередко лишь забава, то для ребёнка это волшебное средство для развития чувства числа, которое позволит облегчить понимание состава числа и в игровой форме непринуждённо запомнить таблицу сложения.

Для детей дошкольного и младшего школьного возраста, родителей, учителей, методистов и всех любителей головоломок.

В. Г. Дубинский «СПИЧКИ!!!! Новые головоломки»(0+)

Книга содержит новые головоломки со спичками и призвана расширить и усовершенствовать уровень пространственного мышления и отточить нетривиальный подход к решению новых задач. Это очень пригодится в жизни. Рассчитана на широкую аудиторию.

Гарет Мур «100 головоломок для детей на каждый день»(0+)

Книга «100 головоломок для детей на каждый день» содержит огромное количество игр, головоломок и заданий, которые не дадут соскучиться и проверят читателя на сообразительность.

Запутанные лабиринты, логические и математические игры позволят натренировать свой ум и воображение, внимание и быстроту реакции, а главное – весело провести время!

Для младшего школьного возраста.

Гарет Мур «Зачётные головоломки» (6+)

Ну что, вы готовы поломать голову?

В этой книжке больше 100 головоломок, математических загадок и числовых пирамид, которые могут поставить в тупик даже признанного гения.

«2500 занимательных головоломок и заданий для детей»(0+)

В книге «2500 занимательных головоломок и заданий для детей» собрано множество разнообразных заданий: ребусов, загадок, лабиринтов, кроссвордов, игр со словами и логических задачек. Головоломки помогут ребёнку потренировать логическое и абстрактное мышление, развить память, наблюдательность, внимание и смекалку. Для дошкольного возраста.

В. Г. Дмитриева «1000 головоломок и заданий на внимательность» (0+)

«1000 головоломок и заданий на внимательность» – отличный тренажёр для развития мышления, внимания, памяти и воображения. В этой книге – логические задачки, лабиринты, игры «найди отличия», задачи на смекалку, занимательные игры со словами и цифрами. Ребята смогут с удовольствием и надолго погрузиться в удивительный мир логических задач и головоломок.

Для дошкольного возраста.

Гарет Мур «Чемпионат мира по головоломкам. TheWorld Puzzle Championship Challenge. 200 реальных заданий»(12+)

Ты такой же умный, как чемпионы мира?

Попробуй решить головоломки из чемпионата мира по головоломкам, где команды со всего мира соревнуются, чтобы найти самого быстрого и лучшего решателя головоломок.

Книга содержит более 200 головоломок различных типов, расположенных в 19 тематических главах, включая широкий спектр уникальных вариантов головоломок, созданных специально для чемпионата мира по головоломкам.

Сравни свои собственные результаты решения головоломок с победителями чемпионата и узнай, на каком ты уровне в мировом масштабе.

Леонид Смирнов «Космические головоломки «Белого кракена»»(12+)

Космос и космонавтика всегда считались популярными темами среди писателей, но пальма первенства, безусловно, принадлежит книгам с фантастическим сюжетом. Однако наша цель – не просто развлечь читателей описанием межпланетной одиссеи, но, в первую очередь, рассказать о реальных космических тайнах и чудесах, разбудить желание напрячь свой ум, разгадывая увлекательные загадки главного героя – отважного звездолетчика Куратова.

Лиза Риган «Головоломки с динозаврами»(0+)

«Головоломки с динозаврами» – это сборник творческих заданий, лабиринтов, головоломок, заданий на логику и внимательность и математических упражнений для детей 6–10 лет. Незаменимая книга во время каникул и замечательное средство от скуки! Ведь с её главными героями – озорными динозаврами – невероятно интересно разгадывать шифры, определять время на часах, решать примеры и находить отличия.

Для младшего школьного возраста.

Юки Сато «Лучшие головоломки: новый метод развития интеллекта и памяти» (12+)

«Встречают по одежке, а провожают по уму» – эта популярная когда-то пословица сегодня не актуальна. Ум стоит во главе угла. Быть интеллектуалом стало очень модно. Бицепсы, конечно, красиво, но ныне рулят вчерашние «ботаники», ставшие сегодня главами крупнейших корпораций.

В этой книге вы познакомитесь с самыми сложными задачами в мире от известных математиков и необычными математическими парадоксами. Поиграете в такие любопытные игры, как кейворд, «китайская стена» и филломино. Побродите по лабиринтам. Поломаете голову над спичками. Разгадаете секреты судоку.

И еще убедитесь в том, что сложные задачки – это не только способ напрячь свои извилины, но и расслабиться, и даже помедитировать. А некоторые головоломки предполагают еще некоторое творчество, так что их решение – еще и проявление своего воображения.

Читайте книги в ЛитРес.

Составление ребусов и других головоломок с Online Test Pad — Дидактор

Продолжаем обзор возможностей онлайн конструктора тестов, кроссвордов и головоломок Online TestPad. В предыдущих двух статьях я дал небольшой общий обзор и остановился на том, как обеспечить обратную связь и создать виртуальный класс. Без сомнения, нам необходимы инструменты не только тестирования, но и конструирования других видов учебных задач, что разнообразит познавательную деятельность учеников. Хочу познакомить вас подробнее с конструированием логических игр.

Online TestPad предлагает 5 видов логических задач:

составление слова из букв
составление фразы из слов
ребусы
загадки
поиск в тексте

Конструирование ребусов.

Ещё пять лет назад Дидактор сообщал о замечательном проекте РЕБУС № 1, где с помощью генератора ребусов в несколько щелчков можно было создать добротные головоломки со всеми присущими ребусам атрибутами и готовыми картинками. Их можно было скопировать, распечатать. Однако времена меняются. Многие учителя обзавелись блогами и тестами. К сожалению, данный сервис не предоставляет возможности вставки ребусов в авторские интернет-ресурсы.

Online TestPad предоставляет такую возможность. После команды Добавить ребус следует написать необходимое слово. Несмотря на заявленное создателями наличие генератора, к сожалению, он отсутствует. Но это вас совсем не огорчит, если вы воспользуетесь встроенными инструментами сервиса. Конструктор обладает большой подборкой функций.

Встроенный каталог готовых картинок.

Если ни одно из изображений вас не устраивает, вы можете загрузить картинку со своего компьютера.

Каждый блок ребуса сопровождается соответствующей подборкой инструментов:

Таким образом, вы можете моделировать блоки на своё усмотрение. Вы можете создать целую группу ребусов на выбранную тему, разослать ученикам или встроить в свой блог или сайт. Результаты решения данных учебных задач отразятся в вашем виртуальном классе.

Посмотрите ребус, посвящённый городам России.

Как видим, данная система ребусов приобретает свою законченность, настраивает ученика на решение однотипных задач.

Конструктор фраз.

О конструкторе составления слова из букв сообщалось в первой статье. Конструктор составления фразы из слов позволяет проектировать новый вид заданий. Это могут быть крылатые выражения, афоризмы, пословицы и т.п.

Вы поочередно добавляете слова в нужном порядке. Впоследствии они будут постоянно перемешиваться. В конструкторе предусмотрены подсказка, дополнительный вопрос к фразе.

Пример.

Между тем, учитель с помощью данного инструмента может предложить восстановление алгоритма действий, последовательности событий. При изучении иностранного языка это может быть порядок слов в предложении.

Конструктор загадок.

Работать с ним легко. Вы вводите текст загадки и указываете ответ.

Русские народные загадки.

Впрочем, это могут быть ваши задания, вопросы, которые требуют от ученика однозначного ответа.

Поиск в тексте.

Безусловно, и данный вид логической задачи предоставляет учителю большие возможности. Указать отдельные буквы (к примеру, ударные или безударные гласные), нужные слова. Это может быть некий текст с заведомыми ошибками, которые ученик должен найти.

Посмотрите пример.

Таким образом, вы можете разнообразить учебную познавательную деятельность учащихся, организовать контроль за их работой не только при решении тестов, но и других учебных задач.

Все составленные логические задачи вы можете сохранить у себя на компьютере и использовать их без Интернет-соединения. Для того, чтобы открыть задание, вам необходимо кликнуть по файлу index. В браузере откроется составленное вами задание.

Такие задания можно демонстрировать на интерактивной доске или распределить ученикам для работы в компьютерном классе.

Числовые ребусы как средство развития логического мышления

Библиографическое описание:

Осипова, Я. А. Числовые ребусы как средство развития логического мышления / Я. А. Осипова. — Текст : непосредственный // Молодой ученый. — 2020. — № 20 (310). — С. 596-597. — URL: https://moluch.ru/archive/310/70183/ (дата обращения: 18.02.2021).

В данной статье рассмотрена роль внеурочной деятельности по математике в учебно-воспитательном процессе, а также место и действенность применения в нем числовых ребусов, представлен самостоятельно разработанный курс внеурочной деятельности по математике «Ребусы +».

Ключевые слова: ребус, внеурочная деятельность, головоломка, арифметический ребус, логическое мышление, задача.

Федеральный государственный образовательный стандарт второго поколения обозначил своей целью социальный заказ общества на воспитание креативной, инициативной личности. Современному российскому государству нужны люди, способные решать нестандартные задачи, самостоятельно мыслящие, умеющие применять и использовать полученные знания, поэтому основная задача российского образования — всестороннее развитие личности. Отечественное математическое образование накопило богатый опыт в развитии мышления ребенка средствами математики. Эта работа идет в двух направлениях — и на уроках математики, и во внеурочной деятельности.

Повышение интереса к предмету, усиление мотивации, стремление к новому знанию — задачи, которые ставит перед собой каждый учитель математики. Одним из дидактических инструментов, позволяющих решить эти задачи, являются головоломки.

Как правило, головоломки считают одним из разделов занимательной математики. Это связано не только с тем, что практически любая головоломка основана на математической идее, но и с тем, что решение головоломки «по своему духу близко к решению математических задач» [1]. Поэтому головоломки являются одним из мощных средств приобщения учащихся к «нескучной» математике, формирования математической культуры и развития математического мышления.

Головоломки специально предназначены для умственного развития детей и подростков, формирования логического мышления, они помогают лучше усваивать и закреплять полученные знания, пробуждают у учащихся живой интерес к математике. Головоломки решают не только познавательные задачи. Безусловно, работа с головоломками способствует развитию памяти, внимания, творческого воображения, формирует навыки анализа и синтеза, сравнения и оценки. С помощью головоломок можно развивать абстрактное мышление, пространственное воображение, конструкторские навыки. Кроме того, работа с головоломками решает и воспитательные задачи, формируя привычку к самоконтролю, стремление доводить начатую работу до конца. Это актуализирует необходимость включения головоломок в учебный процесс как дидактического средства достижения образовательных результатов обучающихся, развития их общих и специальных математических способностей.

Наиболее эффективно головоломки можно использовать во внеурочной деятельности, которая сегодня признается неотъемлемой частью учебно-воспитательного процесса. Внеурочная деятельность по математике может быть реализована в различных видах и формах.

Остановимся на таком виде внеурочной математической деятельности, как математический кружок. В ходе занятий кружка могут рассматриваться различные головоломки или их серии, решаться различные задачи.

В частности, для занятий математического кружка нами был самостоятельно разработан курс внеурочной деятельности «Ребусы +». Он посвящен интересному разделу занимательной математики, а его математическая компонента вполне доступна младшему школьнику, поскольку решение арифметического ребуса требует достаточно ограниченного набора математических знаний.

На занятиях курса рассматриваются правила и свойства, которые примеряются при дешифровке арифметического ребуса. Математическая и методическая ценность изучения арифметического ребуса заключается в том, что при его решении учащимся необходимо анализировать условия, выделять в них существенные признаки, вспоминать общие правила и применять их к решению конкретной задачи. Это позволяет сформировать навыки быстрого счета, использования рациональных вычислительных приемов и методов, развивает память, мышление, творческую инициативу.

Данная программа рассчитана на один учебный год. Все материалы подбирались с учетом возрастных и психолого-педагогических особенностей учащихся 6 класса. За основу курса было взято пособие [1], представляющее не просто сборник числовых ребусов, но и содержащее некоторые математические обоснования способов их решения.

Курс включал в себя 6 разделов:

История числовых ребусов
Числовые ребусы, содержащие операции сложения и вычитания
Числовые ребусы, содержащие операции умножения и деления
Числовые ребусы, содержащие операцию возведения в степень
Системы числовых ребусов
Приложения

На протяжении всего времени работы учащиеся не только изучали правила и секреты решения числовых ребусов, но и сами научились их составлять.

Различные методические подходы к использованию дидактических средств на основе головоломок и ребусов позволяют включать их не только в дополнительное, но и в базовое математическое образование детей и подростков, обеспечивая достижение высоких предметных результатов. Так, например, в 5-м классе арифметические ребусы можно применять при контроле устного счета. Решение ребусов вынуждает учащихся запоминать таблицы умножения и деления, применять рациональные вычислительные приемы, увеличивать скорость арифметических действий и объем памяти. В 6-м классе арифметические ребусы можно применять при изучении признаков делимости. Они не только помогут подтолкнуть учащихся к необходимости знать признаки делимости, но и внесут значительный вклад в развитие логики, комбинаторных способностей, критического мышления, помогут развить математическую память.

Безусловно, опытный учитель сможет найти место ребусам и на других этапах урока математики. Однако надо понимать, что головоломки, как, и любое другое средство обучения, является именно средством, а не целью. Оно позволяет формировать и развивать определенные качества мышления, но не должно заменить другие формы работы на уроке.

В современной педагогико-математической литературе имеется большое число работ, посвященных числовым головоломкам и их решению. Большинство математиков и методистов высоко оценивают возможности головоломок для развития мотивации и познавательного интереса учащихся младшего подросткового возраста. Числовые ребусы, являясь разновидностью головоломок — математических задач повышенной сложности, не только определяют предметные умения учащихся, но и служат мощным средством развития математических способностей: логического мышления, математической памяти, пространственного воображения и т. п.

Решение числовых ребусов благотворно влияет на развитие абстрактного и логического мышления, формирует математическую культуру обучающихся, вызывает большой интерес и предоставляет возможность для проявления самостоятельности и инициативы детей.

Литература:

Лихтарников Л. М. Числовые ребусы и способы их решения. — СПб.: Лань, 2006.

Основные термины (генерируются автоматически): внеурочная деятельность, ребус, арифметический ребус, головоломка, логическое мышление, задача, занимательная математика, математическая память, математический кружок, пространственное воображение.

пазлов для начинающих

Это хорошие головоломки, которые стоит попробовать, когда вы впервые попадаете в мир головоломок:

Согласно традиционной песне, в первый день Рождества (25 декабря) моя настоящая любовь … Попробуйте Puzzle >> Только для смельчаков! В этом квадрате не хватает одиннадцати букв, которые вы должны … Попробуйте головоломку >> Используя любую букву только один раз, какие самые большие и самые маленькие числа вы можете записать …Попробуйте головоломку >> Спагетти известны тем, что все это запутывается на тарелке. Те из вас, кто думает … Попробуйте Puzzle >> Голодный Гораций просматривал семейный фотоальбом, в котором есть фотографии каждого из .

.. Пазл >> Шесть волков ловят шесть ягнят за шесть минут. Сколько потребуется волков, чтобы поймать шестьдесят … Пазл >> Именинного торта уже нет, но осталось двенадцать стопок Smarties. Каждая стопка удерживается … Попробуйте пазл >> На приведенной ниже диаграмме показан прямоугольник в форме креста, содержащий три пронумерованных блока.Головоломка … Попробуйте головоломку >> Если бы я сказал, что через три дня будет четверг, я уверен, что большинство из вас … Попробуйте Puzzle >> Нарисуйте круг радиусом 5 см. Нарисуйте второй круг радиусом 3 см снаружи и … Попробуйте пазл >> Дед Мороз проводит 364 дня в году, дегустируя рождественские пудинги (вот почему … Попробуйте Puzzle >> Сколько треугольников на этой диаграмме? Дополнительный вопрос: сколько четырехугольников? Попробуйте головоломку >> Миссис Месс покупала набор садовой мебели.Счет был семьдесят долларов. Она дала … Попробуйте головоломку >> Это любимое пасхальное яйцо Голодного Горация. Он пошел в магазин, чтобы купить одну .

.. Попробуйте Puzzle >> Дед Мороз должен навещать множество домов в канун Рождества, когда он доставляет подарки …. Попробуйте Puzzle >> У мамы Сэма четверо детей: апрель, май, июнь и … Как называется … Пазл >> Голодный Гораций недавно отправился на спонсируемую прогулку, чтобы собрать средства на приобретение нового оборудования у местных жителей… Попробуйте Puzzle >> Хильда играла со строительными кирпичиками, когда строила башню, подобную той, что изображена ниже: Как … Попробовать пазл >> В чем разница между спичкой и оружием, используемым в начале гонки? Один … Попробуйте головоломку >> Если вы продолжите закрашивать квадраты так, чтобы две пунктирные линии стали линиями симметрии (зеркало … Попробуйте Головоломка >> Рассказывают историю об предприимчивом молодом фермере, который скрестил овцу с лягушкой. Перед … Попробуйте головоломку >> Таким образом, восемь квадратов бумаги одинакового размера были размещены друг на друге… Попробуйте Puzzle >> Дед Мороз простудился.

К счастью, ему удалось передать сообщение через один … Попробуйте Puzzle >> Сумма сложения ниже — это загадка, которую я пытался решить. Идея в том, что каждый тип … Попробуйте Puzzle >> Старая книга по математике содержала эту сумму сложения, которая была правильно отмечена учителем: … Попробуйте головоломку >> Тремя прямыми линиями разделите участок капусты на шесть частей с двумя кочанами … Попробуйте Головоломку >> Время веселиться! На праздник вещи принесли несколько человек разного возраста: Чарли,… Попробуйте Puzzle >> «В какой день ты вернешься в школу, Гораций?» — спросила однажды его бабушка. «Ну,» … Попробуйте Puzzle >>

Логические головоломки

1. Верблюды

Четыре тасманских верблюда, идущие по очень узкому уступу, встречают четырех тасманских верблюдов, идущих в другую сторону.

Как всем известно, тасманские верблюды никогда не идут назад, особенно когда они находятся на опасном выступе. Верблюды будут перелезать друг через друга, но только если на другой стороне есть пространство размером с верблюда.

Верблюды не видели друг друга, пока между двумя группами не оставалось ровно одного верблюда.

Как могут пройти все верблюды, позволяя обеим группам идти своим путем, без движения задним ходом?

Совет: используйте спичечные палочки или монеты, чтобы имитировать головоломку.

Решение: Сначала вперед движется верблюд с одной стороны, затем два верблюда с другой стороны, затем три верблюда с первой стороны и т. Д…

и т.д …

2. Официант

Трое мужчин в кафе заказывают еду, общая стоимость которой составляет 15 долларов. Каждый из них вносит по 5 долларов. Официант передает деньги повару, который узнает троих друзей и просит официанта вернуть 5 долларов мужчинам.

Официант не только плохо разбирается в математике, но и нечестен, и вместо того, чтобы разделить 5 долларов между тремя, он просто дает им по 1 доллару, а оставшиеся 2 доллара кладет себе в карман.

Итак, каждый из мужчин фактически заплатил по 4 доллара, следовательно, общая сумма выплаты составляет 12 долларов. Добавьте 2 доллара в карман официанта, и получится 14 долларов … куда пропал еще 1 доллар по сравнению с первоначальными 15 долларами?

Решение: Выплаты должны быть равны квитанциям. Нет смысла добавлять то, что заплатили мужчины (12 долларов), к тому, что было получено от этой оплаты официантом (2 доллара)

Хотя первоначальная купюра была 15 долларов, одна из пятидолларовых банкнот заменяется на пять.Сумма, которую в конечном итоге заплатили трое мужчин, составила 12 долларов, поскольку они получили обратно троих. Таким образом, из 12 долларов, которые заплатили мужчины, владелец получает 10 долларов, а официант получает разницу в 2 доллара. 15 долларов — 3 доллара = 10 долларов + 2 доллара.

3. Коробки

Есть три коробки. Один помечен «ЯБЛОКИ», другой — «АПЕЛЬСИНЫ». Последний называется «ЯБЛОКИ И АПЕЛЬСИНЫ». Вы знаете, что каждый имеет неправильную маркировку. Вы можете попросить меня собрать один фрукт из одной коробки, которую вы выберете.

Как правильно маркировать коробки?

Решение:

Выберите один из продуктов с надписью «Яблоки и апельсины». В этой коробке должны быть только яблоки или только апельсины.

Например, Если вы найдете апельсин, пометьте поле «Апельсины», затем измените поле «Апельсины» на «Яблоки», а поле «Яблоки» на «Яблоки и апельсины».

4. Каннибалы

Трое каннибалов и трое антропологов должны перейти реку.

Лодка, которая у них есть, рассчитана только на двоих. Каннибалы будут делать то, о чем просят, даже если они находятся на другом берегу реки, за одним исключением. Если в какой-то момент времени на одной стороне реки окажется больше каннибалов, чем антропологов, каннибалы их съедят.

Какой план могут использовать антропологи для перехода через реку, чтобы их не съели?

Примечание: один антрополог не может контролировать двух каннибалов на суше, равно как и один антрополог на суше не может контролировать двух каннибалов на лодке, если все они находятся на одной стороне реки.Это означает, что антрополог не переживет, когда каннибал переплывет реку, если на другом берегу окажется один каннибал.

Решение:

Сначала два каннибала переходят на другую сторону реки, затем возвращается гребец. Затем гребной каннибал проходит через второго, а затем его зовут обратно, так что теперь на дальней стороне двое каннибалов.

Два антрополога переходят, затем один антрополог сопровождает одного каннибала обратно, так что теперь один антрополог и один каннибал по другую сторону.

Два последних антрополога переходят на противоположную сторону, так что теперь все антропологи находятся на другой стороне вместе с лодкой и одним каннибалом.

За два рейса каннибал на дальнем берегу берет лодку и переправляет двух других каннибалов через реку.

5. Отец

Мать на 21 год старше своего ребенка. Ровно через 6 лет мать будет ровно в 5 раз старше ребенка.

Где отец?

Решение: с мамой. Если вы сделаете математику, вы узнаете, что ребенок родится через 9 месяцев.

6. Двойные двери опасности

Вы попали в комнату с двумя дверями. Один ведет к верной смерти, а другой ведет к свободе. Вы не знаете, что есть что.

Двери охраняют два робота. Они позволят вам выбрать одну дверь, но после этого вы должны будете пройти через нее.

Однако вы можете задать одному роботу один вопрос. Проблема в том, что один робот всегда говорит правду, другой всегда лжет, и вы не знаете, что есть что.

Какой вопрос вы задаете?

Подсказка: два робота знают личности друг друга. Что они разговаривают, когда им скучно, одиноко и т. Д. Попытайтесь заставить двух роботов отменить их зло и добро.

Решение: спросите одного робота, что сказал бы другой робот, если бы его спросили, какая дверь безопасна.Затем пройдите в другую дверь.

7. Лягушка

Лягушка на дне 30-метрового колодца. Каждый день он набирает достаточно энергии для одного трехметрового прыжка в колодец. Измученный, он зависает там до конца дня. Ночью, когда он спит, он соскальзывает на 2 метра назад. Сколько дней ему нужно, чтобы выбраться из колодца?

Примечание: после первого прыжка предположим, что его задние лапы находятся на высоте ровно трех метров над колодцем. Его задние лапы должны очистить колодец, чтобы он смог сбежать.

Подсказка: попробуйте продумать задачу для пятиметрового колодца. Что теперь делать для 30-метровой скважины?

Решение: 28

Каждый день он делает еще один метр, а затем на двадцать седьмой день он может прыгнуть на три метра и вылезти наружу.

8. Боббер

Вы можете проплыть на каноэ со скоростью семь миль в час через любое спокойное озеро. Поток течет со скоростью три мили в час.В тот момент, когда вы начинаете плыть вверх по течению, рыбак теряет одну из своих поплавков в воде в четырнадцати милях от вас.

Сколько часов у вас уходит на встречу с поплавком?

Подсказка: предположите, что поток движется с совершенно постоянной скоростью три мили в час.

Решение: 2

Не обращайте внимания на скорость потока, так как пробка будет уноситься со скоростью три мили в час, как и вы. Чтобы проехать четырнадцать миль со скоростью семь миль в час, нужно два часа.

9. Носки

У Кэти в ящике есть двенадцать черных и двенадцать белых носков.

В полной темноте, не глядя, сколько носков она должна вынуть из ящика, чтобы наверняка получить пару подходящих?

Решение: 3

Носки не подходят слева и справа, поэтому любой черный будет сочетаться с любым другим черным, а любой белый будет сочетаться с любым другим белым.Если у вас три носка черного или белого цвета, то у вас будет как минимум два носка одного цвета, что даст вам одну подходящую пару.

10. Есть кое-что о Мэри

У мамы Марии четверо детей.
Первого ребенка зовут Эйприл.
Второе мая.
Третье июня.
Как зовут четвертого ребенка?

Решение: Мэри.

Четвертым ребенком матери Мэри была сама Мэри.

11. Лепестки вокруг розы

Название игры — Petals Around the Rose , и это название очень важно. Новички к игре можно сказать многое. Им также можно сказать, что каждый ответ нулевой или четное число. Им также можно сказать ответ на каждый бросок игральных костей. игра. И это вся информация, которую они получают.

Человек, у которого есть кости и который знает игру, бросает пять кубиков и почти замечает моментально на ответ.Например: в Броске №1 ответ — два.

Рулон №1.

«Ответ какой?» — говорит новый игрок.

«Два».

«На этом рулоне?»

«Да».

«Было бы еще два, если бы я передвинул кости, не переворачивая их, просто переставлять выкройку? »

«Могу сказать только три вещи: название игры, то, что ответ всегда четный, и ответ на каждый конкретный бросок. В этом случае ответ будет два. «

«Так вот как. Что мне делать?»

«Ты должен сказать мне ответ, прежде чем я скажу тебе. Я дам тебе все время, которое хочешь, но не рассказывай мне свою теорию, просто ответ. Если вы это поймете, вы не хочу выдавать эту идею другим шутникам вокруг вас. Заставить их работать на ответы тоже. Если вы получите правильный ответ в шести последовательных бросках, я приму это как прима очевидное свидетельство того, что вы разбираетесь в игре.«

«Хорошо, брось еще раз».

Рулон №2.

«Я сдаюсь. Что делать?»

«Ответ — восемь».

«Брось снова».

Рулон №3.
Ответ четырнадцать.

Рулон №4.
Ответ нулевой.

Рулон №5.
Ответ — четыре.

Рулон №6.

Неотъемлемой частью головоломки является то, что тем, кто ее решил, настоятельно рекомендуется держать решение в секрете, поэтому здесь нет решения. Однако разгадать эту загадку нетрудно.

Утверждение, которое часто сопровождает эти инструкции, состоит в том, что чем умнее человек, тем труднее ему будет его решить.Если такое утверждение верно, это может быть связано с тем фактом, что «более умные» люди, как правило, более осведомлены в широком спектре информации, которую они могут без нужды пытаться использовать для решения головоломки.

12. Выбор Ватсона

Вам показывают набор из четырех карточек, размещенных на столе, каждая из которых имеет номер на одной стороне и цветное пятно на другой стороне. На лицевых сторонах карт изображены 3, 8, красный и коричневый.
Какую карту (карты) вы должны перевернуть, чтобы проверить истинность утверждения о том, что если карта показывает четное число на одной стороне, то ее противоположная сторона красная?

Подсказка: ответ, который определяет карту, которую не нужно перевернуть, или не может определить карту, которую нужно перевернуть, неверен.Первоначальное задание касалось чисел (четные, нечетные) и букв (гласные, согласные).

Решение: правильный ответ — перевернуть 8-ю карту и коричневую карту.

Правило гласило: «Если карта показывает четное число на одной стороне, то ее противоположная сторона красная». Только карта с четным числом на одной стороне и чем-то отличным от красного на другой может аннулировать это правило:

Если 3 карта красная (или коричневая), это не нарушает правила. Правило не делает никаких заявлений о нечетных числах.

Если карта 8 не красная, это нарушает правило.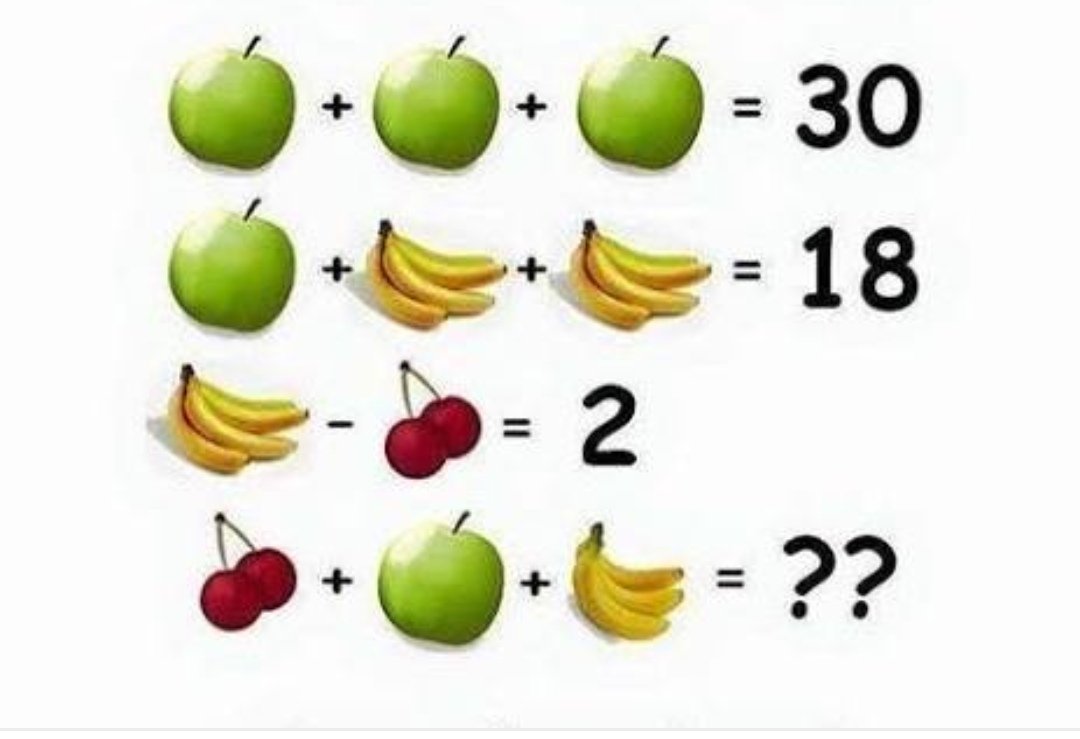

Если красная карточка нечетная (или четная), это не нарушает правила. Красный цвет не ограничивается четными числами.

Если коричневая карта четная, это нарушает правило.

логических головоломок | Brilliant Math & Science Wiki

В головоломке о пересечении реки цель состоит в том, чтобы найти способ перебросить группу людей или предметов через реку (или какое-либо другое препятствие) и сделать это с наименьшими затратами. шагов или наименьшее количество времени.

Известная проблема перехода через реку — это проблема с мостом и факелом Ричарда Ховасса, описанная ниже.

Четыре человека приходят ночью к реке. Есть узкий мост, но он может одновременно удерживать только двух человек. У них есть один фонарик, и, поскольку сейчас ночь, при переходе моста нужно использовать фонарик. Человек A может перейти мост за одну минуту, B за две минуты, C за пять минут и D за восемь минут. Когда два человека вместе переходят мост, они должны двигаться в темпе более медленного человека.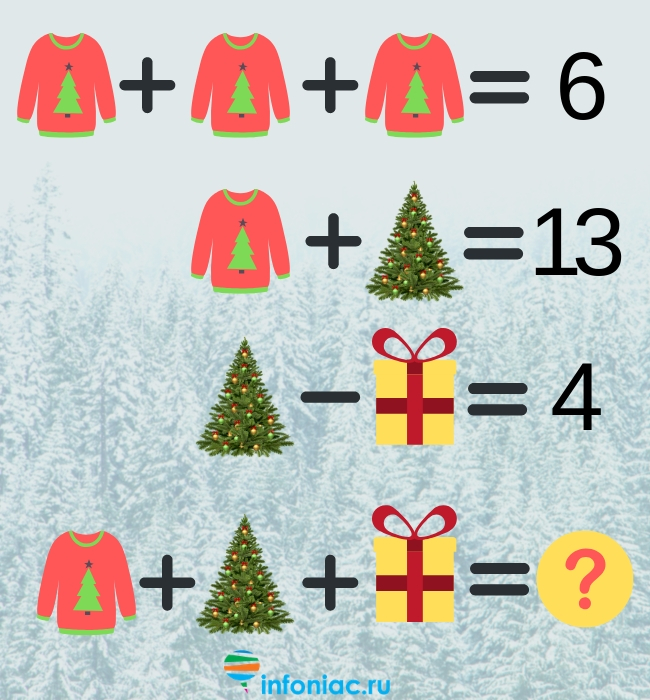 Вопрос в том, смогут ли они все перебраться через мост за 15 минут или меньше?

Предположим, что решение минимизирует общее количество пересечений. Всего получается пять крестов — три парных и два одиночных. Также предположим, что мы всегда выбираем самый быстрый для одиночного кросса.

Во-первых, мы показываем, что если два самых медленных человека (C и D) пересекаются по отдельности, они накапливают общее время пересечения, равное 15. Это делается путем взятия людей A, C, D: D + A + C + A = 8+ 1 + 5 + 1 = 15. (Здесь мы используем A, потому что знаем, что использование A для пересечения C и D по отдельности является наиболее эффективным.) Но время истекло, а люди A и B все еще находятся на стартовой стороне моста и должны перейти. Таким образом, два самых медленных (C и D) не могут пересекаться отдельно.

Во-вторых, мы показываем, что для того, чтобы C и D пересеклись вместе, они должны пересечься во втором парном кресте: то есть не C или D, поэтому A и B должны сначала пересечься. Помните, что наше предположение в начале гласит, что мы должны минимизировать кресты, поэтому у нас есть пять крестов — 3 парных и 2 одиночных.Предположим, что сначала пересекаются C и D. Но затем C или D должны пересечься, чтобы переместить факел на другую сторону, так что тот, кто пересекся в одиночку, должен снова перейти. Следовательно, они будут переходить отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечься ранее, иначе на стартовой стороне будет всего три человека. Таким образом, поскольку есть только три варианта для парных переходов, а C и D не могут пересекаться первым или последним, они должны пересечься вместе при втором или среднем парном переходе.

Собирая все это вместе, A и B должны сначала пересечься, поскольку мы знаем, что C и D не могут, и мы минимизируем пересечения. Затем A должен пересечь следующий, так как мы предполагаем, что должны выбрать самый быстрый, чтобы сделать одиночный кросс. Затем мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны идти. Затем мы решили отправить самый быстрый назад, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься для последнего пересечения пары. Это дает нам B + A + D + B + B = 2 + 1 + 8 + 2 + 2 = 15.

Все четыре человека могут пересечь дорогу за 15 минут.□ _ \ квадрат □

Логическая головоломка | игра | Британника

Логическая головоломка , головоломка, для решения которой требуется использование процесса логической дедукции.

Многие сложные вопросы не связаны с численными или геометрическими соображениями, но требуют дедуктивных выводов, основанных главным образом на логических отношениях. Такие головоломки не следует путать с загадками, которые часто основываются на намеренно вводящих в заблуждение или двусмысленных утверждениях, игре слов или другом приеме, предназначенном для улавливания неосторожных.Логические головоломки не допускают стандартной процедуры или обобщенной схемы для своего решения и обычно решаются каким-либо методом проб и ошибок. Это не значит, что предположение было случайным; напротив, приведенные факты (как правило, минимальные) предполагают несколько гипотез. Они могут быть последовательно отклонены, если обнаружены несоответствия, до тех пор, пока путем замены и исключения не будет окончательно достигнуто решение. Использование различных техник логики иногда может оказаться полезным, но, в конечном счете, успех во многом зависит от той неуловимой способности, которая называется изобретательностью.Для удобства логические задачи условно сгруппированы по следующим категориям.

Пазл тормозник-пожарный-инженер стал классикой. Следующая его версия появилась в книге Освальда Якоби и Уильяма Бенсона «Математика для удовольствия » (1962).

Имена тормозящего, пожарного и машиниста определенного поезда (не обязательно соответственно) были Смит, Джонс и Робинсон. Три пассажира в поезде оказались с одинаковыми именами и, чтобы отличить их от железнодорожных служащих, в дальнейшем будут называться г-ном. Смит, мистер Джонс и мистер Робинсон. Мистер Робинсон жил в Детройте; тормозной мастер жил на полпути между Чикаго и Детройтом; Мистер Джонс зарабатывал ровно 2000 долларов в год; Смит победил пожарного в бильярде; сосед тормозящего, один из пассажиров, зарабатывал ровно в три раза больше, чем тормозной; а у пассажира, который жил в Чикаго, было то же имя, что и у тормозного мастера. Как звали инженера?

Перекрывающиеся группы

Следующая проблема типична для категории перекрывающихся групп.Среди членов языкового клуба в средней школе 21 изучали французский язык; 20, немецкий; 26, испанский; 12, французский и испанский; 10, как французские, так и немецкие; девять, испанские и немецкие; и три, французский, испанский и немецкий. Сколько было членов клуба? Сколько участников изучали только один язык?

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчас

Другой вид загадки логического вывода касается правды и лжи. Одна из разновидностей заключается в следующем: уроженцы определенного острова известны как рыцари или лжецы, хотя внешне они неотличимы.Рыцари всегда говорят правду, а лжецы всегда лгут. Посетитель острова, встречая трех туземцев, спрашивает их, рыцари они или лжецы. Первый говорит что-то неслышное. Второй, указывая на первого, говорит: «Он говорит, что он рыцарь». Третий, указывая на второго, говорит: «Он лжет». Зная заранее, что только один лжец, посетитель решает, кто из троих каждый.

В несколько ином типе, четверо мужчин, один из которых, как известно, совершил определенное преступление, на допросе в полиции сделали следующие заявления:

Арчи : Это сделал Дэйв.
Дэйв: Тони сделал это.
Гас: Я этого не делал.
Тони: Дэйв солгал, когда сказал, что это сделал я.

Если только одно из этих четырех утверждений верно, кто был виноват? С другой стороны, если только одно из этих четырех утверждений ложно, кто был виноват? (Из книги 101 Puzzles in Thought and Logic К. Р. Уайли-младшего; Dover Publications, Inc., Нью-Йорк, 1957 г. Перепечатано с разрешения издателя.)

Проблема смазанных лиц — еще один пример чистой логической дедукции.Трое путешественников были в поезде, который только что вышел из туннеля, и у каждого на лбу осталось пятно сажи. Пока они смеялись друг над другом и прежде чем они смогли взглянуть в зеркало, соседний пассажир предположил, что, хотя никто из троих не знает, был ли он испачкан, есть способ узнать это без использования зеркала. Он предложил: «Каждый из вас троих взглянет на двух других; если ты увидишь хотя бы одного, чей лоб размазан, поднимите руку ». Каждый сразу поднял руку.«Теперь, — сказал сосед, — как только кто-нибудь из вас точно знает, размазан ли у него лоб или нет, он должен опустить руку, но не раньше». Через пару мгновений один из мужчин с удовлетворенной улыбкой опустил руку и сказал: «Я знаю». Откуда этот человек узнал, что его лоб размазан?

Последним примером может быть парадокс неожиданного повешения, замечательная загадка, о которой впервые стало известно из уст в уста в начале 1940-х годов. Одна из форм парадокса заключается в следующем: в субботу был вынесен приговор.Судья объявляет, что «повешение состоится в полдень одного из семи дней следующей недели, но вы не узнаете, какой сегодня день, пока вам не сообщат утро дня повешения». Заключенный, обдумав это, решил, что приговор судьи не может быть приведен в исполнение. «Например, — сказал он, — меня нельзя повесить в следующую субботу, в последний день недели, потому что в пятницу днем я все еще буду жив и я точно буду знать, что меня повесят в субботу. . Но я знал этот до того, как мне сказали об этом в субботу утром, и это противоречило бы заявлению судьи.Точно так же, утверждал он, они не могли повесить его ни в пятницу, ни в четверг, ни в среду, ни во вторник, ни в понедельник. «А завтра меня не повесят, — подумал заключенный, — потому что я знаю это сегодня!»

Тщательный анализ показывает, что этот аргумент неверен и постановление может быть выполнено. Парадокс тонкий. Ключевым моментом является то, что утверждение о будущем событии может быть известно как истинное предсказание одним человеком, но не известно как истинное другому человеку до после того, что событие произошло.

Эта статья была последней редакцией и обновлением Уильямом Л. Хошем, младшим редактором.

Узнайте больше в этих связанных статьях Britannica:

вычет
Логический вывод, строгое доказательство или вывод одного утверждения (заключения) из одного или нескольких утверждений (предпосылок) —i.е., цепочка утверждений, каждое из которых является либо предпосылкой, либо следствием утверждения, сделанного ранее в доказательстве. Это использование является обобщением того, что…
логика
Логика, изучение правильных рассуждений, особенно в том, что касается составления умозаключений. В этой статье обсуждаются основные элементы и проблемы современной логики, а также дается обзор ее различных областей. Для обработки исторического развития логики см. Логика, история России. Для подробного обсуждения конкретных полей…
Кроссворд
Кроссворд, популярная форма словесной головоломки.Кроссворд состоит из диаграммы, обычно прямоугольной, разделенной на пустые (белые) и списанные (черные, заштрихованные или заштрихованные) квадраты. Эта диаграмма сопровождается двумя списками пронумерованных определений или подсказок, один для горизонтального и…

Логические головоломки для подростков и подростков

Недавно я прочитал статью, в которой говорилось о навыках, которые потребуются людям для получения работы в современном мире.

Ушли в прошлое те навыки, которые были необходимы, когда мы учились в школе (запоминание дат, фактов и т. Д.)

На сегодняшнем рынке труда сотрудники должны уметь мыслить, проявлять творческий подход, работать как член команды.

Мой последний пост (творческая задача) — это то, что вы можете сделать со своими внуками, чтобы помочь им расширить и развить свои творческие способности.

Сегодня у меня есть кое-что для вас, чем можно заняться со своими внуками, что поможет им в их логике.(И это может помочь сохранить ваших синапсов , чтобы предотвратить болезнь Альцгеймера!)

Сегодня я представляю вам логические головоломки!

Обожаю логические головоломки. Я обнаружил их, когда сдал тест GRE, чтобы поступить в магистратуру. В тесте были логические задачи, и мне очень понравилось выполнять практические.

Итак, у меня есть кое-что для вас. Некоторые простые для подростков и более сложные для подростков.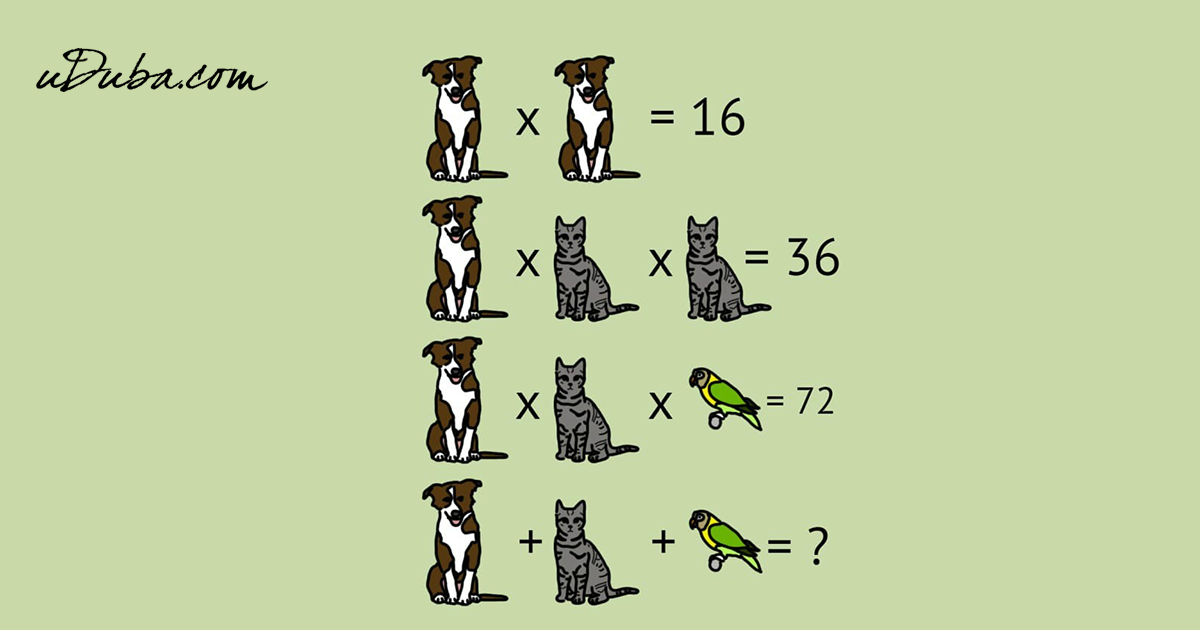

Ваши внуки могут работать над ними индивидуально или они могут работать над ними с одним или двумя другими внуками.(Это дало бы им возможность практиковаться в работе в команде!)

Что такое логические проблемы? спросите вы.

Что ж, позволь тебе рассказать. Это НЕ те надоедливые задачи по математике в былые времена. Нет, Боб! Забудьте о поезде, отправляющемся из Нью-Йорка со скоростью 35 миль в час, и о том, который отправляется из Чикаго со скоростью 45 миль в час. Давайте танцевать и кричать аллилуйя!

Позвольте мне показать вам пример логической задачи. Он называется «Получение питомца» от Брейнгла.com.

Вот в чем проблема.

Три человека однажды купили домашнего питомца. Их звали Зак, Рэйчел и Хьюберт. Они купили змею, попугая и морскую свинку. Они купили своих питомцев за 100, 50 и 25 долларов.

Можете ли вы узнать, какой человек какое животное купил за какую сумму денег, используя эти подсказки?

1. У Зака аллергия на птиц.
2. Хьюберту не удалось получить питомца за 100 долларов, поэтому он купил змею.
3. Рэйчел откладывала 10 долларов в неделю в течение десяти недель, чтобы завести своего питомца.
4. Зверюшка стоила 25 долларов.

Вот сетка, которая поможет вам решить эту проблему. Поставьте X в месте, где информация не применима.

Давайте посмотрим на информацию. Во-первых, у Зака аллергия на птиц. Итак, мы знаем, что он не купит попугая. Поставьте X в поле рядом с именем Зака и в поле под попугаем.

Следующая информация гласит, что Юбер не смог получить питомца за 100 долларов, поэтому он купил змею. Итак, поставьте X в поле в строке информации о Хьюберте, а это в ячейке 100 долларов.В нем говорится, что он купил змею, поэтому вы поставили О в коробке со змеями для Хьюберта.

Следующая информация говорит нам, что Рэйчел откладывала 10 долларов в неделю в течение десяти недель, чтобы завести своего питомца. Здесь нам нужно немного посчитать. Если она сэкономила 10 долларов на 10 недель, чтобы завести своего питомца, это означает, что она потратила 100 долларов на покупку своего питомца. Таким образом, мы можем поставить О в ее строке информации в поле 100 долларов.

Последняя известная нам информация — это млекопитающее стоимостью 25 долларов. Поскольку мы знаем, что морские свинки — это млекопитающие, поставьте букву O под морской свинкой в коробке за 25 долларов.

Теперь вы заполнили квадраты всей предоставленной информацией. Далее идет логическое мышление. Весело!

Поскольку Юбер купил змею, мы знаем, что он покупал не попугая и морскую свинку. Поставьте крестики в эти коробки.

Поскольку мы знаем, что морская свинка стоит 25 долларов, мы можем положить крестики в коробки по 25 долларов под попугаем и змеей.

Вы умеете решать логические головоломки?

Посмотри, сможешь ли ты разобраться с остальным — с помощью внука или самостоятельно.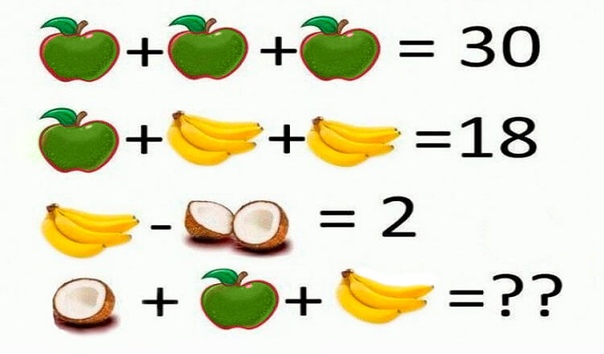

(Вот ответы. Зак купил морскую свинку за 25 долларов. Рэйчел купила попугая за 100 долларов. А Юбер купил змею за 50 долларов).

Вот несколько простых логических головоломок, которые я получил от Kids Love to Know. Вы можете начать с них, чтобы понять, как они работают. Ключ ответа прилагается к головоломке, чтобы вы могли проверить свои ответы.

Вот четыре логические головоломки, которые посложнее. Я получил их от Puzzle Barron.

Вот ответы на эти 4 головоломки.

Отлично проведите время, решая эти головоломки, и развивайте свои навыки критического мышления!

веселых логических головоломок

思方網 • сеть критического мышления

(∀ ∴ & модели; ≠ ↔ ⊥ ∃)

Вот несколько коротких, но забавных логических головоломок. Посмотрим, сможешь ли ты их решить!

1.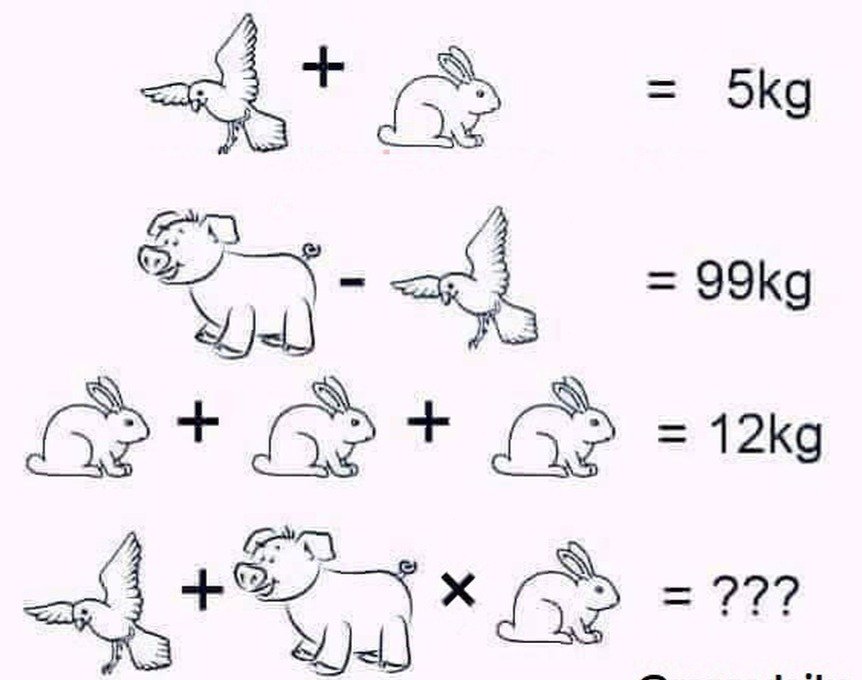 Стивен смотрел на фотографию.Кто-то спросил его: «На чью фотографию ты смотришь?» Он ответил: «У меня нет брата или сестры, но отец этого человека — сын моего отца». Итак, на чью фотографию смотрел Стивен?

отвечать

2. Произошло ограбление, при котором было украдено много товаров. Грабитель уехал на грузовике. Известно, что: (1) Никто другой не мог быть замешан, кроме A, B и C. (2) C никогда не совершает преступления без участия A. (3) Б не умеет водить машину. Итак, виноват А. или невиновен?

ответ

3.Предположим, есть этот маленький городок с ограниченным числом людей: (1) Нет двух жителей с одинаковым количеством волос. (2) Ни у одного жителя нет ровно 409 волос. (3) Жителей больше, чем волос на голове у любого жителя. Итак, какое максимальное количество жителей в этом городке?

ответ

4. Следующий тест на логическую дедукцию, как сообщается, был одним из вопросов, которые задавали 14-летним школьникам на олимпиаде по математике в Сингапуре и азиатских школах. [Подробнее]

Альберт и Бернард только что подружились с Шерил, и они хотят знать, когда у нее день рождения. Шерил дает им список из 10 возможных свиданий.

15 мая, 16 мая, 19 мая
17 июня, 18 июня
14 июля, 16 июля
14 августа, 15 августа, 17 августа

Затем Шерил сообщает Альберту и Бернарду отдельно месяц и день своего дня рождения соответственно.

Тогда Альберт сказал: я не знаю, когда у Шерил день рождения, но я знаю, что Бернар тоже не знает.

Бернард: Сначала я не знал, когда у Шерил день рождения, но теперь знаю.

Альберт: Тогда я также знаю, когда у Шерил день рождения.

Так когда у Шерил день рождения?

отвечать

5. Эта загадка принадлежит покойному логику и математику Раймонду М. Смулляну: дилер купил предмет за 7 долларов, продал за 8 долларов, купил обратно за 9 долларов и продал за 10 долларов. Какую прибыль он получил? ответ

Пазлы рыцари и лжецы

Хотите еще головоломок? Попробуйте наши головоломки рыцарей и мошенников, где вам нужно решить, кто лжет, а кто говорит правду. Их 382 штуки!

математических и логических головоломок по программе Mr Barton Maths

arrow_back Вернуться домой

Математические и логические головоломки

Я обожаю хорошие математические или логические головоломки. Этот страница — это коллекция некоторых из моих любимых, которые я выполнил с годами. Некоторые вы будете знать, но, надеюсь, некоторые вы узнаете нет. Многие пришли из выдающейся игры Numberplay Блог из New York Times.

Головоломки не сгруппированы по темам (это может выдать некоторые секреты их решения) или по возрасту или сложности, потому что это очень сильно зависит от самого решателя головоломки.

Пожалуйста, не присылайте мне какие-либо ответы по электронной почте, поскольку я боюсь У меня нет времени отвечать. В любом случае, это испортило бы удовольствие.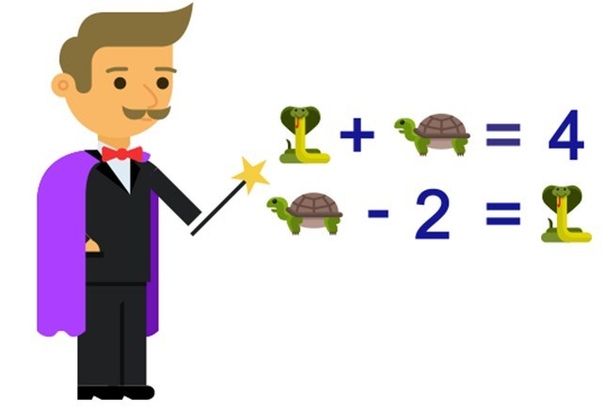 Но Я полагаю, что за относительно большие суммы денег у меня может возникнуть соблазн разгласить некоторую информацию.И если у вас есть любимая головоломка, вы думаете, хорошо впишется в эту коллекцию, пожалуйста, дайте мне знать через Twitter

Содержание

1. Круг смерти

keyboard_arrow_up

В начало

Сто человек в кругу. Они считают начиная с одного и заканчивая сотней.Поскольку они находятся в круг, ОДИН рядом с ДВУМЯ и ОДНОЙ СТО. У ОДНОГО есть меч и убивает ДВОИХ. Он передает меч ТРИ, которые убивают ЧЕТЫРЕХ. И так вперед. ДЕВЯТЬ ДЕВЯТЬ убивает ОДНУ СОТНУ и передает меч ОДНОЙ. Затем ОДИН убивает ТРЕХ и передает меч ПЯТЬ. Это продолжается пока не останется только один человек. Какой он номер?

2.

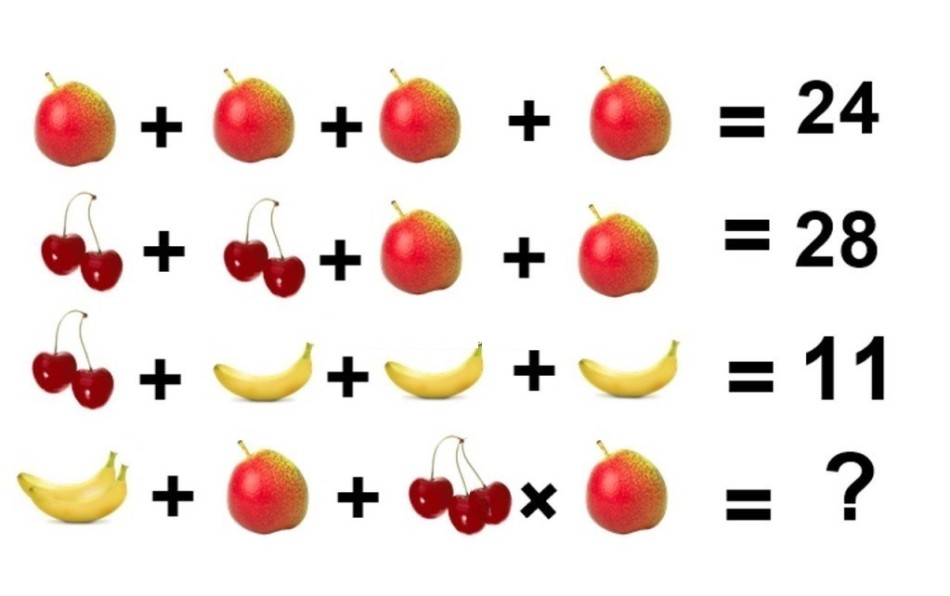Проблема 4 монет keyboard_arrow_up

В начало

Вы создаете новую систему монет для своей страны.Вы должны использовать только четыре достоинства монеты, и вы должны иметь возможность создавать значения 1 через 10, используя минимум одну монету и максимум две монеты. Что 4 монеты вы выбираете, и можете ли вы придумать второй набор из 4 монеты, которые достигают той же цели?

3. Обручальное кольцо

keyboard_arrow_up

В начало

В некоторых сельских районах России собиралась невеста. шесть длинных кусочков соломы или травы и возьмите их в руку.Она затем случайным образом завязывал пары узлов сверху и снизу. Сверху и снизу торчат шесть травинок. руку, она завяжет три узла сверху и три узла на дно. История гласит, что если она образовала одно большое кольцо, она скоро выйдет замуж.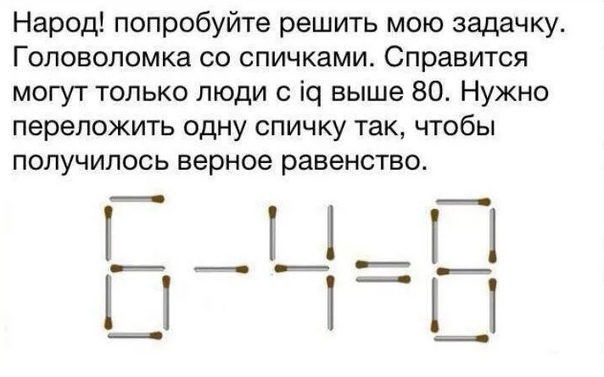 Какова вероятность, что она получит состоите в браке?

4. Задача средних значений

keyboard_arrow_up

В начало

Рассмотрим список всех способов, которыми вы могли бы взять четыре различных цифры от 1 до 9 и расположите их так, чтобы получилась сумма двух 2-значных числа.Некоторые числа могут появляться несколько раз: 134, для Например, 93 + 41, а также 91 + 43.

Каковы среднее значение, медиана и мода всех чисел на этом список? (Среднее — это сумма всех чисел, деленная на количество чисел, медиана — это среднее значение в отсортированном списке числа, а режим — это число, которое встречается чаще всего.)

5. Как избежать тролля

keyboard_arrow_up

В начало

Каждый день вы совершаете поездку из пункта А в пункт Б, расстояние до которого составляет 2 мили.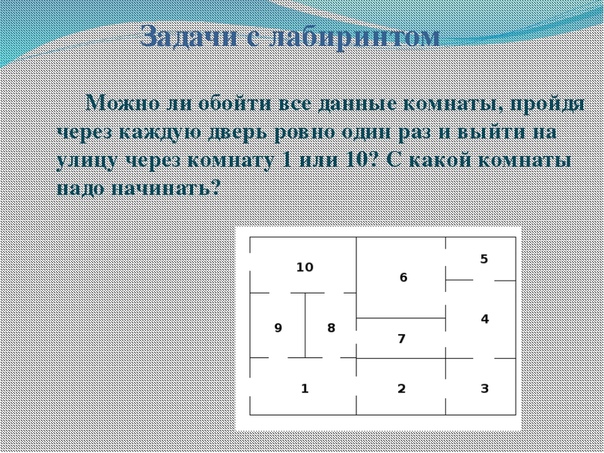 Но твой поездка непредсказуема.

В 50% дней вы можете ходить между А и Б без каких-либо препятствие.

Остальные 50% времени тролль появляется на полпути, блокируя вашу поездку. Тролль также активирует невидимый барьер. которая блокирует 1 милю перпендикулярно в обоих направлениях, заставляя вас обойти его, чтобы завершить поездку.

Вы не можете увидеть тролля или барьер, пока не окажетесь на полпути от От А до Б, поэтому вы не можете заранее спланировать, нужно ли вам ходить вокруг шлагбаума.Вы знаете, что тролль появляется случайно в 50% случаев. время.

Если вы можете идти по прямой к любой точке между A и B, какова ваша лучшая стратегия, чтобы вы прошли наименьшее расстояние средний? Что это за расстояние?

6. Пещера Али-Бабы

keyboard_arrow_up

В начало

Али-Баба нашел пещеру, полную золота и алмазов. Сумка, полная золото весит 200 килограммов, мешок с бриллиантами весит 40 килограммы.Али-Баба может нести за один раз только 100 килограммов. А килограмм золота стоит 20 долларов, а килограмм бриллиантов — 60 долларов. Какую самую большую сумму денег Али-Баба может заработать за золото и бриллианты он может унести сразу (за одну попытку за одну мешок)?

7. Питьевая игра-головоломка

keyboard_arrow_up

В начало

Игра начинается с 6 пустых стаканов подряд, пронумерованных от 1 до 6.Вы бросаете стандартный кубик. Если номер стакана пустой, затем стакан наполняется. Если номер стакана полный, затем вы пьете этот стакан, и он становится пустым.

Есть особое правило, когда 5 стаканов полны. Если вы катите номер для одинокого пустого стакана, затем последний стакан наполняется и надо выпить все 6 стаканов. На этом игра заканчивается.

Какое среднее количество бросков с начала игры пока игра не закончится?

8.Жемчуг раджи

keyboard_arrow_up

В начало

Раджа по своей воле оставил своим дочерям определенное количество жемчуг с инструкциями по их разделению следующим образом: Самый старый дочь должна была получить 1 жемчуг плюс 1/7 того, что осталось. В следующая старшая дочь должна была получить 2 жемчужины плюс 1/7 из них оставили. Следующая старшая дочь должна была получить 3 жемчужины плюс 1/7 что осталось, и так далее таким же образом.Младшая дочь получил то, что осталось после всех остальных дивизий.

Сначала младшая дочь думала, что раздача несправедливо, но после тщательных расчетов она пришла к выводу, что все дочери получат столько же жемчуга.

Сколько всего было жемчуга и дочерей?

9.

Санкт-Петербургская лотерея keyboard_arrow_up

В начало

Предположим, мы играем в следующую игру.Я несколько раз подбрасываю монету пока не поднимется голова. Если выпадет орел при первом броске, я заплатить вам 2 доллара. Если он появится при втором броске, я дам вам 4 доллара; если на третьем я плачу 8 долларов и так далее, каждый раз удваивая.

Сколько вы готовы заплатить мне за эту игру?

10. День рождения Шерил

keyboard_arrow_up

В начало

Альберт и Бернард только что подружились с Шерил, и они хотят узнать, когда у нее день рождения.Шерил дает им список из 10 возможные даты.

15 мая 16 мая 19 мая
17 июня 18 июня
14 июля 16 июля
14 августа 15 августа

Затем Шерил сообщает Бернарду и Альберту месяц и дату по отдельности.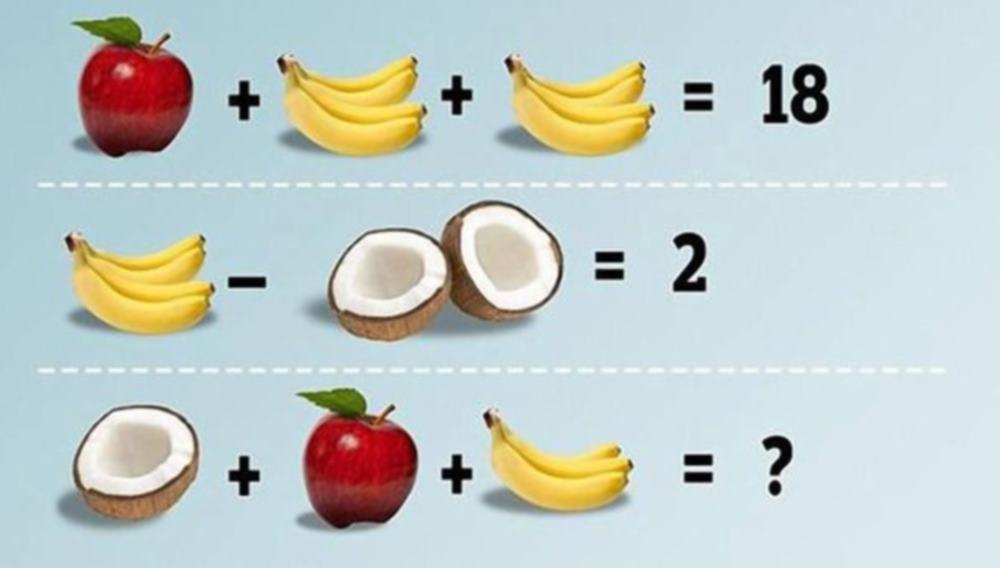 день ее дня рождения соответственно.

Альберт: Я не знаю, когда у Шерил день рождения, но я знаю, что Бернар тоже не знает.
Бернард: Сначала я не знаю, когда у Шерил день рождения, но я знать сейчас.
Альберт: Тогда я также знаю, когда у Шерил день рождения.

Когда у Шерил день рождения?

11. Возраст детей

keyboard_arrow_up

В начало

2 математика встречаются на улице, и один говорит другому: «Я Спорим, ты не можешь угадать возраст моих троих детей «(все целые числа).

Второй математик говорит:» Я приму вашу ставку, но только если вы дайте мне достаточно информации, чтобы решить эту проблему.»

Первый соглашается и говорит:» Продукт возраста моих трех детей — 36. «
» Этой информации недостаточно. «
« Правильно! »- он оглядывается, шпионит за адресом на здании.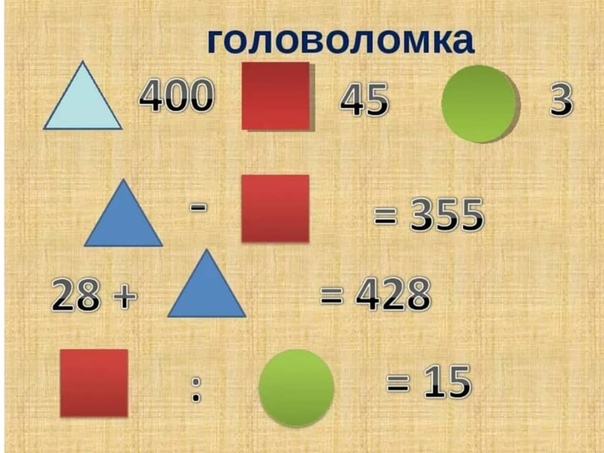 и говорит: «Суммарный возраст моих детей совпадает с адресом вон там «
Немного подумав;» Этой информации все еще недостаточно «
» Ты снова прав! У моего старшего сына рыжие волосы ».
Подумав, второй математик выиграл пари.

12. Кольцо вокруг Земли

keyboard_arrow_up

В начало

Представьте себе стальную полосу вокруг экватора Земли, красиво и уютно (~ 25 000 миль). Если вы затем добавите один фут стали к эта группа, насколько группа поднята над землей? Достаточно высоко подсунуть под него волосы? Твоя рука? Достаточно высоко, чтобы под ним пройти?

13. Школьные шкафчики

keyboard_arrow_up

В начало

Есть школа с 1000 учениками и 1000 шкафчиками.На в первый день семестра директор просит первого ученика уйти и открыть каждый шкафчик, он просит второго пойти в каждый второй шкафчик и закрыть его, третий перейти к каждому третьему шкафчик и закройте его, если он открыт, или откройте, если он закрыт, четвертый пройти в четвертый шкафчик и так далее. Процесс укомплектован тысячным учеником. Сколько шкафчиков открыто в конце?

14.Ставка дьявола

keyboard_arrow_up

В начало

Ты умираешь, а дьявол говорит, что отпустит тебя на небеса, если ты побьешь его в игре. Он усаживает вас за круглый стол. Он делит большая куча четвертей пополам, чтобы у вас обоих было одинаковое количество кварталы в собственной куче. Он говорит: «Хорошо, мы по очереди положить четверти вниз, перекрытия не допускаются, а четверти должен опираться на поверхность стола.Первый парень, который не умеет четверть вниз проигрывает. Вы не можете сдвинуть или попытаться сжать любую четверть в пространство, которое переместится еще на четверть «. Дьявол говорит, что хочет идти первым.

Вы понимаете, что если дьявол пойдет первым, у него, вероятно, есть стратегия, чтобы победить. У вас еще не было времени подумать об этом, поэтому вы спрашиваете какое-то время обдумывать ваши варианты. Он дает вам 15 минут. По истечении этого времени вы знаете, как победить его … но вы также знайте, что вы должны пойти первым, чтобы ваша стратегия выиграла.Ты убедишь его чтобы отпустить вас первым, сказав, что у вас действительно не хватило времени продумайте стратегию, так что вы должны хотя бы пойти первым. Какой твой выигрышная стратегия?

15. Половина яйца

keyboard_arrow_up

В начало

Крестьянка пришла на рынок продать яиц. Первый покупатель взяла половину ее яиц плюс 1/2 яйца. То же произошло и с оставшиеся яйца: второй покупатель-покупатель взял половину своих яиц плюс 1/2 яйцо.Третий купил только то, что осталось: 1 яйцо.

Сколько яиц было изначально?

16.

Сделайте 6 keyboard_arrow_up

В начало

Можно использовать только два математических символа (включая факториалы и квадратные корни), чтобы получить 6

0 0 0 = 6

1 1 1 = 6

2 2 2 = 6

3 3 3 = 6

4 4 4 = 6

5 5 5 = 6

6 6 6 = 6

7 7 7 = 6

8 8 8 = 6

9 9 9 = 6

17.Три лжеца подбрасывают монету

keyboard_arrow_up

В начало

Трое людей имеют тенденцию лгать 1/3 времени. Там это подбрасывание монеты, которую все видят. Все говорят, что это головы. Что вероятность, что это на самом деле Головы?

18. Освободить узников

keyboard_arrow_up

В начало

По прибытии надзиратель встречает 23 новых заключенных.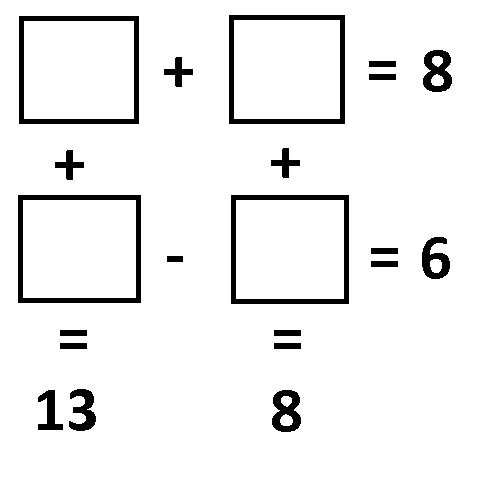 Он говорит им: «Вы можете встретиться сегодня и спланировать стратегию. Но после сегодняшнего дня вы будете в изолированных камерах и не будете общаться с друг друга.

«В тюрьме есть коммутатор, в котором есть два светильника. переключатели с обозначениями 1 и 2, каждый из которых может быть в верхнем или нижнее положение. Я не говорю вам об их нынешнем положении. В переключатели ни к чему не подключены.

«После сегодняшнего дня, время от времени, когда мне так хочется, я случайным образом выберет одного заключенного и сопроводит его к выключателю комната.Этот заключенный выберет один из двух переключателей и изменить свое положение. Он должен щелкнуть одним переключателем, когда посещает коммутатор и может щелкнуть только один из переключателей. Тогда он будет привел обратно в камеру.

«Никому не будет позволено менять переключатели, пока я не приведу следующий заключенный в рубку.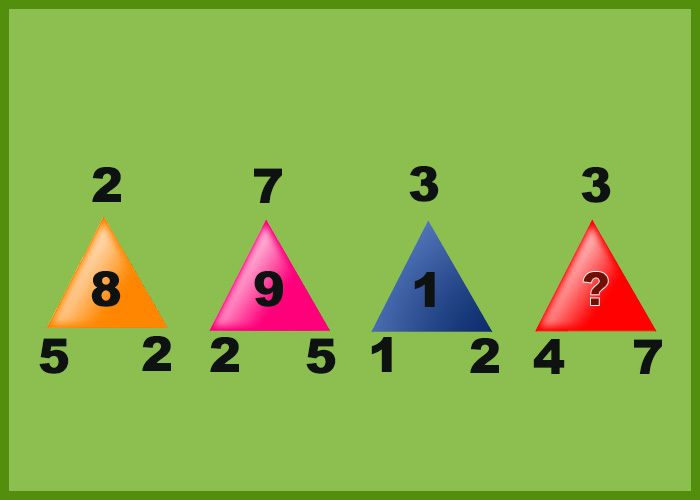 Я собираюсь выбрать заключенные наугад. Я могу выбрать одного и того же парня три раза за грести, или я могу прыгнуть и вернуться.Я не буду трогать выключатели, если бы я хотел, чтобы ты умер, ты бы уже был мертв.

«Если у вас будет достаточно времени, все в конечном итоге посетят коммутатор. номер столько же раз, сколько и все остальные. В любое время, любой может заявить мне: «Мы все посетили коммутатор».
«Если это правда, то вы все будете освобождены. Если это ложь, и кто-то еще не посетил коммутатор, вы все умрете ужасно.За вами будут внимательно наблюдать, и любая попытка нарушение любого из этих правил приведет к мгновенной смерти всех ты »

Какую стратегию они придумали, чтобы быть свободными?

19. Горящие веревки для измерения времени

keyboard_arrow_up

В начало

Разминка: вам дается коробка спичек и кусок веревка.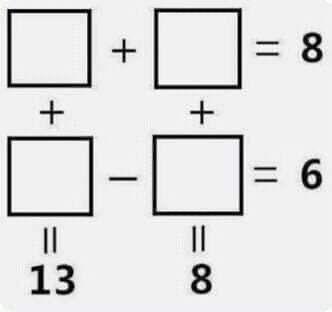 Веревка горит со скоростью одна веревка в час, но он не может гореть равномерно.Например, если вы зажжете веревку на одном конце, пройдет ровно 60 минут, прежде чем вся веревка сгорела, но, возможно, первая 1/10 веревки нужно 50 минут, чтобы сжечь оставшиеся 9/10 веревки горение занимает всего 10 минут. Как можно измерить период ровно 30 минут? Вы можете выбрать стартовый время. Точнее, учитывая спички и веревку, вы должны сказать слова «начало» и «готово» с интервалом ровно 30 минут.

Актуальная проблема: Учитывая коробку спичек и две такие веревки, не обязательно одинаковые, измеряются за 15 минут.

20. Минимальное количество самолетов

keyboard_arrow_up

В начало

На острове Бэгшот есть аэропорт. Аэропорт — это база неограниченного количества одинаковых самолетов.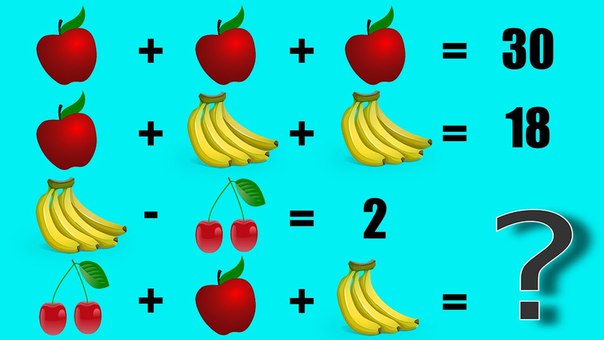 Каждый у самолета есть запас топлива, чтобы он мог лететь ровно на половину пути по всему миру, по большому кругу.Самолеты имеют возможность дозаправки в полете без потери скорости и утечки топливо. Хотя топливо не ограничено, остров является единственным источником топлива.
Какое наименьшее количество самолетов необходимо для получения одного самолета по всему миру при условии, что все самолеты должны благополучно вернуться в аэропорт? Как вы пришли к своему ответу?

Примечания:
(a) Каждый самолет должен вылетать и возвращаться в один и тот же аэропорт, и это единственный аэропорт, в котором они могут приземлиться и заправиться на земле.
(b) У каждого самолета должно быть достаточно топлива, чтобы вернуться в аэропорт.
(c) Время и расход топлива заправки можно не учитывать. (так мы также можем предположить, что один самолет может заправить более одного самолетов в воздухе одновременно. )
(d) Количество топлива, перевозимого самолетами, может быть нулевым до тех пор, пока другой самолет заправляет эти самолеты. Что наименьшее количество самолетов и количество топливных баков, необходимых для выполнить эту работу? (нам нужен только самолет, чтобы облететь мир)

21.Минимальное количество весов

keyboard_arrow_up

В начало

Однажды ко мне пришел оптовый торговец и задал мне эту проблему. Каждый день в своем бизнесе он должен взвешивать суммы от одного фунта до ста двадцати одного фунта, с точностью до фунта. Сделать это, какое минимальное количество гирь ему нужно и насколько тяжелый должен быть каждый вес?

22.Относительно Prime Bet

keyboard_arrow_up

В начало

Есть ящик, в котором хранились разные пронумерованные шары.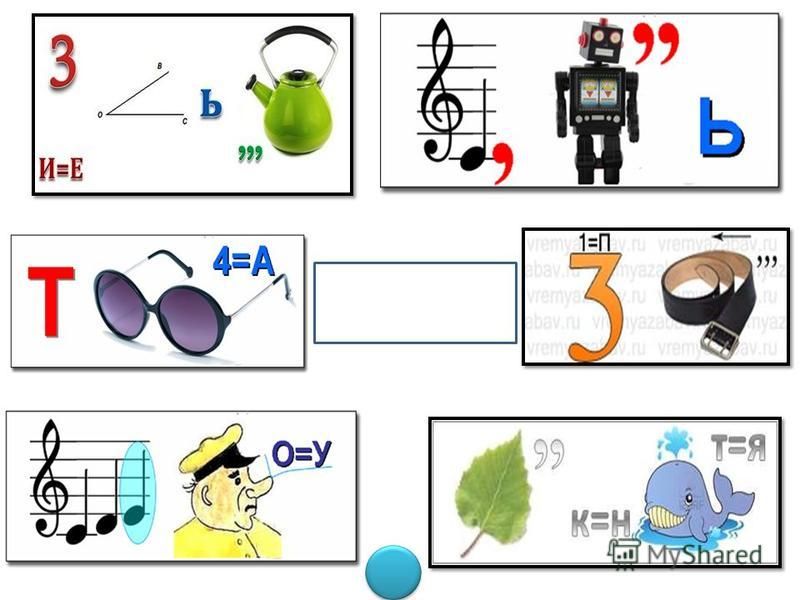 Вы должны случайным образом выбрать два шара из лота.

Если кто-то предлагает вам шанс 2 к 1, то числа будут относительно простое число, например
. Если выбранные вами шары имеют числа 6 и 13, вы теряете 1 доллар.
Если выбранные вами шары имеют номера 5 и 25, вы выигрываете 2 доллара.
Вы примете эту ставку?

23. Переход через мост

keyboard_arrow_up

В начало

Четыре человека должны перейти ночью по шаткому мосту. К сожалению, у них только один фонарик и мост тоже опасно переходить без него. Мост достаточно крепкий для поддержки двух человек одновременно. Не все люди занимают одно и то же время перейти мост.Время для каждого человека: 1 мин., 2 мин., 7 мин. и 10 мин. Какое кратчайшее время нужно всем четверым перейти мост?

24. 25 лошадей, 5 треков

keyboard_arrow_up

В начало

У мистера Джона 25 лошадей, и он хочет выбрать 3 самых быстрых лошади. из этих 25. У него всего 5 гусениц, то есть всего 5 лошадей. может работать одновременно. У него даже нет секундомера.Что минимальное количество скачек, необходимое для поиска трех самых быстрых лошадей?

25. Головоломка с переворачивающимися монетами

keyboard_arrow_up

В начало

На столе лежит двадцать монет, десять в настоящее время решки и десятки. Вы сидите в стол с завязанными глазами и в перчатках. Ты умеешь чувствовать где находятся монеты, но не могут видеть или чувствовать, направляются ли они или решки.Вы должны создать два набора монет. Каждый набор должен иметь такое же количество орлов и решек, что и в другой группе. Вы можете только перемещайте или подбрасывайте монеты, вы не можете определить их Текущее состояние.

Как создать две четные группы монет с одинаковым номером орла и решки в каждой группе?

26.

Случайные места для самолетов keyboard_arrow_up

В начало

Люди стоят в очереди на посадку в 100-местный самолет.Стив первый человек в очереди. Он садится в самолет, но внезапно не может вспомнить номер его места, поэтому выбирает место на случайный. После этого каждый человек, попавший в самолет, садится в назначенное им место, если оно доступно, в противном случае они выберут произвольно открытое место для сидения.

Рейс заполнен, вы последний в очереди. Что вероятность того, что вы сядете на отведенное вам место?

27.Доля девочек и мальчиков

keyboard_arrow_up

В начало

В стране, где все хотят мальчика, каждая семья продолжает иметь детей, пока не родится мальчик. Через какое-то время какой соотношение мальчиков и девочек в стране? (Предполагая вероятность иметь мальчика или девочку одно и то же)

28.

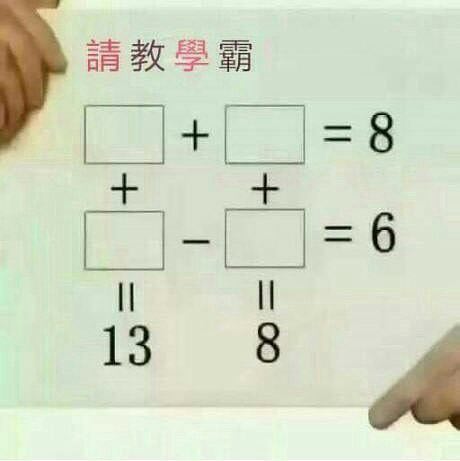Шляпы и монстр keyboard_arrow_up

В начало

Есть остров с 10 жителями.Однажды приходит монстр и говорит, что собирается съесть все до одного, но даст у них шанс выжить следующим образом:
Утром монстр выстроит в очередь всех людей — одиночные файл так, чтобы последний человек видел оставшиеся 9, следующий человек видит оставшиеся 8 и так далее, пока первый человек, который очевидно никого не видит перед собой. Тогда монстр случайным образом наденьте им на головы черные или белые шляпы (они могут быть белый, полностью черный или любое их сочетание).
Монстр предложит каждому человеку, начиная с последнего (кто видит чужие шляпы), чтобы угадать цвет своей шляпы. Ответом может быть только одно слово: «белый» или «черный». Монстр съест всех десяти заложников, как только второй пленник ответит неправильно. Все остальные люди услышат предположение, но не результат предположения. Затем монстр перейдет к следующему до последнего человека (который видит только 8 человек) и так до конца.
Чудовище дает им подумать всю ночь.

The Task:
Разработайте стратегию, которая гарантирует выживание всех пленников.

Допущения:
1) Все 10 человек могут легко понять вашу стратегию и будут выполнить его с безупречной точностью.
2) Если монстр подозревает, что кто-то из людей раздает информация любому из оставшихся членов команды интонацией слова при ответе или любые другие знаки, или наощупь, он съест каждый.
3) Единственно допустимый ответ — короткий, бесстрастный «белый» или «чернить».

29. Яйца из здания

keyboard_arrow_up

В начало

Предположим, что есть 100-этажное здание. Вам дано 2 идентичные яйца.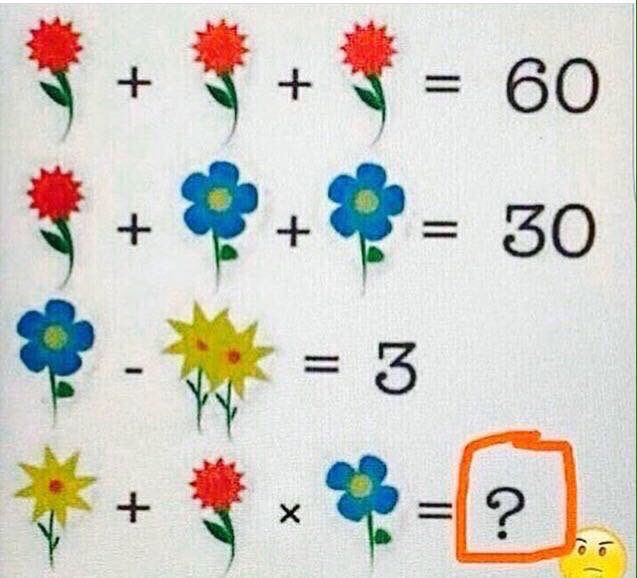 Самое интересное свойство яиц в том, что у каждого яйца есть свой «пороговый» этаж. Назовем этот этаж N. Это означает, что яйцо не разобьется при падении с любым этажом ниже этажа N, но яйцо обязательно сломается любой этаж выше этажа N, включая сам этаж N.

Например, если свойство яиц таково, что N равно 15, эти яйца всегда будут разбиваться на любом этаже выше или равном 15-й этаж, но эти яйца никогда не разобьются ни на одном этаже ниже этаж 15. То же самое верно и для других яиц, поскольку они идентичный.

Это очень крепкие яйца, потому что их можно уронить несколько раз. раз без поломки, пока они падают с пола ниже их «порогового» этажа, этаж N.Но как только яйцо упало этажом выше порога этажа

Вот загадка: какую стратегию следует использовать, чтобы минимизировать количество капель яиц, используемых для поиска этажа N ( порог пол) для яйца? Кроме того, каково минимальное количество падает в худшем случае при использовании этой стратегии?

Помните, что вам дается 2 одинаковых яйца, оба такой же точный порог пола.

30.5 пиратов, 100 золотых монет

keyboard_arrow_up

В начало

Пять корабельных пиратов получили 100 золотых монет и должны поделить добычу. Пираты все очень умны, коварный и эгоистичный (особенно капитан).

Капитан всегда предлагает распределить добычу. Все пираты голосуют за предложение, и если половина экипажа или больше уходит «Да», добыча делится, как предлагается, так как ни один пират не будет готовы сразиться с капитаном без превосходящей силы на их сторона.

Если капитан не заручился поддержкой хотя бы половины своей команды (включая его самого), ему грозит мятеж, и все пираты повернуться против него и заставить его ходить по доске. Пираты начинают снова со следующим старшим пиратом в качестве капитана.

Какое максимальное количество монет может оставить капитан? рискуя своей жизнью?

Решение логических задач — как решать задачи на логику

Самое главное в решении логических задач

Известные техники решения логических задач

Табличный метод

Круги Эйлера

Метод рассуждений

Метод рассуждений «с конца»

Решение логических задач и ребусов.

Логические задачи, ребусы, загадки и головоломки | Статья:

Ребусы. Логические задачи, головоломки, тесты на интеллект, логические игры

Праздник головоломок

Составление ребусов и других головоломок с Online Test Pad — Дидактор

Числовые ребусы как средство развития логического мышления

пазлов для начинающих

Логические головоломки

логических головоломок | Brilliant Math & Science Wiki

Логическая головоломка | игра | Британника

Перекрывающиеся группы

Узнайте больше в этих связанных статьях Britannica:

Логические головоломки для подростков и подростков

веселых логических головоломок

Пазлы рыцари и лжецы

математических и логических головоломок по программе Mr Barton Maths

Математические и логические головоломки

Содержание

1. Круг смерти

2.

3. Обручальное кольцо

4. Задача средних значений

5. Как избежать тролля

6. Пещера Али-Бабы

7. Питьевая игра-головоломка

8.Жемчуг раджи

9.

10. День рождения Шерил

11. Возраст детей

12. Кольцо вокруг Земли

13. Школьные шкафчики

14.Ставка дьявола

15. Половина яйца

16.

17.Три лжеца подбрасывают монету

18. Освободить узников

19. Горящие веревки для измерения времени

20. Минимальное количество самолетов

21.Минимальное количество весов

22.Относительно Prime Bet

23. Переход через мост

24. 25 лошадей, 5 треков

25. Головоломка с переворачивающимися монетами

26.

27.Доля девочек и мальчиков

28.

29. Яйца из здания

30.5 пиратов, 100 золотых монет

Добавить комментарий Отменить ответ