Решение задач онлайн
Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.
Основы математики
Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.
Онлайн программа решения задач курса предварительной алгебры (геометрии)
Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.
Онлайн программа решения задач по алгебре
Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Онлайн программа решения задач по тригонометрии
Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.
Онлайн программа решения задач курса предварительной алгебры
Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.
Онлайн программа решения задач курса высшей математики
Решение задач c определенными, неопределенными интегралами.
Онлайн программа решения статистических задач
Решайте задач с нахождением вероятности, комбинаторные задачи.
Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
www.math10.com
Все онлайн калькуляторы для решения задач · Контрольная Работа РУ · Теперь вы можете задать любой вопрос!
Решение интегралов
Это сервис, где можно вычислить определенные, неопределенные интегралы, а также двойные, несобственные, кратные.
Производная функции
Это сервис, где можно вычислить производную функции, частную производную функции, а также производную неявно заданной функции
Системы уравнений
Позволяет решать системы линейных уравнений методом Крамера, методом Гаусса, а также вообще любые системы уравнений.
Решение систем уравнений »
Решение неравенств
Решает неравенство, а также строит решённое неравенство на графике для наглядности
Решение неравенств »
Решение уравнений
Это сервис позволяет решать уравнения, в том числе получить подробное решение, а также увидеть решение уравнения на графике
Решение пределов
Этот сервис позволяет найти предел функции. Также рассматривается подробное решение правилом Лопиталя.
Комплексные числа
Здесь можно вычислить комплексные выражения: находить формы: алгебраическую, тригонометрическую, показательную; модуль и аргумент, сопряжённое, геометрическую интерпретацию
Комплексные числа »
Разложение в ряд
Здесь приведены последние статьи про использование калькуляторов
Теория вероятности
Теория вероятности онлайн позволяет вычислять без проблем математическое ожидание, дисперсию, число перестановок, сочетаний, размещений и факториал.
Теория вероятности »
Другое
Здесь представлены различные онлайн калькуляторы, и в том числе:
обычный инженерный математический калькулятор
калькулятор онлайн
Другие онлайн калькуляторы »
Физика онлайн
Физика онлайн позволяет посмотреть физические эксперименты он-лайн!
Физика онлайн
www.kontrolnaya-rabota.ru
интересные математические задачи и задания
Математические задачи по возрасту
Заинтересовать дошкольников 5-7 лет, учащихся начальных классов проще всего. Главное — предложить разнообразные занимательные задания, сделать процесс решения задач увлекательным, с элементами игры, и обеспечить умеренную сложность задач.
К 3-4 классу мотивация у школьника часто снижается. Родителям важно не упустить этот момент и объяснить ребёнку, зачем вообще заниматься математикой и учиться решать задачи.
Примеры заданий по возрасту
Занимательные задачи по типу
В плане регулярных тренировок в любом возрасте должно быть выполнение заданий минимум 5-7 типов. Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических способностей.
Среди самых интересных и популярных категорий заданий на логику и смекалку:
- Классические логические задачи. Учат детей анализировать текст, выделять главное, рассуждать и делать выводы.
- Арифметические ребусы. Отличная отработка ключевых мыслительных операций: абстрагирование, анализ и синтез, сравнение и другие.
- Задачи на закономерности, последовательности.
Примеры заданий по типу
logiclike.com
Решение задач по математике онлайн
Данный сайт обращён к учащимся в том или ином объеме изучающим математику и/или геометрию и призван помочь школьникам и
студентам в изучении курса математики, освободить их от многих рутинных вычислений, и подсказать метод решения.
Основу сайта составляют математические программы (калькуляторы) для решения задач онлайн.
Все вычисления производятся на сайте, программы не нужно скачивать и устанавливать на компьютер.
Решение задач приводится в виде, принятом в большинстве школ и вузов, некоторые задачи решаются двумя способами.
Все математические программы (калькуляторы) бесплатные.
Полный список математических и геометрических задач для решения вы можете найти в меню справа.
Вычислить: $$x^2+2x-1=0$$ $$2\frac{1}{3} \cdot \left( 2\frac{3}{4}-1\frac{3}{8} \right) $$ Решение: $$2\frac{1}{3} \cdot \left( 2\frac{3}{4}-1\frac{3}{8} \right) = $$
| Промежуточные результаты: |
| $$2\frac{3}{4}-1\frac{3}{8} = \frac{2\cdot(2\cdot4+3)-1\cdot8-3}{8} = \frac{11}{8}$$ |
Вычислим дискриминант.
$$D = b^2-4ac = 8$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{-2\pm\sqrt{8}}{2} = \frac{-2\pm2\sqrt{2}}{2} $$ Ответ: $$ x_1 = -1+\sqrt{2},\; x_2 = -1-\sqrt{2} $$ Решить неравенство: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1$$ Решение: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1\Rightarrow $$ $$\frac{4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) }{3 x-1} \geq 0$$Упрощение выражения \(4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) \)
$$4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3+ \left( -x+1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3-3 x^2+x+3 x-1= $$ $$x^2-3 x+2$$ Ответ: \( x^2-3 x+2 \) Решим квадратное уравнение \( x^2-3 x+2= 0 \)Решение квадратного уравнения \( x^2-3 x+2= 0 \)
Вычислим дискриминант. $$D = b^2-4ac = 1$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{3\pm\sqrt{1}}{2} = \frac{3\pm1}{2} $$ Ответ: \( x_1 = 2,\; x_2 = 1 \)
Решение по теореме Виета
Т.к. \( \left| a \right|=1 \), то можно воспользоваться теоремой Виета: $$x^2+px+q=0 \Rightarrow \left\{\begin{array}{l} x_1+x_2=-p \\ x_1 \cdot x_2=q \end{array}\right.$$ $$\left\{\begin{array}{l} x_1+x_2=3 \\ x_1 \cdot x_2=2 \end{array}\right. \Rightarrow \left\{\begin{array}{l} x_1=2 \\ x_2=1 \end{array}\right.$$ Ответ: \( x_1= 2,\; x_2= 1 \) Корни квадратного уравнения: $$ x_1 = 1 ;\; x_2 = 2 $$ Решим линейное уравнение \( 3 x-1= 0 \) Корень линейного уравнения: \( x = \frac{1}{3}\)| $$ \frac{1}{3} $$ | $$ 1 $$ | $$ 2 $$ |
Нахождение производной функции
Найти производную функции $$ f(x) = \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}$$ Решение $$ f'(x) = \left( \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( 1+sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot \left( 2 \cdot x\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot 2= $$ $$ = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$ Ответ: $$ f'(x) = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$В разделе Книги вы найдете большой список книг, учебников, решебников, ГДЗ, тестов и контрольных работ с ответами по математике
и геометрии для всех классов общеобразовательных школ.
Все книги в электронном виде и доступны для скачивания бесплатно.
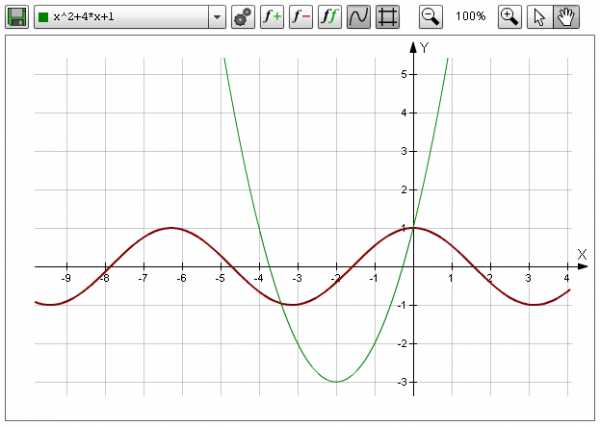
Отдельно стоит упомянуть программу для построения графиков функций онлайн.
Программа работает в вашем браузере, её не нужно устанавливать на компьютер.
Для её работы нужен только установленный Adobe Flash Player.

Возможности программы:
— можно строить несколько графиков в одном окне
— можно менять цвет и толщину линии постоения графика
— можно скрывать и отображать как сетку так и графики
— можно изменять масштаб отображения
— можно трассировать графики
— можно сохранять построение графиков в виде картинки
www.math-solution.ru
Как решать задачи по математике?
Как научить ребенка решать задачи по математике?
Решая задачу о блинчиках мы увидим, что:
• сложными могут оказаться и простые с виду задачи.
• Учить ребенка думать можно и нужно на примере простых задач. Если же с первых классов школы задурить ему мозги, то думать он не научится никогда. Но обнаружится это в классе 6-7. Слишком поздно.
Статья будет длинная и нудная. Она
может быть интересна исключительно родителям, желающим научить собственного ребенка понимать математику. Научить думать.
Простоe и сложное
Чем проще принцип, тем сложнее его доказательство и длиннее объяснение
собственные наблюдения
К примеру, большая теорема Ферма.
Теорема простая, понять ее способен даже ученик начальной школы. А вот доказать её удалось лишь спустя три столетия, в 1994 г. Говорят и сейчас не более двухсот математиков в мире понимают это доказательство. Я в их число не вхожу
Как(не)научить понимать: «Принцип короткого замыкания»
Главный принцип (не)успешного обучения, который я обнаружил — «принцип короткого замыкания»:Понимание не возникает из простоты, оно возникает из сложности. Простота и понимание возникают в процессе и являются результатом обучения . И категорически запрещено укорачивать этот путь!
Именно на этом пункте и спотыкается традиционная школа.
«Игровой подход», как ласково они это называют, цветные картинки, два притопа – три прихлопа … Это НЕ обучение, а его имитация. (Я уже писал о «самолетопоклонниках» Ричарда Фейнмана в книге «Школа понимания».)
«Ах, как все просто и понятно!»
«Ах, как понятно объясняет учительница! Дети все схватывают с первого раза!» Только вот беда: со второго раза, когда встречается чуть видоизмененная задача, путаются и заявляют, что «Они этого не проходили!». Что является абсолютной правдой. И «заслуженному учителю» вновь приходится «в игровой форме» исполнять танец с бубном около «интерактивной доски».
Но и танцевать большинство школьных учителей мастера не великие. Им бы лучше в хор: орать на детей они умеют громко, эмоционально, с душой …
Да, ирония злая. Но большинством школьных функционеров, маскирующихся под Учителей, вполне заслуженная.
На выходе «игрового подхода» к 9-11 классам мы имеем ужасающую статистику непонимания математики, равно, как и других предметов.
Если уже известный ответ задачи, готовое «решение» препарировать, разложить на составляющие, «понятно объяснить», то, естественно, ребенок запомнит «решения» десятка задач. И, также естественно, не научится их решать.
Объяснить готовый ответ и решить задачу – две гигантские разницы!
«Главное — возбудить аппетит и чувства: иначе воспитаете осла, нагруженного книгами …»
Монтень
Кто должен учить?
Основам науки должен учить тот, кто сам эти основы понимает.
Научить думать сможет только тот, кто умеет думать сам.
В начальной же школе работают … ну, вы сами это знаете.
Почему-то считается, что основам математики может научить кто угодно, даже педагог, который сам не умеет решать простейших задач. Но почему-то потом, в старших классах дети массово отказываются понимать математику и что-либо вообще.
Итак,
Задача о блинчиках
«Мама жарит блинчики с творогом. Каждый блинчик она обжаривает с двух сторон: 2 минуты с одной и 1 минуту с другой. На сковороду одновременно умещаются 4 блинчика. Вопрос: за какое минимальное время мама обжарит 7 блинчиков?»
…Поместите эту задачу в раздел самых сложных задач профильного ЕГЭ и процентов 80 выпускников с ней не справятся и/или потеряют неоправданно много времени. Ожидание «подвоха» не позволит выпускникам, чьё математическое мышление за 11 лет так и не было развито, найти верное решение. Смутное чувство интуиции заставит их сомневаться, перебирать варианты в поисках «красивого» ответа…
Решение задачи
Задачи в начальной школе простые, даже примитивные. Ответ получается методом перебора плюс немного здравого смысла и чуть-чуть воображения…
…Сначала мама обжаривает 4 блинчика за 3 минуты ( 2+1=3).
Затем оставшиеся 3 блинчика (7 — 4 = 3), тоже за 3 минуты.
Итого 6 минут. Вроде все верно?
Но:
• Как доказать, что решение верное? Не может же ответ быть настолько простым! Прямо как теорема Ферма …
• И как решить эту же задачу, если мама – директор «блинной фабрики» и за день обжаривает N блинчиков?
Оставим в покое маму – фабриканта и вернемся к условию.
Анализ решения задачи
Сразу бросается в глаза неэффективность использования сковороды. Как-то некрасиво, не по-школьному получается. Незрелый ум школьника замечает: КПД сковороды слишком низкий, одно место при второй обжарке пустует. Сковорода греет воздух, а масло горит …. Можно ли как-нибудь использовать одно свободное место во втором цикле обжарки?
Разумный вопрос: его следует задать и поискать ответ.
Метод перебора
Перебор вариантов это метод. Но не столько метод решения, сколько метод оценки данных, используя который иногда можно нащупать решение.
Но нащупать — не значит доказать, что оно верное.И сомневающийся школьник продолжает в поисках правильного ответа перебирать варианты … То есть действует методически неверно.
«Предположим, что …» — метод
Предположим, что для обжарки требовалось бы три «неделимых» минуты — блинчики обжаривались бы за один раз с одной стороны. Решение оказалось бы настолько тривиальным, что и решать тогда было бы нечего!
Но в условии сказано: блины переворачивают!
Поэтому количество вариантов возрастает и школьник судорожно ищет «что в какую формулу вставить, и что на что разделить»
(по ироничному наблюдению за отличниками академика В.И.Арнольда, одного из крупнейших математиков ХХ века). Смутное чувство интуиции шепчет: здесь что-то не так, не все так просто. Человек бессистемно перебирает варианты, пока не доходит до «перестановок из N по M». Но и комбинаторика в младшешкольной задаче выигрыша во времени не дает …
Человеку кажется: он что-то упустил и судорожные эксперименты с перекладыванием блинов, попытки вспомнить «похожие» задачи и «волшебные» формулы продолжаются. Пока уставший от непродуктивной механической деятельности ум не ошибется и не «нащупает красивый ответ»: 5 минут.
Именно такое «решение» получила учительница начальных классов в школе, которую посещал мой сын. Он тогда поспорил с учительницей, но она настаивала: «Все-таки здесь получается скомбинировать! Сейчас не помню как именно, но точно – получается!». Задачу она дала на уроке «Умники и умницы», поэтому нашлась еще пара «Умников», поддержавших «красивое» решение.
Это вообще не шутка.
«Ум человеческий склонен верить непонятному»
Тацит
Математическая логика и интуиция
Неразвитое мышление активизирует «интуицию». Но ум человеческий не приспособлен адекватно воспринимать мир цифр. Это, кстати, научно подтвержденный факт.
Например: как вы думаете, сколькими способами можно разложить колоду всего лишь из 52 карт? Правильный ответ шокирует: неужели мы способны НАСТОЛЬКО ошибаться?!
Чтобы шок состоялся, прикиньте ответ, а потом посчитайте на калькуляторе факториал 52. Пожалуй, это больше, чем количество атомов в известной Вселенной …
… Без специальной подготовки ум человеческий воспринимает мир цифровой СЛИШКОМ уж несовершенно. Поэтому и возникает «смутное чувство интуиции».
Решение задачи о 6 блинчиках
Предположим, что теперь мама обжаривает только 6 блинчиков. Можно ли теперь уложиться в 5 минут?
Решение.
Итого: 2 + 1 +1 + 1 = 5 минут.
Минуту удалось-таки сэкономить!
Хотя и тут разбазаривание ресурсов налицо: последнюю минуту на сковороде было только 2 блина … . Как говорится, абсолюты в реальном мире недостижимы, считай – не считай …
Арифметика или геометрия? Визуализация VS абстрагирования
Сложно было следить за текстовым изложением решения, не правда ли? А теперь представьте, каково это детям!..Не проще ли изобразить процесс решения графически? Попросту – нарисовать?!
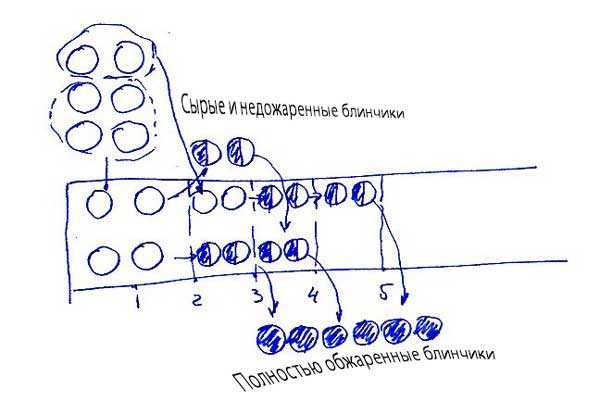
… Детям исключительно полезно решать задачи подобным образом.
С помощью рисунков они приучаются думать (а не запоминать типовые «решения»). Оперирование образами формирует связное, логическое мышление, они узнают, что такое понимание.
Но вряд ли хотя бы 0,1% учителей математики представляет, как работает ум и что в нем происходит во время решения математической задачи! В МПГУ этому не учат.
Родителю – на заметку: всемирно известный академик В.И Арнольд славился доходчивым стилем преподавания и геометрическим подходом к традиционным разделам математики. А также жесткой критикой попыток американцев и, особенно, французов излагать математику на излишне высоком уровне абстракции. «Это великий-то
Вот именно.
Доказательство очевидного: «правильный ответ» задачи
Как узнать, верен ли полученный ответ? Проверка решения это составная часть решения, не менее важная, чем само решение.
Как доказать, что за 5 минут 7 блинчиков обжарить нельзя, а 6 — можно?..
Дроби появляются незаметно …
Как максимальная скорость автомобиля: не обязательно «выживмать» все, можно двигаться и медленнее. Но быстрее — невозможно.
Хотя для такой оценки и требуется понимание дробей, но не очень глубокое.
Дроби, кстати — раздел арифметики, в котором массово «плавает» большинство школьников на ЕГЭ (???). Поэтому, насколько это задача для 3 класса … зависит от способа ее подачи и квалификации «подающего» блинчики к столу решающих задачу
Итак:
при полной загрузке сковороды для обжарки 7 блинчиков требуется больше 5 минут. Не надо больше мучиться и «комбинировать».
А вот для 6 блинчиков можно варианты и поискать.
Задача о блинной фабрике
А что насчет мамы – блинного капиталиста? Если ребенок уяснил метод решения, то теперь ему не составит труда масштабировать решение на любые количества. Но скажите: разве это было очевидно до того, как мы прошли весь этот довольно сложный путь?!
Единственный способ научить ребенка решать задачи это научиться решать их самому. Не так уж и сложно взрослому и заинтересованному человеку научиться решать задачи младшей школы, не так ли? Было бы желание. А если желание отсутствует у наиболее заинтересованных в ребенке людей … тогда дело швах. Сегодня рассчитывать на школу, также, как на репетиторов — абсолютно дохлое дело.
Вернитесь к началу статьи и представьте, что все это происходило в классе. Получилось? А потом представьте, то же самое в присутствии репетитора и ответьте себе на два вопроса:
«Соображайте, мужчина!», — как четверть века назад строго заметила мне смотрительница около турникета метро на «Комсомольской», когда я по ошибке сунулся не в те ворота.
butorov.ru
5 секретов решения всех математических задач
 1. Перед началом решения новых типов задач повторите основы.
1. Перед началом решения новых типов задач повторите основы.
Задачи будут решаться легко, если вы будете стараться понять, как к ним применить основы математики. Большинство студентов не умеют решать задачи по одной причине: они не владеют основными понятиями. Как говорилось ранее, эта проблема решается через повторение программы прошлых лет. Но не думайте, что это займет много времени. Ведь вам нужно прочитать только старые уроки, связанные с новыми математическими задачами. На это уйдет всего несколько минут.
Избегая этой простой работы — заглядывать в старые учебники, — плохие студенты накапливают непонятные моменты, и предмет становится для них сложнее с каждым днем.
Нет необходимости страдать из-за этой проблемы. Поступайте разумно и выясняйте все непонятное, обратившись к старым конспектам, друзьям и преподавателям за помощью. Если знание основ математики у вас крепкое, вы справитесь с любой задачей. Поэтому не допускайте слабости со своей стороны.
2. Стремитесь не запомнить, а понять ход решения задачи.
Большое преимущество математики в том, что не нужно ничего запоминать, кроме формул и единиц измерения. Но стать специалистом можно только одним путем: через постоянную практику.
Чем больше вы решаете задач определенного типа, тем лучше вы понимаете их логику, тем опытнее вы становитесь. Когда вы тренируетесь:
— мозг автоматически записывает решение и предпринимаемые шаги;
— увеличивается скорость решения задач;
— повышается уверенность в себе, которая помогает решать задачи на экзамене спокойно и правильно.
Практикуйтесь в решении задач как можно чаще. Лучше всего для этого перерешать все задачи из учебника. Также решите все задачи, предложенные преподавателем. Выполнив и это, найдите задачи прошлогодних экзаменов и решите их тоже.
3. Подробно записывайте в тетрадь решение задач за преподавателем на уроке.
В математических задачах логика решения так же важна, как и правильный ответ. Поэтому, когда преподаватель объясняет решение задачи, будьте внимательны. Обязательно запишите его в тетрадь в точной последовательности, чтобы потом не забыть все этапы. Усвоив логику решения задач разного типа, вы не растеряетесь на экзамене.
4. Выполняйте домашние задания по математике как можно раньше, пока вы хорошо помните объяснения.
Выполнение домашнего задания в тот же день очень полезно, потому что все еще свежо в памяти. Можно легко вспомнить все рекомендации и сделать задание за более короткое время.
Хотя этот совет касается всех предметов, он особенно важен для математики. Если вы отложите выполнение задания по математике, то можете забыть этапы решения задач. Это важно, если математика сложна для вас. Зная о простом секрете (выполнять домашние задания по математике как можно раньше), вы сделаете этот предмет более легким для себя.
Чтобы математика стала более легким предметом для вас, решайте больше задач, чем задает преподаватель! Эта дополнительная работа поможет прочному усвоению формул и принципов решения. Если вы будете следовать этому совету изо дня в день, математика станет легче вам даваться!
5. Разбирайте все непонятное немедленно.
В отличие от изучения языков, математика является таким предметом, по которому можно набрать 100 %-ное количество баллов! Поэтому добросовестно учите ее, не накапливайте непонятных моментов. Обращайтесь за помощью к преподавателям, друзьям и репетиторам и выясняйте все мелочи.
Решайте много задач, тогда математика вам будет нравиться и ваши баллы станут выше.
blog.zao4nik.ru
Математические головоломки | Логические задачи
Кирпич
Кирпич весит 1 килограмм плюс половину собственного веса.
Сколько весит кирпич?
Муха
Два поезда, находящиеся на расстоянии 200 км, движутся навстречу друг другу со скоростью 50 км/ч каждый. Муха берёт старт с одного из поездов и летит по направлению к другому со скоростью 75 км/ч. Долетев до другого поезда, муха разворачивается и летит назад к первому. Так она летает туда и обратно, пока два поезда не сталкиваются, и насекомое погибает.
Какое расстояние успела пролететь муха?
Есть два способа решить эту задачку, один – простой, другой – тяжёлый.
Поезда
Из Бостона в Нью-Йорк выходит товарный поезд, двигаясь со скоростью 60 км/ч. Через 30 минут навстречу ему из Нью-Йорка в Бостон выходит пассажирский поезд, двигающийся со скоростью 80 км/ч.
Который из поездов будет ближе к Нью-Йорку в момент встречи? (Попросите помощи школьников — они наверняка быстрее справятся с задачкой.)
Средняя скорость
Половину пути до города, находящегося на расстоянии 60 км, я проехал со средней скоростью 30 км/ч.
С какой скоростью я должен ехать остаток пути, чтобы общая средняя скорость всего путешествия была бы 60 км/ч?
Проволка над экватором
Окружность Земли равна примерно 40000 км. Если протянуть проволоку над экватором вокруг Земли так, чтобы длина проволоки была бы только на 10 метров (0,01 км) длиннее окружности земли, сможет ли пролезть под этой проволокой блоха? Мышь? Человек?
Диофант
Мало что известно о жизни одного греческого математика из Александрии, которого называют родоначальником алгебры. Предполагается, что он жил в 3-м веке нашей эры. По рассказам, на его надгробии была высечена следующая эпитафия:
«Детство Диофанта 1/6 жизни заняло; 1/12 жизни Диофант бороду растил; ещё 1/7 жизни Диофанта прошла до того, как он женился. Через 5 лет после свадьбы у Диофанта родился сын, который прожил только половину лет, что прожил его отец. А через 4 года после смерти сына умер Диофант.»
Сколько лет прожил Диофант?

Папирус Ахмеса
В 1858 году Шотландский коллекционер Генри Райнд приобрел древнеегипетский папирус подписанный именем «Ахмес». Этот свиток папируса, шириной 33 см и длинной 5,25 метров, является копией ещё более древнего математического руководства, относящегося ко времени фараона Аменемхета III. Вот одна задача из этого древнейшего из математических сборников:
Сто мер зерна надо поделить между пятью работниками так, чтобы второй получил настолько больше, чем первый, насколько третий больше, чем второй, и на столько же, насколько четвёртый больше, чем третий, и на столько же, насколько пятый больше, чем четвёртый. Сколько мер зерна должен получить каждый, если первый и второй работники вместе получат зерна в семь раз меньше, чем остальные три работника?
Сколько осталось до полуночи?
Через два часа до полуночи останется в два раза меньше, чем оставалось бы через час.
Который сейчас час?
Стрелки часов
В полдень часовая, минутная и секундная стрелки часов совпадают в одной точке циферблата. Чуть больше, чем через час и пять минут, часовая и минутная стрелки совпадут снова. Найдите с точностью до миллисекунды время, когда они совпадут.
Какой угол с ними будет в это время составлять секундная стрелка?
Бассейн
К бассейну подходят четыре трубы, по которым через краны можно контролировать скорость заполнения бассейна. Открыв первый кран, можно заполнить бассейн за 2 дня, второй – за 3 дня, третий – за 4 дня и четвёртый – за 6 часов.
Сколько понадобится времени, чтобы наполнить бассейн, открыв все четыре крана одновременно?
Переезд через пустыню
Военный автомобиль с важным посланием должен пересечь пустыню. Однако полного бензобака хватает только на половину пути. В распоряжении военной базы имеется несколько таких автомобилей, и бензин можно перекачивать из одного бака в другой. Никакими канистрами и тросами они воспользоваться не могут.
Как доставить сообщение, не бросая ни одного автомобиля в пустыне? (Попробуйте для наглядности проиграть ситуацию с игрушечными машинками.)
Авиотур
На одной далёкой планете есть только один аэропорт, находящийся на Севеном полюсе. В распоряжении аэропорта имеются 3 самолёта и неограниченное количество горючего. Бака самолёта хватает ровно до Южного полюса. Самолёты имеют возможность дозаправляться (перекачивать горючее из одного в другой), находясь в полёте.
Как самолёт может облететь вокруг планеты так, чтобы все самолёты вернулись в аэропорт?
Шаг №1. Два смолета летят до первой трети пути, один из них дозаправляет второй и поворачивает назад, а второй продолжает лететь до отметки 2/3 пути.
Шаг №2. Два самолета вновь вылетают из аэропорта до первой третьей пути. Один из них дозаправляет второй и поворачивает назад, а второй продолжает путь до отметки 2/3 пути.
Шаг №3. На отметке 2/3 пути теперь два самолета, бензобаки каждого заполнены на 2/3. Один из них дозаправляет второй и отправляется назад до отметки в 1/3 пути, где его встречает и дозаправляет 1/3 своего топлива третий самолет из аэропорта, оба летят обратно в аэропорт. В это время самолет, бывший на отметке 2/3 пути, с полным баком летит дальше, насколько это возможно (он пролетит над Южным полюсом, обогнет планету и долетит до отметки последней 1/3 пути до аэропорта).
Шаг №4. Остальные действия очевидны. Из аэропорта вылетает еще один самолет (на этот раз в противоположном направлении, то есть навстречу обогнувшему планету самолету), чтобы поделиться 1/3 своего топлива с основным самолетом и вместе с ним вернуться в аэропорт.
Волшебный пояс
Волшебный пояс, исполняющий желания хозяина, уменьшается в два раза в длину и в 3 раза в ширину после каждого исполненного желания. После исполнения трёх желаний площадь лицевой стороны стала 4 см2.
Какова была изначальная длина ремня, если его изначальная ширина была 9 см?
Болдвил
У всех жителей города Болдвил разное количество волос на голове. Нет ни одного жителя, у которого было бы точно 518 волос на голове. Население города превышает число волос на голове любого из жителей Болдвил.
Каково максимально возможное население города Болдвил?
Неверные жёны
Антрополог, изучавший племя в отдалённом уголке джунглей Амазонки, обнаружил странный обычай. Когда муж узнавал, что его жена изменяет, он должен был публично её казнить в полночь того же дня. Про любую женщину, изменяющую мужу, всегда знали все жители племени, кроме её мужа. Но мужу никто никогда не рассказывал об изменах его жены, потому что это противоречило кодексу чести. Тот же кодекс чести не позволял жёнам известить ту жену, чей муж был ей неверен. В противном случае она в тот же вечер пристрелила бы своего мужа. В день своего отъезда антрополог созвал всех представителей племени и объявил: «Я знаю, что в этом племени есть неверные жёны.» И на девятый день все неверные мужья были казнены.
Сколько было неверных мужей?
Предположим, что количество неверных мужей равно единице. Тогда всем, кроме одной, жёнам известно, что среди жителей есть один неверный муж, в то время как жена этого неверного мужа уверена, что все мужья верны своим жёнам. Как только она услышит, что среди жителей есть как минимум один неверный муж, она тут же поймёт, что может быть только её муж, поэтому в тот же вечер она его незадумываясь застрелит.
А теперь представьте, что среди жителей есть два неверных мужа. Каждая жена таких неверных мужей уверена, что среди жителей есть только один неверный муж, поэтому ждёт, пока какая-нибудь из жён пристрелит своего мужа. Но в этот вечер никто никого не застрелил, а это может означать только одно: её СОБСТВЕННЫЙ муж ей ТОЖЕ неверен и является ВТОРЫМ неверным мужем в племени. Первая жена первого неверного мужа приходит к точно таким же выводам (она также ждала, что кто-то из жён застрелит своего мужа). Таким образом, обе оскорбленные жены в первый же вечер понимают, что их мужья им изменяют, и на следующий вечер (второго дня) пристреливают обоих мужей.
Следуя этой логике, нетрудно догадаться, что количество неверных мужей «n» будут пристрелены в «n»-нный вечер.
1 = 2
Найдите ошибку в математических выкладках:
x = 2
x(x-1) = 2(x-1)
x2-x = 2x-2
x2-2x = x-2
x(x-2) = x-2
x = 1
9 точек
Соедините 9 точек четырьмя прямыми линиями не отрывая руки и не обводя линий.
Девиз
В юности я обнаружил, что большой палец ноги рано или поздно проделывает дырку в носке. Поэтому я перестал надевать носки.Альберт Эйнштейн
brainden.com
