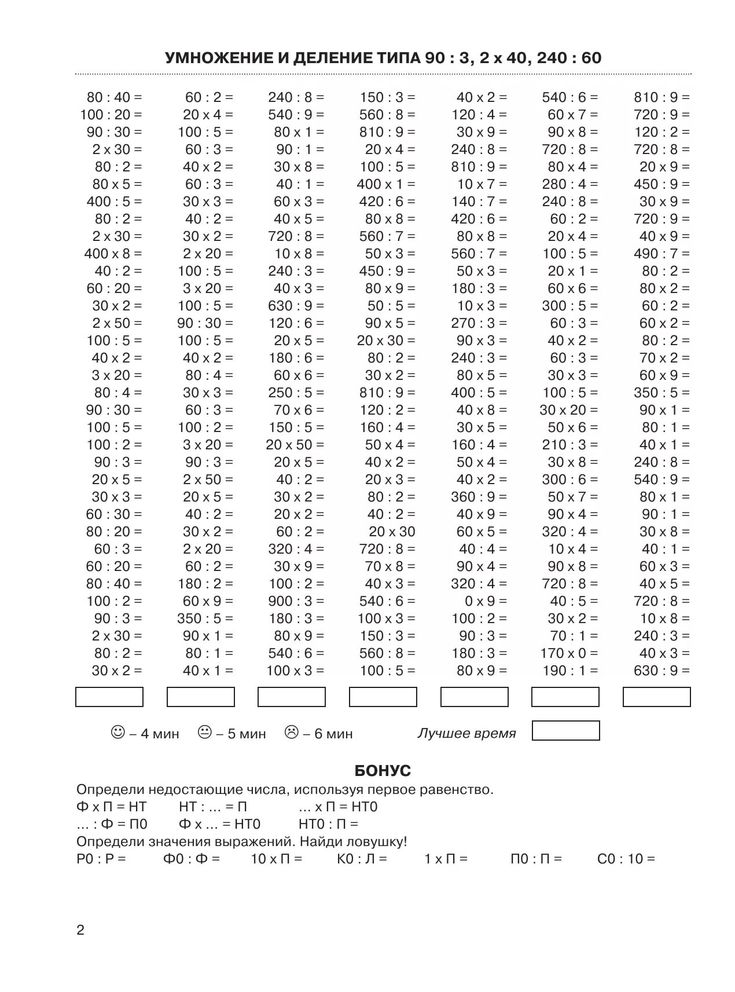
Примеры на умножение и деление. Второе полугодие.
Примеры на умножение и деление. Второе полугодие. Задачи по математике 3 класс
MAT-ZADACHI.RU
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
| | Математика 3 класс ->> Примеры Первое полугодиеВторое полугодие |
| 49 : 7 = 7 | 117 : 9 = 13 | 8 * 16 = 128 | 72 : 9 = 8 | 90 : 6 = 15 | |
| 23 * 7 = 161 | 6 * 17 = 102 | 171 : 9 = 19 | 11 * 4 = 44 | 48 : 2 = 24 | 13 * 2 = 26 |
| 85 : 5 = 17 | 16 : 8 = 2 | 49 : 7 = 7 | 10 * 22 = 220 | 35 : 7 = 5 | 32 : 8 = 4 |
| 24 * 2 = 48 | 56 : 7 = 8 | 189 : 9 = 21 | 12 * 5 = 60 | 4 * 22 = 88 | 126 : 9 = 14 |
| 28 : 7 = 4 | 198 : 9 = 22 | 3 * 21 = 63 | 21 * 5 = 105 | 17 * 2 = 34 | |
| 138 : 6 = 23 | 90 : 5 = 18 | 8 * 16 = 128 | 20 * 10 = 200 | 115 : 5 = 28 | 10 * 17 = 170 |
| 192 : 24 = 8 | 3 * 14 = 42 | 54 : 9 = 6 | 75 : 15 = 5 | 48 : 6 = 8 | 4 * 23 = 92 |
| 18 : 3 = 6 | 198 : 22 = 9 | 9 * 24 = 216 | 12 * 3 = 36 | 7 * 24 = 168 | 12 * 4 = 48 |
| 7 * 15 = 105 | 36 : 12 = 3 | 24 : 3 = 8 | 140 : 20 = 7 | 14 * 8 = 112 | 7 * 16 = 112 |
| 207 : 9 = 23 | 16 : 4 = 4 | 135 : 9 = 15 | 56 : 7 = 8 | 20 * 9 = 180 | 19 * 6 = 114 |
| 55 : 5 = 11 | 72 : 8 = 9 | 30 : 2 = 15 | 12 * 9 = 108 | 6 * 6 = 36 | 99 : 9 = 11 |
| 50 : 5 = 10 | 114 : 6 = 19 | 15 : 5 = 3 | 42 : 3 = 14 | 13 * 4 = 52 | |
| 65 : 5 = 13 | 66 : 6 = 11 | 9 * 9 = 81 | 12 * 8 = 96 | 8 * 17 = 136 | 51 : 17 = 3 |
| 144 : 6 = 24 | 11 * 8 = 88 | 24 * 7 = 168 | 95 : 19 = 5 | 207 : 23 = 9 | 5 * 21 = 105 |
| 15 * 4 = 60 | 114 : 19 = 6 | 48 : 24 = 2 | 17 * 9 = 153 | 18 * 6 = 108 | 152 : 8 = 19 |
| 45 : 3 = 15 | 63 : 3 = 21 | 176 : 8 = 22 | 7 * 16 = 112 | 70 : 14 = 5 | |
| 91 : 13 = 7 | 9 * 22 = 198 | 18 : 3 = 6 | 32 * 6 = 192 | 110 : 5 = 21 | 41 * 3 = 123 |
| 168 : 7 = 24 | 78 : 13 = 6 | 161 : 7 = 23 | 12 * 17 = 204 | 19 * 4 = 76 | 21 * 8 = 168 |
| 115 : 23 = 5 | 56 * 3 = 168 | 32 * 5 = 160 | 27 * 3 = 81 | 207 : 23 = 9 | 60 : 3 = 20 |
| 144 : 16 = 9 | 85 : 5 = 17 | 48 : 12 = 4 | 13 * 10 = 130 | 52 * 2 = 104 | 31 * 4 = 124 |
| 21 : 3 = 7 | 24 : 12 = 2 | 95 : 19 = 5 | 40 * 2 = 80 | 92 * 2 = 184 | 39 * 4 = 156 |
| 72 * 3 = 216 | 124 : 2 = 62 | 147 : 21 = 7 | 77 : 7 = 11 | 126 : 18 = 7 | 3 * 62 = 186 |
| 102 : 17 = 6 | 72 : 4 = 18 | 12 : 4 = 3 | 45 * 3 = 135 | 19 * 6 = 114 | 31 * 2 = 62 |
| 36 : 3 = 12 | 168 : 21 = 8 | 126 : 21 = 6 | 84 : 12 = 6 | 41 * 5 = 205 | 12 * 9 = 108 |
| 33 * 3 = 99 | 85 : 17 = 5 | 77 : 7 = 11 | 114 : 19 = 6 | 32 : 2 = 16 | 44 * 2 = 88 |
| 96 : 3 = 32 | 21 * 6 = 126 | 32 * 7 = 224 | 14 * 7 = 98 | 133 : 7 = 19 | 92 : 4 = 23 |
| 152 : 8 = 19 | 216 : 9 = 24 | 18 * 11 = 198 | 53 * 3 = 159 | 12 * 9 = 108 | 38 : 2 = 19 |
| 49 * 4 = 196 | 0 * 15 = 0 | 12 * 6 = 72 | 48 : 8 =6 | 195 : 3 = 65 | 21 * 10 = 210 |
| 17 * 4 = 68 | 154 : 7 = 22 | 34 * 2 = 68 | 135 : 15 = 9 | 104 : 13 = 8 | 68 * 2 = 136 |
| 11 * 6 = 66 | 96 : 3 = 32 | 87 : 3 = 29 | 37 * 5 = 185 | 44 * 5 = 220 | 98 * 1 = 98 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
примеры на умножение и деление, сложение и вычитание
Ваш ребенок еще только учится в начальной школе, а вы уже задумываетесь о его дальнейшей учебе, развитии и будущем? Это очень похвально. А думали ли вы над тем, что успеваемость ребенка можно улучшить, если заниматься с ним ежедневно по математике всего лишь 15 минут в день дополнительно? И это не выдумки. В материалах этой статьи мы приведем примеры и задачи для школьников начальной школы по математике, а именно, для третьеклассников. (Для удобства решения приведенные ниже задания вы можете распечатать).
А думали ли вы над тем, что успеваемость ребенка можно улучшить, если заниматься с ним ежедневно по математике всего лишь 15 минут в день дополнительно? И это не выдумки. В материалах этой статьи мы приведем примеры и задачи для школьников начальной школы по математике, а именно, для третьеклассников. (Для удобства решения приведенные ниже задания вы можете распечатать).
Содержание
1. Как учить ребенка учиться
2. Примеры и задачи по математике на умножение и деление
3. Примеры и задачи по математике на сложение и вычитание
4. Вместо заключения
Как учить ребенка учиться
Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.
А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.
Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.
Примеры по математике на умножение и деление
Еще во втором классе дети выучили таблицу умножения. Если вы сейчас находитесь в полном заблуждении, как выучить с ребенком таблицу умножения, то рекомендуем к ознакомлению следующий материал по ссылке. На протяжении второго класса школьники постепенно осваивали простые примеры и задачи, используя таблицу умножения, а в третьем классе они оттачивают навыки умножения и сложения.
На протяжении второго класса школьники постепенно осваивали простые примеры и задачи, используя таблицу умножения, а в третьем классе они оттачивают навыки умножения и сложения.
Задание 1
Заменить сложение вычитанием в тех примерах, в которых от замены знака ответ не изменится:
5 + 5 + 5 =
1 + 1 + 1 + 1 =
0 + 0 + 0 + 0 + 0 =
8 + 8 + 8 + 8 =
7 + 7 — 7 + 7 =
7 + 7 + 7 — 7 =
14 + 14 =
61 + 61 =
Подсказка:
5 + 5 + 5 = 15, если заменить знак «+» на знак «•», то получится
5 • 5 • 5 = 125. 15 не равно 125. Значит, в первом равенстве заменить знак «+» на знак «•» нельзя.
По аналогии решаем стальные равенства и делаем выводы о возможной или невозможной замене знака «+» на знак «•».
Задание 2
Какие выражения нельзя заменить суммой, чтобы ответ не изменился:
0 • 4 =
1 • 0 =
1 • 1 =
1 • 6 =
0 • 9 =
7 • 0 =
5 • 2 =
2 • 2 =
Подсказка:
Вспомните, каким правилом следует пользоваться при умножении на ноль.
Задание 3
Решите примеры:
45 : 5 + 1 =
45 : 5 • 1 =
543 — 5 • 1 =
(543 — 5) • 1 =
423 + 7 • 0 =
(423 + 7) • 1 =
10 — 0 + 4 =
10 • 0 + 4 =
Задание 4
Из каждого выражения на умножение составьте выражения на деление:
6 • 8 =
7 • 1 =
4 • 0 =
0 • 3 =
4 • 9 =
Подсказка
6 • 8 = 48
48 : 8 = 6
48 : 8 = 6
Задание 5
Какое значение имеют следующие выражение:
а : а =
а : 1 =
0 : а =
а : 0 =
Задание 6
Решите примеры:
(596 + 374) • 1 =
596 + 374 • 1 =
(596 + 374) • 0 =
596 + 374 + 0 =
0 • 320 : 1 =
0 + 320 : 1 =
Обязательно повторите с ребенком правила умножения и деления числа на единицу и умножения или деления числа на ноль, а также особенности деления ноля на любое число. Часто именно в этих примерах дети делают ошибки, которые влекут за собой дальнейшее неправильное решение примеров, выражений и задач.
Задание 7 (задача)
В оздоровительный лагерь привезли фрукты: 7 ящиков винограда и 5 ящиков персиков. Масса привезенных персиков составляет 40 килограммов. Какая масса винограда, если ящик винограда на 1 килограмм весит больше, чем ящик персиков.
Масса привезенных персиков составляет 40 килограммов. Какая масса винограда, если ящик винограда на 1 килограмм весит больше, чем ящик персиков.
Решение
Найдем, сколько весит один ящик персиков. Известно, что общая масса персиков составляет 40 кг, а всего ящиков – 5.
Первое действие:
40 : 5 = 8 (кг) весит один ящик персиков.
Теперь найдем, сколько весит один ящик винограда, если известно, что он тяжелее на 1 кг, чем ящик персиков.
Второе действие:
8 + 1 = 9 (кг) весит один ящик винограда.
Теперь находим общую массу всего винограда, если известно, что один ящик весит 9 кг, а всего винограда – 7 ящиков.
Третье действие:
9 • 7 = 63 (кг) – общая масса винограда.
Ответ: масса привезенного винограда составляет 63 кг.
Задание 8
Сосна может расти 600 лет, береза – 350 лет. А ива – в 6 раз меньше от сосны. Что может расти дольше береза или ива? И насколько лет?
Решение
Вначале рассчитаем, сколько лет может расти ива, если известно, что она растет в 6 раз меньше, чем сосна.
Первое действие:
600 : 6 = 100 (лет) может расти ива.
Теперь, когда известно, что ива может расти 100 лет, сравним продолжительность «жизни» березы и ивы. Известно, что береза растет 350 лет, а ива – 100. 350 больше чем 100, значит береза может расти дольше ивы. Чтобы рассчитать, на сколько береза может расти дольше ивы, решаем равенство.
Второе действие:
350 — 100 = 250 (лет) – на столько береза может расти дольше ивы
Ответ: береза может расти дольше ивы на 250 лет.
Важно! Если задачу можно решить несколькими способами, обязательно сообщите об этом ребенку. Пусть потренирует логику и начертит все возможные схем решения задачи, т.е. составить схематическое условие. Ведь правильно составленное условие задачи – это 90% успешного решения.
Задание 9
В понедельник гусеница начала ползти вверх по дереву высотой 9 метров. За день она поднялась вверх на 5 метров, а за ночь – опустилась на 2 метра. На какой день гусеница достигнет верхушки дерева?
Решение
Для начала рассчитаем, на сколько метров поднимается гусеница вверх за один день, с учетом того, что ночью на опускается.
Первое действие:
5 — 2 = 3 (м) гусеница проползает за сутки вверх.
Теперь найдем количеств дней, необходимых на преодоление расстояния 9 метров вверх по дереву.
Второе действие:
9 : 3 = 3 (дня) нужно гусенице, чтобы достичь вершины дерева.
Ответ: 3 дня нужно гусенице, чтобы достичь вершины дерева.
Задание 10
В коробке было 18 килограммов печенья. Сначала из нее взяли 13 килограммов печенья, потом досыпали в 4 раза больше, чем оставалось. Сколько килограммов печенья стало в коробке.
Решение
Сначала найдем, сколько килограммов печенья осталось в коробке, после того, как из нее забрали 13 килограммов.
Первое действие:
18 — 13 = 5 (кг) печенья осталось в коробке
Теперь рассчитаем сколько килограммов печенья досыпали в коробку.
Второе действие:
5 • 4 = 20 (кг) досыпали
Сложим тот вес, который оставался в коробке, и тот, который досыпали, чтобы найти, сколько килограммов печения стало в коробке.
Третье действие:
5 + 20 = 25 (кг) стало
Ответ: 25 килограммов печения стало в коробке.
Задание 11
За лето хозяйка вырастила 208 домашних птиц. Кур и уток было 129, а уток и гусей – 115. Сколько кур, уток и гусей вырастила хозяйка за лето?
Решение
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было кур.
Второе действие:
208 (птиц) – 115 (уток + гусей) = 93 кур
Теперь, когда мы знаем количество гусей и кур, а также общее количество домашних птиц, мы можем найти количество уток.
Третье действие:
208 — (79 + 93) = 36 уток
Ответ: за лето хозяйка вырастила 79 гусей, 93 кур и 36 уток.
Второй вариант решения
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было уток
Второе действие:
115 (уток + гусей) – 79 (гусей) = 36 уток
Теперь, когда мы знаем количество гусей и уток по отдельности, а также общее количество домашних птиц, мы можем найти количество кур.
Третье действие:
208 – (79 + 36) = 208 – 115 = 93 кур
Ответ: за лето хозяйка вырастила 79 гусей, 93 кур и 36 уток.
Примеры и задачи по математике на сложение и вычитание
Основной задачей заданий и примеров по математике на сложение и вычитание в третьем классе является популяризация математических знаний и идей, поддержка и развитие математических знаний школьников, стимулирование и мотивация учеников в изучении естественно-математический предметов.
Задание 1
Реши уравнения:
Х – 40 = 60
Х + 4 = 61
Х – 16 = 25
Х + 25 = 84
Х – 45 = 251
Х + 56 = 106
Х + 78 = 301
Задание 2
Расставьте скобки так, чтобы ответом выражения в первом случае было 6, а в втором – 2:
12 : 2 + 2 • 2 =
Подсказка
12 : (2 + 2) • 2 = 6
12 : (2 + 2 • 2) = 2
Важно! Некоторые условия составлены таким образом, чтобы ребенок включал логическое мышление. Прорешивая такие задания он мыслит, делает предположения, размышляет, и находит правильное решение задания.
Прорешивая такие задания он мыслит, делает предположения, размышляет, и находит правильное решение задания.
Задание 3
Перевести в одну систему измерения и решить выражения:
1 м – 5 дм =
1 м – 5 см =
6 м 5 дм – 8 дм =
5 см + 5 см =
15 см + 5 дм =
3 дм – 6 см =
3 дм 5 см – 15 см =
1 дм 2 см – 3 см =
1 м 6 дм – 8 дм =
Задание 4
Из каждого выражения произведения отнять 15 и записать новые выражение и решить их:
7 • 3 =
7 • 6 =
7 • 9 =
8 • 6 =
8 • 4 =
3 • 9 =
4 • 4 =
5 • 7 =
Подсказка
Если 7 • 3 = 21, то 21 – 15 = 6
Задание 5
Решить примеры:
7 • 6 + 7 • 4 =
21 : 3 – 6 =
(35 – 28) • 5 =
(68 – 26) : 7 =
7 + (6 : 2) =
3 – 14 : 2 =
60 – 63 : 7 =
81 – 56 : 7 =
50 + 42 : 7 =
Задание 6 (задача)
В шести одинаковых бочонках 24 литра воды. Сколько литров воды в сети таких же бочонках, на сколько литров больше во втором случае, чем в первом?
Решение
Вначале найдем, сколько воды вмещается в один бочонок.
Первое действие:
24 : 6 = 4 (л) в одном бочонке
Теперь рассчитаем, сколько воды в семи одинаковых бочонках
Второе действие:
4 • 7 = 28 (л) в сети одинаковых бочонках
Найдем ответ на главный вопрос задачи, на сколько литров больше во втором случае, чем в первом.
Третье действие:
28 – 24 = 4 (л) на столько литров больше во втором случае, чем в первом
Ответ: на 4 литра воды больше во втором случае, чем в первом
Задание 7
Отец и сын купили на рынке картошку в 6 одинаковых сетках. Отец принес домой 4 сетки, а сын 2. Всего получилось 18 килограммов картошки. Сколько килограммов принес отец? Сколько килограммов принес сын? На сколько больше килограммов картошки принес отец?
Решение
Рассчитаем, сколько картошки было в одной сетке, если известно, то всего принести 18 килограммов в 6 одинаковых сетках.
Первое действие:
18 : 6 = 3 (кг) в одной сетке.
Теперь узнаем сколько килограммов принес отец и сколько килограммов принес сын.
Второе действие:
3 • 4 = 12 (кг) принес отец
Третье действие:
3 • 2 = 6 (кг) принес сын
Найдем искомую разницу.
Четвертое действие:
12 – 6 = 6 (кг) на столько больше принес отец.
Ответ: Отец принес на 6 килограммов больше картошки, чем сын.
Задание 8
За 5 часов работы двигателя было израсходовано 30 литров бензина. Сколько бензина будет израсходовано за 8 часов работы двигателя. На сколько больше двигатель израсходует бензина за разницу во времени?
Решение
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько составляет разница во времени?
Второе действие:
8 – 5 = 3 (ч) разница во времени
Теперь можно рассчитать, сколько бензина израсходовано за оставшиеся 3 часа.
Третье действие:
3 • 6 = 18 (л) потрачено за 3 часа.
Ответ: за 3 часа двигатель истратил 18 литров бензина
Второй способ решения
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько бензина будет израсходовано за 8 часов работы двигателя.
Второе действие:
8 • 6 = 48 (л) израсходовано за 8 часов работы двигателя
Теперь можно рассчитать разницу потраченного топлива.
Третье действие:
48 – 30 = 18 (л) разница потраченного топлива
Ответ: за 3 часа двигатель истратил 18 литров бензина
Важно! Задания на сложение и вычитание не исключают в своем условии или решении возможность других математических действий, например, умножения или деления. Ученик третьего класса уже должен уметь различать в условии требования к сложению и умножению, делению и вычитанию. Именно потому задания по математике для этого класса часто носят смешанный характер.
Задание 9
В двух прудах плавало 56 уток. Когда из первого пруда во второй перелетело 7 уток, то в нем осталось 25. Сколько уток с самого начала плавало во втором пруду?
Решение
Известно, что после того, как из первого пруда улетело 7 уток, в нем осталось 25. Находим количество уток в первом пруду с самого начала.
Находим количество уток в первом пруду с самого начала.
Первое действие:
7 + 25 = 32 (утки) было в первом пруду.
Теперь можем найти, сколько уток плавало во втором пруду с самого начала.
Второе действие:
56 – 32 = 24 (утки) было во втором пруду.
Ответ: с самого начала во втором пруду было 24 утки.
Задание 10
С первого куста собрали 9 килограммов ягод. Со второго куста собрали на 3 килограммов больше, чем с первого, а с третьего – на 2 килограммов больше, чем со второго. Сколько килограммов ягод собрали с третьего куста? Сколько всего ягод собрали?
Решение
Вначале найдем, сколько килограммов ягод собрали со второго куста.
Первое действие:
9 + 3 = 12 (кг) ягод со второго куста
Теперь определяем, сколько килограммов ягод собрали с третьего куста
Второе действие:
12 + 2 = 14 (кг) год с третьего куста
Когда все составляющие известны, находим ответ на главный вопрос задачи.
Третье действие:
9 + 12 + 14 = 35 (кг) ягод всего
Ответ: всего собрали 35 килограммов ягод.
Вместо заключения
Уделяйте математике достаточно внимания уже с начальной школы. Этот предмет не только тренируем мозг в устном счете, но и умении логически мыслить, развивать смекалку. Постепенно привыкая к выполнению дополнительных и основных заданий, ребенок учится учиться, выполнять требования учителя, грамотно планировать свое время, распределять время для учебы и досуга.
Математические задания для третьеклассников моно составлять самостоятельно по приведенным нами аналогии, это не составит особого труда. Зато ваш ученик сможет больше тренироваться в математике, выполнять задания на каникулах и выходных, а также заниматься дополнительно после школы.
Математика 3 класс | Умножение и деление, часть 1
Учебный план
Детский сад 1 класс 2 класс 3 класс 4 класс 5-й класс 6 класс
7 класс 8 класс 9 класс 10-й класс 11 класс 12 класс
3 класс 4 класс 5-й класс 6 класс 7-й класс 8 класс
Алгебра 1 Геометрия Алгебра 2
Поддержка учителя
Инструменты учителя ELA Инструменты учителя математики Профессиональное обучение Блог Fishtank
Fishtank Plus
Fishtank Plus для ELA Fishtank Plus для математики Усыновление в школе
976B7D1A-2753-4856-9CA8-8A2D57F9F038Учебная программа
F9F71AAC-D645-4DB6-8B51-DCD6337664FDПоддержка учителя
F9F71AAC-D645-4DB6-8B51-DCD6337664FDИнструменты учителя ELA Инструменты учителя математики Профессиональное обучение Блог Fishtank
Fishtank Plus
F9F71AAC-D645-4DB6-8B51-DCD6337664FDFishtank Plus для ELA Fishtank Plus для математики Усыновление в школе
Подпишитесь на обучение Fishtank EE5D2DC5-0343-44FC-BF63-528F33F89D04
Модуль 2
3-й класс
Краткое изложение модуля
Объем и последовательность для 3-го класса по математике были скорректированы в августе 2022 года. в эту единицу.
Модуль 2 открывает глаза учащимся на некоторые из наиболее важных предметов, которые учащиеся изучают в 3 классе — умножение и деление. В этом разделе «учащиеся начинают развивать эти понятия, работая с числами, с которыми они более знакомы, такими как 2, 5 и 10, в дополнение к числам, которые легко пропустить, таким как 3 и 4», что позволяет познавательный спрос на значение самих умножения и деления, а не вычисления (CCSS Toolbox, Sequenced Units for the Common Core State Standards in Mathematics Grade 3). Затем в Блоке 3 учащиеся будут работать над более сложными блоками 0, 1, 6–9., и кратное 10.
Во 2-м классе учащиеся научились считать объекты в массивах, используя многократное сложение (2.OA.4), чтобы получить основу для умножения. Они также проделали большую работу над одно- и двухэтапными задачами на сложение и вычитание, освоив все типы задач, включающие эти операции (2. OA.1). Учащиеся будут полагаться на это основополагающее понимание и ориентацию равных групп при решении контекстуальных проблем в этом модуле.
OA.1). Учащиеся будут полагаться на это основополагающее понимание и ориентацию равных групп при решении контекстуальных проблем в этом модуле.
В начале этого раздела учащиеся получают представление об умножении и делении в контексте задач на равные группы и массивы в теме A. Удерживать внимание на концептуальном понимании умножения и деления (3.OA.1, 3 .OA.2), Тема A не обсуждает конкретные стратегии решения, поэтому учащиеся могут пересчитать все объекты (стратегия 1-го уровня) или вспомнить свой пропуск и повторное сложение (стратегии 2-го уровня) из 2-го класса, чтобы найти неизвестное. товар. Однако в темах B и C основное внимание уделяется разработке более эффективных стратегий для решения задач умножения и деления, включая пропуск счета и многократное сложение (стратегии уровня 2), а также «просто знание» фактов, которое работает для достижения цели. «к концу 3 класса [учащиеся] знают наизусть все произведения двух однозначных чисел и связанные с ними факты деления» (3.OA. 7). Как говорится в книге «Операции и алгебраическое мышление», «освоение этого материала и достижение беглости в умножении однозначных чисел и связанном с ним делении может занять довольно много времени, потому что не существует общих стратегий умножения или деления всех однозначных чисел, как для сложения или вычитание» (OA Progression, стр. 22). Таким образом, поскольку «существует много шаблонов и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в Теме B, поскольку они выучили эти последовательности с пропуском счета во 2-м классе. Затем в Теме C они работать с новыми множителями 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими множителями, учащиеся будут решать с ними более сложные и/или абстрактные задачи, в том числе определение неизвестного целого числа в уравнении умножения или деления, связывающем три целые числа (3.OA.4) и решение двухэтапных текстовых задач с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая обоснованность их ответов для различных типов задач по теме D.
7). Как говорится в книге «Операции и алгебраическое мышление», «освоение этого материала и достижение беглости в умножении однозначных чисел и связанном с ним делении может занять довольно много времени, потому что не существует общих стратегий умножения или деления всех однозначных чисел, как для сложения или вычитание» (OA Progression, стр. 22). Таким образом, поскольку «существует много шаблонов и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в Теме B, поскольку они выучили эти последовательности с пропуском счета во 2-м классе. Затем в Теме C они работать с новыми множителями 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими множителями, учащиеся будут решать с ними более сложные и/или абстрактные задачи, в том числе определение неизвестного целого числа в уравнении умножения или деления, связывающем три целые числа (3.OA.4) и решение двухэтапных текстовых задач с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая обоснованность их ответов для различных типов задач по теме D. Наконец, модуль завершается сосредоточением внимания на категориальных данных, где учащиеся рисуют и решают задачи, связанные с масштабированными графическими изображениями и масштабированными гистограммами, что является хорошим приложением основной работы по умножению и делению. Как отмечают Прогрессии, «эти изменения связаны с упором на умножение в этой степени» (MD Прогрессия, стр. 7). Учащиеся также решают одно- и двухэтапные текстовые задачи, связанные с данными на этих графиках, опираясь на обширную работу, которую учащиеся проделали с текстовыми задачами в течение года. Таким образом, этот поддерживающий стандарт кластера значительно улучшает основную работу, над которой они работали во всем подразделении.
Наконец, модуль завершается сосредоточением внимания на категориальных данных, где учащиеся рисуют и решают задачи, связанные с масштабированными графическими изображениями и масштабированными гистограммами, что является хорошим приложением основной работы по умножению и делению. Как отмечают Прогрессии, «эти изменения связаны с упором на умножение в этой степени» (MD Прогрессия, стр. 7). Учащиеся также решают одно- и двухэтапные текстовые задачи, связанные с данными на этих графиках, опираясь на обширную работу, которую учащиеся проделали с текстовыми задачами в течение года. Таким образом, этот поддерживающий стандарт кластера значительно улучшает основную работу, над которой они работали во всем подразделении.
На протяжении всего раздела учащиеся выполняют различные математические упражнения. Модуль уделяет особое внимание абстрактным и количественным рассуждениям, поскольку учащиеся начинают понимать значение умножения и деления и абстрактных символов, используемых для их представления (MP. 2). Кроме того, учащиеся моделируют математические модели с этими новыми операциями, решая одно- и двухэтапные текстовые задачи с их участием (MP.4).
2). Кроме того, учащиеся моделируют математические модели с этими новыми операциями, решая одно- и двухэтапные текстовые задачи с их участием (MP.4).
Введение в умножение и деление углубляется в Разделе 3, когда учащиеся изучают более сложные множители 0, 1, 6–9.и кратны 10. Затем, в Разделе 4, учащиеся изучат область и ее связи с этими операциями. В 4 классе их понимание умножения и деления станет еще более богатым, когда они начнут понимать мультипликативное сравнение и решать текстовые задачи с ним (4.ОА.1, 4.ОА.2). Кроме того, они будут решать многоэтапные текстовые задачи, включающие все четыре операции, иногда с необходимостью интерпретации остатка в контексте задачи (4.OA.3). Наконец, учащиеся расширят свое вычислительное мастерство до многозначных чисел, умножая целое число до четырех цифр на однозначное целое число и два двузначных числа, а также делят до четырехзначных дивидендов на единицу. -разрядный делитель (4.NBT.5, 4.NBT.6). Умножение и деление обеспечивают основу для множества алгебраических и геометрических тем, от линейных функций до тригонометрии, и, таким образом, это содержание имеет решающее значение для всего будущего изучения математики.
Темп: 24 учебных дня (21 урок, 2 дня гибкого графика, 1 день оценки)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Модуль 2.
Предварительный модуль
Предложите учащимся выполнить предварительную оценку и самооценку учащихся перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить оценку промежуточного модуля после урока 9.
Послемодульный
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Самооценка студентов после окончания обучения
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Предложения по подготовке к обучению данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Plus
Интеллектуальная подготовка для всех модулей
- Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
- Выполните все целевые задания и снабдите их комментариями с учетом «Сводки модуля» и «Основных сведений».
- Пройти итоговую оценку.
Интеллектуальная подготовка для конкретных модулей
- Прочтите статью «Моделирование с помощью математики» на канале Teaching Channel и посмотрите видеоролики о трехактных задачах.

- Прочитайте документ «Типы ситуаций для операций в задачах Word» от Achieve the Core для умножения и деления. Определите типы словесных проблем любых применимых оценочных вопросов.
- (необязательно) Прочтите стр. 22–28 документа «Операции и алгебраическое мышление» («OA») Progressives о 3 классе.
- Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.
| Равные группы | Пример: 4 равные группы по 3 звезды |
| Массив | Пример: 4 ряда по 3 |
| Ленточная схема один к одному | Пример: Есть 10 команд по 4 ученика в каждой. Сколько учеников во всех командах? |
| Диаграмма ленты | Пример: В каждом 4 мешка по 3 сливы. Сколько всего слив? |
| График | |
| Гистограмма |
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- В Соединенных Штатах принято представлять уравнение $$3\times 6 = \square$$ в виде 3 групп по 6 элементов в каждой: 3 шестерки (в отличие от 6 групп).
 из 3). «Но в других странах уравнение 3 × 6 = □ означает, сколько будет 3 вещей, взятых 6 раз (6 групп по 3 вещи в каждой): шесть троек. Некоторые учащиеся приносят эту интерпретацию уравнений умножения в класс. Поэтому полезно обсудите различные интерпретации и позвольте учащимся использовать то, что используется у них дома» (OA Progression, стр. 25).
из 3). «Но в других странах уравнение 3 × 6 = □ означает, сколько будет 3 вещей, взятых 6 раз (6 групп по 3 вещи в каждой): шесть троек. Некоторые учащиеся приносят эту интерпретацию уравнений умножения в класс. Поэтому полезно обсудите различные интерпретации и позвольте учащимся использовать то, что используется у них дома» (OA Progression, стр. 25). - Уравнение $$20\div 4 = \square$$ можно интерпретировать двумя способами: есть 20 объектов, которые нужно разделить на группы по 4, и мы хотим знать, сколько групп мы можем составить (модель измерения деления), или есть 20 объектов, которые нужно разделить на 4 группы, и мы хотим знать, сколько объектов находится в каждой группе (разделительная модель разделения).
- Осмысление задач и настойчивость в их решении — важная практика при решении текстовых задач. Ключевые слова не всегда указывают на правильную работу.
- Задачи на умножение можно решать с помощью различных стратегий возрастающей сложности, включая создание и подсчет всех величин, участвующих в умножении или делении (стратегия уровня 1), повторный счет заданного числа (уровень 2) и использование свойства операций составления и разложения неизвестных фактов на известные (уровень 3).
Материалы
Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Счетчики (максимум 20 на одного учащегося или малую группу) – вместо этого учащиеся могут использовать обычные школьные материалы, такие как скрепки
Запас слов
Термины и обозначения, которые студенты изучают или используют в модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950массив
символ деления, $${\div}$$
деление/деление 2 делимое
делимое
9000равные группы
коэффициент
ключ
символ умножения, $${\times}$$
умножение/умножение
произведение
частное
строка/столбец
масштаб
3 Чтобы увидеть весь словарный запас для модуля 2, просмотрите наш глоссарий лексики для 3-го класса.
Модульная практика
Словесные задачи и упражнения на беглость речи
Получите доступ к ежедневной практике со словесными задачами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
Схема урока
Тема A: Значение умножения и деления
Определите и создайте ситуации с участием равных групп и опишите эти ситуации, используя язык и обозначения умножения.
3.ОА.А.1
Идентифицируйте и создавайте ситуации, связанные с массивами, и описывайте эти ситуации, используя язык и нотацию умножения.
3.ОА.А.1
Идентифицируйте и создавайте ситуации с неизвестным размером группы и находите размер группы в ситуациях.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3
Определить и создать ситуации с участием неизвестного количества групп и найти количество групп в ситуациях.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3
Свяжите умножение и деление и поймите, что деление может представлять ситуации неизвестного размера группы или неизвестного количества групп.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3 3.OA.B.6
Тема B: Умножение и деление на 2, 5 и 10
Добейтесь беглости с фактами умножения, используя единицы 2, 5 и 10.
3.ОА.А.1 3.ОА.С.7
Докажите коммутативность умножения.
3.OA.B.5
Добейтесь беглости с фактами деления, используя единицы 2, 5 и 10.
3.ОА.А.2 3.OA.B.6 3.ОА.С.7
Решите одношаговые текстовые задачи на умножение и деление с использованием единиц 2, 5 и 10.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3
Тема C: Умножение и деление на 3 и 4
Добейтесь беглости с фактами умножения и деления, используя единицы 3.
3.ОА.А.1 3.ОА.А.2 3.OA.B.5 3.OA.B.6 3.ОА.С.7
Развивайте беглость с умножением и делением, используя единицы 4.
3.ОА.А.1 3.ОА.А.2 3.OA.B.5 3.ОА.С.7
Решите одношаговые текстовые задачи на умножение и деление, используя единицы 3 и 4.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3
Тема D: Более сложные задачи на умножение и деление
Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа, включая уравнения с буквой, обозначающей неизвестную величину.
3.ОА.А.4 3.ОА.С.7 3.OA.D.8
Решайте одношаговые текстовые задачи на умножение и деление и записывайте контексты задач, чтобы сопоставить выражения и уравнения.
3.ОА.А.1 3.ОА.А.2 3.ОА.А.3
Решите двухэтапные текстовые задачи на умножение и деление.
3.OA.D.8
Решите двухэтапные текстовые задачи, включающие все четыре операции.
3.OA.D.8
Тема E: масштабированное изображение и гистограммы
Создавайте масштабированные графические изображения, где предусмотрен масштаб.
3.МД.Б.3
Создавайте масштабированные графические изображения, масштаб которых необходимо определить.
3.МД.Б.3
Создавайте гистограммы с масштабированием, где предусмотрен масштаб.
3.МД.Б.3
Создайте гистограммы с масштабированием, где необходимо определить масштаб.
3.МД.Б.3
Решите одно- и двухэтапные задачи со словами, используя информацию, представленную в масштабированном изображении и гистограммах.
3.МД.Б.3 3.OA.D.8
Общие основные стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, описанные в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Измерения и данные
3.МД.Б.3 — Нарисуйте диаграмму в масштабе и гистограмму в масштабе, чтобы представить набор данных с несколькими категориями. Решайте одно- и двухэтапные задачи «насколько больше» и «на сколько меньше», используя информацию, представленную в масштабированных гистограммах. Например, нарисуйте гистограмму, в которой каждый квадрат гистограммы может представлять 5 домашних животных.
Операции и алгебраическое мышление
3.ОА.А.1 — Интерпретируйте произведения целых чисел, например, интерпретируйте 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой.
 Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7. 3.ОА.А.2 — Интерпретировать целочисленные частные целых чисел, например, интерпретировать 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли по 8 объекты каждый. Например, опишите контекст, в котором количество долей или количество групп можно выразить как 56 ÷ 8.
3.ОА.А.3 — Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом для неизвестного числа для представления проблемы.
3.ОА.А.4 — Определить неизвестное целое число в умножении или делении уравнения, связывающего три целых числа.
 Определите неизвестное целое число в умножении или делении уравнения, связывающего три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
Определите неизвестное целое число в умножении или делении уравнения, связывающего три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ? 3.ОА.Б.5 — Применение свойств операций как стратегий умножения и деления. Учащимся не нужно использовать формальные термины для этих свойств. Пример: зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. ( Распределительное свойство.) Пример: если известно 6 × 4 = 24, то известно и 4 × 6 = 24 (перестановочное свойство умножения). 3 × 5 × 2 можно найти из 3 × 5 = 15, тогда 15 × 2 = 30 или на 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения.)
3.ОА.Б.6 — Понимайте деление как проблему неизвестного фактора. Например, найдите 32 ÷ 8, найдя число, которое дает 32 при умножении на 8.

3.ОА.С.7 — Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
3.OA.D.8 — Решите двухэтапные текстовые задачи, используя четыре операции. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление. Этот стандарт ограничивается задачами, поставленными с целыми числами и имеющими целочисленные ответы; учащиеся должны знать, как выполнять операции в общепринятом порядке, когда нет скобок для указания определенного порядка (порядок операций).
Основополагающие стандарты
Стандарты, описанные в предыдущих единицах или классах, которые важны для текущей единицы
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Измерения и данные
2.
 МД.Д.10
МД.Д.10
Число и операции в десятичной системе счисления
2.НБТ.А.2
3.НБТ.А.2
Операции и алгебраическое мышление
2.ОА.А.1
2.OA.C.3
2.ОА.С.4
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Числа и операции в десятичной системе счисления
4.НБТ.Б.5
4.НБТ.Б.6
Числа и операции — дроби
4.
 NF.B.4
NF.B.45.NF.B.3
5.NF.B.4
5.NF.B.5
5.NF.B.6
5.NF.B.7
Операции и алгебраическое мышление
4.ОА.А.1
4.ОА.А.2
4.ОА.А.3
4.ОА.Б.4
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.
 MATH.PRACTICE.MP3
— Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
MATH.PRACTICE.MP3
— Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Модуль 1
Округление, сложение и вычитание
значок/стрелка/вправо/большойМодуль 3
Умножение и деление, часть 2
Планы уроков по умножению и делению 3-й класс
Приобретите или подпишитесь, чтобы получить доступ к этому ресурсу.
7,95 $
Добавить в корзину
Это цифровой продукт.
Включено в премиум-подписку
Подпишитесь, чтобы получить мгновенный доступ к этому и всем ресурсам на TeacherVision.
Подписаться
Добавить в избранноеСОЗДАТЬ НОВУЮ ПАПКУ
Отмена
Управление моим избранным
Найти больше продуктов:
См. продукты
Поделиться
Согласованный со стандартами 11-недельный модульный план с рабочими листами на умножение и деление, планом урока и печатными формами для 3-го класса
Развивайте важные математические навыки с помощью этого комплексного модульного плана, разработанного для Common Core Math Standards for Grade 3. Включая полезные учебные заметки для 11 недель уроков, сопутствующие игры и задания, готовые к использованию тесты и текстовые задачи на умножение и деление, этот план, не требующий подготовки, содержит все необходимое для обучения умножению и делению. в свой 3 класс!
в свой 3 класс!
Что включено в этот план модуля
Для учителя:
- Полноценный 11-недельный план модуля, согласованный с Common Core Math Standards для 3 класса и модуль деления
- Учебные заметки с инструкциями, идеями для дифференциации и стратегиями развития основных математических навыков
Для учащихся:
- Игры на умножение, словесные задачи на умножение и деление, а также множество увлекательных занятий, включая индивидуальные и групповые задания
- Готовые к использованию оценочные листы на умножение и деление для контроля и отслеживания успеваемости учащихся, а также оценочные листы с заданием на время
- Удобные инструменты, сетки, шаблоны и печатные формы, которые помогут учащимся освоить факты умножения и деления
Согласование стандартов:
Этот план раздела по умножению и делению нацелен на следующие общие базовые математические стандарты для 3 класса.
Представление и решение задач на умножение и деление
- CCSS.MATH.CONTENT.3.OA.A.1 — Интерпретация произведений целых чисел, например, интерпретация 5 × 7 как общего количества объектов в 5 группах по 7 объектов каждый. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
- CCSS.MATH.CONTENT.3.OA.A.2 — Интерпретация целочисленных частных целых чисел, например, интерпретация 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли по 8 объектов в каждой. Например, опишите контекст, в котором количество долей или количество групп можно выразить как 56 ÷ 8.
- CCSS.MATH.CONTENT.3.OA.A.3 — Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, с помощью рисунков и уравнений с символом для неизвестный номер для представления проблемы.

- CCSS.MATH.CONTENT.3.OA.A.4 — Определение неизвестного целого числа в умножении или делении уравнения, связывающего три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
Понимать свойства умножения и связь между умножением и делением.
- CCSS.MATH.CONTENT.3.OA.B.5 — Применение свойств операций как стратегий умножения и деления. Примеры: Если известно 6 × 4 = 24, то известно и 4 × 6 = 24. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)
- CCSS.MATH.CONTENT.3.OA.B.6 — Понять деление как задачу с неизвестным фактором. Например, найдите 32 ÷ 8, найдя число, которое дает 32 при умножении на 8.

Умножить и разделить в пределах 100.
- делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел. Решите задачи, связанные с четырьмя операциями, и определите и объясните закономерности в арифметике.
- CCSS.MATH.CONTENT.3.OA.D.8 — Решите двухэтапные текстовые задачи, используя четыре операции. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.
- CCSS.MATH.CONTENT.3.OA.D.9 — Идентифицируйте арифметические шаблоны (включая шаблоны в таблице сложения или таблице умножения) и объясняйте их, используя свойства операций. Например, заметьте, что число, умноженное на 4, всегда будет четным, и объясните, почему число, умноженное на 4, можно разложить на два равных слагаемых.