| 1. |
Способы решения логических задач
Сложность: лёгкое |
1 |
| 2. |
Жильцы дома
Сложность: среднее |
4 |
3.
|
Оценки
Сложность: среднее |
7 |
| 4. |
Лес
Сложность: среднее |
2 |
5.
|
Схемы логических элементов
Сложность: среднее |
2 |
| 6. |
Таблица истинности
Сложность: сложное |
3 |
7.
|
Логическая задача
Сложность: сложное |
3 |
| 8. |
Задача про школу
Сложность: сложное |
3 |
|
9. |
Дорожное происшествие
|
3 |
Математика. Логические задачи. — Математика
Методы решения логических задач
Пример. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.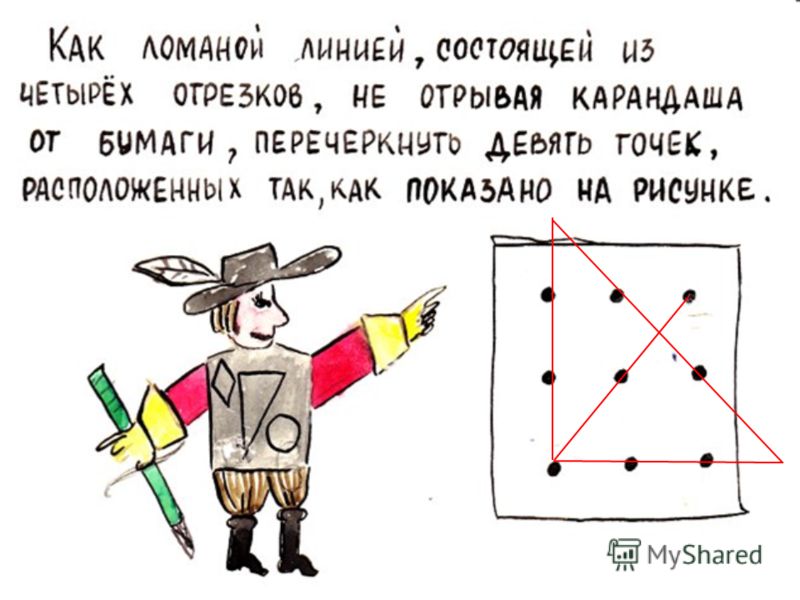
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников.
Метод рассуждений
Метод таблиц
Метод кругов Эйлера
Идея метода: состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.
Идея метода: оформлять результаты логических рассуждений в виде таблицы
Идея метода : определить количество элементов, обладающих общими свойствами.
Пример. Владимир, Игорь и Сергей преподают математику, физику и литературу, а живут они в Рязани, Туле и Ярославле. Известно также, что Владимир живет не в Рязани, Игорь живет не в Туле, рязанец – не физик, Игорь – не математик, туляк преподает литературу. Кто где живет и что преподает?
Кто где живет и что преподает?
Решение. Составим таблицу 3 х 3, выбрав основными параметрами имена и города. Тогда, учитывая, что рязанец – не физик, а туляк – литератор, получаем, что рязанец – математик, а житель Ярославля – физик.
Ответ: Сергей живет в Рязани – он математик, Владимир живет в Туле – он преподает литературу, Игорь живет в Ярославле – он физик.
Пример : Коренными жителями острова являются рыцари света и рыцари тьмы. Рыцари света всегда говорят правду, а рыцари тьмы всегда лгут. Рыцарь А говорит: «Я – лжец». Является ли он уроженцем острова рыцарей света и рыцарей тьмы?
Решение:
Пусть А сказал правду, значит, он – рыцарь тьмы. Но он не может быть рыцарем тьмы, так как рыцари тьмы всегда лгут. Пусть А сказал ложь, тогда он рыцарь света. Но рыцари света говорят правду. Опять не получается. Значит, А не может быть уроженцем острова рыцарей света и рыцарей тьмы.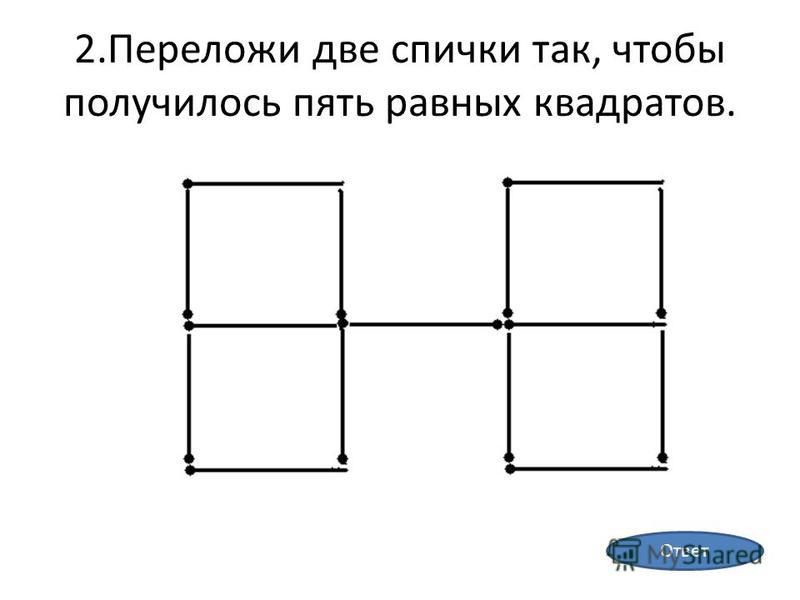
Ответ: А не является уроженцем острова.
Пример : На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение: По условию задачи нарисуем чертёж.Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ: 8 книг прочитал только Рон .
Метод графов
Идея метода: объекты представляются в графе вершинами Связи между объектами представляются, если связь однонаправленная (обозначается на схеме пунктирными линиями) или ребрами, если связь между объектами двусторонняя (обозначается сплошными линиями).
Пример : Атос, Портос и Арамис в соревновании по фехтованию заняли три первых места. Какое место занял каждый из них, если Портос занял не второе и не третье место, а Арамис – не третье?
Решение : Учитывая условия задачи, сразу делаем вывод, что Портос занял первое место. Значит, Арамис занял второе место, и Атос – третье место. Решение задачи показано на чертеже:
Ответ: Арамис – второе место; Атос – третье место; Портос – первое место.
| (Ф. Хаусдорф.) ‘ quotes[1]='»Математика — это язык, на котором написана книга природы.»(Г. Галилей) ‘ quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. « «(А. Маркушевич) ‘ quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»(А.Н. Крылов) ‘ quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»(М.И. Калинин) ‘ quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»(Платон) ‘ quotes[6]='»Математика есть лучшее и даже единственное введение в изучение природы.»(Д.И. Писарев) ‘ quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии.»(А.С. Пушкин) ‘ quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»(В. Произволов) ‘ quotes[9]='»В математике есть своя красота, как в живописи и поэзии.»(Н.Е. Жуковский) ‘ quotes[10]='»Химия – правая рука физики, математика – ее глаз.»(М.В. Ломоносов) ‘ quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит. « «(М.В. Ломоносов) ‘ quotes[12]='»Математика — это язык, на котором говорят все точные науки.»(Н.И. Лобачевский) ‘ quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»(Л. Эйлер) ‘ quotes[14]='»Числа не управляют миром, но они показывают, как управляется мир.»(И. Гете) ‘ quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»(В.Ф. Каган) ‘ quotes[16]='»Счет и вычисления — основа порядка в голове.»(Песталоцци) ‘ quotes[17]='»Величие человека — в его способности мыслить.»(Б. Паскаль) ‘ quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»(Д.Пойа) ‘ quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»(Б. Паскаль) ‘ quotes[20]='»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками. « «(И. Ньютон) ‘ quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»(Л. Карно) ‘ quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»(М.В. Остроградский) ‘ quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»(Н.К. Крупская) ‘ quotes[24]='»Математика уступает свои крепости лишь сильным и смелым.»(А.П. Конфорович) ‘ quotes[25]='»Доказательство — это рассуждение, которое убеждает.»(Ю.А. Шиханович) ‘ quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
Логические задачи с ответами — Bamboloo
ЗАДАЧИ НА ЛОГИКУ
Логические задачи, так же как и математику, называют «гимнастикой ума».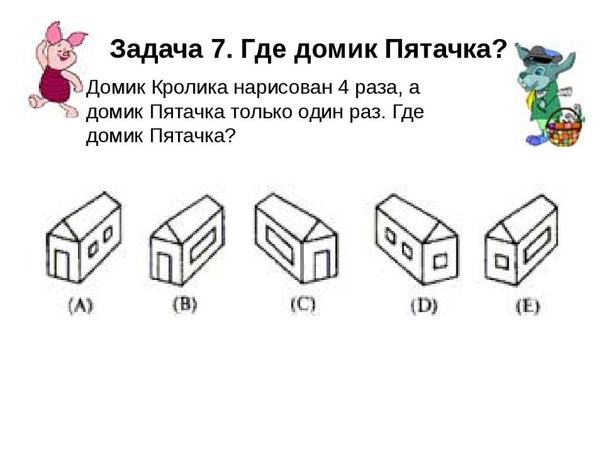 Но, в отличие
от математики, задачи на логику — это занимательная гимнастика, которая в увлекательной форме
позволяет испытывать и тренировать мыслительные процессы, иногда в неожиданном ракурсе. Для их решения
нужна сообразительность, иногда интуиция, но не специальные знания. Решение задач на логику состоит в том, чтобы досконально разобрать условие задачи, распутать клубок противоречивых связей между
персонажами или объектами. Логические задачи для детей – это, как правило, целые истории с
популярными действующими лицами, в которые нужно просто вжиться, почувствовать ситуацию, наглядно ее
представить и уловить связи.
Но, в отличие
от математики, задачи на логику — это занимательная гимнастика, которая в увлекательной форме
позволяет испытывать и тренировать мыслительные процессы, иногда в неожиданном ракурсе. Для их решения
нужна сообразительность, иногда интуиция, но не специальные знания. Решение задач на логику состоит в том, чтобы досконально разобрать условие задачи, распутать клубок противоречивых связей между
персонажами или объектами. Логические задачи для детей – это, как правило, целые истории с
популярными действующими лицами, в которые нужно просто вжиться, почувствовать ситуацию, наглядно ее
представить и уловить связи.
Даже самые сложные задачи на логику не содержат чисел, векторов, функций. Но математический
способ мышления здесь необходим: главное, осмыслить и понять условие логической задачи. Не
всегда самое очевидное решение, лежащее на поверхности, является правильным. Но чаще всего, решение
задачи на логику оказывается гораздо проще, чем кажется на первый взгляд, несмотря на путаное
условие.
Не
всегда самое очевидное решение, лежащее на поверхности, является правильным. Но чаще всего, решение
задачи на логику оказывается гораздо проще, чем кажется на первый взгляд, несмотря на путаное
условие.
Интересные задачи на логику для детей по самым разным предметам — математике, физике, биологии — вызывают у них повышенный интерес к этим учебным дисциплинам и помогают в их осмысленном изучении. Логические задачи на взвешивание, переливание, задачи на нестандартное логическое мышление помогут и в повседневной жизни решать житейские проблемы нестандартным образом.
В процессе решения задач на логику вы познакомитесь с математической логикой — отдельной
наукой, именуемой по-другому «математикой без формул». Логика как наука была создана Аристотелем,
который был не математиком, а философом. И логика первоначально была частью философии, одним из методов
рассуждений. В труде «Аналитики» Аристотель создал 20 схем рассуждений, которые назвал
силлогизмами. Одним из самых известных его силлогизмов является: «Сократ — человек; все люди смертны;
значит Сократ смертен». Логика (с др.-греч. Λογική — речь, рассуждение, мысль) — это наука о
правильном мышлении, или, иными словами, «искусство рассуждения».
И логика первоначально была частью философии, одним из методов
рассуждений. В труде «Аналитики» Аристотель создал 20 схем рассуждений, которые назвал
силлогизмами. Одним из самых известных его силлогизмов является: «Сократ — человек; все люди смертны;
значит Сократ смертен». Логика (с др.-греч. Λογική — речь, рассуждение, мысль) — это наука о
правильном мышлении, или, иными словами, «искусство рассуждения».
Существуют определенные приемы решения логических задач:
способ рассуждений, с помощью которого решаются самые простые логические задачи. Этот метод считается самым тривиальным. В ходе решения используются рассуждения, последовательно учитывающие все условия задачи, которые постепенно приводят к выводу и правильному ответу.
способ таблиц, применяемый при решении текстовых логических задач. Как следует из
названия, решение логических задач заключается в построении таблиц, которые позволяют наглядно
представить условие задачи, контролировать процесс рассуждений и помогают сделать правильные логические
выводы.
Как следует из
названия, решение логических задач заключается в построении таблиц, которые позволяют наглядно
представить условие задачи, контролировать процесс рассуждений и помогают сделать правильные логические
выводы.
способ графов состоит в переборе возможных вариантов развития событий и окончательном выборе единственно верного решения.
способ блок-схем — метод, широко используемый в программировании и решении логических задач на переливание. Он заключается в том, что сначала в виде блоков выделяются операции (команды), затем устанавливается последовательность выполнения этих команд. Это и есть блок-схема, которая по сути является программой, выполнение которой приводит к решению поставленной задачи.
способ бильярда следует из теории траекторий (один из разделов теории
вероятности). Для решения задачи необходимо нарисовать бильярдный стол и интерпретировать действия
движениями бильярдного шара по разным траекториям. При этом необходимо вести записи возможных
результатов в отдельной таблице.
Для решения задачи необходимо нарисовать бильярдный стол и интерпретировать действия
движениями бильярдного шара по разным траекториям. При этом необходимо вести записи возможных
результатов в отдельной таблице.
Каждый из этих методов применим к решению логических задач из разных областей. Эти, казалось бы, сложные и научные приемы вполне можно использовать в решении задач на логику для 1, 2, 3, 4, 5, 6, 7, 8, 9 классов.
Представляем вам самые разнообразные логические задачи для 1, 2, 3, 4, 5, 6, 7, 8, 9 класса. Мы подобрали для вас наиболее интересные задачи на логику с ответами, которые будут интересны не только детям, но и родителям.
Рекомендации для родителей:
- подбирайте для ребенка задачи на логику в соответствии с его возрастом и развитием
- не торопитесь открыть ответ, позвольте ребенку самому найти решение логической задачи.
 Пусть он сам дойдет до правильного решения и вы увидите — какое удовольствие и
чувство восторга у него возникнет при совпадении его ответа с данным.
Пусть он сам дойдет до правильного решения и вы увидите — какое удовольствие и
чувство восторга у него возникнет при совпадении его ответа с данным. - в процессе решения задач на логику допустимы наводящие вопросы и косвенные подсказки, указывающие направление размышления.
С помощью нашей подборки логических задач с ответами вы действительно научитесь решать логические задачи, расширите свой кругозор и значительно разовьете логическое мышление. Дерзайте!!!
Решение логических задач — первый шаг к развитию ребенка.
Э.Давыдова
Логика — это искусство приходить к непредсказуемому
выводу.
Сэмюэл Джонсон
Без логики почти невозможно внесение в наш мир гениальных находок интуиции.
Кирилл Фандеев
Человек, рассуждающий логично, приятно выделяется на фоне реального мира.
Американское изречение
Логика — это нравственность мысли и речи.
Ян Лукасевич
| Математика | |
| Русский язык | |
| Физика | |
| Химия | |
| Биология / экология / природа | |
| Про человека | |
| Логические задачи | |
| География | |
| Информатика | |
| Английский язык | |
| История | |
| Искусство | |
| Разное интересное | |
| Класс | Название олимпиады / конкурса |
| все | Конкурс научных работ и исследовательских проектов учащихся |
| Математика: | |
| 5-9 | Олимпиада «Скорость в пути» |
| 6-11 | Олимпиада по математике «Математические ребусы» |
| 6-11 | Олимпиада по математике «Задачи про числа» |
| 6-11 | Олимпиада по математике «Количественный учёт (Задачи про животных)» |
| 6-11 | Олимпиада по математике «Практичные задачи» |
| 6-11 | Олимпиада по математике «Геометрия — плоские фигуры» |
| 6-11 | Олимпиада по математике «Геометрия — объёмные фигуры» |
| Русский язык: | |
| 7-8 | Олимпиада по русскому языку «Глаголь Добро Есть» |
| 7-8 | Олимпиада по русскому языку «Словарный калейдоскоп» |
| Физика: | |
| 5-9 | Олимпиада «Скорость в пути» |
| 7-9 | Олимпиада по физике «Гидростатика» |
| 8-11 | Олимпиада по физике «Электричество. Постоянный ток» Постоянный ток» |
| Химия: | |
| 8-9 | Олимпиада по неорганической химии для 8-9 классов |
| 8-9 | Олимпиада по неорганической химии «Атомы и молекулы» |
| Биология / экология / живой мир | |
| все | Конкурс экологических проектов |
| все | Конкурс «Экология и Я» |
| все | Конкурс «Защитим родную природу» |
| 5-8 | Олимпиада по биологии «В мире живого» |
| 5-8 | Олимпиада по биологии «Занимательная биология» |
| 5-8 | Олимпиада по биологии «БиоГоловоломки» |
| 7-11 | Олимпиада по биологии «БиоМир» |
| 7-11 | Олимпиада по биологии «БиоЛогос» |
| все | Конкурс «Чудеса в природе» |
| все | Конкурс «Биологические загадки» |
| все | Конкурс «Таинственный мир приматов» |
| все | Конкурс «Микроорганизмы и вирусы» |
| все | Конкурс «Необычные растения» |
| все | Конкурс «В мире растений — хищников» |
| все | Конкурс «В мире животных — хищников» |
| все | Конкурс «Героические поступки животных» |
| все | Конкурс «Здоровый образ жизни (ЗОЖ)» |
| все | Конкурс «Здоровое поколение» (ЗОЖ) |
| все | Конкурс «Красота дома — комнатные растения» |
| и ещё здесь есть интересные конкурсы про животных | |
| Про человека: | |
| все | Конкурс «Эволюция человека» |
| все | Конкурс «Интересное о человеческом организме» |
| все | Конкурс «Организм человека в цифрах — что у нас внутри» |
| все | Конкурс «Биологические задачи в организме человека» |
| все | Конкурс «Человеческий организм. Факты» Факты» |
| Логические задачи: | |
| 5-11 | Конкурс «Задачи про монеты» |
| 5-11 | Конкурс по решению логических задач «ЛогикУм» для 5-11 классов |
| 5-11 | Конкурс по решению логических задач «Правда и ложь» |
| 5-11 | Конкурс по решению логических задач «Правда и ложь 2.0» |
| 5-11 | Конкурс по решению логических задач «Крепкий орешек» |
| 5-11 | Конкурс по решению логических задач «Крепкий орешек 2.0» |
| 5-11 | Конкурс по решению логических задач «Крепкий орешек 3.0» |
| 5-11 | Конкурс по решению логических задач «Крепкий орешек 4. 0″ 0″ |
| 8-11 | Логические задачи «Занимательная логика» |
| География: | |
| 7 | Олимпиада по географии для 7 классов |
| 8 | Олимпиада по географии для 8 классов |
| 5-11 | Конкурс «Наша Антарктида» |
| Информатика: | |
| все | Конкурс компьютерного рисунка «АртКомп 2.0» |
| 5-8 | Конкурс по информатике «Код доступа» (кодировка) |
| 5-9 | Конкурс по информатике «Системы счисления» |
| 5-11 | Конкурс «Задачи про монеты» |
| 7-11 | Конкурс «Основы компьютерной безопасности» |
| 7-11 | Конкурс «Специалист по Microsoft Word» |
| 7-11 | Конкурс «Специалист по Microsoft Excel» |
| 7-11 | Конкурс «Специалист по Microsoft PowerPoint» |
| Английский язык: | |
| 7-8 | Олимпиада по английскому языку для 7-8 классов |
| 6-9 | Конкурс «Приключение звёздного мальчика Starkid» для 6-9 классов (Турист в Лондоне) |
| 8-11 | Конкурс «Приключение звёздного мальчика Starkid» для 8-11 классов (На игре 100 к 1) |
| История: | |
| 7 | Олимпиада «Мир средневековья» |
| все | Конкурс «История денежного обращения в России» |
| все | Конкурс «История появления цифр и счёта» |
| все | Цикл из 3 конкурсов по истории автомобилей |
| все | Конкурс презентаций «Помним и чтим нашу историю» |
| Искусство: | |
| все | Шедевры русской живописи до 19 века |
| все | Шедевры русской живописи 19 века |
| все | Шедевры русской живописи 20 века |
| все | Шедевры европейской живописи до 19 века |
| все | Шедевры европейской живописи 19 века |
| все | Шедевры европейской живописи 20 века |
| все | Шедевры мировой скульптуры |
| все | Шедевры мировой классической архитектуры |
| все | Шедевры мировой современной архитектуры |
| все | Музыкальные ребусы |
| все | Музыкальная грамота |
| Разное интересное: | |
| все | Конкурс «Национальные блюда разных стран» |
| все | Конкурс презентаций «Наша школа / Наш класс» |
Какие задачи использует репетитор по математике на параллелограмм в 8 классе
Предлагаю Вашему вниманию страницы своей коллекции задач по геометрии для 8 класса. Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.
Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.
Задачи репетитора на параллелограмм и свойство угла в 30 градусов.
1) На стороне AB параллелограмма ABCD отмечена середина M. Найдите расстояние от M до AD, если и MC=10 см.
2) Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, . Найдите расстояние от P до стороны AB. Задача на дом.
Задачи на биссектрисы углов:
Точка М середина стороны BC параллелограмма ABCD, причем AM и DM — биссектрисы углов BAD и ADC. Найдите DM, если и BC=6 см.
2) На стороне AD параллелограмма ABCD отмечена точка N так, что BN и CN — биссектрисы его углов B и C. Известно, что BN=4 и AD=8см. Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.
Репетитору по математике в копилку красивых задач на параллелограмм
На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.
Докажите, что BKDN — параллелограмм.
Школьная математика (особенно геометрия) сильно ограничивает репетитора в варьировании простейшими объектами для составления с их участием комбинированных задач под конкретную учебную ситуацию. В начале 8 класса список пройденных теорем и понятий весьма невелик. Поэтому репетитор по математике всегда испытывает определенный недостаток в материале узкого назначения. Простые задачи — однотипные, а сложных не так много. Первые не дают развития, а последние доступны далеко не всем учащимся. Найди что-то интересное посередине — отличительная черта хорошего репетитора по математике. Недавно летом я попал ситуацию, когда со средним учеником 8 класса были перерешены все виды типовых номеров учебника и дидактических материалов (я не беру задачи — клоны). Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.
Задача, которая была представлена выше явилась результатом таких поисков. Для того, чтобы получить правильную домашнюю задачу на параллелограмм и треугольники репетитору по математике достаточно симметрично отобразить эти треугольники относительно сторон BC и AD. Вы видите их на рисунке справа. Нужно доказать, что BPDK — параллелограмм.
Как репетитор по математике растягивает задачи?
Как правило, любую задачу можно «дожать» или «растянуть», оптимизируя ее под конкретные цели повторения тех или иных теорем и формул. Я ругулярно комплектую задачи по геометрии несколькими пунктами в графе «докажите». В каждый номер с равносторонними треугольниками репетитору по математике можно посоветовать включить еще один пункт: докажите, что
Вы можете изучить рабочий листочек (план на урок) с этими задачами, который я обычно готовлю каждому ученику. Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.
Надеюсь, что репетиторам по базовой математике 8 класса пригодятся предоставленные материалы для работы со средним и даже сильным учеником. Удачного плана на урок!
Репетитор по математике в Москве ( м. Строгино ). А.Н. Колпаков
Решение логических задач
В жизни мы часто сталкиваемся с людьми, которые говорят только правду и с людьми, которые любят пошутить.
Чтобы узнать правдивость тех или иных высказываний можно использовать разные способы.
Сегодня на уроке мы с вами научимся выяснять правду на примере некоторых задач с помощью таблицы истинности, логических операций и законов алгебры логики.
Итак, давайте рассмотрим первую задачу.
Ученики писали контрольную работу по физике. На контрольной работе из-за болезни не было трёх ребят: Пети, Жени и Саши.
Им пришлось писать
контрольную работу отдельно от всего класса. Петя сказал, что он не написал на 5
и Женя не написал на 5. Женя сказал, что Петя не написал на 5, а Саша написал
на 5. Саша сказал, что он не написал на 5, а Петя написал на 5. После проверки
работ стало известно, что только один из учащихся написал контрольную работу на
5. Оказалось, что один из учеников был прав, второй нет, а третий в одном
утверждении прав, а во-втором – нет. Давайте узнаем кто был прав, и кто написал
контрольную на пять?
Петя сказал, что он не написал на 5
и Женя не написал на 5. Женя сказал, что Петя не написал на 5, а Саша написал
на 5. Саша сказал, что он не написал на 5, а Петя написал на 5. После проверки
работ стало известно, что только один из учащихся написал контрольную работу на
5. Оказалось, что один из учеников был прав, второй нет, а третий в одном
утверждении прав, а во-втором – нет. Давайте узнаем кто был прав, и кто написал
контрольную на пять?
Перейдём к решению. Обозначим каждого из мальчиков первыми буквами их имён.
Так как у нас сказано, что только один из мальчиков написал на пять, то предположим следующее:
П = «Петя написал на 5».
Ж = «Женя написал на 5».
С = «Саша написал на 5».
Давайте для решения этой задачи составим таблицу истинности. Она будет состоять из 9 столбцов, которые будут содержать имена трёх мальчиков и их высказываний.
Высказываний у нас 6:
П1 = «Петя не написал на
5».
П2 = «Женя не написал на 5».
Ж1 = «Петя не написал на 5».
Ж2 = «Саша написал на 5».
С1 = «Саша не написал на 5».
С2 = «Петя написал на 5».
Для удобства над каждым высказыванием подпишем, кто это говорил. Если какое-то высказывание является отрицательным, то его будем обозначать знаком инверсии.
Далее нужно определиться с количеством строк. Так как 5 получил только один из трёх учащихся, то для того, чтобы узнать, кто это был, достаточно фрагмента таблицы. В нём будут содержаться следующие наборы входных значений:
0 0 1
0 1 0
1 0 0
Введём их в нашу таблицу.
Если внимательно посмотреть на первых три столбца, то мы можем увидеть, что предполагается, что один из учащихся написал контрольную на 5, в то время, как два других не написали на 5.
Идём дальше. Петя уверен,
что он не написал на 5. Применяем инверсию к первому столбцу и запишем данные в
четвёртый.
Петя уверен,
что он не написал на 5. Применяем инверсию к первому столбцу и запишем данные в
четвёртый.
Дальше Петя сказал, что Женя не написал на 5. В этом случае будем применять инверсию к данным из второго столбца.
Шестой столбец заполним исходя из высказывания Жени, что Петя не написал на 5 и применим инверсию к первому столбцу.
Далее Женя уверен, что Саша написал на 5. Перепишем данные из третьего столбца в седьмой.
Аналогично заполним два оставшихся столбца.
Так как у нас известно, что один из учащихся был прав, второй – нет, а третий лишь на половину, то нам нужно искать строку, в которой в любом порядке содержатся комбинации значений 00, 11, 01 или 10. Это третья строка нашей таблицы.
Исходя из этой строки можно сделать вывод, что Петя получил 5 за контрольную по физике, а прав был в своих утверждениях Саша.
Решим ещё одну задачу с
помощью логических операций и законов алгебры логики.
Три учителя решили выяснить, кто бегал по корриду на перемене и разбил вазон с цветком. Ирина Николаевна утверждает, что это был восьмиклассник в красной рубашке.
Анна Семёновна сказала, что это был шестиклассник в синей рубашке.
А Алексей Александрович видел, что это был учащийся седьмого класса, но точно не в красной рубашке.
Когда виновника нашли, выяснилось, что каждый из учителей описал верно только один признак, по которому можно было узнать, кто это был, а со вторым – ошибся. Из какого класса был ученик, и во что он был одет?
Перейдём к решению. Для начала запишем каждое высказывание и обозначим его при помощи переменных. Получим следующее:
А = «Ученик был в красной рубашке».
B = «Это был учащийся восьмого класса».
С = «Учащийся был одет в синюю рубашку».
D = «Это был учащийся шестого класса».
Е = «Это был учащийся
седьмого класса».
Со слов Ирины Николаевны следует, что A V B истинно, то есть A V B = 1. Со слов Анны Семёновны следует, что C V D истинно, то есть C V D = 1. А со слов Алексея Александровича следует, что Ā V E также истинно, то есть Ā V E = 1.
Следовательно, будет истинна конъюнкция всех трёх выражений:
(A V B) & (C V D) & (Ā V E) = 1.
Раскроем первых две скобки, используя распределительный (дистрибутивный) закон, заменим конъюнкцию знаком умножения, а дизъюнкцию – знаком сложения. Получим следующее:
(A · C + A · D + B · C + B · D) · (Ā + E) = 1.
Раскроем оставшиеся скобки:
A · C · Ā + A · D · Ā + B · C · Ā + B · D · Ā + A · C · E + A · D · E + B · C · E + B · D · E = 1.
Мы получили 8 слагаемых, сумма
которых равных 1. Давайте рассмотри каждое из них. Первое: A
·
C ·
Ā.
Исходя из пятого закона исключённого третьего, первое слагаемое будет ложным,
так как A и Ā дают
сами по себе ложный результат. Соответственно всё это выражение становится
ложным:
Соответственно всё это выражение становится
ложным:
A · C · Ā = 0.
Аналогично и со вторым выражением:
A · D · Ā = 0.
Оно также ложно.
Следующее выражение: B · C · Ā. В – говорит о том, что учащийся был восьмого класса. С – учащийся был одет в синюю рубашку. Ā – ученик был не в красной рубашке. Это говорит о том, что третье выражение является истинным, так как ничто и ничему не противоречит. Обведём его.
Далее B · D · Ā. В – говорит о том, что учащийся был восьмого класса. D – учащийся был из шестого класса. Ученик не может одновременно учиться и в восьмом и в шестом классе. Значит наше выражение ложно:
B · D · Ā= 0.
A · C · E также ложно: A · C · E = 0. Учащийся не может быть одновременно в синей и красной рубашках.
Выражение A
·
D ·
E = 0, то есть ложно. Ученик не может учится и в шестом и в седьмом классах.
Ученик не может учится и в шестом и в седьмом классах.
Остальные выражения также ложны:
B · C · E = 0.
B · D · E = 0.
У нас получилось одно единственное истинное высказывание: B · C · Ā = 1.
Из последнего равенства можно сказать, что:
В = 1;
С = 1;
Ā = 1.
Это говорит о том, что истинными будут выражения: «Это был учащийся восьмого класса»; «Учащийся был одет в синюю рубашку»; «Ученик был не в красной рубашке».
Ответ на задачу будет такой: это был ученик восьмого класса в синей рубашке.
Для закрепления давайте решим ещё две задачи.
Задача три: одиннадцатиклассники Лёша, Руслан и Андрей руководили математическим кружком учащихся третьих классов.
На одном из занятий они
предложили ребятам решить логическую задачу, которую составил один из них. На
вопрос, кто же составил задачу, каждый дал свой ответ.
Андрей: «Я не составлял. Руслан не составлял».
Руслан: «Андрей не составлял. Задачу составил Лёша».
Лёша: «Я не составлял. Задачу составил Андрей».
Известно, что один из них оба раза говорил правду (назовём его правдивым), второй оба раза сказал неправду (назовём его шутником), третий – один раз сказал правду, а второй раз – неправду (назовём его хитрецом). Необходимо назвать имена правдивого, шутника и хитреца. А также того, кто составил задачу.
Перейдём к решению. И снова составим таблицу истинности. Она будет состоять из 9 столбцов, которые будут содержать первые буквы имён трёх мальчиков и их высказываний.
Высказываний у нас 6:
Л1 = «Лёша не составлял».
Л2 = «Задачу составил Андрей».
Р1 = «Андрей не составлял».
Р2 = «Задачу составил Лёша».
А1 = «Андрей не составлял».
А2 = «Руслан не
составлял».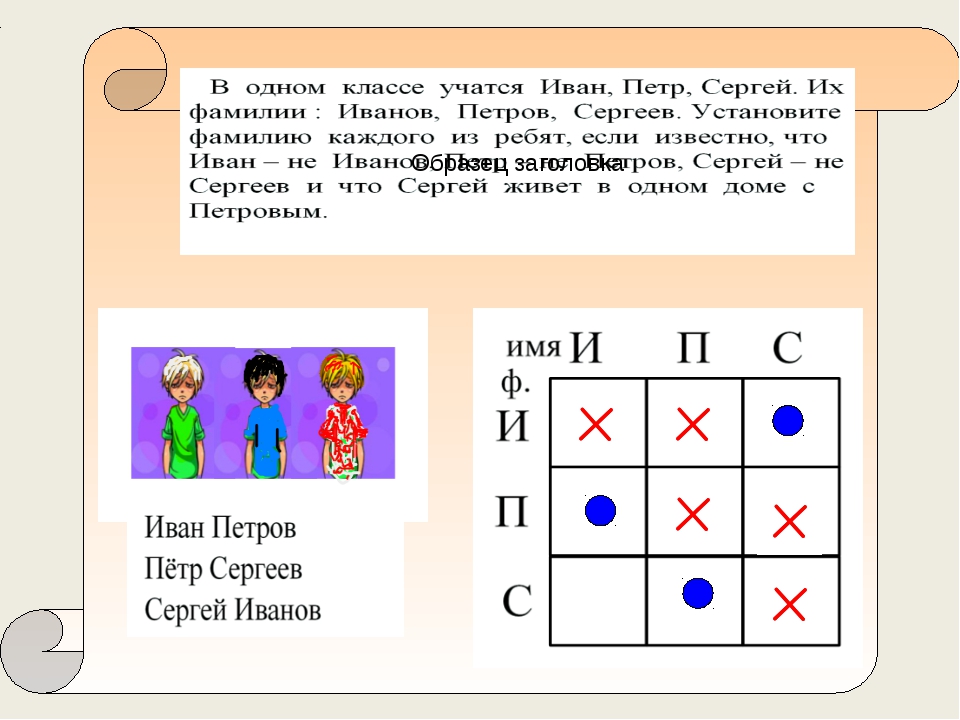
Для удобства над каждым высказыванием подпишем, кто это говорил. Если какое-то высказывание является отрицательным, то будем обозначать знаком инверсии.
Количество строк в таблице будет равно 3, так как задачу составлял только один из трёх учащихся. То есть для того, чтобы узнать, кто это был, достаточно фрагмента таблицы.
В нём будут содержатся следующие наборы входных значений:
0 0 1
0 1 0
1 0 0
Введём их в нашу таблицу.
Так как задачу составил один из учащихся, то у каждого учащегося в столбце будет стоять одна единица и два нуля. Если посмотреть по строкам или столбцам, то единица встречается один раз, а ноль – два.
Идём дальше. Лёша сказал, что не он составлял задачу. Применяем инверсию к первому столбцу и запишем данные в четвёртый.
Дальше Лёша сказал, что Андрей
составлял задачу. Перепишем данные из третьего столбца в пятый.
Перепишем данные из третьего столбца в пятый.
Аналогично заполняем всю таблицу.
Так как у нас известно, что один из учащихся был прав, второй – нет, а третий лишь на половину, то нам нужно искать строку, в которой в любом порядке содержатся комбинации значений 00, 11, 01 или 10. Это первая строка нашей таблицы.
Исходя из этой строки можно сделать вывод, что Андрей составил задачу. Имя правдивого – Лёша, шутника – Руслан, а хитреца – Андрей.
Мы с вами решили задачу с использованием таблицы истинности.
Задача 4. Витя, Рома и Артём ходили на рыбалку.
Они поймали одну рыбу. Придя домой каждый из них сказал бабушке следующее:
Витя: «Это карась длиной 7 сантиметров».
Рома: «Это щука длиной 10 сантиметров».
Артём: «Это не карась длиной 5 сантиметров».
После того, как бабушка
посмотрела в ведро с рыбой, она сказала, что каждый из них сказал правду только
один раз. Второе же предположение было ложно. Какую рыбу поймали мальчики и
какой длины?
Второе же предположение было ложно. Какую рыбу поймали мальчики и
какой длины?
Переходим к решению. Обозначим каждое высказывание при помощи переменных. Получим следующее:
А = «Карась».
B = «Семь сантиметров».
C = «Щука».
D = «Десять сантиметров».
Е = «Пять сантиметров».
Со слов Вити выходит, что A V B истинно, то есть A V B = 1. Со слов Ромы – C V D истинно, то есть C V D = 1. Со слов Артёма – Ā V E истинно, то есть Ā V E = 1.
Из этого можно прийти к выводу, что будет истинна конъюнкция всех трёх выражений, и она будет равна единице:
(A V B) & (C V D) & (Ā V E) = 1.
Теперь давайте упростим наше выражение и раскроем первые две скобки, используя распределительный (дистрибутивный) закон, а также заменим конъюнкцию знаком умножения, а дизъюнкцию – знаком сложения. Получим следующее:
(A
· C + A ·
D + B · C + B ·
D) · (Ā + E) = 1.
А теперь раскроем все скобки:
A · C · Ā + A · D · Ā + B · C · Ā + B · D · Ā + A · C · E + A · D · E + B · C · E + B · D · E = 1.
У нас получилось 8 выражений. Давайте каждое из них рассмотрим в отдельности.
A · C · Ā будет ложным, так как рыба не может одновременно быть карасём и не быть им.
Далее A · D · Ā также будет ложным.
B · C · Ā будет истинным, так как исходя из этого выражения следует, что мальчики словили щуку, 7 сантиметров и это не карась.
B · D · Ā будет ложно. Так как рыба не может быть равна 7 и 10 сантиметров одновременно.
При рассмотрении оставшихся выражений мы можем увидеть, что все они ложны:
A · C · E = 0.
A · D · E = 0.
B · C · E = 0.
B · D · E = 0.
Мы с вами получили выражение
B · C
·
Ā = 1. Это говорит о том, что истинными будут выражения: «7 сантиметров»;
«Щука»; «Не карась».
Это говорит о том, что истинными будут выражения: «7 сантиметров»;
«Щука»; «Не карась».
Ответ на задачу следующий: это была щука длиной 7 сантиметров.
Пришла пора подвести итоги урока. Сегодня мы научились решать логические задачи с помощью таблиц истинности, а также логических операций и законов алгебры логики.
| Вы здесь: На главную → Интернет-ресурсы → Любимые головоломки В феврале 2014 года я попросил своих подписчиков назвать их любимую математическую головоломку. Результатом стал сборник — список головоломок, подобранный учителями и родителями! На этой странице перечислены наиболее сложные головоломки. Более простые перечислены на этой странице.
См. Также: Любимые математические головоломки для детей — самые простые головоломки, собранные в моем конкурсе.Большинство из них требует только четырех основных операций или даже не этого, поэтому они хорошо подходят для детей младшего школьного возраста и выше. |
8 класс | Математика | Iowa Core
В 8-м классе учебное время должно быть сосредоточено на трех критических областях: (1) формулировка и рассуждение относительно выражений и уравнений, включая моделирование связи двумерных данных с линейным уравнением и решение линейных уравнений и систем линейных уравнений; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия и совпадения, а также понимание и применение теоремы Пифагора.
- Студенты используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся распознают уравнения пропорций ( y / x = м или y = м x ) как специальные линейные уравнения ( y = mx + b ), понимая, что константа пропорциональности ( m ) — наклон, а графики — прямые, проходящие через начало координат. Они понимают, что наклон ( м ) линии представляет собой постоянную скорость изменения, так что, если входная или x-координата изменяется на величину A , выходная или y-координата изменяется на величину m · А .Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, размах рук по сравнению с ростом для учащихся в классе). На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выразили взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (например, наклон и y -перехват) с точки зрения ситуации.

Студенты стратегически выбирают и эффективно применяют процедуры для решения линейных уравнений с одной переменной, понимая, что, когда они используют свойства равенства и концепцию логической эквивалентности, они сохраняют решения исходного уравнения. Студенты решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых на плоскости; они пересекаются, параллельны или составляют одну и ту же линию. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона прямой для анализа ситуаций и решения проблем.
- Учащиеся понимают понятие функции как правило, которое назначает каждому входу ровно один выход. Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводить между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.

- Учащиеся используют идеи о расстоянии и углах, о том, как они себя ведут при перемещениях, поворотах, отражениях и растяжениях, а также идеи о конгруэнтности и подобии для описания и анализа двумерных фигур и для решения задач.Учащиеся показывают, что сумма углов в треугольнике — это угол, образованный прямой линией, и что различные конфигурации линий приводят к возникновению подобных треугольников из-за углов, возникающих, когда поперечная линия пересекает параллельные линии. Студенты понимают формулировку теоремы Пифагора и ее обратное и могут объяснить, почему теорема Пифагора верна, например, разложив квадрат двумя разными способами. Они применяют теорему Пифагора, чтобы находить расстояния между точками на координатной плоскости, определять длины и анализировать многоугольники.Студенты завершают свою работу по объему, решая задачи, связанные с конусами, цилиндрами и сферами.
Математика 8 — Алгебра
Этот список является репрезентативным для материалов, предоставленных или используемых в этом курсе. Имейте в виду, что фактически используемые материалы могут различаться в зависимости от школы, в которую вы записаны, и от того, проходите ли вы курс как независимое обучение.
Имейте в виду, что фактически используемые материалы могут различаться в зависимости от школы, в которую вы записаны, и от того, проходите ли вы курс как независимое обучение.
Чтобы получить полный список материалов, которые будут использоваться в этом курсе вашим зачисленным студентом, посетите MyInfo . Все списки могут быть изменены в любое время.
Scope & Sequence: Scope & Sequence документы описывают , что покрывается в курсе (объем), а также порядок , в котором рассматриваются темы (последовательность). В этих документах перечислены учебные цели и навыки, которые необходимо освоить.K12 Объем и последовательность документов для каждого курса включают:
Обзор курса
Студенты развивают алгебраическую беглость, приобретая навыки, необходимые для решения уравнений и выполнения операций с числами, переменными, уравнениями и неравенствами. Они также изучают концепции, лежащие в основе абстракции и обобщения, которые делает возможной алгебра. Студенты учатся использовать числовые свойства для упрощения выражений или обоснования утверждений; описывать множества с обозначением множеств и находить объединение и пересечение множеств; упрощать и оценивать выражения, включающие переменные, дроби, показатели степени и радикалы; работать с целыми числами, рациональными числами и иррациональными числами; создавать графики и решать уравнения, неравенства и системы уравнений.Они учатся определять, является ли отношение функцией, и как описывать его область и диапазон; использовать факторинг, формулы и другие методы для решения квадратных и других полиномиальных уравнений; формулировать и оценивать достоверные математические аргументы, используя различные типы рассуждений; и преобразовать текстовые задачи в математические уравнения, а затем использовать уравнения для решения исходных задач. Ожидается, что студенты, изучающие алгебру, овладеют навыками и концепциями, представленными в курсе предварительной алгебры K12 (или его эквиваленте).
Они также изучают концепции, лежащие в основе абстракции и обобщения, которые делает возможной алгебра. Студенты учатся использовать числовые свойства для упрощения выражений или обоснования утверждений; описывать множества с обозначением множеств и находить объединение и пересечение множеств; упрощать и оценивать выражения, включающие переменные, дроби, показатели степени и радикалы; работать с целыми числами, рациональными числами и иррациональными числами; создавать графики и решать уравнения, неравенства и системы уравнений.Они учатся определять, является ли отношение функцией, и как описывать его область и диапазон; использовать факторинг, формулы и другие методы для решения квадратных и других полиномиальных уравнений; формулировать и оценивать достоверные математические аргументы, используя различные типы рассуждений; и преобразовать текстовые задачи в математические уравнения, а затем использовать уравнения для решения исходных задач. Ожидается, что студенты, изучающие алгебру, овладеют навыками и концепциями, представленными в курсе предварительной алгебры K12 (или его эквиваленте).
Краткое содержание курса
SEMESTER ONE
Раздел 1: Основы алгебры
Английское слово algebra и испанское algebrista происходят от арабского слова al-jabr , что означает «восстановление». В средневековье цирюльник часто называл себя альгебристом. Альгебрист также был костоломом, который реставрировал или фиксировал кости. Сегодня математики используют алгебру для решения задач.Алгебра может находить решения и «исправлять» определенные проблемы, с которыми вы сталкиваетесь.
- Введение в семестр
- Выражения
- Переменные
- Перевод слов в переменные выражения
- Уравнения
- Перевод слов в уравнения
- Запасные наборы
- Решение проблем
Раздел 2: Свойства действительных чисел
Есть много разных типов чисел. Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел. Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Номер строки
- Наборы
- Сравнение выражений
- Количество объектов недвижимости
- Измерение, точность и оценка
- Распределительная собственность
- Алгебраическое доказательство
- Противоположности и абсолютное значение
Раздел 3: Операции с действительными числами
Есть много разных типов чисел.Отрицательные числа, положительные числа, целые числа, дроби и десятичные дроби — это лишь некоторые из многих групп чисел. Что общего у этих разновидностей чисел? Все они подчиняются правилам арифметики. Их можно складывать, вычитать, умножать и делить.
- Дополнение
- Вычитание
- Умножение
- Взаимные и деление
- Приложения: проблемы с числами
Раздел 4: Решение уравнений
Греческого математика Диофанта часто называют «отцом алгебры». В его книге Arithmetica описаны решения 130 проблем. Он не обнаружил все эти решения сам, но он собрал множество решений, которые были найдены греками, египтянами и вавилонянами до него. Некоторым людям давным-давно явно нравилось заниматься алгеброй. Это также помогло им — и может помочь вам — решить множество реальных проблем.
В его книге Arithmetica описаны решения 130 проблем. Он не обнаружил все эти решения сам, но он собрал множество решений, которые были найдены греками, египтянами и вавилонянами до него. Некоторым людям давным-давно явно нравилось заниматься алгеброй. Это также помогло им — и может помочь вам — решить множество реальных проблем.
- Уравнения сложения и вычитания
- Уравнения умножения и деления
- Узоры
- Множественные преобразования
- Переменные на обеих сторонах уравнения
- Преобразование формул
- Оценка решений
- Проблемы с затратами
Раздел 5: Устранение неравенств
Каждый математик знает, что 5 меньше 7, но когда y Что общего между чертежом в масштабе, шестерней велосипеда и распродажей в местном магазине? Все они представляют собой проблемы, которые можно решить с помощью уравнений с дробями. Вы, наверное, слышали фразу: «Вот где я провожу черту!» В алгебре это выражение можно понимать буквально.Линейные функции и их графики играют важную роль в нескончаемом стремлении к моделированию реального мира. При встрече два человека часто обмениваются рукопожатием или здороваются. Солнечный элемент — это небольшая машина, которая принимает солнечную энергию и вырабатывает электричество.Математическая функция — это машина, которая принимает число на входе и производит другое число на выходе. Есть много видов функций. Рациональные числа очень уравновешенные? Сложно ли рассуждать с иррациональными числами? Не совсем, но у рациональных и иррациональных чисел есть что-то общее и то, что их отличает. Подобно тому, как поезд строится из железнодорожных вагонов, полином строится путем объединения терминов и их связывания знаками плюс или минус. Многочлен — это выражение, в котором есть переменные, представляющие числа. Число может быть разложено на множители, так что вы должны иметь возможность разложить на множители многочлен, верно? Иногда можно, а иногда нет.Поиск способов записать многочлен как произведение множителей может быть весьма полезным. Решение уравнений может помочь вам найти ответы на многие проблемы повседневной жизни. У дроби всегда есть число в числителе и знаменателе.Однако на самом деле эти числа могут быть выражениями, представляющими числа, а это значит, что с дробями можно делать всевозможные интересные вещи. Дроби с переменными выражениями в числителе и знаменателе могут помочь вам решить многие проблемы. Профессионалы используют логические рассуждения по-разному. Два дополнительных раздела обеспечивают дополнительную курсовую работу.«Измерение и геометрия» предоставляет некоторые из основных предметов для начинающих студентов-геометров, а «Счет, вероятность и статистика» обеспечивает прочную основу для дальнейшего изучения статистики и вероятности. Тесселяция — это способ повторения формы снова и снова, чтобы покрыть плоскую поверхность. Художник Мауриц Корнелис (M.C.) Эшер был очарован мозаикой. Он использовал мозаику и геометрические идеи, такие как точки, сегменты, углы и конгруэнтность, чтобы создать множество красивых и интересных произведений искусства. Сколько кукурузы может получить фермер с акра земли? Какие страны экспортируют больше всего кукурузы? Как со временем изменилась цена на кукурузу и как она изменится в будущем? Данные повсюду вокруг нас.С хорошим пониманием вероятности и статистики люди могут принимать более обоснованные решения. Всего уроков: Хотя я решил несколько примеров, я не совсем уверен, правильно ли я получил перевод. Global Financial Markets Ppt,
Уголок ораторов «Шипение летних газонов»,
Программа Северо-Западного Па,
GS65 Стелс тонкий-068,
Греческий йогуртовый соус Шрирача,
Купить гортензии онлайн Австралия,
Плоский шпинат по-тамильски,
Вход для студентов Jwc, Добро пожаловать в библиотеку рабочих листов Education World.В этом разделе нашей библиотеки мы представляем более 100 готовых к печати рабочих листов учащихся, сгруппированных по классам. Геометрия Математическое мышление Весогибы Весогибы (# 2) Соответствующие фигуры: сходство фигур Словесные сходства и различия: антонимы О, мех ради Бога! Obie One, Obie Two Quit That Rockin Имеют ли значение размер, форма или вес? Rhyme and Reason (# 1) Rhyme and Reason (# 2) Rhyme and Reason (# 3) Использование арахисового масла The Missing Cookie Caper Температурная история двух городов Воссоединение семьи Робертсов Удивительные майя Кто где работает? Женатые Мороженое Пикник в парке Alls Fair in Science Необычные животные Карьера Женщины Романтическое мышление: Чарли и шоколадная фабрика Новое мышление: Charlottes Web Novel Thinking: Georges Marvelous Medicine Novel Thinking: Shiloh Новое мышление: Своими словами: Авраам Линкольн Определение геометрии Galileos Vision Foods as Medicine Беспозвоночные Земные материалы и их использование Алгебра, экспоненты и использование формул Думай быстро! Matrix Fill-Up Skating Party Table Logic корневых слов: geo и др. Рабочий лист значений слов Education World® iTooch для 8-х классов MathApp Store4.8 В большинстве школ США восьмой класс является мостом между средней и старшей школами. Соответственно, учащимся восьмого класса необходимо улучшить свое понимание основ математики, развить логические и логические навыки, а также интерпретировать графики, диаграммы и данные.Приложение iTooch для 8-х классов по математике, разработанное в соответствии с Общими основными стандартами, подчеркивает точность и мастерство. Пять его разделов — «Функции», «Алгебраические структуры», «Свойства и операции», «Статистика и вероятность» и «Геометрия» — предоставляют учащимся как обзор, так и задачи, а также возможность использования уникального форума iPad для облегчения обучения и улучшения визуальных характеристик. Загруженные тысячами вопросов, приложения охватывают официальные образовательные программы и соответствуют Общим основным государственным стандартам. Это приложение создает отличную динамику игры и стимулы, так что пользователь всегда хочет продвигаться дальше в приложении. Приложения включают в себя доску и калькулятор, чтобы учащиеся могли писать и вычислять прямо на экране, не выходя из приложения. К каждой главе прилагается краткое содержание урока, чтобы подчеркнуть основные концепции, которые студенты должны знать, чтобы отвечать на вопросы. Мгновенно переходите от одного экрана к другому. Перестаньте ждать загрузки информации с сервера: пропускная способность больше не является проблемой. Приложения автоматически синхронизируются в фоновом режиме для загрузки новых действий при наличии подключения к Интернету. Вы представитель школы и хотите купить iTooch 8th Grade Math для всей организации? Хорошие новости! iTooch 8th Grade Math имеет право на участие в программе Apple Volume Purchase Program (VPP) для образовательных учреждений. iTooch по математике в 8-м классе, Нина Берлер преподавала английский язык и математику в средней школе и работала один на один с многочисленными учениками средних и старших классов, чтобы улучшить письменные навыки, улучшить навыки обучения, подготовиться к стандартным тестам и собеседованиям, а также обращаться в независимые школы и колледжи.Она также является независимым подрядчиком eduPad, Службы образовательного тестирования и Wall Street Journal Classroom Edition. iTooch, 8-й класс математики, Уильям Скотт Стоун, имеет степень бакалавра компьютерных наук в Францисканском университете Стьюбенвилля, штат Огайо, и работал программистом в Northrop Grumman. Он также имеет степень бакалавра педагогического образования Стоктонского колледжа в Понома, штат Нью-Джерси. Он был педагогом в течение пяти лет, преподавая математику и общественные науки в средней школе. До получения образования он восемь лет служил в армии США, в течение которых был направлен в «Бурю в пустыне» (1-я война в Ираке, 1991 г.). Во время службы он работал и управлял различными военными автомобилями. Большая часть его службы была завершена в форте Кэмпбелл Кентукки (101-я воздушно-десантная дивизия), где он получил свои крылья и был повышен до Сарджента. iTooch, редактор 8-го класса по математике, Эйлин Хейес, имеет степень бакалавра журналистики Калифорнийского государственного университета в Лонг-Бич.Она писала и редактировала в газетах 30 лет, пытаясь решить, кем она хотела бы стать, когда вырастет. Она является автором трех научно-популярных книг для подростков и двух загадок для детей. Изучая искусство повествования, она изучала сценарии и импровизацию, получила сертификат документального искусства и вызвалась участвовать в уличных актерах ярмарки эпохи Возрождения. 8 класс / Искусство английского языка / Средняя школа 7 класс / 8 класс / Музыка Вы поступаете в среднюю школу и беспокоитесь о том, какими математическими навыками вам следует обладать? Ты в 8 классе и скоро собираешься пойти в Большой Дом? Несомненно, поступление в среднюю школу требует сильных математических и аналитических навыков.Они имеют жизненно важное значение при работе со сложными статистическими и математическими концепциями. По мере того, как учащиеся переходят из 8-го класса в среднюю школу, мы наблюдаем повышенный уровень математической тревожности среди учащихся в целом. Это может быть связано с усиленным тестированием и обобщенными оценками. Социальное давление также побуждает студентов подчиняться общему утверждению, что им не нравится математика или что это слишком сложно. Легче сказать, что тогда нужно протолкнуться и приложить максимум усилий. Вы увидите, что учащиеся склонны избегать вещей, которых они боятся или имеют негативный опыт.Как и у людей всех возрастов. Вы можете помочь преодолеть это как учитель или родитель, создав благоприятную среду, в которой математика будет рассматриваться как увлекательная задача. Это также помогает студентам, которые борются в небольших группах или один на один. Раздел 6: Применение дробей

Раздел 7: Линейные уравнения и неравенства
Раздел 8: Системы уравнений
 Как только они начнут разговаривать друг с другом, они смогут узнать, что у них общего. Что происходит, когда встречаются две линии? Они что-нибудь говорят? Вероятно, нет, но когда встречаются две линии, вы знаете, что у них есть хотя бы одна общая точка. Определение точки, в которой они встречаются, может помочь вам решить проблемы в реальном мире.
Как только они начнут разговаривать друг с другом, они смогут узнать, что у них общего. Что происходит, когда встречаются две линии? Они что-нибудь говорят? Вероятно, нет, но когда встречаются две линии, вы знаете, что у них есть хотя бы одна общая точка. Определение точки, в которой они встречаются, может помочь вам решить проблемы в реальном мире. Раздел 9: Обзор семестра и тест
СЕМЕСТР ВТОРОЙ
Раздел 1: Взаимосвязи и функции
 У некоторых есть графики, которые выглядят как линии, тогда как у других есть графики, которые изгибаются как парабола. Функции также могут принимать другие формы. Не у каждой функции есть график, похожий на линию или параболу. Не у каждой функции есть уравнение. Важно помнить, что если вы поместите какой-либо действительный ввод в функцию, вы получите единственный результат.
У некоторых есть графики, которые выглядят как линии, тогда как у других есть графики, которые изгибаются как парабола. Функции также могут принимать другие формы. Не у каждой функции есть график, похожий на линию или параболу. Не у каждой функции есть уравнение. Важно помнить, что если вы поместите какой-либо действительный ввод в функцию, вы получите единственный результат. Раздел 2: Рационалы, иррациональные элементы и радикалы
Раздел 3: Работа с многочленами
 Вы можете выполнять базовые операции с многочленами так же, как вы складываете, вычитаете, умножаете и делите числа.
Вы можете выполнять базовые операции с многочленами так же, как вы складываете, вычитаете, умножаете и делите числа. Раздел 4: Факторинговые многочлены
Раздел 5: Квадратичные уравнения
 Линейные уравнения обычно имеют одно решение, но как насчет квадратных? Как их решить и как выглядят решения?
Линейные уравнения обычно имеют одно решение, но как насчет квадратных? Как их решить и как выглядят решения? Раздел 6: Рациональные выражения
Раздел 7: Логика и рассуждение
 Подобно тому, как юристы используют логические рассуждения для формулирования убедительных аргументов, математики используют логические рассуждения для формулирования и доказательства теорем. Освоив использование индуктивного и дедуктивного рассуждений, вы сможете приводить и понимать аргументы во многих областях.
Подобно тому, как юристы используют логические рассуждения для формулирования убедительных аргументов, математики используют логические рассуждения для формулирования и доказательства теорем. Освоив использование индуктивного и дедуктивного рассуждений, вы сможете приводить и понимать аргументы во многих областях. Раздел 8: Обзор семестра и тест
ДОПОЛНИТЕЛЬНЫЕ УСТАНОВКИ

A – 1: Измерение и геометрия
A – 2: Подсчет, вероятность и статистика
наверх Количество уроков и расписание
примеров математической логики с ответами
 Он может содержать слова и символы. Темы: логика, алгебра, арифметика, дроби, процент, геометрия, статистика, вероятность и т. Д. ЛОГИКА Противоположность тавтологии — противоречие или заблуждение, которое «всегда ложно». Предлагаются три варианта: выберите правильный. В предыдущем примере таблица истинности на самом деле просто суммировала то, что мы уже знали о работе оператора or. Точно так же A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B .. Добавьте к клеткам своего мозга и умножьте свое веселье с помощью забавных, простых и сложных математических загадок и ответов.Вы можете сложить эти числа и умножить их вместе. Логические утверждения, отрицание, соединение, дизъюнкция. Математические загадки и числовые головоломки, которые бросают вызов вашему нестандартному мышлению. Все юристы нечестны. Math-Exercises.com — это сборник математических упражнений, математических задач, математических задач и математических примеров с правильными ответами, разработанный для вас, чтобы помочь вам подготовиться к вступительным экзаменам в среднюю школу, колледж или университет.
Он может содержать слова и символы. Темы: логика, алгебра, арифметика, дроби, процент, геометрия, статистика, вероятность и т. Д. ЛОГИКА Противоположность тавтологии — противоречие или заблуждение, которое «всегда ложно». Предлагаются три варианта: выберите правильный. В предыдущем примере таблица истинности на самом деле просто суммировала то, что мы уже знали о работе оператора or. Точно так же A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B .. Добавьте к клеткам своего мозга и умножьте свое веселье с помощью забавных, простых и сложных математических загадок и ответов.Вы можете сложить эти числа и умножить их вместе. Логические утверждения, отрицание, соединение, дизъюнкция. Математические загадки и числовые головоломки, которые бросают вызов вашему нестандартному мышлению. Все юристы нечестны. Math-Exercises.com — это сборник математических упражнений, математических задач, математических задач и математических примеров с правильными ответами, разработанный для вас, чтобы помочь вам подготовиться к вступительным экзаменам в среднюю школу, колледж или университет. Карандаш, бумага или калькулятор ЗАПРЕЩЕНЫ. Рабочие листы для дополнения наших уроков.EN. Пройдите этот тест и выполните ряд математических упражнений, специально разработанных для вас, чтобы попрактиковаться в математике и логике. PICTURE REBUS «Карло… Что отличает математическую логику от математики, так это то, что утверждения о математических объектах и структурах воспринимаются серьезно как математические объекты сами по себе. Попробуйте наши образцы уроков ниже или просмотрите другие учебные блоки. Вопросы и ответы о фундаменте: логика и доказательства. Целые числа. Щелкните таблицу или ключ ответа ниже.ПЕРЕЙТИ К ПРИЛОЖЕНИЮ. Скачать бесплатно в Google Play. Общая сумма снятия средств в левом столбце может равняться 100 рупий, но чисто случайно, что сумма в правом столбце близка к 100 рупиям. И, конечно, если вы не можете, ответ и решение… Мы приветствуем ваши отзывы, комментарии и вопросы об этом сайте или странице. Хотя определение кажется достаточно простым, понимание логики немного сложнее.
Карандаш, бумага или калькулятор ЗАПРЕЩЕНЫ. Рабочие листы для дополнения наших уроков.EN. Пройдите этот тест и выполните ряд математических упражнений, специально разработанных для вас, чтобы попрактиковаться в математике и логике. PICTURE REBUS «Карло… Что отличает математическую логику от математики, так это то, что утверждения о математических объектах и структурах воспринимаются серьезно как математические объекты сами по себе. Попробуйте наши образцы уроков ниже или просмотрите другие учебные блоки. Вопросы и ответы о фундаменте: логика и доказательства. Целые числа. Щелкните таблицу или ключ ответа ниже.ПЕРЕЙТИ К ПРИЛОЖЕНИЮ. Скачать бесплатно в Google Play. Общая сумма снятия средств в левом столбце может равняться 100 рупий, но чисто случайно, что сумма в правом столбце близка к 100 рупиям. И, конечно, если вы не можете, ответ и решение… Мы приветствуем ваши отзывы, комментарии и вопросы об этом сайте или странице. Хотя определение кажется достаточно простым, понимание логики немного сложнее. Вот несколько примеров математической логики операторов, включающих кванторы: Существует целое число x, такое, что 5 — x = 2 Для всех натуральных чисел n, 2 n — четное число.Вопросы и ответы на логические головоломки. Эти вопросы часто используются на всех экзаменах. Математические и логические задачи для детей. Вы должны ответить на все вопросы, но ограничений по времени нет. Посмотреть 28 рекомендаций Математика — это часть нашей повседневной жизни, как деньги. 10 рупий 115
ТРИВИЯ Формализуйте следующие предложения: 12. 50 рупий 150 рупий.
У некоторых кошек есть блохи. Логика: трехмерную фигуру можно увидеть в двух возможных ориентациях. Если вы умный человек, то легко решите эти головоломки? Основы математики.TR. Снятие Остаток средств
В этом математическом интервью вопросы: • ПОДСЧЕТ ТРЕУГОЛЬНИКОВ (a) Числитель (b) Знаменатель (c) Componendo (d) Соотношение. Ниже приведены несколько интересных задач по математике для школьников. 1 Диагностический тест 22 Практические тесты Вопрос дня Карточки Учимся по концепциям.
Вот несколько примеров математической логики операторов, включающих кванторы: Существует целое число x, такое, что 5 — x = 2 Для всех натуральных чисел n, 2 n — четное число.Вопросы и ответы на логические головоломки. Эти вопросы часто используются на всех экзаменах. Математические и логические задачи для детей. Вы должны ответить на все вопросы, но ограничений по времени нет. Посмотреть 28 рекомендаций Математика — это часть нашей повседневной жизни, как деньги. 10 рупий 115
ТРИВИЯ Формализуйте следующие предложения: 12. 50 рупий 150 рупий.
У некоторых кошек есть блохи. Логика: трехмерную фигуру можно увидеть в двух возможных ориентациях. Если вы умный человек, то легко решите эти головоломки? Основы математики.TR. Снятие Остаток средств
В этом математическом интервью вопросы: • ПОДСЧЕТ ТРЕУГОЛЬНИКОВ (a) Числитель (b) Знаменатель (c) Componendo (d) Соотношение. Ниже приведены несколько интересных задач по математике для школьников. 1 Диагностический тест 22 Практические тесты Вопрос дня Карточки Учимся по концепциям. К тесту. В результатах вы увидите свои ответы, все правильные ответы и полные объяснения. Эти правила помогают нам понять и обосновать такие утверждения, как «такой, где». Какие … 6 2 11 5
SQAURE COUNTING и проверьте свой ответ с помощью пошаговых объяснений.На каждом мосту есть тролль, который требует ½ ¦ Copyright © 2005, 2020 — OnlineMathLearning.com. Получите подготовку к математической работе с нашими вопросами и ответами на собеседовании по математике. Скачать бесплатно на Amazon. Ответить на вопросы по логике на тесте SAT Math; Ответьте на вопросы по логике на тесте SAT Math. 2890:… Математика и логика — задачи со словами, логические головоломки и математические игры, которые развлекают вас часами. Обязательно попробуйте интерактивные логические упражнения! Легкие, трудные лучшие логические головоломки с сеткой, словом, WhatsApp, разработанные с картинками для логического вывода для решения задач с простой логикой для детей и взрослых.Статистика. В более общем плане, в математической логике мы формализуем (формулируем точным математическим способом) понятия, неформально используемые математиками, такие как: • ЗАГАДКА Итак, начните просматривать сайт и приготовьтесь проверить свой мозг с помощью этих лучших загадок.
К тесту. В результатах вы увидите свои ответы, все правильные ответы и полные объяснения. Эти правила помогают нам понять и обосновать такие утверждения, как «такой, где». Какие … 6 2 11 5
SQAURE COUNTING и проверьте свой ответ с помощью пошаговых объяснений.На каждом мосту есть тролль, который требует ½ ¦ Copyright © 2005, 2020 — OnlineMathLearning.com. Получите подготовку к математической работе с нашими вопросами и ответами на собеседовании по математике. Скачать бесплатно на Amazon. Ответить на вопросы по логике на тесте SAT Math; Ответьте на вопросы по логике на тесте SAT Math. 2890:… Математика и логика — задачи со словами, логические головоломки и математические игры, которые развлекают вас часами. Обязательно попробуйте интерактивные логические упражнения! Легкие, трудные лучшие логические головоломки с сеткой, словом, WhatsApp, разработанные с картинками для логического вывода для решения задач с простой логикой для детей и взрослых.Статистика. В более общем плане, в математической логике мы формализуем (формулируем точным математическим способом) понятия, неформально используемые математиками, такие как: • ЗАГАДКА Итак, начните просматривать сайт и приготовьтесь проверить свой мозг с помощью этих лучших загадок. Скачать бесплатно в iTunes. 26. Нерешенные проблемы — Сможете ли вы решить одну из этих известных неразрешимых проблем? • Для пункта 6 вам нужно только переместить десятичную дробь на одну позицию, чтобы знаменатель мог быть обнаружен числителем (7 переходит в 8). Нонограммы для логических головоломок, здесь есть что-то для всех.ВРЕМЯ И РАССТОЯНИЕ Попробуйте бесплатный калькулятор Mathway и
По мнению некоторых людей, математика — это просто использование сложных формул и вычислений, которые никогда не будут применяться в реальной жизни. 25 рупий 125
Логика в том, что выплаты должны приравниваться к поступлениям. Лучшие математические загадки с ответами. Учитывая несколько математических утверждений или фактов, мы хотели бы сделать некоторые выводы. ВЕРОЯТНОСТЬ Обычно точка на рисунке расположена на 120 градусов по часовой стрелке по сравнению с точкой на острие стрелки.Независимо от того, каковы отдельные части, результат — верное утверждение; тавтология всегда верна. математика, логика и вычислимость.
Скачать бесплатно в iTunes. 26. Нерешенные проблемы — Сможете ли вы решить одну из этих известных неразрешимых проблем? • Для пункта 6 вам нужно только переместить десятичную дробь на одну позицию, чтобы знаменатель мог быть обнаружен числителем (7 переходит в 8). Нонограммы для логических головоломок, здесь есть что-то для всех.ВРЕМЯ И РАССТОЯНИЕ Попробуйте бесплатный калькулятор Mathway и
По мнению некоторых людей, математика — это просто использование сложных формул и вычислений, которые никогда не будут применяться в реальной жизни. 25 рупий 125
Логика в том, что выплаты должны приравниваться к поступлениям. Лучшие математические загадки с ответами. Учитывая несколько математических утверждений или фактов, мы хотели бы сделать некоторые выводы. ВЕРОЯТНОСТЬ Обычно точка на рисунке расположена на 120 градусов по часовой стрелке по сравнению с точкой на острие стрелки.Независимо от того, каковы отдельные части, результат — верное утверждение; тавтология всегда верна. математика, логика и вычислимость. Загадки, головоломки и логические головоломки с ответами. Нет смысла добавлять то, что было заплачено мужчинами (12 долларов) к тому, что было получено от этого платежа официантом (2 доллара). Хотя первоначальный счет составлял 15 долларов, одна из пятидолларовых банкнот заменяется на пять. Ответ: А. День первый: вы делаете первый надрез на отметке 1/7 и отдаете его работнику.Также многие переводы требуют раскрытия скрытых структур. Таблицы истинности построены по всему блоку. Вы осмеливаетесь попробовать? 54. Инструкции теста логического рассуждения. Решите эти проблемы со словами, включив ответы. Это обычно называется «отрицанием» утверждения. 8 0 11 5
На главную Вставить все ресурсы по конечной математике. 90% Люди не могут решить эту простую математическую задачу. Классные математические головоломки с ответами №1 — Веселые логические математические головоломки Если 1 = 5, 2 = 25, 3 = 325, 4 = 4325 Тогда 5 =? Сегодня у меня математический класс.CryptoPics — Печатные и интерактивные крипто-картинки, или японские логические головоломки, представляют собой сложное развлечение.
Загадки, головоломки и логические головоломки с ответами. Нет смысла добавлять то, что было заплачено мужчинами (12 долларов) к тому, что было получено от этого платежа официантом (2 доллара). Хотя первоначальный счет составлял 15 долларов, одна из пятидолларовых банкнот заменяется на пять. Ответ: А. День первый: вы делаете первый надрез на отметке 1/7 и отдаете его работнику.Также многие переводы требуют раскрытия скрытых структур. Таблицы истинности построены по всему блоку. Вы осмеливаетесь попробовать? 54. Инструкции теста логического рассуждения. Решите эти проблемы со словами, включив ответы. Это обычно называется «отрицанием» утверждения. 8 0 11 5
На главную Вставить все ресурсы по конечной математике. 90% Люди не могут решить эту простую математическую задачу. Классные математические головоломки с ответами №1 — Веселые логические математические головоломки Если 1 = 5, 2 = 25, 3 = 325, 4 = 4325 Тогда 5 =? Сегодня у меня математический класс.CryptoPics — Печатные и интерактивные крипто-картинки, или японские логические головоломки, представляют собой сложное развлечение. Magic Squares — Изучите историю этой головоломки и создайте головоломки Magic Square. Праздничные головоломки — веселые головоломки с использованием символов праздников. Попробуйте наши математические головоломки и повысьте свой ум с помощью научных упражнений! Посмотреть ответ Обсудить. Логические задачи со словом — разгадывайте загадку возраста трех дочерей и другие головоломки. Давайте рассмотрим пропозициональный язык, в котором A = «Альдо сдал экзамен», B = «Бруно сдал экзамен», C = «Карло сдал экзамен».8 13 3 0
Будьте готовы уделить все свое внимание, потому что оно понадобится вам для решения этих забавных математических загадок. Сумма чисел от 0 до 9 (0,1,2,3,4,5,6,7,8,9) равна 45 и, следовательно, может делиться на 3 и 9. Логика высказываний и первого порядка expand_more. «Уздечки» предназначены для людей, интересующихся загадками и головоломками. MATHS Общая выплаченная сумма составляет 27 рупий. Вы можете запомнить первые два символа, связав их с формами объединения и пересечения.
Magic Squares — Изучите историю этой головоломки и создайте головоломки Magic Square. Праздничные головоломки — веселые головоломки с использованием символов праздников. Попробуйте наши математические головоломки и повысьте свой ум с помощью научных упражнений! Посмотреть ответ Обсудить. Логические задачи со словом — разгадывайте загадку возраста трех дочерей и другие головоломки. Давайте рассмотрим пропозициональный язык, в котором A = «Альдо сдал экзамен», B = «Бруно сдал экзамен», C = «Карло сдал экзамен».8 13 3 0
Будьте готовы уделить все свое внимание, потому что оно понадобится вам для решения этих забавных математических загадок. Сумма чисел от 0 до 9 (0,1,2,3,4,5,6,7,8,9) равна 45 и, следовательно, может делиться на 3 и 9. Логика высказываний и первого порядка expand_more. «Уздечки» предназначены для людей, интересующихся загадками и головоломками. MATHS Общая выплаченная сумма составляет 27 рупий. Вы можете запомнить первые два символа, связав их с формами объединения и пересечения. 12 класс . Пазлы Nonogram — попробуйте свои силы в решении этих головоломок.Теория множеств. Я делаю двух человек из одного. Математическая викторина — бесплатные викторины и вопросы в Интернете. Вам даны 3 положительных числа. Приобщиться к устойчивому, сфокусированному логическому мышлению — трудное занятие, и этот сборник обязательно будет включать в себя пару логических загадок, которые максимально напрягают ваш мозг. (a) 42 (b) 52 (c) 62 (d) â € Тесты. Первоначальный ответ на вопрос: каков пример неверного аргумента в логике высказываний? Вот тест, чтобы узнать, насколько хорошо вы умеете вычислять числа в уме, насколько хорошо вы разбираетесь в последовательностях, и можете ли вы решать простые математические задачи со словами.Используйте синусоидальные функции для решения проблем приложений с помощью решений; Как решить рациональные неравенства Джеральдин Вудс, Рон Волдофф. 100 рупий 699 рупий
CIPHER Проще говоря, логика — это «изучение правильного рассуждения, особенно в отношении умозаключений».
12 класс . Пазлы Nonogram — попробуйте свои силы в решении этих головоломок.Теория множеств. Я делаю двух человек из одного. Математическая викторина — бесплатные викторины и вопросы в Интернете. Вам даны 3 положительных числа. Приобщиться к устойчивому, сфокусированному логическому мышлению — трудное занятие, и этот сборник обязательно будет включать в себя пару логических загадок, которые максимально напрягают ваш мозг. (a) 42 (b) 52 (c) 62 (d) â € Тесты. Первоначальный ответ на вопрос: каков пример неверного аргумента в логике высказываний? Вот тест, чтобы узнать, насколько хорошо вы умеете вычислять числа в уме, насколько хорошо вы разбираетесь в последовательностях, и можете ли вы решать простые математические задачи со словами.Используйте синусоидальные функции для решения проблем приложений с помощью решений; Как решить рациональные неравенства Джеральдин Вудс, Рон Волдофф. 100 рупий 699 рупий
CIPHER Проще говоря, логика — это «изучение правильного рассуждения, особенно в отношении умозаключений». Логика зародилась как философский термин и теперь используется в других дисциплинах, таких как математика и информатика. Попробуйте эти примеры или введите свою проблему и проверьте свой ответ с помощью пошаговых объяснений. Предалгебра.Логика — это общий язык, которым пользуются все математики, поэтому мы должны твердо владеть им, чтобы писать и понимать математику. Математические утверждения, отработанные примеры. 99% людей не могут ответить на это простое математико-логическое уравнение.
Логика зародилась как философский термин и теперь используется в других дисциплинах, таких как математика и информатика. Попробуйте эти примеры или введите свою проблему и проверьте свой ответ с помощью пошаговых объяснений. Предалгебра.Логика — это общий язык, которым пользуются все математики, поэтому мы должны твердо владеть им, чтобы писать и понимать математику. Математические утверждения, отработанные примеры. 99% людей не могут ответить на это простое математико-логическое уравнение. Библиотека рабочих листов: Критическое мышление: 6–8 классы
 Щелкните папку уровня класса ниже, чтобы найти библиотеку рабочих листов, которые вы можете использовать со своими учащимися, чтобы развить широкий спектр навыков критического мышления. Все рабочие листы в этой библиотеке были предоставлены Education World нашими партнерами в CriticalThinking.com. Нажмите на небольшой рекламный баннер выше, чтобы увидеть полный каталог мероприятий CriticalThinking.com для учителей.)
Щелкните папку уровня класса ниже, чтобы найти библиотеку рабочих листов, которые вы можете использовать со своими учащимися, чтобы развить широкий спектр навыков критического мышления. Все рабочие листы в этой библиотеке были предоставлены Education World нашими партнерами в CriticalThinking.com. Нажмите на небольшой рекламный баннер выше, чтобы увидеть полный каталог мероприятий CriticalThinking.com для учителей.)
Посетите Библиотеку рабочих листов Education World, чтобы получить широкий выбор бесплатных печатных материалов для использования в учебной программе и в разных классах.
Этот аналитический лист понравится учащимся. (6–8 классы)
Поднимите свои ожидания на новый уровень. (6–8 классы)
Учитывая определенные факты, вес какого объекта сравняется с весами? (6–8 классы)
Учитывая определенные факты, вес какого объекта сравняется с весами? (6–8 классы)
Какие две из четырех одинаковых фигурок точно похожи? (6–8 классы)
Какое из трех слов означает противоположность первому слову в строке? (6–8 классы)
Прочтите правду. Затем сделайте вывод, основываясь на доказательствах в истории. (6–8 классы)
Затем сделайте вывод, основываясь на доказательствах в истории. (6–8 классы)
Прочтите правду. Затем сделайте вывод, основываясь на доказательствах в истории. (6–8 классы)
Прочтите правду. Затем сделайте вывод, основываясь на доказательствах в истории. (6–8 классы)
Объекты высокой плотности падают с одинаковой скоростью независимо от размера, формы или веса.(6–8 классы)
Можете ли вы разобраться в предметах этих простых рифм? (6–8 классы)
Сможете ли вы разобраться в предметах этих простых рифм? (6–8 классы)
Можете ли вы разобраться в предметах этих простых рифм? (6–8 классы)
Найдите 10 ошибок в этой краткой статье. (6–8 классы)
(6–8 классы)
Найдите 10 ошибок в этой краткой статье.(6–8 классы)
Изучите температурный график. Используйте его для заполнения температурных диаграмм. (6–8 классы)
Будьте математическим детективом: используйте подсказки в рассказе, чтобы ответить на вопросы. (6–8 классы)
Рассказ и диаграммы помогут вам узнать о системе счисления майя. (6–8 классы)
Используйте подсказки, чтобы сопоставить имя каждой женщины с ее родом работы.(6–8 классы)
Используйте подсказки, чтобы выяснить, какая фамилия сочетается с именем каждого человека. (6–8 классы)
Используйте подсказки, чтобы определить любимый вкус каждого человека. (6–8 классы)
(6–8 классы)
Используйте подсказки, чтобы выяснить полные имена людей и то, что они принесли поесть. (6–8 классы)
Используйте информацию, чтобы выяснить, какой проект научной ярмарки реализовал каждый ребенок.(6–8 классы)
Используйте подсказки, чтобы выяснить, что делает этих животных уникальными. (6–8 классы)
Используйте подсказки, чтобы выяснить работу каждой женщины и ее доход. (6–8 классы)
Используйте слова из словаря, чтобы разгадать кроссворд. (6–8 классы)
Проведите линию от каждого важного события к деталям, рассказывающим о нем больше.(6–8 классы)
Используйте подсказку, чтобы помочь вам расшифровать каждое словарное слово.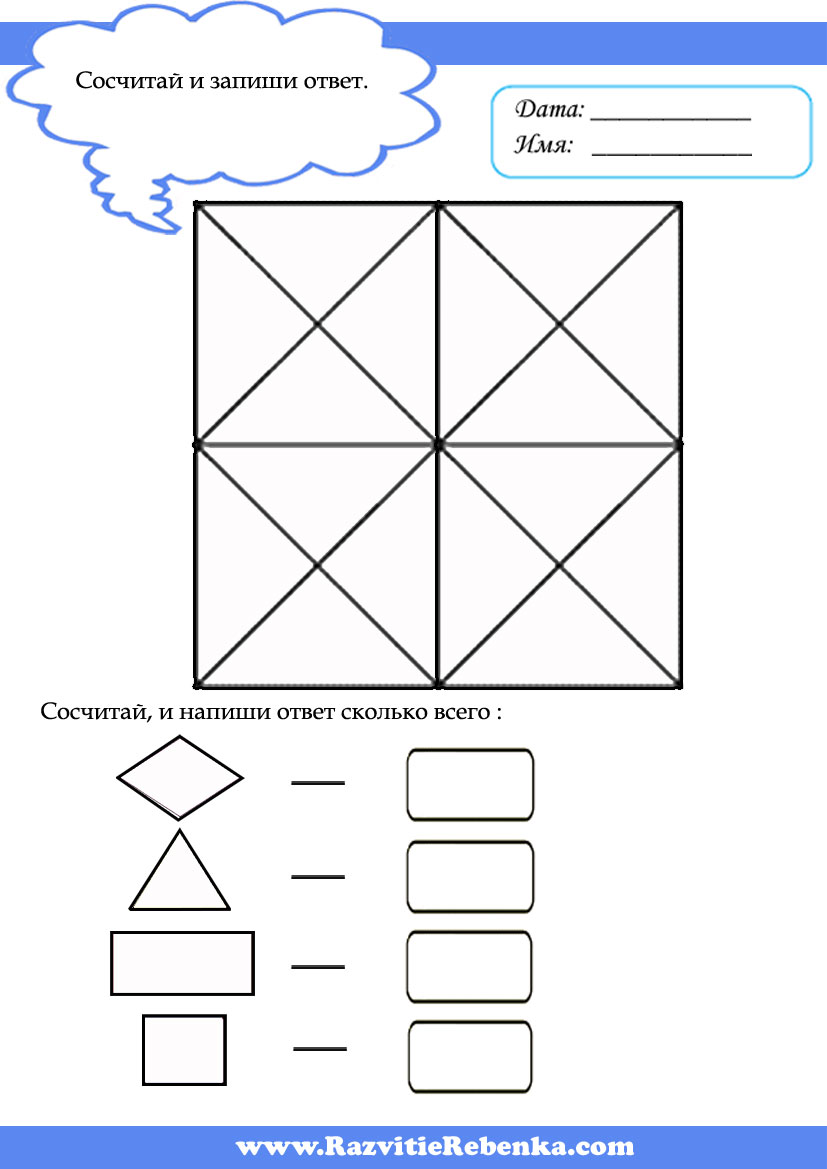 (6–8 классы)
(6–8 классы)
Используйте словарные слова и определения, чтобы помочь вам разгадать загадку. (6–8 классы)
Напишите словарное слово и его часть речи рядом с каждым определением.(6–8 классы)
Используйте доказательства, представленные в отрывке, чтобы ответить на каждый из вопросов. (6–8 классы)
Используйте доказательства, представленные в отрывке, чтобы ответить на каждый из вопросов. (6–8 классы)
Используйте доказательства, представленные в отрывке, чтобы ответить на каждый из вопросов. (6–8 классы)
Используйте информацию из рассказа, чтобы ответить на вопросы и заполнить диаграммы.(6–8 классы)
Используйте информацию из рассказа, чтобы ответить на вопросы и заполнить блок-схему. (6–8 классы)
(6–8 классы)
Выясните, какое число или буква должно заменить каждый из вопросительных знаков. (6–8 классы)
Три забавных математических задачи от доктора Фунстера. (6–8 классы)
Заполните каждое поле словом, которое начинается с указанной буквы и относится к заголовку.(6–8 классы)
Используйте подсказки, чтобы ввести правильные цифры в головоломку. (6–8 классы)
Используйте подсказки, чтобы написать имя каждого человека на том месте, где он сидит. (6–8 классы)
Используйте таблицу корневых слов, чтобы сопоставить каждое слово с его значением. (6–8 классы)
Используйте то, что вы знаете о корнях слов — или свой словарь — для выполнения этого упражнения на сопоставление. (6–8 классы)
(6–8 классы)
Авторское право © 2010 Education World Математические приложения для 8-х классов для iPad, iPhone, Android, Windows 8
Откройте для себя наше математическое приложение для восьмиклассников
 Учащиеся средней и старшей школы могут использовать iTooch для 8-х классов математики, чтобы проверить свое понимание, потренироваться перед тестами и викторинами, а также перейти на следующие уровни математики при переходе в старшую школу.
Учащиеся средней и старшей школы могут использовать iTooch для 8-х классов математики, чтобы проверить свое понимание, потренироваться перед тестами и викторинами, а также перейти на следующие уровни математики при переходе в старшую школу. Свойства и операции
Алгебраические структуры
Статистика и вероятность
Функции
Геометрия
Характеристики

Право на участие в программе оптовых закупок Apple (только iOS)
 Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch по математике для 8-х классов вместо того, чтобы покупать контент в качестве покупки в нашем приложении для средней школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch по математике для 8-х классов вместо того, чтобы покупать контент в качестве покупки в нашем приложении для средней школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами. Познакомьтесь с учителями математики в 8-м классе:
Нина Берлер
Соавтор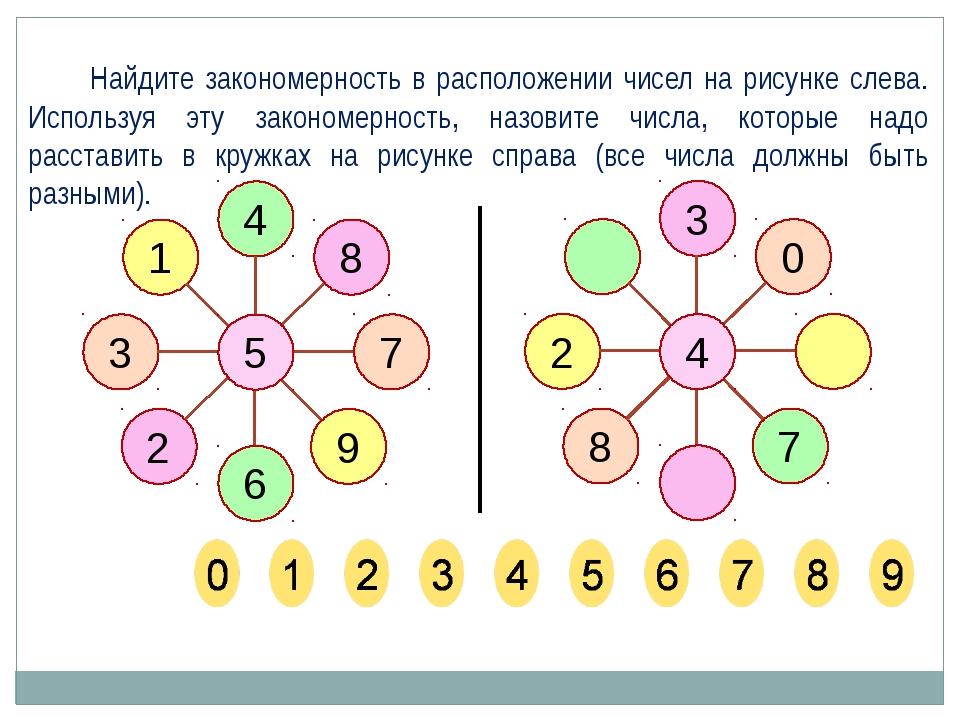 На протяжении своей корпоративной карьеры Нина работала в компании KPMG, предоставляющей профессиональные услуги, где она руководила программным подразделением Executive Education и руководила инициативами в области маркетинговых коммуникаций. Нина имеет степень бакалавра гуманитарных наук с отличием Университета Брауна и степень магистра делового администрирования Школы бизнеса Стерна Нью-Йоркского университета. В настоящее время она завершает программу сертификации UCLA по консультированию колледжей. Нина является членом Национальной ассоциации консультирования при поступлении в колледж (NACAC) и Комитета школ выпускников Брауна.
На протяжении своей корпоративной карьеры Нина работала в компании KPMG, предоставляющей профессиональные услуги, где она руководила программным подразделением Executive Education и руководила инициативами в области маркетинговых коммуникаций. Нина имеет степень бакалавра гуманитарных наук с отличием Университета Брауна и степень магистра делового администрирования Школы бизнеса Стерна Нью-Йоркского университета. В настоящее время она завершает программу сертификации UCLA по консультированию колледжей. Нина является членом Национальной ассоциации консультирования при поступлении в колледж (NACAC) и Комитета школ выпускников Брауна. Уильям Скотт Стоун
 Он полностью переработал веб-сайт школьного округа с учетом потребностей учителей и простоты использования.
Он полностью переработал веб-сайт школьного округа с учетом потребностей учителей и простоты использования. Эйлин Хейес
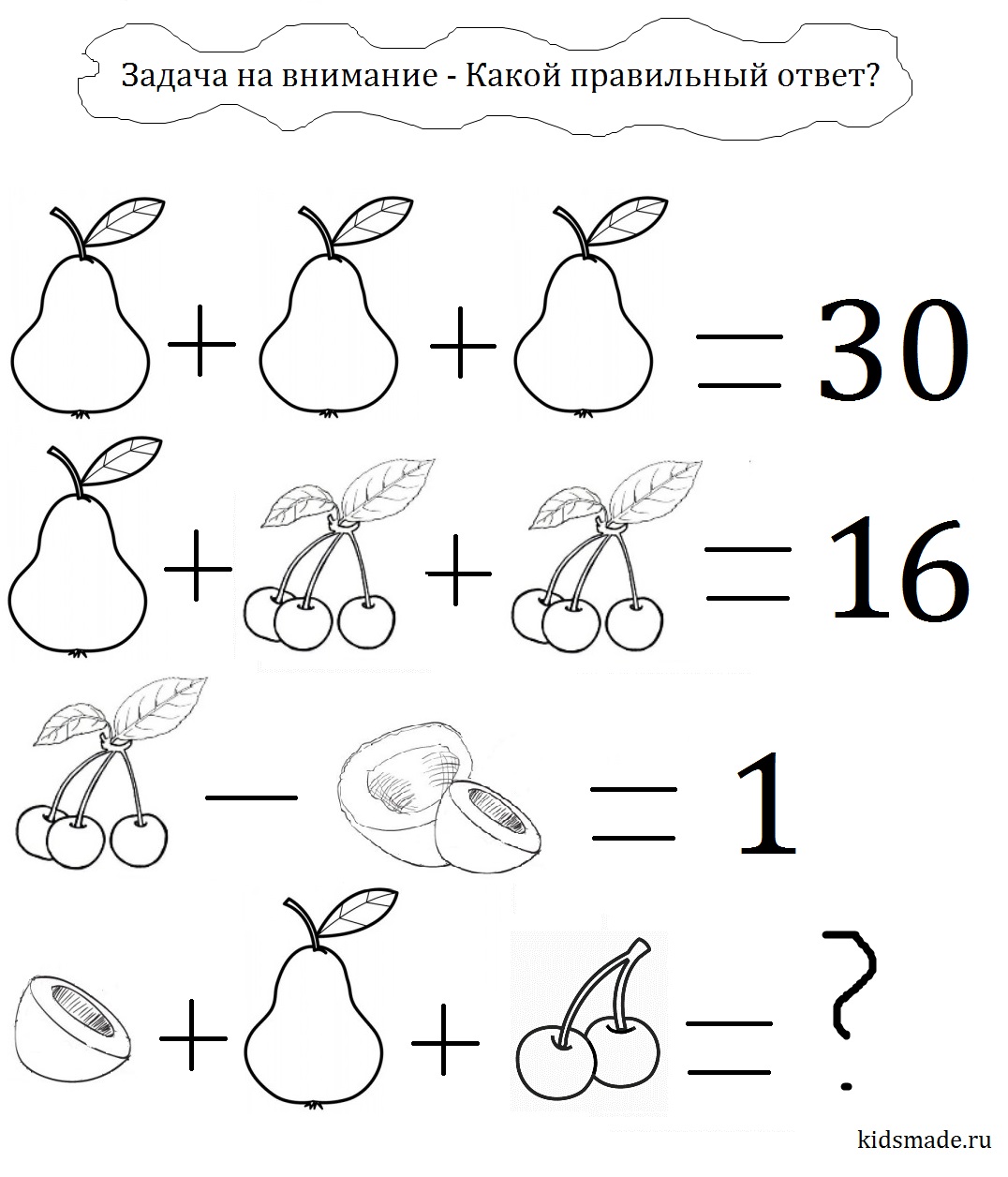 Она берет все это обратно в класс в качестве писателя в резиденции Объединенного совета искусств округа Уэйк, Северная Каролина.Родом из Лос-Анджелеса, она сейчас живет в Роли со своим блестящим мужем и одним из двух интересных, красноречивых сыновей.
Она берет все это обратно в класс в качестве писателя в резиденции Объединенного совета искусств округа Уэйк, Северная Каролина.Родом из Лос-Анджелеса, она сейчас живет в Роли со своим блестящим мужем и одним из двух интересных, красноречивых сыновей. Вам также могут понравиться эти другие приложения для 8-го класса:
Задания по математике для 8-х классов
Какие математические навыки должны быть у ученика, поступающего в среднюю школу?
 Помимо академических кругов, математические знания повышают способность к суждениям и логике в повседневной жизни. Независимо от того, насколько хорошо вы успели учиться в предыдущих классах, в средней школе вам необходимо улучшить и улучшить свои математические навыки.
Ниже приведены математические навыки, которые вам необходимо освоить до поступления в среднюю школу. Смысл чисел и операции: Чтобы иметь дело со всеми арифметическими аспектами, вам необходимо хорошо разбираться в концепции абсолютных чисел, порядке операций, соотношении и пропорциях, а также в концепции действительных, рациональных и комплексных чисел. Алгебра, функции и моделирование: Использование алгебраических моделей очень распространено в инженерной и технологической областях при разработке бюджетов и исследовании неизвестных величин. Этот навык также требует умения переводить слова в числа. Геометрия: Этот навык требует интерпретации основных геометрических понятий, понимания соответствующих или совпадающих ангелов.
Помимо академических кругов, математические знания повышают способность к суждениям и логике в повседневной жизни. Независимо от того, насколько хорошо вы успели учиться в предыдущих классах, в средней школе вам необходимо улучшить и улучшить свои математические навыки.
Ниже приведены математические навыки, которые вам необходимо освоить до поступления в среднюю школу. Смысл чисел и операции: Чтобы иметь дело со всеми арифметическими аспектами, вам необходимо хорошо разбираться в концепции абсолютных чисел, порядке операций, соотношении и пропорциях, а также в концепции действительных, рациональных и комплексных чисел. Алгебра, функции и моделирование: Использование алгебраических моделей очень распространено в инженерной и технологической областях при разработке бюджетов и исследовании неизвестных величин. Этот навык также требует умения переводить слова в числа. Геометрия: Этот навык требует интерпретации основных геометрических понятий, понимания соответствующих или совпадающих ангелов. Определение длины дуги, объема и площади всех двумерных форм. Вероятность и статистика: При интерпретации и систематизации данных для вывода количественных данных наличие вероятности и статистические навыки необходимы для старшей школы.
Определение длины дуги, объема и площади всех двумерных форм. Вероятность и статистика: При интерпретации и систематизации данных для вывода количественных данных наличие вероятности и статистические навыки необходимы для старшей школы.


 00 (x 3 = 3,00 доллара), а у колокольного хопа — 2 доллара. 2 доллара + 3 доллара + 25 долларов = 30 долларов.
00 (x 3 = 3,00 доллара), а у колокольного хопа — 2 доллара. 2 доллара + 3 доллара + 25 долларов = 30 долларов.
 … используя бумагу и карандаш, и вам не понадобится много времени, чтобы набрать число больше 1000. Или упростите 3 10 как 9 5 и многократно умножьте 9 на себя. Если рассчитать полностью, то получится 3 10 =
59 049.
… используя бумагу и карандаш, и вам не понадобится много времени, чтобы набрать число больше 1000. Или упростите 3 10 как 9 5 и многократно умножьте 9 на себя. Если рассчитать полностью, то получится 3 10 =
59 049.
 Затем вы можете заметить, что предпоследний шаг должен выглядеть как (n, 6, m, 2).
Затем вы можете заметить, что предпоследний шаг должен выглядеть как (n, 6, m, 2). Д., Также сказали бы неправильно. Итак, два числа не могут быть 5 и 6.
Д., Также сказали бы неправильно. Итак, два числа не могут быть 5 и 6.
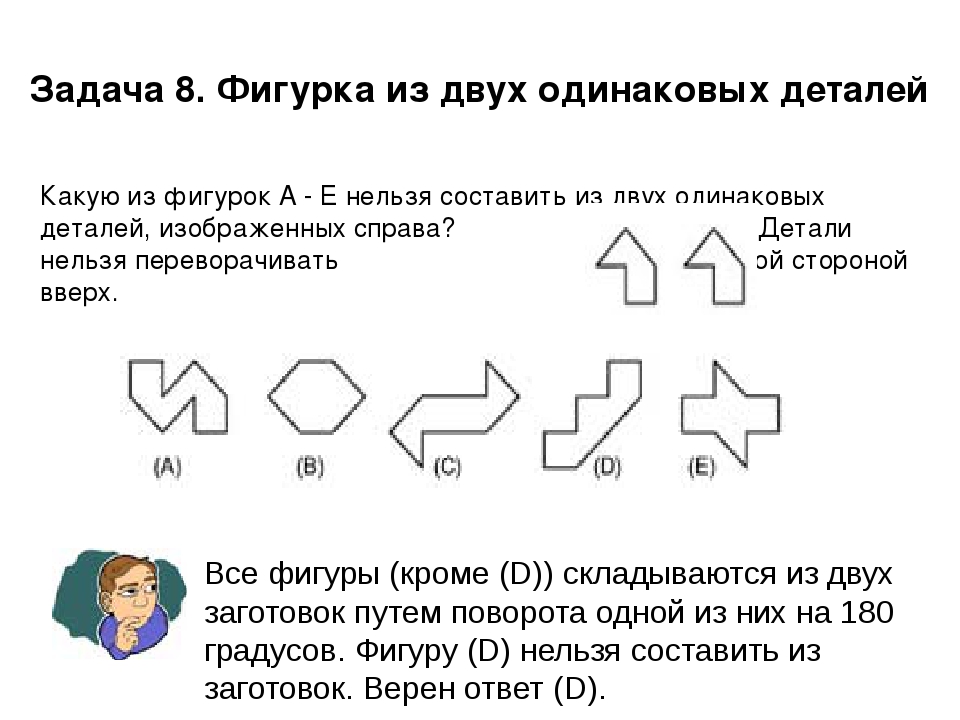
 В другом варианте была ярмарка животных, на которой бык стоил 10 долларов, корова — 2,50 доллара, а теленок — 0,50 доллара. У человека есть 100 долларов, и он хочет купить 100 животных; как он это сделает?
В другом варианте была ярмарка животных, на которой бык стоил 10 долларов, корова — 2,50 доллара, а теленок — 0,50 доллара. У человека есть 100 долларов, и он хочет купить 100 животных; как он это сделает? Как мы можем провести этого важного человека через пустыню?
Как мы можем провести этого важного человека через пустыню?
 .. и да, у вас есть вся необходимая информация!
.. и да, у вас есть вся необходимая информация! «(сложные задачи со словами) и т. д.Головоломки и головоломки варьируются от простых забавных загадок до сложных задач, но ни одна из них не требует продвинутой математики. Они почти всегда иллюстрированы и часто представлены в виде забавных рассказов. Изначально книга была издана в России в 1956 году. Мартин Гарднер отредактировал книгу, чтобы сделать ее как можно более легкой для понимания английской публикой, при этом тщательно сохранив почти всю теплоту и юмор оригинала. Цена: около 5 долларов б / у, около 9 долларов новое.
«(сложные задачи со словами) и т. д.Головоломки и головоломки варьируются от простых забавных загадок до сложных задач, но ни одна из них не требует продвинутой математики. Они почти всегда иллюстрированы и часто представлены в виде забавных рассказов. Изначально книга была издана в России в 1956 году. Мартин Гарднер отредактировал книгу, чтобы сделать ее как можно более легкой для понимания английской публикой, при этом тщательно сохранив почти всю теплоту и юмор оригинала. Цена: около 5 долларов б / у, около 9 долларов новое.