Яркий Дворик | Детские игровые и спортивные площадки

Яркий Дворик | Детские игровые и спортивные площадки

Как умножать и делить в столбик: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.

Опубликовано Автор alexxlabКатегория РазноеОставить комментарий

Содержание

Умножение в столбик | Наука делать уроки

Самое главное правило, с которого мы начинаем изучать умножение в столбик:

Умножение в столбик на двузначное число

Пример: 46 умножить на 73

Этот пример  можно записать в столбик.

Под числом 46 записываем число 73 по правилу:

Единицы записываем под единицами, а десятки  под десятками

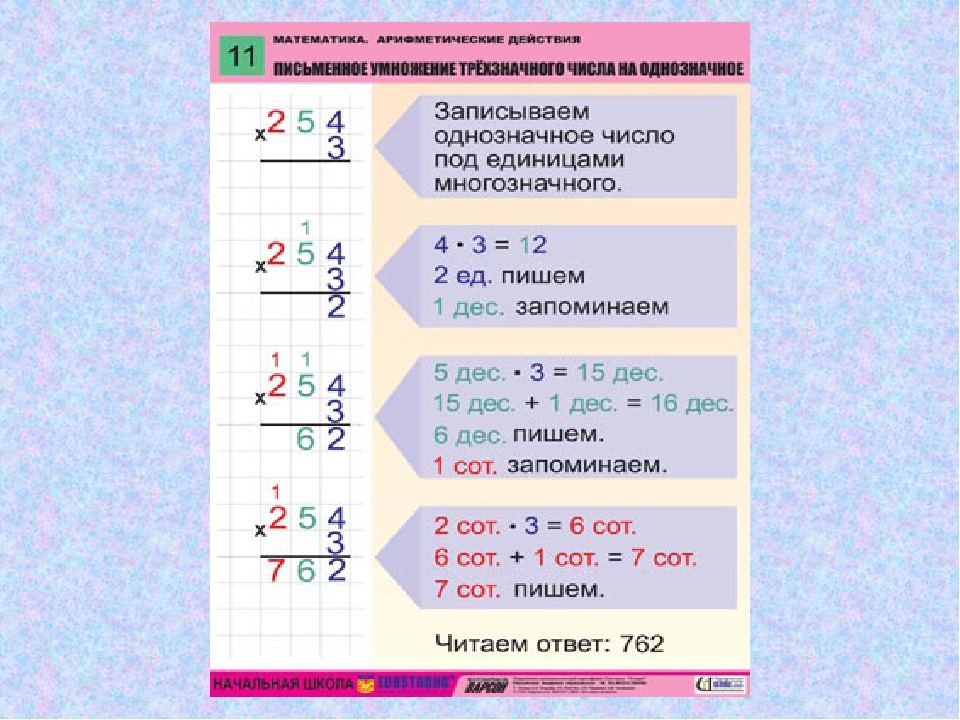
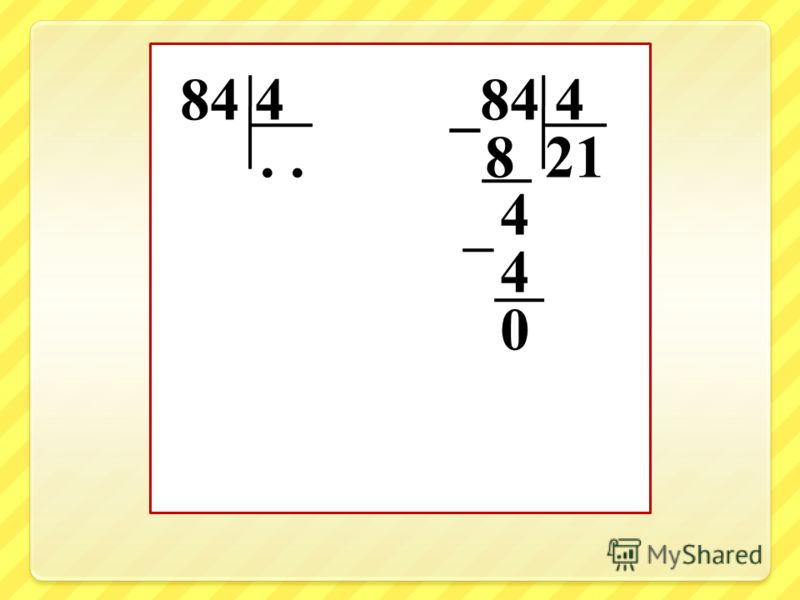
1Умножать начинаем с единиц.

3 умножим на 6. Получится 18.

  • 18 единиц – это 1 десяток и 8 единиц.
  • 8 единиц пишем под единицами, а 1 десяток запоминаем  и прибавим к десяткам.

Теперь 3 умножим на 4 десятка. Получится 12.

12 десятков, да ещё 1, всего 13 десятков.

Сотен в этом примере нет, поэтому сразу на месте сотен пишем 1.

138 — это первое неполное произведение.

2 Умножаем десятки.

7 десятков  умножить на 6 единиц получится 42 десятка.

  • 42 десятка это 4 сотни и 2 десятка.
  • 2 десятка пишем под десятками. 4 запомним и прибавим  к сотням.

7 десятков умножить на 4 десятка получится 28 сотен. 28 сотен, да ещё 4 получится 32 сотни.

  • 32 сотни  – это 3 тысячи и 2 сотни.
  • 2 сотни пишем под сотнями, а 3 тысячи запомним и прибавим к тысячам.

Тысяч в этом примере нет, поэтому сразу на месте тысяч пишу 3.

3220 – это второе неполное произведение.

3Складываем первое и второе неполные произведения по правилу сложения в столбик.

138 плюс 3220  получится 3358.

 

Читаем ответ: 46 умножить на 73 получится 3358

Работаем в столбик

Образец записи

(Кликните по картинке)

Компоненты действия умножения

 

(Кликните по картинке)

Ваша Помощница


— умная и нужная
шпаргалка

Кликните, чтобы скачать и затем распечатать

Образец рассуждения


во время записи
умножения в столбик

 

 

Внимательно просмотрите и примените в своих действиях!

Какие ошибки при умножении


можно сделать и
как их избежать

[Видео]

Внимательно просмотрите,

чтобы не совершать ошибок!

Правила для других случаев умножения

Умножение в столбик на однозначное число

34 х 2

Этот пример  можно записать в столбик.

Под числом 34 записываем число 2 по правилу:

Единицы записываем под единицами, а десятки, если они будут под десятками

1Умножать начинаем с единиц.

2 умножим на 4. Получится 8.

2х4=8

8 пишем под единицами.

Теперь 2 умножим на 3десятка. Получится 6.

2х3=6

6 пишем под десятками.

Читаем ответ: 34 умножить на 2 получится 68.

Умножение в столбик на однозначное число с  переходом через десяток

38 х 2

Этот пример  можно записать в столбик.

Под числом 38 записываем число 2 по правилу:

 Единицы записываем под единицами, а десятки, если они будут под десятками

1Умножать начинаем с единиц.

2 умножим на 8. Получится 16.

  • 16 единиц – это 1 десяток и 8 единиц.
  • 8 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.

Теперь 2 умножим на 3 десятка. Получится 6.

6 десятков да ещё 1 всего 7 десятков.

7 пишем под десятками.

Читаем ответ:

38 умножить на 2 получится 76.

Умножение в столбик на однозначное число с  переходом через десятки

68 х 2

Этот пример  можно записать в столбик.

Под числом 68 записываем число 2 по правилу:

 Единицы записываем под единицами, а десятки, если они будут под десятками

1Умножать начинаем с единиц.

2 умножим на 8. Получится 16.

  • 16 единиц – это 1 десяток и 6 единиц.
  • 6 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.

Теперь 2 умножим на 6 десятков. Получится 12.

12 десятков да ещё 1 всего 13 десятков.

  • 13 десятков – это 1 сотня да ещё 3 десятка.
  • 3 десятка  пишу под десятками. А 1 сотню запомним и прибавим к сотням.

Сотен в этом примере нет, поэтому сразу на месте сотен напишем 1.

Читаем ответ: 68 умножить на 2 получится 136.

Математика. Умножение «в столбик» | Сайт Леонида Некина

Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >

<< Назад  |   Оглавление  |   Далее >>

До сих пор мы умели только умножать на счетах в пределах 24 × 24. Настало время научиться перемножать бóльшие числа, и не на счетах, а на бумаге — с помощью процедуры, которая называется умножением «в столбик».

Надо честно признаться: умножение «в столбик» — это одна из самых неприятных и нудных вещей во всей математике. Хуже нее только деление «уголком», которым мы тоже вскоре займемся. Как только мы освоим умножение «в столбик» и деление «уголком», мы можем смело утверждать, что самый трудный участок на пути изучения математики у нас остался позади.

Прежде всего нам понадобится таблица умножения в пределах от 2 × 2 до 9 × 9. Удобнее всего ее записать в таком виде:

 

    

2

3

4

5

6

7

8

9

2

4

6

8

10

12

14

16

18

3

6

9

12

15

18

21

24

27

4

8

12

16

20

24

28

32

36

5

10

15

20

25

30

35

40

45

6

12

18

24

30

36

42

48

54

7

14

21

28

35

42

49

56

63

8

16

24

32

40

48

56

64

72

9

18

27

36

45

54

63

72

81

Это так называемая таблица Пифагора.

Здесь на пересечении строки, помеченной числом 3, и колонки, помеченной числом 5, стоит как раз произведение чисел 3∙5, то есть 15. Подобным же образом мы можем по этой таблице быстро найти произведение любых однозначных чисел (за исключением нуля и единицы, но умножать на ноль и единицу настолько легко, что никакая таблица не нужна).

В школе эту таблицу заставляют учить наизусть. На мой взгляд, в этом нет никакой необходимости. Пусть она просто будет под рукой, и этого совершенно достаточно. По мере того как мы будем практиковаться в умножении «в столбик», она выучится сама собой.

Таблицу умножения на отдельном листе (в формате pdf) можно взять здесь.

Итак, приступим к умножению чисел. Для начала научимся умножать на однозначное число. Пусть нам надо вычислить

6879∙7.

Воспользовавшись свойствами умножения, которые мы проходили на прошлом уроке, мы можем написать:

6879∙7 =

(9

 + 

7∙10

 + 

8∙100

 + 

6∙1000)∙7

 =

9∙7

 + 

7∙7∙10

 + 

8∙7∙100

 + 

6∙7∙1000

 =

63

 + 

49∙10

 + 

56∙100

 + 

42∙1000

 =

 

6 3

+

4 9 0

+

5 6 0 0

+

 4 2 0 0 0

Перепишем это в виде упрощенной таблицы (очень похожей на ту, какую мы писали, когда учились сложению столбиком):

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 

 6 

 3 

 

 4 

 9 

 

 

 5 

 6 

 

 4 

 2 

 

Теперь остается сложить числа под горизонтальной линией — и ответ готов:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 

 6 

 3 

 

 4 

 9 

 

 

 5 

 6 

 

 4 

 2 

 

 

1

1

 

 

 4 

 8 

 1 

 5 

 3 

Надо ли пояснять, откуда взялись маленькие единички над нашим ответом? Когда мы в разряде десятков сложили 6 и 9, то получили 15. Последнюю цифру этого числа (то есть пятерку) мы записали в ответе в разряде десятков, а первую цифру этого числа (то есть единицу) перенесли в следующий разряд в виде маленькой приподнятой единички. Потом в разряде сотен мы стали складывать 4 и 6, и не забыли добавить сюда же эту самую единичку. Получившееся число 11 тоже записали наискосок: вторую единицу покрупнее и пониже (в аккурат в строке ответа), а первую единицу поменьше и повыше.

Мы теперь, в принципе, умеем умножать на однозначное число. Но давайте подумаем над усовершенствованиями. Во-первых, перепишем нашу табличку в более компактном виде:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 4 

 5 

 4 

 6 

 

 

 2 

 6 

 9 

 3 

 

1

1

 

 

 4 

 8 

 1 

 5 

 3 

А во-вторых, подумаем над возможностью более радикального сокращения записи. Вернемся в исходное положение:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

В разряде единиц умножим 9 на 7. Результат 63 запишем, как и раньше, наискосок, но шестерку сделаем совсем маленькой:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 

 

 

6

 

 

 

 

 

 3 

Теперь умножим в разряде десятков 7 на 7. Получаем 49. Прибавляем сюда нашу «маленькую» шестерку: 49 + 6 = 55. Этот результат опять записываем наискосок:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 

 

5

6

 

 

 

 

 5

 3 

Переходим к разряду сотен: 8∙7 + 5 = 61. Записываем:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

 

6

5

6

 

 

 

 1

 5

 3 

И, наконец, в разряде тысяч получаем 6∙7 + 6 = 48:

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 7 

4

6

5

6

 

 4

 8

 1

 5

 3 

Здесь мы еще перенесли «маленькую» четверку в разряде десятков тысяч вниз, чтобы получить окончательный ответ. Не правда ли, наши вычисления стали короче, а запись еще более компактной?

Теперь возникает резонный вопрос. А как мы будем записывать эти вычисления в нашей тетрадке по математике, разлинованной в клетку? Будем ли мы писать «маленькие» цифры в отдельном ряду клеток или же втискивать их в тот же ряд клеток, где у нас записан ответ? Оба варианта не слишком хороши. Поэтому я предлагаю делать наши вычисления в столбик на отдельных листах бумаги. Для этого прекрасно подойдут обычные белые листы, какие используются для принтеров и копировальных машин. А тех, кому работать на линованной бумаге всё же привычнее, приглашаю воспользоваться листами с особой линовкой.

Лист со специальной линовкой для вычислений можно взять здесь (формат pdf).

Надо отметить, что в школе учат умножать «в столбик» несколько по-другому. Отличие состоит в том, что «маленькие» цифры не записывают на бумагу, а держат в уме — вероятно, по той именно причине, что в стандартных тетрадках в клетку их прото некуда записывать. На мой взгляд, это слишком усложняет процесс счета и только способствует ошибкам.

Переходим к умножению на двузначные числа. Пусть требуется вычислить

6879∙67.

Ну что ж, приступим.

6879∙67 =

6879∙(7 + 6∙10) =

6879∙7
+
6879∙6∙10 =

 

6 3

+

4 9 0

+

5 6 0 0

+

 4 2 0 0 0

 

+

 

5 4 0

+

4 2 0 0

+

4 8 0 0 0

+

 3 6 0 0 0 0

Здесь при умножении на 6 мы воспользовались тем же приемом, что и при умножении на 7, только к каждому получившемуся слагаемому приписали еще 0 из-за дополнительного умножения на 10. Сумму «желтых» слагаемых находим точно так же, как раньше мы находили сумму «зеленых» слагаемых:

 

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 6 

 7 

 

4

6

5

6

 

 

 4 

 8 

 1 

 5 

 3 

4

5

4

5

 

 

 4 

 1 

 2 

 7 

 4 

 

Складываем получившиеся ряды «больших» цифр и получаем окончательный ответ (при этом «маленькие» цифры можно зачеркнуть, чтобы не мешались):

 

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 6 

 7 

 

  4  

  6  

  5  

  6  

 

 

 4 

 8 

 1 

 5 

 3 

  4  

  5  

   4  

  5  

 

 

 4 

 1 

 2 

 7 

 4 

 

 

1

 

 

 

 

 4 

 6

 0

 8

 9

 3

Подобным же образом делается умножение на трехзначные числа. Например:
 

 

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 2

 6 

 7 

 

 

4

6

5

6

 

 

 

 4 

 8 

 1 

 5 

 3 

 

4

5

4

5

 

 

 

 4 

 1 

 2 

 7 

 4 

 

1

1

1

1

 

 

 

 1 

 3

 7

 5

 8

 

 

 

1

1

1

 

 

 

 1 

 8

 3

 6

 6

 9

 3

Если в середине трехзначного числа стоит ноль, то запись выглядит так:
 

 

 

  ×

 6 

 8 

 7 

 9 

 

 

 

 2

 0

 7 

 

 

4

6

5

6

 

 

 

 4 

 8 

 1 

 5 

 3 

1

1

1

1

 

 

 

 1 

 3 

 7

 5

 8

 

 

 

1

1

 

 

 

 

 1 

 4

 2

 3

 9

 5

 3

Наконец, умножение круглых чисел (которые оканчиваются нулями) записывается в таком виде:
 

 

 

  ×

 6 

 8 

 7 

 9 

 0 

 

 

 

 

 

 2

 6 

 7 

 0 

 0 

 

 

 

4

6

5

6

 

 

 

 

 

 

 4 

 8 

 1 

 5 

 3 

 

 

 

 

4

5

4

5

 

 

 

 

 

 

 4 

 1 

 2 

 7 

 4 

 

 

 

 

1

1

1

1

 

 

 

 

 

 

 1 

 3

 7

 5

 8

 

 

 

 

 

 

1

1

1

 

 

 

 

 

 

 1 

 8 

 3 

 6 

 6 

 9 

 3 

 0 

 0 

 0 

Из «бесконечного» сборника типовых упражнений

Умножение на однозначное число

Умножение на двузначное число

Умножение на трехзначное число

 

 

 

Умножение и деление чисел в Excel

Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.

Умножение чисел

Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.

Умножение чисел в ячейке

Для выполнения этой задачи используйте арифметический оператор * (звездочка).

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.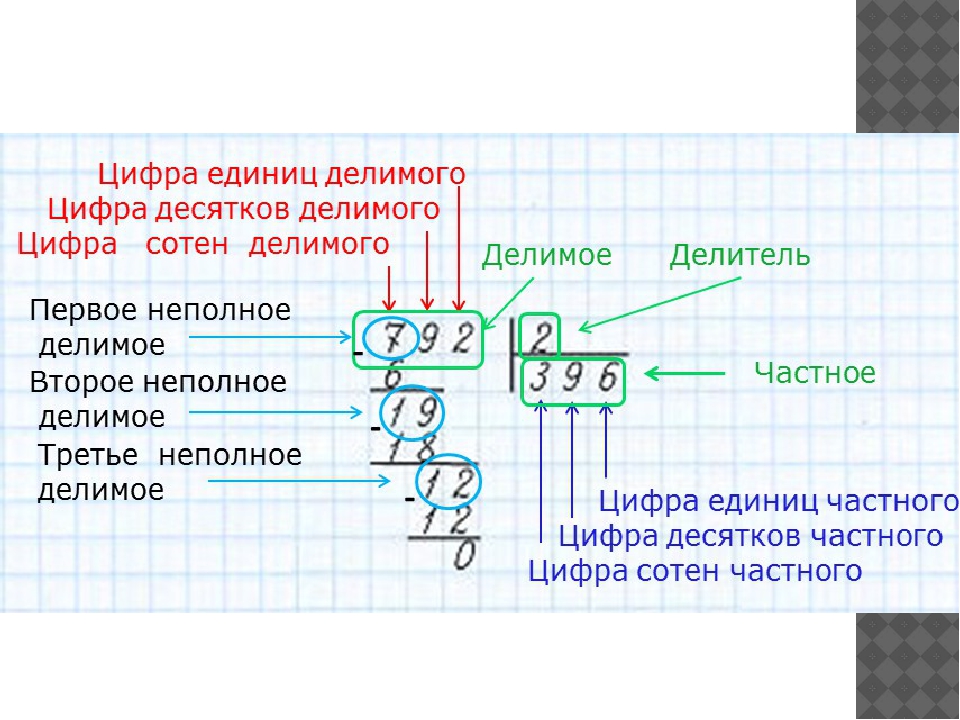

Умножение столбца чисел на константу

Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.

  1. Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.

    Примечание: Символ $ указывает Excel, что ссылка на ячейку B2 является «абсолютной», то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, что не будет работать, так как в ячейке B3 нет значения.

  2. Перетащите формулу вниз в другие ячейки столбца.

    Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.

Перемножение чисел в разных ячейках с использованием формулы

Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.

Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).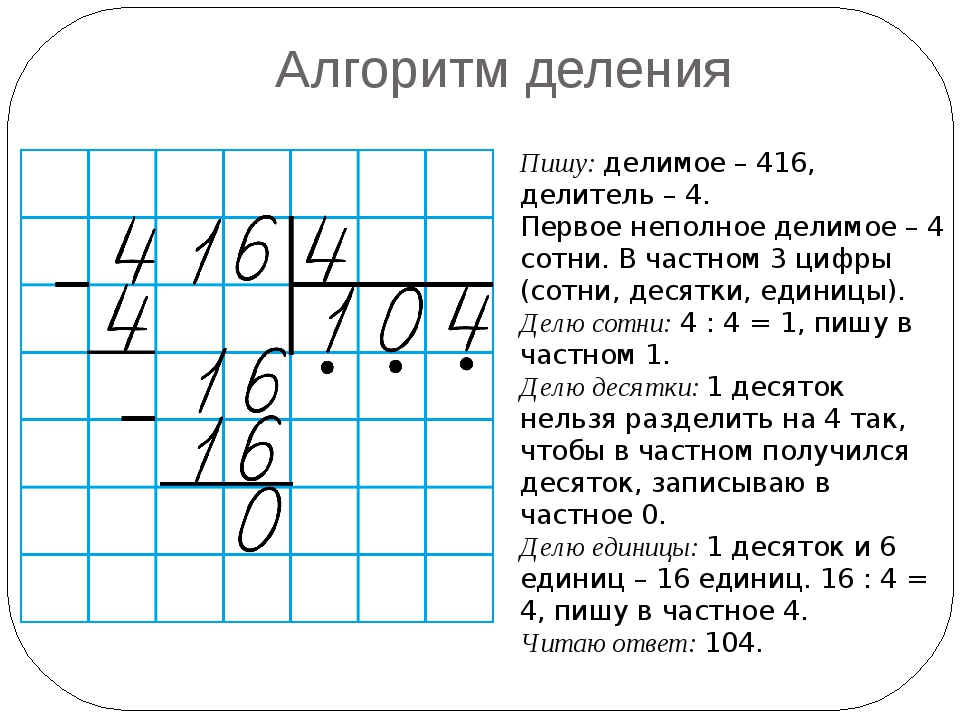

Деление чисел

Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проектов ÷ общее количество людей в проекте) или фактические километры на лилонной скоростью для вашего недавнего меж страны (общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.

Деление чисел в ячейке

Для этого воспользуйтесь арифметическим оператором / (косая черта).

Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.

Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-Июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.12.1936 и отобразит в ячейке значение «1-дек».

Примечание:  В Excel нет функции DIVIDE.

Деление чисел с помощью ссылок на ячейки

Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.

Пример:

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Копирование примера

  1. Создайте пустую книгу или лист.

  2. Выделите пример в разделе справки.

    Примечание: Не выделяйте заголовки строк или столбцов.

    Выделение примера в справке

  3. Нажмите клавиши CTRL+C.

  4. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

  5. Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

A

B

C

1

Данные

Формула

Описание (результат)

2

15000

=A2/A3

Деление 15000 на 12 (1250).

3

12

Деление столбца чисел на константу

Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.

A

B

C

1

Данные

Формула

Константа

2

15000

=A2/$C$2

3

3

12

=A3/$C$2

4

48

=A4/$C$2

5

729

=A5/$C$2

6

1534

=A6/$C$2

7

288

=A7/$C$2

8

4306

=A8/$C$2

  1. В ячейке B2 введите =A2/$C $2. Не забудьте в формуле включить символ $ перед символами C и 2.

  2. Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.

Примечание:  Символ $ указывает Excel, что ссылка на ячейку C2 является «абсолютной», то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

См.

также

Умножение столбца чисел

таблицы

порядка операций

Деление в столбик | интернет проект BeginnerSchool.ru

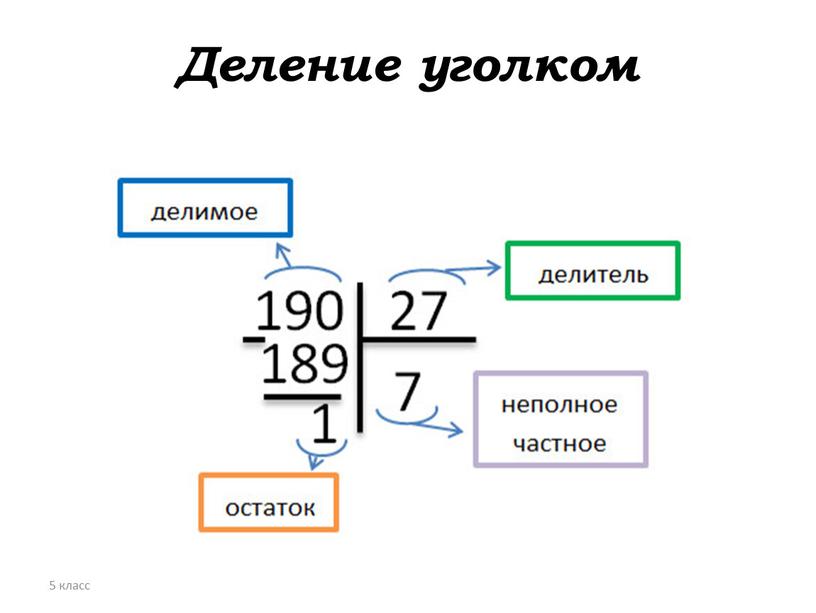
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.

Итак, поделим 354 на 2. Для начала разместим эти числа как показано на рисунке:

Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.

Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с  делителем.

3 больше 2, значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:

Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.

2 × 1 = 2               (2 < 3)

2 × 2 = 4               (4 > 3)

2 меньше 3, а 4 больше, значит, берем первый пример и множитель 1.

Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:

Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:

Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:

Полученное значение сравниваем с делителем. 15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:

2 × 7 = 14             (14 < 15)

2 × 8 = 16             (16 > 15)

Искомый множитель 7, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:

Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:

Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:

2 × 7 = 14

Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:

Разность мы получили равную нулю, значит деление произведено правильно.

Усложним задачу и приведем другой пример:

1020 ÷ 5

Запишем наш пример в столбик и определим первое неполное частное:

Разряд тысяч делимого составляет 1, сравниваем с делителем:

1 < 5

Добавляем в неполное делимое разряд сотен и сравниваем:

10 > 5 – мы нашли неполное делимое.

Делим 10 на 5, получаем 2, записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.

10 – 10 = 0

0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:

Сравниваем второе неполное делимое с делителем.

2 < 5

Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0:

20 ÷ 5 = 4

Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0, значит пример решён правильно.

И ещё 2 правила деления в столбик:

1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:

Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.

2. Если в делимом после деления остались нули, то их следует перенести в частное:

Итак, сформулируем последовательность действий при делении в столбик.

  1. Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
  2. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
  3. Определяем первый неполный делитель:

а) выделяем в неполный делитель старший разряд делимого;

б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;

в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).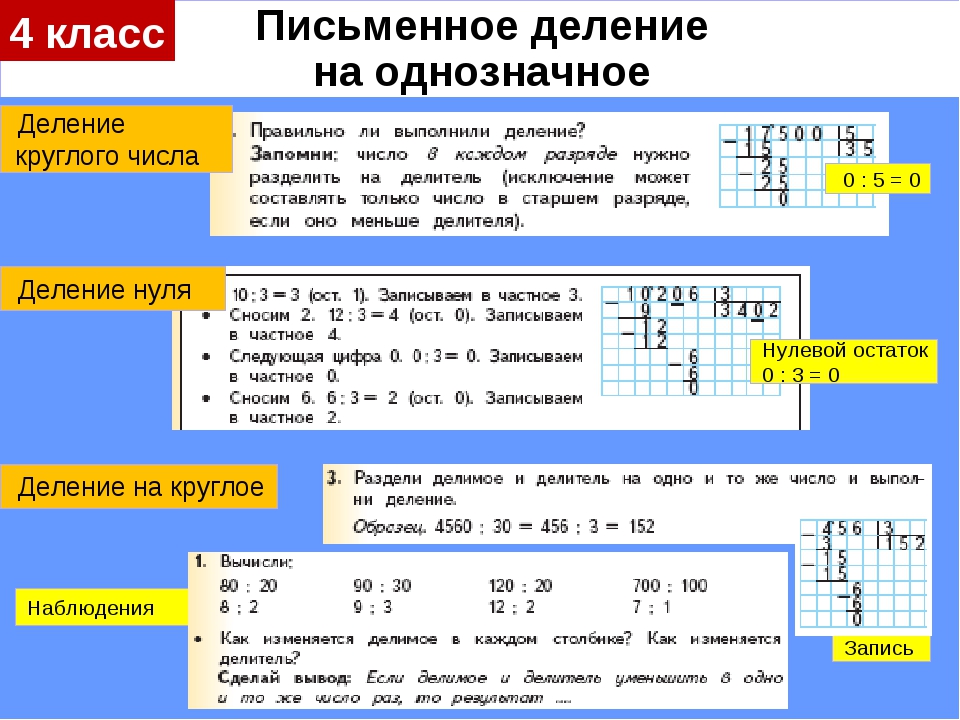

  1. Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
  2. Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
  3. Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
  4. Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
  5. Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
  6. Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:

а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;

б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;

в) переходим к пункту (а).

10. Если мы выполняли деление без остатка и последняя найденная разность равна 0, то мы правильно выполнили деление.

Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:

Спасибо, что вы с нами.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Игра решение столбиком. Умножение столбиком

Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет. Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.

Как научиться умножать столбиком?

В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.

Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать и .

Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…

Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.

За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.

Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)

Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.


Умножение прямо на сайте (онлайн)

*
Таблица умножения (числа от 1 до 20)
×1234567891011121314151617181920
11234567891011121314151617181920
2246810121416182022242628303234363840
33691215182124273033363942454851545760
448121620242832364044485256606468727680
55101520253035404550556065707580859095100
66121824303642485460667278849096102108114120
7714212835424956637077849198105112119126133140
881624324048566472808896104112120128136144152160
9918273645546372819099108117126135144153162171180
10102030405060708090100110120130140150160170180190200
11112233445566778899110121132143154165176187198209220
121224364860728496108120132144156168180192204216228240
1313263952657891104117130143156169182195208221234247260
1414284256708498112126140154168182196210224238252266280
15153045607590105120135150165180195210225240255270285300
16163248648096112128144160176192208224240256272288304320
171734516885102119136153170187204221238255272289306323340
181836547290108126144162180198216234252270288306324342360
191938577695114133152171190209228247266285304323342361380
2020406080100120140160180200220240260280300320340360380400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

В этой игре мы будем учиться складывать столбиком числа до 100. Яркие картинки и подробные пояснения помогут легко понять и запомнить алгоритм сложения столбиком. А тренажер поможет закрепить тему.

Прежде всего нужно запомнить, что при решении примеров на сложение столбиком большее число записывается сверху, а меньшее — под ним. Числа записываются так, чтобы единицы были под единицами, а десятки (если они есть) — под десятками.

Сначала складывают единицы, а затем десятки, при этом возможно 2 варианта:

Если при сложении единиц получается однозначное число, мы просто записываем его под чертой под единицами. Если же при сложении единиц получается двузначное число, включая 10, мы записываем под единицами только вторую цифру(единицы), а 1 (десяток) прибавляем к десяткам.

Первый вариант описан и проиллюстрирован в уроке 1, а второй вариант — в уроке 2 нашей обучающей онлайн игры «Сложение столбиком». После просмотра уроков порешайте примеры на сложение столбиком самостоятельно в разделе «Тренажер»

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

    Найти сумму цифр делимого.

    Поделить на 3 или 9 (в зависимости от того, что вам нужно).

    Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель.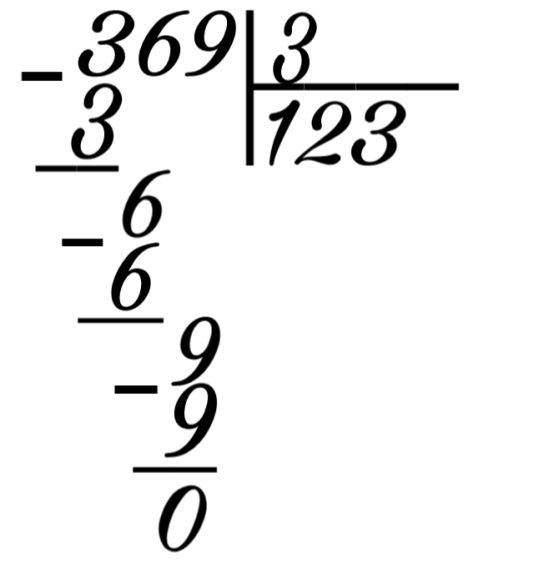 Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Как научиться делить столбиком 3 класс


Деление столбиком — примеры для 3 класса с решением

04 июня 2019

Аверьянова Света

Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить деление уголком, с остатком, выявить пробелы в детских знаниях.

Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее.

Из этой статьи вы узнаете

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

  • Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
  • Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
  • Отнимать, складывать многозначные числа.
  • Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы.

Игровые задания

Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

  • Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
  • Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
  • «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
  • «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
  • Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
  • «Ищем дерево». Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой.

Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком.

Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

2. Посмотреть вместе с ребенком обучающее видео

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай.

На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным.

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

  • Сначала запишите задачу обычным способом: 250:2=?
  • Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
  • Затем сделайте сокращенную запись столбиком (уголком):

  • Рассуждайте вместе так: сначала найдем неполное частное. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
  • После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике. Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.

Деление на однозначное число

Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).

Первый урок можно построить так:

  1. Положите перед ребенком картинку с образцом деления столбиком.
  2. Придумайте собственный пример. Пусть это будет 254:2
  3. Задание нужно записывать уголком. Доверьте это школьнику. Он может посмотреть, как делается запись на картинке.
  4. Спросите третьеклассника: «Какое число нужно делить на 2 первым?». В этот момент важно объяснять, что делимое должно быть равно или большего делителя. Малыш выделит для деления первое число из данной цифры: 2…54
  5. Теперь определите вместе, сколько двоек поместится в числе 2. Ответ: 1.
  6. Записываем частное под уголком.
  7. Умножаем 1 на 2 и записываем результат под делимым.
  8. Вычитаем.
  9. Так как получился 0, сносим следующую цифру под линию после вычитания: 5.
  10. Опять задаем вопрос: «Сколько двоек поместится в 5?» Малыш вспоминает таблицу умножения или подбирает частное с помощью логики. Отвечает: 2.
  11. Записываем 2 в частное, умножаем на 2.
  12. Результат (4) записываем под 5.
  13. Отнимаем.
  14. Остается 1. Единицу разделить на 2 нельзя, поэтому сносим остатки делимого вниз. Получается 14.
  15. Делим 14 на 2. Записываем в частное 7.
  16. Умножаем на 2. Записываем под чертой 14.
  17. Отнимаем.
  18. В конце всегда должен получаться 0.
  19. В результате у ребенка сформируется такая запись:

Для закрепления запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе.

На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия.

Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце.

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

  1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
  2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
  3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

  1. Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
  2. Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
  3. Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
  4. Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370. Важно начинать запись с первого числа слева.
  5. После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
  6. 37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
  7. Теперь делим 370 на 74. Подбираем множитель (5) и записываем его под уголком.
  8. Умножаем 5 на 74, записываем результат в столбик. Получится 370.
  9. Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

  1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
  2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

  1. Объясните, что такое неполное делимое и зачем его выделять.
  2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

  1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
  2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

  1. Подбирайте частное на отдельном листочке или посчитайте в уме.
  2. Распишите результат.
  3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
  4. Продолжайте деление до конца, пока не получится 0.
  5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.

Деление с остатком

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

  1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
  2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике.

Как делать проверку

Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:

Теперь проверим:

Для проверки деления с остатком нужно:

  1. Умножить полное частное на делитель.
  2. Прибавить к результату остаток.

17х2=34

34+1 (остаток) =35

Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.

Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы.

Примеры для тренировки

Научиться быстро решать примеры с делением помогают тренировочные задания. Карточками может оканчиваться каждый урок после прохождения новой темы.

Однозначные

Двузначные

Многозначные

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

 >> Скачать  файл.DOC  для распечатки (деление на однозначное число)<<

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

ВАЖНО! *при копировании материалов статьи обязательно указывайте активную ссылку на первоисточник: https://razvitie-vospitanie. ru/kak_nauchit/rebenka_delit_v_stolbik.html

Если вам понравилась статья — поставьте лайк и оставьте свой комментарий ниже. Нам важно ваше мнение!

Поделиться с друзьями:

Как научить делить в столбик: пошаговый метод

В этой статье я объясню, как обучить делению в столбик в несколько шагов. Вместо того, чтобы показывать студентам сразу весь алгоритм, мы искренне воспринимайте это «шаг за шагом».

До ребенок готов учить деление в столбик, он должен знать:

  • таблицы умножения (по крайней мере неплохо)
  • базовая концепция деления, основанная на таблицах умножения
    (например, 28 ÷ 7 или 56 ÷ 8)
  • базовое деление с остатками (например 54 ÷ 7 или 23 ÷ 5)

Одна из причин, почему деление в столбик затруднено

Длинное деление — это алгоритм, который повторяет основные шаги
1) Делить; 2) Умножить; 3) Вычесть; 4) Отбросьте следующую цифру.

Из этих шагов №2 и №3 могут стать трудными и запутать учащихся, потому что они, по-видимому, не имеют отношения к разделению — они имеют отношение к нахождению остатка. На самом деле, чтобы указать на это, мне нравится объединять их в один «умножить и вычесть» шаг.

Чтобы избежать путаницы, я рекомендую обучать полному делению в таком мода на то, что дети сначала НЕ подвергаются всем этим шагам. Вместо этого вы можете научить этому в несколько «ступенек»:

  • Шаг 1: Все цифры четные.Здесь студенты отрабатывают только разделительную часть.
  • Шаг 2: Остаток в единицах. Сейчас, студенты практикуют часть «умножить и вычесть» и связать это с поиском остаток.
  • Шаг 3: Остаток в десятках. Ученики теперь используйте весь алгоритм, в том числе «отбрасывание следующей цифры», с использованием 2-значного дивиденды.
  • Шаг 4: Остаток в любом месте ценности. Студенты практикуют весь алгоритм, используя более длинные дивиденды.

Шаг 1. Деление четное по всем цифрам


Мы делим числа, в которых каждая цифра сотен, десятков и единиц делится на делитель без остатка. ЦЕЛЬ на этом первом легком шаге чтобы студенты привыкли к двум вещам:

  1. Чтобы привыкнуть к большому делению «угол», чтобы частное писалось сверху.
  2. Чтобы привыкнуть спрашивать, сколько раз делитель переходит в различные цифры делимого.

Ниже приводятся примеры проблем для этого шага. Студенты должны проверить каждый деление на умножение.

,

Ваш третий класс и математика в соответствии со стандартами Common Core

Как лучше всего помочь вашему ребенку в математике? Пищевые фракции! Этот кусок пиццы составляет 1 ⁄ 8 пирога. Сравните 1 ⁄ 2 большого пончика с 1 ⁄ 2 маленького печенья — почему они не одного размера? Вместо того, чтобы разрезать этот бутерброд пополам, поэкспериментируйте с третями, четвертыми и восьмыми. Поговорите с ребенком об этих пищевых дробях, и вы поможете ему понять самую важную математическую концепцию этого года.

К концу третьего класса вашему ребенку необходимо выучить 10 математических навыков (четыре из них связаны с дробями!):

  • Знать наизусть таблицы умножения от 1 до 10.
  • Умножение и деление с числами до 100.
  • Понимание дробей как чисел, представляющих часть целого.
  • Размещение дробей в числовой строке.
  • Нахождение эквивалентных дробей.
  • Сравнение двух дробей с одним и тем же числителем или знаменателем.
  • Округление чисел до ближайших 10 и 100.
  • Определение времени с точностью до минуты.
  • Создание графиков для понимания и решения текстовых задач.
  • Нахождение периметра и площади прямоугольника.

Умножайте, делите и побеждайте математика

Некоторые вещи должны быть сохранены в памяти: имя, адрес, дата рождения — и таблицы умножения от 1 до 10. Так много математики включает в себя умножение, что вашему ребенку необходимо мгновенно вспомнить этих продуктов от 1 x 1 = 1 до 10 x 10 = 100.

Помимо запоминания, третьеклассники должны понимать умножение как способ определения общего количества предметов, не считая каждый отдельно. Думайте об этом как о более быстром и эффективном способе добавления.

Например: если у Джессики есть 4 коробки, каждая из которых наполнена 7 плюшевыми мишками, сколько у нее плюшевых мишек? Джессика могла бросить их на пол и сосчитать один за другим, она могла сложить 7 + 7 + 7 + 7, или она могла умножить количество коробок на количество плюшевых мишек в каждой коробке и быстро прийти к ответу, 4 x 7 = 28 плюшевых мишек в секундах.Быстро получить ответ — это хорошо, но гораздо важнее, чтобы ребенок понимал, как и почему работают все три метода, чтобы получить один и тот же ответ.

Точно так же, как ваш первоклассник научился думать о вычитании как об обратном или «отмене» сложения, вашему третьекласснику необходимо понимать, что деление подобно обратному умножению. Если умножение объединяет вещи, то деление разбивает их на группы равного размера. Математика станет более понятной, если ваш ребенок поймет взаимосвязь между этими двумя важными операциями.

Например: Если 9 x 8 = 72, то 72 ÷ 8 = 9.

Третьеклассники начинают изучать основы алгебры через умножение и деление, подставляя X вместо неизвестного числа и меняя операцию на решить для X .

Например: чтобы решить 6 x X = 24, ваш ребенок разделит 24 ÷ 6 = X. (И, если ваш ребенок запомнил таблицу умножения, он сразу поймет, что X = 4. )

Двухэтапные задачи со словами

Третьеклассники теперь в основном решают двухэтапные задачи со словами, для решения которых требуется использовать любую из четырех операций — сложение, вычитание, умножение, деление.

Например: если 3 ребенка собирают по 4 яблока каждый, а затем группа съедает всего 6, сколько яблок останется? Шаг 1: 3 ребенка х 4 яблока = 12 яблок. Шаг 2: 12 яблок — 6 яблок = осталось 6 яблок.

Округление

Третьеклассники учатся округлять целые числа в большую или меньшую сторону до ближайших десятков или сотен.

Например: Округлите 62 до десяти. (Это 60.) Округлите 287 до ближайшей сотни. (Это 300.)

Ваш ребенок также будет складывать и вычитать в пределах 1 000 и изучать схему умножения чисел на 10: сложение нуля.

Например: если 6 x 6 = 36, то 6 x 60 = 360. Видите, теперь не так страшно.

Дроби имеют значение

Это основные вещи, которые ваш ребенок узнает о дробях в третьем классе.

  • 1. Дроби представляют собой числа и могут отображаться в числовой строке:
  • 2. Дроби представляют собой равные части всего объекта или формы:
  • 3. Целые числа могут быть выражены в виде дробей: Например: 4 = 4 ⁄ 1 и 1 = 4 ⁄ 4
  • 4.Дроби с разными числителями (верхнее число) и знаменателями (нижнее число) могут быть равны: Например: 1 ⁄ 2 = 2 ⁄ 4 , 6 ⁄ 8 = 3 ⁄ 4

Нажмите кнопку повтора сигнала

Третьеклассник точно определяет время, решая задачи на сложение и вычитание времени и считая время с точностью до минуты.

Например: будильник Джейн срабатывает в 7:00. м., но она не встает с постели до 8:25 утра. Сколько еще она спала?

Картинка стоит множества чисел

Третьеклассники учатся рисовать графические изображения и гистограммы, чтобы сравнивать числа в задачах со словами, которые спрашивают, сколько больше или сколько меньше объектов в одной категории, чем в другой.

Третьеклассники измеряют длину предметов с точностью до половины и четверти дюйма и показывают разную длину на линии графика.

Ферма свежих яиц в четырехугольнике

Третьеклассники начинают использовать умножение, чтобы найти площадь формы, умножая длину на ширину.Дети расширяют свое понимание форм на основе общих свойств. Например, не все четырехугольники, называемые четырехугольниками, представляют собой квадраты и прямоугольники: некоторые имеют форму воздушного змея, а некоторые, как трапеции, имеют четыре стороны разной длины. Вашему ребенку будет предложено решить реальные задачи, чтобы найти периметр этих различных форм, добавив длины всех четырех сторон.

Например: для курятника, который строит отец Габриэлы, нужен забор. Четыре стороны имеют размеры 20 футов, 8 футов, 14 футов и 16 футов.Сколько проволочной сетки нужно купить папе Габриэлы?


Между порциями еды — и, возможно, время от времени находя площадь куска хлеба — вы можете очень много сделать дома, чтобы закрепить математические навыки, которые вашему ребенку необходимо выучить в этом году. Ваш ребенок может не благодарить вас около 20 лет, но в конечном итоге он оценит эту важную помощь.

Может ли ваш ребенок умножать и делить, как третьеклассники в нашем видео «Вехи» по математике?

Поделиться в Pinterest

Обновлено: 2 декабря 2019 г.

,

Планы уроков математики для третьего класса

Посмотреть демо наших уроков Переключить меню Зарегистрироваться Войти Поиск Поиск Time4Learning Поиск Time4Learning Войти / Зарегистрироваться Call Time4Learning ВойтиЗарегистрироватьсяКупить сейчас
    org/SiteNavigationElement» role=»menu»>
  • Учебная программа
  • Субъекты
  • Обучение на дому
  • Ресурсы
  • Как это работает
  • Посмотреть демонстрации
  • Учебная программа по классам
  • дошкольный
  • элементарный
  • Средняя школа
  • Старшие классы средней школы
  • Объем и последовательность
  • Языковые искусства
  • математический
  • Наука
  • Социальные исследования
  • Факультативы
  • Наука об окружающей среде
  • Социология
  • Психология
  • Личные финансы
  • Больше факультативов
.

Что случилось с делением | Блог репетитора по математике

Пару лет назад стали попадаться дети, которые не умеют делить в столбик. Причем первый такой ребенок учился в восьмом классе. Этот мог просто разучится, мало ли. Но потом стали появляться пятиклассники, которые не умеют делить в столбик. И это уже повергло меня в шок, потому что как бы плохо у детей не было с математикой, например были такие кто на пальцах считал, тем не менее арифметические действия в столбик выполняли все. А здесь… пустота.

Когда таких детей стало больше, я начала понимать в чем дело, по крайней мере мне так кажется. Сложение, вычитание, умножение в столбик очень алгоритмизированные, а в деление есть элемент творчества. Там нужно подбирать, а как подбирать? Давайте с примером, чтобы понятно было.

Итак, начинаем мы с выбора первого неполного делимого и это довольно просто. 5 на 16 не делится, значит берем 59. А вот дальше нужна магия. Необходимо понять какое максимальное количество чисел 16 можно сложить, чтобы получилось число меньше 59, но близкое к нему.

Как это понять? Можно просто перебирать последовательно числа и искать остатки, пока они не будут меньше 16 (59 — 16 = 43 > 16, 59 — 2*16 = 27 > 16, 59 — 16*3 = 11 < 16). Значит неполное частное — 3. Метод подбора работает, но долго.

Другой способ это оценка. 59 можно округлить до 60, 16 до 20. 60 : 20 = 3. Значит можно попробовать три. Как мы уже знаем, это число подойдёт, в противном случае мы бы брали меньше трех или больше, в зависимости от того какой получается остаток.

Это не единственные способы, но общим для них является наличие поиска ответа и оценка вариантов. Этого нет ни в одном другом арифметическом действии, там нужно просто знать таблицу умножения и уметь считать на пальцах. В делении же ребенок всегда сталкивается с проблемой, маленькой, но проблемой. Хотя не такая уж она и маленькая, для некоторых детей, это просто не разрешимая трудность.

Почему для детей этот поиск стал таким сложным, что некоторые вообще отказываются делить в столбик? Свои размышления по этому вопросу я лучше оставлю при себе.

Детские решения задач умножения и деления слов: продольное исследование

  • Ангилери, Дж. (1985). Мы должны сказать времена? Математика в школе, 14 , 3.

    Google ученый

  • Ангилери Дж. (1989). Исследование понимания детьми умножения. Образовательные исследования по математике, 20 (4), 367–385.

    Артикул Google ученый

  • Белл, А., Костелло, Дж., И Кучманн, Д. (1981). Обзор исследований в области математического образования: исследования в области обучения и преподавания . Лондон: NFER-Nelson.

    Google ученый

  • org/ScholarlyArticle»>

    Белл, А., Фишбейн, Э., и Грир, Б. (1984). Выбор операции в задачах вербальной арифметики: влияние размера числа, структуры задачи и контекста. Образовательные исследования по математике, 15 , 129–147.

    Артикул Google ученый

  • Белл, А., Грир, Б., Гримисон, Л., и Манган, К. (1989). Постановка детей по мультипликативным задачам со словами: элементы описательной теории. Журнал исследований в области математического образования, 20 (5), 434–449.

    Артикул Google ученый

  • Боэро П., Феррари П. и Ферреро Э. (1989). Проблемы разделения: значения и процедуры при переходе к письменному алгоритму. Для изучения математики, 9 (3), 17–25.

    Google ученый

  • org/ScholarlyArticle»>

    Бут, Л. (1981). Детские методы по средней математике. Образовательные исследования по математике, 12 , 29–41.

    Артикул Google ученый

  • Briars, D.J., & Larkin, J.H. (1984). Интегрированная модель умения решать простейшие словесные задачи. Познание и обучение, 1 , 245–296.

    Артикул Google ученый

  • Коричневый, м.Л., Кучеманн Д. (1976). Это добавка, мисс? Часть I. Математика в школе, 5 (5), 15–17.

    Google ученый

  • Brown, M.L., & Kuchemann, D.E. (1977). Это добавка, мисс? Часть II. Математика в школе, 6 (1), 9–10.

    Google ученый

  • Коричневый, M.L. (1981). Числовые операции. В К. Hart (Ed.), Дети понимают математику: 11–16 (стр.23–48). Лондон: Джон Мюррей.

    Google ученый

  • Карпентер Т.П., Хиберт Дж. И Мозер Дж. М. (1981). Структура задачи и процессы решения первоклассниками простых задач на сложение и вычитание. Журнал исследований в области математического образования, 12 (1), 27–39.

    Артикул Google ученый

  • Карпентер, Т.П., & Мозер, Дж.М. (1982). Развитие навыков решения задач на сложение и вычитание. В T.P. Карпентер, Дж.М. Мозер и Т.А. Romberg (Eds. ), Сложение и вычитание: когнитивная перспектива (стр. 9–25). Хиллсдейл, Нью-Джерси: Эрлбаум.

    Google ученый

  • Карпентер Т.П. и Мозер Дж. М. (1984). Освоение концепций сложения и вычитания в классах с первого по третий. Журнал исследований в области математического образования, 15 (3), 179–203.

    Артикул Google ученый

  • Карпентер, Т.П., Мозер, Дж. М., и Бебаут, Х.С. (1988). Представление задач на сложение и вычитание слов. Журнал исследований в области математического образования, 19 , 345–357.

    Артикул Google ученый

  • Карпентер, Т. П., Мозер, Дж. М., и Ромберг, Т.А. (Ред.) (1982). Сложение и вычитание: когнитивная перспектива .Хиллсдейл, Нью-Джерси: Эрлбаум.

    Google ученый

  • Кобб П. и Меркель Г. (1989). Стратегии мышления: обучение арифметике через решение задач. В P.R. Trafton & A.P. Shulte (Eds.), Новые направления в математике начальной школы (стр.70–85). Рестон, Вирджиния: N.C.T.M.

    Google ученый

  • Де Корте, Э., и Вершаффель Л. (1987).Влияние семантической структуры на стратегии первоклассников при решении задач на сложение и вычитание. Журнал исследований в области математического образования, 18 (5), 363–381.

    Артикул Google ученый

  • org/ScholarlyArticle»>

    Де Корте, Э., Вершаффель, Л., и Ван Койли, В. (1988). Влияние структуры задачи и способа ответа на решения детей задач умножения слов. Journal of Mathematical Behavior, 7 , 197–216.

    Google ученый

  • Де Корте, Э., и Вершаффель, Л. (1989). Преподавание словесных задач в начальной школе: что исследование должно сказать учителю. В Б. Грир и Г. Малхерн (ред.), Новые направления в математическом образовании (стр. 85–107). Лондон: Рутледж.

    Google ученый

  • Фишбейн, Э., Дери, М., Нелло, М., и Мерино, М. (1985).Роль неявных моделей в решении вербальных задач умножения и деления. Журнал исследований в области математического образования, 16 (1), 3–17.

    Артикул Google ученый

  • org/Book»>

    Фусон К. (1982). Дополнительно анализируется процедура расчетного решения. В T.P. Карпентер, Дж.М. Мозер и Т.А. Romberg (Eds.), Сложение и вычитание: когнитивная перспектива (стр. 67–81). Хиллсдейл, Нью-Джерси: Эрлбаум.

    Google ученый

  • Гельман Р. и Галлистель К. Р. (1978). Детское понимание числа . Кембридж, Массачусетс: Издательство Гарвардского университета.

    Google ученый

  • Гинзбург, Х. (1977). Детская арифметика: Учебный процесс . Нью-Йорк: Ван Ностранд.

    Google ученый

  • Гинзбург, Х.(1983). Развитие математического мышления . Нью-Йорк: Academic Press.

    Google ученый

  • Грир Б. и Малхерн Г. (ред.). (1989). Новые направления в математическом образовании . Лондон: Рутледж.

    Google ученый

  • Гроен, Г., и Резник, Л. (1977). Могут ли дошкольники изобретать алгоритмы сложения? Журнал педагогической психологии, 69 , 645–692.

    Артикул Google ученый

  • Харт, К.М. (Ред.). (1981). Понимание детьми математики: 11–16 . Лондон: Джон Мюррей.

    Google ученый

  • Хиберт, Дж. (1984). Обучение детей математике: борьба за связь между формой и пониманием. Журнал начальной школы, 5 , 497–513.

    Google ученый

  • Хиберт, Дж., И Бер М. (1989). Числовые понятия и операции в средних классах (Том 2). Рестон, Вирджиния: Эрлбаум / N.C.T.M.

    Google ученый

  • Хиберт, Дж. (1990). Роль рутинных процедур в развитии математической компетентности. В T.J. Куни и К. Р. Хирш (ред.), Преподавание и изучение математики в -е годы 1990-х гг. (Стр. 31–41). Рестон, Вирджиния: N.C.T.M.

    Google ученый

  • Хьюз, М.(1986). Детский и номер . Оксфорд: Бэзил Блэквелл.

    Google ученый

  • Охота, Р. П. (1989). Что предлагает классному руководителю последнее десятилетие исследований рациональных чисел? В Н.Ф. Эллертон и М.А. Клементс (ред.), Школьная математика: вызов переменам (стр. 188–217). Джилонг: Издательство Университета Дикина.

    Google ученый

  • Керанто, Т.(1984). Процессы и стратегии в решении простейших словесных задач умножения и деления: их связь со способностями Пиаже, навыками объема памяти и рациональным числом . Тампере, Финляндия: Университет Тампере, факультет подготовки учителей. (Номер службы размножения документации ERIC ED239906)

    Google ученый

  • org/ScholarlyArticle»>

    Kintsch, W. (1986). Изучение текста. Познание и обучение, 3 , 87–108.

    Артикул Google ученый

  • Килпатрик Дж. (1987). Что за конструктивизм может быть в математическом образовании. В материалах материалов 11-й ежегодной конференции по психологии математического образования (том 1, стр. 3–27). Монреаль: Международная группа психологии математического образования.

    Google ученый

  • Коуба, В.Л. (1986, апрель). Как дети решают задачи на умножение и деление слов . Доклад, представленный на предварительном заседании Национального совета учителей математики, Вашингтон, округ Колумбия

  • org/ScholarlyArticle»>

    Коуба, В.Л. (1989). Детские стратегии решения эквивалентных задач умножения множеств и деления слов. Журнал исследований в области математического образования, 20 (2), 147–158.

    Артикул Google ученый

  • Лабинович, Э.(1985). Обучение у детей: Новое начало в обучении числовому мышлению . Менло-Парк: Эддисон Уэсли.

    Google ученый

  • Лэнгфорд, П. (1988). Арифметические задачи со словами: доказательства для размышлений на столе. Исследования в области математического образования в Австралии, июня, 1–7. Леш Р. и Ландау М. (ред.) (1983). Приобретение математических понятий и процессов . Нью-Йорк: Academic Press.

    Google ученый

  • org/ScholarlyArticle»>

    Mulligan, J.T. (1988). Детские решения сюжетных задач. Простое число, 3 (4), 5–11.

    Google ученый

  • Mulligan, J.T. (1991а, июль). Роль интуитивных моделей в решениях маленьких детей задач умножения и деления слов . Документ, представленный на 15-й ежегодной конференции Исследовательской группы математического образования Австралазии, Перт.

  • Mulligan, J.T. (1991b). Умножение и деление — что мы можем использовать на уроках. Заставляя детей думать, когда они вычисляют . Брисбен: Технологический университет Квинсленда, Центр математики, науки и технологий.

    Google ученый

  • Нешер П. (1982). Уровни описания при анализе задач на сложение и вычитание слов. В T.P Carpenter., J.M. Moser и T.А. Ромберг (ред.), Сложение и вычитание: когнитивная перспектива (стр. 25–39). Хиллсдейл: Эрлбаум.

    Google ученый

  • Нешер П. (1988). Мультипликативные проблемы школьного слова: теоретические подходы и эмпирические данные. В J. Hiebert & M. Behr (Eds.), Числовые концепции и операции в средних классах (Том 2, стр. 19–40). Хиллсдейл, Нью-Джерси: Эрлбаум.

    Google ученый

  • Райли, М., Greeno, J., & Heller, J. (1983). Развитие у детей способностей к решению задач по арифметике. В Х. Гинзбург (ред.), Развитие математического мышления (стр. 153–192). Нью-Йорк: Academic Press.

    Google ученый

  • org/Book»>

    Шварц Дж. (1988). Референт-сохранение и референт-трансформирующие операции над качествами. В J. Hiebert & M. Behr (Eds.), Числовые концепции и операции в средних классах (Vol.2. С. 41–52). Рестон, Вирджиния: Эрлбаум / N.C.T.M ..

    Google ученый

  • Соудер Л. (1988). Детские решения сюжетных задач. Journal of Mathematical Behavior, 7 , 227–238.

    Google ученый

  • Штеффе, Л. (1983). Детские алгоритмы как схемы. Образовательные исследования по математике, 14 , 109–154.

    Артикул Google ученый

  • Штеффе, Л.(1988). Детское построение числовых последовательностей и схем умножения. В J. Hiebert & M. Behr (Eds.), Числовые концепции и операции в средних классах (Том 2, стр.119–140). Рестон, Вирджиния: Эрлбаум / NCTM.

    Google ученый

  • Стеффе, Л., Кобб, П., и Ричардс, В. (1988). Построение арифметических значений и стратегий . Нью-Йорк: Springer-Verlag.

    Google ученый

  • Штеффе, Л., Фон Глазерсфельд, Э., Ричардс, Дж., И Кобб, П. (1983). Детские виды счета: философия, теория и применение . Нью-Йорк: Прегер.

    Google ученый

  • Стеффе Л. и Вуд Т. (1990). Преобразование детского математического образования: международные перспективы . Хиллсдейл, Нью-Джерси: Эрлбаум.

    Google ученый

  • Верно, Г.(1988). Мультипликативные структуры. В J. Hiebert & M. Behr (Eds.), Числовые концепции и операции в средних классах (Том 2, стр. 141–161). Рестон, Вирджиния: Эрлбаум / N.C.T.M.

    Google ученый

  • Фон Глазерсфельд, Э. (1985). Реконструкция концепции знания. Achives de Psychologie, 53 , 91–101.

    Google ученый

    • (PDF) Лонгитюдное исследование успеваемости детей по задачам простого умножения и деления

    как умножение, так и деление.Напротив, при

    высоких уровнях квалификации предполагается независимое представление для

    соответствующих задач умножения и деления (т. е. 21 ⫼3⫽

    7 и 3 ⫻7⫽21 относятся к двум независимым узлам памяти).

    Хотя четвероклассники в этом исследовании освоили таблицы

    с RT менее 2 с и частотой ошибок около 6%, мы не наблюдали диссоциации

    в траекториях развития обеих операций.

    Конечно, мы не можем исключить, что диссоциация между обеими операциями

    возникает на более поздних стадиях развития, с еще более высокими уровнями навыков

    .Но на ранних стадиях развития доказательства, представленные здесь до

    , ясно указывают на общую сеть для умножения

    катионов и фактов деления.

    Откуда взялось параллельное развитие между двумя операциями

    ? Конкретный метод, используемый для обучения арифметике для нашей выборки

    , можно описать как «конструктивистский», что означает, что

    детей были обучены конструировать свои собственные знания, а

    детей придумывали свои собственные стратегии решения (Jonassen, 1991; Steffe &

    Гейл, 1995). Тем не менее, умножение и деление были введены почти одновременно (во втором классе), а детей

    явно учили, что деление — это обратное умножению.

    Даже несмотря на то, что это не преподавалось как строгий алгоритм (учитывая конструктивистский подход

    ), вполне вероятно, что это приводит к быстрой интеграции

    обеих операций. Следовательно, обе операции

    будут прочно связаны в памяти. Поэтому было бы интересно исследовать траектории развития обеих операций в

    учебных ситуациях, в которых умножение и деление выполняются отдельно и / или когда меньше внимания уделяется математической взаимодополняемости

    обеих операций во время инструкция-

    ция.В соответствии с нашими результатами Маллиган и Митчелмор (1997)

    обнаружили, что до получения формального обучения делению дети

    во 2 и 3 классах использовали аналогичные процедуры решения для задач слова

    , включающих умножение и деление, и эти решения были

    . В

    случаях использовались мультипликативные и аддитивные отношения. Если сначала для решения задач деления используются отношения умножения

    , что весьма вероятно в группе детей, участвовавших в этом исследовании

    , из-за метода обучения, то вполне вероятно, что

    представления в памяти фактов умножения будут лежать в основе выполнения деления

    .Это приводит к гипотезе о том, что аналогичные траектории

    будут наблюдаться для сложения и умножения, если катион multipli-

    преподается как повторное сложение. Чтобы прояснить этот вопрос, необходимы дальнейшие исследования

    .

    В совокупности из настоящего исследования мы знаем, что, по крайней мере,

    на ранней стадии разработки, представления в памяти простого умножения и деления

    сильно взаимосвязаны. Наши результаты

    предполагают, что на этих ранних стадиях развития умножение

    и деление следует рассматривать как взаимозависимые и взаимодействующие навыки

    .

    Ссылки

    Эшкрафт, М. Х., & Стазык, Э. Х. (1981). Мысленное дополнение: Тест 3 проверочных моделей

    . Память и познание, 9, 185–196.

    Баруди, А. Дж. (1983). Развитие процедурных знаний: альтернативное объяснение

    хронометрических тенденций ментальной арифметики.

    Обзор развития, 3, 225–230.

    Blo¨te, A. W., Lieffering, L. M., & Ouwehand, K. (2006). Развитие

    счета «многие к одному» у 4-летних детей.Когнитивное развитие,

    21, 332–348.

    Брайант П. и Нуньес Т. (2002). Понимание математики детьми.

    В У. Госвами (ред.), Блэквелл, руководство по когнитивному развитию детей

    (стр. 412–439). Оксфорд, Англия: Блэквелл.

    Кэмпбелл, Дж. И. Д. (1987). Сетевые помехи и умственное умножение.

    Журнал экспериментальной психологии: обучение, память и познание

    tion, 13, 109–123.

    Кэмпбелл, Дж.И. Д. (1994). Архитектуры для числового познания. Познание

    тион, 53 (1), 1–44.

    Кэмпбелл, Дж. И. Д. (1997). О соотношении опытного выполнения простого деления

    и умножения. Журнал экспериментальной психологии:

    Обучение, память и познание, 23, 1140–1159.

    Кэмпбелл, Дж. И. Д. (1999). Деление на умножение. Память и познание —

    tion, 27, 791–802.

    Campbell, J. I. D., Fuchs-Lacelle, S., & Phenix, T.С. (2006). Идентичные

    элементов модели арифметической памяти: Расширение до сложения и суб-

    тяги. Память и познание, 34, 633–647.

    Кэмпбелл, Дж. И. Д., и Грэм, Д. Дж. (1985). Умножение умственных способностей:

    Структура, процесс и приобретение. Канадский журнал психологии, 39,

    338–366.

    Кэмпбелл, Дж. И. Д., & Гюнтер, Р. (2002). Вычисление, культура и эффект повторного операнда

    . Познание, 86, 71–96.

    Кэмпбелл, Дж. И. Д., и Тарлинг, Д. П. М. (1996). Поисковые процессы в арифметическом производстве и проверке

    . Память и познание, 24, 156 —

    172.

    Cerella, J. (1991). Возрастные эффекты могут быть глобальными, а не локальными: комментарий к Fisk

    and Rogers (1991). Журнал экспериментальной психологии: общий, 120,

    215–223.

    Куни, Дж. Б., Суонсон, Х. Л. и Лэдд, С. Ф. (1988). Приобретение умственного умения

    умножения: свидетельство перехода между стратегиями подсчета и

    поиска.Познание и обучение, 5, 323–345.

    Корреа Дж., Нуньес Т. и Брайант П. (1998). Понимание детьми

    деления: взаимосвязь между элементами деления в некомпьютерной задаче

    . Журнал педагогической психологии, 90, 321–329.

    Де Браувер, Дж. (2007). Представления знаний арифметических фактов в памяти

    и их развитие. Неопубликованная докторская диссертация,

    Гентский университет, Гент, Бельгия.

    Де Браувер, Дж., Вергутс, Т., и Фиас, В. (2006). Представление

    фактов умножения: эволюционные изменения в размере задачи, пять,

    и эффекты связи. Журнал экспериментальной детской психологии, 94, 43–56.

    Делазер М., Семенца К. и Денес Г. (1994). Чтение арабских чисел

    и цифровых слов у пациента с дислексией. Мозг и язык, 47,

    437–439.

    Фридман О. (1990). Роль переписки в развитии

    числовых стратегий у детей раннего возраста.Неопубликованная докторская диссертация

    , Оксфордский университет, Оксфорд, Англия.

    Гальфано, Г., Мацца, В., Ангрилли, А., & Умилта, К. (2004). Electrophysi-

    ологических коррелятов извлечения фактов умножения, управляемого стимулами. Neu-

    ropsychologia, 42, 1370–1382.

    Гальфано, Г., Рускони, Э., & Умилта, К. (2003). Автоматическая активация

    фактов умножения: свидетельства из узлов, смежных с продуктом.

    Ежеквартальный журнал экспериментальной психологии: Human Experimental

    Psychology, 56A, 31–61.

    Имбо, И., и Вандиерандонк, А. (2008). Влияние размера задачи, операции,

    и объема рабочей памяти на простые арифметические стратегии: различия

    между детьми и взрослыми? Психологические исследования, 72, 331–346.

    Йонассен Д. (1991). Объективизм vs. конструктивизм. Образовательные технологии —

    ogy Исследования и разработки, 39, 5–14.

    Кайл Р. В. (1991). Развитие изменения скорости обработки в течение

    детства и юности.Психологический бюллетень, 109, 490–501.

    Кайл, Р. В., и Феррер, Э. (2007). Скорость обработки в детстве и

    подростковом возрасте: продольные модели для изучения изменений в развитии.

    Развитие ребенка, 78, 1760–1770.

    Кауфманн, Л., Лохи, А., Дрекслер, А., и Семенца, К. (2004). Дефицит

    Получение арифметических фактов: проблема с хранением или доступом? Пример из практики.

    Neuropsychologia, 42, 482–496.

    1493

    РАЗВИТИЕ УМНОЖЕНИЯ И РАЗДЕЛЕНИЯ

    Продольное исследование успеваемости детей по простым задачам умножения и деления

    Используйте этот URL для цитирования или ссылки на эту публикацию: http: // hdl.handle.net/1854/LU-784327

    MLA

    Де Брауэр, Жолиен и Вим Фиас. «Лонгитюдное исследование успеваемости детей по задачам простого умножения и деления». ПСИХОЛОГИЯ РАЗВИТИЯ 45,5 (2009): 1480–1496. Распечатать.

    APA

    Де Браувер Дж. И Фиас У. (2009). Продольное исследование успеваемости детей по простым задачам умножения и деления. ПСИХОЛОГИЯ РАЗВИТИЯ , 45 (5), 1480–1496.

    Чикаго, дата автора

    Де Брауэр, Жолиен и Вим Фиас. 2009. «Продольное исследование успеваемости детей по задачам простого умножения и деления». Психология развития 45 (5): 1480–1496.

    Дата автора в Чикаго (все авторы)

    Де Брауэр, Жолиен и Вим Фиас.2009. «Продольное исследование успеваемости детей по задачам простого умножения и деления». Психология развития 45 (5): 1480–1496.

    Ванкувер

    1.

    De Brauwer J, Fias W. Продольное исследование успеваемости детей в задачах простого умножения и деления. РАЗВИВАЮЩАЯ ПСИХОЛОГИЯ. 2009. 45 (5): 1480–96.

    IEEE

    [1]

    Дж.Де Браувер и В. Фиас, «Продольное исследование успеваемости детей при решении простых задач умножения и деления», РАЗВИТИЕ ПСИХОЛОГИИ , том. 45, нет. 5. С. 1480–1496, 2009.

    .
     @article {784327,
  abstract = {Авторы исследовали выполнение задач простого умножения и деления 8-летних детей в продольном направлении, чтобы определить траектории развития обеих операций. Дважды в год, в течение двух школьных лет подряд, дети выполняли задание на умножение и деление и задание на сопоставление чисел.Все эффекты, которые наблюдались в производительности умножения (размер задачи, 5, и эффект связи и взаимодействие Tie x Size), также наблюдались в производительности деления.  Описаны траектории развития этих эффектов. Авторы наблюдали сильные параллели развития между обеими операциями. Эти результаты соответствуют сильно взаимосвязанным сетям памяти для умножения и деления фактов, по крайней мере, у маленьких детей. Результаты задачи сопоставления чисел показали, что эффект интерференции развивался по-разному для умножения и деления, указывая на то, что автоматическое распространение активации от операндов деления к ответам деления не работает у детей этого возраста.},
  author = {Де Браувер, Жолин и Фиас, Вим},
  issn = {0012-1649},
  journal = {ПСИХОЛОГИЯ РАЗВИТИЯ},
  ключевые слова = {ФАКТЫ, ОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ НАВЫКИ, МОДЕЛЬ ИДЕНТИФИКАЦИОННЫХ ЭЛЕМЕНТОВ, ФУНКЦИИ ВРЕМЕНИ-ТОЧНОСТИ, МЕНТАЛЬНОЕ УМНОЖЕНИЕ, РАЗВИТИЕ-ИЗМЕНЕНИЕ, ИНДИВИДУАЛЬНЫЕ РАЗЛИЧИЯ, ОБЯЗАТЕЛЬНАЯ АКТИВАЦИЯ, ПРОСТОЕ РАЗЛИЧИЕ, РАЗРАБОТКА ПРОБЛЕМ, арифметическое вычисление размера памяти },
  language = {eng},
  число = {5},
  pages = {1480–1496},
  title = {Продольное исследование успеваемости детей в простых задачах умножения и деления},
  url = {http: // dx. doi.org/10.1037/a0015465},
  объем = {45},
  год = {2009},
}

    Двойное деление | деление клеток

    Бинарное деление , бесполое размножение путем разделения тела на два новых тела. В процессе бинарного деления организм дублирует свой генетический материал или дезоксирибонуклеиновую кислоту (ДНК), а затем делится на две части (цитокинез), при этом каждый новый организм получает одну копию ДНК.

    Бактерии Escherichia coli , подвергающиеся цитокинезу на заключительной стадии бинарного деления (микрофотография с помощью сканирующего электронного микроскопа; увеличение в 21 674 раза).

    Дженис Хейни Карр / CDC

    Подробнее по этой теме

    воспроизведение: Двойное деление

    Из различных видов деления клеток наиболее распространенным является деление клеток на две части, разделение клетки на две отдельные и похожие части . …

    Бинарное деление — основной способ размножения прокариотических организмов. У протистов бинарное деление часто подразделяется на типы, такие как поперечное или продольное, в зависимости от оси разделения клеток.Регулярное поперечное деление у некоторых организмов, таких как ленточные черви и сцифостомные полипы, называется стробиляцией. Обычно в результате образуется цепочка, называемая стробилом, продуктов деления — проглоттиды ленточных червей и эфиры сцифозных медуз; каждая проглоттида или эфира созревает по очереди и отделяется от конца стробила. Несколько видов многоклеточных (многоклеточных) регулярно подвергаются делению тела на несколько единиц одновременно, этот процесс называется фрагментацией. Деление и фрагментация планарии обычно представляют собой прямое воспроизводство, при котором каждая часть восстанавливает недостающие части, чтобы стать совершенно новым животным.Однако продукты стробиляции имеют лишь косвенное воспроизводство: проглоттиды не регенерируют, а несут и выделяют большое количество яиц и погибают; ephyrae не образуют новых полипов, а созревают в медузы, воспроизводящиеся половым путем, личинки которых становятся полипами.

    Продольное исследование выявляет гендерные и расовые различия среди первоклассников

    Национальный центр статистики образования, подразделение Министерства образования США, проводящее исследование, продолжит следить за выборкой учащихся 3 и 5 классов.

    Лонгитюдное исследование в раннем детстве, детский сад 1998–1999 годов, проводится на основе репрезентативной общенациональной выборки примерно из 22 000 детей до весны 5-го класса. На момент отбора детей для исследования они посещали около 1000 детских садов по всей стране.

    Отчет «Успеваемость детей в детском саду и первом классе по чтению и математике» доступен в Национальном центре статистики образования. Также доступно резюме.(Для полного отчета требуется Adobe Acrobat Reader.)

    Последняя часть исследования, выпущенная в этом месяце, укрепляет уверенность в том, что дети, которых часто читают и которые распознают буквы и цифры при поступлении в школу, имеют явное преимущество перед подростками, которым не хватает такой фундамент.

    «Дети, которые демонстрируют ранние навыки грамотности и происходят из благоприятной среды обучения грамоте, которые обладают позитивным подходом к обучению и которые имеют очень хорошее или отличное общее состояние здоровья, по-видимому, после одного и даже двух лет формального обучения достигают более высоких результатов, чем дети, у которых нет этих ресурсов », — говорится в отчете.Исследование показывает, что к концу первого класса большинство детей приобрели навыки чтения в раннем возрасте, которые, по мнению экспертов, необходимы им для будущего успеха.

    Девяносто пять процентов учащихся, участвовавших в исследовании, знали все буквы алфавита к тому моменту, 98 процентов устанавливали связь между буквой и звуком в начале слов, а около 83 процентов узнавали общеупотребительные слова на глаз.

    В математике 96 процентов детей понимали относительное положение предметов к тому времени в учебном году, и около 76 процентов могли складывать и вычитать простые числа — оба навыка, которые, по мнению Национального совета учителей математики, детям следует развивать. 2 класс.Кроме того, около четверти учащихся — чаще мальчиков — умножали и делили простые целые единицы.

    В чтении 85 процентов девочек 1-го класса могли узнавать слова в лицо по сравнению с 80 процентами мальчиков. А по математике 30 процентов мальчиков 1-го класса начинали решать задачи умножения и деления по сравнению с 24 процентами девочек.

    Различия в успеваемости бедных детей и их более обеспеченных сверстников очевидны.

    Только 67 процентов первоклассников из бедных семей могли распознавать слова в лицо, например, по сравнению с 86 процентами первоклассников из небедных семей, как показало исследование. Дети, живущие в бедности, также реже, чем дети из семей с более высоким доходом, прибавляли и вычитали к концу первого класса — 60 процентов по сравнению с 79 процентами.

    Раса и этническая принадлежность детей также являются факторами. К весне 1-го класса белые дети и дети азиатского происхождения с большей вероятностью, чем дети афроамериканского или латиноамериканского происхождения, распознавали слова на вид, понимали слова в контексте, складывали и вычитали, умножали и делили.

    Детские сады разные

    В оценках, основанных на нормах, специально разработанных для исследования в раннем детстве, белые дети, как правило, имели средние по стране результаты как по чтению, так и по математике. Афроамериканские дети поступили в школу с результатами ниже среднего по стране в этих областях и остались там в конце 1-го класса. Дети латиноамериканского происхождения поступили в школу и остались на среднем уровне по стране по математике, но по чтению значительно ниже среднего. Однако к тому времени, когда ученики латиноамериканского происхождения заканчивали первый класс, они сокращали этот пробел.

    Типы школ, которые дети посещали в детском саду, также имели значение. Первоклассники из программ частных детских садов набрали значительно больше, чем в среднем по стране, по чтению и математике, в то время как те, кто посещал программы государственных школ, получили средние оценки.

    Марилу Хайсон, заместитель исполнительного директора Вашингтонской национальной ассоциации образования детей раннего возраста, сказала, что одним из важных выводов отчета является влияние здоровья детей и их отношения к учебе на их успеваемость.

    «Это говорит мне о том, что программы дошкольного образования и дошкольного образования должны уделять пристальное внимание всему ребенку, а также грамотности и другому содержанию», — сказала она.

    Национальный центр статистики образования, подразделение Министерства образования США, проводящее исследование, продолжит следить за выборкой учащихся 3 и 5 классов.

    Перевод и значение продольного деления на арабском, английский Арабский Словарь терминов Страница 1

    Раздел Свинцовые внутренние и внешние каналы

    القنوات الداخلية والخارجية لقادة الأقسام

    Автомобильная промышленность

    Подушки безопасности водителя и пассажира рассчитаны на срабатывание при лобовом и ближнем лобовом столкновении, а не при опрокидывании, боковом ударе или ударе сзади, если только столкновение не вызовет достаточного продольного замедления

    الوسائد الهوائية الخاصة بالسائق أو الراكب الأمامي مصممة بحيث تنفرج في حالة حدوث تصادم من الجانب الأمامي, وليس في حالات انقلاب السيارة أو الصدمات من الجانب أو من الخلف, إلا إذا نجم عن الاصطدام انخفاض مفاجئ في السرعة

    Автомобильная промышленность

    Подушки безопасности водителя и пассажира рассчитаны на срабатывание при лобовом и ближнем лобовом столкновении, а не при опрокидывании, боковом ударе или ударе сзади, если только столкновение не вызывает достаточного продольного замедления

    الوسائد الهوائية الخاصة بالسائق والراكب الأمامي مصممة للانتفاخ في حالة حدوث تصادم من الجانب الأمامي أو بالقرب من الجانب الأمامي, وليس في حالات انقلاب السيارة أو الصدمات من الجانب أو من الخلف, إلا إذا نجم عن الاصطدام انخفاض كافي في السرعة

    Автомобильная промышленность

    Частота FDMA деление множественный доступ

    الوصول المتعدد بتقسيم التردد

    Автомобильная промышленность

    TDMA Time разделение множественный доступ

    الوصول المتعدد بتقسيم الوقت

    Автомобильная промышленность

    Заполните форму, содержащую организационную схему информирования об инцидентах. Наверху находится диспетчер инцидентов, а под ним — планирование, операции и логистика. Ниже представлены три подразделения , / группы и Air

    .

    املأ النموذج الذي يوضح مخطط المنظمة لبيان الحادثة. ي الأعلى يوجد قائد الحادثة مع العمليات المخططة والإمدادات في الأسفل. أدناه يوجد ثلاث مجموعات / أقسام والمجال الجوي

    Автомобильная промышленность

    Передние подушки безопасности и натяжители предназначены для срабатывания только при лобовом и ближнем лобовом столкновении, но не при опрокидывании, боковом ударе или ударе сзади, если только столкновение не вызывает достаточное продольное замедление

    إن الوسائد الهوائية الأمامية والشدادات مصممة بحيث تنشط فقط عند حدوث الاصطدامات الأمامية والقريبة من الجهة الأمامية, وليس في حالات الانقلاب أو الاصطدامات الجانبية أو الاصطدامات الخلفية, ما لم يسبب الاصطدام تقليلا للسرعة

    Автомобильная промышленность

    Двоичное деление — определение, шаги, типы, примеры (по сравнению с митозом)

    Главная »Биология» Бинарное деление — определение, шаги, типы, примеры (по сравнению с митозом)

    Обучающие видео по биологии

    Последнее обновление в мае 23, 2020 Сагар Арьял

    Что такое двойное деление? (Определение)
    • Бинарное деление — это тип бесполого размножения, при котором одна живая клетка или органелла увеличивается в два раза, а затем распадается на две идентичные дочерние клетки, каждая из которых имеет потенциал вырасти до размера исходной клетки или органеллы.
    • Бинарное деление отличается от других типов деления тем, что; только две части формируются из одного объекта.
    • Эта форма воспроизводства называется бесполым, поскольку процесс не включает в себя образование или слияние гамет.
    • Поскольку бинарное деление является типом бесполого размножения, образовавшиеся дочерние клетки имеют тот же генетический материал, что и их родительские клетки.
    • Бинарное деление — это способ размножения у многих прокариот, включая архей, цианобактерий, эубактерий и некоторых эукариот, таких как амеба и Paramecium .
    • Некоторые клеточные органеллы, такие как митохондрии, также подвергаются клеточному делению в процессе бинарного деления.
    • Для того, чтобы оставаться жизнеспособными и конкурентоспособными, бактерия должна делиться в нужное время в нужном месте и предоставлять каждому потомству полную копию своего основного генетического материала.

    Шаги / процесс двойного деления

    Двойное деление у прокариот

    Рисунок: Двойное деление у прокариот. Источник изображения: Википедия.

    • Перед бинарным делением, в отличие от человеческих клеток, в которых генетический материал присутствует внутри ядра, генетический материал прокариота (хромосомы) присутствует в специализированной области клетки в цитоплазме в виде нуклеоида.
    • Хромосомы затем подвергаются репликации, начиная с точки в хромосоме, называемой точкой начала репликации. Затем источник делится, и по мере продолжения репликации два источника перемещаются к противоположным концам клетки, увлекая за собой хромосомы.
    • Когда репликация завершена, различные типы белков, работающих в качестве механизма деления клетки, собираются в месте будущего деления (в центре клетки).
    • Одним из важнейших белков в этом процессе является белок FtsZ, который образует кольцеобразную структуру в центре клетки.
    • Этот процесс важен для гарантии того, что деление расщепляет цитоплазму и не повреждает генетический материал.
    • Теперь, для деления цитоплазмы, мембрана сжимается внутрь, образуя перегородку (новую клеточную стенку), формирующуюся посередине клетки.
    • Наконец, перегородка делится, образуя две независимые клетки.
    • Crenarchaeota, не имеющая ни клеточной стенки, ни белка FstZ, однако, использует примитивный механизм с участием различных белков, называемый системой ESCRT-III.

    Бинарное деление у эукариот
    • Хотя большинство эукариот подвергаются половому размножению, некоторые простейшие, такие как амеба, размножаются бинарным делением, и деление клеток в некоторых органеллах внутри эукариотических клеток происходит аналогичным бактериям.
    • Процесс бинарного деления в этих клетках такой же, как у прокариот с участием белка FtsZ.
    • Органеллы клетки, такие как митохондрии и хлоропласты, делятся бинарным делением, что дает основу для теории эндосимбиотиков , , которая объясняет, что прокариоты эволюционировали в современные митохондрии.

    Типы бинарного деления

    Бинарное деление бывает четырех типов в зависимости от плоскости деления цитоплазмы:

    1. Нерегулярное бинарное деление
    • В данном случае деление цитоплазмы цитокинез) может происходить в любой плоскости, но в основном перпендикулярно плоскости деления хромосом (кариокинез).
    • Этот тип встречается у организмов, подобных амебе.

    1. Поперечное бинарное деление
    • При поперечном бинарном делении цитокинез происходит вдоль поперечной оси клетки.
    • Этот тип деления встречается у мерцательных простейших, таких как Paramecium .

    1. Продольное бинарное деление
    • Здесь деление цитоплазмы происходит вдоль продольной оси клетки.
    • Этот тип деления встречается у жгутиконосцев, таких как Euglena .

    1. Oblique Binary Fission
    • Деление цитоплазмы в данном случае происходит наклонно (т.е. косо слева и справа).
    • Этот тип деления встречается у динофлагеллят, таких как Ceratium .

    Примеры организмов, использующих двоичное деление
    • Группа различных организмов, включая прокариот и эукариот, делится на двоичное деление.
    • Большинство бактерий размножаются этим процессом. Процесс включает деление с использованием белка FtsZ, включая хромосомную репликацию, хромосомную сегрегацию и расщепление клеток.
    • Однако у простейших, таких как амеба , Paramecium , Euglena , процесс может отличаться в расщеплении клеток и в том, как делится цитоплазма.
    • Организмы, которые размножаются бинарным делением, включают Bacillus subtilis, B. cereus, B. pumilus, Escherichia coli, Clostridium perfringens, Corynebacterium diphtheriae, Amoeba, Paramecium, Euglena, Ceratium, и т. Д.

    Бинарное деление против митоза 41 Происходит в некоторых случаях .

    Характеристики

    Бинарное деление

    Митоз

    		 Это происходит только у эукариот.
    Механизм При бинарном делении волокна веретена не образуются. При митозе деление поддерживается за счет образования волокон веретена.
    Стадии Бинарное деление включает три стадии, а именно репликацию хромосом, хромосомную сегрегацию и расщепление цитоплазмы. Митоз включает четыре стадии; профаза, метафаза, анафаза и телофаза.
    Продукт В результате этого процесса образуются две идентичные дочерние клетки, обе с таким же генетическим содержанием, что и родительская клетка. Этот процесс также приводит к образованию двух идентичных дочерних клеток, обе с таким же генетическим содержанием, что и родительская клетка.
    Функция Бинарное деление — это тип бесполого размножения. Митоз участвует в росте (количестве) клеток в многоклеточных организмах.

    Ссылки и источники
    • 4% — https://answers.yahoo. 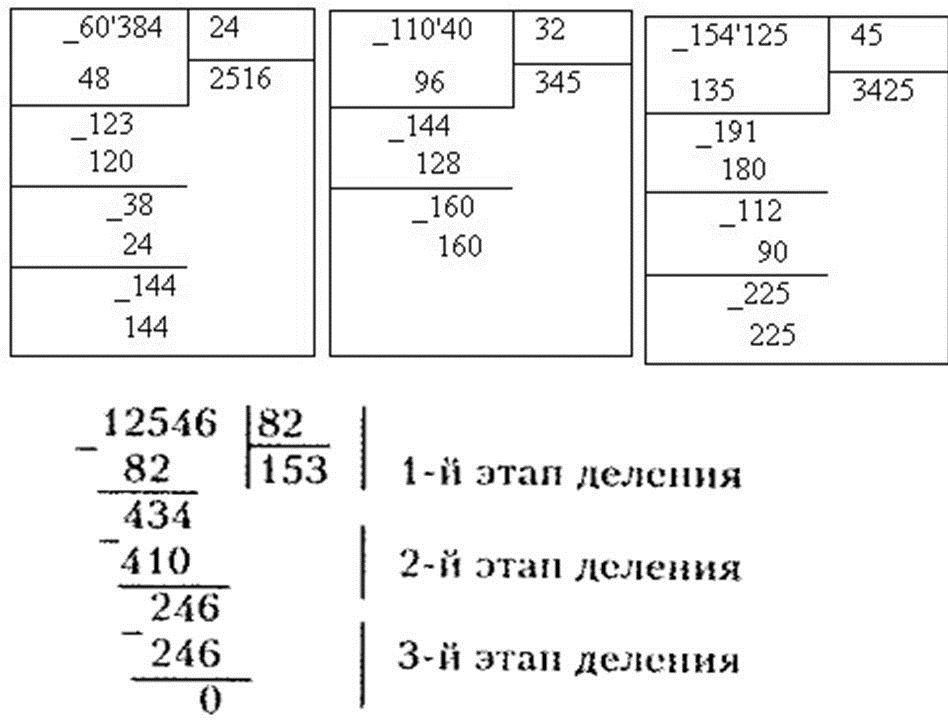com/question/index?qid=20131020212143AACOqLf
    • 2% — https: // www.coursehero.com/file/p28h9gb/results-in-the-formation-of-two-daughter-cells-that-have-the-same-number-and/
    • 2% — https://byjus.com/biology / binary-fission /
    • 2% — https://brainly.com/question/9365782
    • 1% — https://www.oughttco.com/bacterial-reproduction-373273
    • 1% — https: // www.ncbi.nlm.nih.gov/pmc/articles/PMC6126333/
    • 1% — https://www.ncbi.nlm.nih.gov/books/NBK26831/
    • 1% — https: // sciencing. com / 5-stage-mitosis-13121.html
    • 1% — https: // quizlet.com / 6697584 / microbiology-expected-2-flash-cards /
    • 1% — https://en.wikipedia.org/wiki/Fission_(biology)
    • 1% — https://courses.lumenlearning.com/ biology1 / chapter / missing-prokaryotic-cell-division-ch-6-4 /
    • 1% — https://brainly.com/question/839539
    • <1% - https://www.oughttco.com/ types-of-asexual-reproduction-1224623
    • <1% - https://www.biologyonline.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *