Как разделить 8000 на 100 столбиком: 8000:100 решите столбиком — Школьные Знания.com

Калькулятор онлайн — Калькулятор процентов. Найти сколько процентов составляет одно число от другого

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100.

Например:

\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):

\( b = a \cdot \frac{p}{100} \)

Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac{p}{100} \). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

\( p = \frac{b}{a} \cdot 100\% \) Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить \( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:

\( S_n = \left( 1+ \frac{pn}{100} \right) S \)

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)

Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.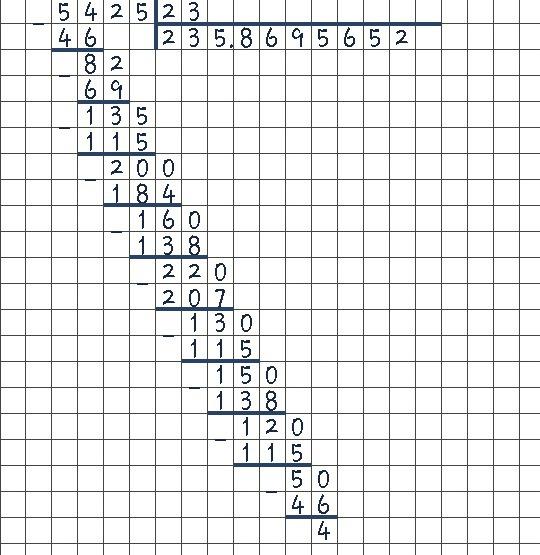 n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Ответы к странице 139 №537-543 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Задание № 537

Сколько процентов площади прямоугольника закрашено (рис.6.10,а−в)?

Решение

а) 100% : 2 = 50% − площади прямоугольника закрашено.
Ответ: 50%.

б) 100% : 4 = 25% − площади прямоугольника закрашено.
Ответ: 25%.

в) 100% : 5 * 2 = 20 * 2 = 40% − площади прямоугольника закрашено.
Ответ: 40%.

Задание № 538

а) Во время киносеанса 3/5 всех мест кинозала было занято, остальные места свободные. Сколько процентов всех мест кинозала было занято и сколько − свободно?
б) Книги на русском языке составляют 11/20 всех книг библиотеки, остальные − на иностранных языках. Сколько процентов всех книг библиотеки на иностранных языках?

Решение

а) 1) $\frac35=\frac6{10}=0,6=60$ % − мест занято;
2) 100% − 60% = 40% − мест свободно.
Ответ: 60% мест занято, 40% мест свободно.

б) 1) $\frac{11}{20}=\frac{55}{100}=0,55=55$ % − книг на русском языке;
2) 100% − 55% = 45% − книг на иностранных языках.
Ответ: 45% книг.

Задание № 539

Тимур бросил мяч в баскетбольное кольцо 50 раз. Определите, какую часть составляет число попаданий от числа бросков, и выразите эту часть в процентах, если он попал в кольцо:
а) 10 раз;
б) 25 раз;
в) 32 раза;
г) 40 раз.

Решение

а) $10:50=\frac{10}{50}=\frac{20}{100}=0,2=20$ % − составляет число попаданий от числа бросков.
Ответ: 20%.

б) $25:50=\frac{25}{50}=\frac{50}{100}=0,5=50$% − составляет число попаданий от числа бросков.
Ответ: 50%.

в) $32:50=\frac{32}{50}=\frac{64}{100}=0,64=64$% − составляет число попаданий от числа бросков.
Ответ: 64%.

г) $40:50=\frac{40}{50}=\frac{80}{100}=0,8=80$% − составляет число попаданий от числа бросков.
Ответ: 80%.

Задание № 540

а) Из 500 ответов, присланных на вопрос телевикторины, правильными оказались 120. Найдите отношение числа правильных ответов к числу всех присланных ответов. Сколько процентов участников викторины ответили правильно?
б) В школе 800 учащихся, 600 из них занимаются спортом. Найдите отношение числа спортсменов к числу всех учащихся школы. Сколько процентов учащихся занимаются спортом?

Решение

а) $120:500=\frac{120}{500}=\frac{24}{100}=0,24=24$ % − участников викторины ответили правильно.
Ответ: 24% участников.

б) $600:800=\frac{600}{800}=\frac{75}{100}=0,75=75$ % − учащихся занимаются спортом.
Ответ: 75% учащихся.

Задание № 541

а) В округе 25000 избирателей. В голосовании приняли участие 13000 из них. Сколько процентов избирателей приняли участие в выборах и сколько не приняли?
б) Из 30000 жителей города 6900 дети. Какой процент всего населения составляют дети? Какой процент всего населения составляют взрослые?

Решение

а) 1) 25000 − 13000 = 12000 (избирателей) − приняли участие в выборах;
2) $12000:25000=\frac{12000}{25000}=\frac{48}{100}=0,48=48$ % − избирателей не приняли участие в выборах;
3) 100% − 48% = 52% − избирателей приняли участие в выборах.
Ответ: 48% − не приняли участие, 52% − приняли участие.

б) 1) $6900:30000=\frac{6900}{30000}=\frac{69}{300}=\frac{23}{100}=0,23=23$ % − населения составляют дети;
2) 100% − 23% = 77% − населения составляют взрослые.
Ответ: 23% составляют дети, 77% населения составляют взрослые.

Задание № 542

а) Из 40−литровой канистры отлили 16 л бензина. Сколько процентов бензина осталось в канистре?
б) Боксер из 60 проведенных боев выиграл 54 боя. Сколько процентов всех боев боксер проиграл?

Решение

а) 1) 40 − 16 = 24 (л) − бензина осталось в канистре;
2) $24:40=\frac6{10}=0,6=60$ % − бензина осталось в канистре.
Ответ: 60%.

б) 1) 60 − 54 = 6 (боев) − боксер проиграл;
2) $6:60=\frac1{10}=0,1=10$ % − боев боксер проиграл.
Ответ: 10%.

Задание № 543

а) В банке был открыт счет на 8000 р. сроком на 1 год. Через год сумма на счете стала равна 8640 р. Сколько процентов от вложенной суммы составляет новая сумма на счете?
б) В осенние месяцы в городе Дальнегорске произошло 45 дорожно−транспортных происшествий (ДТП). В зимние месяцы в связи с ухудшением погодных условий число ДТП выросло до 54. Сколько процентов от числа осенних ДТП составило число ДТП в зимние месяцы?

Решение

а) 8640 : 8000 * 100 = 108% − от вложенной суммы составляет новая сумма на счете.
Ответ: 108%.

б) 54 : 45 * 100% = 1,25 * 100% = 125% − от числа осенних ДТП составило число ДТП в зимние месяцы.
Ответ: 125%.

 

Урок 18. повторение пройденного по теме «величины» — Математика — 4 класс

Математика, 4 класс

Урок №18.Повторение пройденного по теме «Величины»

Перечень вопросов, рассматриваемых в теме:

1. Что относится к величинам?
2. Как узнать о какой величине идёт речь?
3. Можно ли выполнять арифметические действия с величинами?

Глоссарий по теме:

Величина – это то, что можно измерить, сравнить и результат представить в виде числа

Единица измерения – это величина, в которой выражаются другие, однородные с ней величины.

Обязательная литературы и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 53 — 57
2. Моро М. И., Волкова С. И. Для тех, кто любит математику 4 класс.

Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – С. 30

Теоретический материал для самостоятельного изучения

Назовём известные величины: длина, площадь, масса, время.

Называют их величинами, потому, что их можно измерить, сравнить и результат выразить числом.

Выполним задание:

Разбейте числа на две группы по определённому признаку.

43, 5 м 6 дм, 1001, 4 кг, 5 мин, 890, 10 с, 12, 6 кг, 2 т, 7 сут., 98, 120 г, 8 дм², 5 км, 1 ч 20 мин, 8 м², 1000 см², 555

Мы видим, что в этом ряду есть натуральные числа, которые являются результатом вычислений или счёта. И есть именованные числа, которые получают в результате измерения величин и сопровождающих названием единиц измерения.

Группу именованные числа можно разбить на несколько групп по признаку разных величин. Единицы измерения нам укажут на величину, о которой идёт речь. Для этого нужно вспомнить единицы измерения величин.

Единицы измерения длины: км, м, дм, см, мм.

Единицы измерения времени: сутки, час, мин, сек.

Единицы измерения массы: т, ц, кг, г.

Единицы измерения площади: м², дм², см².

Для измерения величин используют различные инструменты и приборы.

	Величины
	Длина	Площадь	Масса	Время
Измерительные приборы		формулы
Единицы измерения	мм, см, дм, м, км	мм², см², дм², м²	г, кг, ц, т	с, мин, ч

Надо всегда помнить одно правило – сравнивать, складывать и вычитать можно только именованные числа с одинаковыми единицами (мерами). Для этого нужно помнить соотношения единиц измерения величин.

Сравним:

555м * 5 км

Для того, чтобы сравнить длину, нужно выразить в одни и те же единицы.

5км = 5000 м

555м < 5 км

8 м² * 80 дм², переведём 8 м² = 800 дм²

8 м²> 80 дм²

4 кг30 г * 5100 г, переведем 4 кг30 г = 4030 г

4 кг30 г < 5100 г

100 мин * 1 ч 40 мин, переведём 1 ч 40 мин = 100 мин

100 мин = 1 ч 40 мин

Решим задачу:

Длина тела кита 26 м, а тюленя – 20 дм. Во сколько раз тюлень короче кита?

26 м = 260 дм

260 : 20 = 13 раз

Ответ: в 13 раз длина тюленя короче длины кита.

Вывод:

Таким образом, длина, площадь, масса и время – это величины.

Величину можно измерить, сравнить и результат представить в виде числа.

Единица измерения – это величина, в которой выражаются другие, однородные с ней величины. При письменных вычислениях значения величин выражают в одних и тех же единицах измерения и выполняют действия с ними так же, как с числами.

Выполним несколько тренировочных заданий.

1. Выберите и отметьте столбик, где написаны только единицы измерения  длины:

а) миллиметр                б)  дециметр                      в)    минута

    грамм                             сантиметр                              тонна

    километр                        миллиметр                            дециметр

    сутки                               километр                              секунда

    дециметр                         метр                                       километр

Ответ: б

2. Выберите вариант, где единицы массы расположены в порядке возрастания:

  а) 3000 г,   30ц,     300 кг,     30 т,   3кг 3г.

  б) 30т,   30 ц,  3кг 3г,  300кг,  3000 г.

  в) 3000г,  3 кг 3г,  300кг,  30ц,  30т.

Ответ: в

3. Выберите ошибочный  ответ:

а) Кирпич массой 5 граммов

б) В пакете 5 килограммов  конфет

в) На уроке физкультуры мы пробежали  100 метров

Ответ : а

4. Найдите ошибку при переводе величин:

5. а) 2м 3дм = 230 см         б) 2м 3дм = 23 дм         в) 2м 3дм = 203см

6. а) 8000кг =  8т                б) 8000 кг = 800000г     в) 8000 кг = 80ц

7. а) 2 ч =  120 мин             б) 2ч =  200 мин            в) 2ч = 7200с

Ответ: в) 2м 3дм = 203см

Калькулятор процентов. Онлайн-калькулятор

Калькулятор процентов позволяет производить любые расчеты с процентами: нахождение процента от числа, сколько процентов составляет число «X» от числа «Y», прибавление процента к числу, вычитание процента из числа

Для расчета необходимо ввести данные в поля калькулятора, после нажать кнопку «Рассчитать» для получения результата.

Нахождение процента от числа. Для того чтобы найти процент от числа введите в первое поле значение процента, которое нужно найти. Во второе поле введите число, из которого нужно найти процент.

Сколько процентов составляет число «X» от числа «Y». В первое поле нужно ввести число, процент которого мы ищем. Во второе поле нужно ввести число, из которого мы будем находить процент первого числа.

Прибавление процента к числу. Чтобы прибавить процент к числу нужно в первое поле ввести значение процента, которое нужно прибавить. Во второе поле ввести число, к которому нужно прибавить процент.

Вычитание процента из числа. Для нахождения результата введите в первое поле число, из которого нужно вычесть процент. Во второе поле введите значение процента, которое нужно вычесть из числа.

Процент (лат. per cent — на сотню) — одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому. Принято считать что 100% = 1, исходя из этого 25% эквивалентно 0,25 или 25/100.

Пример. Для того чтобы вычислить процент от числа нужно в первом поле указать процент который требуется вычислить, например «20». Во втором поле нужно указать число из которого будет вычисляться процент, например «60». После ввода данных нажмите кнопку «Рассчитать», искомый результат «12».

20 %  от числа  60  = ?         →         20 %  от числа  60  = 12.

Как вычитать из 100 столбиком. Вычитание столбиком. Правила вычитания в столбик

Умение считать является одной из основ грамотного человека, хотя последнее время в связи со стремительным развитием электроники важность этого навыка несколько уменьшилась. Сейчас функции калькулятора присутствуют практически в каждом электронном устройстве, однако умение считать без помощи калькулятора может очень пригодиться в жизни. Мы уже вспоминали раньше операцию сложения , а сейчас освежим в памяти еще одну из арифметических операций, а именно вычитание. Считать мы будет на листе бумаги методом вычитания в столбик.

Для примера, найдем разность чисел 5183 и 472. Напомним, что число из которого вычитают другое число называется «уменьшаемым» (5183), число на которое уменьшается исходное число называется «вычитаемым» (472), а результат операции называется «разностью».

Для нахождения разности чисел методом вычитания в столбик, берем листок бумаги и записываем «уменьшаемое», а под ним «вычитаемое» выравнивая их по правому краю. Другими словами, нужно записать единицы под единицами, десятки под десятками, сотни под сотнями и так далее. Таким образом одинаковые разряды обоих чисел оказываются строго друг под другом. После этого проводим под получившимся столбиком горизонтальную черту и ставим слева знак минус.

Вычитание столбиком осуществляется справа налево поразрядно. Начинаем с единиц, считаем 3-2=1 и записываем получившейся результат под чертой.

Переходим к десяткам, нам нужно от 8 отнять 7 и результат опять записать под чертой.

Теперь дошла очередь до сотен, но здесь появляется небольшая проблема, поскольку 1 меньше чем 4. Чтобы ее преодолеть нужно занять десяток у числа слева, в данном случае у тысяч. Получается 10 взятые от числа слева плюс 1 равно 11 и минус 4 равно 7, записываем цифру семь под чертой, а над цифрой 5 в уменьшаемом ставим точку.

Точка над числом указывает, что у него был заимствован десяток и его следовательно нужно будет в дальнейшем уменьшить. Поскольку в вычитаемым больше цифр не осталось, то просто записываем оставшиеся цифры уменьшаемого под чертой. Главное быть внимательным и не забыть, что мы занимали у разряда тысяч, о чем свидетельствует точка над цифрой, поэтому пишем 4.

В результате мы нашли разность двух чисел методом вычитания в столбик и получили результат равный 4711. Все очень просто, главное внимательность.

Хотя есть один момент, который порой вызывает трудности, это необходимость занять, когда слева оказывается ноль. На самом деле все точно также, давайте рассмотрим это на примере и узнаем как вычитать в столбик числа с нулями. В качестве примера вычтем из 104 например 67. Записываем их друг под другом в столбик. Поскольку 4 меньше 7, то нам требуется занять слева. Ставим над нулем точку, однако у нуля нельзя ничего занять, поэтому двигаемся еще левее. Видим единицу, занимаем у нее и ставим над ней точку. В результате мы имеем 10+4=14 и 14-7=7.

Смещаемся влево, здесь мы имеем ноль с точкой, значит на самом деле там цифра 9, поэтому вычитаем из 9 число 6 получается 3.

Снова смещаемся левее, здесь видим 1 с точкой, значит на самом деле здесь 0. В вычитаемом тоже больше не осталось чисел, значит разность равна 37.

Так же требуется запомнить, что способ вычитания столбиком подходит только для случая, когда уменьшаемое больше вычитаемого. Если вам требуется из меньшего числа вычесть в столбик большее число, то просто нужно поменять их местами, то есть вычитать из большего меньшее, а к полученному результату добавить знак минус.

Как видите, все довольно просто, главное помнить простые правила и быть внимательным и даже если у вас не окажется под рукой калькулятора или телефона, вы всегда сможете найти разность двух чисел с помощью бумаги и ручки в столбик. Вы так же можете ознакомиться с правилами выполнения

Для того чтобы вычесть одно число из другого, поместим вычитаемое под уменьшаемым, следующим образом: единицы под единицами, десятки под десятками. Для примера, в качестве уменьшаемого возьмем двузначное число, а в качестве вычитаемого – однозначное.

7 – 5 = 2 результатпишем под единицами.

Теперь вычитаем десятки из десятков, но у вычитаемого нет десятков, поэтому опускаем десяток уменьшаемого в ответ.

27 – 5 = 22

Теперь возьмем оба числа двухзначных:

Вычитаем единицы вычитаемого из единиц уменьшаемого:

6 – 4 = 2 результатпишем под единицами

Теперь вычитаем десятки вычитаемого из десятков уменьшаемого:

8 – 3 = 5 результатпишем под десятками.

В результате получаем разность:

86 – 34 = 52

Давайте попробуем найти разность следующих чисел:

Вычитаем единицы. Из 7 вычесть 9 нельзя, занимаем один десяток из десятков уменьшаемого. Чтобы не забыть ставим точку над десятками.

17 – 9 = 8

Теперь вычитаем десятки из десятков. У вычитаемого нет десятков, но мы занимали один десяток у уменьшаемого:

2 десятка – 1 десяток = 1 десяток

В результате получаем разность:

27 – 9 = 18

Теперь для примера возьмем трехзначные числа:

Вычитаем единицы. 2 меньше 8 , поэтому занимаем один десяток из десятков уменьшаемого: 2 + 10 = 12 (пишем 10 над единицами). Чтобы не забыть ставим точку над десятками.

12 – 8 = 4 результат пишем под единицами.

Мы занимали один десяток из десятков для единиц, значит в уменьшаемом уже не три десятка, а два (3 десятка – 1 десяток = 2 десятка ).

Два десятка меньше чем шесть, занимаем одну сотню или 10 десятков из сотен (2 десятка + 10 десятков = 12 десятков пишем 10 над десятками уменьшаемого), а чтоб не забыть ставим точку над сотнями. Вычитаем десятки:

12 десятков – 6 десятков = 6 десятков результат пишем под десятками.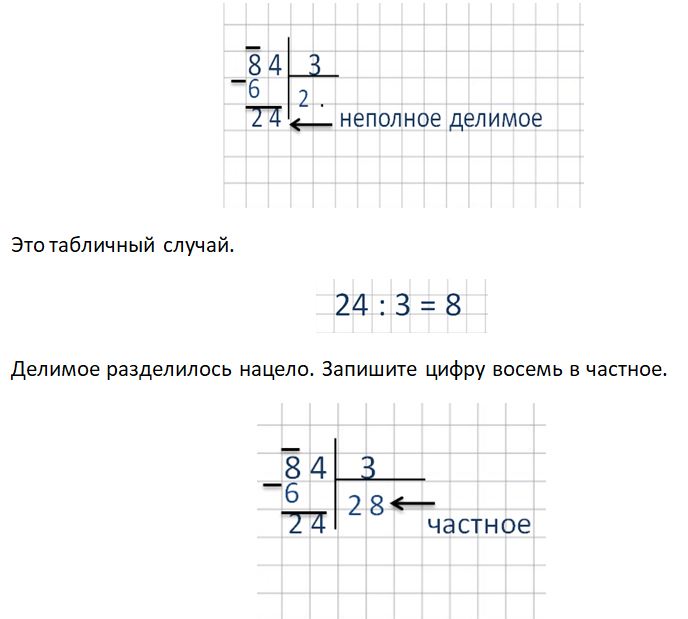

Мы занимали одну сотню из сотен уменьшаемого для десятков, значит у нас не 9 сотен, а 8 сотен (9 сотен – 1 сотня = 8 сотен ). Вычитаем сотни:

8 сотен – 7 сотен = 1 сотня . Результат пишем под сотнями.

В результате получаем:

932 – 768 = 164

Усложним задачу. Что делать если в разряде, из которого надо занять десяток, равен нулю? Например:

Начинаем с единиц. 2 меньше 8 , то есть надо занять из десятков. Но у уменьшаемого в десятках 0 , значит, для десятков надо занимать у сотен. В разряде сотен в уменьшаемом тоже 0 , занимаем из тысяч. Чтобы не забыть ставим над тысячами точку.

В сотнях уменьшаемого остается 9 , так как мы занимаем одну сотню для десятков: 10 – 1 = 9 пишем 9 над сотнями.

В десятках тоже остается 9 , так как мы заняли один десяток для единиц: 10 – 1 = 9 пишем 9 над десятками, а над единицами пишем 10 .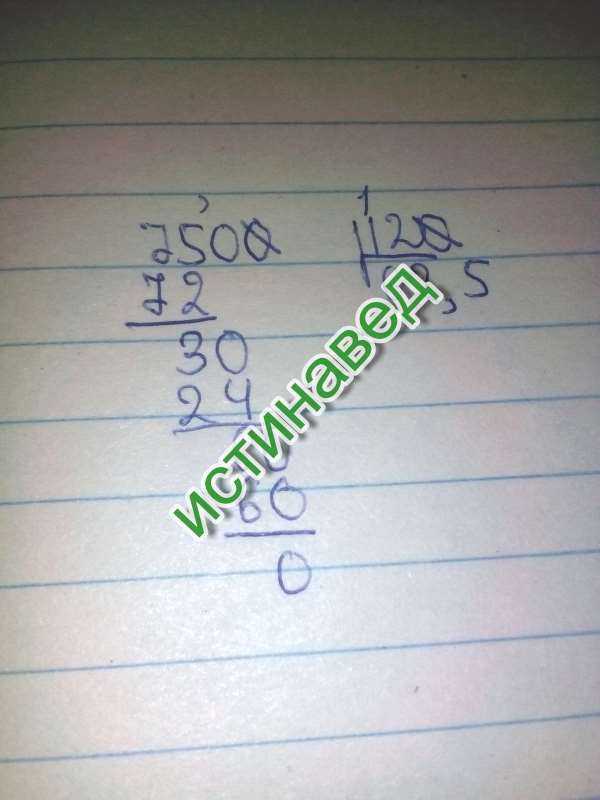

Считаем единицы:

12 – 8 = 4 пишем результат под единицами.

В десятках уменьшаемого осталось 9 , считаем:

9 – 6 = 3 пишем результат под десятками.

В сотнях уменьшаемого осталось 9 , у вычитаемого сотен нет, опускаем 9 в ответ под сотни.

В разряде тысяч уменьшаемого была 1 , мы её занимали (точка над тысячами), значит тысяч больше не осталось. В результате получаем:

1002 – 68 = 934

Итак, подведем итог.

Для того чтобы найти разность двух чисел (вычитание столбиком) :

1. помещаем вычитаемое под уменьшаемым, пишем единицы под единицами, десятки под десятками и так далее.
2. Вычитаем поразрядно.
3. Если надо занять десяток из следующего разряда, то над разрядом, из которого занимали, ставим точку. Над разрядом, для которого занимаем, ставим 10.
4. Если в разряде, из которого занимаем, стоит 0, то для него занимаем из следующего разряда уменьшаемого, над которым ставим точку. Над разрядом, для которого занимали, ставим 9, так как один десяток заняли.

Инструкция

Приступая к обучению, начните с самого простого — со сложения. Для этого возьмите чистый листок, ручку и попросите ребенка записать числа , которые нужно сложить следующим образом: единицы — под единицами, десятки — под десятками, сотни — под сотнями. Далее под самым нижним числом проведите черту.

Объясните, что складывать нужно, начиная с последних цифр, то есть с единиц . При сумме меньше десяти сразу записывайте под единицами. Если же получилось двузначное число, тогда под единицами запишите количество единиц, а количество десятков запомните.

Теперь сложите количество десятков и прибавьте число, которое вы запомнили в уме после сложения единиц. Расскажите, что сотни и тысячи слаживаются таким же образом.

Выполняя операции с вычитанием, поясните, что числа нужно записывать в точности как и при сложении. Если при вычитании количество единиц в уменьшаемом больше, чем в вычитаемом, необходимо «занять» десяток.

Покажите, что при умножении многозначного числа на однозначное сначала умножаются единицы, затем десятки и последующие разряды. Перемножая многозначные числа, действуйте последовательно. Сначала умножьте второй множитель на количество единиц первого множителя и запишите результат под чертой. Затем умножьте на количество десятков первого множителя и снова запишите результат под первым.

Научите ребенка проводить операции и с делением. Для этого запишите рядышком делимое число с делителем и разделите их уголком, а результат запишите под ним.

Ежедневно тренируйтесь, чтобы знания развивались. Но имейте в виду: занятия не должны заключатся в зазубривании, иначе это не даст никаких положительных результатов. Не переходите от одной операции счета столбик ом к другой. То есть пока ребенок не научится складывать в столбик , не приступайте к обучению вычитания.

Многие родители сталкиваются с нежеланием ребенка есть быстро. Малыш может долго ковыряться в тарелке, явно избегая неприятной процедуры. Для того, чтобы ребенок научился есть быстро, вам нужно превратить его завтраки, обеды и ужины из обязательных дел в интересные приключения.

Инструкция

Выясните вкусовые предпочтения ребенка и проконсультируйтесь с диетологом. Часто дети не желают быстро есть, потому что просто не любят то, чем их пичкают родители. Допустим, ребенок ненавидит кашу, но легко соглашается на макароны. Составьте список блюд, которые подойдут ребенку и по составу необходимых веществ, и по вкусовым предпочтениям. И тогда вы наполовину решите свою проблему.

Приучайте ребенка к столовому этикету. Порой детям нелегко справиться самостоятельно с вилкой или тем более с вилкой и ножом. Или научите чадо есть разными приборами, или дайте возможность есть тем, к чему оно привыкло, но тогда не ругайте его за его выбор. Это тоже может ускорить процесс поедания пищи.

Превратите еду в интересное приключение. Можно купить набор красивых тарелок и попросить съесть все, чтобы увидеть рисунок. Если у вас двое детей , можете попробовать устроить соревнования – еда на скорость. Главное, следите, чтобы они не переусердствовали и не подавились. Еще одним хорошим способом является еда перед интересной телепередачей или мультфильмом. Накройте стол за 15-20 минут до начала мультика и попросите его успеть доесть, пока не начнется развлечение.

Позволяйте ребенку есть в разном темпе. Все должно быть в меру. Не обязательно есть быстро всегда. Например, в выходные или вечером за ужином, когда не надо собираться в школу или сад, вполне можно посидеть за столом подольше. Пообщаться, не спеша поесть. Ребенок должен понимать, что медленное поедание пищи – не недостаток, не что-то запретное и привлекательное. Это просто один из вариантов поведения, который стоит использовать не всегда, а когда есть время. Чем расслабленнее он подойдет к вопросу, тем быстрее научится первым съедать все, что ему положили в тарелку.

Видео по теме

Изучение устного счета способствует у детей развитию умственных способностей. Учить ребенка считать в уме можно уже с 4-5 летнего возраста. Чтобы ребенок научился устному счету, занятия должны проходить в увлекательной форме, так как ему легче обучатся тому, что для него интересно.

Инструкция

Теперь можно начать осваивать с ребенком устное сложение и вычитание . Сначала можно показывать ему примеры на каких-нибудь предметах, например яблоках или конфетах, чтобы ребенок понял механизм счета. Нужно ему объяснить, что при сложении получается большая сумма, а при вычитании получается меньшая сумма.

На примерах объясните ребенку, что если поменять слагаемые местами, то сума не изменится. Это поможет ему научиться считать в уме . Также можно научить ребенка считать в уме при помощи специальных обучающих игр. Это могут быть специальные таблицы с числами и точками, специальные кубики или пластмассовые цифры со знаками.

Научите ребенка подсчитывать в пределах 10. Покажите ему результаты всех возможных вариантов вычитания и сложения в пределах этой цифры. Переходить к двузначным числам можно только тогда, когда ребенок нормально ориентируется и не путается в вычитании и сложении однозначных чисел.

Не нужно просто заучивать цифры и варианты, обучение должно проходить в игровой форме . В таком случае ребенок осознанно запомнит цифры и правила счета, а также сможет закрепить свои знания.

Нужно регулярно заниматься с ребенком, но при этом не следует его перегружать. Объясните ребенку порядок счета при сложении и при вычитании, что сначала нужно посмотреть, сколько было, затем, сколько прибавили, потом сколько стало.

При переходе к двухзначным числам, а также к умножению и делению, в более старшем возрасте, также объясните ребенку принцип умножения и деления на простых числах и покажите ему порядок счета.

Связанная статья

Источники:

• как научить ребёнка считать примеры

Для быстрого счета в уме не нужно никаких специальных знаний или способностей, главное — постоянно тренироваться и соблюдать правила счета. Благодаря таким тренировкам, можно без особых усилий научиться считать в голове операции с двузначными и трехзначными числами.

Инструкция

При сложении многозначных слагаемых прибавьте старший разряд меньшего числа, затем младший разряд. Например, при прибавлении двузначного числа, сначала прибавляются десятки, затем единицы. При сложении двухзначных чисел сначала сложите все десятки, затем все единицы, после этого прибавьте единицы к общему числу десятков.

Перед началом изучения деления убедитесь, что ребенок хорошо знает таблицу умножения и понимает механизм, по которому осуществляется данное математическое действие.

Покажите ребенку связь между умножением и делением. Дайте ему интуитивно почувствовать, что это обратное действие. Например, показав на реальном примере, что три умножить на два — это шесть, а шесть поделить на два — это три и так далее.

Постоянно возвращайтесь к этим операциям, например, играйте в деление вне дома. Давайте ребенку задачки, которые отображают действительность. Так, при покупке яблок возьмите, к примеру, шесть штук и спросите, сколько яблок достанется каждому члену вашей семьи. Гуляя на улице , предлагайте ему поделить конфеты между всеми детьми во дворе.

Если ребенок не сразу понимает, что от него требуется — будьте терпеливы и ищите способ объяснить лучше. Но не давите на него, так вы можете вызвать негативную психологическую реакцию, из-за которой ребенку будет тяжело воспринимать информацию. В этом случае процесс обучения займет куда больше времени.

Источники:

• как научить ребёнка делению

При подготовке к школе особенное внимание уделяется обучению счету. Это довольно сложный процесс требует от ребенка многих навыков – умение быстро ориентироваться, абстрагироваться, раскладывать числа на более простые. Учить этому лучше всего с самого раннего возраста.

Инструкция

Используйте для занятий наглядный материал. Маленьким детям трудно абстрагироваться, поэтому возьмите для своих объяснений конфеты, печенье, фрукты, игрушки, карандаши и т.п. Научить ребенка считать и складывать в пределах десяти несложно. У ребенка всегда при себе две ладошки с 10-ю пальчиками, которые помогут быстро посчитать . Чтобы быстро освоить счет на пальцах, ребенок должен потренироваться быстро показывать нужное количество пальчиков. Начните с простых чисел – 1 и 2, 5 и 10, 10 и 9. Помогите ребенку справиться с плохо слушающимися пальцами рук. Не торопитесь, пусть ребенок считает не спеша.

Допишите справа от делимого ноль и поставьте запятую, после цифры 3 в частном (то число, которое получается в ходе деления, и записывается под чертой, проведенной под делителем).

Снесите дописанный в делимом ноль (запишите его справа от 11) и проверьте, есть ли возможность разделить получившееся число на делитель. Ответ – да: 2 (обозначим его, как число G) умножить на 55 равно 110. Ответ — 23,2.Если бы снесенного в предыдущем шаге нуля не хватило бы для того, чтобы остаток с дописанным нулем оказался больше делителя, нужно было бы дописать еще один ноль в делимом и поставить 0 в частном после запятой (получилось бы 23,0. ..).

Деление в столбик десятичных дробей.Перенесите запятую на одинаковое количество знаков вправо в делимом и делителе так, чтобы и там, и там были целые числа. Дальше – алгоритм деления тот же.

Видео по теме

Обратите внимание

Записывайте все числа строго друг под другом согласно изложенным рекомендациям – это не даст возможности допустить ошибку в ходе выполнения расчетов.

Источники:

• Сложение, вычитание, умножение и деление десятичных дробей.

Таблица умножения нравится далеко не всем детям. Между тем выучить ее нужно, иначе через несколько лет у ребенка неизбежно возникнут трудности с вычислениями. Для того, чтобы младший школьник или дошкольник запомнил таблицу умножения , вовсе не обязательно заставлять его зубрить. Любой материал запоминается легко, когда человек его понимает, а сам процесс обучения интересен и увлекателен. Таблица умножения в этом смысле — вовсе не исключение.

Вам понадобится

• — компьютер с текстовым редактором;
• — карточки с цифрами и знаками арифметических действий;
• — большое количество мелких одинаковых предметов — спичек, фишек, кубиков, зверушек.

Инструкция

Объясните ребенку, что такое умножение . Давать математическое определение дошкольнику или младшему школьнику не обязательно, это сделает учитель . Ученик должен понять, что умножение служит для того, чтобы не приходилось много раз прибавлять одно и то же число. Используйте для объяснения однородные предметы. Например, положите перед ребенком два камешка и спросите, что получится, если к камешкам прибавить два. А если добавить еще два? Сколько раз мы брали по 2 предмета, чтобы получилось 6? Повторяйте это задание с разными предметами и с разным их количеством.

Объясните, как записываются примеры на умножение и что означает каждое число. Например, 4х5 значит, что 4 одинаковых предмета взяли 5 раз. Можно переставить сомножители и взять четырежды по пять предметов. Результат получится тот же.

Начертите квадрат. Это можно сделать на листе бумаги или на компьютере. Сделайте 11 столбиков по ширине и 11 строчек по высоте. Правая верхняя клетка остается пустой, в остальных ячейках верхней строчки напишите числа от 1 до 10. То же самое сделайте в крайнем левом столбце. Вместе с ребенком заполните остальные строчки и столбцы. Во втором слева столбике напишите результаты умножения единицы на каждое последующее число. В следующем столбце будут результаты умножения на 2, 3 и т. д. Таким образом, число, стоящее в каждой ячейке, представляет собой произведение чисел первой строчки и первого слева столбца.

Предложите ребенку несколько заданий. Попросите его найти, чему равен результат умножения 3 и 5, 7 и 6 и т. д. Не забывайте спрашивать и о том, как получается число 56 или 45. Ребенок будет с удовольствием искать нужные результаты, в особенности есть таблица сделана на компьютере. Когда малыш научится хорошо ориентироваться в квадрате, предложите ему сделать точно такой же, но для перемножения чисел от 11 до 20, а потом и от 21 до 30 и дальше. Если он понимает принцип умножения, задание это особых трудностей у него не вызовет. Предложите ему в первый момент считать на калькуляторе, что же нужно написать в каждой клеточке.

Таблица Пифагора не всегда может оказаться у ребенка под рукой. Объясните ему, какие существуют подсказки. На 9 можно умножать, например, на пальцах. Предложите своему ученику положить руки перед собой ладонями вниз. Пусть он задумает число, которое нужно умножить на 9. Например, это будет число 4. Отсчитайте его по пальцам слева направо. Получится указательный палец левой руки. Посмотрите, сколько пальцев осталось слева от него и сколько справа на обеих руках. Слева расположены средний, безымянный и мизинец, то есть три. Справа — 6. Соответственно, произведение будет равняться 36.

Выучите несколько считалок. «Пятью пять — двадцать пять» и «шестью шесть — тридцать шесть», равно как и другие рифмованные примеры, позволят ребенку в случае необходимости сориентироваться. Он точно знает, что если шесть раз взять по шесть яблок, то получится 36. Соответственно, 6х7 — это на 6 яблок больше. В дальнейшем можно показать ребенку способы быстрого умножения.

Полезный совет

Показывать принципы умножения можно в любом графическом редакторе. Например, найдите картинку с несколькими одинаковыми предметами. Откройте ее в редакторе, скопируйте и вставьте. Предложите ребенку посчитать фигурки на экране. Если добавлять предметы группами, принцип умножения ваш ученик поймет быстрее.

Младшим школьникам иногда бывает сложно освоить такое математическое действие, как умножение. Надо разобраться в причинах трудностей ребенка. Занятия, направленные на то, чтобы освоить саму суть этого действия и выучить таблицу умножения, обязательно принесут свои плоды.

Вам понадобится

• — счетные палочки или другие мелкие предметы;
• — детские книжки на тему «Умножение»;
• — таблица умножения.

Инструкция

Иной раз ребенок, успешно осваивающий программу начальной школы, вдруг спотыкается при изучении темы «Умножение». Не стоит паниковать по этому поводу и ругать ребенка. Надо просто с ним позаниматься. Но прежде чем приступить к дополнительным занятиям, необходимо понять, в чем дело.

Одной из причин осечек при решении примеров на умножение является то, что ребенок не понял самой сути этого действия. Поэтому постарайтесь объяснить ребенку, что такое умножение.

Возьмите счетные палочки, конфеты или какие-то другие мелкие предметы. Разложите их на столе попарно. Например, 3 пары подряд. Конечно, ребенок быстро сосчитает, сколько конфет лежит на столе.

Предложите записать это в виде примера на сложение. Получится: «2+2+2=6». Понаблюдайте вместе с ребенком, в чем особенность слагаемых. Они одинаковые! А если продолжить ряд? «2+2+2+2+2=10» Теперь задайте ребенку вопрос: «Как иначе можно записать это математическое выражение?» И увидите, как он сам найдет правильный ответ: «2х3=6», «2х5=10».

Проделайте еще несколько опытов с конфетами или счетными палочками. Разложите их по 3, по 4 и т.д. Записывайте сначала примеры на сложение, а потом преобразовывайте их в выражения на умножение. Совместно с ребенком нарисуйте группы различных предметов, чтобы на их основе записать примеры на сложение и на умножение.

Другой причиной трудностей с умножением может быть незнание таблицы умножения. Наберитесь терпения и помогите ребенку заучить таблицу наизусть.

Чтобы эти занятия не были скучными, приобретите книжки с веселыми стихами об умножении чисел. Читайте их вместе с ребенком. Положительные эмоции помогут лучше запомнить сложный школьный материал.

Обратите внимание

Для того чтобы ребенок освоил непонятный ему материал, не надо форсировать события. Возможно одно и то же придется повторить несколько раз.

Полезный совет

Занимаясь с ребенком, старайтесь не раздражаться. Важно, чтобы обстановка была спокойной и доброжелательной. Именно положительные эмоции способствуют лучшему усвоению материала. Кроме этого, будут полезны и поощрения даже за самые маленькие достижения. Наградите ребенка хотя бы конфетами, которые помогли ему понять суть умножения.

Инструкция

Люди разработали множество приемов, позволяющих вычислять в уме большие числа.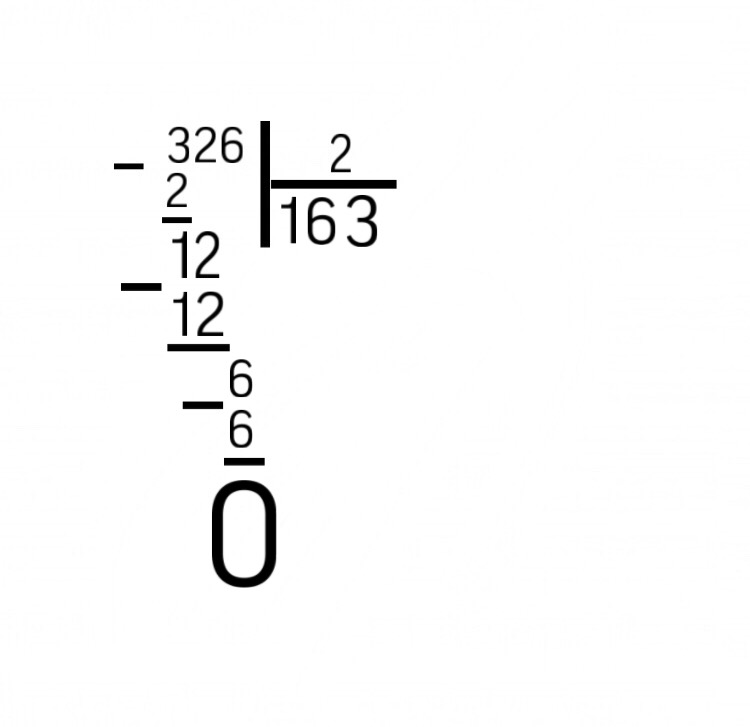 Для того чтобы умножать, делить, возводить в квадрат, вовсе не обязательно пользоваться калькулятором или тетрадным листком. Чтобы производить в уме сложные вычисления, достаточно запомнить ряд простых правил.

Чтобы умножить двузначное число на 11, нужно сложить его первую и вторую цифру и поставить ее в середину числа. Например, требуется умножить на 11 число 27. Сложите 2 и 7 и поместите получившуюся девятку посередине числа. Получится 297. Если сумма первой и второй цифр дает двузначное число, вставлять посередине нужно только вторую его цифру, а к первой цифре исходного числа — прибавлять единицу. Например, умножаем 11 на 49. Сумма 4 и 9 составляет 13. Помещаем между четверкой и девяткой тройку, получается 439. Затем добавляем к четверке единицу — получаем 539.

Чтобы возвести в квадрат число, заканчивающееся на 5, нужно умножить первую цифру на саму себя плюс единица, а затем добавить в конце 25. Например, квадрат 95 равен 9*(9+1)_25 = 9*10_25 = 9025.

Умножать большие числа на 5 тоже легко.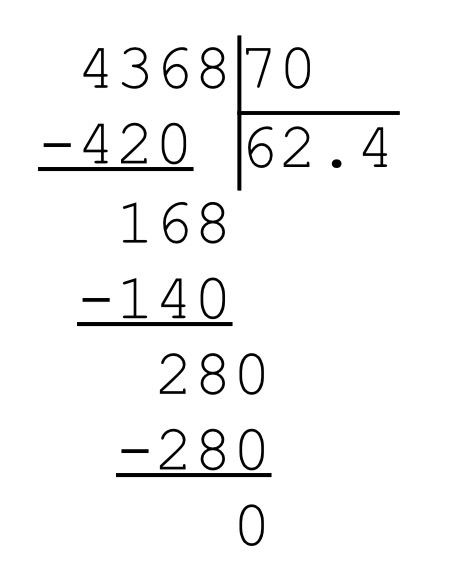 Сначала посмотрите, делится ли число полностью на 2. Если делится, то результатом его умножения на 5 будет результат его деления на 2, в конце которого записан ноль. Например, 620*5 = 310_0 = 3100. Если число не делится на 2 без остатка, отбросьте остаток и добавьте в конце вместо ноля пятерку. Например, 621*5 = 310_5 = 3105.

Чтобы умножить двузначное число на 4, достаточно дважды умножить его на 2. Например, 43*4 = 43*2*2 = 86*2 = 172.

Чтобы перемножить одно большое число на другое, посмотрите, не делится ли одно из них на два без остатка. Если делится, для умножения можно применить метод упрощения множителей, последовательно деля на 2 один множитель и умножая на 2 второй множитель. Например, 32*105 = 16*210 = 8*420 = 4*840 = 3360.

Складывать в уме большие числа лучше, сначала разделив одно из них на части. Например, 3570+5780 = (3000+5000) + (570+780) = 8000+(500+700)+70+80 = 9200+70+80 = 9350. Такой же прием можно использовать и при вычитании, последовательно разбивая числа на части, более удобные для вычисления.

Чтобы вычесть число из 1000, разбейте его на составляющие цифры и вычтите каждую из них из девятки. Последнюю цифру вычитайте не из девятки, а из десятки. Например, 1000-523 = (9-5)_(9-2)_(10-3) = 477.

Чтобы разделить большое число на 5, умножьте его в уме на два и разделите на десять. Например, 182/5 = (182*2)/10 = 364/10 = 36.4.

Обучение любого питомца желательно начинать в щенячьем возрасте. Именно в этот период закладываются основы взаимоотношения с собакой. Научить собаку командам можно самостоятельно, но при первом опыте лучше начинать работу под присмотром инструктора-кинолога.

Как научить собаку команде «Голос»

Иногда бывает нужно, чтобы собака начинала лаять по вашей команде. Подача голоса отрабатывается в момент игры, как и большинство команд. Играя с питомцем, например, в мячик, периодически произносите команду «Голос», дождитесь от него самопроизвольного лая и тут же бурно и радостно похвалите собаку, повторяя «Голос, голос!», дайте лакомство (небольшой кусочек сыра, засушенного ливера).

Повторяйте процесс до полного закрепления команды. При этом важно менять игрушку и ситуации возбуждения, чтобы собака не связала похвалу от вас с игрой, а видела прямую связь между вашей командой, лаем и наградой.

Как научить собаку команде «Сидеть»

Классическое обучение данной команды выглядит следующим образом. В руку берется лакомство, показывается питомцу, но не дается. Рука с лакомством заносится над головой собаки, подается команда «Сидеть», одновременно другая рука надавливает на крестец собаки, принуждая собаку сесть. Как только она сядет, лакомство тут же отдается, следует бурная похвала с повтором команады.

В настоящее время кинологи предпочитают использовать бесконтактный вариант обучения данной команде. То есть, надавливания на крестец не производится, одновременно с произнесением команды «Сидеть», рука с лакомством заносится над головой и подается чуть вперед таким образом, чтобы собака была вынуждена запрокидывать ее назад, не отрывая взгляда от лакомства. В такой позиции для собаки будет естественно сесть, что она и сделает. Тут же нужно отдать лакомство и похвалить питомца.

Как научить собаку команде «Лежать»

Команда «Лежать» разучивается с питомцем по похожей методике. Собаке показывается лакомство, зажатое в левой руке, затем эта рука опускается к полу, одновременно с этим подается команда «Лежать», а правая рука нажимает на холку собаки, принуждая ее тем самым лечь. Как только требуемая позиция будет достигнута, лакомство тут же отдается и следует похвала, перемежаемая с повторением разучиваемой команды «Лежать».

Чтобы найти разность методом «вычитание столбиком » (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:

• поместить вычитаемое под уменьшаемое, записать единицы под единицами, десятки под десятками и т.д.
• вычесть поразрядно.
• если необходимо занять десяток из большего разряда, то над разрядом, в котором заняли, поставить точку. Над разрядом, для которого заняли, поставить 10.
• если в разряде, в котором заняли, стоит 0, тогда занимаем из следующего разряда уменьшаемого и над ним ставим точку. Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.

Ниже рассмотренные примеры покажут вам как происходит вычитание двухзначных, трехзначных и любых многозначных чисел столбиком.

Вычитание чисел в столбик очень помогает при вычитании больших чисел (как и сложение в столбик). Лучше всего научиться на примере.

Необходимо записать числа одно под другим таким образом, чтобы крайняя правая цифра 1-го числа стала под крайней правой цифрой 2-го числа. Число, которое больше (уменьшаемое) записываем сверху. Слева между числами ставим знак действия, здесь это «-» (вычитание).

2 — 1 = 1 . То, что у нас получается пишем под чертой:

10 + 3 = 13.

Из 13 вычтем девять.

13 — 9 = 4.

Так как мы заняли десяток у четверки, то она уменьшилось на 1. Для того, чтобы не забыть об этом у нас и стоит точка.

4 — 1 = 3.

Результат:

Вычитание столбиком из чисел, содержащих нули.

Опять же, разберем на примере:

Записываем числа в столбик. Которое больше — сверху. Начинаем вычитание справа налево по одной цифре. 9 — 3 = 6.

Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.

Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой.

Над нашим нулем есть точка, значит, он стал девяткой. Вычитаем из нее 4. 9 — 4 = 5 . Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать.

Вычитание — одна из основных операций, которую можно производить с числами. Бывает так, что надо срочно произвести какие-то вычисления, а калькулятора под рукой не оказалось. В этом случае вас выручит умение вычитать столбиком .

Вам понадобится

• — бумага для записи;
• — ручка или карандаш.

Инструкция

Запишите два числа друг под другом — меньшее под большим. Числа состоят из разрядов единиц, десятков, сотен и далее по нарастающей. Запишите единицы одного числа под единицами другого, десятки — под десятками и так далее. Например, требуется вычесть из числа 2589 число 1346. Уменьшаемое в этом примере — 2589, вычитаемое — 1346.

Запишите шестерку второго числа под девяткой первого, четверку — под восьмеркой и так далее. Слева между числами запишите знак «-». Подведите под числами черту. Вычитайте с конца, т. е. справа налево. Из единиц первого числа вычтите единицы второго, из десятков первого — десятки второго и так далее.

Если количество одного или нескольких из разрядов в уменьшаемом числе больше, чем в вычитаемом, вычитайте числа друг из друга по обычным правилам. К примеру, из 316 надо вычесть 205.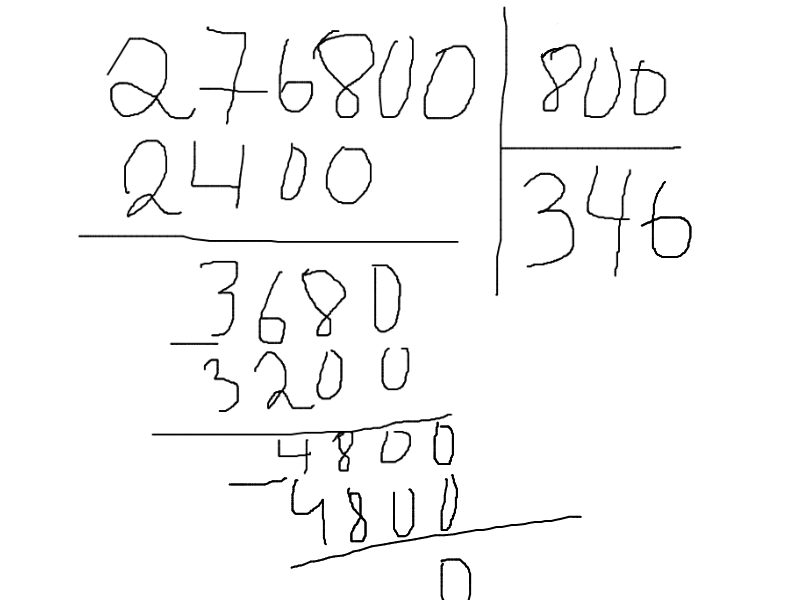 Из 6 вычтите 5. Запишите под чертой единицу. Из 1 вычтите 0, запишите 1. Вычтя из 3 двойку, также получится 1. Результат — 111.

Если количество одного или нескольких из разрядов в уменьшаемом числе меньше, чем в вычитаемом, «займите» десяток. К примеру, если из числа 56 надо вычесть 9, запишите 9 под 6. Поставьте точку над цифрой 5, чтобы занять десяток. Это значит, что вы должны уменьшить количество десятков (5 десятков) на единицу.

Произведите вычитание, как если бы вы вычитали 9 не из 6, а из 16. Вычтите, получив 7. Вычтите из пяти единицу. Вы получите 4. Четверка указывает на количество десятков. Значит в результате будет 4 десятка и 7 единиц — 47. Подобным образом вычитайте сотни, тысячи и другие разряды. Не забывайте ставить точки, чтобы не забыть, у какого числа вы «одалживали».

Вычитание в столбик десятичных дробей производите по этим же правилам, записав целую часть вычитаемого под целой частью уменьшаемого, соответственно дробную часть — под дробной. Например, из числа 843,217 необходимо вычесть 700,628.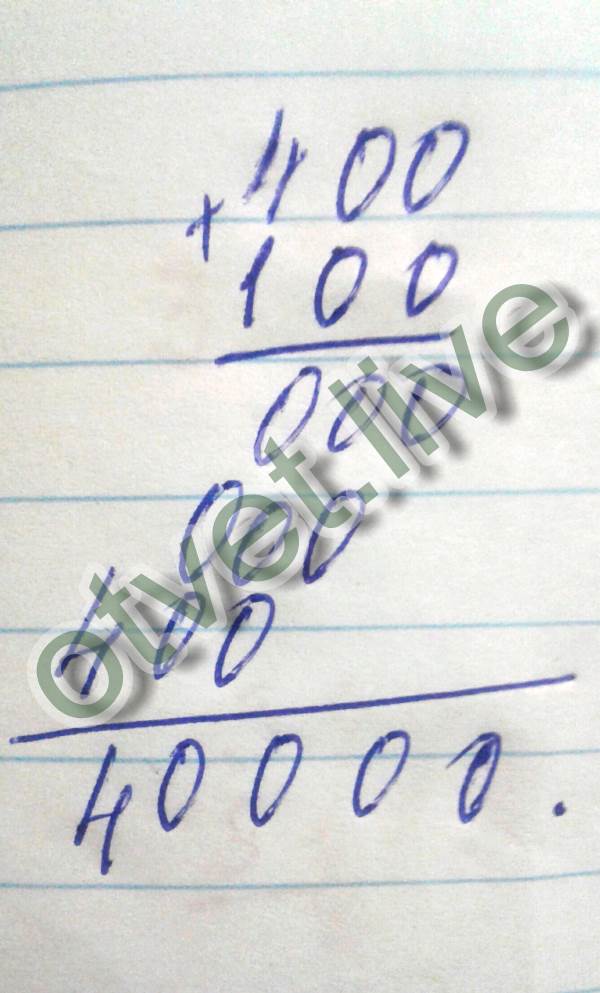 Вычтите из 7 восемь. Поставьте точку над единицей. Это означает, что вы заняли десяток, уменьшив единицу на один. Запишите под чертой 9 (ведь 17-8=9).

Вместо единицы, у которой вы занимали, получается 0. Поставьте точку над двойкой из первого числа, так как из 0 нельзя вычесть двойку. Вы снова заняли десяток, уменьшив двойку из первого числа на единицу. Получается, что из 10 вы вычитаете 2. Запишите 8.

Из 1 вычтите 6. Поставьте точку над тройкой, чтобы занять десяток. Тогда получится, что вы вычитаете из 11 шесть. Запишите под чертой пять. Поставьте запятую. Так как вы заняли у тройки единицу, то запишите под чертой два. Далее вычитайте по известным правилам. Результат — 142,589.

Обратите внимание

Чтобы не запутаться при вычитании столбиком десятичных дробей, обращайте внимание, чтобы запятые, отделяющие в обоих числах целую часть от дробной, находились друг под другом.

Полезный совет

Если справа от уменьшаемого/вычитаемого в десятичной дроби не хватает разрядов дробной части, допишите столько нулей справа, сколько разрядов в вычитаемом/уменьшаемом.

Почему нельзя делить на ноль?

«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.

Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.

Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.

Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.

Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.

Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.

Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.

Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается. )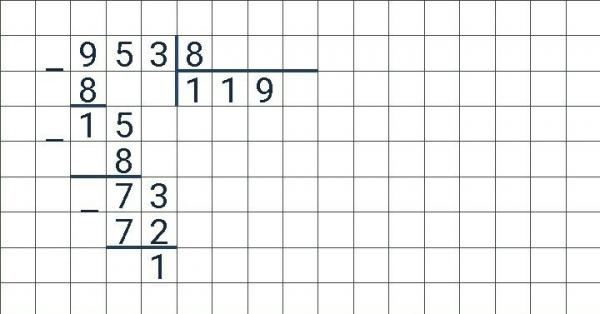

Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль.

Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.

Ответил: Александр Сергеев

арифметических операторов SQLite — w3resource

Последнее обновление 26 февраля 2020 г. 08:08:49 (UTC / GMT +8 часов)

Введение

Арифметические операторы могут выполнять арифметические операции с числовыми операндами. Существует четыре типа арифметических операторов: сложение (+), вычитание (-), умножение (*) и деление (/).

Синтаксис:

 SELECT <Выражение> [арифметический оператор] <выражение> ...
 ОТ [table_name]
 ГДЕ [выражение]; 

Параметр	Описание
Выражение	Выражение, состоящее из одной константы, переменной, скалярной функции или имени столбца, а также может быть частями запроса SQLite, которые сравнивают значения с другими значениями или выполняют арифметические вычисления.
арифметический оператор	Плюс (+), минус (-), умножение (*) и деление (/).
имя_таблицы	Имя таблицы.

Содержание

Пример:

Это простой пример использования арифметических операторов SQLite:

Пример вывода:

 ВЫБРАТЬ 10 ​​+ 12-5 * 4/2;
10 + 12-5 * 4/2
-----------
12 

Оператор SQLite plus (+)

Оператор SQLite plus (+) используется для сложения двух или более выражений или чисел.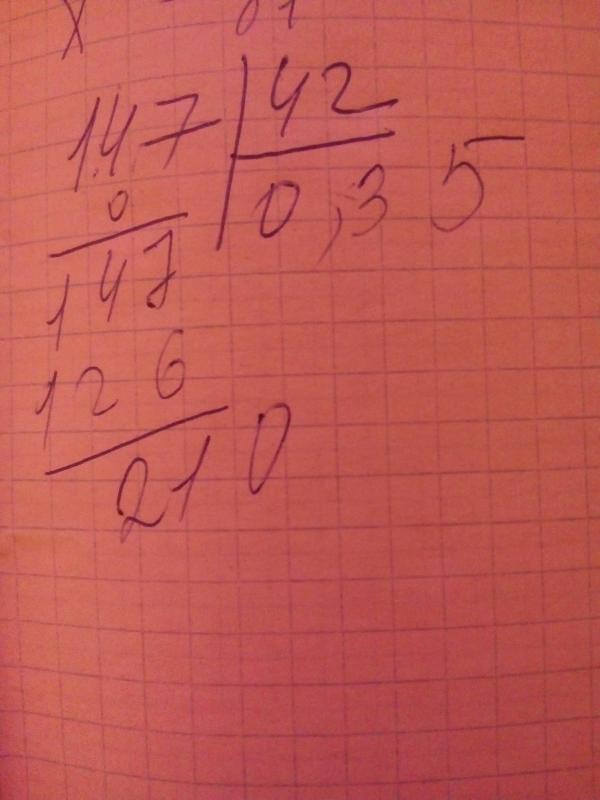

Пример:

Образец таблицы: заказчик

Чтобы получить данные ‘cust_name’, ‘Opening_amt’, ‘receive_amt’, (‘Opening_amt’ + ‘receive_amt’) из таблицы ‘customer’ со следующим условием —

1. сумма «open_amt» и «receive_amt» больше 16000,

можно использовать следующий оператор SQLite :

  ВЫБРАТЬ cust_name, Opening_amt, receive_amt,
(open_amt + receive_amt)
ОТ заказчика
ГДЕ (open_amt + receive_amt)> 16000;
 
 

Вот результат.

Пример вывода:

 CUST_NAME OPENING_AMT RECEIVE_AMT (open_amt + receive_amt)
---------- ----------- ----------- ------------------ ---------
Сасикант 7000 11000 18000
Раманатан 7000 11000 18000
Авинаш 7000 11000 18000
Шилтон 10000 7000 17000
Рангараппа 8000 11000 19000
Венкатпати 8000 11000 19000
Сундария 7000 11000 18000
 

SQLite оператор минус (-)

Оператор SQLite минус (-) используется для вычитания одного выражения или числа из другого выражения или числа.

Пример: >

Чтобы получить данные ‘cust_name’, ‘Opening_amount’, ‘payment_amount’ и ‘oustanding_amount’ из таблицы ‘customer’ со следующим условием —

1. «непогашенный_амт» — «платеж_амт» равно «получить_амт»,

можно использовать следующий оператор SQLite :

  ВЫБРАТЬ cust_name, Opening_amt, inventory_amt
ОТ заказчика
ГДЕ (невыплаченная_амт - платеж_амт) = получить_амт;
 
 

Вот результат.

Пример вывода:

 CUST_NAME OPENING_AMT OUTSTANDING_AMT
---------- ----------- ---------------
Стюарт 6000 11000
 

SQLite оператор умножения (*)

Оператор умножения (*) SQLite используется для умножения двух или более выражений или чисел.

Пример:

Примерная таблица: агенты

Получить данные ‘agent_code’, ‘agent_name’, ‘working_area’ и (‘Commission’ * 2) из ​​таблицы ‘agent’ со следующим условием —

1. двойная комиссия по умолчанию больше 0,25,

можно использовать следующий оператор SQLite:

  ВЫБЕРИТЕ имя_агента, имя_агента, рабочую_зону, (комиссия * 2)
ОТ агентов
ГДЕ (комиссия * 2)> 0,25;
 
 

Вот результат.

 AGENT_NAME AGENT_NAME WORKING_AREA (комиссия * 2)
---------- ---------- ------------ --------------
Рамасундар Рамасундар Бангалор 0,3
Алекс Алекс Лондон 0.26
Рави Кумар Рави Кумар Бангалор 0,3
Сантакумар Сантакумар Ченнаи 0,28
Андерсон Андерсон Брисбан 0,26
Суббарао Суббарао Бангалор 0,28
МакДен МакДен Лондон 0,3
Иван Иван Торенто 0,3
 

SQLite оператор деления (/)

Оператор деления (/) SQLite используется для деления одного выражения или чисел на другое.

Пример:

Чтобы получить данные ‘cust_name’, ‘Opening_amt’, ‘receive_amt’, ‘expected_amt’ и (‘receive_amt’ * 5/100) в виде заголовка столбца ‘Commission’ из таблицы клиентов со следующим условием —

1. ‘unique_amt’ меньше или равно 5000,

можно использовать следующий оператор SQLite:

  ВЫБРАТЬ cust_name, Opening_amt, receive_amt,
задолженность, (receive_amt * 5/100) комиссия
ОТ заказчика
ГДЕ выдающееся_амт
  

Вот результат.

Пример вывода:

 CUST_NAME OPENING_AMT RECEIVE_AMT OUTSTANDING_AMT комиссия
---------- ----------- ----------- --------------- --- -------
Холмс 6000 5000 4000 250
Стюарт 6000 8000 11000 400
Болт 5000 7000 3000350
Флеминг 7000 7000 5000 350
Сасикант 7000 11000 11000 550
Карл 4000 6000 3000 300
Шилтон 10000 7000 11000 350
Чарльз 6000 4000 5000 200
Стивен 5000 7000 3000 350
Каролина 7000 7000 5000 350
Рамеш 8000 7000 12000 350
Рангараппа 8000 11000 12000 550
Венкатпати 8000 11000 12000 550
Сундария 7000 11000 11000 550
 

SQLite, оператор по модулю (%)

Оператор модуля SQLite возвращает остаток (целое число) от деления.

Пример:

  ВЫБРАТЬ 153% 4; 
 

Вот результат.

Пример вывода:

 153% 4
----------
1
 

Предыдущее: Операторы SQLite Введение
Далее: Операторы сравнения

Как сделать длинное деление за 6 шагов [с иллюстрациями]

Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость: Как выполнить деление в столбик. Исследование 2012 года, опубликованное в журнале Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают на уроках математики более высокого уровня — даже с учетом различных социально-экономических факторов. Никакого давления, правда? Если мысль об обучении длинному делению вызывает у вас холодный пот и липкие ладони, не волнуйтесь — мы сделали всю работу за вас. В этом посте вы найдете:

Как выполнить деление в столбик за шесть шагов

1.

Обзор Первый шаг, который вам следует сделать, — это шаг назад. Для ученика 4-го класса деление в столбик — это сложное сочетание различных операций. Чтобы успешно научиться делать длинное деление, им необходимо пересмотреть эти фундаментальные концепции. Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов при определении способности ученика будущий математический успех. Согласно тому же исследованию, деление в столбик — это «синтез всех арифметических знаний.«Убедитесь, что ваши ученики понимают, что умножение — это результат повторного сложения, а деление — это наоборот — повторное вычитание. Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство чисел. Планируйте мероприятия, в которых учащихся просят создать «группы фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.

instagram.com/p/BppfoeEhX84/?utm_source=ig_embed&utm_medium=loading» data-instgrm-version=»12″/> Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся обучением и развить уверенность в математике, прежде чем продолжать.

2. Начните с простого

Давайте начнем с урока лексики. В уравнении деления в длинную строку есть много разных частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать. Дивиденд — это число в правой части уравнения под линией. Он представляет собой разделяемую сумму. Делитель — это число слева — оно делает деление. Частное — это число сверху. Он представляет ответ или количество единиц в каждом значении разряда после завершения уравнения.Остаток — это номер вверху справа. Он представляет собой оставшиеся единицы, которые нельзя равномерно разделить на частное. Во-первых, введите уравнение, в котором нет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что выучили: спросите учащихся, сколько раз 2 вписывается в 4. Это может быть для них непростой концепцией. , поэтому используйте идею совместного использования: если вы хотите поделиться 4 объектами между двумя людьми, сколько объектов получит каждый? Когда они дадут правильный ответ, поставьте 2 над 4.Затем повторите шаг со второй цифрой делимого. Используйте эти простые уравнения, чтобы усилить числовую ценность. Объясните ученикам, что, когда они спрашивают, сколько раз 2 может перейти в 4, они на самом деле спрашивают, сколько раз 2 входит в 40.

3. Оставайтесь в единицах

Попросите ваших учеников практиковать вышеуказанный шаг, пока они не почувствуют себя комфортно с базовым форматом. Тогда пора двигаться дальше. Вместо того, чтобы сразу переходить к уравнению с остатками, начните с другого наглядного урока .Разделите учащихся на группы по три, четыре или шесть человек и раздайте каждой группе по 50 ватных шариков (или мармелад, или помпоны, или зефир — любой маленький предмет, доступный в вашем классе). Попросите учеников разделить предметы так, чтобы каждый член группы группа имеет равное количество, затем наблюдайте и ждите. В конце концов они поймут, что не могут разделить его поровну, и всегда останутся какие-то объекты. Вот где вы приходите, чтобы сэкономить время и объяснить, как выполнить деление в столбик с остатками .Сначала покажите учащимся задачу, в которой остаток находится в единицах: теперь начните со столбца десятков и проработайте задачу: 5 переходит в 5 ровно один раз, так что там ничего не остается. Но сколько раз 5 превратится в 7, и что вы будете делать с остатками? Покажите студентам новые шаги:

• Разделите деленное в столбце единиц на делитель
• Умножьте делитель на частное справа поместить столбец
• Вычтите произведение из столбца единиц

Число, с которым они остались, является остатком.Обязательно смоделируйте несколько задач в классе, чтобы учащиеся могли начать понимать шаги и как правильно писать свои ответы. Это хорошее время на уроке, чтобы научить студентов проверять свои ответы. Попросите их умножить делитель на частное и сложить остаток — ответ должен быть таким же, как и дивиденд, с которого они начали.

4. Остаться в десятках

Теперь пришло время ученикам заняться задачами, в которых делитель не вписывается точно в столбец десятков или единиц.Шаги более или менее одинаковы, за исключением одного нового сложения:

• • Разделите делимое столбца десятков на делитель
  • Умножьте делитель на частное в столбце разряда десятков
  • Вычтите произведение из делителя
  • Уменьшите делимое в столбце единиц и повторите .

Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому не торопитесь и моделируйте задачи на доске.Обсудите, почему эти шаги работают, и помогите им понять, насколько важна роль места в этом процессе.

5. Вводите числа побольше, постепенно

Вот и все. Или это так? Пусть студенты освоятся с формулой и поработают над небольшими проблемами. По мере того, как они разовьются в уверенности и начнут понимать, как выполнять деление в столбик, начните ставить перед ними задачи с трехзначным делителем, а затем задачи с двузначным делителем. Напомните учащимся, что шаги остаются неизменными, независимо от того, насколько велика задача. , и предложите им использовать макулатуру, чтобы «угадывать и проверять» умножение в процессе.Это хорошее место, чтобы убедиться, что они не испытывают затруднений и полностью понимают связь деления с числовой величиной и умножением. Чтобы освежить память, посмотрите это видео из Khan Academy:

6. Как это сделать. деление в столбик с десятичными знаками

Если вы охватили весь свой контент за первые пять шагов, поздравляю! Попросите учащихся продолжать практиковаться в продольном делении больших и малых чисел, а также укреплять взаимосвязь между делением и другими математическими концепциями, которые они изучают.Но процесс еще не завершен — учащимся нужно понимать, как выполнять деление в столбик с десятичными знаками. Для начала вернемся к одной из фундаментальных концепций деления: числовой ценности. Однако на этот раз вы будете двигаться назад, а не вперед.

|

Попросите учащихся решить задачу, как они обычно это делают. Когда они дойдут до шага, на котором они обычно останавливаются на остатке, попросите их поставить десятичную точку в конце частного и деленного и записать несколько нулей после делимого.Попросите их продолжить обычные шаги деления на одно или два разряда, сбивая нули. Соедините десятичную дробь с дробями. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Это должно помочь им понять взаимосвязь между дробями и числовой ценностью и может быть хорошей возможностью более подробно изучить основы дробей.

Как выполнять деление в столбик (без деления в столбик)

Поздравляем! Ваш блок подходит к концу, и вы успешно научили своих учеников делать столбики.Но знаете ли вы, что есть несколько способов разделить большие числа? Обучение студентов другим способам проверки своей работы является важной частью общих математических стандартов и может улучшить понимание учащимися того, что на самом деле означает длинное деление в данном контексте.

Квадратные модели

Квадратные модели — отличный способ для учащихся, изучающих визуальное представление, понять и концептуализировать деление, а также улучшить чувство числа. В этом методе используется сетка, чтобы представить процесс разделения как проблему площади: например, 148 ÷ 4 будет разделено на сетку высотой 4 единицы, площадью 148 квадратных единиц и шириной неизвестного числа единиц.Студенты разбивают сетку на более управляемые области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100 ÷ 4 равно 25, 40 ÷ 4 равно 10, а 8 ÷ 4 равно 2. Эти числа находятся в верхней части модели площади и могут быть добавлены для получения ответа.

Частные частные

Подобно модели площадей, частные частные побуждают учащихся разбивать вопросы с разделением на более «дружелюбные» части. Это помогает учащимся понять, что деление — это определение того, сколько раз одно число может переходить в другое.Задайте задачу (в данном случае 450 ÷ 23) как уравнение деления в столбик. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать их в качестве справочного материала. Спросите, сколько раз 23 входит в 400, но не ищите точное ближайшее число: сделайте его простым для работы, например 230 (десять раз). Вычтите 230 из 450 и положите 10 справа, чтобы отслеживать это. Возьмите разницу и вычтите ее из дивиденда. Ответ должен быть 220. Спросите, сколько раз 23 переходит в 220. 5 x 23 равно 115, поэтому вычтите это из 220 и запишите 5.Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное. Частные частные обладают гибкостью, которой нет при длинном делении. Деление в столбик нужно делать точно, но с частными частными можно просто многократно вычесть делитель из дивиденда и все равно прийти к правильному ответу. Используйте этот метод, чтобы усилить числовую ценность и концепцию деления как повторного вычитания.

Упражнения с длинным делением

Лучший способ для студентов научиться делать длинное деление — это практика, практика, практика. Вот список из восьми заданий, которые увлекут ваших учеников делением в столбик и помогут им развить твердые математические навыки.

1. Prodigy

Prodigy — это увлекательный, увлекательный ресурс с нулевой стоимостью для занятий в классе или дома. Учащиеся исследуют мир, наполненный приключениями, где успех зависит от правильных ответов на математические вопросы.Через панель управления учителя вы можете доставлять контент, согласованный с уроком, в зависимости от оценки, навыков или учащегося. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании . Поощряйте своих учеников практиковать все математические навыки, которые они изучали в классе, включая деление в столбик. Вот как вы можете использовать Prodigy для: Студентам нравится увлекательная игровая платформа, где они могут собирать домашних животных, выполнять задания и сражаться с друзьями.И пока они веселятся, вы помогаете им развить математическую уверенность и навыки деления в столбик. Это победа для всех!

2. Полное деление в натуральную величину

Ученики 5-го класса расширили свои навыки выполнения #long_division с помощью различных занятий @DawhaHighSchool @FawziehHn #kinesthetic #online_division_calculator ➗✔ pic.twitter.com/vuNnKGu9Uc

— najah shams (@najahshams) 19 декабря 2018 г.

Оживите математику с помощью практической головоломки с делением столбиком. Вырежьте из разноцветной бумаги квадраты со всеми числами, которые нужны учащимся, чтобы решить задачу о длинном делении от начала до конца.Используйте клейкую ленту, чтобы провести линии разделения на полу, и раздайте студентам пронумерованные карточки. Начиная с данного уравнения, попросите учащихся разложить все карточки в правильном порядке, чтобы решить уравнение. Это упражнение побуждает учащихся замедлиться и обдумать свои шаги, и это особенно полезно для класса, который все еще пытается освоить шаги умножения.

3. Бинго с длинным делением

|

Бинго — классика не зря. Каждый номер на листе ученика должен соответствовать вопросу, который стоит у вас в передней части класса.Напишите задачу на доске, а затем дайте учащимся бумагу для заметок и возможность решить ее и посмотреть, есть ли она у них на карточке. Как всегда, побеждает первый ученик, который заполнит весь ряд! Бросьте вызов своим ученикам, но убедитесь, что вы уделяете достаточно времени этому заданию — у некоторых учеников могут возникнуть проблемы с быстрым решением проблем, и они могут расстроиться или совершить ошибки, если они не в состоянии угнаться.

4. Книги по математике

Повысьте уровень грамотности и обучения математике с помощью забавных книг, охватывающих сложные математические концепции.Используйте их, чтобы объяснить учащимся разделение и остатки в увлекательной и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут изучать, как выполнять деление в столбик. Некоторые учебники по математике, посвященные делению, включают: [галерея size = «medium» ids = «3833,3837,3834»]

• Остаток одного Элинор Дж. Пинчес
• Бин Тринадцать Мэтью МакЭллиготт
• Дверной звонок Пэт Хатчинс

5. Проявите творческий подход

У длинного деления много ступеней, и нужно делать в правильном порядке, чтобы получить правильный ответ.Учащиеся могут запутаться или расстроиться, если не запомнят шаги, что отрицательно скажется на их уверенности в математике и успеваемости. Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в столбик — разделите , умножьте , вычтите и уменьшите — чтобы проявить творческий потенциал в вашем классе. Попросите их создать плакат, песню, мнемоническое устройство или даже небольшую сценку, которую они могут показать своим одноклассникам. Если они стремятся найти способ запомнить шаги, они с большей вероятностью научатся быстро.

6. Реле с удлиненным разделителем

|

Превратите практику с делением в столбик в увлекательную классную игру с помощью эстафеты с делением в столбик. Разделите свой класс на команды и составьте карточки с задачами в столбик. Выстройте учеников в группы. Каждая группа получает карточку для начала, и первые ученики выполняют первый набор шагов для решения своей проблемы. Когда они это делают, второй ученик ищет ошибки и продолжает решение.Если они решат проблему, они могут позвать вас, чтобы вы пришли проверить их работу и обменять правильный ответ на карточку с новой проблемой. Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!

7. Сундук с сокровищами

Это задание — забавный способ для вашего класса отпраздновать завершение своего подразделения по разделению. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решать в группах, чтобы «открыть» коробку.В качестве дополнительной задачи сделайте это кодом: каждое частное должно совпадать с буквой алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку.

8. Генератор рабочих листов

Рабочие листы — это проверенный временем элемент математического класса. К счастью для вас, существует множество веб-сайтов, которые сделают эту работу за вас и создадут настраиваемый рабочий лист, который даст вашим ученикам возможность попрактиковаться в делении в столбик. Вот некоторые из наших фаворитов:

Заключительные мысли об обучении студентов делению в столбик

Самое важное, что нужно помнить при обучении студентов делению в столбик, — не торопиться с материалом.Это большая концепция, которая отличается от всего, что они изучали раньше, и некоторые (если не все) ваши ученики могут сначала столкнуться с трудностями. Если вам нужно, вернитесь к более простым уравнениям и некоторым из более ранних шагов, которые мы обрисовали в общих чертах. для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно. Продолжайте воодушевлять и бросать вызов своим ученикам, и они будут готовы разделять и побеждать в кратчайшие сроки!

---

Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и ученикам.Он соответствует учебным планам англоязычного мира, его любят более миллиона учителей и 50 миллионов студентов .

Сравнение типов данных VARCHAR (max) и VARCHAR (n) в SQL Server

Я видел, что разработчики SQL используют данные varchar (max) при разработке таблиц или временных таблиц. Возможно, мы не уверены в длине данных или хотим устранить ошибку строки или двоичного усечения.

Рекомендуется ли использовать varchar (max) для каждого случая использования?

Мы можем определить конкретный диапазон для типа данных varchar (n), и это рекомендуемый способ сделать это. Чтобы получить представление об этом типе данных, прочтите статью SQL varchar (n).

В этой статье мы обсудим использование varchar max и его последствия, а также сравнение с типом данных varchar (n).

Обзор типа данных SQL Server VARCHAR (max)

В SQL Server 2005 появился этот тип данных varchar (max). Он заменяет большой объект blob с типами данных Text, NText и Image. Все эти типы данных могут хранить данные размером до 2 ГБ. Как вы, возможно, знаете, основная единица хранения в SQL Server — это страница.Размер страницы составляет 8 КБ (8192 байта) в SQL Server, и он является фиксированным. На странице SQL Server использует 96 байтов для заголовка страницы. Мы можем хранить 8096 байтов (8192-96 байтов) для данных в SQL Server. Помимо этого, страница также содержит служебные данные строки и смещение строки и оставляет 8000 байт для хранения данных. Благодаря этому мы можем хранить до 8000 байт данных, используя тип данных varchar (8000).

Вы можете подумать об использовании типа данных varchar (max) для хранения данных размером 2 ГБ, чтобы решить проблемы с усечением строки.

Давайте создадим несколько примеров таблиц разного размера в типе данных varchar. Мы также создадим таблицу с типом данных varchar (max).

1 2 3 4 5 6 7 8 9 10 11 12 13 14 14 18 19

СОЗДАТЬ ТАБЛИЦУ dbo.Employee_varchar_2000 (id INT IDENTITY PRIMARY KEY, Col1 VARCHAR (2000) ); СОЗДАТЬ ТАБЛИЦУ dbo.Employee_Varchar_4500 (id INT IDENTITY PRIMARY KEY, Col1 VARCHAR (4500) ); СОЗДАТЬ ТАБЛИЦУ dbo.Employee_Varchar_8000 (id INT IDENTITY PRIMARY KEY, Col1 VARCHAR (8000) ); СОЗДАТЬ ТАБЛИЦУ dbo.Employee_Varchar_Max (id INT IDENTITY PRIMARY KEY, Col1 VARCHAR (MAX) );

Давайте вставим записи в эти примеры таблиц, используя следующие запросы.

INSERT INTO Employee_varchar_2000 (Col1) SELECT REPLICATE (‘A’, 2000); INSERT INTO Employee_varchar_4500 (Col1) SELECT REPLICATE (‘A’, 4500); INSERT INTO Employee_varchar_8000 (Col1) SELECT REPLICATE (‘A’, 8000); INSERT INTO Employee_varchar_max (Col1) SELECT REPLICATE (‘A’, 8000);

Мы можем проверить длину данных в этих таблицах, используя следующие запросы.

Используйте SQLShackDemo go SELECT LEN (col1) AS columnlength FROM Employee_varchar_2000; SELECT LEN (col1) AS columnlength FROM Employee_varchar_4500; ВЫБРАТЬ ДЛИНА (col1) AS длина столбца FROM Employee_varchar_8000; SELECT LEN (col1) AS columnlength FROM Employee_varchar_max;

На следующем снимке экрана мы можем убедиться, что длина данных аналогична длине существующего столбца таблицы.

Теперь мы можем проверить статистику объекта, такую ​​как количество страниц, количество строк и единицы распределения, с помощью DMV sys.dm_db_index_physical_stats.

ВЫБРАТЬ ИМЯ ОБЪЕКТА ([object_id]) AS TableName, alloc_unit_type_desc, record_count, page_count, round (avg_page_space_used_in_percent, 0) as avg_page_space_in_in_percent, 0) as avg_page_space_use_in_in_percent, 0) as avg_page_space_use_in_in_percent, 0) as avg_record_space_space_in_in_percent, 0) as avg_page_space_space_in_in_percent, 0) as avg_Record_space_space_Size 9_in000dm_db_index_physical_stats (DB_ID (), NULL, NULL, NULL, ‘DETAILED’) WHERE OBJECT_NAME ([object_id]) LIKE ‘Employee_varchar%’;

Мы видим, что все таблицы содержат единицу распределения IN_ROW_Data. SQL Server хранит все данные в блоке распределения IN_ROW_Data.

Мы не можем вставить больше 8000 байтов данных в тип данных varchar (n). Если мы попытаемся это сделать, мы получим следующее сообщение об ошибке.

INSERT INTO Employee_varchar_8000 (Col1) SELECT REPLICATE (‘A’, 8001); Go INSERT INTO Employee_varchar_8000 (Col1) SELECT REPLICATE (‘A’, 10000);

Он успешно вставляет данные, но усекает значения до 8000 символов.Аналогичное усечение происходит для таблицы Employee_varchar_max, содержащей тип данных varchar (max).

Нам нужно привести значение к varchar (max) и вставить длину более 8000 символов. Мы получаем сообщение об ошибке при попытке вставить записи в таблицу Employee_varchar_8000.

INSERT INTO Employee_varchar_8000 (Col1) SELECT REPLICATE (CONVERT (VARCHAR (max), ‘x’), 8001);

Он успешно вставляет записи в таблицу Employee_varchar_max.

Повторите запрос, чтобы проверить единицу распределения. Мы получаем блок распределения LOB_Data для хранения данных более 8000 байт в таблице Employee_Varchar_Max. У нас есть указатель на эти данные в блоке распределения IN_Row_DATA.

Отсюда можно сделать следующий вывод.

1. SQL Server использует страницу IN_ROW_DATA для типа данных varchar (max), если данные меньше или равны 8000 байтам.
2. Если размер данных превышает 8000 байт, SQL Server использует страницу LOB_DATA для типа данных varchar (max).

Сравнение производительности между типами данных varchar (max) и varchar (n)

Давайте вставим по 10 000 записей в каждую из таблиц, которые мы создали ранее. Мы хотим проверить время вставки данных. Вы можете использовать инструмент ApexSQL Generate для вставки данных без написания для них кода t-SQL.

На следующем снимке экрана вы можете отметить следующее.

• Employee_varchar_2000 время вставки 0,08 секунды
• Employee_varchar_4500 время вставки 0,19 секунды
• Employee_varchar_8000 время вставки 0,31 секунды
• Employee_varchar_Max время вставки 2,72 секунды

Индексы для столбцов VARCHAR (N) и VARCHAR (MAX)

Как администратор базы данных, вы можете не проектировать таблицу.Однако необходимо создать индекс для таблиц, чтобы повысить производительность запроса.

Мы можем создать индекс для ключевого столбца таблицы с типом данных varchar (n).

СОЗДАТЬ ИНДЕКС IX_Employee_varchar_2000_1 ON dbo.Employee_varchar_2000 (col1) GO

Если мы попытаемся сделать то же самое для типа данных varchar (max), появится следующее сообщение об ошибке.

СОЗДАТЬ ИНДЕКС IX_Employee_varchar_max ON dbo. Employee_varchar_max (col1) GO

Сообщение 1919, уровень 16, состояние 1, строка 23 Столбец «col1» в таблице «dbo.Employee_varchar_max» имеет тип, недопустимый для использования в качестве ключевого столбца в индексе.

Мы можем использовать столбец varchar (max) в качестве включенного столбца в индекс, но вы не можете выполнить поиск индекса в этом столбце.Также потребуется дополнительное хранилище. Следовательно, вам следует избегать создания индекса с типом данных varchar (max).

Сравнение планов выполнения

Давайте сравним план выполнения двух операторов select.

В первом запросе мы хотим получить данные из таблицы Employee_Varchar_2000 и получить фактический план выполнения.

В фактическом плане выполнения мы видим оператор поиска по некластеризованному индексу.

Если мы запустим тот же запрос с типом данных varchar (max), он будет использовать оператор сканирования кластерного индекса и может быть ресурсоемким оператором в зависимости от количества строк в таблице.

выберите col1 из Employee_varchar_max, где col1 как «xxxx%»

Давайте сравним план выполнения, используя опцию Сравнить Showplan в SSMS. Чтобы сравнить два плана выполнения, сохраните один план выполнения, щелкнув его правой кнопкой мыши, а затем «Сохранить план выполнения как» и укажите место для сохранения плана.

В другом плане выполнения запроса щелкните правой кнопкой мыши и выберите Сравнить Showplan. Он открывает окно, в котором вы можете указать путь к ранее сохраненному плану выполнения.

На следующем снимке экрана вы можете увидеть сравнение обоих планов выполнения.

• Расчетная стоимость ЦП выше в типе данных varchar (max) для аналогичной активности, как у varchar (2000).
• Для varchar (max) он использует оператор сканирования кластерного индекса и просматривает все записи. Вы можете видеть, что предполагаемое количество строк составляет 10000, в то время как в типе данных varchar (2000) он использует оператор поиска по индексу, а предполагаемое количество строк — 1. 96078
• Предполагаемый размер строки 4035 B больше, чем в varchar (max), по сравнению с 1011 B для типа данных varchar (2000)

Разница между типами данных varchar (max) и varchar (n)

varchar (макс.)	varchar (сущ.)
Мы можем хранить до 2 ГБ данных в этом типе данных.	В этом типе данных мы можем хранить до 8000 байт данных.
Он использует блок распределения IN_ROW_Data до 8000 байт данных.Если размер данных превышает 8000 байт, он использует страницу LOB_Data и сохраняет свой указатель на странице IN_ROW_Data.	Хранит данные на стандартной странице данных
Мы не можем создать индекс для ключевого столбца типа данных varchar (max)	Мы можем создать индекс для этого типа данных
Мы не можем сжать LOB-данные	Мы можем сжать данные для этого типа данных
Получение и обновление данных LOB происходит относительно медленно	Мы не сталкиваемся с такой проблемой в типе данных varchar (n).

Заключение

В этой статье мы продемонстрировали тип данных varchar (max), а также изучили несколько различий между типами данных varchar (max) и varchar (n).Вы должны использовать соответствующий тип данных. Мы должны учитывать дизайн базы данных, производительность, сжатие и индексы. Вам следует просмотреть типы данных в своей базе данных и при необходимости изменить их с помощью надлежащего тестирования.

Будучи сертифицированным MCSA и сертифицированным инструктором Microsoft в Гургаоне, Индия, с 13-летним опытом работы, Раджендра работает в различных крупных компаниях, специализируясь на оптимизации производительности, мониторинге, высокой доступности и стратегиях и внедрении аварийного восстановления.Он является автором сотен авторитетных статей о SQL Server, Azure, MySQL, Linux, Power BI, настройке производительности, AWS / Amazon RDS, Git и связанных технологиях, которые на сегодняшний день просмотрели более 10 миллионов читателей.

Он является создателем одного из крупнейших бесплатных онлайн-сборников статей по одной теме с его серией из 50 статей о группах доступности SQL Server Always On. За свой вклад в сообщество SQL Server он постоянно удостаивался различных наград, включая престижную награду «Лучший автор года» в 2020 и 2021 годах на SQLShack.

Радж всегда заинтересован в новых задачах, поэтому, если вам нужна консультация по любому вопросу, затронутому в его трудах, с ним можно связаться по адресу [email protected]

Просмотреть все сообщения Раджендры Гупты

Последние сообщения Раджендры Гупты ( увидеть все)

Увеличение и уменьшение в процентах: расчет и примеры — Видео и стенограмма урока

После просмотра этого видео-урока вы сможете рассчитать процентное увеличение и уменьшение изменений, происходящих с течением времени.Вы также узнаете, что вам нужно для расчетов.

Изменения в процентах

Изменения происходят каждый день. Например, однажды на улице может быть тепло и приятно, и вы в рубашке и шортах идете поиграть на улице. Но тогда следующий день может быть холодным, и вы в конечном итоге будете носить бабушкин свитер с брюками. В бизнесе необходимо проанализировать важные изменения, такие как сокращение продаж за один год по сравнению с предыдущим годом. Чтобы помочь предприятиям проанализировать эти изменения, мы вычисляем увеличение или уменьшение на процентов, — величину увеличения или уменьшения, выраженную в процентах.

Как рассчитать

Как рассчитать это процентное увеличение или уменьшение? Мы начинаем с вычисления первой суммы, а затем сравниваем ее со второй суммой. Например, если мы анализируем изменение продаж от одного года к другому, наша первая сумма будет продажей за один год, а наша вторая сумма будет продажей следующего года. Затем мы определяем, происходит ли увеличение или уменьшение. Например, у нас есть увеличение, если вторая сумма больше, чем первая, и у нас есть уменьшение, если вторая сумма меньше первой.

После того, как мы определили, является ли изменение увеличением или уменьшением, мы затем вычисляем, насколько это изменение, путем вычитания меньшего из большего. Затем мы делим его на первую сумму. Чтобы найти процентное значение, мы затем умножаем его на 100.

Мы можем написать простую формулу для процентного увеличения или уменьшения. Мы можем сказать, что процентное увеличение или уменьшение составляет (увеличение или уменьшение) / (первая сумма) * 100.

Независимо от того, какая проблема нам дается, до тех пор, пока мы можем найти первую сумму и величину увеличения или уменьшение, тогда мы можем вычислить процент увеличения или уменьшения.Давайте взглянем на пару примеров.

Пример 1

Владелец зоомагазина анализирует свои продажи за этот месяц. Он хочет сравнить это со своими продажами в прошлом месяце. Он не знает, увеличились ли его продажи или уменьшились. Он также хочет узнать, насколько его продажи увеличились или уменьшились. Он может работать со следующими номерами:

Продажи за 1 месяц	Продажа за 2 месяц
Щенки: 400 $	Щенки: 300 $
Котята: 700 $	Котят: 900 $
Рыба: 100 $	Рыба: 50 долларов
Мелкие животные: $ 200	мелких животных: 250 долларов

Глядя на его цифры, мы видим, что сначала нам нужно найти общую сумму за каждый месяц. Итак, за каждый месяц мы складываем все продажи.

• Для первого месяца у нас есть 400 + 700 + 100 + 200 = 1400. Итак, первый месяц дал владельцу всего 1400 долларов.
• Для второго месяца у нас есть 300 + 900 + 50 + 250 = 1500. Итак, во втором месяце общий объем продаж составляет 1500 долларов.

Сравнивая эти две суммы друг с другом, мы видим, что во втором месяце сумма больше, чем в первом. Итак, у нас происходит рост. Сколько у нас прибавки? 1500 долларов на 100 долларов больше, чем 1400 долларов. Итак, наша прибавка составляет 100 долларов.

×

Разблокировать содержимое

Более 83000 уроков по всем основным предметам

Получите доступ без риска на 30 дней,
просто создайте аккаунт.

Попробуй это сейчас

Нет обязательств, отмените в любой момент.

Хотите узнать больше?

Выберите предмет для предварительного просмотра связанных курсов:

Чтобы найти увеличение в процентах, мы делим наши 100 на сумму за месяц. Получаем 100/1400 = 0,0714. Умножьте это на 100, мы получим 7,1%. Таким образом, наши продажи выросли на 7,1%. И готово!

Пример 2

На этот раз у нас есть учительница, которая смотрит на свои графики посещаемости. Она хочет знать, лучше ли посещаемость на этой неделе, чем на прошлой. Она хочет знать, потому что на этой неделе она изменила свой подход к обучению на более юмористический. На прошлой неделе она была очень серьезной и не позволяла дурачиться. Посмотрев свои записи, она видит, что на прошлой неделе у нее был рекорд посещаемости 95%.На этой неделе ее рекорд посещаемости — 90%. У нас есть увеличение или уменьшение?

У нас уменьшение, так как вторая сумма ниже. Насколько наше снижение? У нас 95 — 90 = 5. Мы уменьшились на пять процентов. Насколько это процентное снижение? Делим наши 5/95 * 100. Получаем примерно 5,3%. Итак, имеем процентное снижение на 5,3%. И мы закончили.

Обратите внимание, что в этой задаче мы уже имеем дело с процентами. Но наш процесс все тот же. Итак, пока у нас одинаковый формат наших итогов, мы используем один и тот же процесс, независимо от того, являются ли числа уже процентами или нет.

Резюме урока

Давайте рассмотрим то, что мы узнали. Увеличение или уменьшение на процентов. — это величина увеличения или уменьшения, выраженная в процентах. Чтобы вычислить его, мы сначала вычисляем первую сумму, а затем вторую сумму. Если мы сравниваем два года подряд, первый год дает нам первую сумму, а второй год дает нам вторую сумму.Затем мы определяем, происходит ли увеличение или уменьшение. Затем рассчитываем величину этого увеличения или уменьшения. Чтобы найти процентное значение, мы делим величину увеличения или уменьшения на первую сумму и умножаем на 100.

Результаты обучения

К концу этого урока вы должны быть в состоянии:

• Сформулировать формулу для определения увеличения в процентах или уменьшить
• Рассчитать процент увеличения или уменьшения

Лабораторное упражнение № 9

В приведенной выше таблице 1 будет рассчитана численность популяции (N) через определенный промежуток времени (t). Все, что вам нужно сделать, это указать начальную численность популяции (N или ), скорость роста (r) и продолжительность времени (t). Константа (e) уже введена в уравнение. Это основание натурального логарифма (приблизительно 2,71828). Скорость роста (r) и время (t) должны быть выражены в одной и той же единице времени, например, в годах, днях, часах или минутах. Для людей темп роста населения рассчитан на один год. Если численность населения выросла с 1000 до 1040 за один год, то процентное увеличение или годовой темп роста составит 40/1000 x 100 = 4 процента.Другой способ показать этот естественный темп роста — вычесть уровень смертности из коэффициента рождаемости в течение одного года и преобразовать его в процент. Если коэффициент рождаемости в течение одного года составляет 52 на 1000, а уровень смертности — 12 на 1000, то годовой прирост этого населения составляет 52 — 12 = 40 на 1000. Естественный прирост для этого населения составляет 40/1000 x 100 = 4%. Это называется естественным приростом, потому что он основан только на уровне рождаемости и смертности, а не на иммиграции или эмиграции. Скорость роста бактериальных колоний выражается в минутах, поскольку бактерии могут делиться бесполым путем и удваивать свое общее количество каждые 20 минут.В случае вольфии (самое маленькое цветущее растение в мире и любимый организм мистера Вольфии) рост популяции выражается в днях или часах. Каждое растение вольфия имеет форму микроскопического зеленого футбольного мяча с плоской вершиной. Среднее отдельное растение азиатского вида W. globosa или столь же мелкого австралийского вида W. angusta достаточно маленькое, чтобы пройти через ушко обычной швейной иглы, а 5000 растений легко поместятся в наперсток. В мире насчитывается более 230 000 видов описываемых цветковых растений, и они варьируются по размеру от миниатюрных альпийских ромашек высотой всего несколько дюймов до массивных эвкалиптовых деревьев в Австралии более 300 футов (100 м) в высоту. Но наименьшее Бесспорным мире цветущие растения принадлежат к роду вольфии , минутная безродных растения, которые плавают на поверхности спокойных ручьев и прудов. Два самых мелких вида — азиатский W.globosa и австралийский W. angusta . Среднее индивидуальное растение составляет 0,6 мм в длину (1/42 дюйма) и 0,3 мм в ширину (1/85 дюйма). Он весит около 150 микрограммов (1/1 унции), или примерный вес 2–3 зерен поваренной соли. Одно растение в 165 000 раз короче самого высокого австралийского эвкалипта ( Eucalyptus regnans ) и в семь триллионов раз легче самой массивной секвойи-гиганта ( Sequoiadendron giganteum ). Скорость роста для Wolffia microscopica может быть рассчитана исходя из времени удвоения 30 часов = 1.25 дн. В приведенном выше уравнении роста популяции (N = N o e rt ), когда rt = 0,695 первоначальная начальная популяция (N o ) удвоится. Поэтому простое уравнение (rt = 0,695) можно использовать для решения относительно r и t. Скорость роста (r) может быть определена простым делением 0,695 на t (r = 0,695 / t). Поскольку время удвоения (t) для Wolffia microscopica составляет 1,25 дня, скорость роста (r) составляет 0,695 / 1,25 x 100 = 56 процентов. Попробуйте ввести следующие числа в приведенную выше таблицу: N o = 1, r = 56 и t = 16.Примечание. При использовании калькулятора значение r всегда следует выражать в виде десятичной дроби, а не в процентах. Общее количество растений вольфии через 16 дней составляет 7 785 штук. Этот экспоненциальный рост показан на следующем графике, где размер популяции (ось Y) сравнивается со временем в днях (ось X). Экспоненциальный рост дает характерную J-образную кривую, потому что популяция продолжает удваиваться, пока она постепенно не изгибается вверх и превращается в очень крутой наклон. Если бы график был построен логарифмически, а не экспоненциально, он предполагал бы прямую линию, идущую вверх слева направо. Шестнадцать дней экспоненциального роста у Wolffia microscopica . У растений вольфии самый быстрый рост населения среди представителей королевства Плантаэ. В оптимальных условиях одно растение индийского вида Wolffia microscopica может размножаться вегетативно, давая почки каждые 30 часов.Одно минутное растение математически может дать начало одному нониллиону растений или 1 x 10 30 (один с 30 нулями) примерно за четыре месяца со сферическим объемом, примерно эквивалентным размеру планеты Земля! Примечание: это чисто математический прогноз, и в действительности он никогда не может произойти! На следующем рисунке показано сравнение размеров одноминутного растения вольфия, примерно промежуточного между молекулой воды и планетой Земля! Если молекула воды представлена ​​как 10 0 , то растение вольфия примерно на 10 20 энергии больше, чем молекула воды.Земля примерно на 10 20 энергии больше, чем растение вольфия, или на 10 40 энергии больше, чем молекула воды. 2. Рост населения показан в геометрической прогрессии Геометрическая прогрессия — это упрощенный способ показать экспоненциальный рост населения. Начиная с одной пары, предположим, что у каждой девочки 4 ребенка (2 мальчика и 2 девочки). В следующей таблице сравнивается рост населения в 7 поколениях.Первоначальная пара имеет 4 детей, двое из которых девочки, которые рождают 8 детей (2 x 4). Четверо из 8 детей — девочки, от которых рождается 16 детей (4 x 4) и т. Д. Это экспоненциальный рост, при котором население удваивается с каждым поколением. Население 7-го поколения составляет 2 7 или 128 человек. Номер 2 4 8 16 32 64 128 Поколение (1) (2) (3) (4) (5) (6) (7) Английский священнослужитель и экономист Томас Р. Мальтус указал на геометрический рост населения в 1798 году. В своем трактате о росте населения он заявил, что население увеличивается геометрически, в то время как мировые запасы продовольствия увеличиваются арифметически. Арифметические прогрессии увеличиваются на добавление одной и той же суммы в каждом поколении, например, 2 — 12 — 22 — 32 — 42 — 52 … В предыдущем примере числовая последовательность увеличивается на 10 в каждом поколении. Мальтус пришел к выводу, что снабжение продовольствием никогда не поспеет за ростом населения, а неизбежными последствиями роста населения являются голод, эпидемии и войны.Хотя некоторые биологи и по сей день разделяют пессимистический прогноз Мальтуса, большинство экспертов сходятся во мнении, что рост человеческой популяции намного сложнее простых геометрических прогрессий. Было четко задокументировано, что когда уровень жизни и валовой национальный продукт (ВНП) страны повышаются, темпы роста ее населения фактически снижаются. Фактически, некоторые высокоразвитые страны с очень высоким ВНП фактически достигли нулевого прироста населения. Это также связано с экономическим и культурным давлением.Одним из лучших примеров небольшой страны с высоким ВНП и низким темпом роста населения является Япония. Темпы роста населения США в настоящее время составляют менее одного процента (по данным на 2000 год). Некоторые страны, такие как Китай, предлагают сильные экономические стимулы иметь только одного ребенка в семье. Есть дополнительные аргументы против мрачного прогноза Мальтуса. Благодаря современным методам ведения сельского хозяйства (Зеленая революция) некоторые высокоразвитые страны увеличили свои запасы продовольствия геометрически; однако, учитывая ограниченное количество пахотных земель и давление урбанизации, этот уровень продуктивности не может сохраняться бесконечно.По состоянию на 2000 год избытка пищи достаточно, чтобы накормить весь мир. Проблема заключается в раздаче продуктов питания голодающим в отдаленных регионах мира, а не в поставках. Еще неизвестно, будет ли в следующем столетии излишек продовольствия. Возможно, Мальтус прав в конечном счете. Применение геометрической прогрессии к плодовым мушкам ( Drosophila melanogaster ) дает астрономические числа за относительно короткий период времени.Начиная с двух плодовых мушек, предположим, что каждая самка откладывает 100 яиц каждые две недели (25 поколений в год). Сколько мух будет у 25-го поколения к концу года? Номер 2 100 5000 250000 12500000 1.19 х 10 41 Поколение (1) (2) (3) (4) (5) (25) Чтобы оценить количество мух в 25-м поколении, предположим, что мухи собраны вместе от 1000 до кубического дюйма. Такое количество мух заполнило бы шар диаметром 96 миллионов миль, превышающий расстояние между Землей и Солнцем! Конечно, это чисто теоретически. Естественные управляющие силы природы предотвратят этот ошеломляющий взрыв плодовых мух. Фактически, существует правило природы, которое гласит: «Выживаемость обратно пропорциональна плодовитости ». Другими словами, животные с высокой продуктивностью потомства (высокой плодовитостью) имеют низкую выживаемость среди потомства.У червей, насекомых и рыб, откладывающих тысячи яиц, только несколько яиц достигают зрелости. Следующие примеры роста населения с шестью детьми на пару сравнивают время поколений в 20 и 30 лет: 2 ————— 6 ————— 18 ————— 54 (20 лет) (20 лет) (20 лет) 80 человек через 60 лет 2 ————— 6 ————— 18 (30 лет) (30 лет) 26 человек через 60 лет При 20-летнем интервале между поколениями общее количество людей в конце 60-летнего возраста составляет 80 (2 + 6 + 18 + 54). При 30-летнем интервале между поколениями общее количество людей в конце 60-летнего периода составляет 26. Увеличение интервала между поколениями с 20 до 30 лет снижает прирост населения с 80 до 26 в течение 60-летнего периода, то есть процентное снижение на 67,5%. . Более длительный интервал между поколениями значительно замедляет рост популяции. 3. Прирост населения на основе годового прироста: I = rN Большая биология учебники объясняют следующее классическое уравнение годового увеличения Население: I = rN.I = годовой прирост населения, r = годовой темп прироста и N = начальный размер популяции. Если начальная численность населения в 1000 человек вырастет на 4% в течение одного года, население увеличится на 40 в течение года (I = 1000 x 0,04 = 40). Общая популяция (N) в конце года будет теперь 1000 + 40 = 1040. Начиная с одной модели Wolffia microscopica и используя скорость роста 56 процентов (в день), увеличение (I) для первого поколения составляет 0,56 X 1 = 0,56, и теперь общая численность населения равна 1. 56. Увеличение (I) для второго поколения составляет 0,56 X 1,56 = 0,87, а общая численность населения сейчас составляет 2,43. В следующей таблице и графике показаны прирост (I) и общая популяция для 10 поколений W. microscopica : Поколение № 1 № 2 № 3 № 4 № 5 № 6 № 7 № 8 № 9 № 10 Увеличение (I) 0.56 0,87 1,36 2,12 3,30 5,16 8,05 12. 55 19,58 30,55 Численность населения 1,56 2,43 3,79 5.91 9.21 14,37 22,42 34,97 54,55 85,10 Экспоненциальный рост популяции (J-образная кривая) на основе I = rN для 10 поколений Wolffia microscopica .Чтобы получить J-образную кривую, прирост (I) для каждого поколения (на основе скорости роста 56 процентов) добавляется к последовательным размерам популяции для каждого поколения. Если эти значения популяции вольфии нанесены арифметически для десяти последовательных поколений, вы получите J-образную кривую экспоненциального роста, подобную графику, показанному для роста популяции вольфии с использованием уравнения N = n o e rt .Разница между этими двумя уравнениями заключается в том, что одно показывает увеличение (I) в год при постоянной скорости роста (r) 0,56, а другое показывает окончательную численность населения (N) с постоянной скоростью роста (r) 0,56 в расширенном в течение заданного периода времени (t). Используя уравнение I = rN, вы должны добавить увеличение для каждого поколения к общей численности населения, чтобы получить J-образную кривую. Уравнение годового прироста (I = rN) модифицируется, чтобы получить уравнение логистического роста, описанное в следующем параграфе. 4. Логистический рост населения: I = rN (K — N / K) Рост естественного населения более точно описывается уравнением логистического роста, а не уравнением экспоненциального роста. При логистическом росте населения быстрый рост численности достигает пика, когда популяция достигает своей вместимости. Уравнение для этого типа роста содержит коэффициент несущей способности (K). Переносимость (K) может быть определена как максимальное количество популяции определенного вида, которое может поддерживаться данной экосистемой.Годовой прирост популяции можно показать уравнением: I = rN (KN / K), где I = годовой прирост популяции, r = годовой темп прироста, N = размер популяции и K = несущий емкость. Логистический рост популяции дает характерную S-образную или сигмовидную кривую, потому что популяция быстро увеличивается до тех пор, пока не достигнет предельной емкости, при которой она начинает замедляться и стабилизироваться. Логистический рост популяции дрожжевых клеток показан на следующем графике, где размер популяции (ось Y) сравнивается со временем в часах (ось X).Когда рост дрожжевой популяции достигает предельной емкости (чуть более 500), он начинает замедляться и замедляться. Восемнадцать часов логистического роста дрожжевых клеток. Луга среди соснового леса пондероза на плато Кайбаб, Аризона. Когда размер популяции равен пропускной способности (N = K), скорость роста равна нулю (I = 0) или нулевому приросту населения.Когда размер популяции превышает пропускную способность (N> K), I становится отрицательным числом, и популяция уменьшается. В случае неконтролируемого роста популяции оленей с недостаточным количеством хищников популяция резко сокращается, поскольку чрезмерно заросшая растительность просто не может поддерживать высокую долю оленей. Следовательно, олени умирают от голода и болезней, и популяция быстро сокращается. Этот сценарий действительно произошел на плато Кайбаб в северной Аризоне между 1907 и 1939 годами. В 1907 году поголовье оленей было необычно низким — всего 4000 голов. В то время грузоподъемность составляла 30 000 человек, поэтому была развернута массовая кампания против естественных врагов оленей. Между 1907 и 1923 годами естественные хищники оленей (горные львы, волки и койоты) были уничтожены охотниками с целью увеличения популяции оленей. Как показывает следующий график, популяция оленей быстро увеличилась до 100000 к 1924 году, но затем быстро вымерла до 10000 к 1939 году.Из-за чрезмерного выпаса чрезмерного количества оленей в 1939 году вместимость этого региона сократилась примерно до 10 000, и соответственно сократилась популяция оленей. Популяция оленей на плато Кайбаб в период 1905-1940 гг. Первоначальная вместимость оленей, составлявшая 30 000 голов в 1907 году, была значительно превышена в 1924 году, когда поголовье оленей выросло до 100 000. После 1924 года поголовье оленей быстро сократилось до 10 000 в 1939 году. 5. Рост населения по сравнению со сложным процентом 100 долл. США ежегодно на 10 лет под 6% N = N o (1 + r) n N o = 100, n = 10, r = 0,06 N = 179,08 долл. США 100 долл. США ежемесячно на 10 лет под 6% N = N o (1 + r / q) nq N o = 100, n = 10, r = 0.06, д = 12 N = 181,94 долл. США 100 долл. США ежедневно на 10 лет под 6% N = N o (1 + r / q) nq N o = 100, n = 10, r = 0,06, q = 365 N = 182,20 долл. США 100 долл. США непрерывно накапливаются на 10 лет под 6% ** N = N o e rt N o = 100, n = 10, r = 0.06, т = 10 N = 182,21 доллара США Таблица 2A. Сложные проценты против экспоненциального роста населения. ** Это та же формула, которая используется для расчета прироста населения. начальная сумма компаунд суточный составной непрерывно непрерывно минус ежедневно $ 100 182 долл. США.20 182,21 долл. США 0,01 доллара США $ 1000 1822,03 долл. США $ 1822,12 0,09 доллара США $ 10000 18220 долл. США.29 $ 18221,19 $ 0,90 $ 100000 $ 1822 202.90 $ 182211,88 8,98 долл. США Таблица 2B.Деньги начисляются ежедневно по сравнению с непрерывным начислением. [Деньги составлены на 10 лет по ставке 6 процентов, как в таблице 2A.] Таблица 2C. JavaScript для сложных процентов (начисляется ежегодно). Обязательно введите темп роста (r) целым числом, а не десятичным. [Например, введите 6 для 6%. Не вводите десятичное значение 0,6.] Сложные проценты JavaScript предоставлено исходным кодом JavaScript 6.Определение времени удвоения: t = 0,695 / r Таблица 3. Определение времени удвоения популяции. 7. Определение скорости роста: r = 0,695 / т Таблица 4. Определение темпов роста населения. 8. Замена репродукции vs.Нулевой рост населения Замещающее размножение просто определяется как замена супружеской пары (мужчины и женщины) одинаковым количеством людей (в среднем один мальчик и одна девочка). Его также можно определить как по одной дочери, рожденной от каждой матери. В зависимости от условий жизни в стране замещающее воспроизводство должно быть более двух потомков из-за фактора смертности. В Соединенных Штатах в конце 1900-х годов замещающее воспроизводство составляло примерно 2,2 или 2,3.Замещающее воспроизводство отличается от нулевого прироста населения, когда количество рождений равно количеству смертей в год. Годовой нулевой прирост населения для данной страны рассчитывается по следующему уравнению: Количество рождений + количество иммигрантов = количество смертей + количество эмигрантов Хотя в Соединенных Штатах средний размер семьи приближается к воспроизводству замещения, у них нет ежегодного нулевого прироста населения. Это связано с тем, что уровень рождаемости превышает уровень смертности в год, в стране наблюдается значительная чистая иммиграция, а в возрастной структуре присутствует множество бэби-бумеров, которые теперь являются родителями. 9. Земля как источник пищи для населения мира Хотя, по оценкам, на континентах мира есть только около 10 миллиардов акров пахотных земель (лишь часть общей площади мирового океана), именно здесь добывается большая часть пищи для людей. По массе (в тоннах) общий урожай аквакультуры в Мировом океане, включая водоросли, рыбу и моллюсков, составляет менее 1/600 земледелия. Пища из земли включает зерно (крупы), бобовые, корнеплоды, такие как картофель и ямс, овощи, говядину и птицу.Но даже наша еда из земли — не бесконечный ресурс. Учитывая, что 1/4 акра земли требуется для обеспечения продовольствием одного человека в год, тогда 10 миллиардов акров пахотных земель будут поддерживать 40 миллиардов человек (10 миллиардов акров разделить на 0,25 акра на человека). Учитывая, что в начале 21 века население мира составляет чуть более 6 миллиардов человек (и ежегодный прирост составляет 2%), допустимая емкость для людей (40 миллиардов) может быть достигнута примерно за одно столетие. По следующей ссылке показан счетчик населения мира в реальном времени.Каждую секунду рождается пять человек и два человека умирают. При увеличении населения на три человека в секунду к концу 50-минутной лекции по биологии 100 население мира увеличится на 9000 человек. По итогам года население увеличится почти на 95 миллионов. Начиная с населения в 6 миллиардов человек, это будет ежегодный прирост примерно на 1,58 процента. Численность населения # Год, чтобы добавить миллиард Год 1-й миллиард С начала до 1800 1800 2-й миллиард 130 лет 1930 3-й миллиард 30 лет 1960 4-й миллиард 15 лет 1975 5-й миллиард 12 лет 1987 6-й миллиард 11 лет 1998 7-й миллиард 11 лет 2009 10. Глобальное изменение климата, сельское хозяйство и парниковый эффект Стеклянные стены и крыша теплицы улавливают солнечную энергию, что приводит к повышению температуры внутри. То же явление, называемое «парниковым эффектом», вызывается газами двуокиси углерода и метана в атмосфере Земли. Тенденция к потеплению Земли, вызванная парниковыми газами, известна как «глобальное потепление». Имеются убедительные доказательства того, что по состоянию на 2005 г. происходит глобальное потепление, например таяние ледников Аляски и Канады; однако точная причина глобального потепления является спорным вопросом. Одна из самых интересных гипотез, объясняющих глобальное потепление, обсуждается Уильямом Ф. Руддиманом в мартовском номере журнала Scientific American за 2005 год: «Как люди впервые повлияли на глобальный климат?» ( Sci. Amer. 292 (3): 46-53). По словам доктора Руддимана, глобальное потепление началось за тысячи лет до того, как мы начали сжигать ископаемое топливо на электростанциях, промышленных предприятиях и в двигателях внутреннего сгорания. Этот вывод основан на данных по двуокиси углерода и метану, захваченным в кернах ледяных щитов Гренландии и Антарктики.Количество солнечной радиации, которая достигает Земли каждый год, основано на нескольких сложных орбитальных циклах, включая форму орбиты Земли вокруг Солнца, а также колебание или наклон Земли вокруг своей оси. Руддиман считает, что солнечная радиация достигла пика около 11000 лет назад. Земля имела тенденцию к постепенному похолоданию примерно 8000 лет назад, дата, которая совпадает с появлением человеческого сельского хозяйства. Когда люди начали рубить и сжигать леса и обрабатывать обширные площади земли, в атмосферу были выброшены более высокие уровни углекислого газа и метана.Например, выращивание рисовых полей 5000 лет назад хорошо коррелирует с увеличением метана, продукта бактерий гниения на заболоченных территориях. Колебания похолодания в течение 8000-летнего тренда потепления можно объяснить массовыми смертями, вызванными серьезными человеческими заболеваниями (эпидемиями), в результате которых уменьшились численность населения и выбросы парниковых газов. В заключение, общая тенденция к потеплению коррелирует с человеческим сельским хозяйством и экспоненциальным ростом населения. Фактически, Руддиман предполагает, что без развития сельского хозяйства мы вступили бы в другой период оледенения! Предсказания ученых 1970-х годов о том, что мы столкнемся с новым ледниковым периодом, верны, если вы проследите за тенденцией к похолоданию, которая началась 11000 лет назад.Предсказания ученых о глобальном потеплении в 1980-х годах также верны, если включить парниковый эффект. Текущая тенденция к глобальному потеплению может продлиться еще несколько веков, пока мы не исчерпаем запасы ископаемого топлива. Надеюсь, мы создадим эффективный, экологически чистый источник энергии, который не зависит от ресурсов других стран. Было бы интересно заглянуть в будущее, чтобы увидеть, стихнет ли глобальное потепление, когда ископаемое топливо больше не будет сжигаться. 11.Вопросы о росте населения 1. Начиная с 25 000 человек на 1 января, население достигает 26 000 к 31 декабря. Каков годовой прирост в процентах? 2. Начиная с 25 000 человек в 1966 году, население Эскондидо к 1984 году достигло 75 000. Каков процент увеличения за этот 18-летний период? Если вы спроецируете этот огромный рост на 2001 год, это объяснит затор на шоссе 78. 3.В Кении годовой коэффициент рождаемости составляет 52 на 1000 человек, а уровень смертности — 12 на 1000. Рассчитайте годовой процент роста (r) для Кении. 4. Каково время удвоения в годах для Кении? [Подсказка: N o удваивается, когда rt = 0,695.] 5. Местный кредитный союз выплачивает 10% процентов (начисленных почасово) по сберегательным счетам. Когда ваш первоначальный депозит в размере 100 долларов удвоится? 6. Сколько денег будет на вышеуказанном счете (вопрос 5) через 30 лет? [Предполагается, что процентная ставка составляет 10%, а вы не делаете депозиты и не снимаете средства. ] 7. Рассчитайте приблизительное увеличение в процентах в результате ежедневного роста на 3% в течение 100 лет. 8. Рассчитайте приблизительное увеличение в процентах в результате ежедневного увеличения на 1% в течение 100 лет? 9. Естественный прирост (r) мирового населения составляет примерно 2 процента в год. Какое время удвоения мира основано на этой скорости роста? 10. Начав с 5 миллиардов человек в 1988 году, подсчитайте численность населения мира в 2100 году. 11. Некоторые довольно пессимистические демографы предполагают, что максимальное количество людей, которые могут поддерживаться земледелием, составляет около 40 миллиардов человек. Это означает, что несущая способность (К) для Земли составляет 40 миллиардов. Когда в 1988 году население Земли составляло 5 миллиардов человек, когда земля достигнет 40 миллиардов (по годам)? 12. В оптимальных условиях Wolffia microscopica имеет время удвоения за счет бутонизации 30 часов (1,25 дня). Рассчитайте скорость роста (r) Вт.microscopica в сутки. 13. Начиная с одного растения вольфии (со средним объемом в один кубический миллиметр), рассчитайте окончательную популяцию (N) через 4 месяца (125 дней). [Это число примерно равно объему Земли в кубических миллиметрах!] 14. С шестью потомками от каждой самки (равное соотношение полов) и средним интервалом между поколениями 20 лет, сколько всего потомства пара теоретически может произвести за 60 лет? [Если предположить, что все в семье живут так долго.] 15. Ссылаясь на вопрос № 14 выше, сколько всего людей было бы у вас за 60 лет, если бы интервал между поколениями увеличился до 30 лет? [Всем придется немного подождать, прежде чем появятся дети.] 16. Если у Джека и Джилл будет двое детей в возрасте 20 лет и их дети будут вести себя одинаково, в возрасте 65 лет у них будет всего 8 правнуков, 4 внука и 2 ребенка. Если бы они ждали до 30 лет, чтобы иметь детей (и их дети вели бы себя аналогичным образом), сколько всего потомков у них было бы в возрасте 65 лет? Scantron Choices: Я знаю, что есть 4 а, 4 b, 4 c, 4 d и 4 e. Просто выберите правильный выбор независимо от повторяющихся букв. (а) 2 (а) 12 (а) 75 (а) 1900 (б) 4 б 17,4 б 80 б) 2009 год (в) 6 (в) 26 (в) 104 (в) 4.7 х 10 10 (г) 7 (г) 35 (г) 160 (г) 2,5 x 10 30 (д) 10 (д) 56 (д) 200 е) 2.5 х 10 80

Расчет уровня безработицы | Макроэкономика

Цели обучения

• Рассчитайте процентное соотношение рабочей силы и уровень безработицы

Расчет уровня безработицы

Помните, что безработные — это те, кто не работает и активно ищет работу. Мы можем рассчитать уровень безработицы, разделив количество безработных на общую численность рабочей силы, а затем умножив на 100.

Рисунок 1. Распределение занятого, безработного и неработающего взрослого населения (в возрасте 16 лет и старше), 2016 г. Общая численность взрослого трудоспособного населения в 2016 г. составила 253,5 миллиона человек. Из этой общей численности населения 151,4 миллиона были классифицированы как занятые, а 7,7 миллиона — как безработные. Остальные 94,4 миллиона были отнесены к категории неработающих.Однако, как вы узнаете, эта, казалось бы, простая диаграмма не раскрывает всей истории.

На рисунке 1 показано трехстороннее разделение взрослого населения старше 16 лет. В 2016 году 62,8% взрослого населения было занято; то есть либо работают, либо не работают, но ищут работу. Тех, кто находится в рабочей силе, можно разделить на занятых и безработных. Эти значения также показаны в таблице 1. Уровень безработицы — это не процент от всего взрослого населения, не имеющего работы, а, скорее, процент взрослых, которые работают, но не имеют работы:

[латекс] \ text {Уровень безработицы} = \ frac {\ text {Безработные}} {\ text {Общая рабочая сила}} \ times {100} [/ latex]

Таблица 1. Занятость и безработица в США, 2016 г.
Всего взрослого населения старше 16 лет	253,5 млн
В составе рабочей силы	159,1 млн (62,8%)
Занятые	151,4 млн.
Безработные	7,7 млн.
Вне рабочей силы	94,4 млн (37,2%)
Источник: www.bls.gov

Каков уровень безработицы в 2016 г., исходя из данных таблицы 1? В этом примере уровень безработицы можно рассчитать как 7,7 миллиона безработных, разделенных на 159,1 миллиона человек в составе рабочей силы, что дает 4,8% уровня безработицы. Прочтите, чтобы пройти этапы расчета этого процента.

Расчет процентной доли рабочей силы

Итак, как экономисты приходят к процентному соотношению в составе рабочей силы и вне ее, а также к уровню безработицы? Мы будем использовать значения в таблице 1, чтобы проиллюстрировать шаги.

Для определения доли в рабочей силе:

Шаг 1. Разделите количество работающих (159,1 миллиона) на общую численность взрослого (трудоспособного) населения (253,5 миллиона).

Шаг 2. Умножьте на 100, чтобы получить процентное значение.

[латекс] \ begin {array} {l} \ text {Процент в рабочей силе} = \ frac {159.1} {253,5} \\\ text {Процент в рабочей силе} = 0,628 \\\ text {Процент в рабочая сила} = 62,8 \ text {percent} \ end {array} [/ latex]

Для определения доли вне рабочей силы:

Шаг 1. Разделите количество людей, не занятых в рабочей силе (94,4 миллиона), на общую численность взрослого (трудоспособного) населения (253,5 миллиона).

Шаг 2. Умножьте на 100, чтобы получить процентное значение.

[латекс] \ begin {array} {l} \ text {Процент от рабочей силы} = \ frac {94.4} {253,5} \\\ text {Процент от рабочей силы} = 0,372 \\\ text { Процент от рабочей силы} = 37,2 \ text {percent} \ end {array} [/ latex]

Для определения уровня безработицы:

Шаг 1. Разделите количество безработных (7,7 миллиона) на общую численность рабочей силы (159,2 миллиона).

Шаг 2. Умножьте на 100, чтобы получить коэффициент.

[латекс] \ begin {array} {l} \ text {Уровень безработицы} = \ frac {7.7} {159.2} \\\ text {Уровень безработицы} = 0,0487 \\\ text {Уровень безработицы} = 4,8 \ text { процент} \ end {array} [/ latex]

Даже с категорией «вне рабочей силы» все еще есть некоторые люди, которых неправильно отнесены к категории занятых, безработных или выбывших из рабочей силы.Есть люди, которые работают неполный рабочий день или имеют временную работу и которые ищут полную или постоянную работу, которые считаются занятыми, хотя они не работают так, как им хотелось бы или нужно было. Кроме того, есть человек с неполной занятостью . Сюда входят те, кто обучен или имеет квалификацию для одного вида или уровня работы, которые работают на более низкооплачиваемой работе или на той, которая не использует свои навыки. Например, человек с высшим образованием в области финансов, работающий продавцом, будет считаться частично занятым.Однако они также учитываются в группе работающих. Все эти люди подпадают под действие термина « скрытая безработица . ” Обескураженные работники, те, кто прекратил искать работу и, следовательно, больше не учитывается в числе безработных, также попадают в эту группу.

Уровень участия рабочей силы

Другой важный статистический показатель — это уровень участия в рабочей силе . Это процент взрослых в экономике, которые либо работают, либо безработные и ищут работу.Люди, которые не имеют работы, но в настоящее время не ищут работу, считаются вышедшими из состава рабочей силы и не учитываются в коэффициенте экономической активности. Таким образом, используя данные на Рисунке 1 и Таблице 1, в этот расчет будет включено 159,2 миллиона человек в составе рабочей силы. Ставка рассчитывается путем деления количества взрослых в составе рабочей силы на общую численность взрослого населения и умножения на 100, чтобы получить процентную долю. По данным за 2016 год, уровень экономической активности составляет 62 человека.8%. В Соединенных Штатах уровень участия в рабочей силе обычно составляет около 66–68%, хотя за последнее десятилетие он снизился.

Отчетность о занятости и безработице

Обследование заработной платы на предприятиях

Когда ежемесячно публикуется отчет о безработице, Бюро статистики труда (BLS) также сообщает о количестве созданных рабочих мест, которое берется из обследования фонда заработной платы (EPS). Обследование заработной платы основано на опросе около 140 000 предприятий и государственных учреждений по всей территории Соединенных Штатов.Он генерирует оценки занятости по заработной плате по следующим критериям: все сотрудники, среднее количество отработанных часов в неделю, а также средняя почасовая, недельная и сверхурочная заработная плата. Одно из критических замечаний к этому обзору заключается в том, что он не учитывает самозанятых. Он также не делает различия между новой, минимальной заработной платой, неполной или временной работой и полной занятостью с «достойной» оплатой.

Как собираются данные о безработице в США?

Уровень безработицы, объявленный U.Ежемесячное статистическое исследование S. Bureau of Labor Statistics основано на текущем обследовании населения (CPS), которое ежемесячно проводится с 1940 года Бюро переписи населения США. Большое внимание уделяется тому, чтобы этот опрос был репрезентативным для страны в целом. Страна сначала разделена на 3137 областей. Затем для обследования выбирается 729 из этих участков. Затем 729 районов делятся на районы примерно по 300 домохозяйств в каждом, и каждый район делится на группы примерно по четыре жилых дома.Ежемесячно сотрудники Бюро переписи обзванивают около 15 000 кластеров из четырех домохозяйств, что в общей сложности составляет 60 000 домохозяйств. Домохозяйства опрашиваются в течение четырех месяцев подряд, затем выходят из обследования на восемь месяцев, а затем снова опрашиваются в течение тех же четырех месяцев в следующем году, прежде чем навсегда покинуть выборку.

На основе этого обследования уровни безработицы рассчитываются по штатам, отраслям, городским и сельским районам, полу, возрасту, расе или этнической принадлежности и уровню образования.Доступен также широкий спектр другой информации. Например, как долго люди были без работы? Они стали безработными из-за увольнения, или были уволены, или их работодатель обанкротился? Является ли безработный единственным кормильцем в семье?

CPS и EPS

В то время как текущее обследование населения (CPS) и обследование заработной платы в учреждениях (EPS) предоставляют отчеты о рабочих местах, CPS измеряет процент безработной рабочей силы, а EPS измеряет чистое изменение рабочих мест, созданных за месяц. .

Критика измерения безработицы

При измерении количества безработных всегда возникают сложности. Например, как быть с людьми, у которых нет работы и которые были бы готовы работать, но разочаровались в отсутствии рабочих мест в их районе и перестали искать? Такие люди и их семьи могут страдать от безработицы. Но опрос считает их вышедшими из состава рабочей силы, потому что они не ищут работу активно. Другие люди могут сказать Бюро переписи населения, что они готовы работать и ищут работу, но на самом деле они не очень-то хотят работать и совсем не ищут.Они считаются безработными, хотя более точно их можно отнести к категории безработных. Тем не менее, у других людей может быть работа, например, работа во дворе, уход за детьми или уборка домов, но они не отчитываются о полученных доходах в налоговых органах. Они могут сообщать о том, что они безработные, когда они действительно работают.

Хотя уровень безработицы привлекает большую часть внимания общественности и средств массовой информации, экономические исследователи из Бюро статистики труда публикуют широкий спектр опросов и отчетов, которые пытаются измерить эти виды проблем и разработать более детальное и полное представление о рабочей силе. рынок.То, что экономическая статистика несовершенная, не является горячей новостью. Однако даже несовершенные показатели, такие как уровень безработицы, могут быть достаточно информативными, если их толковать со знанием дела и разумно.

Глоссарий

разочарованные работники:

тех, кто прекратил искать работу из-за отсутствия подходящих вакансий

коэффициент участия в рабочей силе:

это процент взрослых в экономике, которые либо работают, либо безработные и ищут работу

неполная занятость:

человек, занятых на работе ниже их квалификации

уровень безработицы:

процент взрослых, которые работают и поэтому ищут работу, но не имеют работы

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Вот сколько может стоить Starbucks закрытие 8000 магазинов после обеда

Согласно расчетам MarketWatch, закрытие магазинов на один день после обеда, о котором компания Starbucks Inc. объявила во вторник для обучения сотрудников на основе расовых предубеждений, обойдется компании примерно в 12 миллионов долларов в виде упущенной выгоды.

Если принять во внимание годовой объем продаж компании в размере 22,39 миллиарда долларов и разделить его на количество дней в году, но без поправки на относительную силу отдельных дней и их частей, можно предположить, что Starbucks хранит около 61 доллара.3 миллиона каждый день. Поскольку, согласно объявлению, заведения Starbucks закрываются только на часть дня, MarketWatch подсчитал, что заведения могут потерять около 20% своего ежедневного дохода, или 12 миллионов долларов.

Starbucks заявила, что закрывает около 8000 мест в США для обучения расовым предубеждениям. По состоянию на четвертый финансовый квартал Starbucks управлял 13 275 магазинами по всему миру и лицензировал еще 14 064, в том числе 5 708 в США.

Это не первый раз, когда Starbucks закрывает магазины по всей стране для обучения.Когда Starbucks закроет свои двери во второй половине дня 29 мая, прошло десять, три месяца и три дня с момента последнего такого действия.

Остановка в 2008 году, о которой тогдашний генеральный директор Говард Шульц вспоминал в своей книге за 2011 год, обошлась компании примерно в 6 миллионов долларов. «В конечном счете, — писал Шульц, — согласно выдержке из Business Insider, — закрытие наших магазинов было самым сильным символом. Это было потрясающее событие ». В 2008 году компания обслуживала около 7 100 магазинов.

Планируемое в мае приостановление коммерческой деятельности в U.Местонахождение S. происходит после угрожающего репутации инцидента на прошлой неделе в магазине в Филадельфии, где двое чернокожих были насильно выселены, поскольку они, как сообщается, ждали третьего человека, с которым у них была запланирована встреча. Менеджер магазина Starbucks подал жалобу о незаконном проникновении, заявив, что люди не размещали заказ и отказались освободить место. Кофейная компания обвинила недостатки в своей «культуре сообщества», которые она теперь намерена устранить во время майского мероприятия для всех сотрудников.

Появившись рано утром в среду на канале CBS This Morning, Шульц охарактеризовал себя как смущенный и пристыженный.«Я думаю, что произошедшее было предосудительно на всех уровнях». Он подтвердил, что закрытие 8000 магазинов «обойдется в миллионы долларов, но я всегда рассматривал это и подобные вещи не как расходы, а как вложение в наших людей и нашу компанию».

«Мы лучше, чем это», — сказал Шульц корреспонденту CBS Гейл Кинг, — «и я думаю, что люди ожидают, что мы будем на более высоком уровне, чем многие другие компании, и я это понимаю».

Шульц сказал Кингу, что не сомневается в том, что звонок менеджера — по его словам, он уверен, что менеджер магазина сожалеет — был сделан только потому, что упомянутые мужчины были афроамериканцами.

В то время как трехчасовое закрытие в 2008 году было нацелено на более повседневный результат — переориентацию сотрудников на совершенствование «искусства эспрессо» — язык, используемый во вторник в Starbucks SBUX, + 0,93% не так уж сильно отличался от того, что компания тогда говорила: «Речь идет не об обучении. Речь идет о любви, сострадании и приверженности, которые все мы должны испытывать к клиенту ».

В своем заявлении во вторник компания из Сиэтла заявила, что, по ее мнению, расовое профилирование в коммерческих условиях выходит далеко за пределы ее тысяч U.S. хранит, но он намеревался внести изменения там, где это возможно. «Основополагающие ценности компании основаны на гуманности и вовлеченности», — говорится в заявлении Шульца, ныне исполнительного председателя. «Мы будем учиться на своих ошибках и подтвердить нашу приверженность созданию безопасной и гостеприимной среды для каждого клиента».

Читайте дальше: У Говарда Шульца из Starbucks есть мечта Вилли Вонки о флагманском магазине Crate & Barrel в Чикаго

.

No related posts.