Как научить делить столбиком: Как научить ребёнка делить столбиком правильно, числа класс — www.wday.ru

Как научить ребенка решать деление в столбик. Как научиться делить столбиком: примеры и решения

Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.

Как правильно подготовить ребенка к восприятию нового материала?

Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.

Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.

Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.

Как пошагово объяснить алгоритм математического действия?

Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:

1. Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
2. Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
3. При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
4. Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
5. Далее, нужно найти разницу между частью делимого и полученным произведением.
6. Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

1. Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
2. Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
3. 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
4. Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
5. К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
6. Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
7. 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.

Пошаговая инструкция обучения делению столбиком

Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8. Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211.

Результат необходимо перепроверить обратным умножением.

В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:

• Берем первую цифру числа, делим ее на делитель. Сколько раз делитель может содержаться в делимом?
• Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
• Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.
• Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
• Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.

На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.

Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки.

Удивительное открытие сделала наша читательница. Ее сын на уроке не понял, как делить в столбик. Желая помочь сыну, она открыла учебник и увидела, что …ничего не увидела. Никаких пояснений к теме в книге почему-то не было. Как научить ребенка делению столбиком, если в книжке Вашего ребенка допущен подобный методический казус?

Что нужно знать, что бы научиться делить

Математика не любит пропусков.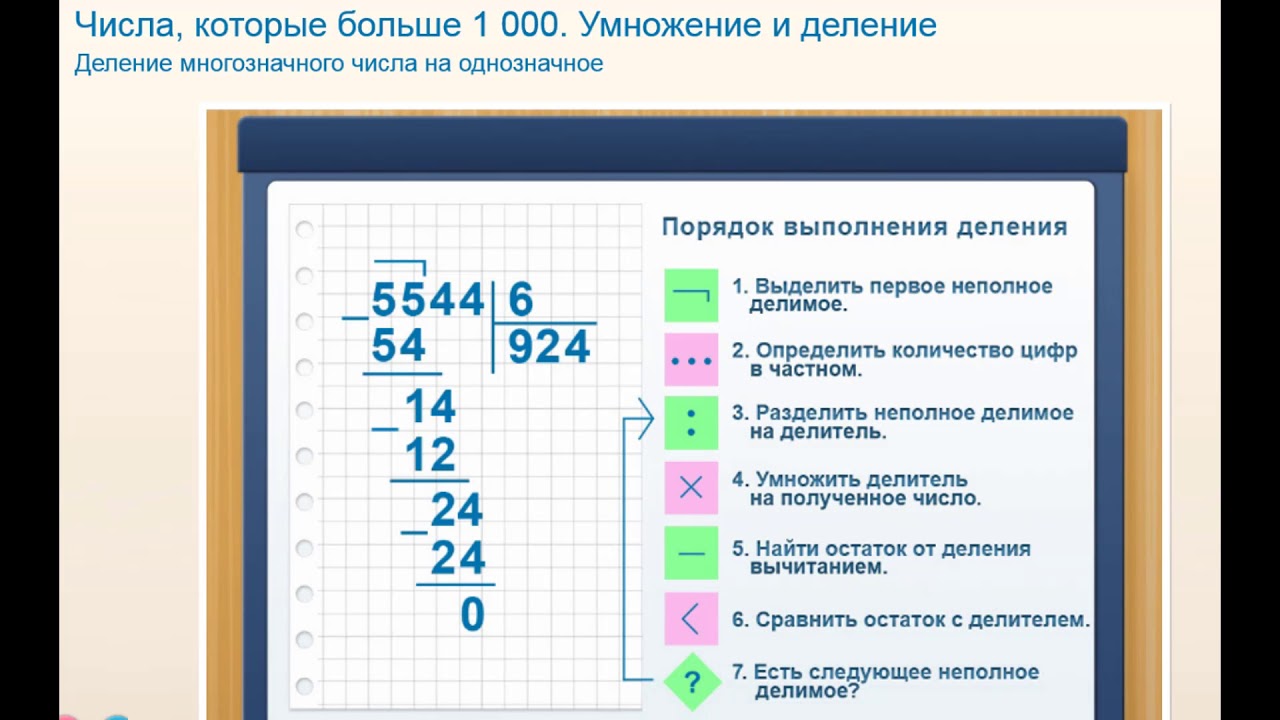 Все знания должны быть крепкими, как кирпичики. Если ребенок не знает основ, с делением будет невероятно трудно. На что следует обратить внимание?

1. Знает ли школьник название элементов при делении.
2. Убедитесь, что ребенок не забыл таблицу умножения.
3. Повторите разряды числа.

Приступаем к делению

Как научить ребенка делить столбиком, мы разберем на конкретных примерах. Следите за рассуждениями и будьте внимательны к цифрам.

Отделяем делимое от делителя скобкой-уголком.

Рассуждаем так: можно ли 4 разделить на 5? Нет, нельзя. Поэтому мы берем не 4, а 46. Вспомним таблицу умножения (можно взять распечатку), какое число в таблице умножения на 5 ближайшее к 46? – 45. Сколько раз 5 помещается в 45? – 9 раз. Подписываем 45 по 46, единицы под единицами, чтобы не запутаться. Девятку пишем «на полочке» – в уголке.

Если от 46 отнять 45, сколько получим? -1. Один меньше пяти? – меньше. Значит, мы разделили правильно.

Один на 5 не делится, сносим оставшееся число – 5, получаем 15. Пятнадцать делится на пять? — делится. Сколько получается? – 3. Тройку записываем в уголке. Проверяем решение: три умножить на 5, будет 15. Подписываем его под предыдущим числом. Из пятнадцати вычесть пятнадцать – будет ноль. Мы использовали все числа из делимого, значит, решили пример правильно.

В уголке мы записали две цифры – 9 и 3, получили число 93. Девяносто три – это частное, которое является решением нашего примера.

Объясняя школьнику, как научиться делить столбиком, выполняйте проверку обратным действием: 93*5. Кроме того, решайте более сложные варианты.

Есть и другие, частные случаи – о них Вы узнаете из программы. Если в учебнике действительно «ничего нет», возьмите за правило сверять решение с классной работой. Из классной тетрадки легко понять, каким методом пользуется учитель, и повторить его при объяснении домашней работы.

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение).

Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше.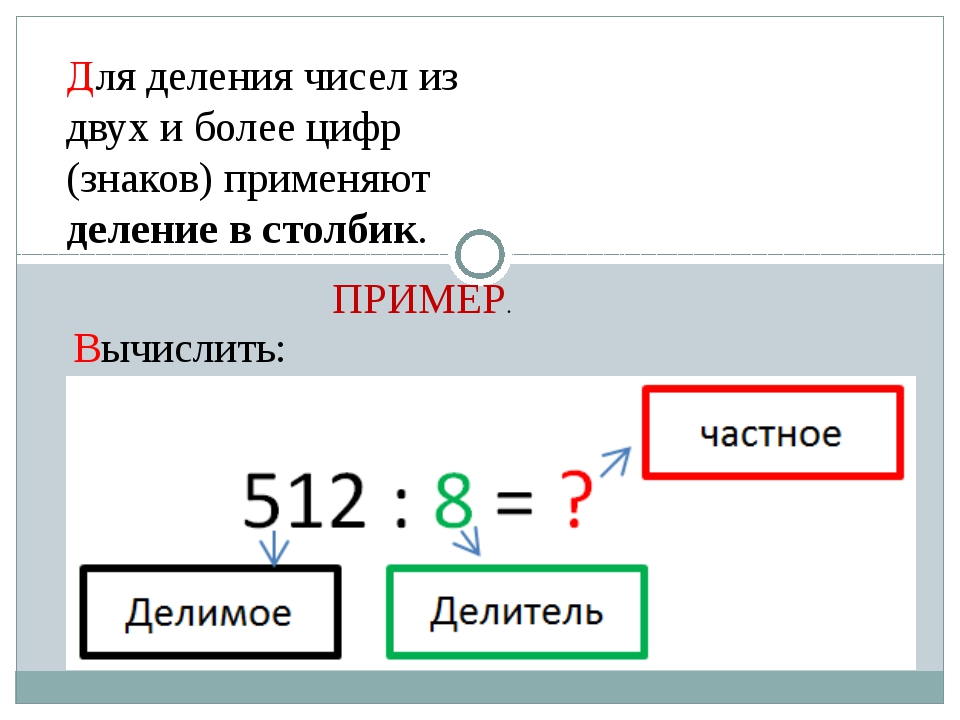 Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера.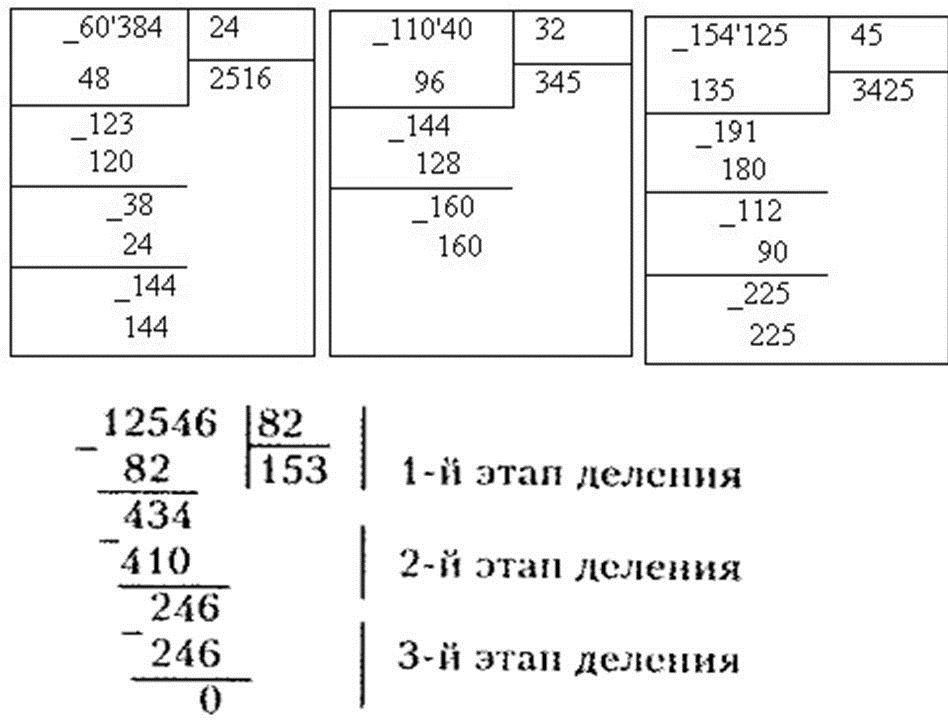 Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.

Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.

Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.

Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.

Как правильно делить числа в столбик: алгоритм деления

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Как объяснить ребенку деление и научить делить столбиком?

Во-первых, учтите ряд вводных факторов:

• ребёнок знает таблицу умножения
• хорошо разбирается и умеет применять на практике действия вычитания и сложения
• понимает разницу между целым и его составными элементами

• поиграйте с таблицей умножения. 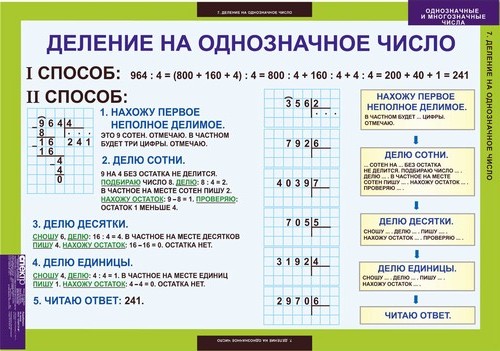Положите её перед ребёнком и на примерах покажите удобство использования при делении,
• объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
• превратите процесс в игру, придумайте историю про цифры и действие деления,
• подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
• первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:

• запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
• предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
• подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
• помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
• следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
• снова помогите с записью действия,
• продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
• закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.

Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение

Приступим к пошаговому разбору примеров на деление в столбик.

Осуществите действие над цифрами 25 и 2:

• запишите их рядом и разделите линиями границы,
• определите нужное количество цифр делимого для первого действия,
• запишите значение под делителем и результат умножения под делимым,
• выполните вычитание,
• допишите вторую цифру делимого и повторите действия на умножение и вычитание.

Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:

Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.

Второй пример. Разделите 87 на 26 в столбик.

Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.

Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.

Ниже пример деления столбиком двузначного числа на двузначное с остатком.

Третий пример. Как разделить число в столбик с нулем в ответе.

Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

Примеры подробного решения ниже.

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

Как делить в столбик с остатком?

Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Как делить столбиком десятичные дроби с запятой?

Существует несколько особенностей при подобном делении. Если вы совершаете действие с:

• десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
• числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
• десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.

Как делить столбиком меньшее число на большее?

При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.

Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:

• первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
• поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
• когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка. В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.

Ниже пример.

Как делить столбиком числа с нулями?

Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.

Из нюансов отметим:

• при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
• если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.

Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.

Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.

Практикуйте полученные знания и помогайте своему чаду осваивать математику.

Видео: как правильно делить числа в столбик?

Как научить ребенка делить столбиком?

Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.

Учить ребенка делить столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно подтянуть знания, ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.

Как научить делить столбиком?

Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.

Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.

Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.

Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.

Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку.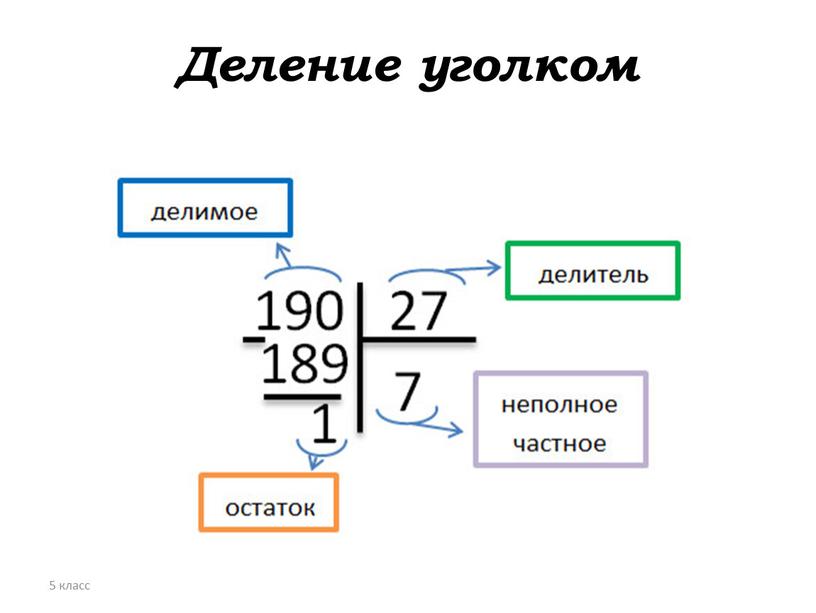 Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.

Попробуйте на различных примерах, и ребенок быстро освоит это действие.

 

Как научиться делить в столбик

Процесс деления в столбик заключается в последовательном выполнении элементарных арифметических действий. Для того чтобы научиться делить в столбик, нужно простопоупражняться в этом несколько раз. Алгоритм деления в столбик рассмотрим на следующих примерах — разделимв столбик целые числа без остатка, с остатком и дробные числа, представленные в виде десятичной дроби.Вам понадобится

Деление без остатка. Разделим 1265 на 55.
Проведите вниз короткую вертикальную линию, высотой в несколько клеток. От этой линии проведите перпендикуляр вправо.Получилась буква «Т», заваленная на левый бок. Над горизонтальной частью заваленной буквы «Т» пишется делитель (55), а слева от него в этой же строчке, за вертикальной частью буквы «Т» – делимое (1265). Обычно, сначала записывается делимое, потом ставится знак деления в столбик (заваленная набок буква «Т»), а после делитель.

Определите, какая часть делимого (отсчет идет слева направо по старшинству разрядов) делится на делитель. То есть: 1 на 55 – нет, 12 на 55 – нет, 126 на 55 – да. Число 126 называется неполным делимым.

Прикиньте в уме, на какое число N нужно умножить делитель, чтобы получилось число равное или максимально приближенное (но не большее) к величине неполного делимого. То есть: 1*55 – маловато, 3*55=165 – многовато. Итак, наш выбор – число 2. Записываем его под делителем (ниже горизонтальной части заваленной буквы «Т»).

Умножьте 2 на 55 и запишите полученное число 110 строго под цифрами неполного делимого – слева направо: 1 под 1, 1 под 2 и 0 под 6. Сверху 126, снизу 110. Проведите под 110 короткую горизонтальную черту.

Вычтите из 126 число 110. Получится 16. Цифры записывайте четко одна под другой под проведенной чертой.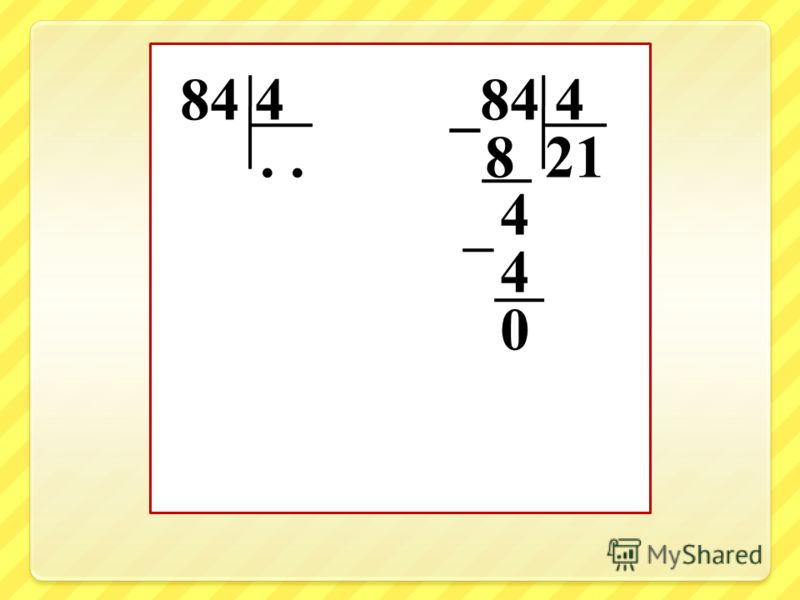 То есть, слева направо: под цифрой 1 числа 110 – пусто, под цифрой 1 – 1 и под цифрой 0 – 6. Число 16 – это остаток, который должен быть меньше делителя. Если он оказался больше делителя, число N было выбрано неправильно – нужно его увеличить и повторить предыдущие действия.

Снесите следующую цифру делимого (цифра 5) и запишите ее справа от числа 16. Получилось 165.

Повторите действия третьего шага для отношения 165 к 55, то есть найдите число Q, при умножении делителя на которое, получается число максимально приближенное к 165 (но не большее его). Это число 3 – 165 делится на 55 без остатка. Запишите цифру 3 справа от цифры 2 под чертой, проведенной под делителем. Это и есть ответ: частное отношения 1265 к 55 равно 23.

Деление с остатком. Разделим 1276 на 55.Повторите все те же действия, что и при делении без остатка. Число N по-прежнему равно 2, но разница между 127 и 110 равна 17. Сносим 6 и определяем число Q. Оно также по-прежнему равно 3, но теперь появляется остаток: 176 – 165 = 11. Остаток 11 меньше 55, вроде бы все нормально. Но сносить-то больше нечего…

Допишите справа от делимого ноль и поставьте запятую, после цифры 3 в частном (то число, которое получается в ходе деления, и записываетсяпод чертой, проведенной под делителем).

Снесите дописанный в делимом ноль (запишите его справа от 11) и проверьте, есть ли возможность разделить получившееся число на делитель. Ответ – да: 2 (обозначим его, как числоG) умножить на 55 равно 110. Ответ- 23,2.Если бы снесенного в предыдущем шаге нуля не хватило бы для того, чтобы остаток с дописанным нулем оказался больше делителя, нужно было бы дописать еще один ноль в делимом и поставить 0 в частном после запятой (получилось бы 23,0…).

Деление в столбик десятичных дробей.Перенесите запятую на одинаковое количество знаков вправо в делимом и делителе так, чтобы и там, и там были целые числа. Дальше – алгоритм деления тот же.

Как объяснить ребенку деление и умножение чисел

Искусство учиться

Как объяснить ребенку деление и умножение чисел

3 апреля 2018 52 673 просмотра

Лиана Хазиахметова

Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.

Умножение чисел

При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

Иллюстрация из книги «Как объяснить ребенку математику»

Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.

Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.

Некоторые числа легко умножать, зная особые приемы. Вот они.

Таблица из книги «Как объяснить ребенку математику»

В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

Деление чисел

Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.

Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.

Деление как распределение. Из книги «Как объяснить ребенку математику»

Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.

Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь.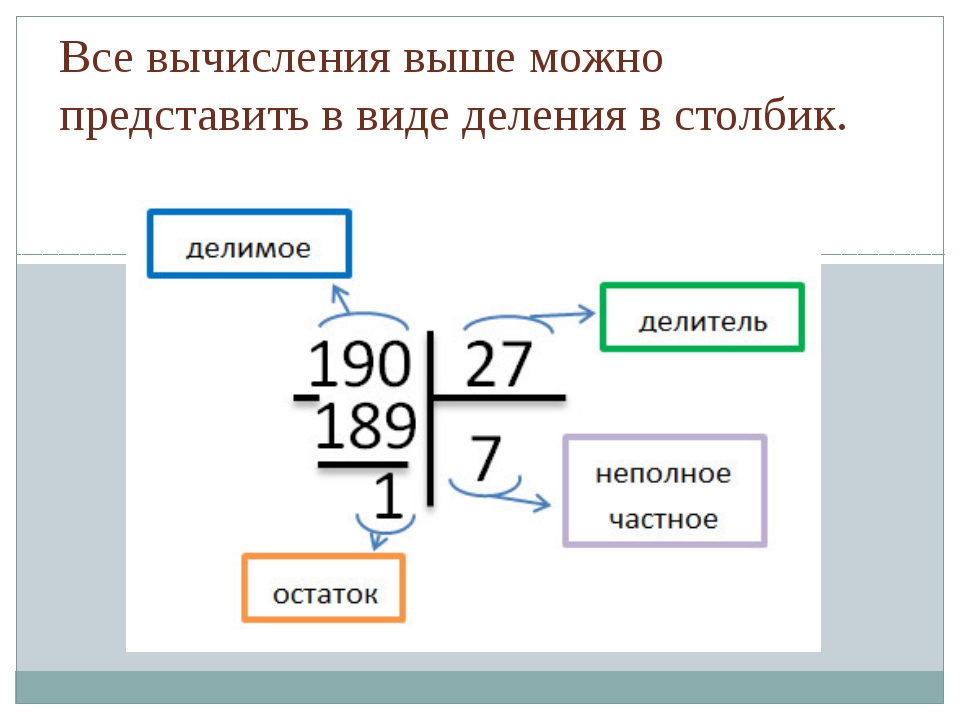 В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.

Рабочие тетради на деление и умножение

Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»

и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.

Пример из тетради «Математика. Деление. Уровень 4»

Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».

По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».

Обложка поста: pixabay.com

Урок 43. приём деления для случаев вида 87 : 29, 66 : 22 — Математика — 3 класс

Математика, 3 класс

Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22

Перечень вопросов, рассматриваемых в теме:

1. Как разделить двузначное число на двузначное?

2. Как выполнить деление вида 87 : 29, 66 : 22?

3. Как проверить правильность результата деления?

Глоссарий по теме:

Деление – это обратное действие умножению

Умножение – это сложение одинаковых слагаемых.

Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.

Обязательная и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М. ; Просвещение, 2017, C-18.

2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.

3. Марченко И.С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.

Теоретический материал для самостоятельного изучения

Рассмотрим решение задачи.

Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?

Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно

используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.

Рассмотрим пример 48 : 12

Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре — не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.

48 : 12

12 ∙ 2 = 24 не подходит

12 ∙ 3 = 36 не подходит

12 ∙ 4 = 48 подходит

Значит,

48 : 12 = 4

В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.

66 : 22

22 ∙ 3 = 66

66 : 22 = 3, так как 22 ∙ 3 = 66

Умножение нужно использовать для проверки правильности вычислений.

88 : 11 = 8, так как 11 ∙ 8 = 88

Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе — цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.

81 : 27 = 3

Делимое 81 — последняя цифра 1

Делитель 27 — последняя цифра 7

7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81

Частное найдено, верно.

Выполним тренировочные задания

Вставьте пропущенные числа:

54 : 27 = ____ , так как 27 ∙ ___ = 54;

Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.

Зачеркните пример с ошибкой:

38 : 19 = 2

42 : 14 = 2

64 : 16 = 3

Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3

Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:

Я 78 : 26

С 99 : 33

В 78 : 13

Й 64 : 16

К 84: 12

О 70 : 14

Е 88 : 11

Ответ:

11 8 7 6 5 4 3

С Е К В О Й Я

Деление в столбик с запятыми калькулятор. Как научиться делить столбиком: примеры и решения

Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.

Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).

Из этой статьи вы узнаете

Принцип деления для малышей

Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.

Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.

Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.

Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.

Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.

Как обучить малыша делению в столбик

Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.

Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.

Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.

При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.

Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.

Умножаем и делим с помощью таблицы

При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.

И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.

Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.

Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.

Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.

В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.

Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.

Делим с помощью столбика

Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.

Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.

В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.

Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.

Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.

Чтобы было проще обучить малыша процессу деления необходимо:

• в 2-3 года понимание отношения целое-часть.
• в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.

Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

• Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
• Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
• Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

• Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
• Спросите у малыша, сколько четверок помещается в двойке — нисколько
• Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
• Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
• Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
• Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
• Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

• Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
• Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

• Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
• Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
• Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
• Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

• Сделать прикидку числа, которое будет стоять в ответе
• Найти первое неполное делимое
• Определить число цифр в частном
• Найти цифры в каждом разряде частного
• Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

• 1428:42
• 2924:68
• 30296:56
• 136576:64
• 16514:718

Для закрепления результата можно использовать такие игры на деление:

• «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340: 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.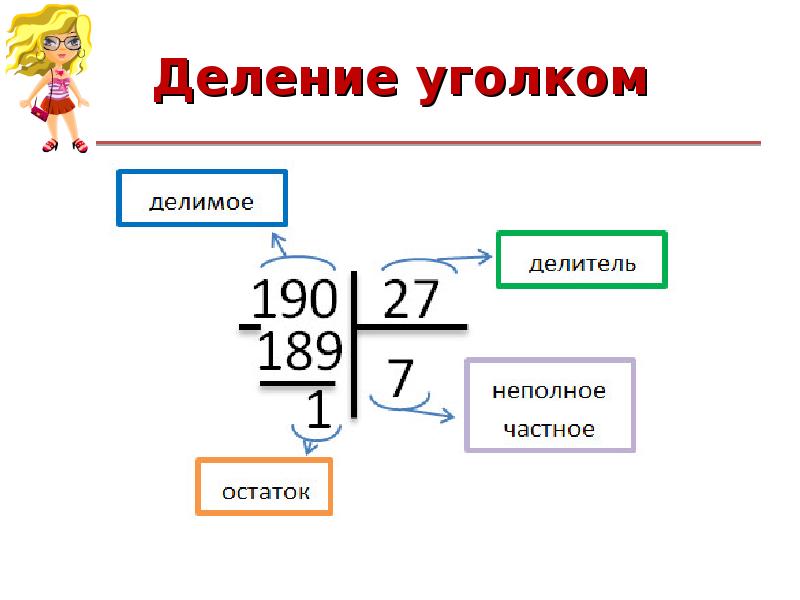

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером.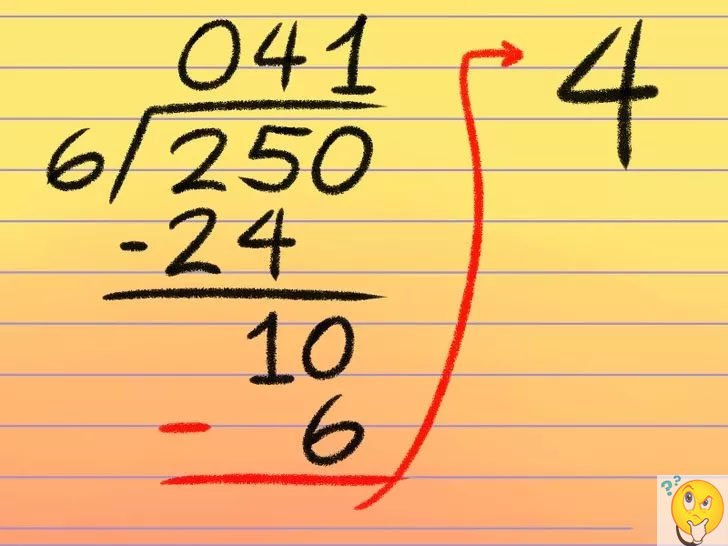 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Деление двузначного числа на однозначное. Примеры

Сначала рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц делится на делитель.

Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы разрядных слагаемых и разделить эту сумму на однозначное число.

Например, чтобы найти значение выражения:

56 : 2

сначала записываем двузначное число  56  в виде суммы разрядных слагаемых:

50 + 6,

то есть просто разбиваем число  56  на сумму пяти десятков и шести единиц. Затем делим сумму  50 + 6  на число  2:

(50 + 6) : 2 = 50 : 2 + 6 : 2 = 25 + 3 = 28,

значит  56 : 2 = 28.

Примеры:

1) 39 : 3 = (30 + 9) : 3 = 30 : 3 + 9 : 3 = 10 + 3 = 13;

2) 75 : 5 = (70 + 5) : 5 = 70 : 5 + 5 : 5 = 14 + 1 = 15;

3) 68 : 4 = (60 + 8) : 4 = 60 : 4 + 8 : 4 = 15 + 2 = 17.

Теперь рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц по отдельности не делятся на делитель.

Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы слагаемых и разделить эту сумму на однозначное число.

Рассмотрим выражение:

52 : 4.

В данном случае разрядные слагаемые числа  52  (50  и  2)  не делятся на  4.  Значит первый способ вычислений здесь не подходит. Тогда можно подобрать ближайшее к  52  круглое число, которое делится на  4,  это будет число  40.  Заменяем делимое  52  на сумму:

40 + 12.

Затем делим сумму  40 + 12  на число  4:

(40 + 12) : 4 = 40 : 4 + 12 : 4 = 10 + 3 = 13,

значит  52 : 4 = 13.

Примеры:

1) 96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12;

2) 51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17;

3) 84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12.

Как видно из примеров, при делении двузначного числа на однозначное используется:

1. представление числа в виде суммы двух чисел или суммы разрядных слагаемых,
2. правило деления суммы на число,
3. знание таблицы умножения.

Краткое деление (метод автобусной остановки) и объяснение длинного деления

Мы работали со специалистами по математике, чтобы создать руководство для родителей по короткому делению (включая метод автобусной остановки) и ужасному длинному делению.

Здесь мы объяснили все, что вам нужно знать, чтобы помочь вашему ребенку с этими сложными темами!

Неважно, деление ли это на короткое или длинное, для многих детей и их родителей простое упоминание о работе «D» может вызвать дрожь по спине у многих молодых математиков, но в этом нет необходимости. по делу!

Здесь, в Third Space Learning, мы стремимся сделать математику доступной для всех, включая короткое и длинное деление …

В прошлом деление преподавалось без особого конкретного моделирования (с использованием физических предметов, чтобы помочь представить математика), поэтому неудивительно, что многим из нас, родителей, и по сей день трудно.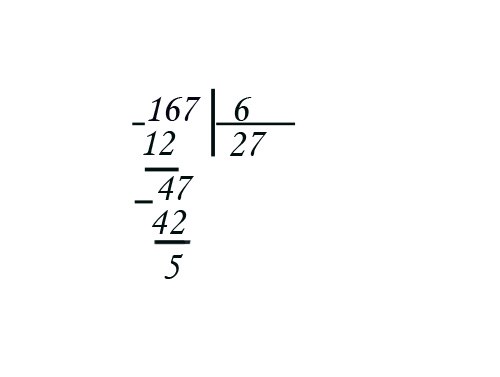

Однако в настоящее время, когда дети проводят много времени в школе, понимая , как работает деление , а не просто запоминают метод, страх по поводу деления KS2 тает, но повторение слов и помощь вашему ребенку в делении дома поможет большая разница

Но прежде чем вы узнаете все, что вам нужно знать о разделении для детей, мы подготовили для вас краткое резюме по разделу!

Эта статья является частью нашей серии, предназначенной для родителей, поддерживающих домашнее обучение и ищущих наборы для домашнего обучения.Он подходит тем семьям, которые проходят обычное или гибкое домашнее обучение, или как часть дополнительной поддержки, которая может вам понадобиться во время карантина и во время отсутствия в школе из-за Covid-19.

---

В двух словах о методах деления

Мы знаем, насколько чертовски трудным может быть деление как для вас, так и для вашего ребенка, поэтому давайте начнем с некоторых определений и краткого обзора того, что вы, возможно, забыли со школы.

Что такое деление в математике?

Деление — это операция, противоположная умножению и включающая разделение на равные части или группы.

В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Это:

• Разделение на части
• Краткое разделение (также известное как метод автобусной остановки)
• Длинное разделение

Что такое разделение на части?

Разделение на части — это метод, который используется для деления больших чисел, которые нельзя разделить мысленно.

При использовании метода сегментирования дочерние элементы будут многократно вычитать делитель из делимого до тех пор, пока не будет получен ответ.Например, 12 ÷ 3 можно решить, выполнив 12-3, чтобы получить 9, 9-3, чтобы получить 6, 6-3, чтобы получить 3, а затем 3-3, чтобы получить 0.

Когда все времена 3 было вычтено из 12, пересчитываются (4), становится ясно, что ответ 4.

Что такое короткое деление?

Короткое деление — это быстрый и эффективный метод определения деления с большими числами.

После того, как ваш ребенок освоится с разбиением на части, он перейдет к короткому разделению, так как его можно использовать для решения задачи разделения с очень большим дивидендом, выполнив ряд простых шагов.

Например:

В этом примере четыре переходит в девять два раза, а остаток остается равным единице.

Этот остаток затем передается на следующее число (шесть), чтобы получилось 16. Четыре четыре раза переходит в 16, поэтому, сложив вместе, получится 24.

Каков метод автобусной остановки?

Метод разделения на автобусных остановках — это просто еще одно название для сокращенного разделения. Он получил свое название от идеи, что дивиденд (число, которое вы хотите разделить) находится внутри автобусной остановки, в то время как делитель ждет снаружи.

Учителя расходятся во мнениях относительно того, действительно ли это изображение полезно при обучении разделению, поэтому в большинстве случаев мы будем называть его сокращенным разделением.

Что такое столбик?

Длинное деление — это метод, который используется при делении большого числа (обычно трех или более цифр) на двузначное (или большее) число. Он изложен аналогично методу автобусной остановки, который используется для сокращения.

Взгляните на наш пример ниже, чтобы увидеть, как деление в столбик объясняется наглядным примером.

Лучше всего это пояснить на примере — см. Ниже.

У нас есть очень подробная статья, написанная для учителей по этому предмету, которая может вам понравиться, если вы хотите более подробно рассказать об обучении методу длинного деления на KS2.

Терминология, которую вам необходимо знать при обучении подразделению

В наших родительских блогах мы стараемся избегать излишнего жаргона, но следующие три термина действительно важны для всех, кто интересуется разделением.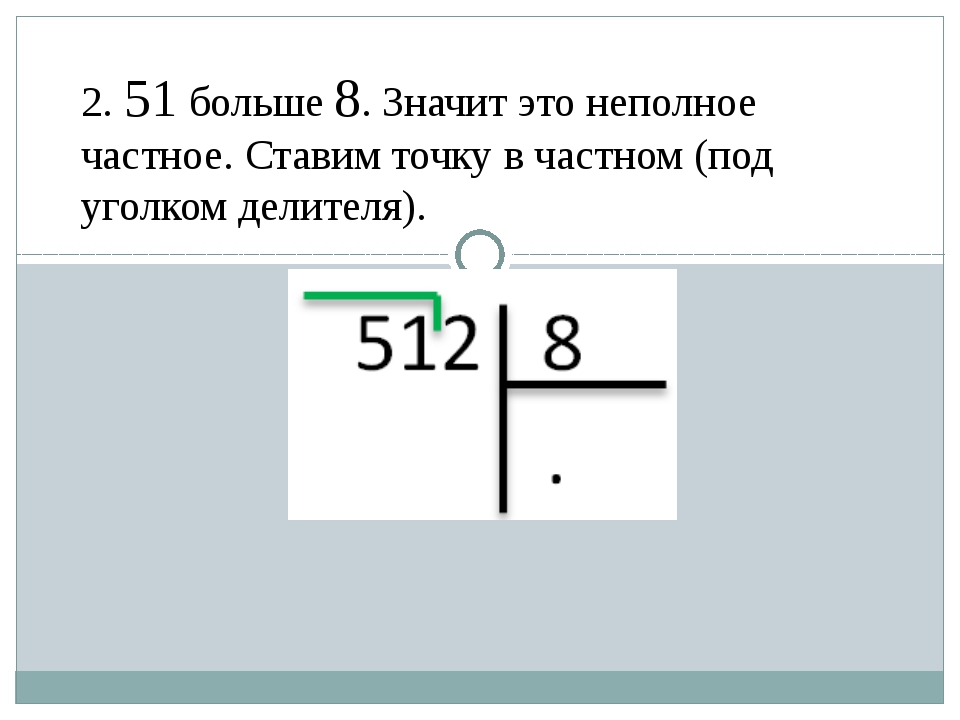

• Дивиденд — это число, которое вы делите (число внутри «автобусной остановки»
• Делитель — это число, на которое вы делите.
• Частное — это сумма, которую получает каждый делитель, то есть ответ в большинстве случаев.

Хороший способ запомнить, что это дивидендов ÷ делитель = частное

Части задачи деления, обозначенные для детей и родителей

Изучая правильный словарь всех частей задачи деления, вы ребенок найдет много элементов деления намного проще.

Что моему ребенку нужно знать о кратком и длинном делении в KS1 и KS2?

Поскольку краткое и длинное деление для детей меняется из года в год на протяжении всей начальной школы, в блоге есть о чем рассказать, но, чтобы помочь вам, мы разбили его по годам.

Дивизион, год 1 : как вы можете помочь

В первом году разделение обычно называется разделением, и оно осуществляется с использованием конкретных предметов, таких как прилавки, блоки или даже такие продукты питания, как макаронные изделия.

Это помогает детям понять разделение как разделение между группами.

Простой пример этого можно найти ниже.

Некоторые простые задачи с разделением слов для первого года обучения

Возьмите набор блоков и помогите своему ребенку решить эти задачи с разделением.

Убедитесь, что вы не забываете использовать такие слова, как share и разделить повсюду, чтобы ваш ребенок познакомился с концепциями.

Начать с 4 блоков. Разделите их на 2 группы одинакового размера.

Начать с 10 блоков. Разделите их на 2 группы одинакового размера.

Начать с 6 блоков. Разделите их на 3 группы одинакового размера.

Присоединяйтесь к Третьему центру космического обучения математике

Чтобы просмотреть всю нашу коллекцию бесплатных и платных ресурсов по математике для учителей и родителей, зарегистрируйтесь, чтобы присоединиться к Третьему центру космического обучения математике. Это быстро, просто и бесплатно! (Пожалуйста, используйте Google Chrome для доступа к Maths Hub)

Division Year 2 : как вы можете помочь

Во 2-м классе дети начинают более глубоко понимать, как работает разделение, и это означает, что есть еще несколько вещи, которым должен научиться ваш ребенок.

Ключевым понятием, которое нужно понять и с которым действительно усвоить в этом возрасте, является коммутативность .

Если вы изо всех сил пытаетесь вспомнить, что именно означает коммутативность, определение простое.

В математике свойство коммутативности утверждает, что порядок не имеет значения.

Умножение коммутативное ; вы можете переключаться между числами, и это не имеет значения.

2 x 3 = 6

3 x 2 = 6

Деление не является коммутативным . Если вы измените порядок чисел, это изменит ответ.

4 ÷ 2 = 2

2 ÷ 4 = 0,5

Деление и коммутативность во 2-м году

В этом возрасте полезно попрактиковаться в изучении таблиц умножения на 2, 5 и 10 с соответствующими фактами деления.Например:

Факт умножения:

2 x 5 = 10

Соответствующие факты деления:

10 ÷ 5 = 2

10 ÷ 2 = 5

Знание этих фактов значительно упрощает деление в дальнейшем, и они отличный пример того, почему коммутативность важна.

Если вашему ребенку комфортно с разницей между 10 ÷ 5 и 10 ÷ 2, даже после того, как он увидел, что 5 x 2 равно 2 x 5, он будет лучше всего подготовлен для комфортного перемещения до короткого деления KS2 и длинного KS2. разделение.

Дивизион 3-й год : как вы можете помочь

В 3-м классе ваш ребенок будет сосредоточиваться на записи вычислений деления и решении простых задач деления, связанных с отсутствием чисел.

Знание фактов умножения и деления здесь очень кстати, поэтому, как и во втором классе, очень важно, чтобы вы практиковали их со своим ребенком.

Эта проблема с отсутствующим числом поможет вам понять, почему знание таблицы умножения значительно упрощает деление:

5 x 4 = 20

__ ÷ 5 = 4

20 ÷ __ = 5

Есть также два письменных метода деления, которые вводятся в этом возрасте, и они разбиты ниже.

Письменные методы деления для детей

Объяснение метода деления на части

Хотя этот метод немного медленнее, чем деление на автобусной остановке, он отлично подходит для развития умственных способностей детей, необходимых для более сложного деления в дальнейшем.

Как выполнить разбиение на части Метод деления

Разделение на части — это когда вы вычисляете, сколько раз одно число умещается в другое число.

Вы решаете это, многократно вычитая делитель (или кратные делителю), пока не дойдете до нуля, чтобы увидеть, сколько раз делитель может войти в число, которое вы делите (делимое).

Разделение на части — хороший способ познакомить вашего ребенка с некоторыми из наиболее основных концепций деления, и когда он смирится с этим, он может перейти к короткому методу деления.

Объяснение метода краткого деления или метода автобусной остановки

Часто его называют методом автобусной остановки из-за того, что при нанесении на лист бумаги расчет имеет некоторое визуальное сходство с автобусной остановкой, этот метод краткого деления KS2 — один из самых популярных методов, которым преподают в школах.

Этот метод быстрее, чем разбиение на части, но важно, чтобы дети понимали, что они делают (а не просто следовали методу).

Это значительно упростит деление в столбик в будущем, но рекомендуется убедиться, что ваш ребенок хорошо справился с делением на части, прежде чем переходить к разделению на короткие.

Как делать короткое деление

Краткое деление в этом возрасте будет включать однозначные делители и трех- или четырехзначные дивиденды.

Сядьте вместе с ребенком и посмотрите на диаграмму ниже, чтобы узнать названия и места для каждой части задачи деления.

Они могут показаться очень незнакомыми, если вы привыкли записывать свои суммы в строку, поэтому поработайте со своим ребенком, чтобы убедиться, что он знает свой делитель по своим дивидендам!

Как помочь своему ребенку разделить трех- или четырехзначное число на однозначное

С этими типами вопросов деления, составляющими большую часть того, что ваш ребенок будет решать в 3-м классе, вот графическое описание того, как разделите трех- или четырехзначное число на однозначное число.

Дивизион 4-й год : как вы можете помочь

В 4-м классе ваш ребенок будет использовать краткое деление (метод деления на автобусной остановке, описанный выше) для деления чисел до четырех цифр на двузначные числа.

Метод точно такой же, как и с однозначными числами, но первый шаг всегда будет включать группировку.

На этом этапе процесс деления становится гораздо более трудным, если ваш ребенок не знает наизусть свои таблицы умножения, поэтому одно из лучших действий, которые вы можете для него сделать, — это поддержать их изучение.

Им также нужно будет выбрать, какой остаток использовать в зависимости от вопроса, а некоторые общие вопросы будут связаны с ситуациями из реальной жизни, например, разделение групп между машинами или предметами между коробками.

Разделение вопросов с остатками

Остатки могут быть сложной задачей для понимания, когда дети впервые знакомятся как с кратким, так и с длинным делением, но важно, чтобы они хорошо их понимали, так как они могут резко измениться в зависимости от вопроса, который спрашивают.

Практикуйтесь в использовании пар факторов в 4-м классе, чтобы облегчить письменное деление

Пары факторов — это два фактора (числа), которые при умножении дают конкретный продукт (результат).

Практика пар факторов с вашим ребенком может помочь ускорить процесс, когда дело доходит до деления, так как знание того, что 4 x 5 = 20, поможет им, когда дело доходит до отработки 20 ÷ 4 = _.

Попросите ребенка найти как можно больше пар факторов для числа, указанного ниже, и почему бы не превратить это в игру?

Сядьте вместе с ребенком, возьмите ручку и лист бумаги и посмотрите, кто сможет вычислить наибольшее количество пар факторов для следующих чисел за минуту.Результаты могут быть ближе, чем вы думаете!

Подробнее: Какой наивысший общий коэффициент

Дивизион 5-й год : как вы можете помочь

К 5-му классу ваш ребенок должен быть в состоянии быстро мысленно сократить вдвое или четверть суммы.

Если им сложно, использование математики в реальном мире может стать отличным способом помочь им разобраться с половинками и четвертями. Например, когда вы находитесь вне дома, спросите их, сколько стоила бы вещь, если бы она была наполовину дешевле, или сколько граммов было бы в половине 1-килограммового мешка сахара.

Умение быстро разделить на 2 (деление пополам) и 4 (четвертование) станет важной частью деления по мере того, как ваш ребенок будет учиться в школе, поэтому будет очень полезно, если он сможет выучить их сейчас.

Краткое деление с десятичными знаками

Краткое деление будет использоваться для чисел, содержащих десятичные дроби, впервые в 5-м классе.

Это означает, что сейчас хорошее время для пересмотра разряда, чтобы ваш ребенок понял, как работают десятичные дроби.

Десятичные дроби — это части целого (аналогично дробям), но важно помнить, когда дело доходит до деления десятичных знаков, это то, что столбцы с размеченными значениями уменьшаются в значении каждый раз, когда вы перемещаетесь вправо.

Пример десятичного деления

Дивизион 6-й год: чем вы можете помочь

В 6-м классе ваш ребенок впервые познакомится с ужасным делением в столбик!

Однако хорошая новость заключается в том, что после того, как вы освоите дробление и короткое деление, длинное деление совсем не плохо!

Ключ, когда дело доходит до длинного деления для детей, — это действовать медленно и поощрять их аккуратно представлять свою работу, чтобы они могли легко замечать ошибки и работать над их исправлением.

Даже зная это, деление в столбик все еще может быть пугающей перспективой для детей (и родителей в равной степени!), Поэтому взгляните на наш пример ниже, чтобы понять, как решить проблему деления в столбик.

Объяснение для детей в длинное деление

Приведенный ниже пример является наиболее популярным методом деления в столбик для детей, и вы, возможно, знакомы с ним еще в начальной школе.

Все, что вам понадобится для выполнения вычисления 528 ÷ 24, — это ручка, немного бумаги и ребенок, который хочет освоить этот метод!

После того, как вы ответите на несколько вопросов о длинных делениях (для начала с вашей помощью), ваш ребенок скоро увидит, что этот метод может помочь ему понять, как решать задачи с длинным делением, независимо от используемых чисел, и окажется бесценным. когда дело доходит до SAT.

Как сделать длинное деление: простой пошаговый метод длинного деления для использования в KS2

Не беспокойтесь, если на то, чтобы по-настоящему встроить процесс, потребуется время. Это длинная цепочка вещей, которые нужно запомнить, поэтому вам потребуется регулярная практика, чтобы запомнить этот метод.

Просто запомните процесс: деление, умножение, вычитание, уменьшение; и повторить.

Тяжелая работа окупится в долгосрочной перспективе, поэтому сейчас стоит уделить время ребенку, чтобы убедиться, что деление в столбик хорошо объяснено на ранней стадии, чтобы уменьшить количество раз, когда вы услышите неизбежное:

“ Ммммммм …….Как у вас деление в столбик…? »

Как узнать, когда делить и какой метод использовать?

Для решения разных вопросов деления требуются разные методы деления, но вот краткое и простое руководство, которое покажет, какой метод и когда следует использовать вашему ребенку:

• Разделение на части лучше всего подходит для меньших чисел и арифметики.
• Краткое деление отлично подходит для деления больших чисел на однозначные числа.
• Длинное деление удобно для деления больших чисел на числа, состоящие из двух и более цифр.

Конечно, могут быть случаи, когда каждый из вышеперечисленных методов может использоваться в немного разных сценариях, но, как правило, этого должно быть достаточно, чтобы помочь вашему ребенку принять правильное решение.

Вопросы по SAT для 6-го класса

Когда придет время сдавать экзамены по SAT по математике, более чем вероятно, что вашему ребенку придется ответить на некоторые вопросы по разделам.

Решение проблем и рассуждения (работы 2 и 3) в 6 классе могут быть непростыми, когда дело доходит до задач разделения.Часто проблемы требуют выполнения более одной операции, что может добавить элемент сложности в и без того напряженную среду, поэтому поощряйте ребенка искать такие слова, как доля или группа , чтобы помочь им определить что нужно сделать для решения проблемы.

Задачи на деление в Задании 1 (арифметика) будут представлены в виде числовых предложений, и ваш ребенок должен будет показать свое решение, если вопрос стоит более 1 балла.

Эти вопросы легко определить, потому что они будут использовать символы деления:

÷

или

, или они могут включать дроби.

Как правило, поощряйте вашего ребенка мысленно делиться там, где это возможно.

Хотя письменные методы отлично подходят для больших чисел, умение мысленно делить дает им преимущество. Это означает, что когда они будут выполнены с использованием письменного метода, они смогут увидеть, является ли их ответ примерно правильным, оценив его.

Наряду с бесплатными рабочими листами для полных делений вы также можете загрузить набор бесплатных вопросов SAT по делению и умножению, чтобы расширить свою практику.

Это должно было охватить все, что вам нужно знать о разделении для детей. Если вы хотите найти больше способов помочь с домашним заданием по математике, мы рекомендуем вам также взглянуть на следующие руководства «по объяснению для родителей и детей».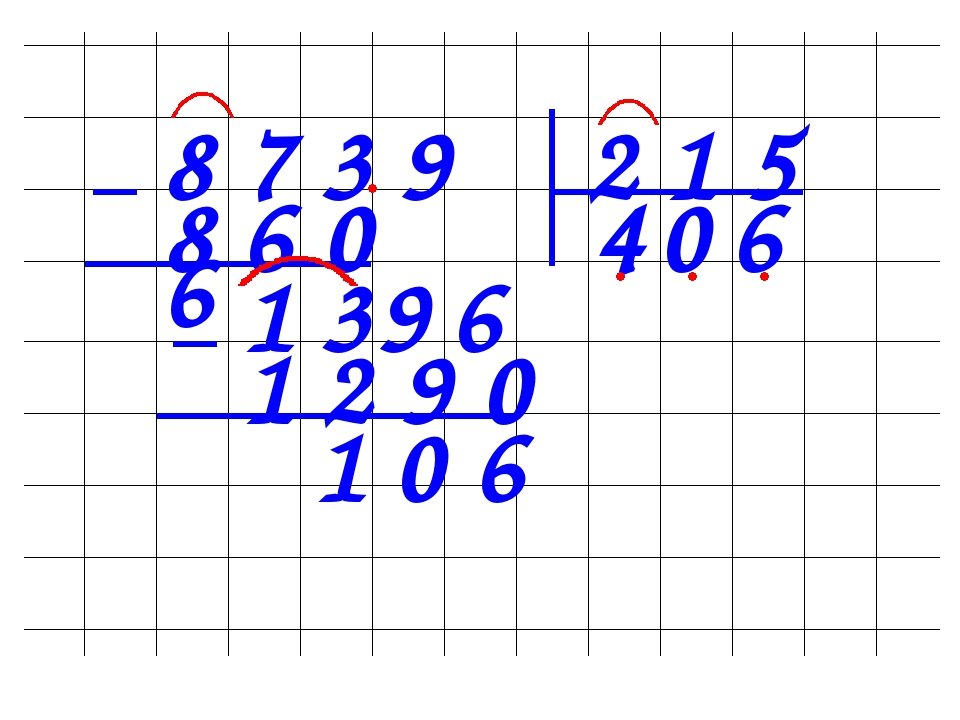

Индивидуальные онлайн-уроки математики, которым доверяют школы и родители.
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи младших школьников, предлагая еженедельные индивидуальные онлайн-уроки и занятия по математике.С 2013 года мы помогли более чем 70 000 детей стать более уверенными и способными математиками. Узнайте, как дети могут быстрее успевать по математике вместе с нами в школах и дома.

Обучение математике для детей в возрасте от 5 до 12 лет, ориентированное на национальную учебную программу и проводимое онлайн

Используйте этот быстрый трюк, чтобы ускорить работу в длинных дивизионах

Научитесь разделять с помощью точек и линий

Если вы когда-нибудь видели японский трюк с умножением с помощью линий, вы знаете, что выполнение математических расчетов вручную не обязательно должно означать выполнение этого по старинке.Если деление в столбик всегда сбивает вас с толку или вы просто хотите попробовать что-то новое, этот трюк может быть для вас.

Начните с выбора числа, которое нужно разделить на другое: мы собираемся попробовать разделить 145 824 на 112. Первый шаг — нарисовать точки на листе бумаги в столбцах, где в каждом столбце есть количество точек, представляющее цифру в число, которое вы делите. Итак, у нас есть столбец с одной точкой, столбец с четырьмя точками, столбец с пятью точками и так далее.

Теперь мы проведем линии между точками.Поскольку мы делим на 112, мы собираемся соединить одну точку из столбца с одной точкой из следующего столбца с двумя точками из третьего столбца. Вы всегда начинаете как можно дальше влево (где есть пустые точки).

Последний шаг включает подсчет количества групп строк, начинающихся в каждом столбце. В нашем примере одна группа начинается в первом столбце (красный), три группы начинаются в следующем столбце (синий), затем нет, а затем две (зеленый). Это дает нам ответ: 1302. Вы должны не забыть поставить ноль для любого столбца, который не начинает новую строку, но вы можете игнорировать столбцы в конце — если ответ не заканчивается нулями.Я рекомендую умножить его, чтобы проверить, нужны ли они вам.

В некоторых случаях этот метод может оказаться немного сложным, если в определенном столбце недостаточно точек. В этом случае вам нужно будет преобразовать одну из точек из столбца в десять точек в следующем столбце. Вот еще один пример, чтобы увидеть, как это работает: 3328/104. В этом случае одна из точек из второго столбца преобразуется в 10 точек в третьем столбце (показано серым).

Посмотрите видео ниже, чтобы увидеть, как эту технику можно использовать и для деления полиномов в длину!

Матрицы

Матрица — это массив чисел:

Матрица
(в ней 2 строки и 3 столбца)

Речь идет об одной матрице , или нескольких матрицах .

Мы можем многое с ними сделать …

Добавление

Чтобы сложить две матрицы: сложите числа в соответствующих позициях:

Это расчеты:

3 + 4 = 7	8 + 0 = 8
4 + 1 = 5	6−9 = −3

Две матрицы должны быть одинакового размера, т.е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.

Пример: матрица с 3 строками и 5 столбцами может быть добавлена ​​к другой матрице из 3 строк и 5 столбцов .

Но не удалось добавить в матрицу с 3 строки и 4 столбца (столбцы не совпадают по размеру)

отрицательный

Негатив матрицы тоже прост:

Это расчеты:

— (2) = — 2	— (- 4) = + 4
— (7) = — 7	— (10) = — 10

Вычитание

Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:

Это расчеты:

3-4 = -1	8−0 = 8
4−1 = 3	6 — (- 9) = 15

Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (−B)

Умножить на константу

Мы можем умножить матрицу на константу (значение 2 в данном случае) :

Это расчеты:

2 × 4 = 8	2 × 0 = 0
2 × 1 = 2	2 × −9 = −18

Мы называем константу скаляром , поэтому официально это называется «скалярное умножение».

Умножение на другую матрицу

Чтобы перемножить две матрицы вместе немного сложнее … прочтите Умножение матриц, чтобы узнать, как.

Разделение

А что с делением? Ну, мы не делим матрицы на , мы делаем это так:

A / B = A × (1 / B) = A × B ^-1

, где B ^-1 означает «обратное» B.

Итак, мы не делим, вместо этого мы умножаем на обратное .

И есть особые способы найти обратное, подробнее см. Обратный к матрице.

Транспонирование

Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.

Мы ставим букву «Т» в верхнем правом углу, чтобы обозначить транспонирование:

Обозначение

Матрица обычно обозначается заглавной буквой (например, A или B)

Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» строки , столбец :

Строки и столбцы Итак, какая строка, а какая колонка? Рядов слева направо Колонны идут вверх-вниз Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : a r, c

Пример:

B =

Вот несколько примеров записей:

b _1,1 = 6 (запись в строке 1, столбце 1 — 6)

b _1,3 = 24 (запись в строке 1, столбце 3 — 24)

b _2,3 = 8 (запись в строке 2, столбце 3 — 8)

Как разделить в Excel

В Excel нет функции РАЗДЕЛЕНИЕ.Просто используйте косую черту (/), чтобы разделить чисел в Excel .

1. Приведенная ниже формула делит числа в ячейке. В качестве оператора деления используйте косую черту (/). Не забывайте, всегда начинайте формулу со знака равенства (=).

2. Приведенная ниже формула делит значение в ячейке A1 на значение в ячейке B1.

3. Excel отображает # DIV / 0! ошибка, когда формула пытается разделить число на 0 или пустую ячейку.

4. Приведенная ниже формула делит 43 на 8. Ничего особенного.

5. Вы можете использовать функцию ЧИСЛО в Excel, чтобы вернуть целую часть деления. Эта функция отбрасывает остаток от деления.

6. Функция МОД в Excel возвращает остаток от деления.

Посмотрите на снимок экрана ниже. Чтобы разделить числа в одном столбце на числа в другом столбце, выполните следующие действия.

7а. Сначала разделите значение в ячейке A1 на значение в ячейке B1.

7б. Затем выберите ячейку C1, щелкните в правом нижнем углу ячейки C1 и перетащите ее в ячейку C6.

Посмотрите на снимок экрана ниже. Чтобы разделить столбец чисел на постоянное число, выполните следующие шаги.

8а. Сначала разделите значение в ячейке A1 на значение в ячейке A8. Исправьте ссылку на ячейку A8, поместив символ $ перед буквой столбца и номером строки ($ A $ 8).

8б. Затем выберите ячейку B1, щелкните в правом нижнем углу ячейки B1 и перетащите ее в ячейку B6.

Объяснение: когда мы перетаскиваем формулу вниз, абсолютная ссылка ($ A $ 8) остается неизменной, а относительная ссылка (A1) изменяется на A2, A3, A4 и т. Д.

Если вы не являетесь героем формул, используйте Специальную вставку для деления в Excel без использования формул!

9. Например, выберите ячейку C1.

10. Щелкните правой кнопкой мыши и выберите «Копировать» (или нажмите CTRL + c). 2} -7x + 18 [/ latex], а остаток равен –31.Процесс будет более понятен в следующих примерах.

A Общее примечание: Подразделение синтетических материалов

Синтетическое деление — это ярлык, который можно использовать, когда делитель является биномом в форме x — k . В синтетическом делении в процессе деления используются только коэффициенты.

Как сделать: даны два многочлена, используйте синтетическое деление, чтобы разделить

1. Запишите k вместо делителя.
2. Напишите коэффициенты дивиденда.
3. Понизьте ведущий коэффициент.
4. Умножьте старший коэффициент на k . Напишите продукт в следующем столбце.
5. Добавьте условия второго столбца.
6. Умножьте результат на k . Напишите продукт в следующем столбце.
7. Повторите шаги 5 и 6 для остальных столбцов.
8. Используйте нижние числа для записи частного. Число в последнем столбце является остатком и имеет степень 0, следующее число справа имеет степень 1, следующее число справа имеет степень 2 и т. Д.{2} -3x — 36 [/ латекс] по [латекс] х — 3 [/ латекс].
   Показать решение

   Начнем с создания синтетического подразделения. Напишите k и коэффициенты.

   Понизьте ведущий коэффициент. Умножьте старший коэффициент на k .

   Продолжайте, добавляя числа во второй столбец. Умножьте полученное число на k . Запишите результат в следующий столбец. Затем сложите числа в третьем столбце.

   Результат: [латекс] 5x + 12 [/ латекс].{2} + 21x — 150+ \ frac {1,090} {x + 7} [/ латекс]

   https://www.myopenmath.com/multiembedq.php?id=29483&theme=oea&iframe_resize_id=mom1

   Полиномиальное деление можно использовать для решения множества прикладных задач, связанных с выражениями для площади и объема. Мы рассмотрели приложение в начале этого раздела. Теперь мы решим эту проблему на следующем примере. {2} + 54x = 3x \ cdot \ left (x — 2 \ right) \ cdot h \ end {array} [/ latex]

   Чтобы найти h , сначала разделите обе части на 3 x .{2} -4x + 1 [/ латекс]

   Внесите свой вклад!

   У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

   Улучшить эту страницуПодробнее

   Массивы, умножение и деление

   Массивы, умножение и деление

   Дженни Пеннант с помощью Дженни Уэй и Майка Аскью исследует, как использовать массив в качестве инструмента мышления, чтобы помочь детям развить глубокое понимание умножения и деления.

   Использование массивов для исследования чисел

   Массивы — это полезные модели для умножения, которые можно использовать по-разному, от высоко структурированных уроков до игр и открытых исследований.

   Массив формируется путем размещения набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, что и другие столбцы, и каждая строка должна иметь то же количество объектов, что и другие строки.

   Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12, 4 x 3 = 12, 3 + 3 + 3 + 3 = 12 и 4 + 4 + 4 = 12.

   Построение фактов и таблиц умножения

   Массивы можно использовать для конструктивного построения фактов умножения.Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты выводятся. Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить себе трехкратные таблицы. Это представление не только помогает понять процесс, но и дает визуальное изображение для детей, на которых можно рисовать, когда они начнут использовать и запоминать основные числовые факты.

   Использование массивов для исследования больших чисел

   Массивы могут быть полезны для изучения вычислений, таких как 13 x 5, где массив можно разделить на полезные части, такие как 10 и 3.Это означает, что дети могут использовать свои известные числовые факты для вычислений.

   Здесь 13 x 5 = (10 x 5) + (3 x 5).

   Через некоторое время рисование всех точек может стать очень утомительным! Пустой массив становится очень полезным инструментом, помогающим детям моделировать свое мышление и разрабатывать более сложные операции умножения в неформальной обстановке.

   Вот ребенок, использующий пустой массив в качестве инструмента мышления, чтобы помочь им вычислить 15 x 14.

   Пустой массив помогает детям использовать другие стратегии, такие как компенсация, при выполнении умножения.Здесь, чтобы вычислить 34 x 9, ребенок решил сделать 34 x 10, а затем снять 34 x 1.

   Помимо пустого массива, эта стратегия «деления умножения на простые части» может быть формализована в виде сеточный метод. Дети могут видеть, как «абстрактный» метод сетки накладывает на массив и формализует пустой массив в стандартной форме.

   Деление как обратная операция умножения

   Из четырех операций деление является наиболее сложной задачей для молодых студентов.Полное понимание деления обычно сильно отстает от других операций. Для многих детей возможности исследовать концепцию на конкретных материалах ограничиваются задолго до того, как они осознают взаимосвязь между разделением и тремя другими операциями. Одна из таких отношений, обратная связь Между делением и умножением можно эффективно проиллюстрировать использование массивов.

   Например; 3 × 5 = 15 или 3 строки из 5 составляют 15, могут быть представлены следующим массивом.

   Если взглянуть на массив по-другому, можно увидеть обратное, то есть
   15 ÷ 3 = 5 или 15, помещенные в 3 строки, дают 5 столбцов — или 5 в каждой строке.

   Язык явно играет важную роль в способности выражать математические отношения, и физический массив поддерживает этот аспект понимания, давая детям конкретный образ, о котором можно говорить.

   Размещение математики в контексте реальной жизни с помощью словесных задач может облегчить как понимание взаимосвязи, так и ее выражение в словах.

   Например, «Садовник посадил 3 ряда по 5 семян. Сколько семян она посадила?» представляет собой совсем другую проблему, чем «Садовник посадил 15 семян в 3 равных ряда. Сколько семян в каждом ряду?» тем не менее, обе эти проблемы со словами можно смоделировать с использованием одного и того же массива.

   Дальнейшее изучение массива обнаруживает еще два способа выражения обратных отношений: 5 × 3 = 15 и 15 ÷ 3 = 5.

   Слова «проблемы» могут быть адаптированы для описания этих операций и выделения сходства и различий между четырьмя выражениями, смоделированными одним массивом.

   Использование пустого массива
   Предположим, вы хотите вычислить 176 ÷ 8. Мы можем настроить его как массив с отсутствующим значением одной стороны.

   Используя известные факты умножения, можно построить значение отсутствующей стороны.
   
   Итак, ребенок может видеть, что 22 лота из 8 — это то же самое, что и 176.

   Массив — очень мощный инструмент для поддержки развития детского мышления как в отношении умножения, так и деления.

   Дополнительная литература
   Чтобы прочитать об использовании массивов для иллюстрации числовых свойств, перейдите сюда, чтобы прочитать статью Дженни Уэй, озаглавленную «Иллюстрирование числовых свойств с помощью массивов».

   Вот версия этой статьи в формате PDF.

   Синтетическое подразделение

   Синтетика Подразделение: Процесс (стр. 1 из 4) Разделы: Введение, Наработанные примеры, поиск нули, факторинговые многочлены Синтетическое подразделение сокращенный или сокращенный метод полинома разделение в частный случай деления на линейный множитель — а это только работает в этом случае.Синтетическое деление обычно используется, но не для разделения множителей, но для нахождения нулей (или корней) многочленов. Подробнее об этом позже. Если вам дается, скажем, полиномиальное уравнение y = x 2 + 5x + 6, вы можете разложить полином на множители как y = ( x + 3) ( x + 2). потом вы можете найти нули y установив каждый коэффициент равным нулю и решив.Вы обнаружите, что x = 2 и x = 3 — два нуля от до . Однако вы также можете работать в обратном направлении от нулей, чтобы найти исходный многочлен. За Например, если вам дано x = 2 и x = 3 — нули квадратичной, то вы знаете, что x + 2 = 0, поэтому x + 2 — коэффициент, а х + 3 = 0, поэтому x +3 — фактор.Следовательно, вы знаете, что квадратичный должен иметь вид y = a ( x + 3) ( x + 2). (Дополнительный номер « а » в этом последнем предложении есть, потому что, когда вы работаете назад от нули, вы не знаете, к какой квадратичной вы работаете. За любое ненулевое значение « a «, ваш квадратичный по-прежнему будет иметь те же нули.Но вопрос стоимости из « а » это просто техническое соображение; пока вы видите отношения между нулями и множителями, это все, что вам действительно нужно знать для этого урока.) В любом случае, это многословный способ сказать, что если x n — коэффициент, затем x = n равно ноль, и если x = n это ноль, тогда x n — фактор.И это тот факт, который вы используете, когда делаете синтетическое деление. Давайте еще раз посмотрим на квадратичная сверху: y = x 2 + 5 x + 6. Из Рационального Тест на корни, ты знаю это 1, 2, 3 и 6 возможных нулей квадратичной. (И из приведенного выше факторинга вы знаете, что нули на самом деле 3 и 2.) Как бы вы использовали синтетическое деление для проверки потенциальных нулей? Что ж, подумай, как долго полиномиальное деление работает. Если мы догадаемся, что x = 1 — ноль, тогда это означает, что x 1 — коэффициент квадратичный. А если это фактор, то он будет делиться поровну; который есть, если разделить x 2 + 5 x + 6 по х 1, мы получили бы нулевой остаток.Проверим: Как и ожидалось (поскольку мы знаем что x 1 не является фактором), мы получили ненулевой остаток. Как это выглядит в синтетическом дивизионе? Авторские права Элизабет Стапель 2002-2011 Все права защищены Сначала напишите ТОЛЬКО коэффициенты внутри перевернутого символа деления: Убедитесь, что вы ушли комната внутри, под строкой коэффициентов, чтобы написать еще ряд чисел позже. Поставь тестовый ноль, х = 1, слева: Возьмите первое число внутри, представляя ведущий коэффициент, и переносим его вниз, без изменений, до символа деления ниже: Умножить это понижающее значение на тестовый ноль, и переносим результат вверх в следующий столбец: Добавить столбец: Умножить предыдущее значение переноса на тестовый ноль, а новый результат перенести в последний столбец: Добавить столбец: Этот последний перенос значение — остаток. Сравнивая, можно увидеть что мы получили тот же результат от синтетического деления, такое же частное (а именно 1 x + 6) и тот же остаток в конце (а именно 12), как когда мы делали длинное деление: Результаты отформатированы по-разному, но вы должны понимать, что каждый формат предоставил нам результат, являющийся частным x + 6, а остаток из 12. Вы уже знаете (из приведенного выше факторинга), что x + 3 — фактор полинома, и, следовательно, x = 3 — ноль. Теперь сравните результаты деления в столбик и синтетического деления. когда мы используем коэффициент x + 3 (для длинное деление) и ноль x = 3 (для синтетическое подразделение): Как видно выше, в то время как результаты имеют другой формат, в остальном результаты такие же: В длинном дивизионе я делится на коэффициент x + 3 и достигли результат x + 2 с остатком нуля.Это означает, что x + 3 — коэффициент, а что x + 2 осталось после факторинга из x + 3. Установка факторов равно нулю, я получаю x = 3 и x = 2 — нули квадратичной. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт