Как научить дауна математике: НУМИКОН — методика изучения математики для детей с синдромом Дауна. Практические советы применение для «солнечных детей» — Яркий Дворик

Содержание

НУМИКОН — методика изучения математики для детей с синдромом Дауна. Практические советы применение для «солнечных детей»

Синдром Дауна — это генетическая аномалия, которая проявляет себя в присутствии лишней хромосомы в 21 паре. Пока нет окончательного утверждения какие именно факторы могут повлечь или предотвратить развитие этой аномалии.

Когда родители узнают о диагнозе своего ребенка, то часто впадают в панику, испытывают страх и волнения. Но несмотря на все, они мечтают о комфортной и счастливой жизни для своего ребенка. Перед ними стоит задача — создать достойные условия для жизни ребенка, сделать ее длительной и насыщенной, помочь ребенку приспособиться к этому миру. Благодаря совместной работе родителей и специалистов можно достичь значительных успехов в учебе, социализации. «Солнечные дети» ходят в детские сады, учатся в школе и даже вступают в высшие учебные заведения.

У многих детей, включая детей с синдромом Дауна возникают трудности при изучении математики. На помощь родителям и педагогам приходит программа Нумикон, которая имеет доказанную эффективность в обучении.

Начинать работать с Нумикон нужно как можно быстрее, но ребенок к этому должен быть подготовлен.

Что нужно знать до Нумикона?

Развиваем мышление через внимание, память и логику.

Прежде всего важна концентрация внимания — содержание информации об определенном объекте в кратковременной памяти. Это происходит не только из-за визуализации, но и через тактильные ощущения. Внимательно дышим, едим, играем. Без развития внимание не будет математики.

Пространственное восприятие — это возможность стоять, двигаться, ориентироваться, принимать решения, анализировать. Обычно происходит через детские игры — прятки, игры с мячом, кубиками, пальчиками и др. Ребенок учится пониманию — большой-маленький, узкий-широкий, низкий-высокий, ближе-дальше. Это и есть начальные математические представления.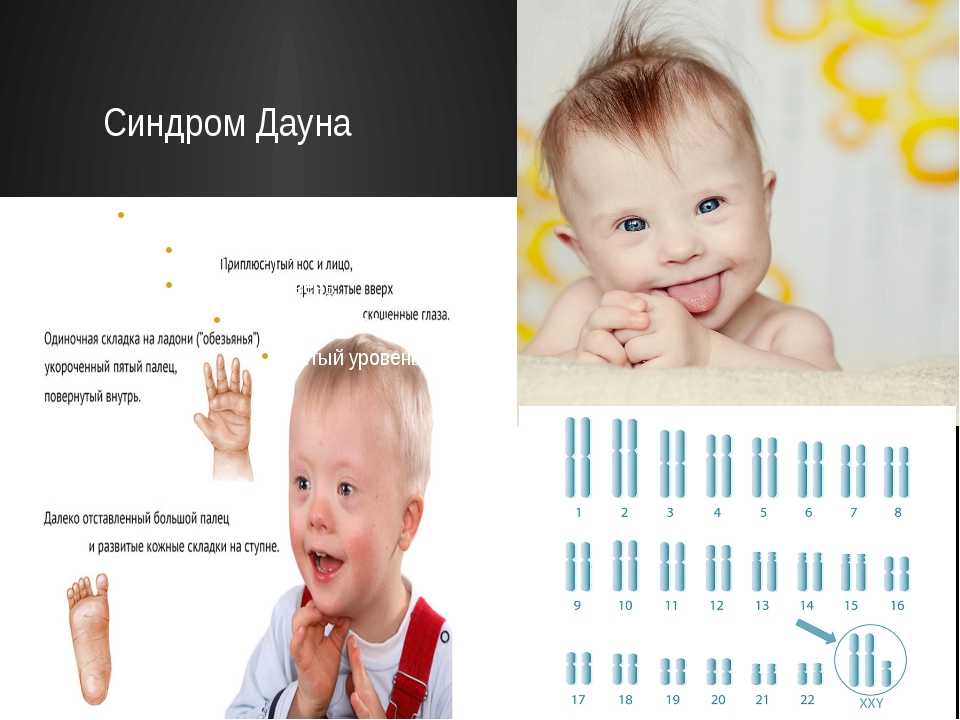

Устойчивость внимания показывает, как долго ребенок может сосредоточиться на объекте или задаче, которую выполняет. Это можно проверить через игры с правилами или ролевые игры.

Развитие внимания очень важно, но это чрезвычайно сложный процесс для ребенка с синдромом Дауна. Поэтому нужно много общаться, хвалить, верить и поддерживать ребенка. Не допускать нервного напряжения, делать перерывы и при необходимости остановиться или даже вернуться на шаг назад.

Память

Информация должна быть яркой и образной. Обычно мы запоминаем то, что нас поразило и вызвало эмоции. Важно не только увидеть определенный объект, а прощупать, понюхать или даже попробовать на вкус. Нужно обеспечить применение этого предмета в быту. А еще здесь хорошо работают ассоциации. На примере Нумикона в дальнейшем можно применять такую ассоциацию: четные числа — кроватки, нечетные — стульчики.

Логика

Книги и журналы с логическими задачами и загадками, кроссворды, сканворды, головоломки, настольные игры. Такого материала множество. Но с ним стоит подождать. Начинать развивать логическое мышление нужно с самого простого. Пригодятся игрушки, одежда, обувь, кухонные принадлежности и другие бытовые предметы. Самый простой пример с кубиком и шариком. Почему шарик катится, а кубик нет?

Этапы работы с Нумикон

На первом этапе (сенсорном) преобразуем математику в игру и важно здесь задействовать все органы чувств.

Основная задача — освоить формы, запомнить их имена — Один, Два, Три и т.д. Очень важно в дальнейшем так и называть детали.

Практические советы

— Сюжетные игры. Формы становятся героями сказок, игр, театра. Один идет в гости к Два, Три съезжает с горки, Пять гуляет с Сем. Из подручных средств делаем домики, в которых будут жить наши герои или транспорт, в котором они будут путешествовать. А также формы могут «оживать» на рисунках ребенка.

— Заполняем пространство — делаем квадрат, используя один набор от 1 до 10, заполняем формами уже заранее подготовленный рисунок, складываем формы в коробку.

— Выкладываем и чередуем узоры из форм и счетных трубочек. Можно воспользоваться примерами рисунков, которые есть в наборах Нумикон или подключать фантазию и создавать свои изображения.

— Сортируем формы по цвету и по разным емкостях.

— Готовим печенье и потом кушаем его.

— Прячем формы под подушку, в мешочек, носки, песок, крупы, воду. Затем достаем, угадываем на ощупь. Каждому ребенку может подойти разный тактильный материал.

— Обводим, отбиваем на кинетическом песке, пластилине, глине. Купаем в ванне, бассейне.

— Строим башни, высотные дома, лестницы.

— Чтобы ребенку было интереснее, добавляем к играм и занятиям стишки, песенки, считалки. А также меняем игры. Возможностей множество и это все прекрасно работает.

На сенсорном периоде нужно задержаться минимум на 3 месяца. Кроме игр, счет используем в быту, на прогулках, во время путешествий, в очередях и тому подобное.

На втором этапе выстраиваем числовой ряд, сопоставляем с цифрами, разбираем числовой ряд. На этом этапе постоянно все озвучиваем, обсуждаем, повторяем.

Практические советы

Повесить на стену числовую ленту и постоянно ею пользоваться. Ее можно сделать самостоятельно или использовать из набора Нумикон. По совету специалистов, ленту не нужно крепить около рабочего стола. Если она будет находиться в другой комнате, ребенок приложит больше усилий для того, чтобы запомнить и донести нужную информацию с первого или второго раза. Таким образом тренируется оперативная память.

— Строим числовой ряд в виде ступенек. Перечисляем его в прямом и обратном порядке. Для этого тоже придумываем интересный рассказ или игру — зайчик прыгает по ступенькам, космонавт летит на Луну. Ребенку будет интересно и весело, это будет побуждать его к повторению и лучшему запоминанию.

— Соединяем Нумикон с числами. Продолжаем использовать сенсорный материал. На этом моменте можно познакомить ребенка с понятием часа, а уже на следующих этапах научить ориентироваться во времени. Сопоставим цифры на часах с формами Нумикон.

— Начинаем учить «соседей» числа. Сравниваем числа — больше, меньше, поровну. Для знака больше-меньше используйте «крокодила», который захочет «съесть» больше число. Изучаем парные и непарные числа. Для занятий используем игрушки, сказки, рисунки. Также выполняем небольшие примеры, но только ради игры, не акцентируя внимания на математическом действие.

Занятия на втором этапе хорошо подготовят ребенка к школе и станут базой для дальнейшего изучения математики.

Третий этап направлен на изучение состава числа, перехода через десяток, счета до ста, математических действий — сложения, вычитания, умножения, деления.

Практические советы.

— Для зрительного узнавания количества предметов заполняем отверстия форм Нумикон шариками, изюмом, камешками, конфетами и перечисляем их. Ребенок поймет, что количество отверстий совпадает с количеством предметов. Такое занятие поможет понять хранения чисел и узнавания числовых множеств.

— Для понимания состава числа строим башни, дорожки из форм и трубочек Нумикон.

— Используем плакаты с изображением цифр и соответствующим количеством предметов.

— Для занятий на этом этапе подойдут весы Нумикон.

— Используем пластины Нумикон как материал для арифметических действий. Кроме этого печатаем примеры на карточках, пользуемся другими дидактическими материалами, играем в настольные игры: «Лото», «Домино», «Турбосчет», «Халли-Галли», «10 свинок», «Котосовы», «7на9», «Цветариум» и многие другие. Для игр — бродилок берем два кубика, таким образом кроме счета, ребенок будет выполнять действие сложения.

— Важным моментом является научить ребенка считать деньги. Для этого следует сделать или приобрести копилку, играть в магазин, а в будущем поручать мелкие покупки и спланировать вместе бюджет на месяц.

— Чтобы достичь хорошего результата на третьем этапе нужно решать много примеров и задач, заниматься регулярно. Придумайте вознаграждение за выполненную работу.

Нумикон прекрасно подойдет для всех детей. А игры с Нумикон заинтересуют и взрослых. Поэтому играйте всей семьей. Пусть ребенок будет уверен, что его поддерживают, верят в него, помогают ему. Это станет лучшей мотивацией для развития и обучения.

Наборы Нумикон доступны в интернет-магазине «инклюзии: реабилитационное и коррекционное оборудование» в разделе «Учебно-методические средства».

ч.1, Особенности детей и взрослых с синдромом Дауна, оказывающие влияние на освоение математических понятий.

Преподавание математики детям с синдромом Дауна, основные навыки: часть 1, Особенности детей и взрослых с синдромом Дауна, оказывающие влияние на освоение математических понятий

Преподавание математики детям с синдромом Дауна: ч.1, Особенности детей и взрослых с синдромом Дауна, оказывающие влияние на освоение математических понятий.

(с) Horstmeier, DeAnna (Ph.D.). Teaching Math to People with Down Syndrome and Other Hands-on Learners. Basic Survival Skills. Woodbine House, 2004. Книга предоставлена Натальей Баженовой.
(с) Перевод, реферирование Ольги Лисенковой. При перепечатке ссылка на sunchildren.narod.ru обязательна.

Жан Пиаже, швейцарский психолог, выделяет следующие стадии когнитивного развития (т.е. развития мышления).

(1) Сенсомоторное развитие (в норме младенчество и период примерно до 2 лет). Ребенок изучает мир, трогая его, получая различные ощущения через различные каналы (зрение, слух, осязание, обоняние, вкус), передвигаясь и исследуя.
(2) Период подготовки конкретных операций (в норме примерно 2-7 лет). Ребенок осваивает сюжетную игру, подключает воображение и абстрактное мышление. На первый план выходит предметно-изобразительное действие. Если взять два одинаковых куска глины, из первого куска скатать шарик, а из второго сделать «змейку», ребенок скорее всего скажет, что во втором куске было больше глины – в этом суждении он опирается на размер, на бОльшую длину.

(3) Период конкретных логических операций (в норме примерно 7-12 лет). Ребенок учится решать задачи в уме, используя правила логики. Однако он способен это делать пока только на основе конкретной информации, которую он может непосредственно воспринять. Например, он может посчитать количество ягод в своей тарелке и в тарелке брата. Он может затем выполнить операцию сложения и узнать, сколько всего ягод, либо сравнить количество ягод и выяснить, что у брата на две ягодки больше. Однако, если дать ему задачу с абстрактными числами, ребенок может не справиться с подобной задачей. В данной книге объясняется, как заниматься математикой с людьми, мыслящими конкретно, остающимися на этом уровне.
(4) Период формальных операций (в норме от 12 лет и старше). Ребенок способен мыслить абстрактно и не нуждается в иллюстрациях и конкретных, осязаемых примерах.
(Подробнее о концепции интеллекта Ж.Пиаже читайте, например, здесь.)

Какие практические навыки, связанные с математическими понятиями и операциями, рассмотрены в этой книге

— навыки работы с калькулятором
— математические понятия, которые ребенок должен освоить до понятия числа
— простые сравнения
— сопоставление, классификация
— понятие числа
— навык счета
— навык примерного определения количества (малых количеств) без счета «на глаз»
— распознавание цифр
— использование числовой прямой
— счет до больших чисел
— счет с пропуском
— вес разряда
— написание цифр: рисование прямых и кружочков, как научить ребенка писать цифры, как можно обойтись без этого
— порядковые числительные
— расположение чисел по порядку
— слова, используемые для сравнения
— простые графики (по желанию)
— сложение: сложение простых и сложных чисел, сложение с помощью калькулятора, решение задач на сложение
— вычитание: вычитание простых и сложных чисел, вычитание с помощью калькулятора, решение задач на вычитание, как посчитать сдачу в магазине
— понятие времени
— понятие временных отрезков (дни, недели, месяцы)
— расписание
— как определить время по часам
— измерение: длина, емкость (вместимость), вес
— температура
— формы (двумерные и трехмерные)
— последовательности (продолжи ряд…)
— деньги

Прим. : Дальнейшие навыки (дроби, умножение и деление, проценты и проч.) рассматриваются в следующей книге того же автора.

Характеристики детей/людей с синдромом Дауна, мешающие освоению математических понятий

Следует отметить, что не все люди (в дальнейшем – ученики) с синдромом Дауна будут обладать всеми следующими характеристиками. Возможно, в вашем случае ученик будет обладать лишь некоторыми из этих особенностей.

1. У учеников с синдромом Дауна обычно отмечаются сложности с кратковременной и оперативной памятью. Если информация для них неинтересна, не обладает эмоциональным зарядом (а арифметические примеры, как правило, им не обладают), ученик с синдромом Дауна часто склонен забывать о том, чему его учили. Однако, если информация или навык запечатлелись в долговременной памяти, он будет помнить их долго, наверное, даже дольше, чем его родители.

2. У детей с синдромом Дауна отмечается отставание в развитии навыков мелкой моторики. Им трудно писать цифры в клеточках, трудно попадать на нужные кнопочки калькулятора.

Если ребенок прикладывает все старания, чтобы аккуратно вывести цифру в тетради, он вряд ли может сосредоточиться на том, чтобы правильно выполнить арифметическое действие.

3. Люди с синдромом Дауна обычно сталкиваются с трудностями при развитии речи (подробнее об этом см. здесь: особенности детей с синдромом Дауна, оказывающие влияние на развитие речи). Хотя они, как правило, понимают больше, чем хотят сказать, им все равно бывает трудно понять, например, задание в учебнике, условие задачи или инструкцию учителя, и еще труднее – объяснить, чего именно они не поняли. Это нередко приводит к тому, что учитель считает ребенка неспособным вообще освоить математику, однако это не так.

4. Человеку с синдромом Дауна трудно понять задания, особенно если они всегда формулируются по-разному. Например, ему нелегко разобраться, что от него требуется в следующих случаях (пример заданий из учебника):

— Впиши пропущенные числа.
— Напиши число меньше на одну единицу.
— Впиши числа в промежутках.
— Расставь числа в правильном порядке.

Ученикам с синдромом Дауна очень помогает, если задачу можно разбить на несколько действий. Например, рассмотрим следующую задачу. «У Яна 1 шоколадка, у Элла 7 шоколадок, а у Хайнца 4 шоколадки. Сколько шоколадок было бы у каждого, если бы они поделили шоколадки поровну?». Задача кажется очень трудной. Но ученик с синдромом Дауна вполне способен с нею справиться, если подсказать ему, что сначала нужно сложить все шоколадки, а затем уже поделить их на три. (Если ребенок еще не освоил деление, он способен выполнить это действие вручную с конкретными шоколадками.)

5. Людям с синдромом Дауна гораздо сложнее воспринимать информацию на слух. Учителя должны об этом помнить. Нужно всегда представлять задания в письменном виде, желательно с наглядными пособиями (положить перед учеником настоящие рубли и копейки и т.д.).

6. У детей с синдромом Дауна, как правило,

недостаточно повседневного опыта в решении практических математических задач, по сравнению с обычными детьми.

Вот несколько примеров. Родители склонны чрезмерно опекать детей с синдромом Дауна, они гораздо позже начинают ходить в магазин за хлебом одни (если вообще начинают), да и отправляясь в магазин сами, родители зачастую предпочитают оставить малыша с синдромом Дауна дома, чтобы он чего не натворил. Таким образом, ребенок лишается возможности посчитать яблоки и апельсины во фруктовом отделе или найти кассу №4. Поскольку дети с синдромом Дауна бывают медлительны, их братья и сестры могут опережать их и считать предметы, называть количество очков в игре и пр. за них. Из-за трудностей с мелкой моторикой и проблем с памятью вы предпочтете внести телефонный номер подруги ребенка с синдромом Дауна в память телефона, вместо того чтобы каждый раз позволять ребенку потренироваться и набрать его самому, и так далее.

7. Дети с синдромом Дауна обычно развиваются с некоторой задержкой. Они проходят все те же стадии развития, что обычные дети, но медленнее. Таким образом, если вернуться к стадиям, выделенным Пиаже (выше), мы можем сказать, что большинство детей с синдромом Дауна в школьном возрасте остаются на стадии конкретного мышления.

Если вы покажете ребенку с СД пирог, разрезанный на 6 кусков, и спросите, сколько кусков останется, если взять и съесть два куска, он может ответить правильно. Если же вы дадите ему пример «1 – 2/6», это поставит его в тупик. Еще труднее ребенку с синдромом Дауна даются условные обозначения, например, иксы и игреки, которые могут означать все, что угодно. Люди с синдромом Дауна хорошо справляются с заданиями, практический смысл которых им ясен.

8. Нередко бывает так, что у ученика с синдромом Дауна

нет мотивации, т.к. он испытал уже слишком много неудач в попытках освоить сложные математические понятия. Он даже не хочет пытаться. А еще ему может казаться, что математика – чисто абстрактная наука, которая совершенно не пригодится ему в повседневной жизни.
К счастью, интересные задания в игровой форме и реальные ситуации способны исправить эту проблему.

Характеристики учеников с синдромом Дауна, помогающие освоению математических понятий

Следует снова отметить, что не все люди (в дальнейшем – ученики) с синдромом Дауна будут обладать всеми следующими характеристикам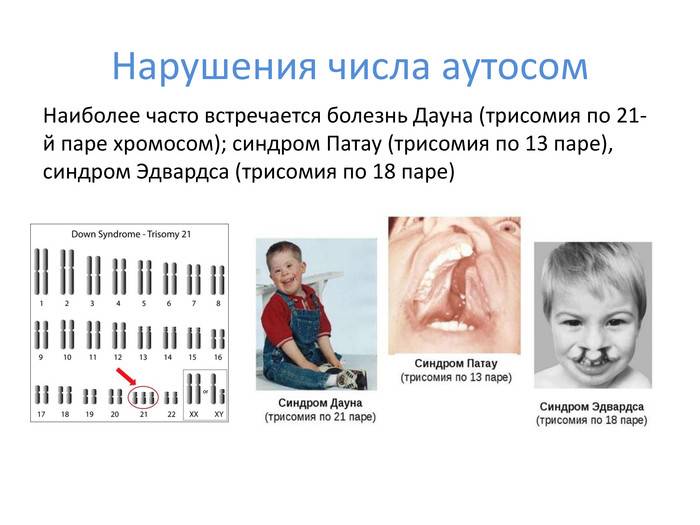и.

Возможно, в вашем случае ученик будет обладать лишь некоторыми из этих особенностей.

1. Большинство людей (особенно детей) с синдромом Дауна хотят понравиться учителю. Если учитель им симпатичен, они с энтузиазмом приступают к занятиям. Согласно некоторым исследованиям, у детей с синдромом Дауна отмечается меньше проблем с поведением, чем у детей с умственной отсталостью, вызванной другими причинами.

2. Многие люди с синдромом Дауна хорошо обучаются при помощи зрительных опор. Картинки, символы, графики, написанные условия задач помогают им понять задание.

3. Даже если речь ученика с синдромом Дауна не слишком разборчива, как правило, он способен изъясняться так, чтобы его поняли, с помощью мимики, жестов, знаков.

4. Дети с синдромом Дауна проходят все те же стадии в освоении понятий, что обычные дети, но медленнее. Им просто нужно намного больше практики. Однако им не нужны бесконечные автоматические повторения и зубрежка, их интересует творческий подход.

5. Ученикам с синдромом Дауна часто нравится работать с калькуляторами и компьютерами.

6. Детям с синдромом Дауна нравится общаться со сверстниками, они склонны подражать им. Во многих случаях одноклассник может лучше, чем учитель, объяснить материал ребенку с синдромом Дауна. Все учителя, пробовавшие подключать к обучению детей с синдромом Дауна их обычных сверстников, отмечали положительные результаты.

OZON.ru — Книги | Особенности развития мышления у детей с особыми нуждами и потребностями | Библиотека педагога-практика | Купить книги: интернет-магазин / ISBN 978-5-89502-343-3, 978-5-89395-755-6

Приводимые в книге Деанны Хорстмайер примеры, игры, принципы занятий подходят не только ученикам с синдромом Дауна, но и некоторым людям с аутизмом, СДВГ и умственной отсталостью различной степени и происхождения.

Основные принципы занятий

Опирайтесь на зрительные впечатления, зрительную память. Используйте наглядные пособия.

2. Используйте практические задания и пособия, которые можно потрогать. Вспомните, как вам легче научиться работать с какой-то компьютерной программой – прочитать инструкцию или если вам кто-нибудь покажет, что и в какой последовательности делать? Конечно, второе. Заставляйте учеников что-то делать, а не только смотреть на страницы задачнкиа, полные цифр и букв, например, попросите всех учеников в классе, кому нравится красный цвет, встать и подойти к двери, а потом предложите посчитать, скольким ученикам нравится красный.

3. Используйте структурированный подход с некоторой долей гибкости. Ученикам с синдромом Дауна очень нужна стабильность, когда они знают, что за чем следует, чего ожидать. Это позволяет им чувствовать себя увереннее. Можно нарисовать иллюстрированный план урока и следовать этой структуре. Можно также чуточку заранее предупреждать учеников о том, что их сейчас ждет, при переходе от одного вида деятельности к другой: «Сейчас мы будем считать. Ваня, пожалуйста, собери у своего ряда ножницы».

4. Старайтесь сделать так, чтобы ученик мог применить свои навыки в реальной жизни. Отправляйтесь с ним в магазин, чтобы купить конфет или диски с мультиками, попросите его переключить каналы телевизора на пульте дистанционного управления и т.п. Внимательно следите за тем, чтобы эти задания не были слишком сложны для ребенка и вселяли в него большую уверенность в себе, создавали дополнительную мотивацию.

5. Старайтесь, чтобы ученик был сосредоточен на задании. Оцените, как долго могут оставаться сосредоточенными обычные дети его возраста. Продумайте, как привлечь и удержать внимание ребенка. Ваш голос не должен быть монотонным. Если вы приступаете к освоению чего-то нового, придумайте какой-нибудь завлекательный трюк. Часто ученикам с синдромом Дауна трудно понять, что, если они не будут стараться, они не получат хорошую отметку – это для них слишком отдаленное будущее. Продумайте систему немедленных наград, например, наклейки в тетрадку.

6. Проверьте, чтобы в заданиях не было ничего, что отвлекает внимание. Ученикам с синдромом Дауна трудно бывает сосредоточиться, если на одной странице учебника содержится слишком много задач, используется слишком много различных шрифтов, цветов, картинок. Задачи в несколько действий могут сразу сбить их с толку и заставить «отключиться». Один из способов, как можно исправить ситуацию, — взять листок бумаги с вырезанным окошком и закрыть им все ненужное на странице. Другой способ – ксерокопировать задания таким образом, чтобы нужное задание было набрано увеличенным шрифтом и на странице больше ничего не было, — только само задание и место, где нужно вписать ответ. Тщательно проверяйте, хорошо ли пропечатано задание, нельзя ли спутать единицу и семерку, например.

7. Минимизируйте требования к мелким движениям. Так, ребенок с синдромом Дауна может ошибаться при решении примеров в столбик, потому что ему трудно писать единицы под единицами, а десятки – под десятками в маленьких клеточках. Используйте тетради с крупными клетками, можно использовать «подсказки». Например, если в столбик написан пример 30+70, можно подвести под столбиком черту и несильно закрасить простым карандашом ТРИ клеточки под разрядами единиц, десятков и сотен, чтобы ребенок мог догадаться, где именно начинать писать правильный ответ «100».

8. Структурируйте время, отведенное на домашнее задание. Договоритесь с учителем, как именно надо строить выполнение домашнего задания. Если ребенок старательно пытался понять, что от него требуется, в течение 20-30 минут и все равно не понимает, пойдет отрицательная реакция, он расстроится и перестанет стараться. Поговорите с учителем, что делать в таких случаях. Не давите на ребенка чрезмерно. Старайтесь выполнять домашнее задание каждый день в одно и то же время.

9. Если ребенок ведет себя плохо, например, закатывает истерику и не хочет учить уроки, постарайтесь разобраться в причинах такого поведения. Проведенный в Великобритании опрос учителей инклюзивных школ показал, что для детей с синдромом Дауна самым эффективным способом регулировать поведение является похвала и выдача каких-то «наград» (наклеек и т. п.). Регуляция поведения с помощью оценок плохо работает с такими детьми. Наказание или игнорирование ребенка в случае плохого поведения также не слишком успешны, т.к. иногда дети с синдромом Дауна не способны понять причинно-следственную связь между своим собственным поведением и наказанием со стороны учителя. Дома вы также можете применять систему наград, но дети (любые дети) зачастую не воспринимают родителя как учителя. Попробуйте подключать к обучению братьев и сестер, друзей ребенка или наймите репетитора.

10. Создавайте «ситуацию успеха» в самом начале занятия. До того как приступить к занятию, спросите у ребенка о чем-то, что он точно знает, и с энтузиазмом похвалите его за правильный ответ. Старшие дети с синдромом Дауна, особенно если они обучаются вместе с обычными детьми, заранее настроены на неудачу, на то, что у них все будет получаться медленнее. Не забывайте хвалить ребенка за старание, за попытку – не только за успех. Однако не перехваливайте ученика. Он не должен работать только за вашу похвалу. Постепенно учите его находить отдачу в самом выполнении задания, это пригодится ему гораздо больше.

11. По возможности подключайте в качестве учителя, помощника ровесников ребенка.

12. Тренируйте кратковременную и долговременную память ребенка. Отличный способ это сделать – музыка. Подыщите детские песенки, которые помогут запомнить последовательность чисел. Это хорошо всем знакомые «Раз, два, три, четыре, пять, вышел зайчик погулять» и другие (обратите внимание, например, на вот этот материал по пальчиковым играм — сколько здесь возможностей для освоения порядковых и количественных числительных! См. также ссылки ниже). Не забывайте о наглядности. Для освоения дробей покажите ребенку нарезанный пирог, при изучении времени сконструируйте с ним вместе модель часов. Используйте мнемонические приемы (так, известен прием российской учительницы, которая объясняла знак «больше >» как открытую пасть крокодила).

13. Учите ребенка пользоваться калькулятором достаточно рано.

14. Сделайте так, чтобы занятия проходили в теплой, веселой атмосфере.

15. Подключайте компьютерные программы. Людям с синдромом Дауна, как правило, нравится работать на компьютере. Существуют обучающие программы и программы, закрепляющие навыки. Яркие образы, веселые звуки, немедленное подкрепление правильного ответа или порицание за неправильный ответ привлекают детей и взрослых.

16. Разбивайте сложные задачи на пошаговые действия.

В данной книге приводится 9 способов адаптации ОБЫЧНЫХ заданий для учеников с синдромом Дауна.

1. Уменьшайте количество заданий.

2. Выделяйте больше времени на освоение каждого навыка, выполнение каждого задания.

3. Больше помогайте ученику.

4. Приспосабливайте предъявление задания для вашего ребенка, например, читайте с ним условие вслух или подыскивайте наглядные пособия.

5. Упрощайте условия задач, например, разрешите ему использовать калькулятор.

6. Приспосабливайтесь к конкретному ученику в плане проверки знаний. Убедитесь, что вы проверяете именно математический навык, а не сопутствующий! Например, из-за отставания в развитии мелкой моторики ребенку может быть трудно самому написать нужные цифры, но он может выполнить арифметическое действие и сможет приклеить наклейку с изображением числа = правильного ответа на задачу.

7. Позволяйте ученику с синдромом Дауна участвовать в решении хотя бы ЧАСТИ сложного задания, например, он может посчитать, сколько его одноклассников любят ванильное мороженое, а остальные одноклассники переведут эту цифру в проценты.

8. Приспосабливайте уровень целей и задач, заявленных в учебном плане, к конкретному ученику с синдромом Дауна. Возможно, его одноклассники уже будут складывать трехзначные числа, пока он сражается с однозначными, в этом нет ничего страшного. У него свой темп развития.

Продолжение следует: Математические понятия, осваиваемые ребенком до понятия числа (можно заниматься с ребенком с 2-3 лет).

Преподавание математики детям с синдромом Дауна, основные навыки: часть 2, Навыки, осваиваемые до понятия числа
Преподавание математики детям с синдромом Дауна, основные навыки: часть 3, Понятие числа
Преподавание математики детям с синдромом Дауна: ч. 4, Узнаём и запоминаем цифры
Преподавание математики детям с синдромом Дауна: ч.5, Тренируем счет
Чернова В.И., Тарасов М.А., Надтока М.В. Формирование элементарных математических представлений у детей с речевыми нарушениями/ под общей редакцией В.И. Черновой: Методическое пособие. — Хабаровск, 2003. на сайте PedLib.ru.
Перова М.Н. Особенности усвоения математических знаний, умений и навыков учащимися специальной (коррекционной) школы 8 вида // Перова М.Н. Методика преподавания математики в специальной (коррекционной) школе 8 вида. — М.: Просвещение, 1999 на сайте PedLib.ru.
Сайт «Музыка с мамой», где можно заказать тексты и диски развивающих песенок, в т.ч. тренирующих числительные — Екатерина Железнова.
Купить диски Железновых можно на сайте Развивалки.ру.
Особенности преподавания математики в коррекционной школе
Количественная математика — на персональном сайте Алисы Пушинской
Александр Звонкин, Вадим Левин. Домашняя школа для дошкольников
Купить:

OZON.

ru — Книги | Малыши и математика. Домашний кружок для дошкольников | А. К. Звонкин | Купить книги: интернет-магазин / ISBN 978-5-94057-315-9

Каталог ресурсов нашего сайта
На главную
Напишите мне

Пиаже Ж. Как дети образуют математические понятия
Математика: состав числа (ЖЖ Елены Величко)
Пишем цифры, пост в ЖЖ imacom
Сайт «Математика для дошкольников

Передовой опыт преподавания математики

Вы, наверное, слышали, как один или несколько учеников говорят: «Я не математик». У некоторых, возможно, был опыт, из-за которого они не любили математику. У других есть идея, что они не могут быть хороши в математике из-за своего пола.

Но некоторые ученики, которые говорят, что они не «математики», могут быть среди 25-35 процентов учеников, которые действительно борются с математикой. Они могут быть даже среди тех 5-8% учащихся, у которых есть серьезные проблемы с математикой.

Тем не менее, мы знаем, что прочная математическая база важна для всех учащихся. Это открывает двери для курсов математики более высокого уровня и для карьеры в области STEM.

Хорошая новость заключается в том, что существуют эффективные, основанные на фактических данных способы преподавания математики, которые можно использовать в текущей учебной программе. Вы можете использовать эти методы обучения, чтобы помочь каждому учащемуся изучать математику на всех уровнях обучения — от сложения до алгоритмов.

Что такое научно обоснованное обучение математике?

Эффективное преподавание математики состоит из четырех элементов.

1. Эксплицитное обучение с кумулятивной практикой

Что это такое: Эксплицитное инструктаж – это способ обучения, который делает процесс обучения полностью понятным для учащихся. С подробными инструкциями вы моделируете навык и вербализуете свой мыслительный процесс, используя ясный и лаконичный язык. Вы даете учащимся возможности для управляемой и самостоятельной практики, в том числе для отработки нового навыка и повторения навыков, которые они изучили в прошлом. Вы также даете учащимся быструю обратную связь, чтобы они не сбились с курса.

Исследования показали, что использование явных математических инструкций может улучшить способность учащихся выполнять действия и решать текстовые задачи.

Почему это помогает: Когда вы используете эту практику, вы моделируете навык настолько четко, что учащимся не нужно догадываться, что они должны делать. Кумулятивная практика явного обучения особенно полезна, потому что она сохраняет старые навыки свежими в памяти учащихся. Это большой плюс для студентов, у которых проблемы с рабочей памятью. Повторяющаяся практика связанных навыков с течением времени помогает им быстро извлекать информацию и поддерживать беглость математических фактов.

Разобраться в инструкциях (например, в многошаговых математических задачах) — сложная задача для учащихся, у которых есть проблемы с обработкой речи. Математика требует от учащихся большого количества языковых навыков, как устных, так и письменных. Явные инструкции могут уменьшить объем этой обработки, которую должен выполнить студент.

Советы преподавателям

Поставьте перед учащимися четкую цель обучения.
Используйте «сделай сейчас», которые активизируют ранее полученные знания, например, решите задачу в начале урока, чтобы вернуться к навыку, которому вы научились накануне.
Дайте кристально ясное объяснение навыка или стратегии.
Используйте несколько примеров, чтобы показать все шаги. (В некоторых случаях используйте разные примеры, например, в некоторых задачах на сложение сначала ставится большее слагаемое, а в других задачах на сложение — сначала меньшее слагаемое.)
Подумайте вслух, чтобы вербализовать свои мысли.
Предоставьте множество возможностей для управляемой и независимой практики.
Варьируйте, как вы запрашиваете ответы учащихся, например устные (например, хоровые ответы), письменные (например, стоп-и-заметки) и невербальные сигналы (большой палец вверх/большой палец вниз).
Включите ранее полученные навыки в практику.
Дайте учащимся немедленную обратную связь.

2. Визуальное представление

Что это такое: Визуальное представление – это способ для учащихся увидеть математику. Вы можете визуально представить математику с помощью числовых линий, ленточных диаграмм (также известных как гистограммы), изображений, графиков и графических органайзеров.

Визуальное представление часто используется в учебном подходе, называемом конкретным-репрезентативным-абстрактным или CRA. (Некоторые учителя называют этот подход конкретно-образно-абстрактным.)

CRA позволяет использовать визуальные представления, чтобы помочь учащимся понять абстрактные математические понятия. Например, учащиеся могут использовать бетон, например кубики Unifix, для решения задачи на сложение. (Несмотря на то, что конкретные манипуляции чаще используются в начальных классах, они также могут помочь учащимся старшего возраста. )

Учащиеся могут также использовать рисунки или картинки (опять же, больше наглядных материалов), чтобы продемонстрировать ту же математическую концепцию. Например, учащиеся могут использовать подсчеты для представления задачи на сложение. В то же время вы можете показать это же понятие в абстрактном виде в виде дополнения к предложению с цифрами и символами.

С CRA вам не нужно следовать порядку: конкретное, затем репрезентативное, затем абстрактное. Вы можете предложить учащимся использовать конкретные инструменты, в то время как вы моделируете ту же концепцию в абстрактном виде. Кроме того, вы можете переключаться между тремя представлениями в зависимости от потребностей ваших учеников.

Почему это помогает: Визуальные представления помогают всем учащимся понимать абстрактные математические понятия и решать задачи. Эти представления могут устранить языковые барьеры, связанные с задачами со словами, для учащихся, которые учатся и думают по-другому, а также для изучающих английский язык.

Когда учащиеся создают свои собственные визуальные представления, у них есть способ продемонстрировать свое понимание (или непонимание, которое вы затем можете исправить). Фактически, исследования показывают, что учащиеся, которые используют точные визуальные представления, в шесть раз чаще правильно решают задачи по сравнению со учащимися, которые их не используют.

Примечание: Эта стратегия может оказаться не столь полезной для учащихся, у которых проблемы с математикой из-за проблем с пространственным мышлением или визуализацией. Это также может создавать проблемы для слепых или слабовидящих учащихся. Для этих учащихся вы можете сделать приспособления, например, использовать тексты, напечатанные крупным шрифтом, или тактильную графику.

Тактильная графика — это простое трехмерное представление пространственных представлений, например изображения, карты, графики, диаграммы и другие изображения. Они используют выпуклые линии и другие тактильные элементы, чтобы предоставить информацию, необходимую вашему ученику. Поговорите со своим окружным консультантом по слабовидящим о том, как научить учащихся пользоваться этими инструментами.

Советы преподавателям

Научите учащихся пользоваться числовыми линиями, ленточными диаграммами, рисунками, графиками и математическими графическими органайзерами.
Предложите учащимся использовать визуальные представления, чтобы продемонстрировать свое математическое мышление, например, использовать таблицу сотен, когда они тренируются в счете с пропусками.
Познакомьте с понятиями и навыками, используя конкретные манипулятивные приемы, такие как использование блоков с основанием 10 для обучения разрядному значению.
Продемонстрируйте понятия и навыки, используя представления и изображения, такие как подсчеты, точки и круги.
Моделирование понятий и навыков на абстрактном уровне, например использование чисел и символов.
Предоставьте учащимся возможность попрактиковаться на каждом этапе.

3. Обучение на основе схемы

Что это такое: Один из наиболее эффективных способов помочь учащимся решать текстовые задачи — научить их определять типы текстовых задач. Согласно исследованиям, эта практика особенно полезна для учащихся, у которых проблемы с математикой.

Вы можете специально научить учащихся распознавать закономерности в текстовых задачах. Это называется обучением на основе схемы, что означает, что учащиеся используют то, что они знают о шаблонах в текстовых задачах, для решения проблемы. Существует два основных типа схем: аддитивные и мультипликативные. Аддитивные включают задачи на сложение и вычитание. Мультипликатив включает задачи на умножение и деление.

Рассмотрим задачу со словами: «У Эрин 4 цветных карандаша. У Алейши 3 мелка. Сколько карандашей у них вместе? » Учащиеся могут понять, что это соответствует шаблону, состоящему из двух наборов предметов и слова «вместе». Это может привести учащихся к распознаванию аддитивной схемы.

После того, как учащиеся определят схему, они могут представить информацию с помощью диаграммы или уравнения перед решением.

Почему это помогает: Учащиеся, у которых проблемы с математикой, могут испытывать трудности с распознаванием закономерностей и взаимосвязей в новых ситуациях. (Это известно как гибкое рассуждение.) Инструкция по схеме явно учит учащихся, как идентифицировать шаблоны, чтобы связать их с правильной стратегией решения словесных задач этого типа.

Учащиеся, которые учатся и думают по-другому, особенно те, у кого есть проблемы с исполнительными навыками , , также могут иметь проблемы с рабочей памятью и многоступенчатыми инструкциями. Исследования показывают, что учащиеся, которые обучались на основе схемы, лучше справлялись как со знакомыми, так и с новыми многошаговыми задачами.

Советы преподавателям

Научите учащихся анализировать текстовые задачи и определять шаблон .
Определите для учащихся уникальные особенности каждого типа задач.
Явно обучайте математическому словарю, необходимому для этой задачи.
Покажите, как представлять информацию, используя сначала конкретное представление, а затем визуальное представление.
Показать несколько способов решения одной и той же проблемы.

4. Взаимодействие со сверстниками

Что это такое: При взаимодействии со сверстниками вы объединяете учащихся в пары для совместной работы и обсуждения математики. Например, студенты могут выполнять самостоятельную практику, а затем встретиться с партнером, чтобы поделиться тем, что они узнали. Вы можете использовать гибкую группировку, чтобы сопоставить учеников, например, объединить учеников с одинаковыми математическими способностями или с разными сильными сторонами.

Почему это помогает: Обсуждения со сверстниками могут развивать математический язык и словарный запас учащихся, а также помогают учащимся выражать свои рассуждения. Это также может помочь им лучше узнать о процессах решения проблем — как о том, как они решили проблему, так и о том, как ее решили другие. Учащиеся, у которых проблемы с математикой, могут найти эту процедуру полезной, потому что их сверстники могут объяснить концепцию так, как они лучше понимают. Всем учащимся будет полезно увидеть, что одну и ту же задачу можно решить несколькими способами.

Советы преподавателям

Предварительно научите, как вести обсуждения между коллегами. Работайте всем классом, чтобы установить правила (например, не обсуждать друг друга) и подсказки для обсуждения (например, «Что вы можете добавить к моему объяснению?»).
Предложите учащимся сравнить способы решения задачи и обсудить различия в их подходах.
Выделите время в конце уроков, чтобы учащиеся могли поразмышлять друг с другом о возможностях самостоятельной практики. Вы даже можете просто показать часть студенческой работы и спросить студентов: «Что вы заметили?»
Предоставьте учащимся время для выполнения математических заданий с партнерами или в малых группах.

Кому помогает научно обоснованное обучение математике?

Эффективное преподавание математики может помочь всем учащимся, но особенно полезно для учащихся, у которых проблемы с математикой.

Учащиеся с дискалькулией , неспособностью к обучению, влияющей на математику, могут испытывать трудности с пониманием понятий, связанных с числами. Например, им может быть трудно понять, что цифра 5 — это то же самое, что группа из пяти предметов и слово 9.0023 пять . У них также могут возникнуть проблемы с использованием математических символов или пониманием математических понятий, таких как больше или меньше .

Обучение математике, основанное на фактических данных, помогает учащимся с дискалькулией, потому что дает им четкое руководство и поддержку, необходимые для приобретения навыков и понимания.

Ученики также могут испытывать трудности с математикой из-за проблем с исполнительными функциями. Математика требует от учащихся внимания к деталям, планирования и самоконтроля. Студенты также должны отслеживать шаги и, возможно, даже менять направление во время работы. Обучение математике, основанное на фактических данных, помогает этим учащимся, потому что оно разбивает задачи на несколько шагов и уменьшает количество отвлекающих факторов.

Как начать преподавание математики на основе фактических данных в моем классе?

Учебная программа по математике в вашей школе может не включать все эти элементы. Или, может быть, ваша подготовка не охватывала этот тип преподавания математики. Если вы хотите лучше понять эти стратегии, вы также можете выступать за профессиональное развитие в вашей школе по этой теме.

Но даже без формального обучения вы можете опробовать любой из элементов доказательного обучения математике в своем классе. Например, если у учащегося возникают проблемы с понятием разряда, начните с предоставления десятичных блоков, чтобы показать, как из двух блоков сотен, трех блоков десятков и четырех блоков единиц получается число 234 (бетон). Затем перейдите к тому, чтобы учащийся нарисовал его (репрезентативный), и, наконец, перейдите к 200 + 30 + 4 = 234 (абстрактный).

Изучите эти стратегии, которые включают в себя ключевые элементы обучения математике на основе фактических данных:

Представление чисел
Счет с помощью манипуляций
Разместите значение с помощью связок соломинок
Разместите значение с помощью дисков
Построение дробного числа 90 Дробная беглость
Разделение дробей полосками дробей

Как семьи могут поддерживать это дома?

Основные математические стандарты. «Новая математика». Это лишь некоторые термины, которые члены семьи могли слышать о математике. Перед родительским собранием поделитесь этим контрольным списком (испанская версия здесь) с семьями.

Он был создан Паули Эвансон, стипендиатом программы «Понятный учитель». Контрольный список поможет семьям подготовить свои вопросы по математике перед собранием.

Как использовать доказательное обучение математике во время дистанционного обучения?

Отдайте предпочтение наиболее важным компонентам учебной программы.
Поговорите с семьями ваших учеников, чтобы узнать, какие ресурсы у них есть и что им может понадобиться для обучения дома.
Используйте синхронные уроки, чтобы проводить обсуждения, проверять понимание, давать целевые инструкции и строить отношения.
Обеспечьте асинхронные возможности, такие как записанные уроки, чтобы учащиеся могли просматривать и просматривать содержимое в удобное для них время.
Предлагайте учащимся учебные задания, такие как управляемые заметки, чтобы помочь им сосредоточиться и сохранить информацию во время всего асинхронного обучения.
Используйте небольшие гибкие группы, чтобы давать более целенаправленные инструкции и возможности для взаимодействия со сверстниками. Предложите учащимся поделиться своими мыслями с вами и друг с другом.
Если возможно, отправьте манипуляторы домой для использования учащимися. В противном случае попросите учащихся использовать виртуальные манипуляторы, обычные предметы домашнего обихода или манипуляторы, вырезанные из бумаги.

Как только вы начнете использовать обучение математике на основе фактических данных, вы увидите, что лучшие практики, которые помогают учащимся, испытывающим трудности с математикой, также подходят для всех учащихся.

Смежные темы

Поддержка школы

Передовой опыт преподавания математики

Что такое научно обоснованное обучение математике?

Эффективное преподавание математики состоит из четырех элементов.

1. Подробная инструкция с кумулятивной практикой

Что это: Подробное обучение — это способ обучения, который делает процесс обучения полностью понятным для учащихся. С подробными инструкциями вы моделируете навык и вербализуете свой мыслительный процесс, используя ясный и лаконичный язык. Вы даете учащимся возможности для управляемой и самостоятельной практики, в том числе для отработки нового навыка и повторения навыков, которые они изучили в прошлом. Вы также даете учащимся быструю обратную связь, чтобы они не сбились с курса.

Советы преподавателям

Поставьте перед учащимися четкую цель обучения.
Используйте «сделай сейчас», которые активизируют ранее полученные знания, например, решите задачу в начале урока, чтобы вернуться к навыку, которому вы научились накануне.
Дайте кристально ясное объяснение навыка или стратегии.
Используйте несколько примеров, чтобы показать все шаги. (В некоторых случаях используйте разные примеры, например, в некоторых задачах на сложение сначала ставится большее слагаемое, а в других задачах на сложение — сначала меньшее слагаемое.)
Подумайте вслух, чтобы вербализовать свои мысли.
Предоставьте множество возможностей для управляемой и независимой практики.
Варьируйте, как вы запрашиваете ответы учащихся, например устные (например, хоровые ответы), письменные (например, стоп-и-заметки) и невербальные сигналы (большой палец вверх/большой палец вниз).
Включите ранее полученные навыки в практику.
Дайте учащимся немедленную обратную связь.