Интересные задачи по алгебре: Занимательные задачи по математике для 7 класса (ФГОС) — Яркий Дворик

Содержание

Занимательные задачи

1 260

Занимательные задачи!

Чем хороши занимательные задачи — ими можно интересно занять детей по в дороге, по пути в школу или устроить конкурс на школьном празднике. Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.

Занимательные задачи по математике

1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек?

2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца?

3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок?

4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?

5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?

6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?

7.Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?

8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?

9. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения?

10. Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?

Ответы:

1.4

2.Одной девочке дали клетку с кроликом.

3.9марта

4.7

5. 6 рыбаков за день едят 1 судака.
Один рыбак есть 1/6 судака в день.
10 рыбаков едят за день 10/6 судака.
10 судаков делим на 10/6 судака = 6 дней

6.Все улетели

7. 2

8. Дед, отец и внук = 2 отца и 2 сына

9.Через 7/12 суток.

10. Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.

Подумай и сосчитай

Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
Ответ:четверо

Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя

Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?
Ответ: три
******************
К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?
Ответ: четверо

Задачи на внимание

1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?

2. Подумай и скажи — какого цвета волосы у колобка?

3. Отгадай загадку:
Лежали конфетки в кучке.
Две матери, две дочки

Да бабушка с внучкой
Взяли конфет по штучке,
И не стало этой кучки.
Сколько конфет было в кучке?

4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?

5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?

6. На каких деревьях вьют свои гнезда страусы?

7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?

8. Подумай и скажи — кто громче рычит: тигр или буйвол?

9. Посмотрел Ваня утром в окно и говорит:
— А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться.
Как он догадался, что на улице ветер? Что он увидел?

10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика.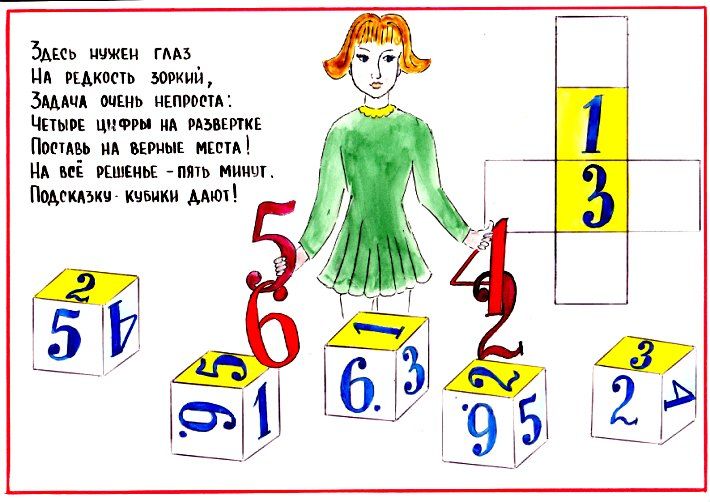 Сколько всего детей идет в лес? (подсказка: 2 — остальные идут обратно)

11. В комнате горело 5 свечей. Зашел человек, потушил 2 свечи. Сколько осталось? ( подсказка: 2- остальные сгорели)

12. Бревно распилили на 4 части. Сколько сделали распилов?

13. Прочитай слова и скажи — какое слово лишнее в каждом ряду?
— диван, стул, шкаф, конура, тумбочка,
— гвоздика, ромашка, камыш, лилия, астра,
— боровик, мухомор, сыроежка, подберезовик, лисичка.

14. Подумай и скажи — сколько земли будет в яме глубиной 1 метр, длиной 1 метр и шириной 1 метр?

15. У шестилетней девочки была кошка с коротким хвостом. Она съела мышку с длинным хвостом, а мышка проглотила 2 зернышка и съела тонкий кусочек сыра. Скажи, сколько лет было девочке, у которой была кошка?

16. На одном берегу реки стоит петух, а на другом индюк. Посреди реки — островок. Кто из этих птиц быстрее долетит до островка?

17. Скажи сколько грибов можно вырастить из 5 семечек?

18. Скажи, кто обитает в море на большей глубине: щука, рак или форель?

19. Гусь на двух ногах весит 2 кг. Сколько он будет весить, стоя на одной ноге?

20. На клене 5 веток. На каждой ветке по 2 яблока. Cколько яблок на клене?

Мой блог находят по следующим фразам

kak opredelit pol rebenka
позы при зачатии ребенка фото
логические задания для детей 5-6 лет
красивые картинки где дети играют с песком
загадки для детей 13 лет с ответами
интересные задания для детей

Интересные задачи по математике — Со Вкусом

Учебный год в самом разгаре, и уже многие успели освежить в памяти некоторые

математические теоремы. Не только дети, но и родители.

Для многих алгебра и геометрия ассоциируются с чем-то скучным или сложным. Однако истинная причина такого отношения кроется в устаревших методиках и скучных упражнениях. Мы подготовили для вас интересные задачи по математике, которые могут быстро исправить это!

Наша редакция подобрала несколько примеров, которые помогут быстро привести мозги в тонус. Эти задания будут интересны как детям, так и взрослым. Ведь не стоит забывать, что кулинария — это, прежде всего,

наука о пропорциях!

Интересные математические задачи

50 + 50 – 25 * 0 + 2 + 2 = ?
Не спешите брать бумагу и карандаш. Решить этот пример с подвохом нужно в уме. Так сказать, для разминки!
Следующий пример основан на закономерности. Попробуйте выяснить, сколько будет 11 + 5, если:

7 + 3 = 10421

5 + 4 = 9120

9 + 6 = 15354

На кусте висело 12 яблок. Прохожий сорвал половину по пути домой и еще половину по пути из дома. Вопрос: сколько яблок сорвал прохожий?

У повара было 6 яиц. Два он разбил, два приготовил и два съел. Вопрос: сколько осталось яиц?

143 мышки пробрались в сырный амбар и слопали 33 головки сыра. Все ели поровну, но половина мышек объелась, и на следующий день пришло 13 мышей. Снова ели поровну, но в 3 раза меньше. Вопрос: сколько было съедено головок сыра за два дня?

Ответы к задачам

Перейдем к самому интересному — к ответам. На самом деле здесь 2 из 5 примеров на логику. Давайте разбираться!

Ответ: 104.
Это упражнение нужно для того, чтобы вспомнить: сначала делают умножение и деление, а потом сложение и вычитание.
Ответ: 16655.
Смущает длина числа? Это ничего, ведь пример основан на закономерности, а не на сложении! В этом числе по очереди записаны результат сложение, вычитание и умножение первых двух чисел из уравнения — 11 и 5.
Математический ответ, конечно же, 9. Но внимательные садоводы подметят: на кустах не растут яблоки! А значит, и у прохожего таковых нет.

Ответ: 4 яйца. Всё просто: чтобы съесть яйца их нужно разбить и приготовить.
Ответ: 34. 13 мышей — это в 11 раз меньше, чем в первый раз. Они бы съели 3 головки, но в этот раз их аппетит поугас в 3 раза. Значит, съели на второй день одну головку. 33 + 1 = 34.

Хорошие

познания в математике просто необходимы в повседневной жизни! Подсчитать сдачу в магазине, рассчитать продукты для приготовления блюда и даже на неделю. Что уж говорить о подсчете калорий? Здесь главное — держать ум в тонусе. Подобные задачи дети решают с удовольствием, а взрослые используют подобные им в знаменитом «Что? Где? Когда?».

Автор статьи

Александра Береза

В кулинарной книге Александры есть сотни необычных рецептов с бережными заметками. Даже простой омлет Саша способна превратить в волшебное блюдо, завершенное листочком ароматной кинзы. Редактор

«Со Вкусом» не боится экспериментировать и ежедневно оттачивает свое кулинарное мастерство. Утонченные десерты и выпечка — то, что делает Александра с особым вдохновением: чего только стоит клюквенно-апельсиновый кекс в ее исполнении!

математическая педагогика — Поиск простых «интересных» математических задач, которые без алгебры не решить легко

спросил 8 лет, 7 месяцев назад

Изменено 2 года, 9 месяцев назад

Просмотрено 13 тысяч раз

$\begingroup$

Я часто встречаю студентов, которым не нравится алгебра. Они предпочитают работать с числами при решении задач. Я считаю, что есть много проблем, которые трудно решить без алгебры. Например:

Нахождение значения $x$, при котором объем коробки без крышки достигает максимального значения.
Резервуар содержит 40 галлонов раствора, состоящего из 90 % воды и 10 % алкоголь. Второй раствор, содержащий половину воды и половину спирта, добавляют к бак со скоростью 4 галлона в минуту. При этом бак опорожняется со скоростью 4 галлона в минуту, как показано ниже. При условии, что раствор постоянно помешивается, сколько спирта будет в баке через 10 минут?
И т. д. и т. д.

Не могли бы вы предоставить мне другие простые «интересные и сложные» примеры, чтобы я мог представить их своим ученикам?

математическая педагогика

$\endgroup$

$\begingroup$

Проблема с коробкой может быть сложной для учащихся, не знакомых с алгеброй. Мне нравится использовать глупые головоломки с числами, когда я начинаю учить алгебру.

Выберите число от 1 до 25.
Добавьте к нему 9.
Умножьте результат на 3.
Вычесть 6.
Разделить на 3.
Вычтите исходное число.

Затем вы можете пойти и тихо сказать: «У тебя есть 7, верно?» каждому. Как только они узнают, что у всех по 7, становится интересно выяснить, почему.

Мне пришла в голову идея использовать это на уроке алгебры из курса «Элементарная алгебра 9» Гарольда Джейкобса.0062 .

$\endgroup$

$\begingroup$

Думаю, загадка Диофанта — хороший пример.

 Бог дал ему отрочество одну шестую часть его жизни,
На одну двенадцатую больше в молодости, пока росли бакенбарды;
А потом еще одна седьмая до свадьбы;
Через пять лет появился прыгающий новый сын.
Увы, дорогое дитя мастера и мудреца
Достигнув половины отцовской меры жизни, его взяла холодная судьба. 
Четыре года утешая свою судьбу наукой о числах,
Он закончил свою жизнь.

$\endgroup$

$\begingroup$

Вот отличная загадка:

Бутылка вина стоит 20 евро. Вино стоит на 19 евро дороже, чем пустая бутылка. Сколько стоит пустая бутылка?

Каждый ответит €1. Но 1 + (19 + 1) = 21. Подставив его в уравнение, мы получим ответ в размере 0,50 евро.

$\endgroup$

$\begingroup$

Недавно я наткнулся на загадку, что $\frac{3}{16} — \frac{3}{19} =\frac{3}{16} \cdot \frac{3}{19}$, и, таким образом, вопрос, какие значения переменных дают замечательное совпадение $$ \frac{a}{b} — \frac{a}{d} =\frac{a}{b} \cdot \frac{a}{d} $$ Дело в том, что алгебра дает простое объяснение загадочному явлению.

$\endgroup$

$\begingroup$

Вот хороший способ возвести в квадрат число, оканчивающееся на «5»; давайте возьмем 75 в качестве примера. Вы отсекаете «5»; осталось 7. Затем вы умножаете его на следующее: 7×8=56. Затем вы пишете «25» после «56» и получаете результат: 5625. 92+100а+25=100а(а+1)+25$$ и они (надеюсь) понимают момент «ага! так что алгебра не бесполезна, в конце концов…».

$\endgroup$

$\begingroup$

Наиболее ярким примером этого для меня является достаточно сложное уравнение первой степени.

Что это, говорите вы? Нет сложных уравнений первой степени? Все они просто $ax+b=0\подразумевает x=-b/a$? Это потому, что вы знаете алгебру — совсем не очевидно, что их можно представить в стандартной форме.

$$3\cdot(2\cdot\_\_+5)-2\cdot(\_\_+5)=3\cdot\_\_+14$$

Какое число может стоять в пробелах сделать это правдой?

Причина, по которой я нахожу это таким поразительным, заключается в том, что, если вы вообще не знаете алгебры, все вышеперечисленное выглядит невероятно сложным, но с алгеброй настолько просто, что вы можете сделать это в уме менее чем за минуту, с небольшой практикой.

Мне хотелось бы думать, что простая головоломка «заполни пустое место» достаточно проста и интересна, чтобы мотивировать всех, кроме самых математически фобных учеников, если вы начнете с простого.

$$\_\_+5=12$$

$$7\cdot\_\_=42$$

Легко, особенно после того, как вы потренируетесь, вы сможете получить ответ, не угадывая, выполняя деление и вычитание.

$$3\cdot\_\_+9=90$$

Немного сложнее, но не требуется формального обучения алгебре, чтобы увидеть, что вы можете получить это с вычитанием, за которым следует деление. Обратите внимание, что задача теперь становится слишком сложной, чтобы сделать угадывание жизнеспособным.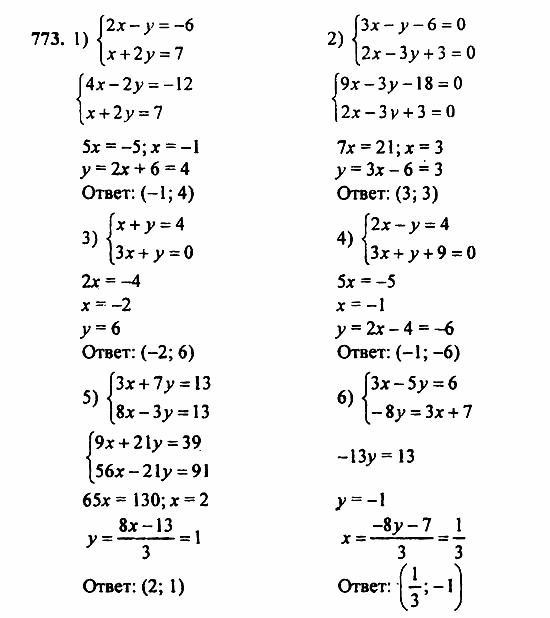 Затем, как только вы доберетесь до чего-то вроде того, что я написал выше, ситуация станет безнадежной, если вы не знаете о дистрибутивности и уравнениях балансировки.

Помню, когда мне было лет 10, я примерно знал, что значит «решить для $x$», и хотел придумать что-нибудь, чтобы поставить папу в тупик. Мне нужно что-то достаточно простое, чтобы я сам мог это решить. Если я правильно помню, моим лучшим усилием после 15 минут мозгового штурма было что-то вроде $x+1=2x$, если не проще. Он решил ее в уме примерно за полсекунды, и я был ошеломлен.

$\endgroup$

$\begingroup$

Вы можете найти множество таких задач (в свободном доступе в Интернете) среди Арифметических задач в первых выпусках American Mathematical Monthly и в учебниках по алгебре 1800-х годов. Ниже приведены три таких примера.

Решение арифметической задачи № 116 , American Mathematical Monthly 6 № 10 (октябрь 1899 г. ), 238–239. [Проблема также появляется на с. 120 из Advanced Algebra Джозефа Виктора Коллинза (1918).]

Постановка задачи: Две свечи одинаковой длины. Один потребляется равномерно за $4$ часов, а другой — за $5$ часов. Если свечи зажечь одновременно, когда одна будет в три раза длиннее другой?

Джозеф Рэй, Элементы алгебры , 1865.

Задача 24 на стр. 117 В бак подается вода от трех насосов. Первый и второй заполнят его за 30$ часов, первый и третий – за 40$ часов, а второй и третий – за 50$ часов. За какое время каждый может заполнить его отдельно?

Горацио Нельсон Робинсон, Элементарный трактат по алгебре , 1846.

Задача 24 на с. 64 (переменные изменены мной на числовые значения): Человек, привлеченный к работе 24$ дней на следующих условиях: За каждый отработанный день он должен был получать 25$ центов, за каждый день бездействия он должен был лишиться 15$ центов. . По истечении $24$ дней он получил $320$ центов. Сколько дней он простоял?

$\endgroup$

$\begingroup$

Решите для необходимой оценки в конце курса. Обычный вопрос, который многие из нас получают от студентов: «Что мне нужно набрать на выпускном экзамене, чтобы получить пятерку по курсу?» или что-то в этом роде. Теперь я всегда отвечаю: «Вы только что задали мне вопрос по алгебре, вы должны решить его сами».

Я установил свою формулу оценки специально для поддержки этого упражнения: $W = 15\%Q + 50\%T + 35\%F$, где W = взвешенная сумма за курс, Q = среднее значение теста, T = тест средний балл, F = итоговый балл за экзамен. Для курса «А» требуется не менее W = 90, «B», по крайней мере, W = 80 и т. д. На последней неделе, если у учащегося есть определенная целевая оценка, это диктует W, а Q и T известны, поэтому единственным неизвестным является F.

В моей начальной алгебры, я трачу на это час как на отдельное упражнение где-то в середине семестра. На курсах более высокого уровня, если студент задает вопрос на прошлой неделе, я помогу напомнить/установить формулу оценки, и пусть они решают ее сами. Иногда это становится довольно интенсивным «вау!» реакция, как будто впервые проблема, которую они лично спровоцировали, решается с помощью алгебры; иногда выходят телефоны и они это фотографируют и т.д.

$\endgroup$

$\begingroup$

Этот тип задач почти невозможен без алгебры:

Если Джон покрасит дом за 3 часа, а Джейн покрасит дом за 2 часа, сколько времени потребуется им, чтобы вместе покрасить 5 домов?

$\endgroup$

$\begingroup$

А вот мой еще один, но не относящийся к делу ответ. Иногда я делал (более или менее) следующее: показывал старшеклассникам квадратную формулу (т. е. формулу дискриминанта и решения квадратного уравнения) и говорил им что-то вроде: «Вот формула, которая дает способ решить это уравнение. Теперь попробуйте объяснить способ решить без алгебры ». Затем я открываю страницу Википедии с формулой решения для квартики и говорю: «И удачи с этим!». Может быть, это не интересно (для них), но я нахожу убедительным тот факт, что алгебра на самом деле может решить проблемы, а не создать их (в данном случае проблема краткого и точного описания способа выполнения некоторых вычислений). $\endgroup$

$\begingroup$

«Хорошо, класс: что получится, если разделить 1 на 0?»

Почти неизбежно вы получите ответ: «Бесконечность!»

Но это неверно, и вы можете показать это с помощью алгебры: Сам вопрос — это замаскированная алгебра. Он просит решить для x: $$0*x = 1$$

В этот момент вы можете написать на доске самое простое алгебраическое уравнение: $$Solve\quad for\quad x:\quad\quad\quad ax = b$$

«Это, класс, алгебраическое уравнение. Его также можно записать так…» $$х=б/а$$ 9{9})=0\ne 1$

«Правильно, даже если мы подставим 1 триллион миллиардов зиллионов +1, умножив его на 0, мы получим 0, который не равен 1.»

Правильный ответ в чисто алгебраическом контексте состоит в том, что x неопределенно: не существует действительного числа, которое решит это уравнение. На самом деле ответ «бесконечность» может возникнуть только в контексте пределов до расчета/расчета:

$$x = \lim_{a\downarrow 0}\frac{1}{a}=\infty$$

Но это ответ на вопрос «Каков предел 1/а при стремлении а к нулю?» Это не тот же вопрос, который мы изначально задавали, а именно: «Какое число х мы получим, если разделим 1 на 0». .»

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.
100 Трудные задачи по алгебре
Ниже вы найдете множество сложных задач по алгебре. Здесь рассматриваются самые сложные и трудные задачи по алгебре. Если вы можете решить их, вы, вероятно, сможете решить любые задачи по алгебре.
Учителя! Не стесняйтесь выбирать из этого списка и давать их своим ученикам, чтобы проверить, освоили ли они, как решать сложные задачи по алгебре.
Узнайте ниже, как распечатать эти задачи. При необходимости вы также можете приобрести раствор.
1. бензин подорожал на 2 цента за литр. на прошлой неделе мужчина купил 20 литров по старой цене. На этой неделе он купил 10 литров в новом цена. В целом бензин стоит 9,20 доллара. Какая была старая цена 1 литр?
2. Учителя разделил студентов на группы по 3 человека. Каждая группа из 3 человек написала отчет в котором было 9 картинок. Всего студенты использовали 585 изображений. Сколько всего было учеников?
3. Вера и Викки сестры. Вере 4 года, а Викки 13 лет. Сколько лет будет каждой из сестер, когда Викки будет вдвое старше Веры?
4. А может выполнить работу за 14 дней, и, работая вместе, А и В могут сделать то же самое работа через 10 дней. За какое время В один может выполнить эту работу?
5. 7 рабочие могут изготовить 210 пар чашек за 6 дней. Сколько рабочих требуется сделать 450 пар чашек за 10 дней?
6. Десять лет назад соотношение между возрастами Мохана и Сумана было 3:5. 11 лет, следовательно, это будет 11:16. Каков нынешний возраст Мохана?
7. соотношение девочек и мальчиков в классе 9 к 7, а в классе 80 учеников класс. Сколько девочек в классе?
8. Один унция раствора X содержит только ингредиенты a и b в соотношении 2:3. Одна унция раствора Y содержит только ингредиенты a и b в соотношении 1:2. Если раствор Z создается путем смешивания растворов X и Y в соотношении 3:11, затем 25:20 унций раствора Z содержит сколько унций a?
9. Это неделю Боб заправляет свой грузовик бензином когда бак был примерно наполовину пуст. Пять дней спустя Боб снова заправляет газом, когда в баке было около трех четверти заполнены. Если Боб купил 24 галлона бензина, сколько галлонов бак держит?
10. А коммерческий самолет, летящий со скоростью 700 миль/ч, обнаружен на расстоянии 1000 миль прочь с радаром. Через полчаса самолет-перехватчик, летевший с скорость 800 миль / ч отправляется. Сколько времени потребуется перехватчику самолет, чтобы встретиться с другим самолетом?
11. Есть 40 свиней и кур на ферме. Джозеф насчитал 100 ног за все. Сколько свиней и сколько кур?
12. Верх коробки представляет собой прямоугольник с периметром 72 дюйма. Если поле высота 8 дюймов, какие размеры дадут максимальный объем?
13. Вы собирают деньги на благотворительность. Кто-то сделал фиксированное пожертвование в размере 500. Затем вы требуете, чтобы каждый участник внес залог в размере 25 долларов. Какова минимальная сумма сбора, если участников 224 .
14. сумма двух положительных чисел равна 4, а сумма их квадратов 28. Какие два числа?
15. Полет против реактивного течения реактивный самолет проходит 1880 миль за 4 часа. Полет с реактивный поток, тот же реактивный самолет проходит 5820 миль за 6 часов. Что это скорость струи в неподвижном воздухе и какова скорость струйного течения?
16. Дженна и ее друг Халил соревнуются, кто сможет спасти больше всего денег. Дженна уже накопила 110 долларов и каждую неделю откладывает дополнительные 20 долларов. Халил уже накопил 80 долларов и каждую неделю откладывает дополнительные 25 долларов. Пусть x представляет количество недель, а y представляет общая сумма сэкономленных денег. Определите, через сколько недель Дженна и Халил будет столько же денег.
17. сумма трех последовательных членов геометрической прогрессии равна 104, а их продукт 13824.узнать условия.
18. сумма первого и последнего из четырех последовательных нечетных целых чисел равна 52. Что четыре целых числа?
19. А оздоровительный клуб взимает единовременный вступительный взнос и ежемесячная плата. Джон заплатил 100 долларов за 2 месяца членства. Однако Питер заплатил 200 за 6 месяцев членства. Сколько Сильвия заплатит за 1 год членство?
20. сумма двух положительных чисел равна 4, а сумма их кубов равна 28. Что произведение двух чисел?
21. А человек, продающий компьютерные комплектующие, понимает, что когда он продает 16 компьютерных комплектующих, его заработок составляет 1700 долларов. Когда он продает 56 компьютерных комплектующих, его доход составляет 4300 долларов. Каков будет доход, если мужчина продаст 30 деталей для компьютеров?
22. А у человека в карманах 15 монет. Эти монеты десятицентовики и четверти которые добавляют до 2,4 долларов. Сколько четвертаков и сколько десятицентовиков у человека?
23. длины сторон треугольника относятся как 4:3:5. Находить длины сторон, если периметр равен 18 дм.
24. отношение основания к высоте равностороннего треугольник 3:4. Если площадь треугольник равен 6, чему равен периметр треугольника?
25. процентная доходность фонда роста, фонда дохода и денежного рынка 10%, 7% и 5% соответственно. Предположим, у вас есть 3200 долларов США для инвестирования, и вы хотите вложить в фонд роста вдвое больше, чем на денежный рынок, чтобы максимизировать ваше возвращение. Как вы должны инвестировать, чтобы получить доход в 250 долларов за 1 год?
26. А была поймана акула, хвост которой весил 200 фунтов. Глава акула взвешенная столько, сколько его хвост плюс половина его тела. Его тело весило столько как его голова и хвост. Каков вес акулы?
27. квадратный корень из число плюс два равно количество. какая это количество?
28. Допустим у вас есть купон на 6 долларов на любой товар в торговом центре. Вы идете на магазин в торговом центре со скидкой 20%. Что вам нужно делать сэкономить больше всего денег?
29. Допустим ваши оценки на трех экзаменах по математике: 80, 93 и 91. Какую оценку вы нужно на следующем экзамене иметь средний балл не ниже 90 по четырем экзаменам?
30. Питер имеет фотографию шириной 5 дюймов и длиной 6 дюймов. Она увеличила с каждой стороны на одинаковую сумму. Насколько увеличена фотография если новая площадь составляет 182 квадратных дюйма?
31. стоимость создания книги составляет 1200 для начала плюс 9 долларов за книгу. книга продается по 15 долларов каждая. Сколько книг нужно продать, чтобы получить прибыль?
32. Магазин А продает компакт-диски по 2 доллара за штуку при единовременной оплате комиссия 104 долларов. Магазин B предлагает 12 бесплатных компакт-дисков и взимает 10 долларов за каждый дополнительный CD. Сколько компакт-дисков вы должны купить, чтобы они стоили одинаково в обоих случаях? планы?
33. Когда К двум числам добавляется 4, соотношение 5:6. Когда 4 вычитается из двух чисел соотношение 1:2. Найдите два числа.
34. А владелец магазина хочет продать 200 фунтов смеси фисташек и грецких орехов вместе. Грецкие орехи стоят 4 доллара за фунт, а фисташки — 6. долларов за фунты. Сколько фунтов каждого вида орехов нужно смешать, если владелец магазина будет брать 5 долларов за смесь?
35. А производитель коробок с хлопьями изготавливает коробки с хлопьями на 32 унции. В идеальном мира, коробка будет весить 32 унции каждый раз. Однако, поскольку мир не идеален, они допускают разницу в 0,06 унции. Найди диапазон допустимых размеров коробки с хлопьями.
36. А мужчина весом 600 кг каждый месяц теряет 3,12% своего веса с некоторыми тяжелые упражнения и правильное питание. Сколько будет весить человек после 20 месяцев?
37. Ан предмет подброшен в воздух на высоту 60 футов. Через 1 секунду и 2 секунды объект находится в воздухе на высоте 88 футов и 84 фута соответственно. какая начальная скорость тела?
38. А транзит находится в 200 футах от основания здания. есть человек стоит на крыше здания. Углы подъема сверху и низ мужчины 45 градусов и 44 градуса. Что это рост человека?
39. А лимонад состоит из 6% лимонного сока и клубничного сока состоит из 15% чистого фруктового сока. Сколько каждого вида должно быть смешать вместе, чтобы получить 4 литра фруктов с концентрацией 10% сок?
40. Эллен может помыть машину за 60 минут. Ее старшая сестра Сара может сделать та же работа за 45 минут. Сколько времени это займет, если они помоют машину вместе?
41. А самолет летит со скоростью 500 миль в час. Самолет может пролететь 1100 миль с ветром за то же время, за которое он проходит 900 миль против ветра. Какова скорость ветра?
42. А Компания производит коробки длиной 5 футов, шириной 4 фута и 3 фута. высокая. Компания хочет увеличить каждое измерение на одинаковую величину. чтобы новый объем был в два раза больше. На сколько увеличивается измерение?
43. Джеймс вложил половину своих денег в землю, десятую часть в акции и двадцатую в сберегательных облигациях. Затем он вложил оставшиеся 21000 в компакт-диск. Сколько деньги Джеймс сэкономил или вложил?
44. материнские платы для настольного компьютера могут быть изготовлены за 50 долларов каждый. Стоимость разработки 250000. Первые 20 материнских плат являются образцами и продаваться не будет. Сколько продаваемых материнских плат будет иметь среднюю стоимость 6325 долларов?
45. Как большая часть 70-процентного апельсинового сока должна быть смешана с 44 галлонами 20% апельсинового сока выпить, чтобы получить смесь, состоящую из 50% апельсинового сока?
46. А Компания реализует орехи оптом. При покупке оптом арахис продавать по 1,20 доллара США за фунт, миндаль по 2,20 доллара США за фунт и кешью по 3,20 доллара за фунт. Предположим, специализированному магазину нужна смесь из 280 фунтов, что будет стоить 2,59 доллара за фунт. Найдите количество фунтов каждого вида ореха, если сумма количества фунтов миндаля и орехов кешью в три раза больше, чем арахиса. Вокруг вашего ответы с точностью до фунта.
47. А Баскетболист успешно выполнил 36 из своих последних 48 штрафных бросает. Находить количество штрафных бросков подряд, необходимое игроку, чтобы увеличить вероятность успеха до 80%.
48. Джон может мыть машины в 3 раза быстрее, чем его сын Эрик. Работать вместе, им нужно помыть 30 машин за 6 часов. Сколько часов это займет каждый из них работает в одиночку?
49. В колледже, около 36% студентов моложе 20 лет и 15% старше 40 лет. Какова вероятность того, что студент, выбранный в random моложе 20 лет или старше 40 лет? 92 . Какова сила света на расстоянии 2 метров от лампочки?
52. длины двух сторон треугольника равны 2 и 6. найдите радиус значения возможных длин третьей стороны.
53. Найти три последовательных целых числа, половина их суммы находится между 15 и 21.
54. После вы открываете книгу, вы замечаете, что продукт два номера страниц на лицевых страниц 650. Каковы два номера страниц?
55. Допустим вы начинаете с числа. Вы умножаете число на 3, прибавляете 7, делите на ½, вычесть 5, а затем разделить на 12. В результате получится 5. Что число, с которого вы начали?
56. Вы иметь 156 футов ограждения, чтобы окружить прямоугольный сад. Ты хочешь длина сада в 5 раз больше его ширины. Найдите размеры сада.
57. количество воды, которую сбрасывает капающий кран, зависит от количество времени, в течение которого кран капает. Если из крана капает 2 стакана воды каждые 6 минут, узнайте, сколько времени потребуется крану, чтобы капнуть 10,6465 литров воды.
58. А стиральная машина стоит на 25% дороже сушилки. Если продавец магазина дал скидку 10 % на сушилку и скидка 20% на стиральную машину, сколько стоит стиральная машина перед скидкой, если вы заплатили 1900 долларов.
59. Выпечка на поднос кексов с черникой уходит 4 стакана молока и 3 стакана пшеницы мука. На поднос тыквенных кексов уходит 2 стакана молока и 3 стакана пшеничная мука. У пекаря есть 16 чашек молока и 15 чашек пшеничной муки. Вы зарабатываете 3 доллара прибыли за поднос черничных кексов и 2 доллара прибыль с лотка тыквенных кексов. Сколько лотков каждого типа кексы вы должны сделать, чтобы максимизировать прибыль?
60. А компания установила, что -2p + 1000 моделей количество телевизоров, продаваемых в месяц где p может быть установлено от 200 до 300. Как может компания максимизирует доход?

Другие сложные задачи по алгебре
61. Ваш друзья говорят, что у него есть 2 доллара 40 центов равным количеством четвертаков, десятицентовиков, и никель. Сколько у него каждой монеты?
62. Я двузначное число, цифра в десятом разряде которого на 1 меньше удвоенная цифра в разряде единиц. Когда цифра на десятом месте делится на цифру, стоящую в разряде единиц, частное равно 1, а остаток равен 4. Какой у меня номер?
63. А двузначное число формируется путем случайного выбора из цифр 2, 4, 5, и 7 без замены. Какова вероятность того, что двузначное число содержит 2 или 7?
64. Допустим вы берете интервью у 30 девушек и 20 юношей в вашей школе, чтобы выяснить, кто среди них используют электрическую зубную щетку. Ваш опрос показал что только 2 мужчины используют электрическую зубную щетку, а 6 женщин. Какова вероятность того, что респондент не пользовался электричеством? зубная щетка, учитывая, что респондент — женщина?
65. Ан работодатель платит 15 долларов в час плюс дополнительные 5 долларов в час за каждый час, отработанный сверх 8 часов, до максимальной дневной заработной платы 220 долларов. Находить кусочная функция, моделирующая эту ситуацию.
66. Разделить меня на 7, остаток равен 5. Раздели меня на 3, остаток равен 1 и мое частное в 2 раза меньше, чем мое предыдущее частное. Какой номер я?
67. А компании, производящей багаж, должны соблюдать эти требования. Длина на 15 дюймов больше глубины и суммы длины, ширины и глубина не должна превышать 50 дюймов. Какое максимальное значение для глубина, если производитель будет использовать только целые числа?
68. Кому сделать открытую коробку, человек отрезает равные квадраты от каждого угла лист металла шириной 12 дюймов и длиной 16 дюймов. Найдите выражение объема через х.
69. Десять кандидаты баллотируются на пост президента, вице-президента и секретаря в студенческом самоуправлении. Вы можете проголосовать не более чем за 3 кандидатов. Сколькими способами можно проголосовать за 3 или менее кандидатов?
70. период полувыведения лекарства, назначенного врачом, составляет 6 часов. Как много мг этого лекарства остается через 78 часов, если врач прописал 100 мг?
71. Допустим вы бросаете красный кубик с числами и желтый кубик с числами. Находить P(красный 2, желтый 2) и вероятность получить любые совпадающие пары числа.
72. А кинотеатр в маленьком городе обычно открывает свои двери 3 дня подряд а затем закрывается на следующий день на техническое обслуживание. Другой кинотеатр 3 миль открыто 4 дня подряд, а затем закрывается на следующий день для та же самая причина. Предположим, оба кинотеатра закрыты сегодня и сегодня среда, когда в следующий раз они оба снова будут закрыты тот же день?
73. Ан инвестор вкладывает 5000 долларов под 10%, остальное под 5%. Сколько было инвестируется под 5%, если доход составляет одну пятую от суммы, инвестированной в 10%?
74. 20000 учащиеся сдали стандартизированный тест по математике. Баллы по тесту такие нормально распределены, со средним баллом 85 и стандартным отклонение 5. Сколько студентов набрали от 90 до 95 баллов?
75. А спутник, расположенный на высоте 2400 км над поверхностью Земли, находится в круговом орбиту вокруг земли. Если для завершения спутника требуется 3 часа 1 орбита, на каком расстоянии находится спутник через 1 час?
76. В группе из 10 человек, какова вероятность того, что хотя бы двое люди в у группы один день рождения?
77. Во время сбор средств для борьбы с раком на гала-концерте, все пожимают друг другу руки все остальные в комнате до события и после события законченный. Если n человек посетили торжество, сколько различных рукопожатий произошло?
78. Два кубы имеют длины сторон, равные 2x и 4x. Во сколько раз больше чем поверхность маленького куба, равна площади поверхности большого куб?
79. Допустим у вас есть работа в ресторане, где вам платят 8 долларов в час. У вас также есть работа в Walmart с оплатой 10 долларов в час. Вы хотите зарабатывать как минимум 200 в неделю. Однако вы хотите работать не более 25 часов в сутки. неделя . Покажите 3 различных способа, которыми вы могли бы работать на каждой работе.
80. Два Компания предлагает услуги репетитора. Компания А понимает, что когда они репетитора на 3 часа, они делают 45 долларов. Когда репетитор по 7 часов они составляют 105 часов. Компания B понимает, что, когда они занимаются репетиторством за 2 часов, они составляют 34 доллара. Когда они занимаются репетиторством по 6 часов, они делают 102 часа. Предполагая, что количество часов, которое студенты подписали за репетиторство одинаково для обеих компаний, какая компания будет генерировать больше доходов?
81. Вы хочу огородить прямоугольную детскую площадку во дворе. Чтобы сэкономить на заборы, вы будете использовать заднюю часть вашего дома в качестве одной из четырех сторон. Найдите возможные размеры, если дом имеет ширину 60 футов и вы хотите использовать по крайней мере 160 футов ограждения.
82. Когда число увеличивается на 20%, результат тот же, когда оно уменьшилось на 10% плюс 12. Какое число?
83. среднее из трех чисел равно 47. Самое большое число на пять больше, чем в два раза меньше. Диапазон 35. Какие три числа?
84. процент увеличения числа от его исходного количества до 36 составляет 80%. какая исходная сумма числа?
85. Когда Питер едет на работу со средней скоростью 45 миль в час из-за движение. На обратном пути домой он набирает в среднем 60 миль в час, потому что трафик не такой плохой. Общее время в пути 2 часа. Как далеко Дом Питера с работы?
86. Ан рекламная компания берет 20% со всей выручки, которую она генерирует для его филиалы. Если бы аффилиатам в этом месяце заплатили 15200 долларов, какой доход рекламная компания сгенерировала в этом месяце?
87. А Выручка компании может быть смоделирована с помощью квадратного уравнения. Компания заметила, что когда они продают 2 или 12 товаров, доход равен 0. Каков доход, когда они продают 20 предметов?
88. А мяч отскочил 4 раза, достигнув трех четвертей своей предыдущей высоты с каждым отскоком. После четвертого отскока мяч достиг высоты 25 см. На какой высоте находился мяч в момент падения?
89. А Компания по прокату взимает 40 долларов в день плюс 0,30 доллара за милю. Ты арендовать автомобиль и вернуть его через 4 дня. Сколько миль вы проехали автомобиль, если вы заплатили 325,5 долларов, включая 5% налога с продаж?
90. Два ученики покидают школу в одно и то же время и едут в противоположном направлении направления по той же дороге. Одна прогулка со скоростью 3 км/ч. другие велосипеды со скоростью 8,5 миль в час. Через сколько им будет 23 часть миль?
91. Коричневый имеет столько же братьев, сколько и сестер. Его сестра Сильвия как вдвое больше братьев, чем сестер. Сколько детей в семья?
92. Итан имеет такое же количество одноклассников мужского пола, как и одноклассников женского пола. Его у одноклассницы Оливии на три четверти больше одноклассниц, чем мужчин одноклассники. Сколько учеников в классе?
93. Ной хочет разделить определенную сумму денег с 10 человек. Однако на в последнюю минуту он думает о том, чтобы уменьшить сумму на 20, поэтому он может оставить себе 20 и разделить деньги только с 5 людьми. Сколько денег Ной пытается разделить, если каждый человек по-прежнему получает то же количество?
94. квадратный корень из меня плюс квадратный корень из меня — это я. Кто я?
95. А Денежный ящик содержит 160 купюр, все 10 и 50. Если общая стоимость из 10-х и 50-х годов составляет 1760 долларов. Сколько купюр каждого типа находится в чертежник?
96. Вы хотите приготовить 28 грамм протеиновой смеси для закусок с арахисом и мюсли. Арахис содержит 7 граммов белка на унцию и мюсли содержат 3 грамма белка на унцию. Сколько унций мюсли вы должны использовать на 1 унцию арахиса?
97. длина прямоугольной призмы вчетверо, ширина в два раза, а высота урезана пополам. Если V — объем прямоугольного призмы перед модификацией, выразить объем после модификация с точки зрения V.
98. А Прокат автомобилей имеет проигрыватели компакт-дисков в 85% своих автомобилей. Проигрыватели компакт-дисков случайным образом распределены по автопарку. Если человек арендует 4 машины, какова вероятность того, что хотя бы 3 из них будут с КД игроки?
99. Джейкобс почасовая оплата в 4 раза больше, чем у Ноя. Когда Джейкоб получил рейз на 2 долларов, Ной согласился на новую должность, на которой ему платят на 2 доллара меньше. в час. Джейкоб теперь зарабатывает в 5 раз больше денег, чем Ной. Сколько сколько денег они зарабатывают в час после того, как Джейкоб получил прибавку?
100.
Ты собственный ресторанный бизнес, который делает фирменные торты. Ваша компания имеет решили создать три вида тортов. Для создания таких тортов принимает команду, состоящую из декоратора, пекаря и дизайнера консультант. Торт А занимает у декоратора 9 часов, у пекаря 6 часов, и консультант по дизайну 1 час. Торт B берет декоратор 10 часов, пекарь 4 часа и консультант по дизайну 2 часы. Торт C занимает у декоратора 12 часов, у пекаря 4 часа, а у пекаря консультант по дизайну 1 час. Без найма дополнительных сотрудников 39Доступно 8 часов декоратора, 164 часа пекаря и 58 часов.
No related posts.