Урок 17. деление с остатком — Математика — 5 класс
Математика
5 класс
Урок № 17
Деление с остатком
Перечень вопросов, рассматриваемых в теме:
— деление с остатком;
— неполное частное;
— остаток.
Тезаурус
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы.

- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Не всегда можно полностью разделить одно число на другое. В примерах на деление может оставаться остаток. Такое деление называется деление с остатком.
Рассмотрим пример. Разделим 16 на 5.
Запишем этот пример в столбик:
Получилось, что 5 помещается в 16 три раза, но остаётся 1 – это остаток.
Читается данное выражение следующим образом: «16 разделить на 5 получится 3, и остаток – 1».
Деление с остатком – это деление одного натурального числа на другое, при котором остаток меньше делителя.
Если при делении натуральных чисел остаток равен нулю, то договорились считать, что делимое делится на делитель без остатка, или делится нацело.
Запишем деление с остатком в общем виде.
Порядок решения выражений на деление с остатком:
1. находим наибольшее число до
2. вычитаем из делимого найденное число c.
a – c = r
Сравниваем остаток с делителем. Остаток всегда меньше делителя: r < b.
Если получилось, что остаток больше делителя – значит, наибольшее число, которое делится на делитель без остатка, найдено неверно.
При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1. Иногда для этого необходимо произвести дополнительные расчёты в столбик.
Рассмотрим ещё один пример.
297 : 25 = ?
Запишем это выражение в столбик:
Получили остаток 22, он меньше, чем 25, значит:
297 : 25 = 11 ост (22)
Как проверить деление с остатком:
- умножить неполное частное на делитель;
- прибавить к полученному результату остаток;
- сравнить полученный результат с делимым.

Проверим ответ предыдущего примера.
297 : 25 = 11 ост (22)
25 · 11 = 275
275 + 22 = 297
Деление с остатком выполнено верно.
Разбор решения заданий модуля
№ 1. Вычислите выражение 312 : 15 = _____ ост (____)
Решение: выполним деление уголком:
Сравним неполное частное с делителем: 12 < 15.
Теперь проверим, верно ли мы нашли неполное частное и остаток:
20 ∙ 15 + 12 = 300 + 12 = 312
Ответ: 312 : 15 = 20 ост (12)
№ 2. Найдите неизвестное делимое в выражении:
х : 17= 18 (остаток 4)
Выберите верный ответ: х = 310; х = 120; х = 250; х = 110.
Решение: чтобы найти неизвестное делимое, надо неполное частное умножить на делитель и прибавить остаток.
х = 18 ∙ 17 + 4
х = 306 + 4
х = 310
Ответ: х = 310.
Презентация «Повторение по теме: «Деление «Столбиком»».
библиотека
материалов
Содержание слайдов
Повторение по теме: «Деление столбиком»
Номер слайда 3
Номер слайда 6
Номер слайда 9
Задания для закрепления
Математика: уроки, тесты, задания.
 Математика: уроки, тесты, задания.
Математика: уроки, тесты, задания.
-
-
Сравнение предметов
-
Точка, прямая линия, кривая и отрезок
-
Квадрат, круг, прямоугольник, треугольник
-
Пространственные и временные представления
-
Пары и группы предметов
-
Больше, меньше, столько же
-
Знаки сравнения, знаки действий и знак равенства
-
-
-
Нумерация.
 Сколько? От 1 до 5
Сколько? От 1 до 5
-
Примеры на сложение и вычитание от 1 до 5
-
Сравнение чисел от 1 до 5
-
Текстовые задачи (от 1 до 5)
-
Задачи на смекалку (от 1 до 5)
-
-
-
Примеры на сумму
-
Текстовые задачи (сумма)
-
-
Переместительный закон сложения
-
-
Примеры на разность
-
Текстовые задачи (разность)
-
-
Таблица сложения.
 Числа от 1 до 9
Числа от 1 до 9
-
-
Нумерация. Сколько? От 0 до 10
-
Примеры от 0 до 10
-
Сравнение чисел от 0 до 10 и выражений
-
Текстовые задачи (от 0 до 10)
-
Задачи на смекалку (от 0 до 10)
-
-
Увеличить или уменьшить на…
-
-
Сантиметр
-
Дециметр
-
-
На сколько больше? На сколько меньше?
-
-
Счёт десятками
-
Круглые числа
-
-
-
Нумерация.
 Сколько? От 11 до 20
Сколько? От 11 до 20
-
Примеры от 11 до 20
-
Сравнение чисел от 11 до 20
-
Текстовые задачи (от 11 до 20)
-
Задачи на смекалку (от 11 до 20)
-
-
Числа от 20 до 100.
 Нумерация. Числа и цифры
Нумерация. Числа и цифры
-
-
Скобки. Сочетательный закон сложения
-
Таблица сложения. Числа от 0 до 18
-
Вычитание суммы из числа
-
Сложение и вычитание чисел в пределах 20 с переходом через десяток
-
Сложение и вычитание чисел в пределах 100 без перехода через десяток
-
Сложение и вычитание чисел в пределах 100 с переходом через десяток
-
Сложение и вычитание чисел в пределах 100
-
-
-
Периметр
-
Решение задач в два действия
-
-
-
Метр
-
Килограмм
-
Литр
-
-
-
Уравнения (сумма)
-
Уравнения (разность)
-
-
-
Понятие умножения
-
Переместительный закон умножения
-
Таблица умножения на 2
-
Таблица умножения на 3
-
Таблица умножения на 4
-
Таблица умножения на 5
-
-
Деление
-
Чётные и нечётные числа
-
-
Выражения без скобок
-
Выражения со скобками
-
-
-
Луч
-
Угол
-
Прямой, тупой и острые углы
-
-
-
Увеличить на.
 .. Увеличить в… Уменьшить на… Уменьшить в…
.. Увеличить в… Уменьшить на… Уменьшить в…
-
Больше на… больше в… меньше на… меньше в…
-
-
-
Таблица умножения на 6
-
Таблица умножения на 7
-
Таблица умножения на 8
-
Таблица умножения на 9
-
-
-
Нахождение неизвестного множителя
-
Нахождение неизвестного делимого
-
Нахождение неизвестного делителя
-
-
-
Ломаная линия
-
Треугольники
-
-
-
Умножение и деление на 0, 1, 10.
 Деление числа на само себя
Деление числа на само себя
-
Умножение и деление круглого числа на однозначное число
-
Деление круглого числа на круглое число
-
-
-
Умножение суммы на число
-
Умножение двузначного числа на однозначное число
-
-
-
Деление суммы на число
-
Деление двузначного числа на однозначное
-
Деление двузначного числа на двузначное
-
Деление с остатком
-
-
-
Нахождение доли числа
-
Сравнение долей
-
Нахождение числа по доле
-
-
-
Нумерация
-
Сложение и вычитание трёхзначных чисел
-
Умножение и деление трёхзначного числа на однозначное число
-
Связь между величинами
-
-
Календарь
-
-
Нумерация
-
Сложение и вычитание многозначных чисел
-
Сочетательный закон умножения
-
Умножение и деление чисел на 10, 100 и 1000
-
Умножение и деление круглых чисел
-
-
-
Час.
 Минута. Сутки
Минута. Сутки
-
Миллиметр
-
Километр
-
-
-
Площадь фигуры. Площадь прямоугольника
-
Единицы измерения площади
-
-
-
Умножение на однозначное число.
 Распределительный закон умножения относительно сложения
Распределительный закон умножения относительно сложения
-
Умножение круглого числа на однозначное число
-
Умножение на круглое число
-
Умножение круглых чисел
-
Умножение на двузначное число
-
Умножение на трёхзначное число
-
-
-
Деление многозначного числа на однозначное число
-
Деление круглого многозначного числа на однозначное
-
Деление многозначного числа на 10, 100, 1000 с остатком
-
Деление многозначного числа с остатком на однозначное число
-
Деление трёхзначного числа на двузначное число
-
Деление трёхзначного числа на двузначное с остатком
-
Деление многозначного числа на двузначное число
-
Деление на двузначное число с остатком
-
Деление на трёхзначное число
-
Деление на трёхзначное число с остатком
-
Деление круглого многозначного числа на круглое число
-
-
-
Секунда.
 Измерение времени
Измерение времени
-
Гектар. Центнер. Тонна
-
-
-
Понятие дроби
-
Сравнение дробей
-
Нахождение части числа
-
Нахождение числа по его части
-
-
-
Скорость.
 Время. Расстояние
Время. Расстояние
-
Работа. Время. Производительность
-
Цена. Количество. Стоимость
-
-
-
Десятичная система счисления. Римская нумерация
-
Числовые и буквенные выражения
-
Начальные геометрические понятия: прямая, отрезок, луч, ломаная, прямоугольник
-
Определение координатного луча
-
Округление чисел.
 Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
-
Законы арифметических действий. Вычисления с многозначными числами
-
Решение текстовых задач арифметическим способом
-
Формулы. Уравнения. Упрощение выражений
-
Математический язык и математическая модель
-
-
-
Деление с остатком.
 Понятие обыкновенной дроби
Понятие обыкновенной дроби
-
Основное свойство дроби. Сокращение и расширение дробей
-
Правильные и неправильные дроби. Смешанные числа. Понятие, запись и чтение
-
Сравнение обыкновенных дробей
-
Сложение и вычитание обыкновенных дробей и смешанных чисел
-
Умножение и деление обыкновенной дроби на натуральное число
-
Нахождение части от целого и числа по его части
-
Геометрические понятия: окружность и круг
-
-
-
Угол.
 Измерение углов
Измерение углов
-
Биссектриса угла. Свойство биссектрисы угла
-
Треугольник. Площадь треугольника
-
Свойство углов треугольника. Размеры объектов окружающего мира (масштаб)
-
Расстояния между двумя точками.
 Масштаб. Виды масштаба
Масштаб. Виды масштаба
-
Перпендикулярность прямых. Расстояние от точки до прямой. Серединный перпендикуляр
-
-
-
Понятие десятичной дроби. Представление десятичной дроби в виде обыкновенной дроби и наоборот
-
Десятичные дроби.
 Сравнение
Сравнение
-
Десятичные дроби. Сложение и вычитание
-
Десятичные дроби. Умножение
-
Степень с натуральным показателем
-
Десятичные дроби.
 Среднее арифметическое, деление на натуральное число
Среднее арифметическое, деление на натуральное число
-
Десятичные дроби. Деление на десятичную дробь
-
Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту
-
-
-
Прямоугольный параллелепипед.
 Определение, свойства
Определение, свойства
-
Прямоугольный параллелепипед. Развёртка
-
Прямоугольный параллелепипед. Объём
-
-
-
Делимость натуральных чисел
-
Признаки делимости на 2, 3, 5, 9, 10
-
Простые и составные числа.
 Разложение натурального числа на простые множители
Разложение натурального числа на простые множители
-
Наибольший общий делитель и наименьшее общее кратное
-
-
-
Положительные и отрицательные числа. Определение координатной прямой
-
Противоположные числа.
 Модуль числа. Целые и рациональные числа
Модуль числа. Целые и рациональные числа
-
Сравнение рациональных чисел
-
Сложение рациональных чисел с помощью координатной прямой
-
Алгебраическая сумма. Свойства
-
Алгебраическая сумма рациональных чисел с одинаковыми знаками
-
Алгебраическая сумма рациональных чисел с разными знаками
-
Умножение и деление рациональных чисел
-
Умножение и деление обыкновенных дробей
-
Дробные выражения
-
Координаты.
 Координатная плоскость. Координаты точки
Координатная плоскость. Координаты точки
-
-
-
Отношение двух чисел
-
Пропорция. Основное свойство пропорции
-
Прямая и обратная пропорциональность
-
Решение задач с помощью пропорций
-
Разные задачи
-
-
-
Упрощение выражений, раскрытие скобок
-
Решение линейных уравнений
-
Этапы решения линейных уравнений
-
-
-
Начальные понятия и факты курса геометрии
-
Параллельность прямых
-
Осевая и центральная симметрия
-
Окружность и круг.
 Число Пи. Длина окружности. Площадь круга
Число Пи. Длина окружности. Площадь круга
-
Наглядные представления о шаре, сфере. Формулы площади поверхности сферы и объёма шара
-
-
Коллекция интерактивных моделей
-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницуТакой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Русский язык 7 класс
- Алгебра 7 класс
- Математика 6 класс
- Русский язык 6 класс
- Русский язык 5 класс
- Наименьшее общее кратное
- Математика 5 класс
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Деление и дроби
- Квадратный корень из неотрицательного числа
- Алгебра 8 класс
- Доли. Обыкновенные дроби
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Деление в столбик больших чисел примеры. Деление столбиком на двузначное число
Как в столбик делить — один из основных навыков, необходимых для работы с двух- и трёхзначными числами. Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Этот полезный математический навык необходим не только для успешного освоения школьной программы по математике и ряду других предметов. Умение делить наверняка поможет каждому в повседневной жизни.
Умение делить наверняка поможет каждому в повседневной жизни.
Итак, делимое, то есть число, которое нужно разделить, надо записать слева. Число, на которое делят, называют делителем и записывают справа.
Под делителем проводится черта, под которой пишут частное (решение).
Под делимым необходимо оставить место, требующееся для вычислений.
Сама задача выглядит следующим образом: пакет, где лежат шесть грибов, весит 250 грамм. Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Сейчас предстоит вычислить, сколько целых раз делится первая цифра (отсчёт ведётся с левого конца) делимого на делитель.
Для решения нашей задачи нужно узнать, сколько раз цифра 2 делится на 6. Так как это невозможно, то в ответе — 0, который записывается под делителем. В этом случае нуль является первым числом частного, однако допускается отказ от такой записи.
Теперь предстоит узнать, сколько целых раз делятся две первые цифры делимого на делитель.
Если в предшествующем действии в ответе был получен 0, надо рассмотреть две первые цифры делимого. В рассматриваемой задаче надо вычислить, сколько раз 25 делится на 6.
Если делитель является двух- и более значным числом, надо разделить на него первые три (четыре, пять и т. д.) цифры делимого. Наша цель: получить целое число.
Далее начинается работа с целыми числами. Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Результат, полученный в третьем этапе, записывается прямо под соответствующей цифрой делителя — под чертой. Данный итог будет первой цифрой искомого частного, то есть ответа.
Результат обязательно нужно писать под соответствующей цифрой делителя. Если пренебречь этим требованием, будет допущена ошибка, которая скажется и на конечном результате: он будет неверным.
В рассматриваемом случае 4 записывается под 5, так как на 6 делится число 25, а не 2.
Часть вторая. УмножениеЭтот этап представляет собой переход к новой части работы «как считать в столбик». Деление в данном случае сменятся… умножением.
Делитель умножается на число, которое было под ним записано. Это означает, что речь идёт о первой цифре искомого частного.
Результат этого произведения размещается под делимым.
В рассматриваемом примере 6 х 4 = 24. Число, стоящее в ответе, то есть 24, записывается под 25. Важно: 2 должна стоять под 2, а 4 — под 5.
Результат произведения подчёркивается. В нашем случае речь идёт о подчёркивании числа 24.
Здесь происходит переход к вычитанию и опусканию цифр.
Результат записывается под чертой, которая в свою очередь проводится под числом, поставленным под делимым.
Нам предстоит произвести вычитание 24 из 25. Получаемый при этом результат: 1.
Получаемый при этом результат: 1.
Опускается третья цифра делимого, то есть она записывается рядом с результатом вычитания.
В нашем случае 1 не может делиться на 6. В силу этого спускают третью цифру делимого (третьей цифрой числа 250 является 0). Она размещается рядом с 1. Мы получаем число 10, которое может быть разделено на 6.
Теперь требуется повторить процесс с новым числом.
Для этого полученное число делится на наш делитель, а получаемый при этом результат размещается под делителем, в качестве которого будет выступать вторая цифра частного, то есть нашего ответа.
В решаемом примере 10 делим на 6, что даёт в итоге 1. Единичка записывается в частное — рядом с 4. После этого 6 умножается на 1 и из 10 вычитают результат. У нас должно получиться 4 (остаток).
Если делимое представляет собой двух-, трёх-, четырёх- и более значное число, изложенный процесс повторяется до тех пор, пока не будут опущены все цифры делимого. Пример для иллюстрации: если известно, что вес грибов равен 2 506 г, надо опустить цифру 6, то есть записать её рядом с 4.
Теперь переходим к записи частного с остатком или в виде десятичной дроби.
Наш остаток был равен 4, что связано с тем, что это число — 4 — не делится на 6 и у нас не осталось цифр, которые можно спустить.
Ответ при этом будет выглядеть следующим образом: 41 (ост. 4).
Вычисления на данном этапе могут быть завершены, если в задаче сформулировано требование найти что-то, выражаемое исключительно в целых числах. Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Если есть необходимость в ответе в виде десятичной дроби, можно перейти к следующим действиям алгоритма «как разделить в столбик».
Если нет желания записывать ответ с остатком, можно найти ответ в виде десятичной дроби. При получении остатка, не поддающегося делению на делитель, надо добавить десятичный знак (к частному).
В нашем случае число 250 может быть записано в виде десятичной дроби: 250. 000.
000.
Теперь, когда в наличии цифры (только нули), которые могут быть опущены, можно продолжить вычисления. Опускаем нуль и подсчитываем, сколько целых раз можно поделить полученное число на делитель.
В нашем примере после частного 41 (которое размещаем прямо под делителем) пишем десятичную запятую и приписываем 0 к остатку (4). Затем делим полученное число, то есть 40, на делитель (в роли которого выступает 6). Получаем опять 6, которую пишем в частное после десятичного знака. Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
В ряде ситуаций при поиске ответа в виде десятичной дроби приходится столкнуться с повторяющимися числами. Для этого надо прервать вычисления и округлить уже полученный ответ — вниз или вверх.
В частности, в рассматриваемом примере надо отказаться от бесконечного получения цифры 4. Нужно просто прервать вычисления и округлить частное. В силу того, что 6 больше 5, округление производится вверх, в результате чего получается ответ в виде дробного числа 41.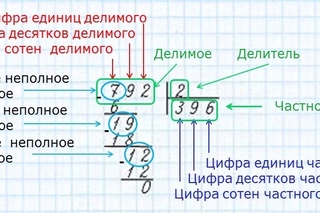 67.
67.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.
Пошаговая инструкция обучения делению столбиком
Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8. Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211. Результат необходимо перепроверить обратным умножением.
В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:
Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:
- Берем первую цифру числа, делим ее на делитель. Сколько раз делитель может содержаться в делимом?
- Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
- Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.
- Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
- Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.
На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.
1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.
Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников.
Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты.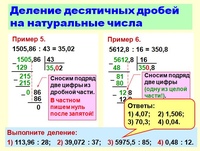 Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.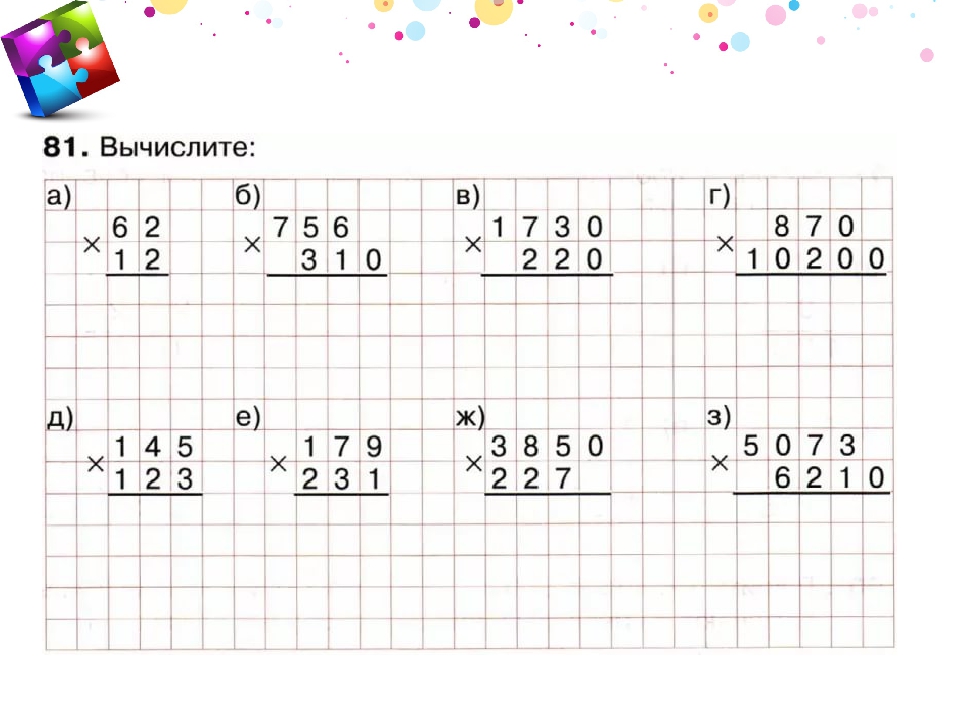
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.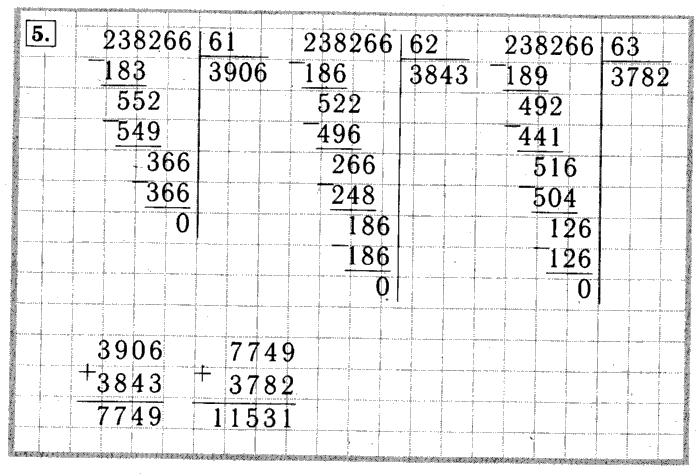
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10.
 Получится 0.
Получится 0. - Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.

- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
как объяснить ребенку деление в столбик
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.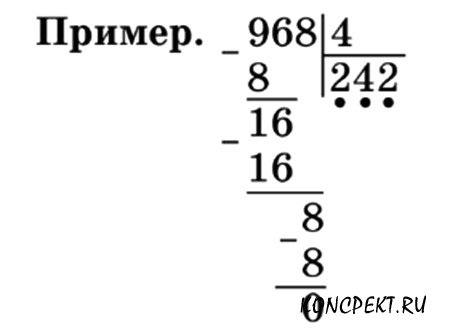
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Вам понадобятся:
Азы математики
Сначала убедитесь в том, что ваш ребенок усвоил более простые операции: сложение, вычитание, умножение.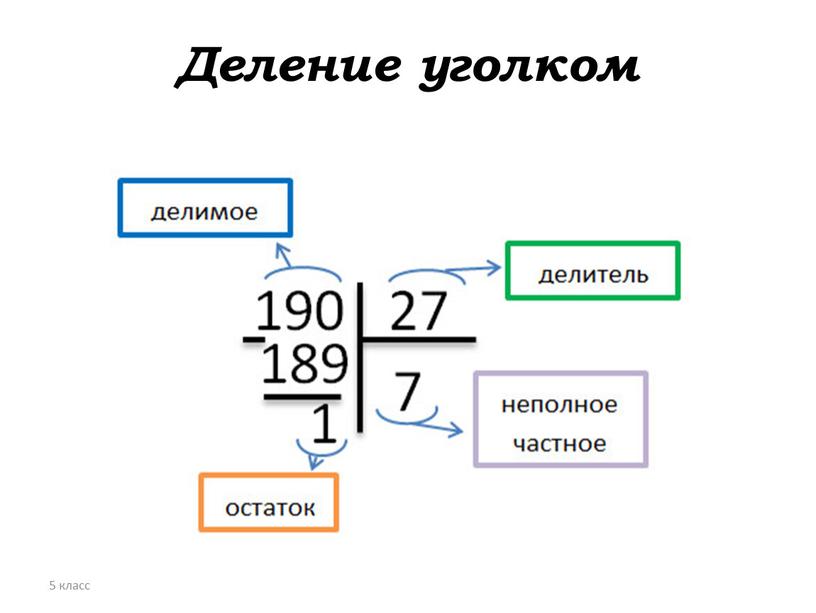 Без этих азов ему будет сложно понять деление.
Без этих азов ему будет сложно понять деление.
Если вы видите какие-то пробелы в знаниях, то повторите предыдущий материал.
Принцип деления
Прежде чем приступать к объяснению алгоритма деления следует сформировать у ребенка понимание самого процесса.
Объясните маленькому ученику, что «деление» – это разделение единого целого на равные части.
Возьмите коробку карандашей, которая будет выступать единым целым (можно взять любые предметы – кубики, спички, яблоки и т. д.), и предложите ребенку разделить их поровну между собой и вами. Затем, попросите его сосчитать сколько карандашей было изначально в коробке и сколько он раздал каждому.
По мере понимания ребенка, увеличивайте число предметов и количество участников. Далее, следует отметить, что не всегда получается разделить поровну и некоторые предметы остаются «ничейными». Например, предложите разделить 9 груш между бабушкой, дедушкой, папой и мамой. Ребенок должен усвоить, что все получат по 2 груши, а одна окажется в остатке.
Взаимосвязь с таблицей умножения
Покажите ребенку, что «деление» противоположное действие «умножению».
- Возьмите таблицу умножения и покажите ученику взаимосвязь между двумя операциями.
- Например, 4х5=20. Напомните ребенку, что число 20 результат произведения двух чисел 4 и 5.
- Затем, наглядно покажите, что деление противоположный процесс: 20/5=4, 20/4=5.
Обратите внимание ребенка на то, что правильным ответом всегда будет множитель, не участвующий в делении.
- Разберите другие примеры.
Если ваш ребенок отлично будет знать таблицу умножения, и поймет взаимосвязь между двумя математическими операциями, он легко освоит деление. Стоит ли запоминать ее в обратном порядке – выбор за вами.
Определение понятий
Перед началом занятий определите и выучите названия элементов, которые участвуют в процессе деления.
«Делимое» – число, которое следует разделить.
«Делитель» – это число на которое разделяется «делимое».
«Частное» – это результат, который получаем в процессе вычисления.
Для наглядности можете привести пример:
На день рождения сына/дочки вы купили 96 конфет, чтобы ребенок угостил своих друзей. Всего приглашенных – 8.
Объясните, что пакет с 96 конфетами – это «делимое». Восьмеро детей – «делитель». А количество конфет, которое получит каждый ребенок – «частное».
Алгоритм деления в столбик без остатка
Теперь покажите ребенку на примере о конфетах алгоритм вычисления.
- Возьмите чистый лист бумаги/тетрадь и напишите цифры 96 и 8.
- Разделите их перпендикулярными линиями.
- Покажите наглядно элементы.
- Укажите на то, что результат вычисления записывается под «делителем», а вычисления – под «делимым».
- Предложите маленькому ученику посмотреть на число 96 и определить цифру, которая больше 8.
- Из двух цифр 9 и 6, такой цифрой окажется 9.
- Спросите ребенка, сколько цифр 8 может «уместиться» в 9.
 Малыш, помня таблицу умножения, легко определит, что только раз. Поэтому запишите цифру 1 под подчеркиванием.
Малыш, помня таблицу умножения, легко определит, что только раз. Поэтому запишите цифру 1 под подчеркиванием. - Далее, умножьте делитель 8 на результат 1. Полученную цифру 8 запишите под первой цифрой делимого числа.
- Между ними поставьте знак «вычитания», и подведите итог. То есть, если от 9 отнять 8 получиться 1. Запишите результат.
На этом этапе объясните ребенку, что результат вычитания всегда должен быть меньше делителя. Если вышло наоборот, значит, малыш неправильно определил сколько 8 содержится в 9.
- Попросите снова ребенка определить цифру, которая больше делителя 8. Как видим, число 1 меньше 8. Поэтому нам следует объединить его со следующей цифрой делимого числа – 6.
- Припишите к единице 6 и получите 16.
- Далее, спросите у малыша сколько 8 содержится в 16. Правильный ответ 2 добавьте к первому.
- Снова умножьте 8 на 2. Полученный результат запишите под цифру 16.
- Путем «вычитания» (16-16) мы получим 0, что говорит о том, что наш результат вычисления – 12.
Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
В качестве примера, разделим 17 на 5.
Основные этапы :
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2.
 Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные : 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного .
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение .(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой формеТаким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбикПрежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
- Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.
Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Тогда все у вас получится.
Удивительное открытие сделала наша читательница. Ее сын на уроке не понял, как делить в столбик. Желая помочь сыну, она открыла учебник и увидела, что …ничего не увидела. Никаких пояснений к теме в книге почему-то не было. Как научить ребенка делению столбиком, если в книжке Вашего ребенка допущен подобный методический казус?
Что нужно знать, что бы научиться делить
Математика не любит пропусков. Все знания должны быть крепкими, как кирпичики. Если ребенок не знает основ, с делением будет невероятно трудно. На что следует обратить внимание?
- Знает ли школьник название элементов при делении.
- Убедитесь, что ребенок не забыл таблицу умножения.
- Повторите разряды числа.
Приступаем к делению
Как научить ребенка делить столбиком, мы разберем на конкретных примерах. Следите за рассуждениями и будьте внимательны к цифрам.
Отделяем делимое от делителя скобкой-уголком.
Рассуждаем так: можно ли 4 разделить на 5? Нет, нельзя. Поэтому мы берем не 4, а 46. Вспомним таблицу умножения (можно взять распечатку), какое число в таблице умножения на 5 ближайшее к 46? – 45. Сколько раз 5 помещается в 45? – 9 раз. Подписываем 45 по 46, единицы под единицами, чтобы не запутаться. Девятку пишем «на полочке» – в уголке.
Поэтому мы берем не 4, а 46. Вспомним таблицу умножения (можно взять распечатку), какое число в таблице умножения на 5 ближайшее к 46? – 45. Сколько раз 5 помещается в 45? – 9 раз. Подписываем 45 по 46, единицы под единицами, чтобы не запутаться. Девятку пишем «на полочке» – в уголке.
Если от 46 отнять 45, сколько получим? -1. Один меньше пяти? – меньше. Значит, мы разделили правильно.
Один на 5 не делится, сносим оставшееся число – 5, получаем 15. Пятнадцать делится на пять? — делится. Сколько получается? – 3. Тройку записываем в уголке. Проверяем решение: три умножить на 5, будет 15. Подписываем его под предыдущим числом. Из пятнадцати вычесть пятнадцать – будет ноль. Мы использовали все числа из делимого, значит, решили пример правильно.
В уголке мы записали две цифры – 9 и 3, получили число 93. Девяносто три – это частное, которое является решением нашего примера.
Объясняя школьнику, как научиться делить столбиком, выполняйте проверку обратным действием: 93*5. Кроме того, решайте более сложные варианты.
Кроме того, решайте более сложные варианты.
Есть и другие, частные случаи – о них Вы узнаете из программы. Если в учебнике действительно «ничего нет», возьмите за правило сверять решение с классной работой. Из классной тетрадки легко понять, каким методом пользуется учитель, и повторить его при объяснении домашней работы.
Деление в столбик — Математика
Урок №33
Тема: деление в столбик
Цели: закреплять знания, умения и навыки учащихся делить многозначные числа на многозначные; учить применять изученное при выполнении заданий; формировать навык самоконтроля; развивать зрительное и слуховое восприятия, вычислительные навыки; воспитывать положительную мотивацию учения, устойчивое внимание трудолюбие.
Тип урока: комбинированный
Методы обучения: словесный, наглядный, практический
Форма обучения: фронтальная, индивидуальная.
Ход урока
Организационный момент
Проверка домашнего задания (устно с места)
Актуализация опорных знаний учащихся
Ответить на вопросы:
Как называются члены деления?
Что значит разделить нацело a на b?
На какие числа делятся натуральные числа без остатка?
На что делить нельзя?
Какими свойствами обладает частное?
Постановка темы урока, цели и задач
Изучение нового материала
Вы помните, с чего всегда необходимо начинать деление? Надо выделить первое неполное делимое. После этого определяем количество цифр в частном и ставим точки на месте частного. Так как восемь меньше девяти, в качестве первого неполного делимого берём две цифры. Это число восемьдесят один. Ставим точку. В делимом есть ещё две цифры, значит, на месте частного ставим ещё две точки.
Так как восемь меньше девяти, в качестве первого неполного делимого берём две цифры. Это число восемьдесят один. Ставим точку. В делимом есть ещё две цифры, значит, на месте частного ставим ещё две точки.
Восемьдесят один делим на девять, получается девять. Это первая цифра частного. Умножаем девять на девять для того, чтобы узнать, сколько именно мы разделили. Это восемьдесят один. Вычитаем, чтобы узнать остаток. Он равен нулю, который, если деление не окончено, мы не пишем. И, конечно, остаток нуль меньше делителя.
Выделяем второе неполное делимое. Для этого переносим вниз следующую за первым неполным делимым цифру. Второе неполно делимое – пять. Делим его на девять. Так как делимое меньше делителя, то в частном получается нуль. Умножаем нуль на девять. Нуль. Вычитаем. Остаток пять. Сравниваем остаток с делителем. Он меньше делителя.
Выделяем третье неполное делимое. Это пять, что получилось в остатке, и справа от пятёрки дописываем следующую цифру из делимого. Третье неполное делимое – пятьдесят четыре. Делим его на девять, получается шесть. Умножаем. Шестью девять – пятьдесят четыре. Вычитаем. Остаток нуль. Деление закончено.
Третье неполное делимое – пятьдесят четыре. Делим его на девять, получается шесть. Умножаем. Шестью девять – пятьдесят четыре. Вычитаем. Остаток нуль. Деление закончено.
Вы обратили внимание на то, что в приёме письменного деления по нескольку раз повторяются одни и те же фразы?
Сначала выделяется неполное делимое. Затем его делят на делитель. Полученную цифру умножают на делитель. Полученное произведение вычитают из неполного делимого. Остаток сравнивают с делителем. И вновь: выделяем неполное делимое, делим его на делитель, полученную цифру умножаем на делитель, полученное произведение вычитаем из неполного делимого, остаток сравниваем с делителем. И так до тех пор, пока не закончится деление.
Вот у нас и получился алгоритм письменного деления многозначных чисел.
Ну а теперь я предлагаю вам посмотреть, как можно запись этого же примера выполнить немного короче.
Начинаю действовать по алгоритму. Выделяю первое неполное делимое, определяю количество цифр в значении частного, делю первое неполное делимое, умножаю полученную цифру, вычитаю полученное произведение. Остаток нуль не пишем, но знаем, что он меньше делителя. Следующее неполное делимое – пять. Так как оно меньше делителя, мы знаем, что, разделив его на девять, получим нуль. Вот теперь ВНИМАНИЕ!!! Мы не будем письменно выполнять деление пяти на девять. Сделаем это устно. Только не забудем записать нуль в частное. А после этого сразу возле пятёрки пишем следующую цифру делимого – четыре. Пятьдесят четыре делим на девять – получается шесть. Умножаем шесть на девять. Вычитаем. Остаток нуль. .
А теперь сравните записи решения одного и того же примера. Как видите, вторая запись немного короче первой, хотя оба примера имеют одинаковый ответ.
Правда, выполняя укороченную запись, очень легко допустить ошибку.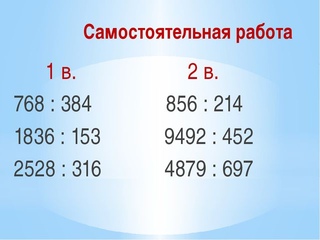 Иногда дети перед тем как перенести вниз вторую цифру неполного делимого, забывают поставить в частное нуль.
Иногда дети перед тем как перенести вниз вторую цифру неполного делимого, забывают поставить в частное нуль.
Чтобы этого не допустить, запомните ребята: если неполное делимое меньше делителя, к нему можно дописать следующую цифру из делимого. Но перед этим в частном обязательно написать нуль!
Вот сейчас попробуйте решить следующий пример, пользуясь укороченной записью.
А теперь проверьте ваше решение. Никто из вас не забыл перед тем, как перенести вниз цифру восемь, написать нуль в частное?
Не забудьте, Если для выделения неполного делимого вниз переносятся две цифры, необходимо в частное написать нуль.
А сейчас я покажу вам ещё один вид примеров, запись которых тоже можно выполнить короче. Это примеры, в которых делимое оканчивается нулями.
Вот, например, разделим двести сорок семь тысяч на пять.
Первое неполное делимое – двадцать четыре. В частном будет пять цифр. Делим двадцать четыре на пять – пишем в частное четыре. Четырежды пять – двадцать. Остаток – четыре. Четыре меньше пяти. Второе неполное делимое – сорок семь. Делим на пять – девять. Умножаем. Сорок пять. Вычитаем. Остаток два. Он меньше делителя. Третье неполное делимое – двадцать. Делим его на пять – четыре. Умножаем. Вычитаем. Остаток нуль. Дальше в делимом стоят два нуля, каждый из которых должен быть неполным делимым. Но когда мы их будем делить, в частном тоже будут нули. Поэтому не будем терять время, а просто перенесём эти два нуля из делимого в частное. Вот так мы сможем сэкономить время и укоротить нашу запись. Но это можно делать только в том случае, если нули стоят в конце делимого. И из делимого в частное переносятся не все нули, а только те, которые должны быть самостоятельными неполными делимыми.
В частном будет пять цифр. Делим двадцать четыре на пять – пишем в частное четыре. Четырежды пять – двадцать. Остаток – четыре. Четыре меньше пяти. Второе неполное делимое – сорок семь. Делим на пять – девять. Умножаем. Сорок пять. Вычитаем. Остаток два. Он меньше делителя. Третье неполное делимое – двадцать. Делим его на пять – четыре. Умножаем. Вычитаем. Остаток нуль. Дальше в делимом стоят два нуля, каждый из которых должен быть неполным делимым. Но когда мы их будем делить, в частном тоже будут нули. Поэтому не будем терять время, а просто перенесём эти два нуля из делимого в частное. Вот так мы сможем сэкономить время и укоротить нашу запись. Но это можно делать только в том случае, если нули стоят в конце делимого. И из делимого в частное переносятся не все нули, а только те, которые должны быть самостоятельными неполными делимыми.
Ну вот, пожалуй, и всё, о чём я сегодня хотела вам рассказать. Но перед тем как попрощаться, я хочу вам напомнить алгоритм приёма письменного деления.
И ещё. Если вы выполняете укороченную запись письменного деления, не забудьте: Переносить из делимого вниз можно только одну цифру. Если же вам нужно перенести и записать рядом вторую цифру, перед этим поставьте в частное нуль.
Ну, а если вы всё-таки забыли это сделать, ещё одна точка в частном, на которой не написали цифру, подскажет вам, что вы допустили ошибку. Так что не забывайте определять количество цифр в частном.
Физкультминутка
Один из учащихся класса проводит физкультминутку
Первичное формирование знаний, умений и навыков
Вычислить (варианты на усмотрение учителя):
9520 : 8 = 1190
21000 : 210 =100
5500 : 11 =500
22000 : 20 =1100
6860 : 7 =980
78400 : 56 = 1400
228000 : 38 =6000
905000 : 50 =18100
844000 : 20 =42200
18000 : 450 =40
2610 : 9 = 290
29600 : 740 =40
2400 : 48 =50
80000 : 80 =1000
66300 : 30 =2210
50400 : 63 = 800
94500 : 35 =2700
264000 : 300 =880
84600 : 600 =141
68000 : 680 =100
8720 : 4 = 2180
32000 : 400 =80
51700 : 47 =1100
102000 : 600 =170
10000 : 200 =50
98800 : 260 = 380
9880 : 26 =380
282000 : 60 =4700
692000 : 40 =17300
426000 : 71 =6000
76300 : 700 = 109
81600 : 510 =160
8400 : 70 =120
60900 : 70 =870
136000 : 80 =1700
777000 : 37 = 21000
71500 : 650 =110
84800 : 800 =106
450000 : 900 =500
72000 : 200 =360
83200 : 400 = 208
6120 : 9 =680
41800 : 380 =110
68400 : 6 =11400
252000 : 900 =280
69000 : 50 = 1380
660000 : 550 =1200
48000 : 96 =500
43400 : 700 =62
108000 : 300 =360
671000 : 61 = 11000
8520 : 2 =4260
89000 : 89 =1000
79200 : 880 =90
312000 : 80 =3900
390000 : 300 =1300
7700 : 77 =100
188000 : 940 =200
405000 : 500 =810
436000 : 400 =1090
600000 : 24 = 25000
7400 : 200 =37
884000 : 17 =52000
498000 : 30 =16600
74200 : 200 =371
7200 : 72 = 100
940 : 94 =10
83200 : 800 =104
3200 : 8 =400
66300 : 17 =3900
5820 : 6 = 970
630000 : 900 =700
910000 : 70 =13000
98000 : 50 =1960
1280 : 8 =160
83000 : 830 = 100
15000 : 75 =200
540000 : 900 =600
310000 : 500 =620
120000 : 10 =12000
80000 : 80 =1000
52800 : 44 =1200
7150 : 55 =130
636000 : 40 =15900
2790 : 9 =310
297000 : 270 =1100
969000 : 300 =3230
67000 : 67 =1000
86000 : 40 = 2150
894000 : 30 =29800
332000 : 20 =16600
583000 : 530 =1100
882000 : 980 =900
148000 : 20 =7400
9325 : 25 =373
7790 : 41 =190
350000 : 250 =1400
12600 : 60 =210
48000 : 600 =80
2100 : 70 =30
432000 : 540 =800
90300 : 300 =301
26500 : 500 =53
390 : 39 =10
52600 : 200 =263
64400 : 23 =2800
19200 : 960 =20
78000 : 200 =390
552000 : 200 =2760
65000 : 95 =67000
61000 : 610 =100
3180 : 6 =530
696000 : 400 =1740
7100 : 71 =100
738000 : 60 =12300
98000 : 70 =1400
385000 : 11 =35000
1120 : 7 =160
89100 : 90 =990
36400 : 91 =400
4000 : 200 =20
8900 : 89 =100
98000 : 50 =1960
6650 : 95 =70
1500 : 2 =750
546000 : 91 =6000
55300 : 7 =7900
10000 : 20 =500
328000 : 40 =8200
192000 : 960 = 200
33000 : 110 =300
540000 : 600 =900
952000 : 400 =2380
39600 : 44 =900
860 : 2 =430
18000 : 150 =120
18200 : 26 =700
4500 : 5 =900
6060 : 2 =3030
408000 : 51 =8000
53700 : 30 =1790
54900 : 900 =61
666000 : 370 =1800
71200 : 400 =178
4950 : 55 =90
48800 : 61 =800
203000 : 70 =2900
450 : 9 =50
170000 : 17 =10000
81900 : 90 =910
Подведение итогов урока
Сообщение домашнего задания
Вычислить:
Что такое длинное деление? [Определение, факты и пример]
Игры с длинным разделением
Разделить на 2-значные числа Разделить 4-значные числа на 2-значные числа, при этом при делении не остается остатка. Вы начнете с оценки частных.
Вы начнете с оценки частных.
Разделите 4-значные числа на 2-значные числа. Начните с оценки частных, которые пригодятся при делении на 2-значные числа.
охватывает общий основной учебный план 5.NBT.6Играть сейчасПосмотреть все игры с разделением >>Учитесь с помощью полной программы обучения математике K-5
Что такое длинное деление?В математике деление в столбик — это метод, используемый для деления больших чисел на группы или части.
Длинное деление помогает разбить проблему деления на последовательность более простых шагов. Как и во всех задачах деления, большое число, являющееся делимым, делится на другое число, которое называется делителем, чтобы получить результат, называемый частным, а иногда и остатком.Как вы делаете деление в столбик?
Метод деления в столбик включает в себя основные математические операции.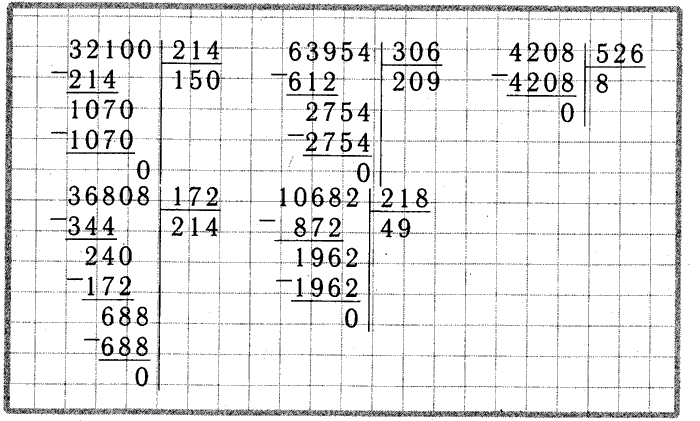
Для деления двух чисел этим методом рисуется таблица. Делитель пишется за пределами правых скобок, а делимое — внутри. Частное указывается над чертой сверху над дивидендом.
Деление в столбик состоит из 5 шагов:
| D | Разделить |
| M | Умножить |
| S | Вычесть |
| B | Сбить |
| R | Повтор или остаток |
Вот пример деления в столбик, где каждый шаг четко показан.
Процесс начинается с деления или определения, сколько раз крайняя левая цифра делимого может быть разделена на делитель.
Затем результат или ответ из шага 1, который становится первой цифрой частного, умножается на делитель и записывается под первой цифрой делимого.
Вычитание производится по первой цифре делимого и записывается остаток.
Следующая цифра делимого уменьшается, а затем процесс повторяется до тех пор, пока все цифры делимого не будут сброшены и не будет найден остаток.
Как разделить десятичные дроби методом длинного деления?
Деление в столбик можно также использовать для разделения десятичных чисел на равные группы. Он выполняет те же шаги, что и при делении в столбик, а именно: деление, умножение, вычитание, уменьшение и повторение или нахождение остатка.
Вот пример деления в столбик с десятичными знаками.
Интересные факты
|
Давайте споем!
Если нужно разделить большие числа,
нарисуйте таблицу для длинного деления сбоку.
Напишите шаги, которые будут вашим руководством,
D, M, S, B и R — Придерживайтесь долгого разделения!
Давайте сделаем это!
Вместо того, чтобы показывать видео для обучения полному делению или раздавать практические задания ученикам 4-го класса, приведите примеры из реальной жизни, когда они могут использовать метод длинного деления для деления.
Скажем, готовя кексы и печенье для продажи в школе, вы можете попросить ребенка подсчитать количество партий, в которых можно приготовить печенье или кексы (исходя из количества форм на подносе), если общее количество печенья и кексы требуются. Вы также можете попросить их подсчитать общее количество необходимых коробок, если в каждую коробку печенья помещается 15 печенья, а в картонную коробку для кексов — 6 кексов. Попросите их вычислить, используя метод длинного деления.
Связанный математический словарь
Двухзначный делитель в столбике
Это полный урок с примерами и упражнениями о двузначном делителе в столбик, предназначенный для начального обучения в 5-м классе.В первых упражнениях есть сетки для завершения деления и место для учеников, чтобы они могли написать таблицу умножения делителя на полях. Кроме того, существуют проблемы преобразования между дюймами / футами и унциями / фунтами, потому что они решаются с помощью деления.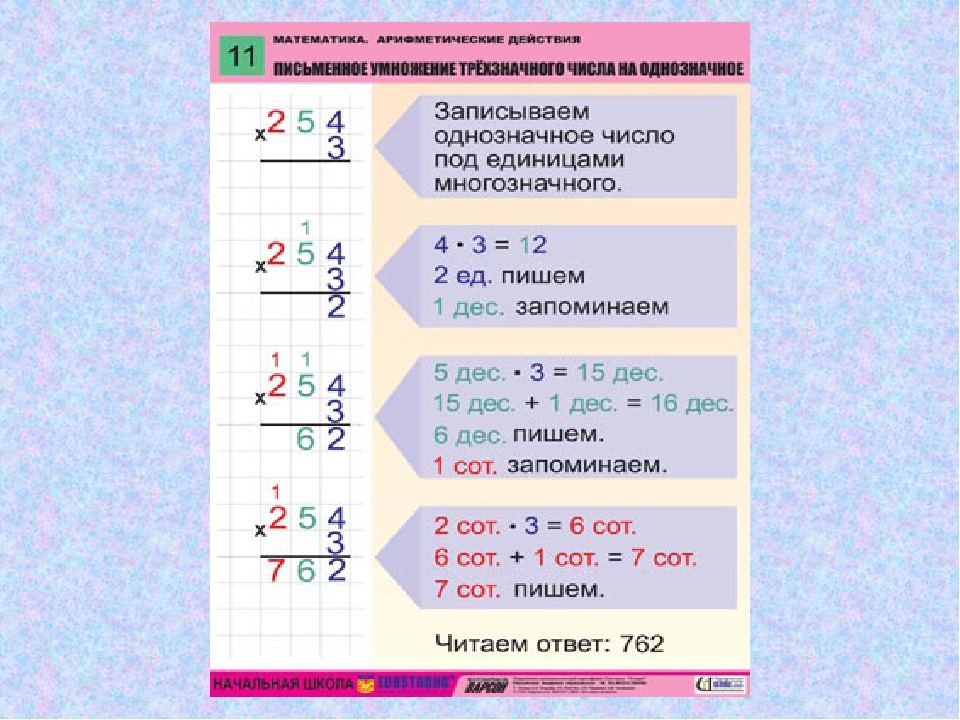
| Часто бывает полезно написать таблицу умножения делителя перед вы разделяете. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1. Деление на 16.Здесь таблица умножения 16: 3 × 16 = 48 |
16 переходит в 5 нулевых раз, поэтому мы смотрим на 55. Сколько раз 16 входит в 55? Отметьте в таблице на слева. Мы видим, что он входит в число 55 три раза. |
А теперь сколько раз 16 переходит в 76? Из таблицы видно, что это четыре раза. |
Наконец, 16 переходит в 128 ровно 8 раз, а разделение окончено. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2. 3 × 32 = 96 |
|
32 переходит в 150
четыре раза. |
32 переходит в 224 семь
раз. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Разделить. Сначала напишите таблица умножения делителя. Проверяйте каждый ответ умножением.
|
2.Разделять. Сначала напишите таблица умножения делителя. Проверяйте каждый ответ умножением.
| |||||
| |||||
| |||||
|
3.Разделять. Проверяйте каждый ответ умножением.
| ||||
| ||||
| ||||
|
4. Ментальная математика! Если 20 переходит в
800 сорок раз, затем 20 переходит в 820 еще раз,
или 41 раз.В каждом поле используйте верхнюю задачу, чтобы решить нижнюю.
проблема.
| а. 800 ÷ 20 = 820 ÷ 20 = | г. 700 ÷ 50 = 750 ÷ 50 = | г. 150 ÷ 15 = 300 ÷ 15 = |
| г. 480 ÷ 40 = 520 ÷ 40 = | e. 600 ÷ 30 = 690 ÷ 30 = | ф. 1,200 ÷ 60 = 1,320 ÷ 60 = |
5. а. Сколько дюймов в одном футе?
а. Сколько дюймов в одном футе?
г. Преобразовать 245 дюймов в футы и дюймы.
с. Преобразование 387 дюймов в футы и дюймы.
6. а. Сколько унций в одном фунте?
г. Перевести 163 унции в фунты
и унции.
с. Перевести 473 унции в фунты
и унции.
7. Новорожденный ребенок набирает вес на 90 161.
примерно одна унция в день.
Допустим, ребенок набрал вес
по этой ставке на ПОЛНЫЙ ГОД.
(На самом деле младенцы этого не делают; их
темп роста замедляется.) сколько
фунты и унции бы ребенок
прибыль за год?
См. Также
Листы с длинным делением
Создайте неограниченное количество листов для деления в столбик (классы 4-6), в том числе с 2-значными и 3-значными делителями.Рабочие листы могут быть выполнены в формате html или PDF — оба легко распечатать.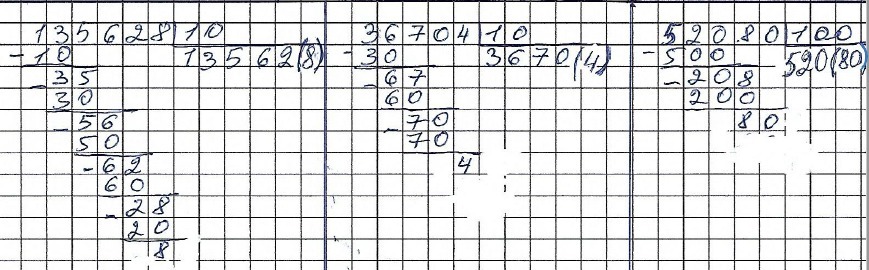 Вы также можете настроить их с помощью генератора.
Вы также можете настроить их с помощью генератора.
/worksheets/long_division.php
Этот урок взят из книги Марии Миллер Math Mammoth Multiplication & Division 3 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Что такое столбик? | TheSchoolRun
Что такое длинное деление?
Метод длинного деления используется, когда вы делите большое число (обычно три или более цифр) на двузначное (или более) число.Он оформлен аналогично сокращенному разделу (метод «автобусной остановки») .
Деление в столбик: пошаговое руководство
Деление в столбик «столбик» определяется следующим образом.
Когда дети учатся использовать разные методы деления?
Дети начинают изучать разделение в 1 году, когда их могут попросить разделить четное количество предметов между двумя людьми.
Они начинают изучать свои таблицы умножения во 2-м классе, в это время они также изучают свои факты деления (например, они узнают, что если 4 x 5 = 20, то 20 ÷ 5 = 4).
Они продолжают изучать остальные таблицы умножения, включая факты деления в течение 3 и 4 лет.
В году 5 они научатся делить трехзначные и четырехзначные числа на однозначное число, раздел (это также известно как метод «автобусной остановки»). Затем они переходят к , деля большие числа на двузначные числа, используя длинное деление , как показано выше.
Раньше учителя обучали детей методу разбиения на части, однако согласно учебной программе 2014 года им рекомендуется использовать краткое и длинное деление.
Использование техники деления в математике
Очень важно, чтобы детей учили делению в контексте решения задач.
На 2-м году обучения их могут попросить решить такую словесную задачу:
У меня 20 конфет.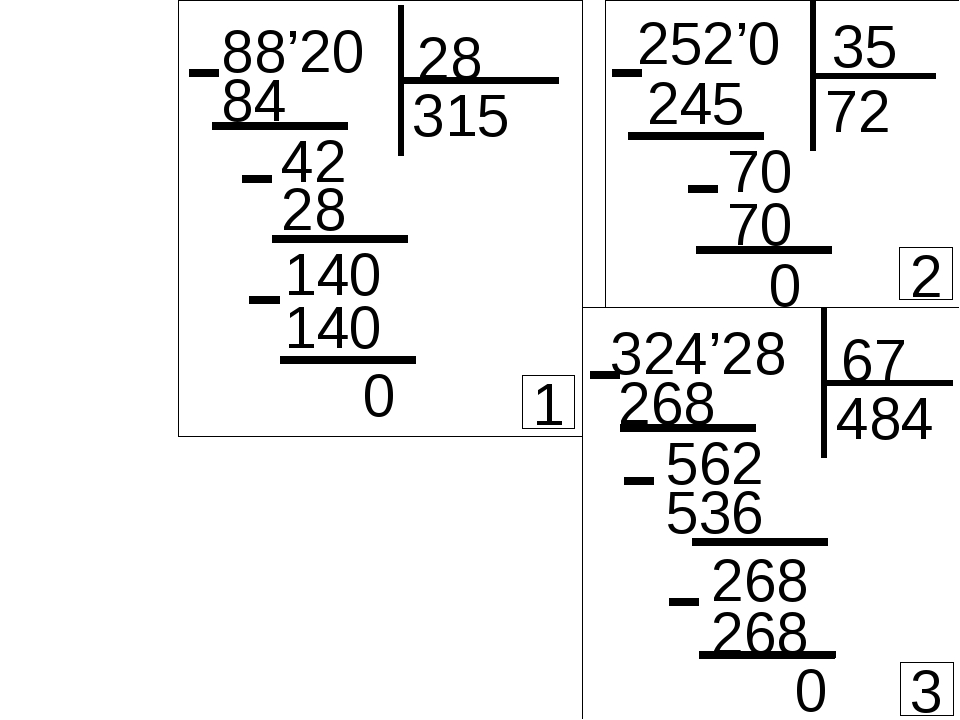 Я делю их между 4 людьми. Сколько сладостей у каждого из них?
Я делю их между 4 людьми. Сколько сладостей у каждого из них?
Их могут побудить использовать счетчики для распределения «сладостей», но они будут побуждены перейти к использованию своих знаний о фактах разделения для решения этой проблемы.
Дети 3-го и 4-го классов будут отвечать на вопросы, используя более сложные таблицы умножения, например:
На детской площадке 42 ребенка. Они разделены на 6 групп по равному количеству детей в каждой. Сколько детей в каждой группе?
В 5-м и 6-м классе им могут задать такие вопросы, как:
В банке 564 бусины. Их нужно поровну разделить на шесть небольших банок. Сколько бусинок будет в каждой баночке?
Я покупаю 23 торта, каждый по той же цене.Общая сумма составляет 11,04 фунта стерлингов. Сколько стоит каждый торт?
Очень важно, чтобы дети разобрались с делением в контексте своих таблиц умножения, прежде чем они смогут приступить к делению больших чисел. Вы действительно можете помочь своему ребенку дома, задав ему множество вопросов умственного деления в соответствии с их таблицей умножения.
Также важно, что в более поздних версиях KS2 они научатся делить числа на 10 и 100 уверенно и эффективно.
Обучайте ребенка делению в столбик за 1,99 фунта стерлингов
Помогите своему ребенку раз и навсегда освоить деление в столбик с помощью пакета действий TheSchoolRun’s Mastering Long Division Step-by-Step : 40 страниц объяснений, примеров, советов и практических вопросов всего 1,99 фунта стерлингов. Загрузите эту целевую электронную книгу сейчас, чтобы повысить уверенность вашего ребенка (и вашего!) И убедиться, что он никогда больше не беспокоится о делении больших чисел.
Как помочь вашему ребенку освоить стратегии деления и длинного деления
Когда моя дочь пошла на деление в четвертом классе, я знал, что нас ждут неприятности (и дополнительные домашние занятия по математике).Как родитель, который изучал математику «старым» способом, мне было очень трудно понять процессы, лежащие в основе ее домашнего задания по математике и задач со словами. (Мне неловко сказать, что задачи по разделению слов для четвертого класса — это не шутка.) Я использовал книгу Эван-Мура Основы математики , чтобы изучить, попрактиковаться и проанализировать стратегии разделения. Визуальные модели и объяснения предоставили пошаговый процесс обучения, который укрепил то, что моя дочь изучала в школе, и углубил ее понимание. Помогая своей дочери освоить деление в столбик, я даже обнаружил стратегии, лежащие в основе процесса деления, которые углубили мое понимание взаимосвязи между делением и умножением.
(Мне неловко сказать, что задачи по разделению слов для четвертого класса — это не шутка.) Я использовал книгу Эван-Мура Основы математики , чтобы изучить, попрактиковаться и проанализировать стратегии разделения. Визуальные модели и объяснения предоставили пошаговый процесс обучения, который укрепил то, что моя дочь изучала в школе, и углубил ее понимание. Помогая своей дочери освоить деление в столбик, я даже обнаружил стратегии, лежащие в основе процесса деления, которые углубили мое понимание взаимосвязи между делением и умножением.
Division — это один из тех математических навыков, которые заслуживают много внимания, объяснений и практики. Вместо того, чтобы преподавать математику как серию систем / шагов для запоминания, сегодняшняя математическая программа включает в себя фундаментальные мыслительные процессы, лежащие в основе каждого навыка и стратегии, которым обучают детей. Сегодняшняя программа по математике требует, чтобы дети понимали, почему они делают эти шаги, и использовали это понимание числовых отношений для более эффективного решения задач. Если дети знают, почему они делают определенные шаги, они могут применять это понимание для решения различных математических задач и понимать беглость чисел на более глубоком уровне.
Если дети знают, почему они делают определенные шаги, они могут применять это понимание для решения различных математических задач и понимать беглость чисел на более глубоком уровне.
Вот некоторые стратегии и концепции, которые мы практиковали, которые помогли мне и моей дочери лучше понять разделение.
Начало деления и умноженияКогда ваш ребенок начинает изучать деление, ему / ей важно понимать взаимосвязь между делением и умножением. Детям необходимо хорошо знать факты умножения. (Если они не знают фактов умножения, потренируйтесь в беглости несколько недель, прежде чем начинать деление.) Ознакомьтесь с дополнительными ссылками ниже, чтобы получить советы и идеи, чтобы узнать факты умножения.
Связь между умножением и делением
«Начало деления» учит простой концепции: чтобы делить, вы должны умножать. Использование наглядных примеров умножения и деления поможет вашему ребенку научиться распознавать разницу между умножением и делением.
Если вы привыкли к старому методу деления, этот процесс может показаться утомительным, но детям важно понимать разницу между умножением и делением.Когда задачи с числами и словами усложняются, это фундаментальное понимание поможет им узнать, когда делить, а когда умножать.
Смоделируйте, как найти неизвестное число умножением или делением.
Чтобы узнать, понимает ли ваш ребенок основную взаимосвязь между умножением и делением, спросите его:
Ответ: факты умножения и деления связаны. Если вы знаете один факт, вы можете решить другой связанный факт.
Стратегии трех подразделений Один из аспектов нынешней учебной программы по математике, который мне нравится, — это акцент на обучении нескольким стратегиям и разрешению детям решать, какая из них лучше всего подходит для них. Такой подход позволяет детям понять и выбрать, какой метод лучше всего подходит для их стиля обучения. Испытание различных подходов может иногда даже иметь значение между неудачей и успехом в математике. Вот три разные стратегии, которым нужно научить, когда начинаете деление.
Испытание различных подходов может иногда даже иметь значение между неудачей и успехом в математике. Вот три разные стратегии, которым нужно научить, когда начинаете деление.
1. Установите связи с помощью шаблонов деления и разбейте числа
Это высшая степень беглости чисел. Обучение детей распознаванию и использованию шаблонов в числовых операциях поможет им эффективно решать проблемы.
6,000 ÷ 3
6 ÷ 3 = 2
6,000 ÷ 3 = 2,000
Просто представьте 6000, разделенные на 3, как 6 тысяч, разделенных на 3, и это 2 тысячи.
2.Разбивка чисел на «дружественные» числа с использованием модели области
260 ÷ 5 = 52 Разбейте числа на «дружественные» числа. Разбивка чисел на числа, которые легко делятся, важно научиться бегло читать. Это может показаться немного утомительным, но понимание того, как разбить большие числа на числа, которыми легче манипулировать, может развить у детей умственные математические способности.
Разбейте 260 на «дружественные» числа 250 и 10. Я выбрал 250, потому что это делитель 5, умноженный на большое число (50).Я выбираю 10, потому что это разница между 250 и 260. Они входят в рамки модели площади. Разделите каждый на делитель, чтобы получить множители, затем сложите множители.
3. Разделить на группы вычитания 623 ÷ 4Я могу составлять группы по 4 человека и вычитать их из 623 до тех пор, пока не останется достаточно, чтобы создать группу. Я начну со 100 групп по 4. Осталось 223. Затем я вычту 50 групп по 4. Теперь у меня осталось 23.5 групп по 4 человека используют большую его часть; осталось недостаточно, чтобы вычесть даже 1 группу из 4. Наконец, я сложу количество групп из 4 и запишу остаток.
Длинное деление: деление многозначных чисел с помощью моделей площадей, частичных частных и стандартного алгоритма
Если я только что потерял вас, используя такие фразы, как «частные частные» и «стандартный алгоритм», не пугайтесь.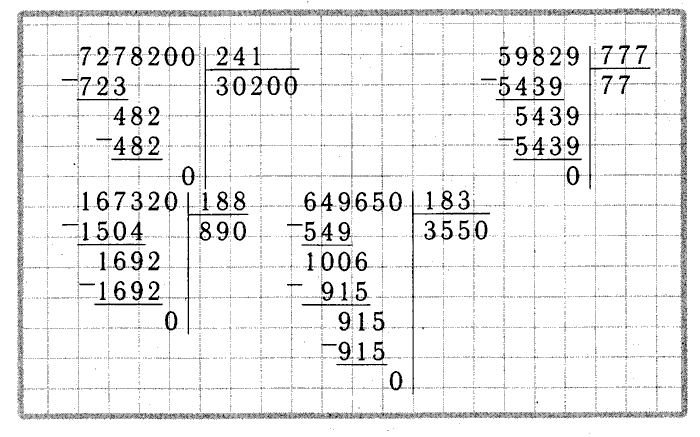 Это просто математическая терминология для пошаговых процессов.Частное — это ответ, а частное — частичное. Стандартный алгоритм — это пошаговый способ решения проблемы. При делении в столбик эти стратегии используются для повторного вычитания, чтобы в конечном итоге найти ответ.
Это просто математическая терминология для пошаговых процессов.Частное — это ответ, а частное — частичное. Стандартный алгоритм — это пошаговый способ решения проблемы. При делении в столбик эти стратегии используются для повторного вычитания, чтобы в конечном итоге найти ответ.
Деление многозначных чисел с использованием модели области
Мы уже занимались этим ранее, начав деление, но теперь числа становятся больше и немного сложнее.
3,182 ÷ 15 = 212 R2
Деление — это просто повторное вычитание.Я сгруппирую по 15 штук и вычту их, пока не останется достаточно средств для вычитания. Затем я сложу количество групп. Поскольку у меня получилось число меньше делителя, я запишу его как остаток.
3,182 ÷ 15 = 212 R2
Разделить на частные
Как и в модели площади, я нахожу группы делителя и вычитаю их. Затем я сложу количество групп и запишу остаток, если он есть.
Разделить по стандартному алгоритму Если вы вздохнете с облегчением на этом примере, я полностью понимаю.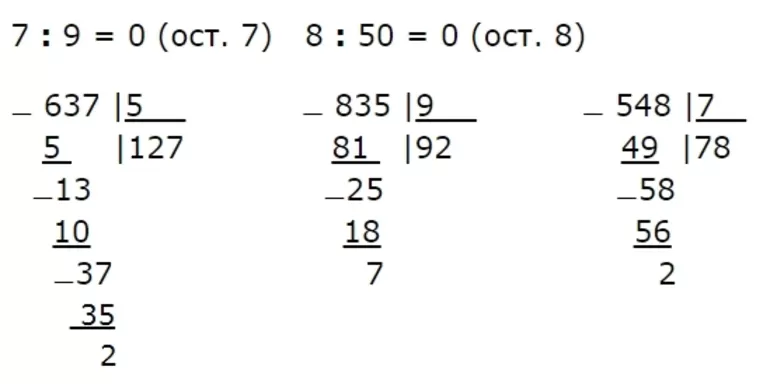 Это традиционный способ обучения разделению, которому большинство из нас научилось много лет назад.
Это традиционный способ обучения разделению, которому большинство из нас научилось много лет назад.
Этот стандартный алгоритм длинного деления повторяется с шагами:
1. Разделить
2. Умножить
3. Вычтем
4. Перейдите к следующей цифре
5.Повторить
* Многие дети путаются с шагами 2 и 3 , потому что вы на самом деле не делите, а умножаете и вычитаете, чтобы найти остаток.
3,182 ÷ 15 = 212 R2
Смотрите только на одно место, начиная с левого. Поскольку 15 не делятся на 3, я перейду к следующему месту. Теперь я прикидываю, сколько раз 15 перейдет в 31, и напишу это над 1. Я вычитаю и убираю цифру со следующего места.Я продолжаю делать это через дивиденд (число). Когда у меня заканчиваются места, я запишу оставшееся число в качестве остатка.
Лучший способ помочь вашему ребенку овладеть трудным навыком разделения — это практика, практика и практика. Выясните, какой метод лучше всего подходит для вашего ребенка, и предложите ему или ей множество практических задач. Кроме того, не забывайте решать проблемы с разделением слов. Решение задач со словами может продемонстрировать, насколько хорошо ваш ребенок понимает концепцию деления и как ее использовать.
Рекомендуемые ресурсы
Все примеры и стратегии были взяты из книги Evan-Moor Math Fundamentals для 1–6 классов. Хотя это учебный ресурс, я обнаружил, что математические модели и практические занятия удобны для использования дома.
Советы по обучению задачам со словами и умножению можно найти в следующих статьях:
Хизер Фоуди — сертифицированный учитель начальных классов с более чем 7-летним опытом работы в качестве преподавателя и волонтера в классе.Ей нравится создавать содержательные и творческие уроки для учеников. В настоящее время она работает в отделе маркетинга и коммуникаций Эван-Моора и любит создавать возможности для обучения, которые являются значимыми и творческими как для студентов, так и для учителей.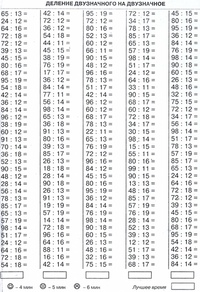
Категории: Классные стратегии, Идеи уроков | Теги: математика 3-го класса, математика 4-го класса, разделение 5-го класса, общее ядро деления, стратегии деления, разделение четвертого класса, как преподавать разделение, математика, разделение третьего класса | Постоянная ссылка
Полиномиальное деление наLong: Примеры | Purplemath
Purplemath
В отличие от примеров на предыдущей странице, почти все полиномиальные деления не «получаются четными»; обычно вы получаете остаток.
Разделить 3
x 3 -5 x 2 + 10 x -3 на 3 x + 1
Я начинаю с настройки длинного деления:
Рассматривая только главные члены, я делю 3 x 3 на 3 x , чтобы получить x 2 . Вот что я поставил поверх:
Вот что я поставил поверх:
MathHelp.com
Я умножаю это x 2 на 3 x + 1, чтобы получить 3 x 3 + 1 x 2 , которое я поместил под:
Затем я меняю знаки, складываю вниз и не забываю перенести «+10 x — 3» из исходного делимого, получив новую нижнюю строку –6 x 2 + 10 x — 3:
Разделив новый ведущий член, –6 x 2 , на ведущий член делителя, 3 x , я получу –2 x , поэтому я поместил это сверху:
Затем я умножаю –2 x на 3 x + 1, чтобы получить –6 x 2 — 2 x , которые я помещаю ниже. Я меняю знаки, складываю и не забываю убрать «–3» из дивиденда:
Я меняю знаки, складываю и не забываю убрать «–3» из дивиденда:
Моя новая последняя строка: «12 x — 3. Разделив новый ведущий член 12 x на ведущий член делителя 3 x , я получаю +4, которое кладу сверху. Я умножаю 4 на 3 x + 1, чтобы получить 12 x + 4. Я переключаю знаки и складываю вниз. В итоге получается остаток –7:
Эта дивизия даже не вышла.Что мне делать с остатком?
Вспомните, когда вы делали в столбик простые числа. Иногда оставался остаток; например, если вы разделите 132 на 5:
… осталось 2. Помните, как вы с этим справились? Вы составили дробь, положив остаток поверх делителя, и написали ответ как «двадцать шесть и две пятых»:
Первая форма без «плюса» посередине — это то, как записываются «смешанные числа», но значение смешанного числа фактически представляет собой форму с добавлением.
Проделаем то же самое с полиномиальным делением. Поскольку остаток в этом случае равен –7 и поскольку делитель равен 3 x + 1, я превращу остаток в дробь (остаток, деленный на исходный делитель) и добавлю эту дробь к многочлену по верхняя часть символа деления. Тогда мой ответ такой:
Предупреждение: , а не , записывают полиномиальное «смешанное число» в том же формате, что и числовые смешанные числа! Если вы просто добавите дробную часть к полиномиальной части, это будет интерпретировано как полиномиальное умножение, которое равно , а не , как вы имеете в виду!
Примечание: разные книги по-разному форматируют полное разделение.При написании выражений в верхней части раздела некоторые книги помещают термины над термином той же степени, а не над термином, над которым работаете. В таком тексте длинное деление выше будет представлено, как показано здесь:
Единственное отличие состоит в том, что члены вверху смещены вправо. В остальном все точно так же; в частности, все вычисления точно такие же. В случае сомнений используйте форматирование, которое использует ваш инструктор.
В остальном все точно так же; в частности, все вычисления точно такие же. В случае сомнений используйте форматирование, которое использует ваш инструктор.
Вам может быть интересно, как я узнал, что нужно остановиться, когда дошел до остатка –7. Это очень похоже на то, как вы знали, когда остановиться при делении в столбик (до того, как узнали о десятичных разрядах). Как только вы дошли до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как могли, поэтому остановились; все, что осталось, было вашим остатком. То же самое и с полиномиальным делением в столбик. –7 — это просто постоянный член; 3 x «слишком велико», чтобы войти в него, точно так же, как 5 было «слишком большим», чтобы войти в 2 в приведенном выше примере числового деления в столбик.Как только вы дойдете до остатка, который «меньше» (в полиномиальной степени), чем делитель, все готово.
Разделить 2
x 3 — 9 x 2 + 15 на 2 x — 5
Прежде всего, я отмечу, что существует разрыв в степенях членов делимого: полином 2 x 3 -9 x 2 + 15 не имеет члена x . Моя работа может усложниться внутри символа разделения, поэтому важно, чтобы я на всякий случай оставил место для столбца размером x . (Это похоже на ноль, скажем, в разряде сотен делимого, в котором столбец открыт для вычитаний под символом деления.) Я могу создать это пространство, превратив делимое в 2 x 3 — 9 х 2 + 0 х + 15.
Моя работа может усложниться внутри символа разделения, поэтому важно, чтобы я на всякий случай оставил место для столбца размером x . (Это похоже на ноль, скажем, в разряде сотен делимого, в котором столбец открыт для вычитаний под символом деления.) Я могу создать это пространство, превратив делимое в 2 x 3 — 9 х 2 + 0 х + 15.
(Это законный математический шаг.Я добавил только ноль, так что фактически ничего не изменил.)
Теперь, когда у меня есть вся «комната», которая может мне понадобиться для работы, я займусь делением. Я начинаю, как обычно, с расстановки длинных делений:
Разделив 2 x 3 на 2 x , я получу x 2 , поэтому я положил это поверх. Затем я умножаю x 2 на 2 x — 5, чтобы получить 2 x 3 — 5 x 2 , которые я поместил под. Затем я меняю знаки, складываю и убираю 0 x + 15 из исходного делимого. Это дает мне –4 x 2 + 0 x + 15 в качестве моей новой чистой прибыли:
Затем я меняю знаки, складываю и убираю 0 x + 15 из исходного делимого. Это дает мне –4 x 2 + 0 x + 15 в качестве моей новой чистой прибыли:
Разделив –4 x 2 на 2 x , я получу –2 x , которые я положил поверх. Умножив это –2 x на 2 x — 5, я получу –4 x 2 + 10 x , которые я поместил внизу.Затем я меняю знаки, складываю и убираю +15 от предыдущего дивиденда. Это дает мне –10 x + 15 в качестве моей новой чистой прибыли:
Разделив –10 x на 2 x , я получу –5, которое кладу поверх. Умножая –5 на 2 x — 5, я получаю 10 x + 25, которые кладу ниже. Затем я меняю знаки и складываю, в результате остается -10:
Мне нужно запомнить, чтобы к добавить остаток к полиномиальной части ответа:
Разделить 4
x 4 + 1 + 3 x 3 + 2 x на x 2 + x + 2
Сначала я переставлю дивиденды, чтобы члены записывались в обычном порядке:
Я заметил, что в дивиденде нет члена x 2 , поэтому я создам его, добавив член 0 x 2 к дивиденду (внутри символа деления), чтобы освободить место для моей работы.
Тогда сделаю деление как обычно. Разделив 4 x 4 на x 2 , я получу 4 x 2 , которые я положил сверху. Затем я перемножаю и так далее, получая новую строку:
Деление — x 3 на x 2 , получаю — x , которое кладу поверх. Затем я умножаю и т. Д. И т. Д .:
Разделив –7 x 2 на x 2 , я получу –7, которое кладу поверх.Затем я умножаю и т. Д. И т. Д .:
И затем я закончил деление, потому что остаток линейный (11 x + 15), а делитель квадратичный. Квадратичный не может делиться на линейный многочлен, поэтому я зашел так далеко, как мог.
Тогда мой ответ:
Чтобы добиться успеха с полиномиальным делением в столбик, вам нужно писать аккуратно, не забывать менять знаки при вычитании и работать аккуратно, правильно выстраивая столбцы. Если вы сделаете это, то эти упражнения не должны быть очень тяжелыми; раздражает, может быть, но не сложно.
Если вы сделаете это, то эти упражнения не должны быть очень тяжелыми; раздражает, может быть, но не сложно.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске, выполняя длинное полиномиальное деление. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Разделить с помощью длинного полиномиального деления», чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/polydiv3.htm
Длинное деление многочленов
Длинное деление многочленов Вот шаги, необходимые для деления на полином, содержащий более одного члена (длинное деление):| Шаг 1: | Убедитесь, что полином записан в порядке убывания. Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). |
| Шаг 2: | Разделите член с наивысшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. |
| Шаг 3: | Умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. |
| Шаг 4: | Вычтите и сократите следующий член. |
| Шаг 5: | Повторяйте шаги 2, 3 и 4 до тех пор, пока не останется терминов, которые нужно сбрасывать. |
| Шаг 6: | Напишите окончательный ответ. Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе. Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе. |
Пример 1 — Разделить:
Пример 2 — Разделить:
Щелкните здесь для практических задач
Пример 3 — Разделить:
Щелкните здесь для практических задач
Пример 4 — Разделить:
| Шаг 1 : Убедитесь, что полином записан в порядке убывания.Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). В этом случае должно получиться: | |
Шаги 2, 3 и 4 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 2x 3 / 2x = x 2 и x 2 (2x + 3).Наконец, вычтите и опустите следующий член. В этом случае мы должны получить 2x 3 / 2x = x 2 и x 2 (2x + 3).Наконец, вычтите и опустите следующий член. | |
| Шаги 5, 6 и 7 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 4x 2 / 2x = 2x и 2x (2x + 3). Наконец, вычтите и опустите следующий член. | |
Шаги 8, 9 и 10 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить –4x / 2x = –2 и –2 (2x + 3). Наконец, вычтите и обратите внимание, что больше нет терминов, которые нужно опускать. | |
| Шаг 11 : Напишите окончательный ответ.Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе. |
Нажмите здесь, чтобы узнать о практических задачах
Пример 5 — Разделить:
| Шаг 1 : Убедитесь, что полином записан в порядке убывания. Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). В этом случае проблема готова как есть. | |
Шаги 2, 3 и 4 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить x 3 / x 2 = x и x (x 2 + x — 6). Наконец, вычтите и опустите следующий член. В этом случае мы должны получить x 3 / x 2 = x и x (x 2 + x — 6). Наконец, вычтите и опустите следующий член. | |
| Шаги 5, 6 и 7 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления.Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 2x 2 / x 2 = 2 и 2 (x 2 + x — 6). Наконец, вычтите и обратите внимание, что больше нет терминов, которые нужно опускать. | |
| Шаг 8 : Напишите окончательный ответ. Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе.В этом случае остатка нет, поэтому дробь записывать не нужно. |
Нажмите здесь, чтобы узнать о практических задачах
Полиномиальное делениев столбик — ChiliMath
В этом уроке я рассмотрю пять (5) примеров с подробными пошаговыми решениями о том, как разделить многочлены с помощью метода деления в столбик . Это очень похоже на то, что вы делали в elementary, когда пытаетесь разделить большие числа, например, у вас есть 1,723 \ div 5.Вы бы решили это так же, как показано ниже, верно?
Это очень похоже на то, что вы делали в elementary, когда пытаетесь разделить большие числа, например, у вас есть 1,723 \ div 5.Вы бы решили это так же, как показано ниже, верно?
Быстрый обзор метода длинного деления чисел
Если вы можете выполнить простое числовое деление длинным методом, как показано выше, я убежден, что вы справитесь с задачами, описанными ниже. Единственное, что добавлено — это разделение переменных.
Примеры деления многочленов с использованием метода длинного деления
Пример 1 : разделить с использованием метода длинного деления
Решение: Мне нужно убедиться, что и дивиденд (материал, который делится), и делитель равны стандартная форма.Многочлен в стандартной форме гарантирует, что их показатели расположены в порядке убывания слева направо. Быстрая проверка этого помогает нам в дальнейшем предотвратить основные ошибки, которых можно избежать.
При быстром рассмотрении, я надеюсь, вы согласны с тем, что и дивиденды, и делитель действительно имеют стандартную форму. Это означает, что теперь мы готовы выполнить процедуру.
Это означает, что теперь мы готовы выполнить процедуру.
ШАГ 1 : Рассмотрите как главные члены дивиденда, так и делителя.
ШАГ 2 : Разделите главный член дивиденда на главный член делителя.
ШАГ 3 : Поместите частное сверху.
ШАГ 4 : Теперь возьмите частное частное, которое вы поместили сверху, 3 x , и распределите по делителю (2 x + 4) .
ШАГ 5 : Поместите произведение ( 3 x) и (2 x +4) под дивидендом. Убедитесь, что вы выровняли их по схожим условиям.
ШАГ 6 : Выполните вычитание, поменяв знаки нижнего многочлена.
STEP 7 : Продолжайте обычное добавление по вертикали. Обратите внимание, что первый столбец слева компенсирует друг друга. Отлично!
ШАГ 8 : Перенести следующий соседний «неиспользованный» член дивиденда.
ШАГ 9 : Затем посмотрите на нижний многочлен −14 x −28 , возьмите его главный член, равный −14 x , и разделите его на ведущий член делителя, 2 x .
ШАГ 10 : Опять же, поместите частное сверху.
ШАГ 11 : Используйте частное частное, которое вы положили, −7 , и распределите его на делитель. Видите узор сейчас?
ШАГ 12 : Поместите произведение −7 и делитель ниже в качестве последней строки полиномиального ввода.
ШАГ 13 : Вычитание означает, что вы поменяете знаки (красный).
ШАГ 14 : Регулярно добавляйте по столбцам схожие термины
ШАГ 15 : Это замечательно, потому что остаток равен нулю.Это означает, что делитель является фактором дивиденда.
Окончательный ответ — это просто содержимое над символом деления.
Пример 2 : Разделите с помощью метода деления в столбик
Решение : Эта проблема также считается «хорошей», как и первая, потому что и делимое, и делитель представлены в стандартной форме.
На этот раз вы делите многочлен с четырьмя членами на бином . Помните, что пример 1 — это деление полинома с тремя членами (трехчленом) на бином.Надеюсь, вы заметите небольшую разницу.
Давайте продолжим и разберемся с этим!
ШАГ 1 : Сосредоточьтесь на крайнем левом члене дивиденда и делителя.
ШАГ 2 : Разделите крайний левый член делимого на крайний левый член делителя.
ШАГ 3 : Поместите частичный ответ вверху.
ШАГ 4 : Используйте этот частичный ответ, x 2 , чтобы умножить его на делитель (3 x −2) .
ШАГ 5 : Поместите свой продукт под дивиденды. Убедитесь, что вы выровняли их по схожим условиям.
Убедитесь, что вы выровняли их по схожим условиям.
ШАГ 6 : Выполните вычитание, меняя знаки нижнего многочлена.
STEP 7 : Продолжайте обычное добавление по вертикали. И снова первый столбец компенсирует друг друга. Мне кажется, это образец!
ШАГ 8 : Перенести следующий соседний «неиспользованный» член дивиденда
ШАГ 9 : Возьмите крайний левый член нижнего полинома и разделите его на крайний левый член делителя.
ШАГ 10 : Как обычно, разместите ответ сверху.
ШАГ 11 : Хорошо, произведем еще одно умножение на частичный ответ 2 x и делитель (3 x −2) . Принесите товар ниже.
ШАГ 12 : Выполните вычитание, меняя знаки, и продолжите обычное сложение.
ШАГ 13 : Перенесите последний неиспользованный срок дивиденда. Мы почти там!
ШАГ 14 : Поднимаемся еще раз. Разделите главный член нижнего многочлена на главный член делителя. Поместите ответ туда!
Разделите главный член нижнего многочлена на главный член делителя. Поместите ответ туда!
ШАГ 15 : Это наша «последняя поездка» вниз, поэтому мы распределяем частичный ответ −1 на делитель (3 x −2) и помещаем произведение «внизу».
ШАГ 16 : Завершите это вычитанием, оставив как с остатком −7 .
ШАГ 17 : Напишите окончательный ответ в следующей форме.
Пример 3 : Разделить с использованием метода длинного деления
Решение : Если вы наблюдаете делимое, в нем отсутствуют некоторые степени переменной x , которые составляют x 3 и x 2 . Мне нужно вставить нулевые коэффициенты в качестве заполнителей для пропущенных степеней переменной. Это важная часть для правильного применения процедур деления в столбик.
Итак, я перепишу исходную задачу как. Теперь учтены все x !
ШАГ 1 : Сосредоточьтесь на ведущих терминах внутри и вне символа деления.
ШАГ 2 : Разделите первый член дивиденда на первый член делителя.
ШАГ 3 : Поместите частичный ответ вверху.
ШАГ 4 : Используйте этот частичный ответ, расположенный сверху, 3 x 2 , чтобы распределить по делителю ( x + 1) .
ШАГ 5 : Поместите результат под дивиденд. Убедитесь, что вы выровняли их по схожим условиям.
ШАГ 6 : Вычтите их вместе, не забудьте поменять местами знаки нижних членов перед сложением.
ШАГ 7 : Перенесите следующий неиспользованный срок дивиденда.
STEP 8 : глядя на нижний многочлен, −3 x 3 + 0 x 2 , используйте ведущий член −3 x 3 и разделите его на старший член делителя, x . Поместите ответ над символом деления.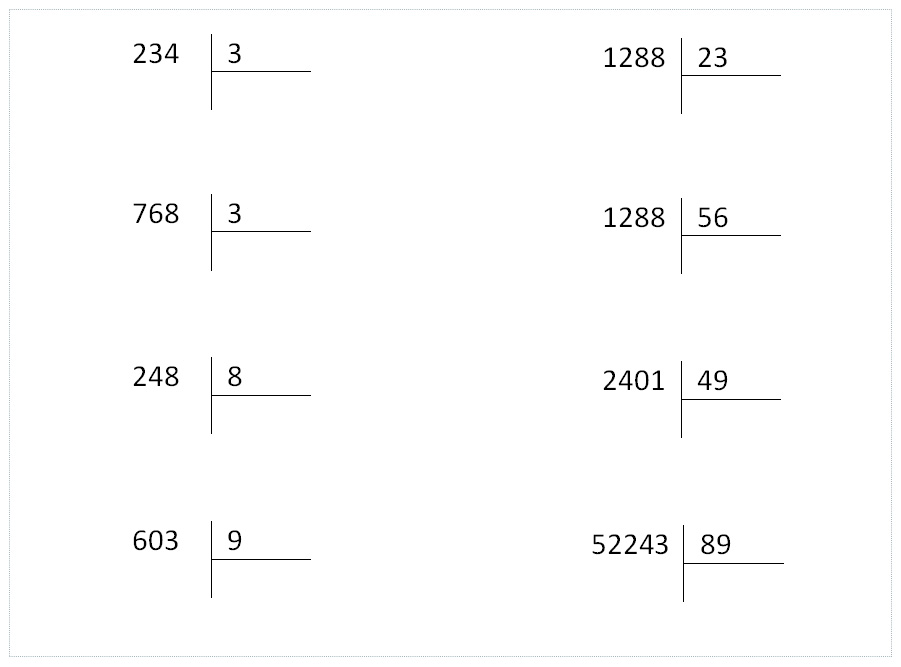
ШАГ 9 : Умножьте полученный ранее ответ на −3 x 3 и распределите его на делитель ( x + 1) .
ШАГ 10 : Поместите ответ ниже и выполните вычитание.
ШАГ 11 : Уменьшите следующий соседний член дивиденда
ШАГ 12 : Поднимитесь снова, разделив главный член ниже на главный член делителя.
ШАГ 13 : Спуститесь вниз, разделив ответ в частном частном на делитель с последующим вычитанием.
Я считаю, что теперь эта закономерность имеет смысл. Да?
ШАГ 14 : Перенесите последнее условие дивиденда.
ШАГ 15 : Поднимитесь снова, выполняя деление.
ШАГ 16 : Вернитесь вниз, выполняя умножение.
ШАГ 17 : Сделайте последнее вычитание, и все готово! Остаток равен 20.
ШАГ 18 : Окончательный ответ:
Пример 4 : Разделить данный многочлен методом длинного деления
Решение : В дивиденде явно отсутствует много переменной x .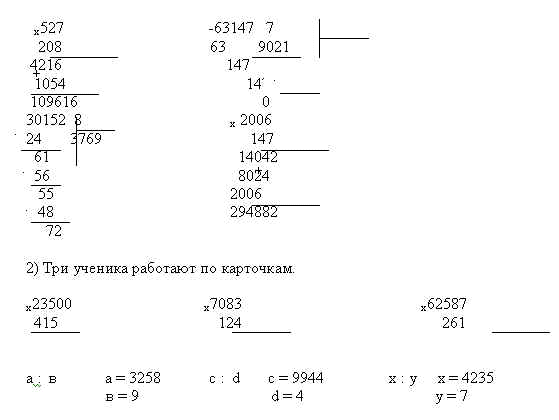 Это означает, что мне нужно вставить нулевые коэффициенты в каждую недостающую степень переменной.
Это означает, что мне нужно вставить нулевые коэффициенты в каждую недостающую степень переменной.
Мне нужно переписать задачу таким образом, чтобы включить все экспоненты x в порядке убывания:
Помните основные шаги в длинном делении:
- При подъеме мы делим
- При понижении распределяем
- Вычесть
- Перенести
- Повторяйте процесс до тех пор, пока не закончите
Убедитесь, что шаги выполняются правильно в примере ниже.
Итак, окончательный ответ:
Пример 5 : Разделите данный многочлен с помощью метода деления в долгую
Решение : У нас есть многочлен с пятью членами, деленными на трехчлен. И делимое, и делитель имеют стандартную форму, и присутствуют все степени переменной x . Это замечательно, потому что теперь мы можем приступить к его решению.
Решение этой проблемы представлено в анимированной картинке. Внимательно наблюдайте за каждым шагом и посмотрите, сможете ли вы ему следовать.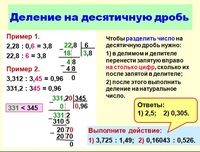

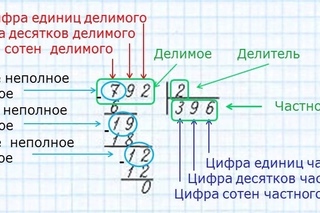

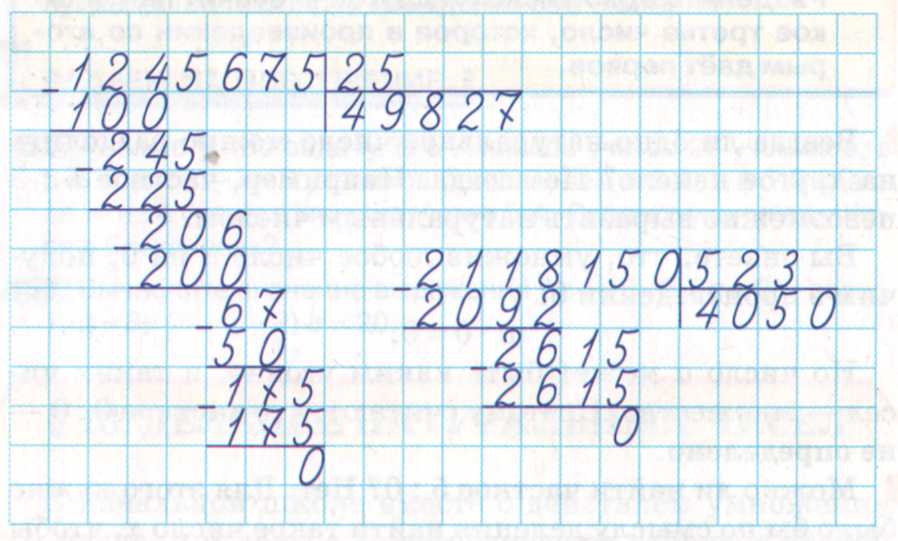 Делим
на 32. Вот
умножение
таблица из 32:
Делим
на 32. Вот
умножение
таблица из 32:
 Обратите внимание, что есть остаток.
Обратите внимание, что есть остаток.


