2Деление в столбик ➗ примеры и правила, как научиться
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трёхзначного числа на однозначное 322:7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя.
3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза. Проверяем 4*7=28, 28<32 все верно. Пишем 4 под чертой — это первая цифра частного. Между 32 и 28 ставим знак «минус», вычитаем по правилам и результат записываем под чертой.
Важно:
Результат вычитания должен быть меньше делителя. Если это не так, значит есть ошибка в расчете. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся 2 и продолжаем размышлять.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
- Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
- Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).
Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
Легкий уровень | Средний уровень | Сложный уровень |
27:3= 48:4= 56:8= 72:9= 95:5= | 270:15= 504:14= 315:5= 728:8= 855:9= | 1749:11= 1080:45= 3888:72= 5248:64= 4818:66= |
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.
В детской школе Skysmart ученики решают примеры вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой. Запишите вашего ребенка на бесплатный вводный урок математики в Skysmart — мы покажем, что математика может быть увлекательным путешествием!
Деление
В данном уроке мы изýчим деление чисел. Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.
Что такое деление?
Деление это действие, позволяющее что-либо разделить. Деление состоит из трёх параметров: делимого, делителя и частного. Делимое это то, что делят. Делитель это число, показывающее на сколько частей нужно разделить делимое. Частное это собственно результат.
К примеру, пусть у нас имеются 4 яблока:
Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:
Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:
В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.
Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос
В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».
Чтобы научиться делить, нужно хорошо знать таблицу умножения.
Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2
Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷
На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.
Деление с остатком
Остаток — это то, что осталось от действия деления неразделённым.
Например, пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Можно проверить это умножением:
(2 × 2) + 1 = 5
Допустим, у нас имеются пять яблок
Разделим их поровну на двоих друзей.
Но разделить поровну пять целых яблок не получится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:
Деление уголком
Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.
Прежде чем делить уголком, человек должен понимать:
- обычное деление маленьких чисел;
- деление с остатком;
- умножение в столбик;
- вычитание в столбик.
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:
Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9.
Записываем эту девятку под делимым:
Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:
Пример 2. Найти значение выражения 8 : 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.
Сначала запишем данное выражение уголком:
Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:
В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три»
Теперь вынимаем остаток.
Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:
Далее из 8 вычитаем 6. Полученное число и будет остатком:
8 : 3 = 2 (2 в остатке)
Проверка: (2 × 3) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя.
Если больше, то разделить, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то разделить, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1. Найти значение выражения 25 : 3
25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше, чем три? Да, больше. Поэтому выполняем деление числа 25 на 3. Записываем в уголком данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему.
Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:
Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
25 : 3 = 8 (1 в остатке)
(8 × 3) + 1 = 24 + 1 = 25
Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.
В приведённом примере последним остатком было число 1, а делителем число 3.
Единица меньше, чем три, поэтому деление завершено. Последний остаток, меньший делителя, говорит о том, что он не содержит чисел, равных делителю.
В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек, поскольку она меньше тройки.
Пример 2. Разделить 326 на 4.
Смотрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да, больше. Поэтому делим. Записываем уголком данное выражение:
Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым.
Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:
Записываем единицу в правом уголке нашего ответа:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
Получили 326 : 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.
Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.
А в примере 25 : 3 первое неполное делимое было 25.
Пример 3. Найти значение выражения 384 : 5
Записываем данное выражение в уголком:
Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение.
Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
Умножаем 7 на 5, получаем 35 и записываем его под 38:
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь из 34 вычитаем 30, получаем 4.
Эта четвёрка будет остатком от деления 384 на 5
384 : 5 = 76 (и 4 в остатке)
Проверка: (76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642 : 4
Этот пример немного посложнее. Записываем уголком данное выражение:
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:
Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.
Далее сносим цифру 6 и делим её на делитель, получаем 1
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого.
Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6
Умножаем 6 на 4, получаем 24. Записываем это число под 24
Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.
Поэтому два разделить на четыре это ноль:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:
8642 : 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел, у которых на конце 0
Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.
Например, разделим 120 : 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.
120 : 3 = 40
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12 : 3 = 4 (делимое без нулей на конце)
120 : 3 = 40 (здесь у делимого один ноль)
1200 : 3 = 400 (здесь у делимого два нуля)
12000 : 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа.
А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно по-отдельности разделить 1000 на 5 и 400 на 5:
1000 : 5 = 200
400 : 5 = 80
и сложить полученные результаты:
200 + 80 = 280
Итого: 1400 : 5 = 280
Решим этот же пример уголком:
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так то просто.
Принцип деления остаётся тем же, что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первые цифры, образующие старший разряд, оставляют без изменений, а остальные цифры заменяют нулями. Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Ещё пример. Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Ещё пример. Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями.
В итоге получаем 2000.
Ещё пример. Превратим число 13 735 в круглое число. Первые две цифры 13 образуют старший разряд (разряд десятков тысяч) — эти две цифры оставляем без изменений, а остальные цифры 735 заменяем нулями. В итоге получаем 13 000.
Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут обобщены.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное приходится находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.
Пример 1. Найти значение выражения 88 : 12
Записываем данное выражение уголком:
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».
Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число, которое меньше делимого, но очень близко к нему или равно ему.
Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит. Угадываем следующее число. Допустим частное равно 5
Что это нам дало? Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка, как частное тоже не подходит. Попробуем сразу взять по 8
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7
Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему.
Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.
88 : 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.
В делении круглых чисел также нет ничего сложного.
Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Если вы заметили, всё в конечном итоге сводится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания. Для начала превращаем делимое и делитель в круглые числа.
Круглым числом для 88 будет число 80.
А круглым числом для 12 будет число 10.
Теперь делим полученные круглые числа:
80 разделить 10 будет 8.
Эту восьмёрку мы пишем в частном:
Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку, как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.
Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:
Как видите, этим способом мы решили этот пример намного быстрее.
Пример 2. Найти значение выражения 1296 : 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
Это деление многозначного числа на многозначное.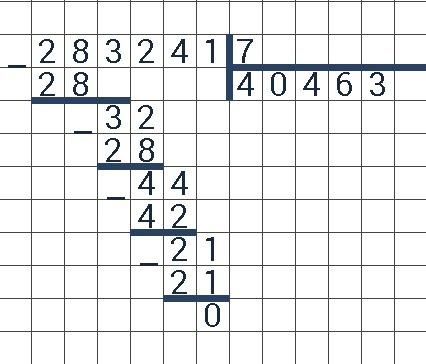
Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144
Десятка не подходит, поскольку при умножении получается число, которое больше делимого.
Попробуем взять по 9, уменьшив десятку на единицу.
Проверяем девятку. Для этого умножаем её на делитель:
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296
1296 : 144 = 9
Проверка: 144 × 9 = 1296
Пример 3. Попробуем решить большой и сложный пример 227 492 : 331
Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274.
Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него.
Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
Теперь делим 2412 на 331. Возьмём по 7
Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:
227 492 : 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок можно завершить.
Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.
Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Задание 2. Выполните деление:
Решение:
Задание 3. Выполните деление:
Решение:
Задание 4. Выполните деление:
Решение:
Задание 5. Выполните деление:
Решение:
Задание 6. Выполните деление:
Решение:
Задание 7. Выполните деление:
Решение:
Задание 8. Выполните деление:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10.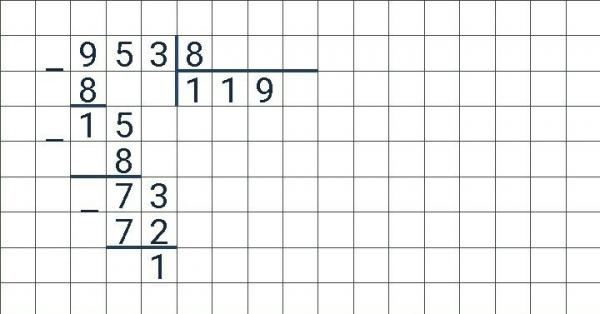
Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Задание 16. Выполните деление:
Решение:
Задание 17. Выполните деление:
Решение:
Задание 18. Выполните деление:
Решение:
Задание 19. Выполните деление:
Решение:
Задание 20. Выполните деление:
Решение:
Задание 21. Выполните деление:
Решение:
Задание 22. Выполните деление:
Решение:
Задание 23. Выполните деление:
Решение:
Задание 24. Выполните деление:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как делить десятичные дроби | Математика
Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.
Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить десятичную дробь на число, не обращая внимания на запятую;
2) когда закончится деление целой части, в частном поставить запятую.
Примеры.
Разделить десятичные дроби:
1) 5,04 : 6
Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04 : 6 = 0,84.
2) 19,26 : 18
Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль.
Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26 : 18 = 1,07.
3) 86,5 : 25
Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5 : 25 = 3,46.
4) 0,1547 : 17
Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547 : 17 = 0,0091.
5) Десятичная дробь может получиться и при делении двух натуральных чисел.
17 : 4
При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую.
2-5x+9$.
Деление натуральных чисел с остатком: правило, примеры решений
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?Разделим натуральное число 273844 на натуральное число 97.
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3.
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7-3=4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет.
Остается 4-3=1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7÷3=2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.Вычислим: 145÷46.
145-46=99.
Число 99 больше, чем 46, поэтому продолжаем последовательное вычитание делителя:
99-46=53.
Повторяем эту операцию еще раз:
53-46=7
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7.
145÷46=3 (остаток 7).
Метод последовательного вычитания непригоден, когда делимое меньше делителя.
В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a<b, то a÷b=0 (остаток a).
Например:
12÷36=0 (остаток 12)47÷88=0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком.
Рассмотрим уравнение d=a-b·c. Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0, 1, 2, 3 и т.д. Применяя формулу d=a-b·c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b. Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбораРазделим 267 на 21.
a=267; b=21. Подберем неполное частное.
Используем формулу d=a-b·c и будем последовательно перебирать c, придавая ему значения 0, 1, 2, 3 и т.д.
Если с=0, имеем: d=a-b·c=267-21·0=267. Число 267 больше, чем 21, поэтому продолжаем подстановку.
При с=1 имеем: d=a-b·c=267-21·1=246.
Т.к. 246>21, снова повторяем процесс.
При с=2 имеем: d=a-b·c=267-21·2=267-42=225; 225>21.
При с=3 имеем: d=a-b·c=267-21·3=267-63=204; 204>21.
…
При с=12 имеем: d=a-b·c=267-21·12=267-252=15;15<21.
На этом этапе процесс деления можно считать законченным. Неполное частное с=12, а остаток деления равен 15.
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a<b, неполное частное равно нулю, а остаток равен делимомому a. Мы будем рассматривать случай, когда a>b.
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b.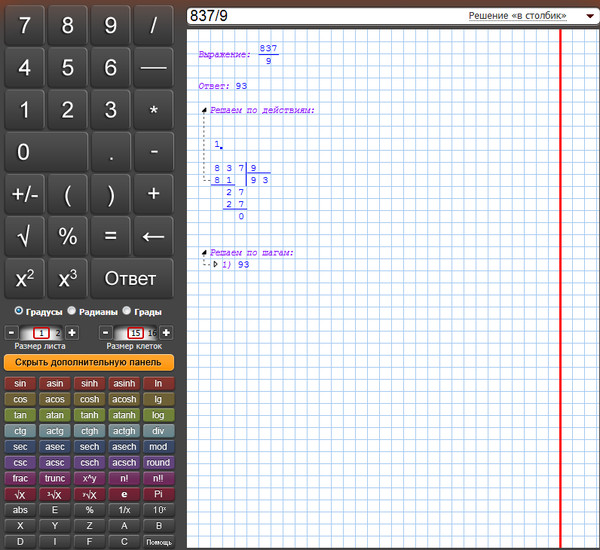
Найти нужно неполное частное c и остаток d.
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a=b·c+d. Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a=b·c+d, тогда мы найдем искомые величины.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеАлгоритм деления, благодаря которому мы представим a в виде суммы a=b·c+d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47.
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
3-2=1
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе.
В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470<899, запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10. В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1, 2, 3.. и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470.
470<899, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47·20=940; 940>899.
Число, которое мы получили на предпоследнем шаге (470=47·10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1-5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1-5, но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899-470=429, 429>47. Повторяем шаги 1-5 алгоритма с числом 429, взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47. Запоминаем разницу — число 1.
2. В записи делимого справа дописываем один нуль. Получаем число 470. Так как 470>429, из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1-1=0. Запоминаем 0.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа.
Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1, 2, 3 .. и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47·9=423<429, 47·10=470>429. Таким образом, второе искомое слагаемое — 47·9=423.
5. Разность между 429 и 423 равна числу 6. Так как 6<47, это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899=470+423+6. Вспоминаем, что 470=47·10, 423=47·9. Перепишем равенство:
899=47·10+47·9+6
Применим распределительное свойство умножения.
899=47·10+47·9+6=47·(10+9)+6
899=47·19+6.
Таким образом, мы представили делимое в виде уже данной ранее формулы a=b·c+d.
Искомые неизвестные:неполное частное с=19, остаток d=6.
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно.
Покажем это:
Разделим числа 42252 и 68.
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800=68·600.
Снова повторяем первые пять шагов алгоритма с числом 1452=42252-40800 и получаем второе слагаемое 1360=68·20
Третий раз проходим шаги аглоритма, но у же с новым числом 92=1452-1360. Третье слагаемое равно 68=68·1. Остаток равен 24=92-68.
В результате получаем:
42252=40800+1360+68+24=68·600+68·20+68·1+24==68·(600+20+1)+24=68·621+24
Неполное частное равно 621, остаток равен 24.
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя.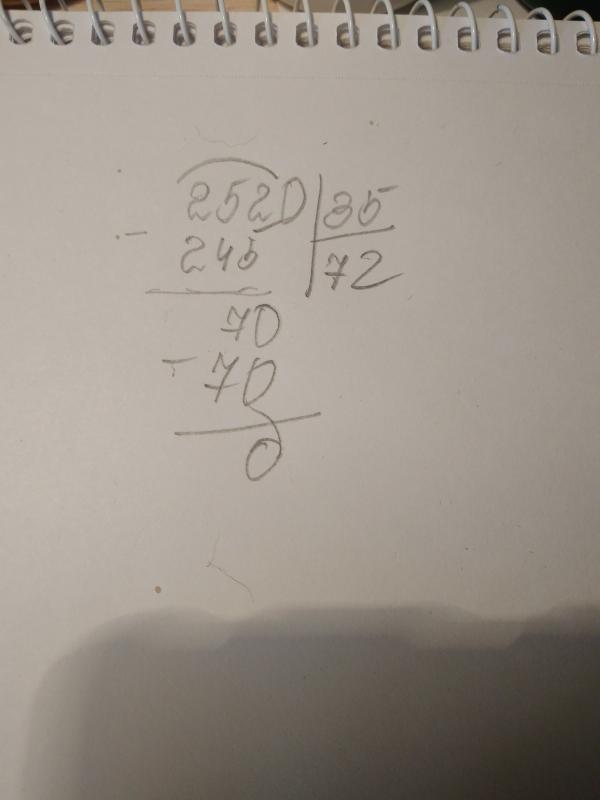
Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Пример 6. Проверка результата деления натуральных чисел с остатком.Проверим, верно ли, что 506÷28=17 (остаток 30).
Сравниваем остаток и делитель: 30>28.
Значит, деление выполнено неверно.
Пример 7. Проверка результата деления натуральных чисел с остатком.Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.
Подставляем значения и сравниваем результаты
13·9+5=117+5=122; 121≠122
Значит, в вычисления школьника где-то закралась ошибка.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.
Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.
После подстановки, имеем:
5998=111·54+4=5994+4=5998.
Равенство корректно, а значит, и деление выполнено верно.
Решение примера столбиком 64 6. Деление столбиком. Игра «Быстрое сложение»
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным.
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя.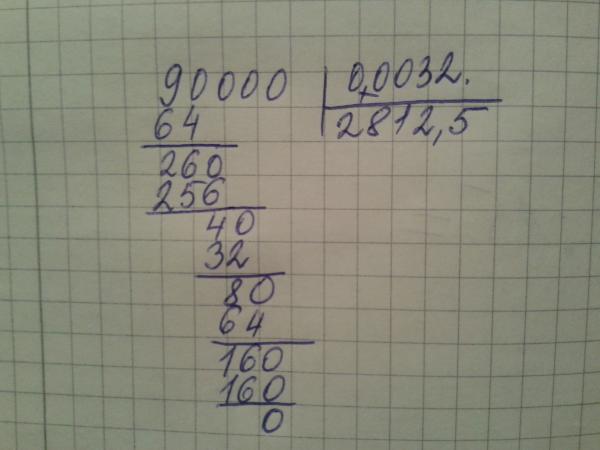
Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.
6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка.
Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение).
Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6.
Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.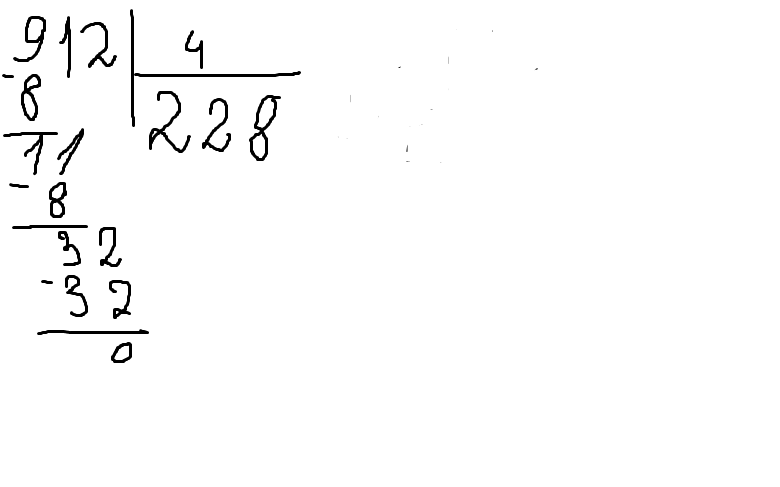
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4.
Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем.
Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть.
частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель.
Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье.
Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре.
В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку.
Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик .
По традиции, разбираться как делить столбиком будем на примере.
Вычислить:
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра «8 ».
Начинаем делить «512 » на «8 » следующим образом:
- Определяем неполное частное . Для этого слева направо
сравниваем
цифры делимого и делитель.
Берём «5 ». Цифра «5 » меньше «8 », значит нужно взять еще одну цифру из делимого.
- «51
» больше «8
». Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Запомните!
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после «51 » стоит только одно цифра «2 ». Значит и добавляем в результат ещё одну точку.
- Приступаем к делению. Вспоминая таблицу умножения на
«8
», находим ближайшее к
«51
» произведение.
«6 · 8 = 48 »
Записываем цифру «6 » в частное.Записываем «48 » под «51 ».
Запомните!
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51 » и «48 » слева поставим «− » (минус). Вычтем по правилам вычитания в столбик «48 » и под чертой запишем результат.
- В остатке получилось «3 ». Сравним остаток с делителем. «3 » меньше «8 ».
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно.
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78.
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули.
Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134.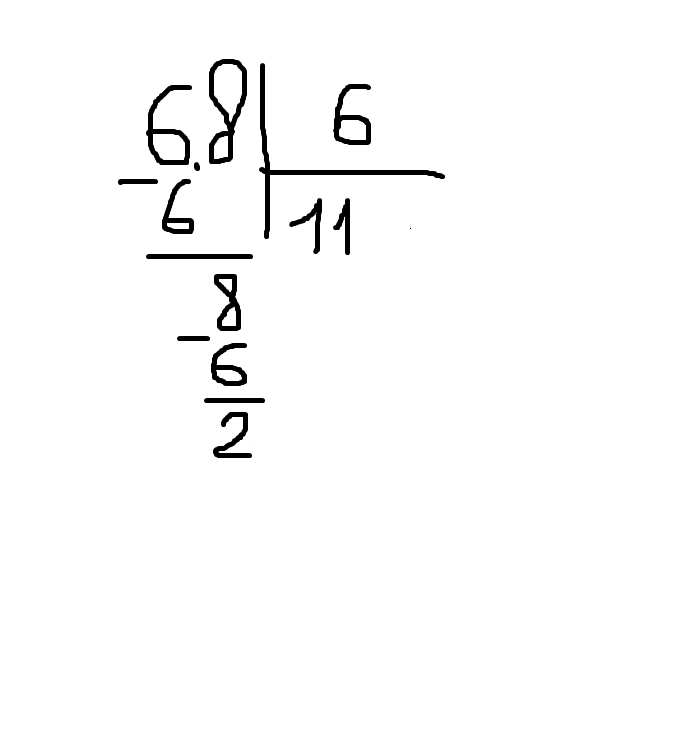
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Дивизион ÷ | Основы арифметики
На этой странице представлены основные сведения о Дивизионе (÷) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение ( + ), Вычитание (-) и Умножение ( × ).
Дивизион
Обычный письменный символ деления — (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять расчеты деления. Как только мы хорошо разбираемся в методе и правилах, мы можем использовать калькулятор для более сложных вычислений, не делая ошибок.
Дивизион позволяет нам делить или «делить» числа, чтобы найти ответ. Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два). Это то же самое, что «разделить» 10 сладостей между 2 детьми.У обоих детей должно получиться одинаковое количество конфет.
В этом примере ответ — 5.
Некоторые быстрые правила о делении:
Если вы разделите 0 на другое число, ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 сладостей, разделенных поровну между 2 детьми — каждый ребенок получает 0 сладостей.
Когда вы делите число на 0, вы вообще не делите (это большая проблема в математике). 2 ÷ 0 невозможно.У вас есть 2 сладости, но нет детей, чтобы разделить их между собой. Нельзя делить на 0.
При делении на 1 ответ будет таким же, как и число, которое вы делили. 2 ÷ 1 = 2. Две сладости на одного ребенка.
Когда вы делите на 2, вы уменьшаете число вдвое. 2 ÷ 2 = 1.
Любое число, разделенное на такое же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет, разделенных на двадцать детей — каждый ребенок получает по одной конфете.
Номера должны быть разделены в правильном порядке.10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять сладостей, разделенных на двоих детей, сильно отличаются от двух сладостей, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ равно 1 ÷ 2. Одна конфета, разделенная на двоих детей. Смотрите нашу страницу Дроби для получения дополнительной информации.
Множественное вычитание
Так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.
Например:
Если у Джона есть 10 галлонов топлива в машине и он использует 2 галлона в день, сколько дней до того, как он закончится?
Мы можем решить эту проблему, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.
- В день 1 Джон начинает с 10 галлона и заканчивается 8 галлона. 10 — 2 = 8
- В день 2 Джон начинает с 8 галлона и заканчивается 6 галлона. 8–2 = 6
- В день 3 Джон начинает с 6 галлона и заканчивается 4 галлона. 6–2 = 4
- В день 4 Джон начинает с 4 галлона и заканчивается 2 галлона. 4–2 = 2
- В день 5 Джон начинает с 2 галлона и заканчивается 0 галлонами. 2–2 = 0
6–2 = 4 У Джона заканчивается топливо на 5-й день.
Более быстрый способ выполнить этот расчет — разделить 10 на 2. То есть, сколько раз 2 уходит в 10 или сколько партий по два галлона в десяти галлонах? 10 ÷ 2 = 5.
Таблица умножения (см. Умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (заштрихованный красным заголовок).Двигайтесь вниз по столбцу, пока не найдете искомый номер: 10 . Перемещайтесь по строке влево, чтобы увидеть ответ (заштрихованный красным заголовок) 5 .
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Мы можем выполнить другие простые вычисления деления, используя тот же метод.
Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Если возможно, вам следует попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет решение простых вычислений умножения и деления.
Деление больших чисел
Вы можете использовать калькулятор для вычисления деления, особенно когда вы делите большие числа, которые сложнее вычислить в уме.Однако важно понимать, как выполнять расчеты деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также важно для того, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может выглядеть устрашающе, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и всю математику, проще всего понять, если мы рассмотрим пример:
Машине Дэйва нужны новые шины.
Ему нужно заменить все четыре шины на машине, а также запасную.
Дэйв получил предложение в местном гараже на сумму 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, — это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 перейдет в 480?
Условно мы пишем это как:
Мы работаем слева направо в логической системе.
Мы начинаем с деления 4 на 5 и сразу же решаем задачу. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «сколько раз 5 входит в 4?».
Мы знаем, что 2 дважды переходит в 4 (4 ÷ 2 = 2), и мы знаем, что 1 переходит в 4 четыре раза (4 ÷ 1 = 4), но 5 не переходит в 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно войти в число, на которое мы делим (в данном случае 4) целое количество раз.
Как вы увидите, это не обязательно должно быть точное целое число.
Так как 5 не входит в 4, мы помещаем 0 в первый столбец (сотни). Для получения справки по столбцам сотен, десятков и единиц см. Нашу страницу , номера .
| Сот | Десятки | шт. | |
| 0 | |||
| 5 | 4 | 8 | 0 |
Затем мы переместимся вправо, чтобы включить столбец десятков.Теперь мы можем увидеть, сколько раз 5 переходит в 48.
5 переходит в 48, так как 48 больше 5. Однако нам нужно выяснить, сколько раз оно идет.
Если мы обратимся к нашей таблице умножения, мы увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 , число, которое мы ищем, находится между этими двумя значениями. Помните, что нас интересует целое число , умноженное на , из которого 5 переходит в 48.
Десять раз — это слишком много.
Мы можем видеть, что 5 переходит в 48 целое число (9) раз, но не точно, с оставшимися 3.
9 × 5 = 45
48-45 = 3
Теперь мы можем сказать, что 5 делится на 48 девять раз, но с остатком 3. Остаток — это то, что остается, когда мы вычитаем найденное число из числа, на которое делим: 48-45 = 3 .
Итак, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбец десятков в качестве ответа для второй части расчета и поставить остаток перед нашим последним числом в столбце единиц.Наше последнее число становится 30.
| Сот | Десятки | шт. | |
| 0 | 9 | ||
| 5 | 4 | 8 | 30 |
Теперь разделим 30 на 5 (или узнаем, сколько раз 5 делится на 30). Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка.
5 × 6 = 30. Запишем 6 в столбце единиц нашего ответа.
| Сот | Десятки | шт. | |
| 0 | 9 | 6 | |
| 5 | 4 | 8 | 30 |
Так как остатков нет, мы закончили расчет и получили ответ 96 .
Новые шины Дэйва будут стоить 96 фунтов каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Отдел рецептов
Наш последний пример деления основан на рецепте. Часто во время приготовления рецепты сообщают вам, сколько еды они собираются приготовить, например, чтобы накормить 6 человек.
Указанные ниже ингредиенты необходимы для изготовления 24 сказочных лепешек, однако мы хотим приготовить только 8 сказочных лепешек. Мы немного изменили ингредиенты для этого примера (оригинальный рецепт на BBC Food).
Первое, что нам нужно установить, это сколько восьмерок в 24 — используйте таблицу умножения выше или свою память.
3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент, указанный ниже, на 3, чтобы получить правильное количество смеси для изготовления 8 сказочных лепешек.
Состав
- 120 г сливочного масла, размягченного при комнатной температуре
- 120 г сахарной пудры
- 3 яйца от кур свободного выгула, слегка взбитые
- 1 чайная ложка ванильного экстракта
- 120 г муки самоподъемной
- 1-2 столовые ложки молока
Количество масла, сахара и муки все одинаково, 120гр.Поэтому необходимо всего один раз проработать 120 ÷ 3, так как для этих трех ингредиентов ответ будет одинаковым.
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, поскольку 3 больше 1. Затем мы смотрим, сколько умноженных на 3 делится на 12. Используя таблицу умножения если необходимо, мы можем увидеть, что 3 переходит в 12 ровно 4 раза по без остатка.
120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г масла, сахара и муки.
Исходный рецепт требует 3 яйца, и мы снова делим на 3. Итак, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.
Далее в рецепте требуется 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 — это то же самое, что ⅓ (одна треть). Вам понадобится чайной ложки ванильного экстракта — хотя на самом деле сложно точно отмерить чайной ложки!
Оценка может быть полезной, а единицы измерения можно менять!
Мы можем взглянуть на это с другой стороны, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.(Если вам нужна помощь с единицами измерения, см. Нашу страницу о «Системы измерения ».) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 делится на 5 один раз (3), а 2 остается. 2 ÷ 3 — это то же самое, что и so, поэтому 5 мл, разделенное на 3, дает 1 ⅔ мл, что в десятичных дробях составляет 1,666 мл.
Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, немного больше полутора миллилитров. Если у вас на кухне есть эти крошечные мерные ложки, вы можете быть очень точными!
Мы можем оценить ответ, чтобы убедиться, что мы правы.Три партии по 1,5 мл дают нам 4,5 мл. Итак, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшое прикидывание может быть забавой и хорошей практикой для нашей ментальной арифметики.
Следующий рецепт требует 1-2 ст. Л. Молока. Это от 1 до 2 столовых ложек молока. У нас нет точного количества, и сколько молока вы добавите, будет зависеть от консистенции вашей смеси.
Мы уже знаем, что 1 ÷ 3 — это, а 2 ÷ 3 -.Поэтому нам понадобится – столовой ложки молока, чтобы приготовить восемь сказочных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому – столовой ложки равно 5–10 мл, то есть 1–2 чайных ложки!
Калькулятор длинного деления
с десятичными знаками
Использование калькулятора
Сделайте долгое деление с десятичными числами и просмотрите пошаговые инструкции по расчету.
Введите положительные или отрицательные десятичные числа для делителя и делимого и вычислите ответ частного.
Как сделать длинное деление с десятичными знаками
- Если число, на которое вы делите, имеет десятичную дробь, переместите десятичную точку до упора вправо, считая количество разрядов, на которое вы ее переместили. Затем переместите десятичную точку в числе, которое вы делите на такое же количество знаков вправо.
- Вставьте десятичную точку в поле частного (ответа) точно над десятичной точкой в числе под полосой деления.
- Делите, пока остаток не станет равен нулю или пока в вашем ответе не будет достаточно десятичных знаков. Вы также можете остановиться, если остаток повторяется, потому что это указывает на то, что ваш ответ является повторяющимся десятичным числом.
Вычислить десятичные разряды для частного ответа
Как далеко вы хотите вычислить десятичные знаки для ответа? Вот несколько примеров:
- 31 разделить на 16 = 1,937500 с учетом 6 десятичных знаков
- 31 разделить на 16 = 1. 937 с точностью до 3 знаков после запятой
- 22 разделить на 15 = 1,466666666 с учетом 9 десятичных знаков
- 22 разделить на 15 = 1,466666 с учетом 6 десятичных знаков
- 22 разделить на 15 = 1,466 с точностью до 3 десятичных знаков
937 с точностью до 3 знаков после запятой Обратите внимание, что это не то же самое, что округление до определенного числа десятичных знаков. Например, 22 разделить на 15 = 1,466, когда вычисляется до 3 десятичных разряда, потому что вы останавливаетесь, как только дойдете до третьего десятичного знака.С другой стороны, 22 делится на 15 = 1,467, когда округлено до 3 десятичных знака. Для округления до третьего знака после запятой необходимо вычислите как минимум до до четвертого десятичного знака, чтобы вы знали, как округлить третий десятичный разряд.
Смотрите наши
Калькулятор чисел округления для получения дополнительной информации.
Также смотрите наши Длинное деление с остатками, чтобы увидеть, как работает длинное деление с остатками.
Части подкласса
Для задачи деления 471 делится на 32:
- 471 — это дивиденд
- 32 — делитель
- 14,718 — это частное, вычисленное до трех знаков после запятой
Как сделать длинное деление с десятичными знаками: пример
В этой задаче мы делим 4.71 на 3,2 с точностью до 3 знаков после запятой в частном ответе.
Устраните проблему с продольным кронштейном. Разместите делимое внутри скобки, а делитель снаружи слева.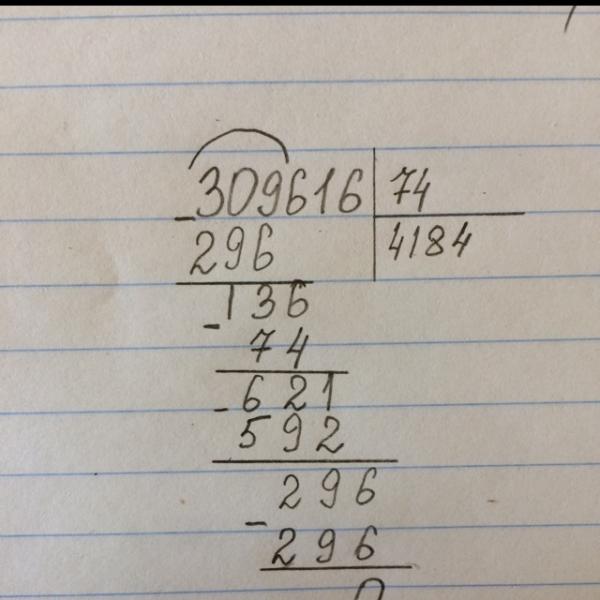
Поскольку 3.2 не является целым числом, переместите десятичную запятую на одну позицию вправо. 32 — целое число. Сделайте то же самое с делимым и переместите десятичную дробь на одну позицию вправо.
Поскольку мы решаем с точностью до 3 десятичных знаков, добавьте к делимому два конечных нуля.
Вставьте десятичную точку над полосой деления, непосредственно над новой десятичной позицией в делимом.
Разделите крайнее левое число делимого на делитель, в данном случае разделите 4 на 32.
Поскольку 4, разделенное на 32, не является целым числом, первая цифра частного — 0.
Умножьте делитель 32 на частное 0, чтобы получить произведение 0. Вычтите 0 из 4, чтобы получить остаток 4.
Затем убавьте 7 из дивиденда, чтобы у вас было 47.
Как 47 делится на 32? Или, другими словами, сколько раз 32 переходит в 47? Один раз, с остатком.Вставьте 1 в частное. Чтобы найти остаток, умножьте делитель на 1 и вычтите произведение 32 из второго делимого 47. Остаток равен 15.
Опять уменьшите следующую цифру делимого, 1, и поместите ее в конец остатка.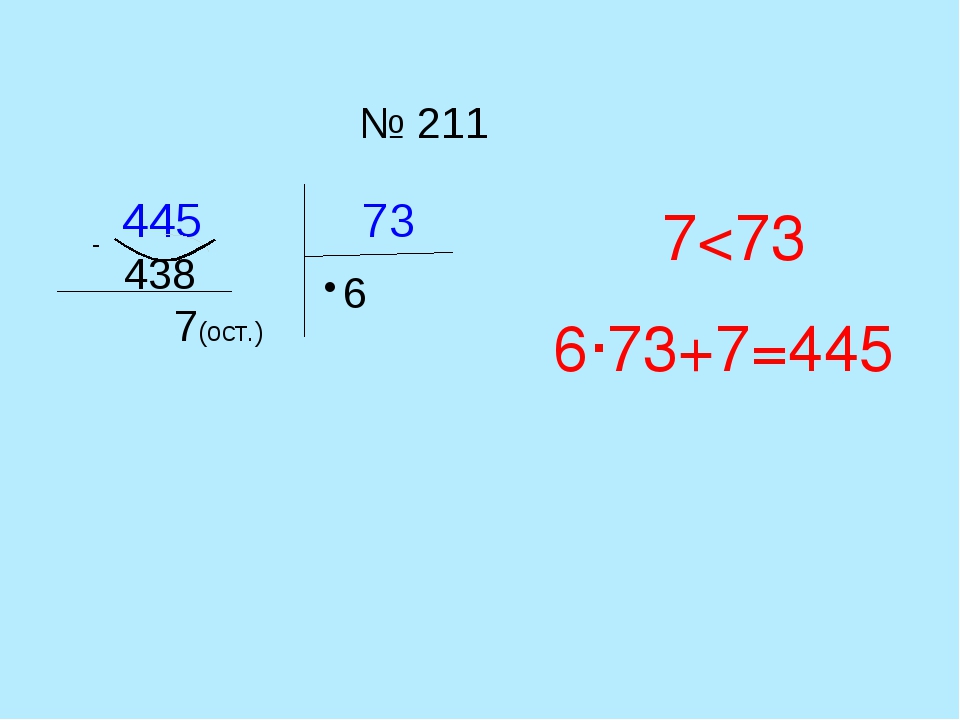
32 переходит в 151 четыре раза. Поставьте 4 на следующее место в частном и умножьте 32 на 4, чтобы получить 128.
Вычтем это произведение из 151, чтобы найти остаток от 23.
Уберите 0 из делимого и вставьте его после 23, чтобы получить 230.
Сколько 230 разделить на 32? 32 переходит в 230 семь раз. Поставьте 7 на следующее место в частном.32 умножить на 7 будет 224.
230 минус 224 остается остаток 6.
Теперь уменьшите следующий ноль делимого и повторите шаги.
32, умноженное на 1, равно 32.
При вычитании 32 из 60 остается 28.
Дополнительная литература
На Спросите доктора математики вы можете найти Инструкции по длинному делению для простых и более сложных задач.
Википедия: Длинный дивизион
Как разделить в Excel и обработать # DIV / 0! ошибка
В руководстве показано, как использовать формулу деления в Excel для деления чисел, ячеек или целых столбцов и как обрабатывать ошибки Div / 0.
Как и другие основные математические операции, Microsoft Excel предоставляет несколько способов деления чисел и ячеек.
Какой из них использовать, зависит от ваших личных предпочтений и конкретной задачи, которую вам нужно решить. В этом руководстве вы найдете несколько хороших примеров использования формулы деления в Excel, которые охватывают наиболее распространенные сценарии.
Символ разделения в Excel
Распространенным способом деления является использование знака деления. В математике операция деления обозначается символом обелуса (÷). В Microsoft Excel символ разделения представляет собой косую черту (/).
При таком подходе вы просто пишете выражение типа = a / b без пробелов, где:
- a — это дивиденд — число, которое вы хотите разделить, и
- b — делитель — число, на которое делится дивиденд.
Как делить числа в Excel
Чтобы разделить два числа в Excel, введите знак равенства (=) в ячейку, затем введите число, которое нужно разделить, затем косую черту, затем число, на которое нужно разделить, и нажмите клавишу Enter, чтобы вычислить формула.
Например, чтобы разделить 10 на 5, введите в ячейку следующее выражение: = 10/5
На снимке экрана ниже показано еще несколько примеров простой формулы деления в Excel:
Когда формула выполняет более одной арифметической операции, важно помнить о порядке вычислений в Excel (PEMDAS): сначала скобки, затем возведение в степень (возведение в степень), затем умножение или деление в зависимости от того, что наступит раньше, а затем сложение или вычитание в зависимости от того, что наступит раньше.
Как разделить ячейку в Excel
Чтобы разделить две ячейки в Excel, используйте символ разделения точно так же, как показано в приведенных выше примерах, но вместо чисел укажите ссылки на ячейки.
Например:
- Чтобы разделить ячейку A2 на 5:
= A2 / 5 - Чтобы разделить ячейку A2 на ячейку B2:
= A2 / B2 - Чтобы разделить нескольких ячеек последовательно, введите ссылки на ячейки, разделенные символом деления. Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте эту формулу:
= A2 / B2 / C2
Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте эту формулу: Функция деления в Excel (QUOTIENT)
Скажу прямо: в Excel нет функции разделения.Всякий раз, когда вы хотите разделить одно число на другое, используйте символ деления, как описано в примерах выше.
Однако, если вы хотите вернуть только часть деления целого числа и отбросить остаток, используйте функцию QUOTIENT:
ЧИСЛО (числитель, знаменатель)
Где:
- Числитель (обязательно) — делимое, т.е. число, которое нужно разделить.
- Знаменатель (обязательный) — делитель, т.е.е. число, на которое нужно разделить.
Когда два числа делят поровну, без остатка , символ деления и формула QUOTIENT возвращают одинаковый результат. Например, и = 10/5 , и = QUOTIENT (10, 5) вернут 2.
Когда после деления остается остаток , знак деления возвращает десятичное число, а функция QUOTIENT возвращает только целую часть. Например, = 5/4 возвращает 1,25, а = QUOTIENT (5,4) возвращает 1.
3 вещи, которые вы должны знать о функции QUOTIENT
Как бы просто ни казалось, функция Excel QUOTIENT все же имеет несколько предостережений, о которых вы должны знать:
- Аргументы числителя , и знаменателя , должны быть представлены в виде чисел, ссылок на ячейки, содержащие числа, или других функций, возвращающих числа.
- Если какой-либо из аргументов не является числовым, формула QUOTIENT возвращает #VALUE! ошибка.
- Если знаменатель равен 0, QUOTIENT возвращает ошибку деления на ноль (# DIV / 0!).
Как разделить столбцы в Excel
Разделить столбцы в Excel тоже просто. Это можно сделать, скопировав формулу обычного деления вниз по столбцу или используя формулу массива.
Зачем использовать формулу массива для такой тривиальной задачи? Вы узнаете причину в мгновение ока 🙂
Как разделить два столбца в Excel, скопировав формулу
Чтобы разделить столбцы в Excel, просто сделайте следующее:
- Разделите две ячейки в самой верхней строке, например:
= A2 / B2 - Вставьте формулу в первую ячейку (скажем, C2) и дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу.Выполнено!
Поскольку мы используем относительные ссылки на ячейки (без знака $), наша формула деления будет изменяться в зависимости от относительного положения ячейки, в которую она копируется:
Наконечник. Аналогичным образом можно разделить две строки в Excel. Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете = A1 / A2 в ячейку A3, а затем копируете формулу вправо в необходимое количество ячеек.
Как разделить один столбец на другой с помощью формулы массива
В ситуациях, когда вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках, вставьте формулу массива во весь диапазон.
Например, чтобы разделить значения в ячейках A2: A8 на значения в B2: B8 построчно, используйте эту формулу: = A2: A8 / B2: B8
Чтобы правильно вставить формулу массива, выполните следующие действия:
- Выберите весь диапазон, в который вы хотите ввести формулу (C2: C8 в этом примере).
- Введите формулу в строке формул и нажмите Ctrl + Shift + Enter, чтобы завершить ее. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
В результате вы получите числа в столбце A, разделенные на числа в столбце B одним махом. Если кто-то попытается изменить вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива нельзя изменить.
Чтобы удалить или изменить формулу , вам нужно сначала выбрать весь диапазон, а затем внести изменения. Чтобы расширил формулу на новые строки, выберите весь диапазон, включая новые строки, измените ссылки на ячейки в строке формул, чтобы разместить новые ячейки, а затем нажмите Ctrl + Shift + Enter, чтобы обновить формулу.
Как разделить столбец на число в Excel
В зависимости от того, хотите ли вы, чтобы выходные данные были формулами или значениями, вы можете разделить числовой столбец на постоянное число с помощью формулы деления или функции Специальная вставка .
Разделите столбец на номер по формуле
Как вы уже знаете, самый быстрый способ выполнить деление в Excel — использовать символ разделения. Итак, чтобы разделить каждое число в данном столбце на одно и то же, вы помещаете обычную формулу деления в первую ячейку, а затем копируете формулу вниз по столбцу.
Вот и все!
Например, чтобы разделить значения в столбце A на число 5, вставьте следующую формулу в A2, а затем скопируйте ее в любое количество ячеек: = A2 / 5
Как объяснено в приведенном выше примере, использование относительной ссылки на ячейку (A2) гарантирует, что формула будет правильно настроена для каждой строки. То есть формула в B3 становится = A3 / 5 , формула в B4 становится = A4 / 5 и т. Д.
Вместо того, чтобы указывать делитель непосредственно в формуле, вы можете ввести его в какую-нибудь ячейку, например, D2, и разделить на эту ячейку.В этом случае важно заблокировать ссылку на ячейку знаком доллара (например, $ D $ 2), сделав ее абсолютной ссылкой, поскольку эта ссылка должна оставаться постоянной независимо от того, куда копируется формула.
Как показано на снимке экрана ниже, формула = A2 / $ D $ 2 возвращает точно такие же результаты, как = A2 / 5 .
Разделите столбец на такое же число с помощью специальной вставки
Если вы хотите, чтобы результаты были значениями, а не формулами, вы можете выполнить деление обычным способом, а затем заменить формулы на значения.
Или вы можете достичь того же результата быстрее с помощью опции Специальная вставка > Делить .
- Если вы не хотите отменять исходные числа, скопируйте их в столбец, в котором вы хотите получить результаты. В этом примере мы копируем числа из столбца A в столбец B.
- Поместите делитель в какую-нибудь ячейку, скажем D2, как показано на скриншоте ниже.
- Выберите ячейку делителя (D5) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выберите ячейки, которые нужно умножить (B2: B8).
- Нажмите Ctrl + Alt + V, затем I, что является ярлыком для Специальная вставка > Divide , и нажмите клавишу Enter.
Или щелкните правой кнопкой мыши выбранные числа, выберите Специальная вставка… из контекстного меню, затем выберите Разделить в разделе Операция и нажмите OK.
В любом случае каждое из выбранных чисел в столбце A будет разделено на число в D5, и результаты будут возвращены в виде значений, а не формул:
Как разделить на процент в Excel
Поскольку проценты являются частями более крупного целого, некоторые люди думают, что для вычисления процента от данного числа вы должны разделить это число на процент.
Но это же заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, вы умножаете 80 на 20% и в результате получаете 16: 80 * 20% = 16 или 80 * 0,2 = 16.
В каких ситуациях вы делите число на процент? Например, чтобы найти X, если определенный процент от X равен Y. Чтобы прояснить ситуацию, давайте решим эту задачу: 100 — это 25% от какого числа?
Чтобы получить ответ, преобразуйте задачу в это простое уравнение:
X = Y / P%
Если Y равно 100, а P равно 25%, формула принимает следующий вид: = 100/25%
Поскольку 25% — это 25 частей от сотни, можно смело заменять процентное значение десятичным числом: = 100/0.25
Как показано на скриншоте ниже, результат обеих формул будет 400:
Дополнительные примеры процентных формул см. В разделе Как рассчитать проценты в Excel.
Excel DIV / 0 ошибка
Деление на ноль — это операция, для которой нет ответа, поэтому она запрещена.
Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (# DIV / 0!). В некоторых ситуациях эта индикация ошибки может быть полезной, предупреждая вас о возможных сбоях в вашем наборе данных.
В других сценариях формулы могут просто ждать ввода, поэтому вы можете заменить обозначения ошибок Excel Div 0 пустыми ячейками или собственным сообщением. Это можно сделать с помощью формулы ЕСЛИ или функции ЕСЛИОШИБКА.
Подавить ошибку # DIV / 0 с помощью IFERROR
Самый простой способ справиться с # DIV / 0! ошибка в Excel заключается в том, чтобы заключить формулу деления в функцию ЕСЛИОШИБКА следующим образом:
= ЕСЛИ ОШИБКА (A2 / B2; "")
Формула проверяет результат деления, и, если она оценивается как ошибка, возвращает пустую строку («»), иначе результат деления.
Обратите внимание на два рабочих листа ниже. Какой из них эстетичнее?
Примечание .
Функция ЕСЛИОШИБКА в Excel маскирует не только # ДЕЛ / 0! ошибок, но все другие типы ошибок, такие как # N / A, #NAME ?, #REF !, #VALUE !, и т. д. Если вы хотите подавить конкретные ошибки DIV / 0, используйте формулу IF, как показано в следующий пример.
Обработка ошибки Excel DIV / 0 с помощью формулы IF
Чтобы замаскировать только ошибки Div / 0 в Excel, используйте формулу ЕСЛИ, которая проверяет, равен ли делитель (или не равен) нулю.
Например:
= ЕСЛИ (B2 = 0, "", A2 / B2)
или
= ЕСЛИ (B2 <> 0, A2 / B2, "")
Если делителем является любое число, кроме нуля, формулы делят ячейку A2 на B2. Если B2 равно 0 или пусто, формулы ничего не возвращают (пустая строка).
Вместо пустой ячейки вы также можете отобразить собственное сообщение, подобное этому:
= ЕСЛИ (B2 <> 0, A2 / B2, «Ошибка в вычислении»)
Как разделить с помощью Ultimate Suite для Excel
Если вы делаете первые шаги в Excel и еще не чувствуете себя комфортно с формулами, вы можете выполнить деление с помощью мыши.
Все, что для этого требуется, — это установить наш Ultimate Suite в ваш Excel.
В одном из примеров, обсужденных ранее, мы разделили столбец на число с помощью специальной вставки Excel. Это потребовало большого количества движений мыши и двух ярлыков. А теперь позвольте мне показать вам более короткий способ сделать то же самое.
- Скопируйте числа, которые вы хотите разделить, в столбец «Результаты», чтобы предотвратить переопределение исходных чисел.
- Выберите скопированные значения (C2: C5 на скриншоте ниже).
- Перейдите на вкладку Инструменты Ablebits > Группа Расчет и выполните следующие действия:
- Выберите знак разделения (/) в поле Operation .
- Введите число для деления в поле Значение .
- Нажмите кнопку Рассчитать .
Готово! Весь столбец в мгновение ока делится на указанное число:
Как и в случае с Excel Paste Special, результатом деления будет значений , а не формулы.
Таким образом, вы можете безопасно переместить или скопировать вывод в другое место, не беспокоясь об обновлении ссылок на формулы. Вы даже можете переместить или удалить исходные числа, и ваши рассчитанные числа останутся в целости и сохранности.
Вот как вы делите в Excel с помощью формул или инструментов вычислений. Если вам интересно попробовать эту и многие другие полезные функции, включенные в Ultimate Suite for Excel, вы можете загрузить 14-дневную пробную версию.
Чтобы ближе познакомиться с формулами, обсуждаемыми в этом руководстве, загрузите наши примеры формул Excel Division.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Дивизион
Подразделение делится на равные части или группы.
Это результат «честного обмена».
Пример: есть 12 шоколадных конфет, и 3 друга хотят ими поделиться, как они делят шоколадные конфеты?
12 конфет
12 шоколадных конфет, разделенных на 3
Ответ: 12 разделить на 3 равно 4.
Каждый получает по 4.
Обозначения
÷ /
Мы используем символ ÷ или иногда символ / для обозначения деления:
Давайте использовать здесь оба символа, чтобы мы к ним привыкли.
Другие примеры
Вот еще несколько примеров:
Противоположность умножению
Деление — это , противоположное умножению . Когда мы знаем факт умножения, мы можем найти факт деления:
Пример: 3 × 5 = 15, поэтому 15/5 = 3.
Также 15/3 = 5.
Почему? Что ж, подумайте о числах в строках и столбцах, как на этой иллюстрации:
| Умножение… | … Отдел | |
|---|---|---|
| 3 группы по 5 составляют 15 … | … 15, разделенное на 3, равно 5 | |
а также: | ||
| 5 групп по 3 штуки 15 … | . .. 15, разделенное на 5, дает 3. | |
Итак, есть четыре связанных факта :
- 3 × 5 = 15
- 5 × 3 = 15
- 15/3 = 5
- 15/5 = 3
Знание таблицы умножения может помочь вам с делением!
Пример: что такое 28 ÷ 7?
Обыскивая таблицу умножения, мы обнаруживаем, что 28 равно 4 × 7, поэтому 28, разделенное на 7, должно быть равно 4.
Ответ: 28 ÷ 7 = 4
Имена
Для каждого числа в дивизионе есть специальные названия:
дивиденд ÷ делитель = частное
Пример: в 12 ÷ 3 = 4:
- 12 — это дивиденд
- 3 — делитель
- 4 — частное
Но иногда он не работает идеально!
Иногда мы не можем точно разделить вещи… может быть что-то осталось.
Пример: Есть 7 костей, которые можно разделить с 2 детенышами. Но 7 нельзя разделить точно на 2 группы,
так что каждый щенок получает по 3 кости,
, но останется 1 :
Мы называем это остатком .
Подробнее об этом см. Раздел и остатки
Упражнения
Попробуйте эти листы деления.
Умножайте и делите числа в Excel
Умножение и деление в Excel легко, но для этого нужно создать простую формулу. Просто помните, что все формулы в Excel начинаются со знака равенства (=), и вы можете использовать панель формул для их создания.
Умножение чисел
Предположим, вы хотите выяснить, сколько воды в бутылках вам нужно для конференции с клиентами (общее количество участников × 4 дня × 3 бутылки в день) или возмещать командировочные расходы для деловой поездки (общее количество миль × 0.46). Есть несколько способов умножать числа.
Умножение чисел в ячейке
Для выполнения этой задачи используйте арифметический оператор * (звездочка).
Например, если вы введете в ячейке = 5 * 10 , в ячейке отобразится результат: 50 .
Умножить числовой столбец на постоянное число
Предположим, вы хотите умножить каждую ячейку в столбце из семи чисел на число, содержащееся в другой ячейке.В этом примере число, на которое вы хотите умножить, — 3, содержащееся в ячейке C2.
Введите = A2 * $ B $ 2 в новом столбце вашей электронной таблицы (в приведенном выше примере используется столбец D).
Обязательно включите в формулу символ $ перед B и перед 2 и нажмите ENTER.Примечание. Использование символов $ сообщает Excel, что ссылка на B2 является «абсолютной», что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel изменит формулу на = A3 * C3, что не сработает, поскольку в B3 нет значения.
Перетащите формулу вниз в другие ячейки столбца.
Примечание. В Excel 2016 для Windows ячейки заполняются автоматически.
Обязательно включите в формулу символ $ перед B и перед 2 и нажмите ENTER.Умножайте числа в разных ячейках по формуле
Вы можете использовать функцию ПРОИЗВОД для умножения чисел, ячеек и диапазонов.
Вы можете использовать любую комбинацию до 255 чисел или ссылок на ячейки в функции PRODUCT . Например, формула = ПРОДУКТ (A2, A4: A15,12, E3: E5,150, G4, h5: J6) умножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазоны (A4: A15, E3: E5 и h5: J6).
Разделить числа
Предположим, вы хотите узнать, сколько человеко-часов ушло на завершение проекта (общее количество часов проекта ÷ общее количество людей в проекте) или фактический расход миль на галлон для вашей недавней поездки по пересеченной местности (общее количество миль ÷ общее количество галлонов).Есть несколько способов делить числа.
Делим числа в ячейке
Для выполнения этой задачи используйте арифметический оператор / (косая черта).
Например, если вы введете в ячейке = 10/5 , в ячейке отобразится 2 .
Важно: Обязательно введите в ячейку знак равенства ( = ), прежде чем вводить числа и оператор /; в противном случае Excel будет интерпретировать вводимое вами сообщение как дату.Например, если вы введете 7/30, Excel может отобразить в ячейке 30 июля. Или, если вы введете 12/36, Excel сначала преобразует это значение в 12/1/1936 и отобразит 1 декабря в ячейке.
Примечание: В Excel нет функции РАЗДЕЛ .
Разделите числа с помощью ссылок на ячейки
Вместо того, чтобы вводить числа непосредственно в формуле, вы можете использовать ссылки на ячейки, такие как A2 и A3, для ссылки на числа, которые вы хотите разделить и разделить на.
Пример:
Пример может быть легче понять, если вы скопируете его на пустой рабочий лист.
Как скопировать пример
Создайте пустую книгу или рабочий лист.
Нажмите CTRL + C.
На листе выделите ячейку A1 и нажмите CTRL + V.
Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих результаты, нажмите CTRL + `(серьезное ударение) или на вкладке Формулы нажмите кнопку Показать формулы .
org/ListItem»>Выберите пример в разделе справки.
Примечание. Не выбирайте заголовки строк или столбцов.
Выбор примера из справки
А | B | С | |
1 | Данные | Формула | Описание (результат) |
2 | 15000 | = A2 / A3 | Делит 15000 на 12 (1250) |
3 | 12 |
Разделите числовой столбец на постоянное число
Предположим, вы хотите разделить каждую ячейку в столбце из семи чисел на число, содержащееся в другой ячейке.
В этом примере число, на которое вы хотите разделить 3, содержится в ячейке C2.
А | B | С | |
1 | Данные | Формула | Константа |
2 | 15000 | = A2 / $ 2 | 3 |
3 | 12 | = A3 / 2 канадских доллара | |
4 | 48 | = A4 / 2 канадских доллара | |
5 | 729 | = A5 / C $ 2 | |
6 | 1534 | = A6 / C $ 2 | |
7 | 288 | = A7 / C $ 2 | |
8 | 4306 | = A8 / 2 канадских доллара |
org/ItemList»>Введите = A2 / $ C $ 2 в ячейку B2.Обязательно включите в формулу символ $ перед C и перед 2.
Перетащите формулу в B2 вниз в другие ячейки в столбце B.
Примечание. Использование символов $ сообщает Excel, что ссылка на C2 является «абсолютной», что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel изменит формулу на = A3 / C3, что не сработает, потому что в C3 нет значения.
Нужна дополнительная помощь?
Вы всегда можете спросить эксперта в техническом сообществе Excel, получить поддержку в сообществе Answers или предложить новую функцию или улучшение в Excel User Voice.
См. Также
Умножьте столбец чисел на такое же число
Умножить на процент
Создайте таблицу умножения
Операторы вычисления и порядок операций
Деление на 100 — Математика с мамой
Чтобы разделить число на 100, переместите каждую цифру в этом числе на два столбца значений разряда вправо на .Если число заканчивается двумя нулевыми цифрами в столбце десятков и единиц, то деление на 100 имеет тот же эффект, что и удаление этих двух нулевых цифр.
Этот трюк работает только с для целых чисел, которые находятся в таблице умножения на 100 (оканчиваются двумя нулями).
В приведенном выше примере 400 ÷ 100 = 4.
Чтобы разделить число на 100, переместите все его цифры на два столбца значений разряда вправо.
Цифра «4» перемещается из столбца сотен в столбец единиц.
Цифра «0» в столбце десятков перемещается в столбец десятых сразу после десятичной точки.
Цифра «0» в столбце единиц переместится в столбец сотых.
400 ÷ 100 равно 4,00.
Если у числа есть только нули после десятичной точки, то это целое число, и нет необходимости писать эти нули.
Лучше написать: 400 ÷ 100 = 4.
Видно, что мы просто «убрали два нуля».
Этот трюк работает только для целых чисел , которые на самом деле имеют два нуля в столбцах десятков и единиц, которые необходимо удалить.
Важно понимать, как работает деление любого числа на 100, потому что не все числа, которые мы делим на 100, оканчиваются двумя нулями.
Например:
Чтобы разделить 527 на 100, мы перемещаем каждой цифры на 527 на две позиции вправо .
Начнем с перемещения «5» из столбца сотен на два места в столбец единиц .
«2» и «7» затем последуют за «5».
2 перемещается из столбца десятков в столбец десятков , а 7 перемещается из столбца единиц в столбец сотых .
Каждая цифра переместилась на две позиции вправо, поэтому 527 ÷ 100 = 5,27.
Если наибольшая цифра числа находится в столбце сотен, то эта цифра переместится в столбец единиц, когда она будет разделена на 100.
Оставшиеся цифры справа появятся в том же порядке справа от десятичной точки.
Итак, в этом примере «5» — это цифра слева от десятичной точки, а затем «2» и «7» будут расположены в том же порядке, сразу после десятичной точки.
В следующем примере нам дано число меньше 100 и состоит только из двух цифр. Мы по-прежнему следуем тем же правилам для деления на 100 и перемещаем каждую цифру на два места вправо на .
Начнем с перемещения «1» на две позиции вправо , из столбца десятков в столбец десятков .Затем следует цифра «9». Мы перемещаем его из столбца единиц в столбец сотых .
Если слева от десятичной точки не остается цифр, в столбце единиц записывается одна цифра «0».
Следовательно, 19 ÷ 100 = 0,19.
Нас могут попросить разделить однозначное число на 100.
Например:
Хотя 6 состоит только из одной цифры, мы все еще следуем тому же правилу деления на 100.Перемещаем 6 на два места вправо . Он перемещается из столбца единиц в столбец десятых долей .
Поскольку больше нет цифры в столбце единиц и есть пробел в столбце десятых долей , мы записываем ноль в оба столбца, чтобы показать, что их значения равны нулю.
Следовательно, 6 ÷ 100 = 0,06.
Нам нужно быть осторожными при работе с числами, в которых между двумя другими ненулевыми цифрами стоит ноль.
Например:
Чтобы разделить на 100, мы должны убедиться, что мы перемещаем каждую цифру на 30,2 на два места вправо, , включая ноль . Мы перемещаем 3 из столбца десятков в столбец десятых , перемещаем ноль из столбца единиц в столбец сотых и перемещаем 2 из столбца десятых в столбец тысячных .
Цифры остаются в порядке в том же порядке .Итак, 30,2 ÷ 100 = 0,302.
Краткое деление — Умножение и деление — KS3 Maths Revision
Чтобы разделить большое число на \ ({1} \) — разрядное число, вы можете указать его следующим образом:
- \ (6 \) переходит в \ (9 \) один раз с оставшимся \ (3 \) (остаток \ (3 \)), поэтому поместите \ (1 \) над столбцом сотен и перенесите \ (3 \) в столбец десятков.
- \ (6 \) входит в \ (31 \) пять раз, остаток \ (1 \), поэтому поместите \ (5 \) над столбцом десятков и перенесите \ (1 \) в столбец единиц.
- \ (6 \) входит в \ (18 \) ровно три раза, поэтому поместите \ (3 \) над столбцом единиц.
0.0.0.1:0.1.0.$0.$1.$3″> Итак, \ ({918} \ div {6} = {153} \)Иногда одно число не делится на другое число точно.
В этом случае мы можем дать ответ в виде целого числа вместе с остатком или дать ответ в виде десятичного числа. Десятичный ответ может быть завершающим десятичным или повторяющимся десятичным. Часто десятичные ответы могут быть округлены до необходимого количества десятичных знаков.
Например:
\ [{964} \ div {7} \]
Метод 1 — ответ в виде целого числа с остатком.
- \ (7 \) переходит в \ (9 \) один раз с оставшимся \ (2 \) (остаток \ (2 \)), поэтому поместите \ (1 \) над столбцом сотен и перенесите \ (2 \ ) в столбец десятков.
- \ (7 \) входит в \ (26 \) три раза, остаток \ (5 \), поэтому поместите \ (3 \) над столбцом десятков и перенесите \ (5 \) в столбец единиц.
- \ (7 \) входит в \ (54 \) семь раз, остаток \ (5 \), поэтому поместите \ (7 \) над столбцом единиц измерения и получите остаток от \ (5 \).
Итак, \ (964 \ div 7 = 137 \) остаток \ (5 \).
Мы записываем это с \ (r \) для «остатка», поэтому он выглядит так:
\ [{964} \ div {7} = {137 ~ r5} \]
Метод 2 — десятичный ответ, округленный до десятичного знака \ ({1} \).
1.0.$0.$2.$2″>