Примеры по математике для подготовки к школе: задания для детей 6-7 лет для подготовки к школе распечатать бесплатно: 6 тыс изображе…

Курчатовская школа.

Сегодня в Москве существует несколько очень сильных физико- математических школ, для зачисления в которые недостаточно подачи заявления на прием. Многие проводят свои экзамены с олимпиадными задачами, к которым необходимо проводить специализированную подготовку. Одна из них — Курчатовская школа. Долгое время школа имела номер 1189 и до сих пор жива традиция называть ее именно так. Набор в 5 класс традиционно проходит в конце апреля — начале мая сразу по двум предметам: математика и русский язык. Работа по математике носит ярко выраженный олимпиадный характер и представляет из себя достаточно серьезное для среднего школьника испытание. Если Вы не поступили после 4 класса, можно дождаться соответствующей вступительной олимпиады через 2 года.

Варианты работ, предлагавшихся для поступления в 5 класс в последние годы:
Удаленная Курчатовская олимпиада по математике для 4 класса от 24 мая 2020г. Основной тур.
Курчатовская олимпиада от 9 февраля 2020 года
Курчатовская олимпиада 2019г (20 апреля, основной тур)
Курчатовская олимпиада от 10 февраля 2019г (пробный тур)
Олимпиада по математике для 4 класса. Курчатовская школа, апрель 2018 г.
Олимпиада по математике в Курчатовской школе от 23 апреля 2017 г.
Курчатовская олимпиада по математике 2015

Почитать о формате проведения вступительного экзамена можно на отдельной странице Курчатовская олимпиада

Какую помощь в поступлении в 5 класс Курчатовской школы может оказать репетитор по математике?

Немного странно звучит «репетитор для 5-го класса». Неужели в таком возрасте родители тоже приглашают ребенку преподавателя? И каков в этом случае должен быть характер индивидуальных уроков?

Безусловно, нужно разбирать олимпиадные задачи для 4 класса на смекалку и логику. Привязка к возрасту и программе в них достаточно условная, ибо они проверяют не столько знания ученика, сколько его умение мыслить в нестандартных ситуациях. Способность к олимпиадным задачам отражает главным образом уровень развития школьника: силу его внимания, памяти, мышления, зрительного представления о рассматриваемых объектах. Поэтому главным направлением стратегии подготовки в школу имени Курчатова, принимаемая репетитором по математике, становится развивающая тематика заданий. Без развития (математического и общего интеллектуального) на экзамене будет очень сложно, ибо искать выход из нестандартных ситуации на олимпиаде придется «с чистого листа», без применения известных схем и типов задач.

Как проводит подготовку в Курчатовскую школу репетитор по математике?

Изучение ребенка

Нужно очень аккуратно и внимательно протестировать Курчатовского ученика, изучить его способности мышления и при получении неудовлетворительных результатов поставить родителей в известность о вероятных проблемах при поступлении. Не всем детям по зубам олимпиадный уровень, каким бы старательным, опытным и талантливым ни был ваш репетитор по математике. Чудеса случаются редко. Превратить троечника (или даже хорошиста) в маленького гения, — не сможет даже самый лучший преподаватель математики на планете. Поэтому реально оценивайте свои возможности.
Вы можете пройти мой предварительный олимпиадный тест для Курчатовской школы — 4 класс и прислать его результы мне на почту.

Оглядка на школу

Иногда требуется подготовительная школьная работа. Пятерки по математике тоже бывают разными. Репетитору необходимо быть на 100% уверенным в том, что все базовые навыки не просто присутствуют, но и могут с успехом работать в разнотипных задачах, нагруженных большим количеством операций (арифметических и логических). Для этого в начале процесса подготовки желательно уделить время последним (усложненным) номерам вариантов типовых контрольных работ. Они используются репетитором не только для подготовки к более серьезным задачам, но и для всестороннего изучения ученика.

Классификация задач репетитором по математике

На следующем этапе я бы советовал обратиться к классическим типовым задачам, традиционно включаемым в олимпиадные сборники. В них, как правило, рассматриваются ситуации, на базе которых можно составить еще с десяток аналогичных. На их основе репетитору по математике легче организовать самостоятельную работу ученика. Если задавать на дом только сложные, уникальные и нестандартные задачи, то должной логической нагрузки при выполнении домашней работы ребенок не получит, ибо просто не сможет ничего решить. Кроме этого нужно разделить задачи на группы: на движение, на пересчет, на монеты, на чистую логику, на переправы, на календарь, на числовые ребусы и др. Лучше их решать сначала раздельно, а затем вперемешку.

Мои материалы для Курчатовской школы

Долгие годы я изучал и сортировал всевозможные олимпиадные задачи из разных источников и для разных классов. Что то сразу отправлялось в мусорную корзину, что то восхищало и принималось «на ура». Сегодня я могу похвастаться огромной пачкой листов А4 с подготовленными для каждого олимпиадного урока задачами. В применении к Курчатовской школе — это кипа листов для поступающих в 5 класс. Вы их видите на соответствующем фото (кликните для увеличения). Помимо подготовленных комплектов по каждой теме отдельной стопкой хранятся листы с конкретными олимпиадами по математике прошлых лет. Все это богатство можно и нужно использовать. Я предлагаю подготовку не только в 5 класс, но и подготовку в 7 класс и далее советовал бы рассмотреть уроки с репетитором как минимум для контроля качества школьного обучения. Как известно кадры решают все и даже в хорошей с виду школе можно нарваться на проблемы.

О режиме занятий
Рекомендуемый график занятий при подготовке в Курчатовскую школу в течение года (начиная с сентября) – раз в неделю. Каждая сложная задача требует неспешного обдумывания и аккуратного оформления. Пауза в неделю – оптимальный режим. Ученик успеет поразмышлять в домашней работе над каждым заданным номером, а в случае возникновения сложностей будет иметь для их преодоления достаточный запас по времени. Опытные репетиторы по математике обычно говорят своим ученикам: «Не бросайте олимпиадную задачу, если она не получается. Отвлекитесь и попробуйте справиться с ней через час, на следующий день, через день, через два дня. И только тогда просите репетитора ее объяснить». Когда индивидуальные урока расположены близко, то времени на размышление не хватает.

Особенности перехода в Курчатовскую школу

Курчатовская школа работает только с 5 класса. Поэтому в нее попадают дети из разных школ, с разной предварительной подготовкой. Олимпиадные занятия у репетитора по математике в большинстве случаев проходят автономно, то есть без жесткой привязки к школьному учебнику, и поэтому после поступления в Курчатовскую школу может потребоваться определенная коррекция под смену программы. Например, если Вы переходите на учебник Петерсон с любого другого, то необходимо пройти темы «углы», «координатный луч», «задачи на проценты», «скорость сближения и удаления», а также еще несколько мелких тем. Для этого как раз есть время в мае, а в случае полнейшей неизвестности вплоть до 1 сентября придется увеличить частоту уроков в первый месяц нового учебного года. В любом случае не желательно прекращать контакты с репетитором по математике.

О гарантии подготовки
Процессы и объекты, которые описываются в условиях конкурсных задач по математике, сильно отклоняются от школьных стандартов и это отклонение на экзамене невозможно заранее предсказать. Поэтому гарантировать успех на олимпиаде в Курчатовской школе невозможно даже при грамотной работе репетитора. Если Вам это обещают, то будьте уверены как минимум в лукавстве преподавателя, преследующем цели повышения привлекательности его уроков.

В чем сложность работы репетитора по математике с олимпиадными задачами?

Главная проблема в решении и объяснении таких задач заключается в том, что рассматриваемые в них ситуации, вычислительные и логические операции, очень трудно отобразить на бумаге. Большую часть смысловых и даже вычислительных действий приходится обрабатывать в уме. Это сильно затрудняет репетитору комментирование решений и поиск ошибок. Чтобы раскрыть логически сложную математическую структуру объекта приходится приводить примеры максимально близких к ним моделей. Например, для анализа ситуаций с большим количеством элементов, репетитор по математике приводит примеры решений меньшим их количеством. Подмечаются закономерности на упрощенной модели, а затем они переносятся на исходную модель. Например, если ребенок не понимает, как репетитор математики складывает все натуральные числа от 1 до 100, лучше сначала рассмотреть пример с меньшим числом слагаемых, например 1+2+3+4+5+6+8+9+10. Упрощенная модель позволит увидеть все пары слагаемых с суммой 11 без непривычного для маленького ученика пропуска чисел в записи 1+2+3+…+100.

О проблемах учеников

Серьезную проблему при подготовке в Курчатовскую школу составляет отсутствие у ребенка практического опыта в работе с окружающими его объектами и процессами (в том числе и математическими). Составитель варианта может заложить в олимпиадную задачу какую-нибудь особенность, выявить которую без репетитора по математике ребенок сможет только проявив наблюдательность в процессе решения других задач (простых или сложных). Например, при ответе на вопрос о количестве нулей в произведении понадобиться не вычислительный опыт, а способность обращать внимание на то, как зависит результат от набора множителей. Правильный репетитор по математике раскрывает эти взаимосвязи в ходе практической работы с обычными не олимпиадными заданиями в уже 4 классе. Если ученик не запоминает указания репетитора, приходится заниматься весьма трудоемкой работой по подбору или составлению отдельных номеров на каждую подмеченную особенность. Проблем в олимпиадной подготовке имеется великое множество. Ребенок приходит к репетитору по математике в 4 классе не имея, порой даже навыков умножения или деления в столбик. А родители, тем не менее, болеют Курчатовской школой. Репетитору по математике приходится заниматься базовыми уроками и поднимать развивать простейшие практические навыки.

Связанные со школой странички сайта:
Курчатовская школа. Помощь в учебе

Немного о Курчатовской школе

Школа 1189 была создана в 1991 году усилиями И.Н. Полякова и М.Ю. Галицкого и сначала имела статус экспериментальной. Олимпиады по математике стали проводиться с 1993 года и в этот же год был создан первый физико-математический класс. Преподавателями школы — ведущие ученые Курчатовского института, с которыми дети общаются с ранних лет.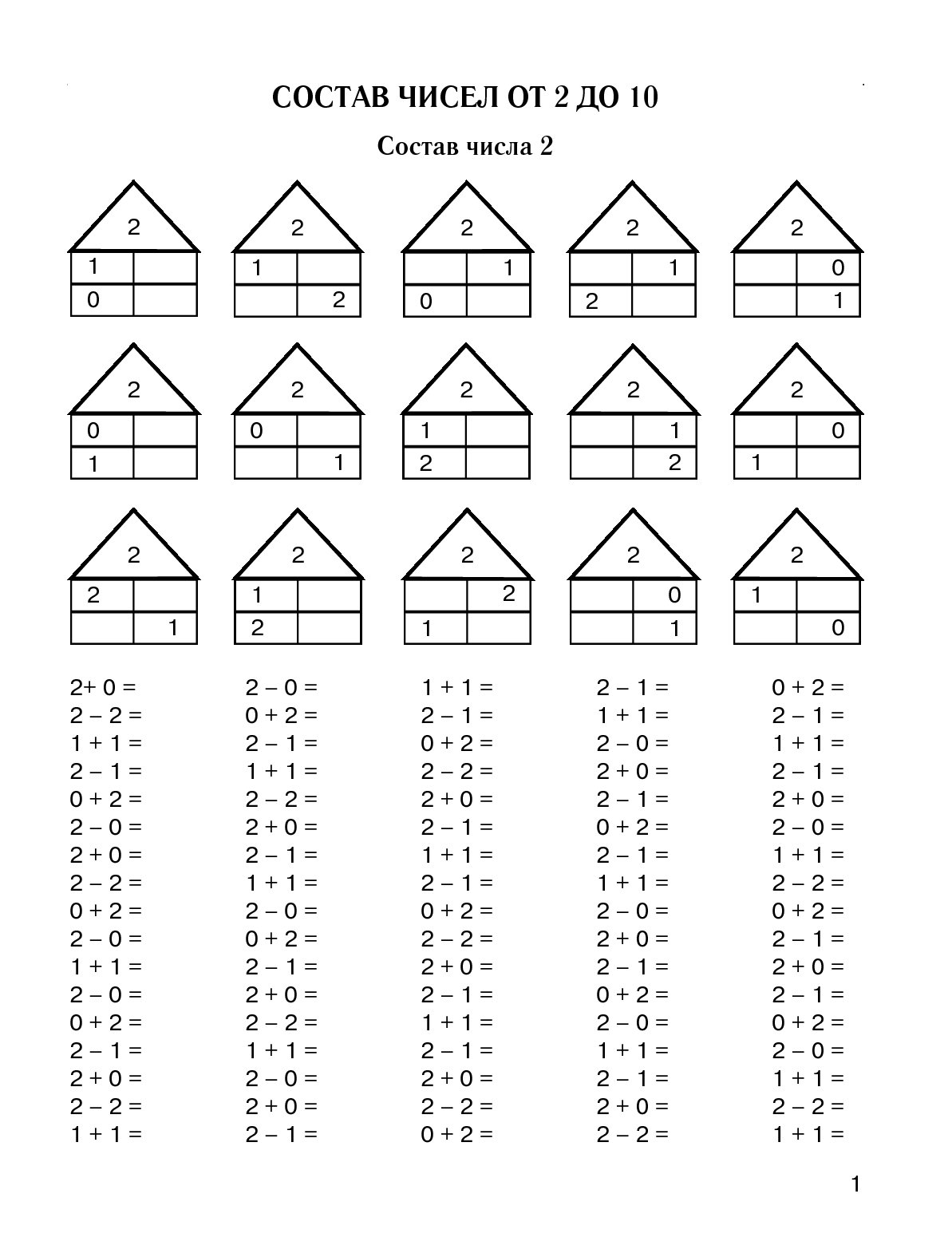 Несмотря на богатую традициями историю, Школа 1189 всегда считалась одной из самых престижных в Москве. В 2006-м она вошла в пятерку ведущих школ по рейтингу «Известий» на основе результатов олимпиад в старших классах. В прошлом учебном году согласно новому рейтингу МИОО, составленного по тем же олимпиадам, Курчатовская школа из этой десятки, к сожалению, выпала, заняв не самое почетное для себя 12 место. Однако в СЗАО и уж точно в районе Строгино — м. Щукинкская лучшего места учебы не найти. По Москве в лидерах рейтинга идут 57-я школа и лицей «вторая школа».

В новейшей истории Курчатовской школы мы видим значительные изменения. Начиная с 26.09.2012 года по приказу Департамента образования г. Москвы произошло соединение сразу нескольких школ в районе м.Щукинская. Соединились 7-я, 77-я, 702-я, 703-я и 738-я школы. Далее с 28.08.2013 года по 04.03. 2015 года происходит целая серия реорганизации через соединение нескольких дошкольных (№2713 и № 2177) учреждений, в числе которых коррекционная общеобразовательная школа-интернат № 101, со сменой вывески на «Школа № 2077». Интересно, что старая добрая Курчатовская школа №1189 формально присоединилась к этому локомотиву последней, а именно в 2015 году. В общем, мутная история, в которую репетиторам по математике, занимающимся подготовкой Курчатовских учеников в 5 -7 классы, нет смысла вникать. По крайней мере у меня все происходит по тем же олимпиадным графикам и платам без оглядки на начальную школу. Раньше в 1189 ее не было, и сейчас, насколько я знаю, никто из обучающихся в присоединенных школах не имеет проходных льгот для поступления в 5 класс. Также проводится по математике олимпиада в 4 классе и также около 60 человек зачисляются (2 класса).

О курчатовском комплексе

Идея трансформации нескольких учреждений под единое управление на базе Курчатовского института создало для жителей района Октябрьское поле — м.Щукинская — Строгино полноценный образовательный комплекс со множеством направлений и дополнительных услуг. Чего только не встретишь: в одном крыле интернат, в другом коррекционные классы для детей с ограниченными возможностями, есть платные курсы для дошкольников и девятиклассников (с октября по апрель), встречаются даже курчатовские кадеты с изучением основ военной медицины. Надо сказать, что к созданному комплексу серьезно «приложился» МГМУ им. Сеченова и «Первый медицинский институт». Под их началом работают медико-биологическое направление, преподаватели институтов читают лекции. ведут курсы «младшая медицинская сестра». Медицине уделяется большое внимание. Все серьезно: переводные предпрофильные экзамены, лекции, переводные тесты.

Вернемся к математике

Если оценивать работу математической части школы по информации, предоставляемой репетитору его учениками, то какого-то серьезного послабления уровня не замечено. Механика отбора при поступлении сохранена: олимпиада по математике, с довольно высоким порогом даже для талантливых деток. С 7 класса принимаются профильные учебники, а в 5-6 классах обычные (Мерзляк, Полонский), но с профильным предметом ПРЗ (практикум по решению задач). Он сохраняется, насколько я знаю, вплоть до 9 класса. На нем детям дается дополнительная олимпиадная нагрузка (или близкая к ней).

Базовая математика в 5 классе раньше была посложней обычной школьной программы, но в основном за счет решения усложненных задач с вариантов «В» пособия Ершовой и Голобородько. Но все меняется и каждый преподаватель Курчатовской школы приносит в учебные планы свое видение профильного обучения. Посмотрим, что будет в 2018 -2019 году. В прошлые годы следили за строгостью в оформлении решений, а в задании на дом встречались интересные логические и занимательные задачки. Многие из них удавалось решить только с родителями или репетитором по математике. В связи с этим я бы советовал не полагаться только на школу и сохранить занятия у репетитора. За ребенком нужно следить постоянно.

Поучительный случай в Курчатовской школе

Лет 8 назад, еще в пору обособленной бытности Курчатовского обучения (до мании объединения), детей, поступивших в 5 класс, как обычно в соответствии с набранными баллами по вступительной олимпиаде, поделили на 2 класса: сильный и послабее. Более слабый класс занимался по обычной программе, а сильному предоставили «крутого» преподавателя из МФТИ, который больше внимания уделял не программе, а решал с детьми сложные олимпиадные задачки. В итоге на переводной контрольной работе в 6 класс «слабые дети» показали результаты лучше, чем «сильные». Вот так. Не стоит успокаиваться полностью доверять школе. Любой. Продолжайте занимайтесь с хорошим репетитором. В большинстве случаев это лучшее средство достижения высоких показателей по математике.

Раньше мне казался странным выбор учебника в 1189 для 5 класса, ибо в большем почете у математиков значился Петерсон, но после того, как на его программу 1-4 классов «накатили бочку» — он полностью сошел с тренда, уступив даже профильное первенство классической программе Виленкина и его производной — Мерзляку. Есть еще Никольский (лицей Вторая школа его принимает как базовый), но он мне еще больше не нравится. Лучший вариант в работе репетитора по математике, по крайней мере я так советую заниматься, — синтез Виленкина и Петерсон. Приезжайте ко мне в Строгино на уроки и я расскажу о своей системе подробнее.

Важная информация о школе

Адрес физико-математического корпуса : Москва, СЗАО, ул. маршала Василевского, дом 9, корпус 1.
Главный телефон школы (директор и администратор): (499) 194-10-44
Директор — Пушина Маргарита Алексеевна
Администратор — Болотина Инна Владимировна
Электронная почта [email protected]

Позиция рейтинга в списке лучших школ Москвы — 20 место
Начальная школа — есть. На физ-мат отделение нужно поступать по итогам апрельской олимпиады в конце 4 класса.

Местонахождение — недалеко от Строгино, поэтому Вам будет удобно заниматься у меня дома.

Если Вы когда-либо учились в 1189 — напишите свое мнение о Курчатовской школе.

Курчатовская школа на карте:

2 года назад Курчатовская школа объединилась со школой номер 2077, которая тоже стала именоваться Курчатовской, в связи с чем родители часто путают их географически.

Адрес второй Курчатовской школы таков:
Ул. Маршала Конева дом 10. Телефон (495) 194-10-44. Расположена школа дальше от м.Щукинская и Строгино чем ее приемная мама 1189, а именно в 600 метрах от м. Октябрьское поле.

На вступительных олимпиадах это не сильно отразилось. По прежнему в 5 класс проходит набор учеников через вступительное испытание. Правда несколько изменился характер задач. В 2016 и 2017 годах увеличилось число задач, пришедших на олимпиаду для 4 класса из обычных программ по математике для 5-6 класса. В 2018 году таких вольностей мной замечено не было. Каков будет баланс в следующем 2019 году — посмотрим.

Вопросы родителей по подготовке в Курчатовскую школу

Здравствуйте! Мы учимся в обычной школе, мальчик — отличник, 4 класс. В прошлом году прошел по конкурсу в математический лагерь под Костромой. Участвовал в олимпиаде за 4 класс осенью, в призеры не вышел, по баллам где-то 4 место. Заинтересован в математике. К сожалению в математический кружок пойти не удалось. Занимаемся дома. Подумываем попробовать силы в Курчатник. Не подскажете, пожалуйста, каких-нибудь методички, книжки, ссылки по Курчатовским задачкам (они отличаются от всех олимпиадных задачек, как я вижу)? Спасибо.

Репетитор по математике об олимпиадных материалах: специализированных методичек именно по Курчатовской — нет, как и критериев отбора задач (кроме их уровня и соответствия пройденному материалу в 1 — 4 классах). Я использую свою базу, наработанную за годы подготовки в 1189. В ней есть как редкие и уникальные задачи, так и достаточно распространенные типовые, ставшие олимпиадной классикой. Аналогичные материалы можно найти в различных сборниках, но, как правило, прежде чем садится решать все то, что в них имеется, нужно а) подготовить ребенка к восприятию сложных решений б) отсортировать материал по его тематической и программной пригодности. С сортировкой задач по классам дела обстоят неважно практически в любом пособии и это не принимая в расчет индивидуальные особенности маленького ученика. Часто в один список попадают задачи для разных классов. Работу по отбору задач должен выполнить репетитор по математике.

В случае отсутствия подготовленной дидактики репетитору нужно купить сразу несколько книжек и сначала перерешать задачи самостоятельно (без ребенка), а уже затем совместно. Надо иметь ввиду, что олимпиадные задачи для 4 — 5 класса часто заимствуются авторами пособий друг у друга и в среднем из 3-5 задач конкретному ученику может подойти лишь одна-две. Если взять какую-нибудь среднестатистическую олимпиадную подборку (на сайте или в книге), то наверняка половину имеющегося в ней материала придется отложить в сторону по причине несоответствия конкретному ученику и конкретной ситуации. Поэтому «сырье», из которого репетитор по математике подготавливает олимпиадный урок, должно быть куплено с большим запасом. Можно заказать книжечку Е.Г. Козловой «Сказки и подсказки» или Спивака «1001 задача по математике». Будет время — подготовлю страничку со ссылками на олимпиадные сайты, наиболее полезными и удобными для подготовки в Курчатовскую школу.

Подборка видео объяснений репетитора реальных задач с апрельского экзамена по математике в Курчатовскую школу в 2018г

Наконец дошли руки снять и разместить несколько примеров живых объяснений с последней Курчатовской олимпиады в 2018г. На первых двух видео — Ваш покорный слуга, на последнем (задача на куб) — мой хороший коллега, репетитор по математике, Валентин Юрьевич Колосов.

В шахматном турнире, сыгранном по принципу «каждый с каждым играет по 1 матчу» было сыграно 45 матчей. Сколько в этом турнире приняло участие шахматистов?

Для того, чтобы пронумеровать все страницы некоторой книжки потребовалось 354 цифры. Сколько было страниц?

Полный список задач варианта за 2018 год можно посмотреть по соответствующей ссылке в верхней части этой страницы.

О технических особенностях моих видеосъемок можно прочитать по ссылке Особенности записи видеоуроков репетитором по математике

Колпаков А. Н, Подготовка в Курчатовскую школу.

Дар или навык? Что такое математические способности и как их развить

Успехи других людей – это всегда немного загадка. Почему у одних получается решать сложные математические задачи, а другие, как бы ни старались, не могут выйти на новый уровень? Неужели математика и правда подвластна не всем? На эти вопросы ответил Назар Агаханов, председатель Центральной предметно-методической комиссии по математике Всероссийской олимпиады школьников. С 1995 года руководил национальной командой России на международных математических олимпиадах. 

В 2010 году Назар Хангельдыевич стал лауреатом премии Правительства РФ в области образования за научно-практическую разработку «Система развития всероссийских предметных олимпиад школьников, отбора и подготовки национальных сборных команд России на международные олимпиады по физике и математике». Когда проявляются математические способности, как их развивать и кому не стоит идти в олимпиадное движение – рассказал эксперт.

Фото: https://mipt.ru/

Математические способности – это умение построить новые модели, не повторяющие стандартные алгоритмы, которым научили в школе. На базе таких маленьких открытий и строятся наука и технологии. Именно поэтому математика позволяет находить способных детей. 

Некоторые ученые считают, что порядка 10% людей обладают высокими математическими способностями. И это нормально. Если нет математических способностей, значит, есть что-то другое. Важно помогать детям открывать интересные сферы, но не навязывать. 

«Каждый родитель хочет, чтобы его ребенок вырос успешным человеком, и сейчас очень популярна позиция, что развивать нужно с пеленок. Может быть, так и есть, но в  любом случае лучше отталкиваться от искреннего интереса ребенка. Талант погибнет, если заставлять его делать несвойственное. Часто родители хотят использовать любые возможности, в частности, например, отправляют заниматься ментальной арифметикой, ложно полагая, что это шаг в математику, но это бессмысленная трата времени, ведь математика – это творчество. Не зря же задачи и решения называют красивыми», – говорит Назар Агаханов.

Чаще всего склонность к математике начинает проявляться в начальной школе, но это не значит, что сразу нужно вести ребенка на несколько кружков и интенсивно развивать эти способности. Достаточно одного урока занимательной математики в неделю. 

Более серьезные кружки начинают работу с учениками 5-6 классов. На этом этапе изучения математики обогнать сверстников очень легко. Круг задач еще достаточно узок и владение приемами их решения позволяет обойти даже, возможно, потенциально более сильных сверстников именно за счет знаний, а вот дальше, в 7-8 классах, для высоких результатов нужно чувствовать математику, здесь и проявляются математические способности. В это время преподаватели работают со школьником на развитие математического аппарата, укрепляется который уже в старших классах. 

Поэтому нередко бывает, что ярко проявляющие себя в 5-7 классах школьники начинают терять свои позиции в старших классах и выгорают от непонимания, почему теперь не получается быть сильнее других. Хотя выгорание возможно и по другой причине –  слишком долгие занятия олимпиадными задачами. Интерес все-таки нужно поддерживать, переключаясь на другую деятельность. 

Характер и воля: что помогает добиваться успехов в олимпиадах

Трудолюбие и готовность много работать – наверное, самые очевидные качества, которые нужны в любой сфере для достижения высоких результатов. 

«Способности – это фундамент. Чтобы подняться на несколько ступенек вверх, нужно работать. При наличии этих двух пунктов и еще хорошего педагога, все остальное уходит на второй план. Даже атмосфера в семье и материальное благополучие. В сборную часто попадают дети,  у которых не очень устроено семейное положение. Можно даже сделать частный вывод, что чем больше благоустроен быт, тем меньше ребенок настроен трудиться», – рассказывает Назар Агаханов.

Еще один важный пункт, над которым нужно работать каждому олимпиаднику, – психологическая устойчивость. На олимпиаде ребенок от волнения может показать результат хуже, чем его потенциал. Более ярко это проявляется в спорте, когда ребенок, приезжая на международные соревнования, проваливается. Нужно уметь воспринимать состязания не как конкурс, где тебе придется преодолевать невероятные сложности, а как  удовольствие от того, что ты встретишься с интересными задачами и попробуешь их решить. Самостоятельно психологическую устойчивость развивать сложно. Для этого важна среда. 

«Задумайтесь, почему в хороших математических школах так много детей, показывающих высокие результаты? Во-первых, конечно, в лучших школах собираются лучшие учителя. Во-вторых, в конкурентной борьбе с равными тебе сверстниками ты привыкаешь – нужно доказывать, что ты лучший. Несколько раз сначала ты можешь сорваться из-за волнения, а дальше уже будешь спокоен», – говорит Назар Агаханов.

Интересуйтесь всем: советы по эффективному олимпиадному тренингу

Если юный математик идет в олимпиадное движение только ради поступления в университет, лучше оставить эту затею. По словам эксперта, количество бюджетных мест по России определенно превосходит количество способных ребят, заканчивающих школы. Проблемы с тем, чтобы ребенок был талантлив в математике, а его не хотели брать на учебу в вуз, нет. Такие ребята с легкостью сдают экзамены. Повторимся, этот фактор абсолютно для математики не работает. 

Пожалуй, нужно искренне любить соревноваться, чтобы спокойнее переживать возможный стресс. А педагог поможет раскрыть способности и стать лучше. Заниматься с преподавателями можно и онлайн, и оффлайн. Но эксперт уверен, что онлайн-формы не заменят личного общения.

«Важен не объем пройденного материала, а то, как преподаватель послушал решение и рассуждения ребенка. Именно поэтому подготовка к международным олимпиадам во всех странах проходит примерно одинаково – учитель помогает разобрать ошибки, а не начитывает лекции. Школьник может увидеть решения тысяч задач и от этого не продвинуться, но, если он сам углубился в вопрос, попробовал решить, увидел трудные места, ему приоткроется новое знание. Дистанционные формы, к сожалению, в этом не столь эффективны, потому что важен живой диалог и прямая беседа. При этом место проживания – не крест для успехов. Хорошие преподаватели есть в регионах и это факт», – утверждает Назар Агаханов. 

Еще одна возможность прокачаться – различные турниры и летние школы, которые есть практически в каждом регионе. Можно подобрать для себя наиболее подходящие. Такие площадки собирают большое количество ребят из разных городов в одном месте, дают возможность и пообщаться, и вместе решать задачи, и познакомиться с  педагогами, которые входят в жюри.

Еще один важный пункт на пути к эффективным занятиям – вовремя отдыхать. Спорт, прогулки, активный отдых – хороший инструмент для качественной перезагрузки между занятиями. Но не единственный. 

«Большое количество открытий в математике происходит на стыке дисциплин, когда ты можешь переключиться, перенести свои способности на другое направление, в котором не являешься специалистом самого высокого уровня. Поэтому при стремлении добиться чего-то серьезного в математике, стоит интересоваться всеми предметами в школе и вообще разносторонне развиваться», – говорит Назар Агаханов. 

Отсюда возникает вопрос, если тратить время на другие интересы, то сколько тогда нужно заниматься именно математикой? Конкретного ответа здесь нет, все очень индивидуально. Формулу поможет выработать внутреннее ощущение – заниматься нужно ровно столько, чтобы чувствовать, что ты находишься в форме. А вот перед олимпиадными турами важно не перегружать мозг слишком интенсивными занятиями, чтобы не устать. 

Обрати внимание: самые распространенные ошибки начинающих олимпиадников

Многие начинающие олимпиадники делают ошибки из-за того, что не продумывают решение глубоко. Чаще всего это происходит из-за невнимательности и игнорирования части условий. Поэтому Назар Агаханов рекомендует, как банально бы это ни было, детально читать условия задач и использовать в решении все обозначенные параметры.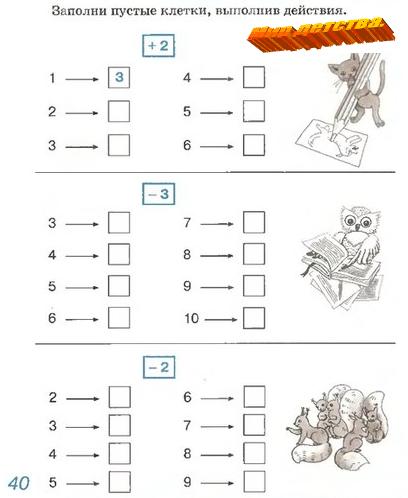  

В решении геометрических задач чаще всего встречаются логические ошибки, когда то, что надо доказать, каким-то образом встраивается в логику решения. Пример:  нужно доказать равенство углов. Школьник отталкивается от фразы «так как эти углы равны», решает задачу и попадает в логическую ловушку, делая некорректные выводы. 

Распространенная ошибка в алгебре и комбинаторике – длинное решение с перебором вместо короткого. Решение методом перебора – нормальный подход, но, если пропускается какой-то случай, решение может не засчитаться, потому что именно в этом случае и было верное решение.

Подготовка – Факультет математики – Национальный исследовательский университет «Высшая школа экономики»

Эта страница называется “Подготовка”. Но речь не про подготовку к поступлению на наш факультет, т.е. не про ЕГЭ и олимпиады. Речь идет о теме, которая освещена в Сети гораздо хуже — о подготовке к обучению на нашем факультете (или, более широко, на любой программе высшего образования по специальности Фундаментальная математика).

Эту тему делает актуальной существование «ничейной земли» между школьной и университетской программами — круга вопросов, которым во многих школах уделяют недостаточное, на наш взгляд, внимание, и на которых нет возможности надолго задержаться на первом курсе.

Приведенный ниже перечень тем очерчивает эту “ничейную землю”. Если Вы заранее разберете незнакомые Вам темы из этого списка по предложенной литературе, то обеспечите себе намного более успешное и комфортное начало обучения на нашем факультете (равно как и на любом другом, где предполагается серьезная математическая подготовка).

Более того, знакомство со многими из предложенных тем может оказаться полезным уже для участия в математических олимпиадах старших классов. По большей части эти темы не предполагают знания материала 10-11 классов, поэтому приступить к их изучению стоит уже в 9 классе или даже раньше — так же, как делают на курсах “спецматематики” или “математического анализа” в ведущих математических школах. Типичное начало такого курса представлено, например, в следующей книге (она будет полезна также при работе над темами 1-6 нашего списка):

Т. И. Голенищева–Кутузова, А. Д. Казанцев, Ю. Г. Кудряшов, А. А. Кустарёв, Г. А. Мерзон, И. В. Ященко. Элементы математики в задачах (с решениями и комментариями). Части I и II, М., МЦНМО, 2010

Хорошо приспособлена для самостоятельной работы книга  М. Вялый, В. Подольский, А. Рубцов, Д. Шварц, А. Шень «Лекции по дискретной математике», в которой части 1 и 2 посвящены тем же разделам.

Хорошие подборки задач по этим разделам можно найти в других опубликованных курсах московских школ 57  и 179, а также в задачнике  А.А.Заславский, А.Б.Скопенков, М.Б.Скопенков «Элементы математики в задачах».

Тем, кому удобен формат видеолекций, рекомендуем онлайн-курс В.А.Кириченко «Основания алгебры и геометрии» (запись в осеннем семестре открыта до 15 сентября!)

Видеолекции также содержатся в материалах летней школы «Матфак: предисловие», которая ежегодно проводится на факультете в конце августа для поступивших на факультет.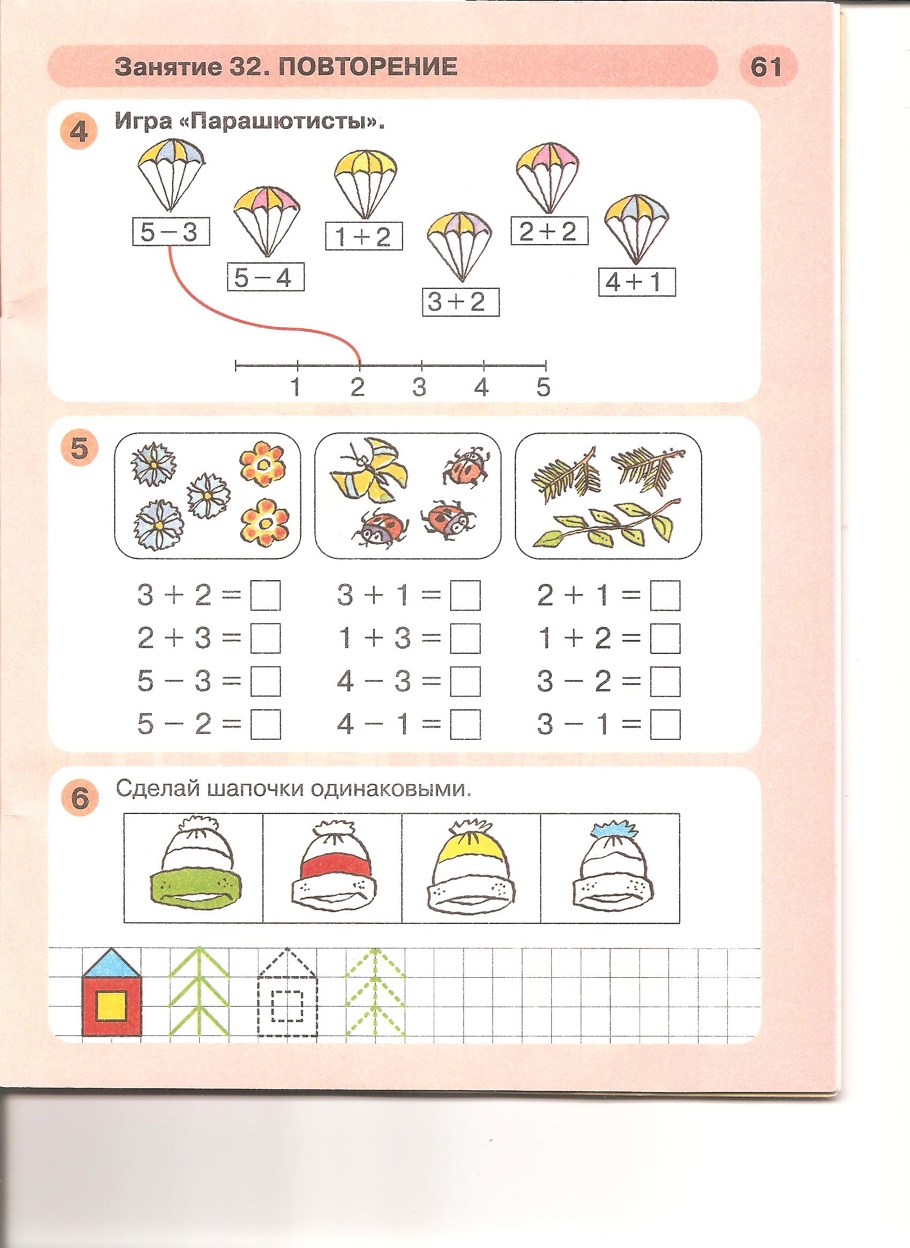

Темы нашего перечня перечислены в порядке, в котором их наиболее естественно изучать. Правда, некоторые из них указаны в скобках (курсивом) — они в наименьшей степени могут считаться первоочередными для школьного математического образования, и потому их можно оставить “на десерт”.

Если книга в списке литературы идёт под номером (0) — это идеальный текст для первого знакомства с предметом и, в частности, его просто очень интересно читать. Знакомство с этими книгами можно считать обязательным для каждого, кто любит математику.

Помимо конкретных книг, в качестве главного общего источника информации мы рекомендуем сайт Московского Центра Непрерывного Математического Образования — его миссия состоит как раз в преодолении зазора между “школьной” и “высшей” математикой. На его страницу свободно распространяемых изданий ведет большая часть ссылок в нашем списке.

Помимо приведенного ниже базового списка тем, у нас на сайте можно ознакомиться с перечнем книг “на вырост”, а на сайте Независимого Московского Университета — с существенно более амбициозной программой “Матшкольник”. Конечно, мы ни в коем случае не ожидаем от наших абитуриентов знакомства с перечисленными там книгами и темами.

1. Множества, практика доказательства их равенства, отображения множеств и их композиции

(1) Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. 4-е изд., доп., М: МЦНМО, 2012 [глава 1]

2. Логические операции, кванторы, построение отрицаний

(1) Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 2. Языки и исчисления. 4-е изд., испр., М.: МЦНМО, 2012 [главы 1-3]

3. Математический уровень строгости, неопределимые понятия и определения, аксиомы и доказательства, (

(1) И.В. Арнольд. Теоретическая арифметика, М., Учпедгиз, 1938 [глава 2: аксиомы Пеано]

4. Индукция, комбинаторика — числа сочетаний и перестановок, бином Ньютона

(2) А. Шень. Математическая индукция, 3-е изд., М., МЦНМО, 2007

(3) Н. Я. Виленкин, А. Н. Виленкин, П. А. Виленкин, Комбинаторика, М., МЦНМО, 2006 [главы 1 и 2]

5. Делимость, разложение на простые, деление с остатком чисел и многочленов, НОД, алгоритм Евклида, арифметика вычетов

(2) Р. Курант, Г. Роббинс. Что такое математика? М., МЦНМО, 2013 [разделы 1 и 4 дополнения к главе 1 (раздел 2 дополнения к главе 1)]

(3) Подборка статей журнала “Квант” про арифметику вычетов.

6. Рациональные числа, отношения и классы эквивалентности, вещественные числа, (

(2) Р. Курант, Г. Роббинс. Что такое математика? М., МЦНМО, 2013 [раздел 2.2 (2.2.6)]

7. Комплексные числа, их тригонометрическая форма

(2) В.И. Арнольд. Геометрия комплексных чисел, кватернионов и спинов, М., МЦНМО, 2002 [раздел “Комплексные числа”]

(3) Я.П.Понарин.  Алгебра комплексных чисел в геометрических задачах,  М., МЦНМО, 2004.

8. Векторы на плоскости и в пространстве, суммы и кратные векторов в координатах, преобразования евклидовой плоскости и пространства, их композиции

(2) Подборки статей журнала “Квант” на темы “векторы” и “преобразования”.

(3) Кострикин А.И. Введение в алгебру. Часть 1: Основы алгебры, МЦНМО, 2012 (Издание 2-е, стереотипное) [главы 1-3]

(4) И. М.Гельфанд. Линейная алгебра, М.: Добросвет, МЦНМО, 1998. Издание пятое, исправленное [разделы 1.1, 1.2, 1.9]

обучающие наборы «Школа будущего» математика и украинский алфавит

Подготовка к школе

Каждый комплект приходит в удобной коробке с открывающейся крышкой, которая также выполняет роль «школьной доски».

В комплекте есть обучающие карточки, специальный фломастер с «резинкой», магнитные фигурки и тетрадь с заданиями для ученика. Выполнять задания и решать задачки можно как на карточках, так на магнитной доске и в тетради.

Обучающий набор математика

Синий фломастер, который есть в наборе, отлично пишет на магнитной доске сверху, над деревьями с зелеными кронами. Спонжик на конце колпачка фломастера позволяет легко стирать написанное.

Кроме этого, в комплекте есть тетрадь по математике для дошкольников.

В этой тетради много интересных примеров на сложение, вычитание и сравнение предметов, а также веселые задачки для детей.

Украинский алфавит (абетка)

В комплекте есть синий фломастер со специальной «губкой» на колпачке, с помощью которой можно стирать написанное на магнитной доске или карточках. Да, на каждой из 36 карточек можно писать фломастером.

С одной стороны указана буква с картинкой (и названием изображенного предмета), набор букв или весь алфавит, а с другой стороны точечками показано, как можно правильно написать букву (печатную).

Так ребенок может фломастером обводить по контуру буквы, стирать и начинать заново.

С ее помощью можно учить буквы и звуки, гласные и согласные.

Другими словами, это удобный способ для родителей грамотно объяснить, что такое украинский алфавит, какие есть гласные и согласные буквы, какие есть звуки и т.д.

Магнитный алфавит из 33 украинских букв представлен в двух цветах: гласные буквы зеленые, согласные синие. Его можно прикреплять к магнитной доске, составляя слова.

как сдать ОГЭ по математике — Учёба.ру

Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Ольга Евсеева,

преподаватель математики физико-математической школы Института довузовской подготовки

Московского технологического университета (МИРЭА, МИТХТ, МГУПИ)

По вашему мнению, насколько хорошо девятиклассники сейчас знают математику? Насколько сложен для них этот ОГЭ?

Не сказала бы, что школьники не знают математику. Как правило, к нам на занятия приходят ребята с неплохим начальным уровнем, с хорошими навыками выполнения арифметических действий и преобразования выражений, знакомые с методами решения линейных, квадратных уравнений и неравенств — то есть со всем тем, что они должны знать к началу 9 класса. Конечно, глубина знаний и умение ими пользоваться напрямую зависят от количества часов математики в школе: при изучении предмета на базовом уровне это три-четыре часа алгебры и два часа геометрии в неделю, на углубленном уровне — пять-семь часов алгебры и три часа геометрии. Поскольку ОГЭ состоит из двух частей, первая из которых проверяет базовый уровень подготовки, а вторая включает более сложные задания, ребятам, изучающим в школе базовую математику, необходимо выделить дополнительное время для подготовки.

Иногда школьных уроков и самостоятельной работы достаточно, чтобы сдать ОГЭ на хорошо и отлично. В качестве подспорья можно использовать различные сайты и учебную литературу в открытом доступе. Возникающие вопросы можно обсудить на форумах или со школьным учителем. Но занятия на курсах помогают последовательно разобрать темы, систематизировать материал, проверить глубину его усвоения. Ведь после ОГЭ ребят через два года ждет более трудное испытание — ЕГЭ, в котором часть базовых заданий аналогичны заданиям повышенной и высокой сложности из ОГЭ. Девятиклассники впервые сдают экзамен, содержащий так много заданий, и его длительность составляет 3 часа 55 минут. Безусловно, для ребят это непросто.

Расскажите про структуру экзамена и систему начисления баллов. За какие задания на ОГЭ по математике ставится наибольшее количество баллов?

Всего школьникам предлагается 26 заданий. До недавнего времени экзамен состоял из трех частей — «Математика», «Реальная математика» и «Геометрия».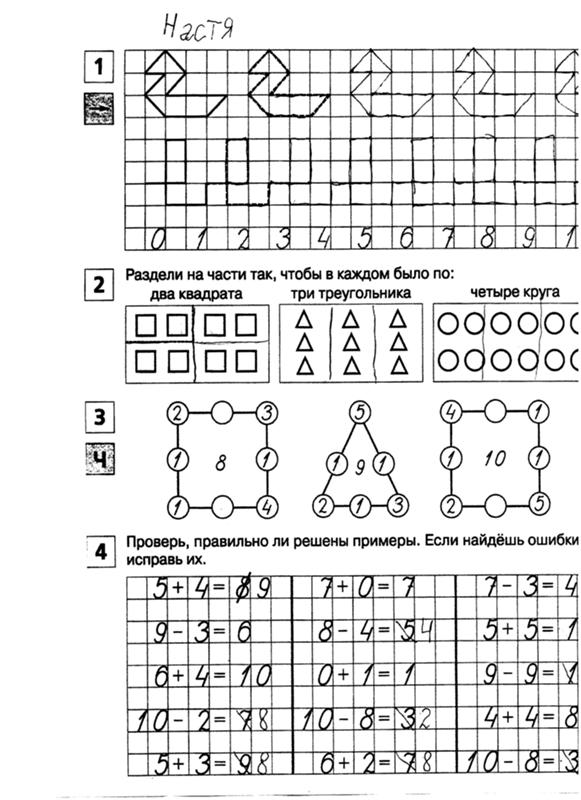 С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».

Ребятам предстоит решить 17 задач по алгебре (14 задач в части 1 и три в части 2) и девять задач по геометрии (шесть задач в части 1 и три в части 2). Задания части 1 требуют краткого ответа в виде числа или последовательности цифр, которые вносятся в бланк ответов № 1. Развернутые решения заданий части 2 и ответы к ним записываются на бланке ответов № 2. За правильный ответ на каждое из заданий № 1-20 ставится 1 балл. Эти задания проверяются автоматически при сканировании бланков. Задания № 21-26 проверяют двое независимых экспертов, хотя при значительном расхождении оценок назначается проверка третьим экспертом. Эти задания могут быть оценены от 0 до 2 баллов. Таким образом, максимально за работу можно получить 32 первичных балла. Пятерка ставится за результат от 22 баллов, четверка — от 15 баллов, тройка — от 8 баллов (из них не менее 4 баллов по алгебре и 2 баллов по геометрии).

Как видите, для положительной оценки достаточно решить лишь восемь задач из части 1, а для пятерки — безошибочно выполнить базовую часть экзамена и только одно из заданий повышенной сложности. Вроде бы задача «сдать ОГЭ на отлично» не кажется такой уж сложной. Однако с заданиями повышенной сложности из части 2 ребятам придется снова столкнуться на ЕГЭ, уже в его базовой части. Например, задание № 22 повышенного уровня сложности — «текстовая задача» — аналогично заданию № 11 из части 1 ЕГЭ. Поэтому, как мне кажется, ребятам уже в 9 классе надо освоить методы и приемы решения заданий из части 2.

По вашему опыту преподавания, какие разделы математики самые сложные для школьников и вызывают наибольшее затруднение? Какие темы самые простые?

В модуле «Алгебра» это, прежде всего, исследование функций и построение их графиков. Задания на эту тему входят и в часть 1, и в часть 2 ОГЭ. В задании № 10 нужно установить соответствие между графиками функции и формулами, которые их задают. Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.

В модуле «Геометрия» в части 1 включены задачи, относящиеся к ключевым разделам курса геометрии. И все же, если в задании встречаются такие темы, как «вписанная и описанная окружности», «вписанные углы», «соотношения между сторонами и углами прямоугольного треугольника», «подобие треугольников», показатель его решаемости падает.

Меньше всего ошибок девятиклассники допускают в заданиях на чтение таблиц и диаграмм, нахождение вероятности случайного события.

Какие есть «подводные камни» в заданиях части 2? На что нужно обратить внимание при подготовке к заданиям повышенной сложности?

Задание № 21	В этом задании необходимо решить уравнение или неравенство, преобразовать алгебраическое выражение. При решении рациональных и дробно-рациональных уравнений, а также уравнений высших степеней необходимо обращать внимание на возможность потери решения (при сокращении на выражение, которое может быть равным нулю) или получение посторонних решений (которые обнуляют знаменатель или обращают исходное уравнение в выражение, не имеющее смысла). При решении неравенств надо помнить, что при умножении неравенства на отрицательное выражение оно меняет знак. Зачастую школьники либо просто не обращают внимание на знак величины, на которую умножают неравенство, либо умножают неравенство на выражение, содержащее переменную.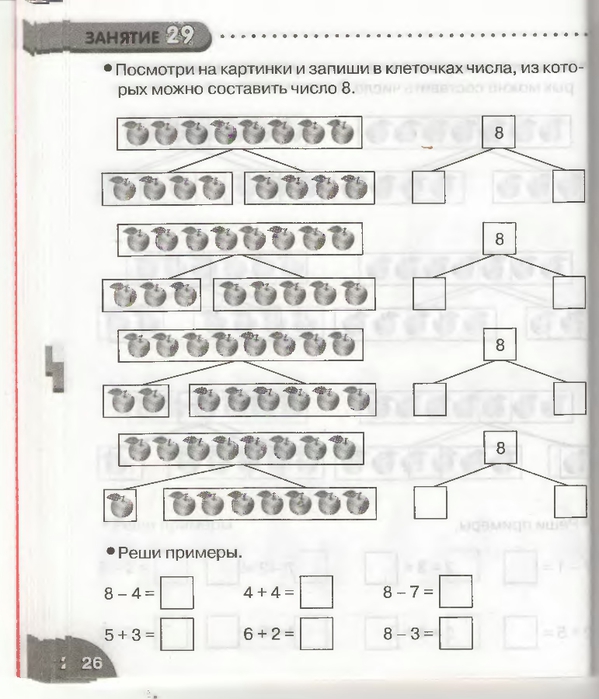
Задание № 22	Это текстовая задача, как правило, на «движение», «работу», «концентрации растворов» или «смеси и сплавы». Для ее решения необходимо составить уравнение или систему уравнений. Я бы посоветовала ребятам для наглядности обязательно заполнять таблицу, в которую вносятся известные по условию величины, выбранная переменная или переменные, после чего в пустые клетки вписываются соответствующие им величины, выраженные через введенные переменные, и только потом приступать к составлению уравнения (или системы).
Задание № 23	Построение графика функции. Для правильного выполнения этого задания необходимо знать свойства следующих функций: линейная, квадратичная, либо функция, описывающая обратно пропорциональную зависимость. Также необходимо уметь строить графики этих функций, знать правила преобразования графиков. Очень часто встречаются задания, в которых формулу, задающую исходную функцию, можно преобразовать, после чего она значительно упрощается. Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать.
Задание № 24	Геометрическая задача вычислительного характера. Школьник должен решить планиметрическую задачу, применяя различные теоретические знания из курса геометрии.
Задание № 25	Геометрическая задача на доказательство с использованием стандартных приемов. Здесь надо обратить внимание на умение математически грамотно и ясно записать решения, приведя все необходимые обоснования и пояснения.
Задание № 26	Для решения этой задачи школьникам нужно владеть широким спектром приемов и способов рассуждений. Здесь возможно потребуются и дополнительные построения, и знание утверждений, не так часто используемых в школьном курсе. Например, теорема об угле между касательной и хордой; теорема о секущих и касательной; свойства высоты прямоугольного треугольника, опущенной из прямого угла; свойства биссектрис, медиан, высот треугольника; теорема Чевы; теорема Менелая.

Что нужно делать школьнику, чтобы подготовиться к экзамену наилучшим образом? Как вы посоветуете им распределить свое время?

На занятиях со школьниками я обычно придерживаюсь следующей стратегии. Во-первых, мы полностью проходим программу 9 класса, начиная с отработки основных навыков и умений по следующим темам: преобразование алгебраических выражений, решение уравнений и неравенств, числовые последовательности, функции, их свойства и графики, элементы статистики и теории вероятностей. Постепенно повышая уровень заданий, мы переходим к решению задач повышенной и высокой сложности и стараемся уделить этим заданиям как можно больше внимания. Не менее трети времени следует посвятить геометрии, и здесь также нужно двигаться «от простого к сложному».

Во-вторых, необходимо готовиться к самому формату ОГЭ, к его структуре. Если ученик хорошо умеет решать задачи, но ни разу не пробовал написать работу в этом формате, ему сложно будет оценить количество затрачиваемого времени на часть 1 и 2. Обязательно нужно научиться правильно распределять свои силы.

Многие девятиклассники не используют предлагаемое на экзамене время полностью, у них просто не хватает усидчивости. Ребята сдают работу раньше, хотя еще остались нерешенными задания повышенной сложности. Зачастую и в заданиях части 1 бывают ошибки по невнимательности, которые сам школьник не смог найти и исправить. На ЕГЭ же складывается обратная ситуация. Выпускники прилежно готовятся к экзамену, считают, что времени мало. Им хочется еще раз проверить свои решения и подумать над заданиями высокой сложности.

Какие источники вы рекомендуете использовать для самостоятельной подготовки к экзамену?

• «Сайт ФИПИ». На нем вы найдете открытый банк заданий ОГЭ.
• Сборник «ОГЭ. Математика 2018. Типовые и тестовые задания». Таких сборников очень много, нужно обращать внимание на гриф «рекомендовано ФИПИ».
• Учебные пособия Центра непрерывного математического образования. Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения.
• «Сайт Alexlarin.net». Здесь каждую неделю выкладывается новый вариант ОГЭ и новый вариант ЕГЭ. Ребятам дается семь дней на размышление. Они могут обсуждать свои решения на специальном форуме. Потом вывешиваются правильные ответы.
• «РешуЕГЭ». На сайте доступен большой банк заданий. Тесты можно составлять самостоятельно, выбирая лишь те темы, над которыми необходимо поработать. Небольшой минус — тесты часто получаются похожими друг на друга.

Список интернет-ресурсов для учителей и обучающихся

http://100ege.ru/ Онлайн подготовка к ЕГЭ
http://soc.reshuege.ru/ Образовательный портал для подготовки к экзаменам
http://www.ege.edu.ru/ Официальный информационный портал подготовки к ЕГЭ
http://gia.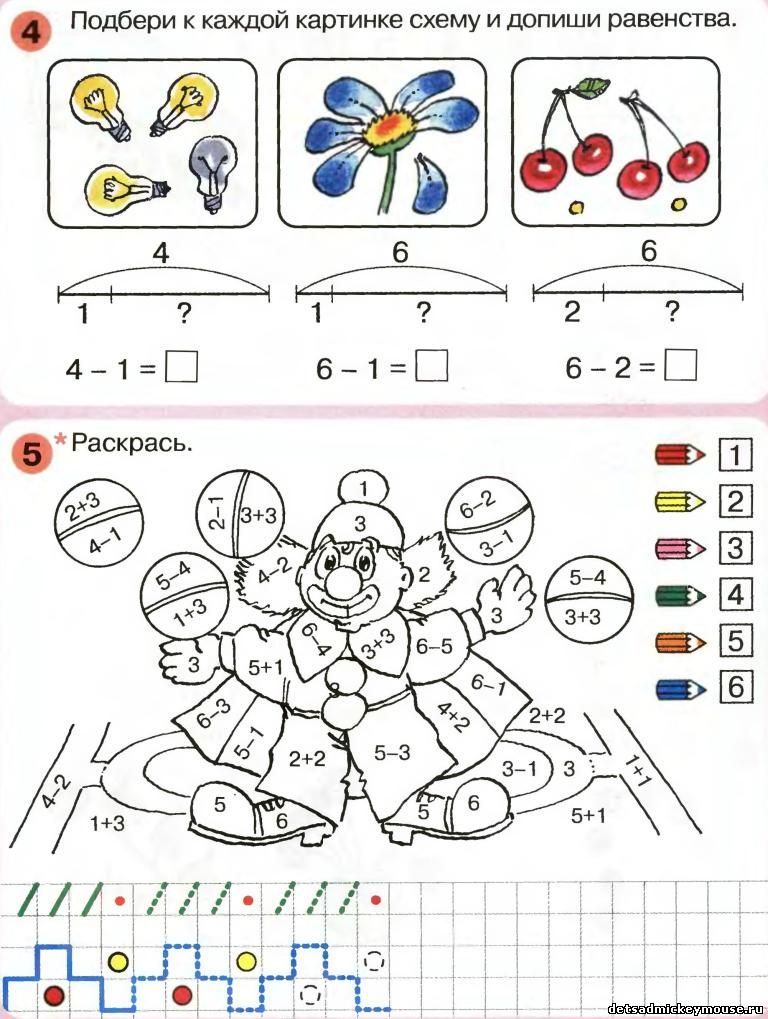 edu.ru/ Официальный информационный портал подготовки к ГИА
http://www.ege.ru/ Сайт поддержки проведения ЕГЭ в компьютерной форме
http://4ege.ru Портал подготовки к ЕГЭ
http://www.menobr.ru/about/res_obr/ Информационный центр цифровых ресурсов
http://www.alleng.ru/ Сайт «Всем кто учится». Электронные учебники
http://eor-np.ru/ Основной сайт по ЭОР
http://fcior.edu.ru/ Федеральный центр информационно-образовательный ресурсов
http://www.edu.ru/db/portal/sites/res_page.htm Федеральные образовательные ресурсы для общего образования
http://window.edu.ru/library?p_rubr=2.1 Единое окно доступа к образовательным ресурсам
http://school-collection.edu.ru/ Единая коллекция ЦОР
http://katalog.iot.ru/ Образовательные ресурсы сети Интернет
http://school.edu.ru/doc.asp?ob_no=53721 Единая коллекция ЦОР
http://www.digital-edu.ru/fcior/133/373 Единая коллекция ФЦИОР
http://www.openclass.ru/dig_resources Открытый класс
http://festival.1september.ru/ Фестиваль педагогических идей «открытый урок»
http://www. uchportal.ru/ Учительский портал

Предметный список ЭОР
Математика
http://www.math.ru Портал Math.ru: библиотека, медиатека, олимпиады, задачи, научные школы, учительская, история математики
http://school-collection.edu.ru/collection/matematika Материалы по математике в Единой коллекции цифровых образовательных ресурсов
http://www.mccme.ru Московский центр непрерывного математического образования
http://www.bymath.net Вся элементарная математика: Средняя математическая интернет-школа
http://mat.1september.ru Газета «Математика» Издательского дома «Первое сентября»
http://www.uztest.ru ЕГЭ по математике: подготовка к тестированию
http://zadachi.mccme.ru Задачи по геометрии: информационно-поисковая система
http://www.problems.ru Интернет-проект «Задачи»
http://edu.of.ru/computermath Компьютерная математика в школе
http://www.mathematics.ru Математика в «Открытом колледже»
http://www.mathtest.ru Математика в помощь школьнику и студенту (тесты по математике online)
http://school. msu.ru Математика в школе: консультационный центр
http://www.shevkin.ru Математика. Школа. Будущее. Сайт учителя математики А.В. Шевкина
http://www.etudes.ru Математические этюды: SD-графика, анимация и визуализация математических сюжетов
http://www.athedu.ruМатематическое образование: прошлое и настоящее. Интернет-библиотека по методике преподавания математики
http://www.mce.su Международные конференции «Математика. Компьютер. Образование»
http://eqworld.ipmnet.ru Научно-образовательный сайт EqWorld — Мир математических уравнений
http://kvant.mccme.ru Научно-популярный физико-математический журнал «Квант»
http://www.exponenta.ru Образовательный математический сайт Exponenta.ru
http://www.allmath.ru Портал Allmath.ru — Вся математика в одном месте
http://www.pm298.ruПрикладная математике: справочник математических формул, примеры и задачи с решениями
http://www.mathnet.spb.ru Сайт элементарной математики Дмитрия Гущина
http://www.bashmakov.ru Учимся по Башмакову — Математика в школе
http://math. rusolymp.ru Олимпиады, конкурсы по математике для школьников Всероссийская олимпиада по математике
http://tasks.ceemat.ru Задачник для подготовки к олимпиадам по математике
http://www.math-on-line.com Занимательная математика — Олимпиады, игры, конкурсы по математике для школьников
http://www.olimpiada.ru Математические олимпиады для школьников
http://wwwzaba.ru Математические олимпиады и олимпиадные задачи

Физика.
http://school-collection.edu.ru/collection Предметная коллекция «Физика»
http://experiment.edu.ru Естественно-научные эксперименты — Физика: Коллекция Российского общеобраз. Портала
http://www.physics.ru Открытый колледж: Физика
http://www.elementy.ru Элементы: популярный сайт о фундаментальной науке
http://nano-edu.ulsu.ru Введение в нанотехнологии
http://www.gomulina.orc.ru Виртуальный методический кабинет учителя физики и астрономии: сайт Н.Н. Гомулиной
http://www.fizmatklass.ru Виртуальный физмат-класс: общегородской сайт саратовских учителей
http://www. effects.ru Виртуальный фонд естественно-научных и научно-технических эффектов «Эффективная физика»
http://fiz.1september.ru Газета «Физика» Издательского дома «Первое сентября»
http://ens.tpu.ru Естественно-научная школа Томского политехнического университета
http://elkin52.narod.ru Занимательная физика в вопросах и ответах: сайт В. Елькина
http://www.zensh.ru Заочная естественно-научная школа (Красноярск): учебные материалы по физике для школьников
http://ido.tsu.ru/schools/physmat Заочная физико-математическая школа Томского государственного университета
http://www.school.mipt.ru Заочная физико-техническая школа при МФТИ
http://teach-shzz.narod.ru Информатика и физика: сайт учителя физики и информатики З.З.Шакурова
http://ifilip.narod.ru Информационные технологии в преподавании физики: сайт И.Я. Филипповой
http://somit.ru Информационные технологии на уроках физики. Интерактивная анимация

Информатика и информационные технологии.
http://www. ict.edu.ru Информационно-коммуникационные технологии в образовании: федеральный образовательный портал
http://www.iot.ru Информационные образовательные технологии: блог-портал
http://icttest.edu.ru Отраслевая система мониторинга и сертификации компьютерной грамотности и ИКТ-компетентности
http://portal.ntf.ru Проект «Информатизация системы образования» Национального фонда подготовки кадров
http://linux.armd.ru Проект «Пакет программного обеспечения для образовательных учреждений России»
http://shkola.edu.ru Проект «Первая Помощь»: Стандартный базовый пакет программного обеспечения для школ
http://mo.itdrom.com Виртуальное методическое объединение учителей информатики и ИКТ на портале «Школьный университет»
http://www.computer-museum.ru Виртуальный компьютерный музей
http://www.problems.ru/inf Задачи по информатике
http://iit.metodist.ru Информатика и информационные технологии: сайт лаборатории информатики МИОО
http://www.intuit.ru Интернет-университет информационных технологий (ИНТУИТ. ру)
http://www.edu-it.ru ИТ-образование в России: сайт открытого е-консорциума
http://www.edusite.ru Конструктор школьных сайтов (Некоммерческое партнерство «Школьный сайт»)
http://edu.of.ru Конструктор образовательных сайтов (проект Российского общеобразовательного портала)

Химия.
Портал фундаментального химического образования ChemNet.
http://www.chemnet.ru Химическая информационная сеть: Наука, образование, технологии
http://him.1september.ru Газета «Химия» и сайт для учителя «Я иду на урок химии»
http://school-collection.edu.ru/collection/chemistry Единая коллекция ЦОР: Предметная коллекция «Химия»
http://experiment.edu.ru Естественно-научные эксперименты: химия. Коллекция Российского общеобразовательного портала
http://www.alhimik.ru АЛХИМИК: сайт Л.Ю. Аликберовой
http://chem.rusolymp.ru Всероссийская олимпиада школьников по химии
http://www.chemistry.ssu.samara.ru Органическая химия: электронный учебник для средней школы
http://www.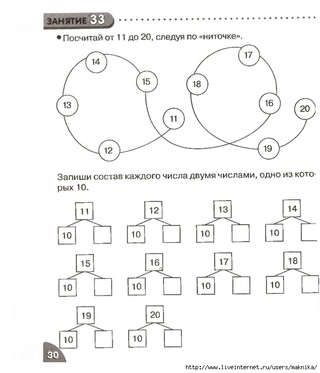 hemi.nsu.ru Основы химии: электронный учебник
http://www.chemistry.ru Открытый колледж: Химия
http://www.edu.yar.ru/russian/projects/predmets/chemistry Дистанционная олимпиада по химии: телекоммуникационный образовательный проект
http://www.eidos.ru/olymp/chemistry Дистанционные эвристические олимпиады по химии

Биология и экология.
http://school-collection.edu.ru/collection Единая коллекция ЦОР. Предметная коллекция «Биология»
http://bio.1september.ru Газета «Биология» и сайт для учителей «Я иду на урок биологии»
http://college.ru/biology Открытый колледж: Биология
http://fns.nspu.ru/resurs/nat Помощь учителю биологии: образовательный сайт ИЕСЭН НГПУ
http://www.eco.nw.ru Внешкольная экология. Программа «Школьная экологическая инициатива»
http://www.sbio.info Вся биология: научно-образовательный портал
http://www.biolog188.narod.ru В помощь моим ученикам: сайт учителя биологии А.П. Позднякова
http://www.darwin.museum.ru Государственный Дарвиновский музей
http://www. livt.net Живые существа: электронная иллюстрированная энциклопедия
http://www.zensh.ru Заочная естественно-научная школа (Красноярск): учебные материалы по биологии для школьников
http://zelenyshluz.narod.ru Зеленый шлюз: путеводитель по экологическим ресурсам
http://www.zooclub.ru Зооклуб: мегаэнциклопедия о животных
http://www.zin.ru/museum Зоологический музей в Санкт-Петербурге

Русский язык.
http://www.gramota.ru Справочно-информационный портал «Русский язык» — ГРАМОТА.РУ
http://rus.1september.ru Сайт «Я иду на урок русского языка» и электронная версия газеты «Русский язык»
http://language.edu.ru Коллекция диктантов по русскому языку Российского общеобразовательного портала
http://rus.rusolymp.ru Всероссийская олимпиада школьников по русскому языку
http://www.philolog.ru/dahl Владимир Даль. Проект портала Philolog.ru
http://www.rus-ege.com ЕГЭ по русскому языку: электронный репетитор
http://www.ruslang.ru Институт русского языка им. В.В. Виноградова Российской академии наук
http://www.ruthenia.ru Интернет-проект исследователей-русистов Ruthenia.ru
http://ruslit.ioso.ru Кабинет русского языка и литературы
http://www.rm.kirov.ru Конкурс «Русский Медвежонок — языкознание для всех»
http://www.gramma.ru Культура письменной речи

Иностранные языки.
http://www.translate.ru Онлайн-словари, переводчики, тезаурусы Онлайн-переводчики «ПРОМТ»
http://online.multilex.ru Онлайн-словари «Мультилекс»
http://www.multitran.ru Онлайн-словари «Мультитран»
http://www.abbyyonline.ru Онлайн-словари ABBYY Lingvo
http://www.rambler.ru/dict Онлайн-словари на портале «Рамблер»
http://slovari.yandex.ru Служба «Яндекс.Словари»
http://dictionary.cambridge.org Dictionary.com Cambridge Dictionaries Online
http://dictionary.reference.com онлайн-словари и переводчики
http://www.thefreedictionary.comTheFreeDictionary.com: онлайн-словари и переводчики
http://www.yourdictionary.com YourDictionary. com: онлайн-словари и переводчики
http://www.websters-online-dictionary.org Webster’s Online Dictionary
http://www.englishforkids.ru Английский язык Английский для детей

История
История России. Обществознание: Учебно-методический комплект для школы
http://biography.globala.ru Биографии известных людей
http://www.stolypin.ru/ посвященных личности и реформаторскому наследию П.А.Столыпина
http://bibliofond.ru Библиотека научной и студенческой информации
http://www.hrono.info Всемирная история в интернете
http://www.lensart.ru Художественные фотографии
http://historydoc.edu.ru Коллекция «Исторические документы» Российского общеобразовательного портала
http://www.lectures.edu.ru Лекции по истории on-line для любознательных
http://www.pish.ru Преподавание истории в школе: научно-методический и теоретический журнал
http://his.1september.ru
Сайт «Я иду на урок истории» и электронная версия газеты «История»
http://school-collection. edu.ru/collection Тематические коллекции по истории Единой коллекции ЦОР по истории
http://hist.rusolymp.ruВсероссийская олимпиада школьников
http://www.teacher.syktsu.ru Инновационные технологии в гуманитарном образовании: материалы по преподаванию истории
http://www.hrono.ru Проект ХРОНОС — Всемирная история в Интернете

География.
GeoSite — все о географии
http://www.geosite.com.ru Библиотека по географии
http://geoman.ru География. Планета Земля
http://ru.wikipedia.org/wiki/География Раздел «География» в энциклопедии Википедия
http://www.rgo.ru География.ру: клуб путешествий
http://migranov.ru Авторский проект Руслана Мигранова
http://geo-tur.narod.ru Гео-Тур: все, что вы хотели знать о географии
http://www.myplanet-earth.com Планета Земля
http://geopub.narod.ru Страноведческий каталог «EconRus» http://catalog.fmb.ru GeoPublisher (архив научных публикаций географического факультета МГУ им. М.В.Ломоносова)
http://geo.1september. ru Газета «География» и сайт для учителя «Я иду на урок географии»
http://geo.metodist.ru Учебно-методическая лаборатория географии Московского института открытого образования
http://afromberg.narod.ru Уроки географии и экономики: сайт учителя географии А.Э. Фромберга

Новая математика: Руководство для родителей | Разобрался

Вас смущает незнакомые математические задачи в домашней работе вашего ребенка? Подход к обучению математике в последние годы изменился. Приведенные ниже примеры, созданные с помощью специалиста по математике Хайди Коэн, могут помочь вашему ребенку освоить «новую математику».

Десять рамок — это набор из 10 прямоугольников с точками в некоторых или всех прямоугольниках. Дети могут увидеть, как разные комбинации чисел дают в сумме 10. Десятикадровый просмотр особенно хорош для демонстрации того, как работает вычитание.

В числовой связке используются линии, связывающие группу чисел вместе, показывая, как они связаны. На первом рисунке соотношение между числами 3 и 10 показано добавлением числа 7 к пустому кружку (3 + 7 = 10). Это помогает детям понять, как одно число можно разбить на более мелкие части.

В открытой числовой строке нет цифр, которые уже были записаны. Учащийся может использовать любой номер в качестве отправной точки. (Здесь 37 — это начальная точка, потому что именно столько ярдов прошел Бретт.Затем добавляются 26 ярдов, которые прошел Адам.) Открытая числовая линия позволяет детям складывать или вычитать визуально. Его часто используют для решения словесных задач.

Декомпозиция (также называемая «развернутой формой»)

Декомпозиция — это стратегия решения математических задач путем разбиения числа на его цифровые значения. Например, 37 превращается в 30 и 7. После того, как вы разделите число, вы можете сложить или вычесть отдельные цифровые значения, чтобы получить ответ.

Основание десять — это стратегия решения задач на сложение и вычитание с использованием таблицы, разделенной на сотни, десятки и единицы. Вероятно, вы встретите термин «перегруппировка», используемый для этого метода. Каждое число попадает в таблицу в соответствии с его разрядовым значением. Например, 43 будет означать 4 десятка и 3 единицы. Это помогает детям понять, когда «одалживать» и «переносить» числа из одной разряда в другую.

Умножение прямоугольников — это метод разбиения чисел на цифровые значения. В таблице числа разбиты по стоимости и отдельно умножены. После умножения каждого числа общие значения складываются.Этот метод может быть полезен для детей, у которых есть проблемы с традиционным умножением с использованием больших чисел.

Модель площади использует длину и ширину прямоугольника или квадрата, чтобы разобрать задачу умножения. Каждая фигура рассчитывается, и ответы складываются. Это еще один способ сделать математику более наглядной для детей.

Подобно модели области, массив представляет собой набор объектов, которые представляют собой числа. Эта модель часто используется, чтобы помочь детям увидеть различные качества сложения и умножения.

Столбиковое моделирование (также известное как «ленточная диаграмма»)

Столбиковая модель использует столбцы для визуального представления чисел и неизвестных в словесной задаче. Это может помочь детям увидеть, как количества сравниваются друг с другом. Дети могут адаптировать модель штанги для решения многих задач.

6 способов помочь учащимся понять математику

Конечная цель обучения математике состоит в том, чтобы учащиеся понимали представленный материал, применяли навыки и вспоминали концепции в будущем.Мало пользы от того, что учащиеся вспомнят формулу или процедуру для подготовки к завтрашнему экзамену, а к следующей неделе забывают основную концепцию. Учителям необходимо сосредоточиться на том, чтобы ученики понимали материал, а не просто запоминали процедуры.

Вот шесть способов научить понимать в классе математики:

1. Создайте эффективный вводный курс.

Первые пять минут урока задают тон всему уроку.В идеале учителя должны начать с того, что поделятся повесткой дня урока, чтобы ученики знали, чего ожидать от того, что будет происходить. Затем учителя могут разместить и сформулировать цель обучения или основной вопрос классу, чтобы учащиеся знали цель и в конце урока могли самостоятельно оценить, была ли цель для них достигнута. Наконец, вводный курс может включать в себя одну или несколько задач для разминки как способ проанализировать и оценить предыдущие знания учащихся при подготовке к ознакомлению с новым материалом.В этом видеоролике показано начало урока седьмого класса по прямоугольным призмам:

2. Представляйте темы, используя несколько представлений.

Чем больше типов представлений вы можете представить студентам, обращаясь к их различным стилям обучения, тем с большей вероятностью они действительно поймут представляемую концепцию. Различные представления могут включать в себя использование манипуляторов, показ изображения, рисование проблемы и предложение символического представления. Например, представляя линейные отношения с одним неизвестным, проиллюстрируйте учащимся ту же задачу в виде уравнения в числовой строке, словами и картинками. Учащиеся, которые подвергаются воздействию и могут распознать одни и те же отношения, представленные в различных режимах представления, с большей вероятностью будут иметь концептуальное понимание отношений и лучше справляться с оценками (PDF).

3. Решать проблемы разными способами.

В оптимальной обстановке в классе учитель может показать разные способы решения одной и той же проблемы и побудить учеников придумывать собственные творческие способы их решения. Чем больше стратегий и подходов используют студенты, тем глубже становится их концептуальное понимание темы.Предоставление ученикам возможности создавать собственные методы решения проблем может заставить учителя нервничать. Что, если мы не будем следовать их логике? Что, если они неверны? Однако стоит рискнуть, чтобы они исследовали. После того, как один, пара или небольшая группа учащихся завершат решение задачи класса с помощью одного метода, предложите им поискать альтернативные способы найти такое же правильное решение. Когда учащиеся разрабатывают свои собственные методы, а затем делятся с классом правильными шагами, это очень мощный учебный опыт.На видео ниже показано, как учитель предлагает ученикам несколько способов решить одну и ту же задачу на прямоугольных призмах:

4. Покажите приложение.

В идеальном мире мы всегда сможем продемонстрировать, как каждая концепция может быть применена к реальному миру — и, когда это возможно, это поможет улучшить понимание учащимися. Когда концепция не может быть применена таким образом, мы все равно можем рассказать, как ее можно применить в математике или другой предметной области. Другой вариант — показать, как эта концепция развивалась на протяжении истории математики.Выделите минутку из каждого урока, чтобы показать своим ученикам, где и как математику можно увидеть или использовать в жизни за пределами класса.

5. Предложите учащимся изложить свои соображения.

Студенты должны объяснять свои рассуждения при решении задач.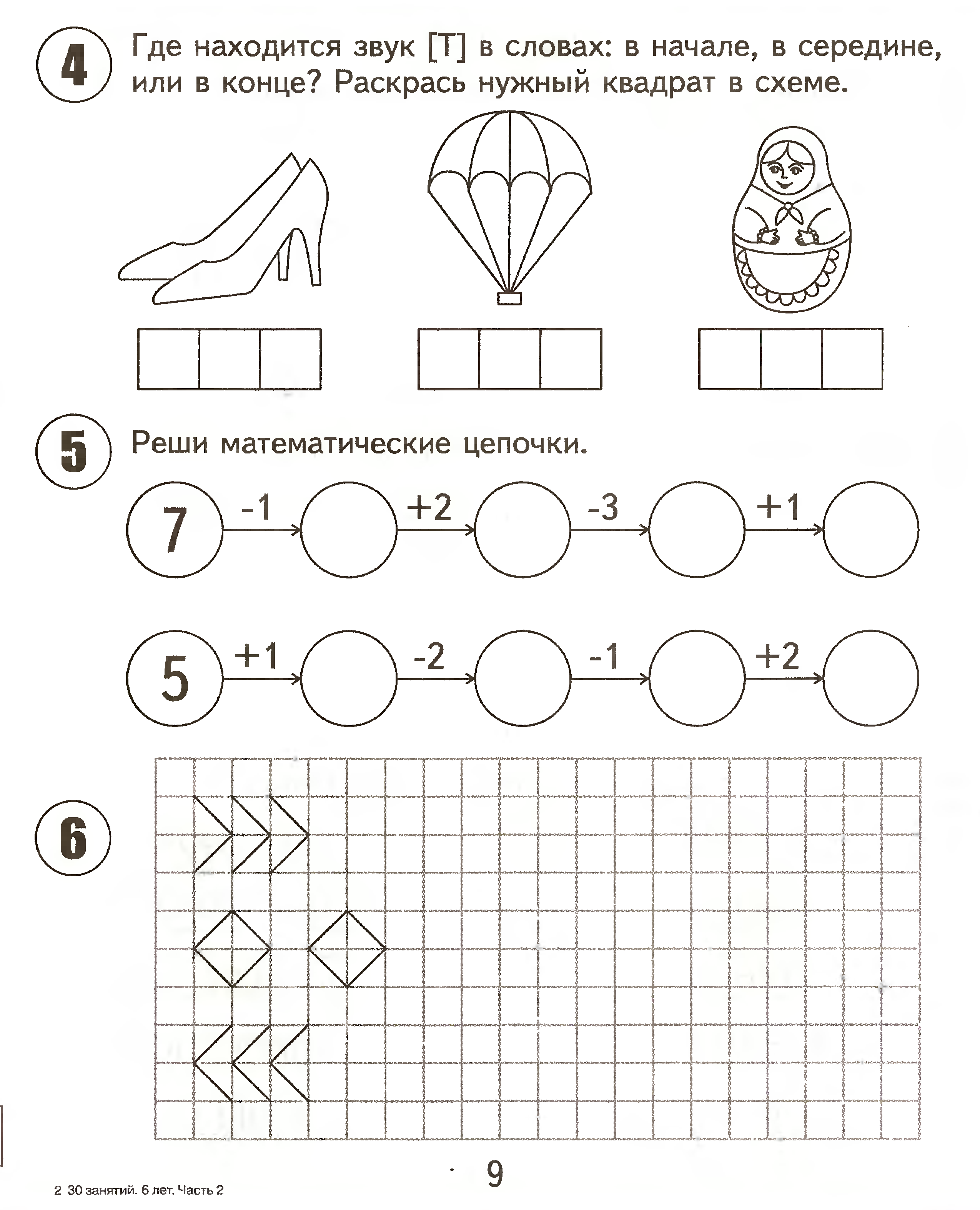 Чтобы учитель мог определить, действительно ли каждый ученик понимает цель урока, каждому ученику необходимо общаться как устно, так и письменно. Предоставив классу десять минут для обсуждения их рассуждений друг с другом, изучая различные способы решения проблем, вы обеспечите отличное взаимодействие и обучение.Не всегда легко заставить учеников говорить в классе, но есть способы их поощрить (PDF).

6. Завершить занятие с аннотацией.

Каждый может заблудиться во время урока, и легко потерять счет времени, пока не прозвенит звонок и урок не закончится. Последние семь минут могут оказаться наиболее важными для того, чтобы студенты поняли учебную цель дня. Вы можете использовать это время для выполнения трех очень важных задач:

• Быстрая формирующая оценка, чтобы определить, сколько было усвоено, например, учащиеся самостоятельно оценивают свой комфорт с концепцией по шкале от 1 до 5
• Обзор цели для время урока и краткое обсуждение того, где будет проходить урок в следующий раз.
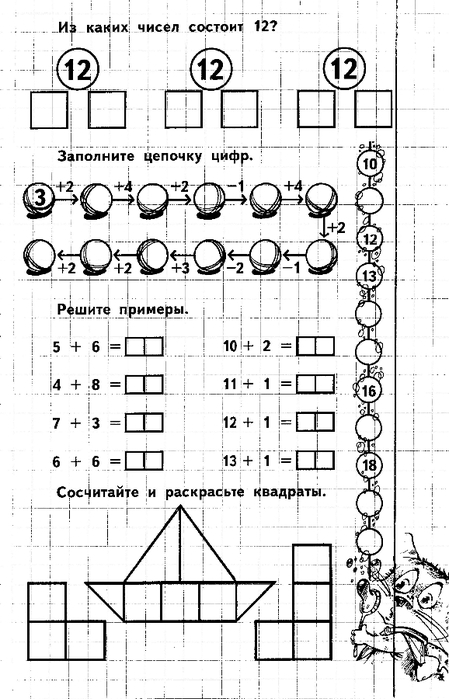
• Предварительный просмотр домашнего задания вместе, чтобы избежать путаницы.

Это лишь некоторые из заданий в конце урока.Есть как минимум 22 дополнительных действия по закрытию. В этом видео показана итоговая фаза того же урока:

В разделе комментариев ниже поделитесь своими собственными советами и приемами, которые помогут учащимся понять математику.

Как подготовить учеников начальной школы к алгебре

Педагоги проявляют все больший интерес к переходу от арифметики к алгебре, сопровождаемый интересом к алгебраическому мышлению в начальных классах. Этот интерес усилился, потому что у очень многих студентов, похоже, возникают проблемы с изучением алгебры.Нередко можно услышать от взрослых, что они отлично справлялись с математикой, пока не дошло до трех последних букв алфавита. Хотя некоторые люди определяют алгебру как «обобщенную арифметику», на самом деле это совсем другой способ мышления, чем просто числовая или вычислительная арифметика. Это система логических рассуждений. Это репрезентативная система, включающая манипулирование символами, а не числами, и предмет изучения математики. Речь идет о структурах и отношениях.

Например, если студенту дается уравнение 2x + 5 = 15 , хороший студент, изучающий арифметику, может решить его мысленно, а не найти эквивалентное уравнение, которое выделяет неизвестное.Возможно, лучше было бы попросить учащегося написать уравнение, представляющее вопрос: «5 больше, чем удвоение, число равно 15, какое это число?» Этот вопрос фокусируется на представлении отношений с помощью переменной, а не на конкретных числах.

Переход от арифметики к алгебре является сложной задачей, но если учащиеся знакомятся с концепциями алгебры на протяжении всех младших классов, этот переход становится проще. Это можно сделать, во-первых, убедившись, что учащиеся достаточно понимают и свободно владеют такими важными темами, как вычисление целых чисел, дроби, отношения и пропорциональность, а во-вторых, явно обучая критическим алгебраическим идеям и рассуждениям. Некоторые из явно преподаваемых тем включают обобщения, распознавание структур, свойств, эквивалентность, использование переменных и создание визуальных моделей для решения алгебраических задач.

Обобщения

Математика — это изучение обобщений — поиска взаимосвязи, применимой к набору объектов. Это требует поиска сходств, различий и определяемых общих черт среди объектов и случаев. Это ведет к абстракции, к удалению контекста.

Например, учеников в начале третьего класса просят рассмотреть эффекты добавления четного числа к четному, нечетного числа к нечетному и четного числа к нечетному.После тестирования нескольких версий каждого из них студентов спрашивают, всегда ли это соотношение верно. Студенты часто приводят дополнительные примеры в качестве доказательства того, что получается четная сумма, когда два слагаемых четны или когда оба нечетны. Затем учителю предлагается спросить, почему это соотношение сохраняется, что заставляет учеников отойти от дополнительных примеров и вместо этого сосредоточиться на значении четных и нечетных чисел. Что общего у всех четных чисел и что общего у всех нечетных чисел?

Использование манипуляторов побуждает учащихся рассматривать четные числа как пары, а нечетные числа как пары плюс 1.В более поздних классах это будет 2n и 2n + 1 . Студенты обсудят, является ли 0 четным числом, а затем в этом году студенты будут смотреть на таблицу умножения таким же образом и делать обобщения относительно произведений четных и нечетных чисел. Они ответят на вопросы, есть ли на столе больше четных или нечетных продуктов и почему.

Конструкции

Когда факты умножения преподаются как связанные факты, и учащиеся изучают факты, используя эти отношения, они знакомятся со структурами и свойствами.

Как включить «реальный мир» в уравнение обучения математике

Учитель математики, с которым я когда-то работал, поделился историей о встрече с бывшим учеником.

Этот конкретный студент был , тот ребенок , если не сказать лучше. Вы знаете, что это за тип: отстраненный, иногда деструктивный и готовый ответить на любое предложение поработать с вневременной классикой: «Я все равно никогда не буду использовать это».

Но он был здесь лет десять спустя.И что первое, что он сказал своему бывшему учителю?

Я наконец понял, почему все это было важно.

Почему?

Он не стал инженером, физиком-ядерщиком или главным архитектором адронного коллайдера. На самом деле он так и не закончил среднюю школу. Вместо этого он изучал ремесло.

И все же он использовал математику каждый день своей трудовой жизни. Геометрия, углы и сложные измерения были его хлебом с маслом.

Был крановщиком.

Каким бы отрадным ни был этот рассказ для учителя математики, он также обнажает одну из самых сложных частей преподавания предмета. Никто не мог сказать этому студенту в тринадцать лет, что евклидова геометрия станет стержневой частью его карьеры. Для него «математика» была просто серией чернильных пятен на бумаге, полностью оторванных от реального мира.

Для многих наших учеников момент, когда они осознают, что математика существует в реальном мире, наступает в после школы .В нем есть все необходимые компоненты взрослой жизни, требующие базового владения числами; налоги, личные финансы, покупка или продажа вещей, сборка мебели IKEA с растущим нетерпением — список можно продолжить.

Но что, если бы мы могли сделать так, чтобы этот момент с лампочкой случился в наших классах?

Можем ли мы с самого начала преподавать математику для реального мира?

Это не всегда легко, но можно. А с этим приходит большее участие и новая приверженность обучению.

Давайте взглянем на некоторые стратегии, которые можно использовать, чтобы перенести математику со страницы в реальный мир.

Попросите своих учеников найти математику в своей жизни

Перед тем, как вы решите полностью изменить математическое образование в рамках одного урока, попросите своих учеников выполнить часть работы.

Учащимся легко по умолчанию использовать образ мышления «Мы никогда не будем использовать это в реальном мире», когда у них возникают проблемы с математикой или когда они просто не готовы учиться в определенный день.Но так легко им не отделаться.

Были ли они когда-нибудь на самом деле искали для математики в реальном мире?

Вы когда-нибудь просили их найти математику в реальном мире?

Скорее всего, ответ на оба вопроса отрицательный.

Часто наш первый ответ на обвинения в несущественности — это сплотить нашу защиту и начать становиться немного слишком страстно. («Клянусь, это актуально. ВЫ БЛАГОДАРЮ МНЕ ОДИН ДЕНЬ!»).

Но открытие математики в реальном мире намного мощнее, если оно исходит от самих студентов.Так что не думайте, что вы автоматически должны оправдывать существование математики как предмета. Верните его ученикам вместо .

Попробуйте предложить им найти три дела, которые они делали дома, связанные с математикой любого рода, а затем поделиться ими с остальным классом в качестве еженедельного задания. Студенты поймут, что возможности взаимодействия математики в реальном мире поистине безграничны.

Конечно, вы тоже должны сыграть в этом свою роль.Вы также можете попробовать…

Используйте математику для создания ресурсов, которые помогут ученикам в реальном мире

Возможно, вам удастся заставить учеников осознать, что они уже занимаются математикой вне класса, но следующий шаг — доказать им, что есть другие эффективные способы использования математики в повседневной жизни.

Самый простой пример — расписание. Между уроками музыки, спортом, домашними заданиями, свиданиями, семейными обязательствами и т. Д. Дети в наши дни управляют внеклассной жизнью настолько сложной, что им в основном нужен постоянный помощник врача (к сожалению, это всего лишь еще одна часть работы мамы 21 века. описание).

Попросите учащихся составить расписание своих занятий до и после школы, и вы научите их активно использовать разделение в реальных жизненных целях. Естественно, это также учит их кое-чему об управлении временем.

Список потенциальных приложений продолжает расти по мере взросления учащихся. Например, личный бюджет или базовый финансовый план являются бесценным активом, поскольку все больше и больше наших студентов приходят к нам с банковскими счетами, неполной занятостью и тарифами на мобильную связь.

Собирая воедино то, что студенты могут на самом деле использовать , подчеркивает, что математика не просто «где-то там», а всплывает на поверхность лишь изредка, когда нам нужно подсчитать мелочь.Вместо этого математика — это то, чем студенты могут активно заниматься, чтобы жить лучше .

Установите домашнее задание, которое задействует навыки математики в реальном мире

Домашнее задание — прекрасная возможность преподавать математику в реальном мире. В конце концов, ученики буквально используют математические рассуждения вне школьных занятий и вне уроков. Наконец-то они в «реальном мире».

Тем не менее, мы часто настойчиво выполняем домашнее задание, которое на самом деле является продолжением классной деятельности.Завершите рабочий лист, ответьте на вопросы в учебнике, переходите к следующей главе… вы поняли.

Почему бы не воспользоваться преимуществами домашней обстановки, побудив учащихся познакомиться с математическими понятиями, которые делают дом функцией? Вот несколько идей:

• Бюджет продуктовых покупок на неделю. Тот факт, что у большинства супермаркетов есть полный онлайн-каталог, делает это намного проще, потому что его можно полностью спланировать, потратив столько времени, сколько необходимо.И это тоже не может быть конфетой. Несколько пунктов в списке, указанных родителями, заставят их нести обязательные расходы.
• Готовьте по рецепту. Прекрасная возможность попрактиковаться в измерениях с реальным, съедобным стимулом. У этого есть дополнительный бонус в виде победы над родителями!
• Простой подсчет предметов в доме — это очень простая стратегия для молодых людей, которая позволяет им увидеть числовые свойства физической среды. По мере того, как они становятся старше, вы можете назначать более сложные задания — например, масштабный ремонт спальни в стиле фантастики.

По возможности пользуйтесь домашним окружением. Дополнительным преимуществом является то, что в этих занятиях участвуют родители и семьи, так что математика становится совместной деятельностью в реальном мире, а не изолированной.

Свяжите математику с другими областями учебной программы

Нетрудно понять, почему учащиеся воспринимают математику как отдельный мир. Он использует совершенно другой язык по сравнению с другими предметами и требует собственных методов решения проблем и рассуждений.

Если мы свяжем математику с другими предметами в учебной программе, мы покажем нашим ученикам, что математика не стоит особняком. Это часть интегрированной системы знаний, которая помогает нам понимать мир.

Однажды я наблюдал, как учитель математики и учитель английского языка вместе проводили урок по книжкам с картинками. Умы учащихся были потрясены, когда они увидели их в одном классе, но их соответствующие учебные точки совпали таким образом, что никто бы не мог предсказать (включая меня).

Учитель математики сначала попросил учеников проанализировать композицию рисунков в книге. Учащиеся наложили на изображения сетку и использовали ее, чтобы обсудить, каким образом одним объектам было отдано преимущество перед другими, и как можно было бы привлечь внимание к конкретным особенностям для выделения.

Учитель английского языка затем использовал это, чтобы начать обсуждение эмоциональных и критических ответов учащихся на изображения, которые затем послужили основой для интерпретации сопроводительного текста.

Это было не что иное, как гениальность. Интерпретация текста учащимися была намного богаче с учетом ввода обоих предметов, и они покинули класс, увидев, что математика — это не просто серия холодных и жестких правил, управляющих абстрактным миром.

Математика заставила их думать и чувствовать. Есть ли что-нибудь более «реальный мир», чем это?

Используйте своих коллег вне математического факультета. Да, межучебное сотрудничество требует времени и координации, которых часто не хватает, но награда того стоит.

И последнее, но не менее важное: стоит сделать шаг от учебника и перейти в реальную жизнь во время вашего реального обучения, ориентированного на содержание.

Вместо абстрактного объяснения концепции, вы можете связать ее с любым количеством бесчисленных явлений реального мира, которые так или иначе вращаются вокруг математики. Задачи со словами и исследовательская деятельность могут помочь, но вы можете улучшить игру, используя физический, материальный реальный ресурс в классе (или за его пределами).

Допустим, вы обучаете шаблонам. Скорее всего, где-то в школе есть образец в застроенной среде. Это может быть мозаичный пол, брусчатка снаружи или даже просто кирпичная стена. Вместо того, чтобы работать с фотокопией, вы можете использовать ее как подлинный ресурс.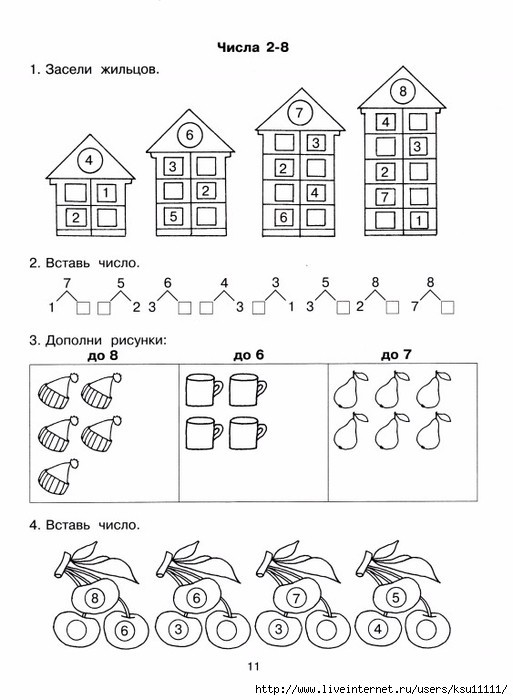 У вас может быть студентов:

• Продолжите выкройку на бумаге или, возможно, используя практический материал.
• Опишите его партнеру, у которого , а не его видели, и он может попытаться воспроизвести его в соответствии с его инструкциями.
• Используйте мел или стираемый маркер, чтобы выделить другие знакомые формы в узоре.

Вы могли подумать, что одно и то же действие можно было бы просто воспроизвести на листе, чтобы избавиться от логистических проблем, но это не даст вам возможности вникать в реальные приложения математической теории.

Итак, в приведенном выше примере вам не нужно останавливаться, как только учащиеся смогут идентифицировать и объяснять закономерность. Следующий вопрос, который вы можете задать (если они не спросят вас сначала):

Почему строитель может выбрать этот шаблон?

И в конце этого обсуждения:

Итак, почему, по вашему мнению, нам важно знать о паттернах ?

Способность мыслить независимо и с любопытством — один из востребованных математических навыков, которые все чаще будут развиваться у студентов. Использование этого подхода действительно работает в этом направлении. Он показывает, что в большинстве случаев вам не нужно объяснять , как актуальна для студентов в реальном мире. Вам просто нужно привести их к этому.

Как изучать математику в колледже

Кузов

Введение

Почему вы не получаете лучших оценок по математике? Чувствуете ли вы, что потратили на это все время, которого от вас можно ожидать, и что вы все еще не получаете результатов? Или ты просто ленивый? Если вы ленивы, этот материал не для вас.Но если вы пытались, и ваши оценки по-прежнему не показывают ваших способностей, или если вы получали хорошие оценки, но все же чувствуете, что математика для вас не так уж много значит, весьма вероятно, что вы не знаете, как это сделать. учиться эффективно. Этот материал призван помочь вам эффективно изучать математику.

Некоторые из вас могут почувствовать, что у вас есть собственные успешные методы обучения, отличные от описанных здесь. В этом случае вам не нужно думать, что вы должны менять свои методы, хотя вы можете получить пользу от сравнения своих методов с ними.

С другой стороны, некоторым из вас может показаться, что предложения на следующих страницах чрезмерно амбициозны — они потребуют больше времени и усилий, чем вы готовы вложить. Вы, наверное, будете правы. Мы не можем ожидать, что сделаем все до совершенства, но мы можем сделать все, что в наших силах. Из предложенных предложений вы можете выбрать те, которые могут вам больше всего помочь, и, когда вы обнаружите, что ваша работа улучшается, вы можете попробовать дальнейшие предложения. Так что насмехайтесь над этими амбициозными предложениями, если хотите, но затем попробуйте некоторые из них, честно попробуйте и посмотрите результаты.

Как учиться:

В начало

Домашнее задание

Существует распространенное заблуждение, что домашнее задание — это в первую очередь то, что в конечном итоге передается учителю. На самом деле домашнее задание — это прежде всего средство изучения фундаментальных идей и процессов в математике, а также развития навыков аккуратности и точности. То, что передается учителю, является лишь побочным продуктом этого процесса обучения. Следующий четырехступенчатый распорядок поможет сделать домашнее обучение эффективным:

1. Ориентируйтесь.Потратьте несколько минут, чтобы подумать, просмотрите свои заметки и просмотрите книгу, чтобы четко увидеть, над какими идеями вы работали.
2. Выровняйте идеи. Подумайте об идеях, законах и методах ежедневного задания или урока. Не забывайте знакомиться с любыми новыми словами в своем математическом словаре. Постарайтесь напомнить себе о любых предупреждениях об ошибках, чтобы избежать их, о которых мог упомянуть учитель. Просмотрите все приведенные примеры, чтобы убедиться, что вы действительно понимаете иллюстрированные концепции.
3. Выполните задание. Подумайте об идеях, которые иллюстрируют упражнения. 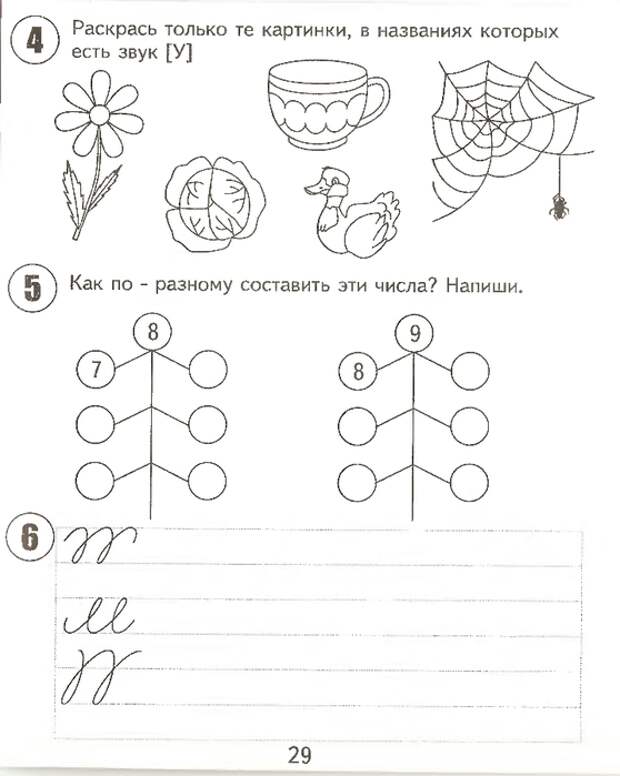Вы должны углублять свое понимание, а также получать ответы. Следующие указатели помогут вам улучшить работу:
   1. Точно возьмите задание с доски. Отведите в блокноте определенное место, куда вы записываете задание или урок. Если вам непонятно задание, не стесняйтесь спрашивать.
   2. Следуйте инструкциям.
   3. Работаем аккуратно и аккуратно.
   4. Покажите свою работу полностью, а не только ответ. Это поможет вам и вашему учителю, когда вы проверяете ошибки.
   5. Всегда проверяйте, правильно ли вы выполнили все простые арифметические операции.
   6. Выполняйте работу как можно скорее, пока не забыли все инструкции.
   7. Если вы застряли, не сдавайтесь! Вернитесь к книге и своим заметкам, чтобы найти идеи, связанные с проблемой. Если ваша работа над проблемой кажется совершенно запутанной, иногда полезно полностью отказаться от работы и начать все заново.Если вы все еще не можете прояснить свое мышление, как можно скорее спросите учителя о проблеме.
4. Помогите кому-нибудь еще, если можете. Нет лучшего способа изучить тему, чем пытаться ее преподать! Кроме того, часто бывает полезно позвонить однокласснику, если вы не понимаете проблему. Часто они могут объяснить эту концепцию и вам (если не лучше) учителю.

В начало

Как сделать ошибки, которые помогут вам научиться

Что вы делаете, если в домашнем задании или на тесте ответ неправильный? Вы выбрасываете его и забываете — а затем совершаете ту же ошибку в следующий раз? Если вы поступите мудро, эти ошибки научат вас чему-то.Вот что вы можете сделать:

1. Проанализируйте ошибку, чтобы определить, что вы сделали неправильно.
2. Если это ошибка по неосторожности и вы действительно знали, как правильно выполнять работу, запишите ее, и если вы обнаружите, что продолжаете часто делать ошибки по неосторожности, начните работать более осторожно.
3. Если вы не можете найти свою ошибку, попросите учителя или одноклассника помочь вам.
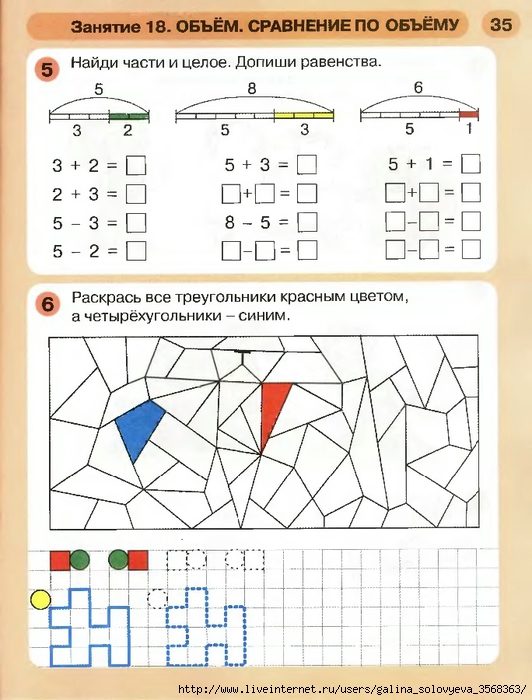
4. Заведите в блокноте страницу с заголовком «Предупреждение: ошибки, которых следует избегать». На этой же странице напишите описание исправленного способа выполнения такого упражнения, обязательно подчеркнув важную идею, лежащую в основе этого упражнения.

В начало

Классные работы: Как максимально эффективно использовать свое время в классе

1. Приготовьтесь. За пару минут до начала урока подумайте над тем, над чем вы работали в последнее время.
2. Имеется все необходимое: книга, карандаши или ручки, тетрадь, домашнее задание.
3. Выполните задание быстро и точно.
4. Концентрат. Это требует усилий, если вы из тех, чей ум склонен блуждать.
5. Задавайте вопросы, если не понимаете.
6. Слушайте вопросы и ответы других в классе. Когда другой ученик отвечает на вопрос, подумайте, как бы вы ответили на этот вопрос.
7. Примите участие в обсуждении в классе.
8. Не пишите в неподходящее время. Когда вы делаете заметки, убедитесь, что вы не пропустили ничего из того, что было сказано при этом. Делая заметки, вы должны попытаться сделать две противоречивые вещи. Один из них — сделать ваши записи достаточно полными и точными, чтобы они были вам полезны в дальнейшем.Другой — сделать свои записи достаточно краткими, чтобы вы могли продолжать слушать то, что говорится в классе.

В начало

Как пользоваться учебником

1. Используйте указатель и глоссарий в конце книги, особенно если вы забыли значение слова.
2. Когда в вашей книге приводится пример для иллюстрации идеи, внимательно проанализируйте этот пример на предмет идей, лежащих в его основе, вместо того, чтобы просто пытаться сделать свои упражнения похожими на этот пример.
3. Если вы не можете выполнить упражнение, перечитайте пояснительный материал в книге и / или просмотрите свои классные заметки.
4. Извлеките максимум из помощи для изучения в конце каждой главы.

В начало

Как просмотреть тесты

1. Начните проверять достаточно заблаговременно, чтобы у вас было время выполнить осторожную неторопливую работу, и при этом вы все еще могли лечь спать рано вечером перед экзаменом.
2. Обязательно просмотрите свои заметки и примеры, которые там есть.Если они вам не понятны, значит, вы сделали недостаточно заметок!
3. Если есть какие-то формулы, за которые вы отвечаете, составьте их список, а затем потренируйтесь произносить или записывать их.
4. Используйте обзорные материалы в конце каждой главы. Если у вас возникли проблемы с проблемой, вернитесь к этому разделу в книге и исправьте там некоторые проблемы.
5. Если бы вы были учителем, какие вопросы вы бы задали на тесте? Подготовьтесь к этим вопросам.
6. Поскольку говорится, что «практика ведет к совершенству», один из лучших способов подготовиться к тесту — это выполнить некоторые задачи, которые были ранее поручены вам. Просмотрите домашнее задание, чтобы убедиться, что вы понимаете процедуру, которую использовали в каждом разделе.
7. Хорошо отдохните в ночь перед экзаменом!
8. НЕ БОЙТЕСЬ!

В начало

Как сдавать анализы

1. Когда вы сдаете тест, проявляйте правильное отношение — гордитесь тем, что делаете все, что в ваших силах.Не пытайтесь «обойтись», делая как можно меньше. Будьте уверены в своих силах.
2. Будьте серьезны и достаточно озабочены тестом, чтобы сделать все возможное, но не беспокойтесь до точки беспокойства. Один только страх может заставить человека плохо сдать экзамен, независимо от его способностей и знаний.
3. Есть все необходимое оборудование.
4. СЛЕДУЙТЕ НАПРАВЛЕНИЯМ. Внимательно прочтите и внимательно прислушайтесь к любым специальным инструкциям, например, где должны быть написаны ответы, любые изменения или исправления и т. Д.
5. Вначале быстро просмотрите весь тест и, если от вас не требуется отвечать на вопросы в указанном порядке, сначала выполните те, в которых вы уверены.
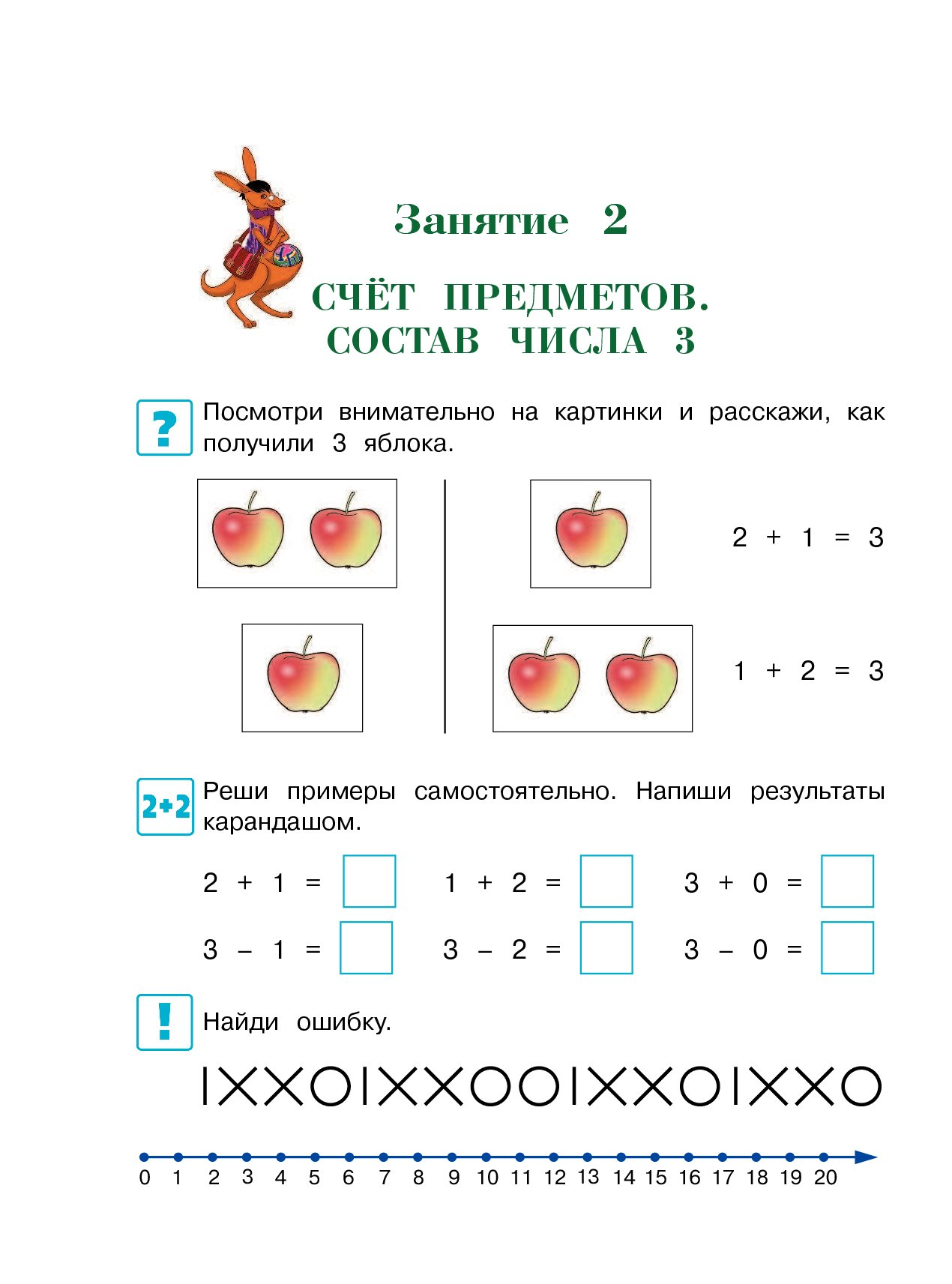
6. Если вы не можете ответить на вопрос, оставьте его и переходите к другому, вернувшись к сложному позже. Часто, начав все сначала, вы вдруг намного лучше поймете, что делать.
7. Будьте осторожны, чтобы четко показать, что вы делаете. Помните, что учитель не умеет читать мысли, и ваша оценка может зависеть от того, видит ли учитель по вашей работе, что вы понимаете, что делаете.
8. Работаем аккуратно. На учителя производит хорошее впечатление!
9. Проверяйте точность по мере продвижения. Неосторожные ошибки могут существенно повлиять на ваш счет.
10. При правильном отношении и тщательной подготовке к экзамену вы, вероятно, хорошо сдадите экзамен.
11. Помните: один или два часа теста — это всего лишь короткие моменты в вашей жизни, поэтому НЕ ПАНИКА!

В начало

Тест ACT Практические вопросы по математике

акт. org, actprofile.org, act.org, actstudent.org, act.alertline.com, services.actstudent.org, Care4.successfactors.com, Engagement.act.org, discoveractaspire.org, qc.vantage.com, myworkkeys. act.org, twitter.com, facebook.com, youtube.com, plus.google.com, linkedin.com, preview.act.org, workreadycommunities.org, pearson.com, instagram.com, actaspire.org, run2. карьерыready101.com, run2.keytrain.com, лидерствоblog.act.org

Обновления COVID-19

Спасибо за терпение, пока мы продолжаем бороться с пандемией COVID-19.Посетите Ресурсы по COVID-19 , чтобы получить обновления и ресурсы для цифрового обучения, которые помогут учащимся, учителям, школам и работникам, пострадавшим от COVID-19.

Математика

Тестовые подсказки

Настоящий тест по математике ACT содержит 60 вопросов, на которые нужно ответить за 60 минут.

• Внимательно прочтите каждый вопрос, чтобы убедиться, что вы понимаете тип требуемого ответа.
• Если вы решите использовать калькулятор, убедитесь, что он разрешен, работает в день проверки и имеет надежные батареи.
• Используйте свой калькулятор с умом.
• Решите проблему.
• Найдите ваше решение среди вариантов ответа.
• Убедитесь, что вы ответили на заданный вопрос.
• Убедитесь, что ваш ответ разумный.
• Проверьте свою работу.

Наконечники калькулятора

• Просмотрите последнюю информацию о разрешенных и запрещенных калькуляторах.
• Вы не обязаны использовать калькулятор. Все проблемы можно решить без калькулятора.
• Если вы регулярно используете калькулятор в математической работе, воспользуйтесь уже знакомым вам калькулятором при прохождении теста по математике. Использование более мощного, но незнакомого калькулятора вряд ли даст вам преимущество перед тем, что вы обычно используете.

Нажмите на выбранные буквы ниже, чтобы просмотреть правильный ответ и пояснения.

Для полного взаимодействия с Практикой просмотрите эту страницу на планшете или настольном устройстве.

НАПРАВЛЕНИЯ: Решите каждую задачу, выберите правильный ответ, а затем закрасьте соответствующий овал в своем ответе.

Не зацикливайтесь на проблемах, которые отнимают слишком много времени. Решите как можно больше; затем вернитесь к остальным за время, отведенное для этого теста.

Вам разрешается использовать калькулятор в этом тесте. Вы можете использовать свой калькулятор для решения любых задач по вашему выбору, но некоторые из них лучше всего решать без использования калькулятора.

Примечание. Если не указано иное, следует исходить из следующего.

1. Иллюстрации НЕ обязательно выполнены в масштабе.
2. Геометрические фигуры лежат на плоскости.
3. Слово в строке обозначает прямую линию.
4. Слово среднее обозначает среднее арифметическое.

Это действие откроет новое окно. Вы хотите продолжить?

Если вы заходите на этот сайт из-за пределов США, Пуэрто-Рико или США.S. Territories, перейдите на неамериканскую версию нашего веб-сайта.

Верх

30 способов развлечься с математикой для детей младшего школьного возраста

Развлекать математику можно как вызов. Но я здесь, чтобы сказать, что это просто неправда. Есть много способов сделать математику интересной и интересной для наших детей.

Вот полный список способов сделать математику увлекательной (и по-прежнему образовательной):

1.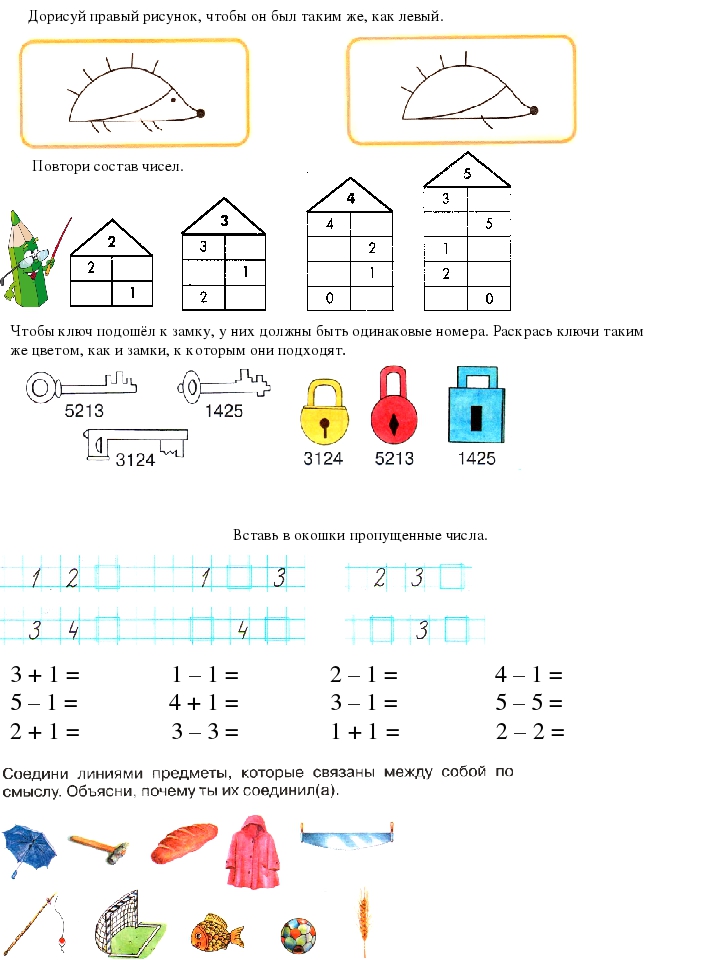 Сделайте это практическим

Вы когда-нибудь были на семинаре или собрании, где ведущий говорил и продолжал? Вы нервничаете или мысли блуждает где-то еще? Что ж, у меня есть секрет.Дети думают так же. Попробуйте превратить урок, который обычно может включать лекцию и рабочий лист, в интерактивный. Например, вы можете попросить детей разместить числа на интерактивной числовой строке или угадать количество предметов в таинственном мешочке.

Есть так много замечательных книжек с картинками, которые можно использовать на уроках математики. Вы можете найти темы, которые варьируются от счета до умножения. Чтение по телефону идеально подходит для привлечения детей к математическим навыкам, которым они будут обучать.

Кто не любит играть в игры? Игры для печати или цифровые игры — это идеальный способ для студентов учиться и получать удовольствие одновременно. Существует множество типов игр, которые вы можете использовать при обучении математическим концепциям или изучении их. В голове у меня возникают мысли о BINGO, War, Concentration, и этот список можно продолжить…

Думаю, все согласятся, что детям нравится разговаривать. Смоделируйте, как вести содержательный разговор о математике.А затем дайте время для этих разговоров во время математического блока.

Это восходит к приведенному выше утверждению. Дети любят поговорить! Так что давайте зададим им больше открытых вопросов. Примером этого может быть вопрос: «Почему вы использовали эту стратегию для решения проблемы?» Также попробуйте задавать вопросы, на которые может быть несколько ответов. У детей появится желание найти их всех.

Иногда небольшое повторение — это неплохо. За свою педагогическую карьеру я заметил, что одно верно. Дети любят рутины (даже если они иногда борются с ними). Процедуры помогут вам максимально сэкономить время, потому что ваши ученики знают установленные ожидания. До тех пор, пока вы будете продолжать заниматься, студенты будут настроены на это и с нетерпением ждут большего.

Дети любят, когда мы делаем обучение более достоверным. Попробуйте заменить имена учащихся в задачах со словом или использовать математическое задание, чтобы представиться друг другу в начале года.

Есть так много классных математических веб-сайтов и приложений, которые вы можете загрузить, чтобы проверить свои математические навыки. Некоторые из моих любимых — Kahoot! и время математической игры.

Уроки, которые я запомнил больше всего, когда я был в начальной школе, предполагали, что учитель использовал реальные предметы для обучения концепции. Вы можете проявить творческий подход, когда преподаете такие темы, как геометрия, измерение, построение графиков, сложение … просто по любой математической теме.Попробуйте использовать тыкву, чтобы научить сложению, или используйте настоящие предметы, чтобы решить задачу со словами.

Мы знаем, что у детей и взрослых разные стили обучения, поэтому немного смешайте вещи и включите упражнения, в которых учащимся нужно вставать и двигаться. Это может быть короткий мозговой перерыв, включающий математику, или более длительное задание, на котором учащиеся должны разбить себя на группы. В любом случае, ваши кинестетики будут вам благодарны.

Создание благоприятной атмосферы может помочь рассеять страх некоторых наших детей по поводу математики. Приветствия — отличный способ мотивировать студентов. Еще более эффективно, когда ученики аплодируют друг другу.

12. Рисование математических моделей

Рисование может быть веселым и познавательным. Я твердо верю в модель CPA (Concrete-Pictorial-Abstract). При обучении математической концепции с использованием модели CPA дети сначала манипулируют конкретными объектами , затем переходят к рисованию моделей через представления изображений и, наконец, используют только числа и математические символы (что для них составляет абстрактное ). ).Дайте учащимся несколько возможностей рисовать изображения. Здесь вы действительно можете увидеть, усвоили ли учащиеся концепцию.

Математические манипуляции для всех! Вопреки распространенному мнению, математические манипуляторы предназначены не только для школьников. Они полезны на всех уровнях начальной школы. Возвращаясь к модели CPA, я заметил, что учителя часто пропускают этот шаг. Я тоже был виноват! Однако этот шаг важен для концептуального обучения.А если у вас нет доступа к какой-либо вашей школе, вы можете создать свою собственную.

Review не обязательно должен сводиться только к тренировкам и убийствам. Карточки с заданиями по математике предлагают учащимся множество увлекательных способов проверить и попрактиковаться в математических навыках. Вы можете использовать их для партнерских тренировок, соревнований или для игры в SCOOT.

Не знаю, как вы, но я заметил, что студенты очень внимательны во время естественных и общественных занятий.Используйте их естественное любопытство к этим темам, чтобы закрепить их на уроках математики. Например, если вы преподаете о товарах и услугах в области социальных наук, деньги будут идеальной связующей темой. Если вы изучаете растения, измерьте их длину линейкой. Будь креативным!

Создайте среду, в которой учащиеся обычно работают в парах или небольших группах. Они могут решать математические задачи и нести ответственность друг перед другом. Им также понравится работать со своими сверстниками.

Да! Это ОБЯЗАТЕЛЬНО! Расскажите родителям, как развлечься математикой. Вы даже можете отправить домой идеи для простых практических занятий, которыми родители могут заниматься со своими детьми. Таким образом, дети получают сообщение дома и в школе о том, что математика — не страшный предмет.

Попробуйте включить математические темы в то, что происходит в это время года. Может быть сезонным. Или особенный праздник не за горами? Вы можете легко выбрать ту же математическую тему (например,дополнение) и сделать его свежим, используя различные материалы (например, яблоки, пауки, тыквы и т. д.)

Свежий воздух полезен всем. Выйдите на улицу и проведите тот же урок математики. Вместо бумаги и карандаша возьмите мел. Ваши дети будут вам благодарны.

Сделайте БОЛЬШУЮ сделку из этого особенного времени года для математики. А именно 100-й день школы и День числа числа. Хотя это большая двойка, вы можете придумать творческие способы отметить достижения учащихся по математике (т.е. зная все факты их умножения).

«Конкуренция» не должно быть плохим словом. Как только учащиеся узнают о ваших ожиданиях в отношении соревнований, вы увидите высокий уровень вовлеченности учащихся. И не забывайте, что конкуренция не всегда должна быть против другой команды или ученика. Некоторые студенты любят ставить личные цели и соревноваться сами с собой. Итак, приглашаем на соревнования по математическим фактам!

Что вашим ученикам нравится в математике? Что им кажется сложным? Создайте опрос по интересам к математике и узнайте, что они хотят узнать.

Замените математическое задание вместо рабочего листа. Есть много мест, где вы можете найти задания по математике, подходящие для вашего класса. Ознакомьтесь с ними и посмотрите, что лучше всего подойдет вашим детям.

Еда и математика просто идут рука об руку.Фактически, я посвятил ему целую доску Pinterest. Получайте удовольствие, складывая, вычитая, умножая, деля, измеряя и отображая в графиках любимые блюда ваших учеников.

Что может быть лучше, чем заинтересовать детей в собственном обучении, чем заставить их создавать задачи для решения одноклассников? Я использовал эту стратегию в прошлом и добился большого успеха. Студентам нравится видеть, как проблемы, которые они создают, решаются их друзьями.Им особенно нравится вставлять свои имена в задачи со словами.

Это для всех вас, изучающих визуальное восприятие! Ясные и удобные для студентов визуальные представления всегда необходимы, когда речь идет о вовлечении студентов. Визуализация привлечет их внимание и поможет им лучше понять абстрактные идеи.

Часто наши дети попадают в тупик, пытаясь решить словесную задачу. Предложите студентам разыграть словесную задачу, используя реальные предметы.Это поможет им «увидеть», что на самом деле происходит в слове «проблема». Дополнительным бонусом является то, что студенты работают над своим актерским мастерством.

Музыка — отличный способ начать урок математики. Вы даже можете использовать это как перерыв для мозга. В сети много музыкальных ресурсов. Осмотритесь и посмотрите, что вы можете найти для вашего класса.

Есть так много способов выделить урок математики.Вы можете отличить содержанием (что изучается), процессом (фактическая деятельность) или продуктом (как студент продемонстрировал мастерство). Вы можете преодолеть множество препятствий для детей, встретив их там, где они находятся на пути к математике.

STEM-проекты по своей природе очень практичны и носят межучебный характер. Они также сосредоточены на реальных проблемах и обычно работают совместно.Пока что это включало 4 рекомендации из этого списка. STEM-проекты могут стать для детей надежным способом полюбить математику (и естественные науки).

Уф! Это был длинный список. Я надеюсь, что вы уберете одну-две идеи из этого списка и сделаете математику интересной! Не забудьте скачать БЕСПЛАТНЫЙ контрольный список, чтобы в любое время вернуться к этому исчерпывающему списку способов развлечься с математикой.